Microstructure-based simulations of the viscous densification of snow and firn

Accurate models for the viscous densification of snow (understood here as a density below 550 kg m⁻³) and firn (a density above 550 kg m⁻³) under mechanical stress are of primary importance for various applications, including avalanche prediction and the interpretation of ice cores. Formulations of snow and firn compaction in models are still largely empirical instead of using microstructures from micro-computed tomography to numerically compute the mechanical behavior directly from the physics at the microscale. The main difficulty of the latter approach is the choice of the correct rheology/constitutive law governing the deformation of the ice matrix, which is still controversially discussed. Being aware of these uncertainties, we conducted a first systematic attempt of microstructure-based modeling of snow and firn compaction. We employed the finite element suite Elmer FEM using snow and firn microstructures from different sites in the Alps and Antarctica to explore which ice rheologies are able to reproduce observations. We thereby extended the ParStokes solver in Elmer FEM to facilitate parallel computing of transverse isotropic material laws for monocrystalline ice. We found that firn densification can be reasonably well simulated across different sites assuming a polycrystalline rheology (Glen's law) that is traditionally used in glacier or ice sheet modeling. In contrast, for snow, the observations are in contradiction with this rheology. To further comprehend this finding, we conducted a sensitivity study on different ice rheologies. None of the material models is able to explain the observed high compactive viscosity of depth hoar compared to rounded grains having the same density. While, on one hand, our results re-emphasize the limitations of our current mechanical understanding of the ice in snow, they constitute, on the other hand, a confirmation of the common picture of firn as a foam of polycrystalline ice through microstructure-based simulations.

1 Introduction

Once deposited on the ground, snow and firn are subject to the overburden stress imposed by the weight of the overlying snow or firn column. This causes the slow and viscous compaction of the snow and firn layers and their densification over time (e.g., Kojima, 1975; Herron and Langway, 1980). Accurate prediction of the rate of the compaction is of primary importance for various applications. For instance, the densification of firn determines the timescale at which atmospheric gases are enclosed in polar ice (Schwander et al., 1993). Faithful modeling of firn densification is, thus, a critical component for the interpretation of ice cores (Goujon et al., 2003; Witrant et al., 2012; Buizert, 2021). However, observed variations in the densification rate of different layers of similar density that are subjected to similar overburden stress still lack a conclusive explanation in view of either microstructural or compositional origins (Hörhold et al., 2012; Fujita et al., 2016). This situation is remarkably similar in snow. The slow densification of seasonal snow determines the timescale for the existence of persistent weak layers as a major source of avalanche danger (Schweizer and Lütschg, 2001). Faithful modeling of snow densification would greatly improve the capacity of a detailed snowpack model to predict this timescale and the presence of persistent weak layers over the winter season. Still, for snow, there are well-known differences in densification rates between different layers (rounded grains and depth hoar) (Kojima, 1975; Calonne et al., 2020a) that still lack a conclusive explanation. In view of these similarities, holistic approaches to snow and firn densification are desired in order to identify common microstructural controls.

Due to the progress in micro-computed tomography (μCT) in cryospheric sciences within the last decade, 3D microstructures of snow and firn samples are now widely used (e.g., Löwe et al., 2013; Calonne et al., 2019; Letcher et al., 2022). Based on μCT, effective material properties of snow or firn can now be derived in a physically consistent manner, based on the underlying microstructure and the physics at the pore scale. This leads to an effective (upscaled) material characterization using homogenization methods and numerical simulations (Torquato, 2002; Auriault et al., 2009). For example, for the thermal conductivity of snow and firn, upscaling methods have been widely used, yielding a fairly consistent picture of how the microstructure determines the effective thermal properties (Calonne et al., 2011, 2019; Löwe et al., 2013; Riche and Schneebeli, 2013; Fourteau et al., 2021). For snow and firn compaction, such a consistent picture is still lacking.

Despite the pressing need for an accurate model, the formulation of the slow compaction of snow and firn in models remains largely empirical (e.g., Vionnet et al., 2012; Lundin et al., 2017) and lacks a detailed microstructure-based justification. To the best of our knowledge, so far only Theile et al. (2011), Chandel et al. (2014), and Wautier et al. (2017) have attempted to estimate the effective viscous response of snow using μCT images and microstructure-based nonelastic (plastic or viscoplastic) simulations. While all of them led to an apparent agreement with measurements, they were based on very different assumptions about the rheology of the ice material accommodating the deformation at the microscale. The main difficulty for developing a microstructure-based formulation of compaction and its integration in snow and firn models is the present disagreement concerning the dominating mechanism(s) driving the mechanical deformation of the ice material at the microscale. While it is generally accepted that firn densification occurs through creep in the ice matrix, several types of creep have been proposed in the literature. For instance, Arthern et al. (2010) assume the ice to deform according to a Nabarro–Herring creep, where deformation occurs through vacancy diffusion in the crystals, while Barnola et al. (1991) or Salamatin et al. (2009) assume a power-law creep that originates from dislocation creep. For snow, the mechanism of deformation remains even more elusive. Some studies support the idea that the ice in snow deforms through a dislocation-creep mechanism (Kirchner et al., 2001; Scapozza and Bartelt, 2003; Wautier et al., 2017). This led to the appealing concept of snow as being a foam of (polycrystalline) ice (Kirchner et al., 2001). Other studies, rather, support the idea that the compaction of snow involves grain boundary sliding (Alley, 1987; Salamatin et al., 2009; Schultz et al., 2022). This uncertainty is, for instance, reflected by the choice of Wautier et al. (2017) who considered three different ice power-law rheologies with an ice fluidity about 1000 times higher than the usually reported value (e.g., in Chap. 3 of Cuffey and Paterson, 2010). Therefore, the most promising approach is to allow for flexibility in the material model when comparing simulated densification rates with observations using diverse data sets.

The aim of this article is to study whether the viscous compaction of snow and firn can be simulated consistently directly from the microstructure using a common numerical approach. We use different microstructures (rounded snow, faceted snow, and dense firn) to assess the validity of this modeling approach over a broad range of possible microstructures. Snow and firn microstructures were obtained by μCT imaging of snow and firn cores from different sites in the Alps and in Antarctica where observed densification rates are also available. We employ and extend Elmer FEM as the computational platform, as it is already established in the ice flow modeling community. In this setup, we investigate which viscous ice matrix rheology (variants of Glen's law) is able, or not able, to appropriately reproduce the observations of snow and firn compaction.

The paper is organized as follows. Section 2 presents the minimal theoretical background used throughout this work. Section 3 details the setup of the data and numerical simulations that were used for the study, and Sect. 4 presents and discusses our results.

2 Theoretical background

In snowpack and firn models, it would be impossible to explicitly represent the 3D microstructure of a whole snowpack or firn column. Instead, these models rely on an upscaled (or volume averaged) description where the snow/firn can be described as a homogeneous medium characterized by effective material properties (Torquato, 2002; Auriault et al., 2009) that are often referred to as macroscopic in order to emphasize the separation of scales from the characteristic (microscopic) length scales where the theoretical description is formulated. Accordingly, the compaction of snow and firn is described in terms of a macroscopic strain rate $\dot{E}$ resulting from the macroscopic overburden stress Σ. For snow or firn modeling purposes, a macroscopic constitutive law $\dot{E}=f\left(\mathrm{\Sigma }\right)$ is required. Here, f is a function that characterizes the mechanical response of snow/firn that depends on the snow/firn microstructure and other relevant variables, such as the temperature (Arnaud et al., 2000; Bartelt and Lehning, 2002; Vionnet et al., 2012). The aim of this section is to provide some general considerations about the functional form of f.

2.1 Conservation laws

We start from the equations governing the mechanical response at the microscale. As we are interested in the slow compaction of snow and firn over timescales of days to years, we resort to the common assumption that elastic stresses have been relaxed and that the ice in the microstructure is responding in a purely viscous fashion. This assumption is supported by the relaxation timescale, in the order of hours (Theile et al., 2011), of elastic stresses in snow. Technically, this assumption allows us to describe the ice as an incompressible, (nonlinear) viscous fluid, and the deformation of the viscous ice matrix is then governed by the Stokes equations as

$$\begin{array}{}\text{(1)}& {\displaystyle }\mathrm{\nabla }\cdot \mathit{\sigma }\left(\mathit{x}\right)=\mathrm{0}& {\displaystyle }\mathit{x}\in {\mathrm{\Omega }}_{\mathrm{i}},\text{(2)}& {\displaystyle }\mathrm{\nabla }\cdot \mathit{u}\left(\mathit{x}\right)=\mathrm{0}& {\displaystyle }\mathit{x}\in {\mathrm{\Omega }}_{\mathrm{i}},\end{array}$$

where x is the three-dimensional position vector, σ(x) is the microscopic stress tensor field, u(x) is the microscopic deformation velocity field, Ω_i is the three-dimensional domain that is occupied by the ice matrix, and ∇⋅ denotes the divergence operator. The Stokes equations need to be complemented by a constitutive law that characterizes the rheology of the ice.

2.2 Constitutive law

The constitutive laws considered in this work, which are variants of Glen's law, involve a power-law nonlinearity of the form

$$\begin{array}{}\text{(3)}& \dot{\mathit{ϵ}}\left(\mathit{x}\right)=s_{\text{eq}}^{n-\mathrm{1}}\mathbf{a}(\mathit{x},T):\mathbf{s}.\end{array}$$

Here, $\dot{\mathit{ϵ}}\left(\mathit{x}\right)$ is the microscopic strain rate tensor, s is the deviatoric part of the microscopic stress tensor σ, $s_{\text{eq}}=\sqrt{s_{ij}{s}_{ij}}$ is the equivalent deviatoric stress, n is a nonlinearity exponent, and a is referred to as the fluidity. In the general case, the fluidity a is a fourth-order tensor that depends on temperature T and potentially on the position x in the microstructure if, for example, the c-axis orientation is allowed to vary in space. The double product a:s yields a second-order tensor whose ijth component is ∑_kla_ijkls_kl. The tensorial nature of a is required to represent anisotropic materials that deform preferentially in some directions (such as the ice monocrystal; e.g., Meyssonnier and Philip, 1996; Gagliardini and Meyssonnier, 1999). In the case of an isotropic rheology, the fluidity a is a scalar a times the unit tensor (e.g., Schulson and Duval, 2009). The constitutive material law given by Eq. (3) corresponds to viscoplastic creep, where the deformation occurs through dislocation movement within the ice material.

With the constitutive law given by Eq. (3), it can be shown (Auriault et al., 1992; Suquet, 1993; Orgéas et al., 2007; Tsuda et al., 2010) that the macroscopic strain rate of a sample under compression in a snowpack or in a firn column can be expressed in the form

$$\begin{array}{}\text{(4)}& \dot{E}=A(\mathit{\mu },T){\mathrm{\Sigma }}^n,\end{array}$$

where A is a scalar that does not depend on the overburden stress Σ but on the snow/firn microstructure μ and potentially on the temperature T. Physically, A represents a form of fluidity, analogous to the fluidity tensor a at the microscopic scale. We also stress that the macroscopic nonlinearity exponent n in Eq. (4) is the same as in the microscopic deformation law of Eq. (3). In snow sciences, the viscous compaction of snow and firn is traditionally expressed in the form

$$\begin{array}{}\text{(5)}& \dot{E}={\displaystyle \frac{{\mathrm{\Sigma }}^n}{\mathit{\eta }}},\end{array}$$

where we refer to $\mathit{\eta }=A^{-\mathrm{1}}$ as the compactive viscosity (factor). Again, η does not depend on the magnitude of the loading Σ but only on the microstructure and the temperature of the sample. We note that the compactive viscosity is sometimes defined by the ratio $\mathrm{\Sigma }/\dot{E}$ (e.g., Kojima, 1967; Wiese and Schneebeli, 2017) irrespective of the nonlinearity of the constitutive law. While only the latter definition of the compactive viscosity also has physical units of a viscosity (i.e., Pa s), we do not follow this convention here as, in this case, the compactive viscosity is not an intrinsic (microstructure- and temperature-dependent) property of the snow/firn sample. It would also depend on the overburden stress Σ. Also, this study is limited to the investigation of vertical compaction in snowpacks/firn columns and does not consider other directions of deformation (e.g., lateral compaction). Therefore, we do not quantify the potential anisotropy of the compactive viscosity.

Since the microscopic constitutive law characterizes visco-plastic processes in the ice, the microscopic rheology depends on temperature. This temperature dependence is inherited by the macroscopic compactive viscosity η (Kirchner et al., 2001). Typically, the fluidity a in the microscopic law involves an Arrhenius factor with an activation energy Q, which implies the same temperature dependence,

$$\begin{array}{}\text{(6)}& A(\mathit{\mu },T)=A_{\mathrm{0}}\left(\mathit{\mu }\right)\exp \left[{\displaystyle \frac{Q}{R}}\left({\displaystyle \frac{\mathrm{1}}{T_{\mathrm{0}}}}-{\displaystyle \frac{\mathrm{1}}{T}}\right)\right],\end{array}$$

at the macroscopic scale. Here, A₀ is a reference macroscopic fluidity that only depends on the microstructure, and T₀ is a reference temperature. Re-expressed in terms of compactive viscosity, this implies

$$\begin{array}{}\text{(7)}& \mathit{\eta }(\mathit{\mu },T)={\mathit{\eta }}_{\mathrm{0}}\left(\mathit{\mu }\right)\exp \left[{\displaystyle \frac{-Q}{R}}\left({\displaystyle \frac{\mathrm{1}}{T_{\mathrm{0}}}}-{\displaystyle \frac{\mathrm{1}}{T}}\right)\right],\end{array}$$

where ${\mathit{\eta }}_{\mathrm{0}}=\mathrm{1}/A_{\mathrm{0}}$ is a reference compactive viscosity that only depends on the microstructure.

2.3 Viscosity ratios

For the comparison of the macroscopic mechanical behavior of different microstructures, it is helpful to utilize viscosity ratios. For two snow/firn samples under the same mechanical load Σ at the same temperature, the ratio of their respective macroscopic strain rates ${\dot{E}}_A$ and ${\dot{E}}_B$ is given by

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{{\dot{E}}_A}{{\dot{E}}_B}}={\displaystyle \frac{{\mathit{\eta }}_B}{{\mathit{\eta }}_A}}={\displaystyle \frac{{\mathit{\eta }}_{\mathrm{0}B}}{{\mathit{\eta }}_{\mathrm{0}A}}}.\end{array}$$

The ratio is independent of any scalar prefactor in the microscopic deformation law. Indeed, halving the fluidity a results in a doubling of both η_0A and η_0B, and, thus, their ratio remains unchanged. Viscosity ratios are an interesting metric to test the applicability of different ice rheologies to snow/firn modeling, as they remove the influence of a potentially poorly constrained scalar prefactor in the microscopic deformation law, leaving only the nonlinearity exponent n and the space dependence of the rheology as relevant parameters.

3 Data and methods

3.1 Benchmark densification rates and μCT images

In order to compare our simulations with independent estimates, we selected different Alpine and Antarctic field campaigns with available μCT data and complementary measurements that can be used to constrain observed densification rates.

3.1.1 Alpine snow

For Alpine snow, we rely on the RHOSSA campaign (Calonne et al., 2020a). This extensive data set provides daily density profiles of a snowpack over the 2015–2016 snow season at the Weissfluhjoch observation site in the Swiss Alps. Four snow layers have been carefully tracked and measured with several instruments over the entire season, including a rounded grains (RG) snow layer and a depth hoar (DH) snow layer (following the classification of Fierz et al., 2009). From these data, the observed macroscopic strain rate of a given layer can be estimated from

$$\begin{array}{}\text{(9)}& \dot{E}={\displaystyle \frac{\dot{\mathit{\rho }}}{\mathit{\rho }}},\end{array}$$

where ρ and $\dot{\mathit{\rho }}$ are the density of a layer and its time derivative, respectively. By convention, the strain rate is positive in the case of compaction. The relevant overburden stress Σ imposed on a given layer can be obtained by integrating the density profile above that layer to the snow surface as

$$\begin{array}{}\text{(10)}& \mathrm{\Sigma }=\underset{\text{layer}}{\overset{\text{surface}}{\int }}\mathrm{d}zg\mathit{\rho }\left(z\right),\end{array}$$

where ρ(z) is the density at height z in the snowpack, and g is the acceleration due to gravity.

The density time series of the layers were obtained on a daily basis using a snow penetrometer (SnowMicroPen; Calonne et al., 2020a). The resulting data include an apparent day-to-day variability that stems from spatial variability, resulting in a strongly fluctuating strain rate estimate when using Eq. (9) directly. This variability can cause an apparent decrease in density from one day to the other, which would be interpreted as a negative strain rate. To avoid such issues, the time evolution of the tracked snow layers was smoothed by visually selecting tie points in the profiles in order to reconstruct a piecewise linear and strictly increasing density time series. In order to estimate the uncertainty in this method, 25 time series were manually created for both the DH and RG layers. Their median values were taken as the observed strain rate of the layer and used to deduce the compactive viscosity. The upper and lower bounds of this procedure were used to characterize the spread of this method.

The density time series of the tracked layers in the RHOSSA campaign were regularly validated by μCT measurements, however at a much lower temporal resolution. Therefore, the snow was regularly sampled, and the microstructure was obtained with μCT at a resolution of 18 µm (Calonne et al., 2020a). For our study, we selected μCT scans from the DH and RG layers on 13 January 2016 and 16 February 2016. This selection was motivated by the fact that on 13 January 2016, the RG and DH samples have a similar density but different compaction rates, while on 16 February 2016, the two snow layers have a similar compaction rate but different densities. Moreover, the DH and RG layer in the RHOSSA snowpack were almost adjacent and, therefore, subject to a similar overburden stress and a similar temperature of about −3 °C. Differences between these two layers thus cannot be explained by a difference in stress or temperature but should rather reflect a difference in their intrinsic mechanical properties.

These RHOSSA layers provide an ideal benchmark for simulations, which should be able to predict that DH snow tends to be much more resistant to compaction than RG snow (Kojima, 1967, 1975), which is an important feature of snow mechanics that models need to account for (Vionnet et al., 2012).

3.1.2 Antarctic firn

For the estimation of firn compaction rates with simultaneous microstructure measurements, we rely on an Antarctic field campaign. Our data originate from the B34 and B54 ice cores, both drilled on the East Antarctic Plateau. The B34 core was drilled at Kohnen Station, which is a site characterized by a 10 m borehole temperature of −44.5 °C (Weinhart et al., 2020). The B54 core was drilled near the OIR (Oldest Ice Reconnaissance) camp (displayed in Fig. 1 of Weinhart et al., 2020), a site with a measured 10 m borehole temperature of −53 °C.

For each firn core, a bulk density versus depth and an ice-age versus depth profile were produced based on firn core weighting and temporal synchronization with other cores. Assuming that the firn density profile represents a steady state, the compaction rate of the firn column at a given depth can be estimated by

$$\begin{array}{}\text{(11)}& \dot{E}={\displaystyle \frac{\mathrm{1}}{\mathit{\rho }}}{\displaystyle \frac{\mathrm{d}\mathit{\rho }}{\mathrm{d}\mathit{\tau }}}.\end{array}$$

Here, $\frac{\mathrm{d}\mathit{\rho }}{\mathrm{d}\mathit{\tau }}$ is the derivative of the density with respect to the age τ. In order to obtain the density versus age profile, we combine the density–depth and the age–depth profiles. As in the case of the Alpine snowpack, the overburden stress Σ for a layer at a given depth is calculated from the integration of the density of the overlying firn column.

As the density profiles were obtained by weighing 1 m long cores, they do not resolve the layer-to-layer variability, and the derived strain rate can already be regarded as an averaged (smoothed) bulk value. The strain rate of an individual layer in a 1 m core might still differ from this bulk value if its mechanical and microstructural properties differ from the average ones in the core.

While the firn density profiles are therefore sufficiently smooth and do not include any decrease in density with depth (which would be interpreted as expansion in Eq. 11), the deduced strain rate profiles still fluctuate, resulting in large and nonphysical variations in the compactive viscosity at the meter scale. As with the Alpine case, we therefore smoothed the profiles by manually selecting tie points to create a piecewise linear profile from which the compactive viscosity is deduced. In order to characterize the uncertainty in the method, profiles corresponding to the outer envelopes of the strain rate profile were also created and used to derive upper and lower bonds for the strain rate profiles.

Finally, these firn core data are complemented by 36 μCT scans (4 from B34 with a 40 µm resolution and 32 from B54 with a 30 µm resolution) with ice volume fractions ranging from 0.428 to 0.933 (that is to say, densities ranging from about 390 to 860 kg m⁻³, assuming a density of ice of 917 kg m⁻³).

3.2 Finite element modeling

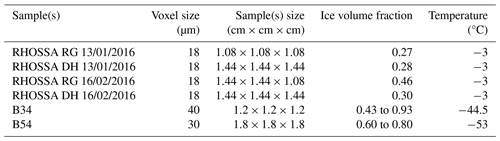
The experimental observations of snow and firn compaction were complemented with simulations using the finite element method (FEM). The goal of these simulations was to estimate the compaction rate of a sample based on its microstructure and a given microscopic ice rheology. Our simulation workflow, from μCT scanning to the estimation of the compactive viscosity, is schematically summarized in Fig. 1 and detailed below.

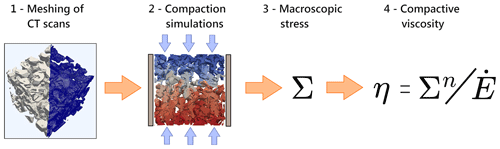
Figure 1 Simulation workflow used in this study in order to estimate the compactive viscosity of a snow/firn sample. The first steps shows the production of a tetrahedral mesh from the μCT images using CGAL. The second step shows a simulation of strain-rate-imposed compaction using Elmer FEM (the color scale stands for the vertical velocity). Step three shows the computation of the resulting macroscopic stress exerted at the top and bottom of the sample. Step four shows the computation of the compactive viscosity of the microstructure.

3.2.1 Image segmentation and mesh generation

The first step of our simulation workflow is to produce tetrahedral meshes representing the snow/firn microstructures. As detailed below, we performed simulations using both isotropic and anisotropic constitutive laws for the ice. Depending on whether a simulation was performed with an isotropic or an anisotropic material, the mesh generation process was slightly different.

For the isotropic ice simulations, each μCT image was first segmented into a binary voxel image of ice and air (as detailed in Calonne et al., 2020a), which was used as input for the CGAL¹ meshing library (Fabri et al., 2000) in order to produce a tetrahedral mesh of the ice matrix. Disconnected parts of the mesh were removed by component labeling in order to obtain a simply connected region for the ice microstructure. The last step is necessary as disconnected regions cannot carry mechanical loads and lead to an ill-defined mathematical problem in the finite element formulation.

As the goal of using an anisotropic ice material was to model snow microstructure as an ensemble of monocrystals with a crystallographic texture, the μCT images were also segmented into individual ice crystals as in Theile and Schneebeli (2011), Hagenmuller et al. (2014), or Willibald et al. (2020). As μCT does not carry any information about the crystallographic orientation of the ice, this segmentation was done on a purely geometrical basis using a watershed algorithm, following Willibald et al. (2020). The resulting segmented images for two RHOSSA samples are shown in the left column of Fig. 2. The segmentation appears to be realistic when compared to c-axis orientation measurements in snow from thin sections (Riche et al., 2013, Fig. 3). We note that while such a technique was not available for our study, the crystallographic orientation in snow could also be experimentally determined through X-ray diffraction tomography (Rolland du Roscoat et al., 2011; Reischig et al., 2013; Granger et al., 2021). The crystal-segmented μCT images were then meshed using the CGAL software, and the disconnected parts were removed, following the same procedure as for the standard binarized μCT images. Visualizations of segmented 3D FEM meshes, composed of various individual ice crystals, are displayed in the right column of Fig. 2.

Figure 2 Geometrical segmentation of μCT images into individual grains (a, c) and the corresponding 3D meshes (b, d). Each grain is represented by a given color. Samples correspond to the DH and RG snow sampled, as part of the RHOSSA campaign, on 13 January 2016.

In each case, we used the full size of the μCT images in order to have volumes that are as representative as possible. Specifically, the size of the RHOSSA snow samples corresponds to $\mathrm{1.44}\mathrm{cm}\times \mathrm{1.44}\mathrm{cm}\times \mathrm{1.44}\mathrm{cm}$ cubes for both the DH samples and the RG sample of 16 February 2016 and a $\mathrm{1.08}\mathrm{cm}\times \mathrm{1.08}\mathrm{cm}\times \mathrm{1.08}\mathrm{cm}$ cube for the RG sample of 13 January 2016. The B34 samples correspond to $\mathrm{1.2}\mathrm{cm}\times \mathrm{1.2}\mathrm{cm}\times \mathrm{1.2}\mathrm{cm}$ cubes, and the B54 samples correspond to $\mathrm{1.8}\mathrm{cm}\times \mathrm{1.8}\mathrm{cm}\times \mathrm{1.8}\mathrm{cm}$ cubes. The samples used for FEM modeling and their characteristics are summarized in Table 1.

Table 1 Description of the Alpine snow and Antarctic firn μ-CT images used for finite element simulations.

3.2.2 Finite element solution

Once a tetrahedral mesh is obtained, the Stokes equations as given in Eq. (1) are solved using the finite element method to estimate the compactive viscosity of a given microstructure for a given microscopic rheology, as outlined in Sect. 2. As we consider a purely viscous material without elasticity, we do not need to isolate the viscous response from an elastic part (as, for instance, done in Wautier et al., 2017). The simulations were carried out with the Elmer FEM² software, which is regularly used in ice sheet modeling. In this way, we can build on existing work in the context of ice flow that is typically done on larger scales (Gagliardini et al., 2013; Law et al., 2023).

As our meshes typically contain tens of millions of elements, we used the ParStokes equation solver that was specifically developed for solving the Stokes equations for a large number of elements on a parallel computer (used, for instance, in Schannwell et al., 2020). However, the ParStokes solver was originally developed for isotropic materials only. For the purpose of our study, we extended the ParStokes solver to also cope with a linear anisotropic material in order to emulate the behavior of ice monocrystals (Gagliardini and Meyssonnier, 1999; Burr et al., 2017). For this implementation in Elmer FEM (or any other FEM framework) of an anisotropic visco-plastic material, one needs to define the constitutive law that relates the deviatoric stress tensor s to the strain rate tensor $\dot{\mathit{ϵ}}$. In the case of a linear and anisotropic rheology, this constitutive law can be applied thanks to a fourth-order viscosity tensor M, i.e., $\mathbf{s}=\mathbf{M}:\dot{\mathit{ϵ}}$. While we do not consider this case in our study, one could also use a nonlinear rheology. In this case, this constitutive law would need to be linearized around the current estimate of the solution, and this linearized law would need to be expressed through a fourth-order tensor. The solution would then be iteratively approached (typically through Picard or Newton iterations).

In order to represent the deformation of a monocrystal, we used the constitutive law of Gagliardini and Meyssonnier (1999), which is given in Voigt notation in Eq. (7) of their article. This constitutive law represents a transverse isotropic ice material with its c axis oriented towards the vertical. The viscosity while shearing in the plane perpendicular to this c axis is assumed to only be a fraction of the viscosity while shearing in the planes containing the c axis. In our case, we set this fraction to be 0.01 (following Burr et al., 2017). Note that in Gagliardini and Meyssonnier (1999), the constitutive law is expressed as the relation yielding $\dot{\mathit{ϵ}}$ as a function of s, i.e., $\dot{\mathit{ϵ}}=\mathbf{a}:\mathbf{s}$, with a being a fluidity tensor. For the implementation in Elmer FEM, such a law needs to be inverted in order to have $\mathbf{s}=\mathbf{M}:\dot{\mathit{ϵ}}$. Due to the incompressibility of ice, the computation of M from a is not unique (Loredo and Klöcker, 1997). However, as the Voigt representation of the a tensor in Gagliardini and Meyssonnier (1999) is invertible, we can simply take the inverse as the tensor M. The tensor M, obtained by following the expression of Gagliardini and Meyssonnier (1999), is only valid for an ice crystal having its c axis oriented vertically. In order to be applied in a 3D FEM simulation, this constitutive law needs to be rotated according to the actual orientation of the crystal. This is achieved through rotation matrices and using the colatitude and longitude angles of the c axes (Meyssonnier and Philip, 1996; Gagliardini and Meyssonnier, 1999).

One of the particularities of the ParStokes solver used in this work is its use of block preconditioning. Ideally, this block preconditioner would be based on a Schur complement (similarly to Worthen et al., 2014). However, as the computation of a Schur complement can be costly, the isotropic version of the ParStokes solver approximates it as a FEM mass matrix divided by the element-wise scalar viscosity. However, in the case of anisotropy, the viscosity is not scalar anymore. For the approximation of the Schur complement in the anisotropic version of ParStokes, we instead used the first invariant of the viscosity tensor (Betten, 1982), normalized such that it equals the scalar viscosity in the limiting case of an isotropic rheology.

Finally, for solving the linearized FEM equations, we relied on the BiCGSTAB or the GMRES iterative methods, and convergence was assumed when the relative residual of the system reached at least $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ (some simulations reached a lower convergence criterion, but others showed quite slow convergence rates after passing $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{4}}$, which prevented them from reaching smaller criteria). For nonlinear problems, the nonlinear iterations were considered to have converged when the relative difference between two consecutive iterations was smaller than $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{4}}$.

3.2.3 Boundary conditions

For the simulations, boundary conditions need to be prescribed on the sides of the snow/firn sample. For the compression of snow and firn samples, we used the so-called periodicity-compatible mixed uniform boundary conditions (PMUBC; Pahr and Zysset, 2008). The vertical strain rate is imposed by prescribing the top and bottom vertical velocities, while a vanishing normal velocity is imposed on the sides. The advantage of such boundary conditions is twofold. First, these conditions mimic the natural, laterally constrained situation during compaction in snowpacks and firn columns. Second, these boundary conditions require the smallest volumes to achieve a representative behavior (Pahr and Zysset, 2008). Finally, we note that in the anisotropic simulations, the condition at the interface between monocrystals is simply characterized by the continuity of displacement rates.

Once the simulation has completed, the total reaction forces acting on the top and bottom faces are calculated. The macroscopic overburden stress is computed as the resulting average force divided by the sample surface area. Finally, the compactive viscosity η of the sample is obtained as the ratio between the macroscopic stress, with the appropriate nonlinearity exponent, and the prescribed macroscopic strain rate, as given by Eq. (5).

3.3 Testing the finite element setup

To provide some confidence in the correctness of the finite element setup, we conducted two numerical test experiments.

First, we verified that the macroscopic response of a microstructure with the microscopic constitutive law in Eq. (3) follows the same power law with the same stress exponent n. To this end, we used the microstructure obtained from one of the B34 firn samples. The deformation law chosen for the constituting material is an isotropic power law with n=3 and a fluidity prefactor a=1 ${\mathrm{Pa}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$. Using our finite element framework, the microstructure was deformed with different imposed macroscopic strain rates, and the macroscopic stress was obtained from the output of the simulations. The results are shown in Fig. 3 and confirm that the macroscopic strain rate versus stress curve indeed follows a power law with n=3, as predicted by Eq. (5). The corresponding compactive viscosity of this microstructure can be evaluated as η=28.1 Pa³ s (this value, of course, depends on the specific choice of the nonlinear exponent n and of the fluidity prefactor a).

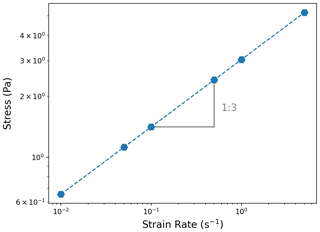
Figure 3 Stress versus strain rate curve characterizing the response of a firn microstructure composed of isotropic ice under compression (and assuming a fluidity prefactor a=1 ${\mathrm{Pa}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$). The macroscopic response follows a power law with the same exponent as the ice material, here with n=3.

Second, we tested the anisotropic behavior of the implemented transverse isotropic constitutive law, which is supposed to represent the rheology of an ice monocrystal. To this end, we performed simulations of the compression of a cylinder composed of a single monocrystal with a flattened top and bottom, which is referred to as the flattened Brazilian test (Wu et al., 2018). For the boundary conditions, the bottom boundary of the sample is fixed, while a constant vertical velocity is imposed at the top. The results of the simulations are displayed in Fig. 4 and show the appearance of the well-known shear band when the crystallographic orientation is tilted compared to the direction of compression. While the precise position and orientation of this shear band are nontrivial and depend on the geometry of the sample (notably through stress concentrations developing near corners, as visible in, for example, Fig. 8 of Patel and Martin, 2018), such a shear band is characteristic for an anisotropic material and does not appear in the isotropic case. Moreover, the resulting macroscopic stress required to obtain the same imposed macroscopic strain rate is about 23 times smaller in the case of a tilted c axis, showing the softening of the material depending on the respective orientation between the compression and the crystal.

Figure 4 Compressive response of a flattened cylinder composed of a transverse isotropic material, depending on the orientation of the crystal axis (0 and 30° compared to the vertical). The small gray arrows indicate the velocity of the ice material, and the color scale indicates the vertical component of the velocity field.

4 Results and discussion

We start with the simplest rheology for the ice matrix commonly used in the literature, namely Glen's law for isotropic, polycrystalline ice.

4.1 Firn is a foam of polycrystalline ice; snow is not

Several works in the literature have proposed that the deformation of the ice matrix in snow and firn is similar to the deformation of isotropic polycrystalline ice, i.e., glacier ice. This idea dates back to Mellor and Smith (1966), where the deformation of snow was experimentally studied alongside polycrystalline ice in order to unravel the similarities between the two. This approach has been supported by subsequent work by Kirchner et al. (2001), who concluded that the viscous compaction of snow has the same nonlinear properties as polycrystalline ice. In this respect, snow is viewed as a “foam of ice” (Kirchner et al., 2001) or, more precisely, a foam of polycrystalline ice. The viscoplastic deformation of polycrystalline ice is, nowadays, reasonably well understood and usually described by Glen's law, an isotropic power-law rheology with n=3 and known fluidity values depending on the temperature of the ice (Schulson and Duval, 2009; Cuffey and Paterson, 2010). As the benchmark densification rates for snow and firn were obtained with temperatures around −3, −44.5, and −53 °C, the corresponding ice fluidities are $\mathrm{1.7}\times {\mathrm{10}}^{-\mathrm{24}}$, $\mathrm{5.2}\times {\mathrm{10}}^{-\mathrm{27}}$, and $\mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{27}}$ ${\mathrm{Pa}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$, respectively.

Our first attempt was, thus, to simulate the deformation of snow and firn assuming Glen's law as the rheology for the ice matrix. Figure 5 shows the comparison between the compactive viscosities obtained with FEM simulations and those derived from the experimental data.

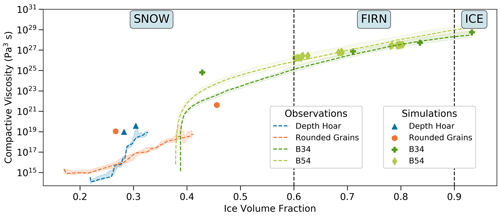
Figure 5 Comparison between simulated and observed compactive viscosities of snow and firn samples, assuming Glen's law for the ice rheology. The samples and data from the depth hoar and rounded grains are taken from the RHOSSA campaign, and the B34 and B54 samples and data are taken from the firn cores. The ice volume fractions of the simulated points are computed based on the CT scans. The shaded areas correspond to the uncertainties in deriving the compactive viscosity values, as described in Sect. 3.1.

Concerning firn (ice volume fraction above 0.6), the figure shows a general agreement, despite a cluster of simulated B54 samples that appear not viscous enough. Our interpretation is that since all these samples were taken at a similar location in the firn, this very location in the firn column may not be representative of the bulk and steady-state firn column due to the vertical variability existing in firn (Hörhold et al., 2011; Fourteau et al., 2019). Concerning snow (ice volume fraction below 0.6), Fig. 5 reveals a large overestimation of the compactive viscosities for all samples. This overestimation of the compactive viscosity when using Glen's law is consistent with the results of Theile et al. (2011), who reached a similar conclusion. The overestimation also exceeds the uncertainties in the observations that were computed as explained in Sect. 3 and shown as shaded areas in Fig. 5.

Moreover, Fig. 6 shows that while the RHOSSA observations indicate that on 13 January 2016 and 16 February 2016 the DH sample is, respectively, about 5 times and 1 times as viscous as the RG sample, our simulations using Glen's law predict a DH sample that is, respectively, 0.83 and 0.0093 times as viscous as the RG sample. Thus, not only is Glen's rheology largely overestimating the viscosity of snow, but it also fails in explaining relative differences (viscosity ratios) and as to why DH is such a viscous snow type compared to RG at the same density, temperature, and overburden stress.

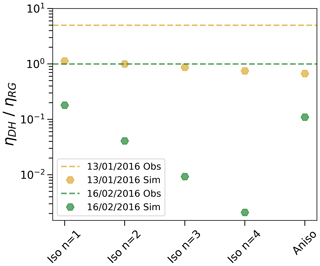
Figure 6 Comparison of simulated compactive viscosity ratios (DH over RG, represented by the green and yellow markers) with observations (dashed lines) from 13 January 2016 and 16 February 2016 for different versions of the microscale constitutive law (x axis).

Our results confirm that Glen's law is appropriate to model firn compaction, but clearly another microscopic ice rheology is required to explain the viscous compaction of snow.

4.2 Sensitivity study of isotropic rheologies

The disagreement of Glen's (isotropic polycrystalline) law could be resolved in a pragmatic but physically unjustified way by artificially increasing the fluidity a in Glen's law. Such a rheology could still be an interesting trade-off between physical rigor and practical considerations, as long as the obtained simulated compactive viscosities reasonably reproduce experimental observations. For instance, using an ice rheology with adjusted parameters, different from Glen's law, Wautier et al. (2017) were able to simulate compaction rates that are much more in line with experimental observations. However, such a fudge factor would still be in contradiction with our results: as explained in Sect. 2, the viscosity ratio between samples is independent of any potential (unjustified) modification of the ice fluidity a. In other words, while modifying the fluidity of the ice can be used to attenuate the general overestimation of the simulated snow viscosity, it would still fail in explaining why the simulated compactive viscosity of rounded grains is (relatively) too high when compared to DH snow, as seen in Fig. 5. Since this relative difference between RG and DH is a prominent feature in the densification of snow, we conclude that isotropic power-law rheologies with n=3 are not suited for snow modeling.

Detailed snow models rather employ a Newtonian rheology (n=1) instead (Bartelt and Lehning, 2002; Vionnet et al., 2012). Macroscopic Newtonian rheologies are also used in low-density firn studies (Schultz et al., 2022). Therefore, exploring rheologies besides Glen's law, with related numerical experiments, would benefit our understanding of homogenization in snow compaction. Accordingly, we conducted a sensitivity analysis on microscopic, isotropic constitutive laws using different exponents (n=1, n=2, and n=4 in our case) following Wautier et al. (2017). We note that, while some of these rheologies could be justified based on mechanisms of ice deformation (such as the Nabarro–Herring creep resulting in n=1; Herring, 1950; Arthern et al., 2010), our analysis of n≠3 was not conducted with specific physical mechanisms in mind. Rather, our motivation is to determine if an isotropic deformation law could explain snow compaction, independently of a specific underlying physical mechanism. For these simulations, physically constrained values for the scalar fluidity a of the ice rheologies are not available. Hence, comparing simulated and observed absolute values of compactive viscosities is not meaningful. We therefore focus here on viscosity ratios of DH and RG during the RHOSSA campaign, as this ratio is independent of the ice fluidity.

The results of our sensitivity study are shown in Fig. 6 and summarized in Table 2. Similar to Glen's law for both investigated days, and independent of the microscopic rheology, the simulations predict a viscosity ratio that is not in agreement with the observations. One may either consider this as RG snow being too viscous or DH snow being not viscous enough. Moreover, increasing the nonlinearity exponent n leads to a decrease in the viscosity ratio moving farther away from the observations. We interpret this result through the differences in geometry between RG and DH. DH is characterized by smaller necks than RG. This leads to higher local stress concentrations in DH than in RG, which can be confirmed from the simulated stress distribution in the DH and RG samples. These higher stress concentrations result in higher local strain rates, which are exacerbated by the nonlinear nature of the power-law rheology (for n>1). This effect is particularly marked on the DH and RG samples from 16 February 2016, as shown by the sharp decrease in the DH viscosity compared to that of RG as n increases. Thus, further increasing the value of n beyond n=4 appears unlikely to explain the compactive behavior of DH and RG snow. The insight from this sensitivity study consolidates our conclusion that the viscous compaction of snow cannot be explained by assuming that the ice matrix deforms according to a simple isotropic power law, whether linear or nonlinear.

4.3 Snow as an ensemble of monocrystals

The inability of Glen's (isotropic polycrystalline) law to explain snow viscous compaction is consistent with the fact that microstructural geometrical grains in snow are, in fact, monocrystalline units (Riche et al., 2013). The mechanical behavior of polycrystalline ice arises from the collective behavior of neighboring monocrystals blocking each other, as their preferential directions of deformation are not compatible with one another. In contrast, the monocrystalline grains in snow have many free surfaces at the ice–pore interfaces, where the crystals are free to deform (Scapozza and Bartelt, 2003). Thus, the ice matrix composing snow can be expected to deform much easier than polycrystalline ice. Note that this reasoning is also compatible with the applicability of Glen's law in firn. Here, due to the lower porosity, there are not so many interfaces with the pores, and individual ice-crystals tend to block one another, resulting in an ice rheology close to that of polycrystalline ice. Thus, there would be a transition in the ice matrix rheology from snow, characterized by freely deforming monocrystals, to firn, characterized by the interaction of incompatibly oriented crystals (i.e.,  polycrystalline ice), as the microstructure becomes denser and the crystals start blocking one another. This vision is consistent with experimental observations of the nonlinear exponent n of snow and firn that show a transition from n ∼ 2 to n ∼ 3.5 (Scapozza and Bartelt, 2003). Such a transition in behavior, which is assumed to be driven by a transition in density, is widely adopted (Alley, 1987; Arnaud et al., 2000; Salamatin et al., 2009; Morris et al., 2022).

Therefore, as a natural generalization of our work on snow compaction, we extended our study to an anisotropic rheology in order to advance in the direction of representing the grains in snow as monocrystals. To this end, we conducted simulations using a transverse isotropic rheology (Meyssonnier and Philip, 1996; Gagliardini and Meyssonnier, 1999). In contrast to the isotropic rheologies used above, this anisotropic rheology introduces a novel feature at the microscale, namely anisotropic deformations of grains that shear much easier in their basal plane than in other directions (Montagnat et al., 2014b). This idea of modeling snow as an ensemble of monocrystals has been previously proposed by Theile et al. (2011). They found that this rheology yielded smaller compactive viscosities more in line with observed values. However, Theile et al. (2011) considered only RG microstructures on geometrically simplified meshes. Therefore, the relative comparison between DH and RG, in terms of viscosity ratios using the full microstructure, constitutes an important cross-validation of this finding related to the aim of the present work.

For the simulation, the ice crystals were randomly binned into 100 different crystallographic orientation classes, each with a randomly given c-axis orientation. The distribution of the orientations of the c axes correspond to an isotropic texture (i.e., with no preferential orientation for the c axes). In order to simplify the comparison between the DH and RG snow simulations, the same distributions of the c axes were used for snow samples taken from the same day. For the present purpose, we limited ourselves to the linear transverse isotropic rheology that has been proposed for ice (as in Gagliardini and Meyssonnier, 1999).

Results of the simulations for the anisotropic rheology are shown in Fig. 6 and Table 2. They confirm the same disagreement that was found with the simulations for the isotropic rheology: the viscosity ratio between DH and RG is too low. Comparing the viscosity ratios from the anisotropic model, with their isotropic counterpart having the same exponent (n = 1), shows that the performance is even reduced, with a slight decrease in the viscosity of DH relative to RG. The use of a linear transverse isotropic rheology, meant to represent monocrystal behavior, cannot be considered more realistic. While we have only considered the linear anisotropic case here, it can be expected that a nonlinear anisotropic material law (when using exactly the same grain segmentation) would further increase the difference to the observations for the same reasons as detailed in the isotropic case.

Table 2 Ratio between the DH and RG compactive viscosities from various ice rheologies.

In order to illustrate the main differences between the anisotropic and the isotropic constitutive law, we computed the deviatoric stress field in the RHOSSA 13 January 2016 RG microstructure for both material laws. The distribution of the s₃₃ component (i.e., vertical component) of the deviatoric tensor is displayed in Fig. 7a. It reveals that, overall, the two deviatoric stress distributions are relatively similar, once normalized by the macroscopic stress. Only the tails of the distribution differ. Thus, while stress concentrations could be expected due to deformation incompatibilities of neighboring crystals, they appear to be relatively limited. This is confirmed by Fig. 7b, which displays the spatial field of the normalized s₃₃ component within a slice of the RG microstructure. The anisotropic and isotropic cases show similar spatial patterns of stress concentrations, which appear to be dictated by ice matrix geometry rather than crystallographic effects. In our simulations, the stress pattern driving the deformation is only affected a little by the use of an anisotropic material with crystallographic orientations. In the case of an isotropic crystallographic texture, where crystal orientations are not correlated with zones of stress concentration, the RG and DH can be expected to be impacted in a similar fashion by their random crystal orientation in zones of stress concentrations. Thus, the use of an anisotropic material with planes of preferential deformation modifies the compactive viscosity of a given sample compared to the isotropic case. However, the viscosity ratio between two samples remains relatively constant (see Fig. 6).

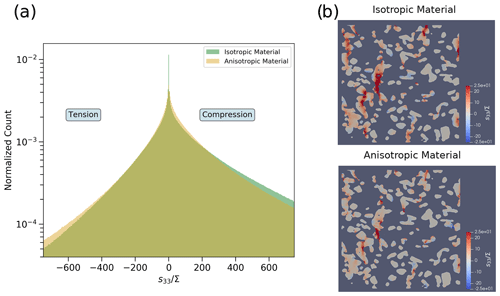
Figure 7 (a) Distribution of the s₃₃ component of the deviatoric tensor normalized by the macroscopic stress Σ in an RG microstructure, using either an isotropic or anisotropic constitutive law for the ice matrix. (b) Field of the normalized s₃₃ component of the deviatoric tensor in a RG microstructure, using either an isotropic or anisotropic constitutive law for the ice matrix. Red colors stand for compressive zones and blue colors stand for tensile zones.

4.4 Perspectives for the viscous compaction of snow and firn

By considering the viscous compaction of snow and firn in the same computational, microstructure-based framework, we were able to support and contradict underlying mechanisms that were previously hypothesized in the snow and firn literature.

The overall agreement of the isotropic simulations with observed firn densification rates using a published fluidity for the actual firn temperature supports the notion of firn as a foam of (isotropic, polycrystalline) ice (Kirchner et al., 2001), where the deformation stems from (intracrystalline) dislocation creep (Schulson and Duval, 2009). We note that in our study, the rheology for polycrystalline ice was taken from Cuffey and Paterson (2010), who report a nonlinear exponent n=3. The nonlinear exponent of firn has recently been experimentally studied by Li and Baker (2022), who, rather, report a nonlinear exponent of n ∼ 4. This value is consistent with the laboratory experiments of Sundu et al. (2024), who report n ∼ 4.4 for large-grained snow. As noted by Li and Baker (2022), a nonlinear exponent closer to 4 is also compatible with observations of polycrystalline ice (e.g., Goldsby and Kohlstedt, 2001; Bons et al., 2018). While the question of the best choice for n remains open, these inconsistencies in the specific n value do not contradict our result that firn compaction can be adequately simulated using an ice rheology based on polycrystalline ice observations. Remaining differences between simulations and firn core observations could be further explored if microstructure profiles were continuously available at a high vertical resolution, similar to Montagnat et al. (2020). In this way, the difference in scales between observations (strain rates averaged over 1 m) and simulations (centimeter-sized samples), and the associated uncertainty, could be further narrowed down.

In contrast, the notion of snow as a foam of ice following the same creep mechanism as high density firn is clearly ruled out by our study. While this result seems trivial in view of the number of studies highlighting the difference between snow and firn (e.g., Herron and Langway, 1980; Arnaud et al., 2000; Morris et al., 2022), we stress that these differences were hitherto never explored by microstructure-based simulations.

Our results for snow reinitiate the question about the dominant deformation mechanisms. Using viscosity ratios (see Fig. 6), we were able to show that DH and RG snow cannot be consistently modeled using the same microscale constitutive law (isotropic or anisotropic), strongly suggesting a fundamental difference in the underlying physics. Viscosity ratios provide a complementary benchmark, since biases resulting from the numerics or the prefactor in the microscale constitutive law should cancel out.

On one hand, this raises the question of whether the agreement for the anisotropic rheology found in Theile et al. (2011) would still hold when including different snow types at the same temperature and relaxing the mesh simplification step in representing the microstructure. Likewise, exploring anisotropic rheologies should be extended further, for instance, by including nonlinearity effects (Schulson and Duval, 2009; Montagnat et al., 2014b) or a preferential orientation of the c axes (Riche et al., 2013). Our extension of the ParStokes solver in Elmer FEM could provide an efficient modeling starting point in the direction of viscous and transverse-isotropic rheologies with a texture. Concurrent measurements of the texture are then unavoidable, either through thin sections of snow (Riche et al., 2013; Montagnat et al., 2020) or through X-ray diffraction tomography (Rolland du Roscoat et al., 2011; Reischig et al., 2013; Granger et al., 2021). Alternatively, microscale constitutive laws may be directly adopted from crystal plasticity and simulated using dedicated numerical techniques based on fast Fourier transformation (Knezevic et al., 2009; Hure, 2019). A deeper understanding of the influence of the snow texture on its mechanical properties would enable the study of the interaction between structural (i.e., due to the microstructure) and textural (i.e., due to the crystallographic orientations) anisotropies.

On the other hand, our viscosity ratios also raise the question of whether the density (of snow or firn) is actually the relevant property that discerns between different deformation mechanisms (Alley, 1987; Morris et al., 2022). Our snow samples were selected to include cases (Fig. 5) with virtually the same density but clear differences in the observed densification rates. Consistent with this idea, the recent experimental study of Sundu et al. (2024) suggests that the transition in the ice matrix rheology (characterized in their work by a transition from n ∼ 1.9 to n ∼ 4.4) is better captured by grain size than by density. While the comparison to observations (for snow and firn) is subject to the same uncertainty (separation of scales between centimeter-sized simulations and layer-averaged densification rates in the observations), care needs to be taken in assuming a density-driven transition to a different deformation mechanism, e.g., grain boundary sliding (GBS) (Raj and Ashby, 1971; Langdon, 2006). Such a GBS mechanism provides an alternative to the intracrystalline deformation discussed so far (Theile et al., 2011). Indeed, it is often assumed that at low density the deformation of snow occurs through localized stress relaxation at the junctions between grains (Alley, 1987; Salamatin et al., 2009; Schultz et al., 2022). However, the implementation of such a deformation mechanism in FEM, and an extension of the sensitivity analysis Fig. 6 to fundamentally different forms of the microscale constitutive law in Eq. (3), is not straightforward. Standard FEM techniques are not suited for localized, discontinuous deformations. Simulations of grain boundary sliding at the microscale would require more complex numerical methods, such as the extended finite element method (Khoei, 2014). This method has been developed to account for discontinuities and was successfully applied to model grain boundary sliding in the past (Simone et al., 2006).

Finding the relevant drivers for transitions in the compactive viscosity is even complicated by recent experimental studies such as the study by Wiese and Schneebeli (2017). This work found an immediate increase in the compactive viscosity during temperature gradient metamorphism (compared to isothermal samples), despite the absence of strong differences in structural parameters such as density, SSA (specific surface area), or structural anisotropy. We believe that these kinds of studies constitute a good experimental direction to identify active, microscopic deformation mechanism(s) and should be able to explain why very small microstructural differences can lead to large compactive viscosity differences. Moreover, the acquisition of μCT images during the controlled deformation of snow in the laboratory could help to identify the microscopic mechanism(s) at play during deformation and be a guide to select the appropriate physics for microstructure-based simulations.

Besides snow compaction, the simulations using a transverse isotropic rheology showcased that the ability of Elmer FEM's ParStokes solver to handle highly parallelized simulations (as in Schannwell et al., 2020) can be extended to account for complex anisotropic rheologies. Such a possibility could, for instance, be useful for large-scale ice sheet modeling, where the ice material can present an anisotropic behavior due to texture development (e.g., Gillet-Chaulet et al., 2006; Montagnat et al., 2014a). As mentioned in Sect. 3.2.2, the ParStokes solver relies on an approximation of a Schur complement for block preconditioning. A path of future development for the ParStokes solver, and its ability to robustly handle anisotropic materials, could be to derive a better approximation of the Schur complement, which could improve the block preconditioning stage.

5 Conclusions

Modeling the viscous densification of snow and firn directly from the microstructure of samples constitutes an important step towards replacing empirical parametrizations in models with physics-based laws. These computationally demanding, microstructure-based simulations can now be conveniently carried out with the required accuracy (mesh representation) using parallel computing. A holistic snow and firn densification picture is still hampered though by the limited insight into the microscale rheology of the ice matrix. This study explored several rheologies in microstructures taken from field campaigns and compared them to independent estimates. Using firn cores drilled in East Antarctica, our simulations largely confirmed that the ice matrix deforms according to an isotropic polycrystalline rheology, as classically used to model ice from glaciers or ice sheets. For snow, none of the tested rheologies (isotropic vs. anisotropic, linear vs. nonlinear) are able to quantitatively predict the large viscosity ratio between depth hoar and rounded grains, which is a critical requirement in snowpack modeling. Future (experimental and numerical) work is urgently needed in order to further constrain the form and the parameters in the microscale constitutive law of ice in snow.