the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Monitoring snow depth change across a range of landscapes with ephemeral snowpacks using structure from motion applied to lightweight unmanned aerial vehicle videos
Richard Fernandes
Christian Prevost
Francis Canisius
Sylvain G. Leblanc
Matt Maloley
Sarah Oakes
Kiyomi Holman
Anders Knudby
Differencing of digital surface models derived from structure from motion (SfM) processing of airborne imagery has been used to produce snow depth (SD) maps with between ∼2 and ∼15 cm horizontal resolution and accuracies of ±10 cm over relatively flat surfaces with little or no vegetation and over alpine regions. This study builds on these findings by testing two hypotheses across a broader range of conditions: (i) that the vertical accuracy of SfM processing of imagery acquired by commercial low-cost unmanned aerial vehicle (UAV) systems can be adequately modelled using conventional photogrammetric theory and (ii) that SD change can be more accurately estimated by differencing snow-covered elevation surfaces rather than differencing a snow-covered and snow-free surface. A total of 71 UAV missions were flown over five sites, ranging from short grass to a regenerating forest, with ephemeral snowpacks. Point cloud geolocation performance agreed with photogrammetric theory that predicts uncertainty is proportional to UAV altitude and linearly related to horizontal uncertainty. The root-mean-square difference (RMSD) over the observation period, in comparison to the average of in situ measurements along ∼50 m transects, ranged from 1.58 to 10.56 cm for weekly SD and from 2.54 to 8.68 cm for weekly SD change. RMSD was not related to microtopography as quantified by the snow-free surface roughness. SD change uncertainty was unrelated to vegetation cover but was dominated by outliers corresponding to rapid in situ melt or onset; the median absolute difference of SD change ranged from 0.65 to 2.71 cm. These results indicate that the accuracy of UAV-based estimates of weekly snow depth change was, excepting conditions with deep fresh snow, substantially better than for snow depth and was comparable to in situ methods.
- Article
(5927 KB) - Full-text XML
-
Supplement
(1289 KB) - BibTeX
- EndNote
The temporal and spatial pattern of snow depth (SD) is of importance to hydrological, ecological and climate studies (GCOS, 2016). Together with representative estimates of snow density, time series of SD are indicative of changes in snow water equivalent that in turn are of importance to streamflow forecasting and management of hydroelectric resources (Clyde, 1939; Barnett et al., 2005; DeWall and Rango, 2008). In many ecosystems, SD is an important determinant of winter habitat in terms of range and access to forage (Bokhorst et al., 2016). Snow depth also exerts an influence on local climate through insulation of permafrost and ice and global climate through its role in snow albedo feedbacks (IPCC, 2013, 2014; Bokhorst et al., 2016).
Systematic monitoring of SD is currently performed using in situ networks (e.g. Worley et al., 2015; Reges et al., 2016; https://globalcryospherewatch.org/projects/snowreporting.html, last access: 24 October 2018) providing daily measurements using automated sensors and less frequent measurements using manual sampling with rulers. The former are typically fixed in location with spatial sampling footprints from 1 to 10 m2 (e.g. Ryan et al., 2008; de Haij, 2011) with the exception of Global Positioning System (GPS) instruments that can estimate the mean snow depth over a footprint of ∼104 m2 (Larson, 2014). The sampled footprint for manual measurements is typically under 10 m2 (US Department of Commerce, 1997; Ryan et al., 2008; Meteorological Service of Canada, 2016). While in situ monitoring networks offer frequent temporal sampling, with the exception of GPS approaches, their spatial sampling can be imprecise and is often biased in terms of their representativeness of surrounding landscapes (Gelfan, 2004; Essery and Pomeroy, 2004; Neumann et al., 2010; Wrzesien et al., 2017). A GPS survey may offer a solution for an average SD estimation over open terrain, although measurement error is larger than for manual methods (e.g. Larson et al., 2014, report bias and precision of −5.7 cm and 10.3 cm respectively when estimating SD of a snowpack typically under 1 m in depth). Irrespective of measurement method, in situ SD monitoring sites can have vastly different microclimates and topographic conditions than less accessible areas nearby, thus increasing the potential for biases in estimated SD (Brown et al., 2003). One solution to address the limitation of sparse and potentially spatially biased in situ SD monitoring is to estimate the spatio-temporal SD pattern by combining in situ SD time series and maps of SD change (ΔSD) derived from remote-sensing methods (e.g. Liu et al., 2017). Remote SD mapping at a similar or better resolution of automated in situ measurements (i.e. <1 m2) can be performed using airborne survey with lidar (e.g. Deems et al., 2013; Harpold et al., 2014) or photogrammetric imaging (e.g. Nolan et al., 2015). Here we consider photogrammetric imaging approaches due to both their potential cost effectiveness and the widespread availability of unmanned aerial vehicle (UAV) systems. Nolan et al. (2015) used structure from motion (SfM; Westoby et al., 2012) processing of 15 cm ground sampling distance (GSD) digital images from a manned aircraft at an altitude of ∼750 m above ground level (a.g.l.) to map SD with an accuracy (precision) of ±10 cm (8 cm at 1 standard deviation) in comparison to individual probe measurements over relatively flat surfaces. Similar results were subsequently reported using UAV systems, with a GSD ranging from ∼2 to ∼10 cm and altitude from 60 to 130 m a.g.l., over prairies (Harder et al., 2016), alpine shrub lands (Bühler et al., 2016; De Michele et al., 2016; Harder et al., 2016; Avanzi et al., 2017) and glaciers (Gindraux et al., 2017). Even greater accuracy (1.5 to 3.8 cm) and precision (4.2 to 9.8 cm at 1 standard deviation) have been reported for ΔSD mapping over tundra (Cimoli et al., 2017) and alpine terrain (Vander Jagt et al., 2015) when using very low (10–30 m a.g.l.) altitude acquisitions with a GSD less than 4 cm.
While current studies provide increasing evidence of the potential for SD mapping over certain landscapes using multi-date UAV imagery, there are a number of issues that must be addressed if this approach is to be applicable for routine seasonal estimation of SD or ΔSD over natural landscapes. A pressing issue is the need to test the performance of this approach over a range of snowpack, vegetation and terrain conditions (De Michele et al., 2016). Studies indicate the presence of large (>10 cm) errors under specific illumination, snowpack, vegetation or terrain conditions. The reduced contrast in imagery of homogenous snowpacks (due to fresh snow covering all vegetation) under overcast conditions results in reduced point cloud density (Nolan et al., 2015; Bühler et al., 2017) and can lead to the failure of commercial SfM algorithms (Harder et al., 2016). While this issue may be partly addressed by using both visible and near-infrared imaging (Bühler et al., 2017), it may also be less of a factor when there is structure in the snowpack due to emergent vegetation and when GSD is sufficiently high to identify the intersection of snow and vegetation. Dense low vegetation compressed by the snowpack can result in SD underestimates due to a positive elevation bias in the snow-free reference image (Nolan et al., 2015; Bühler et al., 2016; Cimoli et al., 2017; De Michele et al., 2016). Vegetation above the snowpack can result in local overestimates of SD if it is incorrectly interpreted as the snowpack surface (Nolan et al., 2015; Harder et al., 2016). Topographic shadowing can have the same impact as overcast conditions when estimating SD over homogenous snowpacks (Bühler et al., 2017). However, the shading from vegetation and microtopography on SD estimates has not been studied systematically in the sense of considering different terrain roughness under the same snowpack and acquisition conditions.
A second issue that has yet to be addressed is the performance of UAV imaging approaches for estimating ΔSD between two dates with partial or complete snow cover. Current UAV imaging methods may have a practical lower limit of ∼30 cm SD due to the combined errors in estimating the snow-covered and snow-free surface elevation (Harder et al., 2016; Schirmer and Pomeroy, 2018). However, in many circumstances ΔSD may still have relevance (e.g. for temporal monitoring or for estimating SD using a single reference snow-covered date when SD is well approximated using in situ methods). Errors due to factors such as vegetation and terrain may be spatially correlated so that estimates of ΔSD among short periods (e.g. weekly) may be substantially more accurate than estimates of SD itself. There is a need to compare the relative accuracy and temporal precision of SD and ΔSD estimates, especially for areas with ephemeral snow packs.
A third issue is the need to model the uncertainty of elevation estimates as a function of UAV mission parameters. This is required to both guide mission parameters and understand the potential limits of current technologies and prospects for improvements in UAV performance and camera systems. Nasrullah (2016) demonstrated that photogrammetric theory could be used for this purpose when estimating the elevation of fabricated targets using UAV imagery and SfM over fabricated targets. A similar modelling approach has yet to be tested over snow-covered surfaces.
A fourth issue is the need to have robust low-cost equipment and software for data acquisition and processing (Nolan et al., 2015). Lightweight systems that require minimal flight certification are especially desirable considering that snow surveys may be episodic in both time and space. Nasrullah (2016) found that using commercial SfM software (Pix4D version 2.1.100) with imagery from off-the-shelf UAV systems weighing less than 2 kg and costing under USD 1000 (Phantom 2 Vision+) provided performance comparable to larger drones. There is a need to evaluate similar systems for ΔSD mapping over a range of environmental and surface conditions.
The issues that remain to be addressed regarding UAV-based mapping of SD require multiple experimental treatments including climate and snow conditions that cannot easily be controlled and land surface conditions that can be controlled. Here we chose to control the survey methodology by using a single low-cost commercially available solution for UAV-based mapping of three-dimensional point clouds and select mission parameters that should maximize the accuracy of elevation estimation based on photogrammetric theory, even if the solution may not be optimal in the sense of logistical constraints of time or cost. Secondly, we select sites with a range of microtopography and vegetation cover but limit vegetation cover to <50 % and only validate SD in openings. This strategy simplifies the approach used to extract surface locations within three-dimensional point clouds leaving the issue of UAV-based SD mapping under closed canopies for further study. Thirdly, we locate the sites within regions of ephemeral snowpack since this should correspond to a worst-case assessment of uncertainty, especially with respect to ΔSD. Given these limitations, the initial broad research question regarding snow depth mapping is refined into two specific research questions addressed in this study:
-
What is the accuracy and uncertainty of SD and weekly ΔSD maps derived using small commercial UAVs and commercial SfM technology as a function of varying microtopography and snowpack condition in sparsely vegetated regions with ephemeral snowpacks?
-
How well does the uncertainty of ΔSD maps and their corresponding digital surface models correspond to a priori estimates based on photogrammetric theory?
Our null hypothesis is that SD accuracy will be similar to that of previous studies, with greater biases in the presence of vegetation, but the accuracy of weekly ΔSD will be lower due to correlated errors related to surface conditions. Further, we hypothesize that, except for very smooth snowpack conditions, the accuracy of weekly ΔSD and digital surface models will correspond to the expected accuracy from photogrammetric theory. For very smooth snowpack conditions we hypothesize that there will be a decrease in key point matching density (as observed over glaciers by Gindraux et al., 2017) that in turn will result in accuracy less than expected from theory.
In Sect. 2 the study sites and methods used to estimate and validate ΔSD maps are described. A theoretical estimate of the precision of ΔSD as a function of mission parameters is also proposed. Results are presented in Sect. 3. Section 4 discusses these results in the context of the experimental conditions and their applicability to the research question. Conclusions with respect to the two research questions are given in Sect. 5.
2.1 Study sites
Five study sites were located in two study regions: Gatineau and Acadia. To simplify the acquisition of permits for in situ and UAV surveys, both study regions corresponded to land owned by the government of Canada. The separation between regions was partly due to the availability of staff to perform surveys but also due to a desire to sample different snowpack and land surface conditions. Climate and weather data were acquired from Environment and Climate Change Canada data (http://climate.weather.gc.ca/historical_data/search_historic_data_e.html, last access: 24 October 2018).
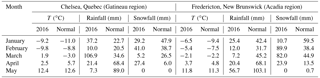
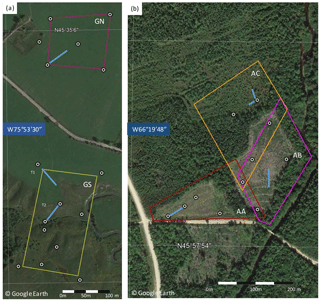
The Gatineau region (Fig. 1) was located at 45∘35′ N latitude and 75∘54′ W longitude in Gatineau Park (a 391 km2 federal park near Ottawa, Canada). The region consisted of land used for hay production with the meandering Meech Creek flowing across the southern half. Table 1 indicates recorded and climatological monthly rain, snow and temperatures for the nearest climate station (Chelsea, Quebec, at 45∘31′ N, 75∘47′ W, 112.50 m above sea level (a.s.l.)). During 2016, monthly air temperature was similar to the climate normal but rain (snow) was substantially higher (lower) than normal for March and lower (higher) for April. Two sites with alternatively flat and hilly macrotopography were established in the Gatineau region.
Gatineau North (GN) was a rectangular site of ∼2.0 ha with grass cover less than 5 cm high over a flat surface. Gatineau South (GS) was a rectangular site of ∼3.2 ha centred on Meech Creek. The northern portion of GS (Fig. 1) shared the same conditions as GN. The centre and southern portion of GS covered the river valley including spur hillslopes. Northern hillslopes where in situ transects were located were covered by low shrubs and grasses (<10 cm). Shrubs up to 1 m in height covered southern hillslopes. A small forested area was located at the southwest corner of GS.
The Acadia region (Fig. 1) was located at 45∘58′ N latitude and 66∘19′ W longitude in the Acadian Research Forest (a 91.6 km2 managed forest near Fredericton, Canada; Swift et al., 2006). The region consisted of three parcels of managed forest land, corresponding to sites Acadia A (AA), Acadia B (AB) and Acadia C (AC), separated by mature forest boundaries on gently undulating terrain. Table 1 indicates recorded and climatological monthly rain, snow and temperatures for the nearest climate station (Fredericton, New Brunswick, at 45∘52′08 N, 66∘32′14 W, 20.70 m a.s.l.). During 2016, air temperature was similar to the climate normal but rain (snow) was substantially lower (higher) than normal from February to April.
AA was a relatively flat trapezoidal site of ∼3 ha with grass (<5 cm) and stumps (<20 cm). AB was a hummocky rectangular site of ∼4.5 ha with stumps (<20 cm) and substantial brush and shrubs (<1 m) left over from clearing. AC was a rectangular site of ∼4.5 ha with recently planted balsam fir (Abies balsamea (L.) Mill.) ranging from 1 to 5 m in height. AC was also hummocky, although shrubs and herbs had covered most stumps. The sites were separated by mature mixed wood stands up to 20 m in height with balsam fir, red maple (Acer rubrum L.) and white birch (Betula papyrifera Marsh.).
2.2 Ground control points
Ground control points (GCPs) were established for each site for geolocation of UAV imagery and derived maps. The number and location of GCPs were determined based on the work of Tonkin and Midgley (2016), who assessed the performance of a digital surface model (DSM) derived from SfM processing of UAV imagery acquired at 100 m a.g.l. over a grassy landscape. Following their recommendation, at least five GCPs were positioned within the UAV coverage at each site and at least one GCP near the corner of each site. AC was an exception as GCPs could not be located at the northern edge due to access constraints. Six GCPs were located in GN and 10 GCPs in GS with 95 % circular error of probably less than 2.05 cm (Prévost et al., 2016a). For Acadia, four GCPs were located in AA, five GCPs in AB and two GCPs in AC with a 95 % circular error of probably less than 2.46 cm (Prévost et al., 2016b). GCP targets of either 30 cm square plywood or 15 cm diameter plastic disks were suspended between 1 and 1.3 m above ground level to avoid artificially increasing the accuracy of SD estimates by placing control points on the snowpack surface (Supplement Sect. S1). GCPs were located using ASHTECH Z-Xtreme dual-frequency instruments using precise point positioning.
2.3 In situ ΔSD measurement
Transects of ∼50 m in length (see Fig. 1) were positioned at each site within 5 m of a GCP. Each site had one transect except for GS where two transects were located (GS-1 in the flat northern portion and GS-2 along and across a spur hillslope leading into the floodplain). Along each transect, 12 48 wooden stakes were placed equally spaced apart ∼10 cm deep and approximately vertical. The attitude of the stakes was measured at the start and end of the field season using a digital level to a precision of 0.1∘. The elevation of the stakes above the soil layer was measured at the end of the field season using a plumb line and tape measure to a precision of better than ±0.5 cm (95 % confidence interval). In situ ΔSD was estimated at each stake using the protocol described in Oakes et al. (2016) to process digital images of stakes taken using a 14 Mpixel camera with a telephoto lens (Sect. S2). When comparing snow-covered conditions, the uncertainty for measuring the ΔSD assuming independent errors in determining the exposed stake freeboard is ∼2.06 cm (95 % confidence interval) for typical uncertainties in delineating the snowpack at the base of a stake and measuring the stake angle (Oakes et al., 2016). As both sources of uncertainty are spatially random, the uncertainty in estimating the average snow depth using all 12 stakes in a transect is estimated at ∼0.60 cm (95 % confidence interval).
2.4 UAV missions
Missions were performed weekly at Gatineau (26 January 2016 to 19 April 2016) and Acadia (10 February 2016 to 14 April 2016), during periods without precipitation at the start of the mission, using a Phantom Pro 3 Plus UAV (https://www.dji.com/phantom-3-pro, last access: 24 October 2018; P3P). The same UAV was used for all missions in a region. Imagery was acquired using the provided gimbal mounted 12.4 Mpixel rolling-shutter camera with a f2.8 fixed aperture in auto-exposure mode recording in 4K MPEG-4 AVC/H.264 format (MP4) (see Table S1). MP4 was used in preference to full-resolution photographs since (i) the system firmware limited the maximum photograph sampling rate to 1 frame per 2 s and (ii) the 4K video frames have almost identical resolution to the full-resolution photographs (Leblanc, 2018). Auto-exposure mode was used since the flights encountered rapid variations between sunlit and shaded snow and vegetation areas making it challenging to adjust exposure manually during the flight.
Litchi v3.0.4 (https://flylitchi.com/new, last access: 24 October 2018) flight planning software was used to create flight plans. The same flight plan was used for all missions at a site. Flight plans were defined using equally spaced parallel linear tracks flying oriented north to ensure consistent locations of shadows among dates. The exception was AC where tracks were oriented parallel to the GPS targets at AB to maximize overlap over these targets. Cross tracks were not used since this would increase flight time and since Nasrullah (2016) found that they did not significantly improve point cloud accuracy or density when using data acquired using a similar consumer-grade UAV and SfM software. Flight plans, using nadir view geometry, were defined to cover rectangular (triangular in the case of AA) regions with a buffer of 100 m to ensure adequate side views at the edges of each study area and to include GCPs from adjacent sites. Flights were planned such that the UAV was always flying along the vertical axis of the camera to minimize post-processing complexity. Turns were limited to 90∘ with smoothing of arcs to provide adequate side overlap during the turn.
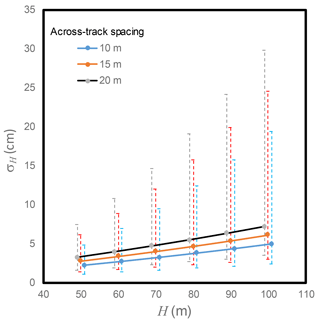
Mission parameters were optimized to minimize the vertical precision error in altitude H (σH) derived from the block triangulation of images at matching key points covering a nominal mapped extent of 10 ha assuming a 15 min flight (Sect. S3). For a matching key point found in K images, each acquired at a lateral distance of dk from the key point, the vertical precision error is modelled as (Forstner, 1998)
where σx is the average horizontal uncertainty when matching the location in each image pair on the camera focal plane and c is the lens focal length. Ignoring edges of flight tracks, {dk}, and σH will therefore be a function of the along-track image spacing (by), the across-track image spacing (bx) and H. With 4K video it is generally possible to choose a frame sampling rate f such that by≤bx.
Equation (1) assumes that matches are found in all overlapping images. Based strictly on geometric considerations, for the P3P with H≤100 m and bx<40 m, we expect K>20 matches. In practice, K is much lower than 20 due to the difficulty in matching the same feature in multiple images (Nasrullah, 2016). Adopting the worst-case assumption that the matched images are closest to the key point location and assuming similar along- and across-track spacing, from Forstner (1998),
Here, σx was estimated as the Euclidean sum of the mean reprojection error after block adjustment σre, the uncorrected motion blur during integration of the detector signal (σm) and the uncorrected rolling shutter motion (σrs).
Mean reprojection error is computed during block adjustment by the Pix4Dmapper Pro. Motion blur is given by
where vy is the along-track velocity, c is the lens focal length, τe is the exposure time and l is the detector size along the track. Rolling-shutter correction error is determined by the uncertainty in v and the sensor readout time τs:
Estimates of K, σre, σm and σrs were required to model σH. Trial flights (Supplement Sect. 3) were used to determine ranges for K (4.3 matches to 7.4 matches), σre (0.179 pixels to 0.209 pixels) and τe (0.017 to 0.005 s). Worst-case values of σre=0.25 pixels and τe=0.02 s were used for selecting flight parameters. We did not have sufficiently accurate on-board sensors to provide reference values of σv. Instead, we relied on a published comparison of v based on imagery from a Pix4D block adjustment and on-board measurement (Vautherin et al., 2016) indicating σv≈0.05v.
Using measurements from the training flights, the relationship between σH and H was modelled for the average and extreme values of K using the 10 ha minimum area constraint to relate vy to bx. Figure 2 indicates that σH increases almost linearly with H for any given K, although the rate of increase is steeper for low K. This result indicates it is critical to select the lowest feasible H. At H=50 m the sensitivity of σH to bx is negligible (<10 % σH) for m. Here we selected bx=15 m to maximize across-track overlap since we were able to increase f to achieve a constant along-track overlap irrespective of bx. This was important since the density of key point matches per square metre mapped (D) increases with overlap with all other parameters fixed (Nasrullah, 2016). The selected flight parameters predict a σH=1.44 cm for K=5 matches (ranging from σH=0.92 cm for K=8 matches to σH=3.73 cm for K=3) matches. As ΔSD was later estimated by computing the temporal difference of DSM (Sect. 2.7), the precision error in ΔSD, assuming uncorrelated errors in H between two dates, corresponds to the Euclidean sum of σH for each date. Ignoring uncertainty due to surface roughness for snow-free conditions, σΔSD=1.2 cm where both dates have K=8 matches, σΔSD=2.14 cm where both dates have K=5 matches and a worst-case σΔSD=5.25 cm where both dates have K=3 matches.
Each UAV mission resulted in two consecutive MP4 videos (due to a limitation of 3.91 GB for a single MP4 file) and an ephemeris file providing the P3P position and attitude with a temporal resolution of about 0.1 s. Data from each mission were processed in Pix4Dmapper Pro version3.2 (https://pix4d.com/product/pix4dmapper-photogrammetry-software/, last access: 24 October 2018) as described in Sect. S5.
2.5 Assessment of microtopography
Microtopography was assessed for each transect within each site using a snow-free point cloud acquired within 1 week of complete snowmelt. Compressed vegetation was included within microtopography since it also acts to bias estimates of SD (Harder et al., 2016). Microtopography was quantified as the deviation from a local robust linear slope trend (MATLAB function “lmfit” with robust option, https://www.mathworks.com/help/stats/fitlm.html, last access: 24 October 2018) with a 15 m moving window oriented along the transect. Deviations greater than the maximum snowpack elevation at each transect during the season were removed when computing the RMSD over a transect to eliminate overstory vegetation that normally would be above the snowpack.
2.6 Elevation and overstory cover extraction
Surface elevations were extracted from each point cloud in a sampling region at a constant sampling region around each stake. The sampling region corresponded to a 2 m tall vertical elliptic cylinder centred on the nominal horizontal location of a stake and extended 50 cm below the nominal vertical location of a stake. The horizontal (vertical) centre of the sampling region was specified as the average (average less 50 cm) of the visually determined location of the base of the stake from the colourized point clouds for two missions acquired during sunny conditions with less than 5 cm of snow depth. The 50 cm vertical offset was required to account for both point cloud geolocation uncertainty and local topography (including snow pits due to melt at the base of the stake) close to the stake. The horizontal major and minor axes of the cylinder were specified to approximate twice the Euclidean sum of geolocation uncertainty of the point cloud and the typical geolocation uncertainty of the stake corresponding to the difference between both reference image locations. These considerations typically resulted in horizontal axis lengths ranging from 10 to 24 cm depending on the precision of the stake geolocation among reference images.
The average overstory vegetation cover in the vicinity of transect sampling locations was estimated for each UAV mission. Overstory vegetation cover near each stake was estimated for a 1 m radius cylinder centred horizontally at each nominal stake location as the fraction of grid cells where at least one other point was found vertically above a surface point. A 1 m radius was used as an approximation of points within the field of view of images used to map the elevation in the smaller region used around each stake.
2.7 ΔSD estimation from point clouds
ΔSD was estimated for each transect using geolocated point clouds. For each point cloud, snow cover points were identified in each sampling region using points exceeding the 50th percentile of the blue band in a sampling region. The blue band was used as a simple indication of snow considering that vegetation and shadows should both have substantially lower blue intensity in a region with similar view geometry and similar top-of-canopy illumination conditions (Miller et al., 1997). To minimize bias due to the presence of melt depressions at the base of each stake and due to snow on vegetation, the median elevation of snow cover points within the sampling region was used to estimate the snow surface elevation at the corresponding stake.
The snow-free surface elevation was derived from a point cloud produced using an UAV flight over snow-free conditions within 1 week after complete snowmelt. For each sampling region, the snow-free elevation was estimated as the median elevation of all points unobstructed by points vertically below them. For each UAV flight, the average ΔSD across all sampling windows for the transect was used to estimate the transect ΔSD. The precision of ΔSD was estimated using the central percentile 67.5 interval of sampled ΔSD within the transect to include both measurement error and natural variability.
2.8 Performance assessments
The performance of geolocated DSMs and ΔSD, in comparison to reference values from GCPs and in situ transects respectively, was quantified in terms of accuracy, precision and uncertainty statistics following ANSI/NCSL (1997). Here accuracy is defined as the mean difference between validated and referenced data (i.e. the bias), precision is the RMSD after subtracting the accuracy from the validated data and uncertainty is the RMSD between the validated and reference data. For convenience, we use the term “bias” for accuracy and “RMSD” for uncertainty when discussing DSMs and ΔSD performance. In contrast to previous studies that report RMSD in comparison to individual in situ sample locations, assessments were performed using transect averages since addressing the broader research goal of combining in situ and UAV-based ΔSD requires an assessment of UAV estimates of ΔSD over a sampling footprint comparable to the reported in situ measurement (i.e. transect average at ruler locations). Camera calibration performance was assessed in terms of the percentage of images (P) successfully calibrated using a single block adjustment, the number of key point matches per image and D.
3.1 Data acquisition
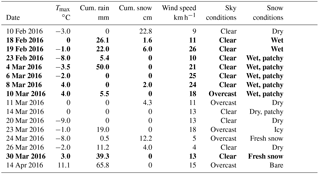
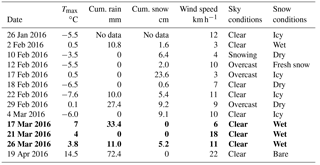
UAV flights were conducted on 13 days at Gatineau and 16 days at Acadia, resulting in 74 missions. For brevity, results for a mission are referenced using the site acronym followed by the date (e.g. GS 26 January 2016 is the Gatineau South mission for 26 January 2016). Flights were performed between 10:00 and 14:00 local time. Environmental conditions for each date are provided in Tables 2 and 3 based on the nearest climate station. Maximum daily temperatures at Gatineau (Acadia) ranged from −7.6 ∘C (−9.0 ∘C) to 14.5 ∘C (11.5 ∘C) and can be considered representative of typical temperature variability during late winter and spring melt periods. Hourly average wind speed at 10 m a.g.l. ranged from 3 to 26 km h−1, although the higher value may not be representative of local conditions since flights were not conducted if there was strong evidence of surface gusts or swaying conifer trunks. Sky conditions included both cloudy and overcast with one instance (GN 10 February 2016) in which snow was falling. Snowpack conditions included fresh snow, icy snow, wet snow, patchy snow (incomplete cover) and no snow. Ephemeral melt, preceded by over 10 mm of rain, occurred at both Gatineau (2 February 2016) and Acadia (18 February 2019). Three missions were not processed due to issues with the recorded data (see Sect. S6).
Table 2Environmental conditions during P3P missions over Gatineau. Rain and snow correspond to cumulated totals since the previous mission. Melt periods are in bold font.
3.2 UAV data processing
A total of 71 missions were processed with Pix4D (details in Sect. S6). Of these, three missions over GN, corresponding to either snowing or icy snow conditions, resulted in <500 matches per image and subsequently <50 %. Two other missions (GN 29 February 2016 and AB 8 March 2016) also resulted in P<50 %. During both of these missions, there was spatially uniform fresh snow that possibly reduced the number of spatial features suitable for matching. The remainder of the missions were each processed using a single block adjustment with a median P=97 % (minimum = 80 %).
The key point match density varied substantially between missions and sites (Fig. 3). Fresh snow or ice conditions resulted in D<10 matches m−2 irrespective of the site. Season average D was higher over Acadia (83 matches m−2) than Gatineau (28 matches m−2), even considering only dates without icy or fresh snow (91 matches m−2 for Acadia versus 42 matches m−2 for Gatineau). For dates at or exceeding the median D, K ranged from 4 to 8 (not shown). Pix4D does not provide a similar statistic over sub-areas. Missions with differing sky conditions but constant snowpack conditions only occurred at AA for one pair of dates (8 March 2016 and 10 March 2016) when missions were repeated due to instrument failure on the first date at AB. For these two missions, D was higher under clear versus overcast conditions but there was insufficient replication to determine if this impacted ΔSD estimation.
Horizontal accuracy ranged from −0.68 to 0.57 cm (median −0.01 cm) and vertical accuracy ranged from −1.10 to 0.48 cm (median −0.04 cm) (Fig. 4a). There was evidence of a linear relationship between vertical and horizontal accuracy after accounting for outliers. Horizontal uncertainty ranged from 0.44 to 11 cm with a median of 1.87 cm while the vertical uncertainty ranged from 0.045 to 4.6 cm with a median of 1.02 cm (Fig. 4b). Over 75 % of missions resulted in a geolocation uncertainty under 4 cm in both horizontal and vertical directions. Uncertainty less than 0.5 cm RMSD was only observed for missions with D>50 matches m−2 but uncertainty was unrelated to D past this matching density. Horizontal precision ranged from 0.04 to 10.7 cm (median 1.76 cm) and vertical precision ranged from 0.04 to 4.5 cm (median 0.99 cm) (not shown). A least absolute residual regression (https://www.mathworks.com/help/stats/robustfit.html, last access: 24 October 2018) of vertical versus horizontal precision gave an adjusted r2 of 0.97 with a slope of 1.11 (95 % confidence interval [1.04, 1.18]). Precision error was closely related to uncertainty due to the low bias relative to uncertainty (not shown). Similar to accuracy, a least absolute residual regression of vertical versus horizontal precision gave an adjusted r2 of 0.95 with a slope of 0.58 (95 % confidence interval [0.54, 0.62]). The effect of sky conditions on geolocation performance was not systematic across the entire dataset. There were insufficient replicates having the same surface conditions but different sky conditions to perform a quantitative analysis of this effect on geolocation performance.
As expected, microtopographic roughness increased from qualitatively smooth to rough sites with average RMSD values under 5 cm at Gatineau, between 5 cm and 10 cm at AA and AB, and 42 cm at AC (Fig. 5). AC indicated the presence of high-spatial-frequency variation (length scales <10 cm) that was due to low vegetation rather than variations in ground surface elevation per se. Figure 6 indicates that for conditions other than icy/fresh snow, except for the forested AC site, D increased with microtopographic roughness. Key point density was lower for icy/fresh snow conditions versus other conditions at all sites; decreases ranged from ∼35 % at AC to ∼1000 % at GS. The season average decrease was only different from zero at a significance level of 0.05 when the RMSD related to topographic roughness was less than 0.08 (i.e. GN, GS and AA).
The effect of hourly average wind speed on D, geolocation accuracy or geolocation uncertainty was also evaluated at each site using ordinary least-squares regression. For each site, the r2 was below 0.5 and the slope was not significantly different from 0 at p=0.05. As with sky conditions there were insufficient trials to control for snow surface conditions when evaluating the effect of wind speed.
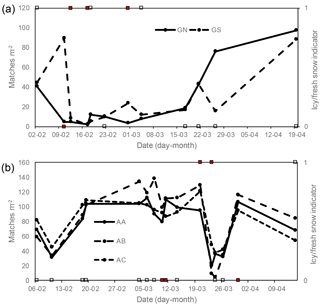
Figure 3Pix4D automated key point match density for (a) Gatineau and (b) Acadia together with an indicator of fresh snow (square symbols). Missions (solid circular symbols) for the same site are connected by lines. Red squares indicated overcast conditions.
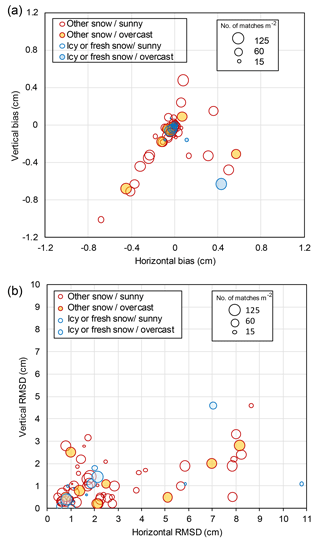
Figure 4(a) Accuracy and (b) uncertainty of absolute geolocation for digital surface models based on cross-validation with GCPs. Symbol area proportional to mission average key point match density.
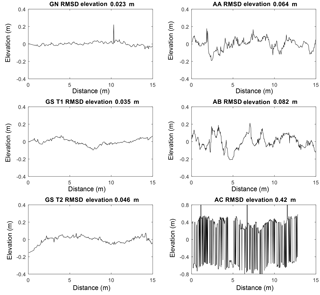
Figure 5Deviations from the local robust linear trend (based on 15 m moving window) of densified point cloud elevations along each transect. Only the first 15 m of each transect is shown for clarity. The root-mean-square deviation (RMSD) for elevations over the entire transect is also indicated. AC is truncated as the transect consisted of shorter line segments.
3.3 ΔSD mapping performance
The performance of ΔSD mapping was evaluated in terms of both changes between successive dates and changes between a given date and snow-free conditions. Figure 7a shows the ΔSD between successive dates for each transect. Vertical (horizontal) bars indicate the 1 standard deviation confidence interval due to within-transect variation in ΔSD from the image data (in situ data). The bars indicate that spatial variability in ΔSD within a transect was often larger than the 2.6 cm (1 standard deviation) uncertainty for in situ ΔSD estimation for a transect assuming no spatial variability. As such, the in situ measurement method was considered sufficiently precise for reference estimates. Nevertheless, due to within-transect variation in ΔSD, the precision of both in situ and image-based methods was often similar in magnitude to observed ΔSD so that statistically significant comparisons could not be conducted for individual dates. Rather, in situ and image-based ΔSD values were compared using statistics based on differences observed for all dates for each transect. In this case, uncertainty ranged from 2.54 to 5.12 cm for the non-forested sites to 8.68 cm at AC. The temporal bias was substantially smaller than uncertainty, ranging from −0.80 cm at GS to 0.35 cm at AC. As such, the precision error was only slightly less than the uncertainty (not shown). There were seven instances in which the observed difference exceeded 5 cm. Four were overestimates ranging from 5 to 10 cm at Gatineau and the other three were all at AC, including the largest residual corresponding to an underestimate of 20 cm. Four of these instances, including the 20 cm error, involved at least one date with either extremely icy snow and another with deep fresh snow. In such cases the D can be low (Fig. 3) while the snowpack itself has changed substantially among dates. Two other cases involved rapid melt, leading to exposed ground surfaces on the last date. We also noted that at AC, the identified key points were often at snow–vegetation intersections (not shown), which may differ systematically in ΔSD when compared to the stakes that were placed within openings.
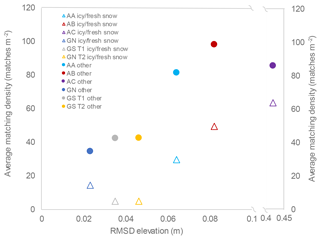
Figure 6Season average key point matching density versus root-mean-square deviation (RMSD) of elevation deviation along the transect for icy and fresh snow missions (hollow triangles) and “other” missions with snow cover (solid circles) during snow-covered periods. The difference in season average matching density between icy/fresh snow and other was statistically significant at p=0.05 for RMSD < 0.8 (plots GN, GS, AA) but not statistically different at p=0.15 for RMSD < 0.8 (plots AB, AC).
Figure 7b compares ΔSD between snow-covered and snow-free conditions (i.e. estimated SD). In this case, the confidence interval of ΔSD for a transect was on average [+5.2, −6.3 cm] for in situ and [+4.1, −7.8 cm] for image-based estimates. Uncertainty ranged from 1.58 cm at AB to 10.56 cm at GN. Accuracy varied among sites. Bias was below 1.2 cm for GS T1, AA and AB. In contrast, bias at the other sites exceeded ±5 cm (−10.05 cm at GN T1, −6.23 cm at GS T1 and 5.5CM at AC). Moreover, the bias was consistent over time with the exception of large (>5 cm) underestimates for the date just prior to snowmelt for all sites except AB.
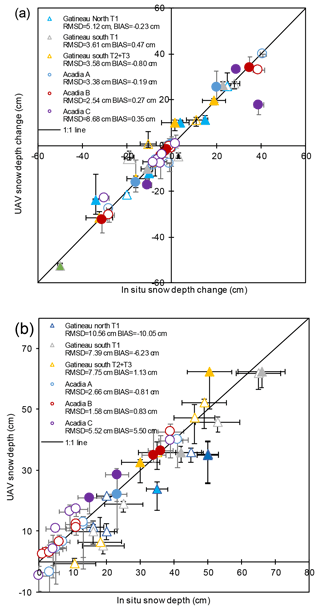
Figure 7Validation of (a) snow depth change for successive (∼ weekly) measurements and (b) corresponding snow depth over transects. Shaded symbols correspond to icy or fresh snow conditions. Horizontal (vertical) bars correspond to the ±34th percentile interval of within-transect in situ (UAV) snow depth estimates.
4.1 Temporal and spatial variation in snowpack conditions
Missions were conducted over a range of snowpack conditions including peak snowpack with both fresh and aged snow, ice-covered snow, partial snow cover during melt and no snow just after melt. In this sense, the experiment offers a realistic sampling of ephemeral snowpacks for the temperate climate regions of our study sites. In contrast to studies reviewed in Sect. 1, snowpack conditions were often icy (5 of 29 dates) and patchy (6 of 29 dates) due to frequent rain-on-snow events. Ideally, the temporal sampling could have been enhanced by adding additional missions during the same day or adjacent days to assess the impact of sky and weather conditions on ΔSD estimates.
The uncertainty of in situ ΔSD was primarily due to precision error from spatial variability rather than measurement error. This aspect is important when evaluating image-based estimates of ΔSD since the difference between a single in situ and remote measurement will include some element of spatial uncertainty due to differences in the compared area. A number of previous studies have directly reported the RMSD between image-based ΔSD and point measurements (e.g. Nolan et al., 2015; Harder et al., 2016; Vander Jagt et al., 2015). One may argue that single-measurement comparisons include the horizontal uncertainty of the image-based map but practically speaking users of ΔSD maps are likely interested in the transect average in the same manner that users of current in situ networks require transect averages rather than the spatial distribution of ΔSD at centimetre resolution. Nevertheless, the within-transect range of ΔSD from both in situ and image-based approaches is important for understanding the representativeness of the measurements as well as potential biases. In this regard, the within-transect variation for image-based ΔSD was approximately the same magnitude as for in situ ΔSD but skewed towards lower ΔSD when considering snow depth due to local positive biases in the snow-free DSM in the presence of vegetation. Similar biases have been reported in previous studies (Vander Jagt et al., 2015; Gindraux et al., 2017).
4.2 SfM performance with snowpack condition, microtopography and wind speed
The mission performance of the consumer-grade UAV was encouraging given that it was often operated at the edge of its performance envelope in terms of wind speed and air temperature and under varying illumination conditions. The percentage of calibrated images and D decreased substantially in the presence of precipitation or very smooth surface conditions such as fresh snow or ice. The decrease was greatest over sites with low microtopographic roughness (GN, GS and AA), although the lack of statistical significance for the decrease at AB and AC may be due to the limited number of icy/fresh snow dates (three). Qualitative assessment of imagery during snow-covered conditions indicated that, in contrast to AB and AC, which had substantial exposed vegetation and rough topography, key points at the other sites were chiefly found along ridges and shadows cast by snowdrifts. Bühler et al. (2017) and Gindraux et al. (2017) reported similar findings with other UAV systems for fresh snow but not for glacier ice. In our study, ice was typically in the form of a flat surface pond or smoothed snowpack, while in these studies ice was the surface of a glacier that included topographic roughness. In any case, the lower key point density in both their study and ours was due to smooth surfaces. In principle one could interpolate ΔSD across smooth regions using the ΔSD at their perimeter. Otherwise, the percentage of calibrated images did not vary substantially across sites and was consistently not a limiting factor in terms of performance (i.e. >97 %).
Key point density decreased by almost 1 order of magnitude when comparing missions flown with snow more than 1 day old and missions with either deep fresh snow or smooth icy snowpacks. Previous studies have identified the drop in both elevation and SD accuracy due to deep fresh snow (Nolan et al. 2015; Avanzi et al., 2017) and icy conditions (Gindraux et al., 2017). Here we demonstrate that D may be a useful indicator of such conditions and hence an indicator of the quality of ΔSD estimates. The experiment did not control for sky conditions. The one pair of missions with similar snow conditions but different sky conditions did not show substantial changes in either the percentage of calibrated images or D. Nevertheless, the lack of dense canopy conditions and controlled sky conditions means that this study does not address the issue of large cast shadows (or lack thereof) in estimating snow depth changes using a low-flying UAV. Bühler et al. (2017) reported that digital surface models from UAV images acquired in cast shadows appeared to be qualitatively noisier than those without shadows and resulted in unrealistic (both negative and very high) estimates of SD after differencing from bare-earth accuracy models. They suggested that a combination of visible and near-infrared imagery might reduce uncertainty in areas of cast shadow. Alternatively, measurements during overcast conditions may be sufficient to map ΔSD with sufficient accuracy in areas of persistent shadows.
Previous studies have not systematically evaluated the sensitivity of ΔSD estimation to microtopography or vegetation density. The sites selected for this experiment were nominally flat at length scales of tens of metres, except in the vicinity of GS T3. However, microtopography varied among sites. All of the Gatineau sites had little or no microtopographic variation while the Acadia sites progressed from tree stumps (AA) to mounds covered with shrubs (AB) to mounds covered with shrubs and a regenerating canopy (AC). Overstory vegetation cover was less than 10 % along transects, except at AC where cover within a 1 m radius vertical cylinder centred at each stake was estimated to average 38 % (range [0 %, 52 %]). However, GN and GS T1 have substantial thatch exceeding 5cm in height under the snow that was present during the snow-free mission while AC had cover of understory herbs and low shrubs ranging from 5 to 10 cm in height. As such, this experiment provides new results for a range of microtopography and understory/low vegetation but is limited in terms of overstory cover. As previously indicated, this was a conscious decision due to the difficulty of adequate non-destructive in situ sampling in forested areas and our desire not to further complicate the point cloud processing when having to deal with snow on vegetation. Excluding fresh and icy snow, which varied in frequency between Gatineau and Acadia, D was generally proportional to microtopographic roughness for sites without overstory. The behaviour with overstory (AC) may have been due more to our inclusion of vegetation point cloud points within our microtopography index since the matching density at AC was similar to AB where the understory and surface topography was subjectively similar. Assuming this is the case, these results suggest a compensating effect between increasing variability in ΔSD due to microtopographic complexity and increasing D that may explain why, outside of icy and fresh snow, RMSD and accuracy were similar across sites when estimating ΔSD change.
The absence of a statistically significant linear relationship between hourly average wind speed and either D or geolocation performance was not surprising. Firstly, we did not perform missions where all other factors but wind speed were controlled. In addition, our wind speed data may not have been representative of actual conditions. Daily maximum gusts, corresponding to instantaneous recordings, were often twice the magnitude of hourly average wind speed, suggesting that the UAV may have experienced higher wind speeds during its mission on calmer days. Additionally, missions were delayed if extreme local gusts were observed. We also did not control for snow and illumination conditions when considering the effect of wind speed (e.g. by performing missions on subsequent days with different wind speed by the same illumination). We hypothesize that, except for very large gusts, the Pix4D block adjustment procedure is capable of accounting for uncertainty in camera attitude and location since we observed little or no sensitivity of either D or geolocation performance when using imagery with or without ephemeris (not shown). Rather, the major difference was the decrease in time for key point matching and block adjustment when providing accurate ephemeris in comparison to no ephemeris information except for the time of acquisition.
4.3 Geolocation and ΔSD validation
The geolocation performance of derived DSMs was exceptional considering that the UAV was a consumer-grade device. Bias errors were smaller than the precision of the GCPs themselves, suggesting that spatial variation in DSM errors may have a large random component. We could not test this hypothesis as we had limited control points that were all in relatively open areas. The DSM accuracy over GCPs was higher than reported in other studies over natural landscapes (e.g. Nolan et al., 2015; Harder et al., 2016; Gindraux et al., 2017) but similar to performance over fabricated targets (Nasrullah et al., 2016). This is partly explained by the high spatial resolution of the imagery in our study but we hypothesize it was also due to use of easily visible elevated GCP targets that were identified in many images. For example, the number of image matches at GCPs ranged from 10 to 30. Assuming independent errors at each GCP, the number of image matches corresponds to a theoretical ratio of vertical to horizontal accuracy of between 0.9 and 5 at a single point or 0.42 and 2.2 over five GCPs. The observed ratio based on a robust line fit was 1.1, indicating agreement with theory. The strong correlation observed between horizontal and vertical accuracy error was also in line with the theoretical error model. We did not have sufficient spatial sampling of surface elevations over snow-covered areas to test the model in terms of snow surface elevation. This should be performed in future studies using reference measurements from surface instruments (e.g. Avanzi et al., 2017).
Validation of ΔSD requires minimally invasive reference estimates using methods that also do not substantially change the performance of UAV estimates. Considering the potential for large variations in SD and ΔSD with microtopography, we decided to control the reference locations by using fixed stakes. This strategy could have led to an (artificial) increase in precision if the stakes led to an increase in the D as well as an increase in accuracy if the same key points on stakes were detected in multiple images within or among missions. A posteriori examination of maps of automated key points indicated that the Pix4D algorithm rarely found a key point along a stake (e.g. Sect. S7). Furthermore, the few cases in which a key point was identified on a stake corresponded to locations with exposed vegetation around the stake that would potentially exhibit a match in any event. Pix4Dmapper uses a proprietary implementation of a reduced set of features derived from the scale-invariant feature transformation (SIFT) (Strecha et al., 2011). SIFT features are defined to specifically eliminate key points that have poorly determined locations but high edge responses, especially corner features (Lowe, 2004). We hypothesize that, especially for snow-covered conditions, the relatively narrow stakes correspond to such features and are subsequently avoided by Pix4Dmapper when identifying key points. If so, our results may actually be somewhat pessimistic since there are potentially fewer key points near stakes.
Validation of weekly ΔSD indicates that bias across all sites and dates was smaller than the typical uncertainty for a given transect from both in situ and image-based methods and of the same order of magnitude of conventional automated or manual measurements at point locations. There was evidence of two larger (>5 cm) over- and underestimates at the forested AC site that may be due to snow present on vegetation near the ground (overestimates) or under-sampling of the point cloud due to fresh snow (underestimates). There were also instances of underestimates exceeding 5 cm during melt over the Gatineau sites. Both of these cases corresponded to icy anterior conditions that may have favoured point cloud matches in areas with rougher snow that had not yet melted. In each of these cases, one of the compared elevation surfaces had far lower D than typical for the site, suggesting that D may be a useful indicator of confidence in estimated ΔSD. Notwithstanding these issues, the typical uncertainty of ΔSD was close to the theoretical error of ∼2.44 cm for a single estimate. This suggests that sources of error within a transect are likely correlated since one would expect substantial reduction in the ΔSD for the transect considering that hundreds of point cloud samples are averaged. The correlation is potentially explained by the fact that the stakes in each transect share the same images for the most part and therefore potentially suffer the same lateral displacement errors.
Validation of SD (comparing snow and snow-free conditions) indicated that the range of RMSD (from ∼1.5 to ∼10.5 cm) falls within the ±10 cm uncertainty reported in previous studies (see Sect. 1), with a tendency for underestimation in areas with substantial ground thatch layer. The underestimate in these conditions was approximately the same magnitude of the thatch height, leading us to hypothesize that they are related to an overestimate in the local DSM height as previously suggested (Nolan et al., 2015; Avanzi et al., 2017). This hypothesis could be tested in future studies using supplementary in situ elevation measurements (e.g. Avanzi et al., 2017), although it is also consistent with the relatively unbiased estimate of ΔSD changes among snow-covered dates. We also hypothesize that the overestimate at AC may be due to snow-covered vegetation being included in the sampled point cloud around each stake when estimating the DSM for snow-covered areas. Harder et al. (2016) noted a similar bias due to stubble protruding from shallow snowpacks. Here, we used the median snow surface elevation based on point cloud colour processing that seemed to avoid this effect for other sites. More sophisticated algorithms for separating snow-covered surfaces from overstory vegetation should be evaluated.
Snow depth is an important geophysical quantity that exhibits substantial variation in space over distances of metres and in time over daily intervals. Systematic snow depth monitoring to date has emphasized temporal resolution. This study evaluated the potential for lightweight UAV imagery, processed using off-the-shelf SfM software, for mapping the change in snow depth over natural vegetated landscapes. The primary goal of this study was to compare this approach when mapping changes in snow depth between successive snow-covered dates versus between a snow-covered and snow-free date over land cover with varying vegetation density and microtopography and with ephemeral snowpacks. The sampled sites exhibited only modest variation in overstory vegetation cover (from 0 to 38 % averaged over a transect) but substantial variability in microtopography, including tree stumps, hummocky terrain and mowed pasture. The study also addressed a second goal of comparing observed accuracy and precision of snow depth change and associated surface elevations with estimates based on photogrammetric theory.
A total of 71 UAV missions were flown in a range of conditions with surface elevation maps derived at a horizontal ground sampling distance of between 2 and 3 cm and with a median (range) of horizontal and vertical uncertainty of 1.87 cm (0.44 to 11 cm) and 1.02 cm (0.045 to 4.6 cm) respectively in comparison to man-made ground control points. Validation over five different study sites from mid-winter to snow-free conditions indicated an uncertainty of 6.45 cm (1.58 to 10.56 cm) and accuracy of 3.33 cm (−10.05 to 5.05 cm) for the average snow depth over a ∼50 m long transect. Snow depth was systematically underestimated over sites with dense low vegetation by ∼5 cm. As the underestimate was the same magnitude as the vegetation height during snow-free conditions, we hypothesize the underestimate is related to an overestimate of the snow-free ground elevation. Validation for the average change of snow depth over a transect among successive (∼ weekly) missions indicated a uncertainty of 3.40 cm (2.54 to 8.68 cm) and accuracy of 0.31 cm (−0.19 to 0.80 cm).
Observed uncertainty for snow depth change agreed with the theoretical uncertainty (mean value of 2.44 cm and range of 1.2 to 5.25 cm depending on the number of matches at a key point) when considering the difference between two snow-covered dates. In general, uncertainty in associated surface elevations agreed with theoretical estimates in both magnitude and in terms of the expected correlation between horizontal and vertical errors. The observed uncertainty in absolute snow depth was larger than theoretical uncertainty chiefly due to bias in estimates of the bare-ground elevation in the presence of vegetation within the snow-free reference image. In this case the bias is likely to be specific to local conditions and it may be possible to use in situ measurements to calibrate for this bias if UAV-based estimates of snow depth are combined with in situ measurements. Even so, the uncertainty of UAV-based weekly snow depth change is comparable to typical in situ measurement approaches, suggesting that a combination of both measurements should be considered for producing maps of snow depth change in complex terrain with high spatio-temporal resolution. We recommend that future studies consider the potential of using UAV information on snow depth change rather than absolute snow depth.
Further studies are required to investigate the performance of snow depth change mapping using similar UAV data in terms of sensitivity to changes in key point sampling density due to changing illumination and wind speed, in terms of the precision of snow depth change estimates under denser canopies where the non-vegetated surface is substantially obscured and to quantify performance as a function of UAV mission and SfM software parameters. Nevertheless, the results from our multi-site and multi-operator study suggest that UAV-based estimates of snow depth and snow depth change over areas corresponding to a typical in situ transect have uncertainty comparable to current manual in situ estimates while offering substantially greater coverage. Moreover, the technology can be applied with widely available off-the-shelf equipment and software. While our study had a ∼10 ha limit due to using a single mission, spatial coverage can be extended to line of site using multiple missions or multiple cameras on the same UAV or even past line of sight given adequate certification. Moreover, in situ GPS targets may not be required if baseline networks can be processed using post-processed kinematic methods. Assuming these results are representative of wider landscapes and snow conditions, we recommend that subsequent studies address the problem of combining airborne UAV survey-based information on snow depth change with high-temporal-resolution satellite and in situ information to improve snowpack characterization and reduce uncertainty in estimates of streamflow.
Data can be accessed as indicated in Fernandes et al. (2017).
The supplement related to this article is available online at: https://doi.org/10.5194/tc-12-3535-2018-supplement.
RF designed the experiment, performed observations and analysis, and prepared the paper. CP, FC and SL designed the experiment and performed observations. MM and SO performed observations and analysis. KH and AK performed analysis.
The authors declare that they have no conflict of interest.
The authors acknowledge funding from Public Safety Canada and Natural
Resources Canada and field data acquisition by Brigitte Leblon,
Armand Laroque and Melanie Poirier. The authors thank Najib Djamai,
Robert Fraser and Morgan Macfarlane-Winchester and the two anonymous
external reviewers for reviewing the paper.
Edited by: Etienne Berthier
Reviewed by: two anonymous referees
ANSI/NCSL, Z540-2-1997.: U.S. Guide to the Expression of Uncertainty in Measurement, 1st ed., National Conference of Standards Laboratory, Boulder, USA, 1997.
Avanzi, F., Bianchi, A., Cina, A., De Michele, C., Maschio, P., Pagliari, D., Passoni, D., Pinto, L., Piras, M., and Rossi, L.: Measuring the snowpack depth with Unmanned Aerial System photogrammetry: comparison with manual probing and a 3D laser scanning over a sample plot, The Cryosphere Discuss., https://doi.org/10.5194/tc-2017-57, 2017.
Barnett, T. P., Adam, J. C., and Lettenmaier, D. P.: Potential impacts of a warming climate on water availability in snow-dominated regions, Nature, 438, 303–309, 2005.
Bokhorst, S., Pedersen, S. H., Brucker, L., Anisimov, O., Bjerke, J. W., Brown, R. D., Ehrich, D., Essery, R., Heilig, A., Ingvander, S., Johansson, C., Johansson, M., Jónsdóttir, I. S., Inga, N., Luojus, K., Macelloni, G., Mariash, H., McLennan, D., Rosqvist, G. N., Sato, A., Savela, H., Schneebeli, M., Sokolov, A., Sokratov, S. A., Terzago, S., Vikhamar-Schuler, D., Williamson, S., Qiu, Y., and Callaghan, T. V.: Changing Arctic snow cover: A review of recent developments and assessment of future needs for observations, modelling, and impacts, Ambio, 45, 516–553, 2016.
Brown, R., Brasnett, B., and Robinson, D.: Gridded North American monthly snow depth and snow water equivalent for GCM evaluation, Atmos.-Ocean, 41, 1–14, 2003.
Bühler, Y., Adams, M. S., Bösch, R., and Stoffel, A.: Mapping snow depth in alpine terrain with unmanned aerial systems (UASs): potential and limitations, The Cryosphere, 10, 1075–1088, https://doi.org/10.5194/tc-10-1075-2016, 2016.
Bühler, Y., Adams, M. S., Stoffel, A., and Boesch, R.: Photogrammetric reconstruction of homogenous snow surfaces in alpine terrain applying near-infrared UAS imagery, Int. J. Remote Sens., 38, 3135–3158, 2017.
Cimoli, E., Marcer, M., Vandecrux, B., Boggil, C. E., Williams, G., and Simonsen, S. B.: Application of low-cost UASs and digital photogrammetry for high-resolution snow depth mapping in the Arctic, Remote Sens., 9, 1144, 2017.
Clyde, G. D.: Stream-flow forecasting by snow-surveying, Eos Trans. AGU, 20, 194–195, 1939.
Deems, J. S., Painter, T. H., and Finnegan, D. C.: Lidar measurement of snow depth: a review, J. Glaciol., 59, 467–479, https://doi.org/10.3189/2013JoG12J154, 2013.
de Haij, M.: Field test of the Jenoptik SHM30 laser snow depth sensor, KNMI, available at: http://bibliotheek.knmi.nl/knmipubTR/TR325.pdf (last access: 24 October 2018), De Bilt, Technical report, TR-325, 35 pp., 2011.
De Michele, C., Avanzi, F., Passoni, D., Barzaghi, R., Pinto, L., Dosso, P., Ghezzi, A., Gianatti, R., and Della Vedova, G.: Using a fixed-wing UAS to map snow depth distribution: an evaluation at peak accumulation, The Cryosphere, 10, 511–522, https://doi.org/10.5194/tc-10-511-2016, 2016.
DeWalle, D. R. and Rango, A.: Principles of snow hydrology, Cambridge University Press, Cambridge, 428 pp., 2008.
Essery, R. and Pomeroy, J.: Implications of spatial distributions of snow mass and melt rate for snow-cover depletion: theoretical considerations, Ann. Glaciol., 38, 206–265, 2004.
Fernandes, R. A., Canisius, F., Leblanc, S. G., Maloley, M., Oakes, S., Prévost, C., and Schmidt, C.: Assessment of UAV-based photogrammetry for snow-depth mapping: data collection and processing, Geomatics Canada, Open File 32, 50 p., https://doi.org/10.4095/300553, 2017.
Forstner, W.: On the theoretical accuracy of multi image matching, restoration and triangulation, Bonn, Universität Bonn, available at: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.42.8370, last access: 24 October 2018.
GCOS: The global observation system for climate: implementation needs, GCOS-200, World Meteorological Organization, 313 pp., 2016.
Geflan, A. N.: Modelling Forest Cover Influences on Snow Accumulation, Sublimation and Melt, J.f Hydrometeorol., 5, 785–803, 2004.
Gindraux, S., Boesch, R., and Farinotti, D.: Accuracy Assessment of Digital Surface Models from Unmanned Aerial Vehicles' Imagery on Glaciers, Remote Sens., 9, 186, https://doi.org/10.3390/rs9020186, 2017.
Harder, P., Schirmer, M., Pomeroy, J., and Helgason, W.: Accuracy of snow depth estimation in mountain and prairie environments by an unmanned aerial vehicle, The Cryosphere, 10, 2559–2571, https://doi.org/10.5194/tc-10-2559-2016, 2016.
Harpold, A. A., Guo, Q., Molotch, N., Brooks, P., Bales, R., Fernandez-Diaz, J. C., Musselman, K. N., Swetnam, T., Kirchner, P., Meadows, M., Flannagan, J., and Lucas, R.: A LiDAR derived snowpack dataset from mixed conifer forests in the Western U.S., Water Resour. Res., 50, 2749–2755, https://doi.org/10.1002/2013WR013935, 2014.
IPCC: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 1535 pp., 2013.
IPCC: Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Field, C. B., Barros, V. R., Dokken, D. J., Mach, K. J., Mastrandrea, M. D., Bilir, T. E., Chatterjee, M., Ebi, K. L., Estrada, Y. O., Genova, R. C., Girma, B., Kissel, E. S., Levy, A. N., MacCracken, S., Mastrandrea, P. R., and White, L. L., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 1132 pp., 2014.
Larson, K. M.: Snow depth, density, and SWE estimates derived from GPS reflection data: Validation in the western U. S., Water Resour. Res., 50, 6892–6909, https://doi.org/10.1002/2014WR015561, 2014.
Leblanc, S. G.: Off-the-Shelf Unmanned Aerial Vehicles for 3D Vegetation Mapping, Geomatics Canada, Open File 32, 28 pp., 2018.
Liu, Y., Li, L., Yang, J. Chen, X., and Hao, J.: Estimating Snow Depth Using Multi-Source Data Fusion Based on the D-InSAR Method and 3DVAR Fusion Algorithm, Remote Sens., 9, 1195, 2017.
Lowe, David G.: Distinctive Image Features from Scale-Invariant Key points, Int. J. Comput. Vision, 60, 91–110, https://doi.org/10.1023/B:VISI.0000029664.99615.94, 2004.
Meteorological Service of Canada: MANOBS – Manual of Surface Weather Observations, Seventh Edition, Amendment 19, Environment and Climate Change Canada, available at: https://www.ec.gc.ca/manobs/73BC3152-E142-4AEE-AC7D-CF30DAFF9F70/MANOBS_7E-A19_Eng_web.pdf (last access: 24 October 2018), 431 pp., 2016.
Miller, J. R., White, H. P., Chen, J. M., Peddle, D. R., McDermid, G., Fournier, R. A., Shepherd, P., Rubinstein, O., Freemantle, J., Soffer, R., and LeDrew, E.: Seasonal change in understory reflectance of boreal forests and influence on canopy vegetation indices, J. Geophys. Res., 102, 29475–29482, https://doi.org/10.1029/97JD02558, 1997.
Nasrullah, A.: Systematic analysis of Unmanned Aerial Vehicle Derived Product Quality, MSc, Thesis, available at: https://webapps.itc.utwente.nl/librarywww/papers_2016/msc/gfm/nasrullah.pdf (last access: 24 October 2018), 2016.
Neumann, N. N., Derksen, C., Smith, C., and Goodison, B.: Characterizing local scale snow cover using point measurements during the winter season, Atmos.-Ocean, 44, 257–269, 2010.
Nolan, M., Larsen, C., and Sturm, M.: Mapping snow depth from manned aircraft on landscape scales at centimeter resolution using structure-from-motion photogrammetry, The Cryosphere, 9, 1445–1463, https://doi.org/10.5194/tc-9-1445-2015, 2015.
Oakes, S., Prévost, C., Fernandes, R., and Canisius, F.: Method of Determining In-Situ Snow Depth in UAV Snow Monitoring Missions, Geomatics Canada, Open File 28, 9 pp., 2016.
Prévost, C., Fernandes, R., and Canisius, F.: Ground control point acquisition for Acadia Forest, New Brunswick, during winter 2016, in support of Canada Centre for Mapping and Earth Observation snow depth from unmanned aerial vehicle activities, Geomatics Canada, Open File 27, 42 pp., 2016a.
Prévost, C. and Fernandes, R.: Relevé GPS de cibles de référence au site test de Gatineau, Québec, dans le cadre du projet d'évaluation de l'épaisseur de neige par aéronef sans pilote, Geomatics Canada, Open File 26, 67 pp., 2016b.
Reges, H. W., Doesken, N., Turner, J., Newman, N., Bergantino, A., and Schwalbe, Z.: COCORAHS: The evolution and accomplishments of a volunteer rain gauge network, B. Am. Meteorol. Soc., 97, 1831–1846, 2016.
Ryan, W. A., Doesken, N. J., and Fassnacht, S. R.: Evaluation of Ultrasonic Snow Depth Sensors for U.S. Snow Measurements, J. Atmos. Ocean. Technol., 25, 667–684, 2008.
Schirmer, M. and Pomeroy, J. W.: Factors influencing spring and summer areal snow ablation and snowcover depletion in alpine terrain: detailed measurements from the Canadian Rockies, Hydrol. Earth Syst. Sci. Discuss., https://doi.org/10.5194/hess-2018-254, in review, 2018.
Strecha, C., Bronstein, A., Michael, M., Bronstein, M., and Fua, P.: LDAHash: Improved matching with smaller Descriptors, IEEE Transactions on Pattern Analysis and Machine Intelligence, 34, 66–78, 2012.
Swift, D. E., Kilpatrick, B., Murray, T. S., Toole, D., Henderson, J. M., and Pitt, C. M.: Acadia Research Forest: a brief introduction to a living laboratory, in: Long-term Silvicultural & Ecological Studies. Results for Science and Management, edited by: Irland, L. C., Camp, A. E., Brissette, J. C., and Donohew, Z. R., Yale University, School of Forestry and Environmental Studies, Global Institute of Sustainable Forestry, New Haven, CT, USA, 104–118, 2006.
Tonkin, T. and Midgley, N.: Ground-Control Networks for Image Based Surface Reconstruction: An Investigation of Optimum Survey Designs Using UAV Derived Imagery and Structure-from-Motion Photogrammetry, Remote Sens., 8, 786, https://doi.org/10.3390/rs8090786, 2016.
U.S. Department of Commerce: Snow Measurement Guidelines for National Weather Service Cooperative Observers, Silver Spring, MD, 1997.
Vander Jagt, B., Lucieer, A., Wallace, L., Turner, D.. and Durand, M.: Snow Depth Retrieval with UAS Using Photogrammetric Techniques, Geosciences, 5, 264–285, 2015.
Vautherin, J., Rutishauser, S., Schneider-Zapp, K., Choi, H. F., Chovancova, V., Glass, A., and Strecha, C.: Photogrammetric accuracy and modelling of rolling shutter cameras, ISPRS Comission III, available at: https://pix4d.com/wp-content/uploads/2016/05/pix4d-isprs-paper-rolling-shutter-final-edited.pdf (last access: 24 October 2018), 2016.
Westoby, M., Brasington, J., Glasser, N., Hambrey, M., and Reynolds, J.: “Structure-from-Motion” photogrammetry: A lowcost, effective tool for geoscience applications, Geomorphology, 179, 300–314, 2012.
Worley, S, Chi-Fan, S., Fetterer, F., Yarmey , L., Uttal, T., Starkweather, S.: Current data holdings of historical in situ snow cover observations, available at: http://www.coreclimax.eu/sites/coreclimax.itc.nl/files/documents/Workshops/SnowWorkshop/presentation_Worley_NCAR_data_holdings.pdf (last access: 24 October 2018), 2015.
Wrzesien, M. L., Durand, M. T., Pavelsky, T. M., Howat, I. M., Margulis, S. A., and Huning, L. S.: Comparison of methods to estimate snow water equivalent at the mountain range scale: A case study of the California Sierra Nevada, J. Hydrometeorol., 18, 1101, https://doi.org/10.1175/JHM-D-16-0246.1, 2017.