Inter-model differences in 21st century glacier runoff for the world's major river basins

Projected glacier change has important downstream consequences, including sea level rise, changing freshwater supply, and loss of important cultural sites. While the glacier contribution to global sea level rise and associated uncertainties have been quantified in model intercomparison studies, comparatively less focus has been directed towards the interannual changes in runoff caused by glacier recession. The observed effect of glacier runoff on basin-level water availability makes simulated future runoff a particularly consequential target for analysis. In this study, we compare century-scale runoff simulated by three global glacier evolution models. Aggregating annual glacier runoff contributions to 75 globally distributed major river basins, we find that the three models agree closely in some basins but differ dramatically (up to a factor of 3.8) in others. However, when we analyze century-scale runoff changes relative to a glacier model's historical runoff baseline, annual runoff projections are much more consistent across glacier models. Glacier models project broadly consistent relative changes in seasonal runoff supply, with some differences across climatic regions. Estimates of the year of peak water are more consistent across glacier models (when driven by a climate model ensemble) than across individual climate forcings within a single glacier model. We identify the glacier models' different approaches to modifying precipitation forcing as the dominant source of inter-model differences in projected runoff. Our findings highlight the comparative roles of glacier evolution model, global climate model forcing, and emissions scenario as important sources of uncertainty across different metrics of projected glacier runoff. For example, inter-glacier-model uncertainty in absolute annual runoff is large, but the year of projected peak water has much greater inter-climate-model uncertainty. We recommend that users pay particular attention to how a selected glacier model parameterizes and calibrates the glacier climatic mass balance in glaciohydrological modeling efforts.

1 Introduction

21st century glacier change has substantial downstream consequences, including sea level rise (e.g., Marzeion et al., 2012; Gardner et al., 2013), changing freshwater supply (e.g., Kaser et al., 2010; Immerzeel et al., 2020), altering ecosystems (e.g., Bosson et al., 2023; Jacobsen et al., 2012), increasing natural hazard risk (e.g., Taylor et al., 2023), and loss of important cultural sites (e.g., Bosson et al., 2019). In recent decades the effects of these changes have already become visible. Cities such as La Paz (Kinouchi et al., 2019) and Santiago (McCarthy et al., 2022) have had to adopt severe water management strategies, while numerous Himalayan communities have had to enact new preventative measures against glacial lake outburst floods (Ahmed et al., 2021). The diverse downstream consequences of glacier recession highlight the importance of refining projections of glacier change to support adaptation and mitigation strategies.

Though the relative importance of glacier runoff varies by basin (Immerzeel et al., 2020), glaciers are projected to provide critical drought buffering, especially in arid basins (Ultee et al., 2022), despite already surpassing the year of greatest annual runoff (“peak water”) in many regions (Huss and Hock, 2018). Our ability to predict glacier mass and runoff changes is thus important for water planning and management. Unfortunately, global climate models (GCMs) do not simulate glacier change, and global hydrological models can only crudely represent it due to a lack of input data and parameterization constraints (van Tiel et al., 2020a). While global hydrological models can explicitly represent glaciers through coupling to a glacier evolution model, computational expense generally limits such efforts to a single hydrological model coupled to a single glacier model (Wiersma et al., 2022; Hanus et al., 2024). There is thus an urgent need to quantify uncertainties associated with projected glacier runoff from different global glacier evolution models (hereafter “glacier models”) to properly inform glaciohydrological modeling studies.

Uncertainties in glacier runoff projections come from differences in glacier models as well as uncertainty in climate forcing. GCM-projected precipitation and land-surface runoff vary widely across GCMs and climate scenarios; in some regions, models disagree even on the sign of the expected changes (Lee et al., 2021; Wang et al., 2022). Runoff simulated by glacier models may either amplify or temper inter-GCM variability in projected hydrologic changes because glaciers respond nonlinearly to climate forcing (Oerlemans, 1989; Christian et al., 2022). The inherent nonlinearity of the glacier response is further obscured because glacier models use different methods to modify precipitation forcing and account for un-simulated processes. For example, “glacier-centric” models like the ones we study here, which simulate each of the world's glaciers individually, must downscale and bias-correct coarse-gridded climate forcing data to the individual glacier scale. Each glacier model applies slightly different schemes to do so, calibrating parameters such as temperature lapse rates, temperature biases, and multiplicative precipitation factors to match the observed glacier mass balance. The calibrated parameters often make climate biases or missing mass balance processes implicit (Rounce et al., 2020b). Further, because only one observation per glacier is globally available for calibration (Hugonnet et al., 2021), all glacier models are over-parameterized. Thus, multiple combinations of parameters may match the observations equally well but produce different runoff projections (Schuster et al., 2023a).

While previous glacier model intercomparison projects have revealed considerable differences in glacier mass projections due to differences in models (e.g., model parameterizations, initializations, calibration data and techniques, reanalysis data, and bias corrections) (Hock et al., 2019; Marzeion et al., 2020), uncertainties in projected glacier runoff from a multi-glacier-model ensemble have yet to be quantified. Here, we analyze the first estimate of glacier runoff projections for the three most advanced, globally capable glacier models, forced by an ensemble of CMIP6 GCMs and Shared Socioeconomic Pathways (SSPs), for 75 glaciated major river basins. For each basin, we analyze annual glacier runoff, the year of peak water, and seasonal runoff cycle projected by each glacier evolution model until the year 2100. We quantify the consistency of projections across glacier models by comparing the inter-glacier-model range with the inter-GCM range. We also examine inter-SSP ranges to determine the effect of the future emission scenario on the year of peak water. Ultimately, the study aims to summarize inter-model similarities and differences in runoff projections, discern general reasons for observed differences, and provide guidance for practitioners and hydrologists seeking to incorporate readily available glacier model projections into future planning.

2 Methods

We evaluate projected glacier runoff at annual and seasonal timescales for all 75 of the world's large river basins (> 3000 km²) with considerable glacier cover (> 30 km²). Glacier outlines are provided by the Randolph Glacier Inventory (RGI version 6; RGI Consortium, 2017), and we include all glaciers falling within Global Runoff Data Centre (2020) major river basins, including those in Europe, Asia, the Americas, and New Zealand (Figs. 1 and A1). Here, we define glacier runoff as the sum of ice melt, snowmelt, and liquid precipitation minus refreezing (when modeled). We use a “fixed-gauge” station approach (e.g., Huss and Hock, 2018) where each model estimates runoff for a constant area such that it accounts for ice melt and snowmelt as well as rainfall over the initially glaciated areas as the glacier retreats.

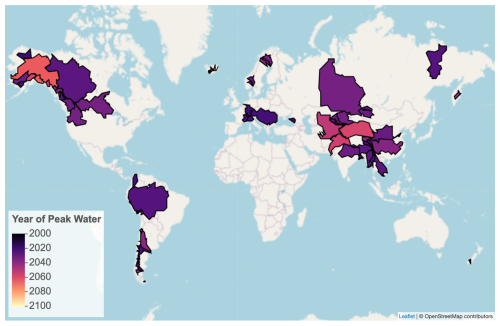
Figure 1 All 75 basins analyzed in the study. The color fill corresponds to the basin's year of peak water as estimated by the multi-glacier-model median under the SSP2-4.5 scenario. This map was generated by our online interactive mapping tool (Wimberly, 2024b), available at https://fwimberly.shinyapps.io/Global_Glacier_Runoff/ (last access: 31 March 2025).

2.1 Glacier evolution models

The three glacier models included in our study are the Global Glacier Evolution Model (GloGEM; Huss and Hock, 2015), Open Global Glacier Model (OGGM; Maussion et al., 2019), and Python Glacier Evolution Model (PyGEM; Rounce et al., 2023). All three are glacier-centric, simulating each of the world's glaciers individually. Each simulated glacier is initialized with a Randolph Glacier Inventory outline (RGI Consortium, 2017), calibrated using different reanalysis data and calibration strategies against glacier-wide mass balance from 2000–2019 for each glacier (Hugonnet et al., 2021) and forced in the future with an ensemble of GCMs and SSPs from CMIP6 (Eyring et al., 2016). Melt is estimated using a temperature index approach and accumulation using a temperature threshold to distinguish rain from snow. GloGEM and PyGEM also include a parameterization to estimate refreezing, while OGGM does not. All three glacier models have previously been validated against seasonal mass balances from in situ measurements of a few hundred glaciers worldwide (WGMS, 2020), showing good agreement at regional scales, even though deviations for individual glaciers can be considerable. All three models also bias-correct the GCMs to align closely with the reanalysis dataset utilized during calibration by matching temperature (mean and standard deviation) and precipitation (mean) over a historical period (see, e.g., Zekollari et al., 2019). Below we describe the key features of each glacier model; for further details, we refer readers to the associated description papers cited above and to Zekollari et al. (2024).

2.1.1 Global Glacier Evolution Model (GloGEM)

GloGEM estimates monthly snow accumulation, snowmelt and ice melt, and refreezing for 10 m elevation bands on each glacier. Glacier dynamics are modeled using an empirical relation that describes ice thickness change as a function of the normalized elevation range (Huss and Hock, 2015). The model is forced with ERA5 reanalysis data (Hersbach et al., 2020) and is calibrated in a three-step calibration procedure. The main calibration parameters are the degree-day factors for relation of positive air temperature to melt and a precipitation correction factor that accounts for differences between the reanalysis cell forcing and the actual precipitation on the glacier. All model parameters are calibrated for every glacier individually to match observed glacier-wide mass balances (Hugonnet et al., 2021). The multiplicative precipitation correction is constrained to remain within bounds of approximately 1.0 to 2.5. These bounds vary between RGI regions and are chosen such that the misfit of modeled and measured winter balance according to sparse observations obtained from the World Glacier Monitoring Service (Zemp et al., 2023; WGMS, 2024) is minimized. GloGEM employs separate degree-day factors for snow, firn, and ice, scaled by a multiplicative factor to account for their differing melt rates. The reanalysis climate forcing is used until 2020, after which GCM output forces the future evolution. A bias correction between the reanalysis data and future GCMs is applied based on the years 1980 to 2019. The glacier area (geometry) is assumed to be constant until the date associated with the RGI outline, after which the glacier geometry evolves. The constant catchment area for the runoff computation is the RGI v6.0 glacier area in each basin.

2.1.2 Open Global Glacier Model (OGGM) – v1.6.1

OGGM is a modular, open-source, community-based glacier evolution model framework that estimates the monthly mass balance using a temperature index model (Marzeion et al., 2012; Maussion et al., 2019). Glacier dynamics are modeled using the shallow-ice approximation along elevation-band flowlines. The model is calibrated for every glacier individually to match observed glacier-wide mass balances (Hugonnet et al., 2021) when forced with the W5E5v2.0 climate dataset (Lange et al., 2021). The glacier-specific multiplicative precipitation factor is computed from an empirical function of total winter precipitation, leading to smaller factors for glaciers located in wetter grid points and larger factors for drier grid points. This relationship was derived by calibrating the model on 114 glaciers (Schuster et al., 2023a) with in situ winter mass balance data (WGMS, 2024). The local precipitation factor can range from 0.1 to 10, but 90 % of the global values lie between 1.6 and 6.7 (median: 3.6). High precipitation factor values may be partly explained by the fact that W5E5 is drier than ERA5 and that OGGM does not apply a precipitation gradient with elevation like PyGEM or GloGEM. OGGM calibrates a single degree-day factor for temperature index melt estimation, with no surface-type distinction. We analyze the standard OGGM projection option of OGGMv1.6.1 (Maussion et al., 2023), which performs a bias correction between the reanalysis data and each GCM and/or scenario based on 2000–2019. OGGMv1.6.1 uses a dynamic spin-up and calibration routine to initialize glacier states in the year 2000 and ensure that glacier mass balance during the 2000–2019 historical simulation still matches observations taking elevation feedback into account (Aguayo et al., 2023; Zekollari et al., 2024). The spin-up ensures that glacier areas at the inventory date are matched within 1 %. The constant catchment area for the runoff computation is the glacier area in each basin in the year 2000 according to the dynamic spin-up routine and may differ from the RGI. In this study, the GCM forcing is used from 2000 onwards.

2.1.3 Python Glacier Evolution Model (PyGEM)

PyGEM is a modular, open-source, glacier evolution model that estimates the monthly mass balance at ∼ 10 m elevation bins (Rounce et al., 2023). Sub-debris melt enhancement factors are used to account for the enhanced or reduced melting associated with debris thickness for debris-covered glaciers (Rounce et al., 2021). Glacier dynamics are modeled using OGGM's shallow-ice approximation along elevation-band flowlines (OGGMv1.3). The model is calibrated using Bayesian inference (Rounce et al., 2020b, 2023) on observed glacier-wide mass balances (Hugonnet et al., 2021) forced by ERA5 reanalysis data (Lange et al., 2021). Prior distributions for each model parameter are determined at a subregional level based on a three-step calibration procedure for each glacier that constrains the multiplicative precipitation factor between 0.5 and 5. During the Bayesian inference, the multiplicative precipitation factor is not constrained, but the choice of prior distribution ensures positivity. PyGEM uses two degree-day factors to capture snow and ice melt, along with spatially dependent sub-debris melt enhancement factors, enhancing its ability to simulate debris-covered glaciers. The GCM bias correction is performed for the period 2000–2019 and the GCM forcing is used from 2000 onwards. The initial glacier area from the RGI outline is assumed to be at 2000, i.e., unlike the prior two models which used the specific RGI date for each glacier, after which the glacier evolves. The constant catchment area for the runoff computation is the RGI v6.0 glacier area in each basin.

2.1.4 Future climatic forcing

Each glacier model simulated monthly glacier runoff for all RGI glaciers from 2000–2100, forced by an ensemble of single realizations from 12 GCMs and four SSPs of the Coupled Model Intercomparison Project Phase 6 (CMIP6, Eyring et al., 2016). The SSPs include SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5. The 12 GCMs were chosen to be consistent with prior studies (Compagno et al., 2022; Rounce et al., 2023) and included BCC-CSM2-MR, CESM2, CESM2-WACCM, EC-Earth3, EC-Earth3-Veg, FGOALS-f3-L, GFDL-ESM4, INM-CM4-8, INM-CM5-0, MPI-ESM1-2-HR, MRI-ESM2-0, and NorESM2-MM. For consistency, we used the “r1i1p1f1”-tagged ensemble member for each GCM from the CMIP6 archive (see Taylor et al., 2022,  for a description of ripf tags).

2.2 Metrics analyzed

We report annual runoff as the multi-GCM median and quartile values for each glacier evolution model in each basin for each SSP. Our results thus highlight the range and central tendency of projected annual runoff totals for each glacier model for the ensemble of GCMs. We also compare single-glacier-model percent-change runoff projections (i.e., for every glacier model, we divide the annual runoff by the average historical runoff):

$$\begin{array}{}\text{(1)}& {\mathrm{\Delta }}_{\mathit{\%}}Q\left(y\right)={\displaystyle \frac{Q\left(y\right)-\widehat{Q}}{\widehat{Q}}}\times \mathrm{100}\mathit{\%},\end{array}$$

where Q(y) is the single-glacier-model, single-GCM annual runoff in a given year y and $\widehat{Q}$ is the average annual runoff for the same glacier model (and GCM, if applicable) over the historical period (2000–2019). This eliminates baseline differences and allows for a more direct comparison of differences between the models' interannual tendencies.

For both the annual and percent-change runoff projections, we calculated an explicit “multi-GCM range” by computing the spread (maximum – minimum) in single-GCM runoff projections for each year and averaging across the century and then across glacier models for each basin. Similarly, our metric of “multi-glacier-model range” is the spread (maximum – minimum) of the multi-GCM median projections for the three glacier models, averaged across the century for each basin. We note that our 12 forcing GCM realizations are a small sample of more than 250 realizations from the CMIP6 archive, while the three glacier models are the entire population available for global glacier runoff simulation; the expected distribution of glacier runoff for all CMIP6 realizations and all possible glacier model parameter sets is not known. As such, the multi-GCM and multi-glacier-model ranges we present do not give a complete characterization of uncertainties. Rather, we use them to contextualize whether the projections from different glacier models should be interpreted as “similar” in light of typical GCM ensemble uncertainty.

Peak water, i.e., the year of maximum glacier runoff after which runoff declines, is calculated using an 11-year rolling mean (Huss and Hock, 2018). We computed the year of peak water from single-GCM time series and then found the multi-GCM median year for each glacier model and scenario. We also provide GCM, glacier model, and SSP ranges for the year of peak water projections (see Fig. 4). The GCM range (for the year of peak water) is calculated by finding the spread (maximum – minimum) of single-GCM realizations for each glacier model and then taking the median value. We calculated the glacier model range by finding the multi-GCM median year of peak water for each glacier model and then took the range of these three values. The SSP range refers to the range across all glacier models' multi-GCM median peak water projections for all SSPs.

We aggregated the annual on- and off-glacier solid and liquid precipitation totals for each glacier model and basin over the historical period, 2000–2019. We report the mean annual precipitation over that period for each glacier model to highlight differences in how the models process the raw precipitation from the climate forcing. We also calculate inter-glacier-model “relative” runoff and precipitation values. These values take the annual runoff (across the entire period) or annual precipitation (across the historical period) and divide by the mean of all three glacier models' projected annual runoff or historical precipitation. We then calculated the mean by summing the annual values and dividing by the number of years:

$$\begin{array}{}\text{(2)}& \text{Relative}Q={\displaystyle \frac{\mathrm{1}}{\mathrm{100}}}\sum _{y=\mathrm{2000}}^{\mathrm{2099}}{\displaystyle \frac{Q_y}{{\stackrel{\mathrm{‾}}{Q}}_y}},\end{array}$$

where Q_y indicates the single-GCM runoff for a single glacier model in a given year and ${\stackrel{\mathrm{‾}}{Q}}_y$ indicates the multi-glacier-model mean of single-GCM runoff for the same year. Note that we compute these values per GCM and per glacier model and then take a multi-GCM median to arrive at a single value per glacier model for the projected period. Similarly,

$$\begin{array}{}\text{(3)}& \text{Relative}P={\displaystyle \frac{\mathrm{1}}{\mathrm{20}}}\sum _{y=\mathrm{2000}}^{\mathrm{2019}}{\displaystyle \frac{{\text{P}}_y}{{\stackrel{\mathrm{‾}}{P}}_y}},\end{array}$$

where P_y indicates multi-GCM median total precipitation as downscaled and bias-corrected by a single glacier model, summed over the initially glaciated area of the basin, for a year between 2000 and 2019, and ${\stackrel{\mathrm{‾}}{P}}_y$ indicates the multi-glacier-model mean of that quantity. Note that we compute these values for only a single forcing (the calibration dataset of each glacier model) and therefore arrive immediately at a single value per glacier model over the historical period. These metrics quantify how the magnitude of one model's runoff projection or input precipitation compares to the multi-glacier-model mean.

3 Results

3.1 Annual glacier runoff by basin

Across the majority of basins, the three glacier models project similar interannual runoff changes with a noticeable difference in magnitude such that each model's projected runoff appears to be translated up or down relative to the others (Figs. 2 and A1). The glacier model that predicts the most runoff varies by river basin (e.g., Fig. 2), with some regional consistency. OGGM projects the largest amount of glacier runoff across the entire century for nearly all basins located within Alaska, Iceland, the European Alps, central Asia, and the low latitudes. GloGEM projects the largest annual runoff totals for all basins located within northern Asia, the southern Andes, and New Zealand. PyGEM projects the most runoff in Scandinavia. Analyses of climatological and geographical factors (e.g., historical aridity index, mean precipitation, central latitude, mean glacier altitude) did not reveal regionally consistent drivers of inter-glacier-model differences in runoff; we elaborate on two drivers of differences at a global scale in the Discussion section. While the evolution of runoff over the century differs between SSPs, the dependence of annual glacier runoff on SSP appears to be consistent across glacier models. Generally, maritime regions exhibit a more extreme dependence on emission scenarios. In most coastal North American basins (e.g., Yukon, Alsek, and Copper), more severe emission scenarios result in an increase in precipitation and thus an increase in annual runoff across the century (this paper in Fig. 2 and Wimberly, 2024b).

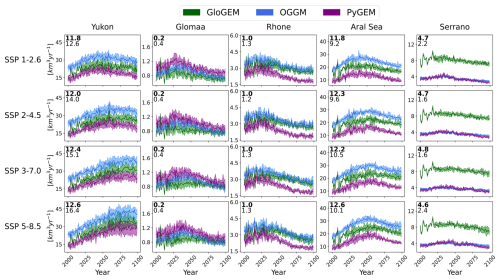
Figure 2 Projected multi-GCM median annual glacier runoff for each glacier model and SSP for selected basins: the Yukon basin (1.2 % initial glacier cover, North America), the Glomaa basin (0.7 %, Europe), the Rhône basin (1.0 % Europe), the Aral Sea basin (0.9 %, Asia), and the Serrano basin (1.1 %, South America). The shaded area shows the interquartile range of the 12 single-GCM projections. Annotations in each panel state the multi-glacier-model range (n=3, bold text) and multi-GCM range (n=12) of projections, both in km³ yr⁻¹, computed following Sect. 2.2. These basins were selected to sample the range of regions in which glacier models project more or less absolute runoff.

During the historical period (2000–2019), GloGEM outputs forced by only the ERA5 reanalysis are highly variable, while OGGM and PyGEM forced by GCM output produce smoother median projections with an inter-GCM range (e.g., Serrano basin in Fig. 2). The modeler choice to simulate the historical period with climate reanalysis (as in GloGEM) or bias-corrected GCM output (as in OGGM or PyGEM) affects the range in the baseline for future runoff projections.

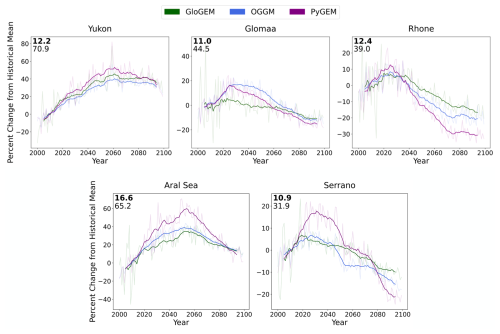
Figure 3 Smoothed (11-year rolling mean) annual multi-GCM median glacier runoff projections as a percent change relative to the historical (2000–2019) average under SSP2-4.5. The multi-glacier-model range and multi-GCM range are given as in Fig. 2 but in units of percent.

The inter-glacier-model range in annual runoff is comparable to inter-GCM range in most basins (“glacier model range” and “GCM range” annotations, Fig. 2). For the Yukon, Glomaa, and Rhône basin, the inter-GCM ranges are slightly larger than the inter-glacier-model ranges. By contrast, the glacier model ranges are larger than the inter-GCM ranges in the Aral Sea and Serrano river basins, where the range in historical baseline runoff is also large.

Normalizing runoff as a percent change relative to the model's historical mean dramatically reduces the range in glacier model projections (Fig. 3). While the Yukon basin's glacier model range was comparable to its GCM range, the normalized glacier model range was one-seventh of the normalized GCM range. Even more drastically, the Serrano basin's projections have a glacier model range 3 times the GCM range, but normalization decreases the inter-glacier-model range to one-third the GCM range. Beyond significantly reducing inter-glacier-model uncertainty, normalization allows for a more direct visual comparison of differences in glacier model tendencies. For example, Fig. 3 reveals that PyGEM runoff decreases much more rapidly from its projected year of peak water than the other two glacier models in the Aral Sea, Serrano, and Rhône basins. We present both absolute and normalized examples here to illustrate their differences; we encourage those interested in a particular region to carefully study runoff series of both types (see Sect. 4 as well).

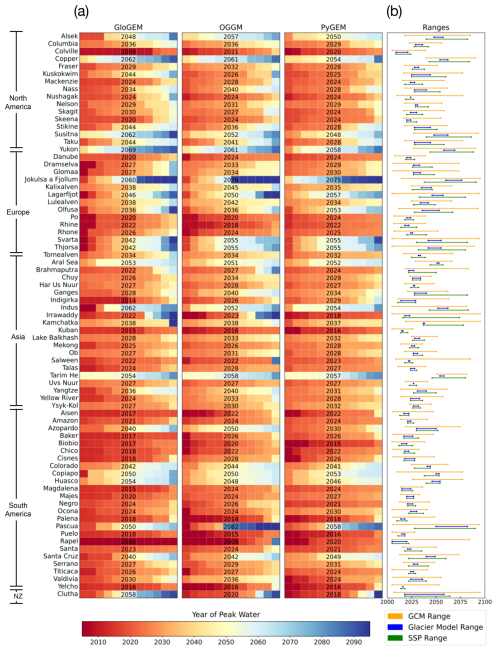
Figure 4 Panel (a) shows the projected peak water year for all 75 basins (rows) for each GCM (columns) and glacier model (panels) for SSP2-4.5. The GCMs (i.e., pixels) are ordered by ascending year of peak water, which varies across basins and glacier models (i.e., the first pixel in the first row is not necessarily the same GCM as the first pixel in the second row or the first pixel in the first row of the second panel). The black text laid over the pixels gives the multi-GCM median year of peak water. Panel (b) depicts the inter-GCM (n=12 at SSP2-4.5), inter-glacier-model (n=3 at SSP2-4.5), and inter-SSP (n=4) range of the year of peak water.

3.2 Timing of peak water

In most basins, the projected year of peak water is similar across glacier models (Figs. 4 and A1). Generally, the inter-glacier-model range is minimal compared to the inter-GCM range (Fig. 4b). For SSP2-4.5, the median (across all basins) inter-GCM range is 40 years, while the median inter-glacier-model range is 6 years. However, the timing of peak water does vary considerably between glacier models for a few basins (e.g., Clutha basin; see Fig. A1). These differences primarily appear in basins with minimal runoff variability over time; i.e., projected runoff is more or less constant over the century. In such basins, the year of peak water is predominantly determined by any shorter-timescale fluctuations that persist through the smoothing process of the rolling mean analysis. Thus, these peak water estimates are determined primarily by GCM variability and have a high degree of uncertainty.

Basins that have already passed observed peak water may nevertheless show an early-century year of peak water in the projections. This discrepancy arises because glacier models are initialized under the assumption of equilibrium, whereas many glaciers are far from equilibrium. As a result, runoff may exhibit an artificial peak at the beginning of the simulation that does not align with real-world observations. The Skagit River basin, which is well past peak water based on observations, highlights this limitation in our simulated peak water years (Riedel and Larrabee, 2016; Pelto et al., 2022).

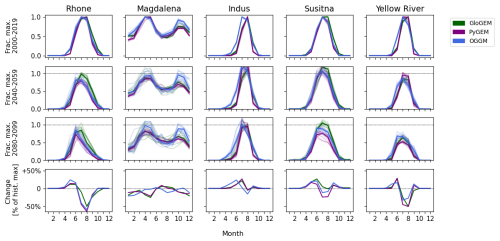
Figure 5 Variability in relative monthly glacier runoff for each glacier model for five example basins over 2000–2019 (top row), 2040–2059 (second row), and 2080–2099 (third row), as well as the change between the beginning-of-century and end-of-century periods (bottom row). Monthly glacier runoff for 2000–2019 and 2080–2099 is normalized by the maximum monthly runoff over the 2000–2019 period, computed for each glacier model and GCM individually. The percent change over the two time periods is expressed as a percentage of the 2000–2019 maximum monthly runoff, shown only for the multi-GCM median. Heavier lines show the multi-GCM median for each glacier model; light lines show individual GCMs. Results for all basins are shown in Figs. A2–A3.

3.3 Seasonality

In most basins, all three glacier models show the seasonal glacier runoff peak shifting earlier by the end of the century (Figs. 5 and A3). GloGEM tends to maintain wider, less defined peaks, i.e., more months with a high fraction of maximum monthly runoff, while OGGM and PyGEM have narrower seasonal peaks at the end of the century compared with 2000–2019 (Fig. A2). The shift in the timing of glacier runoff is highly affected by the variability in GCMs as the spread associated with individual GCMs is considerably wider at the end of the century relative to the start of the century (Fig. 5).

Future changes in seasonal cycle show some differences across different climate regions. Many basins in the midlatitudes of North America, South America, and Europe tend to show some months of increasing runoff and some decreasing, consistent with a change in shape of the seasonal peak (e.g., Rhône, Fig. 5). By contrast, basins in tropical South America have a weaker seasonal cycle overall, consistent with a tropical climate, and show relatively small changes in monthly runoff (e.g., Magdalena, Fig. 5). A few basins in arid central Asia (e.g., Indus, Tarim He, Aral Sea) and maritime North America (Yukon, Copper, Skagit) show a net increase in magnitude of the seasonal glacier runoff peak in most simulations (Figs. 5 and A2). Annual runoff projections for these basins peak in the mid-century to late century and do not diminish much afterward (Fig. A1).

In several heavily populated Asian basins (Yellow River, Yangtze, Brahmaputra, Ganges, Indigirka, Salween, Mekong) all three glacier models project the magnitude of the seasonal runoff peak to substantially decrease by the end of the century (Figs. 5 and A2). Annual peak water in these basins occurs at the start of the century (Fig. A1). As such, the 2000–2019 reference period is likely on the ascending branch of the peak water curve, while the end of the century is far past the peak, when melt-season runoff has tapered off (Huss and Hock, 2018).

There are several basins where one of the three glacier models projects a net increase in the seasonal runoff peak (e.g., Susitna, Colville, Nushagak, Dramselva, Irrawaddy, Santa, Majes, Ocona) while the others project a decrease; across those basins, it is not consistent which glacier model projects an increase and which models project a decrease. The glacier model that projects an increase in seasonal runoff is also not necessarily the glacier model that projects the highest absolute runoff. For example, GloGEM is the only glacier model that projects an increase in monthly runoff for the Susitna basin (Fig. 5), but its end-of-century annual runoff is similar to OGGM. Likewise, PyGEM projects the greatest net increase in monthly runoff across multiple months for the Jokulsa a Fjollum but projects the lowest absolute runoff at the end of the century for that basin (Figs. A1–A2). Projections of seasonal change in such basins may benefit from a more detailed regional study using a multi-glacier-model ensemble and validating against historical observations where available.

4 Discussion

We have found that different metrics of future glacier runoff – absolute annual runoff, runoff change from a historical baseline, year of peak water, and change in seasonal runoff distribution – have different dominant sources of uncertainty in 21st century projections. While the multi-GCM and multi-glacier-model ranges have statistical limitations, comparing them to each other indicates whether glacier models produce broadly similar projections (Sect. 2.2). Absolute annual runoff projections are at least as affected by the choice of glacier model as by the choice of forcing GCM. For 29 of the 75 examined basins, the inter-glacier-model range in annual runoff is larger than the inter-GCM range (Figs. 2 and A1). For the remaining 46 basins the inter-glacier-model range is relatively comparable to the inter-GCM range.

Glacier models have generally been calibrated using single-glacier mass change observations from global datasets (Hugonnet et al., 2021) rather than local or regional-scale glacier runoff metrics. Runoff has been a variable of secondary interest to model development focused on glacier contributions to sea level (e.g., Hock et al., 2019; Marzeion et al., 2020); further, local- and regional-scale runoff data are too limited to permit their use in global model calibration (van Tiel et al., 2020b). The scarcity of historical observations of glacier change and the different approaches to initialization in each glacier model lead to wide spread in model initial conditions that persist in the future projections (Eis et al., 2019; Schuster et al., 2023a; Aguayo et al., 2023). Expressing projections as a percent difference from a historical baseline – where the baseline may be different for each model – corrects this spread in initial conditions and makes the future changes more consistent across glacier models (Fig. 3). Studies using glacier runoff projections should account for the wide spread in glacier model initial conditions, for example by analyzing percent change rather than absolute runoff or by calibrating new regional model runs with additional observations (such as winter accumulation) that are not globally available.

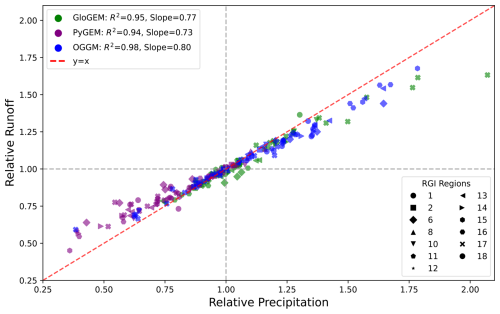
Figure 6 Relative average annual runoff (2000–2099) for SSP2-4.5 vs. relative average (annual) historical (2000–2019) precipitation. The above values are made “relative” by dividing the multi-GCM median annual runoff (or average historical precipitation) by the mean of all three glacier models and averaging across the period such that, if one model projects 20 % more runoff than the mean of all three models, its relative runoff value is 1.2 (see Sect. 2.2) The slopes of our calculated regression lines and the corresponding correlation coefficients are provided for each glacier model. The RGI region, within which the given basin resides, is indicated by the shape of the marker.

Variability in glacier runoff projections between glacier models and GCMs is driven by differences in temperature (i.e., melt) and solid and liquid precipitation. While the future climate data were consistent across the glacier models, the models varied in the reference climate datasets used to bias-correct the future climate data, as well as the calibration framework used to estimate the degree-day factors, temperature biases, and precipitation factors (Sect. 2.1). We thus evaluate the relation between projected glacier runoff and precipitation over the historical period, since the latter captures both the reference climate data and adjustments caused by the calibrated precipitation factors. We find that the extent to which one glacier model projects more or less runoff than the others for a given basin is directly related to its precipitation adjustment (Fig. 6) and the area over which precipitation is summed for runoff. Further, the linear correlation explicitly shows that the inter-model offsets in the magnitudes of projected runoff (Fig. 2) are driven by modeler decisions related to the reference climate data and calibration frameworks used. However, though the relation is clearly linear, the slopes of the regression lines are all less than 1. This indicates that while increasing precipitation will increase runoff, runoff is also affected by the amount of melt occurring. The melt in turn depends on additional calibrated model parameters (degree-day factors and temperature biases) and the implementation of the surface-type-dependent melt parameterization (Schuster et al., 2023a; and see Methods above) as well as the air temperature forcing. For example, Schuster et al. (2023a) found slightly larger projected runoff when surface-type distinction was not used and smaller runoff when monthly temperature data, instead of superimposed daily data, were applied (OGGM vs. PyGEM and GloGEM, which use both surface-type distinction and superimposed daily data). Differences in model adjusted precipitation are further amplified or reduced by secondary variables. Notably, differences in a basin's initially glaciated area (apparent from Appendix Table A1) would result in differing input precipitation totals even prior to glacier model calibration. Such differences may arise due to slight discrepancies in the number of glaciers simulated by each model in a given basin (Appendix Table A1) or as a result of OGGM's dynamic spin-up routine for initial area (as contrasted with GloGEM and PyGEM's use of the RGI outline; Sect. 2.1).

Projections of peak water year vary across single GCMs – in some cases spanning the entire 21st century – but are consistent across glacier models for each basin (Fig. 4). Indeed, the century-wide range in peak water projections between GCMs suggests that single-GCM simulations cannot be trusted to accurately project peak water years (Fig. 4). Further, the influence of GCM on runoff varies by basin; i.e., there is no single GCM with consistently earlier or later peak water years than the others, which makes it difficult to interpret single-GCM results in isolation. Users interested in the timing of peak water could use any one of the three glacier models for projections but should be sure to use the full ensemble of simulations forced by different GCMs.

The sensitivity of peak water year to future warming scenario is consistent across GCMs and glacier models but not consistent across basins. Where peak water occurs early in the century, runoff declines after the peak in every scenario. In basins where peak water occurs later, the timing of peak water depends more clearly on SSP scenario (see Figs. 4b and A4). Basins with later peak water tend to be more heavily glaciated (not shown) and/or in regions that receive more precipitation (e.g., Copper, Yukon, Indus). In those basins, increasing future warming may melt more ice later in the century as well as altering precipitation trends. Both phenomena would serve to push the peak water year later in the century with increasing radiative forcing, which produces the apparent sensitivity of peak water year to SSP scenario (Fig. A4). Although our study did not analyze runoff components due to data limitations, the partitioning of runoff into glacier wastage or “excess melt”, equilibrium ice melt, seasonal snowmelt, and precipitation could support additional insights into peak water year sensitivity to SSP scenario. For example, Rounce et al. (2020a) found that basins with large excess meltwater signals (e.g., Amu Darya, Indus, and Tarim) had a later-century peak water whose timing was sensitive to SSP scenario. Moore et al. (2020) found that for several smaller Canadian basins, excess melt had already passed its peak in 2019 and that observed streamflow was already below what would be expected if glaciers were in equilibrium. The latter study emphasizes the need for glaciohydrological modeling studies with evolving glacier cover.

Runoff seasonality changes in a globally consistent way across all three glacier models, with seasonal runoff peaks shifting earlier and decreasing in magnitude in most basins (Figs. 5 and A2–A3). Seasonality of simulated runoff is controlled by the temperature downscaled to the glacier sites as well as by the partitioning between solid and liquid precipitation. Each glacier model uses different methods for those tasks, which we expect to produce some slight differences among their projections. In the basins with apparent differences in multi-GCM median seasonal runoff, we note that GloGEM tends to maintain wider seasonal peaks toward the end of the century (e.g., Columbia through Yukon panels of Fig. A2). OGGM tends to maintain the strongest seasonal peaks – i.e., monthly runoff in the peak month that is closest to the historical maximum monthly runoff (e.g., Colville, Indigirka, Balkhash, Mekong, Amazon, Ocona, and Titicaca basins in Fig. A2). PyGEM tends to project the strongest percent change in runoff distribution (Fig. A3), which is consistent with PyGEM's historical baseline values being the lowest in many basins (Fig. A1): the same absolute change in monthly runoff will be a larger percentage of a small baseline value. These slight differences in seasonality may reflect differences among the models in the underlying components of runoff (ice melt, snowmelt, liquid precipitation), all of which have distinct seasonal curves; a detailed analysis of hydrological components could guide basin-level seasonal runoff projections. However, despite these small differences, we emphasize the broad similarity across glacier models in projected seasonal runoff decreasing and shifting earlier in the year.

In both arid central Asia and maritime North America, there are several basins where all three models project increases in the magnitude of the seasonal runoff peak at the end of the century (Sect. 3.3 and Fig. A2). Both regions are projected to see increased winter (December–February) precipitation (Lee et al., 2021); if the magnitude of the seasonal runoff peak depends most strongly on winter snow accumulation, increased snowfall could drive a larger seasonal runoff peak in both regions. Another possible driver would be stronger seasonal melting in both regions due to summer warming in glaciated areas that were previously close to the freezing point; the seasonal warming signals in the CMIP6 projections are not robust in these regions (Lee et al., 2021), so further regional analysis would be needed to confirm that possibility. An analysis of projected solid versus liquid precipitation in each basin – not pursued here due to data limitations – would also clarify the regional dynamics contributing to projected increases in seasonal runoff.

Although the runoff projections from different glacier models have large offsets in absolute annual runoff, the same projections expressed in relative terms – percent change from a historical baseline – exhibit strongly reduced offsets (Figs. 2–3). The temporal pattern of runoff increase, peak water, and subsequent runoff decrease in each basin is similar for all three glacier models; as a result, the year of peak water and its response to increasing climate warming have little glacier model uncertainty (Figs. 4 and A1). Future changes in runoff seasonality also show similarities in basins with similar peak water years (Sect. 3.3). Thus, although peak water is limited to a very general description of glacier runoff, which does not account for broader basin hydrology or within-basin differences among glaciers, we believe that the year of peak water, with its consistency across glacier models, can serve as a helpful heuristic for other runoff metrics.

We emphasize that the results we present are a sample of 12 GCM realizations per scenario, selected from the more than 250 plausible realizations from the CMIP6 archive. Our results thus likely under-sample the true uncertainty arising from CMIP6 projections. All GCMs struggle to represent precipitation processes, particularly in areas of high relief typical of glaciated basins (Douville et al., 2021). In addition, the spread in surface air temperature among GCM realizations, which we have not quantified here, will produce differences in melt and in how much precipitation falls as solid or liquid phase, and that will affect both the magnitude and timing of glacier runoff. As such, there is a high likelihood of systematic biases in the GCM forcing that cannot be quantified and that are not easily addressed with bias correction (e.g., if bias impacts longer-timescale climate variability and change). Those interested in water availability for a specific basin should conduct a regional analysis to select an ensemble of GCMs that best represents precipitation and temperature trends and variability for that basin.

Similarly, the glacier runoff projections we analyze come from the three globally capable glacier evolution models. No other global glacier-centric runoff projections are publicly available, and we do not quantify glacier model parameter uncertainty in any of our results. As such, our results do not map a full probability distribution of future glacier runoff (Aguayo et al., 2023). Glacier models' differing approaches to handling precipitation input have a strong effect on their runoff output (Fig. 6). In a given basin, a glacier model forced with more precipitation during the historical period (due to either the choice of reanalysis data or model calibration) usually also projects more runoff during the 21st century. A multiplicative “precipitation factor” that scales up GCM precipitation will have a corresponding effect on the precipitation component of glacier runoff (Sect. 2.1). The three glacier models also used different climate reanalysis datasets for their bias correction and calibration period (Sect. 2.1.1–2.1.3), but all were calibrated to match the same global glacier mass change dataset (Hugonnet et al., 2021). A glacier model that is calibrated with higher precipitation may therefore also produce higher melt to match the observed mass change (Schuster et al., 2023a), which means that the influence of the precipitation factor is not limited to the first-order precipitation response but that it also has an influence on the partitioning and seasonality of ice melt.

Ultimately, the importance of glacier runoff in a given basin depends on the local hydrology. Glacier runoff may infiltrate to groundwater reservoirs (Somers et al., 2016; Mackay et al., 2020), sustain high-altitude wetlands (López-Moreno et al., 2022), flow through proglacial lakes or streams, evaporate while transiting arid downstream regions (Wang et al., 2013), and encounter human management interventions such as diverting runoff towards agricultural lands, hydroelectric plants, or storage reservoirs. Simulating those dynamics will require coupled glaciohydrological models (Hanus et al., 2024). Ideally, projections of regional water availability will calibrate and apply a coupled glaciohydrological model; however, such models are strongly under-constrained, perhaps even more so than the glacier models we have presented (Somers and McKenzie, 2020; Drenkhan et al., 2023). Without sufficient calibration data, one of the coupled model components may inadvertently be calibrated to overcompensate for the shortcomings of the other. Although we have presented an analysis of glacier runoff in isolation, our work highlights the urgent need for additional observations of mountain hydrology (Somers and McKenzie, 2020) and meteorology (Shahgedanova et al., 2021) to support glaciohydrological simulations.

5 Conclusions

Aggregation of annual runoff series among the three glacier models reveals regionally dependent offsets. The offsets arise from differences in historical baseline conditions for the three glacier models; their effect can be removed by normalizing relative to those conditions to produce percent change in runoff. Remaining differences are the result of different approaches to correcting GCM precipitation across the glacier models, which can only be refined with more complete observations of mountain hydrology. Despite differences in annual runoff, changes in runoff seasonality are qualitatively consistent across glacier models, with most basins' seasonal runoff peaks moving earlier and having lower magnitude than their historical runoff peaks. These robust seasonal shifts could be expected to impact drought risk in mountain areas, though changes in glacial drought buffering were not apparent in an analysis of the standardized precipitation–evapotranspiration index (Ultee et al., 2022). The inter-GCM range in basin peak water year, which is otherwise consistent across glacier models, highlights the need for judicious selection of climate forcings to simulate hydrologic change in glaciated river basins.

Appendix A: Global results – total annual runoff projections

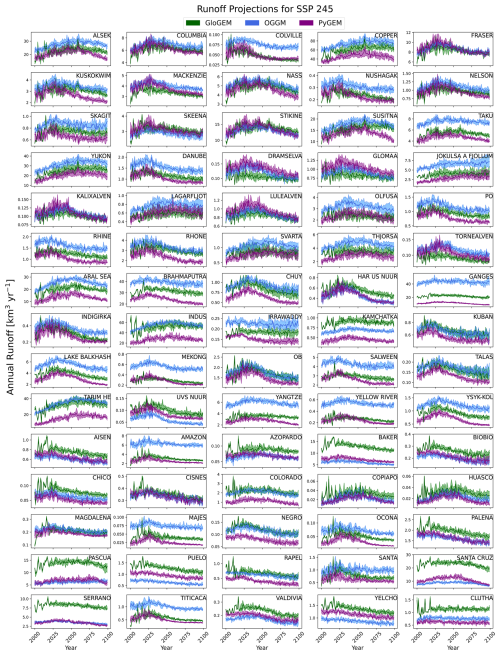
Figure A1 Total annual runoff projections for all 75 glaciated major river basins given in SSP2-4.5. The multi-GCM range is highlighted in the same way as in Fig. 2.

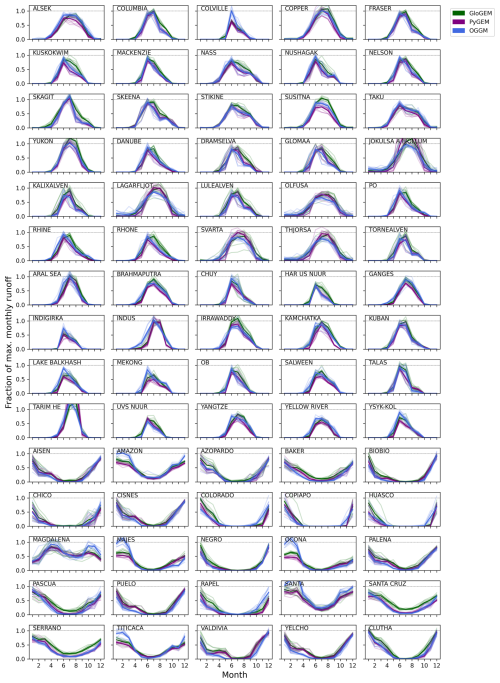
Figure A2 Seasonal cycle of runoff in 2080–2099, expressed as a fraction of maximum monthly runoff during the 2000–2019 baseline period, as in the middle row of Fig. 5, for all basins. Heavier lines show the multi-GCM median for each glacier model; light lines show individual GCMs. Lines that cross the dashed line at 1.0 show a seasonal peak with a higher magnitude than the historical period.

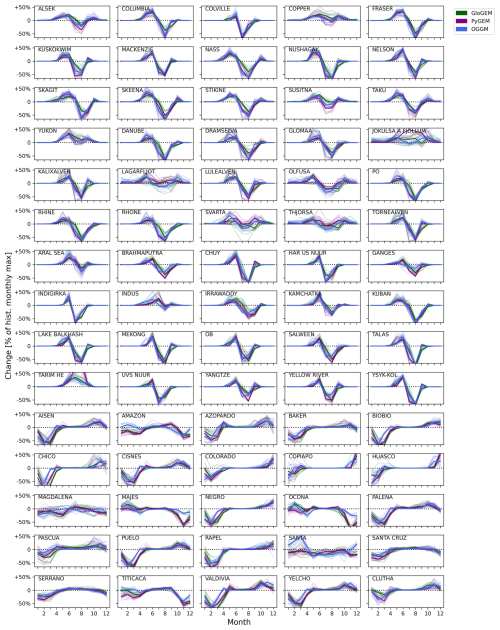
Figure A3 Seasonal shift in runoff from the early century (2000–2019) to late century (2080–2099), as in the bottom row of Fig. 5, for all basins. Shifts are expressed in differences per month as a fraction of historical (2000–2019) maximum monthly runoff for each basin. Heavier lines show the multi-GCM median for each glacier model; light lines show individual GCMs. Positive y-axis values indicate a net increase in that month's runoff at the end of the century compared with the baseline period (2000–2019); negative y-axis values indicate a decrease.

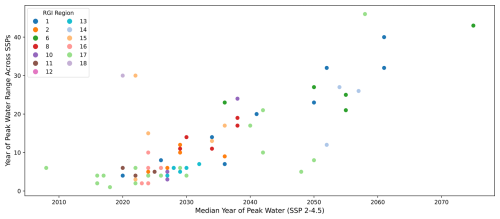
Figure A4 Range of predicted year of peak water across emission scenarios (SSPs) compared to the multi-glacier-model median year of peak water for SSP2-4.5. Points of the same color represent different basins within one RGI region.

Table A1 Initial (year 2000) areas and number of glaciers for each glacier model.