The future of Upernavik Isstrøm through the ISMIP6 framework: sensitivity analysis and Bayesian calibration of ensemble prediction

This study investigates the uncertain future contribution to sea-level rise in response to global warming of Upernavik Isstrøm, a tidewater glacier in Greenland. We analyse multiple sources of uncertainty, including Shared Socioeconomic Pathways (SSPs), climate models (global and regional), ice–ocean interactions, and ice sheet model (ISM) parameters. We use weighting methods based on spatio-temporal velocity and elevation data to reduce ice flow model uncertainty and evaluate their ability to prevent overconfidence. Our developed initialization method demonstrates the capability of Elmer/Ice to accurately replicate the hindcast mass loss of Upernavik Isstrøm. Future mass loss predictions in 2100 range from a contribution to sea-level rise from 1.5 to 7.2 mm, with an already committed sea-level contribution projection from 0.6 to 1.3 mm. At the end of the century, SSP-related uncertainty constitutes the predominant component of total uncertainty, accounting for 40 %, while uncertainty linked to the ISM represents 15 % of the overall uncertainty. We find that calibration does not reduce uncertainty in the future mass loss between today and 2100 (+2 %) but significantly reduces uncertainty in the hindcast mass loss between 1985 and 2015 (−32 % to −61 % depending on the weighting method). Combining calibration of the ice sheet model with SSP weighting yields uncertainty reductions in future mass loss in 2050 (−1.5 %) and in 2100 (−32 %).

1 Introduction

The primary cause of present-day sea-level change is human-induced climate change, which will have far-reaching effects on coastal communities worldwide. To make informed decisions on protective measures, it is crucial to understand the extent and timing of sea-level rise. Predicting future local sea-level rise is a challenging task as it depends on many factors, such as the mean sea-level rise (SLR); ocean dynamics; local context; and, of course, future mitigation of greenhouse gas emissions (Durand et al., 2022). As an important component of the local solution, it is essential to predict future mean sea-level rise for the end of the 21st century. As recent assessments by the Intergovernmental Panel on Climate Change have highlighted (Masson-Delmotte et al., 2021), future sea-level change is highly uncertain, especially the high-end scenarios. The main source of uncertainty in SLR stems from the constrained ability to model the future mass loss of the Antarctic Ice Sheet (AIS) and Greenland Ice Sheet (GrIS) due to limited understanding of their climate forcings and initial state, as well as uncertainties in ice sheet models (ISMs) (Goelzer et al., 2018; Seroussi et al., 2019; Goelzer et al., 2020; Seroussi et al., 2020).

To better understand uncertainties and enhance projections of the two ice sheets, a collective initiative has emerged: the Ice Sheet Model Intercomparison Project for CMIP6 (ISMIP6) framework (Nowicki et al., 2020). The outcomes of this endeavour have provided valuable insights into the behaviour of ISMs and the range of their variability. However, to improve estimates for decision-makers, Aschwanden et al. (2021) suggest two key areas of improvement. First, although ISMIP6 quantifies uncertainty in model structure, the intrinsic uncertainties associated with model parameters, as well as initial and boundary conditions, must be more thoroughly accounted for. Second, simulations should accurately reflect current observations within the limits of their uncertainty.

In addition to providing a more comprehensive quantification of uncertainties, sensitivity analyses play a crucial role in classifying uncertainties and prioritizing their reduction. This approach has gained popularity in glaciology, as evident in case studies conducted with a single ISM in Antarctica (Bulthuis et al., 2019; Hill et al., 2021) and Greenland (Aschwanden et al., 2019), as well as the ISMIP6 analyses (Goelzer et al., 2020; Seroussi et al., 2020, 2023), which also facilitate the examination of model structure uncertainty through multiple ISMs. The first two individual ISM studies revealed that the dominant origins of uncertainty were atmospheric forcings for Greenland and oceanic forcings for Antarctica. The ISMIP6 outcomes, in contrast, emphasize that uncertainties linked to ISMs persist significantly, akin to uncertainties originating from forcings and their application. These findings underscore the potential for reducing uncertainty in model projection by reconciling the differences among ISMs. In this regard, a better use of observational data to calibrate these models and ensure their skill in reproducing recent data holds promise (Aschwanden and Brinkerhoff, 2022; Nias et al., 2023).

Bayesian calibration using observations has become a common practice in glaciology, as is evident in previous studies on the SLR contribution of the GrIS (Applegate et al., 2012; McNeall et al., 2013; Chang et al., 2014; Aschwanden and Brinkerhoff, 2022; Nias et al., 2023), the AIS (Gladstone et al., 2012; Ritz et al., 2015; DeConto and Pollard, 2016; Nias et al., 2019; Gilford et al., 2020; Wernecke et al., 2020), or likewise the mountain glaciers (Rounce et al., 2023), and a review of previous studies is given in the supplementary material of Aschwanden and Brinkerhoff (2022). These studies typically involve two steps: (i) establishing prior distributions over uncertain model parameters to obtain an ensemble and projecting it into the future to forecast a prior future SLR contribution and (ii) adjusting prior distributions by giving weights to the members according to their ability to reproduce past observations. However, due to the limited availability of observational data, these studies often employ all available observational data for calibration without incorporating any form of validation to assess the improved performance of the calibrated ensemble compared to the non-calibrated one. This gives rise to concerns regarding the potential for overfitting and excessive confidence in future predictions of sea-level rise, especially in the context of a dataset of considerable size like ours.

In a previous study (Jager et al., 2024), the focus was directed towards investigating the ability of the ISM Elmer/Ice to replicate past variations in Upernavik Isstrøm (UI) during the period from 1985 to 2019. UI is a tidewater glacier situated in the northwest sector of Greenland and is characterized by four distinct catchments: UI-N, UI-C, UI-S, and UI-SS (Fig. 1), as named in Mouginot et al. (2019). The diverse dynamics of their front enable multiple tidewater glacier studies to be conducted within this comprehensive catchment. This approach mitigates the risk of over-interpretation that may arise when focusing on a single tidewater glacier, providing more robust results; i.e. if the model successfully reproduces these varied behaviours, it is likely to do so for other tidewater glaciers as well. Moreover, UI has experienced substantial mass loss since 1985, contributing to 0.47 mm of sea-level rise, more than 3 % of Greenland's total contribution during this period, indicating significant temporal changes (Mouginot et al., 2019). The extensive satellite observations spanning 1985 to 2019 make UI an ideal candidate for evaluating the ability of a large-scale ISM to reproduce available observations of a local glacier. Furthermore, the pronounced spatial and temporal heterogeneity of this case study helps prevent unwarranted overconfidence in the model's performance.

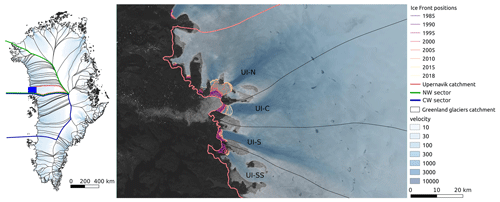
Figure 1 Left: GrIS drainage catchments with the catchment of UI in pale red, northwest (NW) in green, and central-west (CW) in blue as defined in Slater et al. (2019). The blue box is the validation area shown on the right. Right: the four different catchments (UI-N, UI-C, UI-S, and UI-SS), the front positions between 1985 and 2018 (Wood et al., 2021), and the surface ice speed (Mouginot et al., 2019) overlaid on a Landsat image (13 August 2017). All the data collected are from within this validation area.

To reproduce past changes in UI using Elmer/Ice, Jager et al. (2024) introduced a new initialization method employing a model ensemble that incorporates various uncertainties within the ISM, including different basal friction field calibrations, initial surface elevation, and model parameters. Additionally, the front positions and surface mass balance (SMB) were prescribed for each year. Subsequently, the performance of two ensembles, using two different basal friction relationships, was compared against a comprehensive dataset comprising spatio-temporal series of velocities and elevations, ice discharge, and mass loss. Jager et al. (2024) indicate the necessity of accounting for a reduction in friction near the glacier front to accurately reproduce these observational data. The sensitivity analysis, made possible by the ensemble approach, underscored the predominant role of the initial friction field compared to the initial surface or surface mass balance in shaping the hindcast variations in ice mass loss.

The objective of this study is to assess UI's contribution to SLR throughout the 21st century and to enhance the quantification of associated uncertainties. The following aspects will be addressed:

1. a sensitivity analysis to project the future SLR contribution and quantify the contribution of the ISM and forcings to the forecast uncertainty

2. a Bayesian calibration to robustly adjust prior information using available observations.

To address the first question, we adopt the ISMIP6 framework for the GrIS (Nowicki et al., 2020). The forcings for the future are an SMB and a parameterization for the position of the glacier fronts. The SMB is derived from a regional climate model (RCM) that downscales outputs from an atmosphere–ocean general circulation model (AOGCM) associated with a specific Shared Socioeconomic Pathway (SSP). Future front positions are estimated using a parameterization that incorporates RCM runoff and AOGCM ocean temperatures as input variables while allowing for consideration of different front-retreat sensitivities. By incorporating uncertainties associated with RCMs, AOGCMs, SSPs, front-retreat sensitivities, and the ISM itself, this approach enables a comprehensive analysis of the impacts of these various sources of uncertainty in SLR. Additionally, it quantifies the potential reduction in uncertainty attributable to the ISM.

To address the second aspect, we propose several weighting methods and have designed a rigorous cross-validation approach to ensure robust calibration of the model ensemble. The validation process assesses the performance of the calibrated ensemble against independent data. Additionally, we investigate the sensitivity of the calibration to different assumptions, evaluating calibration performance through the validation procedure. Once the optimal calibration has been determined, we analyse the implications of this calibration for the selection of model parameters and its impact on SLR predictions. We also study the reduction potential when we change the weighting of the SSPs used.

2 Method

2.1 Model ensemble

In this sub-section, we delineate the methodology employed for initializing and propagating the ensemble into the future, utilizing a single ice sheet model (ISM) and following a framework akin to the ISMIP6 framework for the GrIS (Nowicki et al., 2020). Figure 2 summarize our workflow, which is described as follows:

1. The shared hindcast prior ensemble (Hpr) covers the period from 1985 to 2019 following the methodology of Jager et al. (2024) and serves as a starting point for the two other ensembles.

2. The control prior ensemble (Cpr) extends the ISM into the future from 2015 to 2100 with constant forcing.

3. The predicted prior ensemble (Ppr) extends the ISM into the future from 2015 to 2100 with realistic forcing.

For the ISM we use Elmer/Ice, which is a parallel finite-element model (Gagliardini et al., 2013). Several sources of uncertainty were identified within the ISM, and based on the findings from our prior study (Jager et al., 2024), we have exclusively retained those parameters that exert a substantial influence, employing factor fixing. Parameters leading to undesirable model outputs, when compared to observational data, were excluded through factor mapping. Factor fixing, also known as screening, serves to pinpoint model components that have a minimal impact on either the variability in the outputs or the metrics of interest. Conversely, factor mapping is employed to ascertain which uncertain model factors correlate with specific model behaviours (refer to the glossary in Reed et al., 2022). Additional information regarding the model characteristics and parameter selection is available in Appendix A and C1, respectively.

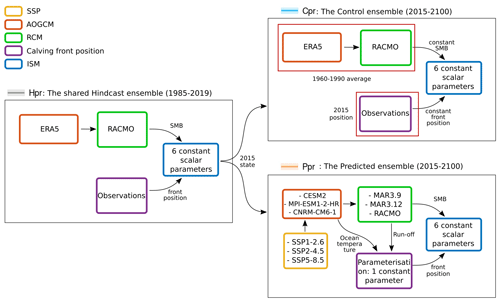
Figure 2 Ensemble model and sensitivity analysis. Illustration of the forcings (surface mass balance, front position) used by the three ensembles: Hpr, Cpr, and Ppr. SSP: Shared Socioeconomic Pathway; AOGCM: atmosphere–ocean general circulation model; RCM: regional climate model; ISM: ice sheet model.

Finally, the ISM uncertainty depends on six constant scalar parameters (Fig. 2), with two parameters influencing the calibration of the friction field (λ_reg and OBS_inv), three parameters influencing the friction law (f_law, f_param, and m), and one parameter influencing the ice rheology (E). See Appendix A to understand what the ISM parameters are.

2.1.1 Shared hindcast prior ensemble (1985–2019)

The ensemble is initialized in 1985 and covers the observational period.

The SMB is prescribed using annual values from the regional climate model RACMO forced with the global reanalysis ERA5 (Noël et al., 2018). Our previous study showed that using RACMO as a regional climate model instead of MAR led to better performance in reproducing the observed surface elevations while having a small influence on the other model outputs. Here, using only RACMO, we improve the overall performance of the ensemble and restrict the parameter space to better cover the other sources of uncertainty.

The position of the UI calving fronts is prescribed at each time step based on observations (Wood et al., 2021). Given that the uncertainty associated with these observations is small compared to the model mesh size (less than 60 m versus more than 150 m), we do not account for this potential forcing uncertainty during the shared hindcast period. The state of the ensemble members in 2015 is used as a starting point for the next two ensembles that cover the period 2015 to 2100.

2.1.2 Control prior ensemble (2015–2100)

Cpr is a control ensemble where the forcings are kept constant.

The SMB is the average of RACMO between 1960 and 1990 to be consistent with the anomaly procedure for the forecast (see below).

The position of the front is kept constant using the observation in 2015.

2.1.3 Predicted prior ensemble (2015–2100)

For the SMB, we adopt the ISMIP6 framework for the GrIS (Nowicki et al., 2020; Goelzer et al., 2020). This approach employs a RCM to downscale an AOGCM associated with a specific SSP at the GrIS scale. These results are then prescribed as anomalies which are added to the reference SMB used for Cpr. The procedure also parameterizes the feedback with the elevation by proving the SMB altitudinal gradients. The various combinations of SSP–AOGCM–RCM are presented in Table 1. As an initial approach, we assign different probabilities to the various SSP–AOGCM–RCM combinations (Table 1) to mitigate potential biases arising from the over-representation of specific SSPs ($\mathrm{7}/\mathrm{24}$, $\mathrm{8}/\mathrm{24}$, and $\mathrm{9}/\mathrm{24}$ for SSP1-2.6, SSP2-4.5, and SSP5-8.5) while trying to maintain balanced proportions between AOGCMs ($\mathrm{1}/\mathrm{2}$, $\mathrm{1}/\mathrm{4}$, and $\mathrm{1}/\mathrm{4}$ for CESM2, MPI-ESM1-2-HR, and CNRM-CM6-1) and RCMs ($\mathrm{1}/\mathrm{3}$ for each). In Sect. 5, we explore alternative probability distributions for the SSPs.

Table 1 SSP–AOGCM–RCM combinations and their probabilities used in the Latin hypercube sampling.

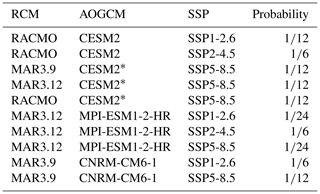
^*For practical purposes, this is the same physical model as CESM2 (CMIP6) but a different ensemble member.

For the future position of the front, we used the ISMIP6 parameterization (Slater et al., 2019, 2020) for which the variation in front position ΔL is given by

$$\begin{array}{}\text{(1)}& \mathrm{\Delta }L=\mathit{\kappa }\mathrm{\Delta }(Q^{\mathrm{0.4}}\times \mathrm{TF}),\end{array}$$

where Q denotes the mean summer (June–July–August) subglacial runoff (in m³ s⁻¹) from the RCM and TF represents the ocean thermal forcing (in °C) outside of the fjord from the AOGCM. κ is the front sensitivity, and it has been calibrated independently for different sectors of the GrIS using available observations (Slater et al., 2019). The distribution of κ effectively encapsulates the uncertainties arising from several critical parameters, e.g. calving rates and thermal transport into the fjord.

To examine the uncertainty associated with the future position of the front, we use six distinct values of κ. UI is located in the northwest (NW) sector, just above the central-west (CW) sector (Fig. 1). Given the distinct sensitivity of these two sectors, both are considered in our analysis to mitigate overconfidence. For the distribution of κ, we adopt three distinct levels: low, medium, and high. Specifically, the low sensitivity encompasses the smallest 25 % of the κ values, medium sensitivity includes the smallest 50 %, and high sensitivity comprises the smallest 75 %. In total, this results in six different κ values (three levels across two sectors), each assigned equal probability. To simplify, the sensitivity of this front parameterization is hereafter referred to as front_s.

2.1.4 Propagation of uncertainty

Having identified the different sources of uncertainty, we proceed to propagate them through the model. To explore the various sources of uncertainty in the three ensembles (Hpr, Cpr, and Ppr), we use a 200-member Latin hypercube sampling technique to cover the 10 different parameters: 6 ISM parameters and 4 for the forcing (SSP, AOGCM, RCM, and front_s). As defined by our set-up, the uncertain parameters of the forcing (SSP, AOGCM, RCM, front_s) do not affect Hpr and Cpr (Fig. 2).

We use the first-order sensitivity indices to analyse the sensitivity of Ppr to the different parameters (Sobol, 2001):

$$\begin{array}{}\text{(2)}& S_i={\displaystyle \frac{\mathrm{Var}\left(E\right[Y\left|X_i\right])}{\mathrm{Var}Y}},\end{array}$$

where Var Y is the variance of an output Y and E[Y|X_i] is the expectation of having Y given the parameter X_i. Here, X_i is 1 of the 10 different parameters. We provide more details on the calculation of these first-order sensitivity indices in Appendix C2.

2.2 Model ensemble evaluation

2.2.1 Observational data

To evaluate the performance of Hpr, we compiled an extensive dataset comprising observations of surface velocity, surface elevation, ice discharge, and ice mass loss. This is summarized in Table 2, and more details on how we obtain these data are provided in Appendix B.

Jager et al. (2024)Jager et al. (2024)Mankoff et al. (2019)King et al. (2018)Mouginot et al. (2019)(Noël et al., 2018)

Table 2 Summary of observation data types and sources.

^* MougniotV2 is described in Appendix B.

2.2.2 Metrics

To evaluate the performance of Hpr, we use several ensemble metrics. The continuous rank probability score (CRPS) measures the accuracy and sharpness (opposite of uncertainty/spread) of the ensemble, where lower values indicate improved alignment between the ensemble mean and observations, as well as similarity between ensemble spread and observational uncertainty. To investigate whether changes in the CRPS result from a reduction in the difference between the ensemble mean and observations, we examine the mean absolute error (MAE) of the ensemble mean. Similarly, to determine whether changes in the CRPS stem from alterations in the ensemble's sharpness, we analyse the spatio-temporal average of the standard deviation (SD) of the ensemble. Ultimately, the RMSE will serve as a metric for assessing the performance of individual ensemble members, allowing us to calibrate the ensemble based on their respective performance.

$$\begin{array}{}\text{(3)}& {\displaystyle }\mathrm{CRPS}={\displaystyle \frac{\mathrm{1}}{n_{\mathrm{obs}}}}\sum _{j=\mathrm{1}}^{n_{\mathrm{obs}}}\underset{\mathbb{R}}{\int }\left(F_{\mathrm{m}}^j\right(Q)-F_{\mathrm{o}}^j(Q){)}^{\mathrm{2}}\mathrm{d}Q,\text{(4)}& {\displaystyle }\mathrm{MAE}={\displaystyle \frac{\mathrm{1}}{n_{\mathrm{obs}}}}\sum _{j=\mathrm{1}}^{n_{\mathrm{obs}}}\left|{\stackrel{\mathrm{‾}}{Q}}_{\mathrm{m}}^j-Q_{\mathrm{o}}^j\right|,\text{(5)}& {\displaystyle }\mathrm{SD}={\displaystyle \frac{\mathrm{1}}{n_{\mathrm{obs}}}}\sum _{j=\mathrm{1}}^{n_{\mathrm{obs}}}\sqrt{{\displaystyle \frac{\mathrm{1}}{n_{\mathrm{m}}}}\sum _{i=\mathrm{1}}^{n_{\mathrm{m}}}{\left(Q_{\mathrm{m},i}^j-{\stackrel{\mathrm{‾}}{Q}}_{\mathrm{m}}^j\right)}^{\mathrm{2}}},\text{(6)}& {\displaystyle }{\mathrm{RMSE}}_i=\sqrt{{\displaystyle \frac{\mathrm{1}}{n_{\mathrm{obs}}}}\sum _{j=\mathrm{1}}^{n_{\mathrm{obs}}}{\left(Q_{\mathrm{o}}^j-Q_{\mathrm{m},i}^j\right)}^{\mathrm{2}}},\end{array}$$

where n_obs is the number of different observations in space and time, n_m is the number of members, Q is a physical quantity (velocity, elevation, ice discharge, change in volume), ${\stackrel{\mathrm{‾}}{Q}}_{\mathrm{m}}$ is the ensemble mean, and F_m(Q) is the cumulative distribution function of the ensemble. The subscript i is associated with the ith member of the ensemble, and the superscript j is associated with the jth observation. As is common for F_o(Q), we use the Heaviside function, where $F_{\mathrm{o}}(Q,Q_{\mathrm{o}})=\mathrm{0}$ for Q<Q_o and $F_{\mathrm{o}}(Q,Q_{\mathrm{o}})=\mathrm{1}$ otherwise, with Q_o being the observation (Brown, 1974; Matheson and Winkler, 1976; Unger, 1985; Hersbach, 2000).

2.3 Bayesian calibration

In the context of ice sheet forecasting, the focus is on predicting the future contribution to global mean sea-level rise (SLR) while leveraging a diverse array of information, including models, observations, and previous studies (see review in the supplementary material of Aschwanden and Brinkerhoff, 2022). In this study, we adopt the formalism introduced by Aschwanden and Brinkerhoff (2022), which updates a model prediction by considering a vector of model parameters M from the parameter space Σ, a collection of untraversed model assumptions ℋ, the evolution of external forcings ℱ, and a set of observations ℬ:

$$\begin{array}{}\text{(7)}& \underset{\text{posterior prediction}}{\underbrace{P\left(\mathrm{SLR}\right|\mathcal{B},\mathcal{H},\mathcal{F})}}=\underset{\mathrm{\Sigma }}{\int }\underset{\text{model prediction}}{\underbrace{P\left(\mathrm{SLR}\right|\mathit{M},\mathcal{H},\mathcal{F})}}\cdot \underset{\text{calibration}}{\underbrace{P\left(\mathit{M}\right|\mathcal{B})}}\mathrm{d}\mathit{M}.\end{array}$$

In the rest of this sub-section, we will describe how the calibration term P(M|ℬ) is obtained from a prior ensemble thanks to the Bayes formula.

2.3.1 Bayesian problem approached by weighted bootstrap

To compute the calibration term P(M|ℬ), we employ an ensemble sampling method named weighted bootstrap (Smith and Gelfand, 1992), which uses an ensemble of n_m particles M_i, corresponding to different members, to approximate the prior probability of the model P(M) by

$$\begin{array}{}\text{(8)}& P\left(\mathit{M}\right)={\displaystyle \frac{\mathrm{1}}{n_{\mathrm{m}}}}\sum _{i=\mathrm{1}}^{n_{\mathrm{m}}}\mathit{\delta }(\mathit{M}-{\mathit{M}}_i),\end{array}$$

where δ is the Dirac function.

The posterior distribution, conditioned by the observations, is approximated by

$$\begin{array}{}\text{(9)}& P\left(\mathit{M}\right|\mathcal{B})=\sum _{i=\mathrm{1}}^{n_{\mathrm{m}}}{w}_i\cdot \mathit{\delta }(\mathit{M}-{\mathit{M}}_i).\end{array}$$

The weight w_i represents the likelihood, i.e. the probability of observing the data for member i, and is therefore higher for members that are the closest to the observations. It is defined as

$$\begin{array}{}\text{(10)}& w_i={\displaystyle \frac{P\left(\mathcal{B}\right|{\mathit{M}}_i)}{\sum _{k=\mathrm{1}}^{n_{\mathrm{m}}}P\left(\mathcal{B}\right|{\mathit{M}}_k)}}.\end{array}$$

Assuming that the n_obs values are independent and that the error is Gaussian with a constant standard deviation, it is possible to express P(ℬ|M_i) as a function of the RMSE as

$$\begin{array}{}\text{(11)}& {\displaystyle }P\left(\mathcal{B}\right|{\mathit{M}}_i)& {\displaystyle }=C\exp \left[-\sum _{j=\mathrm{1}}^{n_{\mathrm{obs}}}{\displaystyle \frac{(Q_{\mathrm{o}}^j-Q_{\mathrm{m},i}^j{)}^{\mathrm{2}}}{\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}}}}\right]\text{(12)}& {\displaystyle }& {\displaystyle }=C\exp \left[-{\displaystyle \frac{n_{\mathrm{obs}}}{\mathrm{2}}}\cdot {\displaystyle \frac{{\mathrm{RMSE}}_i^{\mathrm{2}}}{{\mathit{\sigma }}^{\mathrm{2}}}}\right].\end{array}$$

As these assumptions are difficult to fulfil and verify in practice, we adopt the following expression to compute the weights:

$$\begin{array}{}\text{(13)}& w_i={\displaystyle \frac{\prod _{s=\mathrm{1}}^{n_{\mathrm{s}}}f({\mathrm{RMSE}}_{i,s},\mathit{\sigma })}{\sum _{j=\mathrm{1}}^N\prod _{s=\mathrm{1}}^{n_{\mathrm{s}}}f({\mathrm{RMSE}}_{j,s},\mathit{\sigma })}},\end{array}$$

with f(RMSE,σ) being a probability density function (Gaussian or Student; see below) which depends on the parameter σ that represents both the observation and the model error and n_s being the number of different error metrics (RMSEs) used to compute the performance of the ensemble members.

In our study, Eq. (12) cannot be used directly for three main reasons. First, due to the substantial volume of data at hand, we encounter a challenge similar to that of the particle filter framework, which tends to retain only one member and leads to overfitting (Leeuwen, 2010). To overcome this issue, a number of ensemble members comparable to the number of observations would be necessary. However, achieving such a large ensemble size proves impractical in this case, as the number of observations exceeds 4 million, even with a surrogate model as proposed in Aschwanden and Brinkerhoff (2022). Secondly, the assumption of independent and identically distributed observations is difficult to justify given the strong temporal and spatial correlations of velocities and surface elevations. Higher values observed at one grid point or time step are likely to be similarly high at adjacent locations or subsequent time steps. Thirdly, even supposing observational uncertainties to be independent and identically distributed, it is clear that the modelling errors are not. Ultimately, the crux of the matter lies in our lack of a suitable likelihood function for effective model–data comparison.

Equation (13) uses a performance metric approach to address the challenge of spatial and temporal correlation. The distance between the observed and modelled fields is then only assessed on average using the RMSE, effectively treating the multiple observations as a single observation (Pollard et al., 2016; Bondzio et al., 2018; Albrecht et al., 2020). This method substantially diminishes the influence of observations, thereby mitigating the risk of overfitting while potentially introducing underfitting, as previously identified (Wernecke et al., 2020). This performance metric is applicable across various model outputs, encompassing velocity, surface elevation, ice discharge, and cumulative ice discharge. Furthermore, this metric can be computed for each sub-catchment (UI-N, UI-C, UI-S, and UI-SS, as illustrated in Fig. 1) and, potentially, for distinct sub-periods (as detailed in the sub-period weighting in Sect. 2.3.2). When these n_s metrics are independent (e.g. an RMSE applied to UI-N is quasi-independent of the RMSE applied to UI-C), they can be combined by multiplication, as shown in Eq. (13). These different combinations will be tested for the full-period weighting (Sect. 2.3.2 for the methodology and Sect. 4.1 for the results).

In addition, the challenge of selecting a single member could stem from the restrictive nature of the probability density function f(RMSE,σ) outlined in Eq. (13). This issue may arise from the specific form of f(RMSE,σ) – for example, a Gaussian distribution has lower tails than Student's t distribution, thereby reducing the influence of higher RMSE values – or from the selection of the parameter σ. The parameter σ, which is partially derived from the standard deviation of the observation error as specified in Eq. (12), additionally encompasses the structural errors inherent in the model. The model simplifications of reality hinder an exact representation of the real world, thereby manifesting the discrepancies between the optimized model parameters and empirical observations (Nias et al., 2019; Edwards et al., 2019). However, accurately quantifying structural error remains a persistent challenge, often necessitating retrospective estimation. To mitigate this limitation, we adopt an assumption that leverages the distribution of RMSE values to estimate σ. Specifically, we will evaluate the minimum, median, and maximum RMSE values as potential estimates for σ. This assumption underpins the weighting methodology adopted in earlier studies which employ a singular performance metric; for instance, in Pollard et al. (2016) and Albrecht et al. (2020), the median of such a performance metric is utilized as an estimate for σ. The effect of the choice of σ will be assessed using the full-period weighting, as described in the methodology (Sect. 2.3.2) and presented in the results (Sect. 4.1).

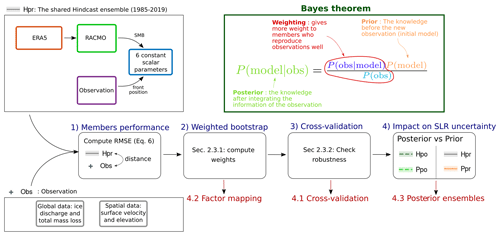
Figure 3 Bayesian calibration (Sect. 2.3). Different steps of our methodology to obtain a robust Bayesian calibration from a hindcast ensemble (Hpr) and observations. Titles in red refer to the sub-sections where the results are presented (Sect. 4), while the remainder relate to the Bayesian calibration method (Sect. 2.3). In the top-right box, a simple explanation of Bayes' theorem (Eq. 9 in the case of weighted bootstrap) with the three main components: in green the posterior model, in red the weighting (Eqs. 10 and 13), and in orange the prior model.

2.3.2 Cross-validation and weighting choices

At the heart of this Bayesian calibration is the calculation of weights (Eq. 13). Several choices are possible for calculating them, as discussed above. To assess the performance of these different choices, we have developed a cross-validation method. This process entails computing weights and calibrating the ensemble using data from three out of the four sub-catchments and subsequently employing the ensemble-based metrics previously defined (CRPS, MAE, and SD) to appraise the performance of the posterior ensemble with respect to the fourth sub-catchment. These metrics are normalized with metrics obtained with the prior ensemble, wherein a value exceeding 1 signifies inferior performance of the posterior ensemble in contrast to the prior ensemble (Hpr), whereas a value of less than 1 signifies enhanced performance.

The evaluation encompasses three distinct weighting approaches:

1. full-period weighting

2. sub-period weighting

3. f_param weighting.

Full-period weighting

In the case of full-period weighting, the weighting of ensemble members depends on their ability to, on average, replicate the temporal evolution of various sub-catchments throughout the entire period from 1985 to 2019. To determine the final weight, we compute the RMSE for each sub-catchment over the entire observation period and then apply Eq. (13) to combine these RMSEs, with n_s being the number of sub-catchments; i.e. n_s=3 for the cross-validation and n_s=4 for posterior ensemble.

In the context of full-period weighting, several assumptions are also examined:

1. The selection of probability density is Gaussian, following Nias et al. (2023), or Student's t, as in Aschwanden and Brinkerhoff (2022).

2. The choice of the σ estimate is the minimum, mean, or median of the RMSE distribution.

3. The choice of data source is surface elevations, surface velocities, ice discharge, or cumulative ice discharge.

Sub-period weighting

In the case of sub-period weighting, the weighting of ensemble members depends on their ability to, on average, replicate the temporal evolution of different sub-catchments across various sub-periods, such as the pre-retreat, retreat, and post-retreat periods. To accomplish this, distinct RMSE values are calculated for each combination of sub-catchment and sub-period. For instance, for UI-N, RMSEs are computed for the periods 1985–2004, 2004–2010, and 2010–2019, while for UI-C, RMSEs are determined for the periods 1985–2009, 2009–2015, and 2015–2019 (see evolution of front in Fig. 1). Conversely, for sub-catchments UI-S and UI-SS, RMSEs are assessed over the entire period. To determine the final weight, we apply Eq. (13) to combine all these RMSEs with, this time, n_s, the total number of periods, i.e. eight for the posterior ensemble (three for UI-N and UI-C, one for UI-S and UI-SS). Similarly to the full-period weighting approach, the assessment of the posterior ensemble through cross-validation employs ensemble metrics spanning the entire period from 1985 to 2019. Because this weighting involves more RMSEs than the full-period weighting (eight versus four), it leads to a narrower posterior distribution.

f_param weighting

This alternative weighting approach was investigated based on insights from our previous study, which demonstrated that the model's ability to reproduce observation data improved significantly when accounting for the reduction in friction near the front (Jager et al., 2024). Indeed, in most of the large-scale applications of Elmer/Ice (e.g. Goelzer et al., 2018; Seroussi et al., 2020; Hill et al., 2023), friction is considered to be constant over time with no dependence on subglacial hydrology. The parameterization developed in this previous study addresses this limitation. This also allows us (i) to see the effect of our parameterization in terms of the predicted future sea-level-rise contribution of Upernavik Isstrøm and (ii) to compare this weighting with the other weightings to see if they are able to highlight this characteristic without going into as much detail as this previous study.

In the case of f_param weighting, the weighting of ensemble members depends on the presence or the absence of the parameterization of the sub-hydrology effect on friction (Eq. A3). We then give a weight of w_i=w for members with parameterization (f_param= true) and a weight $w_i=(\mathrm{1}-w)$ for members without parameterization (f_param= false) and test different values of w (0.6, 0.7, 0.8, 0.9, and 1). Then we evaluate the performance of this ensemble with the CRPS, MAE, and SD for each weighting.

2.3.3 Summary

The main steps of the Bayesian calibration and the sub-sections where the results are discussed are summarized in Fig. 3.

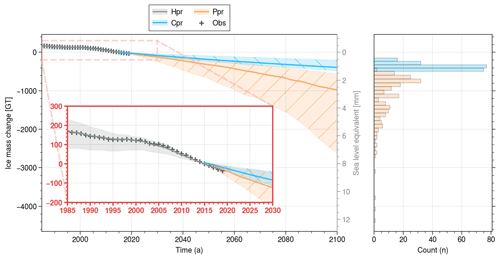
Figure 4 UI ice mass change relative to 2015 for the hindcast (grey), the predicted (orange with /) and the committed mass loss (blue with ∖). For each ensemble, the mean is represented by a solid line and the shading includes 95 % of the ensemble members. Observations of the 1985–2019 period are represented by +. The red box shows a zoomed-in view of the 1985–2030 period. The histogram on the right illustrates the distribution of the predicted (orange) and the committed (blue) mass loss UI contribution to sea-level rise spanning 2015 to 2100.

3 Results: sensitivity analysis

To comprehensively assess the future sea-level-rise contribution of Upernavik Isstrøm in our sensitivity analysis, we begin by projecting the ensemble into the future using the initialization method established in Jager et al. (2024). This initial exploration sets the stage for determining a reference sea-level-rise contribution and understanding the components of Upernavik Isstrøm's mass loss, particularly focusing on ice discharge and surface mass balance. Additionally, it highlights disparities between the predicted prior ensemble (Ppr) and the control prior ensemble (Cpr). Following this, we dissect the uncertainty within the predicted prior ensemble, examining the importance of different sources such as Shared Socioeconomic Pathways (SSPs), atmosphere–ocean general circulation models (AOGCMs), regional climate models (RCMs), frontal sensitivity (front_s), and the ice sheet model (ISM). This analysis underscores the potential of ISM calibration to effectively reduce overall uncertainty.

3.1 Model prediction

In Fig. 4, the ice mass change is depicted relative to 2015 for observations and three simulation ensembles (Fig. 2): the shared hindcast prior ensemble (Hpr), the control prior ensemble (Cpr), and the predicted prior ensemble (Ppr). The figure encompasses the various SSPs for Ppr, and the results for the individual scenarios are given in Fig. S1 in the Supplement.

The shared hindcast prior ensemble (Hpr) yields a median mass loss of 200 Gt between 1985 and 2019, ranging from 100 to 250 Gt (95 % confidence interval). The Hpr median reproduces the observations very faithfully. This result confirms the ability of the methodology established in Jager et al. (2024) to reproduce past observations.

By 2015, UI had already contributed 0.47 [0.23, 0.64] mm to sea-level rise (SLR) since 1985, and the mass loss of Cpr and Ppr is projected to add an additional 1.1 [0.6, 1.3] mm and 2.7 [1.5, 7.2] mm, respectively, by 2100. Notably, the most extreme values of Ppr indicate a contribution to SLR exceeding 10 mm, while the majority of Ppr values range from 1 to 3.5 mm. It is worth noting that the distribution's tail for values above this interval is wider than for values below, which is similar to other results in glaciology studies (e.g. Robel et al., 2019). Finally, the loss of mass due to future warming, given by subtracting Cpr members from Ppr members, gives us an additional contribution to SLR of 1.7 [0.7, 6.3] mm.

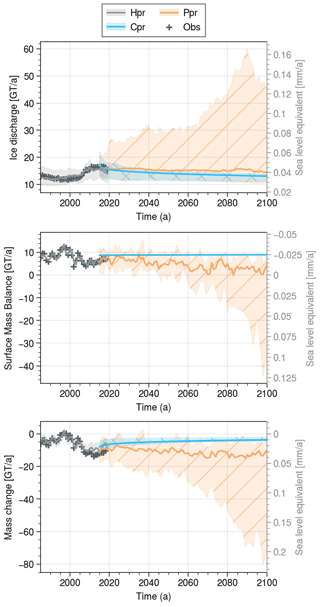
Figure 5 The UI ice discharge and SMB over the period 1985–2100 for the hindcast (grey), the predicted (orange with /), and the committed (blue with ∖) mass loss ensemble simulations. For each ensemble, the mean is represented by a solid line and the shading includes 95 % of the ensemble members. Observations from Mouginot et al. (2019) of the 1985–2019 period are represented by +.

The SMB and the ice discharge have two opposite trends at the end of the century (Fig. 5). Until the 2090s, some members following the SSP5-8.5 see their discharge increasing sharply, reaching high values of 60 Gt a⁻¹, but with a sharp decrease between 2090 and 2100. We attribute this late-period decrease to the fact that two of the three marine-terminating glaciers of the UI catchment become land-terminating from this point onwards for members with large retreat forcings. On the other hand, the median SMB remains close to current levels at around 6 Gt a⁻¹ (mass gain) until the 2050s, before falling slowly to around 3 Gt a⁻¹. In 2050, members forced by SSP5-8.5 start to have a negative SMB, which becomes permanently negative from 2070 onwards. Looking at the discharge and SMB of Cpr, it can be seen that UI has still not reached an equilibrium in 2100, with a discharge of 13 [11.1,13.9] Gt a⁻¹, while the SMB is 9 Gt a⁻¹, resulting in a negative mass balance.

3.2 Uncertainty partitioning

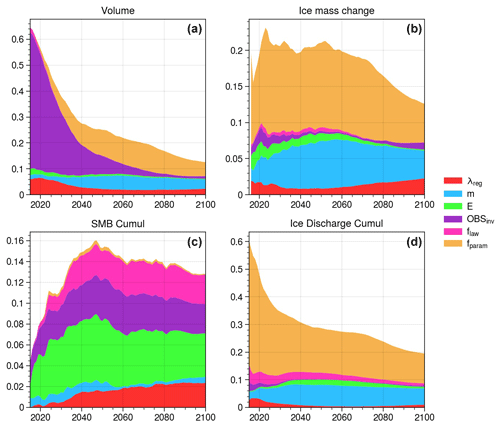
Figure 6 depicts the evolution from 2015 to 2100 of the sensitivity indices computed with the predicted prior ensemble (Ppr) for the volume, the ice mass change, the cumulative SMB, and the cumulative ice discharge. Sensitivity to ice mass change is equivalent to the sensitivity of UI's contribution to SLR. To make things simpler, we sum all the indices influencing the ISM (f_law, f_param, m, E, λ_reg, OBS_inv) and compare them with the indices associated with the SSP, AOGCM, RCM, and front parameterization. Neglecting the sensitivity indices of the parameter combinations leads to a small underestimation of the impact of the dynamics, since part of its influence comes from the parameter combinations.

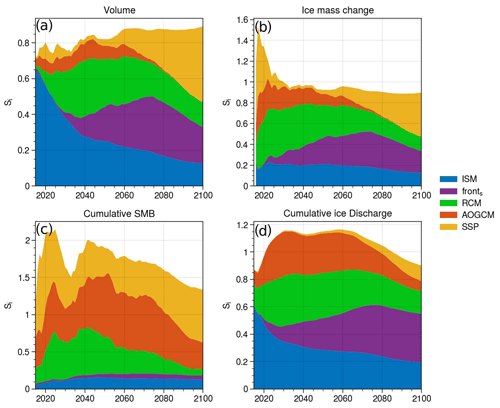
Figure 6 Sensitivity indices for the five sources of uncertainty in Ppr (the ISM, the front parameterization, the RCM, the AOGCM, and the SSP) for the volume (a), the ice mass change relative to 2015 (b), the cumulative SMB since 2015 (c), and the cumulative ice discharge since 2015 (d).

The sensitivity indices provided in the figure are presented in their non-normalized form. It should be emphasized that a sum of sensitivity indices of less than 1 means a substantial impact of specific parameter combinations, e.g. the fact that the influence of the combination of the emission scenario and front sensitivity is stronger than the sum of the influences of each due to non-linearities. Otherwise, if the sum is greater than 1, this implies interdependencies between input parameters, e.g. the fact that the SSP, AOGCM, and RCM are not independent in our case.

As expected, in 2015 the initial volume is independent of the choice of SSP, RCM, AOGCM, and front_s (Fig. 6a), and the sum of the ISM sensitivity indices is equal to 0.65. The value being smaller than 1 is attributed to the interactions between various ISM parameters. The influence of the ISM only diminishes as we move away from this initial state, with the influence of the other sources increasing with very different characteristics.

By 2040, the RCM exhibits the most significant increase in influence on the volume, with a sensitivity index of 0.3, equal to that of the ISM (Fig. 6a). Subsequently, from 2040 to 2075, the sensitivity indices associated with the RCM and ISM gradually decrease to 0.2. During this period, the influence of the AOGCM diminishes from 0.1 to 0. Conversely, the sensitivity index associated with the front parameterization experiences the most pronounced increase, rising from 0.1 in 2040 to 0.3 in 2075.

Beyond 2075, the sensitivity indices of the ISM, front parameterization, and RCM, in terms of the volume, gradually decline until they reach 0.1, 0.2, and 0.1, respectively (Fig. 6a). Meanwhile, the impact of the SSP starts to emerge, becoming non-negligible in the 2050s and significantly accelerating from 2070 onwards. By 2100, the SSP becomes the most influential parameter, with a sensitivity index of 0.45. Throughout this period, the influence of the AOGCM remains at zero.

For the ice mass change in the year 2100, the impact of the parameters exhibits similarities to their influence on total volume, contrasting with the cumulative SMB and cumulative ice discharge (refer to Fig. 6b, c, d). Specifically, for total mass loss, the influence of the SSP is substantial (0.4), while the front parameterization (0.2), the RCM (0.1), and the ISM (0.15) also exhibit discernible but lesser effects. In contrast, the AOGCM demonstrates no discernible influence on total mass loss.

As anticipated, the cumulative ice discharge is primarily influenced by the ISM parameters and the front parameterization front_s. Additionally, the roles played by the SSP, AOGCM, and RCM are not negligible. The combined sensitivity indices of ISM and front_s exhibit a peak value of 0.6 by 2075 and 0.55 by 2100. This heightened influence is also reflected in ice mass loss, with a peak sensitivity index sum of 0.5 in 2075. In contrast, the sensitivity indices of the SSP, AOGCM, and RCM peak at 0.65 in 2030 and gradually decrease to 0.35 towards the later stages.

Conversely, the cumulative SMB demonstrates strong sensitivity almost exclusively to the SSP, AOGCM, and RCM, with their sensitivity indices reaching approximately 2 at the maximum and 1.1 towards the end of the analysis period. For the ISM and front_s, their influence on the cumulative SMB remains limited, with sensitivity indices not exceeding 0.2 (maximum 0.15 for dynamics and 0.05 for front parameterization), owing to feedback interactions with the elevation and ice-covered area.

Significant changes in the influence of the SSP emerge after 2050, notably impacting the cumulative ice discharge, the total mass loss, the volume, and the cumulative SMB. Except for the cumulative SMB, the SSP influence is almost zero before 2050, before becoming the most important parameter after 2090 for the total mass loss, the volume, and the cumulative SMB.

The influence of the AOGCM demonstrates an intriguing trend. From 2050 to 2080, the AOGCM's impact gradually decreases until it reaches zero for ice volume and ice mass change. Concurrently, its effect on the cumulative SMB and cumulative ice discharge also diminishes, though it never reaches zero. This intriguing behaviour is a result of an equilibrium phenomenon, where AOGCMs with the smallest surface mass balance gains correspond to those associated with the lowest ice discharge losses.

Concerning the sensitivity indices of the ISM parameters for the volume, ice mass loss, cumulative SMB, and cumulative ice discharge, the friction parameterization f_param exhibits the highest significance at the end of the analysis period (Fig. C1). In 2100, its sensitivity index is 0.06 for volume, 0.05 for ice mass loss, and 0.1 for cumulative ice discharge, i.e. at least a third of the ISM total. Additionally, the observation used for the friction calibration OBS_inv has a substantial impact at the beginning, with a sensitivity index of 0.5 for volume. However, its influence gradually diminishes over time and becomes negligible by 2080 (less than 0.01). Lastly, the exponent of the friction law m emerges as another significant factor in 2100 for dynamics, with a sensitivity index of 0.04 for volume, ice mass loss, and cumulative ice discharge.

4 Results: Bayesian calibration

This section present the results of the different steps of our Bayesian calibration as given in Fig. 3. First, we present our cross-validation process, which evaluates the robustness of the calibration methodology and allows us to select only the robust weightings. Second, we perform a factor mapping analysis to assess the impact of these weightings on our six ISM parameters (λ_reg, OBS_inv, f_law, f_param, m, and E). Third, we examine the impact of weightings on the model predictions of UI's contribution to sea-level rise.

4.1 Cross-validation

This section presents the key findings of the cross-validation. As detailed in Sect. 2.3.2, the cross-validation is used to assess the ability of the calibration to improve the ensemble performance. The ensemble performance is assessed with the CRPS (Eq. 3) computed using several sets of observations that were not used for the calibration. A detailed analysis is given in Appendix D, and the main conclusions are summarized below.

1. Weighting using the Student distribution generally exhibited superior performance compared to the Gaussian distribution: by assigning less preference to the best members, the Student distribution effectively reduced total variance and mitigated overfitting. Similarly, increasing σ led to reduced emphasis on the best members and aided in avoiding overfitting. However, excessively high values of σ resulted in decreased CRPS performance due to underfitting. We determined that an optimal compromise is achieved by utilizing the median or mean of the RMSE distribution for determining σ.

2. Utilizing surface elevations and velocities in the weighting process yielded the most robust outcomes, reducing the CRPS across all variables. Weighting solely based on ice discharge or volume change improved the CRPS for these specific quantities but not for surface velocities and elevations.

3. The introduction of multiple periods into the weighting process enhanced the CRPS for volume changes but not for surface elevation and velocity, as it excessively reduced overall variance. To mitigate this effect, it is advisable to increase σ by selecting the third quartile of the RMSE distribution, thereby balancing undesirable reductions in variance while preserving desirable outcomes.

4. The f_param weighting scheme generally yielded a superior CRPS for volume change and ice discharge but exhibited poorer performance for surface elevation and velocity compared to alternative weighting approaches.

4.2 Factor mapping

Figure 7 shows the prior and posterior distributions of our six ISM parameters for two weighting methods. For full-period weighting, we adopt Student's distribution with the median as the estimate of σ, along with the integration of the combination of velocity and surface elevation data (ZSxV). In the case of sub-period weighting, we maintain these characteristics, except for the σ estimate, which is determined by the 75th percentile (SP_Q75) of the RMSE distribution.

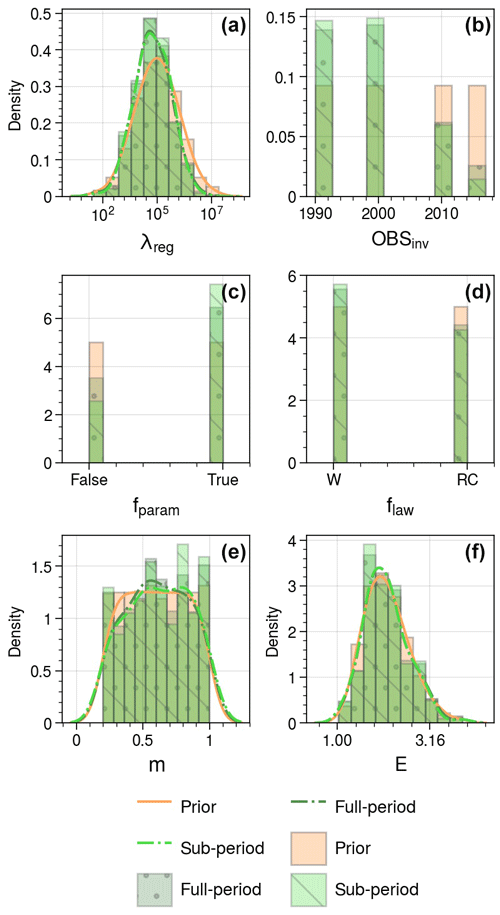
Figure 7 Distribution of λ_reg (a), OBS_inv (b), f_param (c), f_law (d), m (e), and E (f) for the prior ensembles (Hpr, Ppr, and Cpr) in orange and for the calibrated ensembles (Hpo, Ppo, and Cpo) in green: full-period weighting in dark green with • and sub-period weighting in light green with ∖.

While the primary findings are presented herein, additional details can be accessed in Appendix C4:

1. Full-period weighting favours members initialized with friction data from the 1990s and 2000s due to lower RMSE values, while members with inversions conducted in 2010 or 2017 exhibit poorer performance, particularly in ice-free areas pre-retreat, due to extrapolation needs. Confidence in predictions increases as data are faithfully reproduced after the ice front retreats.

2. The presence or absence of f_param is a significant factor influencing the distribution shift between the prior and posterior in full-period weighting, highlighting its crucial role in accurately reproducing data.

3. Excessively high regularization weight (λ_reg) values result in elevated RMSEs due to overly smooth friction fields, emphasizing the importance of balancing regularization strength and model fidelity.

4. Parameters m, f_law, and E show no substantial trends in the difference between prior and posterior distributions. However, higher weights are observed for certain values of m, E, and f_law=W due to the influence of λ_reg, OBS_inv, and f_param.

5. Sub-period weighting amplifies discrepancies in f_param selection, indicating a greater likelihood of accurately replicating distinct periods. This indicates that the members that best reproduce changes in dynamics are those that use the parameterization proposed in Jager et al. (2024).

4.3 Posterior ensembles

Mass changes between 1989 and 2100 for the prior end posterior ensembles are shown in Fig. 8. Results are shown for the full-period, sub-period, and f_param weightings. For the full-period and sub-period weightings, we use both surface velocities and elevations for the calibration with a Student distribution. For the full-period weighting, σ is the median of the RMSE distribution, along with the integration of a combination of velocity and surface elevation data (ZSxV). In the case of sub-period weighting, we maintain these characteristics, except for the σ estimate, which is determined by the 75th percentile (SP_Q75) of the RMSE distribution.

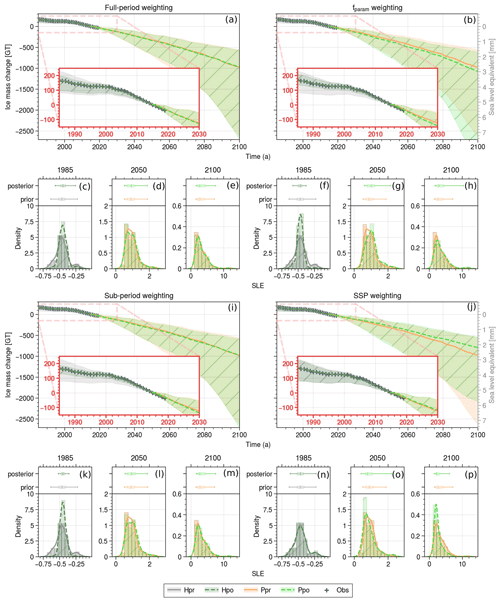
Figure 8 Evolution of Upernavik Isstrøm ice mass loss over the period 1985–2100 for the hindcast prior (grey), the hindcast posterior (dark green with /), the predicted prior (orange), and the predicted posterior (light green with /) for different weightings (full-period weighting in a, c, d, and e; f_param weighting in b, f, g, and h; sub-period weighting in i, k, l, and m; and SSP weighting in j, n, o, and p). Each ensemble's median is represented by a solid (prior) or dotted (posterior) line, and the shaded area encompasses 95 % of the ensemble members. Observations from the 1985–2019 period are indicated by the symbol +. The red box highlights a zoomed-in view of the 1985–2030 period. Sub-plots (c)–(h) and (k)–(p) show changes in the histogram, distribution, and box plot (95 % interval, interquartile interval, and median) between the SLE prior and posterior in 1985, 2050, and 2100.

4.3.1 Hindcast ensemble

Throughout the hindcast period, weightings based on ISM performance over the period 1985–2019, as the full-period, sub-period, and f_param weightings, have considerably narrowed the mass loss distribution around the observations (Fig. 8). This narrowing of the distribution is particularly pronounced for the f_param weighting (−51 % of the 95 % confidence interval in 1985) and sub-period weighting (−61 %), surpassing that achieved by full-period weighting (−32 %). For the f_param weighting, the notable reduction in uncertainty mainly arises from adjusting the weights assigned to members with the greatest mass loss rather than adjusting those assigned to members with the lowest mass loss. Conversely, the opposite trend is observed for the other two weighting methods. This second pattern is attributed to the selection of members based on the year of inversion (Fig. 7) rather than on the presence or absence of the f_param parameterization. Specifically, members initialized before the retreat and not employing f_param show lower mass losses, which is less consistent with the observed data. Sub-period weighting emerges as a compromise between the other two weighting approaches. It incorporates the more precise selection criterion of the f_param weighting while retaining the inclusion of members with a lower mass loss, which are members using inversion data before the retreat.

4.3.2 Control ensemble

The results of the mass loss analysis of the posterior control ensemble (Cpo) are not shown in this section, but these results present trends similar to those observed over the hindcast period. In particular, the reduction in uncertainty is greater for the f_param weighting and the sub-period weighting approaches. In these cases, the main impact is the exclusion of ensemble members characterized by the lowest mass loss, leading to projected contributions in 2100 of 0.83 to 1.31 and 0.83 to 1.25 mm sea-level equivalent (SLE), respectively. This contrasts with the prior ensemble (Cpr), which ranges from 0.56 to 1.31 mm SLE. For the full-period weighting approach, the uncertainty reduction is more symmetrical, affecting the ensemble members with the highest and lowest mass loss, resulting in a range of 0.64 to 1.26 mm SLE.

4.3.3 Predicted ensemble

Regarding the prediction for the year 2050 and 2100, both the full-period weighting and the sub-period weighting methods exhibit minimal changes in the posterior ensemble, as depicted in Fig. 8. The median contribution of Upernavik Isstrøm to sea-level rise by the end of the century remains unchanged at 2.7 mm, consistent with the earlier ensemble. Moreover, few revisions are observed in the 50 % and the 95 % confidence interval, which has been adjusted upwards for both weighting (Fig. 8d, e, i, m).

In contrast, when using f_param weighting for weighting, significant changes are observed in the prediction of the posterior ensemble, leading to a larger projected loss of mass. The median SLR contribution in 2100 increases to 3.0 mm compared to 2.7 mm in the prior ensemble. Moreover, the 50 % interval and the 95 % confidence interval expand significantly (Fig. 8g, h).

5 Results: dependence on SSP

To complete this results section, we explored an alternative probability distribution for the SSPs given its pronounced uncertainty in 2100 (Fig. 6). Contrary to many studies where the results are discussed for different SSPs, our results encompass three scenarios that were almost equally weighted. This allowed us to discuss the sensitivity to the SSP with respect to the other sources of uncertainty. Without any preconceived ideas about their distribution, we have assigned an almost equal weighting to each SSP (Sect. 2.1.3). However, recent evidence suggests that each SSP is not equally likely to occur in the future, with higher probabilities associated with scenarios projected to reach 2 to 3.5 °C of warming by 2100 (Raftery et al., 2017; Hausfather and Peters, 2020; Intergovernmental Panel on Climate Change (IPCC), 2022; Hausfather and Moore, 2022; Pielke et al., 2022). Drawing from the survey results presented in Tollefson (2021), we propose allocating probabilities of $\mathrm{1}/\mathrm{10}$, $\mathrm{6}/\mathrm{10}$, and $\mathrm{3}/\mathrm{10}$ to SSP5-8.5 (representing more than or equal to 4 °C of warming), SSP2-4.5 (indicative of warming between 2.5 and 3.5 °C), and SSP1-2.6 (corresponding to warming below or equal to 2 °C), respectively. We base these probabilities on the challenges we face in achieving SSP5-8.5 under current policies (Intergovernmental Panel on Climate Change (IPCC), 2022), which leads us to give more weight to SSP2-4.5. Similarly, SSP1-2.6 is deemed improbable due to the limited extent of CO₂ emission reductions to date (Raftery et al., 2017). However, it is important to acknowledge that these probabilities are approximate estimates and should not be taken at face value. By construction, these probabilities have no effect on Hpr, and the performance in terms of the CRPS, MAE, and SD cannot be evaluated.

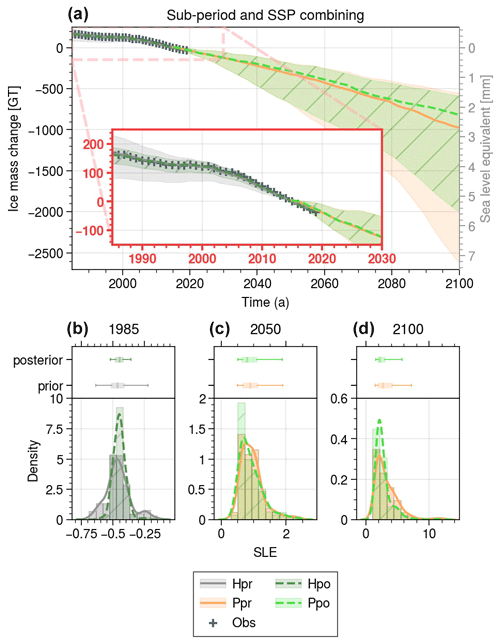
Figure 9 Evolution of UI ice mass loss over the period 1985–2100 for the hindcast prior (grey), the hindcast posterior (dark green with /), the predicted prior (orange), and the predicted posterior (light green with /) for the combined sub-period and SSP weightings, achieved by multiplying the weights of these two weightings. For each ensemble, the median is represented by a solid (prior) or dotted (posterior) line and the shading includes 95 % of the ensemble members. Observations of the 1985–2019 period are represented by +. The red box shows a zoomed-in view of the 1985–2030 period. Sub-plots (b)–(d) show changes in the histogram, distribution, and box plot (95 % interval, interquartile interval, and median) between the SLE prior and posterior in 1985, 2050, and 2100.

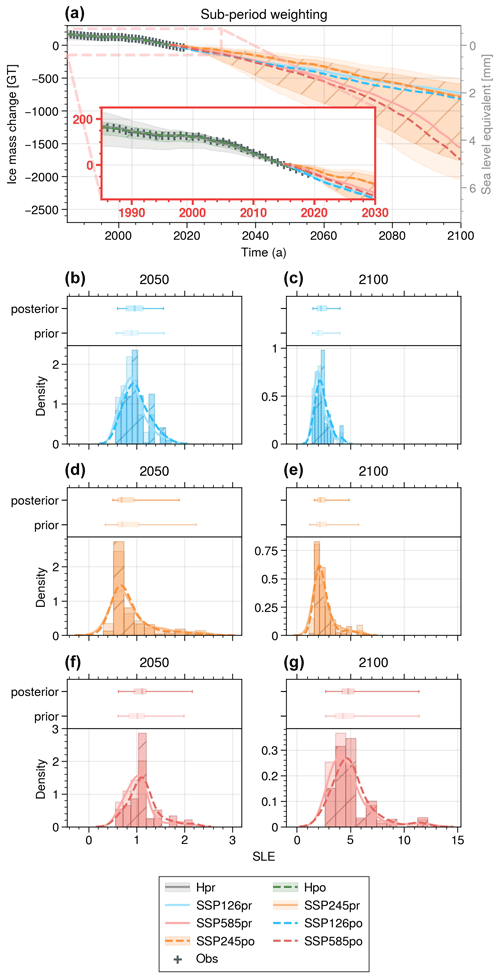
Figure 10 Evolution of UI ice mass loss over the period 1985–2100 (a) for the hindcast prior (grey), the hindcast posterior (dark green with /), the SSP1-2.6 prior and posterior (blue), the SSP2-4.5 prior (light orange) and posterior (dark orange with /), and the SSP5-8.5 prior and posterior (red) ensemble simulations for the sub-period weighting. For each ensemble, the median is represented by a solid (prior) or dotted (posterior) line and the shading includes 95 % of the ensemble members. Observations of the 1985–2019 period are represented by +. The red box shows a zoomed-in view of the 1985–2030 period. Sub-plots (b)–(g) show changes in the histogram, distribution, and box plot (95 % interval, interquartile interval, and median) between the prior and posterior in 2050 and 2100.

The SSP weighting on the future prediction has a very significant effect, reducing the median contribution of UI in 2100 from 2.7 to 2.2 mm. The 50 % and 95 % confidence intervals are also revised downwards (Fig. 8p). In 2050, on the other hand, the range of the 95 % confidence interval becomes wider, while the median is revised downwards, from 0.90 to 0.79 mm (Fig. 8o).

Through the combination of ISM weighting, specifically sub-period weighting, with the existing SSP weighting (Fig. 9), we are able to constrain the wider 95 % interval in short-term predictions (2050) compared to using the SSP weighting alone (Figs. 8o and 9c). This combined approach results in a reduced interval of [0.53, 1.89] compared to the [0.46, 2.05] interval achieved by SSP weighting alone (Fig. 8o) and is slightly smaller than the prior interval of [0.52, 1.90]. Moreover, the combination remains essentially unchanged with the median shifting upwards from 0.79 to 0.80 mm.

In the context of long-term predictions (2100), the combination with sub-period weighting also results in an upward shift compared to SSP weighting alone (Figs. 8p, 9d). The 95 % confidence interval shifts from [1.5, 5.7] to [1.6, 5.5], while the median experiences a slight increase from 2.18 to 2.25 mm.

By employing this weighting combination, we are able to capitalize on the long-term reduction achieved by SSP weighting while simultaneously leveraging the uncertainty reduction facilitated by dynamic performance-based weighting in the short and medium term. Notably, dynamic performance-based weighting also contributes to the reduction in long-term uncertainty by excluding members that underestimate past mass loss and provide the lowest SLR contributions.

An alternative method to assess the influence of Bayesian calibration with reduced SSP-related uncertainty entails presenting results for each distinct SSP (Fig. 10). This approach reveals effects that the aggregation of SSPs otherwise conceals. For SSP2-4.5 (Fig. 10d, e), the application of sub-period weighting significantly tightens the 95 % confidence interval across medium-term (30 % in 2050) and long-term (20 % in 2100) projections. Concerning SSP1-2.6 (Fig. 10b, c) and SSP5-8.5 (Fig. 10f, g), the reduction in uncertainty is less pronounced, not mirroring the levels seen in previous studies about the Greenland Ice Sheet (e.g. Aschwanden and Brinkerhoff, 2022). This modest reduction is attributed to the robustness of our model, with a prior close to observations. Nonetheless, a notable shift in probability towards higher values is observed for each SSP, as shown by histograms, box plots, and median values in Fig. 10b–g. Similar results for the full-period and f_param weightings are illustrated in the Supplement (Fig. S2).

To conclude this section, our exploration yielded two notable findings: (i) incorporating information about the primary source of uncertainty (Fig. 6) and adjusting its probabilities can notably diminish overall uncertainty; (ii) subsequent to reducing this uncertainty, integrating ISM Bayesian calibration further diminishes total uncertainty to a greater extent compared to applying ISM Bayesian calibration alone without updating SSP probabilities.

6 Discussion

6.1 Prior ensemble

One of the reasons behind the use of a control run in ISMIP6 was to address the limitations of the models in accurately reproducing recently observed changes in the ice sheets due to artificial model drift, thus making it easier to assess the deviation of each projection from this drift (Goelzer et al., 2020; Seroussi et al., 2020; Nowicki et al., 2020). However, the control run represents the average state of the recent period, accounting for both model drift and climate change already experienced, such as a 0.5 °C warming in 1990 compared to pre-industrial conditions (Masson-Delmotte et al., 2021). Consequently, the results obtained by differentiating between a simulation with realistic forcing and a control simulation with constant forcing do not allow us to predict the future evolution of sea-level rise (SLR), as they do not take into account the mass loss already underway as a result of past global warming.

The initialization method developed in Jager et al. (2024) effectively reproduces the past UI trend, negating the need for control run differentiation as practised in the ISMIP6 framework. In our case, since we can successfully reproduce recent observations, the prediction (Ppr) offers a comprehensive SLR prediction encompassing this committed mass loss. Subtracting the control (Cpr) from the prediction of the prior ensemble (Ppr) would have underestimated UI's contribution to SLR by approximately 1 mm (i.e. the median contribution of Cpr), almost 35 % of the median value of Ppr. This also implies that stabilizing the forcing at present levels does not stabilize the ice sheet, which would continue to melt. However, it is important to note that in this study, we do not employ a constant forcing from the present day in the control experiment or Cpr. Instead, we utilize a prescribed SMB representative of the period between 1960 and 1990, along with a prescribed front characteristic of the year 2015. It is worth mentioning that using an SMB averaged over more recent years, such as those from the 2010 decade, would yield a higher estimate of melt for Cpr and consequently result in an even greater committed mass loss. Additionally, considering the current climate conditions, it is more likely for the front to retreat than to advance, leading to increased discharge and more mass loss.

6.2 Uncertainty in future prediction

Our sensitivity study on the contribution of sea-level rise differs from previous studies (Aschwanden et al., 2019; Goelzer et al., 2020; Hill et al., 2021) by incorporating the SSP into the parameters, rather than conducting separate analyses for each SSP. However, this approach is not unique and is similar to studies carried out for glaciers outside the Greenland and Antarctic ice sheets (Marzeion et al., 2020), as well as for global temperature and precipitation (Hawkins and Sutton, 2009). As the SSP is included in our sensitivity analysis, in contrast to previous studies on the Greenland Ice Sheet up to at least 2100, such as those of Goelzer et al. (2020) and Aschwanden et al. (2019), we have had to reassess the estimates of uncertainty associated with the SSP, the ISM, the RCM, and the AOGCM used in those studies. Herein, we describe our approach to this reassessment process and demonstrate that these revised estimates yield results consistent with those obtained in our study.

Specifically, the ISMIP6 study highlights a substantial difference of approximately 58 mm of sea-level equivalent between the means of the RCP8.5 and RCP2.6 scenarios (RCP denotes Representative Concentration Pathway), with the combined uncertainty spanning 125 mm of sea-level equivalent, representing a variability of over 45 %. Similarly, the variance between RCPs in Aschwanden et al. (2019) accounts for nearly 35 % of the overall uncertainty. In our study, which focuses on a single tidewater glacier in Greenland, we observe a comparable magnitude of uncertainty (40 %). Notably, when examining the ISM, the uncertainty attributed to this factor is considerably lower in our study (15 %) compared to ISMIP6 (35 %). Conversely, the uncertainty associated with front parameterization is higher in our study (20 %) than in ISMIP6 (15 %) because we are looking at uncertainty due to parametric differences in one model compared to different models in ISMIP6. The uncertainty in the RCM is not investigated in ISMIP6, preventing direct comparisons. Furthermore, our study reveals zero sensitivity of the AOGCM, in contrast to ISMIP6 where it accounts for almost 30 % of the overall variability (36 mm of the 125 mm total uncertainty). This lack of influence can be attributed to a compensatory effect: the AOGCM exerts a non-zero influence on both the ice discharge and the SMB as depicted in Fig. 6. Nevertheless, AOGCMs with higher discharge rates are associated with a higher SMB, and vice versa, culminating in a comparable net ice mass change across different AOGCMs (Fig. S1). Finally, Rohmer et al. (2022) demonstrated that spatial resolution and front parameterization were the two most influential parameters in the ISMIP6 framework, which notably does not account for RCM and SSP uncertainties. Regarding the significance of front-retreat parameterization, our study aligns with this observation, demonstrating its substantial influence. In fact, it emerges as the second most influential factor after SSP, which was not explored in the mentioned study. For the spatial resolution, our sensitivity analysis does not take it into account. However, we conducted mesh sensitivity tests during the hindcast period, changing the resolution by factors of 0.5, 2, and 4. These tests revealed that such modifications resulted in approximately a 30 % alteration in local velocities at a given time, which depends on the precise timing of the front's position as it moves discretely along the edges of the elements. Nevertheless, the overall mass loss across these varying meshes exhibited minimal variation, amounting to less than 5 %.

6.2.1 Reducing uncertainty through ISM calibration

Considering the small sensitivity of the ice mass loss to the ISM, our calibration analysis reaffirms the limitation of reducing uncertainty solely through ISM calibration. Notably, our prior results indicate a considerable reduction in uncertainty compared to broader intercomparison studies like ISMIP6 when employing a single model. This discrepancy can be partly attributed to ISMIP6's more comprehensive consideration of structural uncertainties within the models. Additionally, the prior ensemble already demonstrates a high level of skill in reproducing past observations, as shown in Fig. 4. However, it is important to acknowledge that all models must overcome this challenge before a future intercomparison study like ISMIP7, as suggested in Aschwanden et al. (2021). Once this hurdle has been successfully addressed by the ice sheet dynamics modelling community, it will be essential to focus on reducing other sources of uncertainty.

6.2.2 Reducing uncertainty through climate forcing calibration

Our findings regarding the weighting of SSPs underscore the significant reduction in uncertainty, particularly for long-term predictions with a 20 % reduction in the 95 % confidence interval, that can be achieved through this approach. This opens up possibilities of conducting similar studies aimed at assigning weights to other model assumptions, such as front parameterization, the selection of RCMs, or the selection of AOGCMs. For short-term predictions, which are of great interest to some practitioners, it appears that the primary sources of uncertainty are associated with RCMs, AOGCMs, and front parameterization. Although significant uncertainty remains regarding ice sheet dynamics for UI, with certain aspects still unexplored (e.g. bed elevation), we appear to be approaching the practical limit for uncertainty reduction while preserving the robustness of our results related to these dynamic processes of the GrIS, unless other sources of uncertainty are addressed first. Specifically, after reducing the uncertainty associated with the SSPs, applying a weighting to the ISM further reduces uncertainty by 10 % by 2100 (Ppo in Fig. 8j and a).

In the context of front-retreat parameterization, despite its foundation in observational data, there remains significant room for reducing associated uncertainties. In our study, we have considered two sectors, CW and NW, at three distinct sensitivity levels (low, medium, and high) to prevent unwarranted confidence in our findings. Applying the parameterization to the hindcast period results in a uniform retreat of all branches, with 6 km for the highest sensitivity (high sensitivity of the central-west sector) and 0.9 km for the lowest sensitivity (low sensitivity of the northwest sector). In comparison, UI-N retreated by 5.7 km and UI-S by 1.1 km over the same period (Fig. 1). To improve the parameterization, it will be necessary to take into account additional factors beyond currently considered runoff and far-field ocean temperature changes, which do not allow for the difference in ice dynamics between the different ice streams as shown here for Upernavik Isstrøm. Furthermore, given the significant influence of this front parameterization on the ice discharge and the mass loss of UI, as revealed by the sensitivity analysis, it seems important for the scientific community to engage in further research aimed at improving this characterization of front retreat and introducing a more physics-based formulation of this parameterization. Such efforts would require a comprehensive analysis of past behaviour, along the lines of previous studies (Wood et al., 2021), followed by calibration efforts for an appropriate calving law (Bondzio et al., 2018) and investigations into the complex interactions between ocean, atmosphere, and outlet glaciers (Slater et al., 2019).

In the realm of RCMs, multiple studies have been conducted to compare these models with data obtained from the Greenland Ice Sheet (Fettweis et al., 2020; Vernon et al., 2013). These comparative analyses serve to identify the biases inherent in different RCMs and guide efforts towards their correction in subsequent iterations. However, despite these endeavours, the various models continue to yield significantly divergent results, attributable in part to disparities in the underlying physics employed and the downscaling techniques used. For example, in our previous study (Jager et al., 2024), we demonstrated that members using RACMO, which employs a 1 km statistical downscaling approach to the 5.5 km grid (Noël et al., 2016), reproduce past trends in surface elevation better than those using the MAR model without statistical downscaling (Fettweis et al., 2017). One potential solution to address the disparities among RCMs is to incorporate multiple ensemble members from these models, accounting for their associated uncertainties. This presupposes that the RCMs themselves undertake uncertainty quantification to follow the Bayesian approach proposed in Aschwanden et al. (2021). By doing so, it becomes possible to generate a range of forcing scenarios for both hindcast and forecast periods and evaluate their performance against past surface elevation observations. Efforts can also be directed towards reducing uncertainty by promoting convergence among different RCMs, contingent upon them duly accounting for their intrinsic uncertainties.

Considering the substantial impact of the SSP on uncertainty, it would be valuable to conduct a more thorough examination of this uncertainty, particularly given that SSP2-4.5 and SSP1-2.6 exhibit similar outcomes in this study. Currently, many studies primarily focus on the SSP5-8.5 scenario, which yields striking results due to its high level of warming (Hausfather and Peters, 2020), and only a few include SSP1-2.6 or SSP2-4.5, as used in this study. However, considering the notable differences in results between SSP2-4.5 and SSP5-8.5, a more refined discretization of future scenarios would provide more comprehensive understanding of uncertainty in future sea-level-rise projections. This will also help macro-studies such as that of McKay et al. (2022) to better identify at what level of warming the GrIS and AIS tipping points may be exceeded.

6.3 Cross-validation method for Bayesian calibration

To address the challenge of spatial and temporal correlation and its impact on model weighting, various approaches have been previously explored. We discuss three methods here. The first approach involves the utilization of aggregated data, such as volume and discharge changes, as they were used with a single global value in Ritz et al. (2015) for calibrating the future of the Antarctic Ice Sheet with the mean rate of change for each sub-catchment. However, using time series, the approach does not effectively resolve the issue of temporal correlation as used in Aschwanden and Brinkerhoff (2022) with the mass calibration. The second approach employs a performance metric, which can be interpreted as the distance between the observed and modelled fields, effectively treating multiple observations as a single observation (i.e. n_obs is then equal to 1 in Eq. 12). This is the method used in our study. For example, in a different context focused on constraining a calving law, Bondzio et al. (2018) proposed an approach to weight ensemble members using a metric that measures the distance between each member's front and the observed one. In other contexts of Antarctic Ice Sheet modelling, Pollard et al. (2016) and Albrecht et al. (2020) also proposed weighting methods based on a metric that measures the performance of each member. A third option is to use one observation for each mode (a distinct group of ensemble members with similar characteristics) of the ensemble using principal component decomposition. In the domain of glaciology, Wernecke et al. (2020) implemented the third approach by employing it in the context of the Amundsen Sea embayment. The calibration process utilized two-dimensional satellite data reflecting surface elevation change. Notably, this investigation conducted a comparative analysis by comparing this mode-based approach with both the first method (i.e. aggregated data approach) and an approach that kept all the information encapsulated in the field of view (Eq. 12). The study's results indicated that this mode-based approach succeeded in reducing uncertainty to a greater extent compared to the approach utilizing aggregated data but not as effectively as an approach that harnessed the complete observation field. The study postulated that this second aspect could signify potential overconfidence in the retrieved parameter values or, conversely, more efficient exploitation of the available information. However, it is worth noting that the study did not perform an evaluation of the calibrated ensemble's performance, leaving a distinction between these two possibilities uncharted.

Our validation method responds to the limitations raised above and represents a significant advance in Bayesian calibration within model ensembles of ice sheet modelling. We used a cross-validation approach that allows us to examine the diverse impacts of weighting choices and mitigate the risk of overfitting. However, it is important to acknowledge that the selection of hyper-parameters (e.g. the number of parameters taking into account the ISM sensitivity analysis) itself may contribute to overfitting, and we have yet to identify an effective strategy to address this challenge.

While there is room for further improvement in our method, the unique characteristics of glaciology pose challenges in drawing inspiration from other scientific disciplines. In contrast to hydrology, meteorology, or oceanography, where a wealth of events can be used for weighting or calibration, glaciology often deals with a limited number of observed events. For instance, in hydrology, multiple flood events can be employed for weighting and calibration, with additional events available for validation (Hallouin et al., 2020). In contrast, glaciology typically involves only a single observed retreat event per catchment, as demonstrated in our study of UI. Consequently, the application of such techniques becomes unfeasible in glaciology. Nonetheless, the notion of calibrating and validating parameters on a catchment-specific basis holds great promise, as it would enable a more targeted parameter selection within individual catchments rather than considering the entire ice sheet as a whole. To effectively validate the calibration of parameters on a per-catchment basis, it is imperative to identify a glacier exhibiting dual events (e.g. two major retreats of the same front since the 1980s). Subsequently, the model ensemble can be calibrated using the initial retreat data, followed by a comparison of the calibrated model's CRPS performance against that of the non-calibrated model. Such a case study could also serve as a basis for comparing the calibration with weights as developed here to other transient data assimilation methods as developed in Goldberg et al. (2015).

Furthermore, the validation approach employed in this study has demonstrated the additional benefits of transient calibration compared to snapshot inversion, i.e. the traditional inverse method of friction calibration. This is particularly the case in scenarios where a front retreat occurs, as is evident in the case of the substantial retreat of the UI-N and UI-C fronts. In contrast, when there are no significant front retreats (UI-S) or velocities are low, implying a limited role of dynamics (UI-SS), calibration does not seem to offer any discernible improvements. This observation is likely attributable to the fact that, in the absence of substantial changes in dynamics, all ensemble members can effectively reproduce these dynamics through inversion alone.

Our study underscores the substantial impact of calibrating with velocity and elevation data (full-period weighting) in diminishing the uncertainty linked to hindcast ice mass loss in the UI region, especially when considering their temporal aspects (sub-period weighting). This reduction in uncertainty opens up possibilities for data assimilation of past velocity and elevation data inspired by Goldberg et al. (2015) or Gillet-Chaulet (2020), offering a way to reconstruct discharge with better-characterized uncertainties compared to the conventional input–output method. Using advanced transient data assimilation techniques can lead to enhanced performance in terms of cumulative ice discharge, moving beyond the limitations of the simplistic gate-based approach. By incorporating velocity and elevation data through data assimilation, uncertainties related to velocities, surface elevation, and bed elevation can be effectively addressed, making the use of gates unnecessary. This approach represents a promising advancement in improving the accuracy and reliability of ice discharge reconstructions.

6.4 Insights for future studies

Thanks to our validation methodology, designed to mitigate the risk of overfitting, we can assert the reliability of our findings concerning future sea-level rise and the interpretation of related outcomes. In this context, we offer valuable insights that hold significance for ice sheet modellers concerned with Bayesian calibration through the weighting choices and retrospective modelling.

6.4.1 Use of Bayesian calibration

Our investigation reveals that the selection of weighting strategies for Bayesian calibration, encompassing the probability distribution shape, the determination of an appropriate standard deviation (σ), and the incorporation of multiple periods, can precipitate over-adjustment during the calibration process. Opting for an overly narrow distribution or favouring a distribution with very thin tails such as Gaussian over a distribution with fatter tails as Student's t can result in overfitting, wherein only a few high-performing members are emphasized, thereby disregarding crucial information. This observation resonates with findings presented by Jiang and Forssén (2022), wherein they highlight significant challenges arising from the utilization of complex likelihood functions (as encountered in our study with multiple periods) or extremely small data errors (represented by excessively small σ values). Such circumstances may lead to the selection of a limited number of members, potentially overlooking vital aspects of the posterior distribution. Consequently, cautious consideration is warranted when employing these techniques, and our validation approach serves as a safeguard against such pitfalls.

Regarding the selection of data, our analysis revealed a notable asymmetry between spatialized data, such as speeds and elevations, and global data, such as ice discharge and total mass loss. Specifically, when members were chosen based on their ability to accurately reproduce velocities and elevations, it resulted in an overall enhancement in the ensemble's performance for both spatialized data and global indicators like ice discharge and mass loss. However, the converse was not observed to hold true. This discrepancy can be attributed to potential compensatory effects, wherein a model that closely matches the observed discharge may exhibit excessively high velocities and disproportionately low elevations. Conversely, a model that accurately represents velocities and elevations will inherently yield a satisfactory discharge estimation. Additionally, selecting members based on spatialized data also facilitates improved reproduction of other phenomena that indirectly influence discharge, such as shear margins.

We conducted an analysis of the influence of sub-periods that characterize different phases, namely before, during, and after glacier retreat. Our findings indicate that the use of sub-periods results in a slightly improved selection of members using parameterization compared to full-period weighting, as the former exhibits better representation of glacier acceleration. This approach can be considered an intermediate method between f_param weighting and full-period weighting, particularly during the hindcast period. However, it should be noted that the selection process is still strongly influenced by the choice of inversion data, which becomes less influential in future predictions. A potential future approach could involve using only pre-retreat data to create a new ensemble, enabling a slightly more refined selection based on other model parameters. This calibration method also provides more relevant information, as it demonstrates the model's ability to accurately reproduce past total mass change data, which aligns with our ultimate objective. Consequently, we place slightly more confidence in sub-period weighting than we do in full-period weighting.

6.4.2 Friction law

The most influential parameter within the ISM, regarding the reproduction of past Upernavik Isstrøm behaviour, is the choice of input data for the inverse method of the friction field. Weights are notably larger when using inversion data from the pre-retreat period (1990s and 2000s). This is because no extrapolation is needed in the ice-free areas during this period, in contrast to post-retreat inversions where extrapolation is necessary due to ice front retreat, introducing additional uncertainties into their performance assessment. Consequently, post-retreat inversions exhibit lower performance in ice-free areas before the retreat. The accurate reproduction of data when the front retreats instils greater confidence in our predictions, aligning with the observed trend of front retreat. However, if one wishes to delve further back in time or undertake a paleo-climatic study, extrapolation becomes necessary (e.g. Haubner et al., 2018). Thus, the choice of friction field extrapolation will become a crucial issue as it significantly influences the result, as previously shown in Jager et al. (2024).

Concerning the shape of the friction law, our findings emphasize that incorporating the sub-hydrological effect – albeit in a parameterized manner as demonstrated in this study – is crucial for accurately simulating the historical dynamics of UI. Additionally, inclusion of this effect is associated with an amplification of projected future mass loss of the glacier, consistent with expectations outlined in Jager et al. (2024). In that study, we highlighted the significance of the sub-hydrological effect and posited that its consideration would likely exacerbate glacial mass loss. Moreover, the findings related to parameter selection indicate that the role of parameterization is more crucial than the specific choice of friction law formulation when it comes to reproducing the observed data. In Joughin et al. (2019), reducing friction near the front probably contributed as much as, if not more than, using a regularized Coulomb law to obtaining better agreement with observed data. This suggests that a Budd law, whose formulation is close to that used here for members using Weertman's law and which takes subglacial hydrology into account, at least in a parameterized way, would perform just as well as the regularized Coulomb law in reproducing past acceleration of UI. For Greenland tidewater glaciers, Choi et al. (2022) also showed that friction laws that include a parameterized dependence on the effective pressure better reproduce the observed acceleration and mass loss of the past decade in northwest Greenland. However, despite the promising results from our previous paper, the predominance of inversion data had a moderating effect on the extent of the observed improvements. In the previous study, only front-end post-processing data were employed for the inversion process. In contrast, the current study incorporates data from both the pre- and the post-retreat periods, which noticeably influenced the calibration due to the necessity for extrapolation. In the future, as the front continues to retreat, it is anticipated that this influence will diminish, rendering extrapolation unnecessary in ice-covered regions.

7 Conclusions

In conclusion, we have shown that our initialization method for Elmer/Ice effectively captures trends of ice mass change and enhances the credibility of future tidewater glacier contributions to sea-level rise, aligning with recommendations from Aschwanden et al. (2021). This approach not only characterizes model uncertainties but also reproduces past observations, akin to successful efforts with ISMs such as ISSM and PISM for Greenland (Aschwanden and Brinkerhoff, 2022; Nias et al., 2023). By addressing model drift, our study moves beyond conventional projections and sensitivity analyses (Goelzer et al., 2020; Seroussi et al., 2020), signalling a paradigm shift towards more localized and precise sea-level-rise predictions, particularly for polar ice sheets.

Our sensitivity analysis emphasizes that, in 2100, the most significant factors affecting the future contribution of Upernavik Isstrøm to sea-level rise are the Shared Socioeconomic Pathways (SSPs) followed by the front-retreat parameterization. Regional climate models (RCMs) and ISMs have a slightly lower impact on sea-level-rise contribution in the long term, while atmosphere–ocean general circulation models (AOGCMs) play a minor role. However, in the short and medium term, for results that may be of interest to public policy, the influence of the SSP is much lower, with uncertainties coming mainly from the four other sources.

Furthermore, our ISM calibration with different weightings brings about marginal improvements in 2100 due to its relatively low impact on the ice mass loss sensitivity. However, the combination of multiple weightings shows promise, suggesting that a more holistic approach may yield greater benefits. In addition, our methodology combining Bayesian calibration and cross-validation has generated noteworthy findings that are of relevance to the scientific community: (i) spatially based weighting demonstrates enhanced robustness compared to globally based weighting strategies; (ii) temporal partitioning of the calibration period, particularly considering calving events (prior to calving, during calving, and post-calving), significantly reduces overall uncertainty while preserving comparable model performance; (iii) the model initialization using inverse methods exhibits robustness, particularly in scenarios involving glacier front retreat, with friction initializations derived from pre-retreat data yielding superior performance. These insights contribute to advancing our understanding of ice sheet modelling and calibration techniques, offering avenues for further research and improvement in future studies.

Looking ahead, it would be interesting to extend our methodology to the scale of the Greenland Ice Sheet. This would involve creating frontal masks dating back to the 1980s, collecting velocity and elevation data over this hindcast period for the peripheral regions of the ice sheet, and running ensemble simulations for comprehensive comparisons. Such an undertaking could lead to better understanding of ice sheet dynamics and improved forecasting capabilities.

Appendix A: Model description

The ISM employed in this study is the parallel finite-element code Elmer/Ice (Gagliardini et al., 2013). The model domain corresponds to the UI catchment, as depicted in Fig. 1. The model used here follows the methodology presented in Jager et al. (2024), and we provide a concise overview of its main aspects in this section. For more comprehensive understanding, we refer readers to the original paper.

The shelfy-stream approximation, also called shallow-shelf approximation (SSA; MacAyeal, 1989), is used for the force balance equations together with Glen's flow law (Glen and Perutz, 1955), which is non-linear, for the constitutive relation. It relies on three parameters: the Glen exponent n, the rate factor A, and the enhancement factor E. Thermo-mechanical coupling is disregarded due to the short time period considered (Seroussi et al., 2013), and for simplicity, the rate factor A is assumed to be constant over time. The initialization of A involves using a present-day 3D ice temperature field computed with SICOPOLIS (Greve, 1997), which is preceded by paleo-climatic spin-up and incorporates the prefactors and activation energies provided by Cuffey and Paterson (2010). Uncertainties related to this flow law are commonly accounted for through the enhancement factor E, which serves as a scaling factor for A.

In this study, two distinct friction laws (f_law=W or RC) governing the relationship between basal velocity u_b and basal shear stress τ_b are employed for grounded areas:

• a Weertman friction law (Weertman, 1957),

  $$\begin{array}{}\text{(A1)}& {\mathit{\tau }}_{\mathrm{b}}=-{\mathit{\beta }}_W\left|\right|{\mathit{u}}_{\mathrm{b}}|{|}^{\frac{\mathrm{1}}{m}}{\displaystyle \frac{{\mathit{u}}_{\mathrm{b}}}{\left|\right|{\mathit{u}}_{\mathrm{b}}\left|\right|}};\end{array}$$

• a regularized Coulomb friction law (Joughin et al., 2019),

  $$\begin{array}{}\text{(A2)}& {\mathit{\tau }}_{\mathrm{b}}=-{\mathit{\beta }}_{\mathrm{RC}}{\left({\displaystyle \frac{\left|\right|{\mathit{u}}_{\mathrm{b}}\left|\right|}{\left|\right|{\mathit{u}}_{\mathrm{b}}\left|\right|+u_{\mathrm{0}}}}\right)}^{\frac{\mathrm{1}}{m}}{\displaystyle \frac{{\mathit{u}}_{\mathrm{b}}}{\left|\right|\mathit{u}\left|\right|}}.\end{array}$$

Both Eq. (A1) and Eq. (A2) involve a friction parameter (β_W or β_RC, respectively) and a positive exponent m, and a threshold velocity u₀ is included in the case of the regularized Coulomb friction law (Joughin et al., 2019). The friction parameter β can either remain constant over time (f_param= false) or take into account the effective pressure in a parameterized way as in Jager et al. (2024) (f_param= true):

$$\begin{array}{}\text{(A3)}& \mathit{\beta }={\mathit{\beta }}_{\mathrm{ref}}+{\mathit{\beta }}_{\lim }{\displaystyle \frac{d}{d+d_{\lim }}},\end{array}$$

where β_ref represents a time-independent reference field, d denotes the distance to the front, and β_lim and d_lim are two parameters accounting for the dependence of β on this distance.

Significant uncertainties surround the parameter β, often initialized based on current topography and surface velocity observations (OBS_inv) using an inverse approach that minimizes a composite cost function. This cost function comprises terms assessing the discrepancy between observed and modelled velocities, a regularization term promoting a smooth friction field solution, and a third term that penalizes flux divergence anomalies (Gillet-Chaulet et al., 2012). These last two terms are weighted with the parameters λ_reg and λ_div that are adjusted using an L-curve approach (Gillet-Chaulet et al., 2012). The inversions in this study are conducted at the UI scale, distinguishing it from our previous study that used inversions previously made at the GrIS scale (Gillet-Chaulet et al., 2012).

For the evolution of the bottom and top free surfaces, we solve the continuity equation for the ice thickness using the flotation condition. As we do not resolve the thermo-mechanical coupling, we neglect the basal melt rate in grounded areas. We also set it to 0 in floating areas, as they remain small during our simulations. For the surface mass balance ${\dot{a}}_{\mathrm{s}}$, we use outputs from an RCM. The unstructured mesh is refined near the ice front and in areas where high velocity or thickness curvatures are observed, featuring element sizes ranging from 150 to 600 m within the initial 50 km and increasing to around 5 km further upstream. A time step of 5 d is used.

The temporal variation in the glacier fronts is treated as an external forcing, with the fronts' positions considered fixed within each time step. The mesh remains unchanged, and the effective ice–ocean boundary is defined by the edges connecting glaciated and deglaciated elements, resulting in discrete changes over time. Deglaciated elements are subsequently deactivated and excluded from the numerical solution.

Appendix B: Observation description

For surface velocity and surface elevation, we used the same spatio-temporal data as presented in our previous work (Jager et al., 2024). These observational data have a grid resolution of 150 m and are annually averaged to improve spatial coverage. However, these data are somewhat unbalanced, exhibiting better coverage in both time and space from the 2010s onwards compared to earlier years. To facilitate model–data comparison, the model fields are bilinearly interpolated onto the same regular grid as the observations.

The ice discharge data used in our analysis comprise a compilation of published data from Mankoff et al. (2019), King et al. (2018), and Mouginot et al. (2019). These data correspond to the flow of ice through the gates, assuming that the average velocity over the thickness is equal to the observed surface velocity. As a result, the derived ice discharge data may exhibit variations depending on the positioning of the gates, the selection of ice heights, and the velocity measurements used. In addition, Jérémie Mouginot has recalculated a set of discharges, this time using BedMachine rather than a flight line, which we call MouginotV2, and the data obtained are close to those of Mankoff et al. (2019). Our observation of ice discharge is then an average of these four datasets. For the model, we used the same methodology by taking the gate defined in Mankoff et al. (2019).

The total ice mass loss at the catchment scale is assessed using the input–output method (Mouginot et al., 2019). This method entails subtracting the ice discharge from the surface mass balance outputs of RACMO. In the ISM, the volume is an output obtained by integrating the thickness over the entire active domain. Consequently, the change in volume encompasses the variations due to front retreat, which are not considered in the input–output approach. Nevertheless, this change in volume was found to be negligible (less than 1 %).

Appendix C: ISM parameters

C1 Factor fixing and factor mapping

As detailed in the main paper, modifications have been made to the dynamic parameters in comparison to parameters used in Jager et al. (2024).

• The ice rheology. Considering the enhancement factor (E), we ascertained that members with E between 1 and 3.5 yield better results. Consequently, we transformed the distribution from continuous between 0.5 and 5 to a log-normal distribution with parameters μ=0.8 and σ=0.5 to enhance the values within the range [1, 3.5].

• The friction law, To distinguish between the influence of the choice of friction law and the presence of the parameterization described in Jager et al. (2024), we introduce two new parameters. The first parameter, denoted f_law, is characterized by two states: “RC” when the member employs the regularized Coulomb friction law and “W” when utilizing the Weertman friction law. The second parameter, termed f_param, possesses binary values: “true” to signify the friction parameter β_RC or β_W evolving according to Eq. (A3) and “false” when the friction parameter remains constant. We also keep in our parameter space the choice of exponent of the friction law m. Finally, the impact of u₀ on model outputs was found to be less significant than that of the other ISM parameters. We therefore use a single u₀ of 300 m a⁻¹, which is similar to the median value of our previous study and to the one used in Joughin et al. (2019).

• The calibration of the friction field. For the friction field, we do not take into account the uncertainty in the whole field (i.e. one parameter per mesh node), but we consider only the uncertainty in the hyper-parameters of the inverse method, which considerably reduces the parameter space. Our two hyper-parameters are the regularization weight λ_reg and the observed data used for the inversion OBS_inv. In the previous study, the impact of λ_div on friction was found to be less significant than that of the other ISM parameters, and we therefore use a single λ_div. In terms of the overarching framework, we have implemented modifications to our inversion procedure. In our previous study, a 40-member inversion had previously been carried out at the scale of Greenland. In contrast, the present study involves individual inversions for each member at the Upernavik Isstrøm scale, affording enhanced continuity within the parameter space of inversion. An L-curve analysis was conducted to determine the revised distribution profile of λ_reg, alongside the optimal value for λ_div. While our previous study used five observational velocity datasets from the 2010s, aligned with BedMachine surface elevations, the current approach employs average velocities and altitudes representative of the entire temporal span from 1985 to 2019. These averages were computed using our own dataset, spanning distinct periods for OBS_inv: 1985–1995, 1995–2005, 2005–2015, and 2015–2019. Due to the presence of ice-free regions in certain areas of the glacier following its retreat around 2005, it is imperative to extrapolate the friction field in these regions for members using observational data from 2005–2015 or 2015–2019. When the parameterization of the effective pressure change effect is enabled (i.e. f_param=true), the time-independent reference field β_ref is set to 0 in the extrapolated areas. Conversely, when parameterization is disabled (f_param=false), either β_W or β_RC set to 0 is utilized. The implications of the chosen extrapolation method are further examined and discussed in Jager et al. (2024).

• The initial geometry. With regard to the initial surface elevation, we have established that it exerts a minimal influence on both ice mass loss and ultimate volume. Compared with the previous study, we have therefore fixed the parameters influencing only this initial surface, namely the period for relaxation, which we set at 5 years, and the period over which the SMB was averaged, which is now the average over the period 1960–1990. By doing so, the initial surface depends only on the ISM parameters (material property, friction law, and friction field calibration).

Figure C1 Sensitivity indices for the six ISM parameters of Ppr (λ_reg, m, E, OBS_inv, f_law, f_param) for the volume (a), the ice mass change relative to 2015 (b), the cumulative SMB since 2015 (c), and the cumulative ice discharge since 2015 (d).

C2 Calculation of sensitivity indices

Accurately computing sensitivity indices of an order greater than 1 usually requires a large number of simulations, and methods have been developed to optimize the experimental design (Reed et al., 2022). However, due to the extensive computational demands of our model, conducting such a large number of simulations is impractical. Therefore, to simplify the approach, we opted to focus solely on first-order sensitivity indices (Eq. 2), which assess the individual impacts of the parameters without considering their interactions; these interactions correspond to higher index orders. These sensitivity indices are computed using the ANOVA method (Brevault et al., 2013; Lamboni et al., 2011). When the probability distribution of X_i is discrete, determining Var (E [Y|X_i]) involves averaging the Y values for each value that X_i assumes and then calculating the variance of the means of these distinct subgroups. For continuous probability distributions of X_i, we discretized the distribution, assuming only four distinct values for X_i. This approach simplifies the problem significantly but results in the loss of subtleties present in continuous distributions. Brevault et al. (2013) emphasized the importance of the number of levels chosen for discretization. Different levels can lead to variations in the sensitivity indices, as small-scale variations in continuous parameters may be smoothed out during discretization. So we tested the convergence of these indices as a function of the number of members considered and found that they converged towards a value that changed by less than 3 % from 50 members upwards. Given the primary objective of the qualitative discussion of results rather than precise estimation, the ANOVA method is well-suited for this purpose. Our focus remains on the identification of principal influences and overarching patterns, supported by Figs. 6 and C1, that offer approximate magnitudes of the observed effects.

C3 Sensitivity analysis

Figure C1 illustrates the evolution of sensitivity indices for ISM parameters from 2015 to 2100, computed using the predicted prior ensemble (Ppr), concerning the ice mass, ice mass change, cumulative SMB, and cumulative ice discharge. The sensitivity indices provided in the figure are presented in their non-normalized form.

C4 Weighted parameters

The full-period weighting method used shows a clear preference for members for whom friction initialization was carried out with data from the 1990s and 2000s, as shown by the weights assigned (Fig. 7b). This preference is attributed to the comparatively low RMSE values observed for these members. Conversely, members with inversions conducted in 2010 or 2017 necessitate extrapolation in regions where the ice front has retreated, thereby introducing additional uncertainties into their performance assessment. Consequently, these later inversions exhibit poorer performance in ice-free areas before the retreat due to the need for extrapolation. Notably, the influence of the inversion year diminishes considerably after the retreat of the ice front. The fact that we faithfully reproduce the data when the front retreats gives greater confidence in the results of our predictions, as the front tends to retreat.

The presence or absence of the f_param emerges as the second prominent factor influencing the distribution shift between the prior and posterior in the full-period weighting process, subsequent to OBS_inv (Fig. 7c). This finding aligns with the findings of our previous study (Jager et al., 2024), where we demonstrated the crucial role of this parameterization in enabling the model to accurately reproduce data spanning the period from 1985 to 2019.

Regarding the regularization weight of the cost function, λ_reg, the distribution tends to shift towards lower values (Fig. 7a). This implies that excessively high λ_reg values result in elevated RMSEs due to an overly smooth friction field. This result is noteworthy, as it suggests that solutions with less smoothness, potentially influenced by data noise, are not necessarily of inferior quality. This scenario is preferred over excessive regularization, highlighting the importance of striking a balance between regularization strength and model fidelity.

Regarding the parameters m, f_law, and E, there are no substantial trends in the difference between the prior and posterior distributions (see Fig. 7d, e, and f). However, for the parameter m, members with values exceeding 0.4 or approximately 0.25 exhibit higher weights, although this outcome could be attributed largely to the influence of λ_reg, OBS_inv, and f_param. Likewise, members characterized by an E value near 1.9 and f_law=W demonstrate increased weights. In hindsight, our initial choice of distribution for these three parameters proves to be suitable due to the absence of significant changes observed in their posterior distributions.

In terms of sub-period weighting (Fig. 7), the notable alteration is the amplification of the discrepancy in f_param selection. Specifically, the posterior probability rises from 6.4 to 7.4, indicating a greater likelihood for parameterized members to accurately replicate distinct periods. These findings provide further validation of and support for the outcomes reported in Jager et al. (2024).

Appendix D: Cross-validation of Bayesian calibration choices

Figure D1 visually presents the normalized continuous rank probability score (CRPS) as a performance metric for distinct calibrated ensemble configurations. These configurations encompass full-period weighting, sub-period weighting, and f_param weighting approaches. The CRPSs are computed for ice discharge, cumulative ice discharge, surface elevation, and surface velocity, providing a comprehensive view of the calibrated ensembles' performance across various datasets. In addition, it is important to note that similar figures illustrating the mean absolute error of the ensemble mean (MAE, Eq. 4), the standard deviation of the ensemble (SD, Eq. 5), and the non-normalized values are not included to avoid duplication (see Supplement, Figs. S1 to S5). Moving beyond the graphical presentation, this section undertakes a thorough analysis of the calibrated ensemble's performance in relation to Hpr under different weightings. We begin by scrutinizing the full-period weighting approach, delving into how variations in probability density form, the estimate used for σ, and the data choice for the calibration. Subsequently, we evaluate the outcomes of sub-period weighting and f_param weighting methodologies.

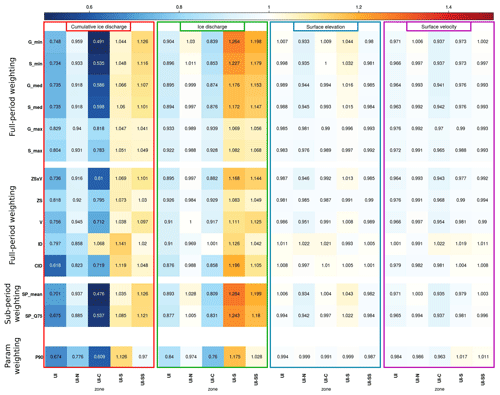
Figure D1 Normalized CRPS applied to cumulative ice discharge (red), ice discharge (green), surface elevation (blue), and surface velocity (purple) for different calibrated ensembles: full-period weighting (G_min: Gaussian distribution with $\mathit{\sigma }=min\left(\mathrm{RMSEs}\right)$; G_max: Gaussian distribution with $\mathit{\sigma }=max\left(\mathrm{RMSEs}\right)$; G_med: Gaussian distribution with σ=median(RMSEs); S_min: Student's distribution with σ=min(RMSEs); S_max: Student's distribution with $\mathit{\sigma }=max\left(\mathrm{RMSEs}\right)$; S_med: Student's distribution with σ=median(RMSEs); ZSxV: calibration with RMSE for surface elevation and velocity; ZS: calibration with RMSE for surface elevation; V: calibration with RMSE for surface velocity; ID: calibration with RMSE for ice discharge; CID: calibration with RMSE for cumulative ice discharge), sub-period weighting (SP_mean: σ=mean(RMSEs); SP_Q75: σ=quantile_0.75(RMSEs)), and f_param weighting (P90: w_i=0.9 if $f_{\mathrm{param}}^i=\text{true}$, else w_i=0.1). The “UI” line represents the calibration using data from all four sub-catchments and is evaluated over the entire validation area. On the other hand, the “UI-N”, “UI-C”, “UI-S”, and “UI-SS” lines correspond to calibrations using data from the three other sub-catchments, and they are evaluated over their respective sub-catchments (Fig. 1).

In general, all the various calibrations result in notable improvements in the CRPS of the ensemble. This improvement is evident in the prevalence of blue shades (67 %), indicating lower CRPS values, compared to yellow–red shades (33 %), indicating higher CRPS values, and the presence of more dark-blue shades than dark-red shades. For all combinations, the SD is reduced by 20 [4,56] % for cumulative ice discharge, 18 [5,47] % for ice discharge, 10 [2,23] % for surface elevation, and 17 [2,34] % for velocity. Furthermore, the MAE is also reduced overall, with a decrease observed in 70 % of the cases.

Notably, significant differences are observed between the CRPS of the different sub-catchments: for the cumulative ice discharge and ice discharge, the CRPS rarely increases for UI-S and UI-SS, while the opposite is true for UI-N and UI-C. This disparity corresponds to lower CRPS values for cumulative ice discharge and ice discharge before calibration. For UI-S and UI-SS, the CRPS before calibration applied to cumulative ice discharge is 0.07 and 0.06 Gt, respectively, compared to 0.22 and 0.43 Gt for UI-N and UI-C. Similarly, their CRPS applied to ice discharge is also lower, at 1.1 and 0.8 Gt a⁻¹, compared to 1.7 and 4.1 Gt a⁻¹ for UI-N and UI-C, respectively. The regions where the CRPS is lower before calibration correspond to areas where the front retreat was not brief, as is seen in the case of UI-N and UI-C. This can be attributed to the fact that, due to the inversion process and with no major change in dynamics like that observed for UI-N and UI-C, all the members are already capable of reproducing the observed data, rendering the calibration process less impactful on the inversion ensemble in these cases.

Additionally, a disparity is observed in the response of different data types, with notably greater reductions or increases observed for global data, such as cumulative ice discharge and ice discharge, compared to spatio-temporal data, such as surface elevation and velocity. Furthermore, no significant patterns are discernible between sub-catchments concerning these spatio-temporal data.

D1 Influence of the data used

Among the full-period weightings using different data, the calibration using the RMSE of both surface velocity and surface elevation (ZSxV) demonstrates the highest robustness in reducing the CRPS for various observations. For the UI-N sub-catchment, ZSxV significantly reduces the CRPS for cumulative ice discharge, ice discharge, surface elevation, and velocity by −8.4 %, −0.3 %, −5.4 %, and −0.7 %, respectively. Similarly, for the UI-C sub-catchment, it leads to substantial reductions in the CRPS for cumulative ice discharge, ice discharge, surface elevation, and velocity by −39 %, −11.8 %, −0.8 %, and −5.7 %, respectively. Additionally, ZSxV contributes to reducing almost all the CRPS values for surface elevation and velocity in the UI-S sub-catchment by +1.3 % and −2.3 %, respectively, and in the UI-SS sub-catchment by −1.5 % and −0.8 %, respectively. This is due to a reduction in the MAE in the majority of cases (75 %), as well to a reduction of −17 [−11, −25] % in the SD. On the other hand, the cumulative-ice-discharge (CID) calibration enhances the CRPS for the UI-N and UI-C sub-catchments concerning cumulative ice discharge (−18 % and −28 %), ice discharge (−1 % and −14 %), and velocity (−2 % and −2 %) but does not yield significant improvements for surface elevation (+0 % and +1 %). However, for the UI-S and UI-SS sub-catchments, cumulative-ice-discharge calibration results in increased CRPS values (88 % of the cases). These observed increases are likely indicative of overfitting, as evidenced by a reduction in the MAE in most cases and in the SD in all cases.

In the case of the ice discharge (ID) calibration, it primarily improves the CRPS for ice discharge itself but does not have a considerable impact on other observations, such as cumulative ice discharge, surface elevation, and velocity. For most instances, this improvement is accompanied by an increase in the MAE, suggesting that the ice discharge calibration may not effectively identify the “best” members due to the presence of noisy or imprecise data.

Lastly, applying a weighting system based on surface elevation (ZS) or velocity (V) leads to improved the CRPS for each type of observation in the UI-N and UI-C sub-catchments, including cumulative ice discharge, ice discharge, surface elevation, and velocity. However, the degree of improvement is less pronounced compared to the weighting with the combined use of both variables (ZSxV), e.g. −29 % and −20 % for ZS and V calibrations for the cumulative-ice-discharge CRPS in UI-C as opposed to −39 % for ZSxV. Notably, there is a reduction in the MAE, primarily for surface elevation and velocity observations, and SD, though it is not as significant as when employing the combined data. Consequently, relying solely on velocity or surface elevation (ZS) for calibration assignment appears to result in under-utilization of data.

D2 Influence of the form of the probability density on ZSxV

To assess the sensitivity of the calibration to the choice of probability density functions, we explore two distinct distributions: Gaussian (G) and Student's with 2 degrees of freedom (S). These distributions are combined with three different estimates for the parameter σ, which are based on the minimum (min), median (med), and maximum (max) values within the ensemble of RMSEs. We do not show the results with the mean, which are almost identical to those with the median. In Fig. D1, the first letter (G or S) denotes the distribution type, while the second part signifies the specific σ estimate employed.

Among the six different distribution shapes (G_min, G_max, G_med, S_min, S_max, S_med) used for calibration, the utilization of the Student distribution leads to a marginally lower CRPS compared to its Gaussian counterpart across all variables and catchments, with an average reduction of −1.6 % compared to −1.3 %. In most cases, employing Student's distribution for weighting leads to a lower reduction in SD (−14 % against −15 % on average) but a lower increase in the MAE (+0.18 % against +0.42 % on average). However, based on these results, it remains inconclusive whether weighting using a Gaussian distribution yields a poorer CRPS because it is less close to observations with the MAE or because it is too confident with the SD, i.e. too low a sharpness.

Similarly, calibration using the median or the mean of RMSE as an estimate of σ demonstrates a better CRPS in most cases compared to those using the minimum or maximum of RMSE as an estimate, which assigns greater and lower weights, respectively, to members that fit the data best. Thus, there is an average CRPS reduction of −1.8 % for the median versus −1.0 % for the minimum and −1.2 % for the maximum. Weighting with the maximum leads to a reduction in the mean absolute error (MAE) by an average of −0.69 %, whereas using the minimum and median weights results in an increase of +1.2 % and +0.43 %, respectively. However, when considering the SD, the values of the minimum estimate are consistently lower, with reductions of −23 % on average for the minimum compared to −15 % and −6 % for the median and maximum. Therefore, the relatively modest reduction in the CRPS with the minimum estimate can be attributed to its overconfident nature, whereas the limited reduction in the CRPS with the maximum estimate is indicative of its underconfident nature. The median RMSE estimate for σ appears to strike the best balance, with additional tests indicating that using the mean as an estimate of σ yields results similar to those obtained with the median.

D3 Use of sub-periods

The sub-period weighting SP_mean uses the following characteristics: Student's distribution, the mean of RMSEs for the estimate of σ, and utilization of surface elevation and velocity data (ZSxV); it does not yield improvements in the CRPS for ice discharge, surface elevation, and velocity (+8 %, −0.9 %, and −2 %, respectively, against an average of +4.6 %, −1.6 %, and −2.4 %, respectively). However, a reduction in the CRPS is observed for cumulative ice discharge (−10.6 % against an average of −7.7 %). Despite this, SP_mean leads to a decrease in the MAE of the mean in 69 % of the cases and a significant decrease in SD for these variables (−26 % against an average of −14 %). These findings indicate that the SP_mean weighting may be overconfident, as it excessively reduces the model's uncertainty.

To address the issue of overconfidence, alternative proxies for σ were tested. It was found that using the 75th percentile (SP_Q75) of the RMSE distribution as an estimate for σ resulted in better CRPS values for ice discharge, surface elevation, and velocity (+6.5 %, −1.4 %, −2.3 %, respectively, compared to +8 %, −0.9 %, and −2 %, respectively, for SP_mean previously). However, the CRPS for cumulative ice discharge becomes worse and closer to S_med (−9.3 % versus −10.6 % for SP_mean previously). Consequently, we decided to analyse the results of this calibration choice as the sub-period weighting.

D4 The f_param weighting

To evaluate the effectiveness of an ensemble that assigns greater significance to the parameterization developed in Jager et al. (2024), we conducted an analysis of the f_param weighting's performance in terms of the CRPS, MAE, and SD. This also enables us to assess whether the intricacies of the validation analysis conducted in the initial study, which encompassed elements such as initial state maps and the temporal evolution of velocity and surface elevation, can be effectively captured within the broader scope of this global analysis.

The CRPS analysis reveals that the f_param weighting outperforms both the full-period and the sub-period weightings for cumulative ice discharge and ice discharge, achieving reductions of −1.6 % and −13 %, respectively, for P90. In contrast, the SP_Q75 weighting shows CRPS changes of +5.5 % and −7.7 % for cumulative ice discharge and ice discharge, while the S_med weighting yields CRPS changes of +4.6 % and −7.7 % for the same variables on average. However, for surface elevation and velocity, the f_param weighting results in slightly lower CRPS reduction (−0.6 % and −0.8 % for P90) compared to the CRPS reduction of −1.6 % and −2.2 % for SP_Q75 and −1.6 % and −2.4 % for S_med on average.

Consistent patterns are observed for the MAE of the mean and the SD. For cumulative ice discharge and ice discharge, the P90 weighting yields lower MAE values (−2 % and +1.6 % for P90, respectively) compared to the SP_Q75 weighting (+4.8 % and +7 %). Similarly, the P90 weighting leads to lower SD values for cumulative ice discharge and ice discharge (−19.6 % and −23.4 %, respectively) in contrast to the SP_Q75 weighting (−19.1 % and −21.4 %). However, for surface elevation and velocity, the P90 weighting results in higher MAE values (−1.7 % and −2.1 %, respectively) compared to the SP_Q75 weighting (−3 % and −5.3 %). Similarly, the P90 weighting leads to higher SD values for surface elevation and velocity (−8.4 % and −11.2 %, respectively) in contrast to the SP_Q75 weighting (−10.6 % and −19.6 %).