the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A model for French-press experiments of dry snow compaction
Colin R. Meyer
Kaitlin M. Keegan
Ian Baker
Robert L. Hawley
Snow densification stores water in alpine regions and transforms snow into ice on the surface of glaciers. Despite its importance in determining snow-water equivalent and glacier-induced sea level rise, we still lack a complete understanding of the physical mechanisms underlying snow compaction. In essence, compaction is a rheological process, where the rheology evolves with depth due to variation in temperature, pressure, humidity, and meltwater. The rheology of snow compaction can be determined in a few ways, for example, through empirical investigations (e.g., Herron and Langway, 1980), by microstructural considerations (e.g., Alley, 1987), or by measuring the rheology directly, which is the approach we take here. Using a “French-press” or “cafetière-à-piston” compression stage, Wang and Baker (2013) compressed numerous snow samples of different densities. Here we derive a mixture theory for compaction and airflow through the porous snow to compare against these experimental data. We find that a plastic compaction law explains experimental results. Taking standard forms for the permeability and effective pressure as functions of the porosity, we show that this compaction mode persists for a range of densities and overburden loads. These findings suggest that measuring compaction in the lab is a promising direction for determining the rheology of snow through its many stages of densification.
- Article
(1828 KB) - Full-text XML
- BibTeX
- EndNote
Snow densification in alpine and polar regions transforms snowflakes into ice crystals. On the surface of glaciers and ice sheets, fresh snow is buried by new snow each winter, thereby slowly transforming into firn and then glacial ice as it compresses and descends. In cold and dry environments (e.g., melt-free accumulation areas of mountain glaciers, interior Greenland, and Antarctica), surface snow evolves due to temperature gradient metamorphism and atmospheric interactions (Dadic et al., 2008; Chen and Baker, 2010b). In the region below the surface, snow compaction is thought to occur in three stages (Herron and Langway, 1980; Arnaud et al., 2000; Cuffey and Paterson, 2010). In the first stage near the surface, compaction occurs by grain growth and rearrangement due to grain boundary sliding (Alley, 1987). In the second stage, compaction occurs through increasing overburden pressure inducing creep deformation and sintering (Wilkinson and Ashby, 1975; Wilkinson, 1988; Arnaud et al., 1998; Spencer et al., 2001). In the final stage, interconnected pores have closed off, and further compaction is caused by air bubble compression (Alley and Bentley, 1988; Salamatin et al., 1997; Gregory et al., 2014). In wet environments, such as the percolation zone of mountain glaciers and Greenland as well as many ice shelves of Antarctica, compaction occurs by a combination of dry snow compaction processes and refreezing of meltwater, which can either enhance or detract from the densification processes just mentioned (Colbeck, 1976; Machguth et al., 2016; Meyer and Hewitt, 2017). Although meltwater percolation is an important part of the compaction process in many areas (e.g., Colbeck, 1972; Bartelt and Lehning, 2002; Wever et al., 2014; Steger et al., 2017), we will only consider dry snow compaction here.
An important reason for studying snow compaction on glaciers, ice sheets, and snowfields is to connect a change in surface elevation to a volume of stored water. The total water volume stored in glaciers and snowpacks is important to know for current as well as future water resources and sea level rise considerations. Additionally, compaction is important for ice core analysis (Barnola et al., 1991; Goujon et al., 2003; Cuffey and Paterson, 2010). At the bottom of the firn column, the difference between the ice age and the gas age is an important input into paleoclimate reconstructions of temperature in ice cores and must be estimated using a compaction model (Arnaud et al., 2000). Compaction can be measured through tracking relative displacements of metal markers (Hawley et al., 2004) or snow features in optical stratigraphy (Hawley and Waddington, 2011), autonomous phase-sensitive radio-echo sounding (Nicholls et al., 2015), vertical strain fiber-optic sensors (Zumberge et al., 2002), the relative-displacement “coffee can” technique (Hamilton et al., 1998; Hamilton and Whillans, 2000), and a continuously recording coffee can method (Arthern et al., 2010; Stevens, 2018).
In one-dimensional compaction, the body force acting on the snow is gravity, leading to an overburden pressure σo, which increases with depth z below the surface zs. Given mass and momentum conservation, all that is needed to predict the densification rate (i.e., surface ice velocity wi(zs) and strain rate within the snow column ) is a constitutive relationship between stress σo and strain rate in one vertical dimension. Thus, snow compaction can be thought of as a problem of rheology, where the rheology is complicated due to variation with depth, temperature, humidity, and water content, among many other physical processes. Three common approaches to characterizing the rheology of a material (Tanner, 2000) are empirical analysis (e.g., Herron and Langway, 1980), microstructural analysis (e.g., Alley, 1987), and experimental analysis. It is this last approach that we describe in this paper.
The standard compaction law applied to most glaciers and ice sheets is a one-dimensional relationship for the rate of change of snow density ρ with depth; i.e.,
where 𝒞 is the compaction function and can depend on the snow density ρ, ice density ρi, temperature T, accumulation rate , overburden pressure σo, vertical strain rate , humidity, water saturation, grain size, and potentially many other physical processes (Spiegelman, 1993; Arthern et al., 2010; Lundin et al., 2017). Herron and Langway (1980) take , where c is an empirical function. However, including the accumulation rate in the compaction function is dubious as it really should enter the mass conservation equations as a boundary condition (Meyer and Hewitt, 2017). Other forms of the righthand side of Eq. (1) are discussed in Zwally and Li (2002), Reeh (2008), Morris and Wingham (2014), and Morris (2018). In this paper, we experimentally and mathematically analyze the function dependence of 𝒞 on overburden pressure and strain rate.
We now summarize the outline of the paper. In Sect. 2, we describe the laboratory compaction experiments of Wang and Baker (2013) and the samples used. In Sect. 3, we construct a continuum model to describe the experiments and implement our model numerically. Lastly, in Sect. 4, we compare the theoretical predictions for the snow compaction with the Wang and Baker (2013) data, showing that the theory does an excellent job explaining the snow compaction. We additionally discuss how this can be implemented into a compaction model such as Eq. (1) and our plans for future work, before a short conclusion section.
Table 1Initial values of density and specific surface area for the four sintered low-temperature snow samples used in Wang and Baker (2013). Naming convention follows Fierz et al. (2009).
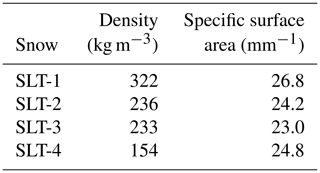
To understand the microstructural origin of macroscopic snow material properties, the role of snow microstructure in avalanche initiation, and snow metamorphosis, Wang and Baker (2013) performed continuous compression tests on snow samples collected near Dartmouth College in Hanover, NH (USA). In their experiments, Wang and Baker (2013) focused on nine samples, ranging from (i) relatively warm, freshly fallen, low-density snow to (ii) snow that was collected during cold air temperatures (ca. −7 to −9 ∘C) and placed in a −30 ∘C cold room for 1 year, allowing for the snow crystals to sinter. In the sintering process, bonds form between snow crystals (Male, 1980; Chen and Baker, 2010a; Wang and Baker, 2017) and the snow evolved into round and well-connected snow grains during the year in the cold room (Chen and Baker, 2010b). In this paper, we focus on the four sintered samples from Wang and Baker (2013), as they are most applicable to alpine snowpacks and firn on glaciers. The naming convention for these sintered low-temperature (SLT) samples follows Fierz et al. (2009), where the highest density sample is SLT-1 and the lowest density sample is SLT-4 (see Table 1). Before compaction, the samples were vibrated to construct samples with different densities, undoubtedly breaking some of the sintered bounds. These sintered and vibrated samples represent a range of densities with relatively small differences in specific surface area (SSA; surface-to-volume ratio, viz. Table 1). The snow samples were then extruded as cylinders, 15.7 mm in diameter and 18 mm tall, and placed on a Skyscan material testing compression stage (i.e., a French-press or cafetière-à-piston-style coffee maker) inside of a microscopic computed tomography (micro CT) machine. A schematic of the compression stage is shown in Fig. 1. Both the top and bottom plates are impermeable but the air contained within the snow is able to flow out the side of the open sample. The samples were compressed at a constant rate of 12.7 mm h−1 (i.e., 111 m yr−1 or a pore-scale Reynolds number of with 1 mm as a characteristic pore size) for the full 5.7 mm dynamic range of the Skyscan compression stage. To avoid termination effects, we only consider the first 5 mm of the range (Wang and Baker, 2013). The compression stage measured the load required to maintain a constant displacement rate for each snow sample. Wang and Baker (2013) then plot the loading stress as a function of the displacement, from which we can derive a stress-strain curve. In the next section, we develop a model for constant-displacement-rate compaction experiments, and in Sect. 4 we compare the model predictions for stress versus displacement against the Wang and Baker (2013) experimental data.
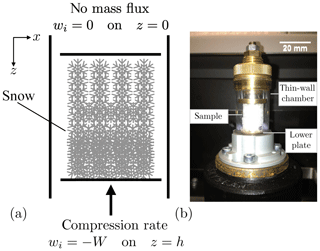
Figure 1Schematic diagram of the snow French press: (a) idealized framework for the theory, including the boundary conditions; and (b) experimental setup from Wang and Baker (2013) showing the snow sample housed within the sample chamber and the upward motion of the lower plate. The sample is small enough that the effects of gravity can be ignored. The top and bottom plates are impermeable, but air can flow out of the sides of the snow sample.
Compaction occurs in a variety of natural and industrial processes, such as sedimentary basin formation, paper pulp dewatering, and particle flocculation, and has motivated numerous experiments and mathematical models (e.g., Landman et al., 1991; Fowler and Noon, 1999; Fowler, 2011; Hewitt et al., 2016a, b; Paterson et al., 2019). In this section, we describe the theory outlined by Hewitt et al. (2016b), although we write the theory in terms of porosity ϕ rather than the solid fraction.
For dry snow that is composed of solely air and ice particles, snow density ρ is given as
where ϕ is the porosity, i.e., the void space (Gray, 1996). The density of air is ρa and the density of pure ice is ρi, both of which we treat as constant. Although air density increases when pressurized in a confined space, in an open system where the air is able to flow, the air density is approximately constant. In the firn column of a glacier or ice sheet, the transition between freely flowing air and confined air is known as the pore-close-off depth. Below the pore-close-off depth the air density will increase with pressure, and above the pore-close-off depth, the air is approximately constant density.
Now from the expression in Eq. (2), it is clear that density variation in snow is equivalent to variation in porosity: near the surface of a glacier or snowpack, the snow air content is high and then density is closer to ρa, whereas at depth, the snow air content is low, and the density approaches ρi. Treating snow as a mixture of air and ice, mass conservation of each component may be written as
where ua is the air velocity, ui is the ice velocity, and ms is the mass exchange between each phase due to sublimation. Again, we treat the densities of each substance as constant, meaning that it is so easy for air to escape from the snow that the air density does not change. We also neglect phase change (i.e., ms=0) and restrict our attention to one vertical dimension. Thus, we can write this model as
Now adding Eqs. (5) and (6) gives the insight that decreasing the porosity requires evacuating the incompressible air out of the pore space or, alternatively, air motion allows for snow compaction; i.e.,
In other words, there is an exact volumetric trade-off where the pore space occupied by air is filled by ice during compaction.
In the Wang and Baker (2013) experiments, the sample has an initial height of mm (see Fig. 1), and, therefore, the overburden pressure is negligible when compared to the applied stress. We take the vertical coordinate system to increase downward. At the top of the sample z=0, the wall is impermeable; i.e., . Thus, we can integrate Eq. (7) to find that
We model the airflow through porous snow using Darcy's law, which is given as
for permeability k(ϕ), air viscosity μ, and air pressure p. As described by Hewitt et al. (2016b), Eq. (8) relates the solid ice velocity wi to the Darcy velocity of the airflow through the pores. Thus, combining Eqs. (8) and (9), we find that
that is, the ice particle velocity is determined by the pressure gradient driving air motion.
Force balance in the vertical direction is given as
where Σ is the vertical bulk compressive stress (Hewitt et al., 2016b). We define effective pressure N as the difference between the compressive stress and air pressure, i.e., , and write Eq. (10) as
As is typical in soil mechanics (Tulaczyk et al., 2000) and other applications of compaction (Fowler, 2011), we can relate the effective pressure N to the porosity ϕ through an empirical constitutive relationship, so that N is identically equal to N(ϕ). This relationship is a form of plasticity as there is a one-to-one correspondence between load and density without reference to displacement, strain rate, or stress history. Inserting this into Eq. (12) and putting that into Eq. (6) gives
which is a nonlinear diffusion equation for the porosity, and is the derivative of the effective pressure with respect to the porosity.
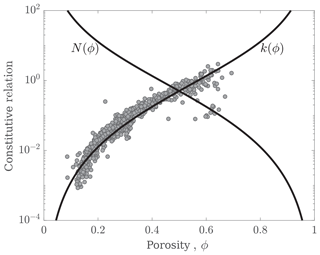
Figure 2Effective pressure N(ϕ) and permeability k(ϕ) constitutive relations as functions of the porosity ϕ for the snow compaction theory. The gray dots are permeability measurements of firn cores from Summit, Greenland (Adolph and Albert, 2014), and show excellent agreement with the Kozeny–Carman permeability model, Eq. (14) with a=3 and b=2.
3.1 Constitutive relations
Equation (13) is a general model for mechanical compaction, and the application to a specific system comes largely from the choice of constitutive relations for k(ϕ) and N(ϕ). A common choice for the permeability is the Kozeny–Carman model; i.e.,
which is commonly used throughout poromechanics (Rice and Cleary, 1976; McKenzie, 1984; Schoof and Hewitt, 2016) and has been extensively evaluated for snow and firn (Albert and Shultz, 2002; Adolph and Albert, 2013, 2014; Keegan et al., 2014), as shown in Fig. 2. Typical values for the exponents are a=3 and b=2. A competing model is a logarithmic permeability (Tait and Jaupart, 1992; Katz and Worster, 2008), of the form
and there are many other permeability models (e.g., Hewitt et al., 2016b). Here we use the Kozeny–Carman model. However, before future compaction experiments, we will measure the permeability and determine the constitutive relation as well as associated parameters that best represent each sample.
The dependence of effective pressure on the porosity of a sample has not to our knowledge been measured for snow or firn. In other systems (e.g., Hewitt et al., 2016b), a plastic constitutive relationship between the effective pressure and porosity is given by
where typical exponents are n=3 and m=2 (see Fig. 2). An exponent of in the numerator is sometimes used for very porous materials (Hewitt et al., 2016b). Just as for the permeability, in the future we plan to measure the constitutive relation for effective pressure with porosity of each sample.
3.2 Boundary and initial conditions
As shown in Fig. 1, the samples were small and loaded from the bottom. The mathematical model for mechanical compaction results in a nonlinear diffusion equation for the porosity ϕ, given in Eq. (13). Regardless of the choice of constitutive relations, two boundary conditions and one initial condition are required. At the top of the sample, as we mentioned before, the ice and airflow must go to zero; therefore, the first boundary condition is
In terms of the porosity, this boundary condition translates into
which is a Neumann boundary condition.
At the bottom of the sample z=h, we apply a constant displacement rate, W; i.e.,
or equivalently
which is also a Neumann boundary condition. Importantly, the constitutive equations play a role at the surface and not at depth. The air pressure at the bottom of the sample is approximately atmospheric, i.e., p=0, due to the ease at which air can escape the sample. The varying load required to compress the sample at a constant rate is
which we will compare to the Wang and Baker (2013) experimental data in the next section.
The initial condition is that the snow sample starts with a uniform porosity throughout; i.e.,
Additionally, the height of the snow sample evolves as a free boundary during compaction according to
with the initial condition
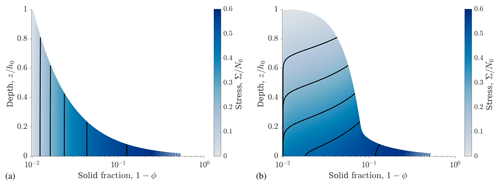
Figure 3Compaction profiles for the theoretical model showing solid fraction change (1−ϕ, where ϕ is the porosity) with depth (cf. Hewitt et al., 2016b). Color map shows nondimensional stress and the black lines show the profiles at nondimensional time . Panels: (a) slow compaction (γ=1000), where the solid fraction is uniform with depth; and (b) fast compaction (γ=1), where significant compaction occurs near the lower part of the sample.
3.3 Nondimensional equations and numerical solution
In our theory for the snow compaction experiments of Wang and Baker (2013), we solve for the evolution of porosity with depth and time, as determined by Eq. (13) with the constitutive relations (14) and (16), the boundary conditions (18) and (20), and the initial conditions (22) and (24). Taking the initial sample height h0 to be a representative length scale, the displacement rate W to be a characteristic velocity, the initial height to displacement rate as a timescale , and k0 and N0 to be scales for the permeability and effective pressure, respectively, we can nondimensionalize the variables as
, , , ,
where the hats represent nondimensionalization, although, for ease of notation, we immediately drop the hats. Inserting this nondimensionalization into the equations, we have the following:
the governing equation
constitutive equations
boundary conditions
and initial conditions
where
is the ratio of pressure gradient N0∕h0 to viscous resistance μW∕k0. Alternatively, this group can be thought of as the ratio of effective pressure N0 to viscous pressure μW∕h0 multiplied by the Darcy number (Bear, 1972).
We solve Eqs. (25)–(28) numerically using a finite volume discretization and the method of lines implemented in Python (LeVeque, 2002). To facilitate the numerical computations, we map the compaction domain into a stationary domain by using the change of variables , which introduces a fictitious advection term into Eq. (25) (Hewitt et al., 2016b). Solutions for two different values of γ and the standard exponents (i.e., a=3, b=2, n=3, m=2) are shown in Fig. 3. The two panels show the two primary regimes: for large values of γ (left panel, γ=1000; Fig. 3a), the porosity ϕ (or equivalently solid fraction, 1−ϕ) is constant with depth. For smaller values of γ (right panel, γ=1; Fig. 3b), compression begins at the bottom of the sample and the top of the sample remains at the starting porosity. As time goes on the sample is compressed and more of the sample compacts.
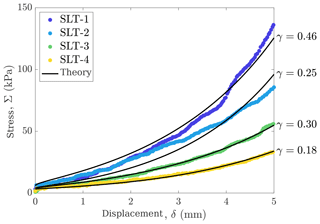
Figure 4Comparison of theory with French-press experiments from Wang and Baker (2013): four snow samples were compacted in a Skyscan micro CT scanner at a constant displacement rate (see Sect. 2 and Fig. 1). Using the theory outlined in Sect. 3, the starting density of each sample, and reasonable parameters, we show agreement between theory and experimental data. For the theory, the constitutive exponents are the typical values (a=3, b=2, m=2, n=2), the stress was scaled (i.e., prefactor N0=30 kPa, friction σf=3 kPa), and the values of γ for each curve are shown on the right.
Here we compare the predictions of the theory outlined in the previous section with the experimental data of Wang and Baker (2013), which we described in the Sect. 2. A key output of these experiments was the applied load required to compact the snow as a function of displacement, during the constant-displacement-rate experiments. These data are shown in Fig. 4. The lowest density snow SLT-1 withstands the least stress as a function of displacement. As the density of the snow samples increases, so does the required stress for a given displacement. A similar observation can be made for the theory: the applied load is given by Eq. (21) and can be written dimensionally as
which states that the applied load Σ increases as the porosity ϕ decreases (see Fig. 2). In other words, for a given displacement, the stress in the theory will also increase as the initial density increases, which is also true for the experimental data, meaning that we have chosen a sensible constitutive law. The theory for the load as a function of the displacement makes sense qualitatively, but we can compare the theory to the experiments in the following way: we run the full model, Eqs. (25)–(28), and evaluate the stress in Eq. (30) using the value of the porosity ϕ at the bottom of the sample z=h and plot it against the displacement . The results for reasonable parameters are shown as black lines in Fig. 4.
The model, therefore, contains three inputs and seven parameters. The most important and most uncertain parameter is γ. Due to the fact that the permeability prefactor k0 and the plastic effective pressure prefactor N0 are unconstrained, we choose representative values for each sample. The permeability prefactor k0 only appears within γ, whereas the plasticity prefactor N0 appears in γ and is required to scale the theory output to compare with experiments. The next four parameters are the exponents a, b, m, and n, which have expected values, but again have not been measured for these samples. Therefore, we only examine small departures from typical values. Additionally, as we will see, there is a small amount of friction in the compression device, and so a small constant stress σf is added to the stress output from the theory; i.e., at z=h. This approach was also used by Hewitt et al. (2016b) in their experiments. The inputs are the initial porosity of the sample, which is set by the initial density measured by Wang and Baker (2013). Another input to the problem is the initial height of the sample, h0. The total experiment run time tf is also an input and set by the final displacement divided by the displacement rate; i.e., , which is about 24 min.
The values of the fixed parameters used for the theory lines in Fig. 4 are the typical exponents (i.e., a=3, b=2, m=2, n=2) and the load information σf=3 kPa and N0=30 kPa. The value of γ for each curve is shown on the figure and is γ=0.46 (SLT-1), γ=0.25 (SLT-2), γ=0.29 (SLT-3), and γ=0.18 (SLT-4). In selecting these values, we successfully (1) found fixed load parameters that worked for all of the experiments and (2) kept the constitutive exponents as the typical values. Thus, γ is the only parameter that varies between theory predictions for each experiment, which is to be expected due to potential variation of k0 with grain size. It is worth emphasizing that this is not a systemic nonlinear best-fit analysis for seven parameters; rather, the agreement between theory and experiment demonstrates a physically motivated model with a single underconstrained parameter.
In general, there is excellent agreement between the theoretical predictions and the experimental data. For the bottom two samples, SLT-3 and SLT-4, the theory captures all of the major data trends and all falls well within any experimental scatter. For the top sample SLT-1, the theory does a reasonable job in capturing the data trend, yet for these parameters it does not follow the data points exactly. A better fit can be obtained by changing the parameters, indicating that this sample may be a different compaction regime than SLT-3 or SLT-4. However, the fit is reasonable enough that this sample is likely just on the edge of a new regime, if at all. In contrast to the other samples, the theory does not adequately capture the data trend of the middle sample, SLT-2. This sample is interesting because it has almost the same density and specific surface area as SLT-3, yet it responded very differently to compression loading. Due to the small size of the samples, i.e., 15.7 mm in diameter and 18 mm tall, the likelihood of defects or inhomogeneities dominating the results is quite high. Thus, the snow bonds in SLT-2 from prior sintering could have been particularly stubborn, requiring more load for a given displacement.
Another possibility for why the two snow samples SLT-1 and SLT-2 did not agree as well with the theory as SLT-3 and SLT-4 is that pressure sintering during the experiment allowed for greater bonding of snow crystals. Adding pressure is an efficient method of accelerating the rate of sintering and can lead to sinter rates that are orders of magnitude faster than by ambient surface energy differences alone (Rahaman, 2007). For this reason, Wang and Baker (2013) attribute the increase in required load to accelerating the sintering and coarsening processes occurring within the snow samples. Willibald et al. (2019) also analyze sintering during compaction experiments and find that the sintering rate is enhanced. The plastic compaction theory we present in this paper does not include pressure processes and, therefore, would not be able to describe the stress required to break sintered bonds, although this is a promising direction for future research.
The plastic compaction theory presented here can be related back to the general firn compaction model given in Eq. (1). Rearranging Eq. (6) gives
which is in the form of Eq. (1). Inserting Darcy's law (9) with mass conservation (5) and (6), the compaction function 𝒞 is given by
which shows the connection between compaction and air evacuating pore space as well as the role of the constitutive relations N(ϕ) and k(ϕ). In this way, measuring the parameters of these constitutive relations in the laboratory allows for predictions of compaction using 𝒞 from Eq. (32).
For generalized viscous compaction, McKenzie (1984) starts from Eq. (31) and connects the divergence to an effective pressure Pe through a compaction viscosity ηc; i.e.,
which is the compaction law used in studies of temperate ice (Schoof and Hewitt, 2016; Hewitt and Schoof, 2017; Meyer et al., 2018) and is equivalent to the viscous closure of a Röthlisberger channel (Nye, 1953; Fowler, 1984; Meyer et al., 2016, 2017). The McKenzie (1984) compaction law, Eq. (33), implies that
If we take the effective pressure Pe to be the overburden pressure, i.e., Pe=ρgz, thereby setting the air pressure to zero, we find the pressure-compaction model described by Cuffey and Paterson (2010) following Arthern et al. (2010). Although this compaction model is attractive because it connects viscous processes to compaction, by setting the air pressure to zero (or even a constant), this compaction model fails to capture the evacuation of air from the pore space, which we have shown to be a very important process in the mechanical compaction of laboratory snow samples. In future work, we will adapt the model we present here to include viscous compaction following McKenzie (1984). Instead of neglecting the air pressure, as in the Arthern et al. (2010) work, we will explicitly solve Darcy's law and determine the resulting compaction.
In this paper, we articulated a mathematical model to describe the snow compaction experiments of Wang and Baker (2013). This model consists of mass and momentum conservation as well as porosity-dependent permeability and plastic effective pressure constitutive equations. The outputs of the model are the snow density as a function of time and space as well as the stress as a function of displacement. Comparing the model outputs to the experimental data of Wang and Baker (2013) shows excellent agreement, especially for the low-density sintered snow. As the density increased, small discrepancies between model and theory emerged, potentially due to the necessity of creep or sample defects. Nevertheless, the excellent agreement between theory and experiments suggests that measuring compaction in the lab is a promising direction forward for understanding snow compaction and that the plastic effective pressure as a function of porosity may be a key constitutive relation to quantify.
The data used in this paper are published and the numerical model is publicly available at https://github.com/colinrmeyer/french-press-compaction (last access: 30 April 2020).
CRM and KMK started the project. CRM performed the numerical simulations, compared the model to the Wang and Baker (2013) data, and wrote the first draft of the paper. All authors contributed to subsequent writing and editing.
The authors declare that they have no conflict of interest.
This paper was edited by Guillaume Chambon and reviewed by two anonymous referees.
Adolph, A. and Albert, M. R.: An improved technique to measure firn diffusivity, Int. J. Heat Mass Transfer, 61, 598–604, https://doi.org/10.1016/j.ijheatmasstransfer.2013.02.029, 2013. a
Adolph, A. C. and Albert, M. R.: Gas diffusivity and permeability through the firn column at Summit, Greenland: measurements and comparison to microstructural properties, The Cryosphere, 8, 319–328, https://doi.org/10.5194/tc-8-319-2014, 2014. a, b
Albert, M. R. and Shultz, E. F.: Snow and firn properties and air–snow transport processes at Summit, Greenland, Atmos. Environ., 36, 2789–2797, https://doi.org/10.1016/S1352-2310(02)00119-X, 2002. a
Alley, R. B.: Firn densification by grain-boundary sliding: a first model, J. Phys. Colloques, 48, 249–256, https://doi.org/10.1051/jphyscol:1987135, 1987. a, b
Alley, R. B. and Bentley, C. R.: Ice-core analysis on the Siple Coast of West Antarctica, Ann. Glaciol., 11, 1–7, https://doi.org/10.3189/S0260305500006236, 1988. a
Arnaud, L., Lipenkov, V., Barnola, J.-M., Gay, M., and Duval, P.: Modelling of the densification of polar firn: characterization of the snow–firn transition, Ann. Glaciol., 26, 39–44, https://doi.org/10.3189/1998AoG26-1-39-44, 1998. a
Arnaud, L., Barnola, J. M., and Duval, P.: Physical modeling of the densification of snow/firn and ice in the upper part of polar ice sheets, in: Physics of ice core records, edited by: Hondoh, T., Hokkaido University Press, 285–305, 2000. a, b
Arthern, R. J., Vaughan, D. G., Rankin, A. M., Mulvaney, R., and Thomas, E. R.: In situ measurements of Antarctic snow compaction compared with predictions of models, J. Geophys. Res., 115, F03011, https://doi.org/10.1029/2009JF001306, 2010. a, b, c, d
Barnola, J. M., Pimienta, P., Raynaud, D., and Korotkevich, Y. S.: CO2-climate relationship as deduced from the Vostok ice core: a re-examination based on new measurements and on a re-evaluation of the air dating, Tellus B, 43, 83–90, https://doi.org/10.1034/j.1600-0889.1991.t01-1-00002.x, 1991. a
Bartelt, P. and Lehning, M.: A physical SNOWPACK model for the Swiss avalanche warning: Part I: numerical model, Cold Reg. Sci. Technol., 35, 123–145, https://doi.org/10.1016/S0165-232X(02)00074-5, 2002. a
Bear, J.: Dynamics of flow in porous media, Dover, 1972. a
Chen, S. and Baker, I.: Structural evolution during ice-sphere sintering, Hydrol. Proc., 24, 2034–2040, https://doi.org/10.1002/hyp.7787, 2010a. a
Chen, S. and Baker, I.: Evolution of individual snowflakes during metamorphism, J. Geophys. Res., 115, D21114, https://doi.org/10.1029/2010JD014132, 2010b. a, b
Colbeck, S. C.: A theory of water percolation in snow, J. Glaciol., 11, 369–385, https://doi.org/10.3198/1972JoG11-63-369-385, 1972. a
Colbeck, S. C.: An analysis of water flow in dry snow, Water Resour. Res., 12, 523–527, https://doi.org/10.1029/WR012i003p00523, 1976. a
Cuffey, K. M. and Paterson, W. S. B.: The Physics of Glaciers, 4th edn., ISBN 9780123694614, Butterworth-Heinemann/Elsevier, Burlington, 2010. a, b, c
Dadic, R., Schneebeli, M., Lehning, M., Hutterli, M. A., and Ohmura, A.: Impact of the microstructure of snow on its temperature: A model validation with measurements from Summit, Greenland, J. Geophys. Res., 113, D14303, https://doi.org/10.1029/2007JD009562, 2008. a
Fierz, C. R. L. A., Armstrong, R. L., Durand, Y., Etchevers, P., Greene, E., McClung, D. M., Nishimura, K., Satyawali, P. K., and Sokratov, S. A.: The International Classification for Seasonal Snow on the Ground, vol. 5, UNESCO/IHP, 2009. a, b
Fowler, A. C.: On the transport of moisture in polythermal glaciers, Geophys. Astrophys. Fluid Dyn., 28, 99–140, https://doi.org/10.1080/03091928408222846, 1984. a
Fowler, A. C.: Mathematical geoscience, vol. 36, Springer Science & Business Media, London, 2011. a, b
Fowler, A. C. and Noon, C. G.: Mathematical models of compaction, consolidation and regional groundwater flow, Geophys. J. Int., 136, 251–260, https://doi.org/10.1046/j.1365-246X.1999.00717.x, 1999. a
Goujon, C., Barnola, J.-M., and Ritz, C.: Modeling the densification of polar firn including heat diffusion: Application to close-off characteristics and gas isotopic fractionation for Antarctica and Greenland sites, J. Geophys. Res., 108, 4792, https://doi.org/10.1029/2002JD003319, 2003. a
Gray, J. M. N. T.: Water movement in wet snow, Philos. Trans. R. Soc. London, Ser. A, 354, 465–500, https://doi.org/10.1098/rsta.1996.0017, 1996. a
Gregory, S. A., Albert, M. R., and Baker, I.: Impact of physical properties and accumulation rate on pore close-off in layered firn, The Cryosphere, 8, 91–105, https://doi.org/10.5194/tc-8-91-2014, 2014. a
Hamilton, G. S. and Whillans, I. M.: Point measurements of mass balance of the Greenland Ice Sheet using precision vertical Global Positioning System (GPS) surveys, J. Geophys. Res., 105, 16295–16301, https://doi.org/10.1029/2000JB900102, 2000. a
Hamilton, G. S., Whillans, I. M., and Morgan, P. J.: First point measurements of ice-sheet thickness change in Antarctica, Ann. Glaciol., 27, 125–129, https://doi.org/10.3189/1998AoG27-1-125-129, 1998. a
Hawley, R. L. and Waddington, E. D.: In situ measurements of firn compaction profiles using borehole optical stratigraphy, J. Glaciol., 57, 289–294, https://doi.org/10.3189/002214311796405889, 2011. a
Hawley, R. L., Waddington, E. D., Lamorey, G. W., and Taylor, K. C.: Vertical-strain measurements in firn at Siple Dome, Antarctica, J. Glaciol., 50, 447–452, https://doi.org/10.3189/172756504781829972, 2004. a
Herron, M. M. and Langway, C. C.: Firn densification: an empirical model, J. Glaciol., 25, 373–385, https://doi.org/10.1017/S0022143000015239, 1980. a, b, c
Hewitt, D. R., Nijjer, J. S., Worster, M. G., and Neufeld, J. A.: Flow-induced compaction of a deformable porous medium, Phys. Rev. E, 93, 023116, https://doi.org/10.1103/PhysRevE.93.023116, 2016a. a
Hewitt, D. R., Paterson, D. T., Balmforth, N. J., and Martinez, D. M.: Dewatering of fibre suspensions by pressure filtration, Phys. Fluids, 28, 1–23, https://doi.org/10.1063/1.4952582, 2016b. a, b, c, d, e, f, g, h, i, j
Hewitt, I. J. and Schoof, C.: Models for polythermal ice sheets and glaciers, The Cryosphere, 11, 541–551, https://doi.org/10.5194/tc-11-541-2017, 2017. a
Katz, R. F. and Worster, M. G.: Simulation of directional solidification, thermochemical convection, and chimney formation in a Hele-Shaw cell, J. Comput. Phys., 227, 9823–9840, https://doi.org/10.1016/j.jcp.2008.06.039, 2008. a
Keegan, K., Albert, M. R., and Baker, I.: The impact of ice layers on gas transport through firn at the North Greenland Eemian Ice Drilling (NEEM) site, Greenland, The Cryosphere, 8, 1801–1806, https://doi.org/10.5194/tc-8-1801-2014, 2014. a
Landman, K. A., Sirakoff, C., and White, L. R.: Dewatering of flocculated suspensions by pressure filtration, Phys. Fluids, 3, 1495–1509, https://doi.org/10.1063/1.857986, 1991. a
LeVeque, R. J.: Finite volume methods for hyperbolic problems, vol. 31, Cambridge University Press, 2002. a
Lundin, J. M. D., Stevens, C. M., Arthern, R., Buizert, C., Orsi, A., Ligtenberg, S. R. M., Simonsen, S. B., Cummings, E., Essery, R., Leahy, W., Harris, P., Helsen, M. M., and Waddington, E. D.: Firn Model Intercomparison Experiment (FirnMICE), J. Glaciol., 63, 401–422, https://doi.org/10.1017/jog.2016.114, 2017. a
Machguth, H., MacFerrin, M., van As, D., Charalampidis, C., Colgan, W., Fausto, R. S., Meijer, H. A. J., Mosley-Thompson, E., and van de Wal, R. S. W.: Greenland meltwater storage in firn limited by near-surface ice formation, Nat. Clim. Change, 6, 390–393, https://doi.org/10.1038/nclimate2899, 2016. a
Male, D. H.: The seasonal snowcover, in: Dynamics of Snow and Ice Masses, edited by: Colbeck, S., Academic Press (Toronto, ON), 305–395, https://doi.org/10.1016/B978-0-12-179450-7.50011-5, 1980. a
McKenzie, D.: The generation and compaction of partially molten rock, J. Petrol., 25, 713–765, https://doi.org/10.1093/petrology/25.3.713, 1984. a, b, c, d
Meyer, C. R. and Hewitt, I. J.: A continuum model for meltwater flow through compacting snow, The Cryosphere, 11, 2799–2813, https://doi.org/10.5194/tc-11-2799-2017, 2017. a, b
Meyer, C. R., Fernandes, M. C., Creyts, T. T., and Rice, J. R.: Effects of ice deformation on Röthlisberger channels and implications for transitions in subglacial hydrology, J. Glaciol., 62, 750–762, https://doi.org/10.1017/jog.2016.65, 2016. a
Meyer, C. R., Hutchinson, J. W., and Rice, J. R.: The Path-Independent M Integral Implies the Creep Closure of Englacial and Subglacial Channels, J. Appl. Mech., 84, 011006, https://doi.org/10.1115/1.4034828, 2017. a
Meyer, C. R., Yehya, A., Minchew, B., and Rice, J. R.: A Model for the Downstream Evolution of Temperate Ice and Subglacial Hydrology Along Ice Stream Shear Margins, J. Geophys. Res., 123, 1682–1698, https://doi.org/10.1029/2018JF004669, 2018. a
Morris, E.: Modeling Dry-Snow Densification without Abrupt Transition, Geosci., 8, 464, https://doi.org/10.3390/geosciences8120464, 2018. a
Morris, E. M. and Wingham, D. J.: Densification of polar snow: Measurements, modeling, and implications for altimetry, J. Geophys. Res., 119, 349–365, https://doi.org/10.1002/2013JF002898, 2014. a
Nicholls, K. W., Corr, H. F. J., Stewart, C. L., Lok, L. B., Brennan, P. V., and Vaughan, D. G.: A ground-based radar for measuring vertical strain rates and time-varying basal melt rates in ice sheets and shelves, J. Glaciol., 61, 1079–1087, https://doi.org/10.3189/2015JoG15J073, 2015. a
Nye, J. F.: The flow law of ice from measurements in glacier tunnels, laboratory experiments and the Jungfraufirn borehole experiment, Proc. R. Soc. Lond. Ser. A, 219, 477–489, https://doi.org/10.1098/rspa.1953.0161, 1953. a
Paterson, D. T., Eaves, T. S., Hewitt, D. R., Balmforth, N. J., and Martinez, D. M.: Flow-driven compaction of a fibrous porous medium, Phys. Rev. Fluids, 4, 074306, https://doi.org/10.1103/PhysRevFluids.4.074306, 2019. a
Rahaman, M. N.: Sintering of ceramics, CRC press, Boca Raton, Florida, 2007. a
Reeh, N.: A nonsteady-state firn-densification model for the percolation zone of a glacier, J. Geophys. Res., 113, F03023, https://doi.org/10.1029/2007JF000746, 2008. a
Rice, J. R. and Cleary, M. P.: Some basic stress diffusion solutions for fluid-saturated elastic porous media with compressible constituents, Rev. Geophys., 14, 227–241, https://doi.org/10.1029/RG014i002p00227, 1976. a
Salamatin, A. N., Lipenkov, V. Y., and Duval, P.: Bubbly-ice densification in ice sheets: I. Theory, J. Glaciol., 43, 387–396, https://doi.org/10.3189/S0022143000034961, 1997. a
Schoof, C. and Hewitt, I. J.: A model for polythermal ice incorporating gravity-driven moisture transport, J. Fluid Mech., 797, 504–535, https://doi.org/10.1017/jfm.2016.251, 2016. a, b
Spencer, M. K., Alley, R. B., and Creyts, T. T.: Preliminary firn-densification model with 38-site dataset, J. Glaciol., 47, 671–676, https://doi.org/10.3189/172756501781831765, 2001. a
Spiegelman, M.: Flow in deformable porous media. Part 1 Simple analysis, J. Fluid Mech., 247, 17–38, https://doi.org/10.1017/S0022112093000369, 1993. a
Steger, C. R., Reijmer, C. H., and van den Broeke, M. R.: The modelled liquid water balance of the Greenland Ice Sheet, The Cryosphere, 11, 2507–2526, https://doi.org/10.5194/tc-11-2507-2017, 2017. a
Stevens, C. M.: Investigations of physical processes in polar firn through modeling and field measurements, PhD thesis, Earth and Space Sciences, 2018. a
Tait, S. and Jaupart, C.: Compositional convection in a reactive crystalline mush and melt differentiation, J. Geophys. Res., 97, 6735–6756, https://doi.org/10.1029/92JB00016, 1992. a
Tanner, R. I.: Engineering rheology, vol. 52, Oxford University Press, 2000. a
Tulaczyk, S., Kamb, W. B., and Engelhardt, H. F.: Basal mechanics of Ice Stream B, West Antarctica: 1. Till mechanics, J. Geophys. Res., 105, 463–481, https://doi.org/10.1029/1999JB900329, 2000. a
Wang, X. and Baker, I.: Observation of the microstructural evolution of snow under uniaxial compression using X-ray computed microtomography, J. Geophys. Res., 118, 371–382, https://doi.org/10.1002/2013JD020352, 2013. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t
Wang, X. and Baker, I.: Comparison of the effects of unidirectional and sign-alternating temperature gradients on the sintering of ice spheres, Hydrol. Proc., 31, 871–879, https://doi.org/10.1002/hyp.11067, 2017. a
Wever, N., Fierz, C., Mitterer, C., Hirashima, H., and Lehning, M.: Solving Richards Equation for snow improves snowpack meltwater runoff estimations in detailed multi-layer snowpack model, The Cryosphere, 8, 257–274, https://doi.org/10.5194/tc-8-257-2014, 2014. a
Wilkinson, D. S.: A pressure-sintering model for the densification of polar firn and glacier ice, J. Glaciol., 34, 40–45, https://doi.org/10.3189/S0022143000009047, 1988. a
Wilkinson, D. S. and Ashby, M. F.: Pressure sintering by power law creep, Acta Metall., 23, 1277–1285, https://doi.org/10.1016/0001-6160(75)90136-4, 1975. a
Willibald, C., Scheuber, S., Löwe, H., Dual, J., and Schneebeli, M.: Ice Spheres as Model Snow: Tumbling, Sintering, and Mechanical Tests, Front. Earth Sci., 7, 229, https://doi.org/10.3389/feart.2019.00229, 2019. a
Zumberge, M. A., Elsberg, D. H., Harrison, W. D., Husmann, E., Morack, J. L., Pettit, E. C., and Waddington, E. D.: Measurement of vertical strain and velocity at Siple Dome, Antarctica, with optical sensors, J. Glaciol., 48, 217–225, https://doi.org/10.3189/172756502781831421, 2002. a
Zwally, H. J. and Li, J.: Seasonal and interannual variations of firn densification and ice-sheet surface elevation at the Greenland summit, J. Glaciol., 48, 199–207, https://doi.org/10.3189/172756502781831403, 2002. a





