the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The tipping points and early warning indicators for Pine Island Glacier, West Antarctica
Sebastian H. R. Rosier
Ronja Reese
Jonathan F. Donges
Jan De Rydt
G. Hilmar Gudmundsson
Ricarda Winkelmann
Mass loss from the Antarctic Ice Sheet is the main source of uncertainty in projections of future sea-level rise, with important implications for coastal regions worldwide. Central to ongoing and future changes is the marine ice sheet instability: once a critical threshold, or tipping point, is crossed, ice internal dynamics can drive a self-sustaining retreat committing a glacier to irreversible, rapid and substantial ice loss. This process might have already been triggered in the Amundsen Sea region, where Pine Island and Thwaites glaciers dominate the current mass loss from Antarctica, but modelling and observational techniques have not been able to establish this rigorously, leading to divergent views on the future mass loss of the West Antarctic Ice Sheet. Here, we aim at closing this knowledge gap by conducting a systematic investigation of the stability regime of Pine Island Glacier. To this end we show that early warning indicators in model simulations robustly detect the onset of the marine ice sheet instability. We are thereby able to identify three distinct tipping points in response to increases in ocean-induced melt. The third and final event, triggered by an ocean warming of approximately 1.2 ∘C from the steady-state model configuration, leads to a retreat of the entire glacier that could initiate a collapse of the West Antarctic Ice Sheet.
- Article
(3300 KB) - Full-text XML
- BibTeX
- EndNote
The West Antarctic Ice Sheet (WAIS) is regarded as a tipping element in the Earth's climate system, defined as a major component of the Earth system susceptible to tipping-point behaviour (Lenton et al., 2008). Its collapse, potentially driven by the marine ice sheet instability (MISI; Feldmann and Levermann, 2015), would result in over 3 m of sea-level rise (Fretwell et al., 2013). Key to MISI are the conditions at the grounding line – the transition across which grounded ice begins to float on the ocean forming ice shelves. In a steady state, ice flux across the grounding line balances the surface accumulation upstream. If grounding-line retreat causes grounding-line flux to increase and this is not balanced by a corresponding increase in accumulation, the net mass balance is negative and retreat will continue (Weertman, 1974; Schoof, 2007). Conversely, grounding-line advance leading to an increase in accumulation greater than the change in flux will lead to a continued advance. In this regime, a small perturbation in the system can result in the system crossing a tipping point, beyond which a positive feedback propels the system to a contrasting state (Fig. 1c). A complex range of factors can either cause or suppress MISI (Haseloff and Sergienko, 2018; Pegler, 2018; O'Leary et al., 2013; Gomez et al., 2010; Robel et al., 2016), and the difficulties in predicting this behaviour are a major source of uncertainty for future sea-level-rise projections (Church et al., 2013; Bamber et al., 2019; Oppenheimer et al., 2019; Robel et al., 2019).
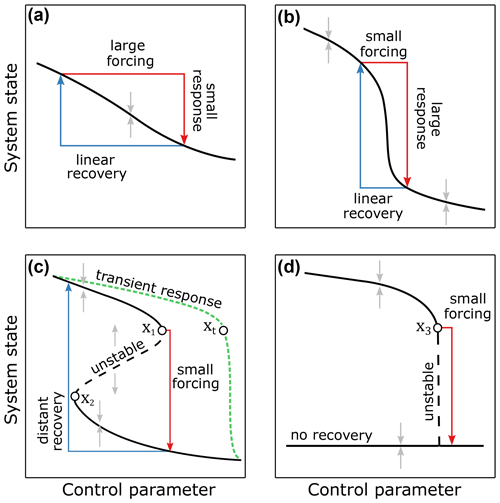
Figure 1Possible range of behaviours for a system state (e.g. ice flux) in response to perturbations in a control parameter (e.g. ocean temperature). A system can (a) respond to a perturbation in a linear way that is directly recoverable with a reversal of the forcing; (b) have a large response to a small perturbation that is still directly recoverable; (c) have a large response to a small perturbation that is irreversible (hysteresis behaviour); and (d) have a large response that is irreversible for any change in the tested range of the control parameter, a behaviour we refer to as permanently irreversible (no recovery possible even if forcing is reversed well below the initial level). Tipping points are crossed only in panels (c) and (d) and are indicated by x1, x2 and x3. Panel (c) also shows a transient response in which the system state lags behind changes in the control parameter as is the case for ice sheets and thus crosses the irreversible system state at a later point, xt.
One area of particular concern is the Amundsen Sea region. Pine Island (PIG) and Thwaites glaciers, the two largest glaciers in the area, are believed to be particularly vulnerable to MISI (Favier et al., 2014; Rignot et al., 2014). Palaeo-records and observational records of PIG show a history of retreat, driven by both natural and anthropogenic variability in ocean forcing (Jenkins et al., 2018; Holland et al., 2019). One possible MISI-driven retreat might have happened when PIG unpinned from a submarine ridge in the 1940s (Jenkins et al., 2010; Smith et al., 2016). Recent modelling studies indicate that a larger-scale MISI event may now be underway for both Pine Island and Thwaites glaciers that would lead to substantial and sustained mass loss throughout the coming centuries (Favier et al., 2014; Jenkins et al., 2016; Joughin et al., 2010). Being able to identify a MISI-driven retreat and differentiate this from a retreat where a tipping point has not been crossed is vital information for projections of future sea-level rise. One of the major hurdles in determining whether a tipping point has been crossed is that currently this necessitates time-consuming steady-state simulations to calculate the hysteresis behaviour of an identified period of retreat (e.g. Garbe et al., 2020). An alternative methodology that can be applied directly to transient simulations as a post-processing step would therefore be useful to the ice sheet modelling community. Such tools based on early warning indicators are presented in this paper.
The tipping behaviour of MISI is an example of a saddle-node (or fold) bifurcation in which three equilibria exist: an upper and lower stable branch and a middle unstable branch (Fig. 1c; Schoof, 2012). Starting on the upper stable branch, perturbing the system beyond a tipping point (x1 in Fig. 1c) will induce a qualitative shift to the lower and contrasting stable state. Importantly (and in contrast to a system such as that shown in Fig. 1a and b), in order to restore conditions to the state prior to a collapse it is not sufficient to simply reverse the forcing to its previous value. Instead, the forcing must be taken back further (to point x2), which in some cases may be far beyond the parameter range that triggered the initial collapse. This type of behaviour is known as hysteresis. A large change in response to a small forcing is not necessarily indicative of hysteresis, as shown in Fig. 1b. Tipping points are crossed in both Fig. 1c and Fig. 1d, and both cases are often referred to as irreversible, although the two are distinct in that only Fig. 1d is irreversible for any change in the tested range of the control parameter. Hereafter we will refer to the former as irreversible, in line with previous studies, and the latter as permanently irreversible, to differentiate the two. Diagnosing whether a tipping point has been crossed without some prior knowledge of the system is not generally possible without reversing the forcing to see if hysteresis has occurred. An alternative approach to identify tipping points is based on a process known as critical slowing down, which is known to precede saddle-node bifurcations of this type (Wissel, 1984; van Nes and Scheffer, 2007; Dakos et al., 2008; Scheffer et al., 2009). Critical slowing down is a general feature of non-linear systems and refers to an increase in the time a system takes to recover from perturbations as a tipping point is approached (Wissel, 1984). We will explore both hysteresis and critical slowing down as indicators of tipping points in our model simulations.
In Sect. 2, we explain critical slowing down and early warning indicators in the context of MISI. We then map out the stability regime of PIG using numerical model simulations. We force the model with a slowly increasing ocean melt rate and identify three periods of rapid retreat with the methodology explained in Sect. 3.1. Using statistical tools from dynamical systems theory we find critical slowing down preceding each of these retreat events and go on to demonstrate that these are indeed tipping points in Sect. 4. This is confirmed by analysing the hysteresis behaviour of the glacier, showing the existence of unstable grounding-line positions. To our knowledge, this is the first time that the stability regime of PIG has been investigated in this detail and the first time that tipping-point indicators have been applied to ice sheet model simulations. Our results reveal the existence of multiple tipping points leading to the collapse of PIG, rather than one single event, that when crossed could easily be misidentified as simply periods of rapid retreat, with the irreversible and the self-sustained aspect of the retreat being missed.
As certain classes of complex systems approach a tipping point, they show early warning signals (i.e. specific changes in system behaviour as detailed below) which can allow us to anticipate or even predict the onset of a tipping event by means of statistical tools called early warning indicators (EWIs; Wissel, 1984). Early warning signals have been found to precede, for example, collapse of the thermohaline circulation (Held and Kleinen, 2014; Lenton, 2011), onset of epileptic seizures (Litt et al., 2001; McSharry and Tarassenko, 2003), crashes in financial markets (May et al., 2008; Diks et al., 2018), onset of glacial terminations (Lenton, 2011) and wildlife population collapses (Scheffer et al., 2001). Although most commonly used to detect the onset of saddle-node bifurcations, of which MISI is an example, they are not strictly limited to bifurcations of this type and have, for example, also been successfully used to indicate the onset of Hopf bifurcations (Chisholm and Filotas, 2009).
2.1 Critical slowing down preceding the marine ice sheet instability
Critical slowing down is one example of an early warning signal that has been used in the past for both model output and observational records such as palaeoclimate data, with the aim of detecting an approaching bifurcation (Held and Kleinen, 2004; Livina and Lenton, 2007; Dakos et al., 2008; Lenton et al., 2009, 2012b). Critical slowing down is so called because, as a non-linear system is gradually forced towards a bifurcation, that system will become more “sluggish” in its response to perturbations (see middle panel of Fig. 2). This can be shown mathematically, because the dominant eigenvalue of the system tends to zero as a bifurcation point is approached (Wissel, 1984) or, equivalently, the recovery time (i.e. the time it takes for a system to return to a steady state after small perturbations) tends to infinity. The response time of a glacier to external forcing has also been shown analytically to increase as a MISI bifurcation is approached (Robel et al., 2018). While critical slowing down is a general characteristic behaviour of the dynamics underlying MISI, the question remains whether it can be reliably detected in the context of a complex glacier where many other processes are at play.
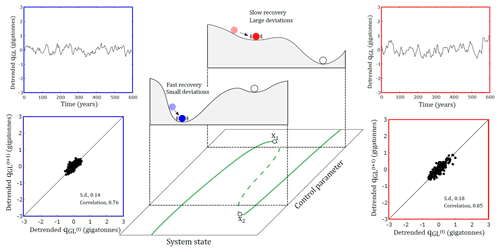
Figure 2Critical slowing down can serve as an indicator that the system is approaching a tipping point. This can be understood conceptually using the common “ball on a slope” analogy (middle panel), where the ball represents the system state and minima are stable equilibrium states. Two example cases are superimposed onto their corresponding positions in the hysteresis plot of MISI shown by the green line and equivalent to Fig. 1c. The processed model results demonstrate how critical slowing down manifests itself, as shown in the blue and red panels at the sides. If the system is far from a tipping point (blue case), the system state (which is in this study the grounding-line flux qGL, upper left panel) recovers quickly from perturbations in the control parameter (which is here the basal melt variability). This means that from one measurement (at time t) to the next (at time t+1) the grounding-line flux changes rapidly and has a low lag-1 auto-correlation (lower left panel). Conversely, close to a tipping point (red case), critical slowing down manifests and the system state responds more slowly to perturbations in the control parameter (upper right panel). Since the state variable is changing more slowly, successive measurements are more similar, resulting in a higher lag-1 auto-correlation (lower right panel).
As a first step to addressing this question, we model MISI in an idealised flow line setup of a marine ice sheet. In this setup, we determine the change in recovery time before a tipping point directly through multiple stepwise perturbations of the control parameter (Appendix A). Our setup closely resembles the MISMIP experiments (Pattyn et al., 2012), and indeed hints of critical slowing down can be identified in that paper (Fig. 2 in Pattyn et al., 2012). The results in Appendix A show that critical slowing down is easily identified preceding both MISI-driven advance and retreat bifurcations. This demonstrates that there is at least the potential that critical slowing down could be found in a less simplified modelling framework. This is not clear a priori, and, for example, adding noise to the bed topography reduces the ability to identify early warning, as detailed in the Appendix. Identifying critical slowing down in this stepwise perturbation manner is appealing because it directly extracts the change in response time that we are searching for; however it is not practical for a realistic model forcing which would not normally take the form of a step function. A more general approach, which we adopt for our simulation of PIG, is to use EWIs to analyse the recovery time of the system as it is forced with natural variability.
2.2 Early warning indicators
As the field of EWIs has expanded, more methods have been developed for extracting critical-slowing-down information from model results and observational records. These methods seek to approximate the system recovery time from some measure of the system state. The challenge is that, for most real-world applications, natural forcing does not take the form of a step function and the system is continuously perturbed and so cannot return to a true steady state. However, if the recovery time of a system is indeed increasing, the response to a continual stochastic forcing could be detected as a tendency for each measurement of the system state to become increasingly similar to the previous measurement, sometimes referred to as an increase in “memory” of small perturbations. This is shown conceptually and with examples extracted from our PIG model in Fig. 2. One common way to measure this effect is by sampling the data at discrete time intervals and calculating the lag-1 auto-correlation, i.e. the correlation between values that are one time interval apart (examples given in Fig. 2). This measure, which we refer to hereafter as the ACF indicator, should increase as a tipping point is approached (Dakos et al., 2008; Ives, 1995). Since recovery time tends to infinity as the bifurcation is approached, successive system states should become more and more similar and the ACF indicator should tend to 1. This threshold of an indicator, corresponding to the point when a tipping point would be crossed as predicted by theory, is referred to hereafter as the critical value. An alternative measure that also seeks to identify changes in recovery time is to use the detrended fluctuation analysis algorithm (Livina and Lenton, 2007; Lenton et al., 2012a, b). This first calculates the mean-centred cumulative sum of the time series, splits the result into epochs of length n which are detrended and then calculates the rms F(n) for each epoch. This is repeated for epochs of different length, and finally an exponent α can be fitted in log–log space such that F(n)∝nα. This exponent yields information on the self-correlation of the original time series, whereby a value of 0.5 corresponds to uncorrelated white noise and greater values indicate increasing “memory” up to a maximum of 1.5. To aid comparison with the ACF indicator and following Livina and Lenton (2007), we rescale the exponent so that it reaches a critical value of 1 and call this the DFA indicator. These indicators can be supported by analysing the variance of the system state. Variance can be shown to increase as a tipping point is approached, since perturbations to the system decay more slowly and thus large shifts from the mean state will persist for longer (Scheffer et al., 2009). No critical value exists in this case, but a persistent positive trend in variance serves as additional evidence that a tipping point is being approached.
We conduct a quasi-steady modelling experiment whereby we subject PIG to slowly increasing rates of basal melt beneath its adjacent ice shelf (Fig. 3). Conducting a transient simulation with an evolving basal melt that exactly tracks the equilibrium curve (Fig. 1c) is not computationally feasible or necessary for our purposes. Thus, we adopt this quasi-steady modelling approach in which the forcing increases slowly enough that it approximates the steady-state behaviour but faster than the long response timescales the glacier would require to be truly in equilibrium. Quasi-steady-state experiments have previously been successfully applied to identify the tipping point of the Greenland Ice Sheet with respect to the melt–elevation feedback (Robinson et al., 2012) and to identify hysteresis of the Antarctic Ice Sheet (Garbe et al., 2020). In Garbe et al. (2020) it was shown that such transient experiments enable identification of hysteresis behaviour, while the exact shape of the curve must be mapped out with equilibrium simulations. We accompany the quasi-steady simulations with simulations that run to a steady state for constant values of the control parameter at discrete values (these simulations continue until the change in ice volume is approximately equal to zero). We use basal melt rate as the control parameter, i.e. the parameter that we will change to drive the system towards a tipping point. We make this choice since erosion of ice shelves by the intrusion of warm ocean currents is widely accepted as the mechanism responsible for the considerable changes currently observed in this region (Shepherd et al., 2004; Rignot et al., 2014; Rignot, 1998; Joughin et al., 2010; Park et al., 2013; Gudmundsson et al., 2019). Sub-ice-shelf melt rates are increased linearly (with additional variability as explained below) from a value that generates a steady state for the present-day glacier configuration. Based on the numerical experiments we then evaluate EWIs to test for critical slowing down.
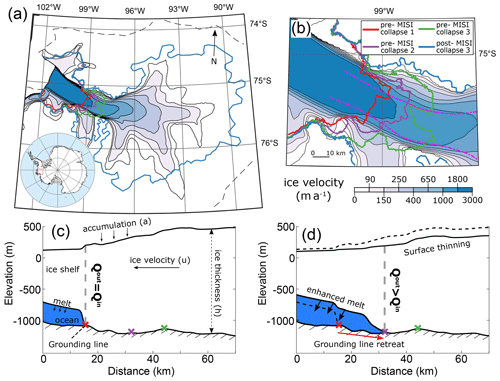
Figure 3Marine ice sheet instability events for Pine Island Glacier. Shown are (a) grounding-line positions before and after the three MISI-driven glacier collapses with (b) a zoom-in on the initial events (coloured lines). The colour map indicates initially modelled ice velocity, and the model domain boundary is indicated by a dashed black contour in panel (a). Panels (c) and (d) show a transect through the main trunk of PIG, calculated as an average of properties between the two dashed magenta lines in (b). The vertical section along the transect is shown (c) at the initial steady state where fluxes (Qin and Qout) are in balance and (d) during a MISI event where retreat causes an increase in Qout, pushing the glacier to be out of balance and leading to further retreat.
3.1 Model description
All simulations use the community Úa ice-flow model (Gudmundsson et al., 2012; Gudmundsson, 2013, 2020), which solves the dynamical equations for ice flow in the shallow-ice-stream approximation (SSTREAM or SSA; Hutter, 1983). Bedrock geometry for the PIG domain is a combination of the R topo2 dataset (Schaffer et al., 2016) and, where available, an updated bathymetry of the Amundsen Sea embayment (Millan et al., 2017). Surface ice topography is from CryoSat-2 altimetry (Slater et al., 2018). Depth-averaged ice density is calculated using a meteoric ice density of 917 kg m−3 together with firn depths obtained from the RACMO2.1 firn densification model (Ligtenberg et al., 2011). Snow accumulation is a climatological record obtained from RACMO2.1 and constant in time (Lenaerts et al., 2012).
Viscous ice deformation is described by the Glen–Steinemann flow law with exponent n=3, and basal motion is modelled using a Weertman sliding law with exponent m=3. The constitutive law and the sliding law use spatially varying parameters for the ice rate factor (A) and basal slipperiness (C), respectively, to initialise the model with present-day ice velocities. These are obtained via optimisation methods using satellite observations of surface ice velocity from the Landsat 8 dataset (Scambos et al., 2016; Fahnestock et al., 2016). An optimal solution is obtained by minimising a cost function that includes both the misfit between observed and modelled velocities and regularisation terms. An additional term in the cost function penalises initial rates of ice thickness change in order to ensure that these are close to zero at the start of simulations. This approach helps to provide a steady-state configuration of PIG from which we can conduct our perturbation experiments.
The Úa model solves the system of equations with the finite-element method on an unstructured mesh, generated with MESH2D (Engwirda et al., 2014). The mesh remains fixed throughout the simulation to avoid contaminating the time series with errors resulting from remapping fields onto a new mesh. The mesh is refined in regions of high strain rate gradients and fast ice flow as well as around the grounding line. The region of grounding-line mesh refinement, in which the average element size is ∼ 750 m, extends upstream sufficiently far so that the grounding line always remains within this region until after the final MISI collapse.
Basal melt rates are calculated using a widely used, local quadratic dependency on thermal forcing:
where γT is the constant heat exchange velocity, ρw is seawater density, cp is the specific heat capacity of water, ρi is ice density, Li is the latent heat of fusion of ice, T0 is the thermal forcing and Tf is the freezing temperature (Favier et al., 2019). Melt rates are only applied beneath fully floating elements to ensure that no melting can possibly occur upstream of the grounding line (Seroussi and Morlinghem, 2018). The initial melt rate factor (f) is chosen such that the model finds a steady state with a grounding line approximately coincident with its position as given in Bedmap2 (Fretwell et al., 2013). This melt rate factor is the aforementioned control parameter that drives changes in the model, some of which may be identifiable as tipping points.
To effectively extract information about the system's recovery time using the statistical methods outlined in Sect. 2, we need to perturb the model in a way that has some measurable impact on the system state. A slow and monotonically increasing forcing would make our chosen approach impractical and is arguably as unrealistic as a stepwise perturbation. We therefore add natural variability to the linearly increasing melt rate factor (f). There is strong evidence that the inferred and observed changes in PIG over the last century can be linked to changes in thermocline depth of the Amundsen Sea shelf, which in turn is influenced by an atmospheric Rossby wave train originating in the Pacific Ocean (Jenkins et al., 2018). Following Jenkins et al. (2018), we use a ∼ 130-year time series of central tropical Pacific sea surface temperature anomalies as a proxy for relevant variability in our melt rate forcing. We create an autoregressive (AR) model-based surrogate from this time series using the Yule–Walker method to fit the AR model and minimum description length to determine the maximum order of the model. This new surrogate time series has the same decadal variability that would be expected for the melting beneath PIG and can be extended to any length required. As shown in more detail below, by superimposing this signal onto the linearly increasing melt rate factor we ensure that the system response contains sufficient variability to extract information about critical slowing down and thereby enable the calculation of EWIs. Furthermore, using natural variability enables us to test the versatility of EWIs if they were to be applied directly to observations.
3.2 Detecting critical slowing down
We have already established the control parameter for our model, but another important decision to make is what model output should be used as a measure of the system state. One choice could be changes in ice volume, since they can be related to sea-level rise and ice sheet model simulations tend to focus on this result. However, ice volume varies very smoothly over time, making it difficult to detect changes in the system recovery time. Instead, we use the integrated grounding-line flux, which shows greater temporal variability and whose change is directly related to the MISI mechanism. As with other studies of this type, the model output is processed prior to the calculation of EWIs. This consists of aggregating the output (i.e. data binning) to remove variability with a frequency higher than that directly relevant to the internal ice dynamics considered here and thus not related to the system recovery time, together with detrending to remove non-stationarities (detrending is included in the DFA algorithm and therefore not required before calculation of the DFA indicator). Detrending was carried out using a Gaussian kernel smoothing function that has been shown to perform better than linear detrending (Lenton et al., 2012a). A smoothing bandwidth was selected that removed long-term trends without overfitting the model time series. Indicators are calculated over a moving window with a length of 300 years. The optimal window length is further discussed in Sect. 4.3.
From the processed time series, we calculate three different EWIs:
-
Critical slowing down is measurable as an increase in the state variable auto-correlation. We measure this here using the lag-1 auto-correlation function (Dakos et al., 2008; Scheffer et al., 2009; Held and Kleinen, 2004) applied to the grounding-line flux over a 300-year moving window preceding each tipping point (ACF indicator).
-
Similarly, DFA (Peng et al., 1994) measures increasing auto-correlation in a time series and we apply this with the same moving-window approach.
-
An additional consequence of critical slowing down is that variance will increase as a tipping point is approached (Scheffer et al., 2009). We calculate variance of grounding-line flux for each moving window, and this can be used in conjunction with other indicators to increase robustness.
As described in Sect. 2, recovery time should tend to infinity as a tipping point is approached. This corresponds to the ACF and scaled DFA indicators reaching a critical value of 1. In practice, for a complex model there are a wide variety of reasons why a tipping point might be crossed before the EWI reaches a critical value. For example, this can be a result of variability in the control variable pushing the system over a tipping point despite its long-term mean still being some distance from its critical value. For this reason, most studies adopt an alternative approach of looking for a consistent increase in the EWIs in the run up to a tipping event. This is often measured by calculating the nonparametric Kendall's τ coefficient, a measure of the ranking or ordering of a variable, which equals 1 if the indicator is monotonically increasing with time (Dakos et al., 2008; Kendall, 1948). This single value enables a simple interpretation of our results, since means the EWI is tending to increase with time, suggesting an imminent tipping point. The closer to 1 the calculated τ coefficient is, the greater the tendency for an indicator to be increasing with time, and conversely a τ coefficient close to zero suggests no clear tendency for an indicator to be changing with time. We present our results in terms of both aforementioned criteria: whether an EWI reaches a critical value preceding the tipping point and whether the EWI is consistently increasing for a period of time before the tipping point.
The quasi-equilibrium simulation shows three potential tipping points with respect to the applied melt (Fig. 4). Upon crossing each threshold, indicated by the numbered blue dots in Fig. 4, PIG undergoes periods of not only rapid but also (as we show below) self-sustained and irreversible mass loss. At this stage, relying only on a record of changes in ice volume resulting from an increasing forcing (solid black line in Fig. 4), one can only speculate that these are indeed tipping points and more analysis is necessary to confirm this hypothesis, and we will address this point in Sect. 4.2. The last of the three events causes a permanently irreversible collapse within the entire model domain (Fig. 4a). We focus our results on these three major changes in the glacier configuration and ignore any possible smaller tipping points that do not result in significant grounding-line retreat or changes in ice volume. We increase basal melt rates gradually and in a quasi-steady-state manner to ensure that successive retreat events can be isolated and their effects do not overlap during the simulation. A more rapidly increasing forcing could lead to one tipping point cascading into the next and result in three individual tipping points being misinterpreted as only one event.
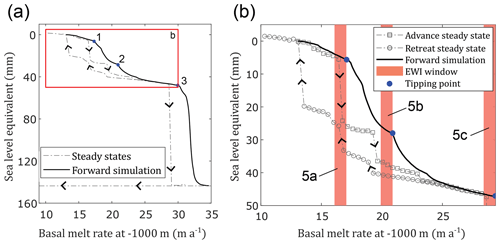
Figure 4Change in system state in terms of sea-level equivalent ice volume as a function of the control parameter, which is the melt rate at the ice–ocean interface. (a) The model is run forward with a slowly increasing basal melt rate (solid black line) and shows three distinct tipping points (blue dots). From the start of the transient simulation to the third tipping point is approximately 10 kyr. The steady states for a given melt rate in both an advance and retreat configuration are plotted as dashed grey lines, with details shown in panel (b). Arrows indicate the direction of the hysteresis. Panel (b) focuses on the model response before the larger tipping point (event 3) and shows the three windows that we analyse for early warning indicators as shaded red boxes (Fig. 5). Circle and square symbols represent steady-state configurations for a given forcing, and the dashed grey line is a linear interpolation between these points. Each step in melt rate for the steady-state runs from ∼ 10 to ∼ 30 m a−1 is approximately equivalent to 0.4 m a−1 of basal melting, or 250 years in the transient simulation. The lower branch in panel (a) represents a simulation starting from the PIG configuration after the third major retreat event and reverses the basal melt rate factor to its lowest value, showing no recovery in ice volume.
Grounding-line positions before each of these retreat events and after the final collapse are shown in Fig. 3. Events 1 and 2 each contribute approximately 20 mm of sea-level rise, while event 3, which arises after slightly more than doubling current melt rates, contributes approximately 100 mm. The actual sea-level rise that would result from this third and largest event is likely to be larger since in our simulation the effects stop at the domain boundary and in reality neighbouring drainage basins would be affected.
4.1 Early warning for the marine ice sheet instability
The three periods of MISI-driven retreat, each following the crossing of an associated tipping point, can be identified clearly using EWIs (Fig. 5). The ACF indicator increases and tends to 1 as the tipping points are approached (Fig. 5a–c), indicating a tendency towards an infinitely long recovery time as predicted by theory. We calculate Kendall's τ coefficient to identify trends in the indicator, with a value of 1 representing a monotonic increase in the indicator with time. The positive Kendall's τ coefficient shows that in all three cases, the lag-1 auto-correlation increases before the onset of unstable retreat. Furthermore, the ACF indicator reaches a critical value of 1 relatively close in time to when the MISI event begins.
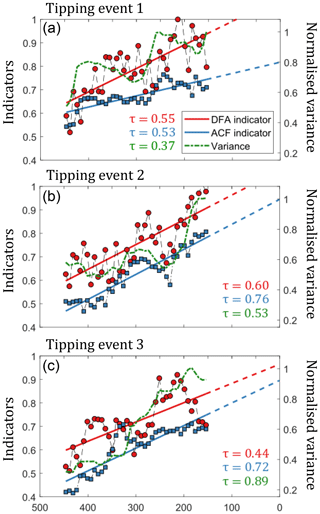
Figure 5EWIs for the marine ice sheet instability in Pine Island Glacier. Each panel shows the EWIs preceding each of the three MISI tipping-point events marked in Fig. 3b, along with the linear trend extrapolated to the point in the simulation when the respective tipping event occurs. Increasing trends in all indicators are shown by a positive Kendall's τ coefficient which measures the correlation between each indicator and time at between −1 and 1.
These findings are supported by the DFA indicator, described in Sect. 2. As with the ACF indicator, Kendall's τ coefficient is positive and the DFA indicator trends towards a critical value of 1 as each tipping point is approached. We show the change in normalised variance calculated over each time window, and in all cases this increases ahead of the tipping points being crossed with a positive Kendall's τ coefficient. The increase in variance gives greater confidence to the findings of the other two EWIs, although variance cannot be used directly to predict when that threshold will be crossed since it does not approach a critical value before a tipping point is crossed.
4.2 Hysteresis of Pine Island Glacier
In order to verify that we have correctly identified tipping points using the EWIs, we run the model to a steady state for a given melt rate to search for hysteresis loops that indicate the presence of unstable grounding-line positions. These simulations start from either the initial model setup (advance steady state) or the configuration just prior to the final tipping point (retreat steady state). Each of these simulations samples a discrete mean melt factor between these two states that is held constant (but with the addition of the same natural variability as in the forward simulations) and is run forward in time until the modelled ice volume reaches a steady state. The first two tipping events show relatively small but clearly identifiable hysteresis loops (Fig. 4b), for which recovery of the grounding-line position requires reversing the forcing beyond the point at which retreat was triggered (i.e. as shown in Fig. 1c). The third event marks the onset of an almost complete collapse of PIG (Fig. 4a). Unlike the previous two, this collapse cannot be reversed to regrow the glacier for any value of the control parameter. This is an example of a permanently irreversible tipping point, as shown in Fig. 1d. Note that this permanent irreversibility is only true for the glacier modelled in isolation and by expanding the domain it would presumably be possible for other catchments that may not have collapsed to enable this glacier to regrow.
4.3 Robustness of the indicators
We carry out several tests to assess the robustness of the EWIs and their sensitivity to the pre-processing carried out on the model output prior to calculating each indicator. Two parameters in this processing step are the bin size into which data are aggregated and the bandwidth of the smoothing kernel that removes long-term trends in the time series. To check that the increasing trends in our indicators are a robust feature of our results, regardless of these choices, we conducted a sensitivity analysis. The parameters were varied by ±50 %, and the indicators were recalculated for each resulting time series. As before, we assess the utility of an indicator by whether it shows an increasing trend before each tipping point, as measured by a positive Kendall's τ coefficient. The results of this sensitivity analysis are presented for each MISI event in Fig. 6. Kendall's τ coefficient is positive for all tested combinations of parameters and all MISI events, although MISI event 2 is particularly insensitive to these parameter choices, whereas the spread in Kendall's τ coefficient is greater for the other two events.
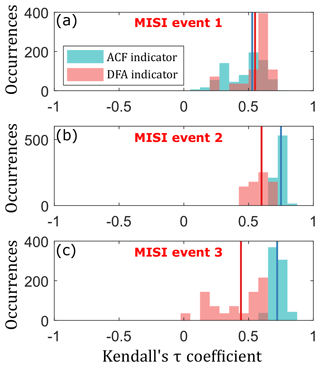
Figure 6Sensitivity analysis for the ACF and DFA indicators. Each occurrence is Kendall's τ coefficient for a different choice of filtering bandwidth and data aggregation. The solid red and blue lines show Kendall's τ coefficient for the DFA and ACF indicators, respectively, as calculated for the choice of parameters used in Fig. 5.
In general, critical slowing down will only occur close to a tipping point. Determining how close to a tipping point a system must be in order to anticipate the approaching critical transition, i.e. the prediction radius, is an important question and also informs the selection of palaeo-records that could be used to detect an upcoming MISI event. The results presented above are for a window size of 300 years (i.e. a record length of 600 years), which is the shortest window size for which the DFA indicator provides a clear prediction for all tipping events. We explored the prediction radius of our model by calculating Kendall's τ for the ACF and DFA indicators and the variance for a range of window lengths; see Fig. 7. For the main tipping event, preceded by the longest stable period, the indicators gradually lose their ability to anticipate a tipping event. This is shown by Kendall's τ values approaching zero or in some cases becoming negative, meaning that the EWIs are not robustly increasing before each tipping point as a result of more data being included further from the bifurcation. The same is true for the two smaller tipping events, but the drop-off is quicker such that the indicators break down for window lengths > 500 years. These results suggest that the prediction radius is relatively small, and thus window sizes that are too large, which hence include data far from a tipping point, become less useful for the application of EWIs.
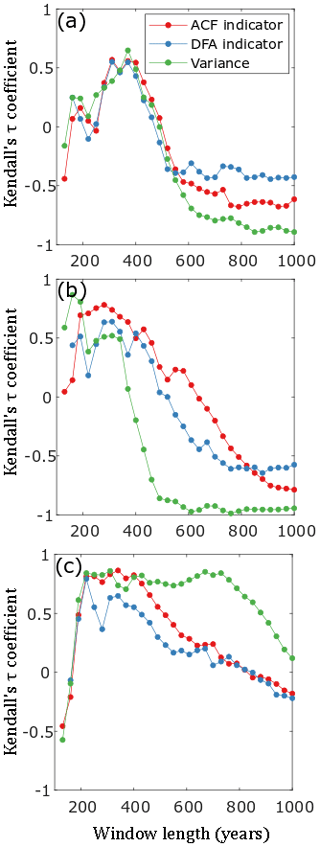
Figure 7The effect of window length on the predictive power of EWIs for MISI. The three panels show the change in Kendall's τ coefficient as calculated for each indicator versus window length for MISI events 1, 2 and 3 (panels a, b and c, respectively).
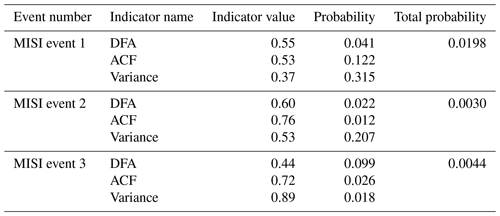
In addition to a sensitivity analysis, it is important to check that trends in the calculated indicators are statistically significant and not the result of random fluctuations. We follow the method originally proposed by Dakos et al. (2012) and produce surrogate datasets from the model time series that have many of the same properties but should not contain any critical-slowing-down trends. We generate 1000 of these datasets using an autoregressive AR(1) process-based surrogate. For each of these datasets we calculate the ACF and DFA indicators and variance in the same way as with the model time series and then estimate the trend with values of Kendall's τ coefficient. We calculate the probability of our results being a result of chance for each indicator and for all three combined as the proportion of cases for which the surrogate dataset was found to have a higher correlation than the model time series. We find that P<0.1 in all but one instance for the ACF and DFA indicators but variance trends were generally less significant (Table 1). However, the combined probability that all three indicators would be equally positive as a result of chance was less than 0.02 for the first MISI event and less than 0.005 for the second and third events.
Table 1Probability of Kendall's τ correlation for each indicator being a result of chance. A total of 1000 surrogate time series of the state variable are generated, and the indicators and Kendall's τ correlations are calculated for each one. The probability of Kendall's τ value is then the fraction of these surrogate time series with a higher correlation coefficient. The total probability is the fraction of surrogates for which all three indicators have a higher correlation coefficient than is observed in the original model time series.
The indicators we have tested provide early warning of tipping points as they are approached in our transient simulation with gradually increasing melt rates. Tipping points driven by MISI represent potential “high-impact” shifts in the Earth climate system, since they may lead to considerable changes in the configuration of the Antarctic Ice Sheet that are effectively irreversible on human timescales. Computational models are frequently used to forecast future changes in the Antarctic Ice Sheet in response to various greenhouse gas emission and warming scenarios. Predictive studies of this kind sometimes label periods of rapid retreat as “unstable” without further analysis of the type performed here (e.g. Joughin et al., 2014; Ritz et al., 2015; Favier et al., 2014) or avoid making this diagnosis altogether (DeConto and Pollard, 2016). Here, we have demonstrated that EWIs robustly approach critical thresholds preceding tipping points driven by MISI. Our results show that EWIs can be used as a method to identify instabilities without the need for the aforementioned modelling approach based on computationally expensive equilibrium simulations.
It is important to clearly understand what critical threshold is identified by the EWIs. In Fig. 4 the simulated steady states show the crossing of the tipping point earlier than identified by the indicators in the transient simulation. Since the timescales of ice flow are longer than the forcing timescale, the ice sheet system modelled here does not evolve along the steady-state branch (as shown schematically in Fig. 1c). Relaxation to a steady state takes centuries to millennia in the simulations. This means that while technically the critical value of the control parameter (basal melt rate) might have already been crossed, the glacier could return to its previous state in the transient simulation at that point if the basal melt rate was reduced below the critical threshold. This is true until the system state variable crosses its critical value (point xt in Fig. 1c) – and this is the point identified by the EWIs. This complication in interpreting EWIs is inherent to ice dynamics because of its long response timescales.
We find that both the ACF and the DFA indicators not only increase as a tipping point is approached, as shown by positive Kendall coefficients, but also generally approach the critical value of 1, although with varying degrees of precision (Fig. 5). This enhances their predictive power, since by extending a positive trend line it is possible to approximate what value of the control parameter will eventually cause a tipping point to be crossed. While our experiments in Appendix A showed that critical slowing down can accurately predict onset of tipping points in an idealised setup, applying this method to a more complex case study may fail, and in this context our finding that these indicators largely retain their predictive power is very encouraging. One area of additional complexity in our model of PIG compared to the setup in Appendix A is the bed geometry, which is obtained from observations and so is much less smooth than the synthetic retrograde bed used in the MISMIP experiments. We explored how the addition of “bumpiness” to bed geometry affects the performance of EWIs and found that it reduces how clearly we can resolve the change in response time (Appendix A). This effect may account for the fact that EWIs do not precisely reach a value of 1 at the bifurcation point, but confirming this would require further testing.
There are several important caveats to the use of EWIs as presented here. Firstly, and as explained above, the tipping point identified is that of the transient system not in a steady state. Although the transient behaviour is arguably of greater societal relevance and an ice sheet is unlikely to ever truly be in a steady state, this is an important distinction to make. Secondly, the predictive power of this method decreases as the distance to tipping increases and must eventually break down altogether. This effect can be clearly seen in Fig. 7 as Kendall's τ coefficient decreases with increasing window length. Thirdly, there is a risk of so-called “false alarms” and “missed alarms” (Lenton, 2011). False alarms, whereby a positive trend in an indicator that is incorrectly interpreted as a tipping point being imminent, can occur for a wide variety of reasons. First and foremost, interpreting EWIs requires robust statistical analysis and judicious data processing to ensure that the response time being measured is that of the critical mode (Lenton, 2011). It is possible that rising auto-correlation is a result of other processes, and using more than one indicator together with changes in variance can help mitigate this risk (Ditlevsen and Johnsen, 2010). It is also possible for a tipping point to be crossed with no apparent warning i.e. missed alarms. This could happen if the internal variability in a system is high so that it changes state before a bifurcation point is reached or similarly if the forcing is too sudden. This last point is particularly pertinent, since we intentionally perturb our model slowly and do not explore how a change in forcing rate affects the performance of our chosen EWIs. Increasing the forcing rate might present further difficulties in identifying tipping points by leading to multiple tipping points being crossed coincidentally. Since in our methodology the control parameter is not held constant after a tipping point is crossed, then if that parameter changes sufficiently during the time it takes for one tipping event to conclude, it might reach a second threshold while the first event is still underway, disguising the fact that two distinct tipping points have been crossed. Changing the control parameter very slowly alleviates this issue, since it will only have altered slightly during the time it takes for a tipping event to happen. This issue, along with the related issue of cascading tipping points, is one that we try to avoid in our experiments to simplify the analysis but is known to influence EWI performance (Dakos et al., 2015; Brock and Carpenter, 2010). Despite our use of a very slow forcing rate, it is possible that more than three tipping points exist in our model configuration. Finding all possible tipping points would necessitate infinitesimally small changes in the control parameter, in either the steady-state or the transient simulations, greatly increasing computational cost but with little benefit in terms of detecting tipping events that constitute substantial mass loss.
In this paper we have presented an application of EWIs to model output to anticipate tipping points. This is a useful approach in and of itself, since it could be used in model studies to detect bifurcations in the system with minimal computational expense or to check whether a model might be on a trajectory to cross a tipping point at some point in time beyond the simulation. Alternatively, it may be possible to use this method on observational data, palaeo-records or some combination thereof. This raises the question of what data might qualify as useful for the application of EWIs, which can be broken down further into (1) the type of data needed and (2) the length of record necessary. As mentioned previously, ice volume or related measures of an ice sheet's size do not show sufficient variability for information on the recovery time to be extracted. Ice speed however can change significantly over very short timescales; for example many ice streams show large variability over timescales as short as tidal periods (Anandakrishnan and Alley, 1997; Gudmundsson, 2006; Minchew et al., 2017). Ice flux was chosen in this study since it is closely related to the MISI mechanism and because flux is proportional to velocity, but it is possible that other metrics related to ice velocity might also exhibit critical slowing down in a similar way. With regards to record length, we find in this study that early warning of tipping points becomes less reliable (with a low or even negative Kendall's τ coefficient) for a moving-window size shorter than 200–300 years. However, this does not mean that this represents the minimum window size in general and is likely sensitive to a number of the choices in our methodology. For example, this value is likely to be sensitive to the rate of forcing applied to the system. In the limiting case of a forcing rate approaching zero, the necessary window length must increase since EWIs are only expected to work relatively close to the tipping point. Both of these points require further study in order to establish suitable datasets for prediction of MISI onset.
Conducting quasi-steady numerical experiments, whereby the underside of the PIG ice shelf is forced with a slowly increasing ocean-induced melt, we have established the existence of at least three distinct tipping points. Crossing each tipping point initiates periods of irreversible and self-sustained retreat of the grounding line (MISI) with significant contributions to global sea-level rise. The tipping points are identified through critical slowing down, a general behavioural characteristic of non-linear systems as they approach a tipping point. EWIs have been successfully applied to detect critical slowing down in other complex systems. We show here that they robustly detect the onset of the marine ice sheet instability in the simulations of the realistic PIG configuration which is promising for application of early warning to further cryospheric systems and beyond. While the possibility of PIG undergoing unstable retreat has been raised and discussed previously, this is to our knowledge the first time the stability regime of PIG has been mapped out in this fashion. The first and second tipping events are relatively small and could be missed without careful analysis of model results but nevertheless are important in that they lead to considerable sea-level rise and would require a large reversal in ocean conditions for recovery. The third and final tipping point is crossed with an increase in sub-shelf melt rates equivalent to a +1.2 ∘C increase in ocean temperatures from initial conditions and leads to a complete collapse of PIG. Long-term warming and shoaling trends in Circumpolar Deep Water (Holland et al., 2019), in combination with changing wind patterns in the Amundsen Sea (Turner et al., 2017), can expose the PIG ice shelf to warmer waters for longer periods of time and make temperature changes of this magnitude increasingly likely.
MISI has been a major focus of modelling efforts within the glaciological community in recent years. In an effort to assess how ice-flow models capture this behaviour, a model inter-comparison experiment was performed to calculate the hysteresis loop of advance and retreat of a marine ice sheet on a retrograde slope, known as MISMIP experiment 3 (referred to as EXP 3 hereafter; Pattyn et al., 2012). As a first step to establishing whether critical slowing down can be observed prior to MISI, we undertook a slightly modified version of this experiment using the Úa ice-flow model (Gudmundsson, 2012, 2013; see Methods). In our modified experiment, the marine ice sheet is forced towards tipping points through step perturbations in the control parameter as before but with smaller steps and the additional constraint that the model must be in a steady state after each perturbation before moving on to the next. In this experiment the chosen control parameter is the ice rate factor, a parameter linked to ice viscosity and temperature.
Following each perturbation in the ice rate factor, we analyse the e-folding relaxation time (TR) of the state variable (in this case, grounding-line position) to directly extract the recovery time of the model as it approaches each tipping point (both advance and retreat). Theory predicts that TR→∞ close to a tipping point and that the point at which (as plotted versus the control parameter) reaches 0 thus identifies the critical value of the control parameter, beyond which a tipping point is crossed (Wissel, 1984). We show this plot for both the advance and retreat scenarios of EXP 3 in Fig. A1. In both cases the relaxation time increases ( decreases) as predicted by theory, even far from the tipping point. A linear fit through the last six perturbations yields a good agreement with theory and accurately predicts the critical value of the control parameter when compared to the analytical solution (red arrows in Fig. A1) given by Schoof (2007). Critical slowing down still occurs outside of this range (equivalent to a change in ice temperature of > 5 ∘C), but using these more distant points to forecast the tipping point would yield a less accurate prediction. These results therefore provide some insight into how far from the tipping point we can expect the predicted linear response.
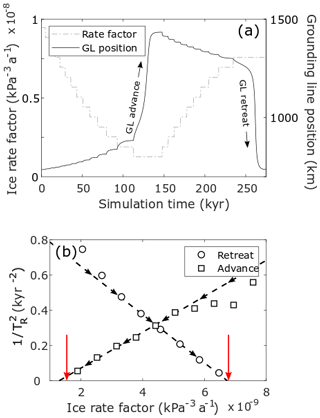
Figure A1Results of EXP 3, showing change in grounding-line position with time resulting from step perturbations in the ice rate factor (a). The calculated inverse relaxation time for each corresponding step change in rate factor in both the advance (square symbols) and retreat (circular symbols) phase is shown in panel (b). The dashed line in panel (b) is a line of best fit, calculated for the five steps in rate factor that preceded the advance or retreat MISI phase. Red arrows indicate the rate factors for which the analytical solution predicts a MISI event, and black arrows show the direction of the forcing towards each tipping point.
One major simplification in this idealised experiment is the bed geometry, which is synthetic and arguably unrealistically smooth. To test whether the addition of bumpiness to the bed affects how accurately the critical value of the control parameter can be predicted, we conducted further experiments in which the bed was made successively less smooth. One simple but flexible way to generate the desired roughness is to add Perlin noise to the bed. Perlin noise is a commonly used method in terrain generation that adds noise at a number of levels with successively smaller wavelengths and amplitudes. The number of levels is denoted by the octave; the rate at which each octave changes frequency is the lacunarity, and the rate at which each octave changes amplitude is the persistence. We made the common choice of a lacunarity greater than 1 and a persistence less than one, meaning that each octave adds noise of a higher frequency and lower amplitude. For a starting octave amplitude of 25 m the difference between the analytical solution and linear fit is less than 1 %, but this grows to ∼ 5 % with an amplitude of 50 m (note the change in height from peak to trough in the retrograde region of the smooth bed is ∼ 120 m). This suggests that more realistic bed geometries with increased roughness might make the task of predicting tipping points more challenging than it is in this simplified case.
The source code of the Úa ice-flow model is available from https://github.com/ghilmarg/UaSource (last access: 30 June 2020, https://doi.org/10.5281/zenodo.3706624, Gudmundsson, 2020), and raw model output is available from the authors upon request.
SHRR and RR conceived the study, SHRR conducted the modelling experiments; JFD contributed to the statistical analysis and surrogate time series; JDR provided an initial model setup. SHRR and RR wrote the manuscript with contributions from all authors.
The authors declare that they have no conflict of interest.
We are grateful to the anonymous reviewer, Alexander Robel and the editor Pippa Whitehouse for their comments, which have greatly improved our paper.
This research has been supported by the Natural Environment Research Council (grant nos. NE/L013770/1 and NE/S006745/1), the Deutsche Forschungsgemeinschaft (grant no. WI4556/3-1) and Horizon 2020 (TiPACCs (grant no. 820575)).
This paper was edited by Pippa Whitehouse and reviewed by Alexander Robel and one anonymous referee.
Anandakrishnan, S. and Alley, R.: Tidal forcing of basal seismicity of ice stream C, West Antarctica, observed far inland, J. Geophys. Res., 102, 15813–15196, 1997.
Bamber, J. L., Oppenheimer, M., Kopp, R. E., Aspinall, W. P., and Cooke, R. M.: Ice sheet contributions to future sea-level rise from structured expert judgment, P. Natl. Acad. Sci. USA, 116, 11195–11200 https://doi.org/10.1073/pnas.1817205116, 2019.
Brock, W. A. and Carpenter, S. R.: Interacting regime shifts in ecosystems: implication for early warnings, Ecol. Monogr., 80, 353–367, 2010.
Chisholm, R. A. and Filotas, E.: Critical slowing down as an indicator of transitions in two-species models, J. Theor. Biol., 257, 142–149, 2009.
Church, J. A., Clark, P. U., Cazenave, A., Gregory, J. M., Jevrejeva, S., Levermann, A., Merrifield, M. A., Milne, G. A., Nerem, R. S., Nunn, P. D., Payne, A. J., Pfeffer, W. T., Stammer, D., and Unnikrishnan, A. S.: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., and Plattner, G.-K., Cambridge University Press, Cambridge, UK, 1137–1216, 2013.
Dakos, V., Scheffer, M., van Nes, E. H., Brovkin, V., Petoukhov, V., and Held, H.: Slowing down as an early warning signal for abrupt climate change, P. Natl. Acad. Sci. USA, 105, 14308–14312, https://doi.org/10.1073/pnas.0802430105, 2008.
Dakos, V., Carpenter, S. R., Brock, W. A., Ellison, A. M., Guttal, V., Ives, A. R., Kefi, S., Livina, V., Seekell, D. A., van Nes, E. H., and Scheffer, M.: Methods for Detecting Early Warnings of Critical Transitions in Time Series Illustrated Using Simulated Ecological Data, Plos One, 7, 1–20, https://doi.org/10.1371/journal.pone.0041010, 2012.
Dakos, V., Carpenter, S. R., van Nes, E. H., and Scheffer, M.: Resilience indicators: prospects and limitations for early warnings of regime shifts, Philos. T. R. Soc. B, 370, 20130263, https://doi.org/10.1098/rstb.2013.0263, 2015.
DeConto, R. and Pollard, D.: Contribution of Antarctica to past and future sea-level rise, Nature, 531, 591–597, https://doi.org/10.1038/nature17145, 2016.
Diks, C., Hommes, C., and Wang, J.: Critical slowing down as an early warning signal for financial crises?, Empir. Econ., 57, 1201–1228, https://doi.org/10.1007/s00181-018-1527-3, 2018.
Ditlevsen, P. D. and Johnsen, S. J.: Tipping points: Early warning and wishful thinking, Geophys. Res. Lett., 37, L19703, https://doi.org/10.1029/2010GL044486, 2010.
Engwirda, D.: Locally-optimal Delaunay-refinement and optimisation-based mesh generation, PhD Thesis, School of Mathematics and Statistics, The University of Sydney, Sydney, Australia, 215 pp., 2014.
Fahnestock, M., Scambos, T., Moon, T., Gardner, A., Haran, T., and Klinger, M.: Rapid large-area mapping of ice flow using Landsat 8, Remote Sens. Environ., 185, 84–94, https://doi.org/10.1016/j.rse.2015.11.023, 2016.
Favier, L., Durand, G., Cornford, S. L., Gudmundsson, G. H., Gagliardini, O., Gillet-Chaulet, F., Zwinger, T., Payne, A. J., and Le Brocq, A. M.: Retreat of Pine Island Glacier controlled by marine ice-sheet instability, Nat. Clim. Change, 4, 117–121, https://doi.org/10.1038/nclimate2094, 2014.
Favier, L., Jourdain, N. C., Jenkins, A., Merino, N., Durand, G., Gagliardini, O., Gillet-Chaulet, F., and Mathiot, P.: Assessment of sub-shelf melting parameterisations using the ocean–ice-sheet coupled model NEMO(v3.6)–Elmer/Ice(v8.3) , Geosci. Model Dev., 12, 2255–2283, https://doi.org/10.5194/gmd-12-2255-2019, 2019.
Feldmann, J. and Levermann, A.: Collapse of the West Antarctic Ice Sheet after local destabilization of the Amundsen Basin, P. Natl. Acad. Sci. USA, 112, 14191–14196, https://doi.org/10.1073/pnas.1512482112, 2015.
Fretwell, P., Pritchard, H. D., Vaughan, D. G., Bamber, J. L., Barrand, N. E., Bell, R., Bianchi, C., Bingham, R. G., Blankenship, D. D., Casassa, G., Catania, G., Callens, D., Conway, H., Cook, A. J., Corr, H. F. J., Damaske, D., Damm, V., Ferraccioli, F., Forsberg, R., Fujita, S., Gim, Y., Gogineni, P., Griggs, J. A., Hindmarsh, R. C. A., Holmlund, P., Holt, J. W., Jacobel, R. W., Jenkins, A., Jokat, W., Jordan, T., King, E. C., Kohler, J., Krabill, W., Riger-Kusk, M., Langley, K. A., Leitchenkov, G., Leuschen, C., Luyendyk, B. P., Matsuoka, K., Mouginot, J., Nitsche, F. O., Nogi, Y., Nost, O. A., Popov, S. V., Rignot, E., Rippin, D. M., Rivera, A., Roberts, J., Ross, N., Siegert, M. J., Smith, A. M., Steinhage, D., Studinger, M., Sun, B., Tinto, B. K., Welch, B. C., Wilson, D., Young, D. A., Xiangbin, C., and Zirizzotti, A.: Bedmap2: improved ice bed, surface and thickness datasets for Antarctica, The Cryosphere, 7, 375–393, https://doi.org/10.5194/tc-7-375-2013, 2013.
Garbe, J., Albrecht, T., Leverman, A., Donges, J. F., and Winkelmann, R.: The hysteresis of the Antarctic Ice Sheet, Nature, 585, 538–544, https://doi.org/10.1038/s41586-020-2727-5, 2020.
Gomez, N., Mitrovica, J. X., Huybers, P., and Clark, P. U.: Sea level as a stabilizing factor for marine-ice-sheet grounding lines, Nat. Geosci., 3, 850–853, 2010.
Gudmundsson, G. H.: Fortnightly variations in the flow velocity of Rutford Ice Stream, West Antarctica, Nature, 444, 1063–1064, 2006.
Gudmundsson, G. H.: Ice-shelf buttressing and the stability of marine ice sheets, The Cryosphere, 7, 647–655, https://doi.org/10.5194/tc-7-647-2013, 2013.
Gudmundsson, G. H.: GHilmarG/UaSource: Ua2019b (Version v2019b), Zenodo, https://doi.org/10.5281/zenodo.3706624, 2020.
Gudmundsson, G. H., Krug, J., Durand, G., Favier, L., and Gagliardini, O.: The stability of grounding lines on retrograde slopes, The Cryosphere, 6, 1497–1505, https://doi.org/10.5194/tc-6-1497-2012, 2012.
Gudmundsson, G. H., Paolo, F. S., Adusumilli, S., and Fricker, H. A.: Instantaneous Antarctic ice- sheet mass loss driven by thinning ice shelves, Geophys. Res. Lett., 46, 13903–13909, https://doi.org/10.1029/2019GL085027, 2019.
Haseloff, M. and Sergienko, O.: The effect of buttressing on grounding line dynamics, J. Glaciol., 64, 417–431, https://doi.org/10.1017/jog.2018.30, 2018.
Held, H. and Kleinen, T.: Detection of climate system bifurcations by degenerate fingerprinting, Geophys. Res. Lett., 31, 1–4, https://doi.org/10.1029/2004GL020972, 2004.
Holland, P. R., Bracegirdle, T. J., Dutrieux, P., Jenkins, A., and Steig, E. J.: West Antarctic ice loss influenced by internal climate variability and anthropogenic forcing, Nat. Geosci., 12, 718–724, https://doi.org/10.1038/s41561-019-0420-9, 2019.
Hutter, K.: Theoretical Glaciology, Springer, Dordrecht, Netherlands, 1983.
Ives, A. R.: Measuring Resilience in Stochastic Systems, Ecol. Monogr., 65, 217–233, 1995.
Jenkins, A., Dutrieux, P., Jacobs, S. S., McPhail, S. D., Perrett, J. R., Webb, A. T., and White, D.: Observations beneath Pine Island Glacier in West Antarctica and implications for its retreat, Nat. Geosci., 3, 468–472, https://doi.org/10.1038/ngeo890, 2010.
Jenkins, A., Dutrieux, P., Jacobs, S., Steig, E. J., Gudmundsson, G. H., Smith, J., and Heywood, K. J.: Decadal Ocean Forcing and Antarctic Ice Sheet Response: Lessons from the Amundsen Sea, Oceanography, 29, 106–117, https://doi.org/10.5670/oceanog.2016.103, 2016.
Jenkins, A., Shoosmith, D., Dutrieux, P., Jacobs, S., Kim, T. W., Lee, S. H., Ha, H. K., and Stammerjohn, S.: West Antarctic Ice Sheet retreat in the Amundsen Sea driven by decadal oceanic variability, Nat. Geosci., 11, 733–738, https://doi.org/10.1038/s41561-018-0207-4, 2018.
Joughin, I., Smith, B. E., and Holland, D. M.: Sensitivity of 21st century sea level to ocean-induced thinning of Pine Island Glacier, Antarctica, Geophys. Res. Lett., 37, L20502, https://doi.org/10.1029/2010GL044819, 2010.
Joughin, I., Smith, B. E., and Medley, B.: Marine ice sheet collapse potentially under way for the Thwaites Glacier basin, West Antarctica, Science, 344, 735–738, https://doi.org/10.1126/science.1249055, 2014.
Kendall, M. G.: Rank correlation methods, Griffen, Oxford, UK, 1948.
Lenaerts, J. T. M., van den Broeke, M. R., van de Berg, W. J., van Mejigaard, E., and Kuipers Munneke, P.: A new, high-resolution surface mass balance map of Antarctica (1979–2010) based on regional atmospheric climate modeling, Geophys. Res. Lett., 39, L04501, https://doi.org/10.1029/2011GL050713, 2012.
Lenton, T. M.: Early warning of climate tipping points, Nat. Clim. Change, 1, 201–209, https://doi.org/10.1038/nclimate1143, 2011.
Lenton, T. M., Held, H., Kriegler, E., Hall, J. W., Lucht, W., Rahmstorf, S., and Schellnhuber, H. J.: Tipping elements in the Earth's climate system, P. Natl. Acad. Sci. USA, 105, 1786–1793, https://doi.org/10.1073/pnas.0705414105, 2008.
Lenton, T. M., Myerscough, R. J., Marsh, R., Livinia, V. N., Price, A. R., and Cox, S. J.: Using GENIE to study a tipping point in the climate system, Philos. T. R. Soc. A, 367, 871–884, 2009.
Lenton, T. M., Livina, V. N., Dakos, V., and Scheffer, M.: Climate bifurcation during the last deglaciation?, Clim. Past, 8, 1127–1139, https://doi.org/10.5194/cp-8-1127-2012, 2012a.
Lenton, T. M., Livina, V. N., Dakos, V., van Nes, E. H., and Scheffer, M.: Early warning of climate tipping points from critical slowing down: comparing methods to improve robustness, Philos. T. R. Soc. A, 370, 1185–1204, https://doi.org/10.1098/rsta.2011.0304, 2012b.
Ligtenberg, S. R. M., Helsen, M. M., and van den Broeke, M. R.: An improved semi-empirical model for the densification of Antarctic firn, The Cryosphere, 5, 809–819, https://doi.org/10.5194/tc-5-809-2011, 2011.
Litt, B., Esteller, R., Echauz, J., D'Alessandro, M., Shor, R., Henry, T., Pennell, P., Epstein, C., Bakay, R., Dichter, M., and Vachtsevanos, G.: Epileptic Seizures May Begin Hours in Advance of Clinical Onset: A Report of Five Patients, Neuron, 30, 51–64, https://doi.org/10.1016/S0896-6273(01)00262-8, 2001.
Livina, V. N. and Lenton, T. M.: A modified method for detecting incipient bifurcations in a dynamical system, Geophys. Res. Lett., 34, 1–5, https://doi.org/10.1029/2006GL028672, 2007.
May, R., Levin, S. A., and Sugihara, G.: Ecology for bankers, Nature, 451, 893–895, https://doi.org/10.1038/451893a, 2008.
McSharry, P. E. A. S. L. and Tarassenko, L.: Prediction of epileptic seizures: are nonlinear methods relevant?, Nat. Med., 9, 241–242, https://doi.org/10.1038/nm0303-241, 2003.
Millan, R., Rignot, E., Bernier, V., Morlighem, M., and Dutrieux, P.: Bathymetry of the Amundsen Sea Embayment sector of West Antarctica from Operation IceBridge gravity and other data, Geophys. Res. Lett., 44, 1360–1368, https://doi.org/10.1002/2016GL072071, 2017.
Minchew, B. M., Simons, M., Riel, B., and Milillo, P.: Tidally induced variations in vertical and horizontal motion on Rutford Ice Stream, West Antarctica, inferred from remotely sensed observations, J. Geophys. Res.-Earth Surf., 122, 167–190, https://doi.org/10.1002/2016JF003971, 2017.
O'Leary, M., Hearty, P., Thompson, W., Raymo, M. E., Mitrovica, J. X., and Webster, J. M.: Ice sheet collapse following a prolonged period of stable sea level during the last interglacial, Nat. Geosci. 6, 796–800, https://doi.org/10.1038/ngeo1890, 2013.
Oppenheimer, M., Glavovic, B. C., Hinkel, J., van de Wal, R., Magnan, A. K., Abd-Elgawad, A., Cai, R., Cifuentes-Jara, M., DeConto, R. M., Ghosh, T., Hay, J., Isla, F., Marzeion, B., Meyssignac, B., and Sebesvari, Z.: Sea Level Rise and Implications for Low-Lying Islands, Coasts and Communities, in: IPCC Special Report on the Ocean and Cryosphere in a Changing Climate, edited by: Portner, H.-O., Roberts, D. C., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegriìa, A., Nicolai, M., Okem, A., Petzold, J., Rama, B., and Weyer, N. M., Cambridge University Press, Cambridge, UK, 2019.
Park, J. W., Gourmelen, N., Shepherd, A., Kim, S. W., Vaughan, D. G., and Wingham, D. J.: Sustained retreat of the Pine Island Glacier, Geophys. Res. Lett., 40, 2137–2142, https://doi.org/10.1002/grl.50379, 2013.
Pattyn, F., Schoof, C., Perichon, L., Hindmarsh, R. C. A., Bueler, E., de Fleurian, B., Durand, G., Gagliardini, O., Gladstone, R., Goldberg, D., Gudmundsson, G. H., Huybrechts, P., Lee, V., Nick, F. M., Payne, A. J., Pollard, D., Rybak, O., Saito, F., and Vieli, A.: Results of the Marine Ice Sheet Model Intercomparison Project, MISMIP, The Cryosphere, 6, 573–588, https://doi.org/10.5194/tc-6-573-2012, 2012.
Pegler, S.: Marine ice sheet dynamics: The impacts of ice-shelf buttressing, J. Fluid Mech., 857, 605–647, https://doi.org/10.1017/jfm.2018.741, 2018.
Peng, C. K., Buldyrev, S. V., Havlin, S., Simons, M., Stanley, H. E., and Goldberger, A. L.: Mosaic organization of DNA nucleotides, Phys. Rev. E, 49, 1685–1689, https://doi.org/10.1103/PhysRevE.49.1685, 1994.
Rignot, E. J.: Fast Recession of a West Antarctic Glacier, Science, 281, 549–551, https://doi.org/10.1126/science.281.5376.549, 1998.
Rignot, E., Mouginot, J., Morlighem, M., Seroussi, H., and Scheuchl, B.: Widespread, rapid grounding line retreat of Pine Island, Thwaites, Smith, and Kohler glaciers, West Antarctica, from 1992 to 2011, Geophys. Res. Lett., 41, 3502–3509, https://doi.org/10.1002/2014GL060140, 2014.
Ritz, C., Edwards, T., Durand, G., Payne, A. J., Peyaud, V., and Hindmarsh, R. C. A.: Potential sea-level rise from Antarctic ice-sheet instability constrained by observations, Nature, 528, 115–118, https://doi.org/10.1038/nature16147, 2015.
Robel, A. A., Schoof, C., and Tziperman, E.: Persistence and variability of ice-stream grounding lines on retrograde bed slopes, The Cryosphere, 10, 1883–1896, https://doi.org/10.5194/tc-10-1883-2016, 2016.
Robel, A. A., Roe, G. H., and Haseloff, M.: Response of marine-terminating glaciers to forcing: Time scales, sensitivities, instabilities, and stochastic dynamics, J. Geophys. Res.-Earth, 123, 2205–2227, https://doi.org/10.1029/2018JF004709, 2018.
Robel, A. A., Seroussi, H., and Roe, G. H.: Marine ice sheet instability amplifies and skews uncertainty in projections of future sea-level rise, P. Natl. Acad. Sci. USA, 116, 14887–14892, https://doi.org/10.1073/pnas.1904822116, 2019.
Robinson, A., Calov, R., and Ganopolski, A.: Multistability and critical thresholds of the Greenland ice sheet, Nat. Clim. Change 2, 429–432, https://doi.org/10.1038/nclimate1449, 2012.
Scambos, T., Fahnestock, M., Moon, T., Gardner, A., and Klinger, M.: Global Land Ice Velocity Extraction from Landsat 8 (GoLIVE), Version 1, NSIDC: National Snow and Ice Data Center, Boulder, USA, https://doi.org/10.7265/N5ZP442B, 2016.
Schaffer, J., Timmermann, R., Arndt, J. E., Kristensen, S. S., Mayer, C., Morlighem, M., and Steinhage, D.: A global, high-resolution data set of ice sheet topography, cavity geometry, and ocean bathymetry, Earth Syst. Sci. Data, 8, 543–557, https://doi.org/10.5194/essd-8-543-2016, 2016.
Scheffer, M., Carpenter, S., Foley, J. A., Folke, C., and Walker, B.: Catastrophic shifts in ecosystems, Nature, 413, 591–596, https://doi.org/10.1038/35098000, 2001.
Scheffer, M., Bascompte, J., Brock, W. A., Brovkin, V., Carpenter, S. R., Dakos, V., Held, H., van Nes, E. H., Rietkerk, M., and Sugihara, G.: Early-warning signals for critical transitions, Nature, 461, 53–59, https://doi.org/10.1038/nature08227, 2009.
Schoof, C.: Ice sheet grounding line dynamics: Steady states, stability, and hysteresis, J. Geophys. Res., 112, F03S28, https://doi.org/10.1029/2006JF000664, 2007.
Schoof, C.: Marine ice sheet stability, J. Fluid Mech., 698, 62–72, https://doi.org/10.1017/jfm.2012.43, 2012.
Seroussi, H. and Morlighem, M.: Representation of basal melting at the grounding line in ice flow models, The Cryosphere, 12, 3085–3096, https://doi.org/10.5194/tc-12-3085-2018, 2018.
Shepherd, A., Wingham, D., and Rignot, E.: Warm ocean is eroding West Antarctic Ice Sheet, Geophys. Res. Lett., 31, L23402, https://doi.org/10.1029/2004GL021106, 2004.
Slater, T., Shepherd, A., McMillan, M., Muir, A., Gilbert, L., Hogg, A. E., Konrad, H., and Parrinello, T.: A new digital elevation model of Antarctica derived from CryoSat-2 altimetry, The Cryosphere, 12, 1551–1562, https://doi.org/10.5194/tc-12-1551-2018, 2018.
Smith, J. A., Andersen, T. J., Shortt, M., Gaffney, A. M., Truffer, M., Stanton, T. P.,Bindschadler, R., Dutrieux, P.,Jenkins, A., Hillenbrand, C.-D. Ehrmann, W., Corr, H. F. J., Farley, N., Crowhurst, S., and Vaughan, D. G.: Sub-ice-shelf sediments record history of twentieth-century retreat of Pine Island Glacier, Nature, 541, 77–80, https://doi.org/10.1038/nature20136, 2016.
Turner, J., Orr, A., Gudmundsson, G. H., Jenkins, A., Bingham, R. G., Hillenbrand, C.-D., and Bracegirdle, T. J.: Atmosphere-ocean-ice interactions in the Amundsen Sea Embayment, West Antarctica, Rev. Geophys., 55, 235–276, https://https://doi.org/10.1002/2016RG000532, 2017.
van Nes, E. H. and Scheffer, M.: Slow Recovery from Perturbations as a Generic Indicator of a Nearby Catastrophic Shift, Am. Nat., 169), 738–747, https://doi.org/10.1086/516845, 2007.
Weertman, J.: Stability of the Junction of an Ice Sheet and an Ice Shelf, J. Glaciol., 13, 3–11, https://doi.org/10.3189/S0022143000023327, 1974.
Wissel, C.: A universal law of The characteristic return time near thresholds, Oecologia, 65, 101–107, https://doi.org/10.1007/BF00384470, 1984.





