the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Snow albedo sensitivity to macroscopic surface roughness using a new ray-tracing model
Fanny Larue
Ghislain Picard
Laurent Arnaud
Inès Ollivier
Clément Delcourt
Maxim Lamare
François Tuzet
Jesus Revuelto
Marie Dumont
Most models simulating snow albedo assume a flat and smooth surface, neglecting surface roughness. However, the presence of macroscopic roughness leads to a systematic decrease in albedo due to two effects: (1) photons are trapped in concavities (multiple reflection effect) and (2) when the sun is low, the roughness sides facing the sun experience an overall decrease in the local incidence angle relative to a smooth surface, promoting higher absorption, whilst the other sides have weak contributions because of the increased incidence angle or because they are shadowed (called the effective-angle effect here). This paper aims to quantify the impact of surface roughness on albedo and to assess the respective role of these two effects, with (1) observations over varying amounts of surface roughness and (2) simulations using the new rough surface ray-tracing (RSRT) model, based on a Monte Carlo method for photon transport calculation.
The observations include spectral albedo (400–1050 nm) over manually created roughness surfaces with multiple geometrical characteristics. Measurements highlight that even a low fraction of surface roughness features (7 % of the surface) causes an albedo decrease of 0.02 at 1000 nm when the solar zenith angle (θs) is larger than 50∘. For higher fractions (13 %, 27 % and 63 %), and when the roughness orientation is perpendicular to the sun, the decrease is of 0.03–0.04 at 700 nm and of 0.06–0.10 at 1000 nm. The impact is 20 % lower when roughness orientation is parallel to the sun. The observations are subsequently compared to RSRT simulations. Accounting for surface roughness improves the model observation agreement by a factor of 2 at 700 and 1000 nm (errors of 0.03 and 0.04, respectively) compared to simulations considering a flat smooth surface. The model is used to explore the albedo sensitivity to surface roughness with varying snow properties and illumination conditions. Both multiple reflections and the effective-angle effect have a greater impact with low specific surface area (SSA; <10 m2 kg−1). The effective-angle effect also increases rapidly with θs at large θs. This latter effect is larger when the overall slope of the surface is facing away from the sun and has a roughness orientation perpendicular to the sun.
For a snowpack where artificial surface roughness features were created, we showed that a broadband albedo decrease of 0.05 may cause an increase in the net shortwave radiation of 80 % (from 15 to 27 W m−2). This paper highlights the necessity of considering surface roughness in the estimation of the surface energy budget and opens the way for considering natural rough surfaces in snow modelling.
- Article
(2274 KB) - Full-text XML
- BibTeX
- EndNote
Spectral albedo quantifies the proportion of solar energy reflected by a surface for each wavelength and governs the quantity of solar radiation absorbed in the snowpack. Because snow has an overall high albedo in the solar spectrum, a small decrease in albedo (e.g. from 0.85 to 0.75) drastically increases the proportion of absorbed energy (from 25 % to 15 %; Genthon, 1994). Thus, a reduction in albedo has important consequences for the surface energy budget, impacting surface temperature (Mondet and Fily, 1999; Picard et al., 2012; Fréville et al., 2014), and the hydrology of watersheds (e.g. Flanner et al., 2009; Painter et al., 2010; Oaida et al., 2015). Several studies have investigated the spatial and temporal variability in snow albedo using in situ data (Brock et al., 2000; Wuttke et al., 2006; Dumont et al., 2017) or satellite observations (Atlaskina et al., 2015; Naegeli and Huss, 2017). Snow spectral albedo generally depends, in a complex way, on several factors, including (1) the snow physical and chemical properties, mainly the specific surface area (SSA) of snow grains (Gallet et al., 2009), the snow grain shapes (Tanikawa et al., 2006; Jin et al., 2008; Libois et al., 2013, 2014) and the concentration of snow light-absorbing particles (referred to as LAPs; Skiles et al., 2018); (2) the spectral and angular characteristics of the incident radiation (Warren, 1982); and (3) the presence of macroscopic surface roughness (Kuhn, 1985; Warren et al., 1998; Mondet and Fily, 1999). The first two points have been thoroughly studied, showing that for a smooth surface, snow albedo decreases as SSA lowers (coarsening snow granularity), and with a higher sun elevation (i.e. a decrease in solar zenith angle), both of which lead to an increased absorption (Warren et al., 1998; Kokhanovsky and Zege, 2004). Nevertheless, the effects of roughness are often neglected due to the difficulty of characterising the actual surface roughness within the footprint of the sensor.
Snow-covered surfaces often exhibit macroscopic roughness, resulting from snow transport or erosion by the wind or snowmelt (Filhol and Sturm, 2015). In Antarctica, roughness height ranges from a few centimetres to a few metres (Warren et al., 1998; Wuttke et al., 2006), and the features' axis is usually aligned along the prevailing wind direction (Furukawa et al., 1996), whereas in alpine areas the spatial distribution of macroscopic roughness mainly depends on topography, which drives wind direction and its intensity (Naaim-Bouvet et al., 2011). As reported by Warren et al. (1998), Kuhn (1974) was the first to observe a reduction of the forward peak of the bidirectional reflectance distribution function (BRDF) over a sastrugi field and attributed this fact to shadows when the solar azimuth angle is perpendicular to the sastrugi. This motivated further studies that showed a systematic albedo decrease in the presence of roughness (Carroll and Fitch, 1981; Leroux and Fily, 1998; Corbett and Su, 2015). The amplitude of the reduction in albedo depends on illumination conditions, snow properties, and the size and the orientation of roughness features (Hudson and Warren, 2007; L'Hermitte et al., 2014). For instance, in high-altitude mountain glaciers, the presence of penitentes, which can reach several metres in height (Lliboutry, 1953), causes a measured albedo decrease of 8 %–10 % (Corripio and Purves, 2006). These studies underlined the difficulty of precisely quantifying the impact of roughness, since the illumination conditions and snow properties also vary during albedo measurements, making it difficult to evaluate the reduction in albedo due to roughness only. A protocol was proposed by Kuchiki et al. (2011), using a controlled environment where the precise roughness shapes, orientation and dimensions, snow properties, and illumination conditions were known. Over a manually created artificial roughness field, they showed that the hemispherical–directional reflectance (HRDF) factor varies by more than ±50 % relative to a smooth surface. Nevertheless, they did not acquire albedo measurements, i.e. bi-hemispherical reflectance.
Warren et al. (1998) showed that the albedo decrease over a roughness field is controlled by two effects: (1) a decrease in the insolation-weighted average incidence angle relative to a flat surface (further referred to as the effective-angle effect) and (2) multiple reflections in the concavities. The first effect is explained by the fact that the sides of the roughness shapes facing the sun experience stronger radiation with a smaller angle than the solar zenith angle, which enhances absorption in the case of snow surface (Warren, 1982), and the sides facing away from the sun receive less radiation due to shadows or grazing angles. The insolation-weighted average albedo is therefore reduced relatively to a flat and smooth surface (Warren, 1982; Warren et al., 1998; Kokhanovsky and Zege, 2004). The effective-angle effect varies with the shape, size and orientation of the roughness features (Carroll and Fitch, 1981; L'Hermitte et al., 2014) and is significant under direct illumination and for low sun elevations only (Warren et al., 1998). The second effect of roughness involves multiple reflections caused by the trapping of photons between roughness shapes (Pfeffer and Bretherton, 1987). Over a smooth surface, a photon only hits the surface once and is either absorbed or reflected to the sky. Over a rough surface, photons can not only be absorbed or reflected to the sky but also be reflected back to the surface. In the latter case, they have another probability of being absorbed, at every hit. This results in a systematic increase in absorption and thus a decrease in albedo. The impact is maximal when the probabilities of reflection and absorption are balanced, i.e. for intermediate values of albedo (close to 0.5 in the near-infrared – NIR – at 700–1100 nm). Instead in the visible range, where albedo is close to 1, the probability of absorption is too low to trap the photons, and oppositely in the mid-infrared where the albedo is close to 0, the impact of multiple reflections is negligible. This trapping effect operates under direct and diffuse illumination. Although these two effects have never been quantified separately, Warren et al. (1998) suggested acquiring measurements in diffuse illumination to estimate the impact of multiple reflections only.
Photometric models based on analytical equations were developed to simulate the effects of roughness on albedo using idealised geometric shapes (Carroll, 1982; Pfeffer and Bretherton, 1987; Wendler and Kelley, 1988; Leroux and Fily, 1998; Cathles et al., 2011, 2014; Zhuravleva and Kokhanovsky; 2010, 2011). Leroux and Fily (1998) predicted a decrease in albedo over a sastrugi field of 5 %–9 % at 900 nm, depending on the sastrugi orientation with respect to the sun position. Despite being of interest for drawing general conclusions on the albedo sensitivity to roughness characteristics, these models are of limited interest for real roughness features due to the idealisation of the shapes (Warren et al., 1998). In addition, they use the Lambertian approximation to represent the surface reflectivity and do not consider the intrinsic BRDF of the snow, meaning that they cannot simulate the effective-angle effect. To explore the real impact of surface roughness, a 3-D radiative transfer model is needed. Monte Carlo photon transport algorithms are convenient approaches (Lafortune, 1995; O'Rawe, 1991; Iwabuchi, 2006; Kuchiki et al., 2011). However, most studies using these numerical methods aim to evaluate the BRDF or HRDF instead of albedo, as their application domain was remote sensing (Kuchiki et al., 2011; L'Hermitte et al., 2014; Corbet and Su, 2015).
The aims of this paper are twofold: (1) to quantify the impact of surface roughness on snow albedo, as a function of roughness features, illumination conditions and snow properties, and (2) to assess the respective roles of the effective-angle effect and multiple reflections with a new model able to represent surface roughness. Firstly, we collected albedo measurements in controlled experiments following the idea of Kuchiki et al. (2011). We produced various artificial rough surfaces during four field campaigns in the French Alps in 2018 and 2019 (Sect. 2). In each experiment, albedo measurements were acquired for several illumination conditions and with numerous geometrical characteristics at the surface. Observations were also acquired over nearby smooth surfaces to serve as references. Secondly, we developed a new model based on the Monte Carlo photon transport method, the rough surface ray-tracing (RSRT) model, to simulate albedo by considering surface roughness (Sect. 3). The RSRT model was evaluated using the albedo observations (Sect. 4.1). In Sect. 4.2, the model was used to explore the albedo sensitivity to surface roughness according to SSA, terrain slope, roughness orientation and solar zenith angle. The model was applied to assess the respective roles played by the effective-angle effect and multiple reflections (Sect. 4.3). At last, the sensitivity of the net shortwave radiation to the presence of surface roughness is discussed to estimate the potential impact on the surface energy balance (Sect. 4.4).
In situ measurements of albedo were acquired in the French Alps over smooth and rough snow surfaces. This section details how the rough surfaces were created and measurements were acquired in the field.
2.1 Artificial rough snow surfaces
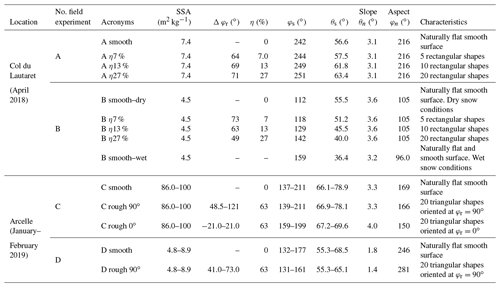
Artificial rough snow surfaces were created by delineating squares of 2.5 m×2.5 m. Roughness features were manually created on natural smooth surfaces by varying their number and orientation. The features were produced parallel to each other, regularly spaced with a period Λ and with an azimuth angle φr, taken clockwise from the north. The roughness orientation with respect to the solar azimuth angle (φs) was defined by Δφr, the difference φs–φr. Figure 1 shows the experimental set-up and the variables involved. Each surface was characterised by its aspect, its slope and its roughness properties (number, shape, size and orientation). Two types of experiments were performed.
-
(a) Sensitivity to the fraction of roughness features. The fraction of roughness features in the 2.5 m×2.5 m area is described with the width-to-period ratio η (i.e. , expressed in percentage, where W is the width of roughness shapes). The albedo sensitivity to η was studied during two experiments at the Col du Lautaret site (45∘2′ N, 6∘2′ E; 2100 m a.s.l.) over two different dates (6 and 17 April 2018), respectively called experiments A and B. Figure 2 illustrates the field experiment A, and Table 1 details the characteristics, acronyms and parameters for each studied surface. Snow albedo was first measured over the smooth surface (called A smooth and B smooth–dry in Table 1), and then the roughness shapes were created on the smooth surface by uniformly pressing a rectangular metal bar into the snow (H=2 cm – depth – and W=4 cm – width) in the north–south direction (φr=0∘–180∘). The rectangular shapes were created with a period Λ=55 cm (5 shapes over 2.5 m; η=7 %). After albedo measurements were acquired, identical rectangular shapes were added to reach a period Λ=30 cm (10 shapes over 2.5 m; η=13 %) then Λ=15 cm (20 shapes over 2.5 m; η=27 %) (Fig. 2 and Table 1). Because it takes approximately 1 h to make a series of measurements, the increasing fraction of roughness features is correlated to solar zenith angle (θs) variations that also change albedo. To attempt to decouple the two effects, experiment A was conducted when the sun was going down (θs went from 56.6 to 63.7∘), whereas in experiment B, the sun was going up (θs went from 56.0 to 40.0∘). Other changes may also occur during that time. In experiment B for instance, melting was observed on the B η27 % surface (the sun was close to the nadir), which leads to an increase in snow wetness and a decrease in surface SSA compared to the B smooth–dry surface analysed at the beginning of the day. To allow for more reliable comparisons, we simultaneously measured albedo over the B η27 % surface and a nearby smooth surface (called B smooth–wet in Table 1).
-
(b) Sensitivity to the roughness orientation. The albedo sensitivity to roughness orientation was studied with two experiments at the Arcelle site (45∘6′ N, 5∘52′ E; 1729 m a.s.l.) over two dates (11 January and 22 February 2019), respectively called experiments C and D. The roughness shapes were triangular, with a H=6 cm depth and W=7 cm width, and created with a period Λ=11 cm (η=63 %). Figure 1b and Table 1 detail the experimental set-up. In experiment C, measurements were simultaneously acquired every 20 min over a surface with roughness features oriented at φr=90∘ (called C rough 90∘), another one with roughness features at φr=0∘ (called C rough 0∘) and a smooth surface for reference (called C smooth). In experiment D, only two surfaces were compared every 20 min: a rough surface with roughness features at φr=90∘ (called D rough 90∘) and a smooth surface (called D smooth). For both experiments, studied surfaces were close enough to consider that snow properties evolved with the same dynamics. Note that it took about 5 min to acquire one set of albedo measurements and to move it to the next surface. Measurements were acquired all day in experiment C (sun going up and down) and in the morning in experiment D (sun going up only).
The albedo sensitivity to roughness features is quantified by comparing rough and smooth surfaces for each experiment.
In reality, it is difficult to find perfectly flat surfaces, and all studied surfaces have small slopes. In particular, it is noteworthy that experiments A, B and C have a small sun-facing slope.
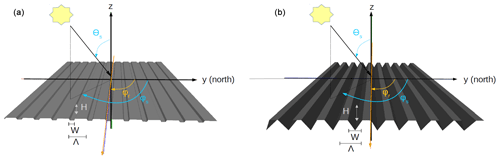
Figure 1Illustration of the set-ups for (a) A η27 % and B η27 % experiments and (b) C rough 90∘ and D rough 90∘ experiments (Table 1 for acronyms). The grey surfaces are modelled meshes with parallel shapes (rectangular or triangular), similar to the artificial roughness surfaces created in the field. The two sites are areas of 2.5 m×2.5 m. H is the height, W the width and Λ the period of roughness features. φr is the roughness orientation, φs the solar azimuth angle and θs the solar zenith angle. Azimuth angles are clockwise from north (y axis).

Figure 2Studied surfaces of experiment A (Table 1), from (a) to (d): A smooth, A η7 %, A η13 % and A η27 % sites.
2.2 Spectral albedo measurements
Spectral albedo, or more precisely bi-hemispherical reflectance (Schaepman-Strub et al., 2006), is the ratio of the upwelling and the downwelling spectral irradiance. Snow spectral albedo measurements were acquired with the Solalb instrument, a manual version of the albedometer Autosolexs described by Picard et al. (2016). Solalb is a hand-held instrument using a single light collector with a near-cosine response and equipped with an inclinometer located at the end of a 3 m boom. The boom was rotated by the operator to successively acquire the downward and upward solar radiation with a horizontal sensor (±0.1∘ accuracy). This operation usually takes up to a maximum time of 30 s. Variations in incident illumination caused by clouds between two acquisitions were also measured with a photodiode receiving ambient radiation. Only spectra with stable incident illumination within 1 % were selected. Spectra were acquired over the 400–1050 nm wavelength range, with an effective resolution of 3 nm. The height of the sensor impacts the measured roughness effects by changing the footprint of the sensor (L'Hermitte et al., 2014). To study this sensitivity, albedo was measured with sensor heights of 45, 55 and 65 cm in experiments A and B (not shown). We found a weak influence on measured albedo (0.4 %±0.5 % of differences between spectra), showing that this sensitivity was negligible given the type of roughness considered here and the sensor's height. Therefore, the sensor was set to be 65 cm high for all experiments. At this height, the footprint is about 2.3 m×2.3 m (99 % of the signal is coming from a viewing angle of 60∘; Picard et al., 2016). The ratio of diffuse to total irradiance (rdiff−tot) was also measured shortly after the albedo measurement by screening the sun to record the diffuse irradiance, with the total irradiance being measured with the sensor looking upward.
Post-processing was applied to each acquired spectrum following Picard et al. (2016). This includes dark current correction, considering the integration time, and the correction of the collector angular responses.
The observed apparent albedo, hereinafter referred to as αobs, is the processed spectrum measured with Solalb, considering the sensor in a horizontal position (Sicart et al., 2001).
The accuracy of αobs mainly depends on that of the levelling of the arm. To estimate αobs uncertainties, measurements were duplicated three times for six different sites. A maximal variation of 1.6 % was estimated between the αobs spectra acquired in the same field conditions.
2.3 Snow surface properties
Snow SSA was measured at the surface using the Alpine Snowpack Specific Surface Area Profiler (ASSSAP) instrument, which has an accuracy of 10 % (Arnaud et al., 2011). For the two experiments A and B, we measured the surface SSA in the middle of the experiment (corresponding to η=13 %), and the SSA was assumed to be constant throughout the experiments (3 h). The albedo sensitivity to SSA variations and associated uncertainties is discussed in Sect. 4.2 in order to untwine these contributions from those of roughness. Note that compacting to create the roughness features may have lowered the SSA locally. As the compaction was small (2 cm depth), and as the SSA values were initially low over the studied surfaces, we assumed here that the effect of the compaction on the observed albedo is negligible. For the two experiments C and D, three SSA measurements were taken at the surface at each albedo acquisition: two in the cavities (one over the side facing the sun, one over the side facing away from the sun) and one over the smooth surface between cavities. The standard deviations of these three SSA values are always lower than 10 % of the mean SSA, showing that the compaction effect is negligible compared to measurement uncertainties. The mean of these three SSA values is used in our albedo simulations.
To limit the scope of this study, the concentration of LAPs, such as mineral dust and black carbon, was not measured, although they strongly lower the spectral signature in the visible range (Warren, 1982), especially at the end of the season, when the concentration of impurities is high at the surface (Flanner et al., 2009). This was the case for experiments A and B (measurements acquired in April). Figure 3 shows the spectrum measured over the A smooth surface. The albedo decrease in the 400–600 nm range is a clear signature of the presence of snow impurities. Even a small number of LAPs led to a high decrease in the albedo in the visible domain (Tuzet et al., 2019, 2020). This sensitivity is well described in Dumont et al. (2017). To minimise this contribution, we chose to quantify the effects of roughness in the 600–1050 nm wavelength range.
2.4 Surface slope effects on the measured albedo
In the case of a tilted surface, Solalb is not perfectly parallel to the snow surface, and therefore the ratio of values acquired by the sensor when it measures the downwelling and the upwelling spectral irradiance (called the apparent or measured albedo, here αobs) differs from the intrinsic surface albedo (called true albedo in previous studies; Picard et al., 2020). Indeed, when the sensor is horizontal, the titled surface receives sun radiation with a different incidence angle and is viewed with a reduced solid angle by the sensor (Grenfell et al., 1994; Wuttke et al., 2006; Dumont et al., 2017). With surfaces that have a sun-facing slope, it has been demonstrated that measured albedo values may be over 1 in the visible range because there is a higher interception probability of the sun beam by these slopes facing the sun compared to the horizontal sensor (Picard et al., 2020). Therefore, apparent albedo may exceed 1 in the visible range. In contrast, the intrinsic albedo strictly ranges between 0 and 1.
In this study, surfaces of experiments A, B and C have small sun-facing slopes (Table 3), and the slope effects cannot be neglected in albedo simulations, since even a small slope (2∘) facing the sun may induce a variation in measured albedo by up to 5 % over a smooth surface (Dumont et al., 2017).
In the field, an inclinometer fixed at the end of a 2 m ruler was used to measure the slope in the sensor's footprint. The aspect of the slope is defined as the azimuthal direction of the steepest slope, clockwise in degrees from the north. However, as the studied surfaces were chosen to be as flat as possible, the steepest inclination was not visually detectable. Thus, a first inclination measurement was acquired with the ruler parallel to the roughness features, and a second one was acquired by rotating the ruler by 90∘ in order to estimate the normal of the surface (n = (nx, ny, nz)). The slope and the aspect were deduced as follows:
where θn is the steepest slope angle, and φn is the aspect of the slope. In this study, all surface slopes were below 5∘. The uncertainty of slope measurements was estimated to be ±1∘ due to natural ripples of the studied surfaces. The impact of this uncertainty in our roughness analysis is discussed in Sect. 4.3.2.
The RSRT model was developed to simulate snow albedo considering macroscopic surface roughness. This combines both (1) the asymptotic radiative transfer theory (Sect. 3.1) to compute the spectral albedo each time a photon hits the modelled surface and (2) a Monte Carlo technique (Sect. 3.2) to estimate the geometric effects introduced by roughness and represented with a 3-D mesh of the studied area. Section 3.3 details the simulation framework and sensitivity analysis. A simple approach is applied to illustrate the impact of roughness on the quantity of energy absorbed in the snowpack (Sect. 3.4).
3.1 Asymptotic radiative transfer theory
In the RSRT algorithm, an ensemble of photons is launched over a modelled surface. This surface is represented with a triangular mesh composed of small facets. Both the spectral albedo and the BRDF distribution are computed for each facet hit by a photon. The asymptotic radiative transfer (ART) theory provides analytical equations to estimate spectral albedo for highly reflective materials, which applies well to snow in the visible and the NIR domains, typically from 400 to 1100 nm (Zege et al., 1991; Kokhanovsky and Zege, 2004). Several models use this theory (Negi et al., 2011; Libois et al., 2013; Wang et al., 2017), which is based on three assumptions: (1) the snowpack is represented with vertically and horizontally homogeneous plane-parallel layers; (2) the surface is perfectly smooth and horizontal (flat); and (3) single-scattering albedo and the snow phase function are described with the asymmetry factor, g, the absorption enhancement parameter, B, and the SSA of the snow. The albedo simulated with the ART theory has shown good accuracy compared to observations over smooth surfaces (Dumont et al., 2017; Wang et al., 2017). The facets of the mesh are small enough to be considered smooth surfaces. The direct and the diffuse part of the albedo at the wavelength λ and θs, αdir(λ,θs) and αdiff(λ) are estimated with Eqs. (3) and (4):
where ρice=917 kg m−3 is the bulk density of ice at 0 ∘C, and γ(λ) is the wavelength-dependent absorption coefficient of ice, taken from Picard et al. (2016). B and g are the snow shape coefficients and are assumed to be constant. Theoretically, g should be directly linked with the wavelength and the ice particle shapes, but as g is not measurable, we used constant values estimated by Libois et al. (2014), who combined simulations and in situ measurements of reflectance in Antarctica and the French Alps. They found that using B=1.6 and g=0.86 is more realistic for modelling snow optical properties than considering spherical grains.
The albedo of a flat smooth surface obtained with ART (αflat) at wavelength λ and at θs is deduced as follows:
where rdiff−tot (λ,θs) is the ratio of diffuse to total illumination at wavelength λ and at θs, measured in the field shortly after each albedo measurement.
These formulations apply to a strictly levelled terrain (better than 0.5∘). To account for the slope and compute the apparent albedo of a titled smooth surface, called αsim,smooth, a K factor is applied (Dumont et al., 2017), such as
and
where is the effective θs modified with the slope. As shown by Dumont et al. (2017), the K factor is the relative change in the cosine of the sun effective incidence angle to the slope and makes it possible to reproduce the distortion of the spectra due to the presence of the slope (with potential albedo values above 1 in the case of a sun-facing slope; Picard et al., 2020).
Following the ART theory, Kokhanovsky and Zege (2004) (further referred as the KZ04 approximations) estimated the snow BRDF distribution by calculating reflectance over a hemisphere with the reflection function of a semi-infinite medium:
where the function R0(Φ, cosθs, cosθv) is the reflection function at ω0=1 (Kokhanovsky, 2013), with ω0 being the single-scattering albedo. Φ is the relative azimuth angle, cosθv is the cosine of the viewing zenith angle, cosθs is the cosine of the solar zenith angle and A is estimated as follows:
ks and kv are called the escape functions and are given by Kokhanovsky (2003) as
and
3.2 Algorithms and model architecture
The Monte Carlo photon light transport algorithm propagates a large number of photons from their source to termination (i.e. that escape from the scene).
A photon is a particle of light carrying a flux and described by its power (intensity), its origin r and its propagation direction i. Each photon starts its trajectory with an intensity equal to 1 (unitless quantity of energy) and a direction i described with the couple (θs, φs) given as input. Photons are either absorbed or reflected at each hit according to the facet albedo value (Iwabuchi, 2006), which is estimated with the single-scattering properties in case of the KZ04 configuration or as a constant snow reflectance in case of the Lambertian configuration. The algorithm works as follows.
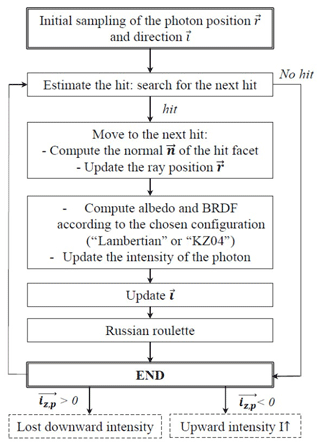
A flow chart of a photon path as computed with RSRT is presented in Fig. 4. This is computed in four main steps.
-
Step 1: estimate the next intersection of the photon with the mesh of the surface (called “hit”). The bounding volume hierarchies (BVH) technique (Ize, 2013) is used to efficiently search for the first facet in the photon propagation direction. It uses a simple recursive intersection routine to test if the photon hits or does not hit the bounding volume, and when positive, the hitting point is searched using a BVH algorithm (Wald et al., 2007). The precise intersection point within the facet is determined by applying the watertight ray–triangle intersection algorithm (Woop et al., 2013). If the photon hits a facet, its origin r is updated on the intersected facet. The normal of the facet is estimated. If there is no hit, the photon escapes from the mesh, and depending on its direction (upward or downward), its intensity is added to the downwelling or upwelling radiation bin (Fig. 4).
-
Step 2: Update the intensity. The photon intensity at hit n (called ip,n) is weighted by the spectral albedo, accounting for the incoming direction angles αflat (λ,θi) as follows:
Two configurations are possible: with the KZ04 configuration, the hit facet is considered to be a snow surface and αflat (λ,θi) is estimated by considering the local incidence angle θi and snow properties (SSA, B, g; i.e. with ART; Eq. 5). With the Lambertian configuration, the hit facet is a Lambertian surface (i.e. isotropic diffusion), and the αflat (λ,θi) is a constant value equal to αflat (λ), given as an input of RSRT.
-
Step 3: Sample the outgoing direction. The most likely outgoing direction of the photon after a hit is estimated from the BRDF distribution computed with the KZ04 approximations (Sect. 3.1). Thus, the next direction after the scattering depends on the incidence angle of the photon and snow properties. With the KZ04 approximation, the surface is more forward scattering than for a Lambertian surface (Warren, 1982). BRDF values are estimated for all directions, defined by the (cosθv, φv) pair. The outgoing direction is sampled from the BRDF distribution using a rejection algorithm as follows: in a first step, the azimuth φv is sampled from a uniform distribution between 0 and 2π, and cosθv with a uniform distribution between 0 and 1, so that the hemisphere is sampled with a cosine weighting distribution (Greenwood, 2002). In a second step, a probability of acceptance is given to each direction (θv, φv). This probability of acceptance is estimated by the BRDF value in this direction, normalised by the maximum value of the BRDF distribution.
-
Step 4: Update the direction i. The new photon direction in+1 after the hit n is updated as follows:
with ix,n and iy,n being the photon directions in the x and y axis before the hit n, respectively.
The algorithm returns to step 1 until the photon escapes from the scene (Fig. 4) or until its intensity is lower than a threshold (set to 0.01 in RSRT). To ensure an unbiased termination in the latter case, a “Russian roulette” method is applied (Iwabuchi, 2006), which consists of accepting or rejecting the termination with probabilities 1−p and p, respectively (p=0.2 in RSRT). In case of rejection, the weak intensity of the photon is rescaled by the factor 1∕p, and the algorithm goes again to step 1. As explained by Iwabuchi (2006), the total energy is conserved for any p value, and this approach can be applied at any step of the algorithm.
At the end of its path, the photon intensity is counted in (1) the total upward intensity (I↑) if the photon escapes with an upward direction and (2) the intensity lost downward if its final z-axis direction is downward (this is possible with a tilted surface for instance). If the latter contribution is higher than 10−3 for a horizontal rough surface, we consider that too many photons have been lost to output a realistic albedo, meaning that the simulation used too wide a radiation source or conversely too small a mesh area.
3.3 Simulation framework
3.3.1 Model simulations
RSRT is run here by considering the snow surface to be either (1) Lambertian (Lambertian configuration), where the albedo is not sensitive to the incidence angle and each photon hitting the mesh is reflected with a constant facet albedo equal to αflat(λ), or (2) a snow surface using KZ04 analytical equations (referred to as the KZ04 configuration). In the latter configuration, each photon hitting the mesh is reflected with αflat (λ,θi), which depends on the incidence angle θi, SSA, and B and g values, i.e. by considering the intrinsic BRDF of the snow. The two configurations are compared in Sect. 4.4. The KZ04 configuration is used by default for all other simulations to compare with observations.
RSRT inputs are described in Table 2. Triangular meshes of rough surfaces are modelled by reproducing same linear shapes as those created in the field with an orientation φr, a height H, a width W and spaced by a constant distance defined with the period Λ (as shown in Fig. 1, with the same values as in Table 1). Meshes have a spatial resolution of 1 cm and are produced large enough to be considered infinite (no edge effects). When an RSRT simulation is started, an ensemble of photons is first created on a horizontal plane above the surface mesh and distributed quasi-randomly to produce a parallel source. The size of the photon ensemble is set to 106 photons as a compromise between the computing time and a good representation of the emission source. The direction of propagation of the ensemble of photons is initialised, with the solar zenith and azimuth angles given as inputs.
RSRT outputs the snow spectral albedo, either in direct or diffuse illumination conditions: αdir,rough (λ,θs) and αdiff,rough(λ), respectively, considering that the plane of the mesh is perfectly flat. Then, αdir,rough (λ,θs) and αdiff,rough (λ) are combined with Eqs. (6) and (7) to simulate the apparent snow albedo of a titled rough surface, called αsim,rough (λ,θs), and therefore the simulated apparent albedo accounts for the slope characteristics and surface roughness. Each simulation assumes clear-sky conditions, and no atmosphere scattering and absorption is considered in the Monte Carlo algorithm. The only atmospheric parameter used in the model is the diffuse-to-total illumination ratio (which depends on atmospheric conditions). This parameter was measured in the field at each albedo acquisition (see Sect. 2.1). At the small scale of this study, the effect of the atmosphere is negligible between the sensor and the surface. Future work should add the atmosphere in RSRT for applications over large-scale natural surfaces (mountainous areas).
3.3.2 Evaluation of simulations
The evaluation of simulations was treated over a set of N observations using the root-mean-square deviation (RMSD), defined as follows:
where αsim,i (λ,θs) is the ith simulation (either αsim,smooth or αsim,rough) at the wavelength λ and θs, and αobs,i (λ,θs) is the ith measured albedo.
The accuracies of αsim,smooth (λ,θs) and αsim,rough (λ,θs) are compared to evaluate the accuracy gain acquired by taking into account surface roughness. The main goal of this study is to quantify the roughness effect on albedo values and to determine if this effect is wavelength dependent. Therefore, statistical results are given at two wavelengths: one in the visible domain at 700 nm and one in the NIR domain at 1000 nm. The relation between the roughness effect and SSA is investigated at 1000 nm, since at this wavelength the albedo sensitivity to SSA is larger (Domine et al., 2006).
3.3.3 Impact of uncertainties
Albedo observations may have been affected by uncertainties or unmeasured variations in the field. To investigate the potential impact, we conducted the following simulations.
Firstly, SSA may have varied over time in the experiments A and B, whereas albedo was simulated with a constant SSA. In order to estimate these variations, we retrieved SSA at the beginning of the experiments from albedo observations over the smooth surfaces by fitting αsim,smooth with αobs, using the same approach as described by Libois et al. (2015). RSRT was then run by considering retrieved SSA values (SSAr) for simulations over A smooth and B smooth–dry surfaces and the measured SSA values (SSAm) for simulations over the rough surfaces. Results are studied at 1000 nm, where the albedo sensitivity to SSA is higher.
Secondly, the difference between retrieved and measured SSA may be related to the uncertainty in SSA measurements. We explored the impact of SSA uncertainties with RSRT simulations by varying SSAm by ±10 % over the rough surfaces at 1000 nm.
Thirdly, the impact of slope uncertainties was studied with RSRT simulations by varying the slope of the rough surfaces by ±1∘ in the experiments C rough 90∘ and D rough 90∘ at 1000 nm. We used C and D experiments only, since observations over the rough and smooth surfaces were acquired simultaneously, with similar θs values (to not influence , the effective θs modified with the slope).
3.3.4 Analysis of processes introduced by surface roughness
The variations in illumination conditions and SSA may attenuate or accentuate roughness effects by playing a role either in the effective-angle effect or in multiple reflections. We thus investigated separately these effects as a function of illumination conditions and SSA to better characterise roughness effects.
The effective-angle effect is the alteration of the local incidence angle over roughness shapes. It was simulated with RSRT using the KZ04 configuration (albedo varying with θs) and by requiring that photons hit the surface only once, i.e. without multiple reflections. The total upward and downward intensities were then added to count all the photons that were not absorbed after the first hit. We also conducted the same simulations with the Lambertian configuration to check that there was no angular dependence. These simulations were performed with various illumination conditions.
The effect of multiple reflections caused by the photon trapping depends on the albedo value. While the effective-angle effect is significant under direct sunlight only, this second effect is significant under both direct and diffuse illumination (Warren et al., 1998). Therefore, it was simulated by running RSRT under diffuse sunlight. Simulations were conducted for various SSA values.
First, the new RSRT model is evaluated with in situ measurements (Sect. 4.1). Second, we explore the albedo sensitivity to macroscopic surface roughness through three questions: (1) is it possible to quantify the change in albedo caused by surface roughness and to model this contribution (Sect. 4.2)? (2) What is the impact of SSA and slope uncertainties on the quantification of roughness effects (Sect. 4.3)? (3) What are the respective roles of the effective-angle effect and multiple reflections according to snow properties and illumination conditions (Sect. 4.4)? The impact of roughness on the absorbed energy is also investigated (Sect. 4.5).
4.1 RSRT evaluation
Table 3 shows RMSDs of albedo simulated by considering or neglecting the presence of roughness (αsim,rough and αsim,smooth, respectively) at 700 and 1000 nm for each experiment.
For experiments A and B (Sect. 2.1), αsim,smooth RMSD increases with the fraction of roughness features ( and is higher at 1000 nm than at 700 nm. By considering roughness, the simulations are more accurate by about a factor of 2 at 700 and 1000 nm compared to αsim,smooth (average αsim,rough RMSD of 0.02 at 700 and 1000 nm), which is significant.
Figure 5 shows measured and simulated spectral albedo acquired when the surface is smooth and when the fraction of roughness features is the largest (η=27 %) for experiments A and B. Both surfaces have a sun-facing slope (3.1∘ for experiment A and 3.6∘ for experiment B; see Table 1), so albedo values above 1 in the visible range are not surprising, as explained in Sect. 2.4. For both experiments, the αobs spectra are lower in the presence of surface roughness than the spectra acquired over the smooth surface. Indeed, when the number of roughness shapes increases, more photons are trapped between concavities. The photons have a larger probability to be absorbed (one probability at each hit) relative to a smooth surface (only one hit), causing the observed albedo to decrease.
The αsim,rough spectra follow the observed trend. Simulations are improved compared to αsim,smooth, which neglects surface roughness (average RMSD=0.02 when η=27 %). For both experiments, the pattern of the measured spectra between 600 and 700 nm is probably led by the presence of impurities (not visible to the naked eye in the field). Previous studies showed that even a small concentration of snow LAPs induces a drastic decrease in the albedo in the visible range (Warren, 1982; Dumont et al., 2017) and may explain why measurements and simulations differ in the 600–700 nm range. Moreover, the spectra do not overlap perfectly in the NIR domain, but differences are below 0.01, and this is probably because of a small bias in SSA measurements (10 % uncertainty). Overall, taking into account the measurement errors, αsim,rough spectra reproduce the observed spectra well for both experiments, and the RSRT model improves the spectral albedo simulations by accounting for roughness, compared to those which neglect them (Fig. 5).
Table 3The RMSD of αsim,smooth and αsim,rough at 700 and 1000 nm. The RMSD is calculated with Eq. (16). N is the number of studied surfaces. For experiments C and D, RMSDs are calculated for the simulations over the rough surface.
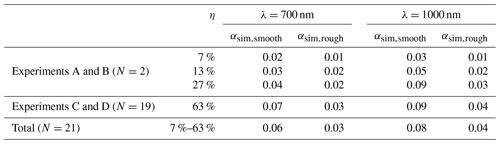
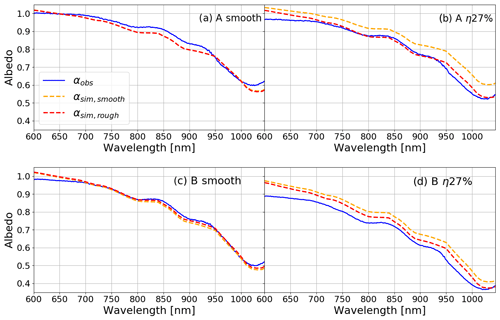
Figure 5Measured spectral albedo αobs (blue solid lines), and spectral albedo simulated with RSRT by considering the surface as smooth (αsim,smooth; orange dashed lines) and by considering surface roughness (αsim,rough; red dashed lines) for (a) A smooth, (b) A η27 %, (c) B smooth and (d) B η27 %.
In experiments C and D, albedo measurements are simultaneously acquired over a rough surface and a nearby smooth surface for multiple illumination conditions every 20 min. Albedo simulations over the rough surface are significantly improved by modelling surface roughness compared to those modelling a smooth surface: the average RMSD of αsim,rough is of 0.03 at 700 nm and 0.04 at 1000 nm (against an average RMSD of 0.07 at 700 nm and 0.09 at 1000 nm for αsim,smooth; Table 3).
To illustrate the spectral performance of the RSRT model, Figure 6 shows albedo measurements and simulations from 600 to 1000 nm for the experiments C at θs∼68∘ and D at θs∼59∘. For this example, randomly chosen illumination conditions were chosen for each experiment. For both experiments, the αobs spectra show a significant decrease caused by the presence of surface roughness ( on average), more pronounced in the NIR domain (Fig. 6a and d). For experiment C, the apparent albedo exceeds 1 in the visible range because of the presence of a sun-facing slope (3.3–4∘; see Table 1).
By considering the surface roughness, the simulations are in agreement with observations; small differences in the NIR domain may be due to weak measured SSA uncertainties. The 0.05 decrease is reproduced well by the RSRT model when it accounts for surface roughness. This pattern is not reproduced at all by simulations considering the rough surface to be smooth.
For experiment D, αsim,rough spectra do not overlap with the observations perfectly, though the decrease is followed (Fig. 6d). This bias is due to several factors that are discussed further. Nevertheless, αsim,rough simulations have an average RMSD of 0.04 and are more accurate compared to simulations which do not take surface roughness into account (αsim,smooth) and which have a RMSD of 0.06.
Considering all observations, albedo simulations with the RSRT model are improved by a factor of 2 by accounting for surface roughness (αsim,rough) at 700 and 1000 nm compared to those neglecting them (αsim,smooth), with an average RMSD of 0.03 at 700 nm and 0.04 at 1000 nm (Table 3). To the best of our knowledge, this is the first model capable of simulating spectral albedo by taking into account the actual surface roughness, the topography and snow optical properties using a Monte Carlo photon transport algorithm.
Nevertheless, reductions in albedo due to roughness effects only are not clearly quantifiable here, since several contributions change the albedo (illuminations and snow conditions also vary), and they have different impacts according to the frequency domain studied. The albedo sensitivity is thus further investigated at two wavelengths only, 700 and 1000 nm.
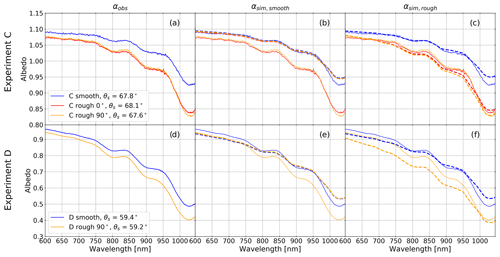
Figure 6Spectral albedo variations for experiment C at θs∼68∘ with (a) αobs, (b) αobs (solid lines) and αsim,smooth (dashed lines), and (c) αobs (solid lines) and αsim,rough (dashed lines). Red lines represent the C rough 0∘ surface, yellow lines the C rough 90∘ surface and blue lines the C smooth surface. Panels (d), (e) and (f) are the same but for experiment D at θs∼59∘. Orange lines represent the D rough 0∘ surface and blue lines the D smooth surface.
4.2 Albedo sensitivity to roughness features
4.2.1 Sensitivity to the fraction of roughness features
To highlight the roughness effect, Fig. 7 shows the change in albedo with increasing roughness fraction η () relative to the initial smooth surface, for both observations and simulations of experiments A and B, i.e. Δαobs(λ,θs) =αobs(λ,θs)–αobs() and Δαsim,rough(λ,θs) (λ,θs) –αsim,smooth(). However, this change in albedo is also affected by concomitant variations in the solar zenith angle θs, as roughness features were added progressively to the initially smooth surface (Fig. 2). To quantify the impact of this spurious change, Fig. 7 also shows the simulated change in albedo if the surface had remained smooth (Δαsim,smooth(λ,θs) = αsim,smooth(λ,θs)–αsim,smooth()).
In experiment A, the stronger Δαobs decrease is of 0.03 at 700 nm, and of 0.07 at 1000 nm, from A smooth (η=0 %, θs, 0=56.7∘) to A η27 % (η=27 %, θs=63.6∘; Fig. 7a and c). Even a low fraction of roughness features (η=7 %) causes an albedo decrease of 0.02 compared to that of a smooth surface at 700 nm (and of 0.03 at 1000 nm). In theory, if the surface remained smooth throughout the experiment, αobs should increase when θs increases (i.e. the sun goes up): photons penetrate less deeply into the snowpack, as they enter with a grazing angle (large θs). They encounter the first scattering event near the surface and have a larger probability of escaping compared to a photon penetrating deeper with a low θs (Carroll and Fitch, 1981; Warren, 1982). By adding surface roughness, αobs shows the inverse trend (Fig. 7a and b) and decreases with the increase in θs, showing that albedo is more sensitive to roughness effects than to θs variations here. This result highlights the need to consider the presence of roughness in albedo simulations.
Simulations neglecting roughness follow the theory for a smooth surface; Δαsim,smooth increases while θs becomes larger by 0.02 at 700 nm and by 0.03 at 1000 nm between A smooth and A η27 % (Fig. 7a and c). Simulations considering roughness follow the observation trend; Δαsim,rough decreases by 0.01 at 700 nm and by 0.03 at 1000 nm between A smooth and A η27 %. Nevertheless, RSRT (i.e. αsim,rough) underestimates, by almost a factor of 2, the observed albedo reduction. The reason for this underestimation may be linked to the SSA variations throughout the experiment.
In experiment B, Δαobs shows a strong decrease of 0.11 at 700 nm and 0.15 at 1000 nm between B smooth–dry (η=0 %, θs=55.4∘) and B η27 % (η=27 %, θs=39.9∘; Fig. 7b and d). In this experiment, αobs decreases due both to the θs decrease (the sun went up; Sect. 2.1) and the η increase. To remove the θs contribution, we use the Δαsim,smooth trend that depends on θs variations only: Δαsim,smooth lowers when θs decreases, and the reduction is half of that of Δαobs (Fig. 7). In other words, half of the αobs decrease is attributable to the decrease in θs, and the other half is attributable to the presence of roughness. More precisely, by calculating Δαobs–Δαsim,smooth we quantify the roughness effect on the albedo. The presence of roughness lowers the albedo of 0.06 at 700 nm and of 0.08 at 1000 nm when η=27 %.
Δαsim,rough decreases by 0.07 at 700 nm, and 0.11 at 1000 nm, between B smooth–dry and B η27 % (Fig. 7b and d). Simulations are consistent with observations by considering the presence of roughness, but the simulated decrease is still underestimated compared to measurements, as for experiment A.
To accurately quantify roughness effects on albedo, it is important to compare rough and smooth surfaces for similar snow and illumination conditions. This is why we simultaneously measured albedo over B η27 % (η=27 %, θs=39.9∘) and a nearby smooth surface (the B smooth–wet surface: η=0 %, θs=36.4∘; Table 1 and Fig. 7b and d). The concurrent measurements show a decrease of 0.05 at 700 nm and 0.07 at 1000 nm. This reduction is solely attributable to the presence of roughness. It is similar to the Δαobs decrease by subtracting the Δαsim,smooth that is caused by the θs decrease only (Fig. 7).
For both experiments, observations show that the albedo decrease is stronger (1) when the number of roughness features is larger and (2) at the longer wavelengths. As albedo is lower in the NIR domain, the impact of multiple reflections is stronger. Indeed, the effect of multiple reflection is more important for intermediate values than for albedo close to 0 or 1 (i.e. systematic absorption or reflection; Warren et al., 1998).
Figure 7Variations in albedo differences between the albedo at θs and the albedo at θs,o, corresponding to that of the smooth surface, as a function of the η ratio (W∕Λ in %). Blue points are Δαobs (λ,θs) (=αobs (λ,θs)–αobs ()), and orange lines are Δαsim,smooth ( (λ,θs)–αsim,smooth ()), where variations are due to θs changes only (η=0 % for all simulations) and red lines are Δαsim,rough ( (λ,θs)–αsim,smooth ()), which varies with η and θs. Blue squares are the Δαobs,wet (λ,θs) (=αobs (λ,θs)–αobs,wet ()), where αobs,wet is the measured albedo over the B smooth–wet surface (η=0 % and θs=39.9∘; Table 1). Grey vertical lines describe the solar zenith angle (θs) when measurements were acquired. Results are given for (a) experiment A at 700 nm. (b) Same as (a) but for experiment B and (c) experiment A at 1000 nm. (d) Same as (c) but for experiment B.
4.2.2 Sensitivity to the roughness orientation
The albedo sensitivity to the roughness orientation with respect to the solar azimuthal angle (Δφr) is investigated at 700 and 1000 nm with experiments C and D, where measurements are simultaneously acquired over a smooth and a rough surface. Figure 8 shows the change in albedo as a function of Δφr for both wavelengths. Δαobs is the difference between αobs acquired over the rough and smooth surfaces at the same moment. Similarly, Δαsim,rough is the difference between αsim,rough simulated over the rough surface and αsim,smooth simulated over the smooth surface at the same illumination conditions. Thus, the change in albedo is not correlated to θs here but to φs that leads the roughness orientation with respect to the sun position.
When roughness features are parallel to the sun (i.e. when Δφr=0∘ in Fig. 8a and d), αobs decreases by 0.01 at 700 nm and to 0.08 at 1000 nm relative to a smooth surface. The impact becomes larger when the roughness orientation is perpendicular to the sun (when Δφr=90∘ in Fig. 8b and e), with an αobs decrease of 0.02 at 700 nm and of 0.10 at 1000 nm. Thus, for experiment C, the reduction in albedo is 20 % stronger when roughness features lie perpendicular to the sun than when they are parallel. This is explained by the fact that, when the sun elevation is low, if the roughness orientation is perpendicular to the sun, the effective incidence angle over sides facing the sun is decreased compared to that of a smooth surface. In addition, the fraction of shadow is higher when Δφr=90∘. This effective-angle effect leads to an average decrease in snow albedo relative to a smooth surface. However, for the C rough 90∘ experiment (Fig. 8b and e), Δφr varies from 50 to 122∘, and Δαobs does not show the strongest albedo reduction around 90∘. Similarly, for C rough 0∘ (Fig. 8a and d), Δαobs values were not symmetrical to Δφr=0∘. This is caused by other contributions that are added to the roughness effects. First, the effect of the slope on albedo varies over time with the solar angle changes. Here we selected a smooth surface with a similar slope to that of the rough surface so as to minimise the contribution of the slope by comparing rough–smooth albedo at similar illumination conditions (Δαobs). The slope sensitivity to roughness effects is studied in Sect. 4.3.2. Second, the particularly high values of SSA for this experiment (∼100 m2 kg−1) induce lower absorption (Warren et al., 1998), and this may explain the albedo insensitivity to small variations in roughness orientation. Moreover, instead of a clear dependence between Δαobs and Δφr, the Δαobs pattern shows oscillations, probably caused by the small differences in snow properties between the smooth and the rough surfaces. Indeed, SSA values over the smooth surface are homogeneous, while SSA values over the rough surface evolve unevenly according to the illumination received in the concavities during the day. The SSA sensitivity to roughness effect on albedo measurements is investigated in Sect. 4.3.1.
In experiment C, Δαsim,rough variations reproduce the Δαobs decrease well, with the same order of magnitude: the average decrease is of 0.01 at 700 nm and 0.08 at 1000 nm for C rough 0∘ and of 0.02 at 700 nm and 0.10 at 1000 nm for C rough 90∘ (Fig. 8a and d).
In experiment D rough 90∘, measurements were acquired in the morning, so Δφr varies from 42 to 72∘ (Fig. 8c and f). We measured an average Δαobs decrease of 0.02 at 700 nm and 0.09 at 1000 nm, which is in agreement with results found for C rough 90∘. In Fig. 8c and f, the Δαobs increases when Δφr goes from 42 to 72∘, while in theory, it should decrease when Δφr approaches 90∘. A possible explanation is that melting was observed at the surface in the field, resulting in a smoothing of our roughness shapes during the day, which attenuates the roughness effect on albedo values. Therefore, we cannot conclude on this observed trend, since several contributions drove the measured albedo.
Figure 8c and f show that αsim,rough overestimates, by almost a factor of 2, the reduction in αobs: the average Δαsim,rough decrease is of 0.06 at 700 nm and of 0.15 at 1000 nm. By considering roughness shapes that are constant throughout the day, Δαsim,rough decreases when Δφr goes from 42 to 72∘ (i.e. Δφr gets closer to 90∘). This trend is coherent with the theory, but more in situ measurements are needed to fully quantify the dependence of the apparent albedo on the roughness orientation.
To sum up, observations show that an increase in the number of roughness features leads to a larger reduction in αobs, with a higher sensitivity in the NIR domain. Roughness effects are also larger when the roughness orientation is perpendicular to the sun rather than parallel. αsim,rough shows an overestimation of the observed albedo decrease, but observations may have been affected by uncertainties or unmeasured variations.
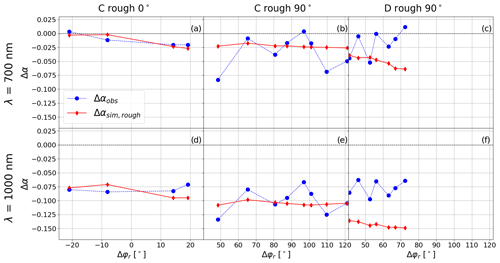
Figure 8Measured and simulated variations in Δα ([rough–smooth] at the same θs) at 700 nm as a function of Δφr for (a) the C rough 0∘ experiment, (b) the C rough 90∘ experiment and (c) the D rough 90∘ experiment. (d), (e) and (f) are the same but at 1000 nm. Blue points are Δαobs, and red lines with diamonds are Δαsim,rough. The horizontal black dashed lines show 0.
4.3 Analysis of uncertainties
In a first step, we explore the possible SSA variations in the experiments A and B and the impact on snow albedo. In a second step, we integrate SSA and slope uncertainties into our roughness analysis.
4.3.1 Sensitivity to SSA
We estimate an SSA (written SSAr) of 9.4 m2 kg−1 over A smooth and 5.3 m2 kg−1 over B smooth by fitting αsim,smooth and αobs (see Sect. 3.3.3 for the methodology). Measured SSA values (SSAm) are equal to 7.4 m2 kg−1 over A η13 % and 4.5 m2 kg−1 over B η13 %. Hence, for both experiments, there is a decrease in SSA from the beginning (smooth surface, η=0 %) to η=13 %, which is compatible with the observation of melt at the surface during these two experiments performed in April. Indeed, Grenfell and Maykut (1977) explained that snow albedo decreases when liquid water replaces air between ice grains, and as the refractive index of the water is very close to that of ice, this results in an increase in the effective grain size (i.e. a decrease in SSA).
To explore the impact of a decreasing SSA on albedo, RSRT is run by considering SSAr for simulations over A smooth and B smooth–dry surfaces (SSAr equal to 9.4 and 5.3 m2 kg−1, respectively) and SSAm for simulations over the rough surfaces (from η=7 % to 27 %, SSAm equal to 7.4 and 4.5 m2 kg−1; see Table 1). Results are presented in Fig. 9a and b, where is the difference αsim,rough (λ,θs, SSAm)–αsim,smooth (, SSAr). Compared to Δαsim,rough (i.e. constant SSA), the decrease is multiplied by a factor of 2 by considering both the increase in the fraction of roughness features and the SSA decline, from 9.4 to 7.4 m2 kg−1 (−15 %) for experiment A or from 5.3 to 4.5 m2 kg−1 (−21 %) for experiment B (Fig. 9a and b). reproduces the Δαobs decrease well, with the same order of magnitude. Thus, the use of a constant SSA for αsim,rough simulations in the experiments A and B probably explains the underestimation of the albedo reduction due to the presence of surface roughness and observed in Sect. 4.2.1. Both SSA variations and roughness effects overlap and lower snow albedo in these two experiments, making it difficult to accurately isolate roughness effects.
Differences between retrieved and measured SSA may be explained by the uncertainty in SSA measurements (∼10 %; Arnaud et al., 2011). The impact of SSA uncertainties is investigated by varying SSA by ±10 % in RSRT αsim,rough simulations for all experiments. Obtained values range within the grey shading shown in Fig. 9. Experiment C presents large measured SSAs (∼100 m2 kg−1), typical of freshly fallen snow, and SSA uncertainties affect Δαsim,rough slightly (Fig. 9c). On the contrary, a variation in ±10 % in SSA strongly impacts the experiments with low SSAs: varies between 0.05 and 0.10 in experiment A η27 % (Fig. 9a), between 0.11 and 0.16 in experiment B η27 % (Fig. 9b), and between 0.13 and 0.18 in experiment D when Δφr=72∘ (Fig. 9d). The reduction in albedo is stronger when SSA is lower due to higher absorption. More precisely, the grains at the surface control the first scattering event, and large-coarse grains (i.e. low SSA) are both more absorptive and more forward scattering relative to fine grains, since photons have to pass through longer paths in ice before being potentially scattered at the ice–air interfaces (Warren et al., 1998). Domine et al. (2006) have shown that the SSA–albedo relationship is non-linear and that albedo varies slightly in the NIR domain when SSA >30 m2 kg−1, while it is highly sensitive to SSA variations for SSA values below 10 m2 kg−1. Hence, in presence of surface roughness, a large SSA leads to a weaker impact of multiple reflections (high albedo), while the impact of the photon trapping is more important at low SSA (<10 m2 kg−1). There is a strong and nonlinear relationship between the roughness effect on the snow albedo and SSA values.
Moreover, experiment D highlights that the impact of SSA uncertainties in albedo is linked to the roughness orientation (Fig. 9d). Albedo is twice as sensitive to SSA when Δφr=72∘ as when Δφr=42∘. This is caused by the effective-angle effect introduced by roughness: photons penetrate deeper over sides facing the sun when the roughness orientation is perpendicular to the sun (lower incidence angle) than if it was oblique or parallel. When SSA is low, absorptions increase and a photon has a larger probability to be absorbed by penetrating deeply into the snowpack. Hence, the effective-angle effect is more pronounced when roughness orientation is perpendicular to the sun and for low SSA.
The joint impact of roughness effects and SSA in the NIR domain has consequences on the accuracy of SSA retrievals. Several studies directly used the ART equations to retrieve SSA from spectral albedo observations in the NIR (Dominé et al., 2006; Gallet et al., 2011; Libois et al., 2015; Picard et al., 2016). By neglecting roughness, SSA retrievals are underestimated to compensate for the albedo reduction caused by the presence of roughness. We retrieved SSAs for experiments C and D at each Δφr by fitting αsim,smooth and αobs acquired over the rough surfaces (not shown). Compared to measured SSAs taken over the smooth surface, results demonstrate that roughness introduces a significant underestimation of the retrieved SSA, reaching 21 % for the roughness features considered here. Thus, it is important to use a model considering roughness to retrieve accurate SSAs from albedo observations.
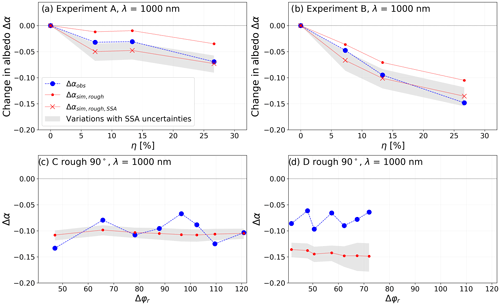
Figure 9(a) and (b) are changes in albedo as a function of the η ratio at 1000 nm for experiments A and B, respectively. Blue dashed lines are Δαobs (αobs (λ,θs)–αobs ()). Red dashed lines with points are Δαsim,rough (αsim,rough (λ,θs)–αsim,smooth ()) obtained using a constant SSA in RSRT (7.4 m2 kg−1 for A and 4.5 m2 kg−1 for B). Red lines with crosses are (αsim,rough (λ,θs, SSAr)–αsim,smooth (, SSAm)) obtained using SSAr for the smooth surface (at η=0 %, SSAr = 9.4 m2 kg−1 for A and 5.3 m2 kg−1 for B) and SSAm for rough surfaces (η from 7 % to 27 %, SSAm = 7.4 m2 kg−1 for A and 4.5 m2 kg−1 for B). (c) and (d) are variations in Δα with Δφr at 1000 nm for experiments C and D, respectively (similar to Fig. 7e and f). Δαobs and Δαsim,rough are the observed and simulated albedo differences between the rough and the smooth surfaces at Δφr. Grey shading represents the range of Δα obtained by varying the SSA by ±10 % in RSRT simulations.
4.3.2 Sensitivity to the surface slope
The impact of slope uncertainties is explored by varying the slope by ±1∘ for simulations over the rough surfaces for experiments C and D at 1000 nm (Sect. 3.3). Obtained values range within the grey shading shown in Fig. 10. The albedo sensitivity to the slope depends of the slope aspect φn, with respect to the solar azimuthal angle φs, since the aspect controls the change in the incidence angle () relative to θs. The slopes have no impacts on albedo if the slope aspect is perpendicular to the solar azimuthal angle ([φs–φn] = 90 or 270∘), since it does not affect the solar incidence angle. On the other hand, impacts change rapidly when the aspect φn becomes parallel to φs ([φs–φn] = 0 or 180∘), as is shown using Eqs. (6) and (7). Over a titled rough surface with roughness orientation perpendicular to the sun (Δφr=90∘) and a slope direction opposite to that of the sun (φs–φn=180∘), roughness sides facing the sun experience a lower effective incidence angle relative to a flat rough surface, leading to a lower albedo. Figure 10b illustrates this point for experiment D rough 90∘: the albedo sensitivity is twice as strong when the slope direction is closer to 180∘ ([φs–φn] = −150∘, i.e. a slope opposite to that of the sun) than when it gets closer to 90∘ ([φs–φn] = −120∘). Note that this experiment has low SSA, leading to a strong sensitivity to a change of the incidence angle, as explained in previous section. Therefore, for low SSA, the impact of roughness on albedo is accentuated when the slope direction is opposite to the sun and attenuated when the slope is facing the sun.
In experiment C (Fig. 10a), the albedo is highly sensitive to slope uncertainties (variations of 0.05–0.15). However, due to high SSA there is a low albedo sensitivity to the φs–φn angle (the effective-angle effect is negligible). Therefore, the observed albedo sensitivity may be explained by a larger effect of multiple reflections, accentuated by the fact that θ is particularly large for this experiment (>60∘).
To sum up, we showed that the albedo sensitivity to roughness is larger when the SSA is low (<10 m2 kg−1), when roughness features are perpendicular to the sun and when the surface slope aspect is facing away from the sun. The roughness effect is strongly linked to SSA values, which affect (1) the impact of the effective-angle effect, since the decrease in the incidence angle on roughness sides facing the sun has more consequences on the albedo when SSA is low (high absorption), and (2) the impact of multiple reflections, which is larger when the probability of a photon to be absorbed or reflected is well balanced. To accurately quantify roughness effects, it is crucial to measure SSA regularly (a small variation may overlap the roughness effects) and to determine the slope. In our experiments C and D, where SSA was measured at each albedo acquisition, we showed that even considering uncertainties of ±10 % of SSA and of ±1∘ of slopes, roughness effects are significant and cause at least an albedo decrease of 0.06 in the experiment C rough 90∘ and a decrease of 0.11 in the experiment D rough 90∘ at 1000 nm.
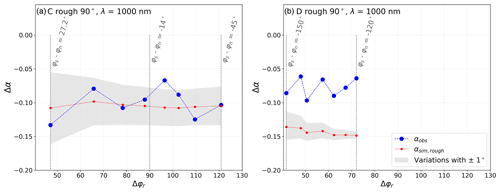
Figure 10Same as Fig. 9c and d, except that the grey shading represents the range of Δα obtained by varying the slope by ±1∘ in RSRT simulations for (a) experiment C rough 90∘ and (b) D rough 90∘. φn is the aspect of the slope and φs is the solar azimuthal angle, separately given in Table 1. Vertical black lines indicate [φs–φn] angles at the beginning and at the end of experiments (and at Δφr=90∘ for experiment C).
4.3.3 Analysis of the two roughness effects
The two processes introduced by surface roughness are decoupled using RSRT to better characterise roughness effects as a function of snow properties and illumination conditions.
4.3.4 Effective-angle effect
To simulate the effective-angle effect, we count all photons that were not absorbed after the first hit. RSRT is run at 1000 nm with a KZ04 configuration, and we sum the total upward and downward intensity considering one hit only. Simulations are performed for various θs and Δφr values. The initial conditions of the A η27 % experiment without slope and under direct sunlight are used. Roughness shapes are rectangular and the SSA is low (7.4 m2 kg−1), which leads to a maximal effect of incidence angle variations.
Figure 11a and b show the simulated Δαsim,rough ([rough-smooth] with similar illumination) as a function of θs and Δφr. The Lambertian configuration yields a constant albedo, as expected, since there is no incidence angle dependence. The albedo decrease of 0.04 is due to shadow areas that are introduced by roughness features and that receive less radiation.
With the KZ04 configuration, Fig. 11a and b show that the effective-angle effect is strongly linked to illumination conditions. Firstly, as previously observed, the model predicts a strong drop in albedo when θs increases (Fig. 11a). When θs>50∘, with the rectangular roughness shapes of experiment A, the local incidence angle of photons hitting the vertical sides facing the sun is lower than that of a smooth surface when θs>45∘ if Δφr=90∘. Thus, photons penetrate deeply into the snowpack before being eventually redirected upward, which induces a stronger decrease in albedo relative to a smooth surface. Conversely, when θs<50∘, the effective incidence angle is higher over roughness sides facing the sun compared to that of a smooth surface. This leads to an increase in albedo, and this is why Δα is higher with the KZ04 configuration than with the Lambertian configuration when θs<50∘ (Fig. 11a). Hence, the reduction in albedo depends on the slope of roughness sides (i.e. their shapes). Figure 11a also illustrates that in the presence of roughness, albedo decreases more rapidly with θs at large values of θs. Therefore, surface roughness plays a more important role at a grazing angle (large θs). Moreover, our results show that the effects of roughness become negligible at 1000 nm, when θs<30∘. The albedo decrease caused by the effective-angle effect only is of 0.04 for experiment A η27 %, when θs=63∘ (Fig. 11a; [Lambert – KZ04]). Secondly, by changing the incidence angle, the roughness orientation also plays an important role (Fig. 11b). The reduction in albedo caused by the effective-angle effect goes from 0 when Δφr=0∘ to 0.09 when Δφr=90∘ for experiment A.
To sum up, the albedo decrease due to the effective-angle effect becomes rapidly stronger with θs at large θs (θs>50∘) and when Δφr=90∘. In experiment A, the model predicts a decrease in albedo of 0.07 when θs=80∘ ([Lambert – KZ04] in Fig. 11a), caused by the effective-angle effect only, i.e. a drop 75 % stronger compared to that of θs=63∘. Therefore, it is necessary to account for the intrinsic BRDF of the snow to simulate realistic albedo over rough surfaces, in particular in polar regions where θs is high.
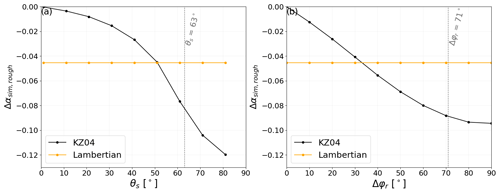
Figure 11Variations in Δαsim,rough ([rough–smooth] at same illumination) simulated with RSRT at 1000 nm with the initial condition of the experiment A η27 %, without slope as a function of (a) θs (in degrees) and a constant Δφr=71∘ and (b) Δφr and a constant θs=63∘. Simulations are performed with the Lambertian configuration (in orange) and the KZ04 configuration (in black). Vertical dashed lines indicate the initial condition of the experiment A η27 % (Table 1).
4.3.5 Multiple reflections
RSRT is run by varying SSA values with the KZ04 configuration and under diffuse sunlight to simulate the trapping effect of photons only (for the A η27 % experiment, see Sect. 3.3 for details). Simulations are performed over a smooth and a rough surface to compute Δαsim,rough. Results are shown in Fig. 12 as a function of SSA. The impact of multiple reflections is higher for SSA between 8 and 14 m2 kg−1, with a maximum effect at SSA=9 m2 kg−1. For the experiment A η27 %, the measured SSA is 7.4 m2 kg−1, and it induces a simulated albedo equal to 0.6 at 1000 nm. Figure 12 shows that at SSA=7.4 m2 kg−1, Δαsim,rough decreases by 0.035 with multiple reflections, which is significant. The impact of multiple reflections is larger for intermediate values of albedo, since photons have the same probability to be absorbed or reflected at each collision. Figure 12 also illustrates that multiple reflections are less sensitive at large SSA, as discussed in Sect. 4.3.1. Hence, this leads to albedo close to 1, and the absorption is too low to trap the photons. Similar results were found in the literature (O'Rawe, 1991; Warren et al., 1998).
Therefore, for the experiment A η27 %, we predict that albedo decreases by 0.04 with multiple reflections and by 0.04 with the effective-angle effect, i.e. a total albedo decrease of 0.08 due to the presence of surface roughness only. Effective-angle effects increase with large θs and low SSA, while the impact of multiple reflections becomes larger when SSA values correspond to an intermediate albedo value in the near-infrared wavelengths. Both effects are stronger when the roughness orientation is perpendicular to the sun.
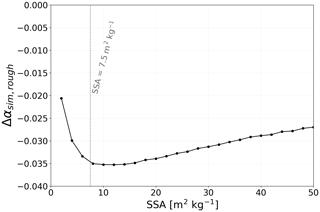
Figure 12Δαsim,rough variations as a function of SSA (m2 kg−1). RSRT simulations are computed with the KZ04 configuration at λ=1000 nm, with the initial conditions of the experiment A η27% (rectangular shapes, θs=63∘, Δφr=71∘, without slope; Table 1). The vertical dashed lines indicate the measured SSA (7.4 m2 kg−1).
4.4 Impact on the radiative balance
In this study, the observed albedo change due to the presence of surface roughness may seem low, of the order of a few percent. However, even a small decrease in albedo may strongly impact the radiative balance by increasing the proportion of absorbed energy, estimated with the net shortwave radiation (SWnet). To illustrate the importance of such an albedo decrease on the radiative balance, we compute SWnet using RSRT with the simple approach described in the following. The net shortwave radiation in the 0.35–4 µm range (in W m−2) is estimated with Eq. (17):
where αdir(λ,θs) and αdiff(λ) are the direct and diffuse albedo, and Irrdir(λ) and Irrdiff(λ) are the direct and diffuse solar spectral irradiance (W m−2 µm−1) computed with the Santa Barbara DISORT Atmospheric Radiative Transfer (SBDART; Ricchiazzi et al., 1998). SBDART is an atmospheric model computing radiative transfer within the Earth's atmosphere and at the surface in clear-sky (direct illumination) and cloudy conditions (diffuse illumination).
The net shortwave radiation is estimated with Eq. (17) over the C smooth 90∘ and C rough 90∘ surfaces using αsim,smooth and αsim,rough, respectively, at θs=68∘. For this simulation, we assume that there are no impurities in the snow and that the presence of roughness is the only cause of the albedo decrease. SBDART is run with a mid-latitude winter atmospheric profile at a height of 1729 m (elevation of the site of experiment C) and at noon.
The broadband albedo simulated by considering surface roughness is 0.05 lower than the one simulated with the smooth surface. This results in an increase in the SW net from 15 to 27 W m−2, caused by the presence of surface roughness. In other words, the energy absorbed by the snowpack may increase by almost a factor of 2 (+80 %) with the presence of roughness. Note that this is an illustration of the potential impact of roughness on the SW net more than a real estimate because RSRT has not been fully validated at wavelength below 600 nm and above 1050 nm and because we simulate artificial roughness, which may not be representative of the whole alpine snowpack. Nevertheless, these results illustrate the necessity of considering surface roughness in the estimation of the surface energy budget. Further work and measurements are needed to validate the radiative balance simulation, and this is out of the scope of this study.
The RSRT model was evaluated with artificial roughness here, and the next step will logically concern natural rough surfaces. An interesting perspective would be to apply this model at a larger scale for remote-sensing applications, in particular in complex terrain (mountainous area). Nevertheless, this work will prove challenging, since, at such a scale, the atmosphere scatterings have to be integrated into the Monte Carlo algorithm, which will increase the number of photon hits.
Four controlled experiments using artificial roughness fields with various geometrical characteristics (fraction of roughness features, orientation, etc.) were studied. Our observations show that the presence of macroscopic surface roughness significantly decreases snow albedo. More specifically, the following can be concluded:
-
Even a low fraction of roughness features (η=7 %) causes a detectable albedo decrease of up to 0.02 at 1000 nm relative to a smooth surface.
-
For higher fractions (η=27 % and 63 %), and when the roughness orientation is perpendicular to the sun, the decrease ranges between 0.03 and 0.05 at 700 nm and 0.07 and 0.10 at 1000 nm. The impact is 20 % lower when the orientation is parallel to the sun.
-
At low SSA (10 m2 kg−1), the albedo sensitivity to surface roughness is twice as large at 1000 nm (NIR) than at 700 nm (visible) due to the higher intrinsic absorption of the snow.
We developed a new model to account for surface roughness in snow albedo simulations. RSRT considers both the 3-D geometric effects introduced by roughness and snow optical properties using a Monte Carlo photon transport algorithm. By considering roughness, albedo simulations are improved by a factor of 2 compared to those assuming a smooth surface (RMSD of 0.03 at 700 nm and 0.04 at 1000 nm).
Using RSRT, we analysed how the contributions usually affecting albedo interact with the effects of roughness.
Firstly, we investigated the impact of SSA and slope uncertainties on our roughness analysis. The amplitude of roughness effects is insensitive to SSA variations at high SSA. On the contrary, at low SSA, an SSA decrease of 50 % induces the same reduction in albedo as the one due to the presence of roughness. Hence, the albedo decrease due to the presence of roughness is drastically accentuated when SSA is low (<10 m2 kg−1) and when the roughness orientation is perpendicular to the sun. This is explained by the fact that (1) when the sun elevation is low, the reduction of the local incidence angle of roughness sides facing the sun has more consequences on the albedo when SSA is low (higher absorption of photons) and that (2) the impact of multiple reflections is larger when the probability of a photon to be absorbed or reflected is well balanced, which is mainly controlled by low SSA in the NIR (albedo∼0.6). In addition, the overall slope of the rough surface changes the local incidence angle and accentuates roughness effects when the surface aspect is facing away from the sun. Therefore, to accurately quantify the effects of roughness, it is necessary to know SSA variations when albedo measurements are acquired and the slope of the surface.
Secondly, the two processes governing roughness effects were quantified separately with RSRT. We showed that the albedo decrease due to the effective-angle effect becomes rapidly stronger with θs at large θs (θs>50∘) and when Δφr=90∘. For instance, the effective-angle effect causes a reduction in albedo 40 % stronger when θs goes from 63 to 80∘ for roughness shapes considered here. The impact of multiple reflections is larger for SSA between 8 and 14 m2 kg−1. Thus, the impact of roughness is strongly linked to SSA, slope, the solar zenith angle and the roughness orientation. RSRT provides a useful tool to better characterise the albedo sensitivity to macroscopic surface roughness.
Roughness effects are significant, and many biases are introduced by neglecting these contributions. For approaches considering a smooth surface and using simulated and observed albedo to retrieve SSA, the presence of roughness causes a strong underestimation of SSA, which can be of the order of 20 % for roughness features perpendicular to the sun. Moreover, the albedo decrease leads to an increase in the absorbed energy in the snowpack. In one of our experiences, we found that a decrease in the broadband albedo of 0.05 causes +80 % of additional net shortwave radiations relative to a smooth surface. This result highlights the necessity of taking into account the roughness effects to compute the surface energy budget. RSRT was evaluated on metre-scale artificial roughness. In further work, this will be applied both for natural roughness and at a larger scale in complex terrain (mountainous area).
The albedo observations and auxiliary data will be assembled in an open dataset to be released on https://doi.org/10.18709/perscido.2020.05.ds314 (Larue et al., 2020) after the review process.
FL, GP and LA contributed to the conceptualisation and design of the work. All authors contributed to the observation acquisition, analysis and interpretation of data. GP wrote RSRT, FL led the analysis and wrote the paper, and all the authors contributed to revisions of the paper.
The authors declare that they have no conflict of interest.
The authors would like to thank Bertrand Cluzet (Centre d'Études de la Neige, Météo-France) for his help during the field campaigns.
This project was supported under the Agence Nationale de la Recherche, programmes EAIIST (grant no. ANR-25 16-CE01-0011), MONISNOW (grant no. 1-JS56-005-01) and EBONI (grant no. ANR-16-CE01-0006). We also acknowledge the Centre National d’Études Spatiales (CNES). This research was at least partially supported by Lautaret Garden – UMS 3370 (Univ. Grenoble Alpes, CNRS, SAJF, 38000 Grenoble, France), a member of AnaEE France (ANR-11-INBS- 0001AnaEE-Services, Investissements d’Avenir frame) and of the eLTER European network (Univ. Grenoble Alpes, CNRS, LTSER Zone Atelier Alpes, 38000 Grenoble, France). CNRM-CEN and IGE are part of Labex OSUG@2020 (investissement d’avenir – ANR10 LABX56).
This paper was edited by Mark Flanner and reviewed by two anonymous referees.
Arnaud, L., Picard, G., Champollion, N., Domine, F., Gallet, J. C., Lefebvre, E., and Barnola, J. M.: Measurement of vertical profiles of snow specific surface area with a 1 cm resolution using infrared reflectance: instrument description and validation, J. Glaciol., 57, 17–29, https://doi.org/10.3189/002214311795306664, 2011.
Atlaskina, K., Berninger, F., and de Leeuw, G.: Satellite observations of changes in snow-covered land surface albedo during spring in the Northern Hemisphere, The Cryosphere, 9, 1879–1893, https://doi.org/10.5194/tc-9-1879-2015, 2015.
Brock, B. W., Willis, I. C., and Sharp, M. J.: Measurement and parameterization of albedo variations at Haut Glacier d'Arolla, Switzerland, J. Glaciol., 46, 675–688, 2000.
Carroll, J. J.: The effect of surface striations on the absorption of shortwave radiation, J. Geophys. Res., 87, 9647–9652, 1982b
Carroll, J. J. and Fitch, B. W.: Effects of solar elevation and cloudiness on snow albedo at the South Pole, J. Geophys. Res., 86, 5271–5276, https://doi.org/10.1029/JC086iC06p05271, 1981.
Cathles, L. M., Abbot, D. S., Bassis, J. N., and MacAyeal, D. R.: Modeling surface-roughness/solar-ablation feedback: Application to small-scale surface channels and crevasses of the Greenland ice sheet, Ann. Glaciol., 52, 99–108, https://doi.org/10.3189/172756411799096268, 2011.
Cathles, L. M., Abbot, D. S., and MacAyeal, D. R.: Intra-surface radiative transfer limits the geographic extent of snow penitents on horizontal snowfields, J. Glaciol., 60, 147–154, https://doi.org/10.3189/2014JoG13J124, 2014.
Corbett, J. and Su, W.: Accounting for the effects of sastrugi in the CERES clear-sky Antarctic shortwave angular distribution models, Atmos. Meas. Tech., 8, 3163–3175, https://doi.org/10.5194/amt-8-3163-2015, 2015.
Corripio, J. and Purves, R.: Surface Energy Balance of High-Altitude Glaciers in the Central Andes: The Effect of Snow Penitentes, Wiley Online Library, https://doi.org/10.1002/0470858249.ch3, 2006.
Domine, F., Salvatori, R., Legagneux, L., Salzano, R., Fily, M., and Casacchia, R.: Correlation between the specific surface area and the short-wave infrared (SWIR) reflectance of snow, Cold Reg. Sci. Technol., 46, 60–68, https://doi.org/10.1016/j.coldregions.2006.06.002, 2006.
Dumont, M., Arnaud, L., Picard, G., Libois, Q., Lejeune, Y., Nabat, P., Voisin, D., and Morin, S.: In situ continuous visible and near-infrared spectroscopy of an alpine snowpack, The Cryosphere, 11, 1091–1110, https://doi.org/10.5194/tc-11-1091-2017, 2017.
Filhol, S. and Sturm, M.: Snow bedforms: a review, new data, and a formation model, J. Geophys. Res.-Earth Surf., 120, 1645–1669, https://doi.org/10.1002/2015JF003529, 2015.
Flanner, M. G., Zender, C. S., Hess, P. G., Mahowald, N. M., Painter, T. H., Ramanathan, V., and Rasch, P. J.: Springtime warming and reduced snow cover from carbonaceous particles, Atmos. Chem. Phys., 9, 2481–2497, https://doi.org/10.5194/acp-9-2481-2009, 2009.
Fréville, H., Brun, E., Picard, G., Tatarinova, N., Arnaud, L., Lanconelli, C., Reijmer, C., and van den Broeke, M.: Using MODIS land surface temperatures and the Crocus snow model to understand the warm bias of ERA-Interim reanalyses at the surface in Antarctica, The Cryosphere, 8, 1361–1373, https://doi.org/10.5194/tc-8-1361-2014, 2014.
Furukawa, T., Kamiyama, K., and Maeno, H.: Snow surface features along the traverse route from the coast to Dome Fuji Station, Queen Maud Land, Antarctica, Proc. NIPR Symposium Polar Meteorol. Glaciol., 10, 13–24, 1996.
Gallet, J.-C., Domine, F., Zender, C. S., and Picard, G.: Measurement of the specific surface area of snow using infrared reflectance in an integrating sphere at 1310 and 1550 nm, The Cryosphere, 3, 167–182, https://doi.org/10.5194/tc-3-167-2009, 2009.
Gallet, J.-C., Domine, F., Arnaud, L., Picard, G., and Savarino, J.: Vertical profile of the specific surface area and density of the snow at Dome C and on a transect to Dumont D'Urville, Antarctica – albedo calculations and comparison to remote sensing products, The Cryosphere, 5, 631–649, https://doi.org/10.5194/tc-5-631-2011, 2011.
Genthon, C.: Antarctic climate modelling with general circulation models of the atmosphere, J. Geophys. Res., 99, 12953, https://doi.org/10.1029/94JD00574, 1994.
Greenwood, J.: The correct and incorrect generation of a cosine distribution of scattered particles for Monte-Carlo modelling of vacuum systems, Vacuum, 67, 217–222, https://doi.org/10.1016/S0042-207X(02)00173-2, 2002.
Grenfell, T. C. and Maykut, G. A.: The optical properties of ice and snow in the Arctic Basin, J. Glaciol., 18, 445–463, https://doi.org/10.3189/s0022143000021122, 1977.
Grenfell, C., Warren, G., and Mullen, C.: Reflection of solar radiation by the Antarctic snow surface at ultraviolet, visible, and near-infrared wavelengths, J. Geophys. Res., 99, 18669–18684, 1994.
Hudson, S. R. and Warren, S. G.: An explanation for the effect of clouds over snow on the top-of-atmosphere bidirectional reflectance, J. Geophys. Res., 112, D19202, https://doi.org/10.1029/2007JD008541, 2007.
Iwabuchi, H.: Efficient Monte Carlo Methods for Radiative Transfer Modeling, J. Atmos. Sci., 63, 2324–2339, https://doi.org/10.1175/JAS3755.1, 2006.
Ize, T.: Robust BVH Ray Traversal, Jcgt. Org., 2, 12–27, available at: http://jcgt.org/published/0002/02/02/paper.pdf (last access: 5 April 2020), 2013.
Jin, Z., Charlock, T. P., Yang, P., Xie, Y., and Miller, W.: Snow optical properties for different particle shapes with application to snow grain size retrieval and MODIS/CERES radiance comparison over Antarctica, Remote Sens. Environ., 112, 3563–3581, https://doi.org/10.1016/j.rse.2008.04.011, 2008.
Kokhanovsky, A. A.: A semi analytical cloud retrieval algorithm using backscattered radiation in 0.4–2.4 μm spectral region, J. Geophys. Res., 108, 1–19, https://doi.org/10.1029/2001jd001543, 2003.
Kokhanovsky, A.: Spectral reflectance of solar light from dirty snow: a simple theoretical model and its validation, The Cryosphere, 7, 1325–1331, https://doi.org/10.5194/tc-7-1325-2013, 2013.
Kokhanovsky, A. A. and Zege, E. P.: Scattering optics of snow, Appl. Opt., 43, 1589–1602, 2004.
Kuchiki, K., Aoki, T., Niwano, M., Motoyoshi, H., and Iwabuchi, H.: Effect of sastrugi on snow bidirectional reflectance and its application to MODIS data, J. Geophys. Res.-Atmos., 116, 1–15, https://doi.org/10.1029/2011JD016070, 2011.
Kuhn, M.: Anisotropic reflection from sastrugi fields, Antarct. J. U.S., 9, 123–125, 1974.
Kuhn, M.: Bidirectional Reflectance of Polar and Alpine Snow Surfaces, Ann. Glaciol., 6, 164–167, 1985.
Lafortune, E. P.: Mathematical Models and Monte Carlo Algorithms for Physically based Rendering, Ph.d. thesis, Katholieke University, Leuven, Belgium, 1995.
Larue, F., Arnaud, L., Ollivier, I., Delcourt, C., Lamare, M., Tuzet, F., Dumont, M., and Picard, G.: Snow albedo over artificial macroscopic surface roughness, Data set, Published 2020 via Perscido-Grenoble-Alpes, https://doi.org/10.18709/perscido.2020.05.ds314, 2020.
Leroux, C. and Fily, M.: Modeling the effect of sastrugi on snow reflectance, J. Geophys. Res., 103, 25779–25788, https://doi.org/10.1029/98JE00558, 1998.
Lhermitte, S., Abermann, J., and Kinnard, C.: Albedo over rough snow and ice surfaces, The Cryosphere, 8, 1069–1086, https://doi.org/10.5194/tc-8-1069-2014, 2014.
Libois, Q., Picard, G., France, J. L., Arnaud, L., Dumont, M., Carmagnola, C. M., and King, M. D.: Influence of grain shape on light penetration in snow, The Cryosphere, 7, 1803–1818, https://doi.org/10.5194/tc-7-1803-2013, 2013.
Libois, Q., Picard, G., Dumont, M., Arnaud, L., Sergent, C., Pougatch, E., Sudul, M., and Vial, D.: Experimental determination of the absorption enhancement parameter of snow, J. Glaciol., 60, 714–724, https://doi.org/10.3189/2014jog14j015, 2014.
Libois, Q., Picard, G., Arnaud, L., Dumont, M., Lafaysse, M., Morin, S., and Lefebvre, E.: Summertime evolution of snow specific surface area close to the surface on the Antarctic Plateau, The Cryosphere, 9, 2383–2398, https://doi.org/10.5194/tc-9-2383-2015, 2015.
Lliboutry, L.: La région du Fitz-Roy (Andes de Patagonie), Rev. Géog. Alpine, 41, 607–694, 1953.
Mondet, J. and Fily, M.: The reflectance of rough snow surfaces in Antarctica from POLDER/ADEOS remote sensing data, Geophys. Res. Lett., 26, 3477–3480, https://doi.org/10.1029/1999GL010913, 1999.
Naaim-Bouvet, F., Naaim, M., Bellot, H., and Nishimura, K.: Wind and drifting-snow gust factor in an Alpine context, Ann. Glaciol., 52, 223–230, https://doi.org/10.3189/172756411797252112, 2011.
Naegeli, K. and Huss, M.: Sensitivity of mountain glacier mass balance to changes in bare-ice albedo, Ann. Glaciol., 58, 119–129, https://doi.org/10.1017/aog.2017.25, 2017.
Negi, H. S., Kokhanovsky, A., and Perovich, D. K.: Application of asymptotic radiative transfer theory for the retrievals of snow parameters using reflection and transmission observations, The Cryosphere Discuss., 5, 1239–1262, https://doi.org/10.5194/tcd-5-1239-2011, 2011.
Oaida, C. M., Xue, Y., Flanner, M. G., Skiles, S. M. K., De Sales, F., and Painter, T. H.: Improving snow albedo processes in WRF/SSiB regional climate model to assess impact of dust and black carbon in snow on surface energy balance and hydrology over western U.S, J. Geophys. Res., 120, 3228–3248, https://doi.org/10.1002/2014JD022444, 2015.
O'Rawe: Monte Carlo models for the reflection of sunlight from rough snow surfaces: suncups and sastrugi, M.S Thesis – University of Washington, available at: https://www.researchgate.net/publication/34100391 (last access: 6 June 2019), 1991.
Painter, T. H., Deems, J. S., Belnap, J., Hamlet, A. F., Landry, C. C., and Udall, B.: Response of Colorado River runoff to dust radiative forcing in snow, P. Natl. Acad. Sci. USA, 107, 17125–17130, https://doi.org/10.1073/pnas.0913139107, 2010.
Pfeffer, W. T. and Bretherton, C. S.: The effect of crevasses on the solar heating of a glacier surface, IAHS Red Book, 170, 191–206, 1987.
Picard, G., Domine, F., Krinner, G., Arnaud, L., and Lefebvre, E.: Inhibition of the positive snow-albedo feedback by precipitation in interior Antarctica, Nat. Clim. Change, 2, 795–798, https://doi.org/10.1038/nclimate1590, 2012.
Picard, G., Libois, Q., Arnaud, L., Verin, G., and Dumont, M.: Development and calibration of an automatic spectral albedometer to estimate near-surface snow SSA time series, The Cryosphere, 10, 1297–1316, https://doi.org/10.5194/tc-10-1297-2016, 2016.
Picard, G., Dumont, M., Lamare, M., Tuzet, F., Larue, F., Pirazzini, R., and Arnaud, L.: Spectral albedo measurements over snow-covered slopes: theory and slope effect corrections, The Cryosphere Discuss., https://doi.org/10.5194/tc-2019-267, in review, 2020.
Ricchiazzi, P., Yang, S., Gautier, C., and Sowle, D.: SB DART: A Research and Teaching Software Tool for Plane-Parallel Radiative Transfer in the Earth's Atmosphere, B. Am. Meteorol. Soc., 79, 2101–2114, https://doi.org/10.1175/1520-0477(1998)079<2101:SARATS>2.0.CO;2, 1998.
Schaepman-Strub, G., Schaepman, M. E., Painter, T. H., Dangel, S., and Martonchik, J. V.: Reflectance quantities in optical remote sensing-definitions and case studies, Remote Sens. Environ., 103, 27–42, https://doi.org/10.1016/j.rse.2006.03.002, 2006.
Sicart, J. E., Ribstein, P., Wagnon, P., and Brunstein, D.: Clear-sky albedo measurements on a sloping glacier surface: A case study in the Bolivian Andes, J. Geophys. Res.-Atmos., 106, 31729–31737, https://doi.org/10.1029/2000JD000153, 2001.
Skiles, S. M., Flanner, M., Cook, J. M., Dumont, M., and Painter, T. H.: Radiative forcing by light-absorbing particles in snow, Nat. Clim. Change, 8, 964–971, https://doi.org/10.1038/s41558-018-0296-5, 2018.
Tanikawa, T., Aoki, T., Hori, M., Hachikubo, A., Abe, O., and Aniya, M.: Monte Carlo simulations of spectral albedo for artificial snowpacks composed of spherical and non spherical particles, Appl. Opt., 45, 5310–5319, https://doi.org/10.1364/AO.45.005310, 2006.
Tuzet, F., Dumont, M., Arnaud, L., Voisin, D., Lamare, M., Larue, F., Revuelto, J., and Picard, G.: Influence of light-absorbing particles on snow spectral irradiance profiles, The Cryosphere, 13, 2169–2187, https://doi.org/10.5194/tc-13-2169-2019, 2019.
Tuzet, F., Dumont, M., Picard, G., Lamare, M., Voisin, D., Nabat, P., Lafaysse, M., Larue, F., Revuelto, J., and Arnaud, L.: Quantification of the radiative impact of light-absorbing particles during two contrasted snow seasons at Col du Lautaret (2058 m a.s.l., French Alps), The Cryosphere Discuss., https://doi.org/10.5194/tc-2019-287, in review, 2020.
Wald, I., Boulos, S., and Shirley, P.: Ray tracing deformable scenes using dynamic bounding volume hierarchies, ACM Trans. Graph., 26, 6–es, https://doi.org/10.1145/1189762.1206075, 2007.
Wang, X., Pu, W., Ren, Y., Zhang, X., Zhang, X., Shi, J., Jin, H., Dai, M., and Chen, Q.: Observations and model simulations of snow albedo reduction in seasonal snow due to insoluble light-absorbing particles during 2014 Chinese survey, Atmos. Chem. Phys., 17, 2279–2296, https://doi.org/10.5194/acp-17-2279-2017, 2017.
Warren, S. G.: Optical properties of snow, Rev. Geophys., 20, 67–89, https://doi.org/10.1029/RG020i001p00067, 1982.
Warren, S. G., Brandt, R. E., and O'Rawe Hinton, P.: Effect of surface roughness on bi-directional reflectance of Antarctic snow, J. Geophys. Res.-Planets, 103, 25789–25807, https://doi.org/10.1029/98JE01898, 1998.
Wendler, G. and Kelley, J.: On the albedo of snow in Antarctica: a contribution to I.A.G.O*, J. Glaciol., 34, 19–25, 1988.
Woop, S., Benthin, C., and Wald, I.: Watertight ray/triangle intersection, J. Comput. Graph. Tech., 2, 65–82, 2013.
Wuttke, S., Seckmeyer, G., and König-Langlo, G.: Measurements of spectral snow albedo at Neumayer, Antarctica, Ann. Geophys., 24, 7–21, 2006.
Zege, E., P., Ivanov, A., P., and Katsev, I., L.: Image transfer through a scattering medium, Berlin, Springer, 1991,
Zhuravleva, T. B. and Kokhanovsky, A. A.: Influence of horizontal inhomogeneity on albedo and absorptivity of snow cover, Russ. Meteorol. Hydrol., 35, 590–595, https://doi.org/10.3103/S1068373910090025, 2010.
Zhuravleva, T. B. and Kokhanovsky, A. A.: Influence of surface roughness on the reflective properties of snow, J. Quant. Spectrosc. Rad. Transf., 112, 1353–1368, https://doi.org/10.1016/J.JQSRT.2011.01.004, 2011.