Unlocking the potential of melting calorimetry: a field protocol for liquid water content measurement in snow

Melting calorimetry, a classic experiment often conducted in high-school chemistry laboratories, holds significant untapped potential for scientific applications beyond its educational context. Traditionally, this technique has been applied to measure the liquid water content in snow using two different formulations: melting calorimetry and freezing calorimetry. In contrast to freezing calorimetry, which is considered the reference method for measuring liquid water content, melting calorimetry has been perceived as prone to generating significant inaccuracies. This research revisits the formulations for both melting and freezing calorimeters to assess volumetric liquid water content in snow. By incorporating the calorimetric constant, we account for heat exchange with the calorimeter, a critical factor often neglected in melting-calorimetry experiments. This paper identifies the most effective and least uncertain method for determining this constant. A central contribution of this work is the introduction of a framework for estimating uncertainty in volumetric liquid water content measurements, adhering to established guidelines for uncertainty expression. This novel framework allows us to revisit past mathematical analyses and demonstrate that melting calorimetry delivers reliable measurements with an uncertainty 0.25 % greater than freezing calorimetry. Notably, despite this slightly higher uncertainty, melting calorimetry offers significant practical advantages for field applications. Moreover, we show how the proposed uncertainty framework can be expanded beyond instrumental uncertainty and also take into account the variability from environmental factors and operators, providing a more comprehensive characterization of the uncertainty. By exploiting the proposed uncertainty framework, we finally conduct an in-depth analysis for the optimal tuning of the experiment parameters. This analysis culminates in a robust field protocol for melting calorimetry that transcends commonsense procedural guidelines. Strict adherence to this protocol will maximize measurement accuracy. Applied in field tests in Italy and Switzerland, the melting calorimetry was demonstrated to accurately track the wet front penetration in the snowpacks, producing results comparable to independent dielectric measurements. These findings highlight the accuracy and the practical advantages of melting calorimetry as a reliable field tool for quantifying snowpack liquid water content. Melting calorimetry can potentially serve as a valuable tool for the independent calibration and validation of proximal and remote sensing techniques used for liquid water content retrieval.

1 Introduction

The presence of liquid water has a profound impact on the physical characteristics of snow, including heat advection through preferential flow, thermal conductivity, density, and mechanical properties, consequently influencing its hydrological and stability responses (Techel and Pielmeier, 2011; Avanzi et al., 2017; Wever et al., 2016; Moure et al., 2023; Valence et al., 2022; Donahue et al., 2022; Schlumpf et al., 2024; Leroux et al., 2020). Therefore, the precise measurement of liquid water content (LWC) within the snowpack assumes critical importance as it provides invaluable information to properly describe the current conditions of the snowpack and predict its evolution (Hirashima et al., 2019; Wever et al., 2014). Moreover, a proper characterization of liquid water content in the snowpack is essential to characterize the backscattering of radar signals (e.g., Gagliano et al., 2023; Marin et al., 2020).

Calorimetry is the scientific technique used to measure the heat energy transferred during a physical or chemical process, such as a reaction or a state change. This is achieved by utilizing a calorimeter, a specialized device designed to accurately measure the heat exchanged between a system and its surroundings. It has emerged as a promising technique for LWC determination within the snowpack (e.g., Yosida, 1960; Jones et al., 1983; Kawashima et al., 1998; Jones, 1979; Boyne and Fisk, 1987; Kinar and Pomeroy, 2015). To measure the LWC in snowpacks, calorimetry offers two distinct approaches based on the process involved: melting and freezing calorimetry. In a melting calorimeter, a snow sample is immersed in hot water. This results in the transition of the solid portion of the sample to a liquid phase and the heating of the melted ice portion and LWC to the equilibrium temperature. The measurement of the energy required for this transition is directly related to the amount of ice present in the snow sample. Consequently, LWC can be derived as the difference between the mass (or the volume) of the sample and the ice content. This is why melting calorimetry is considered an indirect measurement (Colbeck, 1978). On the contrary, a freezing calorimeter involves immersing a snow sample in a freezing agent such as cooled silicon oil that induces the transition of any liquid water in the sample to a solid phase and the cooling of the ice fraction and of the freezed LWC to the equilibrium temperature. The measurement of the energy required for this transition is directly related to the amount of LWC present in the snow sample. Freezing calorimetry is generally accepted as a reference standard for measurements (Colbeck, 1978), and it was used in the past to calibrate and validate non-destructive methods for LWC measurements (e.g., Denoth et al., 1984; Stein et al., 1997; Kendra et al., 1994).

The selection of the most suitable approach for implementing calorimetry demands consideration of both field usage and the accuracy of the obtained results. Firstly, it becomes evident that the practical handling of these methods significantly varies. Specifically, the usage of freezing calorimetry presents several challenges. This type of calorimetry requires the use of a freezing agent such as silicone oils or toluene, which possess characteristics that make them less desirable for use. For instance, these agents may be toxic and pose difficulties in terms of the proper disposal and cleaning of the instruments after their employment. Due to the variability in the freezing agents employed, their specific heat has to be retrieved through a dedicated analysis every time a new agent is used. Furthermore, operating a freezing calorimeter poses challenges associated with maintaining the freezing agent within a temperature range of −50 to −20 °C. Additionally, active monitoring of temperature changes is required throughout the experiment, lasting at least 15 min (Jones et al., 1983), to ensure the complete freezing of LWC and the system reaches thermal equilibrium. During this period, thermal losses can be substantial, introducing significant uncertainties. In contrast, melting calorimetry offers the advantage of using water as the melting agent, which can be kept warm using a portable stove. This also eliminates concerns about conserving the melting agent for multiple measurements in the field. Furthermore, melting calorimetry ensures rapid thermal equilibrium, minimizing heat losses through the calorimeter. These factors contribute to a more efficient experimental process compared to freezing calorimetry.

Regardless of being the established benchmark for measuring LWC, the freezing-calorimetry limitations have stimulated the development of alternative methods. These include, among the most established and used methods, alcohol calorimetry, which utilizes methanol (Fisk, 1986), and the dilution technique, which employs a 0.01 normality (N) hydrochloric acid stock solution (Davis et al., 1985). Laboratory comparisons have demonstrated that these two methods yield results equivalent to the freezing calorimeter and the Denoth meter (Boyne and Fisk, 1987), a portable instrument calibrated with freezing-calorimetry measurements that measures LWC in snow using its dielectric properties (Denoth and Foglar, 1986). The advantage of the dilution technique lies mainly in its speed compared to the freezing calorimeter. This has allowed the gathering of extensive data for calibrating and validating various dielectric models (Perla and Banner, 1988; Perla, 1991), revealing limitations in these models, including in the one used by the Denoth meter. Indeed, the variability in snowpack internal compositions, influenced by the specific conditions, can limit the applicability of dielectric models to all cases (Colbeck, 1980; Camp, 1992; Picard et al., 2022). Therefore, a crucial step towards a more accurate dielectric model is collecting a large number of field measurements. In this sense, melting calorimetry offers several advantages, not only over freezing calorimetry but also over alcohol and dilution methods: (i) it eliminates the need to prepare a specific stock solution, (ii) it has less stringent temperature requirements for the solution (it does not need to be precisely at 0 °C), and (iii) it allows for easier mixing. Interestingly, despite these advantages, melting calorimeters have not been widely adopted in the past.

The fact that the melting calorimeter has been avoided is likely due to the perception of large errors associated with it (Colbeck, 1978; Fisk, 1986; Boyne and Fisk, 1987; Denoth and Foglar, 1986). In particular, the study conducted by Colbeck (1978), where several measuring techniques including freezing and melting calorimetry were compared within a theoretical framework of uncertainty propagation, identifies the melting calorimeter as “inherently inaccurate”. The primary objective of Colbeck (1978) was to determine the measuring methodology that would result in lower uncertainty when deriving the water saturation and porosity. The analysis revealed that the uncertainty propagates in a larger quantity when starting from a measurement of ice volume, i.e., utilizing the melting calorimeter, compared to starting from a measurement of water volume, i.e., employing the freezing calorimeter. Based on this analysis, assuming that the relative uncertainty in measuring the ice volume is similar to or greater than that in measuring the water volume, the freezing calorimeter was deemed preferable to the melting calorimeter. However, the study provided only an intuitive explanation to support this assumption without actually calculating the relative uncertainties in ice and water, suggesting that freezing a smaller amount of water leads to a reduced error compared to melting a larger amount of ice. Nonetheless, this overlooks the practical challenges associated with freezing a small amount of water within a snow sample under real-world conditions, as discussed previously. Despite Kawashima et al. (1998) attempting to address Colbeck (1978) criticisms of melting calorimetry, their work suffers from limitations. Firstly, they do not account for heat exchange with the calorimeter. This issue has been recognized since early applications of the melting calorimeter (Halliday, 1950) and has been recently re-emphasized by Fasani et al. (2023). Secondly, their mathematical uncertainty propagation probably relies on simplified assumptions. These shortcomings likely compromise the accuracy of LWC measurements obtained using the melting calorimeter. Furthermore, these limitations have already propagated into subsequent studies like those of Fasani et al. (2023), Webb et al. (2021), and Mavrovic et al. (2020), potentially invalidating their findings. Therefore, while the field applicability of the melting calorimetry is attractive, a critical reevaluation of this technique is necessary.

Our paper addresses and rectifies the limitations of the state of the art for calorimetric analysis for liquid water measurement by proposing a sound mathematical formulation. In this sense, this paper prioritizes unlocking the full potential of the melting calorimeter for LWC measurement, rather than providing a comprehensive review of all existing measurement methods. Moreover, while certain concepts may resemble those in previous works in broad terms, our formulation and its application differ significantly, constituting the primary novelty of our paper. In detail, the novelties lie in the following points:

• We present the formulations for both melting and freezing calorimeters, expressed in volume percent and incorporating the calorimetric constant.

• We clarify the most effective method for estimating the calorimetric constant (E).

• We introduce the formulations for estimating the uncertainty in the volumetric LWC measurement for both melting and freezing calorimetry. We test the influence of the environment and operator on measurement uncertainty and find, through statistical analysis, that the results fall within the range of instrumental uncertainty.

• We provide a sensitivity analysis that allows an operator to become more aware of the impact of each measured variable when taking measurements.

• While Colbeck (1978) argued that melting calorimetry is “inherently inaccurate”, a view echoed in later studies, we revisit and refine this analysis. This mathematical refinement, occurring 45 years after Colbeck's original paper, fundamentally alters the prevailing understanding that the melting calorimeter, an instrument to indirectly measure liquid water content, is not inherently inaccurate, a significant breakthrough that we believe researchers in the field will appreciate.

• We have devised a field protocol that effectively minimizes uncertainties. The protocol includes specific instructions on the amount of hot water to be used, its temperature, the masses involved, and other crucial details for controlling the uncertainty during the experiment replication.

• The proposed protocol was applied at two different test sites in Italy and Switzerland by two different research groups with different calorimeters to profile LWC. The results, compared to stratigraphic and Denoth meter sampling, show the effectiveness of the proposed melting-calorimetry protocol.

• We have made available all the codes necessary for calculating LWC and its associated uncertainty based on the measured variables.

2 Formulation of melting and freezing calorimetry

The calorimeter experiment is formulated as an energy budget problem. Each term in the energy budget associated with a change in temperature depends on the mass involved, its specific heat, and the temperature difference. Conversely, terms related to phase transitions are determined by the mass involved and the latent heat. Before dealing with the computation of the energy balance, some practical considerations of the setup and measurement operations will be provided.

The setup for calorimetry used to measure LWC in snow involves three essential instruments: (i) a specialized instrument known as a calorimeter (see Fig. 1), (ii) a scale, and (iii) a thermometer. The calorimeter is designed as an insulated container to maintain a given temperature and create an insulated environment from the outside, ensuring ideal heat exchange between the snow sample and the melting or freezing agent. The thermometer is generally already part of the calorimeter. It is inserted into the insulated cap of the calorimeter, with particular attention paid to not introducing any points for heat exchanges, and it is used to monitor temperature changes during the experiment. Prior to the wide availability of modern materials and construction techniques, Yosida conducted extensive research on optimizing calorimeter design (Yosida, 1960). Today, calorimeters can be as simple as a commercially available insulated bottle, which provides thermal insulation superior to the Yosida design. The vacuum between the vessels significantly reduces heat transfer by both conduction and convection. Additionally, silvered internal walls minimize heat loss through thermal radiation. These advancements extend the time during which the calorimeter can work as a perfectly insulated environment, eliminating the need for the double-container design (one for hot water and one for snow) and the stirrer introduced by Yosida (1967).

Figure 1 A cross-section of the calorimeter, depicting a schematic representation of its components.

From a practical point of view, the calorimetric experiment starts with the placement of a precise mass of either melting agent (M_w) or freezing agent (M_o) into the insulated container. The most commonly used melting agent is hot water, while the most used freezing agent is silicone oil. The initial temperature of the melting agent (T_w≫0 °C) or the freezing agent (T_o≪0 °C) is recorded. Subsequently, a snow sample of mass M_s and volume V_s is added to the calorimeter. The resulting mixture is stirred to facilitate rapid mixing and efficient heat transfer. During this process, the temperature of the mixture is monitored until it reaches equilibrium (T_f), indicating the completion of the heat exchange between the snow sample and the agent. Minimizing the duration of these steps is essential to maintain the assumption of an adiabatic system. Any potential losses of the calorimeter, which may be large in the freezing calorimeter given the longer time of operation, must be accounted for in the analysis, e.g., by monitoring the temperature for a long time (Jones et al., 1983). Calorimetric experiments involve heat exchange between the snow sample and the fluid. During the calorimetric experiment, heat exchange occurs not only between the snow sample and the fluid, but also with the internal metallic calorimeter wall. The wall, due to its high thermal conductivity and vacuum insulation, rapidly reaches thermal equilibrium. While thermal radiative heat transfer represents the most significant energy loss for the calorimeter, the impact of radiation can be considered negligible when compared to the timescale of the experiment (around 1 min). Therefore in this study, we will focus primarily on heat conduction as the dominant mechanism for heat exchange, as also done in Jones et al. (1983). All the quantities mentioned are then used to calculate the heat exchanged during the process, allowing for an estimation of LWC within the snowpack. As we progress with the paper, when we discuss liquid water content, we will be specifically referring to the volumetric liquid water content (Fierz et al., 2009), which is a measurement defined as the ratio of the volume of liquid water content to the volume of the snow sample. Regarding the notation, ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ refers to the volumetric LWC measured with the melting calorimeter, ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{F}}$ denotes the same quantity measured with the freezing calorimeter, while θ_w refers to the general case as reported in Appendix C.

From the heat exchange point of view, in the melting calorimeter, the energy introduced by the hot water Q_hot water and the calorimeter internal wall Q_calorimeter must be balanced with the sum of energy terms for the sinks. These terms include the heat needed for melting the ice content Q_ice melting and the heat required to bring the melted ice and the liquid water already present in the snow to the equilibrium temperature, Q_melted ice and Q_LWC. In Eq. (1) is shown the energy budget, detailing the different terms of the equations as follows:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}\underset{M_{\mathrm{w}}C(T_{\mathrm{f}}-T_{\mathrm{w}})}{\underbrace{Q_{\text{hot water}}}}& +\underset{M_{\text{cal}}{C}_{\text{cal}}(T_{\mathrm{f}}-T_{\mathrm{w}})}{\underbrace{Q_{\text{calorimeter}}}}+\underset{L{M}_{\mathrm{i}}}{\underbrace{Q_{\text{ice melting}}}}\\ & +\underset{M_{\mathrm{i}}C(T_{\mathrm{f}}-T_{\mathrm{s}})}{\underbrace{Q_{\text{melted ice}}}}+\underset{M_{\text{LWC}}C(T_{\mathrm{f}}-T_{\mathrm{s}})}{\underbrace{Q_{\text{LWC}}}}=\mathrm{0},\end{array}\end{array}$$

where

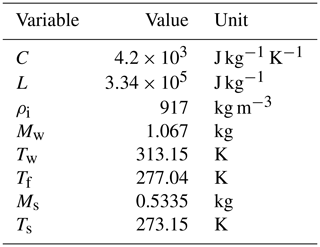
• C represents the specific heat of water (4.2×10³ J kg⁻¹ K⁻¹);

• L represents the latent heat of the fusion of ice (3.34×10⁵ J kg⁻¹);

• T_s is the temperature of the snow sample, which is 273.15 K if no ionic impurities are involved;

• M_cal represents the mass of the internal wall of the calorimeter in contact with the water;

• C_cal represents the specific heat of the internal wall of the calorimeter in contact with the water;

• M_LWC is the mass of the liquid water in the snow sample and can be expressed as $M_{\text{LWC}}={\mathit{\theta }}_{\mathrm{w}}{M}_{\mathrm{s}}\frac{{\mathit{\rho }}_{\mathrm{w}}}{{\mathit{\rho }}_{\mathrm{s}}}$;

• M_i is the mass of the ice fraction of the snow sample and can be expressed as
  $M_{\mathrm{i}}=M_{\mathrm{s}}-M_{\text{LWC}}$.

In the operative formulation of the melting calorimeter, the heat exchange contribution of the calorimeter internal wall is expressed as a term added to the water mass, introducing the so-called calorimetric constant E (Jones et al., 1983; Fasani et al., 2023). Therefore, as an inherent material property of the calorimeter, the computation of E can be accomplished as follows:

$$\begin{array}{}\text{(2)}& E={\displaystyle \frac{M_{\text{cal}}{C}_{\text{cal}}}{C}}.\end{array}$$

An accurate estimation of E requires precise information about the calorimeter construction. Ideally, the manufacturer can provide detailed specifications, including the weight of the internal container and the material used in its construction (typically stainless steel). As a last resort, a destructive approach can be employed. This involves carefully dismantling the calorimeter and precisely measuring the weight of the internal container. Several non-destructive methods for estimating E have been proposed, such as mixing fluids at different temperatures (e.g., Jones et al., 1983; Austin, 1990) or inverting Eq. (3) (e.g., Fasani et al., 2023), given that wet-snow samples are prepared at a given θ_w. However, these methods often suffer from significant uncertainty propagation. For instance, applying the method used by Jones et al. (1983), Austin (1990) yields a relative uncertainty in E of 40 % in a standard calorimetry configuration. Similarly, creating artificial wet-snow samples (Fasani et al., 2023) can further increase relative uncertainty to unacceptable levels i.e., 75 %, even if we assume that θ_w is known without uncertainty. Therefore, although non-destructive, these methods are associated with significant uncertainties and are thus recommended to be avoided. The complete mathematical derivations for estimating the uncertainty associated with E using various methods from the literature are provided in Appendix A.

From Eqs. (1) and (2), ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ can be derived as follows:

$$\begin{array}{}\text{(3)}& {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}={\displaystyle \frac{M_{\mathrm{s}}}{V_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}}}}\left(\mathrm{1}-{\displaystyle \frac{C}{L}}\left[{\displaystyle \frac{(M_{\mathrm{w}}+E)(T_{\mathrm{w}}-T_{\mathrm{f}})}{M_{\mathrm{s}}}}-(T_{\mathrm{f}}-T_{\mathrm{s}})\right]\right).\end{array}$$

This formulation differs from that of Kawashima et al. (1998) in the inclusion of the parameter E, its simplification of the involved masses, and its use of density for volumetric conversion (i.e., snow density $M_{\mathrm{s}}/V_{\mathrm{s}}$ and water density ρ_w).

The freezing calorimeter operates on a principle similar to that of the melting calorimeter; however in this case the freezing agent and the container extract heat from the ice content and θ_w in the snow, causing it to freeze. The corresponding energy balance equation is given by

$$\begin{array}{}\text{(4)}& \begin{array}{rl}\underset{M_{\mathrm{o}}{C}_{\mathrm{o}}(T_{\mathrm{f}}-T_{\mathrm{o}})}{\underbrace{Q_{\text{freezing agent}}}}& +\underset{M_{\text{cal}}{C}_{\text{cal}}(T_{\mathrm{f}}-T_{\mathrm{o}})}{\underbrace{Q_{\mathrm{calorimeter}}}}+\underset{M_{\mathrm{i}}{C}_{\mathrm{i}}(T_{\mathrm{f}}-T_{\mathrm{s}})}{\underbrace{Q_{\text{cooling ice}}}}\\ & +\underset{-M_{\mathrm{LWC}}L}{\underbrace{Q_{\text{freezed}}{\mathit{\theta }}_{\mathrm{w}}}}+\underset{M_{\mathrm{LWC}}{C}_{\mathrm{i}}(T_{\mathrm{f}}-T_{\mathrm{s}})}{\underbrace{Q_{\text{cooling\hspace{0.33em}freezed}}{\mathit{\theta }}_{\mathrm{w}}}}=\mathrm{0},\end{array}\end{array}$$

where

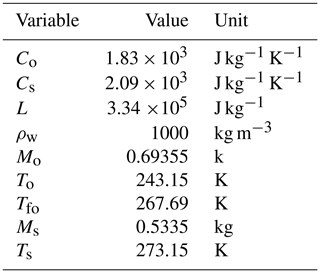
• C_o is the heat capacity of the freezing agent and C_i is the heat capacity of ice (2.09×10³ J kg⁻¹ K⁻¹), where C_o is 1.83×10³ J kg⁻¹ K⁻¹ at −10 °C in the case of using silicone oil;

• C_i is the heat capacity of ice (2.09×10³ J kg⁻¹ K⁻¹).

As for the melting calorimeter, the heat exchange contribution of the calorimeter internal wall is expressed as an additive term but this time added to the freezing agent mass M_o. The calorimetric constant E^F in that case can be obtained as

$$\begin{array}{}\text{(5)}& E^{\mathrm{F}}={\displaystyle \frac{M_{\text{cal}}{C}_{\text{cal}}}{C_{\mathrm{o}}}}.\end{array}$$

In the freezing case, the ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{F}}$ is directly related to the temperature difference induced by the freezing of water present in the snow and, as shown in Jones et al. (1983), is derived from Eqs. (4) and (5) as follows:

$$\begin{array}{}\text{(6)}& {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{F}}={\displaystyle \frac{M_{\mathrm{s}}}{V_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}}}}\left({\displaystyle \frac{(M_{\mathrm{o}}+E^{\mathrm{F}})C_{\mathrm{o}}(T_{\mathrm{f}}-T_{\mathrm{o}})}{L{M}_{\mathrm{s}}}}-{\displaystyle \frac{C_{\mathrm{i}}(T_{\mathrm{s}}-T_{\mathrm{f}})}{L}}\right).\end{array}$$

3 Propagation of the uncertainty in calorimetry

3.1 Instrumental uncertainty propagation: melting vs. freezing calorimetry

Instrumental uncertainty, which arises from the limitations and imperfections of the measuring instruments used in the calorimetric experiment, propagates into the final estimation of θ_w. In both melting and freezing calorimetry, the uncertainties are associated with temperature measurements and mass determinations. To quantify uncertainty propagation, we employ a statistical method for uncertainty propagation in accordance with the Guide to the Expression of Uncertainty in Measurement (GUM) (IEC et al., 1993). In previous studies, different uncertainty estimators have been used, like the sum of the relative uncertainty (Colbeck, 1978) or the sum of the absolute uncertainty (Jones, 1979; Kawashima et al., 1998), to calculate the uncertainty in the percentage of mass liquid water content. This paper breaks new ground by providing the uncertainty in the volume LWC that adheres to the GUM guidelines.

In detail, the uncertainty ${\mathit{\sigma }}_{{\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M},\mathrm{F}}}$ can be determined as the square root of the sum of the squared partial derivatives of ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M},\mathrm{F}}$ with respect to the variables with an associated uncertainty, each multiplied by the squared associated error. By assuming independent variables, the general formulation is reported in Eq. (7) (IEC et al., 1993; Moffat, 1988).

$$\begin{array}{}\text{(7)}& {\mathit{\sigma }}_{{\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M},\mathrm{F}}}=\sqrt{\sum _{m_i}{\left({\displaystyle \frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M},\mathrm{F}}}{\partial m_i}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{m_i}^{\mathrm{2}}}\end{array}$$

In Eq. (7), m_i represents a single measurement affected by uncertainty and ${\mathit{\sigma }}_{m_i}$ is the associated uncertainty. For the melting calorimeter, the required measurements are V_s, M_w, M_s, T_w, T_f, and E (see Eq. 3) with associated instrumental uncertainties ${\mathit{\sigma }}_{M_{\mathrm{w}}}$ and ${\mathit{\sigma }}_{M_{\mathrm{s}}}$, which depend on the accuracy of the scale; ${\mathit{\sigma }}_{T_{\mathrm{w}}}$ and ${\mathit{\sigma }}_{T_{\mathrm{f}}}$, which depend on the accuracy of the thermometer; ${\mathit{\sigma }}_{V_{\mathrm{s}}}$, which depend on the uncertainties in measuring the volume of the sampler; and finally σ_E, which depends on the uncertainty in the estimation of E (see Appendix A).

Equation (7) can be applied to Eq. (3) and expanded as follows:

$$\begin{array}{}\text{(8)}& {\displaystyle }{\mathit{\sigma }}_{{\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}=\sqrt{\begin{array}{l}{\left(\frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}{\partial M_{\mathrm{w}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{M_{\mathrm{w}}}^{\mathrm{2}}+{\left(\frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}{\partial M_{\mathrm{s}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{M_{\mathrm{s}}}^{\mathrm{2}}+{\left(\frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}{\partial T_{\mathrm{w}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{T_{\mathrm{w}}}^{\mathrm{2}}\\ +{\left(\frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}{\partial T_{\mathrm{f}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{T_{\mathrm{f}}}^{\mathrm{2}}+{\left(\frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}{\partial V_{\mathrm{s}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{V_{\mathrm{s}}}^{\mathrm{2}}+{\left(\frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}{\partial E}\right)}^{\mathrm{2}}{\mathit{\sigma }}_E^{\mathrm{2}}\end{array}}.\end{array}$$

The partial derivatives in Eq. (8), known as sensitivity coefficients, are calculated as follows (to preserve the explicit dependence on snow density, i.e., ${\mathit{\rho }}_{\mathrm{s}}=M_{\mathrm{s}}/V_{\mathrm{s}}$, we refrain from simplifying terms involving M_s):

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}{\partial M_{\mathrm{w}}}}=-{\displaystyle \frac{M_{\mathrm{s}}}{V_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}}}}{\displaystyle \frac{C}{L}}{\displaystyle \frac{T_{\mathrm{w}}-T_{\mathrm{f}}}{M_{\mathrm{s}}}},\text{(10)}& {\displaystyle \frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}{\partial T_{\mathrm{w}}}}=-{\displaystyle \frac{M_{\mathrm{s}}}{V_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}}}}{\displaystyle \frac{C}{L}}{\displaystyle \frac{M_{\mathrm{w}}+E}{M_{\mathrm{s}}}},\text{(11)}& {\displaystyle \frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}{\partial T_{\mathrm{f}}}}={\displaystyle \frac{M_{\mathrm{s}}}{V_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}}}}{\displaystyle \frac{C}{L}}\left({\displaystyle \frac{M_{\mathrm{w}}+E}{M_{\mathrm{s}}}}+\mathrm{1}\right),\text{(12)}& {\displaystyle \frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}{\partial M_{\mathrm{s}}}}={\displaystyle \frac{\mathrm{1}}{V_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}}}}\left(\mathrm{1}-{\displaystyle \frac{C}{L}}\left(T_{\mathrm{f}}-T_{\mathrm{s}}\right)\right),\text{(13)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}{\partial V_{\mathrm{s}}}}& =-{\displaystyle \frac{M_{\mathrm{s}}}{V_{\mathrm{s}}^{\mathrm{2}}{\mathit{\rho }}_{\mathrm{w}}}}\\ & \left(\mathrm{1}-{\displaystyle \frac{C}{L}}\left({\displaystyle \frac{(M_{\mathrm{w}}+E)(T_{\mathrm{w}}-T_{\mathrm{f}})}{M_{\mathrm{s}}}}-(T_{\mathrm{f}}-T_{\mathrm{s}})\right)\right),\end{array}\text{(14)}& {\displaystyle \frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}{\partial E}}=-{\displaystyle \frac{M_{\mathrm{s}}}{V_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}}}}{\displaystyle \frac{C}{L}}{\displaystyle \frac{T_{\mathrm{w}}-T_{\mathrm{f}}}{M_{\mathrm{s}}}}.\end{array}$$

It is important to note that although there are significant differences in our calorimetric equations, Kawashima et al. (1998) calculated some of the same derivatives as we present. However, they used an approximation to transition from Eq. (1) to Eq. (4) in their original paper, via Eq. (3), that is not clear. This ambiguity results in different values when properly calculating the derivatives.

Similarly, for the freezing calorimeter, we can analyze the error propagation associated with temperature and weight measurements of Eq. (6). In detail, by applying Eq. (7), we obtain

$$\begin{array}{}\text{(15)}& {\mathit{\sigma }}_{{\mathit{\theta }}_{\mathrm{w}}^{\mathrm{F}}}=\sqrt{\begin{array}{l}{\left(\frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{F}}}{\partial M_{\mathrm{o}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{M_{\mathrm{o}}}^{\mathrm{2}}+{\left(\frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{F}}}{\partial M_{\mathrm{s}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{M_{\mathrm{s}}}^{\mathrm{2}}+{\left(\frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{F}}}{\partial T_{\mathrm{o}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{T_{\mathrm{o}}}^{\mathrm{2}}\\ +{\left(\frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{F}}}{\partial T_{\mathrm{f}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{T_{\mathrm{f}}}^{\mathrm{2}}+{\left(\frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}{\partial V_{\mathrm{s}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{V_{\mathrm{s}}}^{\mathrm{2}}+{\left(\frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{F}}}{\partial E}\right)}^{\mathrm{2}}{\mathit{\sigma }}_E^{\mathrm{2}}\end{array}}.\end{array}$$

The partial derivatives in Eq. (15) are calculated as follows:

$$\begin{array}{}\text{(16)}& {\displaystyle \frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{F}}}{\partial M_{\mathrm{o}}}}={\displaystyle \frac{M_{\mathrm{s}}}{V_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}}}}{\displaystyle \frac{C_{\mathrm{o}}(T_{\mathrm{f}}-T_{\mathrm{o}})}{L{M}_{\mathrm{s}}}},\text{(17)}& {\displaystyle \frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{F}}}{\partial T_{\mathrm{o}}}}=-{\displaystyle \frac{M_{\mathrm{s}}}{V_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}}}}{\displaystyle \frac{(M_{\mathrm{o}}+E)C_{\mathrm{o}}}{L{M}_{\mathrm{s}}}},\text{(18)}& {\displaystyle \frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{F}}}{\partial T_{\mathrm{f}}}}={\displaystyle \frac{M_{\mathrm{s}}}{V_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}}L}}\left({\displaystyle \frac{(M_{\mathrm{o}}+E)C_{\mathrm{o}}}{M_{\mathrm{s}}}}+C_{\mathrm{i}}\right),\text{(19)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{F}}}{\partial M_{\mathrm{s}}}}& =-{\displaystyle \frac{\mathrm{1}}{L}}\left({\displaystyle \frac{(M_{\mathrm{o}}+E)C_{\mathrm{o}}(T_{\mathrm{f}}-T_{\mathrm{o}})}{V_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}}{M}_{\mathrm{s}}}}+{\displaystyle \frac{\mathrm{1}}{V_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}}}}\right.\\ & \left.\left({\displaystyle \frac{(M_{\mathrm{o}}+E)C_{\mathrm{o}}(T_{\mathrm{f}}-T_{\mathrm{o}})}{M_{\mathrm{s}}}}-C_{\mathrm{i}}(T_{\mathrm{s}}-T_{\mathrm{f}})\right)\right),\end{array}\text{(20)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{F}}}{\partial V_{\mathrm{s}}}}& =-{\displaystyle \frac{M_{\mathrm{s}}}{V_{\mathrm{s}}^{\mathrm{2}}{\mathit{\rho }}_{\mathrm{w}}}}\\ & \left({\displaystyle \frac{(M_{\mathrm{o}}+E)C_{\mathrm{o}}(T_{\mathrm{f}}-T_{\mathrm{o}})}{L{M}_{\mathrm{s}}}}-{\displaystyle \frac{C_{\mathrm{i}}(T_{\mathrm{s}}-T_{\mathrm{f}})}{L}}\right),\end{array}\text{(21)}& {\displaystyle \frac{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{F}}}{\partial E}}={\displaystyle \frac{M_{\mathrm{s}}}{V_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}}}}{\displaystyle \frac{C_{\mathrm{o}}(T_{\mathrm{f}}-T_{\mathrm{o}})}{L{M}_{\mathrm{s}}}}.\end{array}$$

Similar derivatives have been presented in Jones (1979) for the propagation of the instrumental uncertainty for the liquid water content expressed as a percentage of mass LWC.

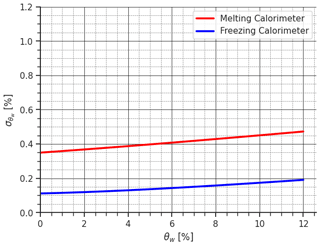
Figure 2 The figure provides a comparison of uncertainty in estimating θ_w by propagating instrumental uncertainty using both the melting-calorimeter and freezing-calorimeter methods.

By evaluating Eqs. (8) and (15), it is possible to compare the two methods as done in Colbeck (1978). In detail, by assuming V_s=200 cm³, a value consistent with the density measurement sampler (Proksch et al., 2016), which ensures compact dimensions for both the snow sampler and the calorimeter and thus facilitates transportation, and considering a snow density of the dry snow of 366 kg m⁻³ as a legacy of Colbeck (1978), to which we add a given percentage of liquid water, that increased the snow density of consequence. We set the temperature and mass of hot water at 40 °C and 2 times M_s, respectively, in line with the analysis of the next section, Sect. 3.2, and with Kawashima et al. (1998). Similarly, we set the temperature and mass of the freezing agent at −30 °C and 1.3 times M_s, respectively, as per Jones et al. (1983). The calorimetric constant was assumed to be equal to 6.58 g. θ_w was varied from 0 % to 12 %, considering the most common values in melting snowpack. Additionally, we consider a scale with an uncertainty of 0.1 g, a thermometer with an uncertainty of 0.2 °C, and an uncertainty in the estimation of the calorimeter constant E of 0.1 g. Regarding the uncertainty associated with the sample volume, to the best of our knowledge, no studies have been conducted in that specific direction. However from our practical experience, a value of 2 cm³ can be realistic according to the tools we are using.

By substituting these values into Eqs. (8) and (2), we quantified the uncertainty associated with θ_w. The results are illustrated in Fig. 2. The comparison demonstrates the superior performance of the freezing calorimeter, particularly for high θ_w values, where the melting calorimetry reaches almost 0.5 % uncertainty, whereas the freezing calorimetry stops at 0.2 % uncertainty, a value similar to that obtained by Jones et al. (1983) and Jones (1979) when converted to the sum of the absolute errors and as a percentage of mass (note that the sum of the absolute uncertainties is always larger than the root mean square of the uncertainties). However, the generally low value of ${\mathit{\sigma }}_{{\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}$ indicates that the melting calorimeter can still provide a significant and reliable measurement of θ_w. Coupled with its notable practical advantages, the melting calorimeter becomes an attractive and compelling choice for field applications, particularly in remote areas.

It is important to highlight that the uncertainty analysis presented here produces the same results as the paper of Colbeck (1978): by applying Eq. (8) for water saturation S_w, we can find that its relative uncertainty ${\mathrm{\Sigma }}_{S_{\mathrm{w}}}$ is 5.1 times the relative uncertainty in the ice volume ${\mathrm{\Sigma }}_{V_{\mathrm{i}}}$, whereas by applying Eq. (15), ${\mathrm{\Sigma }}_{S_{\mathrm{w}}}$ is 0.84 times the relative uncertainty in the water volume ${\mathrm{\Sigma }}_{V_{\mathrm{w}}}$ considering the values used in the original paper of Colbeck (1978). Nevertheless, it is essential to note that the relative uncertainty produced by the melting calorimeter in the estimation of the ice volume ${\mathrm{\Sigma }}_{V_{\mathrm{i}}}$ is 1 order of magnitude lower than the relative uncertainty produced by the freezing calorimeter in the water volume ${\mathrm{\Sigma }}_{V_{\mathrm{w}}}$, something that was not calculated in the original paper. This renders the final uncertainty in the two methods comparable, as shown in Fig. 2. All the mathematical details are reported in Appendix B and relative codes. Therefore, while Colbeck (1978) argued that melting calorimetry is “inherently inaccurate”, our mathematical refinement fundamentally alters the prevailing understanding that the use of a melting calorimeter, an indirect measurement of LWC, is not inherently inaccurate.

Finally, Fig. 2 shows an opposite trend compared to Fig. 3 in Kawashima et al. (1998). In our study, the uncertainty ${\mathit{\sigma }}_{{\mathit{\theta }}_{\mathrm{w}}}$ increases with increasing θ_w. This is because we compared snow samples with the same volume and ice content but varied liquid water content, mimicking an introduction of liquid water into the snow filling the voids. Consequently, as the liquid water content increases, so does the snow density. In contrast, Kawashima et al. (1998) do not account for volume in their formulation, instead adapting the snow mass to the water mass based on the parameter $R=\frac{M_{\mathrm{w}}}{M_{\mathrm{s}}}$ and maintaining a fixed T_f at 10 °C. While both approaches are mathematically correct, adjusting the snow density according to the liquid water content and letting T_f vary accordingly, aligns more closely with the practical reality of measuring LWC in the snowpack.

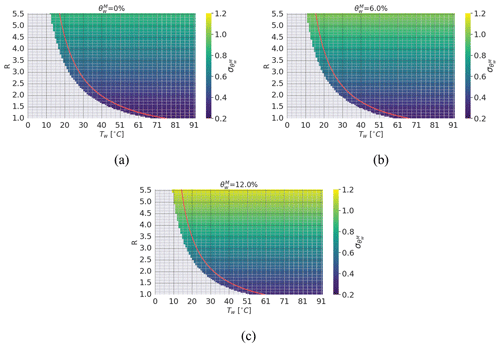
Figure 3 The uncertainty associated with ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ as a function of the experiment parameter R and T_w. In detail, the uncertainty is presented for three representative scenarios of ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$, i.e., 0 %, 6 %, and 12 %. (a) The dry-snow scenario with ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}=\mathrm{0}$ %. (b) The medium-wetness scenario with ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}=\mathrm{6}$ %. (c) The limit wetness scenario with ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}=\mathrm{12}$ %. Gray areas represent the cases where the calorimetric experiment results in a final temperature lower than 0 °C. The red boundary signifies a “safety” threshold constrained by a final temperature of 5 °C; i.e., the points lying on the red line result in T_f=5 °C.

3.2 Minimizing the instrumental uncertainty in the melting calorimetry

Leveraging the framework established in Sect. 3.1, we can now analyze how the uncertainties in variable measurement propagate to the final water content uncertainty ${\mathit{\sigma }}_{{\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}$ through the melting-calorimetry formula (Eq. 3), helping us to identify the optimal operational range for achieving the least uncertain measurements. Given the substantial differences between our approach (volumetric formulation with compensation for the calorimetric constant) and previous methods, a new analysis is necessary with respect to Kawashima et al. (1998). As described in Sect. 2, some of the variables involved in the calorimetry are free to be selected during the experiment. These are V_s, M_s, M_w, T_w, and E (see Eq. 3). However, all these variables are strictly connected to each other with some implications that it is better to account for.

Firstly, by increasing the volume sample V_s, we expect that the uncertainty decreases with V_s in the denominator for all the terms in Eq. (8). Nonetheless, the volume of the sample is linked to its mass, which increases by increasing the volume; this has an effect of compensation on ${\mathit{\sigma }}_{{\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}$. This outcome paves the way for dedicated investigation into employing various sample volumes for characterizing liquid water transport within the snowpack. Although such research lies outside the scope of this paper, here we provide some ideas that explain the volume selected in the context of this paper. As discussed in Sect. 3.1, V_s is generally constrained by the snow sampler used, which is normally fixed, e.g., the Taylor–LaChapelle density cutter. Similarly, with the measuring of the density (Proksch et al., 2016), V_s is selected focusing primarily on the resolution required to describe θ_w in the snowpack: a small snow cutter allows us to sample the small difference in θ_w within the snowpack, whereas a large volume provides more aggregated bulk information. In practice, by considering a calorimeter with a capacity of 0.5 L, V_s should fall between 100 and 300 cm³. For melting snow, this corresponds to an M_s value that ranges between approximately 60 and 150 g. Within these values, the influence of V_s on the overall uncertainty ${\mathit{\sigma }}_{\mathrm{w}}^{\mathrm{M}}$ is limited. For samples of this volume, it is advisable to prioritize a smaller vertical footprint – such as a cylindrical sampler with a diameter of 4 cm and a depth of 18 cm – over a shallower penetration depth with a larger vertical footprint. This strategy aids in identifying saturated layers and ensures smoother insertion of the snow sample into the calorimeter; i.e., the diameter of the sampler is smaller than the opening of the calorimeter.

At this point, the remaining variables are M_w, T_w, and E. It is then mathematically convenient to introduce a new variable $R=\frac{M_{\mathrm{w}}}{M_{\mathrm{s}}}$ as done in Kawashima et al. (1998). This allows us to plot the uncertainty as a function of the water temperature and the ratio between the masses for different levels of θ_w (see Fig. 3). Considering V_s=200 cm³, a dry-snow density of 366 kg m⁻³, and a calorimeter with E=6.58 g, it is possible to show that low values of R and high water temperature T_w are the values that produce the best results in terms of uncertainty. However, high T_w means a large temperature loss when the calorimeter is open to insert the snow sample. To minimize this loss, which otherwise has to be considered in the calorimetric formulation, a T_w of 40 to 50 °C together with a quick insertion of the snow sample in the calorimeter is a good trade-off for all the possible cases, as also indicated by Kawashima et al. (1998). On the other hand, it is worth stressing the fact that, even though low values of R produce the best results, this has two practical implications that should not be neglected: (i) if an immersion thermometer is used (such as the one represented in Fig. 1), particular attention should be devoted to the fact that the probe is properly immersed inside the water–snow mixture, to avoid measuring errors, and (ii) if the snow sample is too big with respect to the water mass or the water temperature is too low, the heat exchange cannot be completed; i.e., T_f<0 °C. As a recommendation, a value of R=2 is a good trade-off for all the possible real cases and T_f>5 °C should be obtained to consider the measurement valid (see Fig. 3).

Finally, it is important to mention that different values of E imply a change in the uncertainty (see Eqs. 9–14). However, we stress the fact that this change is limited, and therefore different sizes, shapes, and qualities of calorimeter can potentially be employed. From a different perspective, an incorrect estimation of the calorimeter constant can have a big impact on the accuracy of the measurement of θ_w (see next section).

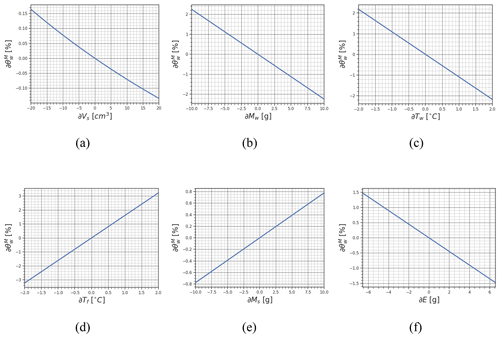
Figure 4 The variation in ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ with respect to the six parameters that define the experiment. In detail, we show in (a) the variation in ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ with respect to V_s, in (b) the variation in ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ with respect to M_w, in (c) the variation in ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ with respect to T_w, in (d) the variation in ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ with respect to T_f, in (e) the variation in ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ with respect to M_s, and in (e) the variation in ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ with respect to E.

3.3 Sensitivity analysis of the melting calorimetry

By studying the so-called sensitivity coefficients, i.e., Eqs. (9)–(14), we can derive important information about the sensitivity of melting calorimetry to variation in the input variables V_s, M_s, M_w, T_w, and E and the final value of ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$. In Fig. 4 the variation in ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ associated with the change in the experiment parameters is shown for a realistic case where the snow density is 416 kg m⁻³, M_s=83.4 g, M_w=166.8 g, T_f=4.8 °C, T_w=40 °C, E=6.58 g, and ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}=\mathrm{5.0}$ %. Note how R and T_w are derived from the considerations discussed in Sect. 3.2. This section, especially Fig. 4, is designed to inform operators about the impacts of potential variations in their measurements on ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$. Experiments in Sect. 5 will show how the strict application of the proposed protocol will avoid the introduction of such errors.

Figure 4a illustrates that the error in V_s is directly proportional to θ_w. However, the impact of this error is relatively limited. For instance, in the considered scenario where a snow box cutter with dimensions of $\mathrm{4}\times \mathrm{2.75}\times \mathrm{18}$ cm =198 cm³ is employed and a portion of 20 cm³ is lost due to incomplete filling – i.e., the snow cutter is not filled to a depth of 2 cm – the resulting θ_w measurement is overestimated by a mere 0.10 %. This suggests the feasibility of utilizing snow samplers with variable depth, such as samplers with a moving piston, to adapt the sample size according to the θ_w distribution in the snowpack.

In Fig. 4b, one can observe how even a small error of a few grams in the measurement of hot water mass can significantly impact the resulting θ_w, causing a nearly 1 % difference. For example, a 1.15° tilt of the scale can result in a measurement error of 0.1 g. This highlights the crucial significance of ensuring a stable, level, and well-prepared position for the scale that is protected by the influence of wind gusts. The plate of the balance should be also sufficiently large compared to the calorimeter.

The accurate measurement of the hot water temperature is equally important (see Fig. 4c). An overestimation of 1 °C in T_w results in an approximate 1 % underestimation of ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$. Additionally, it is crucial to emphasize the importance of measuring T_w only after the entire calorimeter reaches a stable temperature. Using a well-insulated container and promptly inserting the snow sample into the calorimeter so that the hot water does not cool down are vital factors in minimizing errors in the measurement of T_w. The specification regarding the depth of immersion for the thermometer probe must be satisfied; e.g., partially immersing the thermometer can lead to a temperature reading that is up to 1 °C lower than the actual temperature.

The misreading of T_f leads to a directly proportional error in the final θ_w measurement (see Fig. 4d). Achieving an accurate measurement of T_f necessitates ensuring that the heat exchange process is fully completed. To facilitate this, it is recommended to gently shake the calorimeter, and the completion of the process can be verified by observing clear stabilization in the temperature reading. This usually occurs within 30 s of inserting the snow sample into the calorimeter. Even under harsh conditions, heat loss from the closed calorimeter remains minimal. The negligible temperature loss holds true even when the calorimeter is exposed to sunlight or experiences internal–external temperature differences exceeding 40 °C. These conditions far surpass typical operating environmental conditions.

An error in the mass measurement of the snow sample M_s introduces a directly proportional error into ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ (see Fig. 4e). To ensure accurate measurements, the same precautions as those taken for the measurements of M_w should be followed.

Finally, it is crucial to note that an error in E is inversely proportional to θ_w (see Fig. 4f). Neglecting the heat exchange with the calorimeter wall, i.e., assuming E=0 g, results in significant errors in the final measurement of ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$. Therefore, when using a new calorimeter, proper time and effort should be dedicated to accurately estimating E.

The selection of the values will be summarized in Sect. 4 in the form of a protocol that all researchers and practitioners can follow during field experiments.

Figure 5 In (a) is shown the essential materials for the melting-calorimeter experiment. From left to right: the calorimeter, its thermometer, the thermos storing the hot water used in the experiment, and the scale for measuring mass placed on a stable Plexiglas panel. In (b) is shown from left to right, the snow cutter, used for sampling the snowpack at the Weissfluhjoch site and the Denoth meter used during the measurement campaign. In (c) it is possible to see the measurement configuration in case it is not possible to dig a snow pit deep enough to protect the calorimeter from wind and solar radiation. However, measurements under extreme weather conditions are not recommended.

4 Melting-calorimeter protocol

In this section, we will provide a comprehensive summary of the analyses conducted throughout the paper and propose a practical measurement protocol to be followed during field campaigns. First, the necessary materials need to be prepared, including the following:

Calorimeter

This could be a commercially available insulated container designed to maintain the temperature of beverages or food. The calorimeter constant must be known or derived for accurate measurements (e.g., with Eq. 2). In this work we used a commercial insulated container, i.e., a Stanley Classic Legendary Food Jar made of stainless steel (i.e., SAE 304) with C_cal=500 J kg⁻¹ K⁻¹, M_cal=69.1 g, and E=6.58 g. The uncertainty in this measurement is only related to the uncertainty in the scale used to weigh the container, i.e., 0.1 g. These values have been measured, and they are not provided by the producer.

High-precision immersion thermometer

This is used to monitor temperature changes during the experiment (we used a Hanna Instruments HI98501).

Precision balance

This is utilized for measuring the mass of hot water and snow samples. The scale should be at least splash-proof (IPX4). We used an RS PRO 805-6688 and a Kern PCB 10000-1.

Supportive surface

A level, hard, and supportive surface such as Plexiglas is required.

Wind shield

A well-dug shelter or an external barrier, such as a Plexiglas container, can be used to shield the scale from wind.

Insulated bottle

The bottle acts as a reservoir of hot water, ensuring a continuous supply for the experiment.

Snow sampler

This can be any of the available snow samplers for density measurements. The shape and size of the sampler must be compatible with the shape and size of the calorimeter.

The snow pit should be dug so that the snow wall is shaded from the sun. Once the snow pit has been prepared, a shaded area for the scale should be established (see Fig. 5a), protecting it from solar radiation and wind. If shade is unavailable for the scale, measurements should be avoided. Alternatively, a shading protection system like the one shown in Fig. 5c can be used. Another hole should be dug for storing the snow sampler and auxiliary tools needed for sample preparation to maintain them at low temperatures. The outer surface of the pit profile should be smoothed, and the bottom should be level to ensure accurate measurement of the snow height at which the ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ measurement will be taken.

Following these preparations, the following steps should be followed:

1. Dig a snow pit and verify that T_s=273.15 K (0 °C).

2. Warm up the water at a temperature of 40 to 50 °C, and store it in the insulated bottle.

3. Tare the scale with the calorimeter and the lid with the thermometer on top.

4. Prepare the hot water inside the calorimeter in a quantity that meets the minimum immersion requirement of the thermometer and is approximately 2 times the sample mass (label it as M_w). If a volume of 200 cm³ is used, approximately 200 g of hot water should be used.

5. Close the calorimeter and wait for the temperature to stabilize.

6. Record the temperature T_w. It should be around 40 °C.

7. Tare the scale with the calorimeter and hot water (otherwise the uncertainty in the two measurements must be propagated through Eq. 7).

8. Retrieve the snow sampler from the shaded hole and collect a snow sample from the designated height, ensuring no phase changes occur (i.e., take the sample in the shade) and no loss occurs.

9. Open the calorimeter and place the snow sample inside. Minimize the time for this step.

10. Gently shake the calorimeter.

11. Weigh the snow mass M_s by placing the calorimeter on the tared scale, waiting for the temperature to stabilize.

12. Once the temperature has stabilized, approximately 30 s–1 min after sample insertion, read the temperature T_f.

13. Empty and dry the calorimeter thoroughly before subsequent measurements. While carefully drying the calorimeter is advised, the residual water inside the calorimeter will be included in the mass and temperature measurement of the hot water, whereas the potential water or snow attached on the outside part of the calorimeter has to be cleaned out (even though this mass is in general negligible).

By following this protocol meticulously, the measurement of ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ in the snowpack can be conducted with the accuracy and the uncertainty shown in this paper (see next section on the experimental results). Using the shared code provided with the paper, ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ and the relative uncertainty can be derived starting from the measured data.

5 Experimental results: application of the melting-calorimeter protocol

5.1 Dry-snow experiment: the effectiveness of the melting-calorimetry protocol and impact of heat loss

In the first experiment, we used dry-snow samples and measured the final system temperature. This experiment serves as a proxy for evaluating the effectiveness of melting calorimetry when employed by skilled operators. While using reference samples with a known θ_w would be ideal, preparing such samples artificially introduces significant uncertainties. The methods employed by Kawashima et al. (1998) and by Fasani et al. (2023), which introduce liquid water into dry snow, require that the snow sample, the air, and the added liquid water be at exactly 0 °C. Moreover, the mixing operation should be done gently in order to not alter the effective θ_w of the reference sample. Therefore, given the inherent difficulty in achieving such precise control, we avoided this approach. As done for Eq. (1), we can derive the expression for the energy budget in the case of dry snow:

$$\begin{array}{}\text{(22)}& \begin{array}{rl}\underset{M_{\text{w}}C(T_{\mathrm{f}}-T_{\mathrm{w}})}{\underbrace{Q_{\text{hot water}}}}& +\underset{M_{\text{cal}}{C}_{\text{cal}}(T_{\mathrm{f}}-T_{\mathrm{w}})}{\underbrace{Q_{\text{calorimeter}}}}+\underset{M_{\text{dry\_snow}}{C}_{\text{ice}}(T_{\mathrm{f}}-T_{\text{dry\_snow}})}{\underbrace{Q_{\text{warming snow}}}}\\ & +\underset{L{M}_{\text{dry\_snow}}}{\underbrace{Q_{\text{snow melting}}}}-\underset{M_{\text{dry\_snow}}C(T_{\mathrm{f}}-T_{\text{mi}})}{\underbrace{Q_{\text{melted snow}}}}=\mathrm{0}.\end{array}\end{array}$$

From Eq. (22) can be retrieved the final temperature of the system as

$$\begin{array}{}\text{(23)}& T_{\mathrm{f}}={\displaystyle \frac{C_{\mathrm{i}}{M}_{\text{dry\_snow}}{T}_{\text{dry\_snow}}-L{M}_{\text{dry\_snow}}+C(M_{\mathrm{w}}+E)T_{\mathrm{w}}}{C(M_{\mathrm{w}}+E)+M_{\text{dry\_snow}}C}}.\end{array}$$

The associated instrumental uncertainty can be derived as follows (IEC et al., 1993):

$$\begin{array}{}\text{(24)}& {\mathit{\sigma }}_{T_{\mathrm{f}}}^{\text{Ins}}=\sqrt{\begin{array}{l}{\left(\frac{\partial T_{\mathrm{f}}}{\partial M_{\mathrm{s}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{M_{\mathrm{s}}}^{\mathrm{2}}+{\left(\frac{\partial T_{\mathrm{f}}}{\partial T_{\mathrm{s}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{T_{\mathrm{s}}}^{\mathrm{2}}+{\left(\frac{\partial T_{\mathrm{f}}}{\partial M_{\mathrm{w}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{M_{\mathrm{w}}}^{\mathrm{2}}\\ +{\left(\frac{\partial T_{\mathrm{f}}}{\partial T_{\mathrm{w}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{T_{\mathrm{w}}}^{\mathrm{2}}+{\left(\frac{\partial T_{\mathrm{f}}}{\partial E}\right)}^{\mathrm{2}}{\mathit{\sigma }}_E^{\mathrm{2}}\end{array}},\end{array}$$

where T_s and M_s are the temperature and the mass, respectively, of the dry-snow sample.

The dry-snow experiment revealed a lower overall uncertainty than the inherent instrumental uncertainty (refer to Fig. 6a). The results demonstrate that well-trained operators can significantly minimize uncertainties associated with sample handling and lid opening during calorimetric analysis, proving the practical effectiveness of melting calorimetry. Since for this experiment we always obtained an experimental uncertainty lower than the instrumental uncertainty, we performed a total of only five experiments. We instead focus on the heat lost when the calorimeter is opened for snow sample insertion. We observed a temperature loss of 0.2 °C after 10 s with a 40 °C difference between the air and the water temperature. Since sample insertion itself takes a maximum of 2 s by a skilled operator, the heat lost is negligible. This is more evidence that the instrumental uncertainty found in Sect. 3.1 can be applied in this case. This last finding aligns with the observations of Kawashima et al. (1998) (see the section of the original paper called “Effect of Heat Loss by Opening the Lid”).

5.2 Ice cube experiment: effect of different operators measuring at different environmental temperatures

In the second experiment, we investigated the combined effects of performing the calorimetric measurements by different operators under different air temperatures. To this end, we recruited a group of volunteers to perform a large number N of calorimetric experiments; i.e., N>30 following the proposed protocol. To simulate variations in air temperature, we performed the measurements in a controlled chamber spanning temperatures from −5 to 20 °C. In this experiment we used ice cubes as surrogates for wet-snow samples to avoid the introduction of additional uncertainties as described in the previous section. The substantial temperature differential between the ice cubes and the ambient environment enabled us to replicate worst-case scenarios that may arise due to operator inefficiency in adhering to the measurement protocol i.e., slowly moving the ice cube inside the opened calorimeter and/or not waiting for the thermal equilibrium.

The experimental setup, resembling the dry-snow calorimetric experiment described in the section before, aims to compare the measured final temperature ${T_{\mathrm{f}}}^{\text{Exp}}$ of the mixture of hot water after the addition of the ice cube with the theoretical temperature T_f calculated using the calorimetric formula. Specifically, the experiment involved a predetermined mass M_{ice_cube} of ice sample at a known temperature T_{ice_cube} and a mass M_w of water at a known temperature T_w. R was kept equal to 10 for all the experiments in order to guarantee the correct immersion of the thermometer and allow the ice cube ($T_{\text{ice\_cube}}\approx -\mathrm{35}$ °C) to completely melt. The temperature of the ice cubes was determined by leaving the cubes for at least 24 h in a refrigerator with monitored temperature. As done in Eq. (1), we can express the experiment as an energy budget by equalizing the energy carried by the hot water (Q_hot water) and the internal wall of the calorimetry, in thermal equilibrium with the hot water (Q_calorimeter), with the sinks consisting of the ice cube (Q_ice melting) and the water derived by melted ice (Q_melted ice). Starting from the energy balance presented in Eq. (22), the final temperature T_f can be derived from Eq. (23) by changing the mass and temperature of the dry snow with the mass and the temperature of the ice cube.

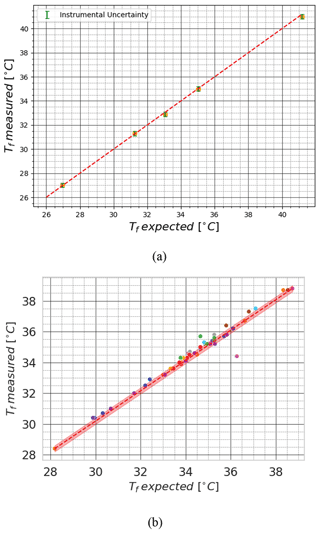
Figure 6 Results of the calorimetric experiment performed by a group of volunteers using (a) dry snow and (b) ice cubes. The measured final temperature (y axis) is compared with the theoretical final temperature (x axis) derived from Eq. (23). In (a) the green bars (barely visible due to their low values) represent the instrumental uncertainty in all the measurements using Eq. (24). In (b) the different colors of the dots represent the different people who performed the experiment. The red area represents the instrumental uncertainty in all the measurements using Eq. (26).

The outcome of the experiment is presented in Fig. 6b. From a qualitative point of view, the figure demonstrates good agreement between the measured and theoretical values, indicating the effectiveness of the melting calorimetry. The small spread of the data indicates that the experiment is largely reproducible among different operators, even though some operators generate larger errors. The lack of a bias indicates that there are no systematic errors. From a quantitative point of view, the experimental uncertainty can be calculated from these data as the root mean square (rms) of the differences between the measured final temperature ${T_{\mathrm{f}}}^{\text{Exp}}$ and the theoretical final temperature T_f as follows (IEC et al., 1993):

$$\begin{array}{}\text{(25)}& {\mathit{\sigma }}_{T_{\mathrm{f}}}^{\text{Exp}}=\sqrt{{\displaystyle \frac{{\sum }_i^N(T_{{\mathrm{f}}_{\mathrm{i}}}-{T_{{\mathrm{f}}_{\mathrm{i}}}}^{\text{Exp}}{)}^{\mathrm{2}}}{N}}}.\end{array}$$

This results in ${\mathit{\sigma }}_{T_{\mathrm{f}}}^{\text{Exp}}=\mathrm{0.5}$ °C. However, strictly speaking, in our setup the thermometer uncertainty of 0.1 °C and the scale uncertainty of 0.1 g limited our ability to definitively isolate the impact of environmental and operator variability on the measured T_f. A z test for null hypothesis verification (Rouder et al., 2009) applied to Eq. (25) sometimes rejected the null hypothesis, i.e., statistically insignificant differences between the estimated and measured temperatures.

Despite the limitations of our current instrumentation, let us explore a hypothetical scenario where ${\mathit{\sigma }}_{T_{\mathrm{f}}}^{\text{Exp}}=\mathrm{0.5}$ °C. This total uncertainty can be further broken down as the sum of the instrumental uncertainty ${\mathit{\sigma }}_{T_{\mathrm{f}}}^{\text{Ins}}$, the operator-induced uncertainty ${\mathit{\sigma }}_{T_{\mathrm{f}}}^{\text{Ope}}$, and the environment-induced uncertainty ${\mathit{\sigma }}_{T_{\mathrm{f}}}^{\text{Env}}$. The instrumental uncertainty ${\mathit{\sigma }}_{T_{\mathrm{f}}}^{\text{Ins}}$ can be calculated as follows (IEC et al., 1993):

$$\begin{array}{}\text{(26)}& {\mathit{\sigma }}_{T_{\mathrm{f}}}^{\text{Ins}}=\sqrt{\begin{array}{l}{\left(\frac{\partial T_{\mathrm{f}}}{\partial M_{\mathrm{i}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{M_{\mathrm{i}}}^{\mathrm{2}}+{\left(\frac{\partial T_{\mathrm{f}}}{\partial T_{\mathrm{i}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{T_{\mathrm{i}}}^{\mathrm{2}}+{\left(\frac{\partial T_{\mathrm{f}}}{\partial M_{\mathrm{w}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{M_{\mathrm{w}}}^{\mathrm{2}}\\ +{\left(\frac{\partial T_{\mathrm{f}}}{\partial T_{\mathrm{w}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{T_{\mathrm{w}}}^{\mathrm{2}}+{\left(\frac{\partial T_{\mathrm{f}}}{\partial E}\right)}^{\mathrm{2}}{\mathit{\sigma }}_E^{\mathrm{2}}\end{array}}.\end{array}$$

At this point, the uncertainty associated with the operator variations ${\mathit{\sigma }}_{T_{\mathrm{f}}}^{\text{Ope}}$ and the environmental factors ${\mathit{\sigma }}_{T_{\mathrm{f}}}^{\text{Env}}$ can be retrieved as a simple difference, i.e., ${\mathit{\sigma }}_{T_{\mathrm{f}}}^{\text{Ope}}+{\mathit{\sigma }}_{T_{\mathrm{f}}}^{\text{Env}}=\mathrm{0.3}$ °C. Given the fact that the operational steps of this experiment are exactly the same as the operational steps for the melting calorimeter, we can use the derived ${\mathit{\sigma }}_{T_{\mathrm{f}}}^{\text{Ope+Env}}$ to update the uncertainty calculated in Sect. 3.1 by adding this uncertainty to ${\mathit{\sigma }}_{T_{\mathrm{f}}}$. In Fig. 7, we observe how this new characterization of the uncertainty affects the uncertainty in the estimation of θ_w with respect to only considering the instrumental uncertainty. While the limitations of our current instrumentation prevent definitive conclusions from this analysis (i.e., not statistically significant results), this exercise demonstrates the value of a quantitative approach to understanding complex uncertainty sources, like the variations due to unskilled operators.

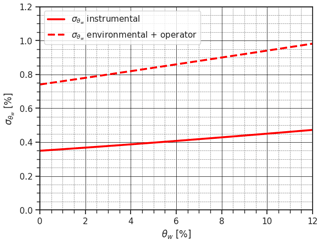
Figure 7 Comparison of the propagation of uncertainty considering the instrumental uncertainty (solid red line) and the potential random uncertainty introduced by variations in operators and environmental temperature (dashed red line) for the melting calorimeter derived from the ice cube experiments.

5.3 Fan experiment: the effect of harsh environmental conditions

Field campaigns often expose researchers or practitioners to challenging environmental conditions, encompassing factors such as wind, snowfall, rain, or high solar radiation. Experiments with excessively harsh environmental conditions and/or those that deviate from established snow pit measurement practices will yield unreliable results and hinder uncertainty estimation, compromising the validity of the measurement. Wind impacting the scale and direct solar radiation exposure of the snow sample are prime examples of such conditions. To quantify the impact of wind on measurement uncertainty, we conducted an experiment where a controlled breeze (of around 15 km h⁻¹) generated by a fan was directed at the scale. This resulted in a 10-fold increase in scale uncertainty, from 0.1 to 1.5 g. By applying ${\mathit{\sigma }}_{M_{\mathrm{w}}}=\mathrm{1.5}$ g and ${\mathit{\sigma }}_{M_{\mathrm{s}}}=\mathrm{1.5}$ g to Eq. (8), a significant uncertainty of more than 1 % will be associated with the measurement of liquid water content. These results highlight that wind is a major factor that can invalidate calorimetric measurements by introducing excessive uncertainty. Similarly to wind, solar radiation and sample handling can significantly impact θ_w. Rough handling, prolonged air exposure, and prolonged sun exposure can all alter the θ_w of the snow sample. As will be shown in the next sections, where profiles of LWC are successfully measured in the fields, following basic snow pit practices like shielding the scale from wind and protecting the sample and instruments from direct sunlight can prevent measurement failure and allow us to regard only the instrumental uncertainty as the main source of uncertainty. However, when the environmental conditions become extreme, calorimetric measurements should be avoided.

Figure 8 An overview of the two sites used for testing the calorimeter. In (a) the two sites can be visualized in the Alpine context, while in (b) and (c) the Senales and Weissfluhjoch sites, respectively, can be visualized in their local contexts. In (d) the Senales site is shown, and in (e) the Weissfluhjoch site is shown.

5.3.1 Weissfluhjoch: an intermediate-complexity ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ profile in the field

The Weissfluhjoch site, located at an altitude of 2536 m a.s.l. in the Davos area of Graubünden, Switzerland, features flat terrain that is partially sheltered from wind. The site includes a fenced research area and two huts equipped with tools, electricity, heating, and internet, making it ideal for high-level snowpack measurement campaigns (see Fig. 8).

On 22 May 2023, measurements began at 08:00 local time (LT) under overcast skies, with an air temperature of 7 °C and negligible winds. The snowpack height was 164 cm, characterized by a smooth surface and no new snowfall in the previous 24 h. Temperature profiles at intervals of 10 cm indicated an isothermal snowpack. Snowpack observations revealed surface melt over a transformed snow layer, with ice lenses identified between H=124 and H=121 cm. Other dry layers were observed until H=98 cm, spaced out by two more ice lenses. Just below the last ice lens, the snow seemed dry, but it was observed to become wetter towards the ground. Finally, water runoff was found at the bottom of the snow pit.

Figure 9a and b show ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ obtained from the melting calorimeter and Denoth method, sampled at 5 and 2 cm intervals, respectively. Figure 9c depicts snow density measured every 3 cm, and Fig. 9d showcases a schematic representation of the profile. Both instruments detected surface melt, though the calorimeter indicated higher surface ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ values. Ice lenses were characterized by drops in ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ and density, blocking the drainage of liquid water. Notably, at 87 cm from the bottom, the highest ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ value corresponded to an extremely wet layer confirmed by the calorimeter, while the Denoth method did not capture this layer, suggesting localized saturation. Measurements indicated that below H=87 cm, the snowpack was releasing meltwater, with ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ values increasing from nearly zero to 2 % and 10 % near the bottom. Comparisons between the Denoth and melting-calorimetry measurements revealed that the Denoth approach tended to underestimate θ_w in non-saturated layers (Perla, 1991). Following the procedure outlined in Boyne and Fisk (1987), we analyzed 16 measurements where both instruments sampled the same LWC conditions for the profile shown in Fig. 9, excluding the measurements at H=87 and H=0 cm. These points were omitted due to the high horizontal variability in LWC, which made it impossible to ensure that we were sampling identical conditions (see Techel and Pielmeier, 2011). The results showed a mean difference of 0.96 % and a standard deviation of 1 % between the two methods, aligning closely with previous findings for alcohol calorimeters and Denoth meters. While the setup for this experiment did not allow sampling at the exact same location with both techniques, the exclusion of certain data points ensures a clearer and more accurate representation of the tool's performance under comparable conditions. The calorimetric profile's vertical consistency and good correlation with density and stratigraphy demonstrate the reliability and stability of melting calorimetry. Lastly, it is interest to note that using the original formulation by Kawashima et al. (1998) may overestimate liquid water content by approximately 3.5 % on average compared to the proposed method.

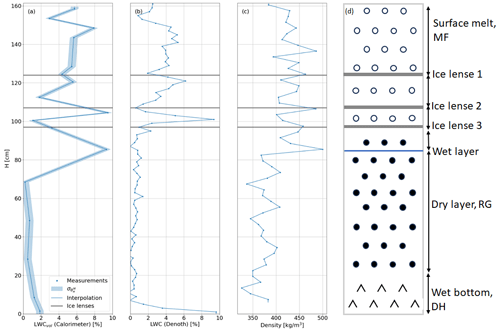
Figure 9 Snow profile at Weissfluhjoch on 22 May 2023. Panel (a) shows the volumetric ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ profile sampled every 5 cm with the melting calorimeter and its associated uncertainty computed with Eqs. (3) and (8). Panel (b) shows the ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ profile sampled every 2 cm with the Denoth meter. Panel (c) shows the snow density sampled every 3 cm with the snow cutter. Panel (d) shows a scheme of the profile.

5.3.2 Schnalstal: a typical ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ profile in the European Alps for late spring 2023

The Italian test site is located in Schnalstal (also referred to as Senales), in South Tyrol. This site has been chosen because the high altitude (approximately 3000 m) guarantees the presence of abundant snow and a long-lasting melting season and is well served by lifts and roads, making it easy to access (see Fig. 8).

The snowpack at the Schnalstal field site, with a height of 79 cm, was profiled on 7 June 2023 at 12:30 LT. During the measurements, the air temperature stood at 1.8 °C and there was negligible wind speed, ensuring relatively stable conditions for the assessment. The snowpack structure was as follows: from the surface down to 65 cm, a layer of recent snow was observed that had undergone wetting due to temperature and solar radiation, which were relatively high that day. The subsequent layer, spanning 65 to 57 cm, contained three prominent ice lenses. Notably, a significant amount of θ_w was trapped within this layer, contributing to its distinctive characteristics.

Continuing downwards, the layer from 57 cm to the base at 0 cm was characterized by coarse snow crystals with size from 1 to 2 mm, exhibiting lower water retention capability. Importantly, there was no noticeable ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ presence within this layer. However, the lowermost 20 cm of the snowpack presented some noticeable challenges. This section displayed loose and coarse crystals, leading to difficulties in proper sampling and ensuring optimal coupling between the Denoth instrument and the snow. Consequently, this lower 20 cm was excluded from the subsequent analysis to ensure data accuracy and reliability.

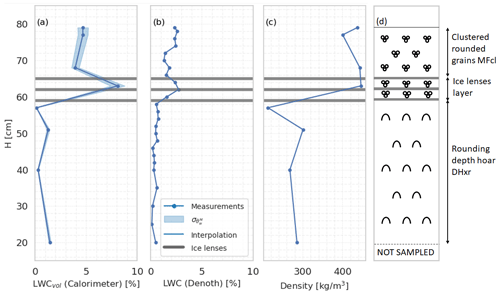
Figure 10 Snow profile at Schnalstal on 7 June 2023. Panel (a) displays the ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$ profile generated using the melting calorimeter, including its associated uncertainty calculated through Eq. (3). Panel (b) exhibits the θ_w profile sampled with the Denoth. Panel (c) illustrates the snow density associated with the calorimeter measurement points. Panel (d) shows a scheme of the profile.

Figure 10a depicts the volumetric liquid water content (${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$) profile, measured with the melting-calorimeter technique, along with its corresponding uncertainty, as computed using Eqs. (3) and (8). Panel (b) of the figure portrays the θ_w profile derived from Denoth measurements. Panel (c) showcases the snow density associated with the measurement points obtained from the calorimeter. These profiles collectively provide valuable insights into the internal structure of the snowpack and its distribution of liquid water. Specifically, the θ_w profile reflects the typical conditions in 2023 of the European Alpine snowpacks, where ice lenses were often present. Despite a significant amount of snowfall occurring in spring, the melting process was hindered by the presence of these ice lenses, impeding the transport of water to the ground. We can notice how the Denoth meter underestimates the superficial θ_w. Although the coherence of the profile along the vertical axis and its correlation with density and stratigraphy are in favor of calorimetric measurements, additional data and analysis are required to fully support the preference of the calorimetry profile over the Denoth meter.

Finally, to better verify the consistency of our measurements, we repeated a subset of measurements at very close distances on a uniform layer. The results of these repeated measurements yielded the following θ_w values: 7.27, 7.10, 7.19, and 7.20, with corresponding standard deviations of 0.50, 0.46, 0.56, and 0.52, respectively. These values were found to be very similar and fell within the uncertainty range, demonstrating the good stability of the melting-calorimetry technique. Additionally, a z test for null hypothesis verification (Rouder et al., 2009) applied at the difference between these values confirmed the evidence.

6 Discussion

The primary objective of this study was to provide a rigorous exposition of the melting-calorimetry technique for estimating liquid water content. The literature outlines two calorimetric approaches used for the estimation of θ_w. Prior to our paper, a rigorous mathematical analysis by Colbeck (1978) argued against the use of melting calorimetry, a stance that was echoed in subsequent works and thus became widely accepted. We have clarified and expanded upon Colbeck's findings, demonstrating unequivocally that the two techniques are comparable in terms of accuracy. While freezing calorimetry still holds an edge, particularly considering instrumental uncertainty alone, our analysis serves to dismiss the melting-calorimetry accusations. The additional sources of uncertainties that stem from the challenging operational conditions of using a freezing calorimeter still require further investigation but might result in large uncertainty, especially when used by inexperienced operators (Fisk, 1986). However, the melting-calorimetry reputation for inaccuracy is partially justified by limitations in its mathematical modeling and uncertainty analysis. Building new concepts upon these unconsolidated works leads to the propagation of errors that may hinder the advancement of liquid water content measurement techniques.

We present formulations, i.e., Eqs. (3) and (6), for melting and freezing calorimeters, respectively, expressed in volume percent and incorporating the calorimetric constant. While the freezing formulation was established upon its introduction into the literature (Jones et al., 1983), the melting formulation lacked compensation for heat exchange within the calorimeter, a discrepancy we noted has existed since Yosida's initial works and was reiterated by Kawashima et al. (1998). This was pointed out from the first applications of the melting calorimeter (Halliday, 1950). The concept of the calorimetric constant was initially introduced for freezing calorimeters (Jones et al., 1983; Boyne and Fisk, 1987; Austin, 1990) but had not been extended to melting calorimetry until a recent study by Fasani et al. (2023). We clarify the most effective method for estimating E, considering various approaches documented in the literature and evaluating their impact on uncertainty, showing that non-destructive methods based on calorimetry itself are largely uncertain and should be avoided.

We generally doubt the effectiveness of preparing artificial samples as reference samples with a given θ_w as done in Fasani et al. (2023) and Kawashima et al. (1998) because the assumption that the added water exchanges heat with the whole ice matrix cannot always be satisfied. Therefore, the selected approach for estimating E in Fasani et al. (2023), which is characterized by significant uncertainty propagation, coupled with strong assumptions and non-stringent experimental protocols such as elevated values of R (as depicted in Fig. 3, the impact of high R values on measurement uncertainty is large), yields results impacted by noise. This renders the interpretation of the presented results challenging and subject to dispute. The impression is that the manner in which water is added to the snow samples introduces a systematic bias, varying with the amount added, to which a large uncertainty is added (see Fig. 5 of the original paper).

We introduce a formulation for estimating volume measurement uncertainty according to GUM (IEC et al., 1993), emphasizing its importance for facilitating comparisons between measurements. While the error propagation for the freezing calorimetry proposed by Jones et al. (1983) aligns with our approach (and leads to similar results when expressed as the sum of absolute uncertainty per mass), the Kawashima et al. (1998) formulation for melting calorimeters relies on erroneous approximations and misleading presentation of the results. In this paper, we also attempt to quantify random uncertainty related to environmental and operator variability. While the limitations of the available instrument prevented a fully comprehensive uncertainty analysis, we believe that the investigation of the impact of more complex sources of uncertainty in θ_w measurements remains an intriguing topic for future research and development.

Leveraging our proposed formulation, we have developed and validated a field protocol for measuring liquid water content using the melting calorimeter. While some steps of the field protocol may resemble those in Kawashima et al. (1998), there are some difference in the theoretical foundation. Our analysis provides guidance on various aspects; however the sample handling during extraction from the snowpack remains a key source of uncertainty. Mechanical shocks, contact with sampler material, large temperature differences from the snow and air, and solar radiation during extraction can all generate liquid water. Additionally, the impact of potentially prolonged pit exposure, a necessity for obtaining spatially detailed liquid water content profiles for deep snowpack, on water transport within the snowpack remains an open question. While our primary focus here is on the melting-calorimeter accuracy for field-based θ_w measurements and not on its application in water transport studies, the results suggest that following the protocol strictly, including measures like shading the pit from solar radiation, can mitigate this issue and provide important information about water transport inside the snowpack. Further investigation is required in any case to properly assess the influence of pit exposure.

In a field comparison at the Italian and Swiss sites, we measured liquid water content using both the melting calorimeter and the Denoth meter. By comparing our findings with results from Boyne and Fisk (1987) (who compared the freezing calorimeter, alcohol calorimeter, dilution technique, and Denoth meter), we established that our novel formulation for the melting calorimeter yields results indirectly comparable to the established freezing and dilution methods. This finding validates our approach and strengthens the case for the melting calorimeter as a reliable measurement tool. This challenges the general notion propagated by Linlor et al. (1975) of the melting-calorimeter overestimation compared to freezing methods, which at this point should be possibly attributed to the missed calorimetric constant. This insight could be leveraged in Webb et al. (2021) and related datasets, which at the moment show a bias similar to our Weissfluhjoch (WFJ) measurements when the calorimetry compensation is not applied.

Finally, the obtained liquid water profiles of Figs. 9 and 10 corroborate the observations in Perla (1991) that show the Denoth meter provides accurate measurements for low liquid water content θ_w – typically below 5 %–8 % with the uncertainty between 0.5 %–1 % – but underestimates it in very wet or soaked snow. The melting calorimeter, when employed with the proposed formulation, has the potential to expand the already substantial dataset established by Perla (1991). This expanded dataset could be instrumental in refining the calibration of the relationship between the wet-snow dielectric constant and θ_w, potentially leading to a clearer understanding of the physical factors that limit the unique determination of water content through dielectric measurements (Picard et al., 2022; Colbeck, 1980; Camp, 1992).

7 Conclusions

The potential of melting calorimetry for measuring snow liquid water content has long been overshadowed by misconceptions about its accuracy.

This paper has challenged this perception by comparing the melting- and freezing-calorimetry techniques, focusing on their applicability for measurements in the field. While freezing calorimetry still holds an edge, our findings indicate that the measurements obtained using the melting calorimeter are still accurate enough for a meaningful analysis of liquid water content in the snowpack, offering at the same time notable practical advantages. To support our claims, we thoroughly examined and propagated uncertainties, encompassing not only instrumental factors but also variations arising from the operational procedures and environmental conditions. As a result, we devised a field protocol that effectively minimizes these uncertainties. The protocol includes specific instructions on the amount of hot water to be used, its temperature, the size of the calorimeter, the masses involved, and other crucial details for controlling the uncertainty during the experiment replication. This protocol was applied at two different test sites in Italy and Switzerland by two different research groups with different melting calorimeters. The results, compared to independent measurements of the dielectric constant of the snow, showed how the application of the proposed protocol to the melting-calorimetry measurements is able to properly track the wet front penetration inside the snowpack in an accurate way.

In conclusion, this research promotes the wider adoption of melting calorimetry as a reliable field tool for quantifying liquid water content in snowpacks. This capability offers significant advantages for calibrating or validating new and potentially non-destructive methods based on electromagnetic interactions with wet snow.

Appendix A

In order to derive the calorimetric constant E, if information regarding the material and mass of the calorimeter cannot be obtained, the heat-balance principle can be applied. In the literature, the calorimeter constant was determined using a basic heat-balance principle (Jones et al., 1983; Austin, 1990). When warm fluid is mixed with cold fluid in the calorimeter bottle, the heat lost by the warm fluid must be equal to the heat gained by the cold fluid and the bottle itself.

For the case of water, the heat-balance equation is given by

$$\begin{array}{}\text{(A1)}& \underset{M_{\mathrm{w}}C(T_{\mathrm{f}}-T_{\mathrm{w}})}{\underbrace{Q_{\text{hot water}}}}+\underset{M_{\text{cw}}C(T_{\mathrm{f}}-T_{\text{cw}})}{\underbrace{Q_{\text{cold water}}}}+\underset{M_{\mathrm{cw}}{C}_{\text{cal}}(T_{\mathrm{f}}-T_{\mathrm{cw}})}{\underbrace{Q_{\text{calorimeter}}}}=\mathrm{0}.\end{array}$$

Therefore we can obtain the calorimetric constant expressed in equivalent water mass as follows:

$$\begin{array}{}\text{(A2)}& E={\displaystyle \frac{M_{\mathrm{w}}(T_{\mathrm{f}}-T_{\mathrm{w}})}{(T_{\mathrm{cw}}-T_{\mathrm{f}})}}-M_{\mathrm{cw}}.\end{array}$$

In this equation, M_w and T_w represent the mass and temperature, respectively, of the hot water, while M_cw and T_cw represent the mass and temperature, respectively, of the cold water. By analyzing the uncertainty propagation of the measurements in E with the same approach as that presented in Sect. 3.1, we can retrieve the uncertainty in the estimation of E, σ_E:

$$\begin{array}{}\text{(A3)}& {\mathit{\sigma }}_E=\sqrt{\begin{array}{l}{\left(\frac{\partial E}{\partial M_{\mathrm{w}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{M_{\mathrm{w}}}^{\mathrm{2}}+{\left(\frac{\partial E}{\partial M_{\mathrm{cw}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{M_{\mathrm{cw}}}^{\mathrm{2}}+{\left(\frac{\partial E}{\partial T_{\mathrm{w}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{T_{\mathrm{w}}}^{\mathrm{2}}\\ +{\left(\frac{\partial E}{\partial T_{\mathrm{f}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{T_{\mathrm{f}}}^{\mathrm{2}}+{\left(\frac{\partial E}{\partial T_{\mathrm{cw}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{T_{\mathrm{cw}}}^{\mathrm{2}}\end{array}}.\end{array}$$

The partial derivatives in Eq. (A3) are calculated as follows:

$$\begin{array}{}\text{(A4)}& {\displaystyle \frac{\partial E}{\partial M_{\mathrm{w}}}}={\displaystyle \frac{T_{\mathrm{f}}-T_{\mathrm{w}}}{T_{\mathrm{cw}}-T_{\mathrm{f}}}},\text{(A5)}& {\displaystyle \frac{\partial E}{\partial M_{\mathrm{cw}}}}=-\mathrm{1},\text{(A6)}& {\displaystyle \frac{\partial E}{\partial T_{\mathrm{w}}}}=-{\displaystyle \frac{M_{\mathrm{w}}}{T_{\mathrm{cw}}-T_{\mathrm{f}}}},\text{(A7)}& {\displaystyle \frac{\partial E}{\partial T_{\mathrm{f}}}}={\displaystyle \frac{M_{\mathrm{w}}(T_{\mathrm{cw}}-T_{\mathrm{f}})+M_{\mathrm{w}}(T_{\mathrm{f}}-T_{\mathrm{w}})}{(T_{\mathrm{cw}}-T_{\mathrm{f}}{)}^{\mathrm{2}}}},\text{(A8)}& {\displaystyle \frac{\partial E}{\partial T_{\mathrm{cw}}}}=-M_{\mathrm{w}}{\displaystyle \frac{T_{\mathrm{f}}-T_{\mathrm{w}}}{(T_{\mathrm{cw}}-T_{\mathrm{f}}{)}^{\mathrm{2}}}}.\end{array}$$

It becomes evident that σ_E is strongly related to the difference T_f−T_cw, which should be maximized. To achieve this, we aim to maximize the difference between T_cw and T_h while minimizing M_cw. However, in a hypothetical scenario with M_cw=5 g, M_w=495 g, T_cw=273 K, T_w=373 K, and E=6.58 g, the uncertainty σ_E associated with E is equal to 2.6 g, which is approximately $\frac{\mathrm{1}}{\mathrm{3}}$ of the value of E. Realistically, this experiment is challenging to conduct, primarily because it would be extremely difficult to maintain thermal equilibrium for 5 g of water with the internal wall. This was also recognized in Austin (1990).

An alternative way to estimate the calorimetric constant E is discussed in Fasani et al. (2023). Here the parameter E is retrieved using the same energy balance as in Eq. (1), and in detail inverting Eq. (3), expliciting E as a function of ${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$. This approach requires the employment of wet-snow samples with known liquid water content, with all the relative associated difficulties in controlling the process. Here we present the analysis of the uncertainty σ_E associated with the parameter E following the same approach as in Sect. 3.1. In detail, by inverting Eq. (3), we can obtain E as

$$\begin{array}{}\text{(A9)}& E={\displaystyle \frac{(T_{\mathrm{f}}-T_{\mathrm{s}})M_{\mathrm{s}}+\frac{L}{C}(M_{\mathrm{s}}-{\mathit{\theta }}_{\mathrm{w}}^M{V}_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}})}{T_{\mathrm{w}}-T_{\mathrm{f}}}}-M_{\mathrm{w}}.\end{array}$$

Analyzing how E is affected by the uncertainty propagation of the measurements with the same approach as presented in Sect. 3.1, we can retrieve the uncertainty in the estimation of E, σ_E:

$$\begin{array}{}\text{(A10)}& {\mathit{\sigma }}_E=\sqrt{\begin{array}{l}{\left(\frac{\partial E}{\partial T_{\mathrm{f}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{T_{\mathrm{f}}}^{\mathrm{2}}+{\left(\frac{\partial E}{\partial T_{\mathrm{w}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{T_{\mathrm{w}}}^{\mathrm{2}}+{\left(\frac{\partial E}{\partial M_{\mathrm{s}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{M_{\mathrm{s}}}^{\mathrm{2}}\\ +{\left(\frac{\partial E}{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{{\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}^{\mathrm{2}}+{\left(\frac{\partial E}{\partial V_{\mathrm{s}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{V_{\mathrm{s}}}^{\mathrm{2}}+{\left(\frac{\partial E}{\partial M_{\mathrm{w}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{M_{\mathrm{w}}}^{\mathrm{2}}\end{array}.}\end{array}$$

The partial derivatives in Eq. (A10) are calculated as follows:

$$\begin{array}{}\text{(A11)}& {\displaystyle \frac{\partial E}{\partial T_{\mathrm{f}}}}={\displaystyle \frac{M_{\mathrm{s}}(T_{\mathrm{w}}-T_{\mathrm{s}})+\frac{L}{C}(M_{\mathrm{s}}-{\mathit{\theta }}_{\mathrm{w}}^M{V}_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}})}{(T_{\mathrm{w}}-T_{\mathrm{f}}{)}^{\mathrm{2}}}},\text{(A12)}& {\displaystyle \frac{\partial E}{\partial T_{\mathrm{w}}}}=-{\displaystyle \frac{M_{\mathrm{s}}(T_{\mathrm{f}}-T_{\mathrm{s}})+\frac{L}{C}(M_{\mathrm{s}}-{\mathit{\theta }}_{\mathrm{w}}^M{V}_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}})}{(T_{\mathrm{w}}-T_{\mathrm{f}}{)}^{\mathrm{2}}}},\text{(A13)}& {\displaystyle \frac{\partial E}{\partial M_{\mathrm{s}}}}={\displaystyle \frac{T_{\mathrm{f}}-T_{\mathrm{s}}}{T_{\mathrm{w}}-T_{\mathrm{f}}}}+{\displaystyle \frac{L}{C(T_{\mathrm{w}}-T_{\mathrm{f}})}},\text{(A14)}& {\displaystyle \frac{\partial E}{\partial {\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}}}=-{\displaystyle \frac{V_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{w}}L}{C(T_{\mathrm{w}}-T_{\mathrm{f}})}},\text{(A15)}& {\displaystyle \frac{\partial E}{\partial V_{\mathrm{s}}}}=-{\displaystyle \frac{{\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}{\mathit{\rho }}_{\mathrm{w}}L}{C(T_{\mathrm{w}}-T_{\mathrm{f}})}},\text{(A16)}& {\displaystyle \frac{\partial E}{\partial M_{\mathrm{w}}}}=-\mathrm{1}.\end{array}$$

It is evident that σ_E is strongly related to the difference T_f−T_w, which should be maximized. However, in a hypothetical scenario with M_w=167 g, M_s=83 g, and T_w=313 K, the uncertainty σ_E associated with E is equal to 4.87 g, which is more than $\frac{\mathrm{2}}{\mathrm{3}}$ of the value of E, here set to 6.58 g.

A possible way to mitigate the large error associated with the estimation of E is to use hot water and ice instead of water at different temperatures. However, it is again important to use the propagation of uncertainty to find how uncertain such a kind of measurement of E is. For the ice–water case, the heat-balance equation to retrieve E becomes

$$\begin{array}{}\text{(A17)}& \begin{array}{rl}\underset{M_{\mathrm{w}}C(T_{\mathrm{f}}-T_{\mathrm{w}})}{\underbrace{Q_{\text{hot water}}}}& +\underset{M_{\text{cal}}{C}_{\text{cal}}(T_{\mathrm{f}}-T_{\mathrm{w}})}{\underbrace{Q_{\text{calorimeter}}}}+\underset{M_{\mathrm{i}}{C}_{\mathrm{i}}(T_{\mathrm{f}}-T_{\mathrm{i}})}{\underbrace{Q_{\text{warming ice}}}}\\ & +\underset{L{M}_{\mathrm{i}}}{\underbrace{Q_{\text{melting ice}}}}+\underset{M_{\mathrm{i}}C(T_{\mathrm{f}}-T_{\mathrm{mi}})}{\underbrace{Q_{\text{melted ice}}}}=\mathrm{0}.\end{array}\end{array}$$

From where we can derive E as follows:

$$\begin{array}{}\text{(A18)}& E={\displaystyle \frac{M_{\mathrm{i}}(C_{\mathrm{i}}{T}_{\mathrm{i}}-L-T_{\mathrm{f}})}{C(T_{\mathrm{f}}-T_{\mathrm{w}})}}-M_{\mathrm{w}}.\end{array}$$

Here, M_i and T_i represent the mass and temperature of ice, while M_w and T_w represent the mass and temperature of hot water. T_mi is the temperature of the water from the melted ice cube, and it is equal to 273.15 K. Also for this case, we can propagate the measurement uncertainty and find the associated σ_E:

$$\begin{array}{}\text{(A19)}& {\mathit{\sigma }}_E=\sqrt{\begin{array}{l}{\left(\frac{\partial E}{\partial M_{\mathrm{i}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{M_{\mathrm{i}}}^{\mathrm{2}}+{\left(\frac{\partial E}{\partial M_{\mathrm{h}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{M_{\mathrm{h}}}^{\mathrm{2}}+{\left(\frac{\partial E}{\partial T_{\mathrm{h}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{T_{\mathrm{h}}}^{\mathrm{2}}\\ +{\left(\frac{\partial E}{\partial T_{\mathrm{f}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{T_{\mathrm{f}}}^{\mathrm{2}}+{\left(\frac{\partial E}{\partial T_{\mathrm{i}}}\right)}^{\mathrm{2}}{\mathit{\sigma }}_{T_{\mathrm{i}}}^{\mathrm{2}}\end{array}}.\end{array}$$

The partial derivatives in Eq. (A19) are calculated as follows:

$$\begin{array}{}\text{(A20)}& {\displaystyle \frac{\partial E}{\partial M_{\mathrm{i}}}}={\displaystyle \frac{C_{\mathrm{i}}{T}_{\mathrm{i}}-L-C{T}_{\mathrm{f}}}{C(T_{\mathrm{f}}-T_{\mathrm{h}})}},\text{(A21)}& {\displaystyle \frac{\partial E}{\partial M_{\mathrm{h}}}}=-\mathrm{1},\text{(A22)}& {\displaystyle \frac{\partial E}{\partial T_{\mathrm{h}}}}={\displaystyle \frac{M_{\mathrm{i}}(C_{\mathrm{i}}{T}_{\mathrm{i}}-L-C{T}_{\mathrm{f}})}{C(T_{\mathrm{f}}-T_{\mathrm{w}}{)}^{\mathrm{2}}}},\text{(A23)}& {\displaystyle \frac{\partial E}{\partial T_{\mathrm{f}}}}={\displaystyle \frac{-C{M}_{\mathrm{i}}(T_{\mathrm{f}}-T_{\mathrm{h}})-M_{\mathrm{i}}(C_{\mathrm{i}}{T}_{\mathrm{i}}-L-C{T}_{\mathrm{f}})}{C(T_{\mathrm{f}}-T_{\mathrm{w}}{)}^{\mathrm{2}}}},\text{(A24)}& {\displaystyle \frac{\partial E}{\partial T_{\mathrm{i}}}}={\displaystyle \frac{M_{\mathrm{i}}{C}_{\mathrm{i}}}{C(T_{\mathrm{f}}-T_{\mathrm{w}})}}.\end{array}$$

Analyzing the error for this case, we observe that it is strongly influenced by the difference between T_f and T_w. In a hypothetical scenario with M_h=300 g, M_i=200 g, T_h=373 K, T_i=244.5 K, and E=6.58 g, the uncertainty σ_E associated with E is equal to 1.6 g, which is approximately $\frac{\mathrm{1}}{\mathrm{4}}$ of the value of E. This is still a high uncertainty, but unlike the water–water case, this experiment does not suffer from the same limitations. Hence, if it is impossible to retrieve the exact mass and specific heat of the calorimeter, the best way to estimate E would be to use hot water and ice. It is important to note that for both cases, using ice and water at extreme temperatures would lead to noticeable heat dispersion in a short amount of time, making it challenging to obtain exact temperature measurements.

Because of these reasons, we destructively analyzed our calorimeters to estimate E using Eq. (2). Fortunately this process has to be done once, and other users can use the E provided in the paper, i.e., E=6.58 g, given that they use the same calorimeter.

Appendix B

In this appendix, we will show all the formulations partly presented in Colbeck (1978) that allow us to prove that the relative uncertainty produced by the melting calorimeter in the estimation of the ice volume is 1 order of magnitude lower than the relative uncertainty produced by the freezing calorimeter in the water volume. With this mathematical step, we unlock the melting calorimeter from being “inherently inaccurate”.

We compute the relative uncertainty produced by the melting calorimeter in the estimation of the ice volume starting from Eq. (3) in the main paper, written in terms of V_i:

$$\begin{array}{}\text{(B1)}& V_{\mathrm{i}}={\displaystyle \frac{C}{{\mathit{\rho }}_{\mathrm{i}}L}}\left[M_{\mathrm{w}}\right(T_{\mathrm{w}}-T_{\mathrm{f}})-M_{\mathrm{s}}(T_{\mathrm{f}}-T_{\mathrm{s}}\left)\right].\end{array}$$

Note that we do not account for E being consistent with Colbeck's formulation. Hence, we compute the partial derivatives for each of the measured variables by assuming $k=\frac{C}{L}$,

$$\begin{array}{}\text{(B2)}& \left\{\begin{array}{rl}{\displaystyle }& {\displaystyle \frac{\partial V_{\mathrm{i}}}{\partial T_{\mathrm{w}}}}={\displaystyle \frac{k}{{\mathit{\rho }}_{\mathrm{i}}}}{M}_{\mathrm{w}}\\ {\displaystyle }& {\displaystyle \frac{\partial V_{\mathrm{i}}}{\partial T_{\mathrm{f}}}}=-{\displaystyle \frac{k}{{\mathit{\rho }}_{\mathrm{i}}}}(M_{\mathrm{w}}+M_{\mathrm{s}})\\ {\displaystyle }& {\displaystyle \frac{\partial V_{\mathrm{i}}}{\partial M_{\mathrm{w}}}}={\displaystyle \frac{k}{{\mathit{\rho }}_{\mathrm{i}}}}(T_{\mathrm{w}}-T_{\mathrm{f}})\\ {\displaystyle }& {\displaystyle \frac{\partial V_{\mathrm{i}}}{\partial M_{\mathrm{s}}}}=-{\displaystyle \frac{k}{{\mathit{\rho }}_{\mathrm{i}}}}(T_{\mathrm{f}}-T_{\mathrm{s}}),\end{array}\right.\end{array}$$

and we calculate the relative uncertainty ${\mathrm{\Sigma }}_{V_{\mathrm{i}}}$ as the sum of each term:

$$\begin{array}{}\text{(B3)}& \begin{array}{rl}{\mathrm{\Sigma }}_{V_{\mathrm{i}}}& =\left|{\displaystyle \frac{\partial V_{\mathrm{i}}}{\partial T_{\mathrm{w}}}}\right|\left|{\displaystyle \frac{T_{\mathrm{w}}}{V_{\mathrm{i}}}}\right|\left|{\displaystyle \frac{\mathrm{d}T}{T_{\mathrm{w}}}}\right|+\left|{\displaystyle \frac{\partial V_{\mathrm{i}}}{\partial T_{\mathrm{f}}}}\right|\left|{\displaystyle \frac{T_{\mathrm{f}}}{V_{\mathrm{i}}}}\right|\left|{\displaystyle \frac{\mathrm{d}T}{T_{\mathrm{f}}}}\right|\\ & +\left|{\displaystyle \frac{\partial V_{\mathrm{i}}}{\partial M_{\mathrm{w}}}}\right|\left|{\displaystyle \frac{M_{\mathrm{w}}}{V_{\mathrm{i}}}}\right|\left|{\displaystyle \frac{\mathrm{d}T}{M_{\mathrm{w}}}}\right|+\left|{\displaystyle \frac{\partial V_{\mathrm{i}}}{\partial M_{\mathrm{s}}}}\right|\left|{\displaystyle \frac{M_{\mathrm{s}}}{V_{\mathrm{i}}}}\right|\left|{\displaystyle \frac{\mathrm{d}T}{M_{\mathrm{s}}}}\right|.\end{array}\end{array}$$

By simplifying, we obtain

$$\begin{array}{}\text{(B4)}& \begin{array}{rl}{\mathrm{\Sigma }}_{V_{\mathrm{i}}}& =\left|{\displaystyle \frac{\partial V_{\mathrm{i}}}{\partial T_{\mathrm{w}}}}\right|\left|{\displaystyle \frac{\mathrm{d}T}{V_{\mathrm{i}}}}\right|+\left|{\displaystyle \frac{\partial V_{\mathrm{i}}}{\partial T_{\mathrm{f}}}}\right|\left|{\displaystyle \frac{\mathrm{d}T}{V_{\mathrm{i}}}}\right|+\left|{\displaystyle \frac{\partial V_{\mathrm{i}}}{\partial M_{\mathrm{w}}}}\right|\left|{\displaystyle \frac{\mathrm{d}M}{V_{\mathrm{i}}}}\right|\\ & +\left|{\displaystyle \frac{\partial V_{\mathrm{i}}}{\partial M_{\mathrm{s}}}}\right|\left|{\displaystyle \frac{\mathrm{d}M}{V_{\mathrm{i}}}}\right|.\end{array}\end{array}$$

By considering the values reported in Table B1, we obtain ${\mathrm{\Sigma }}_{V_{\mathrm{i}}}=\mathrm{0.007426}$ m³. The values in the table are obtained by considering a snow sample with $M_{\mathrm{w}}=\mathrm{2}\times M_{\mathrm{s}}$, $V_{\mathrm{s}}={\mathrm{10}}^{-\mathrm{3}}$ m³, $V_{\mathrm{i}}=\mathrm{500}\times {\mathrm{10}}^{-\mathrm{6}}$ m³, $V_{\mathrm{i}}=\mathrm{75}\times {\mathrm{10}}^{-\mathrm{6}}$ m³, and $V_a=\mathrm{425}\times {\mathrm{10}}^{-\mathrm{6}}$ m³.

Table B1 Variable values used for the computation of the relative uncertainty produced by the melting calorimeter in the estimation of the ice volume.

Similarly, for the freezing calorimeter we can compute the relative uncertainty in the estimation of the water volume starting from the equation of Jones et al. (1983), Eq. (6) in the main paper, written in terms of V_w:

$$\begin{array}{}\text{(B5)}& V_{\mathrm{w}}={\displaystyle \frac{M_{\mathrm{o}}{C}_{\mathrm{o}}(T_{\mathrm{fo}}-T_{\mathrm{o}})+M_{\mathrm{s}}{C}_{\mathrm{s}}(T_{\mathrm{fo}}-T_{\mathrm{s}})}{{\mathit{\rho }}_{\mathrm{w}}L}}.\end{array}$$

Hence, we compute the partial derivatives for each of the measured variables by assuming $k=\frac{C}{L}$,

$$\begin{array}{}\text{(B6)}& \left\{\begin{array}{rl}{\displaystyle }& {\displaystyle \frac{\partial V_{\mathrm{w}}}{\partial T_{\mathrm{o}}}}=-{\displaystyle \frac{M_{\mathrm{o}}{C}_{\mathrm{o}}}{{\mathit{\rho }}_{\mathrm{w}}L}}\\ {\displaystyle }& {\displaystyle \frac{\partial V_{\mathrm{w}}}{\partial T_{fo}}}={\displaystyle \frac{M_{\mathrm{o}}{C}_{\mathrm{o}}+M_{\mathrm{s}}{C}_{\mathrm{s}}}{{\mathit{\rho }}_{\mathrm{w}}L}}\\ {\displaystyle }& {\displaystyle \frac{\partial V_{\mathrm{w}}}{\partial M_{\mathrm{o}}}}={\displaystyle \frac{C_{\mathrm{o}}(T_{\mathrm{fo}}-T_{\mathrm{o}})}{{\mathit{\rho }}_{\mathrm{w}}L}}\\ {\displaystyle }& {\displaystyle \frac{\partial V_{\mathrm{w}}}{\partial M_{\mathrm{s}}}}={\displaystyle \frac{C_{\mathrm{s}}(T_{\mathrm{fo}}-T_{\mathrm{s}})}{{\mathit{\rho }}_{\mathrm{w}}L}},\end{array}\right.\end{array}$$

and we calculate the relative uncertainty ${\mathrm{\Sigma }}_{V_{\mathrm{w}}}$ as the sum of each term:

$$\begin{array}{}\text{(B7)}& \begin{array}{rl}{\mathrm{\Sigma }}_{V_{\mathrm{w}}}& =\left|{\displaystyle \frac{\partial V_{\mathrm{w}}}{\partial T_{\mathrm{o}}}}\right|\left|{\displaystyle \frac{T_{\mathrm{o}}}{V_{\mathrm{w}}}}\right|\left|{\displaystyle \frac{\mathrm{d}T}{T_{\mathrm{o}}}}\right|+\left|{\displaystyle \frac{\partial V_{\mathrm{w}}}{\partial T_{\mathrm{fo}}}}\right|\left|{\displaystyle \frac{T_{\mathrm{fo}}}{V_{\mathrm{w}}}}\right|\left|{\displaystyle \frac{\mathrm{d}T}{T_{\mathrm{fo}}}}\right|\\ & +\left|{\displaystyle \frac{\partial V_{\mathrm{w}}}{\partial M_{\mathrm{o}}}}\right|\left|{\displaystyle \frac{M_{\mathrm{o}}}{V_{\mathrm{w}}}}\right|\left|{\displaystyle \frac{\mathrm{d}M}{M_{\mathrm{o}}}}\right|+\left|{\displaystyle \frac{\partial V_{\mathrm{w}}}{\partial M_{\mathrm{s}}}}\right|\left|{\displaystyle \frac{M_{\mathrm{s}}}{V_{\mathrm{w}}}}\right|\left|{\displaystyle \frac{\mathrm{d}M}{M_{\mathrm{s}}}}\right|.\end{array}\end{array}$$

By simplifying, we obtain

$$\begin{array}{}\text{(B8)}& \begin{array}{rl}{\mathrm{\Sigma }}_{V_{\mathrm{w}}}& =\left|{\displaystyle \frac{\partial V_{\mathrm{w}}}{\partial T_{\mathrm{o}}}}\right|\left|{\displaystyle \frac{\mathrm{d}T}{V_{\mathrm{w}}}}\right|+\left|{\displaystyle \frac{\partial V_{\mathrm{w}}}{\partial T_{\mathrm{fo}}}}\right|\left|{\displaystyle \frac{\mathrm{d}T}{V_{\mathrm{w}}}}\right|+\left|{\displaystyle \frac{\partial V_{\mathrm{w}}}{\partial M_{\mathrm{o}}}}\right|\left|{\displaystyle \frac{\mathrm{d}M}{V_{\mathrm{w}}}}\right|\\ & +\left|{\displaystyle \frac{\partial V_{\mathrm{w}}}{\partial M_{\mathrm{s}}}}\right|\left|{\displaystyle \frac{\mathrm{d}M}{V_{\mathrm{w}}}}\right|.\end{array}\end{array}$$

dM and dT are the instrumental uncertainties and are fixed to 10⁻⁴ g and 0.1 K, respectively. By considering the values reported in Table B2, we obtain ${\mathrm{\Sigma }}_{V_{\mathrm{w}}}=\mathrm{0.014809}$ m³, which results in twice the error ${\mathrm{\Sigma }}_{V_{\mathrm{i}}}$ calculated for the melting calorimeter. The values in the table are obtained by considering a snow sample with $M_{\mathrm{o}}=\mathrm{1.3}\cdot M_{\mathrm{s}}$, $V_{\mathrm{s}}={\mathrm{10}}^{-\mathrm{3}}$ m³, $V_{\mathrm{i}}=\mathrm{500}\times {\mathrm{10}}^{-\mathrm{6}}$ m³, $V_{\mathrm{i}}=\mathrm{75}\times {\mathrm{10}}^{-\mathrm{6}}$ m³, and $V_{\mathrm{a}}=\mathrm{425}\times {\mathrm{10}}^{-\mathrm{6}}$ m³.

Table B2 Variable values used for the computation of the relative uncertainty produced by the freezing calorimeter in the estimation of the water volume.

Appendix C: List of symbols

Symbol	Definition
θw	Volume fraction of liquid water for a given test sample of snow
${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{M}}$	θw obtained with the melting calorimeter
${\mathit{\theta }}_{\mathrm{w}}^{\mathrm{F}}$	θw obtained with the freezing calorimeter
Vs	Volume of the snow sample
Ms	Mass of the snow sample
Mi	Mass of the ice in the snow sample
MLWC	Mass of the liquid water inside the sample, which can be expressed as $M_{\text{LWC}}={\mathit{\theta }}_{\mathrm{w}}{M}_{\mathrm{s}}\frac{{\mathit{\rho }}_{\mathrm{w}}}{{\mathit{\rho }}_{\mathrm{s}}}$
Mw,Mo	Mass of the melting and of the freezing agent, respectively
Mcal	Calorimeter internal vessel mass
R	Ratio of Mw to Ms
E, EF	Calorimetric constant expressed in equivalent water mass for the melting and freezing calorimeter, respectively
Tw,To	Hot water and freezing agent initial temperature
Tf	Final temperature of the system at the end of the experiment
Tmi	Temperature of the ice cube after it is melted, equal to 273.15 K
Tcv	Temperature of the cold water employed for indirect calorimetric constant estimation
Ts	Temperature of the snow sample, which is 273.15 K if no ionic impurities are involved
C	Water specific heat, i.e., 4.2×103 J kg−1 K−1
Ci	Ice heat capacity, i.e., 2.09×103 J kg−1 K−1
Co	Freezing agent specific heat, which, in the case of using silicone oil, is 1.83×103 J kg−1 K−1 at −10 °C
Ccal	Calorimeter internal-wall specific heat
L	Latent heat of ice fusion, i.e., 3.34×105 J kg−1
ρw	Water density, i.e., 1000 kg m−3
${\mathit{\sigma }}_{{\mathit{\theta }}_{\mathrm{w}}}$	Uncertainty associated with the liquid water content measurement
${\mathit{\sigma }}_{M_{\mathrm{w}}},{\mathit{\sigma }}_{M_{\mathrm{w}}}$	Uncertainty associated with the mass of the melting and freezing agent, respectively
${\mathit{\sigma }}_{M_{\mathrm{s}}}$	Uncertainty associated with the mass of the snow sample
${\mathit{\sigma }}_{T_{\mathrm{w}}},{\mathit{\sigma }}_{T_{\mathrm{o}}}$	Uncertainty associated with the measurement of the melting and freezing agent, respectively
${\mathit{\sigma }}_{T_{\mathrm{f}}}$	Uncertainty associated with the final temperature of the system
${\mathit{\sigma }}_{V_{\mathrm{s}}}$	Uncertainty associated with the volume of the snow sample
σE	Uncertainty associated with the calorimetric constant