Probabilistic projections of the Amery Ice Shelf catchment, Antarctica, under conditions of high ice-shelf basal melt

Antarctica's Lambert Glacier drains about one-sixth of the ice from the East Antarctic Ice Sheet and is considered stable due to the strong buttressing provided by the Amery Ice Shelf. While previous projections of the sea-level contribution from this sector of the ice sheet have predicted significant mass loss only with near-complete removal of the ice shelf, the ocean warming necessary for this was deemed unlikely. Recent climate projections through 2300 indicate that sufficient ocean warming is a distinct possibility after 2100. This work explores the impact of parametric uncertainty on projections of the response of the Lambert–Amery system (hereafter “the Amery sector”) to abrupt ocean warming through Bayesian calibration of a perturbed-parameter ice-sheet model ensemble. We address the computational cost of uncertainty quantification for ice-sheet model projections via statistical emulation, which employs surrogate models for fast and inexpensive parameter space exploration while retaining critical features of the high-fidelity simulations. To this end, we build Gaussian process (GP) emulators from simulations of the Amery sector at a medium resolution (4–20 km mesh) using the Model for Prediction Across Scales (MPAS)-Albany Land Ice (MALI) model. We consider six input parameters that control basal friction, ice stiffness, calving, and ice-shelf basal melting. From these, we generate 200 perturbed input parameter initializations using space filling Sobol sampling. For our end-to-end probabilistic modeling workflow, we first train emulators on the simulation ensemble and then calibrate the input parameters using observations of the mass balance, grounding line movement, and calving front movement with priors assigned via expert knowledge. Next, we use MALI to project a subset of simulations to 2300 using ocean and atmosphere forcings from a climate model for both low- and high-greenhouse-gas-emission scenarios. From these simulation outputs, we build multivariate emulators by combining GP regression with principal component dimension reduction to emulate multivariate sea-level contribution time series data from the MALI simulations. We then use these emulators to propagate uncertainty from model input parameters to predictions of glacier mass loss through 2300, demonstrating that the calibrated posterior distributions have both greater mass loss and reduced variance compared to the uncalibrated prior distributions. Parametric uncertainty is large enough through about 2130 that the two projections under different emission scenarios are indistinguishable from one another. However, after rapid ocean warming in the first half of the 22nd century, the projections become statistically distinct within decades. Overall, this study demonstrates an efficient Bayesian calibration and uncertainty propagation workflow for ice-sheet model projections and identifies the potential for large sea-level rise contributions from the Amery sector of the Antarctic Ice Sheet after 2100 under high-greenhouse-gas-emission scenarios.

1 Introduction

With an area of slightly more than 60 000 km² (Andreasen et al., 2023), the Amery Ice Shelf (AmIS) is the third-largest ice shelf in Antarctica and drains approximately 16 % of the ice from East Antarctica (Fricker et al., 2002) (Fig. 1). The AmIS is considered particularly stable due to its location in a narrow embayment with many pinning points (Pittard et al., 2017); the convergent flow of the Lambert, Fisher, and Mellor glaciers entering the ice shelf (Gong et al., 2014); and a prograde bed slope beneath the grounded ice feeding the ice shelf (Morlighem et al., 2020). The most recent in-depth model projection study of the Amery sector (Lambert–Amery system) of the Antarctic Ice Sheet predicts an insignificant sea-level contribution from this sector for the next 500 years, barring extreme ocean temperature increases, which at that time were considered unlikely (Pittard et al., 2017).

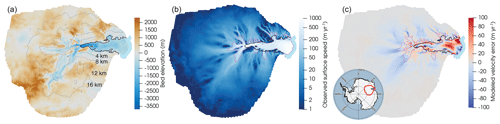
Figure 1 Model domain encompassing the Amery Ice Shelf and Lambert Glacier catchment. The red line in the panel (c) inset map shows the catchment location within the broader Antarctic Ice Sheet. (a) Bedrock elevation (colors), with gray lines contouring the MALI mesh resolution. (b) Observed ice surface speed. (c) Difference between modeled, optimized initial, and observed ice surface speeds. In all panels, the black line represents the grounding line, and the light-blue shading indicates the open ocean in the model domain. The pink line in panels (b) and (c) indicates the observed 50 m yr⁻¹ ice surface speed contour.

However, new projections of the Antarctic Ice Sheet using global climate model (GCM) ocean and atmospheric conditions through 2300 indicate that extreme ocean warming and the subsequent ocean-melt-driven and/or surface-melt-driven removal of most major ice shelves, including the AmIS, are possible after 2100 (Seroussi et al., 2023). Removal or extensive thinning of the ice shelf will accelerate the grounded ice through a reduction in buttressing (Gudmundsson et al., 2019; Zhang et al., 2020), causing a substantially larger contribution to sea-level rise than previously projected. Ice-shelf cavities in Antarctica generally can be characterized as cold or warm, depending on whether their circulation and melting are controlled by cold, saline shelf water or by deeper, relatively warm, saline modified Circumpolar Deep Water (mCDW) (Dinniman et al., 2016). Changes in the access of these water masses to the ice-shelf base can lead to a regime shift and a rapid change in ice-shelf basal melt rates of an order of magnitude (Hazel and Stewart, 2020; Haid et al., 2023). Under present conditions, only small intrusions of mCDW reach the AmIS (Liu et al., 2017). However, in a high-greenhouse-gas-emission scenario, more pervasive access of mCDW to the ice-shelf base appears possible after 2100, as shown in the four GCM projections used by Seroussi et al. (2024) (Fig. 2). With these projections indicating the potential for removal of the AmIS through increased submarine melting, the long-term stability of the AmIS sector should be reevaluated.

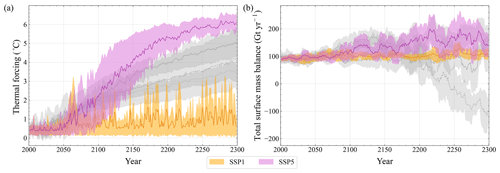
Figure 2 (a) Time series of thermal forcing averaged over the ice-shelf base from approximately the year 2000 for the UK Earth System Model (UKESM) under the Shared Socioeconomic Pathway 1 (SSP1; orange) and SSP5 (purple) scenarios, along with three additional scenarios for Representative Concentration Pathway 8.5 (RCP8.5) and SSP5 from other Earth system models provided by the Ice Sheet Model Intercomparison Project for CMIP6 (ISMIP6): HadGEM2 (solid gray line), CESM2 (dashed gray line), and the Community Climate System Model (CCSM; dotted gray line). (b) Time series of the 10-year running mean of total surface mass balance over the AmIS catchment. Shaded regions denote 1 standard deviation (Seroussi et al., 2024).

Ice-sheet models inherently rely on uncertain model parameterizations (e.g., to represent unresolved sub-grid-scale physical processes or unobserved mechanical and thermodynamic ice characteristics), which introduce uncertainty into the models' predictions of a glacier's dynamic response to changes in climate forcing. Therefore, assessing the AmIS sector's response to a potential sudden increase in ice-shelf basal melting during the 22nd century requires thorough quantification of this parametric uncertainty. Quantifying how uncertainties in input parameters influence future predictions is often achieved through uncertainty propagation, typically using Monte Carlo sampling over the input space. Bayesian calibration, or probabilistic parameter estimation, extends uncertainty propagation by providing a systematic framework for integrating observational data and expert knowledge to constrain the distribution of input uncertainties. This, in turn, allows for the generation of observationally constrained probabilistic projections. Bayesian calibration not only enhances the reliability of ice-sheet model projections but also provides insights into the sources of uncertainties and the impacts of these uncertainties on projections. This calibration workflow, which typically requires Monte Carlo sampling over computationally expensive parametric model ensembles, becomes tractable when combined with statistical emulation of the expensive ice-sheet model. The result is a rigorous method for quantifying and communicating the reliability of model predictions, which aids decision-making in climate science and policy. Numerous studies have introduced formal uncertainty quantification methods into ice-sheet modeling to generate probabilistic projections of future contributions to sea-level change from various glaciers and ice sheets (Bulthuis et al., 2019; Nias et al., 2019, 2023; Alevropoulos-Borrill et al., 2020; Gilford et al., 2020; Wernecke et al., 2020; Lee et al., 2020; Edwards et al., 2021; Berdahl et al., 2021, 2023; Hill et al., 2021; Aschwanden and Brinkerhoff, 2022; Chang et al., 2022; Bevan et al., 2023; Johnson et al., 2023; Seroussi et al., 2023; Van Katwyk et al., 2023). In this study, we apply such methods to the AmIS catchment for the first time to answer the following scientific question: how does parametric uncertainty, when constrained by observations, affect the projected ice-sheet response to abrupt changes in the oceanic forcing of the Amery Ice Shelf sector of Antarctica?

To address this question, we apply a regional ice-sheet model of the AmIS catchment to generate an ensemble of simulations with parameter values perturbed over their likely ranges. Using statistical emulation of the resulting ensemble, we perform Bayesian calibration on the uncertain model parameters, using observations of key glacier quantities from the historical period. By sampling from the posterior distribution of parameter values and combining ensembles of ice-sheet model projections with statistical emulation, we generate calibrated, probabilistic projections of the future contribution of the AmIS sector to sea level under two climate scenarios.

In this work, we first present the ice-sheet model configurations used in our study, followed by a detailed description of the Bayesian modeling framework, including the statistical emulation that enables efficient Monte Carlo sampling. Finally, we share our results and discuss their implications for the future of the AmIS sector of the East Antarctic Ice Sheet (EAIS). We also discuss how these methods may be extended to more complex problems, including those concerning the entire Antarctic Ice Sheet.

2 Ice-sheet model description

For our simulations, we use the MPAS-Albany Land Ice (MALI) model (Hoffman et al., 2018), applied to a regional domain of the AmIS catchment (Fig. 1). Here, we describe the main model features employed in this study, highlighting equations with uncertain model parameters, and refer the reader to references for other details.

2.1 Model configuration

MALI is a variable-resolution mesh-based ice-sheet model that solves the first-order, three-dimensional (3D) Blatter–Pattyn approximation of the Stokes equations for momentum balance using the finite-element method. We use the common constitutive relation ${\mathit{\tau }}_{ij}=\mathrm{2}{\mathit{\eta }}_{\mathrm{e}}{\dot{\mathit{ϵ}}}_{ij}$, where τ_ij is the deviatoric stress tensor, ${\dot{\mathit{ϵ}}}_{ij}$ is the strain rate tensor, and η_e is the effective ice viscosity given by Nye's generalization of Glen's flow law (Glen, 1955; Nye, 1957),

$$\begin{array}{}\text{(1)}& {\displaystyle }{\mathit{\eta }}_{\mathrm{e}}=C_{\mathit{\varphi }}\mathit{\varphi }{A}^{-\frac{\mathrm{1}}{n}}{\dot{\mathit{ϵ}}}_{\mathrm{e}}^{\frac{\mathrm{1}-n}{n}},\end{array}$$

where A is a temperature-dependent rate factor, n is an exponent with a value of 3 for polycrystalline glacier ice, ϕ is a spatially varying ice stiffness factor accounting for the impacts of unresolved processes (e.g., fabric) on ice rheology, and C_ϕ is a spatially uniform ice stiffness adjustment factor taken as an uncertain parameter. We use a power law for basal friction of the form

$$\begin{array}{}\text{(2)}& {\displaystyle }{\mathit{\tau }}_{\mathrm{b}}=C_{\mathit{\mu }}\mathit{\mu }|u_{\mathrm{b}}{|}^{q-\mathrm{1}}{u}_{\mathrm{b}},\end{array}$$

where τ_b is basal shear stress, u_b is the slip velocity at the glacier bed, and $\mathrm{0}<q\le \mathrm{0.333}$ is an uncertain power law exponent representing the degree of plasticity of the bed. Moreover, μ is a spatially varying friction parameter, and C_μ is a scalar basal friction adjustment factor taken as an uncertain parameter.

Thickness and tracer (temperature) advection is performed with a first-order upwind scheme implemented with the finite-volume method. The configuration here employs thermomechanical coupling and a temperature-based thermal solver. MALI uses a forward Euler time integration scheme with an adaptive time step, selected here to be one-fifth of the time interval defined by the advective Courant–Friedrichs–Lewy (CFL) condition. This is smaller than what is typically chosen for MALI, but it minimizes the chances of unstable model behavior when ignoring the diffusive CFL condition and exploring a wide spectrum of parameter space.

We also employ parameterizations for calving, ice-shelf basal melting, and submarine melting of grounded marine termini (as described in Hillebrand et al., 2022). MALI's subglacial hydrology model (Hager et al., 2022) and glacier isostatic adjustment (Book et al., 2022) are not used in this study.

For calving, we apply the von Mises stress calving parameterization from Morlighem et al. (2016),

$$\begin{array}{}\text{(3)}& {\displaystyle }c=\left|\stackrel{\mathrm{‾}}{u}\right|{\displaystyle \frac{\mathit{\sigma }}{{\mathit{\sigma }}_{\text{max}}}},\end{array}$$

where c is calving velocity, $\stackrel{\mathrm{‾}}{u}$ is depth-averaged ice velocity, σ is depth-averaged von Mises tensile stress, and σ_max is yield stress treated as a tuning parameter. Because there are negligible grounded marine calving fronts currently in the Amery catchment, it is not possible to calibrate grounded margin calving, which, in practice, may require a different yield stress parameter than that for floating ice (Choi et al., 2017; Hillebrand et al., 2022). Furthermore, Hillebrand et al. (2022) identify a possible positive feedback between grounded calving and basal slip when both σ_max and q are small, leading to unrealistically catastrophic glacier retreat – behavior that was echoed in preliminary runs of this work. To avoid these complexities, given the large range of parameters being considered, we disable grounded calving entirely. Thus, the glacier retreat in simulations where significant grounded calving fronts develop (following the loss of ice shelves) should be regarded as a conservative projection as it is likely underestimated under such conditions.

For ice-shelf basal melting, we use the scheme by Jourdain et al. (2020), which is designed for Antarctic ice shelves and prescribed in the ISMIP6-Antarctica experimental protocol (Nowicki et al., 2020; Seroussi et al., 2020). This parameterization defines spatially varying ice-shelf basal melt rates (m) as a function of ocean thermal forcing along the ice-shelf base (TF), which is the difference between the ocean temperature and the local ocean freezing temperature:

$$\begin{array}{}\text{(4)}& {\displaystyle }m={\mathit{\gamma }}_{\mathrm{0}}{\left({\displaystyle \frac{{\mathit{\rho }}_{\text{sw}}{c}_{\text{pw}}}{{\mathit{\rho }}_{\mathrm{i}}{L}_{\mathrm{f}}}}\right)}^{\mathrm{2}}(\text{TF}+\mathit{\delta }T)|\langle \text{TF}\rangle +\mathit{\delta }T|,\end{array}$$

where ρ_sw is the density of seawater, c_pw is the specific heat of seawater, ρ_i is the density of glacier ice, L_f is the latent heat of fusion of ice, and 〈TF〉 is the thermal forcing averaged over the entire ice-shelf base. The coefficient γ₀ is an uncertain proportionality constant, and δT is an uncertain bias correction factor.

For grounded marine termini, the melt rate perpendicular to the horizontal calving front (m_g) is parameterized using the form $m_{\mathrm{g}}=(Ah{q}_{\text{sq}}^{\mathit{\alpha }}+B){\text{TF}}_{\mathrm{b}}^{\mathit{\beta }}$ (Rignot et al., 2016; Slater et al., 2020), where A=0.0003 ${\mathrm{m}}^{\mathit{\alpha }}{\mathrm{d}}^{\mathit{\alpha }-\mathrm{1}}\mathrm{°}{\mathrm{C}}^{-\mathit{\beta }}$, h is water depth at the terminus (in meters), q_sq is subglacial runoff (in m d⁻¹), α=0.39, B=0.15 $\mathrm{m}{\mathrm{d}}^{-\mathrm{1}}\mathrm{°}{\mathrm{C}}^{-\mathit{\beta }}$, β=1.18, and TF_b is the ocean thermal forcing at the bed depth. Because the Amery catchment currently has negligible grounded marine margins, we are unable to tune this process and instead use the standard parameter values prescribed for ISMIP6-Greenland (Slater et al., 2020) without uncertainty, conservatively assuming q_sq=0. Despite being negligible in the initial state, significant grounded marine termini develop late in some future scenarios after ice shelves have largely disappeared.

2.2 Amery Ice Shelf catchment domain

The regional simulation domain is defined by the Amery B–C region used in Rignot et al. (2019), which encompasses all ice flowing into the AmIS (Fig. 1). This regional domain is extracted from the whole Antarctic domain used by MALI for the intercomparison study ISMIP6-Projections2300-Antarctica (Seroussi et al., 2023). The mesh resolution is 4 km in areas of fast flow (log ₁₀(u_s)>2.5, where u_s is the observed ice surface speed in m yr⁻¹) or near the 2015 grounding line (<10 km) and coarsens to 20 km in locations of slow flow (log ₁₀(u_s)<0.75) or in locations far (>100 km) from the grounding line (Fig. 1a). The mesh contains a total of 53 523 cells. The vertical coordinate has five terrain-following layers, with a higher resolution near the bed. The overall moderate mesh resolution is chosen to make a large ensemble of simulations computationally feasible.

Ice thickness and bed topography are interpolated from BedMachine Antarctica v2 (Morlighem et al., 2020; Morlighem, 2022) using conservative remapping. The spatially varying and time-invariant basal friction (μ) and ice stiffness (ϕ) fields are solved for the entire Antarctic Ice Sheet using a partial-differential-equation-constrained optimization problem (Perego et al., 2014), minimizing the misfit of ice surface velocity relative to observations from 1996 to 2016 (Mouginot et al., 2017) (Fig. 1c). The solution to the optimization problem satisfies the momentum balance and steady-state thermodynamics, yielding a consistent initial ice temperature and velocity field. For both optimization and forward simulations, the thermal basal boundary condition is provided by the geothermal flux map from Shapiro and Ritzwoller (2004), and the thermal surface boundary condition is the mean annual air temperature from the RACMO2.1 1979–2010 climatology (Lenaerts et al., 2012).

2.3 Climate scenarios

Four climate forcing scenarios are used, each consisting of surface mass balance and 3D ocean thermal forcing. The climate forcing follows the ISMIP6-Projections2300-Antarctica protocol (Seroussi et al., 2023) applied to our regional domain. The two future climate scenarios considered come from the UK Earth System Model (UKESM) (Sellar et al., 2020) – the one climate model used in ISMIP6-Projections2300-Antarctica for which both low- and high-emission scenarios are available. Climate model structural uncertainty is not considered in this study, and the two future scenarios used should be considered broadly representative of high- and low-greenhouse-gas-emission scenarios.

For all the surface mass balance fields used, we add a large negative surface mass balance to land-based locations that are ice-free in our initial condition to prevent ice advance into these areas, where basal friction is unconstrained. The associated mass loss from this approximation is <2 % of the spatially integrated mass balance and is not a significant term in the overall glacier mass balance. Surface air temperature, the upper boundary condition for ice thermodynamics, is kept at its historical value throughout all simulations.

Historical relaxation (RELX).

For each ensemble member, we conduct a 50-year relaxation run from the initial conditions using historical climate forcing to integrate out fast transient behavior. For surface mass balance, we apply a 1995–2017 climatological average from RACMO2.3p1 (Van Wessem et al., 2014; van den Broeke, 2019). The ocean thermal forcing is the observation-based climatology compiled for ISMIP6-Antarctica, which uses data from 1995–2018 (Jourdain et al., 2020; Nowicki et al., 2020). The 50-year relaxation duration is chosen as the most rapid adjustments occur in the first few decades of integration, while long-term adjustment to a fully steady state would take thousands of years. Relaxation to a full steady state would require substantially more computing resources than are available for our entire set of ensembles, which would lead to different runs potentially having very divergent initial states. Future improvements to model initialization that account for surface elevation change (Perego et al., 2014) may reduce initial model drift and enhance this requirement. The final model state in each run at the end of RELX is given the nominal date of 1 January 2015, and all three projection ensembles branch from these states.

Control projection (CTRL).

The CTRL projection ensemble extends from the RELX configurations, continuing with the same surface mass balance and ocean thermal forcing from 1 January 2015 to 1 January 2300. This ensemble is used to assess model drift relative to the forced response of the climate scenarios.

Shared Socioeconomic Pathway 1-2.6 projection (SSP1).

Our SSP1 projection uses annual surface mass balance and ocean thermal forcing derived from a UKESM SSP1-2.6 climate scenario (“expAE10” from Seroussi et al., 2024). To avoid issues with climate model bias and abrupt changes in forcing, surface mass balance and ocean thermal forcing are applied as anomalies relative to the climatological mean forcings in the RELX and CTRL ensembles. The ensemble is run from 1 January 2015 to 1 January 2300.

SSP5-8.5 projection (SSP5).

Our SSP5 projection uses UKESM SSP5-8.5 projection forcings (“expAE05” in Seroussi et al., 2024), again applied as anomalies and covering the period from 2015 to 2300.

3 Bayesian modeling framework

This section details the methodology used to facilitate the end-to-end probabilistic modeling workflow featured in this work.

3.1 Perturbed-parameter ensemble design

To quantify parametric uncertainty, MALI input parameters are varied to generate ensembles of MALI simulations. Here, we elaborate on the input parameters considered in this study, their prior distributions, and the sampling strategy used to generate their values in the MALI simulations.

3.1.1 MALI parameters

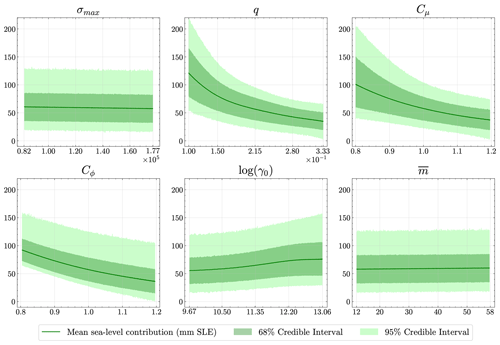
The six MALI input parameters considered are summarized in Table 1. In Fig. 7, the dashed green lines represent the prior probability distribution for each parameter.

Table 1 Summary of the MALI parameters and their prior distributions.

The ranges for ice stiffness scaling and basal friction scaling factors correspond to the values at which yield velocity solutions exceed observational uncertainty and variability, based on sensitivity tests. For the basal slip exponent, the high end of the sampled range is the theoretically derived exponent for a hard bed (Weertman, 1957). The low-end value of 0.1 is less than the estimated exponents for different Antarctic glaciers, i.e., q<0.2 (Gillet-Chaulet et al., 2016) and q=0.11 (Nias et al., 2018). The sampled range for calving yield stress spans the values that produce approximately stable calving front positions in MALI for all major Antarctic regions, based on sensitivity tests exploring model configurations for MALI's contribution to Seroussi et al. (2023). The low end of the sampled range for the ice-shelf melt coefficient is the 5th percentile value for the nonlocal Antarctic-wide (MeanAnt) tuning from Jourdain et al. (2020), while the high end is the 95th percentile value for the high-melt-sensitivity tuning (Pine Island grounding line (PIGL)) derived from the Pine Island Glacier. This spans the range of plausible values proposed by Jourdain et al. (2020) and used in Seroussi et al. (2020). The last uncertain parameter identified in Sect. 2.1 is δT, the ocean temperature bias correction. Because γ₀ and δT are strongly dependent via Eq. (4), it is difficult to prescribe a range and prior distribution for δT, an ad hoc correction factor. Instead, we represent this degree of freedom using the uncertain historical ice-shelf-averaged melt rate ($\stackrel{\mathrm{‾}}{m}$) itself. For a given sample of $\stackrel{\mathrm{‾}}{m}$ and γ₀, we calculate the corresponding value of δT to be used for said sample. For $\stackrel{\mathrm{‾}}{m}$, we use a normal distribution with a mean and standard deviation corresponding to the AmIS, as reported by Rignot et al. (2013). This distribution is truncated at the provided range, interpreted as a 2 σ range around the mean, which we also use to sample the $\stackrel{\mathrm{‾}}{m}$ values.

3.1.2 Space filling sampling strategy

To achieve our objective of training a statistical emulator, we sample the parameter space uniformly within the defined bounds presented in Table 1. This approach helps us to learn the model's response to varying inputs, rather than relying on an expert-defined distribution, which we later use as priors in Bayesian inference. We generate these uniform samples using a low-discrepancy quasi-random Sobol sequence (Sobol', 1967). Sobol sequences possess uniform space filling properties akin to Latin hypercube sampling (McKay et al., 2000; Urban and Fricker, 2010), but they offer the advantage of recursively adding new points while preserving their space filling characteristics. This feature is particularly useful when expanding the ensemble size later. In this study, we design a 200-member ensemble using this method (see Fig. A1). To ensure sufficient coverage, a well-cited paper by Loeppky et al. (2009) recommends using at least 10 data points per input dimension when building an emulator. Given our six input parameters, this implies a minimum of 60 ensemble members. We have selected 200 members to guarantee adequate data, even if some need to be discarded.

3.2 Observations

We use three scalar observational constraints when performing Bayesian calibration of MALI parameters – specifically, mass balance, grounding line movement, and calving front movement. While additional spatially resolved observations can be considered (e.g., ice surface velocity or elevation change rate), we choose to avoid the considerable complexity of weighting spatial misfit and combining spatial and scalar metrics. Instead, we restrict the observational criteria to large-scale scalar metrics. The modeled values of these observables are averaged over the 50-year RELX duration.

Mass balance.

We use mass balance measurements of the grounded ice sheet from Rignot et al. (2019), which employed the input–output method from 1979–2017. We calculate the difference between the 39-year averages of surface mass balance (input) and discharge (output) terms for the AmIS catchment, accounting for their stated uncertainties, to obtain a mean of −1.656 Gt yr⁻¹ and a standard deviation of 5.720 Gt yr⁻¹. Because these measurements are calculated from the input–output method, we compare the values to modeled grounded mass change rates using the normal distribution likelihood $N(-\mathrm{1.656},\mathrm{5.720})$ (instead of using volume above flotation, which is an incomplete representation of mass balance).

Grounding line movement.

Grounding line movement measurements from Konrad et al. (2018), estimated from satellite altimetry measurements collected between 2010 and 2016, are used in this work. We calculate the average grounding line velocity for the three glacier regions within the AmIS catchment (LAM, SCY, and AME, as described in Konrad et al., 2018), using calculations for regions where ice flow speed exceeds 25 m yr⁻¹ and weighting by the length of the grounding line captured in their surveys. While this is the most complete estimate available, the stated coverage for these three basins is 34 %–36 %, and there are additional unsurveyed regions within the AmIS. By repeating the averaging for the 5th and 95th percentile estimates from Konrad et al. (2018) for these regions and assuming that errors are normally distributed, we obtain an estimate of grounding line movement with a mean of 0.467 m yr⁻¹ and a standard deviation of 3.562 m yr⁻¹. For comparison with the modeled glacier state, we multiply this grounding line velocity by the length of the grounding line in our domain (2117 km) to obtain a grounded area change rate of 0.988 ± 7.540 km² yr⁻¹, which we compare against the modeled grounded area change rate using the normal distribution likelihood N(0.988,7.540).

Calving front movement.

Observations indicate that, like other large Antarctic ice shelves, the AmIS has a multidecadal cycle of gradual advance, followed by stepwise retreat through the detachment of large tabular icebergs (Fricker et al., 2002; Greene et al., 2022; Andreasen et al., 2023). At the same time, the advance-and-retreat cycle for the AmIS has a negligible impact on conditions in the central ice shelf (King et al., 2009) as these variations occur well past the portions of the ice shelf that provide significant buttressing (Fürst et al., 2016). Thus, the picture of the AmIS is one of stability, with a long-term front position remaining in the range of the advance-and-retreat cycle. The von Mises calving parameterization used cannot represent the advance-and-retreat cycles because it does not include the processes of damage and fracture formation that lead to tabular-iceberg formation. Instead, it can only represent the long-term average calving behavior. Observations spanning the years 1963 to 2021 indicate that calving front position has varied by 10 000 km², with the 2015 position having retreated about 1000 km² from the most advanced position (Fricker et al., 2002; Greene et al., 2022; Andreasen et al., 2023). To use these observations, we assume that the range from the single observed AmIS calving cycle has a 50 % likelihood of representing the true range of stable calving front variations and define a mean position of −4000 km² relative to the 2015 initial state, with a standard deviation of 7353 km² (resulting in a central 50 % probability region for a normal distribution between −9000 and 1000 km²). For our simulations, we then define long-term stability with the pragmatic criterion that the calving front position over the total simulation duration of 335 years (i.e., the 50-year RELX duration plus the 285-year projection) should remain within the range of the observed calving cycle. By dividing the area change by the total simulation duration, we obtain a mean calving front position change rate of −11.94 km² yr⁻¹, with a standard deviation of 21.95 km² yr⁻¹. This observation-based estimate then is compared to the modeled rate of change in the total ice area using the normal distribution likelihood $N(-\mathrm{11.94},\mathrm{21.95})$, which is as a good proxy for calving front position change given the near absence of terrestrial and grounded marine margins in the catchment.

3.2.1 Ensemble filtering

Before training the RELX ensemble emulator and calibrating the parameters, we filter the runs in the RELX ensemble. The purpose is 2-fold. First, filtering eliminates outliers from potentially complex regions of parameter space that may reduce the skill of the emulators but are negligibly sampled due to the low likelihood of matching observations. Second, because in some cases our prior parameter distributions include regions of parameter space that will be negligibly sampled, eliminating runs from these regions reduces the computational cost of the three MALI projection ensembles. The applied filter removes runs that exceed 4 standard deviations of any of the three observational constraints (covering 99.9 % of the central probability region around the mean in a normal distribution). This results in a filtered ensemble of 119 out of the original 200 runs being retained, ensuring approximately 20 ensemble members per input parameter, which adheres to the general rule of having more than 10 ensemble members per input parameter, as mentioned in Sect. 3.1.2. These 119 filtered ensemble members are used for all subsequent statistical analyses.

3.3 Statistical emulation

The high-fidelity MALI ice-sheet model simulations represent ice-sheet dynamics accurately but are computationally expensive, prohibiting their use in generating a large enough ensemble of simulations for the purposes of uncertainty quantification. To address this challenge, we construct statistical emulators of MALI simulations that approximate MALI's behavior and outputs using statistical techniques (Sacks et al., 1989). Once constructed, the statistical emulators are used to explore the entire parameter space and capture the essential features of the MALI simulations at a negligible computational cost. This also reduces the computational cost of quantifying uncertainty. While existing literature has demonstrated the use of various types of emulators, including regression analysis, Gaussian processes (GPs), neural networks, and machine learning algorithms (Berdahl et al., 2021; Bulthuis et al., 2019; Edwards et al., 2019), this study employs univariate and multivariate (multi-output) emulators based on GP regression.

Gaussian process emulators. GP emulation (Gramacy, 2020) is a Bayesian nonparametric regression technique widely used to model complex systems. Unlike typical polynomial equations, GPs can capture nonlinear and nonparametric relationships without assuming a specific functional form. Moreover, by assuming that the underlying process follows a Gaussian (i.e., normal) distribution, GPs provide a flexible framework for capturing uncertainty and making predictions. GP emulation is a response-surface formulation (Box and Wilson, 1951) that treats the simulator as an unknown function of its input parameters (Gramacy, 2020). Inherently Bayesian, GPs express knowledge about unknown functions through probabilistic means, offering a robust method for modeling and prediction.

3.3.1 Gaussian process emulation of the RELX ensemble

For this work, we construct separate scalar GP emulators to predict the three observables at the end of the 50-year relaxation period, using six MALI parameters in the RELX ensemble.

After performing a thorough search spanning different kernels and their hyperparameters, each GP is constructed using a linear trend function and a separable Matérn covariance kernel with a smoothness parameter (ν=2.5). Our final choice of the Matérn kernel (ν=2.5) ensures that the GP emulator is twice mean square differentiable, providing a high degree of smoothness while avoiding the over-smoothness often introduced by the squared exponential kernel (which renders the fitted GP infinitely differentiable). Following standard practice, the hyperparameters controlling the mean function, as well as the length scales and variance of the kernel, are optimized by minimizing the negative log-likelihood function. The pointwise variance of the posterior prediction of the GP – referred to as code uncertainty – is used as a second independent noise term and is added to the scalar GP emulator's mean prediction during Bayesian calibration. The code uncertainty represents the error introduced by the emulator due to training on a small MALI ensemble (Kennedy and O'Hagan, 2001).

Each emulator is trained using input–output pairs obtained from the filtered 119-member ensemble and consists of realizations of the six input parameters and corresponding scalar outputs. Both the input parameters and the outputs are normalized to have a unit range of [0,1] and to improve the emulator training (we ensure that the GP predictions remain in their original output units).

Emulator validation. We train the emulators using 5-fold cross-validation. To investigate the accuracy of the resulting GPs, we plot the cross-validation residuals (the difference between the predicted and true outputs) in Figs. 3a, 4a, and 5a. The figures indicate that each GP emulator fits the simulation data quite well. Next, we plot the predicted versus actual values of scalar outputs, as well as the corresponding 50 % predictive intervals, to assess the emulation skill of our GP models (Figs. 3b, 4b, and 5b). In each figure, the emulator predictions are close to the 1 : 1 line, and predictive intervals are narrow, highlighting the good emulation skill with minimal uncertainty in the trained GP models. Despite discarding 81 runs during filtering, the cross-validation results (Figs. 3, 4, and 5) show that our GP emulators still perform well. Interestingly, emulators trained with these 119 filtered members are more accurate than those trained with all 200 members, although this comparison is omitted for brevity.

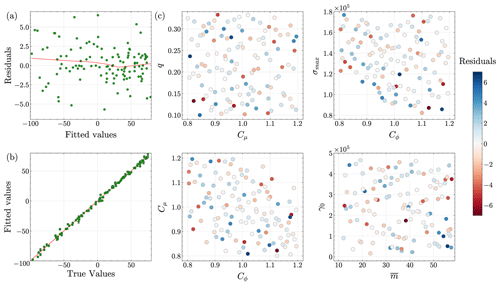
Figure 3 Analysis of the Gaussian process emulator fit for calving front positions. Plots are shown for (a) residuals versus fitted values, (b) predicted values versus actual values, and (c) residuals versus pairwise input parameters.

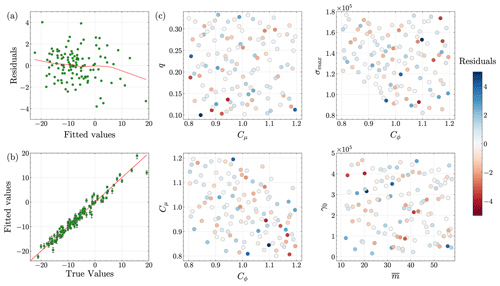
Figure 4 Analysis of the Gaussian process emulator fit for grounding line positions. Plots are shown for (a) residuals versus fitted values, (b) predicted values versus actual values, and (c) residuals versus pairwise input parameters.

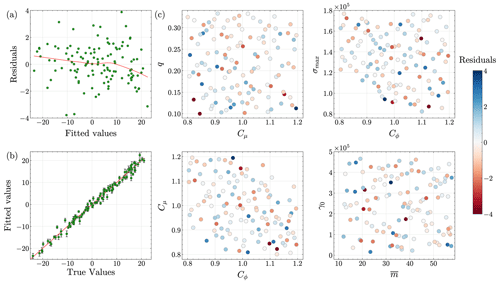
Figure 5 Analysis of the Gaussian process emulator fit for mass change. Plots are shown for (a) residuals versus fitted values, (b) predicted values versus actual values, and (c) residuals versus pairwise input parameters.

We also plot the residuals against the pairwise input parameters to analyze trends associated with specific input parameter values leading to outliers in residuals (Figs. 3c, 4c, and 5c). The figures do not show any significant patterns in the relationships between the outliers in the residuals and input parameters. Finally, we plot predictive-coverage plots, which help assess how well the emulators are calibrated via predictive intervals (Fig. C7). As expected, perfect predictive coverage occurs when the model's predictive intervals align with the actual outcomes, and any deviation from this perfect coverage suggests that the model's uncertainty estimates are either too conservative, i.e., underconfident (blue shaded region below the dashed green line in Fig. C7), or too aggressive, i.e., overconfident (red shaded region above the dashed green line in Fig. C7). Figure C7a–c show that the GP emulators are slightly underconfident, overconfident, and slightly overconfident, respectively.

3.4 Bayesian calibration of MALI parameters

Once cross-validation of the GP emulators is complete, we train the emulators again on the full, filtered ensemble runs for the Bayesian calibration task. These GPs are then used to condition (or calibrate) the prior uncertainty in the MALI parameters on the three observations listed in Sect. 3.2. Specifically, following Kennedy and O'Hagan (2001), we update the prior probability distributions of the MALI parameters using Bayes' rule,

$$p\left(\mathit{\theta }\right|\mathcal{D})\propto p(\mathcal{D}\left|\mathit{\theta }\right)p\left(\mathit{\theta }\right),$$

where p(θ) denotes the prior distribution of MALI parameters; p(𝒟|θ) represents the likelihood function, which is the joint probability of the observed data (𝒟) given the parameters (θ); and p(θ|𝒟) is the posterior distribution of MALI parameters. The prior distributions for the six MALI parameters, determined from past literature and previous model applications, are provided in Fig. 1. The likelihood function is assumed to be a multivariate Gaussian function with a diagonal covariance matrix ($\mathbf{\Sigma }=\text{Diag}[{\mathit{\sigma }}_{\mathrm{1}}^{\mathrm{2}},{\mathit{\sigma }}_{\mathrm{2}}^{\mathrm{2}},{\mathit{\sigma }}_{\mathrm{3}}^{\mathrm{2}}]$) that satisfies

$$p\left(\mathcal{D}\right|\mathit{\theta })\propto \exp \left[-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left(\mathit{f}\right(\mathit{\theta })-\mathit{d}{)}^T{\mathbf{\Sigma }}^{-\mathrm{1}}(\mathit{f}\left(\mathit{\theta }\right)-\mathit{d})\right],$$

which is equivalent to assuming that the noise in each of the three observations is independent. Here, d represents the vector of the three observations taken in 2015, and f is the vector of the three emulator outputs for a given θ value. Additionally, we set the variance term ${\mathit{\sigma }}_j^{\mathrm{2}}$ for the jth scalar output as the sum of observational noise variance (${\mathit{\sigma }}_{\mathrm{o},j}^{\mathrm{2}}$) and code uncertainty (${\mathit{\sigma }}_{\mathrm{c},j}^{\mathrm{2}}$). The values of σ_o,j are presented in Sect. 3.2. We then use the No-U-Turn Sampler (NUTS) (Hoffman and Gelman, 2014), a Hamiltonian Monte Carlo method that requires minimal fine-tuning, to draw samples from the analytically intractable posterior (p(θ|𝒟)).

Remark. We assume independence due to the lack of knowledge about the correlation structure among three observed variables as we only have a single observation for each during calibration. However, our framework can accommodate correlated observables if such information becomes available.

3.5 Principal component emulation of projection ensembles

This study's primary goal is to constrain and quantify the future contribution of the AmIS catchment to global mean sea level using an ensemble of MALI simulations corresponding to those drawn from the posterior distribution of our input parameters. To achieve this, we calculate the sea-level contribution from the years 2015 to 2300 as the change in volume above flotation (VAF) converted to its sea-level equivalent (SLE), following the definitions in Goelzer et al. (2020). We build and employ GP emulators to accelerate the probabilistic SLE projections for three different scenarios (CTRL, SSP1, and SSP5). The VAF in each of our projection ensembles (CTRL, SSP1, and SSP5) is based on time series data from 2015 to 2300. With high autocorrelation, a multivariate (multi-output) emulator is more effective than individual scalar emulators for individual years, which can be cumbersome as additional treatment is required to account for autocorrelated data in consecutive years. To build a multivariate emulator, we employ principal component analysis (PCA) to extract linear reduced-dimensional subspace of the time series, similar to Higdon et al. (2008) and Wilkinson (2010). To this end, PCA provides projected data with maximized variance and dimensions that are uncorrelated but not necessarily independent.

We build the GP emulators using an ensemble of VAF change projections and the input parameter values from the filtered RELX ensemble. The resulting projection ensemble consists of data from 119 simulated time series for VAF change over 285 years. Motivated by Higdon et al. (2008), PCA is used to reduce the dimensionality of this time series data from 285 to K=5 principal components (a detailed description of these steps is available in Appendix B1). The value K=5 is chosen because the retained principal components are able to explain >99 % of the variance in the original data. After this dimensionality reduction, we independently construct GP emulators to approximate the relationship between the input parameters and each of the retained principal components. When training the GPs, we transform the principal components and input parameters using a unit range of [0,1] for the transformations and, again, employ 5-fold cross-validation to validate the resulting PCA-based GP emulators. We reconstruct the mean and variance of the time series predictions from the K emulated principal components using the procedure in Appendix B2.

Figure 6 summarizes the results of the PCA emulator 5-fold cross-validation for the SSP5 projection scenario with respect to the year 2300. Similar results for the CTRL and SSP1 projection ensembles are shown in Figs. C1 and C2, respectively. Figure 6a shows that there is no strong pattern in the plot of residuals versus fitted values. Moreover, the PCA emulator predictions are close to the 1 : 1 line and have narrow predictive intervals (Fig. 6b), and no specific patterns of residuals corresponding to inputs are observed (Fig. 6c). Lastly, the predictive-coverage plot (Fig. C7f) shows good alignment between the model's predictive intervals and the expected outputs for the year 2300. We analyzed years other than 2300 to assess the PCA GP emulator's performance, but we do not include these figures because, relative to the assessment for the year 2300, performance improves closer to the start of the time series. Finally, patterns similar to those described for SSP5 are evident in the CTRL and SSP1 projection ensembles, and the predictive coverage for these scenarios is summarized in Fig. C7d and e.

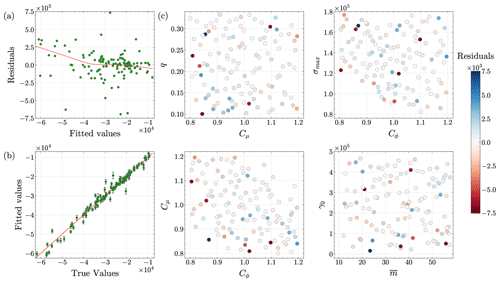
Figure 6 Analysis of the Gaussian process emulator fit using multivariate PCA (five principal components) for change in volume above flotation in the SSP5 projection ensemble for the year 2300. Plots are shown for (a) residuals versus fitted values, (b) predicted values versus actual values, and (c) residuals versus pairwise input parameters.

Once the principal component emulators have been validated, we retrain them using the entire ensemble to provide probabilistic projections of future sea-level contributions from the AmIS catchment. We propagate the MALI parameter posterior samples through the GP emulators and generate samples from the emulator's predictive distribution for each of the K=5 principal components. Finally, we reconstruct the sea-level contribution time series predictions from the principal components, following steps detailed in Appendix B2.

3.6 Sensitivity analysis of MALI parameters

We perform a sensitivity analysis of MALI parameters to assess the individual parameter uncertainty contribution to sea-level contribution uncertainty for the year 2300. Specifically, we employ Sobol's global sensitivity analysis (Sobol', 2001), which decomposes the variance of the sea-level contribution into components attributable to individual input parameters and their interaction effects (i.e., the combined influence of two or more input parameters) for the joint prior distribution. This method requires that the input parameters be independent of each other, a condition satisfied by our joint prior. This approach allows for the systematic quantification of the impact of uncertainty in each input on the output, providing a comprehensive understanding of the primary uncertainty sources. Sobol's method calculates sensitivity indices that measure the contributions of the MALI parameters, including their higher-order interactions with other parameters, to the overall sea-level contribution uncertainty. We report both the first-order Sobol index, which quantifies an input parameter's direct contribution to variance, and the total-order Sobol index, which captures both the individual effect of that input and its interactions with all other parameters. First-order Sobol indices should be less than or equal to total-order indices, and both should be non-negative. However, with finite samples, numerical errors can result in negative indices or first-order indices exceeding total-order indices.

Complementing Sobol's analysis, we also perform a Shapley sensitivity analysis, as proposed by Štrumbelj and Kononenko (2014). Based on game theory, this method calculates the contribution of each input parameter using its Shapley value. A sampling-based algorithm is employed to approximate these Shapley values, which represent the average marginal contributions of the inputs across all possible input combinations. Unlike Sobol's method, the Shapley sensitivity analysis can handle the observationally constrained and correlated joint posterior distribution of the MALI parameters. Specifically, we present Shapley indices for each input parameter under both the joint posterior and prior distributions, offering more flexible insights into parameter importance.

We perform the aforementioned sensitivity analysis using a scalar GP emulator of the change in volume above flotation (VAF) for the SSP5 projection ensemble in the year 2300 to predict the sea-level contributions with uncertainty (described in Sect. 4.2).

4 Results

4.1 Bayesian calibration results

The posterior distributions of MALI parameters, calibrated to three observational constraints, are presented in Fig. 7. While most parameters are informed by the observations, certain observations inform some parameters more than others. Calibration using the calving front position (red lines) leads to posterior distributions that deviate from the prior distributions for calving yield stress (σ_max) and the ice stiffness scaling factor (C_ϕ). The σ_max posterior is symmetric but is shifted toward lower values compared to the prior, with decreased variance indicating that values close to the median have a higher probability. The C_ϕ posterior is slightly skewed toward the lower values, with the probability of values being close to the median slightly increasing. Calibration using grounding line position (blue lines) leads to posteriors that deviate from the priors for the basal slip exponent (q), the basal friction scaling factor (C_μ), and the ice-shelf basal melt rate ($\stackrel{\mathrm{‾}}{m}$). Specifically, the posterior distributions for C_μ and $\stackrel{\mathrm{‾}}{m}$ are skewed toward lower values, and the posterior for q is skewed toward higher values. Additionally, C_μ and $\stackrel{\mathrm{‾}}{m}$ posteriors have narrower high-probability regions compared to their priors, with values close to the median having a higher probability. Calibration using mass change (yellow lines) leads to posterior distributions that deviate from the priors for the basal slip exponent, the basal friction scaling factor, the ice stiffness scaling factor, and the ice-shelf basal melt rate. The q, C_μ, and C_ϕ posteriors are skewed toward lower values, while the posterior for $\stackrel{\mathrm{‾}}{m}$ is skewed toward higher values. C_ϕ has a narrower posterior distribution compared to its prior, with values around the median having a high probability. In all three individual calibrations, the posterior for the ice-shelf melt coefficient (γ₀) does not change noticeably compared to its prior. In summary, each calibration leads to different posterior distributions for the six MALI parameters, highlighting the impact and importance of each observational constraint.

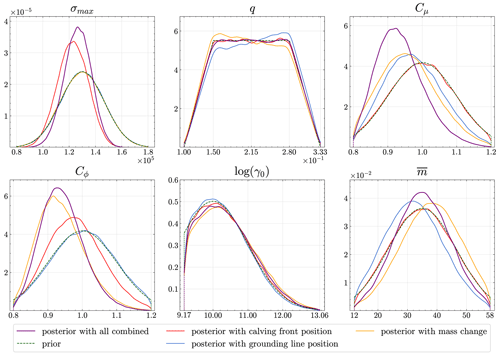
Figure 7 Posterior distributions of MALI parameters using Bayesian calibration on three observables (calving front position, grounding line position, and mass change), along with their combined calibration effect. Prior distributions from Table 1 are shown using dashed green lines.

Next, we detail the effects of simultaneously using all three observational constraints for calibration. As shown in Fig. 7 (purple lines), the posteriors for calving yield stress, the basal friction scaling factor, the ice stiffness scaling factor, and the ice-shelf basal melt rate deviate from their priors. For σ_max, the combination of the three observables leads to a narrower posterior, centered in the middle of the sampled range. For C_μ, the posterior is more skewed toward lower values and has a narrower high-probability region compared to the individual calibration corresponding to grounding line position and mass change. In addition, the C_μ posterior peak shifts further left than that of each individual calibration, possibly because combined calibration samples lower values more frequently than higher ones from the range of possible values. For C_ϕ, the combined calibration produces a posterior skewed toward lower values, with a higher peak and narrower high-probability region compared to individual calibrations based on calving front position and mass change. In contrast, the $\stackrel{\mathrm{‾}}{m}$ posterior is centered in the middle of the sampled range, suggesting that instances of skewness in opposite directions from calibrations corresponding to grounding line position and mass change cancel each other out, amplifying the peak value and leading to a narrower distribution. Similarly, the q posterior is similar to its uncalibrated prior and shows no skewness, suggesting that instances of skewness in opposite directions from calibrations corresponding to grounding line position and mass change cancel each other out. Lastly, as expected, the γ₀ posterior does not change noticeably with respect to its prior because all three individual calibrations leave the posterior for γ₀ close to its prior.

4.2 Probabilistic projection of future sea-level contribution from the Amery Ice Shelf catchment

Using the posterior distributions derived from calibrating all three observables, we generate 10 000 samples of the MALI parameters. Using the prior distributions given in Table 1, we also generate 10 000 samples of model inputs. These samples are propagated through the PCA emulator for the SSP5 projection ensemble, generating the prior- and posterior-predictive sea-level contribution time series, respectively. Figure 8 summarizes the results. The posterior-predictive means are slightly larger than the prior-predictive ones after incorporating all observational constraints. Moreover, the predicted uncertainties in the sea-level contribution, shown by the 68 % and 95 % credible intervals, are narrower for the posterior than for the prior, with an increase in the lower bound of each interval. This underscores the importance of the Bayesian-calibrated ensemble over the RELX ensemble in terms of reducing MALI parameter uncertainties and their resulting impact on future sea-level rise uncertainty. Lastly, Fig. 8c shows how random samples from the posterior distribution of the six input parameters generate future sea-level trajectories when passed through the PCA GP emulator. The 30 trajectories align closely with those actually simulated in the SSP5 projection ensemble (depicted in red in Fig. C3).

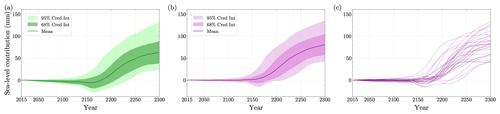
Figure 8 A total of 10 000 samples, drawn from prior distributions and calibrated posterior distributions of MALI parameters, are propagated through the PCA emulator for the SSP5 projection ensemble, leading to reconstructed time series for sea-level contributions (millimeters SLE) for the years 2015–2300. (a, b) The mean and credible intervals at 68 % and 95 % are shown using the prior-predictive (green) and posterior-predictive (purple) sea-level contribution time series samples, respectively. (c) A combined total of 30 randomly selected samples from the posterior-predictive distribution. Cred Int: credible interval.

Next, we propagate the same set of posterior samples through the PCA emulators for the CTRL and SSP1 projection ensembles and generate posterior-predictive sea-level contribution time series. Figure 9 shows a side-by-side comparison of probabilistic projections of future sea-level contributions in three scenarios: CTRL, SSP1, and SSP5. First, we observe a negative drift in the CTRL projection ensemble's sea-level contribution because the initial conditions taken from the end of the RELX ensemble are not fully in equilibrium with historical climate conditions. Second, we observe nearly identical trends in sea-level rise through 2300 in the SSP1 projection ensemble. Assuming that the drift toward a negative sea-level contribution is primarily due to an unequilibrated MALI transient in the control simulation, we can infer a future sea-level contribution of ∼0 mm SLE in the low-emission scenario. Lastly, under the high-emission (SSP5) scenario, the future sea-level contribution is estimated to be significantly higher than 0 mm SLE compared to both the control (CTRL) scenario and the low-emission (SSP1) scenario.

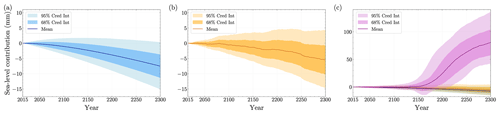
Figure 9 A total of 10 000 samples from the calibrated posterior distributions of MALI parameters are propagated through the principal component emulators for (a) CTRL, (b) SSP1, and (c) SSP5 projection ensembles, leading to reconstructed time series for sea-level contributions (millimeters SLE) for the years 2015–2300. We plot the mean and credible intervals at 68 % and 95 % using the posterior-predictive sea-level contribution time series samples. In panel (c), we include the plots for the CTRL (blue) and SSP1 (orange) ensembles to highlight the differences in sea-level contribution predictions from the SSP5 ensemble.

Finally, we generate predictions for future sea-level contribution for specific years by emulating the individual-year VAF change data from the MALI simulation using a scalar GP emulator. Figures C4, C5, and C6 summarize the scalar GP emulator validation results using 5-fold cross-validation for the CTRL, SSP1, and SSP5 projection ensembles, respectively, for the year 2300. In all three cases, there is no strong pattern in the residuals versus the fitted values. Moreover, the scalar GP emulator predictions are close to the 1 : 1 line, with narrow predictive intervals, and no strong patterns in residuals corresponding to pairwise inputs are evident. Finally, the predictive-coverage plots (Fig. C7g–i) show good alignment of the model's predictive intervals with expected outcomes for the year 2300 across all projection ensembles. Once our scalar GP emulators have been validated, we retrain them using the entire ensemble for a given year to provide probabilistic projections of future sea-level contributions from the AmIS catchment for the respective ensemble. We propagate the MALI parameter posterior samples through the GP emulator and sample from the emulator's predictive distribution. By combining these samples, we construct the posterior-predictive distribution for the future sea-level contribution for a given year in each projection ensemble.

In Fig. 10a, we plot the posterior-predictive distributions of future sea-level contributions under the SSP5 emission scenario for the years 2100, 2150, 2200, 2250, and 2300. We observe that the sea-level contribution in 2100 and 2150 is negligible, with mean values of −0.7 and 1.6 mm SLE. However, by 2200, the sea-level contribution is greater than 0 mm SLE, with a mean value of 21 mm SLE, and uncertainties in the distribution are wider. Moreover, in 2250 and 2300, the sea-level contribution is significantly higher than 0 mm SLE, with mean values of 65 and 79 mm SLE, respectively, while the year 2300 has values that are more highly skewed than those for the year 2250, suggesting a greater future sea-level contribution. We also compare these posterior-predictive distributions with the cross section of the posterior-predictive time series distributions presented in Fig. 8 for the years 2200, 2250, and 2300 in Fig. D1. As PCA involves a lossy compression of data, we switch to individual-year scalar GP emulators that are more accurate compared to the cross section of the posterior-predictive time series distribution for the chosen years. Figure D1 shows slight differences between the posterior-predictive distributions for the chosen years generated by the PCA and the scalar GP emulators. However, in the year 2200, there is a noticeable shift in the peak, which is expected since, as observed in Fig. C3, most of the sea-level contribution time series exhibit sudden change between the years 2150 and 2200. Next, Fig. 10b compares the prior- and posterior-predictive distributions for future sea-level contributions in the years 2200 and 2300. The posterior-predictive means are 21 and 79 mm SLE, which are higher than the prior-predictive means of 8 and 59 mm SLE for those years. The 95 % credible interval (c.i.) of the posterior-predictive distribution is $[-\mathrm{9.6},\mathrm{75}]$ mm SLE for the year 2200 and [46,133] mm SLE for the year 2300. In contrast, the prior-predictive 95 % credible intervals are $[-\mathrm{31},\mathrm{70}]$ mm SLE and [19,123] mm SLE for the same years. This demonstrates that both the means and bounds of the 95 % intervals increase, while the intervals themselves shrink, indicating lower predictive uncertainties in future sea-level projections due to observational constraints for both years. Lastly, Fig. 10c presents the posterior-predictive distributions of future sea-level contributions in the year 2300 for the CTRL, SSP1, and SSP5 projection ensembles. The posterior-predictive mean and 95 % c.i. for the SSP1 ensemble are −5.5 and $[-\mathrm{15},\mathrm{4}]$ mm SLE, which are quite similar to those for the CTRL projection ensemble (−7.7 and $[-\mathrm{15},\mathrm{0.3}]$ mm SLE). In contrast, the posterior-predictive distribution for the SSP5 scenario indicates a significantly higher sea-level contribution in the year 2300, with a mean of 79  and a 95 % c.i. of [46,133] mm SLE. This highlights a major sea-level contribution under the SSP5 scenario compared to the CTRL and SSP1 scenarios.

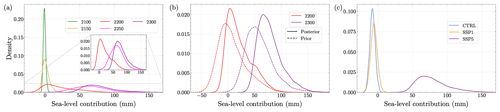
Figure 10 Posterior-predictive distributions for the future sea-level contributions for representative years. (a) Posterior-predictive distributions of future sea-level contributions for the SSP5 scenario in the years 2100, 2150, 2200, 2250, and 2300. We zoom in on the posterior-predictive distributions of the SLE in 2200, 2250, and 2300 to highlight their trends. (b) Prior-predictive distributions (dashed lines) compared with corresponding posterior-predictive distributions for future sea-level contributions for the SSP5 scenario in 2200 and 2300. (c) Posterior-predictive distributions of future sea-level contributions for the year 2300, corresponding to CTRL, SSP1, and SSP5 projection ensembles.

4.3 Individual contributions of MALI parameters to sea-level contribution uncertainty

The results of the sensitivity analysis for the SSP5 projection ensemble with respect to the year 2300 include the first-order and total-order Sobol indices for the MALI parameters shown in Fig. 11a. We observe that uncertainties in the basal slip exponent (q), basal friction scaling factor (C_μ), ice stiffness scaling factor (C_ϕ), and ice-shelf melt exponent (γ₀) make nontrivial contributions to sea-level contribution uncertainty, listed in descending order. Uncertainties in calving yield stress (σ_max) and the ice-shelf basal melt rate ($\stackrel{\mathrm{‾}}{m}$) have negligible contributions.

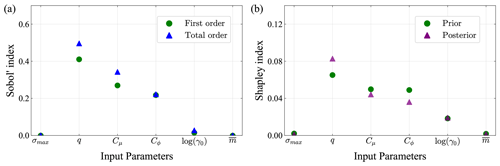
Figure 11 Individual MALI parameter uncertainty contribution to the future sea-level contribution uncertainty for the year 2300, using a scalar GP emulator of VAF change for the SSP5 projection ensemble. (a) Sobol's global sensitivity analysis on the joint prior. We present first-order and total-order Sobol indices for the MALI parameters. (b) Shapley sensitivity analysis on the joint posterior and prior.

In contrast, Fig. 11b presents the sensitivity of MALI parameters using the observationally constrained and correlated joint posterior with Shapley indices. We observe that uncertainties in q, C_μ, C_ϕ, and γ₀ significantly impact sea-level contribution uncertainties in descending order, while the remaining two parameters have negligible effects. Compared to the Shapley indices computed from the joint prior distribution (also in Fig. 11b), Bayesian calibration increases the influence of q while reducing the impact of C_ϕ on sea-level contribution uncertainty.

The aforementioned analysis reveals several key findings. First, despite being significantly constrained by Bayesian calibration, the σ_max parameter does not affect the sea-level contribution of the ice sheet. In contrast, the q parameter, which was not constrained by the calibration, has the largest effect. To illustrate this, Fig. 12 shows mean sea-level contribution predictions, with 68 % and 95 % credible intervals as a function of the MALI parameters. These intervals are estimated by varying each input parameter and sampling the remaining inputs from their joint prior distribution, conditional on the parameter being varied. The samples are propagated through our scalar GP emulator for VAF change in the year 2300 under the SSP5 scenario. We find that higher values of q result in lower sea-level contributions with tighter uncertainty bounds, while lower values lead to higher contributions with wider uncertainty. Similar trends are seen for C_μ. For C_ϕ, higher values reduce the sea-level contribution, but uncertainty remains consistent across its range. In contrast, for γ₀, lower values reduce the sea-level contribution, while higher values slightly increase both the sea-level contribution and its uncertainty bounds. Varying σ_max and $\stackrel{\mathrm{‾}}{m}$ has a negligible impact on sea-level contribution. These findings align with the results from the Sobol and Shapley analyses. It is notable that the three parameters for which sea-level contribution in the year 2300 under the SSP5 scenario is generally insensitive – σ_max, γ₀, and $\stackrel{\mathrm{‾}}{m}$ – all affect the ice-shelf volume and do not directly impact grounded ice. The drastic ocean temperature increase in the 22nd century (Fig. 2) leads to rapid removal of the ice shelf in most of our simulations, after which point parameters specific to ice-shelf processes do not affect the subsequent evolution of the glacier system.

Figure 12 The effect of individual MALI input parameters on sea-level contribution (millimeters SLE), with uncertainty bounds for the year 2300, using a scalar GP emulator of VAF change for the SSP5 projection ensemble.

5 Discussion

5.1 Comparison to previous projections of the Amery Ice Shelf system

Previous modeling studies of Antarctica's AmIS sector suggest that the catchment is stable under a range of likely future climate scenarios, with grounded-ice mass loss occurring only with near-complete loss of the ice shelf (Gong et al., 2014; Pittard et al., 2017). Barring ice-shelf removal, increases in surface mass balance (via increased accumulation in a warmer climate) may outweigh any acceleration in ice discharge caused by reduced ice-shelf buttressing. For scenarios where the AmIS remains intact, Gong et al. (2014) project a mass change of 0 to −15 mm SLE in the year 2200, while Pittard et al. (2017) project a mass change of −43 to 32 mm SLE (with positive values indicating sea-level rise). Given the differences in forcing scenarios and model configurations, our 95 % c.i. for sea-level contribution in the SSP1 ensemble (where the AmIS remains intact) is $[-\mathrm{8.2},\mathrm{4.2}]$ mm SLE for the year 2200, with a −2.1 mm SLE mean value, consistent with these earlier findings. We also point out that the 95 % c.i. for the SLE in the year 2200 in the CTRL ensemble is $[-\mathrm{9},\mathrm{1.5}]$ mm SLE, where the mean SLE of −3.8 mm SLE evolves from an expected mean of 0 mm SLE, likely as a result of model drift. Accounting for this drift in the CTRL ensemble, our SSP1 ensemble results suggest that, on average, we may not expect to see any significant changes in SLE as a result of future AmIS sector evolution. We attribute the narrower projection range in our study to the consideration of a single, intact AmIS scenario and, to a lesser extent, to the observationally constrained calibration.

While these previous studies identify an increase in snowfall accumulation causing surface mass balance to rise, this effect is modest for the UKESM SSP1 atmospheric forcing used here, which yields a 14 % cumulative increase in surface mass balance by the year 2300 (relative to historical conditions (Fig. 2b)). Furthermore, in our simulations, ice discharge increases in the SSP1 scenario, more than offsetting the small uptick in accumulation. Consequently, our SSP1 ensemble contributes slightly more to sea-level rise than the CTRL ensemble (Fig. 9). Intermediate levels of climate warming are more likely to lead to increased accumulation, driving overall mass gain in the catchment (Pittard et al., 2017), but we have not evaluated such scenarios.

The SSP5 scenario applied here includes a sudden and sustained major increase in melting beneath the AmIS, leading to the elimination of the ice shelf around 2130. This is caused by a sustained increase in mean thermal forcing that is not counterbalanced by the modest rise in surface mass balance (Fig. 2). Accordingly, the rapid mass loss in the second half of these simulations is depicted in Fig. 8. The 95 % c.i. for our calibrated posterior distribution is predicted to be [46,133] mm SLE during the final 170 years after the AmIS collapse. For scenarios where the AmIS is suddenly eliminated, Gong et al. (2014) predict up to 11 mm SLE in 200 years, whereas Pittard et al. (2017) forecast about 150 mm SLE after 170 years. It is important to note that these previous studies view the elimination of the AmIS as extreme and unlikely, whereas, in our simulations, it occurs as a consequence of state-of-the-art climate forcing and melt parameterizations (discussed further in Sect. 5.2).

Pittard et al. (2017) attribute the differences in sea-level contribution between their extreme scenario and that of Gong et al. (2014) to different bedrock topography datasets. The ALBMAP dataset (Le Brocq et al., 2010) used by Gong et al. (2014) includes a spurious ridge near the present-day grounding line, and the Bedmap2 dataset (Fretwell et al., 2013) used by Pittard et al. (2017) requires modification to deepen the bedrock near the grounding line by 500 m for consistency with oceanographic observations beneath the ice shelf. The BedMachine dataset, released after these studies, includes a trough along the Mellor Glacier that is up to 2000 m deeper than that in Bedmap2 (Morlighem et al., 2020; Morlighem, 2022) and is consistent with the modifications of Pittard et al. (2017). Thus, the consistency of our results with Pittard et al. (2017) and the differences relative to Gong et al. (2014) appear to be due largely to the representation of the bed topography. Similarly, Gong et al. (2014) report grounding line stabilization within 200 years of the ice-shelf removal, likely due to the relatively shallow bedrock topography. However, we see sustained grounding line retreat through the end of our simulations.

5.2 Ice-shelf collapse and the response of grounded ice

Our results support previous studies that conclude that substantial mass loss from the AmIS system is possible once the ice shelf is removed. However, while Pittard et al. (2017) predict that the ice shelf will remain intact for the next 500 years, we show it melting away within ∼130 years when forced by a state-of-the-art Earth system model under a high-emission scenario. While the UKESM SSP5 ocean forcing is the strongest of the forcings provided by ISMIP6, the other three Earth system models simulating the extended high-emission scenario agree that there will be a strong influx of mCDW within the next few centuries. Meanwhile, surface mass balance exhibits, at most, a modest increase (Fig. 2), unlikely to offset increased ice discharge resulting from substantial ice-shelf thinning and retreat. The mean UKESM thermal forcing of ∼3.5 °C, which causes ice-shelf loss in the 2130s, is reached under the three other high-emission scenarios (SSP5 and RCP8.5; Fig. 2). As significant ocean warming near the AmIS appears to be a robust feature of Coupled Model Intercomparison Project Phase 5 (CMIP5) and CMIP6 models for high-emission scenarios, we expect that calibrated simulations of the AmIS forced by any of these models will predict a significant contribution to sea levels by 2300. Furthermore, we include the potential impact of surface-melt-driven hydrofracture of the ice shelf (Scambos et al., 2009), which, if included, likely will accelerate the ice shelf's demise. Three of the four hydrofracture forcing maps provided by ISMIP6-AIS-2300 for SSP5 and RCP8.5 predict the removal of the AmIS via hydrofracture between 2100 and 2200. While this process is highly uncertain and currently can only be crudely parameterized in ice-sheet models, it represents another potential threat to the AmIS's integrity.

While our projections following ice-shelf removal in the SSP5 ensemble are consistent with the extreme scenario projections in Pittard et al. (2017), there is deep uncertainty about calving processes following the ice-shelf loss. This stems from the lack of observations against which models can be calibrated and from the poorly understood physics (Pollard et al., 2015). As described in Sect. 2.1, we have disabled calving at grounded marine termini because no such termini exist for this glacier system under historical conditions, preventing the possibility of calibrating associated parameters. To explore the impact of this modeling choice on a typical ensemble member, we perform sensitivity experiments, enabling calving at grounded marine termini.

To select a typical run, we first identify the ensemble members from the filtered SSP5 projection ensemble with mass change in the year 2300 between the 40th and 60th percentiles. From this subset, we identify one run with parameter values for the calving yield stress (125 158 Pa), basal slip exponent (0.2245), basal friction scaling factor (0.9602), and ice stiffness scaling factor (0.9601), all of which are close to the means of the respective posterior distributions. In the year 2300, this run has a mass change of 77 mm SLE, which is close to the mean of the sea-level contribution's posterior-predictive distribution for the year 2300, at 79 mm SLE (Fig. 10a). Using this set of parameter values, we conduct additional SSP5 simulations, with the calving yield stress for grounded marine termini set to 1000 kPa, a typical value used for the tensile strength of ice (Petrovic, 2003; Morlighem et al., 2016; Ultee et al., 2020), and a more aggressive threshold set to the value used for floating ice (125 kPa).

Including grounded calving with a threshold stress of 1000 kPa leads to a slightly faster mass loss after the removal of the AmIS, but the glacier mass stabilizes at about the same value as when grounded calving is ignored (Fig. 13a). However, using the same 125 kPa threshold stress as that for floating ice leads to a 10-fold increase in mass loss, yielding nearly 1 m SLE by the year 2300. This behavior is analogous to that of marine ice cliff instability (Bassis and Walker, 2012; Pollard et al., 2015; DeConto and Pollard, 2016). As implemented by Pollard et al. (2015) and DeConto and Pollard (2016), marine ice cliff instability is a calving rate that is a function of ice cliff height above the water line. Here, the analogous behavior comes from the calving rate being a direct function of effective tensile stress. The effect is similar in that large effective tensile stress yields large calving rates and grounded margin retreat, which, in turn, leads to larger effective tensile stresses and faster retreat when the margin withdraws into deeper bedrock (Fig. 13b and c) because the effective tensile stress is strongly affected by subaerial cliff height. The margin retreat and mass loss seen here, with a grounded threshold stress of 125 kPa, are roughly similar to those shown by DeConto and Pollard (2016) for the same region.

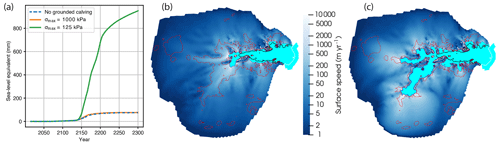
Figure 13 Sensitivity to the treatment of grounded calving. (a) Sea-level contribution when no grounded calving is assumed (dashed blue line), as in the primary results, using a typical value for the tensile strength of grounded ice (σ_max=1000 kPa; orange) and a value for the tensile strength of ice close to the maximum a posteriori value for floating ice in our calibrated ensemble (σ_max=125 kPa; green). (b) Model state in the year 2300 when using σ_max=1000 kPa. The white line indicates the initial calving front, and the black line represents the initial grounding line. Red contours indicate where the bed topography is at sea level. Cyan shading indicates ice-free-ocean portions of the domain. There is effectively no floating ice. (c) Model state in the year 2300 when using σ_max=125 kPa, as in panel (b).

The inability to calibrate the calving yield stress for grounded marine margins complicates future projections for the glacier system under this configuration. The tensile strength of ice has been estimated to be on the order of 1 MPa (Bassis and Walker, 2012; Ultee et al., 2020). The fact that our calibrated value for floating ice (125 kPa) is so much lower may represent unresolved damage and crevassing (Bassis and Ma, 2015; Lhermitte et al., 2020; Kachuck et al., 2022) in our model, which would lead to a yield strength lower than that of intact ice. In this case, a higher threshold stress would be more appropriate for grounded ice than for floating ice because the former is typically less damaged than the latter (Bassis and Ma, 2015; Kachuck et al., 2022). The inability to calibrate this parameter implies an especially large uncertainty with respect to the representation of grounded-ice calving in models. Notably, until relevant direct observations or improved prior understanding become available, this uncertainty will continue to limit the utility of Bayesian inference for quantifying the uncertainty in future sea-level rise from Antarctica.

5.3 Quantification of parametric uncertainty

A notable result of our Bayesian calibration is that the observables constrain both the MALI parameters (Fig. 7) and the projections of the MALI model, as observed by comparing the posterior- and prior-predictive distributions of future sea-level contributions (Figs. 8 and 10b). Combining three observational constraints leads to calibrated posteriors for the calving yield stress, basal friction scaling factor, ice stiffness scaling factor, and ice-shelf basal melt rate, which differ from their uncalibrated priors, whereas the posteriors for the basal slip exponent and the ice-shelf basal melt rate remain similar to their priors (Fig. 7). Consequently, when the posterior samples of the MALI parameters are propagated through the scalar GP emulator of the SSP5 projection ensemble for the year 2300, they yield a posterior-predictive distribution of future sea-level contribution, with a higher mean of 79 mm SLE (Fig. 10b). In contrast, prior samples of the MALI parameters result in a prior-predictive distribution with a mean of 59 mm SLE for the same year. Moreover, the 95 % credible intervals for the posterior- and prior-predictive distributions are [46,133] and [19,123] mm SLE, respectively, for the year 2300. This highlights that both the mean and the bounds of the credible interval have increased, while the interval itself has reduced in size for the posterior-predictive distribution. This indicates lower predictive uncertainties in future sea-level projections due to the calibrated MALI parameter samples. These observations underscore the importance of Bayesian calibration of MALI parameters in constraining and quantifying the future sea-level contribution uncertainties. Potential avenues for reducing uncertainty include (1) collecting new observations with reduced uncertainty, (2) evaluating additional observations (either our existing scalar metrics or additional metrics) at multiple time epochs, or (3) adding new scalar or spatially resolved quantities of interest. Applying Bayesian calibration to the relatively stable AmIS system, with effectively a single time point of observation, limits the amount of information that it can provide as scant information about the dynamical response to external perturbations is included in the calibration. The deep uncertainty associated with calving at grounded marine margins is an extreme case of the lack of observations – observations relevant to the key processes must exist to derive full benefit from the calibration. Incorporating paleodata (Gilford et al., 2020) or additional locations where these processes operate under historical conditions affords additional paths forward.

5.4 Model limitations and future work

There are a number of potential improvements to be made to the ice-sheet model configuration used here. The 4 km resolution used near the grounding line is likely too coarse to fully resolve grounding line dynamics (Gong et al., 2014; Hoffman et al., 2018). This resolution is a computational requirement for running a large enough ensemble to support the generation of emulators. Similarly, the model spin-up procedure results in model drift of up to about −10 mm SLE (Fig. 9a). Conducting multi-millennia spin-ups for each ensemble member (e.g., Berdahl et al., 2023) or improving model initialization techniques to minimize drift (e.g., Perego et al., 2014) would reduce this issue. We note that both approaches introduce other complications through increased simulation costs and additional differences in the initial state between ensemble members.

There are also improvements to be made to the physical-process representations in the model. Although the von Mises stress calving law employed performs well when simulating a stable AmIS calving front (Wilner et al., 2023), it cannot reproduce the historical cycles of calving front retreat and advance (Fricker et al., 2002; Greene et al., 2022; Andreasen et al., 2023). More sophisticated methods that can reproduce these cycles have yet to be implemented in large-scale ice-sheet models, but this is an area of active research (Bassis et al., 2024). The assumption of a time-invariant friction coefficient is also a limitation that requires the implementation of new process models to be resolved. We also neglect glacial isostatic adjustment, which can have strong feedbacks with marine ice-sheet evolution (Gomez et al., 2010) but likely has relatively minor impacts on the timescales considered here and in this region, where mantle viscosity is high (Whitehouse et al., 2019; Coulon et al., 2021). While we present probabilistic projections, we only consider two climate scenarios, and the climate scenario uncertainty is far larger than the parametric uncertainty being considered. Our use of a single Earth system model for climate forcing also presents a limitation necessitated by computational expense. For a given SSP, there is large uncertainty in ice-sheet model projections when applying climate forcing from different climate models (Seroussi et al., 2020, 2023, 2024).

5.5 Limitations and potential improvements for uncertainty quantification methods

Any data–model comparison is limited by the number and dimension of both input uncertainties and output data constraints. This study considers only six scalar inputs as uncertain variables to be estimated. We judge these to be influential based on domain expertise, but the model contains other parameters whose values are not known. In particular, the ice stiffness and basal friction scaling factors are a highly simplified means of representing uncertainties in what are actually two-dimensional spatial fields. Uncertainty quantification of high-dimensional field data is an open mathematical research challenge (Isaac et al., 2015; Petra et al., 2014; Brinkerhoff, 2022; Hartland et al., 2023; Riel and Minchew, 2023; Reese et al., 2024), often resorting to Gaussian posterior approximations or other approximations to accommodate the computational expenses. Another open technical question is how to combine such approximate methods with the fully non-Gaussian, asymptotically convergent Markov chain Monte Carlo methods used here for parameter estimation.

An additional limitation of this work is its reliance on scalar, temporally and spatially averaged observational constraints. We observe that the basal slip exponent (q) and the ice-shelf melt coefficient (γ₀) are largely unconstrained by Bayesian calibration, which suggests that our observational metrics are not informative about these parameters. This may be a result of over-averaging data in space and time, which can remove information. We could consider space- and time-resolved data (where available), although this would introduce additional complexities into modeling the data–model residual space–time covariance structure. This structure is likely intricate, and statistical misspecification of the model discrepancy (error) can bias inference. Calibration against multivariate data using a dimensionally reduced principal component emulator also can introduce bias (Salter et al., 2019; Salter and Williamson, 2022). We could also consider including additional observational constraints. Felikson et al. (2023) demonstrate that the choice of observable can significantly impact the projections of ice-sheet mass change. Finally, a more sophisticated treatment of multiple observational constraints will require careful treatment of the statistical covariance between observables (or, rather, between the model errors for different observables).

6 Conclusion

This study provides a comprehensive analysis of the future sea-level contribution from the AmIS catchment with quantified uncertainties. Three different observables – mass balance, grounding line movement, and calving front movement – are chosen to effectively calibrate the input parameters to the MALI ice-sheet model. Statistical emulation using GPs is used to significantly reduce the computational burden of performing Bayesian calibration and uncertainty propagation. Each observable leads to individual Bayesian calibrations of the MALI parameters using their expert-knowledge-based priors, resulting in posterior distributions. Next, we combine the effects of these three observables to effectively capture the final calibrated posterior distributions of MALI parameters. The combined calibration helps us constrain the calving yield stress, basal friction scaling factor, ice stiffness scaling factor, and ice-shelf basal melt rate parameters, while the basal slip exponent and ice-shelf basal melt rate remain unconstrained. The calibrated posteriors and their respective priors are used to sample the MALI parameters in order to propagate them through the multivariate principal component emulator to obtain posterior- and prior-predictive distributions of future sea-level contributions from the AmIS under two different emission scenarios.

Using the SSP5 high-emission scenario to highlight changes in this relatively stable glacier, our expert prior over the MALI parameters, when propagated through our scalar GP emulator, projects a mean SLE of 59 mm SLE with a 95 % c.i. of [19,123] mm in the year 2300. After constraining the MALI model parameters with observations, this projection changes to a mean SLE of 79 mm SLE with a 95 % c.i. of [46,133] mm. Both the mean and the bounds of the 95 % interval increase, while the interval itself shrinks, indicating lower predictive uncertainties in future sea-level projections due to observational constraints. The reduction in future sea-level contribution uncertainties is modest due to the limited quantity of observations and their inherent uncertainties with regard to the glacial system. In addition, because this system is close to equilibrium, the dynamical constraints on retreat are weak. While the reduced complexity resulting from the AmIS catchment being close to equilibrium makes this a relatively straightforward application of the methodology, applying it to other, more dynamic glacier systems, such as the Thwaites or Totten glaciers, could potentially lead to better-informed projections. We have developed a framework providing an end-to-end probabilistic modeling workflow, consisting of Bayesian calibration and uncertainty propagation, together with Gaussian process emulation, for similar studies that can be undertaken in the glaciological community and beyond. While Bayesian calibration is expected to be more informative for situations with a larger range of observed behaviors, our calibrated projections allow for assessing how parametric uncertainty affects the projected ice-sheet response to abrupt changes in oceanic forcing. The high- and low-greenhouse-gas-emission scenarios yield similar projections of glacier mass change for the 21st century. After abrupt ocean warming and elimination of the AmIS through basal melting, the difference between the scenarios becomes statistically significant within decades, far exceeding the parametric uncertainty in the year 2300. The results align with previous projections of the AmIS catchment, indicating stability with minimal contribution to sea-level change unless large changes in ocean temperature occur, leading to substantial sea-level rise. What has changed since previous studies of the AmIS system were conducted is the subsequent generation of Coupled Model Intercomparison Project (CMIP) model projections, extending to 2300, which predict significant ocean warming under high-greenhouse-gas-emission scenarios that were previously considered unlikely. Our study uses these newer climate projections while quantifying parametric uncertainty, allowing for evaluating the significance of differences between projections of the AmIS catchment under these climate scenarios. Major remaining uncertainties include the processes of calving and marine melting that occur once the ice shelf is removed. Feedbacks between stress state and calving at marine cliffs potentially can lead to mass loss that is 10 times larger than that of our primary ensemble, leaving a deeply uncertain long tail for future projections. Reducing this deep uncertainty will require applying uncertainty quantification methods to locations where these processes have been observed over a diverse range of behaviors and gaining a fundamental understanding of calving processes to confidently transfer this knowledge to places like the AmIS, where such events have not yet occurred.

Appendix A: Input parameters

Figure A1 Input parameter values for 200 MALI simulations generated by a Sobol sequence.

Appendix B: PCA emulator details

B1 Principal component analysis dimensionality reduction steps

This appendix presents the detailed steps for the dimensionality reduction of time series data using principal component analysis (PCA). We begin with a T×N time series data matrix, denoted by S, and extract a reduced K-dimensional principal subspace (Z₁), which has uncorrelated rows, using the linear transformation matrix P₁, consisting of K eigenvectors corresponding to top K eigenvalues. We use the following steps:

1. Compute the vector (μ) of row means of the data matrix S. Center S by subtracting μ from each column to get S_c.

2. Find the singular value decomposition of S_c,

   $$S_{\mathrm{c}}=U\mathrm{\Lambda }{V}^T,$$

   where U is a T×T orthogonal matrix of the left-singular vectors of S_c. V is an N×N orthogonal matrix containing the right-singular vectors of S_c. Λ is a T×N diagonal matrix containing singular values arranged in descending order, and large singular values correspond to the important feature directions in S_c (Shlens, 2014).

3. Let P=U^T; then, we see that

   $$P{S}_{\mathrm{c}}=U^T{S}_{\mathrm{c}}=\mathrm{\Lambda }{V}^T=Z.$$

   The rows of P represent the principal components (PCs) of S_c. Z represents the fully transformed data matrix (or full principal subspace) using all of the PCs.

4. Choose the dimensionality of the reduced principal subspace and denote it by K, where K < T. Let P₁ consist of the first K principal components. Then, P₁ forms the orthonormal basis for the reduced principal subspace. Next, project S_c onto the reduced principal subspace using the K×T transformation matrix P₁ as follows:

   $$P_{\mathrm{1}}{S}_{\mathrm{c}}=Z_{\mathrm{1}},$$

   where Z₁ represents the reduced-dimensional K×N transformed data matrix.

B2 PCA emulator predictive-mean and variance construction

We present the steps for the reconstruction of the mean and variance of the time series predictions from K emulated PCs. First, we back-transform ${\widehat{Z}}_{\mathrm{1}}$, the predictive means of the Gaussian process (GP) emulators of K PCs stacked together row-wise, as follows:

$${\widehat{S}}_{\mathrm{c}}={P_{\mathrm{1}}}^T{\widehat{Z}}_{\mathrm{1}}.$$

Then, we decentralize ${\widehat{S}}_{\mathrm{c}}$ by adding row means (μ) of the data matrix S to obtain the T×N matrix $\widehat{S}$, which represents the mean of the time series predictions. Next, we reconstruct the variance by first reconstructing the entire covariance matrix of each time series prediction as follows:

$${\mathcal{C}}_t={P_{\mathrm{1}}}^T\text{diag}({\mathit{\sigma }}_{\mathrm{1},t}^{\mathrm{2}},\mathrm{\cdots },{\mathit{\sigma }}_{K,t}^{\mathrm{2}})P_{\mathrm{1}},$$

where 𝒞_t represents the covariance matrix for the tth time series prediction and the diagonal entries are variances. Next, we concatenate individual time series variance predictions row-wise to get the T×N matrix Σ. We use Σ to evaluate credible intervals around the mean predictions ($\widehat{S}$).

Appendix C: Emulator validation continued

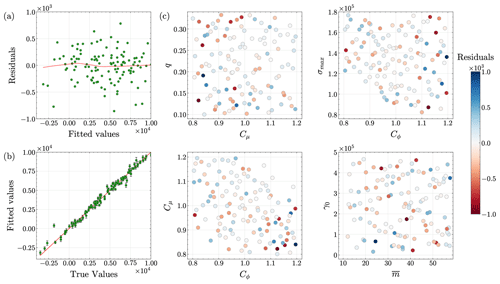
Figure C1 Analysis of the multivariate PCA GP emulator fit (using five principal components) for the change in volume above flotation in the CTRL projection ensemble for the year 2300. Shown are plots for (a) residuals versus fitted values, (b) predicted values versus actual values, and (c) residuals versus pairwise input parameters.

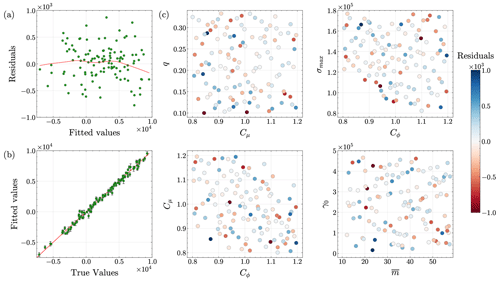
Figure C2 Analysis of the multivariate PCA GP emulator fit (using five principal components) for change in volume above flotation in the SSP1 projection ensemble for the year 2300. Shown are plots for (a) residuals versus fitted values, (b) predicted values versus actual values, and (c) residuals versus pairwise input parameters.

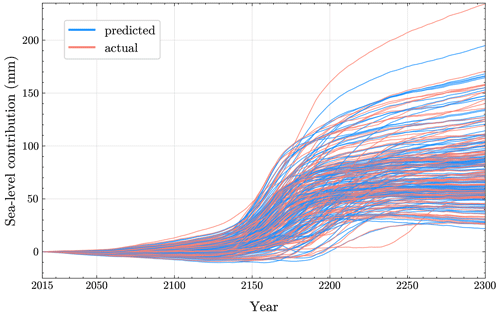
Figure C3 Multivariate PCA GP emulator predictions (using five principal components) during 5-fold cross-validation, compared with actual data for sea-level contributions (in millimeters) until the year 2300.

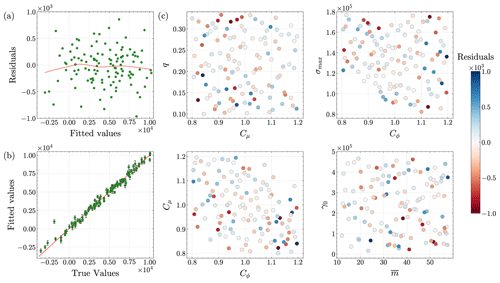
Figure C4 Analysis of the scalar GP emulator fit for change in volume above flotation in the CTRL projection ensemble for the year 2300. Shown are plots for (a) residuals versus fitted values, (b) predicted values versus actual values, and (c) residuals versus pairwise input parameters.

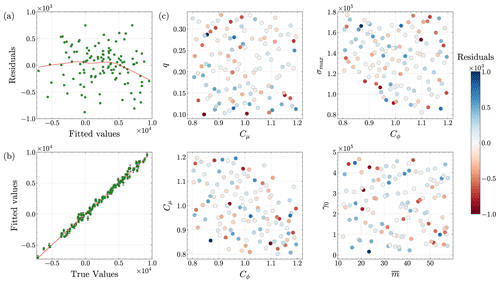
Figure C5 Analysis of the scalar GP emulator fit for change in volume above flotation in the SSP1 projection ensemble for the year 2300. Shown are plots for (a) residuals versus fitted values, (b) predicted values versus actual values, and (c) residuals versus pairwise input parameters.

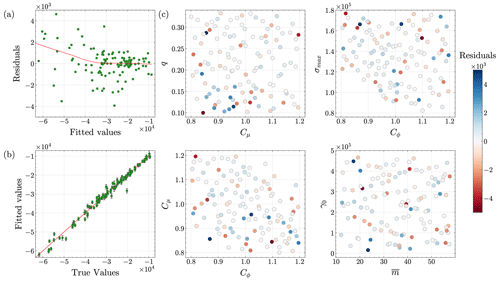
Figure C6 Analysis of the scalar GP emulator fit for change in volume above flotation in the SSP5 projection ensemble for the year 2300. Shown are plots for (a) residuals versus fitted values, (b) predicted values versus actual values, and (c) residuals versus pairwise input parameters.

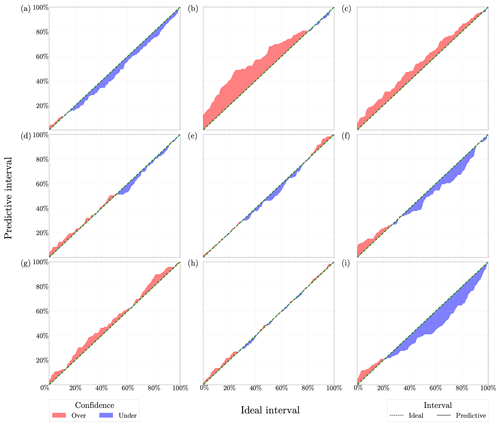
Figure C7 Gaussian process emulator predictive-coverage results for (a) calving front position, (b) grounding line position, (c) mass change, (d) the PCA emulator in the CTRL ensemble, (e) the PCA emulator in the SSP1 ensemble, (f) the PCA emulator in the SSP5 ensemble, (g) the scalar emulator in the CTRL ensemble, (h) the scalar emulator in the SSP1 ensemble, and (i) the scalar emulator in the SSP5 ensemble. The ideal interval, denoted by the dashed green line in each panel, represents the case of perfect confidence. In each panel, overconfidence is represented by the red shaded region, while underconfidence is represented by the blue shaded region. In panels (a)–(c), emulators are applied to the RELX ensemble. In panels (d)–(i), emulators are for changes in volume above flotation for the year 2300.

Appendix D: Comparison between predictions using PCA and scalar Gaussian process emulators

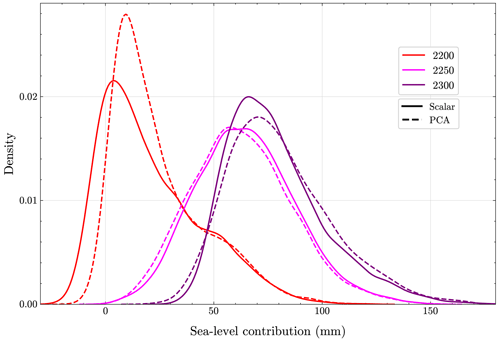
Figure D1 Comparison of posterior-predictive distributions of future sea-level contributions for the SSP5 scenario in the years 2200, 2250, and 2300, obtained using principal component analysis Gaussian process (GP) emulators versus scalar GP emulators fitted to individual-year data from the VAF change projections.