Spatial distribution of vertical density and microstructure profiles in near-surface firn around Dome Fuji, Antarctica

To better understand the near-surface evolution of polar firn in low-accumulation areas (<30 mm w.e. yr⁻¹), we investigated the physical properties – density, microstructural anisotropy of ice matrix and pore space, and specific surface area (SSA) – of six firn cores collected within 60 km of Dome Fuji, East Antarctica. The physical properties were measured at intervals of ≤0.02 m over the top 10 m of the cores. The main findings are (i) a lack of significant density increase in the top ∼4 m, (ii) lower mean density near the dome summit (∼330 kg m⁻³) than in the surrounding slope area (∼355 kg m⁻³) in the top 1 m, (iii) developments of a vertically elongated microstructure and its contrast between layers within the top ∼3 m, (iv) more pronounced vertical elongation at sites and periods with lower accumulation rates than those with higher accumulation rates, (v) a rapid decrease in SSA in the top ∼3 m, and (vi) lower SSA at lower-accumulation sites, but this latter trend is less pronounced than that of microstructural anisotropy. These observations can be explained by a combination of the initial physical properties on the surface set by wind conditions and the metamorphism driven by water vapor transport through the firn column under a strong vertical temperature gradient (temperature gradient metamorphism, TGM). The magnitude of TGM depends on the duration of firn layers under the temperature gradient, determined by the accumulation rate; longer exposure causes a more vertically elongated microstructure and lower SSA. Overall, we highlight the significant spatial variability in the near-surface physical properties over the scale of ∼100 km around Dome Fuji. These findings will help us better understand the densification over the whole firn column and the gas-trapping process in deep firn and possible difference in them between existing deep ice cores and the upcoming “Oldest-Ice” cores collected tens of kilometers apart.

1 Introduction

Understanding the physical characteristics of near-surface firn is important to many glaciological studies. For example, an accurate density profile of near-surface firn is essential to derive the surface mass balance from the change in surface height observed by satellite altimetry (e.g., Zwally et al., 2015; Alexander et al., 2019). The physical properties are also linked to the radiative characteristics in firn; for example, grain size affects surface albedo (Wiscombe and Warren, 1980) and microwave emission (Picard et al., 2014), and the number of layers per unit depth is linked to the microwave polarization ratio (Surdyk and Fily, 1995). Furthermore, the density profile over the entire firn column is affected by the density, the microstructure (the shapes and arrangements of ice matrix and pore space), and the layering in the density (or the microstructure) in the near-surface firn (Alley et al., 1982; Gerland et al., 1999; Freitag et al., 2004; Fujita et al., 2009, 2014, 2016), along with temperature, overburden pressure, and impurity concentrations (e.g., Herron and Langway, 1980; Hörhold et al., 2012; Fujita et al., 2016). The resulting mean density and density variability in deep firn determine the depth range of air enclosure into bubbles (e.g., Schwander, 1989; Mitchell et al., 2015).

Environmental conditions in the atmosphere and at the ice sheet surfaces determine the initial physical properties of firn. The deposition of snow or frost may form a firn layer, which is sometimes altered by wind-driven snow redistribution (e.g., Kameda et al., 2008) and fragmentation (e.g., Domine et al., 2009). The layers in the firn column generally exhibit a vast horizontal extent and seasonal cycles in physical properties (e.g., higher density in summer than in winter) in areas with a high accumulation rate ($>\sim \mathrm{50}$ mm w.e. yr⁻¹, Laepple et al., 2016), suggesting continuous accumulation throughout the year. In contrast, in low-accumulation areas ($<\sim \mathrm{50}$ mm w.e. yr⁻¹, represented by dome areas on the East Antarctic Plateau), the layers are tens of centimeters thick with several meters of horizontal extent and do not show seasonal cycles (e.g., Hörhold et al., 2012; Picard et al., 2019). For example, the age of surface snow can vary from 0 to 300 d within less than 100 m of horizontal distance at Dome C, leading to different initial physical properties of the snow layers (Picard et al., 2019). Also, surface mass balance can vary from −30 to 100 mm w.e. yr⁻¹ within 100 m of horizontal distance at Dome Fuji (Kameda et al., 2008). These facts indicate that snow redistribution, erosion, and precipitation intermittency disrupt homogeneous seasonal snow deposition; instead snow is deposited in patches in low-accumulation areas. After the deposition, the firn layers undergo metamorphism over time by vapor diffusion to decrease the surface free energy, whose rates primarily depend on the firn temperature (e.g., Colbeck, 1989). Moreover, varying surface heating by diurnal and seasonal variations in insolation produces a vertical temperature gradient (TG) in the top few meters, facilitating metamorphism through efficient vertical water vapor transport, where vapor sublimates from warmer grains and condenses to colder grains (e.g., Yosida, 1955; Colbeck, 1983; Pinzer et al., 2012). This process is known as temperature gradient metamorphism (TGM). The accumulation rate is an important factor for the magnitude of TGM because it determines the duration of exposure of a layer to TG (e.g., Hutterli et al., 2009). Wind ventilation may also affect the amount of sublimation and condensation within the firn by disrupting the saturation levels between the ice matrix and surrounding air (Albert, 2002). Because the above environmental conditions vary over the ice sheets, the near-surface firn density and microstructure are also expected to vary. Understanding such variabilities in the physical properties is necessary to better understand differences in the firn densification rate and the depth of air enclosure into bubbles at different sites, such as sites for existing deep ice cores and the upcoming “Oldest-Ice” cores tens of kilometers apart (e.g., Fischer et al., 2013; Parrenin et al., 2017; Obase et al., 2023).

Numerous studies have investigated the physical properties of near-surface firn and their relationship with environmental factors. Near-surface firn densities have been widely measured in Dronning Maud Land, East Antarctica, showing strong dependence of the average density on the annual mean wind speed; lower wind speed leads to lower density (e.g., Sugiyama et al., 2012). Firn cores from multiple polar sites showed that the density variability in the top few meters increases with a decreasing mean annual temperature and accumulation rate (within the ranges of 25–180 mm w.e. yr⁻¹ and −53 to −18 ^∘C, respectively) (Hörhold et al., 2011). Density typically increases with depth due to grain packing and sintering (e.g., Kojima, 1971; Craven and Allison, 1998; Salamatin et al., 2009; Hörhold et al., 2011). However, a few studies have reported a lack of significant density increase in the top 2 or 3 m in the interior plateau, e.g., at Point Barnola (Calonne et al., 2017) and on the Dronning Maud Land plateau (Endo and Fujiwara, 1973; Weinhart et al., 2020), possibly because of a small overburden pressure and high viscosity of firn due to low temperature (Endo and Fujiwara, 1973; Calonne et al., 2017) or strong TGM (Alley, 1987).

Typical methods to investigate the microstructure of polar firn are visual inspection of pit walls or image analysis of thin sections of firn samples (e.g., Koerner, 1971; Rick and Albert, 2004; Courville et al., 2007). Recent studies have also applied X-ray computed tomography (CT), a high-resolution 3-D imaging technique, to investigate polar firn (Freitag et al., 2004; Fujita et al., 2009; Hörhold et al., 2009; Lomonaco et al., 2011; Linow et al., 2012; Calonne et al., 2017; Moser et al., 2020). The X-ray CT has revealed that polar firn has a vertically elongated structure comprising ice matrix and pore spaces, probably formed by TGM. The previous studies have also reported an increase in snow grain size and decrease in snow specific surface area (SSA: the area of the ice–pore interface per unit mass of firn) with depth, particularly in the top few meters (e.g., Linow et al., 2012; Calonne et al., 2017; Moser et al., 2020). Some studies also investigated the spatial variability in the near-surface microstructures. Courville et al. (2007) found larger faceted grains in the top 2 m at a site with an accumulation hiatus compared to those at a site with accumulation (<40 mm w.e. yr⁻¹) in a megadune region, East Antarctica. For West Antarctic sites with an accumulation rate of 160–200 mm w.e. yr⁻¹, lower accumulation rates are associated with a more vertically elongated structure in a 15 m deep firn core (Hörhold et al., 2009). These studies suggested that the accumulation rate influences the magnitude of TGM by controlling the exposure time of layers under TG in the top few meters. Linow et al. (2012) also reported the variability in SSA profiles at six sites with different accumulation rates (25–180 mm w.e. yr⁻¹) and temperatures (−53 to −18 ^∘C). Their SSA profiles were reproduced by an SSA evolution model incorporating the accumulation rate and snow temperature as inputs, suggesting that near-surface SSA depends on the accumulation rate and temperature. The SSA measurement using near-infrared light has also been applied to polar firn (e.g., Gallet et al., 2011; Libois et al., 2014; Picard et al., 2014, 2022). For example, pit wall observations along a traverse route from the coast to Dome C revealed a predominance of rounded grains at the surface of Dome C, and SSA at Dome C was higher than expected from an empirical SSA–density relationship for seasonal snow (Gallet et al., 2011). Thus, this study concluded that wind increases SSA through snow grain transport, fragmentation, and sublimation (Domine et al., 2009) at the surface of Dome C.

However, most of the previous studies have been conducted in high-accumulation sites (>50 mm w.e. yr⁻¹) and key aspects for the evolution of near-surface density and microstructure at low-accumulation sites, such as Dome Fuji, Dome C, or Vostok, remain poorly documented or understood. For example, (i) the inland sites tend to lack density increase in the top few meters, but the mechanisms are uncertain. (ii) The high-resolution microstructure profile in the top few meters has not been investigated beyond visual inspection in the Dome Fuji area. (iii) The differences in the developments of density and microstructure of different layers are not well understood. (iv) It is uncertain whether the effects of the accumulation rate, temperature, and wind speed on density and microstructure, observed over the fairly different environments in previous studies, are noticeable even within smaller environmental changes realistic for low-accumulation areas (e.g., accumulation rates of 13–35 mm w.e. yr⁻¹ during glacial–interglacial cycles at Dome Fuji (Parrenin et al., 2016)).

To address these issues, the density and microstructure must be investigated at high resolution for multiple sites in low-accumulation areas. However, the near-surface firn in these areas is often too fragile to perform detailed on-site or laboratory measurements of physical properties. In particular, thin-section analysis and X-ray CT measurement typically require thin or small cylindrical samples, which, being fragile, are technically challenging and time-consuming to use. These difficulties may have hindered continuous or multi-site measurements of the firn properties. Here, several optical or electrical methods can provide continuous, high-resolution, non-destructive, and time-efficient measurements. For example, gamma-ray or X-ray transmission measurements provide high-resolution density data on millimeter scales (e.g., Gerland et al., 1999; Hori et al., 1999). Near-infrared (NIR) reflectivity measurements determine the SSA of snow and firn (e.g., Matzl and Schneebeli, 2006; Arnaud et al., 2011). Tensorial values of relative permittivity in microwave and millimeter wave frequencies, which can be measured using an open resonator, provide the proxy for microstructural anisotropy of firn (e.g., Fujita et al., 2009, 2014, 2016). Fujita et al. (2009, 2016) applied this method to three firn cores drilled near Dome Fuji Station, but the measurements were limited to depths below 10 m due to poor core recovery at shallower depths.

In this study, we measured the density, microstructural anisotropy, and SSA of six firn cores drilled at five sites around Dome Fuji, continuously at high resolution (0.0025–0.02 m) using optical and electrical methods. Our data provide a first detailed view of the vertical density and microstructure profiles in the top few meters around Dome Fuji. Moreover, they allow for a comparison of the properties among six firn cores collected from the five sites with different environments. Based on the new data, we discuss the key processes for the evolutions in density and microstructure and possible causes for their spatial and temporal variabilities.

2 Methods

2.1 Study area and samples

In Antarctica, the accumulation rate varies depending on the topography and atmospheric circulation (which influences moisture transport) from the coast to inland areas. In Dronning Maud Land, anticyclonic activities play a major role in transporting heat and moisture from lower latitudes toward Dome Fuji (Fig. 1a). These activities tend to originate from the eastern Atlantic Ocean and Indian Ocean (e.g., Suzuki et al., 2008; Hirasawa et al., 2013). At Dome Fuji Station, strong winds mostly blow from the northeast (53±48^∘ for wind speeds above 8 m s⁻¹, black arrow in Fig. 1b). Since air masses tend to release their moisture when they blow in the upslope direction due to orographic lift, snow accumulation is higher on the northeastern side (windward side) of the topographical ridge along the northwest direction compared to on the leeward side (Fujita et al., 2011; Van Liefferinge et al., 2021; Oyabu et al., 2023).

We analyzed six firn cores from five sites around Dome Fuji: NDF, NDFN, DFSE, DFS, and DFNW (Fig. 1b). Information on the sites and cores is listed in Table 1 and briefly described below. The NDF and NDFN sites are located 54 and 48 km south of Dome Fuji Station, respectively. Two cores were collected from the NDF site in December 2012 and 2017, located 0.2 km apart and named NDF13 and NDF18, respectively (Oyabu et al., 2023). A core was collected from the NDFN site in December 2018. The DFSE and DFNW sites are located 44 km southeast and 28 km north of Dome Fuji Station, respectively. A core was collected from each site in 2017–2018. We carefully drilled, handled, and transported the cores to preserve the physical properties in the top several meters. The cores were transported within a temperature range of −30 to −15 ^∘C during the transport from the field to a ship (for ∼20 d, of which ∼5 d was above −20 ^∘C) and at −28 ^∘C during the ship transport (for ∼80 d) and then were stored at −30 ^∘C. The good sample conditions allowed us to perform continuous physical measurements on the near-surface firn around Dome Fuji. In addition, we used published data from the DFS10 core collected 9 km south of Dome Fuji Station (Fujita et al., 2016).

Among our sample locations, the DFNW site has the highest accumulation rate (29.4 mm w.e. yr⁻¹ for 1885–1992 CE), which is 24 % higher than the lowest accumulation rate at NDF13 (23.7 mm w.e. yr⁻¹) (Oyabu et al., 2023). The accumulation rate is one of the most variable environmental factors among the core sites; e.g., 10 m snow temperature shows minor relative differences of 3 % (Table 1).

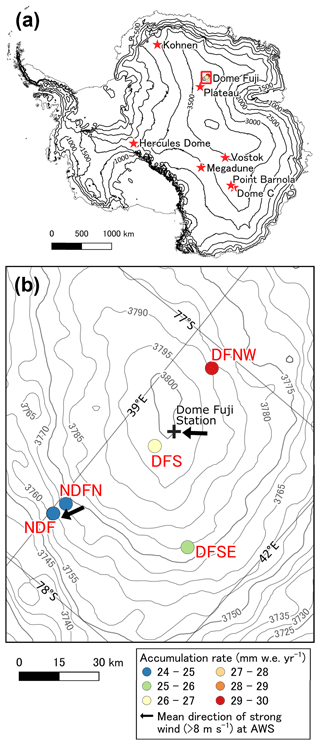
Figure 1 Map of study sites. (a) Topographic map of Antarctica. The red rectangle indicates the Dome Fuji area. (b) Enlarged view of the Dome Fuji area. The solid circle marker indicates a site where one or two firn cores were collected for this study. The color of the marker represents the accumulation rate for 1980–2018 CE (Oyabu et al., 2023). Two black arrows show the mean direction of strong wind (>8 m s⁻¹) measured at the automatic weather station (AWS) located at Dome Fuji Station (53^∘) (Fujita et al., 2011) and the NDF (26^∘) (https://ads.nipr.ac.jp/real-time-monitors/ndf/, last access: 22 March 2022) (this study). Contours in (a) and (b) show elevation (m a.s.l.) based on the CryoSat-2-derived elevation model referenced to WGS84 (Helm et al., 2014).

Table 1 Information on the sampling sites and firn cores.

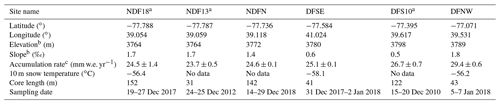
^a The number after the letter designation indicates the year of the field campaign (Fujita et al., 2016; Oyabu et al., 2023). ^b Based on the CryoSat-2-derived elevation model referenced to WGS84 (Helm et al., 2014). ^c Average and 68 % confidence interval for 1885–1992 CE, derived from the depth–age relationships of firn cores (Oyabu et al., 2023).

2.2 Measurements

The density, microstructural anisotropy, and SSA were measured, as described below (summarized in Table 2). All measurements were performed at the National Institute of Polar Research (NIPR), Japan.

2.2.1 Density measurement using the gamma-ray transmission method

The high-resolution density (ρ) profiles were measured using a gamma-ray transmission densimeter (PH-1100, Nanogray Inc., Japan) (Miyashita, 2008) on the NDF18, NDFN, DFSE, and DFNW cores (see Fig. 2a for the measurement setup). The densimeter measures the attenuation of a gamma-ray beam that passes through the firn samples and converts it into ρ using Beer's law. The firn cores were cut into a slab-shaped sample, typically 0.5 m long, 0.06 m wide, and 0.038 m thick. The cut surfaces of the samples were smoothed using a microtome for precise sample parallelism and thickness. We used a slit of lead with an aperture width of 0.0033 m to detect the gamma-ray transmission through samples, and we measured ρ at 0.003 m depth increments. The error in ρ is 1 %–2 %, including the error of sample thickness (1 %) and gamma-ray counting (1.5 %) (e.g., Gerland et al., 1999; Hori et al., 1999).

Table 2 Characteristics of the measurements performed on the six firn cores.

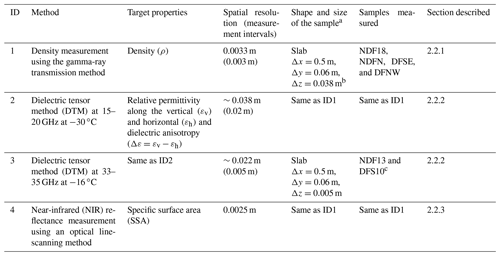
^a Δx, Δy, and Δz are sample length, width, and thickness, respectively. ^b Δz of the NDFN core is 0.063 m for ID1 and 0.043 m for ID2 and ID4. ^c Data from Fujita et al. (2016).

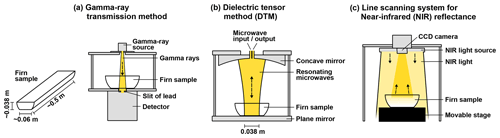
Figure 2 Schematics of the physical measurement setups. (a) Gamma-ray transmission density measurement. (b) Dielectric tensor method (DTM) at 15–20 GHz (in the case of the NDF18, NDFN, DFSE, and DFNW cores). (c) Line-scanning system for NIR reflectance. The schematics illustrate the cross-section of the setups, along with the horizontal sections of firn cores. The firn cores were moved perpendicularly to the page during measurement.

2.2.2 Dielectric tensor method

The relative permittivity of firn at high frequencies between short radio wave (MHz) and millimeter wave (GHz) frequencies primarily depends on the firn density (e.g., Cumming, 1952; Kovacs et al., 1995; Fujita et al., 2014). The relative permittivity (hereinafter, permittivity) is also influenced by the firn microstructure. If the firn has an anisotropic microstructure, that is, comprising ice matrix and pore spaces with anisotropic shapes, the permittivity parallel to the anisotropic longer axis is larger than that along the anisotropic shorter axis (e.g., Lytle and Jezek, 1994; Fujita et al., 2009, 2014, 2016; Leinss et al., 2016).

We detected firn density and microstructural anisotropy through the dielectric tensor method (DTM) (Fig. 2b) (Matsuoka et al., 1998; Fujita et al., 2009, 2014, 2016; Saruya et al., 2022a, b). We used an open resonator to simultaneously measure the permittivity parallel (vertical, ε_v) and perpendicular (horizontal, ε_h) to the core axis. Subsequently, we calculated their difference Δε ($={\mathit{\epsilon }}_{\mathrm{v}}-{\mathit{\epsilon }}_{\mathrm{h}}$), which we define as dielectric anisotropy, as a proxy for microstructural anisotropy. We performed the DTM on the five firn cores: NDF13, NDF18, NDFN, DFSE, and DFNW. Additionally, we used the published data of the DFS10 core (Fujita et al., 2016). The NDF18, NDFN, DFSE, and DFNW cores were measured at 15–20 GHz frequencies at −30 ^∘C in 2019–2021. The Gaussian beam through a sample had a diameter of ∼0.038 m at the $\mathrm{1}/e^{\mathrm{2}}$ intensity level of peak intensity, and we measured ε in 0.02 m depth increments. The samples measured were the same as those for the gamma-ray transmission density measurement. The NDF13 and DFS10 cores were measured at 33–35 GHz at −16 ^∘C in 2012–2015. The beam diameter and depth increment were ∼0.022 and 0.005 m, respectively. The slab-shaped samples were ∼0.005 m thick and 0.06 m wide.

The permittivity (ε_h) was converted to density (ρ_ε) using empirical relationships between ε_h and ρ_ε at the measurement temperature of −16 or −30 ^∘C. For measurements at −30 ^∘C (NDF18, NDFN, DFSE, and DFNW), we used the following empirical equation derived by Oyabu et al. (2023):

$$\begin{array}{}\text{(1)}& {\mathit{\rho }}_{\mathit{\epsilon }}=-\mathrm{20.15}{\mathit{\epsilon }}_{\mathrm{h}}^{\mathrm{3}}+\mathrm{99.801}{\mathit{\epsilon }}_{\mathrm{h}}^{\mathrm{2}}+\mathrm{243.02}{\mathit{\epsilon }}_{\mathrm{h}}-\mathrm{220.57}.\end{array}$$

For measurements at −16 ^∘C (NDF13 and DFS10), Oyabu et al. (2023) derived the following equation from a relationship between ε_h and ρ_ε given by Fujita et al. (2014):

$$\begin{array}{}\text{(2)}& {\mathit{\rho }}_{\mathit{\epsilon }}=-\mathrm{5.556}{\mathit{\epsilon }}_{\mathrm{h}}^{\mathrm{3}}-\mathrm{4.0922}{\mathit{\epsilon }}_{\mathrm{h}}^{\mathrm{2}}+\mathrm{494.14}{\mathit{\epsilon }}_{\mathrm{h}}-\mathrm{436.121}.\end{array}$$

The analytical uncertainty in ε_h is ±0.005, and the total uncertainty in the converted density is ∼9 kg m⁻³ in the top several meters, including errors in ε and density for calibration (Oyabu et al., 2023).

Following Fujita et al. (2009), Δε is related to the axial ratio R, the ratio between the correlation length of pore space in the vertical direction and that in the horizontal direction. It is expressed using the following equation:

$$\begin{array}{}\text{(3)}& R=\mathrm{3.761}\mathrm{\Delta }\mathit{\epsilon }+\mathrm{0.954}.\end{array}$$

The analytical uncertainty in Δε is <0.001 (Fujita et al., 2016; Saruya et al., 2022b), and the total uncertainty in R is 0.08, including the errors in Δε and R for calibration.

2.2.3 SSA

Snow SSA is the area of ice-to-pore interface per unit mass of firn (e.g., Legagneux et al., 2002). Assuming that snow grains are spherical, the relationship between SSA and the sphere radius (r) is expressed as follows (e.g., Gallet et al., 2009):

$$\begin{array}{}\text{(4)}& \mathrm{SSA}={\displaystyle \frac{\mathrm{3}}{r{\mathit{\rho }}_{\mathrm{ice}}}},\end{array}$$

where ρ_ice is the density of pure ice (917 kg m⁻³ at 0 ^∘C). SSA can be estimated by measuring the reflectance of NIR light with a wavelength of 750–1400 nm (e.g., Matzl and Schneebeli, 2006; Gallet et al., 2009, 2011; Libois et al., 2015), based on Mie theory (e.g., Wiscombe and Warren, 1980).

We used an optical line-scanning system (e.g., Takata et al., 2004) (Fig. 2c) to measure the NIR reflectance at high resolution (0.0025 m) on the NDF18, NDFN, DFSE, and DFNW cores. The system comprises LED light sources with a center wavelength of 930 nm and a half-power width of ∼50 nm, along with a charge-coupled device (CCD) camera (C3077-79, Hamamatsu, Japan) with high sensitivity at 800–1100 nm, mounted 0.4 m above the measured surface of a firn sample. A slab-shaped sample, whose surface was smoothed using a microtome, was placed on a movable stage. During the measurement, the sample was irradiated with NIR light while moving the stage at a constant speed, and the CCD camera continuously recorded the brightness of pixels in the direction perpendicular to the moving direction of the sample stage. The individual-pixel data were compiled into an image of the entire firn sample. The brightness was calibrated into reflectance using four reflectance standards: 98.8 %, 81.9 %, 67.7 %, and 23.5 %. Subsequently, we converted the reflectance into SSA using an empirical relationship between the reflectance measured by our system and the SSA measured using the Handheld Integrating Sphere Snow Grain Sizer (Aoki et al., 2023), which is applicable for SSA less than 14 m² kg⁻¹ (see Appendix A for details). Our system has a measurement resolution of 0.00025 m (pixel size), and we obtained the data at 0.0025 m depth increments. The systematic error in SSA measurement is ±2 m² kg⁻¹ for SSA less than 20 m² kg⁻¹ (Aoki et al., 2023), and the error for the regression curve for calibration is 0.4 m² kg⁻¹ for SSA between 2 and 5 m² kg⁻¹ and 0.9 m² kg⁻¹ for SSA between 5 and 14 m² kg⁻¹ (Appendix A). The SSA decrease due to metamorphism during sample transportation is expected to be less than 15 % if SSA is less than 15 m² kg⁻¹, according to the empirical SSA reduction rate (Taillandier et al., 2007). Although metamorphism during transportation may cause a systematic error, it does not affect our discussions on relative variability in SSA (e.g., differences among sites and variations within each core).

2.3 Data processing and analyses

We standardized the depth resolutions of the measured properties (ρ, ε_v, ε_h, Δε, and SSA) and unified the depth intervals using the following procedures. First, we manually removed outliers at the core breaks from the raw data. Then, we smoothed the ρ and SSA data by seven- and eight-point moving averages, respectively, both corresponding to a resolution of ∼0.02 m. For the ε and Δε profiles, the NDF13 and DFS10 data (measured at 33–35 GHz) were smoothed by a four-point moving average (resolution of ∼0.035 m). No smoothing was applied to the NDF18, NDFN, DFSE, and DFNW core data (measured at 15–20 GHz) with a measurement resolution of ∼0.038 m. Finally, we linearly interpolated all data at 0.02 m depth intervals except for the core breaks. The intervals used for interpolation did not affect our result, as long as they were smaller than ∼0.05 m to resolve firn layers in our cores.

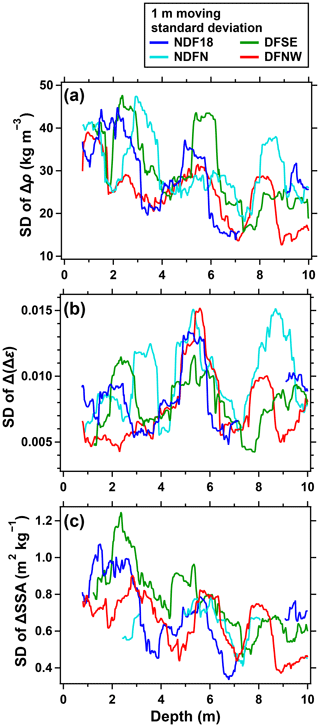
To identify the general trends in ρ, ε_h, Δε, and SSA, we calculated 0.5 m moving averages of their interpolated data at 0.02 m intervals. The average was not calculated for the 0.5 m interval containing nine data points or fewer (<0.1 m) because the data often represent only one layer. To analyze the firn layering, we detrended the ρ, Δε, and SSA data by subtracting their 0.5 m moving averages from the 0.02 m interpolated data. We calculated 1 m moving standard deviations (SDs) of the detrended data as a measure of variability in ρ, Δε, and SSA and linear correlation coefficients between the pairs of properties within 1 m moving intervals to identify the depth ranges with their strong and weak covariations. The moving SD and correlation coefficients were only calculated for the NDF18, NDFN, DFSE, and DFNW cores with the ρ and SSA data. The 1 m intervals containing a data coverage of <0.5 m were excluded from the analyses.

3 Results

We describe the general trend of density (ρ or ρ_ε), Δε, and SSA and their variabilities in the top 10 m of firn at each site. We focus on the top few meters, where initial metamorphism is expected to be large due to large vertical TGs (e.g., Azuma et al., 1997). Figure 3a–d show ρ, ε_v, ε_h, Δε, and SSA of the NDF18 core (see Fig. 3e–t for the data of other cores). The 0.5 m moving averages of ρ, ε_h, Δε, and SSA are shown (dashed black lines in Fig. 3) to identify their general trends and variabilities around the trends.

3.1 Density

The density profiles of the six cores around Dome Fuji are characterized by relatively large variability without significant trends in the top 4 m (Fig. 3), contrary to the expectation from typical firn densification processes such as grain packing and sintering. For the NDF18 core, ρ (and ρ_ε) ranges between 255 and 460 kg m⁻³ at 0–4 m, and the slopes of linear regression for the data are −2 and −4 kg m⁻³ m⁻¹ (i.e., density change per meter depth) for 0–2 and 2–4 m, respectively (p>0.05). Below 4 m depth, significant linear trends of 12, 13, and 15 kg m⁻³ m⁻¹ are observed for 4–6, 6–8, and 8–10 m, respectively (p<0.05). The 0.5 m moving averages of ρ_ε measured in all six cores show no systematic differences exceeding the measurement error of ∼9 kg m⁻³ (Fig. 4a). Similarly to the NDF18 core, the NDFN, DFSE, and DFNW cores do not show significant increasing trends of ρ_ε in the top 2 m (the NDF13 and DFS10 cores were excluded from the analysis due to sparse data). Below ∼2 m, the moving averages of ρ_ε increase to ∼365 kg m⁻³ at ∼4 m and exceed the ρ_ε range in the top ∼2 m.

The density in each core fluctuates significantly around the moving average on scales of ∼0.05–0.3 m, reflecting the density layering of firn (Fig. 3), whose amplitudes appear to decrease with depth. To investigate the evolution of the density variability, we calculated the 1 m moving SD of the deviations (referred to as Δ) of the 0.02 m resolution data from the 0.5 m moving average for the NDF18, NDFN, DFSE, and DFNW cores (Fig. 6a; see Fig. 5 for the deviations Δρ). The moving SD of Δρ decreases from ∼40 kg m⁻³ at 0.75 m to ∼20 kg m⁻³ at 10 m in the four cores; a decreasing trend is typically observed in polar firn (e.g., Fujita et al., 2009, 2016; Hörhold et al., 2011). In addition, the moving SD fluctuates by ∼10–20 kg m⁻³, which is larger than the 95 % confidence interval of ±5 kg m⁻³ based on the chi-square distribution, with large values at the depths with high-density layers, e.g., at around 5.4 m in the NDF18 core (Fig. 5a) and 5.7 m in the DFSE core (Fig. 5c). The local maxima and minima of the moving SD for the four cores tend to appear at similar depths (maxima around 2.5, 5.5, and 8.5 m depths and minima around 4.0 and 7.0 m depths).

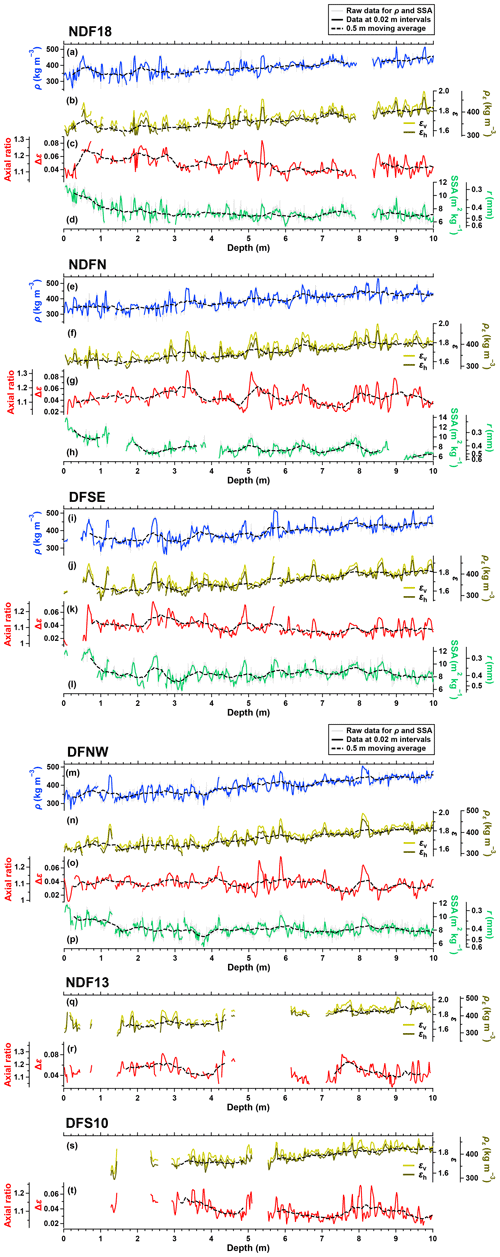
Figure 3 Measured physical properties for 0–10 m of the six firn cores within 60 km of Dome Fuji. (a, e, i, m) Density ρ, (b, f, j, n, q, s) relative permittivity parallel to the core axis ε_v and perpendicular to the core axis ε_h, (c, g, k, o, r, t) dielectric anisotropy Δε ($={\mathit{\epsilon }}_{\mathrm{v}}-{\mathit{\epsilon }}_{\mathrm{h}}$), and (d, h, l, p) SSA. Gray, solid dark, and dashed lines indicate raw data for ρ and SSA, data at 0.02 m intervals, and 0.5 m moving averages, respectively. The axis of ρ_ε next to the ε axis is obtained from the relationship between ε_h and ρ_ε (Eqs. 1 and 2) (Oyabu et al., 2023). The axis of the axial ratio next to the Δε axis is obtained from the empirical relationship between the axial ratio and Δε (Eq. 3) (Fujita et al., 2009). The axis of the grain radius r next to the SSA axis is obtained from SSA (Eq. 4).

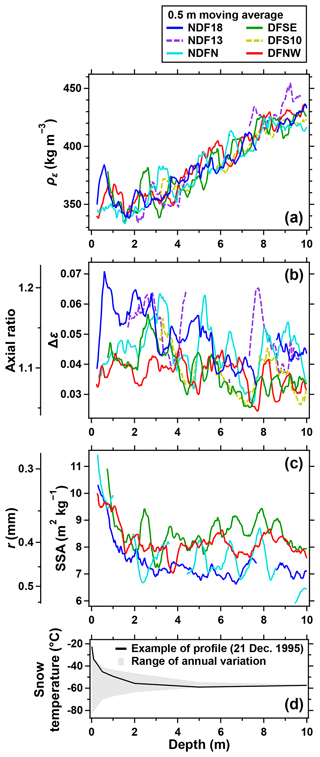
Figure 4 General trends in ρ_ε, Δε, and SSA of the NDF18, NDF13, NDFN, DFSE, DFS10, and DFNW cores. (a) Moving average of ρ_ε using a 0.5 m window. (b, c) The same as (a) but for Δε and SSA, respectively. (d) Snow temperature profile measured in a borehole at Dome Fuji Station (Azuma et al., 1997). The black line is an example profile when TG is high near the surface (12:00 LT on 21 December 1995). The shading indicates the range of the snow temperature during 1995.

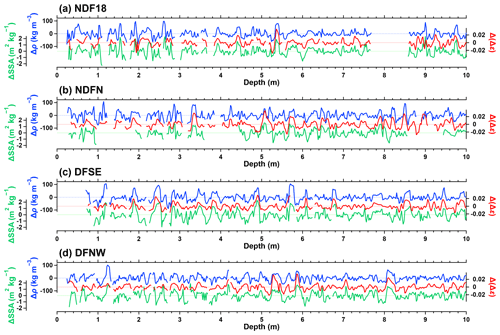
Figure 5 Anomalies (referred to as Δ) of ρ, Δε, and SSA of the (a) NDF18, (b) NDFN, (c) DFSE, and (d) DFNW cores. Δρ, Δ(Δε), and ΔSSA are obtained by subtracting the 0.5 m moving average from their data at 0.02 m intervals. Amplitudes of Δρ and ΔSSA decrease with depth, while the amplitude of Δ(Δε) is low at the shallowest depths and increases toward approximately 5 m. Prominent maxima (or minima) of Δρ, Δ(Δε), and ΔSSA appear at similar depths.

Figure 6 Standard deviations (SDs) of Δρ, Δ(Δε), and ΔSSA of the NDF18, NDFN, DFSE, and DFNW cores. (a) Moving SD of Δρ using a 1 m window. Windows with a data coverage of <0.5 m were excluded from the calculation. (b, c) The same as (a) but for Δ(Δε) and ΔSSA, respectively.

3.2 Dielectric anisotropy

The Δε of the NDF18 core increases rapidly with depth from ∼0.035 near the surface to ∼0.07 at 0.5 m, corresponding to the increasing axial ratio from ∼1.1 to ∼1.2, indicating the development of the vertically elongated structure of ice matrix and pores (Fig. 3c). Below 0.5 m depth, the moving average of Δε generally decreases with depth with fluctuations on scales from several tens of centimeters to meters (e.g., maxima around 2.8 m depth and minima around 3.2 m depth). The initial increase and subsequent general decrease in the moving average of Δε are also observed at other sites around Dome Fuji (Figs. 3g, k, o, r, and t and 4b). Similar development in microstructural anisotropy near the surface has been observed at high-accumulation sites – Hercules Dome in West Antarctica (160–200 mm w.e. yr⁻¹) (Hörhold et al., 2009) and Summit in Greenland (220 mm w.e. yr⁻¹) (Lomonaco et al., 2011) – but not at low-accumulation sites in East Antarctica (<30 mm w.e. yr⁻¹), probably due to a poor core quality or recovery rate in the top several meters in the previous studies (Fujita et al., 2009, 2016). The average Δε for 0.0–0.5 m depth ranges from 0.03 to 0.04 for most of our studied sites. Below 0.5 m depth, Δε values are generally higher at the southern sites (NDF and NDFN) than at the northern sites (DFSE, DFS, and DFNW).

The deviations of Δε from the 0.5 m moving averages, Δ(Δε), show large variations on scales of ∼0.05–0.3 m, indicating the microstructural layering of the firn (Fig. 5). The evolution of Δε variability is represented by the 1 m moving SD of Δ(Δε) for the NDF18, NDFN, DFSE, and DFNW cores (Fig. 6b), which are relatively low at the shallowest depths and increase with depth toward the first local maxima between 2 and 4 m. Below 4 m, the moving SD for each core fluctuates with amplitudes of >0.005 (exceeding the 95 % confidence interval of ±0.001 kg m⁻³ based on the chi-square distribution), and their maxima occur at similar depths (around 5.5 and 8.5 m). The maxima and minima in the moving SD of Δ(Δε) appear at similar depths to those in the moving SD of Δρ (Fig. 6).

Close inspection of the Δ(Δε) from the four cores reveals that their prominent maxima (minima) coincide with those of Δρ (Fig. 5), e.g., at 4.4 and 5.4 (2.0 and 6.0) m in the NDF18 core (Fig. 5a). To investigate the relationship between Δ(Δε) and Δρ, we calculated their correlation coefficients with a 1 m moving window (Fig. 7a). Δ(Δε) and Δρ positively correlated for all cores throughout the 0–10 m depth range. This result is consistent with the previous finding that high-density layers show high Δε (Fujita et al., 2009, 2016). The correlation coefficient is the smallest near the surface and increases until ∼3 m, probably because the variability in Δ(Δε) is small near the surface (for example, large Δρ peaks at ∼1.4 m of the NDF18 core and ∼1.2 m of the NDFN, DFSE, and DFNW cores are not accompanied by marked peaks in Δ(Δε)).

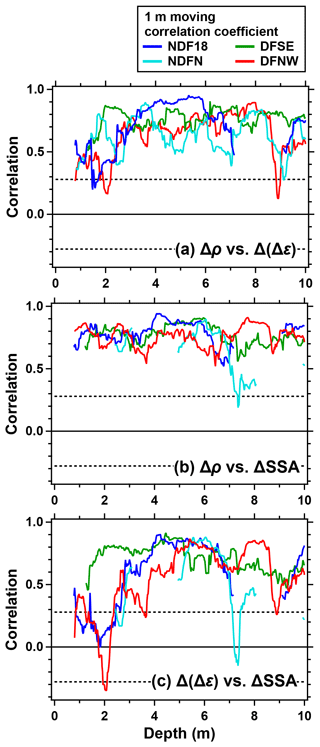
Figure 7 Correlation coefficients between the pairs of Δρ, Δ(Δε), and ΔSSA of the NDF18, NDFN, DFSE, and DFNW cores. (a) The moving correlation coefficient between Δρ and Δ(Δε) using a 1 m window. Windows with a data coverage of <0.5 m were excluded from the calculation. The dotted horizontal lines indicate the 95 % confidence level of the correlation coefficient (data between the two lines are not significant, p>0.05). (b, c) The same as (a) but for the correlation coefficient between Δρ and ΔSSA and between Δ(Δε) and ΔSSA, respectively.

3.3 SSA

The SSA of the NDF18 core decreases from ∼11 m² kg⁻¹ near the surface to ∼7 m² kg⁻¹ at ∼3 m, corresponding to an increase in r from ∼0.3 to ∼0.5 mm (Fig. 3d). The rate of decrease becomes smaller with depth, and the 0.5 m moving average of SSA is stable below ∼3 m. The initial decrease and relatively stable values of SSA below ∼3 m are also observed at NDFN, DFSE, and DFNW (Figs. 3h, l, and p and 4c). The SSA decrease in the top few meters is consistent with the observations at Point Barnola (Calonne et al., 2017), Dome C (Gallet et al., 2011), Kohnen Station, and Hercules Dome (Linow et al., 2012). Furthermore, the southern sites (NDF and NDFN) show smaller SSA than the other sites (DFSE and DFNW) (Fig. 4c). Around the moving averages, SSA fluctuates on scales of ∼0.05–0.3 m (Fig. 3d, h, l, p). The 1 m moving SD of ΔSSA (deviation of SSA from its 0.5 m moving average, Fig. 5) decreases with depth in the NDF18, NDFN, DFSE, and DFNW cores (Fig. 6c). The maxima and minima of the moving SD occur at similar depths in the four cores, coinciding with those of the moving SD of Δρ and Δ(Δε) (maxima around 2.5, 5.5, and 8.5 m and minima around 4.0 and 7.0 m) (Fig. 6).

The evolutions of the relationships of SSA with ρ and Δε are investigated by the correlation coefficients of ΔSSA to Δ(Δε) or Δρ with a 1 m moving window (Fig. 7b and c) (see also Fig. B1 for scatterplots between SSA and ρ with color representing Δε). The prominent maxima and minima of ΔSSA tend to coincide with those of Δρ and Δ(Δε); for example, the high (low) SSA layer at 5.4 (6.0) m shows high (low) Δρ and Δ(Δε) in the NDF18 core (Fig. 5a). The 1 m moving correlation coefficients between Δρ and ΔSSA (Fig. 7b) and between Δ(Δε) and ΔSSA (Fig. 7c) are predominantly positive for the four cores. In addition, while the correlation coefficient between Δρ and ΔSSA is consistently high, the correlation coefficient between Δ(Δε) and ΔSSA (or Δρ) is small or insignificant near the surface and increases until ∼3 m. This is partly due to the absence of prominent Δ(Δε) maxima at the depths of ΔSSA and Δρ maxima near the surface.

4 Discussion

Our continuous and high-resolution data of ρ, ε, Δε, and SSA from six firn cores around Dome Fuji provide detailed views of the vertical profiles of these properties at low-accumulation sites (<30 mm w.e. yr⁻¹). In the following, we discuss the key processes for the evolution of density (Sect. 4.1), microstructural anisotropy (Sect. 4.2), and SSA (Sect. 4.3) in the top few meters that are common to the six cores. Further, we discuss the causes of spatial and temporal variabilities in these properties around Dome Fuji.

4.1 Density evolution

4.1.1 Processes for the density evolution

Our ρ (or ρ_ε) data in the NDF18, NDFN, DFSE, and DFNW cores do not show a significant increase in the ∼0–4 m range, despite being 50–65 years after deposition (Fig. 4a). The lack of density increase in the four cores is consistent with previously published data from pit studies near the respective drilling sites (Fig. 8 and Table 3). Previous studies at other low-accumulation sites at altitudes above 3000 m a.s.l. have also shown a lack of significant density increase in the top 2 or 3 m, e.g., at Point Barnola (Calonne et al., 2017) and the Dronning Maud Land plateau (Endo and Fujiwara, 1973; Weinhart et al., 2020). These observations suggest that the lack of density increase in the top few meters is a common feature in the Antarctic inland plateau.

Endo and Fujiwara (1973) and Calonne et al. (2017) speculated that the lack of mean density increase in near-surface firn is due to insufficient overburden pressure to facilitate the settling of firn with high viscosity and resistance to deformation due to low temperature (e.g., Kojima, 1971; Vionnet et al., 2012). However, the low densification rate cannot explain the decrease in density for the top ∼2 m (Fig. 3a and Table 3). A potential process that may contribute to the density decrease is mass loss of the near-surface firn through TGM; because the near-surface firn is exposed to high TG, which facilitates vapor transports, part of the upward vapor flux may be released to the atmosphere without condensing in the shallower firn, potentially leading to a net mass loss. Another possibility may be that the density decrease in the top 2 m reflects the increasing trend of the surface density over the past few decades, but consistent mean densities of ∼350 kg m⁻³ in the top 1 m were observed around Dome Fuji in 1968, 1994, and 2007 CE (Endo and Fujiwara, 1973; Shiraiwa et al., 1996; Sugiyama et al., 2012), implying that the variability in surface density around Dome Fuji has been small over the past half-century. To quantitatively assess the effects of slight overburden pressure and mass loss processes, observations of the strain rate of the near-surface firn and mass balance by sublimation and condensation in the top few meters would be necessary.

The density variability in the NDF18, NDFN, DFSE, and DFNW cores decreases with depth over the top 10 m (see moving SD in Fig. 6a), consistent with previous observations of polar firn (e.g., Fujita et al., 2009, 2016; Hörhold et al., 2011). Earlier studies have suggested that the decrease in density variability is due to the density dependence of the densification rate; the densification rate of a high-density layer may be lower than that of a low-density layer because the vertical bonds between finer grains in high-density layers provide resistance to deformation (Alley et al., 1982; Freitag et al., 2004; Fujita et al., 2009, 2016). In contrast, a low-density layer, typically composed of coarser grains, settles rapidly because its larger pores are less likely to be filled with ice bonds (e.g., Fujita et al., 2009). Our data are consistent with previous studies showing that the high-density layers (positive Δρ) have a more vertically elongated structure (positive Δ(Δε)) and finer grains (positive ΔSSA) than the low-density layers (Figs. 5 and 7). According to Fujita et al. (2009), the two types are referred to as initially high-density firn (IHDF) and initially low-density firn (ILDF), respectively.

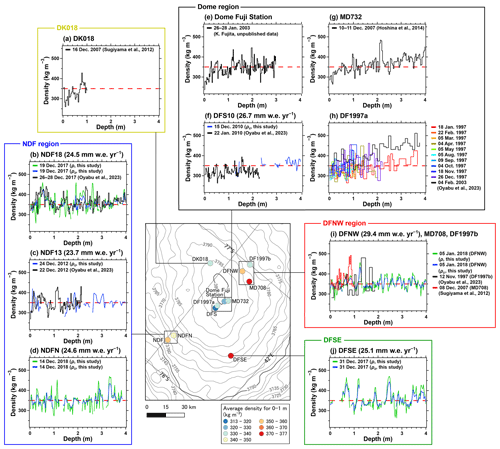
Figure 8 Density profiles from the sites around Dome Fuji listed in Table 3. The dashed red line is the reference line of 350 kg m⁻³. The accumulation rate for sites where the data are available for 1885–1992 CE is shown after the site name (Oyabu et al., 2023). The densities in the top 1 m in the NDF, DFNW, and DFNW regions and at DFSE are higher than those in the Dome region and at DK018.

Table 3 Near-surface density around Dome Fuji.

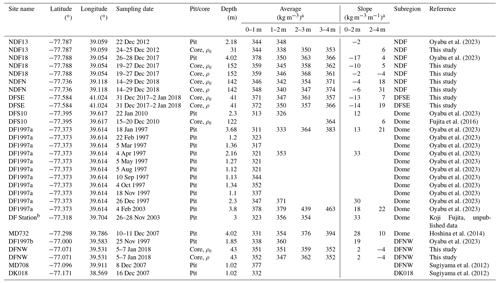
^a Depth intervals with a data coverage of <0.5 m were excluded from the calculation. ^b DF Station denotes Dome Fuji Station.

Furthermore, the SD of Δρ in all four cores shows three maxima at similar depths (Fig. 6a). Because the density variability may be predominantly determined by the occurrence and intensity of IHDF (see Fig. 5), the SD fluctuations may reflect the past environmental conditions that form IHDFs. The intense IHDFs are formed by wind packing (Koerner, 1971; Fujita et al., 2009), and their densities depend on wind speed (e.g., Sugiyama et al., 2012). Thus, the wind environment, such as the mean wind speed or wind gust frequency, is probably a key factor controlling density variability (Fig. 6a) by affecting the frequency of snow redistribution and the degree of packing at the surface. The accumulation rate and temperature may also determine density variability. Previous observations at multiple polar sites have shown a negative correlation between density variability in the top several meters and accumulation rate (temperature) for 25–180 mm w.e. yr⁻¹ (−53 to −18 ^∘C) (Hörhold et al., 2011), although the cause for the correlation is not well understood. In our data, a spatial relationship between the density variability and accumulation rate (or temperature) is not observed (Fig. 6a and Table 1), presumably because of the narrow ranges of the mean accumulation rate (23–30 mm w.e. yr⁻¹) and temperature (−56.2 to −58.1 ^∘C). Thus, we suggest that the accumulation rate or temperature does not explain the density variability around Dome Fuji.

4.1.2 Variability in density evolution around Dome Fuji

The densities of the NDF, NDFN, DFSE, and DFNW cores agree with the published data from pit studies near the respective drilling sites, and the values in the top 1 m (∼355 kg m⁻³) are higher than those near the flat dome summit (central part of the dome summit and along the ridge: dome region and DK018 in Table 3) (∼330 kg m⁻³). Previous studies at the Dronning Maud Land plateau above 3000 m a.s.l. (excluding the dome summit) have observed a similar mean density in the top 1 m (350–355 kg m⁻³) (Endo and Fujiwara, 1973; Shiraiwa et al., 1996; Sugiyama et al., 2012; Weinhart et al., 2020). Shiraiwa et al. (1996) noted that the average density decreases toward the dome summit. Published pit studies at Dome C have also reported low density at the surface (∼280 kg m⁻³), increasing in the top several tens of centimeters (Gallet et al., 2011), similar to the density profiles near the Dome Fuji summit (Fig. 8). Our results and previous observations suggest that relatively low density near the surface is a local characteristic at the dome summit over the vast inland plateau.

To further investigate the density variability around Dome Fuji, we categorized the observed sites into five subregions based on their proximity (Table 3 and Fig. 8) and analyzed the density distribution at 0–1 and 1–2 m depths for each region (Fig. 9). At 0–1 m, densities in the NDF and DFNW regions and DFSE are normally distributed around averages of ∼355 kg m⁻³. Layers with higher densities than the average (e.g., peaks around ∼400 kg m⁻³ at DFSE and in the DFNW region) are wind-packed IHDFs, and layers with lower densities may originate from surface hoar or diamond dust (e.g., Koerner, 1971; Alley, 1988). In contrast, densities in the dome region and DK018 rarely exceed 400 kg m⁻³ and are more often below 300 kg m⁻³ at 0–1 m compared to the NDF and DFNW regions and DFSE, resulting in the lower mean density. The shift of the density distribution toward lower values may reflect snow deposition characteristics at the dome summit, which could be influenced by local topography. For example, the absence of intense IHDFs (>400 kg m⁻³) at the dome may be because wind-blown snow does not tend to ascend slopes and reach the dome. In contrast, distinct ILDFs (<300 kg m⁻³) may occur because surface hoar or diamond dust is deposited predominantly under the calm condition of the dome summit. The ILDFs typically have fragile structures, possibly contributing to the density increase toward 2 m depth (Fig. 9b).

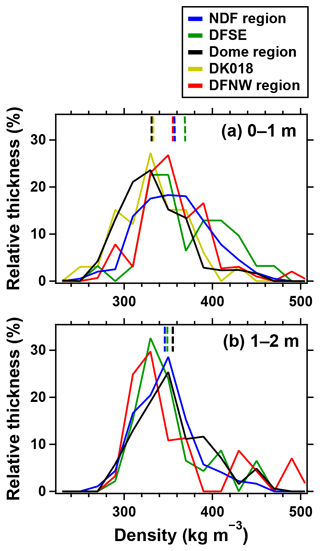
Figure 9 Density distribution of firn cores and pit walls in the five subregions around Dome Fuji. Solid lines indicate the relative cumulative thickness of cores and pit walls in each density range with a bin width of 20 kg m⁻³ for (a) 0–1 m and (b) 1–2 m. The density data are derived from the firn cores (ρ) in this study and pit wall observations in the literature: 5 profiles in the NDF region, 1 profile at DFSE, 15 profiles in the dome region, 1 profile at DK018 (32 km northwest of Dome Fuji Station), and 3 profiles in the DFNW region (see Table 3 for the site information and Fig. 8 for the density profiles). Dashed lines at the top of each panel indicate the average density for the regions.

4.2 Evolution of microstructural anisotropy

4.2.1 Effect of TGM on anisotropy

Microstructural anisotropy of ice and pores in the snow increases with TGM based on laboratory experiments (Pfeffer and Mrugala, 2002; Schneebeli and Sokratov, 2004; Srivastava et al., 2010; Calonne et al., 2014). The TGM may explain the depth profiles of our Δε data in the Dome Fuji area, with the development of microstructural anisotropy within the top ∼3 m (Fig. 4b), where seasonal and diurnal temperature variations create large vertical TGs of up to 15 K m⁻¹ (Fig. 4d). We can assume that a fresh snow layer at the surface has homogeneous or horizontally elongated structure (e.g., Leinss et al., 2016) with Δε (axial ratio) of 0 (1), and Δε (axial ratio) increases to ∼0.03–0.04 (∼1.07–1.10) within the top few tens of centimeters, where TG is the largest. Below ∼3 m depth, where the TG is much smaller than the shallower depths, the vertical anisotropy decreases with depth, probably because a part of the vertical alignment of grains collapses through grain packing (Fujita et al., 2009, 2014, 2016; Löwe et al., 2011).

The increase in the SD of Δ(Δε) (Fig. 6b) and the correlation coefficient between Δ(Δε) and Δρ (or ΔSSA) (Fig. 7a and c) within the top ∼3 m may be caused by selective developments of microstructural anisotropy in the IHDFs (Fig. 5). This observation is consistent with earlier experimental evidence that the magnitude of TGM depends on the density of snow samples (Akitaya, 1974; Pfeffer and Mrugala, 2002; Schneebeli and Sokratov, 2004). For example, Pfeffer and Mrugala (2002) applied realistic TG (20–80 K m⁻¹) to snow block samples with various densities (32–400 kg m⁻³) to investigate the metamorphism with thin-section stereological analysis and hardness measurement after 3 d. They found that the vertical bonds between snow grains associated with snow hardening markedly developed in high-density snow during TGM. Thus, the density-dependent TGM preferentially develops the microstructural anisotropy in IHDFs and may explain the correlation between the SDs of Δ(Δε) and Δρ below ∼3 m depth (Fig. 6a and b).

The causes for the density dependence of TGM are unknown. We suggest that pore size, thermal conductivity, and air permeability play key roles in the density dependence as follows. During the TGM, the smaller pore sizes in the IHDFs may facilitate bond formation between the grains, while larger pores in the ILDFs are less likely to be filled with ice matrix (e.g., Akitaya, 1974; Marbouty, 1980). Furthermore, smaller grains in IHDFs should change their aspect ratios more easily by water vapor condensation at the top or bottom of the grains. In addition, the higher thermal conductivity and lower permeability in IHDFs (Calonne et al., 2011) result in lower TG and less efficient vapor transport through the IHDFs. This may result in net transfer of mass from ILDFs to IHDFs and further facilitate vertical bond formation between grains in IHDFs, developing the contrast of microstructural anisotropy between the layers.

4.2.2 Spatial relationship between the accumulation rate and anisotropy

Our data show higher Δε at the southern sites (NDF and NDFN) than at the other sites (DFSE, DFS, and DFNW) (Fig. 4b). Based on the discussion in Sect. 4.2.1, these microstructural features suggest that the near-surface firn at the southern sites undergoes enhanced TGM compared to at the other sites. We discuss the effects of the mean accumulation rate, one of the most variable environmental factors among the sites (Table 1), as a possible cause of the different magnitudes of TGM.

The accumulation rate determines the residence time of a firn layer in the top few meters where TG is large; thus, it should have a negative correlation with the magnitude of TGM (Courville et al., 2007; Hörhold et al., 2009). The average Δε values for 0–0.5, 0.5–3, 3–6, and 6–9 m in the six cores are plotted against the accumulation rate for 1885–1992 CE (Oyabu et al., 2023) (Fig. 10a). Furthermore, we show the mean residence time of a layer in the top 3 m by dividing the water equivalent depth of 1050 mm, which is the average of the six cores at 3 m depth, by the accumulation rate (shown on the second bottom axis). Δε tends to be high at the NDF and NDFN sites with lower accumulation rates for all the depth ranges compared to the other sites with higher accumulation rates. In all the cores, the largest changes in Δε are observed between 0–0.5 and 0.5–3 m depths (black and red markers in Fig. 10a), where the firn is exposed to large TG (Fig. 4d; also see Sect. 4.2.1). In addition, the magnitudes of Δε changes in the top 3 m appear to be negatively correlated with the accumulation rate; the increase in the axial ratio converted from Δε is ∼3 times larger at NDF and NDFN than at DFNW (Fig. 10a). The axial ratio for 3–6 and 6–9 m depths is larger at the lower-accumulation sites than at the higher-accumulation sites, suggesting that the spatial differences in the microstructural anisotropy developed by TGM are maintained in the deeper firn. Therefore, we conclude that the accumulation rate plays a significant role in controlling the magnitude of TGM around Dome Fuji, primarily through its effect on the residence time of a firn layer in the top few meters.

The sensitivity of Δε to the accumulation rate is higher at lower accumulation rates (Fig. 10a), implying a positive feedback between TGM and microstructural anisotropy. The firn with more vertically elongated structure (created by TGM) becomes more permeable, thereby facilitating vertical vapor transport and potentially leading to stronger TGM. To confirm the non-linearity and this hypothesis, more data from sites with varying accumulation rates should be collected.

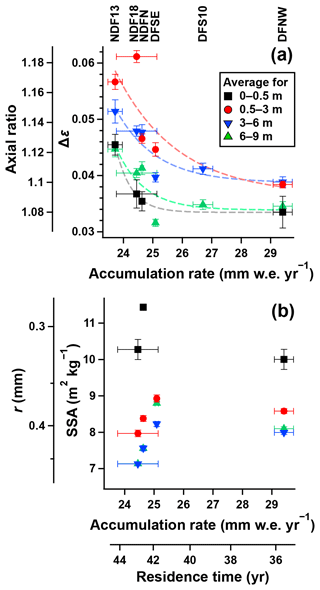
Figure 10 Spatial relationship between Δε (or SSA) and the accumulation rate. (a) Averages of Δε for 0–0.5, 0.5–3, 3–6, and 6–9 m of the six cores plotted against the accumulation rate. Vertical and horizontal error bars indicate standard errors of the Δε average and standard deviations of the accumulation rate, respectively (Oyabu et al., 2023). The Δε average is not calculated when there is a lack of data for more than one-third of each depth range. Dashed lines are exponential fitting lines for each depth range. (b) The same as (a) but for SSA. The second horizontal axis shows the residence time for which a certain layer stays in the top 3 m.

4.2.3 Temporal relationship between the accumulation rate and anisotropy

The 0.5 m moving averages of Δε for all the six cores show fluctuations on scales from several tens of centimeters to meters (Fig. 4b). The fluctuations in microstructural anisotropy may reflect the variations in the past accumulation rate, as observed in the Hercules Dome core (Hörhold et al., 2009). To analyze the fluctuations, we detrended the 0.5 m moving averages of Δε below 1 m (called Δε_det) using the linear regression, and the age scales of our cores are made by linear interpolation between the volcanic peaks (arrows in Fig. 11) with water equivalent depth (Oyabu et al., 2023) (Fig. 11a). Some maxima and minima of the Δε_det for the six cores appear at similar ages (maxima in 1880–1900, 1930–1950, and 1965–1990 CE, and minima in 1900–1930, 1950–1965, and 1990–2005 CE). The mean of the six cores (black line in Fig. 11a) also shows multidecadal fluctuations, exceeding the 68 % confidence interval for the six-core average based on the t distribution (shaded area in Fig. 11a). These results suggest spatial coherence in Δε_det on multidecadal timescales, which may reflect the temporal variations in the mean accumulation rate in the Dome Fuji area.

We compare the fluctuations in Δε_det with past accumulation rates reconstructed for two sites by counting crust layers on pit walls, assuming their formation in summers (Koerner, 1971; Hoshina et al., 2014) (Fig. 11c). The first site is Plateau Station, located 216 km southwest of Dome Fuji Station, covering 1842–1965 CE (Koerner, 1971) (Fig. 1a). The second site is 3 km northeast of Dome Fuji Station, covering 1958–2007 CE (Hoshina et al., 2014). There is no significant difference in the mean accumulation rates between the two sites (the average and standard error for the Dome Fuji and Plateau locations for each period are 29.3±2.5 and 27.8±0.1 mm w.e. yr⁻¹, respectively). We use these data because they are the only available data on a sub-decadal scale for 1880–2005 CE around Dome Fuji. They contain annual variability caused by local factors such as inhomogeneous deposition due to wind-driven redistribution and precipitation intermittency (e.g., Kameda et al., 2008). Thus, we calculated their 8-year moving averages, roughly corresponding to smoothing over ∼0.5 m intervals (thick lines in Fig. 11c), to compare them with the smoothed Δε_det data.

The 8-year moving averages of accumulation rates show maxima in 1900–1920, 1950–1965, and 1980–2005 CE and minima in 1880–1900, 1920–1950, and 1965–1980 CE (Fig. 11c). They are negatively correlated with the Δε_det of the NDF13, NDFN, DFS10, and DFSE cores ($r=-\mathrm{0.52}$ to −0.81), although there is no significant correlation for the NDF18 ($r=-\mathrm{0.24}$) and DFNW ($r=-\mathrm{0.03}$) cores, partly due to specific layers, such as low Δε layers in 1965–1975 CE (3–3.6 m in Fig. 3c) and a thick high-Δε layer in 1910–1915 CE (8–8.3 m in Fig. 3o), respectively. The mean Δε_det of the six cores, which smooths out fluctuations due to such specific layers in each core, shows a strong negative correlation with the smoothed accumulation rates ($r=-\mathrm{0.72}$) (Fig. 12a). To account for the uncertainties in the smoothed accumulation rates (shaded areas in Fig. 11c) in the significance test of the negative correlation, we use a Monte Carlo approach; the 8-year mean accumulation rates and the mean Δε_det of the six cores are randomly varied 1000 times according to their t-distributed probability (error bars in Fig. 12a indicate the 68 % confidence intervals), and linear regression is calculated for each pseudo-data set. The mean slope of the 1000 data set is significantly negative ($-\mathrm{0.0009}\pm \mathrm{0.0006}$ mm w.e. yr⁻¹). The negative correlation suggests that the microstructural anisotropy developed more prominently during low-accumulation periods (long exposure to TG) than high-accumulation periods, highlighting the importance of accumulation rates for the microstructural anisotropy.

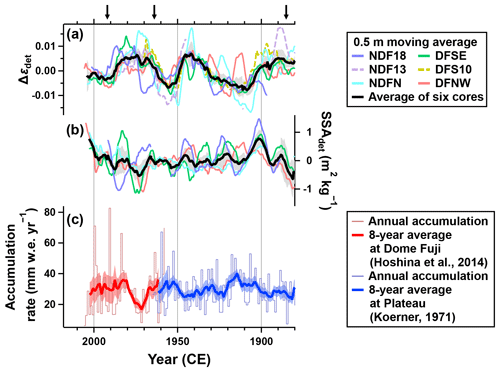
Figure 11 Temporal change in Δε, SSA, and the accumulation rate. (a) Detrended 0.5 m moving averages of Δε (Δε_det) for the six cores, plotted against the year (CE). The age scales of the cores are made by linear interpolation between the volcanic peaks (black arrows) with water equivalent depths (Oyabu et al., 2023). The solid black line and shaded area indicate the average of the six cores and the 68 % confidence interval for the average based on the t distribution, respectively. (b) The same as (a) but for the detrended moving averages of SSA for the four cores. (c) The accumulation rates at Dome Fuji (3 km northeast of Dome Fuji Station) (Hoshina et al., 2014) and Plateau Station (Koerner, 1971), derived by counting summer crust layers on pit walls as annual layer boundaries. The thin lines, thick lines, and shaded areas indicate annual accumulation, an 8-year moving average, and the 68 % confidence interval for the average based on the t-distribution, respectively.

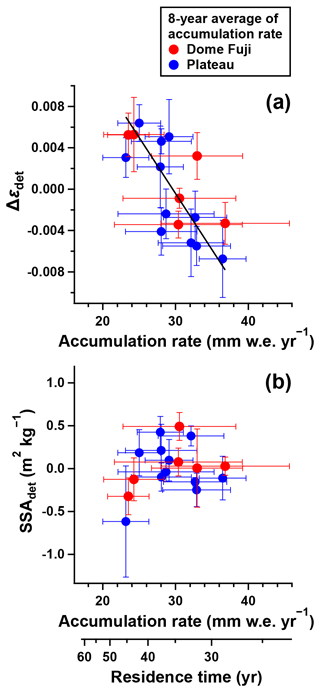
Figure 12 Temporal relationship between Δε (or SSA) and the accumulation rate. (a) Scatterplot of the mean Δε_det for the six cores (Fig. 11a) against the 8-year average of the accumulation rate (Fig. 11c). (b) Scatterplot of the mean SSA_det for the four cores (Fig. 11b) against the 8-year average of the accumulation rate. Vertical and horizontal error bars indicate the 68 % confidence intervals based on the t-distribution for the Δε_det (SSA_det) average and the 8-year average of the accumulation rate, respectively. The black line is a standardized major axis regression to the data. The second horizontal axis shows the residence time for which a certain layer stays in the top 3 m.

4.3 SSA evolution

4.3.1 Effect of TGM on SSA

Grain growth (SSA decrease) during TGM has been observed in laboratory experiments (e.g., Marbouty, 1980; Calonne et al., 2014) and the top few meters of firn in the Antarctic inland (e.g., Gallet et al., 2011; Linow et al., 2012; Calonne et al., 2017). Our data show decreases in SSA in the top ∼3 m in the Dome Fuji area (Fig. 4c), consistent with the earlier studies. Below ∼3 m depth, the SSA decrease is not observed, probably because of small TG.

According to laboratory experiments, TGM is also expected to increase SSA variability (Akitaya, 1974; Marbouty, 1980; Pfeffer and Mrugala, 2002; Schneebeli and Sokratov, 2004) (see Sect. 4.2.1). For example, Marbouty (1980) applied realistic TG (25–66 K m⁻¹) to snow block samples with various densities (180–370 kg m⁻³) and measured the grain size over a month; less grain growth was observed for finer and denser snow. However, we do not observe a significant increase in the SD of ΔSSA in the top ∼3 m of the four cores (Fig. 6c), indicating that the effect of TGM does not significantly change the initial variability in SSA. The ΔSSA is strongly correlated with Δρ from the surface (Figs. 5 and 7b), and both the SD of ΔSSA and the SD of Δρ generally decrease with depth with similar large fluctuations (Fig. 6a and c). These results suggest that SSA is largely determined by the depositional environment at the surface, as is the case for density (see Sect. 4.1.1), and that wind may play a key role. Strong winds may cause higher SSA and density by forming wind-packed layers composed of fragmented fine grains through snow redistribution (Domine et al., 2009).

4.3.2 Relationship between the accumulation rate and SSA

We discuss the differences in SSA among the studied sites and their possible causes. Our data show lower SSA at the southern sites (NDF and NDFN) than the other sites (DFSE and DFNW) (Fig. 4c), possibly because of stronger TGM caused by the longer residence time of a certain layer in the top several meters due to the lower accumulation rates, as discussed from Δε data (see Sect. 4.2.2). The average SSA values for 0–0.5, 0.5–3, 3–6, and 6–9 m in the four cores are plotted against accumulation rates for 1885–1992 CE (Fig. 10b). The largest changes in SSA occur between 0–0.5 and 0.5–3 m (black and red markers in Fig. 10b), where firn is exposed to large TG, in the NDF18, NDFN, and DFNW cores (the DFSE core lacks the data for 0–0.5 m depths). Between the two depth ranges, SSA decreases more at lower-accumulation sites; the increase in grain radius r (second left axis in Fig. 10b) is ∼2 times larger at NDF and NDFN than at DFNW. This stronger reduction in near-surface SSA at the lower-accumulation sites probably explains the lower SSA at NDF and NDFN than at DFNW in the deeper depths (3–6 and 6–9 m). These results suggest that SSA is indeed affected by the accumulation rate through the residence time.

However, the correlations between SSA and the accumulation rate for the four depth ranges are not as pronounced as those between Δε and the accumulation rate (especially for 0–0.5 m depths) (Fig. 10a), with SSA at DFSE showing the largest value despite having an intermediate accumulation rate among the four sites (Fig. 10b). These results suggest that the post-depositional SSA changes through the TGM do not fully replace the initial SSA variations determined by the depositional environments at the surface. For example, the highest SSA at DFSE might be due to the lower surface topographic slope (Table 1), possibly leading to preferential deposition of wind-driven segmented snow with fine grains (Domine et al., 2009). This is consistent with the observation of more intensive wind-packed layers (higher ρ and SSA layers) in the DFSE core compared to the other cores (Fig. 3). To identify the environmental factors controlling SSA at the surface and in the firn, more data from sites with varying depositional environments (e.g., wind speed and topographic slope) are needed.

The spatial relationship between SSA and the accumulation rate (albeit a weak relationship) might hold for their temporal variations, as seen in the relationship between Δε and the accumulation rate (see Sect. 4.2.3). However, the SSA_det values (detrended 0.5 m moving average of SSA below 1 m using the linear regression) do not show significant fluctuations on scales of several tens of centimeters or meters that covary in the four cores (Fig. 11b). Moreover, no correlation is found between the SSA_det for each core (or mean SSA_det of the four cores) and accumulation rate (Fig. 12b). The mean slope of linear regressions for the 1000 data set in a Monte Carlo approach (described in Sect. 4.2.3) is 0.02±0.04 m² kg⁻¹ $/$ mm w.e. yr⁻¹. Thus, we conclude that the role of TGM in SSA evolution in firn is minor compared to the depositional environmental factors, which can significantly alter the initial SSA at the surface. This contrasts with the strong imprint of TGM on microstructural anisotropy, which is essentially isotropic at the surface and is developed primarily by TGM.

5 Conclusions

We continuously measured density, microstructural anisotropy, and SSA at high resolution (0.0025–0.02 m) for the top 10 m of six firn cores collected within 60 km of Dome Fuji. These data provide the first detailed view of the vertical density and microstructure profiles in a low-accumulation area (23–30 mm w.e. yr⁻¹). Furthermore, we investigated the spatial and temporal variabilities in the physical properties of near-surface firn around Dome Fuji. Our main findings are summarized as follows:

1. The density of the NDF18, NDFN, DFSE, and DFNW cores does not significantly increase within the top ∼4 m. The density variability (SD of Δρ) shows fluctuations with a decreasing trend over 10 m depth, with maxima appearing at similar depths in the four cores. These maxima possibly formed during the periods with strong winds that can form wind-packed high-density layers through snow redistribution. The density in the top 1 m is higher at the four sites (∼355 kg m⁻³) than near the flat dome summit or ridge (∼330 kg m⁻³), suggesting that snow deposition patterns (e.g., wind packing and frost) vary around the dome summit.

2. The vertically elongated structure of the ice matrix and pores (i.e., microstructural anisotropy) is developed within the top ∼3 m due to large vertical TGs caused by seasonal and diurnal temperature variations. The variabilities in microstructural anisotropy (SD of Δ(Δε)) increase within the top ∼3 m, with the development of positive correlations between anisotropy and density, suggesting selective developments of microstructural anisotropy in IHDFs. The correlation between the variabilities (SDs) in microstructural anisotropy and density (or SSA) holds below ∼3 m. The microstructural anisotropy is more developed at the southern sites with lower accumulation rates than the northern sites with higher accumulation rates around Dome Fuji. Furthermore, from the surface to ∼10 m depth (roughly over the last century), the layers formed during the periods of relatively low accumulation may have developed higher microstructural anisotropy compared to those formed during the periods of relatively high accumulation. The negative correlations between microstructural anisotropy and accumulation rate suggest that the magnitude of early-stage, post-depositional microstructural development is primarily controlled by the accumulation rate through TGM.

3. Grain growth, as indicated by SSA decrease, is observed in the top ∼3 m probably due to TGM. Lower SSA (stronger TGM) is observed at the southern sites with lower accumulation rates around Dome Fuji. The spatial and temporal correlations between SSA and accumulation rate are weak, suggesting a minor role of TGM in SSA evolution in firn. Instead, the initial SSA at the surface set by the depositional environments (such as wind) may be preserved and dominate the post-depositional SSA variabilities.

The density, microstructural anisotropy, and SSA in the top few meters of the studied sites may influence the densification rates in the deeper firn and the layering in the bubble close-off region, affecting the gas fractionations of trapped air (e.g., Fujita et al., 2009). Understanding these processes in the deeper firn must be investigated in the future to better interpret gas signals in the deep ice cores.

Appendix A: Conversion of NIR reflectance to SSA

We constructed an empirical relationship between SSA and NIR reflectance measured by our optical line-scanning system. For SSA measurements, we used a Handheld Integrating Sphere Snow Grain Sizer (HISSGraS) (Aoki et al., 2023), which has the same measurement principle as the widely used IceCube for SSA measurement (Gallet et al., 2009). HISSGraS can directly measure the plane surface of snow samples with a spatial resolution of 0.025 m. It measures NIR reflectance comprising directional and hemispherical reflectances whose fractions are known, allowing the conversion of reflectance into SSA using a theoretical SSA–reflectance relationship calculated with a radiative transfer model (Aoki et al., 1999). The systematic error in SSA measurement using the HISSGraS is $\pm \sim \mathrm{2}$ m² kg⁻¹ for SSA less than 20 m² kg⁻¹ (Aoki et al., 2023). Here, we measured SSA at 0.02 m intervals for 19 core samples with <0.5 m length from the 0–60 m depth range of the NDFN core and compared SSA with NIR reflectance measured using our system. Figure A1a shows the result for 4.21–4.41 m as an example. We confirm that the NIR reflectance correlates with SSA, with both showing higher values at shallower depths. Figure A1b shows the relationship between measured SSA and NIR reflectance together with the theoretical relationship between SSA and directional (or hemispherical) NIR reflectance at 930 nm with a half-power width of 50 nm, calculated using a radiative transfer model (Aoki et al., 1999). A quadratic regression curve derived from all the NIR reflectance and SSA data is

$$\begin{array}{}\text{(A1)}& \mathrm{SSA}=\mathrm{0.0131}{\mathrm{NIR}}^{\mathrm{2}}-\mathrm{1.20}\text{NIR}+\mathrm{30.1}.\end{array}$$

The regression curve aligns with the two theoretical SSA–reflectance relationships, with our data mostly falling between the two curves, suggesting that the reflectance measured by our system is intermediate between directional and hemispherical reflectance. The root mean square error of the regression curve is 0.4 m² kg⁻¹ for SSA between 2 and 5 m² kg⁻¹ and 0.9 m² kg⁻¹ for SSA between 5 and 14 m² kg⁻¹.

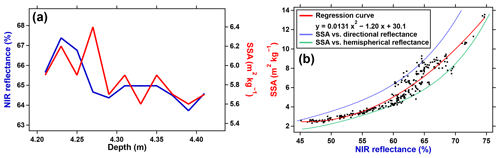
Figure A1 (a) NIR reflectance measured using our optical line scanner system (blue) and SSA measured using HISSGraS (red) for 4.21–4.41 m of the NDFN core. Data at 0.02 m intervals are shown. (b) Relationship between NIR reflectance and SSA. The red line indicates a quadratic regression curve. The blue (green) line indicates the relationship between SSA and directional (hemispherical) NIR reflectance at 930 nm with a half-power width of 50 nm, calculated using a radiative transfer model (Aoki et al., 1999).

Appendix B: Relationship between ρ, Δε, and SSA

The evolutions of the relationships of SSA with ρ and Δε are investigated by scatterplots of SSA against ρ for the four cores, as well as by the correlation coefficients of ΔSSA to Δ(Δε) or Δρ with a 1 m moving window (Fig. 7b and c). The color of marker in the scatterplots represents depth (Fig. B1a, c, e, g) or Δε (Fig. B1b, d, f, h). The variations in ρ and SSA on scales of ∼0.05–0.3 m are consistently correlated. Within the top ∼3 m, Δε becomes higher, especially at depths with higher ρ and SSA.

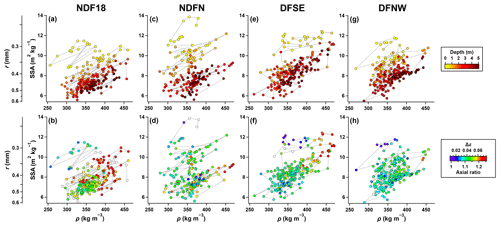
Figure B1 Relationship between ρ, Δε, and SSA of the NDF18, NDFN, DFSE, and DFNW cores. (a, c, e, g) Scatterplot of SSA against ρ for 0–5 m with the color of marker representing depth. Lines connect the symbols in the depth order. (b, d, f, h) The same as (a, c, e, g), but color represents Δε. The white color indicates no data of Δε.