A conceptual model for glacial lake bathymetric distribution

The formation and expansion of glacial lakes worldwide due to global warming and glacier retreat have been well documented in the past few decades. Thousands of glacial lake outburst floods (GLOFs) originating from moraine-dammed and ice-dammed lakes were reported, causing devastating impacts on downstream lives and properties. Detailed glacial lake bathymetry surveys are essential for accurate GLOF simulation and risk assessment. However, these bathymetry surveys are still scarce as glacial lakes located in remote and high-altitude environments hamper a comprehensive investigation. We developed a conceptual model for glacial lake bathymetric distribution using a semi-automatic simulation procedure. The basic idea is that the statistical glacial lake volume–area curves conform to a power-law relationship indicating that the idealized geometric shape of the glacial lake basin should be hemispheres or cones. First, by reviewing the evolution of various types of glacial lakes, we identified nine standard conceptual models to describe the shapes of lake basins. Second, we defined a general conceptual model to depict the continuum transitions between different standard conceptual models for those specific glacial lakes that lie between two standard conceptual models. Third, we nested the optimal conceptual model in the actual glacial lake basin to construct the water depth contours and interpolate the glacial lake bathymetric distribution. We applied the conceptual model to simulate six typical glacial lakes in the Third Pole with in situ bathymetric surveys to verify the algorithm's applicability. The results show a high consistency in the point-to-point comparisons of the measured and simulated water depths, with a total volume difference of approximately ±10 %. The conceptual model has significant implications for understanding glacial lake evolution and modeling GLOFs in the future.

1 Introduction

Globally, glacial recession and thinning have been well documented over the last decades via field observations and remote-sensing techniques (Yao et al., 2012; Zemp et al., 2019; Hugonnet et al., 2021). Such evolution of glaciers due to climate warming and anthropogenic factors could induce related effects (Yao et al., 2019), among them the expansion and formation of glacial lakes (Zhang et al., 2015; Emmer et al., 2016; Wang et al., 2020; Ma et al., 2021). Glacial lakes are water bodies developed within depressions of glacier moraine or mainly fed by contemporary glacier meltwater (Yao et al., 2018). Due to glacier retreats, they are generally impounded by glacier terminal or lateral moraine. Since the 1990s, the glacial lakes within a 1 km buffer of contemporary glaciers worldwide have increased by around 50 % in total number, area, and volume (Shugar et al., 2020). These changes have also been accompanied by glacial lake outburst flood (GLOF) risks.

As a glacier-related hazard, GLOFs have been a frequent incidence in various glacierized areas, causing considerable socioeconomic losses (Anacona et al., 2015a; Nie et al., 2018; Emmer et al., 2022a). According to a compilation, more than 3000 GLOFs from moraine- and ice-dammed lakes have been recorded worldwide and claimed more than 10 000 deaths (Carrivick and Tweed, 2016; Lützow et al., 2023). Under triggering factors such as ice avalanches, landslides, and heavy precipitation, glacial lakes are extremely unstable and subsequently cause a sudden release of water with a peak discharge higher than a dozen times that of monsoon rainfall floods (Richardson and Reynolds, 2000; Westoby et al., 2014; Kougkoulos et al., 2018). However, due to the relatively small volume of the glacial lake, the flooding process generally attenuates rapidly within a few hours. Knowledge of glacial lake volume is critical, as it influences the released water volume and GLOF magnitude (Fujita et al., 2013). Therefore, lake volume is often employed as an essential criterion in numerous cases of GLOF susceptibility and risk assessment (Bolch et al., 2011; Aggarwal et al., 2017; Drenkhan et al., 2019; Falatkova et al., 2019).

Currently, only sporadic bathymetric surveys on glacial lakes have been conducted worldwide. In the Cordillera Blanca, Peru, facing continuous threats by GLOFs (Lliboutry et al., 1977), more than 100 detailed bathymetric surveys of glacial lakes have been carried out to better understand the regional GLOF risks (Muñoz et al., 2020). Government agencies and research institutions have promoted these surveys. In the Third Pole region, the bathymetric surveys are focused on the glacial lakes in the Himalaya (Sharma et al., 2018; Watson et al., 2018), where approximately 60 bathymetric surveys of glacial lakes, such as the Cirenmaco, Jialongco, and Lake Longbasaba, were conducted (Yao et al., 2012; Wang et al., 2018; Li et al., 2021). They measure the water depth with ultrasonic devices on board automatic uncrewed boats or manual hovercrafts.

Carrying out a universal investigation campaign of lake bathymetry is impractical for thousands of glacial lakes in remote areas and at high elevations. Instead, scholars typically utilize single total lake volume data rather than bathymetric distribution in GLOF modeling (Anacona et al., 2015b; Zhang et al., 2021). The lake volume is typically estimated by an empirical equation, e.g., a direct volume–area equation (O'Connor et al., 2001; Huggel et al., 2002; Loriaux and Casassa, 2013) or an indirect area–mean depth–maximum depth–width equation (Wang et al., 2012), which have considerable uncertainty. There is no doubt that the measured and/or interpolated glacial lake bathymetric distributions have great merit that can precisely determine the maximum potential outburst volume of the glacial lake, serving to further simulate the GLOF propagation and evaluate downstream exposures (Frey et al., 2018; Sattar et al., 2021). Moreover, a bathymetry survey is also pivotal to understanding the interactions between the glaciers and their terminating lakes (Zhang et al., 2023), as several studies have revealed that the proglacial lake bathymetric state can dominate the glacier terminal melting and calving regimes (Watson et al., 2020; Sugiyama et al., 2021).

Can we obtain glacial lake bathymetric distributions through modeling rather than in situ investigations? Previous studies have provided insights. Cook and Quincey (2015) preliminarily proposed that the same type of glacial lakes may have their idealized geometric shapes, which depict the evolution of glacial lakes' volume–area (V–A) relationship over time. For instance, the triangular cone is suitable for representing the idealized geometric shapes of ice-dammed lakes dammed by glaciers and formed in the narrow valley. The idealized conceptual models of glacial lakes can be combined with the actual situations to project the glacial lake bathymetric distribution.

An idealized lake basin is also helpful in constructing numerical or physical models. In the study of Veh et al. (2020), the conceptual model of glacial lakes was constructed as a semi-ellipsoid with a circular surface to calculate the released volume after the lake drainage. The surface area and height of the semi-ellipsoid refer to the glacial lake area and maximum water depth, respectively. Based on these instructive designs, we attempted to develop a procedure and algorithm for modeling glacial lake bathymetric distribution in this study. We first (i) retrieved as many conceptual models as possible for various types of glacial lakes by reviewing the evolutions of glacial lakes and analyzing the relationships between lake volumes and areas, (ii) explored the procedure and algorithm to estimate bathymetric distribution in conjunction with actual lake surface and basin shapes, and then (iii) discussed their implications and potential applications.

2 Data and methods

2.1 Compilation of glacial lake bathymetry

Analyzing the existing glacial lake bathymetries can help us reveal glacial lake water depth characteristics. To our knowledge, more than 60 articles have mentioned surveyed bathymetry data from glacial lakes. We integrated the prior studies and established an inventory of global glacial lake bathymetry (Supplement 1). The attributes included the name, location, survey time, area, volume, and maximum water depth. A total of 231 bathymetric data from 220 glacial lakes globally were compiled in the inventory (Fig. 1a). Some large glacial lakes were eliminated since their areas deviate from the majority of concentration zones, which could reduce the fitting accuracy (Cook and Quincey, 2015).

2.2 Classification and evolution of different glacial lake types

The maximum water depth (D) and total volume (V) are the fundamental parameters regarding the idealized geometric shapes of glacial lakes. We used the compiled glacial lake bathymetry data to fit the curves of V–A (glacial lake area) and D–A to understand the potential shapes of an idealized lake basin. Based on the topological positions between the glacial lakes and their parent glaciers, we classified glacial lakes as proglacial, periglacial, extraglacial, supraglacial, and ice-dammed types (Fig. 1b). This classification system considers glaciers' critical role in the evolution of glacial lakes (Petrov et al., 2017; Rick et al., 2022).

We assumed that different types of glacial lakes have different expansion mechanisms and, thus, different conceptual models (Carrivick and Tweed, 2013; Mertes et al., 2017; Minowa et al., 2023). The proglacial lake's expansion mainly proceeds backward by glacial retreat (Minowa et al., 2023). For instance, Lake Longbasaba, located in the central Himalaya, has substantially increased its surface area by occupying space liberated through glacier terminal retreat since 1988, with limited expansion in the frontal and lateral moraine areas (Wei et al., 2021). The periglacial lake and the extraglacial lake are not directly in contact with the glacier, and their expansion depends more on changes in precipitation and glacier meltwater, thereby potentially expanding in all horizontal directions. As for the supraglacial lake, expansion proceeds in all directions, and the temperature difference at the ice–water interface continuously melts the glacier ice in both horizontal and vertical orientations (Watson et al., 2018), while for the ice-dammed lake, the evolution often appears horizontally with glacier retreat, as seen in the expansion of Lake Merzbacher in the Tianshan Mountains (Gu et al., 2023). These various mechanisms in glacial lake expansions showed that the changes in the lake basin among the different glacial lake types are inconsistent, indicating that they may have different conceptual models.

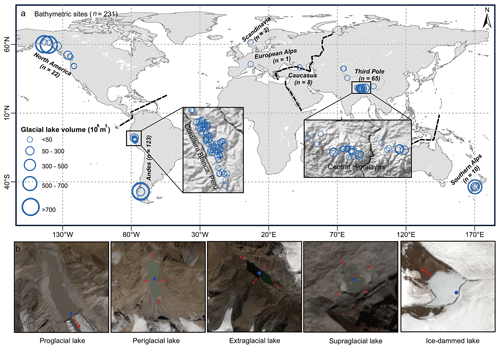
Figure 1 (a) Distribution of glacial lakes whose volume was surveyed in detail. (b) Glacial lakes were divided into five categories, i.e., proglacial (directly in contact with the glacier terminus), periglacial (separated from the glacier and dammed by historical moraine), extraglacial (far from the glacier and generally dammed by landslides), supraglacial (positioned on the glacier surface), and ice-dammed lake (formed when glacier surges block downstream valleys or meltwater fills depressions between retreating tributary and main glaciers). The red arrows indicate the possible main directions of expansion of the glacial lake, and the blue points represent the location of the maximum water depth. Credit: Copernicus Sentinel data.

2.3 Standard conceptual model

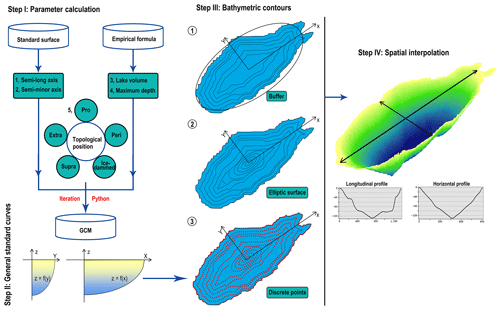
The basic procedure of constructing glacial lake bathymetric distribution is to (i) identify the most appropriate conceptual model that can describe the idealized lake basin, (ii) calculate the theoretical formulation equations of this conceptual model, (iii) nest this conceptual model in the actual glacial lake basin to construct the water depth contours, and (iv) interpolate and calculate the glacial lake bathymetric distribution. The conceptual model was constructed as the scheme presented by Veh et al. (2020). Glacial lakes were assumed to have hemispherical or similar three-dimensional lake basin shapes. The standard surface of the glacial lake was assumed to be an ellipse.

The general formula between the volume and area of glacial lakes fits a power-law relationship (Table 1). It could be expressed as Eq. (1). The best-fit curve for the relationship between maximum water depth and area of glacial lakes also follows the power-law relationship (Eq. 2) (Fig. 2).

$$\begin{array}{}\text{(1)}& {\displaystyle }V=\mathit{\alpha }{A}^{\mathit{\beta }}\text{(2)}& {\displaystyle }D=\mathit{\gamma }{A}^{\mathit{\epsilon }}\end{array}$$

A is the area of the glacial lake; α, β, γ, and ε are the coefficients. The value of β is greater than 1, and ε is less than 1.

The three-dimensional bodies representing the standard shape of a lake basin were required to have a general formula as defined by Eq. (3).

$$\begin{array}{}\text{(3)}& V=\mathit{\delta }AD\end{array}$$

Here, δ is the coefficient, A is the elliptical surface area, and D corresponds to the maximum water depth of the glacial lake. We identified four hemispheres or cones whose volumes can be expressed by Eq. (3): the hemisphere structured by the elliptical side ($V=\mathrm{2}/\mathrm{3}AD$), the hemisphere structured by the upward-opening parabolic side ($V=\mathrm{1}/\mathrm{2}AD$), the cone structured by the straight side ($V=\mathrm{1}/\mathrm{3}AD$), and the cone structured by the rightward-opening parabolic side ($V=\mathrm{1}/\mathrm{5}AD$). These bodies are defined as the standard conceptual model (SCM), and their curves in the X–O–Z quadrant are called the standard curves (Fig. 3a). These four standard curves are progressively concave inward in the quadrant from the elliptical curve to the rightward-opening parabolic curve.

These SCMs for the supraglacial, periglacial, and extraglacial lakes are compatible with the expansion mechanisms partly because their growth direction is comprehensive at the horizontal level. Their maximum water depths were set in the lake center. However, proglacial and ice-dammed lakes are different. Their expansions are focused toward the glacier's or valley's direction, and the maximum water depths are generally situated near the intersection with the glacier, e.g., Longbasaba proglacial lake (Yao et al., 2012; Wei et al., 2021) and Shisper ice-dammed lake (Singh et al., 2023). Under these circumstances, we considered the SCMs of proglacial lakes to be half of the preceding four SCMs, i.e., the semi-hemisphere structured by the elliptical side ($V=\mathrm{1}/\mathrm{3}AD$), the semi-hemisphere structured by the upward-opening parabolic side ($V=\mathrm{1}/\mathrm{4}AD$), the semi-cone structured by the straight side ($V=\mathrm{1}/\mathrm{6}AD$), and the semi-cone structured by the rightward-opening parabolic side ($V=\mathrm{1}/\mathrm{10}AD$). We designed two SCMs for the ice-dammed lake (Fig. 3a): the semi-cone structured by the straight side ($V=\mathrm{1}/\mathrm{6}AD$) and the triangular cone ($V=\mathrm{1}/\mathrm{3}AD$). The deepest points for proglacial and ice-dammed lakes were set near the glacier–lake interface. Most of the actual volume points lie between the volume curves of these SCMs (Fig. 4), and there are one or two closer SCM volume curves for each type of glacial lake's fitted A–V curve. Ultimately, a total of nine different SCMs were designed to express the idealized geometric shapes of glacial lake basins.

Table 1 Empirical equations of the volumes and areas of glacial lakes in previous studies. The applicable region, lake type, and sample size for each empirical equation were indicated during fitting. The volume unit is million cubic meters, and the area unit is square kilometers. In the dam material-based classification method for glacial lakes, a substantial number of proglacial and periglacial lakes can be categorized as moraine-dammed lakes.

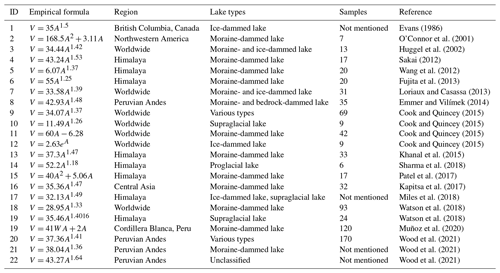
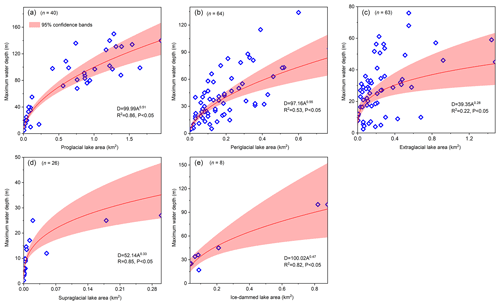
Figure 2 Relationships between maximum water depth and the areas of glacial lakes were compiled in the present study for the following lake types: (a) proglacial lake, (b) periglacial lake, (c) extraglacial lake, (d) supraglacial lake, and (e) ice-dammed lake.

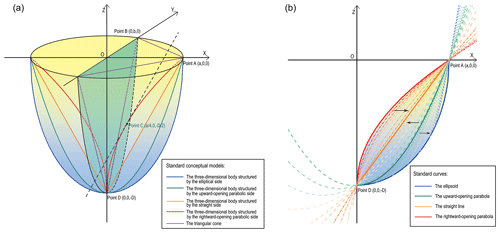
Figure 3 (a) Schematic diagram illustrating the shapes of the SCMs, i.e., the hemisphere structured by the elliptical side or upward-opening parabolic side, the cone structured by the straight side or rightward-opening parabolic side, the triangular cone, and their shapes when symmetrically divided matching the SCMs of the proglacial lake. Here, A is the semi-long axis, B is the elliptical surface's semi-short axis, and D is the maximum water depth. (b) Convergences of the general curves towards the standard curves in the X–O–Z quadrant in different orientations.

Figure 4 Relationships between the volume (V) and area (A) of glacial lakes were compiled in the present study for the following lake types: (a) proglacial lake, (b) periglacial lake, (c) extraglacial lake, (d) supraglacial lake, and (e) ice-dammed lake. The dotted lines indicate the volume curves of different standard conceptual models, which were fitted by Eqs. (2) and (3).

2.4 General conceptual model

If a specific glacial lake has determined its parameters such as surface size, maximum water depth, and volume, it is unlikely that the closest SCM would accurately represent the most appropriate conceptual model. This is because the relatively inherent volume of the SCM is hardly equal to the volume of a specific glacial lake. In other words, the volume curve of the SCM is constant, and therefore the volume point of a specific glacial lake may deviate from the SCM volume curve. Consequently, directly using the SCM to nest and interpolate a realistic glacial lake bathymetric distribution would result in an initial overestimation or underestimation of the total lake volume.

The SCMs can only help us comprehend the various glacial lake morphologies; they cannot be applied directly to estimate the glacial lake bathymetric distribution. We may conceive of the measured volume points between the SCM volume curves as being a result of the transition from one SCM to another. For instance, from the upward-opening parabolic line to the straight line, it is the standard parabolic line continuously approximating the straight line on the X–O–Z quadrant by moving downward and left (Fig. 3b). During the movement process, the rotated-out hemisphere is moving toward the cone structured by the straight side. We can capture these general conceptual models (GCMs) in this transition stage and make their volume consistent with the measured or estimated lake volume. This means we find a GCM that is more effective than the SCM in estimating the lake depth distribution.

Python programming was used to drive the standard curves' transition and parameter calculations. The theoretical description for the GCMs is presented in Supplement 2. By relocating the standard curve's vertices and altering the opening size, it is simple to compute the transition of a standard upward- or rightward-opening parabola to a straight line. The resultant general curves must pass through points A and D. The convergence to the standard elliptic curve from the standard upward-opening parabola is relatively complicated. If we move the vertices of the standard parabola to the right and downward, the maximum height of the produced GCM changes. We used a compound style here. When the second intersection of the moved general parabolic curve and the standard elliptic curve occurs (from right to left), the side of the GCM starts to take on the elliptic curve change. Additionally, the marginal SCMs should be employed when the measured volume is larger (smaller) than the largest (smallest) SCM volume.

2.5 Nesting the actual glacial lake shapes

Once a given glacial lake's GCM has been established, the lake's bathymetric contours may be predicted in relation to actual conditions and parameters. Since the actual shape of the glacial lake surface is irregular rather than the normal elliptic surface we used in the models, it was crucial to determine how the depth contours move inward based on the actual shape.

We tested two hypotheses. First, utilizing the lakeshore line to continually create buffers inward might depict the depth contours because the depth contours near the lakeshore were the consequence of ongoing indentation of the actual glacial lake surface outline inward. Second, on the $\mathrm{1}/\mathrm{4}$ semi-long axis of the standard elliptic surface, the depth contours would become progressively blurred as the inward indentation continues, thus subsequently using the standard elliptic surface to start the inward indentation (Fig. 5). Importantly, these assumptions were supported by observations of hundreds of glacial lake bathymetric distribution cases worldwide. Some similarities exist between the bathymetric contours and the lakeshore shape, suggesting that the area near the lakeshore is possibly impacted by the slopes around the lake and/or other material sources. There are two explanations for this phenomenon: either the glacial lakes were continuously filled with exogenous debris and rocks or the initial lake water level had risen and flooded part of the original slopes.

The $\mathrm{1}/\mathrm{4}$ semi-long axis is the ending position where the glacial lake is not impacted by exogenous materials, as determined by our understanding of those SCMs. Most of the glacial lake SCMs were located closer to the cone structured by the straight side of the hemisphere and the upward-opening parabolic side. It is inferred that the initial deepening of the glacial lake is not particularly large from the outer line to the center (compared to the semi-ellipsoid), indicating that exogenous materials are likely to have impacted it. This situation is better understood when the lake SCM is a cone structured by the rightward-opening parabolic side. Therefore, we hypothesized an extreme circumstance in which a glacial lake starts to be significantly influenced by the lake's surroundings' topography. In this case, the slope of the standard rightward-opening parabolic curve is smaller than the slope of the standard straight line and closer to the ideal deepening state of the lake basin when it is larger. This equal slope point is located on the $\mathrm{1}/\mathrm{4}$ semi-long axis and represents half of the maximum water depth.

Figure 5 The procedure illustrates the parameter calculation of GCMs and processes of creating buffers inward. The water depths on the axes were calculated using the standard curves corresponding to the x and y axes.

2.6 Sites for exhibiting and validating results

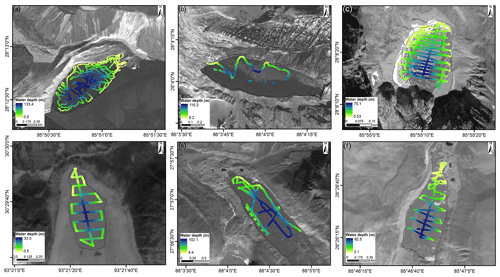
Six sets of bathymetry data were collected for the typical glacial lakes in the Himalaya and Nyainqentanglha (Fig. 6). Among them, Jialongco, Cirenmaco, Poiqu No. 1, and Maqiongco were classified as periglacial lakes, while Lake Longbasaba and Dasuopuco were classified as proglacial lakes. Although it would be desirable to evaluate the performance of our conceptual models across different types, sizes, and geographic locations of glacial lakes, we were limited by the available observational data and could only conduct these examinations in the Third Pole region, focusing on proglacial and periglacial lake types. The topological position, total volume, maximum water depth, and semi-long or minor axis of the standard lake surface were crucial parameters in glacial lake bathymetric distribution modeling (Table 2). The six glacial lake bathymetric distributions were simulated according to the lake sizes in the survey year and eventually compared with the measured points of water depths and the overall parameters (total volume and mean water depth) to verify the feasibility and accuracy of our modeling method.

Table 2 The crucial modeling parameters of the six selected glacial lakes.

Figure 6 The water depths observed along the bathymetric routes for (a) Jialongco, (b) Cirenmaco, (c) Poiqu No. 1, (d) Maqiongco, (e) Lake Longbasaba, and (f) Dasuopuco.

3 Results

We present the SCMs for each type of glacial lake and demonstrate a procedure to identify the most compatible GCM for a specific glacial lake by equalizing the volumes of both. To our knowledge, this is the first model to simulate the bathymetric distribution of glacial lakes at present. The results reveal that the proglacial and periglacial lakes exhibit greater depths as their SCMs are closer to the hemisphere structured by the upward-opening parabolic side. Conversely, the SCMs of the extraglacial and supraglacial lakes are closer to the cone structured by the straight side, indicating relatively shallower depths. As the ice-dammed lakes, their V–A fitting curve is more similar to the V–A curve of the triangular cone (Fig. 4). Hence, we recommend that the bathymetric distribution modeling for ice-dammed lakes proceeds directly using the standard triangular cone.

We determined the optimal GCMs for the six exhibited glacial lakes. Following bathymetric distribution modeling results, the total volume of Jialongco was calculated to be 33.1×10⁶ m³ (with a relative error of −11.7 %) with a mean water depth of 54.6 m (−8.1 %). Its GCM was closer to the cone structured by the straight side (Fig. 7a). The computed total volume and mean depth of Cirenmaco were 17.2×10⁶ m³ (−4.4 %) and 51.7 m (−6.9 %), respectively. The Cirenmaco GCM had similarities to the hemisphere structured by the upward-opening parabolic side (Fig. 7b), meaning a more significant inward deepening rate than Jialongco. The relatively small-sized Poiqu No. 1 and Maqiongco had total volumes of 2.9×10⁶ m³ (7.4 %) and 3×10⁶ m³ (−6.3 %) and mean water depths of 27.3 m (7.1 %) and 12.8 m (−14.7 %), respectively. Their optimal GCMs showed similarities to Jialongco (Fig. 7c, d). The proglacial lake, Longbasaba, was estimated to have a total volume of 71.4×10⁶ m³ (11.5 %) and a mean depth of 61.1 m (22.2 %). Its GCM was more resemblant to the semi-ellipsoid (Fig. 8a). Dasuopuco had the smallest relative error in the total volume (0.2 %) and mean water depth (−1.8 %) (Fig. 8b). Overall, approximately ±10 % volume uncertainty was estimated in the process of nesting the general conceptual models in the actual glacial lake shapes.

The disparity between the area of the assumed standard ellipse surface and the actual lake surface as well as the deviation of the deepest water location likely caused the majority of the inaccuracy. The initial settings of glacial lake conceptual models and the algorithm's applicability were confirmed by comparison with the measured and estimated individual water depths. Between the estimated and measured water depths along the bathymetric routes, the average deviation, mean absolute deviation, and root mean square error for the six glacial lakes all showed good consistency. Neither near the lakeshore nor near the lake center do the estimates show intolerable dispersions.

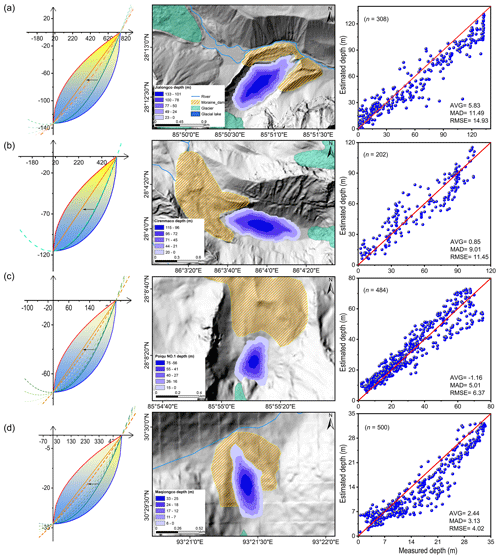
Figure 7 Modeled glacial lake bathymetric distributions of the four selected periglacial lakes. (a) Jialongco, (b) Cirenmaco, (c) Poiqu No. 1, and (d) Maqiongco. The average deviation (AVG), mean absolute deviation (MAD), and root mean square error (RMSE) were selected to depict the consistency between the simulated and measured individual water depths along the boat routes. The movements of the general curves from one standard curve to another are also indicated.

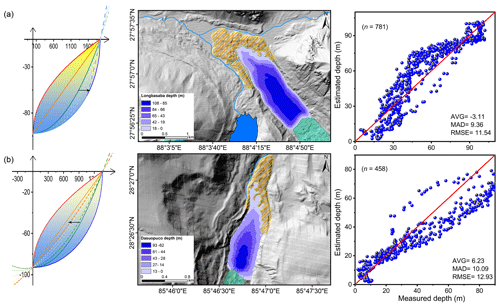
Figure 8 Modeled glacial lake bathymetric distributions of the two selected proglacial lakes. (a) Lake Longbasaba and (b) Dasuopuco. AVG, MAD, and RMSE were selected to depict the consistency between the simulated and measured individual water depths along the boat routes. The movements of the general curves from one standard curve to another are also indicated.

4 Discussion

4.1 Glacial lake basin evolution

Understanding the glacial lake evolution can help us comprehend these idealized geometric shapes in theory. Most moraine- or bedrock-dammed lakes develop in depressions exposed by diminishing glaciers. The supraglacial lakes exist at the glacier snout, eventually facilitating the formation of proglacial and periglacial lakes (Carrivick and Tweed, 2013; Mertes et al., 2017). As the six glacial lakes illustrated, our hypotheses explained the different rates of inward deepening owing to the influence of exogenous materials. The glacier bedrock has been eroded and nudged during historical ice flowing, making the excavation and growth of glacial lake basins.

Contemporary glaciers often have a certain thickness of debris at the snout. For example, approximately 1 m of debris was observed at the snout of Urumqi Glacier No. 1, China (Echelmeyer and Wang, 1987), as a result of glacial erosion. The specific sites of continual eroding and nudging spawn overdeepenings and are considered potential glacial lakes (Linsbauer et al., 2016). Since the glacier velocity in the middle part is often larger than that of both sides, the erosion is stronger in the central line of the initial overdeepening. As glacier flowing continues, the shape of the overdeepening finally reaches equilibrium and is similar to a hemisphere, which is the GCM of the lake basin we assumed. After the overdeepenings are exposed, they can be filled by meltwater to form glacial lakes while also receiving material deposition, resulting in a gradual transition of the idealized geometric basin from a hemisphere to a cone. This conjecture can be inferred from the studies of overdeepenings on glacial beds, whereby the volume and surface area of these potential glacial lakes are also in accordance with the power-law relationship (Zhang et al., 2022).

4.2 Applicability of the conceptual model

Our modeling theory is based on observations of glacial lake bathymetric distribution characteristics worldwide, revealing a geometrical approximation law for glacial lake bathymetry. However, it is strictly limited by several constraints. Firstly, the designed conceptual model is more suitable for those glacial lakes with typically lengthy and elliptical shapes and may be less applicable to very irregularly shaped glacial lakes such as the ice-marginal and thermokarst lakes in the Greenland and Alaska region (Field et al., 2021; Coulombe et al., 2022). Secondly, the designed conceptual model is also more suitable for those glacial lakes with a cirque-valley glacier or a small- or medium-sized valley glacier flowing along a straight valley, ensuring idealized formation conditions for the glacial lake basin with minimal erosion and deposition from tributaries. Although the simulated results were only validated in the periglacial and proglacial lakes of the Himalaya and Nyainqentanglha due to limited observation data, the comparison results of the measured and modeled depth values at different locations of the six glacial lakes demonstrate the rationality and reliability of our conceptual models. Further validation is needed to assess the applicability of our conceptual model across different lake types on a global scale. There is a significant limitation in the availability of glacial lake bathymetric distribution data, with most studies only providing key parameters such as total volume, maximum depth, and mean depth. Moreover, due to the challenges of field investigations, measurements of glacial lakes have predominantly focused on larger, hazardous, or particularly interesting periglacial and proglacial lakes. This makes us unable to find any available bathymetric distribution data for extraglacial, supraglacial, and ice-dammed lakes, preventing validation of our conceptual model for these lake types.

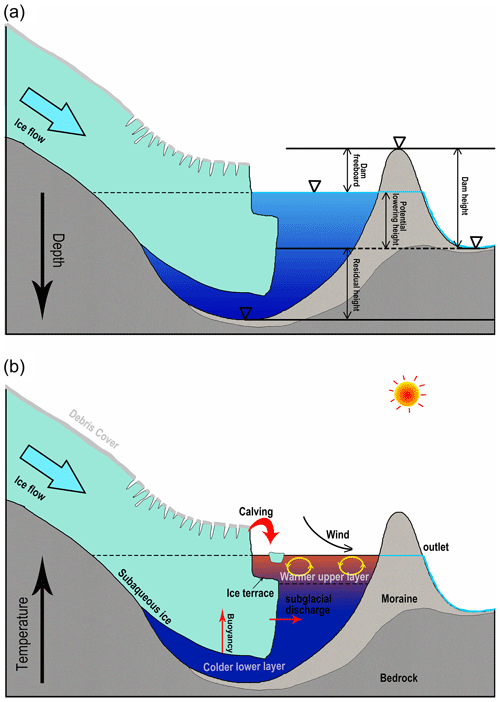
In addition to the subjective and objective errors made during the modeling phase, there are several systematic defects in the algorithm itself. (1) The total volume and maximum water depth are calculated using empirical equations, which may lead to significant deviations when modeling the bathymetric distribution of an arbitrarily selected glacial lake. In particular, the curves of D–A are not robust, with many discrete points appearing (Fig. 2). (2) The estimated depth contours converge inward using the lake shoreline buffers first, followed by the elliptical surfaces. This process may effectively simulate the connections between a bathymetric distribution and glacial lake morphology. However, this is not essential. If the elliptical indentations are always inward relative to the elliptical surface, the modeling accuracy is also not affected significantly in theory. (3) The deepest sites of proglacial lakes have been considered to be near the glacier–lake interface. The developing proglacial lakes, however, are complex. Their deepest sites are constantly located near the glacier terminus before the deepest site of overdeepening is exposed (Fig. 9a), which is in accordance with our hypothesis. With the deepest sites developing more fully, they gradually shift toward the lake center. Our algorithm has not addressed these changes. In the future, the conceptual model will require parameter optimization through learning with a number of measured bathymetry data. Furthermore, the present version of our algorithm relies on simple programming and semi-automated geospatial analysis tool processing. We will further develop this conceptual model to create an interface that can automatically process and reduce subjective errors.

4.3 Rationality of empirical V–A equations

Currently, many studies have attempted to fit V–A equations with regional or global applicability for various types of glacial lakes (Cook and Quincey, 2015; Qi et al., 2022). The most common classification method for glacial lakes is based on dam materials, such as moraine-dammed, bedrock-dammed, and landslide-dammed. However, this study reveals that the different types of glacial lakes have different ideal basin shapes that may be unfavorable to most already-formed V–A empirical formulations, although some have high R² values (Table 1). For instance, most of the proglacial and periglacial lakes are generally dammed by moraine, involving many fitting works of V–A relationships. Unreasonably, the incompletely developed basins of proglacial lakes and the fully developed basins of periglacial lakes are often described by the same empirical formulas (Fig. 9a), disregarding the distinct basin development stages between them. This aspect has been overlooked in the previous studies. In our fitted curves of V–A relationships for various types of glacial lakes (Fig. 4), the V–A relationship for proglacial lakes is robust, indicating possible global applicability. However, the V–A relationships for periglacial and extraglacial lakes exhibit many outliers, suggesting a strong influence from exogenous materials filling in these lakes based on our hypothesis. The V–A relationships of these glacial lakes decoupled with their glaciers at least require parameters related to the glacier characteristics and time of detachment for further description.

There is no single classification method that can adequately capture the refined characteristics of glacial lakes. Even lakes classified as the same type may differ in terms of parent glaciers, bedrock properties, or dam materials. In the modeling of glacial lake bathymetric distribution, accurately estimating the total volume and maximum water depth of glacial lakes is crucial. Therefore, future studies should not only focus on whether the empirical formula is generalizability or global applicability but should also develop more detailed classification criteria for glacial lakes, comprehensively considering dam materials, topological positions, glacier properties, area intervals, geographic locations, and other relevant factors. This will facilitate good fitting of regional empirical relationships of V–A and D–A for various types of glacial lakes, thereby reducing the dispersion between data points.

Figure 9 The schematic diagrams illustrate (a) the potential maximum lowering height of the glacial lake water level after drainage and (b) the interactions between the parent glacier and its terminating lake.

4.4 Applications in GLOF modeling

The conceptual model has been proposed in this study; one such application is in GLOF modeling. The results make two significant contributions to future GLOF modeling: (i) accurately estimate the maximum potential outburst water volume of a glacial lake by combining lake surface elevation, dam bottom elevation, and the optimal GCM; and (ii) facilitate coupling between the various GLOF processes in modeling (trigger–displacement wave–dam breach–flood propagation). Many recent studies have documented reconstruction of the historical GLOFs and simulation of future GLOFs from high-outburst potential glacial lakes (Allen et al., 2015; Anacona et al., 2015b; Erokhin et al., 2017; Kougkoulos et al., 2018). The modeling precision is expected to improve significantly.

On the one hand, most prior studies replaced the potential maximum outburst volume with the total water volume because of the limitations of glacial lake bathymetric investigations (Zhang et al., 2021). Although this could present a maximized risk assessment, an inflated downstream exposure might raise excessive concerns among the authorities and the public regarding inadequate prevention and mitigation measures (Emmer et al., 2022b). As long as the dam's lowest elevation exceeds that of the glacial lake (the potential lowering height is less than the maximum water depth), it could result in incomplete drainage (Fig. 9a). On the other hand, due to the complicated phase transition in the chain process of GLOFs, a segmented simulation has generally been conducted. For instance, Rapid Mass Movement Simulation (RAMMS) can be used to simulate the impact of ice avalanches or landslides on glacial lakes (Frey et al., 2018; Sattar et al., 2021; Duan et al., 2023), and hydrological algorithms are used to calculate the displacement wave (Heller et al., 2009; Evers et al., 2019). Modeling software like IBER, HEC-RAS, or FLO-2D is employed to simulate downstream flood propagation (Alho and Aaltonen, 2008; Osti and Egashira, 2009; Schneider et al., 2014; Somos-Valenzuela et al., 2015; Maurer et al., 2020; Nie et al., 2020).

In contrast to a holistic simulation, such a segmented simulation approach undoubtedly causes poor articulation and increased uncertainty in different processes. With the recent scientific developments, a newly developed three-phase flow model, r.avaflow (Mergili et al., 2017), started to be used to simulate GLOF propagations (Mergili et al., 2018, 2020; Sattar et al., 2023) and can realize the whole hazard cascade modeling with a high performance (Zheng et al., 2021). Our study can provide much-needed glacial lake bathymetry data for such modeling to calculate the displacement wave on the lake surface and the water release process during dam erosion.

4.5 Potential developments of numerical or physical models

The standardized glacial lake basin can facilitate other future model development related to glacial lakes and improve knowledge of how proglacial lakes and lake-terminating glaciers interact. Carrivick et al. (2020) discussed six major challenges in constructing a numerical model of interactions between proglacial lakes and glaciers, which include the imperative for glacial lake bathymetry. The standardized shape implicates the design of the model's basic architecture.

Compared with the somewhat realistic glacier bed topography within the overdeepenings revealed by ice thickness models, a standardized lake basin provides an alternative scheme. For a specific proglacial lake, its water level, water temperature, inflow or outflow, internal circulation, and interface with the glacier vary with glacier–lake dynamics and time, which are very complex processes (Sugiyama et al., 2016; Sutherland et al., 2020). Deep and large proglacial lakes are prone to water stratification due to warmer upper layers and colder lower layers of water because these freshwater-terminating lakes currently have no evidence of active internal circulation (Haresign and Warren, 2005; Boyce et al., 2007). This stratification induces the subaqueous ice differential melting and ice terrace formation (Fig. 9b), impacting the glacier terminal calving regimes (Sugiyama et al., 2019; Mallalieu et al., 2020). On the other hand, the dynamic characteristics of glacier snout, such as bed friction, longitudinal stress, and ice flow velocity, vary distinctively due to the presence of terminating lakes (Sugiyama et al., 2011; Liu et al., 2020). Knowledge and understanding of glacial lake formation and evolution change continually. The ultimate goal is to present these processes via computer numerical simulations. The idealized lake basin can facilitate calculation of the mass and energy transport at the interface.

5 Conclusion

This study was conducted in response to a circumstance that field investigation was the only approach to obtain glacial lake bathymetry. The relationships of volume–area and maximum water depth–area of glacial lakes were reanalyzed via an inventory of the global glacial lake bathymetry data we compiled. The obtained curves were matched with a power-law relationship. Thus, the types of hemispheres or cones were determined as the conceptual models (idealized geometric shapes) of glacial lakes. The standard lake surface was assumed to be an ellipse.

Nine standard conceptual models were identified. The SCMs for the supraglacial, periglacial, and extraglacial lakes are the hemisphere structured by the elliptical side, the hemisphere structured by the upward-opening parabolic side, the cone structured by the straight side, and the cone structured by the rightward-opening parabolic side. The SCMs for the proglacial lakes were determined to be half of the aforementioned four SCMs. Two SCMs were considered for the ice-dammed lakes: the semi-cone structured by the straight side and the triangular cone. To depict the volume between the two SCMs, a general conceptual model was defined to represent the transition from one SCM to another.

Several hypotheses are important in our algorithm for nesting the actual glacial lake shapes from idealized conceptual models and interpolating glacial lake bathymetric distribution. First, the supraglacial, periglacial, and extraglacial lakes' deepest sites were assumed to be in the lake center, whereas the proglacial lakes' and ice-dammed lakes' deepest sites were near the glacier–lake interface. Second, the effects of exogenous materials and boundary conditions were used to explain the different rates of inward deepening of glacial lakes. Six glacial lakes with measured bathymetry data were selected in the Third Pole region for comparison with the simulated bathymetric distributions. The results demonstrated good accuracy and applicability of our conceptual models in estimating lake bathymetry. Relatively high consistency was shown in the point-to-point comparisons of the measured and simulated water depths. This study constructed the glacial lake bathymetric distribution model, which is very rewarding for comprehending the evolution of glacial lakes. Moreover, the quality of GLOF modeling and risk assessment is also enhanced by our outlined general conceptual model. These standardized lake basins implicate the design of the model's basic architecture, which can potentially promote the development of future numerical or physical models of glacial lakes.