the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Towards modelling of corrugation ridges at ice-sheet grounding lines
Katarzyna L. P. Warburton
Alastair G. C. Graham
Jerome A. Neufeld
Duncan R. Hewitt
Julian A. Dowdeswell
Robert D. Larter
Improvements in the resolution of sea-floor mapping techniques have revealed extremely regular, sub-metre-scale ridge landforms produced by the tidal flexure of ice-shelf grounding lines as they retreated very rapidly (i.e. at rates of several kilometres per year). Guided by such novel sea-floor observations from Thwaites Glacier, West Antarctica, we present three mathematical models for the formation of these corrugation ridges at a tidally migrating grounding line (that is retreating at a constant rate), where each ridge is formed by either constant till flux to the grounding line, till extrusion from the grounding line, or the resuspension and transport of grains from the grounding-zone bed. We find that both till extrusion (squeezing out till like toothpaste as the ice sheet re-settles on the sea floor) and resuspension and transport of material can qualitatively reproduce regular, delicate ridges at a retreating grounding line, as described by sea-floor observations. By considering the known properties of subglacial sediments, we agree with existing schematic models that the most likely mechanism for ridge formation is till extrusion at each low-tide position, essentially preserving an imprint of the ice-sheet grounding line as it retreated. However, when realistic (shallow) bed slopes are used in the simulations, ridges start to overprint one another, suggesting that, to preserve the regular ridges that have been observed, grounding line retreat rates (driven by dynamic thinning?) may be even higher than previously thought.
- Article
(5970 KB) - Full-text XML
-
Supplement
(8334 KB) - BibTeX
- EndNote
Motion at the grounding line – that is, the junction between ice that is coupled to the bed and freely floating ice shelves – occurs across a range of timescales and is fundamental to our understanding of marine ice-sheet stability (Thomas, 1979; Schoof, 2007). On short timescales (hours to days), motion is tidally modulated, leading to migration over hundreds of metres to many kilometres across what is known as the grounding zone (e.g. Rignot et al., 2011; Dawson and Bamber, 2020; Drews et al., 2021; Chen et al., 2023). For longer timescales (multiannual to centennial), migration is forced by climatic factors and ice-dynamic feedbacks leading to long-term trends in ice-sheet advance and retreat. Grounding zones are inherently one of the most difficult parts of the ice-sheet–ocean system to access, making observations of the physical processes that control grounding-line movements particularly challenging. Alternative methods of investigation include mathematical models to simulate grounding-line behaviour (e.g. Gudmundsson et al., 2012; Jamieson et al., 2012; Robel et al., 2014, 2017; Walker et al., 2013; Tsai and Gudmundsson, 2015; Warburton et al., 2020), laboratory experiments that replicate grounding-line processes (e.g. Pegler and Worster, 2013; Kowal and Worster, 2020), and the study of post-glacial landscapes that represent former grounding zones (e.g. Jakobsson et al., 2012; Simkins et al., 2018; Shackleton et al., 2020). With recent advances in these methods, notably via increasing the resolution at which models are run and post-glacial landscapes (now marine) are observed, it is now possible to test modelled physical processes against observations of incredibly fine-scale glacial landforms produced at former (marine) grounding zones. The aim of this work is to improve our understanding of the processes acting at ice-sheet grounding lines as they migrate.
One of the most intriguing grounding-zone landforms identified to date are the so-called parallel “ribs” or “rungs” which comprise laterally continuous, low-amplitude ridges (several tens of centimetres), oriented transverse to ice flow, with relatively uniform spacings (metres to tens of metres) and morphologies. These subtle sedimentary ridges exhibit a clear 13–15-ridge periodicity that has led to their interpretation as forming through the tidally modulated motion of ice impacting the sea floor (Graham et al., 2022). Following existing terminology we refer to these landforms as corrugation ridges. Similar ridges are produced in a variety of polar marine settings including iceberg plough marks by the forward motion of iceberg keels (Jakobsson et al., 2011) or beneath ice shelves as ice shelf keels periodically ground during unpinning (Graham et al., 2013; see “Supplementary” in Graham et al., 2022, for a fuller discussion). Recent autonomous underwater vehicle (AUV) deployments have now mapped these features at high (sub-metre) resolution on the tops of wedges of sediment deposited at the former grounding zones of ice streams emanating from both the Larsen Inlet, eastern Antarctic Peninsula (Dowdeswell et al., 2020), and from Thwaites Glacier, West Antarctica (Graham et al., 2022). The regularity of the spacing between ridges, with a clear periodicity, supports their interpretation as the product of tidal motion, as the grounding line lifts and re-settles during an overall pattern of retreat. Because retreat is required to preserve each ridge (Dowdeswell et al., 2020), these landforms and their spacing allow for the calculation of grounding-line retreat rates on daily timescales, as ice receded from what are thought to be stable locations on the constructional sedimentary wedges (see Alley et al., 2007). Such direct, quantitative estimates of grounding-line retreat rates provide critical constraints for numerical models seeking to predict patterns and rates of future ice-sheet retreat under a warming climate.
Schematic models of corrugation ridge formation developed so far are conceptual and favour a mechanism by squeezing out or extrusion of soft sediment from the grounding line as it settles back on the sea floor, following the outgoing tide (Dowdeswell et al., 2020; Graham et al., 2022). However, these interpretations are based somewhat on form analogy with other grounding-line landforms, such as recessional moraines (which form via push during small grounding-line readvances, e.g. Boulton, 1986), and the mechanism that produces the subtle relief of corrugation ridges with their incredibly regular distribution and geometries has not been explored quantitatively. In this study, we consider corrugation ridge formation as a fluid dynamics problem, with both the subglacial till layer and ocean tides (incoming and outgoing) represented as fluids, overlain by an elastic (solid) ice sheet. Adapting a 2D flow-line model of grounding-line migration (Warburton et al., 2020), we investigate three different formation mechanisms for corrugation ridges constrained by observations of these landforms in front of Thwaites Glacier. We consider the model results alongside directly observed sea-floor parameters (ridge size, shape, spacing, acoustic character) and with inferred sedimentological properties to test model predictions of corrugation ridge morphology and composition. Finally, we discuss the plausibility of each mechanism based on the known properties of glacial sediments and grounding-zone processes.
2.1 Grounding-line migration model
Our aim is to explore formation mechanisms for low-amplitude corrugation ridges produced at the grounding line, where one ridge forms during each tidal cycle. In order to preserve each ridge, we require the grounding line to be retreating fast enough that it never overprints its previous low-tide position. Such rapid retreat could be due to an increase in basal melt in the grounding-zone cavity, ice-flow acceleration and dynamic thinning, or a combination. These are the processes that are driving current mass loss trends for the modern Antarctic and Greenland ice sheets (e.g. Pritchard et al., 2009, 2012; Rignot et al., 2013; Smith et al., 2020). We utilise novel marine geophysical observations of corrugation ridges in front of Thwaites Glacier (Graham et al., 2022; Sect. 2.2) to inform the model. Thus, in this case we assume a constant retreat rate inferred from the average ridge spacing at Thwaites (6 m) and a retreat rate of 6 m d−1 is stipulated in our simulations. We use a tidal component appropriate for the Thwaites area in the present day, as produced by the CATS2008 tide model (Padman et al., 2002; Howard et al., 2019). Tides in the southern Amundsen Sea have a dominant diurnal period, with one high tide and one low tide per day; correlations for the Thwaites corrugation ridges indicate that one ridge forms per day, assumed to be at the low-tide position (Graham et al., 2022).
For the model itself, consider an ice sheet with thickness D(x,t) and density ρi resting on a bed b(x), so that the bed slope ddx combined with the ice-thickness gradient produces a subglacial hydraulic pressure gradient ρwgθeff, where ρw is the density of water and the effective slope (Fig. 1a) is
We use the bed slope at the Thwaites corrugation ridges (typically seaward dipping at 0.5∘, corresponding to a value of ddx = tan(0.5∘) of around 0.01) to select an appropriate range of effective slopes for the model. The ice-thickness gradient close to the grounding line at the time of ridge formation is a source of uncertainty in θeff, with every 10 m reduction in ice thickness per kilometre contributing a further 0.009 to the effective slope (i.e. greater ice-thickness gradients along flow contribute to an increased effective slope). Assuming that present-day values of the ice-thickness gradient are representative, we show results for θeff from 0.02 to 0.04. We also discuss the effect of much lower effective slopes, corresponding to an ice-plain setting, cf. Graham et al. (2022), on ridge formation when describing the model results.
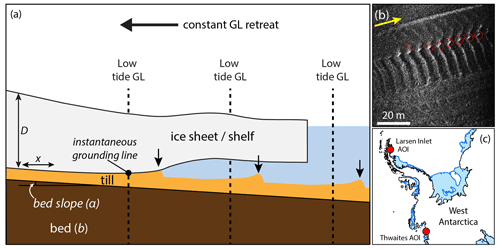
Figure 1(a) Schematic diagram of an ice-sheet grounding line (GL) that is retreating at a constant rate but is also subject to tidal flexure that produces a low-amplitude ridge of sediment (black arrows) at each low-tide grounding-line position. (b) AUV side-scan sonar image of observed corrugation ridges from a former grounding zone of Thwaites Glacier; each ridge represents a former low-tide grounding-line position. Yellow arrow shows the grounding-line retreat direction; red circles highlight sediment “beads” on corrugation ridges as the ridges cross a glacial lineation. (c) Location of the Thwaites and Larsen Inlet areas of interest (AOIs) 26 and 42 km beyond the modern glacier grounding zones, respectively.
In this geometry (Tsai and Gudmundsson, 2015), a change in ocean height Δh produces a change in equilibrium grounding-line position ΔGL
whilst a widespread change in ice thickness ΔD produces the required retreat (or advance) of the grounding line by a distance of
For the current purpose, we assume over a time interval t a constant thinning rate everywhere and an oscillation in ocean height htide(t) due to tides, resulting in a grounding-line migration pattern that combines tidal migration across the grounding zone with the mean retreat of that grounding line, given by
By taking tidal heights (htide(t)) from the CATS2008 tide model for the southern Amundsen Sea area (see middle panels in Fig. 3) and using a mean horizontal grounding-line retreat rate () from the actual ridge spacing at Thwaites (6 m d−1), we only need to estimate θeff to be able to model grounding-line migration across the zone of ridge formation.
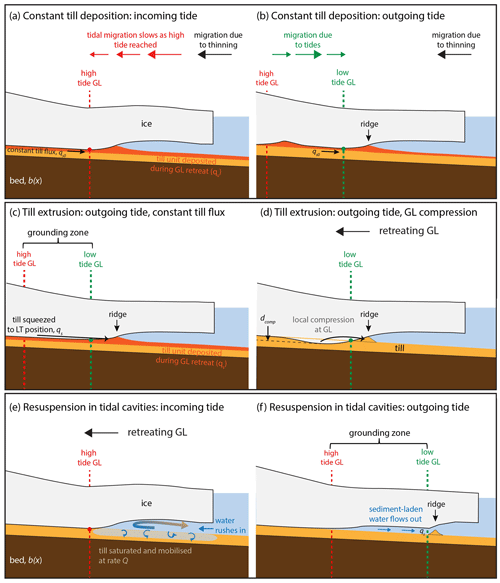
Below, we describe three mechanisms for corrugation ridge formation that can be tested by the above model. All model parameters, their units, and their values (if constant) are given in Table 1. The proposed mechanisms are based on physically plausible processes of tidally forced sediment transport and deposition in a grounding-zone tidal cavity (i.e. the space that opens and closes as the grounding line rises and falls with the tides; see Fig. 2), including a till extrusion mechanism (Sect. 2.1.2) that represents the previous descriptive models put forward for corrugation ridge formation (e.g. Dowdeswell et al., 2020; Graham et al., 2022). Note that in this first study we only consider sediment supply to the grounding line from subglacial till transport or erosion from the existing bed; we do not include the meltout of particles from debris-rich basal ice as a source of material to the grounding zone.
Table 1Definitions, values, and units of parameters used for the modelling. * Note that for an ice shelf that is in hydrostatic equilibrium the angle α will be equal to the θeff; this is assumed for the models presented here.

2.1.1 Constant till flux and deposition
Based on geophysical observations from extant ice-sheet beds, as well as the landform record of grounding-zone wedges, we know that deforming subglacial tills are transported across the grounding zone (Alley et al., 1986, 1989; Anandakrishnan et al., 2007). When they are deposited at a stable grounding-line position, advected sediments can form constructional landforms marking that position (e.g. Alley et al., 1989, 2007; Dowdeswell and Fugelli, 2012). A simple mechanism for producing tidally modulated landforms might arise from this concept of constant till deposition over the grounding zone, as the grounding line moves back and forth across it. The volume of till delivered to any given location will inversely depend on the speed of grounding-line migration across the area, which changes over the tidal cycle.
Suppose that the bed b(x) is initially smooth and that there is a constant sediment flux qs0 (in m3 s−1) delivered subglacially to the grounding line GL(t), as defined in Eq. (4) (Fig. 2a, b). Then, the final depth of sediment deposited at the grounding line (in metres) is given by
where δ is the Dirac delta function. For shallow effective slopes, the range over which the grounding line migrates is large, so the speed of migration is slowest (and deposition is greatest) when migration changes direction. This occurs twice per tidal cycle, at high and low tides, thus generating two ridges per cycle (Fig. 2a, b). In the model for this simple mechanism, the ice sheet does not interact with the ridge after it is formed (e.g. Fig. 2b), leading to a complex pattern of superimposed ridges, unless the retreat rate is sufficiently large that the next low-tide position is inland of the high-tide position. We consider this highly unlikely, given ice-shelf tidal cavity widths have length scales of hundreds of metres to kilometres (Rignot et al., 2011; Mohajerani et al., 2021; Chen et al., 2023), far greater than the observed corrugation ridge spacing. More realistically, a grounding line that migrates seaward after high tide would be expected to interact with recently deposited sediments, eroding or reworking them. The high-tide ridge may be flattened or pushed forwards to the low-tide grounding-line position, as the ice re-settles on the sea floor and migrates downstream resulting in only one ridge per diurnal tide. These processes form the basis of the model in Sect. 2.1.2 and are described by the model code in Hogan et al. (2023).
2.1.2 Till extrusion
Here, we consider the movement of till across the grounding zone into a ridge as ice at the grounding line re-settles on the sea floor (after high tide) and then migrates seaward (and pushes sediment) to the low-tide position (Fig. 2c, d). As a simple idealised model of this process, we assume that the ice has a fixed geometry di at its base and that this shape translates across the bed as the grounding line migrates:
Considering the till as a yield-strength fluid (e.g. Boulton, 1987; Boulton and Hindmarsh, 1987) to allow the till to deform, and invoking mass conservation, we assume that any volume of till that the ice displaces as the grounding line migrates seaward is transported to the point where the ice lifts off from the bed. When the grounding line retreats inland, we assume that any available space below the ice becomes filled with water, and the displaced till remains fixed at the low-tide position.
We explore two possible sources of till to form each ridge with this mechanism: a constant till flux as in the previous mechanism (qs0; Fig. 2c) or mobilisation of existing bed sediments from close to the grounding line due to elastic deformation of the ice, leading to enhanced compression of the sediment by a depth dcomp (Fig. 2d; Sayag and Worster, 2011). Corrugation ridges will be produced as long as one of these processes occurs.
Whichever the source of till flux to the grounding line, as the tide is coming in, a new layer of till is left over the bed (as in the previous mechanism). This layer can then be pushed forwards into a ridge when the tide goes out (Fig. 2c). Thus, the total flux of till towards the grounding line is no longer constant but is given by
For simplicity, since the spacing and volume of sediment in the ribs will not be sensitive to the exact shape taken for the ice lid, we use the steady shape of an ice sheet in hydrostatic balance with the ocean, resting on the till up to the grounding line, at which point the cavity opens at an angle α and (if dcomp>0) includes a highly simplified form of compression near the grounding line, so that
Note that the cavity angle α will be the same as θeff if the ice-sheet–ice-shelf system is in hydrostatic equilibrium, which we shall assume in the results shown. As a result, the exact shape of the corrugation ridges this model produces closely reflects the choice of basal ice topography, but as we have not included any viscous or erosional mechanism that would smooth the shape of the ridges after their formation, we do not expect to be able to compare the detailed ridge morphology (modelled) with observations to evaluate this mechanism.
In general, the total rib volume is given by
where ttotal is the time between high tides. We present results for the two limiting cases, either when dcomp=0 (all till is sourced from constant flux) or when qs0=0 (all till is sourced from compression at the grounding line).
2.1.3 Sediment resuspension in tidal cavities
A third mechanism for ridge formation involves the erosion and deposition of grains as water enters and exits the ice-shelf cavity with the tides. As described in Warburton et al. (2020), when the grounding line migrates downstream, water that was brought in by the incoming tide must drain out again. This flux of water could erode sediments from the water-saturated till that is exposed to the ocean at high tide and deposit it at the low-tide grounding-line position once the outgoing tidal flow ceases (Fig. 2e, f). This mechanism is somewhat based on the concepts of tidal pumping in the ice-shelf cavity and grounding-zone estuaries, both of which have been put forward as processes capable of eroding the grounding-zone sedimentary bed (Domack, 1990; Horgan et al., 2013).
As before, we start from a smooth bed b(x) and deposit a sediment flux qs at the low-tide grounding line. However instead of a constant flux, we now take qs to be made of the sediment eroded by the draining water, which is removed at a rate Q from the region between the high-tide grounding-line position and the current position and is given by
Following the calculation in Warburton et al. (2020), the shear stress τ exerted on the bed in the draining region is given by
where is the speed at which the ocean height lowers, and B is the bending stiffness of the ice sheet as an elastic beam, with flow in the draining region assumed to remain laminar throughout. For physical values of these parameters, the shear stress can reach up to a maximum of approximately 1 N m−2. For simplicity, we take the erosion rate Q in the draining region to be constant, although since U varies over the tidal cycle, a more detailed model could include the effect of variable Q.
2.2 Thwaites marine geophysical datasets
High-resolution multibeam bathymetry and side-scan sonar data were acquired by an autonomous underwater vehicle (AUV) for a 13 km2 area about 3 km offshore from the eastern part of the Thwaites Glacier ice shelf during cruise NBP19-02 of the R/V Nathaniel B. Palmer in 2019 (Fig. 1b). AUV multibeam bathymetric data were cleaned and gridded with horizontal cell sizes of 0.7 and 1.5 m; bottom detect (vertical) resolution is better than 0.02 m. The processed side-scan sonar data, which provide an image of sea-floor reflectivity strength as acoustic backscatter, are dependent on sediment grain size, substrate hardness, and bed roughness, as well as acoustic scattering and incidence. The resultant backscatter images have square 0.05 m pixels. Glacial landform evidence, including subglacial lineations and grounding-zone wedges, confirms that the area surveyed was a former grounding zone for Thwaites Glacier, located on a sea-floor high that the glacier was pinned on during its overall retreat (Hogan et al., 2020b; Graham et al., 2022). Full details of the AUV datasets at Thwaites Glacier and interpretation of the glacial landforms there are given in Graham et al. (2022).
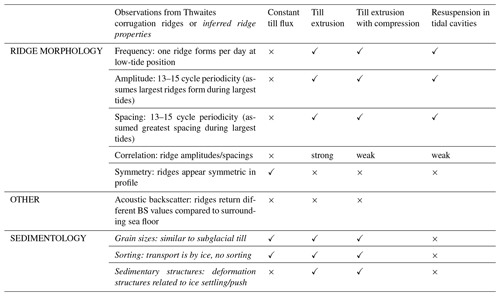
For this study, we focus on the corrugation ridges from the Thwaites AUV dataset (Figs. 1b, S1a in the Supplement). We analysed additional bathymetric profiles across the corrugation ridges to assess ridge morphology in terms of symmetry, lateral continuity, and ridge shape, and we used the side-scan imagery to inform about the acoustic character of the ridges and inter-ridge areas (see Table 2, expanded in Table S1 in the Supplement). In addition to these tabulated characteristics, we provide a short summary of the ridge observations here for comparison with our model outputs. The longest series of corrugation ridges at Thwaites contains 164 individual ridges on a shallow seaward-dipping (0.5–2∘ slopes) sea floor, with amplitudes of 0.1–0.7 m and spacings of 1.6–10.5 m. The ridges exhibit a clear 13–15-ridge periodicity in both their amplitude and peak-to-peak spacing that matches the modelled spring-to-neap tidal periodicity of 14.33 d for the area. The largest spacing between ridges occurs when ridge amplitudes are also highest, meaning that taller ribs are further apart than smaller ones, and it is assumed that the largest spacings/amplitudes were formed by the largest tides (i.e. when the grounding zone is widest and the high-to-low-tide positions will be farthest apart). Detailed analyses of individual ridge morphometry showed that the ridges are symmetric in form. Furthermore, the side-scan sonar data indicate that acoustic reflectivity does vary between the ridges (higher backscatter strength) and inter-ridge (lower backscatter strength) areas, making the ridges particularly easy to identify from this type of data. We have no samples with which to ground truth the side-scan data, and these variations may be due to subtle changes in sediment hardness, roughness, grain size, or illumination of topography (and shadowed areas) during acquisition. The reader is referred to the Graham et al. (2022) paper and its supplementary material for detailed descriptions of the AUV datasets and interpretation of the corrugation ridges (called “ribs” in their paper).
3.1 Modelled formation of grounding-line corrugation ridges
Modelling the constant till flux mechanism (Sect. 2.1.1) with a retreat rate of 6 m per tide produces a complex pattern of ridges, with some with apparent double-peaked (M-shaped) forms and some with multiple peaks (Fig. 3a). These forms result from the close proximity of ridges produced at sequential high-tide positions, and also at low-tide positions, yet there are not consistently 28 ridges per 14 d tidal cycle. Since each pair of ridges formed by a high and low tide can be separated by hundreds of metres, and interleaved by ridges produced by other tides, it is difficult to associate the modelled landforms with the tides that formed them (see Supplement Video S1). The superposition of several ridges forms complex patterns, with large composite ridges evident on a fortnightly cycle, especially on low effective slopes (Fig. 3a). The complex nature of these ridge forms and the production of two ridges per tidal cycle mean that there is no clear correlation between ridge height and spacing (R2=0.103; Fig. 3b).
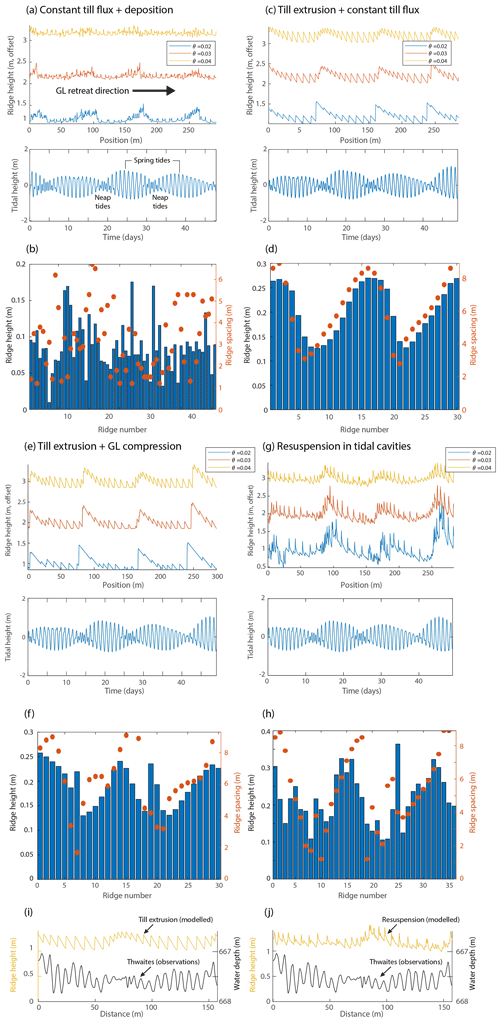
Figure 3Results of modelled corrugation ridges formed by the three mechanisms. (a) Bed and ridge profiles (offset from each other) for different effective bed slopes using the “Constant till flux and deposition” mechanism. (b) Ridge heights and spacings for ridges with θeff=0.04 in panel (a). (c) Bed and ridge profiles for the “Till extrusion with constant till flux” mechanism. (d) Ridge heights and spacings for ridges with θeff=0.04 in panel (d). Note the different vertical scales of panels (b) and (d). (e) Modelled bed and ridge profiles using the “Till extrusion with grounding line compression” mechanism. (f) Ridge heights and spacings for panel (e). (g) Bed and ridge profiles for the “Sediment resuspension in tidal cavities” mechanism. (h) Ridge heights and spacings for panel (g). (i, j) Comparisons of modelled and observed corrugation ridges: (i) till extrusion with constant till flux and a sea-floor profile of ridges at Thwaites Glacier and (j) sediment resuspension in tidal cavities and the sea-floor profile from Thwaites. The Thwaites profile has not been detrended, and model results are shown for θeff=0.04.
For the till extrusion mechanism (Sect. 2.1.2), one ridge per day is produced at the low-tide grounding-line position (Supplement Video S2). As might be expected, ridges become more closely spaced during neap tides (or just after), when the horizontal migration is lowest, and these merge to produce composite forms on lower effective slopes (Fig. 3c). This is because we implement a retreat rate of 6 m d−1 in our models (to preserve individual ridges), so low-tide positions are also close together when the overall retreat best balances (or counters) the increase in grounding-line migration on outgoing tides (cf. Fig. 2b). This “balance spot” appears sometime after neap tides, as the tides transition from neaps to springs (but is balanced by the retreat rate). One way to visualise this is to consider the case where tidal migration of the grounding line is increasing by 6 m d−1, and the rate of grounding-line retreat is also 6 m d−1, then successive low-tide ridges will form in the same location and produce composite ridges. As the tidal cycle progresses, this is followed by the formation of taller ridges during larger tides because the volume of till available to be extruded increases during higher tides. As a result, ridge height and spacing are normally correlated in this mechanism (R2=0.855; Fig. 3d). Outside areas of composite ridge formation, ridge spacing also increases slightly (ridge bases are wider) on lower bed slopes, consistent with an increased range of grounding-line migration on flatter slopes. In Fig. 3e, we show the results of till extrusion but with the till being sourced only from compression at the grounding line (Fig. 2d; Supplement Video S3). As the fundamental mechanism remains the same, the pattern of ridges is similar, but overall ridge heights are slightly smaller and ridge spacing is slightly greater (Fig. 3e, f). This is because the volume of sediment available only depends on the tidal amplitude and associated change in grounding-zone width; in our experiments, the degree of compression is not varied with tidal amplitude (Sayag and Worster, 2013). Outside of areas of composite ridges, ridge spacing more obviously increases as ridge amplitude decreases (compare Fig. 3e to c), leading to more variability in the correlation of ridge height and spacing when compared with the previous till extrusion mechanism (R2=0.447; Fig. 3f).
The final mechanism, resuspension in tidal cavities (Sect. 2.1.3), also produces one ridge at the low-tide position but with less regular shapes than the till extrusion models, notably when there are secondary peaks in the tidal amplitude and during smaller (neap) tides, which tend to occur together (Fig. 3g; Supplement Video S4). Composite forms are also modelled, becoming very pronounced on lower bed slopes and forming on the transitions from neaps to springs to produce large ridges up to 1 m in height (as measured from the sea-floor elevation of neap ridges). Yet ridge spacing reaches its maximum just after this, leading to a poorer correlation between these metrics than for the previous mechanism (Fig. 3f). Outside of composite forms, taller ridges are generally produced by larger tides (springs, Fig. 3g) and on lower bed slopes because a greater area of the grounding zone is exposed and, during larger tides, the drainage rate (velocity) of water out of the cavity is higher. Together, these factors lead to a greater volume of sediment being eroded and available for ridge formation. However, superimposition of ridges formed at lower (neap) tides and at the balance spot described previously leads to some anomalously tall ridges spaced closely together and a poorer correlation of heights and spacing results (R2=0.239; Fig. 3h).
3.2 Implications for the formation of corrugation ridges at grounding lines
To assess whether the formation mechanisms modelled here are robust, we compare the model results with real-world observations from the corrugation ridges observed at Thwaites (see Sect. 2.2, Tables 2, S1). We directly compare modelled output with observations for 14 d periodicity, ridge amplitude, ridge-height-spacing correlation, and the production of individual or composite ridge forms. We also consider, in a more qualitative way, ridge (a)symmetry and consistency of ridge morphology. We then utilise existing knowledge of glacial sediments from former grounding-line settings (e.g. Lindén and Möller, 2005; Demet et al., 2019; Smith et al., 2019) and from well-known sedimentary processes to make inferences about the potential sedimentological properties of corrugation ridges formed by each mechanism. To date, corrugation ridges have not been directly sampled. Our observations from Thwaites and sedimentological inferences for each mechanism are presented in a simplified form in Table 2, and further details and discussion of the evidence for each mechanism supplemented by referenced background information is given in Supplement Table S1. We consider the plausibility of each mechanism in turn.
3.2.1 Constant till flux mechanism
The till flux mechanism produces mostly double-peaked or highly composite ridge forms, with no clear fortnightly pattern to either the spacing or ridge height (Fig. 3a, b). This strongly contrasts our Thwaites observational dataset (Tables 2, S1) with its one ridge per tidal cycle, as well as numerous other tidally modulated ridge landforms (Jakobsson et al., 2011; Graham et al., 2013; Dowdeswell et al., 2020; Supplement Text S1, Fig. S1). So, while this is the simplest conceptual model, we clearly must discount it.
3.2.2 Till extrusion mechanism
The till extrusion models, with either a constant till flux or grounding-line compression, produce ridges that are arguably most similar to the very regular features observed at Thwaites (Fig. 3c, e, i), although some differences do exist. The observed 14-ridge periodicity (Sect. 2.2) is reproduced, as is the normal correlation between ridge height and spacing (Tables 2, S1). As stated in Sect. 2.1.2, we cannot assess the symmetry of ridges produced by this mechanism because we assume that each ridge forms with the same geometry: a landward-facing side reflects the ice-shelf base cavity angle (equal to θeff), and the seaward-facing side is vertical. This is shown clearly in the model results in Fig. 3c and e in comparison with the symmetric forms in Fig. 3i. More complex modelling of the extrusion process, viscous slumping of the ridge, and ice-till coupling during the push process for a subglacial till type of material would be required to allow a detailed comparison of ridge shape. However, we do note that when effective slopes most similar to the observed bed at Thwaites (θeff=0.02) are used, pronounced composite ridges are formed, resulting in a long wavelength (λ∼90 m) cyclicity in bed topography (Fig. 3c, e). By way of comparison with the Thwaites observations, although some corrugation ridges do appear to climb and descend longer wavelength topography, we do not see any clear evidence for either composite ridges or regular bed undulations in the sea-floor data.
An extrusion-type model is the mechanism favoured by marine geoscientists (Dowdeswell et al., 2020; Graham et al., 2022) based on form analogy with other landforms produced at glacier and ice-sheet grounding lines. Recessional or De Geer moraines that form by push as a grounding line readvances over a bed of unconsolidated sediments (Boulton, 1986; Lindén and Möller, 2005) can also have very regularly spaced, repeating morphologies when produced annually by winter readvances of local glacier fronts (e.g. Ottesen and Dowdeswell, 2006; Todd et al., 2007; Burton et al., 2016). However, these moraines tend to be at least an order of magnitude larger in their dimensions (height, width, slope angle) and are often asymmetric in cross section due to the forward motion of grounding-line readvance steepening the ice-distal ridge face (Boulton, 1986). Here, the model only simulates the resettling of ice on to deformable (recently subglacial) sediments at the low-tide position squeezing sediment up into a small ridge, leaving an imprint of the grounding line on the sea floor. As such, we do not expect to recreate ridge asymmetry with this model but note that only the landward side of the corrugation ridge should reflect the shape of the ice base as it touches down onto the bed (Tables 2, S1). We also do not expect any significant modification of ridge shape by post-formation downslope processes (e.g. slumping), owing to the incredibly shallow slopes of their flanks: Graham et al. (2022) report median values of 0.05–0.2∘ for both flanks.
Supporting observational evidence for a till extrusion process of corrugation ridge formation is found in the remarkable consistency from one ridge to the next, i.e. as retreat progressed, at both Thwaites and in the Larsen Inlet (Dowdeswell et al., 2020; Graham et al., 2022). This ridge-to-ridge consistency is the case even when along-ridge form is quite variable, indicating that the small-scale (metres to decimetres) shape of the ice base did not vary as the grounding line retreated (Batchelor et al., 2020), which perhaps supports widespread dynamic thinning as a retreat mechanism over high rates of melting that might alter the shape of the ice-base variably along the grounding line. A process analogy to the squeezing out of sediment that we describe here may come from crevasse-squeeze ridge landforms, which are metres high, sharp-crested, and formed of till and are mostly observed in association with surge-type glaciers. For surging glaciers, the process is squeezing of subglacial till into basal crevasses that opened when high basal water pressures facilitate bottom-up crevassing (Rea and Evans, 2011); however, subglacial till extrusion into existing ice-margin crevasses have also been described for non-surging but radially spreading glaciers (Evans et al., 2016).
In terms of inferred sedimentological properties of the ridges, it is well known from both extant (sampled) glacier beds (e.g. Englehardt et al., 1990; Tulacyk et al., 1998; Christ et al., 2021) and formerly glaciated terrains (e.g. Boulton and Jones Paul, 1976; Evans et al., 2006; Demet et al., 2019) that subglacial sediments (or tills) typically have diamictic grain-size distributions. That is, most or all grain-size fractions are represented in a poorly sorted or homogeneous mixture, often lacking specific structures or textures (e.g. Eyles et al., 1983; Clarke, 1987). With the till extrusion mechanism, either with constant till flux or grounding-line compression, we expect that subglacial till was originally supplied to the grounding zone via a deforming “conveyor belt” at the ice-bed interface (Alley et al., 1987; Kamb, 2001). If the till used in ridge formation is sourced from a constant till flux to the grounding line during its retreat, then this till layer is “fresh”; conversely, if the till is sourced by grounding line compression of material over a former ice-sheet bed, then the till may pre-date the grounding-line retreat phase. In either case, we do not expect any textural or grain-size differences between the ridge and inter-ridge areas beyond the deformational sediment textures and structures typically associated with subglacial traction tills (e.g. van der Meer et al., 2003; Evans et al., 2006; Reinardy et al., 2011; Table S1). Similarly, we would not expect any shearing deformation or stacking of till layers associated with forward motion, or push, as might be found within recessional push moraines or thrusts (e.g. Menzies, 2000; Evans et al., 2007; Table S1).
Based on our model results we cannot properly distinguish between the constant till flux or grounding-line compression source for the ridge material. Both mechanisms produce a series of regular corrugation ridges, although the correlation of ridge height to spacing is stronger, and in line with our observations, for the constant till flux mechanism. We also tend to favour this mechanism for till supply because, when visualising a grounding line that retreats only 6 m d−1, we recognise that almost the same area of sea floor will be compressed every day, as the ice lifts and resettles with the tides. We posit that repeated compression of till across the grounding zone would make this material more difficult to mobilise over time (by compressing, dewatering, and stiffening). Basal properties derived from seismic datasets and inferred from numerical models provide some support for this notion. At Whillans Ice Stream, arguably the best-studied extant Antarctic grounding zone, seismic properties (density ρ, P wave velocity VP, S wave velocity VS) indicate significant stiffening of a 5 m till layer across a sharp transition at the grounding zone (Horgan et al., 2021). This stiff, low-permeability substrate at the grounding zone is consistent with models of ice-shelf flexure (for fixed and tidally migrating grounding lines) that predict compression and potentially dewatering of subglacial till immediately upstream of the grounding zone, as ice bends down into the substrate at high tide (Walker et al., 2013; Sayag and Worster, 2013). Whether this compression and dewatering is enough to prevent material squeezing out from the grounding line after the ice resettles on the sea floor is unknown.
Given the above discussion, we prefer the idea of a constant till flux supplied by the “till conveyor” to form the ridges. With this in mind, we can compare previous estimates of the subglacial sediment flux (to the grounding line) with the volume of a ridge formed once per day at Thwaites Glacier to see if this mechanism of till supply is realistic. Estimated fluxes of 100 m3 yr−1 (per metre of ice stream width) (0.27 m3 d−1) for the extant grounding line of Whillans Ice Stream (Engelhardt and Kamb, 1997; Anandakrishnan et al., 2007), and 800–1000 m3 yr−1 (2.2–2.7 m3 d−1) for large, fast flowing Antarctic and Greenlandic palaeo-ice streams (Dowdeswell et al., 2004; Hogan et al., 2012, 2020a), suggest that daily fluxes of sediment to the grounding line are likely to be on the order of a few tenths of 1 m3 to a few cubic metres. If we consider the average dimensions of a triangular, symmetric corrugation ridge at Thwaites (0.2 m tall, 5 m wide at the base), then we can calculate that every 1 m section along the ridge will contain 0.5 m3 of sediment. Thus, it appears that the subglacial till conveyor is able to supply about the right amount of sediment to build a daily ridge of the same magnitude as the Thwaites corrugation ridges.
One potential contradiction for the till extrusion mechanism comes from the modelling results of Warburton et al. (2020), who found that low subglacial till permeability filters the grounding-line response to tidal forcing, essentially fixing the grounding line at the high-tide position. As pointed out by Graham et al. (2022), the strong tidal periodicity of the corrugation ridge dimensions should, therefore, indicate a high permeability substrate in the region of ridge formation, despite observational evidence that most subglacial tills are cohesive and likely to have low permeabilities. Graham et al. addressed this problem by suggesting that water may drain out of the grounding zone via a series of shallow canals, although another alternative is that the pattern of grounding-line migration at Thwaites is not controlled by fluid connectivity through the till, as has been suggested for the Whillans grounding zone (Horgan et al., 2021).
3.2.3 Resuspension in tidal cavities mechanism
Like the till extrusion mechanism (with either till source), with real-world corrugation ridges, the resuspension of sediment in the tidal cavities mechanism (shortened to “resuspension mechanism” hereafter) produces a series of corrugation ridges with a 13–15 cycle periodicity in their amplitudes and spacings (Fig. 3g, h), although these are only weakly correlated (Tables 2, S1). The shape of the modelled ridges, which are sharp-crested, is also different from the observation of the symmetric ridge cross-sectional shape at Thwaites (Fig. 3j). Again, this is largely due to the simplicity of our model that preserves a vertical seaward slope.
Perhaps of note is that the resuspension mechanism is the only mechanism that would result in a variation in acoustic backscatter over the ridges due to a grain-size change (Tables 2, S1). Smaller particles would be preferentially eroded from the grounding-zone bed and eventually deposited to form the ridges, leading to finer grain sizes in the ridges versus inter-ridge areas. However, the backscatter response on the side-scan sonar images clearly shows higher reflectivity (i.e. brighter returns) on the ridges and lower reflectivity (darker returns) in the inter-ridge areas (Fig. 1b). This is the opposite of what we would expect if the ridges were composed of fine-grained material and the inter-ridge areas consisted of the remaining coarse particles (e.g. Lurton and Lamarche, 2015). In contrast, we can envision that squeezing out of till into a ridge at the grounding line (as in the till extrusion mechanism) may produce a rougher surface texture, producing relatively higher backscatter returns than the inter-ridge areas that have been compressed, or that the stronger returns on the ridges are purely a product of the topography of the ridge fronts. A detailed sampling campaign would be required to ground truth the sedimentology of ridge and inter-ridge areas and so to determine the cause of the backscatter variations.
A sediment suspension mechanism is probably the easiest to interrogate using a combination of empirical datasets and established sediment dynamics theory. Our model simulates water rushing into (and out of) a 1 km wide grounding-zone cavity when set up in a Thwaites configuration and assumes that enough particles can be eroded from the bed of the grounding zone to build a ridge every day. Precedence for such a mechanism comes from the process of “tidal pumping”, whereby tidal flows in a sub-ice-shelf cavity winnow fine-grained particles from glacigenic debris as it melts out from the ice-shelf base near the grounding line and then transports these particles in suspension seaward, eventually depositing them as laminated clayey to fine sandy units. This tidal pumping is well established based on marine sediment core data from the Antarctic continental shelf (Domack and Harris, 1998; Domack et al., 1999) and provides some support for the notion that tidal water velocities can be at least high enough to transport grains up to fine sands in size (0.25 mm diameter). Thus, our mechanism here is similar to tidal pumping because we stipulate (in the model) that the outflows carrying fine-grained particles do not migrate vertically, exiting the grounding zone horizontally and immediately depositing their suspension load to form a ridge.
Accepting this and remembering that every 1 m section along a corrugation ridge will contain around 0.5 m3 of sediment, a basic calculation can be done to determine how much subglacial sediment would need to be eroded from the bed to produce a 0.5 m3 ridge after each tidal cycle (i.e. once per day at Thwaites). Subglacial tills recovered from the western Amundsen Sea in marine sediment cores have similar grain-size distributions, with around 90 % of grains (by weight) being smaller than 2 mm in diameter and around 65 % smaller than 0.25 mm (Smith et al., 2011; see Supplement Table S2). Using a wet bulk density of 1.575 g cm−3 for a standard marine sandy-silty clay (Hamilton and Bachman, 1982), we calculate that around 788 kg of material is required for each 1 m section of ridge. Assuming that grains are eroded across the entire grounding zone, and that only 65 % of them are small enough to be transported to form a ridge, then we calculate that grains would only need to be eroded from the upper ∼ 0.6 mm of the till (wet bulk density 2.1 g cm−3; see Supplement Text B) to provide enough material to form each ridge. This thickness is very small indeed and may indicate that there would have been a plentiful supply of fine-grained particles (from the bed) across the grounding zone with which to form the ridges. However, there are several potential pitfalls with the following simple calculation: (1) with a grounding-zone width of 1 km, tidal water velocities are extremely low, on the order of only a few cm s−1, and therefore below the speeds required for the erosion and transport of fine sands from the bed (e.g. McCave and Hall, 2006); (2) it is unlikely that particles would be resuspended from across the entire 1 km wide grounding zone because as the ice-shelf base becomes less confined (away from the grounding line) the influence of tidal flows would diminish; and (3) it is unclear how fine-grained particles would continue to be mobilised from sub-sea-floor depths once surface sediments had been winnowed, presumably to form either a hardground or lag deposit as is found when strong ocean bottom currents winnow sea-floor sediments (Anderson et al., 1980; Hillenbrand et al., 2003) or to create a granulated facies (with fines removed) similar to those found overlying subglacial tills elsewhere in Antarctica (Domack and Harris, 1998; Domack et al., 1999; Kirshner et al., 2012).
The first of these issues is probably the hardest to counter. Water velocities of only a few centimetres per second, which are in fact in line with the few existing hydrographic observations of extremely low-to-undetectable tidal current velocities in grounding-zone cavities (Begeman et al., 2020; Davis et al., 2023), would only allow for transport of the very finest particles (clay and fine silts < 10 µm). Velocities above ∼ 20 cm s−1 are required to keep sand-sized grains (diameters 63 µm–2 mm) mobile in suspension (McCave and Hall, 2006). Such velocities could be achieved if the grounding zone was much wider; for example, a 10 km wide grounding zone, which is at the upper bound of observed widths around Antarctica (see Brunt et al., 2011), could produce tidal water velocities of ∼ 23 cm s−1 and, therefore, transport sand-sized grains. The occurrence of granulated units elsewhere on the Antarctic continental shelf, including in the Amundsen Sea (Kirshner et al., 2012), might actually indicate that such velocities can be achieved. Turning to the second and third issues, if grains were only eroded from a 100 m wide area adjacent to the grounding line then all particles from the upper ∼ 6 mm of the bed would be required to build a ridge, and mobilising grains from sub-sea-floor layers becomes increasingly difficult to envision (recalling daily retreat rates of only 6 m, so the bed would be repeatedly eroded). If grains can only be mobilised from the newly exposed grounding-zone area (6 m wide) then the depth of erosion increases to an untenable 625 mm (62.5 cm). Even if we accepted this erosion process for some area of the grounding zone, it is also difficult to see how such a “dumping” mechanism would result in all grains being deposited instantaneously (the finest particles would surely be carried further seaward), or how this would produce such consistent ridge-to-ridge morphologies as is observed at both the Thwaites and Larsen Inlet sites (Table S1).
Thus far, we have only considered the transport of grains in suspension and not how easy it is to erode them from the bed. The matrix of subglacial tills, including those recovered from the Amundsen Sea area close to Thwaites Glacier (Smith et al., 2011, 2013; Table S2) and those observed directly at the few Antarctic grounding zones to have been accessed (Langovde Glacier, East Antarctica: Sugiyama et al., 2014; Mackay Glacier: Powell et al., 1996), are dominated by fine grain sizes (typically ∼ 55 %–70 % clays and silts). As a result, subglacial tills behave cohesively (with respect to erosion by water), and the fine grains within them are able to withstand larger values of shear stress without being eroded (Mier and Garcia, 2011). Unidirectional flume experiments designed specifically to assess erosion of glacial till or till-like sediments in rivers or coastal environments have returned critical shear stress values of 4–9 N m−2 to initiate erosion (McNeil et al., 1996; Mier and Garcia, 2011; Pike et al., 2018), whereas our model predicts a shear stress across the grounding-zone bed of only ∼ 1 N m−2. Although this may intuitively indicate that greater shear stresses (or water velocities) are required to erode glacial till across the grounding zone, the additional complexities of being in a grounding-zone setting (tidal currents switching direction and lift-off and re-settling of the ice sheet, compressing but also disturbing the bed every 12 h for diurnal tides as in the Thwaites area) mean that this assumption is not straightforward. In addition, we note that there is a growing body of observations showing that some Antarctic grounding zones are in fact kilometres wide (Mohajerani et al., 2021; Milillo et al., 2022; Chen et al., 2023), an order of magnitude greater than predicted for ice shelves in hydrostatic equilibrium (Mohajerani et al., 2021). Such a wide grounding zone would significantly increase tidal flow velocities, especially in narrow cavities, and potentially allow for much greater erosion and sediment transport. Furthermore, current erosion of the bed may not be the only source of sediment to the tidal cavity. Meltout of basal debris from the ice-sheet base as the cavity opens could be an additional source of particles (see the tidal pumping mechanism described above), although this may be limited to areas very close to the grounding line (Domack and Harris, 1998; Smith et al., 2019), and the disturbance or ploughing of the bed by a rough ice base swiftly followed by lift off as the tidal cavity opens is another process that may mobilise fine-grained sediments into suspension, therefore lowering the current velocities required to transport material out of the grounding zone.
The tidal resuspension mechanism is eminently testable with direct sampling. Sediment samples from an area of corrugation ridges should comprise normally sorted, fine-grained deposits in the ridges and winnowed subglacial sediments (with fines removed at least in their uppermost layers) in intervening bed areas (Supplement Table S1). Although it appears that there is sufficient supply of fine-grained sediments to the grounding zone for this mechanism to be plausible, the cohesive nature of glacial tills and low predicted tidal current velocities make it difficult to see how enough material could be mobilised from the bed every day to produce even the subtle (low amplitude) ridges described from Thwaites or the Larsen Inlet.
3.2.4 Implications for bed geometry
A final yet important consideration is how the models perform with realistic ice-bed geometries, which is represented in the models by θeff. Both the till extrusion and resuspension mechanisms produce tidally correlated ridges for the larger values of θeff but increasingly large composite ridges with a decreasing number of individual ridges, quite unlike the observations that consistently show individual ridge forms were produced at each tidal cycle on low-gradient bed slopes (i.e. smaller values of effective slope; see Sect. 2.2). This conflicts with the suggestion in Graham et al. (2022) that the corrugation ridges at Thwaites may have formed in ice-plain conditions (θeff close to 0) because the thinning or melting rate required to sustain rapid retreat is proportional to θeff and is thus easier to achieve for lower values of effective slope. However, the control on composite ridge formation is the balance between the daily retreat rate (which we take to be directly observable) and the changes in grounding-line migration range over the tidal cycle, which depends only on the tides and the effective slope. While it is possible that present tides do not represent the tidal amplitudes during the time of ridge formation, we assume that θeff is left as our only control parameter. We therefore suggest that it would be impossible to form the observed ridges at small θeff, implying that a large thinning rate was truly necessary to drive the retreat. As such, we reiterate that, in addition to the melting at the grounding line quantified by Graham et al. (2022), dynamic thinning following ice-sheet acceleration likely also contributed to the total thinning rate.
3.3 Larsen Inlet corrugation ridges: model validation
A natural question for model validation is whether the mechanisms described above can produce corrugation ridges in other settings, if the models are run using parameters other than those representative of conditions at Thwaites Glacier. The Larsen Inlet corrugation ridges (Dowdeswell et al., 2020) represent distinctly similar landforms in a somewhat different setting – the ridges are on a shallow landward slope (typical slopes of 0.5–1∘, which equates to lower values of θeff), separated by 20–25 m, in a location where there are two tides per day (corresponding to a suggested retreat rate approximately 10 times larger than at Thwaites). In addition, some of the ridges are double peaked (M shaped), reminiscent of the output with the constant till flux mechanism at Thwaites (e.g. Fig. 3a).
In Fig. 4a we show the results of the three models run using Weddell Sea tides (for the Larsen Inlet site), a retreat rate of 50 m d−1 (as suggested in Dowdeswell et al., 2020), and θeff=0.02. The most notable result is that despite two tides per day, over much of the tidal cycle only one ridge is preserved per day, leading to a ridge spacing that is double the observed values. This is due to the difference in amplitude between the two daily tides, so that alternating low-tide positions eliminate the previous, less-far seaward ridge. Figure 4b shows the result of the same modelling but with a retreat rate of 25 m d−1, which is still extremely high compared to all but the fastest modern retreat rates (cf. Milillo et al., 2022) but half the value previously associated with these bedforms. With this reduced retreat rate, we do reproduce the correct mean corrugation ridge spacing. Further, we see that the constant till flux mechanism still does not produce coherent tidally modulated ridges, while both the till extrusion and sediment resuspension mechanisms produce clear corrugation ridges. We also show that both these preferred mechanisms produce occasional but discrete double-peaked ridges (see arrows in Fig. 4b), as are often observed at Larsen Inlet (Fig. 4c; Table S1) but which were not formed by the models under Thwaites parameters. This reinforces our view that either till extrusion or sediment resuspension represent the most plausible way to form corrugation ridges, whilst also building confidence that our modelling is not overly tuned to Thwaites-like conditions and so may apply more generically around Antarctica.
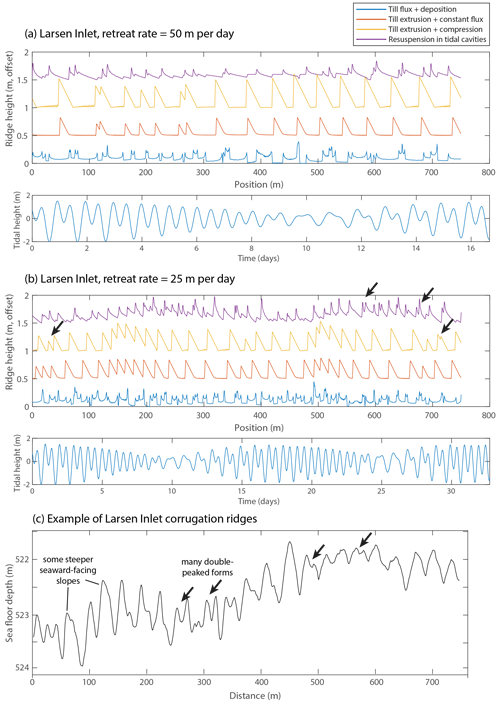
Figure 4Modelled corrugation ridges in the Larsen Inlet study area produced by the three mechanisms and θeff=0.02 for: (a) a “fast” grounding-line retreat of 50 m d−1, as suggested by Dowdeswell et al. (2020), and (b) a grounding-line retreat of 25 m d−1. Black arrows show double-peaked or M-shaped ridges discussed in the text. (c) Sea-floor profile over Larsen Inlet corrugation ridges. Note that the ridges shown have not been detrended nor lined up with modelled forms or tides for the Larsen Inlet.
3.4 Observations necessary to further refine formational mechanisms
In considering all the above discussed mechanisms, we suggest that future work into corrugation ridge landforms, their geometries, and their composition should be undertaken to explore, test, and develop the ideas presented here. One observational approach might be to assess contemporary relationships between grounding-line behaviour and tides in an active ice-stream grounding-zone setting. A candidate environment would be a part of the modern grounding zone, where the glacier is presently sat on a flat bed and is measured to be retreating rapidly over short timescales (e.g. Pope Glacier, one of Thwaites' neighbouring glacial outlets, which retreated at rates of > 10 km yr−1 in 2017 (equates to ∼ 27 m d−1); Milillo et al., 2022). However, these surveys remain a significant challenge given the extreme difficulty in accessing grounding zones around the Antarctic, either from the ocean or from the ice-sheet surface above. Two alternatives we propose are (1) to recover further high-resolution geomorphological information and observations at ice-proximal sites that represent very recently deglaciated proglacial seascapes (cf. Graham et al., 2022) and (2) to seek out candidate grounding-zone wedges on the continental shelf in the open ocean that might preserve additional evidence for rapid retreat phases in their sea-floor landforms (cf. Dowdeswell et al., 2020; Batchelor et al., 2023). In both instances, because of the fine scale of the landforms in question, we argue that even mid-water AUV geophysical mapping is still insufficient to fully understand the mechanisms in question. Remotely operated vehicles (ROVs) with camera capabilities, as well as low-altitude bathymetric lidar scanning equipment, would provide the optimum platform for future investigation. Furthermore, in both cases, we recognise that many of the key tests of corrugation ridge formation rely upon physical sampling of the features. Equipping sea-floor exploration vehicles with mini vibrocoring tools would allow for the recovery of sediments from targeted locations across individual corrugation ridge landforms that can test some of the hypotheses put forward in this paper.
3.5 Potential for further modelling work
The work presented in this paper is a first quantitative modelling effort for several previous conceptual models of corrugation ridge formation (at grounding lines) and has improved our understanding of which mechanisms are most plausible and which parameters (surface slope, average till flux, mean retreat rate) control the basic components of ridge morphology, such as amplitude and spacing. However, these models rely on several simplifying assumptions and do not attempt to replicate the dynamics of ridge formation. As a result, we cannot capture the detailed shape of the ridges, a significant aspect of the observational data that we are presently unable to compare to. Having identified the till extrusion and resuspension models as most able to produce something akin to the real-world tidally modulated corrugation ridges, future modelling should focus on the dynamics of these mechanisms.
In the resuspension mechanism, the parameterisation of sediment erosion could be improved by incorporating more detailed modelling of tidally driven flows between the ocean and the grounding-zone cavity, rather than assuming a sudden transition in the strength of the flow. With a more detailed understanding of the flow speeds throughout the grounding zone, a future model could use the implied spatially and temporally evolving grain-size-dependent sediment flux to model the shape of depositional ridges and to quantify the expected grain-size sorting.
For the till extrusion mechanism, we have neglected the details of the flow field in the till. Future modelling should include the viscous and elastic coupling between the ice and the till, which controls both the till flux towards the grounding line and the shape of the base of the ice, where we have taken these as given and as constant. This modelling could also capture ocean–till interactions at the grounding line as the ice retreats and the viscous relaxation of the ridges after their formation. These processes all depend sensitively on the till rheology, and matching the final shape of the ridges to the observations would therefore help to constrain parameters such as till yield strength and compressibility.
An additional target for future modelling work could be to simulate corrugation ridge formation within iceberg plough marks, as individual icebergs periodically impact the sea floor (e.g. Fig. S1d). Although the details of this process are different from our grounding line setting, i.e. there is no sediment supply from upstream nor compression from a lifting and settling ice sheet, the relative simplicity of this process may help to support a till extrusion (squeeze out) mechanism at grounding lines.
Using mathematical modelling we have investigated three formation mechanisms (constant till flux, till extrusion, and resuspension in tidal cavities) for low-amplitude, regular corrugation ridge landforms at Antarctic grounding lines. The models produce plausible ridges for the only two real-world examples of grounding-line corrugation ridges currently known, at Thwaites Glacier, West Antarctica, and in the Larsen Inlet, eastern Antarctic Peninsula, using different boundary conditions (bed slopes, tides) and indicate that the till extrusion (squeeze out at the grounding line as the ice re-settles on the sea floor at low tides) and resuspension (erosion and flushing out of fine-grained sediments by tidal flows) mechanisms produce ridges most similar to observed landforms. After comparisons with empirical datasets from extant and relict grounding zones, previous modelling studies, and known sedimentary processes, outstanding questions remain around the fine-grained sediment supply (erodibility of tills) for the resuspension mechanism, as well as how it would produce such consistent ridge morphologies. As such, the till extrusion mechanism is the preferred mechanism for corrugation ridge formation.
Given the significance of these landforms as specific markers of quantifiable rapid grounding-line-retreat behaviour, probably with a strong contribution from dynamic thinning, we advocate for their further exploration. High-resolution sea-floor surveying by AUVs or ROVs, and precision sea-floor sampling on ridge crests and inter-ridge areas on a transect across the ridges – followed by detailed sedimentology and dating – would confirm the tidal modulation of the ridges and identify the specific times (and climatic conditions) when rapid grounding-line retreat occurred, as well as help determine the formation mechanism for these intriguing landforms. Additional mathematical modelling, guided by such observations, testing different sediment properties (e.g. permeability, grain-size distributions, cohesion), variable boundary conditions (e.g. ice-shelf cavities and bed shapes), and an elastic (bending) ice shelf should help to determine which grounding-zone conditions and geometries were present during the formation of these landforms and therefore which grounding lines may be vulnerable to (or allow) the very rapid grounding-line retreat (km yr−1) associated with them.
All data needed to evaluate the conclusions in this paper are presented in the paper or in the Supplement including the model code. The model code is also available at the University of Cambridge Apollo Repository (https://doi.org/10.17863/CAM.96524, Warburton et al., 2023). A high-resolution multibeam raster grid over the Thwaites Glacier corrugation ridges (AUV mission 009) is available for download from the figshare repository (https://doi.org/10.6084/m9.figshare.20359920.v1, Graham, 2022); for full details of this dataset see Graham et al. (2022). Gridded multibeam data for the Larsen Inlet corrugation ridges are available upon request from Julian A. Dowdeswell.
The supplement related to this article is available online at: https://doi.org/10.5194/tc-17-2645-2023-supplement.
KAH, KLPW, AGCG, and RDL designed the study; KLPW wrote the model code and performed the simulations with contributions from JAN and DRH; JAD provided the data from the Larsen Inlet; KAH and KLPW wrote the paper draft with contributions from AGCG; and RDL, JAN, DRH, and JAD reviewed and edited the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors thank the masters, officers, and crews of the R/V Nathaniel B. Palmer and S.A. Agulhas II, as well as the science parties of cruises NBP19-02 and The Weddell Sea Expedition 2019 for their valuable support during AUV data collection. We thank Anna Wåhlin, University of Gothenburg, for her generous contribution in collecting the downward-looking AUV data at Thwaites Glacier during NBP19-02 and for her comments on this paper; Claus-Dieter Hillenbrand and James Smith, British Antarctic Survey, are thanked for their helpful discussions relating to the sedimentology of Antarctic tills and glacial sedimentary processes; and Ed Self, Gardline Ltd., is thanked for access to the bathymetry dataset in Supplement Fig. S1d. This work is also an output of the Thwaites Offshore Research (THOR) project, a component of the International Thwaites Glacier Collaboration (ITGC). Logistics for ITGC were provided by the NSF United States Antarctic Program and the NERC British Antarctic Survey (ITGC contribution no. ITGC-103). Finally, we thank the one anonymous reviewer, Sarah Greenwood, and Chris R. Stokes (editor) for their helpful comments that improved the paper.
This research has been supported by the Natural Environment Research Council (grant nos. NE/S006641/1, NE/L002507/1, and NE/S006206/1). Sea-floor data collection in the Larsen Inlet, western Weddell Sea, was funded by the Flotilla Foundation.
This paper was edited by Chris R. Stokes and reviewed by Sarah Greenwood and one anonymous referee.
Alley, R. B., Blankenship, D. D., Bentley, C. R., and Rooney, S.: Deformation of till beneath ice stream B, West Antarctica, Nature, 322, 57–59, 1986.
Alley, R. B., Blankenship, D., Rooney, S., and Bentley, C.: Sedimentation beneath ice shelves – the view from ice stream B, Mar. Geol., 85, 101–120, 1989.
Alley, R. B., Anandakrishnan, S., Dupont, T. K., Parizek, B. R., and Pollard, D.: Effect of sedimentation on ice-sheet grounding-line stability, Science, 315, 1838–1841, 2007.
Anandakrishnan, S., Catania, G. A., Alley, R. B., and Horgan, H. J.: Discovery of till deposition at the grounding line of Whillans Ice Stream, Science, 315, 1835–1838, 2007.
Anderson, J. B., Kurtz, D. D., Domack, E. W., and Balshaw, K. M.: Glacial and glacialmarine sediments of the Antarctic continental shelf, J. Geol., 27, 399e414, https://doi.org/10.1086/628524, 1980.
Batchelor, C. L., Montelli, A., Ottesen, D., Evans, J., Dowdeswell, E. K., Christie, F. D. W., and Dowdeswell, J. A.: New insights into the formation of submarine glacial landforms from high-resolution Autonomous Underwater Vehicle data, Geomorphology, 370, 107396, https://doi.org/10.1016/j.geomorph.2020.107396, 2020.
Batchelor, C. L., Christie, F. D. W., Ottesen, D., Montelli, A., Evans, J., Dowdeswell, E. K., Bjarnadóttir, L. R., and Dowdeswell, J. A.: Rapid, buoyancy-driven ice-sheet retreat of hundreds of metres per day, Nature, 617, 105–110, https://doi.org/10.1038/s41586-023-05876-1, 2023.
Begeman, C. B., Tulaczyk, S., Padman, L., King, M., Siegfried, M. R., Hodson, T. O., and Fricker, H. A.: Tidal Pressurization of the Ocean Cavity Near an Antarctic Ice Shelf Grounding Line, J. Geophys. Res.-Oceans, 125, e2019JC015562, https://doi.org/10.1029/2019JC015562, 2020.
Boulton, G.: Push-moraines and glacier-contact fans in marine and terrestrial environments, Sedimentology, 33, 677–698, 1986.
Boulton, G. S. and Hindmarsh, R. C. A.: Sediment deformation beneath glaciers: Rheology and geological consequences, J. Geophys. Res., 92, 9059–9082, https://doi.org/10.1029/JB092iB09p09059, 1987.
Boulton, G. and Jones Paul, M.: The influence of genetic processes on some geotechnical properties of glacial tills, Q. J. Eng. Geol., 9, 159–194, 1976.
Brunt, K. M., Fricker, H. A., and Laurie, P.: Analysis of ice plains of the Filchner-Ronne Ice Shelf, Antarctica, using ICESat laser altimetry, J. Glaciol., 57, 965–975, 2011.
Burton, D. J., Dowdeswell, J. A., Hogan, K. A., and Noormets, R.: Marginal Fluctuations of a Svalbard Surge-Type Tidewater Glacier, Blomstrandbreen, Since the Little Ice Age: A Record of Three Surges, Arct. Antarct. Alp. Res., 48, 411–426, https://doi.org/10.1657/AAAR0014-094, 2016.
Chen, H., Rignot, E., Scheuchl, B., and Ehrenfeucht, S.: Grounding zone of Amery Ice Shelf, Antarctica, from differential synthetic-aperture radar interferometry, Geophys. Res. Lett., 50, e2022GL102430, https://doi.org/10.1029/2022GL102430, 2023.
Christ, A. J., Bierman, P. R., Schaefer, J. M., Dahl-Jensen, D., Steffensen, J. P., Corbett, L. B., Peteet, D. M., Thomas, E. K., Steig, E. J., and Rittenour, T. M.: A multimillion-year-old record of Greenland vegetation and glacial history preserved in sediment beneath 1.4 km of ice at Camp Century, P. Natl. Acad. Sci. USA, 118, e2021442118, https://doi.org/10.1073/pnas.2021442118, 2021.
Clarke, G. K.: Subglacial till: a physical framework for its properties and processes, J. Geophys. Res.-Sol. Ea., 92, 9023–9036, 1987.
Davis, P. E. D., Nicholls, K. W., Holland, D. M., Schmidt, B. E., Washam, P., Riverman, K. L., Arthern, R. J., Vaňková, I., Eayrs, C., Smith, J. A., Anker, P. G. D., Mullen, A. D., Dichek, D., Lawrence, J. D., Meister, M. M., Clyne, E., Basinski-Ferris, A., Rignot, E., Queste, B. Y., Boehme, L., Heywood, K. J., Anandakrishnan, S., and Makinson, K.: Suppressed basal melting in the eastern Thwaites Glacier grounding zone, Nature, 614, 479–485, https://doi.org/10.1038/s41586-022-05586-0, 2023.
Dawson, G. and Bamber, J.: Antarctic Grounding Line Mapping From CryoSat-2 Radar Altimetry, Geophys. Res. Lett., 44, 11886–811893, 2017.
Demet, B. P., Nittrouer, J. A., Anderson, J. B., and Simkins, L. M.: Sedimentary processes at ice sheet grounding-zone wedges revealed by outcrops, Washington State (USA), Earth Surf. Proc. Land., 44, 1209–1220, 2019.
Domack, E. W.: Laminated terrigenous sediments from the Antarctic Peninsula: the role of subglacial and marine processes, Geological Society, London, Special Publications 53, 91–103, 1990.
Domack, E. W. and Harris, P. T.: A new depositional model for ice shelves, based upon sediment cores from the Ross Sea and the Mac. Robertson shelf, Antarctica, Ann. Glaciol., 27, 281–284, 1998.
Domack, E. W., Jacobson, E. A., Shipp, S., and Anderson, J. B.: Late Pleistocene–Holocene retreat of the West Antarctic Ice-Sheet system in the Ross Sea: Part 2 – Sedimentologic and stratigraphic signature, GSA Bulletin, 111, 1517–1536, 1999.
Dowdeswell, J. and Fugelli, E.: The seismic architecture and geometry of grounding-zone wedges formed at the marine margins of past ice sheets, Bulletin, 124, 1750–1761, 2012.
Dowdeswell, J., Batchelor, C., Montelli, A., Ottesen, D., Christie, F., Dowdeswell, E., and Evans, J.: Delicate seafloor landforms reveal past Antarctic grounding-line retreat of kilometres per year, Science, 368, 1020–1024, 2020.
Dowdeswell, J. A., Cofaigh, C. O., and Pudsey, C. J.: Thickness and extent of the subglacial till layer beneath an Antarctic paleo–ice stream, Geology, 32, 13–16, 2004.
Drews, R., Wild, C. T., Marsh, O. J., Rack, T. A.,Ehlers, N., and Helm, V.: Grounding-Zone Flow Variability of Priestley Glacier, Antarctica, in a Diurnal Tidal Regime, Geophys. Res. Lett., 48, e2021GL093853, https://doi.org/10.1029/2021GL093853, 2021.
Engelhardt, H. and Kamb, B.: Basal hydraulic system of a West Antarctic ice stream: constraints from borehole observations, J. Glaciol., 43, 207–230, 1997.
Engelhardt, H., Humphrey, N., Kamb, B., and Fahnestock, M.: Physical conditions at the base of a fast moving Antarctic ice stream, Science, 248, 57–59, 1990.
Evans, D. J. A., Phillips, E., Hiemstra, J., and Auton, C.: Subglacial till: formation, sedimentary characteristics and classification, Earth-Sci. Rev., 78, 115–176, 2006.
Evans, D. J. A., Hiemstra, J. F., and Ó Cofaigh, C.: An assessment of clast macrofabrics in glacigenic sediments based on A/B plane data, Geogr. Ann., 89, 103–120, 2007.
Evans, D. J. A., Ewertowski, M., and Orton, C., Fláajökull (north lobe), Iceland: active temperate piedmont lobe glacial landsystem, J. Maps, 12, 777–789, https://doi.org/10.1080/17445647.2015.1073185, 2016.
Eyles, N., Eyles, C. H., and Miall, A. D.: Lithofacies types and vertical profile models; an alternative approach to the description and environmental interpretation of glacial diamict and diamictite sequences, Sedimentology, 30, 393–410, 1983.
Graham, A.: Gridded multibeam bathymetry data from “The Bump” at Thwaites Glacier, collected by “Ran” Kongsberg Hugin AUV (Kongsberg EM2040), on the RV Nathaniel B. Palmer during cruise NBP19-02 (2019), figshare [data set], https://doi.org/10.6084/m9.figshare.20359920.v1, 2022.
Graham, A. G., Dutrieux, P., Vaughan, D. G., Nitsche, F. O., Gyllencreutz, R., Greenwood, S. L., Larter, R. D., and Jenkins, A.: Seabed corrugations beneath an Antarctic ice shelf revealed by autonomous underwater vehicle survey: origin and implications for the history of Pine Island Glacier, J. Geophys. Res.-Earth, 118, 1356–1366, 2013.
Graham, A. G. C., Wåhlin, A., Hogan, K. A., Nitsche, F. O., Heywood, K. J., Minzoni, R., Smith, J. A., Hillenbrand, C.-D., Simkins, L., Wellner, J. S., and Larter, R. D.: Rapid tidally-modulated retreat of Thwaites Glacier from a pinning point in the pre-satellite era, Nat. Geosci., 15, 706–713, https://doi.org/10.1038/s41561-022-01019-9, 2022.
Gudmundsson, G. H., Krug, J., Durand, G., Favier, L., and Gagliardini, O.: The stability of grounding lines on retrograde slopes, The Cryosphere, 6, 1497–1505, https://doi.org/10.5194/tc-6-1497-2012, 2012.
Hamilton, E. L. and Bachman, R. T.: Sound velocity and related properties of marine sediments, J. Acoust. Soc. Am., 72, 1891–1904, 1982.
Hillenbrand, C.-D., Grobe, H., Diekmann, B., Kuhn, G. and D. Fütterer: Distribution of clay minerals and proxies for productivity in surface sediments of the Bellingshausen and Amundsen seas (West Antarctica) - Relation to modern environmental conditions, Mar. Geol., 193, 253e271, https://doi.org/10.1016/S0025-3227(02)00659-X, 2003.
Hogan, K. A., Dowdeswell, J. A., and Cofaigh, C. Ó.: Glacimarine sedimentary processes and depositional environments in an embayment fed by West Greenland ice streams, Mar. Geol., 311, 1–16, 2012.
Hogan, K. A., Jakobsson, M., Mayer, L., Reilly, B. T., Jennings, A. E., Stoner, J. S., Nielsen, T., Andresen, K. J., Nørmark, E., Heirman, K. A., Kamla, E., Jerram, K., Stranne, C., and Mix, A.: Glacial sedimentation, fluxes and erosion rates associated with ice retreat in Petermann Fjord and Nares Strait, north-west Greenland, The Cryosphere, 14, 261–286, https://doi.org/10.5194/tc-14-261-2020, 2020a.
Hogan, K. A., Larter, R. D., Graham, A. G. C., Arthern, R., Kirkham, J. D., Totten, R. L., Jordan, T. A., Clark, R., Fitzgerald, V., Wåhlin, A. K., Anderson, J. B., Hillenbrand, C.-D., Nitsche, F. O., Simkins, L., Smith, J. A., Gohl, K., Arndt, J. E., Hong, J., and Wellner, J.: Revealing the former bed of Thwaites Glacier using sea-floor bathymetry: implications for warm-water routing and bed controls on ice flow and buttressing, The Cryosphere, 14, 2883–2908, https://doi.org/10.5194/tc-14-2883-2020, 2020b.
Horgan, H. J., Alley, R. B., Christianson, K., Jacobel, R. W., Anandakrishnan, S., Muto, A., Beem, L. H., and Siegfried, M. R.: Estuaries beneath ice sheets, Geology, 41, 1159–1162, 2013.
Horgan, H. J., van Haastrecht, L., Alley, R. B., Anandakrishnan, S., Beem, L. H., Christianson, K., Muto, A., and Siegfried, M. R.: Grounding zone subglacial properties from calibrated active-source seismic methods, The Cryosphere, 15, 1863–1880, https://doi.org/10.5194/tc-15-1863-2021, 2021.
Howard, S. L., Erofeeva, S., and Padman, L.: CATS2008: Circum-Antarctic Tidal Simulation version 2008, U.S. Antarctic Program (USAP) Data Center [data set], https://doi.org/10.15784/601235, 2019.
Jakobsson, M., Anderson, J. B., Nitsche, F. O., Dowdeswell, J. A., Gyllencreutz, R., Kirchner, N., Mohammad, R., O'Regan, M., Alley, R. B., and Anandakrishnan, S.: Geological record of ice shelf break-up and grounding line retreat, Pine Island Bay, West Antarctica, Geology, 39, 691–694, 2011.
Jakobsson, M., Anderson, J. B., Nitsche, F. O., Gyllencreutz, R., Kirshner, A. E., Kirchner, N., O'Regan, M., Mohammed, R., and Eriksson, B.: Ice sheet retreat dynamics inferred from glacial morphology of the central Pine Island Bay Trough, West Antarctica, Quaternary Sci. Rev., 38, 1–10, https://doi.org/10.1016/j.quascirev.2011.12.017, 2012.
Jamieson, S., Vieli, A., Livingstone, S., O Cofaigh, C., Stokes, C., Hillenbrand, C-. D., and Dowdeswell, J. A.: Ice-stream stability on a reverse bed slope. Nature Geosci., 5, 799–802, https://doi.org/10.1038/ngeo1600, 2012.
Kamb, B.: Basal zone of the West Antarctic ice streams and its role in lubrication of their rapid motion, The West Antarctic ice sheet: behavior and environment, Antarctic Research Series, 77, 157–199, 2001.
Kirshner, A. E., Anderson, J. B., Jakobsson, M., O'Regan, M., Majewski, W., and Nitsche, F. O.: Post-LGM deglaciation in Pine island Bay, west Antarctica, Quaternary Sci. Rev., 38, 11–26, 2012.
Kowal, K. and Worster, M.: The formation of grounding zone wedges: Theory and experiments, J. Fluid Mech., 898, A12, https://doi.org/10.1017/jfm.2020.393, 2020.
Lindén, M. and Möller, P.: Marginal formation of De Geer moraines and their implications to the dynamics of grounding-line recession, J. Quaternary Sci., 20, 113–133, 2005.
Lurton, X. and Lamarche, G. (Eds): Backscatter measurements by seafloor-mapping sonars. Guidelines and Recommendations, 200 pp., https://geohab.org/wp-content/uploads/2018/09/BWSG-REPORT-MAY2015.pdf (last access: 14 June 2023), 2015.
McCave, I. N. and Hall, I. R.: Size sorting in marine muds: Processes, pitfalls, and prospects for paleoflow-speed proxies, Geochem. Geophy. Geosy., 7, Q10N05, https://doi.org/10.1029/2006GC001284, 2006.
McNeil, J., Taylor, C., and Lick, W.: Measurements of Erosion of Undisturbed Bottom Sediments with Depth, J. Hydraul. Eng., 122, 316–324, 1996.
Menzies, J.: Micromorphological analyses of microfabrics and microstructures indicative of deformation processes in glacial sediments, Geological Society, London, Special Publications, 176, 24–257, 2000.
Mier, J. M. and Garcia, M. H.: Erosion of glacial till from the St. Clair River (Great Lakes basin), J. Great Lakes Res., 37, 399–410, 2011.
Milillo, P., Rignot, E., Rizzoli, P., Scheuchl, B., Mouginot, J., Bueso-Bello, J. L., Prats-Iraola, P., and Dini, L. J. N. G.: Rapid glacier retreat rates observed in West Antarctica, Nat. Geosci., 15, 48–53, 2022.
Mohajerani, Y., Jeong, S., Scheuchl, B., Velicogna, I., Rignot, E., and Milillo, P.: Automatic delineation of glacier grounding lines in differential interferometric synthetic-aperture radar data using deep learning, Sci. Rep., 11, 1–10, 2021.
Ottesen, D. and Dowdeswell, J. A.: Assemblages of submarine landforms produced by tidewater glaciers in Svalbard, J. Geophys. Res.-Earth, 111, F01016, https://doi.org/10.1029/2005JF000330, 2006.
Padman, L., Fricker, H. A., Coleman, R., Howard, S., and Erofeeva, L.: A new tide model for the Antarctic ice shelves and seas, Ann. Glaciol., 34, 247–254, 2002.
Pegler, S. and Worster, M.: An experimental and theoretical study of the dynamics of grounding lines, J. Fluid Mech., 728, 5–28, https://doi.org/10.1017/jfm.2013.269, 2013.
Pike, L., Gaskin, S., and Ashmore, P.: Flume tests on fluvial erosion mechanisms in till-bed channels, Earth Surf. Proc. Land., 43, 259–270, 2018.
Powell, R. D., Dawber, M., McInnes, J. N., and Pyne, A. R.: Observations of the grounding-line area at a floating glacier terminus, Ann. Glaciol., 22, 217–223, 1996.
Pritchard, H., Ligtenberg, S. R., Fricker, H. A., Vaughan, D. G., van den Broeke, M. R., and Padman, L.: Antarctic ice-sheet loss driven by basal melting of ice shelves, Nature, 484, 502–505, 2012.
Pritchard, H. D., Arthern, R. J., Vaughan, D. G., and Edwards, L. A.: Extensive dynamic thinning on the margins of the Greenland and Antarctic ice sheets, Nature, 461, 971–975, 2009.
Rea, B. R. and Evans, D. J. A.: An assessment of surge-induced crevassing and the formation of crevasse squeeze ridges, J. Geophys. Res.-Earth, 116, F04005, https://doi.org/10.1029/2011JF001970, 2011.
Reinardy, B. T., Larter, R. D., Hillenbrand, C. D., Murray, T., Hiemstra, J. F. and Booth, A. D.: Streaming flow of an Antarctic Peninsula palaeo-ice stream, both by basal sliding and deformation of substrate, J. Glaciol., 57, 596–608, 2011.
Rignot, E., Mouginot, J., and Scheuchl, B.: Antarctic grounding line mapping from differential satellite radar interferometry, Geophys. Res. Lett., 38, L10504, https://doi.org/10.1029/2011GL047109, 2011.
Rignot, E., Jacobs, S., Mouginot, J., and Scheuchl, B.: Ice-shelf melting around Antarctica, Science, 341, 266–270, 2013.
Robel, A. A., Schoof, C., and Tziperman, E.: Rapid grounding line migration induced by internal ice stream variability, J. Geophys. Res.-Earth, 119, 2430–2447, 2014.
Robel, A., Tsai, V., Minchew, B., and Simons, M.: Tidal modulation of ice shelf buttressing stresses, Ann. Glaciol., 58, 12–20, https://doi.org/10.1017/aog.2017.22, 2017.
Sayag, R. and Worster, M. G.: Elastic dynamics and tidal migration of grounding lines modify subglacial lubrication and melting, Geophys. Res. Lett., 40, 5877–5881, 2013.
Sayag, R. and Worster, M. G.: Elastic response of a grounded ice sheet coupled to a floating ice shelf, Phys. Rev. E, 84, 036111, https://doi.org/10.1103/PhysRevE.84.036111, 2011.
Schoof, C.: Ice sheet grounding line dynamics: Steady states, stability, and hysteresis, J. Geophys. Res.-Earth, 112, F03S28, https://doi.org/10.1029/2006JF000664, 2007.
Shackleton, C. S., Winsborrow, M. C., Andreassen, K., Lucchi, R. G., and Bjarnadóttir, L. R.: Ice-margin retreat and grounding-zone dynamics during initial deglaciation of the Storfjordrenna Ice Stream, western Barents Sea, Boreas, 49, 38–51, 2020.
Simkins, L. M., Greenwood, S. L., and Anderson, J. B.: Diagnosing ice sheet grounding line stability from landform morphology, The Cryosphere, 12, 2707–2726, https://doi.org/10.5194/tc-12-2707-2018, 2018.
Smith, B., Fricker, H. A., Gardner, A. S., Medley, B., Nilsson, J., Paolo, F. S., Holschuh, N., Adusumilli, S., Brunt, K., Csatho, B., Harbeck, K., Markus, T., Neumann, T., Siegfried, M. R., and Zwally, H. J.: Pervasive ice sheet mass loss reflects competing ocean and atmosphere processes, Science, 368, 1239–1242, 2020.
Smith, J. A., Hillenbrand, C.-D., Kuhn, G., Larter, R. D., Graham, A. G. C., Ehrmann, W., Moreton, S. G., and Forwick, M.: Deglacial history of the West Antarctic Ice Sheet in the western Amundsen Sea Embayment, Quaternary Sci. Rev., 30, 488–505, 2011.
Smith, J. A., Hillenbrand, C.-D., Kuhn, G., Klages, J. P., Graham, A. G. C., Larter, R. D., Ehrmann, W., Moreton, S. G., Wiers, S., and Frederichs, T.: New constraints on the timing of West Antarctic Ice Sheet retreat in the eastern Amundsen Sea since the Last Glacial Maximum, Global Planet. Change, 122, 224–237, https://doi.org/10.1016/j.gloplacha.2014.07.015, 2013.
Smith, J. A., Graham, A. G., Post, A. L., Hillenbrand, C.-D., Bart, P. J., and Powell, R. D.: The marine geological imprint of Antarctic ice shelves, Nat. Commun., 10, 1–16, 2019.
Sugiyama, S., Sawagaki, T., Fukuda, T., and Aoki, S.: Active water exchange and life near the grounding line of an Antarctic outlet glacier, Earth Planet. Sc. Lett., 399, 52–60, 2014.
Thomas, R. H.: The dynamics of marine ice sheets, J. Glaciol., 24, 167–177, 1979.
Todd, B. J., Valentine, P. C., Longva, O., And Shaw, J.: Glacial landforms on German Bank, Scotian Shelf: evidence for Late Wisconsinan ice-sheet dynamics and implications for the formation of De Geer moraines, Boreas, 36, 148–169, 2007.
Tsai, V. C. and Gudmundsson, G. H.: An improved model for tidally modulated grounding-line migration, J. Glaciol., 61, 216–222, 2015.
Tulaczyk, S., Kamb, B., Scherer, R. P., and Engelhardt, H. F.: Sedimentary processes at the base of a West Antarctic ice stream; constraints from textural and compositional properties of subglacial debris, J. Sediment. Res., 68, 487–496, 1998.
van der Meer, J. J., Menzies, J., and Rose, J.: Subglacial till: the deforming glacier bed, Quaternary Sci. Rev., 22, 1659–1685, 2003.
Walker, R. T., Parizek, B. R., Alley, R. B., Anandakrishnan, S., Riverman, K. L., and Christianson, K.: Ice-shelf tidal flexure and subglacial pressure variations, Earth Planet. Sc. Lett., 361, 422–428, https://doi.org/10.1016/j.epsl.2012.11.08, 2013.
Warburton, K., Hewitt, D., and Neufeld, J.: Research data supporting Towards modelling of corrugation ridges at ice-sheet grounding lines, Apollo – University of Cambridge Repository [data set], https://doi.org/10.17863/CAM.96524, 2023.
Warburton, K. L. P., Hewitt, D. R., and Neufeld, J. A.: Tidal Grounding-Line Migration Modulated by Subglacial Hydrology, Geophys. Res. Lett., 47, e2020GL089088, https://doi.org/10.1029/2020GL089088, 2020.
till extrusion, whereby deformable sediment is squeezed out from under the ice like toothpaste as it settles down at each low-tide position, as the most likely process.