the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
An 11-year record of wintertime snow-surface energy balance and sublimation at 4863 m a.s.l. on the Chhota Shigri Glacier moraine (western Himalaya, India)
Thupstan Angchuk
Mohd Farooq Azam
Alagappan Ramanathan
Patrick Wagnon
Mohd Soheb
Chetan Singh
Analysis of surface energy balance (SEB) at the glacier/snow surface is the most comprehensive way to explain the atmosphere–glacier/snow interactions, but that requires extensive data. In this study, we have analysed an 11-year (2009–2020) record of the meteorological dataset from an automatic weather station installed at 4863 (above sea level) on a lateral moraine of the Chhota Shigri Glacier, western Himalaya. The study was carried out over the winter months (December to April) to understand SEB drivers and snow loses through sublimation. Furthermore, this study examines the role of cloud cover on SEB and turbulent heat fluxes. The turbulent heat fluxes were calculated using the bulk-aerodynamic method, including stability corrections. The net short-wave radiation was the primary energy source. However, the turbulent heat fluxes dissipated a significant amount of energy. The cloud cover plays an important role in limiting the incoming short-wave radiation by about 70 %. It also restricts the turbulent heat fluxes by more than 60 %, resulting in lower snow sublimation. During winter, turbulent latent heat flux contributed the largest proportion (64 %) in the total SEB, followed by net radiation (25 %) and sensible heat flux (11 %). Sublimation rates were 3 times higher in clear-sky than overcast conditions, indicating a strong role of cloud cover in shaping favourable conditions for turbulent latent heat flux by modulating the near-surface boundary layer conditions. Dry air, along with high snow-surface temperature and wind speed, favours sublimation. Besides, we also observed that strong and cold winds, possibly through mid-latitude western disturbances, impede sublimation by bringing high moisture content to the region and cooling the snow surface. The estimated snow sublimation fraction was 16 %–42 % of the total winter snowfall at the study site. This study substantiates that the snow sublimation is an essential variable to be considered in glaciohydrological modelling at the high-mountain Himalayan glacierised catchments.
- Article
(18727 KB) - Full-text XML
-
Supplement
(1968 KB) - BibTeX
- EndNote
The widespread global glacier imbalance (Slater et al., 2021; Zemp et al., 2019; IPCC, 2019) is a manifestation of ablation dominance compared to accumulation over the last few decades. Ablation processes – including surface melting, sublimation, evaporation and wind-driven transport/erosion – lead to the loss of snow and ice mass (Bintanja, 1995; Nicholson et al., 2013; Giesen and Andreassen, 2009; Schaefer et al., 2020; van den Broeke et al., 2005; Oerlemans, 2000; Conway and Cullen, 2016). Among these, sublimation from snow and ice surfaces is one of the significant contributors to the total ablation (Stigter et al., 2018; Huintjes et al., 2015a) yet is seldom quantified, especially in the Himalaya–Karakoram (HK) region (Azam et al., 2021). Sublimation can be calculated from the surface energy balance (SEB), which requires several meteorological inputs to describe the physical relationship between the glacier/snow surface and meteorological variables (Oerlemans, 2001).
SEB studies are rare in the HK region due to the extreme terrain and the lack of high-altitude meteorological data from glacier and snow-covered sites. SEB studies have been conducted on nearly 11 glacier/snow-covered sites across the HK region (Table S1 and Fig. S1 in the Supplement). However, SEB studies on Tibetan glaciers are relatively more abundant (∼ 17 investigated glacier/ice-covered sites; Table S1), including direct turbulent heat flux measurements (Yang et al., 2011; Zhu et al., 2018) except in the Pamir and Kunlun Mountains (Zhu et al., 2020). Glaciers in the Pamir and Kunlun Mountains are an extreme continental type, with cold temperature and low annual precipitation (Zhu et al., 2020; Li et al., 2019); thus their SEB characteristics are expected to behave differently than the majority of HK glaciers which are an alpine type, with relatively higher precipitation and temperature. In the HK region, a few SEB experiments have been carried out recently, most of them being in the central Himalaya in Nepal, yet at a smaller temporal range, from a month to a few seasons/years (Rounce et al., 2015; Steiner et al., 2018, 2021; Acharya and Kayastha, 2019; Litt et al., 2019; Matthews et al., 2020). SEB studies in the Indian Himalaya are few. Only a single on-glacier SEB experiment was conducted at the Chhota Shigri Glacier in the western Himalaya (Azam et al., 2014a). Recently, Singh et al. (2020) conducted a SEB experiment on a moraine surface with ephemeral snow cover near the Pindari Glacier in Uttarakhand using 2-year data from a weather station. Glacier-wide applications of SEB remain rare to date in the HK region (Srivastava and Azam, 2022).
Apart from the limited number of SEB sampled sites in the HK region, the available literature has mostly focused on the radiative or net radiation fluxes. Net radiation plays a greater role in supplying melt energy to snow/ice than turbulent heat fluxes (Smith et al., 2020). Turbulent fluxes can contribute about 20 % of SEB globally and sometimes above 70 % for a shorter timescale (Thibert et al., 2018). The higher contribution of turbulent heat flux is common in the high-latitudinal glaciers having low altitude, where snow/ice surfaces are exposed to higher air temperatures and dry conditions. The contribution of turbulent heat fluxes on some of the Tibetan and Nepalese glacier/snow-covered sites are also higher, being well larger than 20 %, e.g. Chongche Ice Cap in the Kunlun Mountains and South Col of Everest (Table S1). The SEB experiment on the Everest summit shows that a decrease in turbulent heat flux boosts short-wave radiation efficiency, which results in surface melting despite air temperatures being below the freezing point (Matthews et al., 2020). Overall, the turbulent heat fluxes and their involvement in SEB of the HK glaciers are rarely studied and thus poorly understood.
Snow sublimation is expected to be a significant component of the glacier surface mass balance in the HK region (Azam et al., 2021). Stigter et al. (2018) showed that sublimation loss on the central Himalayan Yala Glacier in Nepal is larger than 20 % of winter snowfall. Srivastava and Azam (2022) studied the glacier-wide SEB on the Chhota Shigri and Dokriani glaciers in the Indian Himalaya and estimated a mass loss through sublimation of up to 20 % of the total annual ablation, with strong spatial and temporal variability. Sublimation contribution is observed to be up to 66 % of the total mass loss on the Purogangri Ice Cap of the north-central Tibetan Plateau (Huintjes et al., 2015b). In the Muji Glacier in northeastern Pamir, the cold season's evaposublimation loss is > 70 % of the corresponding snowfall (Zhu et al., 2020). In the Qilian Mountains at the August-One Glacier in northeast Tibetan Plateau, evaposublimation loss is lower but accounts for about 15 % of annual precipitation (Guo et al., 2021). Recently, Gascoin (2021) reported that the basin-wide mean snow sublimation is ∼ 11 % of the total snow ablation in the Indus basin, with more than 60 % in the Ladakh and western Tibet areas based on satellite-derived datasets (HMASR v1; High Mountain Asia Snow Reanalysis). The HK region's high-altitude meteorological conditions, such as high wind, low atmospheric pressure and dry air, are expected to support sublimation (Wagnon et al., 2013; Shea et al., 2015; Mandal et al., 2020; Matthews et al., 2020; Azam et al., 2018). Therefore, the quantification of high-altitude sublimation is important to improve our understanding of the glacier mass balance components in the HK region.
Direct sublimation measurement requires the use of an eddy-covariance system or pan sublimation technique. The eddy-covariance system is advanced and precise (Sexstone et al., 2016) but expensive; hence it has been used only in two sites in the HK region: the Yala and Lirung glaciers in Nepal (Stigter et al., 2018; Steiner et al., 2018). The pan sublimation or lysimeter measurements are rare in the HK region, likely due to inaccessibility and harsh weather conditions. Alternatively, the bulk-aerodynamic method is widely used for calculating turbulent heat fluxes and thus sublimation. On the Yala Glacier, Stigter et al. (2018) evaluated multiple methods (e.g. the bulk-aerodynamic method, the Penman–Monteith equation and an empirical relation) with eddy-covariance-based sublimation. Results obtained show that the bulk method estimate is similar to observed eddy-covariance-based sublimation. However, parameterisation of the bulk-exchange coefficient and surface roughness length is critical for precisely modelling the turbulent heat fluxes (Smith et al., 2020; Stigter et al., 2018).
This research presents an 11-year-long SEB study on the snow-covered side moraine of the Chhota Shigri Glacier in the western Himalaya using an off-glacier automatic weather station (hereafter AWS-M) installed at 4863 The AWS-M records round-the-year data, but for this study, we considered the snow-covered period between December and April of each hydrological year over 2009–2020. Our primary focus here is to better understand the turbulent heat fluxes and their role in SEB during the winter season when the atmospheric conditions are windier and drier. We also attempt to quantify the snow sublimation and its meteorological drivers. Special attention is given to identify the role of cloud cover on the SEB components and sublimation. We also estimated the fraction of snow sublimation to the winter snowfall at the AWS-M site.
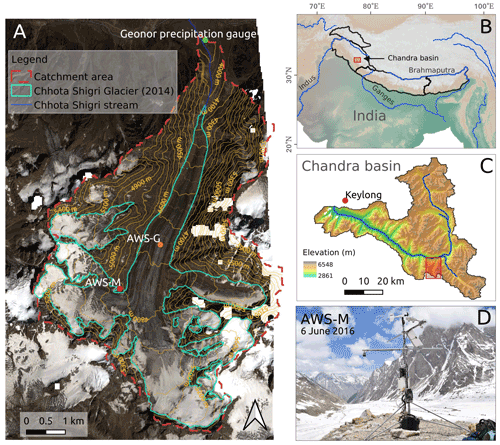
Figure 1(a) Chhota Shigri Glacier catchment showing the location of the AWS-M (red dot), AWS-G (orange dot; middle ablation zone) and Geonor T-200B automatic precipitation gauge (green dot). Glacier outline was derived using the 2014 Pléiades image (Azam et al., 2016). The background is the Pléiades orthoimage of 12 September 2020 (© CNES 2020, distribution Airbus Defence and Space). (b) Location of the Chhota Shigri Glacier region in the western Himalaya. (c) Map of the Chandra basin, with the Chhota Shigri catchment marked (red rectangle). Elevation based on the Shuttle Radar Topography Mission (SRTM) digital elevation model (DEM) obtained from the United States Geological Survey (USGS). (d) Photo of the AWS-M on the lateral moraine (photo credit: Arindan Mandal).
Chhota Shigri moraine site and AWS description
The Chhota Shigri Glacier is located in the Chandra basin (sub-basin of the Indus) of the Lahaul–Spiti Valley situated in the western Himalaya (Fig. 1). The Chandra basin (∼ 30 % glacierised) is located in the monsoon–arid transition zone and is influenced by the Indian summer monsoon (ISM) during summer and the western disturbances during winter (Bookhagen and Burbank, 2010). The mean annual precipitation at the Chhota Shigri base camp was 922 mm, of which 67 % was during the winter season (November–April) and the remaining 33 % was during the summer monsoon (May–October) (Mandal et al., 2020). Chhota Shigri is among the most-studied glaciers in the HK region in terms of surface mass balance and glacial processes. The mean annual glacier-wide mass balance was −0.46 ± 0.40 (water equivalent) over 2002–2019 (Mandal et al., 2020). Azam et al. (2014a) carried out a SEB experiment on this glacier using an on-glacier AWS (hereafter AWS-G; Fig. 1) during 2012–2013 but could not conduct a full-year SEB analysis due to AWS-G failure in winter. They estimated that the net radiation (Rnet) was the primary energy source with about 80 % energy flux to SEB, while the turbulent and conductive heat fluxes shared the rest of the total energy flux.
Table 1Sensor details of the AWS-M (4863 ) and Geonor precipitation gauge at the base camp (3850 ) of the Chhota Shigri Glacier. Variable symbols are also given. Sensor heights indicate the distances to the surface without snow. Long-wave radiation sensors have been operational since May 2010. The snow depth sensor was operational until October 2015.

a Infrared radiometer. b Inlet height
For this study, the meteorological data were collected on the side moraine of the Chhota Shigri Glacier using the AWS-M (32.23∘ N, 77.51∘ E) installed at 4863 (Fig. 1). The AWS-M has been positioned ∼ 50 m away from the Chhota Shigri Glacier margin and on a relatively flat hilltop site. The surface at the AWS-M site remains snow-covered during winter and sand-/sediment-exposed during summer (Fig. 1). The AWS-M has been operating since October 2009. Air temperature (Tair), surface temperature (Ts), relative humidity (RH), wind speed (u) and direction (WD), and incoming and outgoing short-wave (Sin and Sout) and long-wave (Lin and Lout) radiation were being recorded at a frequency of 30 s and stored as half-hourly averages by a Campbell CR1000 data logger. Data before 23 May 2010 were recorded at an hourly time step. Precipitation was recorded at the base camp at 3850 using a Geonor-T200B sensor since July 2012. Description and specifications of the sensors for the AWS-M and Geonor gauge are provided in Table 1.
3.1 Meteorological data and gaps
The meteorological data from the AWS-M were used between 1 December and 30 April (DJFMA) of each hydrological year for 2009–2020. We filtered the snow-covered period for SEB based on the daytime surface albedo threshold value above 0.4 at the AWS-M (the mean bare-ground/snow-free surface albedo was less than 0.25 for July–August; 2009–2020). Additionally, we discarded the data of 74 d (2975 data points) out of a total of 1664 d (76 248 data points; DJFMA 2009–2020) when albedo was below 0.4 (refer to Table S2 in the Supplement for snow-free dates). This albedo threshold value is similar to the minimum albedo (0.41 to 0.46) of continuous snow cover at the Ganja La and Yala sites in Nepal (Stigter et al., 2021; Kirkham et al., 2019).
There was a gap in observation of all variables in the AWS-M data during the night (18:00 to 06:00 IST, Indian standard time) between 22 February 2015 and 2 October 2016 (220 d of DJFMA) due to a disconnected wire between the solar panel and the battery. These gaps were filled using the mean value of the respective variables from available records (1 December 2009–21 February 2015 and 1 December 2016–30 April 2020) of the AWS-M for the particular time steps on the same day. To identify the reliability of the gap-filling method, we applied the same method for non-missing-year data by removing the night values (18:00–06:00 IST) and filled them with mean values from other years. The root mean square error (RMSE) and mean absolute error (MAE) between the original (with night values) and the filled dataset was found to be 3.3 and 2.6 ∘C for Tair, 4.1 and 3.3 ∘C for Ts, 27 % and 22 % for RH, and 2.7 and 2.1 m s−1 for u, respectively, for the test year, 2017/18.
Precipitation data were used from the single-Alter-shielded Geonor gauge operated at the glacier base camp at ∼ 3850 since July 2012 (Fig. 1). All-weather precipitation gauges are known to undercatch precipitation in case of snow (Kochendorfer et al., 2017), and since our precipitation measurements have not been corrected yet, we suspect that precipitation magnitude is underestimated during the snow season (i.e. winter, spring). But those values have only been used to compare with cumulative sublimation in corresponding years, and this does not impact our results. The Geonor gauge has a data gap between October 2013 and July 2014 due to battery failure. Therefore, for the gap period, we used monthly precipitation records from the nearest Indian Meteorological Department (IMD) station at Keylong, which is located at 3119 (https://weathershimla.nic.in/en-IN/climatedata.html, last access: 15 November 2021). Precipitation data from the Keylong station are used because they are the only existing observatory close to the study area (∼ 60 km from the AWS-M site; Fig. 1). Geonor and Keylong precipitation gauges cannot differentiate between snow and rain. Since the daily and monthly Tair did not rise above 0 ∘C during DJFMA (Fig. 2; Table S3 in the Supplement), we considered DJFMA precipitation to be snowfall at both sites. Moreover, the AWS-M site is located 1013 m higher than the Geonor gauge altitude. The measured precipitation of Geonor and Keylong were well correlated (r2 = 0.82); however, the RMSE was higher: 274 mm (Fig. S4 in the Supplement). Therefore, we applied a precipitation gradient of 0.1 m km−1 following Azam et al. (2014b) to extrapolate Keylong's precipitation to the AWS-M altitude (RMSE reduced to 139 mm). For this study, in situ precipitation data from the Geonor gauge are available for only 5 hydrological years (2012–2018; discontinuous).
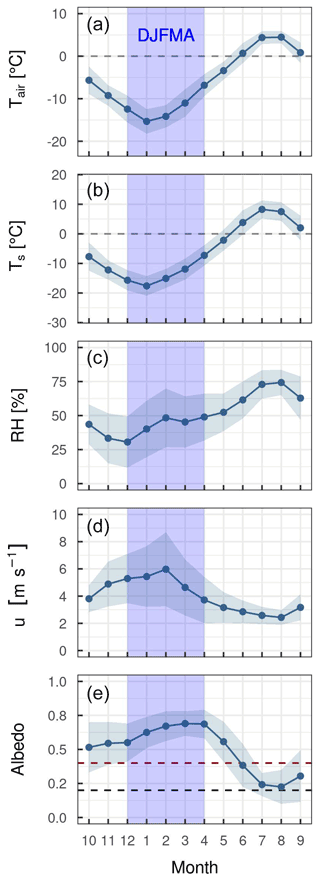
Figure 2Monthly climatology of air (Tair) and surface temperature (Ts), relative humidity (RH), wind speed (u), and surface albedo (αacc) at the AWS-M for 2009–2020. The DJFMA (1 December to 30 April) period is highlighted with a light-blue rectangle in each panel. The shades around the line and scatter points represent the standard deviation (SD). Dashed lines in panel (e) refer to snow-surface albedo (αacc = 0.4; red line) for SEB analysis and bare-surface albedo (αacc = 0.2; black line). Daily values of Tair, Ts, RH, u and albedo for the study period are shown in Fig. S2. Mean yearly values of different variables are provided in Table S4 in the Supplement.
3.2 Surface energy balance (SEB)
SEB has been calculated at a point location for the skin layer using the AWS-M data at a half-hourly time step between 1 December and 30 April (∼ 151 d) of each hydrological year over 2009–2020 (hourly time step for 2009/10). The SEB at the snow surface can be written as (Van den Broeke et al., 2005; Hock, 2005; Oke, 1987)
where Fsurface (W m−2) is the net energy balance of all energy fluxes at the snow surface, Sin and Sout are the incoming and outgoing short-wave radiation, Lin and Lout are the incoming and outgoing long-wave radiation, H and LE are the turbulent sensible and latent heat fluxes, and G and P are the conductive heat flux and heat advected by precipitation, respectively.
Compared to other fluxes, P on glacier/snow is negligible (Hock, 2005; Kayastha et al., 1999) and therefore neglected here. G was found to be negligible or close to 0.0 ± 1.0 W m−2 at the on-glacier AWS-G site on the Chhota Shigri Glacier during winter 2012/13 (Azam et al., 2014a) and thus neglected in the present study. Also, G was neglected in SEB of transient snow cover at the Ganja La and Yala sites, considering inadequate measurement and information of G in the HK region (Stigter et al., 2021). All fluxes are expressed in watts per square metre and defined as positive when directed towards the surface and negative when away from the surface. When Fsurface is larger than 0 W m−2, it will get directed towards the surface/snowpack and warm it up until it reaches the melting point (Ts = 0 ∘C), and then surplus Fsurface will cause melting (Hock, 2005).
3.2.1 Radiative fluxes
Snet (W m−2) and Lnet (W m−2) are represented as Sin−Sout and Lin−Lout, respectively, and all together can be expressed as net radiation, Rnet = Snet+Lnet. However, several corrections were applied to Sin and Sout datasets before using them for SEB. All the night values (determined based on the solar elevation angle) of Sin and Sout were set to be zero. The measured Sout was higher than Sin (1.6 % of total data) during the morning and evening, mainly due to the low solar angle because of poor cosine response of the upward-looking pyranometer (Sin) or due to covering up of the pyranometer by snowfall (Nicholson et al., 2013; Favier et al., 2004). In such cases, Sin was corrected using Sout (raw) and accumulated albedo (αacc) (van den Broeke et al., 2004). αacc is the 24 h sum of Sout divided by the sum of Sin centred around the moment of observation and calculated following van den Broeke et al. (2004):
Lnet was calculated from the difference between observed Lin and Lout. We used raw data from up and down pyrgeometers (CG3) of the radiation sensor (CNR 1) to compute the final Lin and Lout at the AWS-M site.
3.2.2 Turbulent energy flux
The vertical turbulent heat fluxes, H and LE, are calculated using the bulk-aerodynamic method, including stability correction (Brutsaert, 1982). This method is widely used for its applicability because it allows for estimating H and LE from one level of measurement (Chambers et al., 2020; Radić et al., 2017). The bulk-aerodynamic method has already been applied on this glacier at the AWS-G site (on-glacier; Fig. 1) to conduct a SEB experiment during 2012/13, where the SEB-derived ablation showed a good agreement with stake ablation (Azam et al., 2014a). Further, the bulk method showed a good agreement with the eddy-covariance observations over a snow-covered central Himalayan glacier (Stigter et al., 2018). In addition, Denby and Greuell (2000) showed that the bulk-aerodynamic method gives reasonable results in high wind speeds, even in katabatic wind conditions. Therefore, the bulk-aerodynamic method is applied in the present study, as it has already been applied for this glacier and several other studies in the HK region, where atmospheric conditions are similar with high winds (Litt et al., 2019; Stigter et al., 2021; Guo et al., 2022; Azam et al., 2014a). The bulk Richardson number, Rib, describes the stability of the surface layer (Eq. 3), which relates the relative effects of buoyancy to mechanical forces (e.g. Brutsaert, 1982). Therefore, the stability effects were accounted based on Rib:
where g is the acceleration due to gravity (g = 9.81 m s−2); Tair and u are the air temperature (K) and horizontal wind speed (m s−1) at the measurement height, respectively; and Ts is the surface temperature (K). zu and zt are the measurement heights (m) for wind speed and air temperature, respectively. z0m, z0t and z0q are the surface roughness lengths (m) for momentum, temperature and humidity, respectively. Rib is positive in a stable atmosphere. Assuming that local gradients of mean horizontal wind speed, temperature and specific humidity are equal to the finite differences between the measurement height and the surface, the turbulent fluxes, H and LE, are (Brutsaert, 1982)
where ρ is the air density at 4863 (kg m−3) calculated as , where ρ0 is the density (kg m−3) at standard sea level pressure, p0 (1013.25 hPa), and pair is atmospheric pressure (hPa) measured at the site (Cuffey and Paterson, 2010). CP is the specific heat capacity of air () (Cp = Cpd(1+0.84q) with Cpd = 1005 , the specific heat capacity for dry air at constant pressure); k is the von Kármán constant (k=0.4); Ls is the latent heat of sublimation for Ts < 0 ∘C (2.849 × 106 J kg−1); q and qs (kg kg−1) are the specific humidity at height z and the surface, respectively. q and qs were calculated using the measured Tair, Ts and RH. Φm/h/v are the non-dimensional stability functions for momentum, heat and vapour/moisture, respectively. The stability functions are given by Brutsaert (1982) and previously applied in several glacier SEB studies (e.g. Reid and Brock, 2010; Conway et al., 2022) and on the Chhota Shigri Glacier (Azam et al., 2014a). Φm/h/v is expressed in terms of Rib as follows.
For Rib > 0 (stable case),
For Rib < 0 (unstable case),
Half-hourly data of u, Tair, Ts and RH were used to apply the bulk-aerodynamic method when the AWS-M surface was snow-covered (αacc > 0.4). Ts was directly used from the measurement by an infrared radiometer (Table 1). The correlation between infrared measured Ts and Ts derived from Lout (using the Stefan–Boltzmann equation for the snow surface with an emissivity of 1 following Hock and Holmgren, 2005) was r2 = 0.99 (p < 0.001) with RMSE = 0.23 ∘C. The lower and upper limits of Rib were fixed at −0.40 and 0.23, respectively, beyond which all turbulence is suppressed (Denby and Greuell, 2000; Favier et al., 2011). In this way, we discarded about 11 % of the data points beyond the Rib range.
The aerodynamic (z0m) and scalar surface roughness lengths (z0t) play a pivotal role in the bulk method, as the turbulent fluxes are very sensitive to the values of these surface roughness lengths (Chambers et al., 2020; Smith et al., 2020; Nicholson and Stiperski, 2020; Wagnon et al., 1999). Therefore, in this study z0m for snow surface is taken as 0.001 m, which was calculated for the AWS-G site between 16 September 2012 and 17 January 2013 when the AWS-G surface was snow-covered (Azam et al., 2014a). This value was calculated using wind measurements at two different levels following a conventional logarithmic profile (e.g. Moore, 1983). Similarly, z0t and z0q for snow surface are considered 0.001 m following Azam et al. (2014a).
Due to the limitations in the data availability, direct validation of the bulk model used in this study was not possible; therefore, our results are based on the bulk model validation of Azam et al. (2014a) carried out on this glacier in 2012/13, and this proved to deliver robust results compared to observations. We also conducted a sensitivity analysis of our bulk model including surface roughness lengths (Sect. 5.2).
Sublimation (S) was estimated for every DJFMA period between 2009 and 2020 (excluded days are listed in Table S2). S (10−3 kg m−2 or ) was calculated at a half-hourly time step (hourly time step for 2009/10) from negative LE, according to
where Ls denotes latent heat of sublimation and dt is the time step (s).
3.3 Cloud factor
Cloud cover is a good indicator of the contribution of radiation to the surface (Favier et al., 2004). In this study, the cloud factor (CF) is calculated at the AWS-M site between 09:00 and 16:00 IST to avoid the steep valley wall's shading effect during morning and evening. CF is calculated by comparing short-wave incoming (Sin) radiation with the short-wave radiation at the top of the atmosphere (STOA) following Favier et al. (2004):
which represents a quantitative cloud cover estimate and ranges from 0 to 1. The values 1.3 (offset) and 1.4 (scale factor) were derived from a simple linear optimisation process (Favier et al., 2004). Sin was used from the direct measurement from the AWS-M, whereas the theoretical value of STOA for a horizontal surface is calculated following Iqbal (1983).
3.4 Statistical analysis
The standard correlation coefficient (r) and coefficient of determination (r2) were estimated to assess the relationship between various meteorological variables, SEB and sublimation. The two-tailed Student's t test was used to measure the significance of the r and r2. RMSE is calculated to identify the bias/deviation. The k-fold cross-validation method was applied for linear and multiple regression analysis, performed using the “caret” package (Kuhn, 2008) of the R environment (R Core Team, 2021). Cross-validation is a machine learning technique that is used to protect the predictive model against overfitting for better accuracy. We used this method to estimate the meteorological variable's variance in sublimation.
4.1 DJFMA meteorological characteristics
The range of the meteorological variables measured at the AWS-M for DJFMA (2009–2020) is given in Table S3 to provide an overview of the prevailing weather conditions in the study region. During DJFMA, the mean monthly Tair ranged from −15.5 ∘C in January to −6.9 ∘C in April, with a mean of −12.1 ∘C (Fig. 2). Daily mean Tair was below 0 ∘C except during late April in 2010/11 and 2016/17 when daily Tair slightly exceeded 0 ∘C (Fig. S2 in the Supplement). The highest daily Tair was 0.1 ∘C on 27 April 2011, and the lowest was −21.9 ∘C on 26 January 2019. The mean monthly Ts ranged from −17.7 ∘C in January to −7.5 ∘C in April, with a mean of −13.7 ∘C. Daily mean Ts was below 0 ∘C across DJFMA. However, half-hourly Ts was higher than Tair for about 45 % of the data points.
The mean monthly RH ranged from 31 % in January to 49 % in April, with a mean of 43 % (Fig. 2). But for a few days, the mean daily RH in DJFMA was higher than 60 %. The mean daily RH was below 30 % (assumed to be dry air) for 29 % of days and above 60 % (humid air) for 24 % of days during the study period.
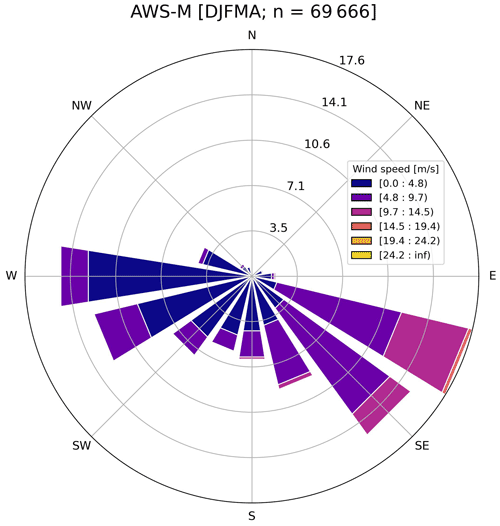
Figure 3Wind rose of the AWS-M for DJFMA (2009–2020). The frequency of wind direction is expressed as a percentage based on n = 69 666 half-hourly data points.
The mean monthly u ranged from 3.7 m s−1 in April to 6.0 m s−1 in February, with a mean of 5.0 m s−1 during DJFMA (Fig. 2). Based on half-hourly records, u < 5.0 m s−1 occurred for 56 % of the data points during the study period, while u > 10.0 m s−1 were observed for only 7 %. The half-hourly mean u reached up to 24.2 m s−1 on 21 February 2019. The highest recorded mean daily u was 15.9 m s−1 on 20 March 2012. The wind rose shows that there is a persistent down-valley wind along the glacier flowline coming from the southeast (90–135∘) during DJFMA with high wind speed (Fig. 3).
Precipitation records from the Geonor gauge were available only for five complete DJFMA periods but discontinuous (Fig. 4). During DJFMA, most of the precipitation in the Chhota Shigri catchment falls due to the western-disturbance storms, accounting for about 67 % of its annual total of ∼ 900 mm (Mandal et al., 2020). The total mean precipitation during DJFMA was 659 mm (2012–2018; Table S3). March received the highest, with 150 mm corresponding to 26 % of total winter precipitation, and the least was in December, with 56 mm corresponding to 10 %. The highest single-day precipitation was observed to be 61 recorded on 30 March 2015.
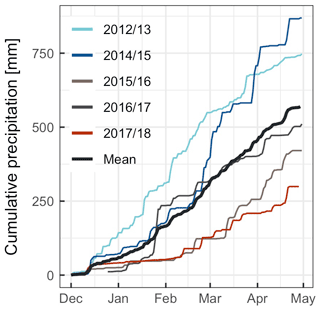
Figure 4Cumulative precipitation at the glacier base camp at 3850 for DJFMA 2012–2018. No data for 2013/14. The bold line is the mean of all years.
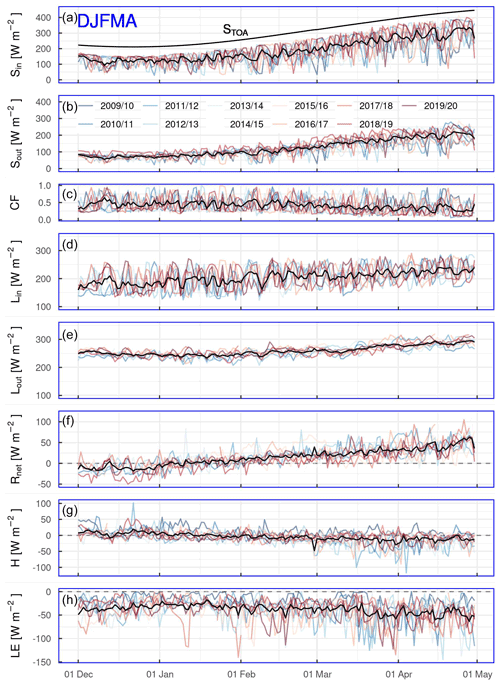
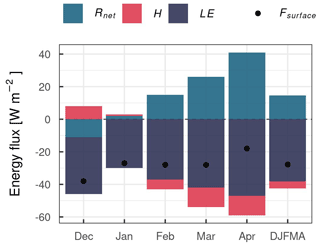
Figure 5The daily mean of short-wave radiation at the top of the atmosphere (STOA), short-wave incoming (Sin) and outgoing (Sout) radiation, the cloud factor (CF), long-wave incoming (Lin) and outgoing (Lout) radiation, net radiation (Rnet), and turbulent sensible (H) and latent (LE) heat fluxes at the AWS-M for DJFMA 2009–2020. Lin, Lout and Rnet start from 1 December 2010. The black line highlights the mean of 2009–2020.
The daily mean variability in incoming and outgoing radiation components and CF are shown in Fig. 5. About 62 % of STOA reached the surface at the AWS-M during DJFMA, indicating the remainder was absorbed and scattered by the cloud cover and atmospheric constituents (e.g. gases, water vapour). Daily mean Sin varied between 28 and 414 W m−2, corresponding to a mean of 191 W m−2 (Table S3). Sin was highest in April with a daily mean of 295 W m−2. The persistent snow cover, especially during the peak winter period, resulted in a strong reflection of Sin (Fig. 5). Sout was the largest in March–April due to the accumulated snow cover (αacc = 0.69). Lin followed the CF pattern (Fig. 5). Low Lin attributed to the low-CF (clear-sky) conditions. Daily mean Lin varied between 123 and 290 W m−2, corresponding to a mean of 203 W m−2 (Table S3). Lin was highest in April with a daily mean of 226 W m−2. Lout was relatively stable throughout DJFMA, ranging from 243 to 285 W m−2, with a mean of 260 W m−2 (Table S3).
4.2 Diurnal cycle of the meteorological variables and SEB components
Figure 6 shows the mean diurnal cycle of meteorological variables and SEB components at the AWS-M for DJFMA (2009–2020). The mean diurnal cycle of Tair and Ts was well below 0 ∘C. However, on certain days Ts was above 0 ∘C (6 % of the half-hourly data points) but limited to peak daytime hours between 11:00 and 14:00 IST. Positive Ts was observed when the snowpack was about 20 cm or lower (based on n = 38 965 half-hourly SR50A data points between December 2009 and April 2015). RH was the lowest around late morning at ∼ 10:00 IST and the highest in the evening at ∼ 18:00 IST. u was maximum during the afternoon (∼ 14:00 IST), which corresponded well with the steep drop of Tair in the afternoon, a typical valley glacier phenomenon (Greuell and Smeets, 2001).
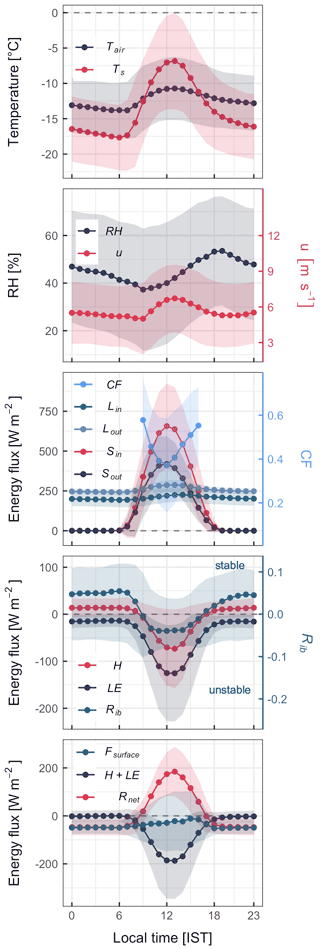
Figure 6Mean diurnal cycle of meteorological and SEB variables at the AWS-M for DJFMA. Half-hourly data were used between 2009 and 2020. CF was calculated between 09:00 and 16:00 IST. Shading is the SD.
Sin, Sout, Lin and Lout were the largest at noon, when the solar zenith angle was at its maximum and the diurnal cycle for CF was reversed. During the daytime, the energy from Snet (balance between Sin and Sout) was absorbed by the skin layer of the snow surface. Snet was compensated by the energy loss through negative Lnet (balance between Lin and Lout). The energy balance between Snet and Lnet, Rnet, was then used to increase the turbulence of the surface boundary layer resulting in unstable conditions (Fig. 6). The turbulent heat flux cycle was opposite of Sin, whereas it was the same as Rib (stability). H was positive throughout the night, and then it started to sink to negative values for a few hours in the afternoon as the surface was heated up and again became positive in the evening. The unstable condition of the surface boundary layer (Rib < 0; Tair−Ts < 0 ∘C) was linked to the negative values of H (Fig. 6). LE, unlike H, was always negative, although less negative in the morning and evening. Rib was mostly positive and small, corresponding to moderately stable surface boundary layer conditions except for about 8 h in the daytime between 09:00 and 16:00 due to the unstable surface boundary layer. Rnet was negative across the night and early morning, whereas it was positive during the daytime following the Sin cycle. The negative Rnet indicated radiative cooling of the surface at night, while the positive Rnet suggested the heat transfer into the snow during the daytime. The Fsurface was consistently negative, being nearly zero during the late afternoons. Despite strong positive Rnet during peak daytime, Fsurface remained negative (Fig. 6). This was because a higher magnitude of negative H + LE considerably compensated a positive Rnet. We found a high negative correlation between half-hourly values of Rnet and H + LE (r = −0.78; p < 0.001, n = 59 131), indicating that Rnet is responsible for the diurnal variation in H and LE.
4.3 Seasonal and interannual variation in SEB components
Rnet was negative in December with a mean of −11 W m−2, which gave rise to near-surface air cooling, whereas it acted as a heat supplier from February to April with a mean value of 15, 26 and 41 W m−2, respectively (Fig. 5, Table S3). H was positive for 56 % of the half-hourly values during December–January, suggesting that heat was carried from the atmosphere to the surface. H was negative for 44 % of the half-hourly values during February–April, down to the monthly mean of −12 W m−2. LE was always negative across DJFMA, suggesting mass loss through sublimation (Fig. 5; refer to Sect. 4.6). The mean monthly LE was most negative in April at −47 W m−2, with a mean DJFMA value of −38 W m−2 (Table S3). We analysed interannual correlations between Rnet and turbulent fluxes to determine their inter-relationship. The correlations were strong and significant for both Rnet and H (r = −0.70; p < 0.05) and Rnet and LE (r = −0.80; p < 0.05). This further confirms that Rnet played an essential role in governing the turbulent fluxes at the AWS-M. The increased energy from Rnet combined with the longer duration of daylight hours along with the progression of winter results in more unstable boundary layer conditions, which supports stronger negative magnitudes of H and LE. Sin showed a stronger indirect relationship with LE and H (r = −0.80 and −0.61, respectively; p < 0.05) than Lin (r = −0.36 and −0.39, respectively; not significant). Together, H + LE contributed a negative budget across DJFMA, with a mean monthly value of −40 W m−2 (Table S3). As a result, the net energy (Fsurface) was negative across DJFMA.
Figure 7 presents the contributions of energy fluxes to SEB. During DJFMA, the proportional contribution of all SEB components showed that LE dominated the contribution (64 %), followed by Rnet (25 %) and H (11 %) (Fig. S3 in the Supplement). The mean monthly contribution showed an increasing contribution of Rnet with decreasing LE and H (Table S3). The largest contribution of Rnet in SEB is well noted across the HMA glaciers (Table S1). However, in this study, during the winter season, such a high contribution of LE (> 60 %) is unique and contrary to the previous findings (e.g. Zhang et al., 2013; Azam et al., 2014a).
4.4 Influence of could cover on SEB components in the daytime
We used CF values to differentiate between clear-sky when CF ≤ 0.2 and overcast conditions when CF ≥ 0.8, following Chen et al. (2018). Around 24 % of the data was categorised as clear-sky conditions, while 10 % was overcast conditions based on n = 23 903 half-hourly data points (09:00–16:00 IST; 2009–2020; Fig. 8). Overcast conditions decrease from January to April with increasing clear-sky conditions.
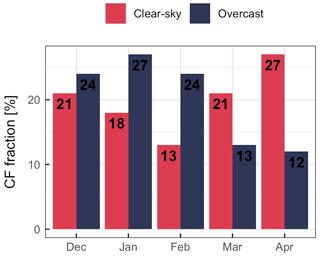
Figure 8Monthly fraction of clear-sky (CF ≤ 0.2) and overcast (CF ≥ 0.8) conditions at the AWS-M. Fraction percentage is calculated from n = 5810 clear-sky and n = 2381 overcast observations from total n = 23 903 half-hourly values between 09:00 and 16:00 IST (DJFMA 2009–2020).
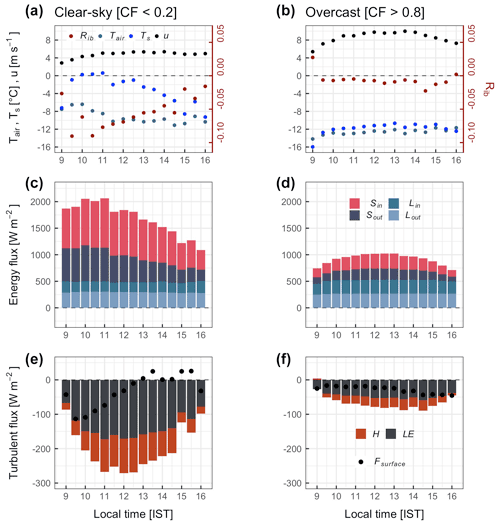
Figure 9Daytime (09:00–16:00 IST) diurnal cycle of Tair, Ts, u, Rib and SEB components under clear-sky (CF ≤ 0.2) and overcast (CF ≥ 0.8) conditions.
Figure 9 shows the daytime half-hourly variation in Tair, Ts, u, Rib and SEB components. The stability of the surface boundary layer is notable in overcast conditions. Due to comparatively lower temperature (both Tair and Ts) and higher u in overcast conditions, the surface boundary layer remains nearly neutral (Rib close to 0 due to low vertical temperature difference; Tair−Ts). Conversely, high negative Rib values (unstable) were observed in clear-sky conditions. All the SEB components were considerably higher in clear-sky than in overcast conditions. On average, cloud cover subdued about 70 % of the daytime mean Sin (744 W m−2 in clear-sky as compared to 228 W m−2 in overcast conditions). Unlike Sin, cloud cover increased the daytime mean Lin by about 25 % (201 W m−2 in clear-sky as compared to 250 W m−2 in overcast conditions).
Turbulent heat fluxes were generally higher in clear-sky conditions due to higher instability of the surface boundary layer (Fig. 9). In clear-sky conditions, the mean daytime H was −66 W m−2, which is 3 times more negative compared to overcast conditions (−21 W m−2), corresponding to a 68 % reduction in H in overcast conditions than in clear-sky conditions. Similarly, the mean daytime LE was also higher in clear-sky conditions, with −136 W m−2 compared to −47 W m−2 in overcast conditions (65 % reduction). The reduced magnitude of turbulent heat fluxes in overcast/cloudy conditions was due to the neutral stability of the surface boundary layer (Fig. 9b; Rib ≈ 0). In neutral stability conditions, cold temperature (Tair−Ts close to 0) restricts the magnitude of H and LE (Fig. 9). In clear-sky conditions, more negative LE was due to the surface's intense heating (Tair−Ts < 0 ∘C), which creates a stronger vertical moisture gradient (q−qs) than overcast conditions. Fsurface showed a slight daytime variation during clear-sky conditions but no significant variation in overcast conditions.
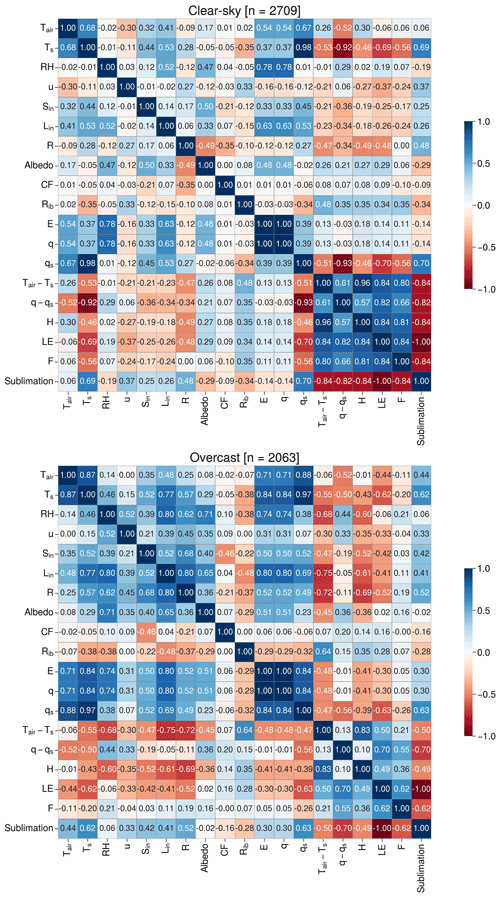
Figure 10Pearson correlation coefficient (r) matrix of various meteorological and SEB components at the AWS-M in clear-sky and overcast conditions between 09:00 and 16:00 IST for 2009–2020. Number (n) of half-hourly data points is shown on top of the panels.
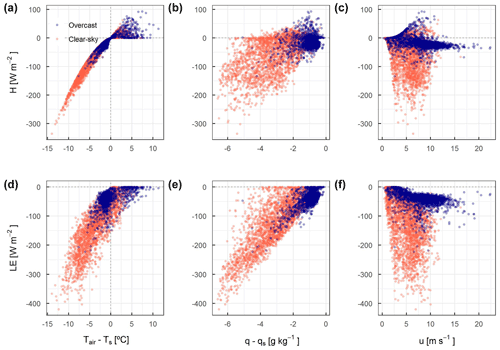
Figure 11Half-hourly values of the vertical temperature difference (Tair−Ts), vertical specific humidity difference (q−qs) and u compared with H and LE between 09:00 and 16:00 IST for DJFMA 2009–2020. Red represents clear-sky conditions (n = 2709), and blue represents overcast conditions (n = 2063).
4.5 Relationship of turbulent heat fluxes and meteorological variables under different cloud conditions
Sub-hourly scale correlations were developed to better understand the relationship between H and LE and meteorological variables (Fig. 10). H was strongly and positively correlated with Tair−Ts in clear-sky (r = 0.96; p < 0.001) and overcast conditions (r = 0.83; p < 0.001). That means H increases as the difference in vertical temperature increases towards a negative direction (Fig. 11). Similarly, LE was strongly correlated with Tair−Ts in clear-sky (r = 0.84; p < 0.001) but moderately correlated in overcast conditions (r = 0.50; p < 0.001), which suggests that the vertical temperature difference significantly controls the near-surface vertical moisture gradient (one of the primary drivers of LE). This attributes to a significantly higher negative LE in clear-sky than in overcast conditions (Fig. 11). The correlation of H with q−qs was moderate in clear-sky (r = 0.57; p < 0.001) and weak in overcast conditions (r = 0.10; p < 0.001). Correlation of LE with q−qs was strong in clear-sky (r = 0.82; p < 0.001) as well as in overcast conditions (r = 0.70; p < 0.001). That means LE increases as the vertical difference in moisture increases towards a negative direction (Fig. 11). Due to higher near-surface heating and convection, the near-surface moisture gradient is steeper in clear-sky than in overcast conditions (Fig. 11). There is a clear pattern of more negative LE with an increasing q−qs; however, the correlations were not very strong (r = 0.82 in clear-sky conditions; r = 0.70 in overcast conditions). This could be partly explained by the overestimation of LE in near-neutral conditions (Rib ≈ 0), which increases the stability function (Φm/h/v), resulting in a higher magnitude of LE. The difference in atmospheric stability in clear-sky and overcast conditions explains the difference in correlations. In this regard, Steiner et al. (2018) discussed that atmospheric stability correction is crucial to estimate H and LE accurately under different cloud conditions and tricky to handle for a rapidly changing mountain atmosphere. No strong correlation was observed between H and u in both clear-sky (r = −0.27; p < 0.001) and overcast conditions (r = −0.35; p < 0.001). Similarly, LE and u were also not strongly correlated both in clear-sky (r = −0.37; p < 0.001) and overcast conditions (r = −0.33; p < 0.001). However, the negative correlation with u suggests that H and LE increase towards a negative direction as u increases and vice versa. The weak correlation between LE and u could be explained in part by the very strong u > ∼ 10 m s−1 at the AWS-M site, with high RH > ∼ 70 % (Fig. S5 in the Supplement), which limits the magnitude of LE. Such strong winds were often observed in overcast conditions with high cloud cover (Fig. S5A) and precipitation (Fig. S5B) and were likely associated with western-disturbance storms. Western-disturbance events are most dominant during winter months around the Chhota Shigri region. This was observed from ERA5's horizontal wind fields and vertically integrated moisture divergence datasets at 500 hPa from 2009 to 2020 (Fig. S6 in the Supplement). Zhu et al. (2021b) and Liu et al. (2020) also indicated that during the winter months in the western Himalaya and western Tibetan regions, western-disturbance storm activities transport a significant amount of moisture and influence the precipitation. A very strong u during western disturbances kept the snow surface cool and maintained a reduced Tair−Ts and q−qs (close to zero), resulting in a low magnitude of LE (Fig. S7 in the Supplement). At the sub-hourly scale, neither Rnet nor Sin and Lin can adequately explain LE in both overcast and clear-sky conditions (r = < 0.50; Fig. 10). Overall, we noted that at the sub-hourly scale near-surface moisture availability (through q−qs) plays a bigger role in determining the magnitude of LE, with the combined effects from several meteorological variables, particularly qs, Ts and u.
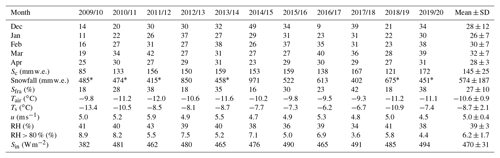
Table 2Monthly sum of sublimation (), cumulative sublimation (Sc; ), snowfall () and the fraction of sublimation to snowfall (Sfra; %) at the AWS-M during 2009–2020. Snowfall is based on Geonor and Keylong (marked with “∗”) precipitation data (see Sect. 3.1). Mean DJFMA meteorology for daytime (09:00 and 16:00 IST) is also shown for corresponding years. RH > 80 % is the frequency of RH > 80 in a particular year.
4.6 Sublimation and its relationship with meteorological variables
Half-hourly LE fluxes were converted to sublimation following Eq. (8). At the AWS-M site, the mean daily sublimation was 1.1 ± 0.5 , corresponding to a cumulative DJFMA mean sublimation loss of 145 ± 25 over 2009–2020 (Table 2). The mean daily sublimation rate was almost 3 times higher in clear-sky (3.7 ± 2.6 ) than in overcast conditions (1.3 ± 0.8 ), indicating the critical role of cloud cover. The mean monthly sublimation was the highest in March, at 32 ± 7 , and it was the lowest in January, at 26 ± 7 , with intra-annual variability in different years. The yearly cumulative sublimation varied across the study period, from a minimum of 85 in 2009/10 to 172 in 2019/20 (Table 2). Notably, the snowfall amounts were often similar over these years (e.g. 2009/10, 2017/18, 2019/20), suggesting a stronger control of other meteorological variables in sublimation, particularly RH, Ts and Sin, than snowfall (Table 2). For example, in 2009/10, cumulative sublimation was the lowest (85 ), which was associated with the lowest Ts (−13.4 ∘C) and the highest frequency of RH > 80 % (8.9 %) during the study period (Table 2, Fig. S8 in the Supplement). Further, Sin was also the lowest in 2009/10 (Table 2). The opposite condition prevailed during 2017/18 and 2019/20 when Ts was considerably higher at −6.7 and −7.4 ∘C, respectively; RH > 80 % was the lowest at 3.6 % and 4.4 %, respectively; and Sin was the highest at 491 and 494 W m−2, respectively. We further assessed the relationship through the interannual correlation analysis based on 11-year sublimation and primary meteorological variables. Interannual correlation between cumulative sublimation and Ts was the highest (r = 0.85; p < 0.01), followed by Sin (r = 0.79; p < 0.05) and RH > 80 % (r = −0.76; p < 0.01) (Table S5 in the Supplement). This suggests that on an interannual scale, high Ts (through higher Sin) and low near-surface moisture conditions support sublimation. Cloud cover, on the other hand, has a significant impact on the primary meteorological variables, particularly Sin, Ts and qs (Fig. 9; Sect. 4.4).
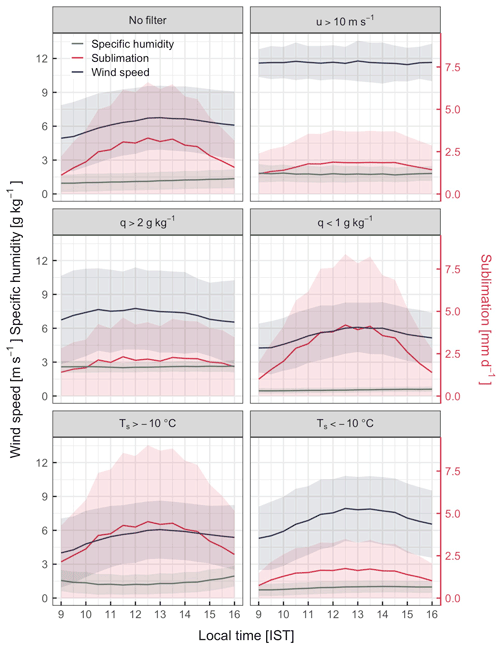
Figure 12Half-hourly daytime (09:00–16:00) records of sublimation (red), wind speed (blue) and specific humidity (green) at the AWS-M for different clusters: no filter, u > 10 m s−1, q > 2 g kg−1, < 1 g kg−1, Ts > −10 ∘C and Ts < −10 ∘C. Data period: DJFMA 2009–2020. Number of data points: n = 30 257, 2347, 12 295, 9762, 10 552 and 12 734 for no filter, u > 10 m s−1, q > 2 g kg−1, q < 1 g kg−1, Ts > −10 ∘C and Ts < −10 ∘C, respectively.
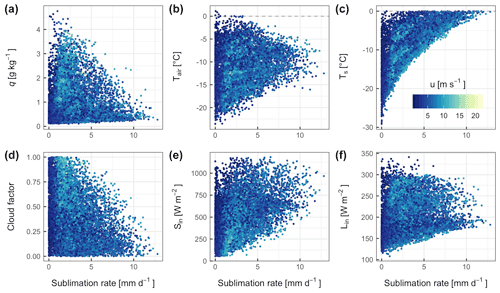
Figure 13Scatter plot of q, Tair, Ts, CF, Sin and Lin against sublimation rate at the AWS-M. The colour of the data points refers to the measured wind speed (u). Total n = 14 088 half-hourly data points between 09:00 and 16:00 IST for DJFMA (2009–2020).
Figure 12 presents the daytime diurnal cycle of sublimation, u and q for six different meteorological clusters: (1) no filter, (2) high u (> 10 m s−1), (3) high q (> 2 g kg−1), (4) low q (< 1 g kg−1), (5) higher Ts (> −10 ∘C) and (6) lower Ts (< −10 ∘C). We omitted measurements during the night when sublimation is negligible. Sublimation peaks in the early afternoon between 12:00 and 14:00 h (Fig. 12), soon after the AWS-M site was sunlit. High insolation during the late morning (10:00–12:00 IST; Fig. 7) increases Tair−Ts, resulting in stronger convection in the early afternoon, which favours sublimation. Once the snow surface is heated up, the sublimation is conditioned by q−qs. A low q below 1 g kg−1 and high Ts above −10 ∘C enhance sublimation (Figs. 12 and 13). Higher q restricts sublimation because the near-surface atmosphere is saturated; consequently, the vertical water vapour pressure gradient is weak. Sublimation was the largest when Tair ranged between −5 and −10 ∘C and also when Ts ranged between 0 and −10 ∘C (Figs. 12 and 13b, c). Sublimation was considerably lower when moisture availability was higher; Ts was significantly lower, with very strong u (Figs. 12 and 13). This was probably associated with the cold storm events through western disturbances, which brings high moisture (Fig. S5) and cold winds in the region (Fig. S7; discussed in Sect. 4.5). Thus, very strong and cold winds with higher moisture from western disturbances impede sublimation in the region. Guo et al. (2022) observed a similar phenomenon in the August-One Glacier in the northeast Tibetan Plateau, where sublimation was significantly constrained by extremely low Ts during strong westerlies.
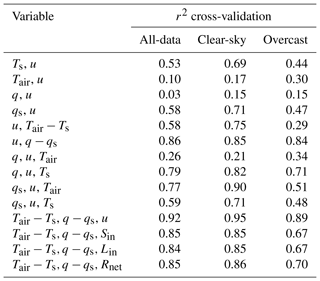
To further understand the combined effect of meteorological variables on sublimation, a multiple linear regression analysis was performed (Table 3). The multiple regression shows that q−qs, Tair−Ts, u and Ts were the best sublimation predictors in clear-sky and overcast conditions as well as in all-data conditions (without a CF filter). Considering two combined predictors, q−qs and u explained the highest variance (> 80 %) in sublimation in clear-sky and overcast conditions as well as in all-data conditions. When three predictors were considered, it is the combination of Tair−Ts, q−qs and u that explained the highest variance, with 95 % in clear-sky and > 90 % in overcast and all-data conditions. However, it is noteworthy that individually u explains the poor variance in sublimation (< 40 % in clear-sky and overcast conditions; Fig. 10). Stigter et al. (2018) noted a slightly higher variance of u (48 %) in sublimation at the Yala Glacier in the central Himalaya.
Table 3Summary of the multiple linear regression analysis (k-fold (k = 10) cross-validation) of sublimation rate and combined meteorological variables. Total n = 13 217, 2708 and 2063 half-hourly data points for all-data, clear-sky and overcast conditions, respectively, between 09:00 and 16:00 IST for DJFMA (2009–2020). The p value of r2 was always < 0.001.
5.1 Factors controlling the latent heat flux/sublimation
We note that the magnitude of LE is governed by a combined effect of different meteorological variables, primarily the vertical moisture and temperature gradients, wind speed, and the state of the surface boundary layer (stability). The relationship between LE and meteorological variables, on the other hand, varied in temporal scale, making it complex. Despite LE and Rnet having a strong relationship on an interannual scale, we did not find a strong relationship in the sub-hourly scale, emphasising the importance of temporal scale in understanding sublimation. On a sub-hourly scale, we found no strong correlation between LE/sublimation and individual meteorological variables (Fig. 10). The absence of a strong correlation between sublimation rate and one or the other meteorological variables is expected because a conducive environment for enhanced sublimation is created by a combination of meteorological variables. For example, cloud cover shapes the prevailing weather conditions at the study site by influencing the stability of the surface boundary layer (Fig. 9). In a stable stratification (Tair−Ts > 0 ∘C), the snow surface remains cooler than the air, which attributes to a gentle near-surface moisture gradient and a lower LE, whereas in an unstable stratification (Tair−Ts < 0 ∘C), steep near-surface moisture gradient results in a high negative LE. The other important aspect is the availability of moisture content in the air, which is a function of various meteorological variables, such as precipitation and the vapour pressure at the surface or above, all of which have a role in promoting sublimation. For example, a low q helps to create a steeper negative moisture gradient which increases sublimation (Fig. 13). Stigter et al. (2018) and Guo et al. (2021) also reported a similar process where an integrated effect was responsible for higher sublimation in the Yala and August-One glaciers. The integrated effect of different meteorological variables in supporting sublimation also explains the weak correlation between LE/sublimation and u (r ≤ 0.40; Fig. 10). Stigter et al. (2018) and Guo et al. (2021) noted a strong direct relationship between LE and u, which does not agree with the present study. This could be partly explained by the highly heterogeneous u at the AWS-M (Fig. 13). For example, the available observations from different sites showed that u generally decreases in overcast conditions (e.g. Stigter et al., 2018; Guo et al., 2021; Conway et al., 2022). However, at the AWS-M, u was often higher in overcast conditions (Figs. 9 and S5) due to westerly activities (discussed in Sects. 4.5 and 4.6). This heterogeneity is likely the cause of the weak correlation between u and sublimation in part. However, the highest multiple regression variance in combination with u (∼ 90 %; Table 3) in clear-sky and overcast conditions emphasise the importance of u in driving LE/sublimation. Fugger et al. (2022) also observed that the relationship between LE and meteorological variables is highly unpredictable, and u fails to explain the variability in LE at five on-glacier sites in the central and eastern Himalaya (see their Fig. 9A). We note the importance of cloud cover in modulating the surface atmosphere at the AWS-M site which favours sublimation; however, the correlation coefficient between CF and LE was poor (r = −0.09 and −0.16 in clear-sky and overcast conditions, respectively; Fig. 10). This is most likely due to the complex influence of cloud cover on meteorological variables, particularly Sin and Lin. Cloud cover reduces Sin, which impedes sublimation, but at the same time it also increases Lin, which promotes sublimation partly by raising Ts. This is well-supported by the higher correlations between sublimation and Sin and Lin, particularly in overcast conditions (Fig. 10). Although Stigter et al. (2018) did not discuss the correlation between sublimation and cloud cover/factor at the Yala Glacier, they did indicate that sublimation was negligible on overcast days when RH was higher. This is supported by the poor correlation of determination (r2 = 0.08) between sublimation and RH at the Yala Glacier. Guo et al. (2021) also did not obtain a statistical relationship between sublimation and cloud cover, but they also noted a weak sublimation rate during cloudy months due to high moisture and warm conditions. Conway et al. (2022) also found that an increase in cloud cover decreases the magnitude of LE at four on-glacier Himalayan sites, including the Chhota Shigri Glacier. Overall, we conclude that the near-surface moisture availability (through q−qs) plays a major role in governing the magnitude of LE at the AWS-M at different temporal scales, while moisture availability was influenced and conditioned by a number of meteorological variables, notably Sin, u, qs and Ts.
5.2 Sublimation sensitivity to meteorology and roughness and uncertainty sources
To test the sensitivity of the calculated sublimation to changes in the input data, we prescribed perturbations of Tair (± 1 ∘C), Ts (± 1 ∘C), u (± 10 %), RH (± 10 %) and z0m (0.0005 m, 0.002 m, 0.003 m and 0.004 m) and re-calculated sublimation for DJFMA 2009–2020. Similar perturbations for the meteorological variables were applied in previous studies (Andreassen et al., 2008; Zhang et al., 2013; Steiner et al., 2018; Liu et al., 2021). For z0m, we chose higher- and lower-order perturbation values, considering the high SD of in situ calculated snow, z0m, at the AWS-G (0.001 ± 0.003 m; Azam et al., 2014a). Results show that sublimation is most sensitive to z0m and Ts (Fig. 14) because they are the direct drivers of LE. Perturbation of higher-order z0m (0.004 m) and a +1 ∘C change in Ts increase the mean cumulative sublimation by 21 % (30 ). For a much lower-order z0m (0.0005 m), the mean cumulative sublimation decreases by 8 % (12 ). Perturbation to ± 10 % change in u yields a ± 8 % change in sublimation. The mean cumulative sublimation is roughly 3 times more sensitive to a ± 1 ∘C change in Ts than a ± 10 % change in RH and u.
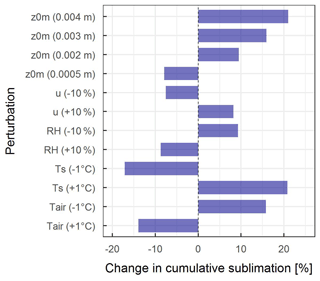
Figure 14Calculated change in mean cumulative sublimation after applying perturbations to Tair (± 1 ∘C), Ts (± 1 ∘C), u (± 10 %), RH (± 10 %) and snow z0m (0.0005, 0.002, 0.003 and 0.004 m).
Table 4Compilation of sublimation rate across the HMA region. “*” refers to the evaporation values. “Do” refers to the same method as in the row immediately above. ELA: equilibrium line altitude.
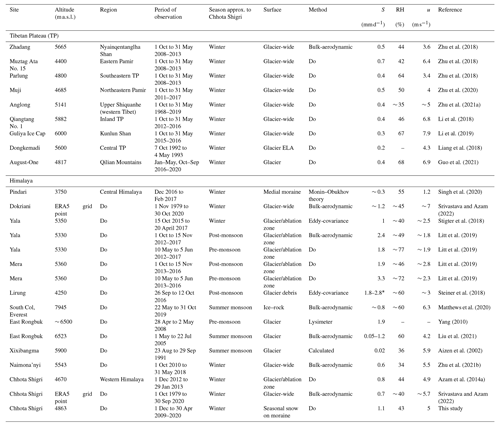
Sublimation/LE sensitivity in this study is similar to that reported for the Lirung Glacier, which, however, has a debris-covered surface (Steiner et al., 2018). They noted that a ± 1 ∘C change in Ts results in a −42 % and 23 % change in LE. They also note that LE is less sensitive (± 8 %) to a ± 10 % change in u. Liu et al. (2021) also reported that LE is considerably less sensitive to change in u and RH (< ± 10 % sensitive) than Ts and z0m (> ± 20 % sensitive) on the clean-ice East Rongbuk Glacier in the Everest region. In general, sublimation is less sensitive to the meteorological variables (Tair, RH and u) than z0m. However, it could be higher or significant, as the change of ± 1 ∘C in Tair or ± 10 % of RH and u can equally be caused by sensor inaccuracies provided by the manufacturer (Table 1). That means the sensitivity to Tair, RH and u could be roughly equal to z0m or Ts. Sensitivities reported in this study have crucial implications in improving the existing hydrological models and distributed SEB models, where sublimation loss is ignored (Srivastava and Azam, 2022; Patel et al., 2021). Another important aspect of the sensitivity to meteorological variables is related to the future atmospheric warming and its consequences to sublimation. Ts exhibited a higher sublimation sensitivity than Tair (Fig. 14), but under melting conditions, Ts will not change much because the temperature of the snow/ice surface cannot rise above the melting point (Ts = 0 ∘C). However, relative potential changes in Tair are likely to be higher across the globe including in the Himalayan region (Hock et al., 2019; Krishnan et al., 2019). Therefore, sublimation sensitivity with respect to Tair could be a major concern in future, due to the expected warming. Considering a future Tair increase of ∼ 0.3 ± 0.2 ∘C per decade for the Himalayan region (Ren et al., 2017; Krishnan et al., 2019), a crude estimate suggests a ∼ 5 % decrease in sublimation per decade from the snow/glacier surfaces. This could possibly lead to a lower energy sink through the LE flux, which will boost the efficiency of Sin/Rnet, resulting in more surface melt. However, since sublimation is a process driven by the combined effect of multiple meteorological variables, it remains to be seen how the sensitivity of a single variable influences the overall sublimation and associated processes. The bulk method was already used in the HK region (Table 4), where the climate setting was similar to that of the Chhota Shigri region, with strong wind and dry conditions. We used z0m (0.001 m), which was calculated at the AWS-G site, applying a logarithmic profile based on wind speed data from two levels (Azam et al., 2014a), which might have reduced the potential bias of choosing a random z0m or one from the existing literature. However, z0m could be higher or lower depending on the snow redistribution at the AWS-M site, which is expected at such a high altitude. Another important uncertainty source of sublimation is blowing snow and erosion (Wagnon et al., 2013), especially over a strong wind-prone site. A wide variation in blowing-snow sublimation rates is reported in the literature, depending on the climate and snow blow model setup (Zwaaftink et al., 2013). However, modelling of blowing-snow sublimation is beyond the scope of this study and might have led to an underestimation of the sublimation. Nevertheless, considering all the above uncertainties, the mean daily sublimation at the AWS-M site (1.1 mm d−1) agrees well with the eddy-covariance-based sublimation of 1 mm d−1 at the Yala Glacier (Stigter et al., 2018), where the reported meteorological condition is similar at the AWS-M.
5.3 Comparison of sublimation rates with other HK and HMA glaciers
This section discusses the existing sublimation rates/studies across the HMA glacier/snow-covered sites compared to the AWS-M site on the Chhota Shigri Glacier (Table 4). The existing sublimation studies in the HK and HMA regions are not uniform with respect to the spatial and temporal scales, which makes it difficult to compare sublimation and associated processes consistently. However, it is worthwhile to use these existing sublimation datasets for comparison, not to conduct a thorough and rigorous comparison but to qualitatively address the sublimation process in the region. The mean daily winter sublimation rate estimated in this study (1.1 ± 0.5 mm d−1) is roughly similar to the mean sublimation (∼ 0.2 to ∼ 2 mm d−1) on the other glacier/snow-covered sites across the HMA region (Table 4). Sublimation rates during winter were slightly higher in the Pamir range, e.g. Muztag Ata No. 15 (Zhu et al., 2018) and the Muji site (Zhu et al., 2020) compared to the inland/central Tibet region, e.g. Qiangtang No. 1 (Li et al., 2018) and the Dongkemadi site (Liang et al., 2018). This is likely due to the relatively drier atmospheric conditions in the Pamir range than the central or eastern parts of Tibet (Table 4; also Liu et al., 2020). However, such spatial understanding needs more studies and direct measurements to confirm. The only in situ lysimeter-based sublimation is available on the East Rongbuk Glacier measured at ∼ 6500 (Yang, 2010). Their measured sublimation rate was 1.9 mm d−1 during late winter, which is similar to the upper limit of our long-term daily sublimation rate. The only eddy-covariance-measured sublimation rate during winter at the Yala Glacier was 1 mm d−1, which is similar to the sublimation calculated at the AWS-M on the Chhota Shigri Glacier. At the Pindari Glacier AWS site (off-glacier at 3750 ), the sublimation rate for transient snow cover was estimated to be ∼ 0.3 mm d−1 during winter (Singh et al., 2020). Sublimation rates calculated using bias-corrected ERA5 data for Dokriani (∼ 1.2 mm d−1) and Chhota Shigri (∼ 0.7 mm d−1) glaciers were also similar to our study. Sublimation rates during the summer-monsoon season, in general, were lower than those in winter (Table 4; also Litt et al., 2019), which could be due to the warm and moist atmospheric conditions driven by the ISM. This also occurs in the westerlies-dominated region such as the Muztag Ata No. 15 Glacier in the Pamir Mountains (Zhu et al., 2018) and the area of transition between the westerlies- and monsoon-dominated climate regimes such as the Xiao Anglong Glacier in the upper Shiquanhe region (Zhu et al., 2021a). Despite high summer-monsoon humidity, sublimation is higher at higher-altitude sites, such as in the East Rongbuk Glacier site (6523 ). This is most likely a result of the strong winds and low air vapour pressure at very high altitudes, which promote sublimation. The high moisture from ISM also impacts Tibetan glaciers, particularly those located in the northern slopes of the Himalaya (Zhu et al., 2021b; Liu et al., 2021) and central Tibet (Mölg et al., 2012; Li et al., 2018). The ratio of summer (June–September) to winter (October–May) sublimation is larger in the monsoon-dominated region such as the Parlung No. 4 and Zhadang glaciers than that in the westerlies and the transition area, e.g. Xiao Anglong Glacier (Zhu et al., 2020). In the Nepalese central Himalaya, we note a higher sublimation value of 2.4 and 1.8 mm d−1, respectively, on the Yala Glacier during the post- and pre-monsoon seasons (Table 4). Litt et al. (2019) also reported a significantly higher sublimation rate of 7.1 and 1.9 mm d−1, respectively, during post- and pre-monsoon seasons on the Mera Glacier in Nepal. Such higher sublimation rates on the Yala and Mera glaciers are unique, particularly during post- and pre-monsoon seasons when air vapour pressure/specific humidity is higher than that in winter season (Shea et al., 2015; Perry et al., 2020). Nevertheless, such higher sublimation can also be partially attributed to snow blowing/redistribution at such high-altitude sites (Barral et al., 2014; Wagnon et al., 2013; Huintjes et al., 2015b). Overall, dry air, low atmospheric pressure and high wind speeds are suitable conditions for sublimation, as reported from various high-altitude sites in the HMA region (Matthews et al., 2020; Litt et al., 2019; Stigter et al., 2018; Zhu et al., 2018) and everywhere in the world (Wagnon et al., 1999; Cullen et al., 2007; Fyffe et al., 2021).
5.4 Sublimation fraction to winter snowfall and its importance
Sublimation is a substantial component of the surface mass balance and hydrological cycle in the HK glacierised catchments (Azam et al., 2021). Sublimation fractions have been reported in different ways, such as fractions of winter/annual snowfall or fractions of total ablation/mass balance. The cumulative sublimation at the AWS-M ranges from 85 to 172 , with a long-term mean of 145 ± 25 for DJFMA during 2009–2020 (Table 2). Cumulative snowfall ranges from 402 to 971 , with a mean of 574 ± 187 recorded at the glacier base camp and Keylong station (reliability of Keylong's precipitation data is discussed in Sect. 3.1) for DJFMA during 2009–2020 (Table 2). The cumulative sublimation loss accounts for 16 %–42 % of the fraction of winter snowfall at the AWS-M site (Table 2). This mass loss is substantial compared to other parts of the HK region. For example, in the central Himalayan Yala Glacier, sublimation loss was 21 % of the snowfall for one winter season (Stigter et al., 2018). Similarly, sublimation loss was about 14 %–18 % of the total snowfall in the Pheriche sub-catchment of the Dudh Koshi basin in Nepal, based on a distributed glaciohydrological model (Mimeau et al., 2019). Based on satellite-derived datasets, Gascoin (2021) showed that the sublimation ratio to snowfall can exceed 60 % in the high-altitude areas in the northwestern part of the Himalaya, e.g. Ladakh and Karakoram. The mean annual glacier-wide sublimation losses were around 20 % of total annual ablation on the Dokriani and Chhota Shigri glaciers over 1979–2020 based on glacier-wide SEB analysis using bias-corrected ERA5 datasets (Srivastava and Azam, 2022). In the Chinese Altai Mountains's Irtysh River basin, sublimation accounts for 19 % of the snowfall estimated through a physically based snow model (Wu et al., 2021). In the Tibetan Plateau, at the Zhadang Glacier, sublimation loss was 26 % of the total mass loss annually (Huintjes et al., 2015a). At the August-One Glacier in the Qilian Mountains, evaposublimation accounts for 15 % of the annual precipitation, with the major part during winter periods (Guo et al., 2021). In some sites of the Tibetan Plateau, the sublimation fraction is considerably higher. For example, in the Muji Glacier in the Pamir Mountains, the cold season's evaposublimation loss is > 70 % of the corresponding snowfall (Zhu et al., 2020). In the Kunlun Mountains on the Guliya Ice Cap, glacier-wide sublimation loss was ∼ 120 % of the winter snowfall and ∼ 50 % of the annual snowfall (Zhu et al., 2022). On the Qiangtang No. 1 Glacier in inland Tibet, the sublimation and evaporation loss fraction were about 65 %–169 % of the snowfall during 2012–2016, showing significantly higher mass loss than gain (Li et al., 2018). Such a higher sublimation fraction at the Qiangtang No. 1 Glacier during non-melt seasons was associated with high wind speed (∼ 7 m s−1), lower RH (∼ 46 %) and low annual precipitation (362–614 mm). This supports that the dry and windy environment fosters sublimation. Although there are limited observations available from various parts of the Himalaya and HMA region, these observations show that the sublimation fraction to winter/annual snowfall/precipitation is higher in the northwestern part of the HK region and western Tibet (e.g. Zhu et al., 2020; Gascoin, 2021). This is likely due to the atmospheric condition of the northwestern part of the HK region and western Tibet, which is drier than the eastern and central Himalaya. Dry atmospheric conditions favour higher sublimation than wet ones due to high near-surface humidity gradients.
Sublimation is the largest mass loss component during winter. Nonetheless, the sum of winter snowfall may have significant uncertainties considering the undercatch of solid precipitation (Collier and Immerzeel, 2015; Shea et al., 2015; Doblas-Reyes et al., 2021) by the Geonor gauge at the glacier base camp and Keylong station due to strong winds. For example, the snowfall catch efficiency of a Geonor T-200B equipped with a single-Alter windshield (the one functional at the glacier base camp) could be about 50 % or less at a wind speed of about 5 m s−1 or higher (Wolff et al., 2015; see their Fig. 5). Despite the uncertainty in winter snowfall, our results indicate that sublimation loss during DJFMA is a significant component of winter mass distribution. Therefore, it is crucial to include sublimation in future surface mass balance and hydrological modelling in the region. We also stress the importance of reporting the sublimation estimates in a consistent and widely acceptable manner so that they can be directly compared between sites.
In this study, we presented an 11-year record of observed meteorology, SEB and sublimation for DJFMA at 4863 on the Chhota Shigri Glacier moraine in the western Himalaya. We investigated the role of turbulent heat fluxes in the SEB along with the influence of cloud cover and the sublimation to understand their importance in winter mass distribution during 2009–2020.
The net short-wave radiation was the primary energy source of SEB. At the same time, turbulent heat fluxes (H + LE) significantly sink the energy, resulting in negative residual energy (Fsurface) at the snow surface throughout DJFMA. Although net short-wave radiation was the largest contributor in the SEB across the HMA region, we found a significant role of latent heat flux, contributing > 60 % during the winter months. The moisture availability primarily controls the magnitude of latent heat flux, with considerable influence from snow-surface temperature and wind speed. Interestingly, we found that the strong and cold winds, probably from the western-disturbance storms, act as an impediment of latent heat flux at the AWS-M site by setting up a high-moisture and cold-temperature regime.
The large variability in the SEB components was directly related to cloud cover, which primarily affects incoming short-wave radiation with a decrease of 70 % and incoming long-wave radiation with an increase of 25 %. The cloud cover also controls the meteorological condition favourable for turbulent heat fluxes and reduces their magnitude by larger than 60 %. The mean daily sublimation at the AWS-M was about 3 times lower on cloudy than clear-sky conditions due to the low incoming short-wave radiation and subsequent alteration in near-surface meteorological conditions. The mean daily sublimation was similar to the sublimation rates of other HK and HMA glaciers during winter. The vertical gradient of temperature and moisture along with surface temperature and wind speed emerged as the best predictors of sublimation based on the multiple linear regression analysis. The sensitivity analysis showed that sublimation is most sensitive to the changes in z0m and Ts, suggesting it is crucial for accurate SEB and sublimation. It is, however, slightly less sensitive to Tair, but it remains a matter of concern from a future warming perspective.
The cumulative DJFMA sublimation was 145 ± 25 , corresponding to 16 %–42 % of the fraction of winter snowfall at the AWS-M site, which is relatively higher than observed in other sites across the HK region, with considerable interannual variations, and is lower than a few of the Tibetan glacier sites. Hence, sublimation emerged as one of the significant mass balance components during winter, especially in a dry–cold–windy environment. However, sublimation estimates and winter snowfall could be uncertain in the high-mountain sites, considering their sensitivity to meteorological forcing, surface roughness length, sensor inaccuracies and calculation errors.
Given the limitations, this 11-year dataset demonstrates how individual glacier-based long-term observations/studies can improve our understanding of local-scale meteorological factors that are affecting SEB and sublimation in the HK region. This study underscores the need for extensive measurements of high-quality, on-glacier weather data observation using the eddy-covariance technique and snowfall for robust region-wide modelling and the inclusion of sublimation schemes in glaciohydrological models.
The codes for SEB calculation and generating the figures are available at https://github.com/arindan/Winter-sublimation-at-the-Chhota-Shigri-Glacier-India (last access: 11 September 2022) (https://doi.org/10.5281/zenodo.6804947; Mandal et al., 2022). AWS-M data used in this study are available on request from the corresponding author.
The supplement related to this article is available online at: https://doi.org/10.5194/tc-16-3775-2022-supplement.
AM, TA, MFA and PW conceptualised the study. AR supervised the study. AM performed the analysis, developed the figures and wrote the paper. MS helped in SEB calculations. CS partly compiled the existing sublimation studies across the HMA region. All authors contributed significantly to preparing the draft manuscript and discussion and supported the data analysis.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Jawaharlal Nehru University, New Delhi, for providing all the facilities to carry out this work. The authors are greatly thankful to the field assistant Bhim Bahadur Adhikari and other field supporters who have taken part in successive field trips in harsh conditions. The funding agencies and project collaborators who fully and partially supported this work are the Department of Science & Technology (Government of India), IFCPAR/CEFIPRA (Indo-French Centre for the Promotion of Advanced Research), INDICE (The response of the hydrological system in India to climate change), GLACINDIA (Water Related Effects of Changes in Glacier Mass Balance and River Runoff in Western Himalaya, India: Past, Present and Future) and CHARIS (Contribution to High Asia Runoff from Ice & Snow), MoES (Ministry of Earth Sciences), and SAC ISRO (Space Applications Centre of the Indian Space Research Organisation). Thanks to Etienne Berthier for the Pléiades image provided under the Pléiades Glacier Observatory (PGO) initiative of the French National Centre for Space Studies (CNES). Arindan Mandal is grateful to UGC RGNF (University Grants Commission; Rajiv Gandhi National Fellowship) and DAAD (German Academic Exchange Service, Germany; Bi-nationally Supervised PhD fellowship) for providing financial support for his PhD. Mohd Farooq Azam acknowledges the research grant through an INSPIRE (Innovation in Science Pursuit for Inspired Research) Faculty Fellowship (no. IFA-14-EAS-22) and the Space Application Centre (ISRO). The Interdisciplinary Centre for Water Research (ICWaR), Indian Institute of Science, is duly acknowledged for supporting Arindan Mandal with a postdoctoral fellowship and necessary research facility at the institute. We thank Masashi Niwano (editor), Jakob Steiner and the other (anonymous) reviewer, and Suryanarayanan Balasubramanian for helping to improve the paper with their comments and suggestions.
This research has been supported by the Science and Engineering Research Board (grant no. SR/DGH-93/2014).
This paper was edited by Masashi Niwano and reviewed by Jakob Steiner and one anonymous referee.
Acharya, A. and Kayastha, R. B.: Mass and Energy Balance Estimation of Yala Glacier (2011–2017), Langtang Valley, Nepal, Water, 11, 6, https://doi.org/10.3390/w11010006, 2019.
Aizen, V. B., Aizen, E. M., and Nikitin, S. A.: Glacier regime on the northern slope of the Himalaya (Xixibangma glaciers), Quatern. Int., 97–98, 27–39, https://doi.org/10.1016/S1040-6182(02)00049-6, 2002.
Andreassen, L. M., van den Broeke, M. R., Giesen, R. H., and Oerlemans, J.: A 5 year record of surface energy and mass balance from the ablation zone of Storbreen, Norway, J. Glaciol., 54, 245–258, https://doi.org/10.3189/002214308784886199, 2008.
Azam, M. F., Wagnon, P., Vincent, C., Ramanathan, AL., Favier, V., Mandal, A., and Pottakkal, J. G.: Processes governing the mass balance of Chhota Shigri Glacier (western Himalaya, India) assessed by point-scale surface energy balance measurements, The Cryosphere, 8, 2195–2217, https://doi.org/10.5194/tc-8-2195-2014, 2014a.
Azam, M. F., Wagnon, P., Vincent, C., Ramanathan, A., Linda, A., and Singh, V. B.: Reconstruction of the annual mass balance of Chhota Shigri glacier, Western Himalaya, India, since 1969, Ann. Glaciol., 55, 69–80, https://doi.org/10.3189/2014AoG66A104, 2014b.
Azam, M. F., Ramanathan, A., Wagnon, P., Vincent, C., Linda, A., Berthier, E., Sharma, P., Mandal, A., Angchuk, T., Singh, V. B., and Pottakkal, J. G.: Meteorological conditions, seasonal and annual mass balances of Chhota Shigri Glacier, western Himalaya, India, Ann. Glaciol., 57, 328–338, https://doi.org/10.3189/2016AoG71A570, 2016.
Azam, M. F., Wagnon, P., Berthier, E., Vincent, C., Fujita, K., and Kargel, J. S.: Review of the status and mass changes of Himalayan-Karakoram glaciers, J. Glaciol., 64, 61–74, https://doi.org/10.1017/jog.2017.86, 2018.
Azam, M. F., Kargel, J. S., Shea, J. M., Nepal, S., Haritashya, U. K., Srivastava, S., Maussion, F., Qazi, N., Chevallier, P., Dimri, A. P., Kulkarni, A. V., Cogley, J. G., and Bahuguna, I. M.: Glaciohydrology of the Himalaya–Karakoram, Science, 373, eabf3668, https://doi.org/10.1126/science.abf3668, 2021.
Barral, H., Genthon, C., Trouvilliez, A., Brun, C., and Amory, C.: Blowing snow in coastal Adélie Land, Antarctica: three atmospheric-moisture issues, The Cryosphere, 8, 1905–1919, https://doi.org/10.5194/tc-8-1905-2014, 2014.
Bintanja, R.: The local surface energy balance of the Ecology Glacier, King George Island, Antarctica: measurements and modelling, Antarct. Sci., 7, 315–325, https://doi.org/10.1017/S0954102095000435, 1995.
Bookhagen, B. and Burbank, D. W.: Toward a complete Himalayan hydrological budget: Spatiotemporal distribution of snowmelt and rainfall and their impact on river discharge, J. Geophys. Res.-Earth, 115, F3, https://doi.org/10.1029/2009JF001426, 2010.
Brutsaert, B.: Evaporation in the Atmosphere: Theory, History and Application, Kluwer Acad., Norwell, Mass, 299 pp., ISBN 9789401714976, https://doi.org/10.1007/978-94-017-1497-6, 1982.
Chambers, J. R., Smith, M. W., Quincey, D. J., Carrivick, J. L., Ross, A. N., and James, M. R.: Glacial Aerodynamic Roughness Estimates: Uncertainty, Sensitivity, and Precision in Field Measurements, J. Geophys. Res.-Earth, 125, e2019JF005167, https://doi.org/10.1029/2019JF005167, 2020.
Chen, J., Qin, X., Kang, S., Du, W., Sun, W., and Liu, Y.: Effects of clouds on surface melting of Laohugou glacier No. 12, western Qilian Mountains, China, J. Glaciol., 64, 89–99, https://doi.org/10.1017/jog.2017.82, 2018.
Collier, E. and Immerzeel, W. W.: High-resolution modeling of atmospheric dynamics in the Nepalese Himalaya, J. Geophys. Res.-Atmos., 120, 9882–9896, doi:10.1002/2015JD023266, 2015.
Conway, J. P. and Cullen, N. J.: Cloud effects on surface energy and mass balance in the ablation area of Brewster Glacier, New Zealand, The Cryosphere, 10, 313–328, https://doi.org/10.5194/tc-10-313-2016, 2016.
Conway, J. P., Abermann, J., Andreassen, L. M., Azam, M. F., Cullen, N. J., Fitzpatrick, N., Giesen, R. H., Langley, K., MacDonell, S., Mölg, T., Radić, V., Reijmer, C. H., and Sicart, J.-E.: Cloud forcing of surface energy balance from in situ measurements in diverse mountain glacier environments, The Cryosphere, 16, 3331–3356, https://doi.org/10.5194/tc-16-3331-2022, 2022.
Cuffey, K. M. and Paterson, W. S. B.: The physics of glaciers, Fourth edition, Butterworth-Heinemann, Oxford, ISBN 9780123694614, 2010.
Cullen, N. J., Mölg, T., Kaser, G., Steffen, K., and Hardy, D. R.: Energy-balance model validation on the top of Kilimanjaro, Tanzania, using eddy covariance data, Ann. Glaciol., 46, 227–233, https://doi.org/10.3189/172756407782871224, 2007.
Denby, B. and Greuell, W.: The use of bulk and profile methods for determining surface heat fluxes in the presence of glacier winds, J. Glaciol., 46, 445–452, https://doi.org/10.3189/172756500781833124, 2000.
Doblas-Reyes, F. J., Sörensson, A. A., Almazroui, M., Dosio, A., Gutowski, W. J., Haarsma, R., Hamdi, R., Hewitson, B., Kwon, W.-T., Lamptey, B. L., Maraun, D., Stephenson, T. S., Takayabu, I., Terray, L., Turner, A., and Zuo, Z.: Linking Global to Regional Climate Change, in: Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S. L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M. I., Huang, M., Leitzell, K., Lonnoy, E., Matthews, J. B. R., Maycock, T. K., Waterfield, T., Yelekçi, O., Yu, R., and Zhou, B., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, https://doi.org/10.1017/9781009157896.012, 2021.
Favier, V., Wagnon, P., Chazarin, J.-P., Maisincho, L., and Coudrain, A.: One-year measurements of surface heat budget on the ablation zone of Antizana Glacier 15, Ecuadorian Andes, J. Geophys. Res.-Atmos., 109, D18105, https://doi.org/10.1029/2003JD004359, 2004.
Favier, V., Agosta, C., Genthon, C., Arnaud, L., Trouvillez, A., and Gallée, H.: Modeling the mass and surface heat budgets in a coastal blue ice area of Adelie Land, Antarctica, J. Geophys. Res.-Earth, 116, F03017, https://doi.org/10.1029/2010JF001939, 2011.
Fugger, S., Fyffe, C. L., Fatichi, S., Miles, E., McCarthy, M., Shaw, T. E., Ding, B., Yang, W., Wagnon, P., Immerzeel, W., Liu, Q., and Pellicciotti, F.: Understanding monsoon controls on the energy and mass balance of glaciers in the Central and Eastern Himalaya, The Cryosphere, 16, 1631–1652, https://doi.org/10.5194/tc-16-1631-2022, 2022.
Fyffe, C. L., Potter, E., Fugger, S., Orr, A., Fatichi, S., Loarte, E., Medina, K., Hellström, Å. R., Bernat, M., Aubry-Wake, C., Gurgiser, W., Perry, L. B., Suarez, W., Quincey, D. J., and Pellicciotti, F.: The energy and mass balance of Peruvian glaciers. J. Geophys. Res.-Atmos., 126, e2021JD034911, https://doi.org/10.1029/2021JD034911, 2021.
Gascoin, S.: Snowmelt and Snow Sublimation in the Indus Basin, Water, 13, 2621, https://doi.org/10.3390/w13192621, 2021.
Giesen, R. H., Andreassen, L. M., van den Broeke, M. R., and Oerlemans, J.: Comparison of the meteorology and surface energy balance at Storbreen and Midtdalsbreen, two glaciers in southern Norway, The Cryosphere, 3, 57–74, https://doi.org/10.5194/tc-3-57-2009, 2009.
Greuell, W. and Smeets, P.: Variations with elevation in the surface energy balance on the Pasterze (Austria), J. Geophys. Res.-Atmos., 106, 31717–31727, https://doi.org/10.1029/2001JD900127, 2001.
Guo, S., Chen, R., Han, C., Liu, J., Wang, X., and Liu, G.: Five-year analysis of evaposublimation characteristics and its role on surface energy balance SEB on a midlatitude continental glacier, Earth Space Sci., 8, e2021EA001901, https://doi.org/10.1029/2021EA001901, 2021.
Guo, S., Chen, R., and Li, H.: Surface Sublimation/Evaporation and Condensation/Deposition and Their Links to Westerlies During 2020 on the August-One Glacier, the Semi-Arid Qilian Mountains of Northeast Tibetan Plateau, J. Geophys. Res.-Atmos., 127, e2022JD036494, https://doi.org/10.1029/2022JD036494, 2022.
Hock, R.: Glacier melt: a review of processes and their modelling, Progress in Physical Geography: Earth and Environment, 29, 362–391, https://doi.org/10.1191/0309133305pp453ra, 2005.
Hock, R. and Holmgren, B.: A distributed surface energy-balance model for complex topography and its application to Storglaciären, Sweden, J. Glaciol., 51, 25–36, 2005.
Hock, R., Rasul, G., Adler, C., Cáceres, B., Gruber, S., Hirabayashi, Y., Jackson, M., Kääb, A., Kang, S., Kutuzov, S., Milner, A., Molau, U., Morin, S., Orlove, B., and Steltzer, H. I.: Chapter 2: High Mountain Areas, in: IPCC Special Report on the Ocean and Cryosphere in a Changing Climate (SROCC), Cambridge University Press, Cambridge, UK and New York, NY, USA, 131–202, https://doi.org/10.1017/9781009157964.004, 2019.
Huintjes, E., Sauter, T., Schröter, B., Maussion, F., Yang, W., Kropáček, J., Buchroithner, M., Scherer, D., Kang, S., and Schneider, C.: Evaluation of a Coupled Snow and Energy Balance Model for Zhadang Glacier, Tibetan Plateau, Using Glaciological Measurements and Time-Lapse Photography, Arctic, Antarctic, and Alpine Research, 47, 573–590, https://doi.org/10.1657/AAAR0014-073, 2015a.
Huintjes, E., Neckel, N., Hochschild, V., and Schneider, C.: Surface energy and mass balance at Purogangri ice cap, central Tibetan Plateau, 2001–2011, J. Glaciol., 61, 1048–1060, https://doi.org/10.3189/2015JoG15J056, 2015b.
IPCC: IPCC Special Report on the Ocean and Cryosphere in a Changing Climate, edited by: Pörtner, H.-O., Roberts, D. C., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegría, A., Nicolai, M., Okem, A., Petzold, J., Rama, B., and Weyer, N. M., Cambridge University Press, Cambridge, UK and New York, NY, USA, https://doi.org/10.1017/9781009157964, 2019.
Iqbal, M.: An introduction to solar radiation, Academic Press, New York, https://doi.org/ISBN: 0123737508, 1983.
Kayastha, R. B., Ohata, T., and Ageta, Y.: Application of a mass-balance model to a Himalayan glacier, J. Glaciol., 45, 559–567, https://doi.org/10.3189/S002214300000143X, 1999.
Kirkham, J. D., Koch, I., Saloranta, T. M., Litt, M., Stigter, E. E., Møen, K., Thapa, A., Melvold, K., and Immerzeel, W. W.: Near Real-Time Measurement of Snow Water Equivalent in the Nepal Himalayas, Front. Earth Sci., 7, 117, https://doi.org/10.3389/feart.2019.00177, 2019.
Kochendorfer, J., Nitu, R., Wolff, M., Mekis, E., Rasmussen, R., Baker, B., Earle, M. E., Reverdin, A., Wong, K., Smith, C. D., Yang, D., Roulet, Y.-A., Buisan, S., Laine, T., Lee, G., Aceituno, J. L. C., Alastrué, J., Isaksen, K., Meyers, T., Brækkan, R., Landolt, S., Jachcik, A., and Poikonen, A.: Analysis of single-Alter-shielded and unshielded measurements of mixed and solid precipitation from WMO-SPICE, Hydrol. Earth Syst. Sci., 21, 3525–3542, https://doi.org/10.5194/hess-21-3525-2017, 2017.
Krishnan, R., Shrestha, A. B., Ren, G., Rajbhandari, R., Saeed, S., Sanjay, J., Syed, Md. A., Vellore, R., Xu, Y., You, Q., and Ren, Y.: Unravelling Climate Change in the Hindu Kush Himalaya: Rapid Warming in the Mountains and Increasing Extremes, in: The Hindu Kush Himalaya Assessment, edited by: Wester, P., Mishra, A., Mukherji, A., and Shrestha, A. B., Springer International Publishing, Cham, 57–97, https://doi.org/10.1007/978-3-319-92288-1_3, 2019.
Kuhn, M.: Building Predictive Models in R Using the caret Package, J. Statist. Softw., 28, 1–26, https://doi.org/10.18637/jss.v028.i05, 2008.
Li, S., Yao, T., Yang, W., Yu, W., and Zhu, M.: Glacier Energy and Mass Balance in the Inland Tibetan Plateau: Seasonal and Interannual Variability in Relation to Atmospheric Changes, J. Geophys. Res.-Atmos., 123, 6390–6409, https://doi.org/10.1029/2017JD028120, 2018.
Li, S., Yao, T., Yu, W., Yang, W., and Zhu, M.: Energy and mass balance characteristics of the Guliya ice cap in the West Kunlun Mountains, Tibetan Plateau, Cold Reg. Sci. Technol., 159, 71–85, https://doi.org/10.1016/j.coldregions.2018.12.001, 2019.
Liang, L., Cuo, L., and Liu, Q.: The energy and mass balance of a continental glacier: Dongkemadi Glacier in central Tibetan Plateau, Sci. Rep.-UK, 8, 12788, https://doi.org/10.1038/s41598-018-31228-5, 2018.
Litt, M., Shea, J., Wagnon, P., Steiner, J., Koch, I., Stigter, E., and Immerzeel, W.: Glacier ablation and temperature indexed melt models in the Nepalese Himalaya, Sci. Rep.-UK, 9, 5264, https://doi.org/10.1038/s41598-019-41657-5, 2019.
Liu, W., Zhang, D., Qin, X., van den Broeke, M. R., Jiang, Y., Yang, D., and Ding, M.: Monsoon Clouds Control the Summer Surface Energy Balance on East Rongbuk glacier (6523 m above sea level), the northern of Mt. Qomolangma (Everest), J. Geophys. Res.-Atmos., e2020JD033998, https://doi.org/10.1029/2020JD033998, 2021.
Liu, X., Liu, Y., Wang, X., and Wu, G.: Large-Scale Dynamics and Moisture Sources of the Precipitation Over the Western Tibetan Plateau in Boreal Winter, J. Geophys. Res.-Atmos., 125, e2019JD032133, https://doi.org/10.1029/2019JD032133, 2020.
Mandal, A., Ramanathan, A., Azam, M. F., Angchuk, T., Soheb, M., Kumar, N., Pottakkal, J. G., Vatsal, S., Mishra, S., and Singh, V. B.: Understanding the interrelationships among mass balance, meteorology, discharge and surface velocity on Chhota Shigri Glacier over 2002–2019 using in situ measurements, J. Glaciol., 1–15, https://doi.org/10.1017/jog.2020.42, 2020.
Mandal, A., Angchuk, T., Azam, M. F., Ramanathan, A., Wagnon, P., Soheb, M., and Singh, C.: Codes used in “11-year record of wintertime snow surface energy balance and sublimation at 4863 m a.s.l. on Chhota Shigri Glacier moraine (western Himalaya, India)” (1.1), Zenodo [code], https://doi.org/10.5281/zenodo.6804947, 2022.
Matthews, T., Perry, L. B., Koch, I., Aryal, D., Khadka, A., Shrestha, D., Abernathy, K., Elmore, A. C., Seimon, A., Tait, A., Elvin, S., Tuladhar, S., Baidya, S. K., Potocki, M., Birkel, S. D., Kang, S., Sherpa, T. C., Gajurel, A., and Mayewski, P. A.: Going to Extremes: Installing the World's Highest Weather Stations on Mount Everest, B. Am. Meteorol. Soc., 101, E1870–E1890, https://doi.org/10.1175/BAMS-D-19-0198.1, 2020.
Mimeau, L., Esteves, M., Zin, I., Jacobi, H.-W., Brun, F., Wagnon, P., Koirala, D., and Arnaud, Y.: Quantification of different flow components in a high-altitude glacierized catchment (Dudh Koshi, Himalaya): some cryospheric-related issues, Hydrol. Earth Syst. Sci., 23, 3969–3996, https://doi.org/10.5194/hess-23-3969-2019, 2019.
Mölg, T., Maussion, F., Yang, W., and Scherer, D.: The footprint of Asian monsoon dynamics in the mass and energy balance of a Tibetan glacier, The Cryosphere, 6, 1445–1461, https://doi.org/10.5194/tc-6-1445-2012, 2012.
Moore, R.: On the use of bulk aerodynamic formulae over melting snow, Nord. Hydrol., 14, 193–206, 1983.
Nicholson, L. and Stiperski, I.: Comparison of turbulent structures and energy fluxes over exposed and debris-covered glacier ice, J. Glaciol., 66, 543–555, https://doi.org/10.1017/jog.2020.23, 2020.
Nicholson, L. I., Prinz, R., Mölg, T., and Kaser, G.: Micrometeorological conditions and surface mass and energy fluxes on Lewis Glacier, Mt Kenya, in relation to other tropical glaciers, The Cryosphere, 7, 1205–1225, https://doi.org/10.5194/tc-7-1205-2013, 2013.
Oerlemans, J.: Analysis of a 3 year meteorological record from the ablation zone of Morteratschgletscher, Switzerland: energy and mass balance, J. Glaciol., 46, 571–579, https://doi.org/10.3189/172756500781832657, 2000.
Oerlemans, J.: Glaciers and Climate Change, CRC Press, Lisse A.A. Balkema Publishers, ISBN 9026518137, 168 pp., 2001.
Oke, T. R.: Boundary Layer Climates, 2nd edn., Routledge, ISBN 9780415043199, 423 pp., 1987.
Patel, A., Goswami, A., Dharpure, J. K., Thamban, M., Sharma, P., Kulkarni, A. V., and Oulkar, S.: Estimation of mass and energy balance of glaciers using a distributed energy balance model over the Chandra river basin (Western Himalaya), Hydrol. Process., 35, e14058, https://doi.org/10.1002/hyp.14058, 2021.
Perry, L. B., Matthews, T., Guy, H., Koch, I., Khadka, A., Elmore, A. C., Shrestha, D., Tuladhar, S., Baidya, S. K., Maharjan, S., Wagnon, P., Aryal, D., Seimon, A., Gajurel, A., and Mayewski, P. A.: Precipitation Characteristics and Moisture Source Regions on Mt. Everest in the Khumbu, Nepal, One Earth, 3, 594–607, https://doi.org/10.1016/j.oneear.2020.10.011, 2020.
R Core Team: R: A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria, https://www.R-project.org/ (last access: 15 July 2022), 2021.
Radić, V., Menounos, B., Shea, J., Fitzpatrick, N., Tessema, M. A., and Déry, S. J.: Evaluation of different methods to model near-surface turbulent fluxes for a mountain glacier in the Cariboo Mountains, BC, Canada, The Cryosphere, 11, 2897–2918, https://doi.org/10.5194/tc-11-2897-2017, 2017.
Reid, T. D. and Brock, B. W.: An energy-balance model for debris-covered glaciers including heat conduction through the debris layer, J. Glaciol., 56, 903–916, https://doi.org/10.3189/002214310794457218, 2010.
Ren, Y. Y., Ren, G. Y., Sun, X. B., Shrestha, A. B., You, Q. L., Zhan, Y. J., Rajbhandari, R., Zhang, P., and Wen, K. M.: Observed changes in surface air temperature and precipitation in the Hindu Kush Himalayan region over the last 100-plus years, Advances in Climate Change Research, 8, 148–156, 2017.
Rounce, D. R., Quincey, D. J., and McKinney, D. C.: Debris-covered glacier energy balance model for Imja–Lhotse Shar Glacier in the Everest region of Nepal, The Cryosphere, 9, 2295–2310, https://doi.org/10.5194/tc-9-2295-2015, 2015.
Schaefer, M., Fonseca-Gallardo, D., Farías-Barahona, D., and Casassa, G.: Surface energy fluxes on Chilean glaciers: measurements and models, The Cryosphere, 14, 2545–2565, https://doi.org/10.5194/tc-14-2545-2020, 2020.
Sexstone, G. A., Clow, D. W., Stannard, D. I., and Fassnacht, S. R.: Comparison of methods for quantifying surface sublimation over seasonally snow-covered terrain, Hydrol. Process., 30, 3373–3389, https://doi.org/10.1002/hyp.10864, 2016.
Shea, J. M., Wagnon, P., Immerzeel, W. W., Biron, R., Brun, F., and Pellicciotti, F.: A comparative high-altitude meteorological analysis from three catchments in the Nepalese Himalaya, Int. J. Water Resour. D., 31, 174–200, https://doi.org/10.1080/07900627.2015.1020417, 2015.
Singh, N., Singhal, M., Chhikara, S., Karakoti, I., Chauhan, P., and Dobhal, D. P.: Radiation and energy balance dynamics over a rapidly receding glacier in the central Himalaya, Int. J. Climatol., 40, 400–420, https://doi.org/10.1002/joc.6218, 2020.
Slater, T., Lawrence, I. R., Otosaka, I. N., Shepherd, A., Gourmelen, N., Jakob, L., Tepes, P., Gilbert, L., and Nienow, P.: Review article: Earth's ice imbalance, The Cryosphere, 15, 233–246, https://doi.org/10.5194/tc-15-233-2021, 2021.
Smith, T., Smith, M. W., Chambers, J. R., Sailer, R., Nicholson, L., Mertes, J., Quincey, D. J., Carrivick, J. L., and Stiperski, I.: A scale-dependent model to represent changing aerodynamic roughness of ablating glacier ice based on repeat topographic surveys, J. Glaciol., 1–15, https://doi.org/10.1017/jog.2020.56, 2020.
Srivastava, S. and Azam, M. F.: Mass- and Energy-Balance Modeling and Sublimation Losses on Dokriani Bamak and Chhota Shigri Glaciers in Himalaya Since 1979, Front. Water, 4, 874240, https://doi.org/10.3389/frwa.2022.874240, 2022.
Steiner, J. F., Litt, M., Stigter, E. E., Shea, J., Bierkens, M. F. P., and Immerzeel, W. W.: The Importance of Turbulent Fluxes in the Surface Energy Balance of a Debris-Covered Glacier in the Himalayas, Front. Earth Sci., 6, 144, https://doi.org/10.3389/feart.2018.00144, 2018.
Steiner, J. F., Kraaijenbrink, P. D. A., and Immerzeel, W. W.: Distributed Melt on a Debris-Covered Glacier: Field Observations and Melt Modeling on the Lirung Glacier in the Himalaya, Front. Earth Sci., 9, 678375, https://doi.org/10.3389/feart.2021.678375, 2021.
Stigter, E. E., Litt, M., Steiner, J. F., Bonekamp, P. N. J., Shea, J. M., Bierkens, M. F. P., and Immerzeel, W. W.: The Importance of Snow Sublimation on a Himalayan Glacier, Front. Earth Sci., 6, 108, https://doi.org/10.3389/feart.2018.00108, 2018.
Stigter, E. E., Steiner, J. F., Koch, I., Saloranta, T. M., Kirkham, J. D., and Immerzeel, W. W.: Energy and mass balance dynamics of the seasonal snowpack at two high-altitude sites in the Himalaya, Cold Reg. Sci. Technol., 183, 103233, https://doi.org/10.1016/j.coldregions.2021.103233, 2021.
Thibert, E., Sielenou, P. D., Vionnet, V., Eckert, N., and Vincent, C.: Causes of Glacier Melt Extremes in the Alps Since 1949, Geophys. Res. Lett., 45, 817–825, https://doi.org/10.1002/2017GL076333, 2018.
van den Broeke, M., van As, D., Reijmer, C., and van de Wal, R.: Assessing and Improving the Quality of Unattended Radiation Observations in Antarctica, J. Atmos. Ocean. Tech., 21, 1417–1431, https://doi.org/10.1175/1520-0426(2004)021<1417:AAITQO>2.0.CO;2, 2004.
van den Broeke, M., Reijmer, C., van As, D., van de Wal, R., and Oerlemans, J.: Seasonal cycles of Antarctic surface energy balance from automatic weather stations, Ann. Glaciol., 41, 131–139, https://doi.org/10.3189/172756405781813168, 2005.
Wagnon, P., Ribstein, P., Francou, B., and Pouyaud, B.: Annual cycle of energy balance of Zongo Glacier, Cordillera Real, Bolivia, J. Geophys. Res.-Atmos., 104, 3907–3923, https://doi.org/10.1029/1998JD200011, 1999.
Wagnon, P., Vincent, C., Arnaud, Y., Berthier, E., Vuillermoz, E., Gruber, S., Ménégoz, M., Gilbert, A., Dumont, M., Shea, J. M., Stumm, D., and Pokhrel, B. K.: Seasonal and annual mass balances of Mera and Pokalde glaciers (Nepal Himalaya) since 2007, The Cryosphere, 7, 1769–1786, https://doi.org/10.5194/tc-7-1769-2013, 2013.
Wolff, M. A., Isaksen, K., Petersen-Øverleir, A., Ødemark, K., Reitan, T., and Brækkan, R.: Derivation of a new continuous adjustment function for correcting wind-induced loss of solid precipitation: results of a Norwegian field study, Hydrol. Earth Syst. Sci., 19, 951–967, https://doi.org/10.5194/hess-19-951-2015, 2015.
Wu, X., Zhang, W., Li, H., Long, Y., Pan, X., and Shen, Y.: Analysis of seasonal snowmelt contribution using a distributed energy balance model for a river basin in the Altai Mountains of northwestern China, J. Hydrol., 35, e14046, https://doi.org/10.1002/hyp.14046, 2021.
Yang, W., Guo, X., Yao, T., Yang, K., Zhao, L., Li, S., and Zhu, M.: Summertime surface energy budget and ablation modeling in the ablation zone of a maritime Tibetan glacier, J. Geophys. Res.-Atmos., 116, https://doi.org/10.1029/2010JD015183, 2011.
Yang, X.: Characteristics of meteorological elements and impact on glacier's change on the north slope of the Mt. Qomolangma Region, Dissertation thesis, p. 125, Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences, Lanzhou, China, 2010.
Zemp, M., Huss, M., Thibert, E., Eckert, N., McNabb, R., Huber, J., Barandun, M., Machguth, H., Nussbaumer, S. U., Gärtner-Roer, I., Thomson, L., Paul, F., Maussion, F., Kutuzov, S., and Cogley, J. G.: Global glacier mass changes and their contributions to sea-level rise from 1961 to 2016, Nature, 568, 382–386, https://doi.org/10.1038/s41586-019-1071-0, 2019.
Zhang, G., Kang, S., Fujita, K., Huintjes, E., Xu, J., Yamazaki, T., Haginoya, S., Wei, Y., Scherer, D., Schneider, C., and Yao, T.: Energy and mass balance of Zhadang glacier surface, central Tibetan Plateau, J. Glaciol., 59, 137–148, https://doi.org/10.3189/2013JoG12J152, 2013.
Zhu, M., Yao, T., Yang, W., Xu, B., Wu, G., and Wang, X.: Differences in mass balance behavior for three glaciers from different climatic regions on the Tibetan Plateau, Clim. Dynam., 50, 3457–3484, https://doi.org/10.1007/s00382-017-3817-4, 2018.
Zhu, M., Yao, T., Xie, Y., Xu, B., Yang, W., and Yang, S.: Mass balance of Muji Glacier, northeastern Pamir, and its controlling climate factors, J. Hydrol., 590, 125447, https://doi.org/10.1016/j.jhydrol.2020.125447, 2020.
Zhu, M., Thompson, L. G., Zhao, H., Yao, T., Yang, W., and Jin, S.: Influence of Atmospheric Circulation on Glacier Mass Balance in Western Tibet: An Analysis Based on Observations and Modeling, J. Climate, 34, 6743–6757, https://doi.org/10.1175/JCLI-D-20-0988.1, 2021a.
Zhu, M., Yang, W., Yao, T., Tian, L., Thompson, L. G., and Zhao, H.: The Influence of Key Climate Variables on Mass Balance of Naimona'nyi Glacier on a North-Facing Slope in the Western Himalayas, J. Geophys. Res.-Atmos., 126, e2020JD033956, https://doi.org/10.1029/2020JD033956, 2021b.
Zhu, M., Yao, T., Yang, W., Wu, G., Li, S., Zhao, H., and Thompson, L. G.: Possible Causes of Anomalous Glacier Mass Balance in the Western Kunlun Mountains, J. Geophys. Res.-Atmos., 127, e2021JD035705, https://doi.org/10.1029/2021JD035705, 2022.
Zwaaftink, C. D. G., Mott, R., and Lehning, M.: Seasonal simulation of drifting snow sublimation in Alpine terrain, Water Resour. Res., 49, 1581–1590, https://doi.org/10.1002/wrcr.20137, 2013.