Glacier geometry and flow speed determine how Arctic marine-terminating glaciers respond to lubricated beds

Basal conditions directly control the glacier sliding rate and the dynamic discharge of ice. Recent glacier destabilization events indicate that some marine-terminating glaciers quickly respond to lubricated beds with increased flow speed, but the underlying physics, especially how this vulnerability relates to glacier geometry and flow characteristics, remains unclear. This paper presents a 1D physical framework for glacier dynamic vulnerability assuming sudden basal lubrication as an initial perturbation. In this new model, two quantities determine the scale and the areal extent of the subsequent thinning and acceleration after the bed is lubricated: Péclet number (Pe) and the product of glacier speed and thickness gradient (dubbed J₀ in this study). To validate the model, this paper calculates Pe and J₀ using multi-sourced data from 1996 to 1998 for outlet glaciers in the Greenland ice sheet and Austfonna ice cap, Svalbard, and compares the results with the glacier speed change during 1996/1998–2018. Glaciers with lower Pe and J₀ are more likely to accelerate during this 20-year span than those with higher Pe and J₀, which matches the model prediction. A combined factor of ice thickness, surface slope, and initial flow speed physically determines how much and how fast glaciers respond to lubricated beds in terms of speed, elevation, and terminus change.

1 Introduction

Marine-terminating glaciers worldwide have undergone significant acceleration, retreat, and mass loss in past decades (e.g., Vaughan et al., 2013; Cook et al., 2016; Carr et al., 2017; Catania et al., 2020; Williams et al., 2021). At the Greenland ice sheet (GrIS), the dynamic discharge of marine-terminating glaciers accounts for 66 % of the region's total mass loss (Mouginot et al., 2019). For the other Arctic regions outside of the GrIS, surface mass balance contributes more mass loss than dynamic discharge (Catania et al., 2020), but several rapid acceleration events also dominate the local land ice budget (e.g., McMillan et al., 2014; Strozzi et al., 2017a; Willis et al., 2018; Haga et al., 2020).

The acceleration and dynamic thinning of marine-terminating glaciers have been attributed to at least two sources: basal lubrication driven by surface melt accessing the bed, and terminus perturbation driven by ice–ocean interactions (Carr et al., 2013). Multiple observations suggest the warming of subsurface ocean waters as the primary and widespread driver across the outlet glaciers in the GrIS (e.g., Nick et al., 2009; Walsh et al., 2012; Tedstone et al., 2013; Catania et al., 2020; Wood et al., 2021; Williams et al., 2021). As a result, models of glacier dynamic loss for estimating sea-level rise usually focus on the glacier terminus and overlook the changing basal conditions (e.g., Nick et al., 2013). Outside of the GrIS, the primary drivers of the dynamic ice loss remain largely uncertain (Carr et al., 2017; Strozzi et al., 2017b), although significant melt-induced lubrication and speedup events have been identified around the Arctic (e.g., Sundal et al., 2011; Dunse et al., 2015; Zheng et al., 2019; Seddik et al., 2019). To date, the response to basal lubrication is mostly studied on a seasonal scale, which links to changing subglacial hydrology within a year (e.g., Zwally et al., 2002; Bartholomew et al., 2010; Sundal et al., 2013; Hewitt, 2013; Rathmann et al., 2017; King et al., 2018; Williams et al., 2020). However, there have been concerns and observations that the bed conditions can evolve and affect glacier dynamics over multiple years. For example, the recent extensive formation of supraglacial lakes in the GrIS can open new moulins that last for years and contribute to long-lived speedups (e.g., Hoffman et al., 2018). During several glacier surge events in Svalbard and the Russian Arctic, initial flow speedups have also created highly crevassed glacier surface and led to further speedups by additional meltwater routing (e.g., Dunse et al., 2015; Strozzi et al., 2017a; Zheng et al., 2019; Sánchez-Gámez et al., 2019). These events potentially alter the basal conditions by allowing meltwater to reach the bed in all seasons, but their interannual impact is still less constrained (Kehrl et al., 2017). In addition, glacier geometry plays a vital role in how a glacier responds to an external perturbation (Carr et al., 2017; Kehrl et al., 2017), but only terminus disruption has been physically well documented and explained (McFadden et al., 2011; Felikson et al., 2017, 2021). Whether some glaciers are more sensitive to basal lubrication than others owing to their geometry is not well known.

To better understand how much and how fast a glacier responds to basal lubrication and its relationship to glacier geometry, this paper presents a physical model with a 1D framework along flowlines formulating the subsequent change (in terms of both glacier speed and surface elevation) after the glacier bed is suddenly lubricated. We use an existing glacier perturbation model (Zheng et al., 2019) and replace the initial thinning condition with a step reduction of basal friction along the glacier channel. This new model identifies key parameters that dominate elevation change rate and ice flow acceleration. Then, using data from the GrIS and Austfonna ice cap, Svalbard, we derive these parameters for each glacier basin and compare them with glacier speed change over 20 years. The entire processing workflows, including data fetching, all calculations, and figure scripts, are available on Github (https://github.com/whyjz/pejzero, Zenodo DOI: https://doi.org/10.5281/zenodo.5641953) and are compiled as a Jupyter Book ready to be cloud executed using the MyBinder service for full reproducibility (Project Jupyter et al., 2018; Executable Books Community, 2020).

2 Model development

We build the model on the perturbation theory developed by Nye (1963), Bindschadler (1997), Felikson et al. (2017), and Zheng et al. (2019). Our goal in this section is to formulate the change rate of ice elevation ($\frac{\mathrm{d}{H}_{\mathrm{1}}}{\mathrm{d}t}$) and ice speed ($\frac{\mathrm{d}{U}_{\mathrm{1}}}{\mathrm{d}t}$) after a glacier bed is lubricated permanently. In this new model, basal lubrication is considered as a sudden perturbation without initial elevation change. The variables defined in the model are listed in Table 1.

Table 1 Variables used in the perturbation model defined in this study. In the dimension column, L is length and T is time. The prime notation used in the text denotes the partial derivative of a variable with respect to x; for example, $H_{\mathrm{1}}^{\prime }\equiv \frac{\partial H_{\mathrm{1}}}{\partial x}$.

2.1 Perturbation due to a permanent change of basal conditions

We set up a glacier with the following initial values along its 1D flowline profile: speed (U₀), thickness (H₀), flux (q₀), surface slope (α₀), and bed friction term (K₀). These values vary along the flowline distance x (positive towards downstream) and do not vary with time (i.e., steady state). We assume that the ice is purely sliding on the bed and does not have any internal deformation, that is,

$$\begin{array}{}\text{(1)}& q_{\mathrm{0}}=U_{\mathrm{0}}{H}_{\mathrm{0}}.\end{array}$$

The glacier speed can be further represented using the hard-bed sliding law (Weertman, 1957):

$$\begin{array}{}\text{(2)}& U_{\mathrm{0}}=K_{\mathrm{0}}{H}_{\mathrm{0}}^m{\mathit{\alpha }}_{\mathrm{0}}^m,\end{array}$$

where m is the flow-law constant and is set to 3 in this study.

At t=0, the bed condition changes and the friction term becomes K₀+K₁. The second term K₁ denotes the amount of change and is positive for a lubrication scenario. There is no initial elevation change associated with this event. We also assume that this is a one-time change and is uniform over the glacier, so K₁ is a constant. The subsequent change of speed, elevation, flux, and slope are represented as U₁, H₁, q₁, and α₁ respectively. Unlike K₁, these quantities vary along the glacier channel and over time. Assuming zero local surface mass balance and zero local stress imbalance (e.g., Felikson et al., 2017; Zheng et al., 2019), the conservation of mass can be expressed as

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{\partial H_{\mathrm{1}}}{\partial t}}=-{\displaystyle \frac{\partial q_{\mathrm{1}}}{\partial x}}.\end{array}$$

Taking the total derivative of q₁ with respect to t yields

$$\begin{array}{}\text{(4)}& q_{\mathrm{1}}={\displaystyle \frac{\partial q_{\mathrm{0}}}{\partial K}}{K}_{\mathrm{1}}+{\displaystyle \frac{\partial q_{\mathrm{0}}}{\partial H}}{H}_{\mathrm{1}}+{\displaystyle \frac{\partial q_{\mathrm{0}}}{\partial \mathit{\alpha }}}{\mathit{\alpha }}_{\mathrm{1}}.\end{array}$$

If we assume a much more gentle slope of the bedrock than that of the ice surface (Felikson et al., 2017; Zheng et al., 2019), the surface slope can also be expressed as the first derivative of ice thickness:

$$\begin{array}{}\text{(5)}& {\mathit{\alpha }}_{\mathrm{1}}=-{\displaystyle \frac{\partial H_{\mathrm{1}}}{\partial x}}.\end{array}$$

Plugging Eqs. (1), (2), (4), and (5) into Eq. (3) yields

$$\begin{array}{}\text{(6)}& \begin{array}{rl}{\displaystyle \frac{\partial H_{\mathrm{1}}}{\partial t}}& =-{\displaystyle \frac{K_{\mathrm{1}}}{K_{\mathrm{0}}}}(C_{\mathrm{0}}{\displaystyle \frac{\partial H_{\mathrm{0}}}{\partial x}}+D_{\mathrm{0}}{\displaystyle \frac{\partial {\mathit{\alpha }}_{\mathrm{0}}}{\partial x}})-{\displaystyle \frac{\partial C_{\mathrm{0}}}{\partial x}}{H}_{\mathrm{1}}\\ & -\left(C_{\mathrm{0}}-{\displaystyle \frac{\partial D_{\mathrm{0}}}{\partial x}}\right){\displaystyle \frac{\partial H_{\mathrm{1}}}{\partial x}}+D_{\mathrm{0}}{\displaystyle \frac{{\partial }^{\mathrm{2}}{H}_{\mathrm{1}}}{\partial x^{\mathrm{2}}}},\end{array}\end{array}$$

where

$$\begin{array}{}\text{(7)}& C_{\mathrm{0}}={\displaystyle \frac{\partial q_{\mathrm{0}}}{\partial H}}\end{array}$$

and

$$\begin{array}{}\text{(8)}& D_{\mathrm{0}}={\displaystyle \frac{\partial q_{\mathrm{0}}}{\partial \mathit{\alpha }}}.\end{array}$$

Since $H_{\mathrm{1}}(t=\mathrm{0},x)=\mathrm{0}$,

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{\partial H_{\mathrm{1}}}{\partial t}}{|}_{t=\mathrm{0}}=-{\displaystyle \frac{K_{\mathrm{1}}}{K_{\mathrm{0}}}}{J}_{\mathrm{0}},\end{array}$$

where

$$\begin{array}{}\text{(10)}& J_{\mathrm{0}}=C_{\mathrm{0}}{H}_{\mathrm{0}}^{\prime }+D_{\mathrm{0}}{\mathit{\alpha }}_{\mathrm{0}}^{\prime }={\displaystyle \frac{\partial q_{\mathrm{0}}}{\partial H}}{\displaystyle \frac{\partial H_{\mathrm{0}}}{\partial x}}+{\displaystyle \frac{\partial q_{\mathrm{0}}}{\partial \mathit{\alpha }}}{\displaystyle \frac{\partial {\mathit{\alpha }}_{\mathrm{0}}}{\partial x}}.\end{array}$$

2.2 J₀ and Péclet number (Pe)

Equation (9) indicates that the ratio of K₁ to K₀ and the value of J₀ both determine the initial elevation change rate. In a lubricating scenario, both K₁ and K₀ are positive, and the initial response of $\frac{\mathrm{d}{H}_{\mathrm{1}}}{\mathrm{d}t}$ is inversely proportional to J₀.

To relate J₀ to the glacier speed change, we start from the change of flux and assume U₁>>H₁. This can be justified by many observations of glacier destabilization as the amount of speed change is usually one to two orders of magnitude higher than the amount of elevation change (e.g., McMillan et al., 2014; Willis et al., 2018). Therefore,

$$\begin{array}{}\text{(11)}& q_{\mathrm{1}}=U_{\mathrm{1}}{H}_{\mathrm{0}}+U_{\mathrm{0}}{H}_{\mathrm{1}}\approx U_{\mathrm{1}}{H}_{\mathrm{0}}.\end{array}$$

As K₁ is a constant, we can derive the glacier speed change using Eqs. (4), (5), (7), (8), and (11):

$$\begin{array}{}\text{(12)}& {\displaystyle \frac{\partial U_{\mathrm{1}}}{\partial t}}={\displaystyle \frac{\mathrm{1}}{H_{\mathrm{0}}}}{\displaystyle \frac{\partial q_{\mathrm{1}}}{\partial t}}={\displaystyle \frac{\mathrm{1}}{H_{\mathrm{0}}}}\left(C_{\mathrm{0}}{\displaystyle \frac{\partial H_{\mathrm{1}}}{\partial t}}-D_{\mathrm{0}}{\displaystyle \frac{\partial }{\partial x}}{\displaystyle \frac{\partial H_{\mathrm{1}}}{\partial t}}\right).\end{array}$$

At t=0,

$$\begin{array}{}\text{(13)}& {\displaystyle \frac{\partial U_{\mathrm{1}}}{\partial t}}{|}_{t=\mathrm{0}}=-J_{\mathrm{0}}{\displaystyle \frac{K_{\mathrm{1}}}{K_{\mathrm{0}}}}{\displaystyle \frac{C_{\mathrm{0}}}{H_{\mathrm{0}}}}.\end{array}$$

Similar to the elevation change, J₀ is inversely proportional to the initial glacier acceleration. If two glacier beds are lubricated with the same amount of $K_{\mathrm{1}}/K_{\mathrm{0}}$, the glacier with a higher absolute value of J₀ (i.e., $\left|J_{\mathrm{0}}\right|$) will be more unstable as the initial speed and elevation change rates are higher.

Also, from Eq. (9) we can predict a subsequent elevation change after t=0. At this point, the last three terms in Eq. (6) begin to take part in the elevation change rate. The second term of Eq. (6) represents an exponential decay of the change rate, and the third and the fourth terms indicate advective and diffusive migration of elevation perturbation, respectively. The coefficients of the latter two terms determine the relative strength between advection and diffusion, with the ratio defined as the Péclet number, Pe:

$$\begin{array}{}\text{(14)}& \mathit{Pe}={\displaystyle \frac{C_{\mathrm{0}}-D_{\mathrm{0}}^{\prime }}{D_{\mathrm{0}}}}\mathrm{\ell },\end{array}$$

where ℓ is the length of a perturbation. If Pe is much higher than 0, forward advection will dominate, and any perturbation of ice thickness will only propagate downstream. This prohibits destabilization in the upper stream if thinning or glacier retreat initiates near the terminus. On the other hand, if Pe∼0 or is negative, either diffusion or backward advection takes place, and a thickness perturbation at the terminus can propagate upstream, changing the dynamics of the entire glacier. Hence, we consider a glacier with a low Pe more vulnerable than one with a high Pe.

Combining Eqs. (1), (2), (7), and (8) with Eq. (14), we can express Pe in terms of ice speed, elevation, and surface slope (see Sect. S4 of Zheng et al., 2019, Eqs. 11 to 16 for derivation details):

$$\begin{array}{}\text{(15)}& \mathit{Pe}=[{\displaystyle \frac{(m+\mathrm{1}){\mathit{\alpha }}_{\mathrm{0}}}{m{H}_{\mathrm{0}}}}-{\displaystyle \frac{U_{\mathrm{0}}^{\prime }}{U_{\mathrm{0}}}}-{\displaystyle \frac{H_{\mathrm{0}}^{\prime }}{H_{\mathrm{0}}}}+{\displaystyle \frac{{\mathit{\alpha }}_{\mathrm{0}}^{\prime }}{{\mathit{\alpha }}_{\mathrm{0}}}}]\mathrm{\ell }.\end{array}$$

The final assumption we adopt in the model is ${\mathit{\alpha }}_{\mathrm{0}}^{\prime }=\frac{\partial {\mathit{\alpha }}_{\mathrm{0}}}{\partial x}\approx \mathrm{0}$ as the estimated value from the data we use in this paper is essentially small. For example, ${\mathit{\alpha }}_{\mathrm{0}}^{\prime }$ of the glacier profile shown in Fig. 3 is only around 10⁻⁶–10⁻⁷ m⁻¹ for the first 100 km, and the last term in Eq. (15) is roughly an order less than the sum of the first three terms. In practice, this assumption might be necessary because ${\mathit{\alpha }}_{\mathrm{0}}^{\prime }$ is highly sensitive to local slope change and may not reflect the glacier's overall mechanism to dissipate the perturbation. With this assumption, Eq. (15) can be reduced to:

$$\begin{array}{}\text{(16)}& {\displaystyle \frac{\mathit{Pe}}{\mathrm{\ell }}}\approx \left[{\displaystyle \frac{(m+\mathrm{1}){\mathit{\alpha }}_{\mathrm{0}}}{m{H}_{\mathrm{0}}}}-{\displaystyle \frac{U_{\mathrm{0}}^{\prime }}{U_{\mathrm{0}}}}-{\displaystyle \frac{H_{\mathrm{0}}^{\prime }}{H_{\mathrm{0}}}}\right].\end{array}$$

Note we now express the Péclet number as the form of $\frac{\mathit{Pe}}{\mathrm{\ell }}$ as we do not focus on a particular perturbation length and instead plan to evaluate the general tendency for the ice flow to dissipate any length of perturbations. Compared with the past models, the expression of Pe in this model has an additional term $\frac{U_{\mathrm{0}}^{\prime }}{U_{\mathrm{0}}}$, implying its relationship to spatially changing basal conditions. This extra dependency on glacier speed also suggests that Pe is a changing variable and needs to be re-calculated if ice flow speeds up or slows down (see Discussion for more details).

With the same assumption about ${\mathit{\alpha }}_{\mathrm{0}}^{\prime }$, the expression of J₀ (Eq. 10) can be also reduced to:

$$\begin{array}{}\text{(17)}& J_{\mathrm{0}}\approx C_{\mathrm{0}}{H}_{\mathrm{0}}^{\prime }=(m+\mathrm{1})U_{\mathrm{0}}{H}_{\mathrm{0}}^{\prime },\end{array}$$

which is proportional to the product of ice speed and the gradient of ice thickness along the flowline. A typical glacier thins toward the terminus, corresponding to a negative $H_{\mathrm{0}}^{\prime }$ and J₀. According to Eq. (13), a negative J₀ suggests that when a lubricating scenario takes place, the glacier might speed up to accommodate the change. From Eq. (9) we can see that the glacier will also get thickened (except at the divide) as thicker ice is sliding and replaces thinner ice downstream.

To summarize, two parameters Pe and J₀ are derived from the 1D basal lubrication model. J₀ represents the strength of initial response to basal lubrication, and Pe gives insights into the mode of mass transport after elevation change occurs. Glaciers with a high $\left|J_{\mathrm{0}}\right|$ and a low Pe (∼0 or negative) are more vulnerable to basal lubrication as reduced friction can lead to a high initial acceleration and elevation change rate, which will then propagate to the entire glacier via diffusion or negative advection.

3 Data and methods for validating the model

To test if the model is suitable for evaluating marine-terminating glaciers, we derive observed $\mathit{Pe}/\mathrm{\ell }$ and J₀ for outlet glaciers in the GrIS and Austfonna ice cap, Svalbard. These two regions are selected primarily because surface elevation, bed elevation, and glacier speed data necessary for our calculation are publicly available. We compare the results with the NASA MEaSUREs ITS_LIVE glacier velocity (Gardner et al., 2018, 2019) and frontal retreat records (Wood et al., 2021) spanning over 20 years and determine if both $\mathit{Pe}/\mathrm{\ell }$ and J₀ are indicative of the vulnerability to basal lubrication.

3.1 Greenland ice sheet

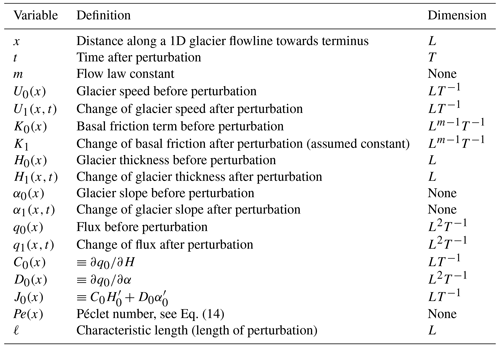
We use the data set published with Felikson et al. (2021), which provides well-constrained flowline data for Greenland's 141 marine-terminating glaciers and their branches (187 basins in total, Fig. 1). These glaciers scatter around the ice sheet and provide a diverse sampling over various climate and oceanic factors. The data set contains six primary flowline shapes for each glacier basin, with vertices sampled every 50 m along the flowlines. We use surface elevations at each vertex, sampled from the Greenland Ice Mapping Project (GIMP, Howat et al., 2014). The GIMP surface elevations come from multiple remote sensing sources and are coregistered with elevations acquired by the Ice, Cloud, and land Elevation Satellite (ICESat), thus best representing the ice sheet elevations during 2003–2009. The flowline vertices also contain the glacier bed elevations, sampled from the BedMachine v3 subglacial topography (Morlighem et al., 2017). Although BedMachine v3 uses the source data collected from 1993 to 2016, we assume that the bed elevations are stable over time and can represent any year in that period. To acquire U₀ and glacier speed change at each flowline vertex, we manually sample the annually mosaicked ITS_LIVE glacier speed data from 1998 and 2018, respectively. The ITS_LIVE data are derived from Landsat 4, 5, 7, and 8 images using the autoRIFT feature tracking software (Gardner et al., 2018; Lei et al., 2021). Finally, each vertex of a flowline has the following key parameters: surface elevation, bed elevation, glacier speed in 1998, and speed difference between 1998 and 2018.

We prepare and process the input data for each flowline using the following steps:

1. As the 1998 speed data do not cover the entire ice sheet, we remove flowlines with only 20 speed readings or less from the input list.

2. Locate vertices with NoData speed values along the flowlines and perform a linear interpolation to fill the missing values. We do not extrapolate the glacier speed; therefore, the NoData vertices at both ends of the flowline are still preserved after this step.

3. Remove flowlines with only 280 valid vertices or less from the input list. A valid vertex should contain all key parameters and no NoData Values.

4. To avoid the effect of small sloping change, we smooth the surface elevation, bed elevation, glacier speed data, and their derivatives using the Savitzky–Golay filter with a window size of 251 vertices (12.5 km) (Savitzky and Golay, 1964; Felikson et al., 2021). We do not apply the smoothing filter to data 0–3 km from the terminus owing to insufficient sampling points within the window size. These unfiltered data will not be used for the next step.

5. Derive $\mathit{Pe}/\mathrm{\ell }$ and J₀ along each flowline using Eqs. (17), (16), and parameters representative of the glacier geometry/speed from 1998. As we empirically derive $\mathit{Pe}/\mathrm{\ell }$ and J₀ for each basin and compare them on the same plot, the results will be insensitive to the selected value of m and the sliding law (Felikson et al., 2021).

6. We also need to include glacier retreat in our analysis to better distinguish the relationship between basal lubrication and speedups. Thus, we use the Greenland Marine-Terminating Glacier Retreat Data (Wood et al., 2021), which contain temporal evolution of terminus positions derived from Landsat 5, 7, and 8 images for 226 glaciers. We use QGIS to manually measure the terminus retreat between 1988 and 2018 for each glacier at its center flowline.

7. Compare $\mathit{Pe}/\mathrm{\ell }$ and J₀ with the frontal retreat and the speed change between 1998 and 2018.

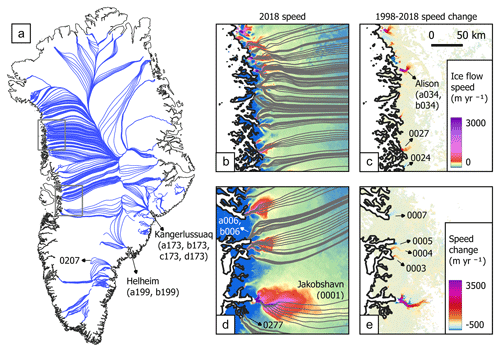
Figure 1 Greenland glacier flowlines used in this study. (a) Location of all selected flowlines from 104 outlet glaciers or glacier branches. Gray boxes indicate map locations for panels (b)–(e). (b, c) The closer view of the flowline distribution, speed from 2018, and speed change during 1998 and 2018 at NW Greenland, a place with the most flowlines across the ice sheet. (d, e) Same panels as (b) and (c) but for W Greenland where Jakobshavn Isbræ is located in the bottom. The glacier speeds from 1998 and 2018 are both sampled from the ITS_LIVE data set. Major glaciers and most glaciers in the zoom-in panels are labeled with names and IDs used in the source data set. Panels (b)–(e) share the scale bar illustrated in panel (c).

3.2 Austfonna ice cap, Svalbard

We perform the same analysis for the marine-terminating glaciers of Austfonna, a polythermal ice cap located in NE Svalbard. Austfonna is only about 100 km wide and is considered to have a more uniform climate and oceanic factors than the GrIS, but its marine outlet glaciers have exhibited diverse speed histories in the past 20 years (Fig. 2). For instance, the glacier speed of basin-3 (Storisstraumen) increased 45-fold during the past two decades, likely triggered by feedback between summer melt, crevasse formation, and basal lubrication (McMillan et al., 2014; Dunse et al., 2015; Gong et al., 2018). The other surge-type glaciers include basin-1 (Bråsvellbreen) and basin-17 (Etonbreen), and the last surge periods of both glaciers are around 1938 (Schytt, 1969; Hagen et al., 1993; Dowdeswell et al., 2008). The other glaciers of Austfonna do not have a surge history, but many of them (e.g., basin-2, -5, -7, and -10) have also significantly increased the flow speed since 1996, as seen from Fig. 2.

To calculate $\mathit{Pe}/\mathrm{\ell }$ and J₀, we use the Ice Thickness Models Intercomparison eXperiment (ITMIX) data set (Farinotti et al., 2017), hosted by the International Association of Cryospheric Sciences (IACS). We use the Austfonna DEM from 1996 (Moholdt and Kääb, 2012), velocity from 1995–1996 (Dowdeswell et al., 2008), and ice thickness from 1996 (Dowdeswell et al., 1986; Farinotti et al., 2017), all included in the ITMIX data set. Eight out of 11 marine-terminated glaciers (basin-1, -3, -4, -5, -6, -7, -10, and -17; Fig. 2) are selected for the analysis; the exceptions are basin-2, -8, and -9 owing to their small length roughly equal to the smoothing window. We construct six glacier flowlines based on the 2018 glacier velocity from the ITS_LIVE annual velocity mosaics (Fig. 2b) and sample ITMIX glacier elevation, ice thickness, and glacier speed data every 50 m along each flowline. Then we follow the same workflow for the outlet glaciers in GrIS (see the previous section) and finally compare $\mathit{Pe}/\mathrm{\ell }$ and J₀ with the ITS_LIVE 2018 glacier speeds.

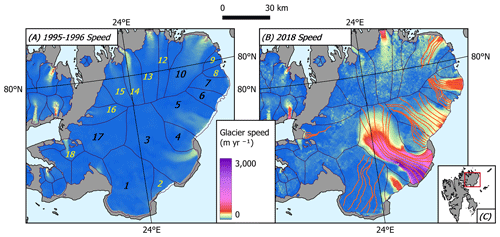
Figure 2 Austfonna ice cap, Svalbard, and glacier flowlines. (a) ITMIX glacier speed in 1995–1996. Each glacier basin is labeled with a number as per Dowdeswell et al. (2008), and glaciers with black numbers are analyzed in this study. (b) ITS_LIVE mosaicked glacier speed in 2018. For each selected basin, we generate six flowlines and plot them on the map as red lines. Glacier outlines are from the Randolph Glacier Inventory (RGI) version 6.0 (RGI Consortium, 2017). (c) Map of Svalbard, Norway; the red box highlights the location of the Austfonna ice cap. Panels (a) and (b) share the scale bar at the top of the figure.

4 Results

4.1 Variation within a single basin

Figures 3 and 4 provide example results within a single basin, showing both input data and the values of $\mathit{Pe}/\mathrm{\ell }$ and J₀ along six major flowlines. The average frontal speed at Glacier 0001 (Jakobshavn Isbræ; 69.18^∘ N, 49.76^∘ W, Figs. 1 and 3) has changed from ∼4000 to ∼7000 m yr⁻¹ during the studied period, suggesting a destabilized status. The value of $\mathit{Pe}/\mathrm{\ell }$ of individual flowlines ranges within $\pm \mathrm{2}\times {\mathrm{10}}^{-\mathrm{4}}$ m⁻¹ for the first 20 km from the terminus, but the average value is more constrained roughly between $-\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ and $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{5}}$ m⁻¹ for the first 10 km. Compared with $\mathit{Pe}/\mathrm{\ell }$, J₀ changes more quickly throughout the first 20 km, from about −1000 to 170 m yr⁻¹. If we plot J₀ versus $\mathit{Pe}/\mathrm{\ell }$ (Fig. 3f) along the first 10 km from the terminus, the average values will roughly form a line going from lower right to upper left in the figure.

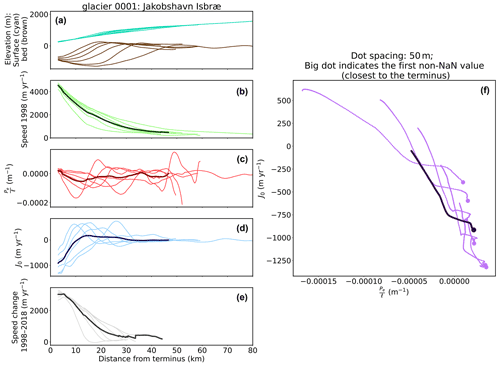
Figure 3 Example results from glacier 0001 (Jakobshavn Isbræ, 69.18^∘ N, 49.76^∘ W). (a) Surface elevation (cyan) and bed elevation (brown). (b) Surface speed in 1998. (c) $\mathit{Pe}/\mathrm{\ell }$. (d) J₀. (e) Speed change between 1998 and 2018. These plots show all six flowline profiles from a single basin in respect of the distance from the glacier terminus. The thick lines represent the average of these flowlines. (f) J₀ versus $\mathit{Pe}/\mathrm{\ell }$ along the first 10 km from the terminus. The big dots represent values at 3 km or the valid values closest to the terminus, and the small dots are plotted every 50 m along the flowline.

On the other hand, glacier 0277 (Alangordliup Sermia, 68.95^∘ N, 50.22^∘ W, ∼30 km south of Jakobshavn Isbræ; Figs. 1 and 4) is more stable than glacier 0001 as the amount of the speed change in the past two decades is only 0–40 m yr⁻¹ and is constrained at the first 6 km from the terminus. $\mathit{Pe}/\mathrm{\ell }$ ranges from $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{4}}$ to $\mathrm{6}\times {\mathrm{10}}^{-\mathrm{4}}$ m⁻¹ within the first 10 km, which is roughly 10 times the values from Jakobshavn Isbræ. Also, the slow glacier speed in 1998 directly results in low $\left|J_{\mathrm{0}}\right|$ (only $\sim -\mathrm{10}$ m yr⁻¹) compared with Jakobshavn Isbræ. These results are supportive for glacier 0277 having a stable condition during the study period. Interestingly, the speed change pattern resembles $\mathit{Pe}/\mathrm{\ell }$ at the first 10 km. The glacier might have dealt with frontal or basal perturbation through advection, as indicated by a large Pe.

Figure 4 Example results from glacier 0277 (Alangordliup Sermia, 68.95^∘ N, 50.22^∘ W). See Fig. 1 for geographical location and Fig. 3 for a detailed description of each panel.

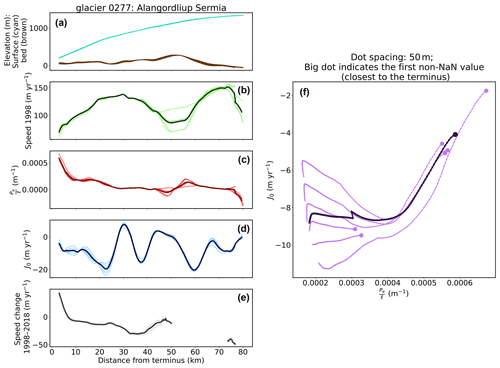
The results of the other GrIS and Austfonna glaciers are available in Github-Zenodo (https://doi.org/10.5281/zenodo.5641953).

4.2 Pe & J₀ versus glacier speed change

This study focuses on the parameter variations close to the glacier terminus for two reasons. First, crevasses and moulins are more likely to form at the terminus region via hydrofracture than at higher elevations (Poinar et al., 2015). Therefore, additional meltwater routing can alter the basal conditions over multiple years. In addition, the J₀ tends to be small for the upper regions of all glaciers where the ice flow is slow, making this metric less distinctive from one basin to another. Considering the limit of spatial smoothing in the processing workflow (see Sect. 3.1, step 4), we select the data at 3 km from the terminus for the following intercomparison. Owing to the incomplete spatial coverage of ITS_LIVE data from 1998, only 104 out of 187 GrIS glacier basins have valid values of $\mathit{Pe}/\mathrm{\ell }$ and J₀ at this terminus distance (Fig. 1).

Although most of these glaciers have sped up during the 20 years, 26 glaciers slowed down by up to −522 m yr⁻¹ (Fig. 5a). To illustrate $\mathit{Pe}/\mathrm{\ell }$ and J₀ at the glacier front and their varying direction along the flowline, we plot J₀ versus $\mathit{Pe}/\mathrm{\ell }$ using ball-head-pin-like curves. Each curve represents the average J₀ and $\mathit{Pe}/\mathrm{\ell }$ values of one glacier basin at 3–5 km with the head mark located at 3 km, color-coded based on the speed change at 3 km as well (Fig. 5b). Glaciers with low speed change (pale color curves) tend to cluster around the area where J₀≈0 m yr⁻¹ and $\mathit{Pe}/\mathrm{\ell }>\mathrm{0.0001}$ m⁻¹. Most of these curves are near horizontal on the plot, indicating a small change of J₀ and a large change of $\mathit{Pe}/\mathrm{\ell }$ at the glacier front. On the other hand, glaciers with high speed change (warm- or cold-color curves, including accelerated and decelerated glaciers) seem to cluster together in a different area where J₀ is much more negative and $\mathit{Pe}/\mathrm{\ell }\approx \mathrm{0}$ m⁻¹. These curves generally show a vertical orientation indicating changing J₀ and constant low $\mathit{Pe}/\mathrm{\ell }$ along the glacier flowline.

To further illustrate the clustering trend, we arbitrarily select a speed change threshold of ±300 m yr⁻¹ and classify the glaciers based on their speed change at 3 km. The threshold value is determined in order to give each classification roughly the same number of samples. Note that glaciers with significant slowdown or speedup are classified into the same group because a glacier vulnerable to basal lubrication would also be sensitive to recovering basal conditions from a lubrication event. Fifty-four glaciers have an absolute value of speed change ≥300 m yr⁻¹, and the other 50 glaciers are considered more stable with an absolute value of speed change <300 m yr⁻¹. We plot J₀ against $\mathit{Pe}/\mathrm{\ell }$ using the values from 3 km as well as the Gaussian kernel density estimates of each classification for both J₀ and $\mathit{Pe}/\mathrm{\ell }$. The results using all glaciers (Fig. 6a) indicate that two classifications have a slightly different distribution for J₀ and $\mathit{Pe}/\mathrm{\ell }$. The unstable glaciers (red group) have J₀ and $\mathit{Pe}/\mathrm{\ell }$ distributions peaked at $\sim -\mathrm{200}$ m yr⁻¹ and ∼0.00003 m⁻¹ respectively, whereas the peaks of stable glaciers (blue group) shift to higher values to $\sim -\mathrm{50}$ m yr⁻¹ for J₀ and ∼0.00013 m⁻¹ for $\mathit{Pe}/\mathrm{\ell }$. Despite the peak shift being small compared with the distributions themselves, the difference is statistically significant found by the Kolmogorov–Smirnov statistic (p=0.003 and 0.006 for J₀ and $\mathit{Pe}/\mathrm{\ell }$, respectively; see the Fig. 6 Jupyter Book page for details). As the major cause of glacier speedups has been attributed to terminus retreat (King et al., 2020), we further group the glaciers by the distance of terminus retreat. Figure 6b plots only the glaciers with a retreat larger than 0.5 km, and the separation between two glacier groups in terms of J₀ and $\mathit{Pe}/\mathrm{\ell }$ becomes much less significant (p=0.366 and 0.050 respectively). On the other hand, Fig. 6c shows the J₀ and $\mathit{Pe}/\mathrm{\ell }$ distributions for glaciers with a retreat ≤0.5 km. Only seven glaciers with little or no retreat have accelerated over 300 m yr⁻¹, which might not be enough to determine the significance of separation for $\mathit{Pe}/\mathrm{\ell }$ (p=0.255). However, it is clear to see two groups divided by the value of J₀ in the plot ($p=\mathrm{2}\times {\mathrm{10}}^{-\mathrm{5}}$).

Among all the glacier outlets, glacier 0207 (65.17^∘ N, 41.16^∘ W; Fig. 1a) seems to be unusual as it is the only one with J₀ over 100 m yr⁻¹ (Fig. 5b). A positive J₀ requires a decreasing ice thickness from terminus to upstream (Eq. 17), which seems to indicate a steeper bed than the glacier surface. In our analysis, glacier 0207 is considered an example with large $\left|J_{\mathrm{0}}\right|$, despite having a different sign than the other glaciers. However, additional data from more glaciers would be required to fully characterize the glaciers with positive J₀ and their sensitivity to basal lubrication.

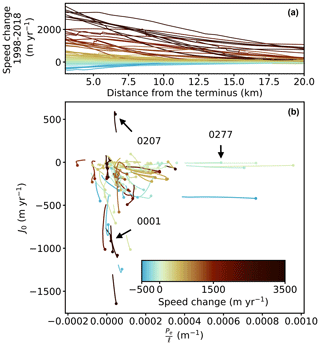
Figure 5 (a) Speed change along Greenland glacier flowlines within the first 20 km from the terminus. Each line represents the average value of a single glacier basin and is color coded based on the speed change value at 3 km (the first valid data point after the Savitzky–Golay filter is applied). (b) The average J₀ versus $\mathit{Pe}/\mathrm{\ell }$ at 3–5 km from the terminus. The value at 3 km is marked with a big dot. Each line uses the same color code from (a). The glacier basins presented in Figs. 3 (0001) and 4 (0277), as well as one extra glacier basin (0207) are annotated.

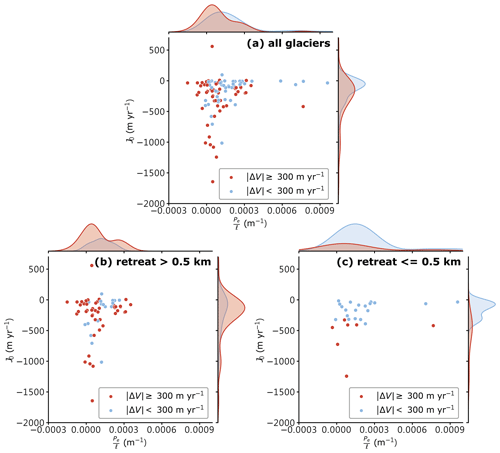
Figure 6 Distribution of J₀ and $\mathit{Pe}/\mathrm{\ell }$ for (a) The Greenland ice sheet's 104 glacier basins analyzed in this study; (b) a subset of panel (a) including only basins with a frontal retreat >0.5 km during 1998–2018; (c) a subset of panel (a) including only basins with a frontal retreat ≤0.5 km during 1998–2018. These plots are similar to Fig. 5b but only show the values at 3 km from the terminus. Each mark is classified based on the 300 m yr⁻¹ threshold of speed change. The joint plots show the Gaussian kernel density estimate along both axes for each class.

We adopt the same method from Fig. 5 to plot the results from eight marine-terminating glaciers in Austfonna (Fig. 7). As all glaciers have accelerated at the terminus for the past two decades, we adjust the color code so that blue represents low change and other colors represent high change. For basin-3 and -5, there are no valid measurements at 3 km, and we only mark the first valid measurements from 7.3 and 6.7 km, respectively, as single points on the plot. Similar to the GrIS, glaciers with higher speed change (basin-3, -5, -7, and -10) roughly occupy the lower left side of the panel where $\mathit{Pe}/\mathrm{\ell }$ and J₀ are small or more negative, and glaciers with lower speed change (basin-1, -4, -6, and -17) fall on a different corner, where $\mathit{Pe}/\mathrm{\ell }$ and J₀ are larger. However, $\left|J_{\mathrm{0}}\right|$ of all eight glaciers have values between 0 and 10 m yr⁻¹, much lower than those from the GrIS (see Fig. 5, where $\left|J_{\mathrm{0}}\right|$ ranges from 0 to over 1500 m yr⁻¹). This is because all eight glaciers are slowly moving in 1996, resulting in a low $\left|J_{\mathrm{0}}\right|$ according to Eq. (17). It is also interesting that basin-1 (Bråsvellbreen) and basin-5 have similar J₀ versus $\mathit{Pe}/\mathrm{\ell }$, but basin-5 has a speed change roughly ten times greater than basin-1. Since basin-1 had a surge record back in 1936–1938 (Schytt, 1969) and is currently in the quiescent stage, its low J₀ and $\mathit{Pe}/\mathrm{\ell }$ values might indicate a future instability when a surge is triggered internally or externally.

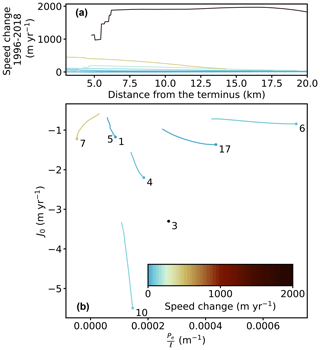
Figure 7 (a) Speed change along Austfonna glacier flowlines within the first 20 km from the terminus. Each line represents the average value of a single glacier basin and is color coded based on the speed change value at 3 km. (b) The average J₀ versus $\mathit{Pe}/\mathrm{\ell }$ at 3–5 km from the terminus. The value at 3 km is marked with a big dot. Each line uses the same color code from (a) and is labeled by the glacier number (see Fig. 2). Note that for basin-3 and -5, there is no valid measurement at 3 km, and only the first valid measurements (at 7.3 and 6.7 km respectively) are plotted.

5 Discussion

5.1 Separation of glacier groups on the J₀ versus $\mathit{Pe}/\mathrm{\ell }$ plot

For the GrIS, the J₀ versus $\mathit{Pe}/\mathrm{\ell }$ plots (Figs. 5–6) seem to capture the characteristics of glaciers vulnerable to basal lubrication. GrIS glaciers with more negative J₀ and $\mathit{Pe}/\mathrm{\ell }$ in 1996–1998 are more likely to speed up in the next 20 years. This tendency is not obvious for glaciers with a significant retreat (Fig. 6b), possibly because instead of changing basal conditions, it is the retreat dominating the flow dynamics of these glaciers. Nevertheless, the separation of peaks at different $\mathit{Pe}/\mathrm{\ell }$ values suggests that the diffusive strength of ice flow might still play a major role in the decades-long speed changes. For glaciers with a more stable terminus position, the clear separation of J₀ (Fig. 6c) supports basal lubrication as a primary cause of glacier speedups and likely highlights the importance of the initial response to changing basal conditions. Even if a glacier has a low P₀ and allows diffusion-dominating dynamics, a small $\left|J_{\mathrm{0}}\right|$ prohibits much elevation and speed change under a lubrication scenario (Eq. 9).

The other factor that might affect the tendency of $\mathit{Pe}/\mathrm{\ell }$ and $\left|J_{\mathrm{0}}\right|$ we see in Fig. 6 is whether the basal lubrication takes place within the study period. Although melt-induced speedups are common for GrIS glaciers (e.g., van de Wal et al., 2008; Bartholomew et al., 2010; Kehrl et al., 2017; Rathmann et al., 2017; Seddik et al., 2019), not all 104 glacier basins analyzed here have been studied well enough to identify when and where a glacier responds to changing basal conditions. A glacier with low $\mathit{Pe}/\mathrm{\ell }$ and high $\left|J_{\mathrm{0}}\right|$ can remain stable if no basal lubrication has taken place in the past decades, mixing up the distributions in Fig. 6. Also, the $\mathit{Pe}/\mathrm{\ell }$ and $\left|J_{\mathrm{0}}\right|$ patterns at the glacier front may not represent the entire glacier length. If moulins can form at a higher elevation than previously thought owing to the warming climate and widespread supraglacial lakes (Hoffman et al., 2018), it might be necessary to reassess the $\mathit{Pe}/\mathrm{\ell }$ and $\left|J_{\mathrm{0}}\right|$ patterns within a wider range of flowline distance.

The three surge-type glaciers of Austfonna (basin-1, -3, and -17) do not cluster in Fig. 7. Compared with the other two glaciers, basin-3 has a higher flow speed in 1995–1996, resulting in a slightly more negative J₀. It has had an unusually long surge evolution over two decades as well: the ice flow speed has gradually increased since the mid-1990s (Dowdeswell et al., 2008; McMillan et al., 2014) and reached a peak velocity of ∼6500 m yr⁻¹ in 2013 (Dunse et al., 2015). The sustaining high flow speed has been attributed to meltwater routing through crevasses formed during the speedup (Dunse et al., 2015; Gong et al., 2018). As the additional supply of surface melt can alter the behavior of a surge-type glacier by reaching a steady state balancing mass and enthalpy conservation through thinner and faster-moving ice (Benn et al., 2019), basin-3 may have entered an ice stream-like regime with higher sensitivity to changing basal conditions. This might explain why basin-3 is away from the other two surge-type but currently quiescent glaciers on Fig. 7. Nevertheless, additional analysis and tests will be required before inferring a general vulnerability for surge-type glaciers to basal lubrication.

5.2 Characteristics of glaciers vulnerable to basal lubrication

Both Pe and J₀ depend on the ice thickness and flow speed (Eqs. 16 and 17), but with a different relationship. Assuming a monotonous decrease in glacier thickness toward the terminus (i.e., no overdeepening area), glaciers with thicker ice and a faster flow yield lower Pe and higher $\left|J_{\mathrm{0}}\right|$ and thus are more susceptible to basal lubrication. However, the thickness change along the flowline (H^′) has a competing contribution to Pe and J₀: a greater change (i.e., a more negative H^′) increases both Pe and $\left|J_{\mathrm{0}}\right|$. Glaciers with a very negative H^′ may not likely be activated through intense diffusion (which is also suggested to be true for a terminus perturbation scenario in Felikson et al., 2021), but a collapse-like destabilization is still possible at the terminus or a localized region along the glacier owing to its high $\left|J_{\mathrm{0}}\right|$. For a glacier with an overdeepening zone, increased ice thickness again lowers Pe and raises $\left|J_{\mathrm{0}}\right|$, making the glacier more vulnerable to basal lubrication at the overdeepened area.

Despite having an additional associating factor J₀ in the model, inferences made to the Péclet number in this study is similar to the previous models based on the perturbation theory. A low or negative Pe allows an ocean-induced terminus perturbation to propagate to a certain inland distance where Pe becomes larger (Felikson et al., 2017, 2021). For an outlet glacier in the GrIS, it is probably common to have terminal perturbation and changing basal conditions in effect at the same time (as indicated by Jakobshavn Isbræ for example; Joughin et al., 2008; Khazendar et al., 2019; Riel et al., 2021). In this case, Pe reflects a general vulnerability to elevation perturbations and is indistinguishable from the source forcing. On the other hand, J₀ as a new term in the lubrication-induced perturbation model seems to be exclusively related to the basal sensitivity as indicated by Fig. 6b and c. Nevertheless, J₀ might still be a key factor for a glacier only subject to the ocean–ice interaction. As warm subsurface water-induced thinning debuttresses the glacier front and increases the longitudinal stretching and glacier speed (Holland et al., 2008), new crevasses can provide additional routes for surface melt accessing and lubricating the bed (Gagliardini and Werder, 2018; Gong et al., 2018). The investigation for surface strain rates indicates that these new crevasses can propagate to up to 1600 m high, corresponding to ∼50 km away from the terminus for GrIS outlet glaciers (Poinar et al., 2015). Thus, J₀ can be used to evaluate the latter mechanism's impact, specifically for subsequent ice flow acceleration or the feedback to additional thinning. This oceanic forcing-induced basal lubrication seems to be important for marine-terminating glaciers to switch to and maintain a fast flow over the years.

Our model does not consider the melt production from strain heating or geothermal heating at the bed. If included, induced glacier speedup owing to basal lubrication can generate energy to melt basal ice (Strozzi et al., 2017b), further increasing K₁ and leading to a higher glacier speed and thinning rate than what Eqs. (6) and (12) indicate.

5.3 Feedback from basal lubrication

One implication from the lubrication-induced perturbation model is that both Pe and J₀ are temporally changing variables. As glacier speed increases due to basal lubrication, Pe will be closer to zero, and $\left|J_{\mathrm{0}}\right|$ will become larger, making the glacier more sensitive to any following change in basal conditions. A potential example to illustrate this feedback is the Vavilov ice cap, Severnaya Zemlya, Russia. The western marine outlet of this ice cap was moving at less than 1 km yr⁻¹ with no apparent summer speedups just before a surge-like collapse took place (Willis et al., 2018). The collapse initiated when the terminus advanced into weak marine sediments, bringing the glacier speed to a maximum of ∼9 km yr⁻¹ in summer 2015, and then the ice flow started to slow down but with a significant seasonal variation (Willis et al., 2018; Zheng et al., 2019). During the collapse, the Péclet number at the thinning center reduced by at least 40 %, suggesting a shift to an ice stream-like dynamic regime more susceptible to basal lubrication (Zheng et al., 2019). However, this transition is not necessarily irreversible as the bed would also be sensitive to a refreezing or efficient draining event, increasing Pe and decreasing $\left|J_{\mathrm{0}}\right|$ back to the pre-perturbation level. Such a cycle is probably happening on a yearly basis as many GrIS glaciers have seasonal speedups closely bonded to summer melt (e.g., Palmer et al., 2011; Sundal et al., 2013; Rathmann et al., 2017). Still, for a multi-year destabilization like Vavilov, it is uncertain whether such a shutdown can completely revert the glacier dynamics because the ice thickness, another critical parameter controlling Pe and J₀ in our model, has changed a great deal during the collapse as well.

As noted in the case of Vavilov, dynamic thinning caused by the lubricated bed can also consequently change the dynamic regime and create another feedback loop. Thinning would decrease the ice thickness and increase the surface slope, potentially raising Pe and $\left|J_{\mathrm{0}}\right|$. Unlike the acceleration feedback from the previous paragraph, this feedback circle seems to be milder as a glacier would gradually switch to advection and prevent further inland thinning. However, dynamic thinning may also contribute to glacier retreat (Thomas and Bentley, 1978; Wood et al., 2021) and the subsequent debuttressing and speedup events. The net effect for dynamic thinning to glacier vulnerability to basal conditions remains ambiguous based on this view and suggests a future research topic as dynamic discharge in GrIS will likely continue to contribute significant ice loss in the near future (Mouginot et al., 2019; Choi et al., 2021).

6 Conclusions

Based on the new lubrication-induced 1D perturbation model, we show that a lubricated bed can initiate a thinning perturbation and destabilize the entire glacier if a particular combination of glacier thickness, thickness gradient, and flow speed is met. The model identifies two controlling physical quantities $\mathit{Pe}/\mathrm{\ell }$ (the Péclet number divided by the characteristic length) and J₀ (essentially the product of glacier speed and thickness gradient). We use observational data from 1996–1998 and derive these numbers for 104 and 8 marine-terminating glaciers in the GrIS and the Austfonna ice cap, Svalbard respectively. The results show that $\mathit{Pe}/\mathrm{\ell }$ and J₀ correlate with the flow speed change during 1996/1998 and 2018, especially for nonsurge glaciers and glaciers without significant terminus retreat, matching the model prediction. Glaciers with thick ice and a fast flow result in low Pe and negative J₀, and reduced basal friction leads to initial speedup and thinning, which can propagate further inland via diffusion. For glaciers in the GrIS subject to ocean–ice interactions, this new model indicates multiple feedback cycles that make glaciers more sensitive to changing basal conditions. Finally, this study highlights glaciers classified as vulnerable to lubricated beds (low Pe and high $\left|J_{\mathrm{0}}\right|$) but with no significant speed change during the past two decades. Frequent monitoring is suggested for these glaciers because they might be more prone to future instabilities and affect the projected sea level rise.