Brief communication: Evaluation of multiple density-dependent empirical snow conductivity relationships in East Antarctica

Nine density-dependent empirical thermal conductivity relationships for firn were compared against data from three automatic weather stations at climatically different sites in East Antarctica (Dome A, Eagle, and LGB69). The empirical relationships were validated using a vertical, 1D thermal diffusion model and a phase-change-based firn diffusivity estimation method. The best relationships for the abovementioned sites were identified by comparing the modeled and observed firn temperature at a depth of 1 and 3 m, and from the mean heat conductivities over two depth intervals (1–3 and 3–10 m). Among the nine relationships, that proposed by Calonne et al. (2011) appeared to show the best performance. The density- and temperature-dependent relationship given in Calonne et al. (2019) does not show clear superiority over other density-dependent relationships. This study provides a useful reference for firn thermal conductivity parameterizations in land modeling or snow–air interaction studies on the Antarctica ice sheet.

1 Introduction

In the Earth's climate system, snow cover has two important physical properties, its high albedo and its low thermal conductivity. Both properties modulate heat exchange between the atmosphere and the surface (Dutra et al., 2010). Heat transport in the near-surface snow layer plays a key role in controlling the upper thermal boundary condition of ice sheets (Ding et al., 2020).

Snow is a porous and inhomogeneous material with thermal conductivity that can be anisotropic and depends on the microstructure of snow, including factors such as the proportion of air and ice, grain shape, grain size, and bond size (Riche and Schneebeli, 2013). Direct measurements of snow heat conductivity can be made with a needle probe, heated plate, and tomographic 3D images (e.g., Sturm et al., 1997; Calonne et al., 2011), all of which require intensive work. Alternative approaches include Fourier analysis methods that can estimate thermal diffusivity and reconstruct snow thermal histories from temperature measurements (Oldroyd et al., 2013), considering that the bulk/apparent heat diffusivity can be more effectively described than the whole physical process of snow metamorphism, as also assumed by needle probe measurement studies (Calonne et al., 2011). Similarly, the spatially averaged thermal diffusivity can be estimated from the changes in amplitude and phase of a temperature cycle with depth in the medium (Hurley and Wiltshire, 1993; Oldroyd et al., 2013). The numerical inverse method (optimal control theory) is another possible approach for recovering thermal diffusivity using a least squares method (Sergienko et al., 2008) or a recursive optimization approach (Oldroyd et al., 2013).

These numerical methods, however, need a relatively large number of temperature measurements, which can be difficult for large-scale model studies. Thus, a widely accepted alternative is to use laboratory-determined empirical relationships to approximate the snow diffusivity and/or conductivity as a function of some typical and easily measured snow parameters such as snow density (e.g., Yen, 1981; Sturm et al., 1997; Calonne et al., 2011).

Density-dependent thermal conductivity relationships are widely used in various model studies. For example, the empirical relationship developed by Jordan (1991) was adopted by the CLM land model, the SNTHERM snow model, and many land surface energy balance studies, such as Wang et al. (2017). Lecomte et al. (2013) used the relationships in Yen (1981) and Sturm et al. (1997) for large-scale sea-ice–ocean coupling models. Applying the density-dependent relationship in Calonne et al. (2011), Hills et al. (2018) investigated the heat transfer characteristics in the Greenland ablation zone. Steger et al. (2017) analyzed the melt water retention in the Greenland ice sheet by adopting the snow density–conductivity relationship given in Anderson (1976). Charalampidis (2016) used the relationship in Sturm et al. (1997) to trace the retained meltwater in the accumulation area of the southern Greenland ice sheet. However, none of those relationships have been carefully validated by in situ data in Antarctica ice sheets.

In this paper, firn temperature data and snow density profiles from three sites in East Antarctica were chosen to validate the applicability of these density–conductivity relationships (Table S1). We first describe the meteorological observations. After introducing the method for validating the empirical density–conductivity relationships, we then present the validation results, followed by discussions and conclusions.

2 Site and observational description

Several solar-powered automatic weather stations (AWSs) have been deployed along a traverse route from Zhongshan to Dome A within the cooperative framework between Chinese and Australian Antarctic programs. These include deployments at LGB69 (in January 2002) and at EAGLE and Dome A (in January 2005). For more than 10 years since then, near-hourly meteorological measurements of air and firn temperature (at several heights and depths), relative humidity, wind, and air pressure have been made. The data from the AWSs are collected remotely and relayed by the ARGOS satellite transmission system. Firn temperatures are measured (using FS23D thermistors in a ratiometric circuit with a resolution of 0.02K) at four depths below the surface; these were 0.1, 1, 3, and 10 m when deployed, but they have slowly deepened with time due to snow accumulation. Due to heavy snowfall at LGB69, these data are only available for 2002–2008.

Figure 1 The locations of Dome Argus, Eagle, and LGB69 in Antarctica.

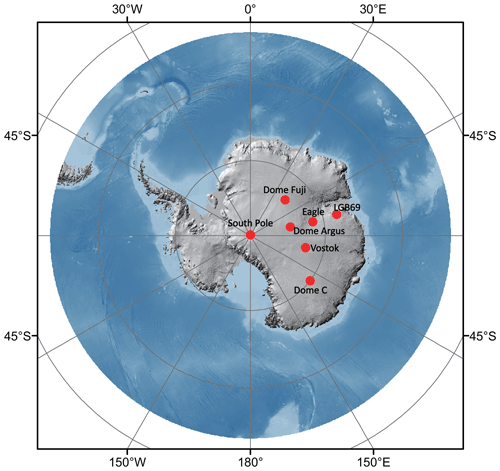
All three sites are located on the western side of the Lambert Glacier basin. LGB69 (70^∘50^′ S, 77^∘04^′ E; 1854 m a.s.l.) is only 192 km from the coast (Fig. 1) and has an annual precipitation of 20 cm w.e. yr⁻¹ (∼50 cm snowfall), strong wind (∼8.5 m s⁻¹ annual), and a mean annual air temperature of approximately −26.10 ^∘C. The snow density increases from ∼400 to 500 kg m⁻³ from the surface to 10 m depth (Fig. S1). EAGLE (76^∘25^′ S; 77^∘01^′ E) is a typical “surface glazed” area with a hard snow crust due to the effect of drift snow. Its snow accumulation is 10 cm w.e. yr⁻¹ (30 cm snowfall), the snow density increases from ∼380 to 550 kg m⁻³ from the surface to 10 m (Fig. S2) depth, and the mean annual air temperature is approximately −40.80 ^∘C. Dome Argus (80^∘22^′ S, 70^∘22^′ E; 4093 m a.s.l.) is the highest point of the east Antarctic ice sheet. It is also the summit of the ice divide of the Lambert Glacier drainage basin, ∼1248 km from the nearest coast, and the surrounding region has a surface slope of only 0.01 % or less. Dome Argus has an extremely low surface air temperature (annual mean of −52.1 ^∘C), specific humidity, and snow accumulation rate (around 2 cm w.e. yr⁻¹), and it experiences no surface melt, even at the peak of summer (Ding et al., 2016). The surface snow is very soft here, and it ranges from ∼270 to 450 kg m⁻³ in the top 10 m (Fig. S3). No radiation measurements were carried out at the site; therefore, it is nearly impossible to build a complete energy balance model at the snow surface of Dome Argus.

3 Methods

3.1 Numerical model method

We validate the heat conductivity by a 1D transient heat diffusion model:

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\partial T}{\partial t}}={\displaystyle \frac{K}{C_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{s}}}}{\displaystyle \frac{{\partial }^{\mathrm{2}}T}{\partial z^{\mathrm{2}}}},\end{array}$$

where T is the firn temperature, K is the heat conductivity, C_s is the heat capacity of snow, ρ_s is the density of snow, and z is the depth below the snow surface. The vertical firn density profiles for three sites are shown in Figs. S1–S3. The heat capacity of snow is estimated by assuming snow is a mixture of air and ice:

$$\begin{array}{}\text{(2)}& C_{\mathrm{s}}=C_{\mathrm{i}}{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{s}}}{{\mathit{\rho }}_{\mathrm{i}}}}+C_{\mathrm{a}}\left(\mathrm{1}-{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{s}}}{{\mathit{\rho }}_{\mathrm{i}}}}\right),\end{array}$$

where C_i and C_a are heat capacity of ice and air, respectively. We constrain the upper and lower model domain using two Dirichlet boundary conditions, the 0.1 and 10 m firn temperatures. The observed and modeled firn temperatures at the depths of 1 and 3 m are then compared over a period of time. The performance of different heat conductivity relationships is then evaluated by the deviation metric of the difference between the modeled and observed temperature data:

$$\begin{array}{}\text{(3)}& {\mathit{\sigma }}^{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{\mathrm{i}}^N(T_{\mathrm{d}}-T_{\mathrm{dm}}),\end{array}$$

where $T_{\mathrm{d}}=\text{abs}(T_{\mathrm{model}}-T_{\mathrm{obs}})$, T_dm is the mean value of T_d, and N is the number of the temperature dataset.

3.2 Temperature phase-change method

In this approach, we approximate the annual temperature cycles as sinusoidal functions (Demetrescu et al., 2007):

$$\begin{array}{}\text{(4)}& T\left(z,t\right)=T_{\mathrm{m}}+A\left(z\right)\sin \left(\mathit{\omega }\cdot t+\mathit{\varphi }\left(z\right)\right),\end{array}$$

where T is the firn temperature expressed as a function of depth z and time t, T_m is the mean annual value of T, A is the amplitude of the annual firn temperature cycle, ω is the frequency of the temperature cycle, and ϕ is the wave phase of the annual cycle.

While it is common to fit a harmonic series (Fourier analysis) rather than a single sine wave to temperature variations, we found that this gave no advantage over Eq. (4) for the data at the three sites because the temperature at the sites shows nonperiodic temperature excursions during the “coreless” Antarctic winter. Assuming the snow is horizontally isotropic, we can estimate the apparent thermal diffusion, k_a, from the changes in phase at different depths:

$$\begin{array}{}\text{(5)}& k_{\mathrm{a}}={\displaystyle \frac{\mathit{\omega }}{\mathrm{2}}}{\displaystyle \frac{{\left(z_{\mathrm{2}}-z_{\mathrm{1}}\right)}^{\mathrm{2}}}{{\left({\mathit{\varphi }}_{\mathrm{1}}-{\mathit{\varphi }}_{\mathrm{2}}\right)}^{\mathrm{2}}}}.\end{array}$$

The conductivity can then be recovered from k_a and the heat capacity of firn.

Table 1 Deviation (σ²) of |T_model−T_obs| (K) for different density-dependent empirical relationships at 1 and 3 m for three stations. The three overall best relationships for different depths are shown using “*”.

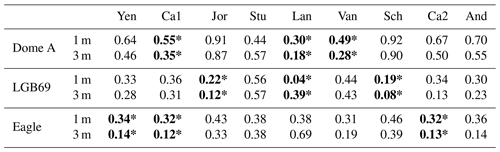
Yen refers to Yen (1981); Ca1 refers to Calonne et al. (2011); Jor refers to Jordan (1991); Stu refers to Sturm et al. (1997); Lan refers to Lange (1985); Van refers to Van Dusen and Washburn (1929); Sch refers to Schwander et al. (1997); Ca2 refers to Calonne et al. (2019); And refers to Anderson (1976).

Figure 2 Comparison of observed and modeled temperatures using different density-dependent conductivity relationships at depths of 1 m (a, c, e) and 3 m (b, d, f) at Dome A (a, b), Eagle (c, d), and LGB69 (e, f).

4 Results and discussions

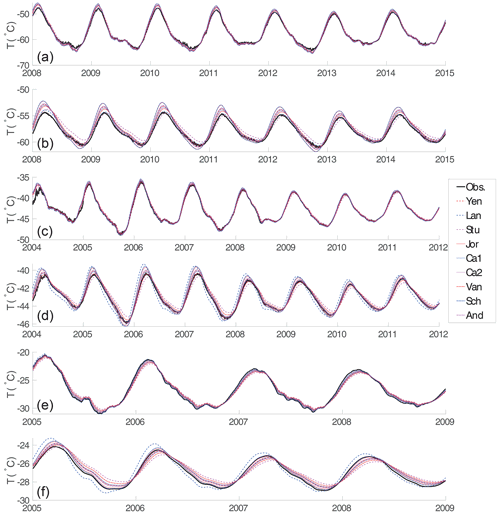
In Figs. S4, S5, and S6, we show the comparisons of observed and modeled firn temperature using nine different density–conductivity relationships at the Dome A, Eagle, and LGB69 AWSs. The deviations of their differences are given in Table 1. At Dome A, the Jor and Sch relationships give us a significant discrepancy between observed and modeled firn temperature (Fig. 2). The modeled firn temperature calculated by the Ca1, Lan, and Van relationships show a closer agreement with the observed firn temperature. The density- and temperature-dependent relationship, Ca2, however, does not appear to have a better performance than its density-dependent version Ca1 at Dome A.

In Fig. 2 and Table 1, we can see that the Lan relationship gives the best performance at the depth of 1 and 3 m at Dome A, followed by the Van and Ca1 relationships. The Lan relationship was derived from in situ snow conductivity measurements on Filchner ice shelf (Lange, 1985). It is the only relationship in this study that is based on in situ firn sample measurements in Antarctica. The Ca1 relationship was derived by analyzing a wide range of different snow samples from a number of different geographical locations with many different snow types (Calonne et al., 2011). The Van relationship is old but is adopted in Cuffey and Paterson (2010) and still shows a nice performance in our model results.

Similarly to the Dome A case, at the Eagle station, the Ca1 relationship outperforms other relationships, followed by the Ca2 and Yen relationships. The Jor, Stu, and Lan relationships, however, appear not to be suitable for parameterizing the firn conductivity, compared with other relationships at the Eagle station. At LGB69, however, the Sch and Jor relationships appear to be superior to other relationships, in contrast to the cases at Dome A. The Jor relationship is based on the experimental measurements in Yen (1962). Sch is also an experimental relationship based on the data given in Mellor (1977). In this case, the Ca2 relationship also gives a smaller temperature difference compared with the Ca1 result. Note that the same relationship may show different performance for different depth ranges. For example, for the Lan relationship, the modeled and observed firn temperature shows very good agreement at a depth of 3 m but has a relatively large discrepancy at a depth of 10 m.

We also estimate the spatially averaged annual mean thermal conductivity from the temperature phase shifts between the depth ranges of 0.1–1, 1–3, and 3–10 m at the Dome A (Fig. S4), Eagle (Fig. S5), and LGB69 (Fig. S6) stations, and we compare them with the mean values corresponding to different density–conductivity relationships (Table S2). The phase at different levels (ϕ_fit) (also the phase shift, Δϕ_fit) is determined from the least squares fit to Eq. (1), and the thermal diffusivity (conductivity) is then calculated using Eq. (5).

Clearly, we can see that there is an increasing trend of conductivity with depth (Table S2). Similar to the case in Table 1, the Ca1 and Ca2 relationships give closer values than the conductivity values recovered from the phase-change method at the three different depth intervals, which is consistent with the comparison results in Table 1. The Lan, Van, and Yen relationships also show closer agreement with the phase-change results. However, we do not see a consistent pattern for the performance of different empirical density–conductivity relationships. At different depth levels, different relationships appear to show varying model performance. This is possibly a result of our assumption that the vertical density profile is kept constant in time and that the heat capacity of firn is a linear relationship of the capacity of air and ice (Eq. 2). In addition, only one relationship is a function of firn temperature (Ca2). As temperature is an important parameter affecting firn heat conductivity (Calonne et al., 2019), considering only density in the other eight relationships may introduce model uncertainties in our evaluation. However, as we consider a long time span of observation and model years (7 years for Dome A, 8 years for Eagle, and 3 years for LGB69), the overall deviation of modeled and observed temperature should be accountable for quantifying the performance of different density-dependent conductivity relationships.

5 Conclusions

In this study, we apply two methods to validate nine different density–conductivity relationships: (1) by applying a 1D vertical heat diffusivity model, we compare the modeled firn temperature at a depth of 1 and 3 m with observations; (2) we compare the mean empirical snow conductivity at three depth intervals (0.1–1, 1–3, and 3–10 m) according to the phase-change-derived temperature variations.

It is found that some empirical density relationships have generally good model performance and agree well with phase-change-recovered conductivity, but they show diverse behaviors at different depth levels. Based on these two methods, we find that the relationship proposed by Calonne et al. (2011) (Ca1) generally has the best overall performance. The Jordan (1991) relationship (used in snow models like CLM and SNTHERM), however, does not present very good model results for Dome A, Eagle, or LGB69. All in all, no density–conductivity relationship is optimal at all sites, and the performance of each varies with depth.

The three AWS sites in the paper cover a large range of elevation and distances from the coast. Thus, we argue that our findings can shed some lights on firn thermal studies (e.g., the applicability of different firn density–conductivity relationships) in Antarctica.