the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Brief communication: Growth and decay of an ice stupa in alpine conditions – a simple model driven by energy-flux observations over a glacier surface
Suryanarayanan Balasubramanian
Conradin Clavuot
Felix Keller
We present a simple model to calculate the evolution of an ice stupa (artificial ice reservoir). The model is formulated for a cone geometry and driven by energy balance measurements over a glacier surface for a 5-year period. An “exposure factor” is introduced to deal with the fact that an ice stupa has a very rough surface and is more exposed to wind than a flat glacier surface. The exposure factor enhances the turbulent fluxes.
For characteristic alpine conditions at 2100 m, an ice stupa may reach a volume of 200 to 400 m3 in early April. We show sensitivities of ice stupa size to temperature changes and exposure factor. The model may also serve as an educational tool, with which the effects of snow cover, switching off water during daytime, different starting dates, switching off water during high wind speeds, etc. can easily be evaluated.
- Article
(2555 KB) - Full-text XML
- BibTeX
- EndNote

Figure 1(a) Ice stupa in Ladakh, India (courtesy of Sonam Wangchuk). (b) Early growing stage of ice stupa with inner structure in Val Roseg, Switzerland (courtesy of Conradin Clavuot). (c) Simple geometrical representation. The ice stupa can have an inner structure (brown). The dashed lines illustrate the growth of an ice stupa from a base with a constant radius.
Ice stupas (Fig. 1), also referred to as artificial ice reservoirs (AIRs), are used more and more as a means to store water in the form of ice (Nüsser et al., 2018). In Ladakh, India, engineer Sonam Wangchuk initiated and developed the use of ice stupas to provide water for irrigation purposes in spring and early summer. The ice stupas grow in winter by sprinkling water on the growing ice structure, and they melt in spring and summer to deliver water; a typical turnover volume is up to 1 × 106 L. Ice stupas also form interesting touristic attractions with a distinct and special artistic flavour. They come in the same class as ice sculptures, which are popular in all regions of the world that have a cold winter.
The possibility to grow ice stupas of appreciable size depends on the meteorological conditions and the availability of water. When a surface has a negative energy balance and water is sprayed on it, ice will form (a well-known technique to make skating rinks). The more effective the latent heat of fusion can be removed by contact with cold air and effective emittance of longwave radiation, the faster the ice layer may grow. In spring and summer incoming solar radiation will dominate and the ice stupa will lose mass.
In this note we present a model of ice stupa growth and decay, based on a simple consideration of the total energy budget, and driven by energy flux observations over a glacier surface (half hourly observations over a 5-year period). We believe that the energy balance of a glacier surface and of an ice stupa have much in common and therefore consider this data set as ideal for a first study. The focus is on alpine conditions at a typical height of 2100 m a.s.l. The purpose of this study is to obtain first-order estimates of how fast an ice stupa may grow and melt and what processes are most important. We emphasize that in this note the focus is on the energetics of the ice stupa system, not on the technical aspects that have to be dealt with in constructing an ice stupa.
Ice stupas have different and often complex shapes. The cone is probably the most appropriate simple geometric shape to represent an ice stupa (Fig. 1), but alternatively a dome (half sphere) could also be considered.
The geometric characteristics of a cone with radius r and height h are
It is useful to introduce a shape parameter . The volume can then also be written as
So for a given volume the height of the ice stupa can be calculated from
In this note we will consider two cases: (i) the shape factor is constant during growth and decay, and (ii) the ice stupa grows upward from a base with a fixed radius, implying that the shape factor gradually increases. The first case may be more appropriate when an inner structure is used or when water supply is by varying sprinkler properties or even manually. Case (ii) describes better the situation when a fixed spray radius is maintained during the growth phase.
Ice stupas exchange energy with the surroundings by absorbing and reflecting solar radiation, absorbing and emitting longwave (terrestrial) radiation, and by turbulent fluxes of sensible and latent heat. Because of the complex shape of an ice stupa, as compared to a horizontal ice/snow surface, it is hard to describe these processes in detail. However, some simplifying assumptions may help to arrive at reasonable approximations.
We use 5 years of energy balance measurements with an automatic weather station (AWS) on the Vadret da Morteratsch (Morteratsch Glacier) (e.g. Oerlemans et al., 2009), which was located at an elevation of about 2280 m a.s.l. The surface energy flux is written as
Sin stands for solar radiation, Sout for reflected solar radiation, Lin for incoming longwave radiation, Lout for emitted longwave radiation, H for the total turbulent heat flux, and G for the ground heat flux (conduction from or into the surface layer – generally small compared to the other components). These quantities are normally expressed in W m−2. So the energy flux is positive when directed towards the surface. A positive energy flux will be used for melting of ice or snow; when the energy flux is negative freezing of water can take place (when available).
We now discuss how these measurements over (almost) flat terrain can be applied to an ice stupa. We first deal with solar radiation and consider the direct part (fraction q) and diffuse part (fraction 1−q) separately. Although the ratio of direct to diffuse solar radiation depends strongly on cloud conditions, outside subtropical climate zones where low cloudiness prevails the components are typically of the same order of magnitude (e.g. Li et al., 2015; Berrizbeitia et al., 2020).
With respect to direct solar radiation, the solar beam can be considered to have a vertical component, impinging on the horizontal surface (base of the ice stupa), and a horizontal component impinging on the vertical cross section (a triangle). Measurements over a flat surface, like those from the glacier AWS, thus underestimate the solar radiation intercepted by an ice stupa. A correction factor f is therefore needed with which the direct radiation as measured by the AWS has to be multiplied. This factor may be large for a low sun, but in alpine conditions where there is always significant shading by the surroundings this situation is rarely found. A simple analysis shows that, for a shape factor of s=2, f varies from 2.5 for a solar elevation of 20∘ to about 1.2 for a solar elevation of 60∘. To account for the fact that the correction factor should be 1 for a flat surface and increase with the shape factor, we use (note that f and s are dimensionless)
For the diffuse part of the solar radiation, illumination is on all sides and the relevant area therefore is the lateral area as given in Eq. (1b). Therefore the total amount of absorbed solar radiation per unit of time can be estimated as (in J s−1)
Alternatively, one may wish to prescribe the albedo α separately, i.e.
For the longwave radiation and turbulent exchange, the exposed surface is also the lateral area. The longwave radiation balance then becomes
The turbulent heat fluxes depend on the roughness and exposure of the surface. Since we do not calculate the surface (skin) temperature, we simply assume that it is close to the melting point. The sensible and latent heat input are calculated using the well-known bulk transfer equations (e.g. Garratt, 1992):
Here C is the bulk turbulent exchange coefficient over a flat surface, T is the air temperature, Ts is the surface temperature (set to the melting point), ρ is air density, Lv is the latent heat of sublimation (2 830 000 J kg−1), cp is the specific heat capacity of air (1004 J kg−1 K−1), e is the vapour pressure, es is the saturation vapour pressure, p is atmospheric pressure, and U is the wind speed. The total turbulent heat flux H is just the sum of the fluxes of sensible and latent heat.
The dimensionless parameter μ is an “exposure/roughness parameter” that deals with the fact that an ice stupa has a rough appearance and forms an obstacle to the wind regime. So μ is expected to be larger than 1 and could perhaps have a value of 2 or more. For a larger shape parameter the exposure will be larger; we therefore use
Equation (9) is no more than an educated guess. It is hard to base estimates of this parameter on information in the literature. Many studies have been carried out on the effect of obstacles on atmospheric boundary layer flow (e.g. trees, but also buildings), but always in an ensemble setting, looking at the bulk effect of an ensemble of obstacles. We deal with a case of a single obstacle in open terrain, and we are confident that the roughness of the surface and the exposure will lead to larger turbulent fluxes. Given the uncertainty in the exposure parameter, later on we will present results for different values.
When water availability is unlimited, the mass gain or loss is given by
M is the mass of the ice stupa and Lm is the latent heat of melting/fusion (334 000 J kg−1). For typical alpine conditions the last term in Eq. (10) is normally quite small. Since the volume of the ice stupa is simply related to the mass (), the height of the stupa can directly be calculated for a given shape factor (case i) or given radius (case ii).
Over the past few years, several ice stupas have been constructed in the Oberengadin, southeast Switzerland. In the winter of 2017/2018 an ice stupa was constructed in the Val Roseg at 2000 m a.s.l. (Fig. 1, maximum height about 12 m). In the winter of 2018/2019 several smaller ice stupas (height about 5 m) were built at a site in the Val Morteratsch at about 1900 m a.s.l. Since February 2021 a test site for ice stupa construction has been in operation at the Diavolezza Talstation at an altitude of 2080 m a.s.l.
To obtain first-order estimates of growth and decay rates for typical climatic conditions in the Oberengadin, we used the energy balance measurements from the automatic weather station on the Vadret da Morteratsch as a proxy for this high alpine region. During the period 1 July 2007–30 September 2012, the AWS on the Vadret da Morteratsch was located at an altitude of about 2280 m a.s.l. and has produced a unique data set without any gaps. The annual melt at the AWS location was between 5 and 7 m of ice. With a focus on the Diavolezza site, which is at an altitude of 2080 m a.s.l., a temperature correction of +1.3 K was applied to the input data (based on a standard atmospheric temperature lapse rate of 0.0065 K m−1). We note that all the locations mentioned above are within a distance of 10 km from each other (interactive map to find locations: https://map.wanderland.ch, last access: 25 June 2021).
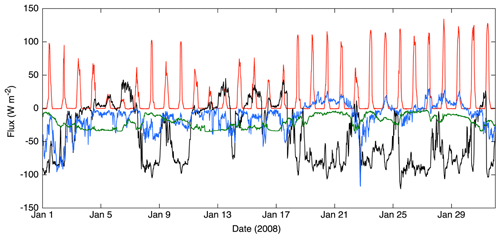
Figure 2 shows an example of data from the AWS. The data have been stored as 30 min averages. The turbulent heat fluxes have been calculated from the wind speed, air temperature, and humidity, where the turbulent exchange coefficient C was used as a tuning parameter (to obtain the correct amount of observed ice melt over a 5-year period). The example shown is just for one relatively sunny winter month (January 2008). Note the large degree of compensation between net solar radiation and net longwave radiation – the well-known effect in clear sky conditions on the radiation balance. As a consequence, the turbulent heat fluxes are more important than it appears at first sight.
Figure 3 summarizes model results in terms of ice stupa height and volume for 5 years. In all calculations we used q=0.5 and α=0.6. It has been assumed that water availability is unlimited. In the first example (Fig. 3a) we show the evolution of an ice stupa on a 5 m high inner structure. In the model this is simply achieved by setting h=5 m at the start of the integration and correct the total volume afterwards for the volume of the inner structure. The use of an inner structure has the advantage that the freezing area is larger from the beginning and that the typical ice stupa shape is achieved relatively fast. The shape factor has been taken constant and equal to 2. We see some differences among the years: the maximum ice stupa height varies between 10 and 12 m and is normally reached in early April. For the last 2 years the simulated ice stupa volume is smaller mainly because of slightly higher temperatures and larger insolation. The decay of the ice stupa is hardly faster than the growth. A faster decay would occur if the albedo were not constant but would be prescribed to decrease during the melt phase (which is more realistic in most cases).
Figure 3b shows a comparison between the fixed-shape simulation just described and a fixed-radius simulation with r=7 m. This value of the radius was chosen to obtain more or less the same ice stupa volume. It can be seen that in the first stage of growth the volume for the fixed-radius case increases somewhat faster than for the fixed-shape case. Nevertheless, the differences in the curves are not large and point to the fact that in the end the energy constraints determine how much ice can form (in the case of unlimited water availability).
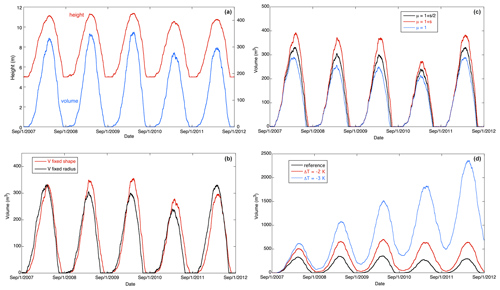
Figure 3Calculated evolution of ice stupa for the case of unlimited water supply for five winters. (a) Height and volume for the case with an inner structure (height 5 m) and fixed shape. (b) Volume for the case with an inner structure and the case with a fixed radius (7 m). (c) The effect of the exposure parameter μ on the volume (fixed radius). (d) The effect of a negative temperature perturbation. For K the stupa does not disappear anymore but is growing from year to year (fixed shape).
Because the value of the exposure parameter μ is highly uncertain, we show the sensitivity of the fixed-radius ice stupa volume to different formulations (Fig. 3c). For μ=1, implying that the situation is equivalent to that of a flat surface, the stupa volume is significantly smaller than in the reference case (). A stronger dependence of μ on the shape factor () increases the stupa volume by about 25 %. For a larger shape factor, the mostly negative turbulent fluxes in winter increase, and this is not compensated by a larger interception of solar radiation.
In the simulations discussed so far the ice stupas disappear in summer. One may ask the question under what conditions an ice stupa may survive the summer and grow to a larger size in the next winter. A possible way to study this question is to decrease the air temperature uniformly (temperature change ΔT). This will imply a stronger negative sensible heat flux in winter and a weaker positive heat flux in summer, thus accelerating stupa growth and slowing down its decay. We found a break-even point for K (Fig. 3d). For larger negative values of ΔT the ice stupa does not disappear in summer and keeps growing from year to year. For K, the maximum volume in the fifth year (∼ 2400 m3) is about 4 times that in the first year (∼ 600 m3). We note that in this calculation the effect of lower temperatures on the net longwave radiation balance has not been taken into account, because the radiation fluxes were prescribed according to the AWS observations. It is likely that we therefore underestimate the effect of lower air temperature.
The data set used to simulate ice stupa growth and decay for typical conditions in the Oberengadin is probably quite appropriate. The setting of the location of the AWS (on the lower tongue of the Vadret da Morteratsch when it still existed) and the Diavolezza Talstation are rather similar: the altitude is about the same, and the valley is relatively wide. However, differences in the wind statistics are likely to exist, but they are difficult to assess. The Morteratsch AWS reveals a steady katabatic (glacier) wind most of the time, whereas the Diavolezza Talstation is more exposed to the larger-scale wind regime. It seems likely that the average wind speed at the Diavolezza Talstation is somewhat higher than at the AWS site, where the 5-year average wind speed is 2.8 m s−1. In contrast, the sites in the Val Roseg and Val Morteratsch are more sheltered and wind speeds are probably lower.
The examples presented here are best-case scenarios with respect to ice stupa growth. In practice it is not always possible to have unlimited water availability, and it may be difficult to sprinkle the water more or less evenly over the stupa, especially at higher wind speeds. The choice of the shape of the ice stupa depends on the sprinkling strategy. It may be more realistic to describe an ice stupa with different shapes for the growth phase (e.g. fixed radius) and decay phase (e.g. constant shape factor). Such an approach can easily be accommodated in the model.
We note that the ice stupa volume calculated here for alpine conditions at ∼ 2100 m a.s.l. (typically 250 m3) is significantly smaller than the volumes obtained in the big ice stupas in Ladakh. Winter conditions in Ladakh are considerably colder and therefore growth rates can be much larger.
In this exploratory study a solid comparison between observed and simulated stupa sizes was not attempted. However, we note that the maximum height of the stupa in the Val Roseg was 12 m, which is in good agreement with the stupa height shown in Fig. 3a.
The model presented here is simple, basically because we consider the ice stupa to be a single unit with a surface temperature close to the melting point. As soon as this constraint is relaxed and the surface temperature of the stupa is considered to be a dependent variable, the whole procedure becomes more complicated, and some processes can be studied more explicitly. Nevertheless, we believe that the simple approach presented in this note, which requires no more than one page of coding, is a useful tool to obtain first-order estimates of growth and decay rates under various conditions. Effects of snow cover, switching off water during daytime, switching of water supply for high wind speeds, different starting dates, differences between warm and cold winters, etc. can be evaluated. We finally note that the model can easily be reformulated for another geometry, e.g. a dome.
The 5-year data set from the weather station on the Vadret da Morteratsch is available on request.
JO designed, coded, and ran the model. Through their experience in constructing ice stupas, SB, CC, and FK have made important contributions concerning the concept and application of the model. JO wrote the text of this communication.
The authors declare that they have no conflict of interest.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank the reviewers and editor for their constructive comments. The operation of the weather station on the Vadret da Morteratsch was made possible by the NWO-SPINOZA grant (Dutch Research Council) to Johannes Oerlemans.
This paper was edited by Chris Derksen and reviewed by Jonathan D. Mackay and two anonymous referees.
Berrizbeitia, S. E., Cago, E. J., and Muneer, T.: Empirical models of the estimation of solar sky-diffusive radiation. A review and experimental analysis, Energies, 13, 701, https://doi.org/10.3390/en13030701, 2020.
Garratt, J.: The Atmospheric Boundary Layer, Cambridge University Press, 316 pp., ISBN 0521380529, 1992.
Li, D. H. W., Lou, S. W., and Lam, J. C.: An analysis of global, direct and diffuse solar radiation, Energy Procedia, 75, 388–393, 2015.
Nüsser, M., Dame, J., Kraus, B., Baghel, R., and Schmidt, S.: Socio-hydrology of artificial glaciers in Ladakh, India: assessing adaptive strategies in a changing cryosphere, Reg. Environ. Change, 19, 1327–1337, https://doi.org/10.1007/s10113-018-1372-0, 2018.
Oerlemans, J., Giesen, R. H., and Van den Broeke, M. R.: Retreating alpine glaciers: increased melt rates due to accumulation of dust (Vadret da Morteratsch, Switzerland), J. Glaciol., 55, 729–736, 2009.