the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Satellite-observed monthly glacier and snow mass changes in southeast Tibet: implication for substantial meltwater contribution to the Brahmaputra
Chunqiao Song
Kosuke Heki
Shichang Kang
Qiuyu Wang
Le Chang
High-Asia glaciers have been observed to be retreating the fastest in the southeastern Tibet Plateau (SETP), where vast numbers of glaciers and amounts of snow feed the streamflow of the Brahmaputra, a transboundary river linking the world's two most populous countries, China and India. However, the low temporal resolutions in previous observations of glacier and snow (GS) mass balance obscured the seasonal accumulation–ablation variations, and their modelling estimates were divergent. Here we use monthly satellite gravimetry observations from August 2002 to June 2017 to estimate GS mass variation in the SETP. We find that the “spring-accumulation-type” glaciers and snow in the SETP reach their maximum in May. This is in stark contrast to seasonal variations in terrestrial water storage, which is controlled by summer precipitation and reaches the maximum in August. These two seasonal variations are mutually orthogonal and can be easily separated in time-variable gravity observations. Our GS mass balance results show a long-term trend of Gt yr−1 (or 0.67±0.08 m w.e. yr−1) and annual mass decreases ranging from −49.3 to −78.3 Gt with an average of Gt in the SETP between August 2002 and June 2017. The contribution of summer meltwater to the Brahmaputra streamflow is estimated to be 51±9 Gt. This result could help to resolve previous divergent modelling estimates and underlines the importance of meltwater to the Brahmaputra streamflow. The high sensitivity between GS melting and temperature on both annual and monthly scales suggests that the Brahmaputra will suffer from not only changes in total annual discharge but also an earlier runoff peak due to ongoing global warming.
- Article
(8548 KB) - Full-text XML
-
Supplement
(7154 KB) - BibTeX
- EndNote
The Tibetan Plateau, considered the Asian water tower, is the source of several major river systems. The upper streams of these rivers are fed by rainfall, base flow, and widespread glacier and snow (GS) melt (Barnett et al., 2005; Immerzeel et al., 2010; Jansson et al., 2003; Lutz et al., 2014). The GS melt is susceptible to climate change, while its sustainable supply is critical to the local freshwater security, flood prevention and control, and hydroelectric development (Bolch et al., 2012; Kaser et al., 2010; Yao et al., 2012). The southeastern Tibetan Plateau (SETP), including the Nyenchen Tanglha Mountains (NTM) and eastern Himalayas, holds 10 439 glaciers with a total area of 9679 km2 (RGI Consortium, 2017) and widespread seasonal snow coverage of up to 100 000 km2. These maritime glaciers are characterized by low equilibrium-line altitudes with large topographic gradients (Yao et al., 2012) and the most severe mass loss in high-mountain Asia (HMA; Brun et al., 2017; Kääb et al., 2015). The GS melt serves as an essential water supplier for the Brahmaputra river system (e.g. Immerzeel et al., 2010; Lutz et al., 2014), which runs through three densely populated countries, China, India and Bangladesh (Fig. 1). The revealed vulnerability of glaciers in the Brahmaputra basin to global warming and emerging controversies over water allocation (e.g. dam building; Tanck and Fazani, 2010) are increasingly attracting scientific and public concerns.
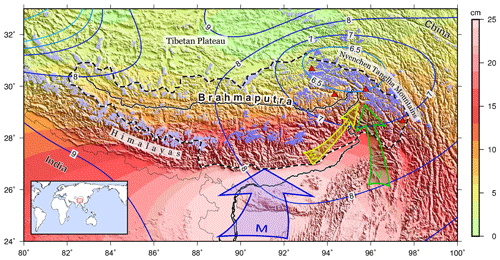
Figure 1Geographic environment of the upper Brahmaputra basin. The boundary of the basin is outlined by the dashed black line. The violet areas in the plateau represent mountain glaciers, but only the darker ones (9679 km2 in total) are studied here. The background colour shows the amplitudes of annual variation in terms of equivalent water height from GRACE, and their peak months (the month with the peak value in a year) are indicated using contours (e.g. 9 means September). The red triangles mark the locations of four meteorological stations. The coloured arrows illustrate major climatic factors influencing this region (M: Indian monsoon; W: westerly winds; V: Bay of Bengal vortex). The red box in the inset marks the location of the study area.
Due to the lack of observational data, most of the previous estimates on the contribution of seasonal meltwater to the upstream flow of the Brahmaputra river were based on modelling approaches that were only calibrated by employing streamflow data. As a result, the previous estimates disagree widely from 19 % to 35 % (Table 1) due to different forcing data and approaches without direct constraints on GS mass balance (Bookhagen and Burbank, 2010; Chen et al., 2017; Huss et al., 2017; Immerzeel et al., 2010; Lutz et al., 2014; Zhang et al., 2013). The amount of meltwater could be even more divergent. For example, Huss et al. (2017) estimated that the amount of annual GS melt to the Brahmaputra river was 138 km3 w.e. (water equivalent) yr−1, which is however triple the estimate of 43 km3 w.e. yr−1 by Lutz et al. (2014). Although these two studies covered different ranges, the glacierized zone in the basin was well enclosed in both, so the estimates should not be so different. Such huge discrepancies in previous estimates make it imperative to incorporate the calibration from GS mass balance observations into future modelling experiments. Recently, the concept of assimilating more GS observations has begun to be implemented in state-of-the-art models (Wijngaard et al., 2017; Biemans et al., 2019), but their glacier results suffered from coarse temporal resolution (two observations over 5 years) and the snow mass changes were partially constrained by area changes.
Table 1Previous model-based estimates of meltwater contribution to the Brahmaputra discharge.
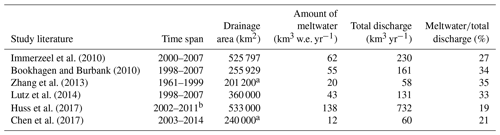
a Excludes large parts of the NTM region. b The time spans vary a bit in different datasets.
Spaceborne sensors can be helpful in this desolate mountain region. Remote sensing techniques for regionwide GS mass balance measurements can be divided into three categories: laser altimetry (e.g. Ice, Cloud and land Elevation Satellite – ICESat – Kääb et al., 2012), multi-temporal digital elevation models (e.g. SPOT, Gardelle et al., 2013; ASTER, Brun et al., 2017), and space gravimetry (Gravity Recovery and Climate Experiment – GRACE – Matsuo and Heki, 2010; Yi and Sun, 2014). The first two geodetic approaches require the average ice density to convert volume changes into mass changes. The ICESat observation suffers from a short operation period (2003–2009) and sparse spatial sampling, both of which can be overcome by the stereo-imagery approach, which has become popular for the whole HMA study recently (Brun et al., 2017; Dehecq et al., 2018). Brun et al. (2017) provided an estimate of the detailed glacier mass balance trends over HMA between 2000 and 2016 and highlighted the regional dissimilarity. Despite recent improvements in spatial resolution in HMA glacier mass change studies, there has been little advance in their temporal resolution.
Observations at a monthly temporal resolution are necessary to separately quantify summer and winter mass balances, two processes dominating the annual glacier mass balance (Cogley et al., 2011, pp. 61–62) and thus crucial for the calibration and validation of glaciological models. The amplitude of seasonal variation in the glaciers in the SETP is up to ∼3 m w.e. (Wang et al., 2017), far exceeding their net annual change of ∼0.6 m w.e. (Brun et al., 2017). Hence, the long-term trend of GS mass changes only reflects a small net imbalance of their ablation and accumulation. Monthly observations by GRACE since its launch in 2002 (Tapley et al., 2004) are promising in identifying these two processes. Up to now, the application of GRACE in HMA glaciers has been focusing on their secular changes with little attention to the seasonal variations (Gardner et al., 2013; Matsuo and Heki, 2010; Yi and Sun, 2014). This is mostly due to the poor spatial resolution of GRACE (>300 km) and the dominance of terrestrial hydrological signals in the seasonal gravity signals, which is difficult to eliminate from glacial signals. The latter limitation is particularly severe in the SETP with intense monsoon precipitation. The GS and hydrological mass changes (mainly including mass changes in rivers, soil moisture and groundwater) dominate the seasonal gravity signals in the SETP observed by GRACE. Despite the general difficulty in separating them in the spatial domain, we find it possible to separate the two signals in the time domain, owing to their contrasting seasonal behaviours.
Precipitation in the SETP is controlled by various atmospheric circulation systems in different seasons, with westerly winds and the Bay of Bengal vortex in winter and spring and the Indian monsoon in summer (Wu et al., 2011; Yang et al., 2013; Yao et al., 2012). The first two systems were found to drive the spring precipitation in the SETP along the Brahmaputra river, thus forming a “spring-accumulation” type of glacier (Yang et al., 2013). The Indian monsoon prevails from June to September and brings intense precipitation to the southern side of the Himalayas, where terrestrial water storage shows tremendous seasonal changes and peaks in late summer. Therefore, according to the climate stations near NTM, we can observe bimodal precipitation variations throughout the year (Yang et al., 2013).
In this work, we will first introduce the precipitation characteristics in this region by both meteorological stations and global precipitation products. We will then use empirical orthogonal function (EOF) analysis to decompose hydrological and GS signals in our study region, which does not exactly coincide with the range of the glacierized zone in the Brahmaputra basin. Our study region covers only 83 % of the basin glaciers (the undetected 17 % are in the western part) and 15 % of non-Brahmaputra glaciers. We will scale our results by a ratio of to obtain the total meltwater in the Brahmaputra, assuming that our observations can represent the basinwide average. The hydrological and GS signals are further compared to the results of other datasets to validate their physical meanings. Such high-time-resolution observations also allow us to compare GS mass variations with temperature records during the ablation season and to study the sensitivity of GS mass change in response to temperature change. Finally, we will compare our results to previous estimates at monthly, annual and interannual scales.
2.1 GRACE data and preprocessing
We adopt the monthly GRACE spherical harmonics Release 06 products from August 2002 to June 2017. The three datasets are solved respectively by three organizations: the Center for Space Research (CSR) at the University of Texas, the GeoForschungsZentrum (GFZ) in Potsdam and the Jet Propulsion Laboratory (JPL). These datasets are available at http://icgem.gfz-potsdam.de (last access: 9 July 2020). The degree 1 terms, which are absent in original GRACE releases, have been added based on the technique proposed by Swenson et al. (2008). The C20 terms have been replaced by those from satellite laser ranging (Cheng et al., 2011), which are considered to be more reliable. A widely used glacial isostatic adjustment (GIA) model by A et al. (2013) is adopted to correct the GIA effect caused by historical polar-ice-sheet changes.
Two different filtering strategies, a combination of a P4M6 decorrelation (Swenson and Wahr, 2006) and 300 km Gaussian filter (hereafter G300 + P4M6) and a DDK4 filter (Kusche et al., 2009), are applied separately. Therefore, there are six combinations, and their average values (with uniform weights) are used in the following figures.
2.2 GRACE error estimation
We adopt different uncertainty estimation strategies for the seasonal variation and the trend due to their intrinsically different error sources. The error in seasonal variation consists of the standard deviations among these six datasets (i.e. errors from the data solution and smoothing methods) and the leakage error, while that in the long-term trend also includes other potentially uncorrected signals. We assume that the majority of the hydrological signal is captured by the first EOF mode. The leakage error is then determined by how effectively the hydrological and GS signals are separated by the EOF technique. Based on the modelled and recovered glacier mass changes, their residuals are estimated to have a seasonal variation of up to 11 % of the modelled glacier mass change (refer to Sect. 3.2 in the Supplement), which is used to calculate the seasonal leakage error. We do not quantify or account for potential hydrological (non-GS) signals in EOF mode 2.
For the long-term trend error, the three different solutions and two smoothing techniques have a total effect of 0.44 Gt yr−1. There are potential errors from other signal sources, like the glacial isostatic adjustment (GIA), Little Ice Age (LIA) and weather denudation. The GIA effect which originates from the polar regions has been corrected by A's GIA model (A et al., 2013), although its influence on the trend is as small as 0.02 Gt yr−1. The main reason is that the spatial pattern of GIA is quite smooth, so it mainly influences the first mode and rarely leaks into the second one. This feature is also applicable for other signal sources: unless they are exactly located in the glacierized area, their influence will be reduced by the EOF decomposition. In the southern and southeastern Tibetan Plateau (over 500 000 km2), the effects of the LIA and denudation are estimated to be Gt yr−1 (Jacob et al., 2012) and 1.6 Gt yr−1 (assuming the sediment has a density of 2 Gt km−3; Sun et al., 2009) respectively. Our glacierized zone and surroundings have an area of about 100 000 km2, accounting for one-fifth of the whole region, so we suppose their contribution to the GS mass estimate is also proportionally one-fifth. However, as we explain above, we could not precisely quantify their contribution without knowing their spatial distribution, and they are more likely to be absorbed by the first mode, so we only include their contribution in the error estimation rather than correcting them in the trend. Table 2 summarizes the sum of GRACE error estimates in the secular trend.
2.3 ICESat altimetry
Version 34 of the ICESat Global Land Surface Altimetry Data is used to derive glacier height changes. The data span is from 2003 to 2009, with two or three observation campaigns per year (Fig. S1 in the Supplement). The processing of ICESat data includes the following steps. (1) Orthometric heights are obtained from original elevation data based on the Earth's gravity model 2008. (2) Footprints of glaciers are identified based on Randolph Glacier Inventory (RGI) 6.0 glacier outlines. (3) For each ICESat footprint, Shuttle Radar Topography Mission (SRTM; Farr et al., 2007) elevations and slopes are extracted by bilinear interpolation of the digital-elevation-model grid cells. Glacier height variation is defined as the elevation differences between the footprints and the SRTM data. (4) We exclude footprints over SRTM voids, footprints with slopes higher than 30∘ and footprints with a height change larger than 100 m (which are attributed to biases caused by cloud cover during the ICESat acquisition). (5) We also discard the calibration campaign L1AB (March 2003) and the incomplete campaign L2F (October 2009). (6) Glacier height variations are averaged and interpolated along the altitude to alleviate the uneven sampling problem in space, and an uncertainty of 0.06 m yr−1 (Kääb et al., 2012) is chosen to account for the uneven sampling bias in time. The steps have been used in previous work (Wang et al., 2017) and have also been described in earlier studies (Gardner et al., 2013; Kääb et al., 2012). The footprint information is given in Fig. S2.
ICESat has shown good ability to estimate snow variation in flat regions (Treichler and Kääb, 2017), but applying the same technique in mountainous areas with high terrain heterogeneity is cumbersome. Therefore, here ICESat is only used to estimate changes in glacier mass. Although our GRACE estimate includes both glaciers and snow, the estimates by GRACE and ICESat are comparable in the late ablation season (i.e. the October–November campaign of ICESat), when the contribution of seasonal snow meltwater is negligible (Sect. 5.1). To convert the glacier thickness changes into mass changes, two parameters are required, i.e. glacier density and total glacier area. We assume an average glacier density of 850±60 kg m−3 (Huss, 2013). According to the glacier inventory RGI 6.0 (RGI Consortium, 2017), the area has a glacierized area of 9679 km2.
2.4 Other auxiliary data
To analyse the impact of temperature and precipitation on GS and water mass balance here, we adopt two types of datasets, gridded reanalysis products and in situ measurements from four meteorological stations (their locations are labelled in Fig. 1, and coordinates are listed in Table S1 in the Supplement). Precipitation and temperature records for each site from 2003 to 2016 (Fig. S4) are available from the China Meteorological Data Service Center (http://data.cma.cn/data/weatherBk.html, last access: 9 July 2020). Only four in situ temperature records may not represent the overall condition of the glacierized zone, so we adopt the gridded temperature product from the ERA5 reanalysis data processed by the European Centre for Medium-Range Weather Forecasts (ECMWF). The data are available at https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5 (last access: 9 July 2020). The gridded data are compared with station observations, and the correlation index ranges from 0.69 to 0.82 in the interannual variation (Fig. S6), indicating a good consistency. The average values in the glacierized zone from the ERA5 temperature product will be used to represent the temperature condition here.
Global gridded precipitation data of the Tropical Rainfall Measuring Mission (TRMM; Huffman et al., 2014) are used to examine the influence of precipitation on water storage. The data are available at https://pmm.nasa.gov/data-access/downloads/trmm (last access: 9 July 2020). Although such a global product is unable to capture the localized spring precipitation in our study area (Sect. 3), it can be used for the investigation of large-scale monsoon precipitation.
Moderate Resolution Imaging Spectroradiometer (MODIS) data MOD10 (Hall et al., 2006) are used to investigate snow coverage here. The MOD10CM product has a temporal resolution of 1 month and spatial resolution of 0.05∘. The Global Land Data Assimilation System (GLDAS) Noah land surface model (Rodell et al., 2004) is adopted to inspect soil moisture changes, which can be compared to changes in total terrestrial water storage estimated by GRACE. Here, the version 2.1 monthly product with 1.0∘ spatial resolution is used (available at https://hydro1.gesdisc.eosdis.nasa.gov/data/GLDAS/GLDAS_NOAH10_M.2.1/, last access: 9 July 2020). The total water storage in this region also contains contributions from rivers and groundwater, which are however difficult to obtain, so only the soil moisture component is investigated here.
The method of this study is based on the fact that the change in GS mass driven by spring precipitation precedes the change in hydrological signals. Therefore, before introducing the method, we want to demonstrate that GRACE can detect mass changes caused by spring precipitation. At two out of four stations (Bomi and Chayu), spring precipitation is noticeable, even surpassing the summer–autumn precipitation brought by the Indian monsoon (Fig. S4). Yang et al. (2013) provided precipitation records at 22 sites in a broader area and outlined the boundary of the impact zone of the spring precipitation, which roughly covers the glacierized area studied here. Summer precipitation and its associated hydrological mass change are enormous and well recognized, while the spring equivalents are not. Therefore, here we only use the TRMM and ERA5 results from January to March in Fig. 2 to show the initiation of spring precipitation. The precipitation begins to spread south and west starting in April, when the monsoon gradually increases (not shown here). The TRMM results show a boundary along the latitude 29∘ N, where the precipitation suddenly decreases to the north. This boundary of change is irrelevant to the terrain and seems to be artificial. This phenomenon cannot be found in the ERA5 result, which shows abundant precipitation in the glacierized zone in these months. The bottom plots give the GRACE monthly mass anomalies from March to May (2 months later than the precipitation), as GRACE observes the cumulative mass change resulting from precipitation. An earlier mass increase from April can be identified in the southeastern part of the Tibetan Plateau.
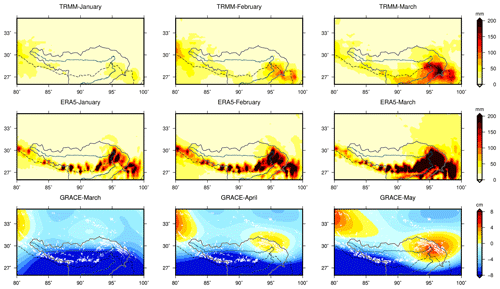
Figure 2Monthly precipitation from January to March by TRMM and ERA5 and mass anomalies from March to May by GRACE. The Brahmaputra and its basin boundary are marked. The white shaded areas in the bottom plots represent glacier distribution.
The performance of TRMM and ERA5 is compared with our station measurements in Fig. S5. According to the in situ records, the spring precipitation, as a part of the bimodal variation, is obvious at the Bomi and Chayu stations. TRMM is capable of revealing the conditions at Chayu at 28.65∘ N but performs poorly in regions north of 29∘ N. The ERA5 data demonstrate higher precipitation in winter and spring at Bomi and Linzhi than the other two datasets.
These results show that spring precipitation can be captured to a limited extent by various reanalysis products and the spring-accumulation pattern of GS mass change in the SETP is recognizable in GRACE observations. The amplitude and phase of the seasonal mass variation from the equivalent water height (EWH) of GRACE are compared in the background of Fig. 1. The seasonal amplitude has a spatial distribution similar to that of the Indian-monsoon-affected area. This pattern reflects the predominance of the monsoon-controlled hydrological process and the weaker glacial signals in this region. However, the peak month of seasonal changes (the contours in Fig. 1) divergently appears earliest in June in the NTM and is gradually delayed to August in the southern Himalayas, where the annual amplitude reaches its maximum. The shift in peak months reflects the increasing–decreasing contribution from the sinusoid of the hydrological and GS seasonal variation. A key point to point out is that the peaks of hydrological and GS seasonal variations have a 3-month time window offset (Sect. 4.4), which is a quarter of the annual oscillation cycle and means that the two signals are mathematically orthogonal.
4.1 EOF analysis of GRACE
GS and hydrological mass changes dominate the seasonal gravity signals observed by GRACE in this region, and they are mathematically orthogonal due to different phases. Therefore, we employ the EOF technique (see the Supplement for mathematic expressions; Björnsson and Venegas, 1997) to decompose hydrological and glacial signals in the GRACE datasets (Fig. 3). We thus extract two modes with significantly higher explained variances than the other modes (i.e. two significant modes are obtained). Results of different datasets and filters show good consistency, indicating that the first two modes are robust.
Each mode consists of one EOF (the spatial pattern) and one principal component (PC; the temporal evolution). Only the first two modes, accounting for 79 %±5 % and 12 %±4 % respectively of the total variance explanation, are shown. Although the first mode is much stronger than the second mode (because the second one is more localized), their signal strength in the glacierized region is comparable on both seasonal and secular temporal scales. Furthermore, after removing the first mode representing the hydrological signal, mass changes in the glacierized zone estimated using the second mode of GRACE are much more consistent with the glacier mass changes using ICESat in terms of seasonal and long-term changes (Fig. S7). Modes above mode 2 are weak and irregularly show much noise, so they are discarded here.
The trends of the GRACE observation and its decomposed modes are shown in Fig. 4. The GRACE observation shows a significant mass loss, which is divided into the first two modes. In the glacierized zone, approximately two-thirds of the negative trend comes from the second mode and approximately one-third comes from the first mode. The trend of higher modes (>2) is quite weak (Fig. 4d).
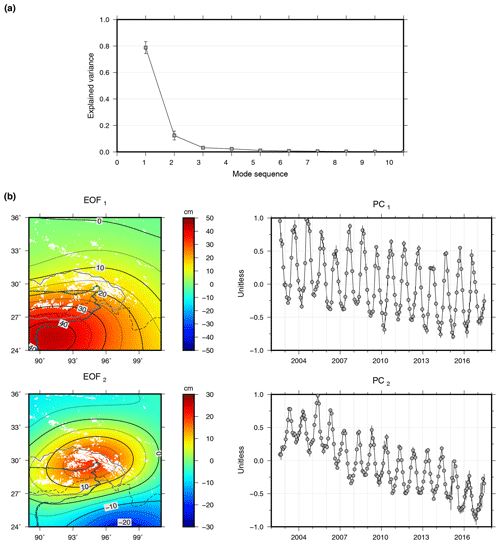
Figure 3EOF decomposition of GRACE observations in the form of EWH in the study region. Six combinations are averaged to generate these plots, and uncertainties are estimated based on the dispersions. (a) Weight of the first 10 components. (b) Spatial distribution (EOF) and temporal variation (PC) in the first two components. The white shaded areas represent glacier distribution.
According to the spatial coverages (EOF1 and EOF2) and their temporal variations (PC1 and PC2), the first mode covering the low altitude areas on the south of the plateau with a peak month in August–September seemingly represents hydrologic signals and the second mode concentrating in the glacierized region with a peak month in May (the peak month of June in Fig. 1 is the mixed result of the first two modes) seemingly represents glaciers. We will verify these hypotheses below.
4.2 GS mass estimation from mode 2
GRACE results only show smooth mass patterns, and we need a strategy to recover the original amount of mass change. If we adopt the second mode to estimate GS mass change, this step is necessary. Therefore, a forward-modelling method (Yi et al., 2016) is chosen to recover the mass in a predefined region iteratively. This method has been widely used (Chen et al., 2015; Wouters et al., 2008), especially in the study of polar ice sheets. In the first step, we divide the glacier mask based on the glacier distribution recorded in RGI 6.0 (RGI Consortium, 2017; Fig. 4e). The lattices have a resolution of 0.5∘ by 0.5∘ and are located in the glacierized area (in this way we assume the snow signal also comes from the glacierized area, but it does not influence the total mass estimates). In the second step, the mass in each lattice is iteratively adjusted until its smoothing signal (Fig. 4f) matches the GRACE observation (Fig. 4c) and becomes stable. The details of each combination of datasets and filters are presented in Figs. S8 and S9. Therefore, we estimate the mass in each combination (Fig. S9). The mass is multiplied by the PC2 series to derive the glacier mass series, and their average is taken as the mass estimate, which will be compared with ICESat observations to test our hypothesis on the estimate's physical meaning.
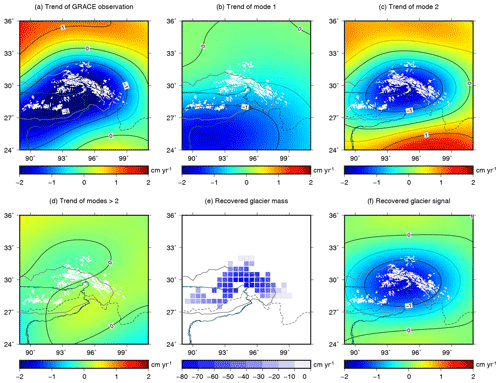
Figure 4Trend of GRACE signals and the GS mass estimation. The CSR product with the DDK4 filter is used here. (a) The trend of GRACE EWH observations between August 2002 and June 2017 is decomposed into (b), (c) and (d). Using the mass changes shown in (e), we obtained (f) by the forward-modelling method to reproduce (c). The white shaded areas represent glacier distribution. The solid black curve marks the basin boundary, and the dashed curve marks the plateau boundary.
4.3 Validation of mode 1 by soil moisture and precipitation datasets
To validate the hypothesis that the first mode represents hydrological signals, we compare it with EOF decomposition results of two other datasets, soil moisture from GLDAS Noah and precipitation data from TRMM (Fig. 5). To make them comparable to GRACE in terms of spatial resolution, they are expanded into spherical harmonics, truncated at degree 60, and smoothed by the same filter. Their results are shown in Fig. 5. Different from GRACE, which has two significant modes, they each only have one due to the lack of a glacial signal. The EOF1 of GLDAS Noah and TRMM is consistent with that of GRACE. The PCs are compared at interannual and seasonal scales as well. Note that precipitation is an instantaneous amount, while water storage is a state value, so the former should be integrated over time to make it comparable to the latter. Here, we integrate precipitation in 6 successive months by an empirical weight function of (1, 2, 3, 4, 5, 6), which will be normalized, and the value is attributed to the sixth month. Different integration methods are tested in the Supplement.
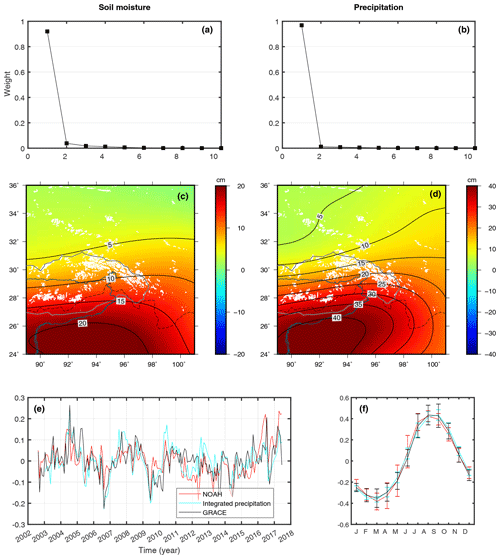
Figure 5EOF analysis of soil moisture using GLDAS Noah (a, c) and of precipitation using TRMM (b, d). The weights of the first 10 modes are shown in the upper panels (a, b). The first EOFs and PCs are shown in the middle and bottom panels (c–f). The PCs are separated into detrended interannual (e) and annual (f) variations for better comparison.
Notably, mass contributions from the Brahmaputra river and groundwater are absent (and they are troublesome to obtain) and precipitation is assumed as the dominant driver of water storage change without considering the influence of runoff and evaporation (Humphrey et al., 2016), so we do not expect that we can reach a thorough agreement between different datasets. This is acceptable if their temporal consistency is targeted. However, long-term trends in runoff, evaporation and groundwater cannot be ignored and they are differently reflected in these three products, so their trends have been removed before the comparison. The exclusion of unavailable surface water and groundwater in the GLDAS result also causes a weaker strength of its EOF1 compared to that of GRACE. We conclude that these datasets should be comparable in terms of seasonal and interannual variations and the pattern of spatial distribution but not in terms of the long-term trend and the amplitude of the spatial distribution. The good resemblance in both the EOF1 (spatial pattern) and PC1 (seasonal and interannual temporal evolution) between GRACE, GLDAS Noah and TRMM indicates that they reflect similar geophysical processes, i.e. hydrological variations.
4.4 Method feasibility and reliability
The phase difference of 3 months is a prerequisite for this method and can be verified retrospectively. We tested different phase differences between hydrological and GS signals and decomposed them by the EOF method (refer to Sect. 3.1 in the Supplement). Only when the GS mass change peaks in May (3 months before the peak month of the hydrological signal) does our simulated result show similarities to the GRACE observation.
Only hydrological and GS signals can explain the first two modes considering their spatial and temporal patterns. The atmosphere contribution has already been removed in GRACE observations (Dobslaw et al., 2017), and mass transports of solid earth are unlikely to have such strong seasonal variations. We cannot quantify the contribution of groundwater in the second mode, but groundwater is apt to be modulated by stronger rainfall in summer (Andermann et al., 2012), rather than by snowfall in winter–spring, and groundwater activity will be reduced in winter–spring when the ground is frozen. Therefore, the groundwater component is inclined to be captured by the first mode. We attribute the negative trend in the first mode to decreasing precipitation in recent years (Fig. S10) and intense groundwater pumping (Shamsudduha et al., 2012). The negative trend in the second mode is supposed to represent GS melting and can be used for estimating GS mass balance.
5.1 Glacier and snow mass balance
The glacier surface elevation changes measured by ICESat are compared with the result estimated from the second mode of GRACE. We interpolate the series of GRACE estimates (2002–2017) into the observation epochs of ICESat (2003–2009) and plot mass changes by GRACE as a function of elevation changes by ICESat (Fig. 6a). After dividing by the glacier density, the slope of the elevation–mass regression line represents the inventorial glacierized area by RGI 6.0. The observations in October–November (blue squares) approximate with the line, indicating the good consistency between ICESat and GRACE in the late ablation season between 2003 and 2009. The MODIS result indicates that the snow coverage increases rapidly from September (Fig. 6b), while the GRACE PC2 series show a moderate increase after October. We speculate that the snow height does not increase much in the first few months, so the contribution of snow mass is not significant. The observations in March and June, as expected, are well above the line, implying an extra snow mass contribution, which can be inferred from the point-to-line vertical distance. The snow contribution relative to the total mass anomalies varies drastically between 0 % and 62 % with a mean value of 38 % within our observation time windows.
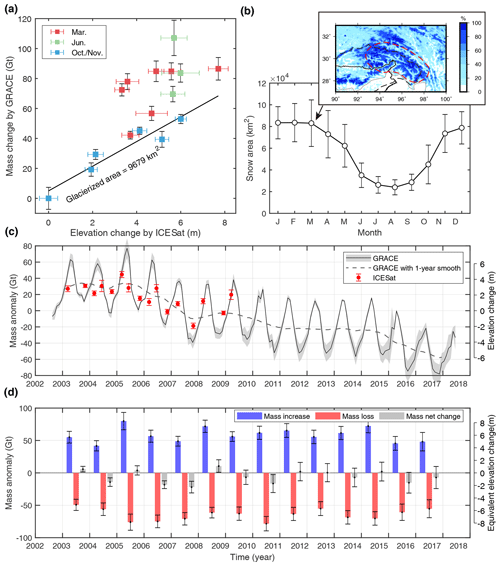
Figure 6GS mass balance in the SETP. (a) GS mass change by GRACE as a function of elevation change from ICESat. The values are anomalies relative to the minimum in October 2007. (b) Seasonal snow coverage changes. The error bars are calculated by the dispersions in the same month in the years from 2003 to 2016. The coverage in March is given in the inset. The dashed red outline marks the region used for the calculation of snow area. (c) Time series of GS mass change estimated by GRACE and glacier mass change by ICESat. The glacierized area of 9679 km2 is used to convert thickness change into mass change. (d) Annual mass increase and decrease from 2003 to 2016 by GRACE.
The difference between GRACE and ICESat-based estimates of mass change indicates that the snowpack outside the glaciers is a non-negligible contributor to the seasonal mass variation. This is quite different from previous glacier trend estimates, where non-glacier snow was neglected. Based on MODIS observations, the snow coverage area in this region varies from approximately 80 000 km2 in winter to 30 000 km2 in summer, both of which are much larger than the inventoried glacier area (Fig. 6b). However, heterogeneous snow depths (Das and Sarwade, 2008) and densities across the vast and rugged area make it difficult to measure their mass change in a non-gravimetric way.
Figure 6c compares the time series of glacial mass in the SETP from GRACE (August 2002–June 2017) and ICESat (2003–2009). The times series from two sensors are consistent in seasonal and interannual variations, despite the absence of the snow component in the ICESat result. Monthly mass change shows that the ablation season is generally between June and October with slightly varied initiation and duration from year to year. The maximum mass increase (10–20 Gt) usually occurs in April, when the spring precipitation peaks, and the severest mass loss (−15 to −30 Gt) usually occurs in July when the temperature peaks. As the temperature rises from April to July, the monthly mass change curve drops steeply from the peak down to the trough, but the ascending process with mass accumulation is relatively moderate and continuous.
We calculate annual mass increase and decrease by the difference in mass anomalies between November and May and between June and October respectively. From 2002 to 2017, the annual mass decrease ranged from −49.3 to −78.3 Gt with an average of Gt, and the annual mass increase ranged from 41.8 to 79.9 Gt with an average of 58.6±11.0 Gt. The seasonal GS mass changes postpone the runoff of ∼60 Gt of winter–spring solid precipitation for several months. This amount plays a vital role in the annual streamflow (130.7 Gt on average) of the upper Brahmaputra (Lutz et al., 2014) and is almost 10 times the annual net meltwater. Without the buffering effect of the seasonal variation, there will be a tremendous reduction in the streamflow in summer and autumn, when the water demand is high, and adaptive management on the dams in the Brahmaputra will be required to reduce seasonal irregularities in the streamflow (Barnett et al., 2005).
5.2 Quantifying the sensitivity of glacier and snow melt to temperature
Temperature is a dominant factor influencing the melting of glaciers (Cogley et al., 2011, pp. 68). Here, the monthly temperature records from the ERA5 product are compared with month-to-month mass changes by GRACE to investigate the sensitivity of the GS mass balance in response to temperature change (Fig. 7). Mass changes are negatively correlated with the temperature anomalies by a factor of Gt per degree during the ablation season (from May to October), but no correlation is found during the accumulation season (from November to April). The mass peaks around May, when either glacier accumulation or ablation could happen. The temperature averaged in this transitional month is taken as the reference for the temperature anomalies used in the figure, and their mass changes are annotated. The highest sensitivity of monthly mass changes in response to temperature is observed in July (3.1±2.5 Gt per degree), when the largest monthly mass loss occurs.
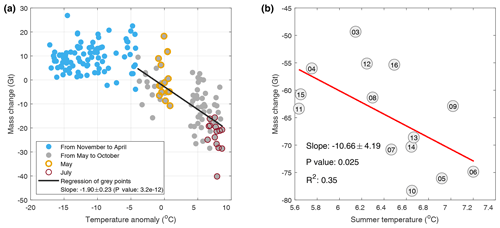
Figure 7Regression between mass change and temperature. (a) Monthly mass changes as a function of monthly temperature anomalies. (b) Linear regression between annual mass decreases and summer temperatures. The number in the circle represents the year of the data (e.g. “15” is 2015).
To investigate the impact of climatic variables on the interannual variations in GS mass, we compare annual mass losses (from May to October) with summer temperatures (from June to August; Fig. 7b). The annual mass loss is significantly correlated with the summer temperature, with a slope of Gt per degree (P value, 0.025; R2 value, 0.35), indicating that the annual GS mass balance is sensitive to summer temperature. The small value of R2 is partly due to the relatively large uncertainties in our mass estimate (10 Gt) in this modest range of variation (30 Gt) and the neglect of other factors influencing GS mass balance. The sensitivity index was provided by a previous study (Sakai and Fujita, 2017), where the whole HMA was examined and the SETP shows a widespread high sensitivity with an average value of −1.23 m w.e. per degree. Based on the glacierized area of 9679 km2, our estimation is m w.e. per degree, which is comparable with the earlier study of Sakai and Fujita (2017). It should be pointed out that annual net mass balance was used in Sakai and Fujita (2017) in comparison with the annual mass loss used in this study, although annual net mass balance is mainly driven by summer melt (Ohmura, 2011).
We could not find a significant relationship between the mass and precipitation changes, probably because our data fail to reflect the strong orographic effect in precipitation and/or because the GS mass gain process is too complex to be attributed to precipitation alone.
5.3 Comparison with previous estimations on glacier and snow meltwater
The trend of glacier elevation change by ICESat in this study is m w.e. yr−1 during 2003–2009, which lies between the values of m w.e. yr−1 (Gardner et al., 2013) and m w.e. yr−1 (Kääb et al., 2015) in eastern NTM by using a similar ICESat dataset (but an older version) and is close to the trend of m w.e. yr−1 during 2000–2016 by using ASTER (Brun et al., 2017). The trend of GS mass change in this study by using GRACE is Gt yr−1 between August 2002 and June 2017. The mass contribution from snow is considerable at the seasonal scale but negligible over 15 years, so the secular trend by using GRACE mainly represents the glacier mass change. Our GRACE trend compares well with the derived glacier mass change of Gt yr−1 by using ASTER (the area-averaged rate in NTM and Bhutan multiplied by the glacierized area of 9679 km2). In conclusion, both of our ICESat and GRACE estimates agree well with the previous ASTER result in terms of the secular trend. The GS mass trend from the second mode is reduced by 25 % compared to the original GRACE signal in the glacierized zone (Fig. 4).
A recent result on changes in interannual glacier flow in this region (Dehecq et al., 2018) indicates a strong correlation between ice flow rate and changes in glacial thickness. The interannual variation in GRACE-based mass changes (the 1-year smoothed sequence in Fig. 6c) notably shows equilibrium during the periods of 2003–2005 and 2011–2014. According to the aforementioned study (Dehecq et al., 2018), thinning glaciers reduce their flow rate by weakening gravitational driving stress; therefore, this balanced mass state may slow down the decreasing flow rate. Coincidentally, we can identify such decelerating phases in the decline in glacier flow rate during 2004–2006 and 2012–2015 (Fig. 1 in Dehecq et al., 2018).
GS mass loss is caused by flow, melting, and evaporation processes, and the last one does not contribute to the river flow. Evaporation is important for continental-type glaciers where the climate is usually cold and dry. For example, it accounts for 12 % of the glacier ablation in Tianshan (Ohno et al., 1992). However, the importance of evaporation is greatly reduced in our maritime glaciers due to the extremely humid air and rapid melting. Therefore, we assume that the mass loss is completely turned into meltwater and can be compared with analogous outputs from models. In our study region, 85 % of its meltwater (estimated according to the area proportion) runs into the Brahmaputra, and this area accounts for 83 % of total glaciers in this basin (9912 km2). Assuming that the unobserved 17 % of glaciers have a similar rate of GS mass change, our estimate of mass change is scaled by a ratio of to represent the GS mass change in the entire Brahmaputra basin. Monthly changes in meltwater estimated by month-to-month difference in GRACE results are compared with model results of Lutz et al. (2014), which showed that GS melt constitutes 33 % of the total discharge in the Brahmaputra and that 50 % of the annual melt occurs in the summer (Fig. 8). GRACE only detects the net change in GS and cannot separate mass ablation and accumulation (see the inset in Fig. 8). Because these two processes concur simultaneously in transitional seasons and are offset to some extent, the annual mass decrease (total mass loss in a year; here, it ranges from 49.3 to 78.3 km3 with an average of 64.5 km3) is smaller than the real GS melt. As a result, the annual mass decrease provides a lower bound on annual GS melt each year, rather than an accurate estimate. Instead, the amount of GS melt can be better determined during the summer (from June to August), when the accumulation is supposed to be small. This value can be used to validate the model output. Our result shows that the summer melt ranges from 37.3 to 62.9 km3 with an average of 51.6 km3, which is over 100 % larger than the 23 km3 GS mass change given in the model of Lutz et al. (2014; Fig. 8). Although extrapolated mass changes for the undetected 17 % of glaciers and the neglected summer evaporation may reduce our estimates of summer meltwater, they definitely cannot explain the difference of more than 100 %. Among all model estimates, the model of Lutz et al. (2014) reported one of the largest proportions of GS melt contribution (33 %) but still largely underestimated the amount of summer meltwater, according to our estimate from satellite observations.
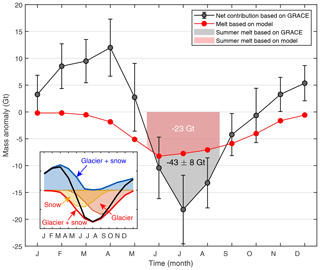
Figure 8Monthly mass change from GS in the upper Brahmaputra basin estimated by GRACE and by the model of Lutz et al. (2014). Negative values mean a net increase in meltwater (i.e. more GS melt than accumulation). Note that Lutz's model only estimated the melt component, while GRACE detects the net change including both melt and accumulation. The estimates of summer melt are annotated. A schematic diagram of seasonal mass balance is shown in the inset (blue text represents mass accumulation, red represents ablation, and the black curve represents the net change). Note 85 % of the meltwater in our study region runs into the Brahmaputra, and this amount comes from 83 % of the glacierized area in this basin; we scale our result by to be comparable with the model estimate.
Our annual mass decrease (average 49.0 Gt) is still much smaller than the 137 Gt of annual meltwater given by Huss et al. (2017). However, this larger value even exceeds the annual streamflow of 130.7 km3 in the upper Brahmaputra where all GS meltwater is included (Lutz et al., 2014). The upper streamflow at the Nuxia station (ahead of the main glacier supply area) is ∼60 km3. Therefore, the difference in streamflow between the main glacier supply area is ∼70 km3, and the annual meltwater is unlikely to exceed this value, considering the additional contribution of precipitation. These values generally represent decadal averages at the beginning of this century (Table 1), and they are therefore comparable.
In this study, we use GRACE gravimetry to estimate the GS mass balance in the SETP from August 2002 to June 2017. The second EOF mode of GRACE observations is attributed to changes in GS mass, which can be validated in the following three steps. First, a simulation experiment shows that two signals with peaks in August and May can be decomposed unbiasedly by EOF. Second, the first decomposed mode shows consistent spatio-temporal patterns with the soil moisture and precipitation variations from the GLDAS and TRMM data and thus can be reasonably attributed to hydrological processes. Thirdly, the second mode of the GRACE signal with a peak in May temporally corresponds to the glacier and snow accumulation and ablation processes and spatially coincides with the glacier distribution, which is also supported by the spring precipitation pattern observed by meteorological stations. Glacier mass change measured by ICESat is further adopted to compare with our GRACE-based GS estimates, and good agreement is reached in the ablation season when the snow contribution is negligible. The ICESat measurements also show that the seasonal glacier mass variation is large, which is consistent with our finding that GS mass change in this region peaks in May.
The GRACE-based GS mass balance not only shows a long-term decreasing trend of Gt yr−1, generally comparable with previous studies on glacier mass balance in the SETP, but also newly reveals a strong seasonal variation which postpones a water supply of about 60 Gt from winter and spring to summer and autumn. The high sensitivity of glacier mass changes responding to temperature shows that warming climate will exert strong impacts on the glacier and snow mass balance from two aspects. On the one hand, under the current glacier condition, the increase in summer temperature will enhance the annual meltwater by a factor of Gt per degree. On the other hand, the seasonal meltwater will shift earlier and reduce its supply in summer and autumn, which will potentially result in 10 times the amount of annual glacier melting. Our estimates of monthly GS meltwater can also give an elaborate calibration on the glacier accumulation and ablation processes in hydrological and glaciological models of the Brahmaputra basin, which were barely calibrated by GS mass observations and diverged largely in terms of the proportion of seasonal meltwater contribution. Given the high vulnerability to warming temperature, the greater contribution of meltwater to the Brahmaputra streamflow than most model estimates indicates that its water resource allocation will face ominous tension in the future.
The data that support this study are mostly publicly open, and their sources are indicated in the “Data” section. The meteorological data and the series of glacier mass balance estimates are available upon request to the corresponding author.
The supplement related to this article is available online at: https://doi.org/10.5194/tc-14-2267-2020-supplement.
SY conceived the study and conducted the calculations. SY and CS analysed the results and wrote the manuscript. KH discussed and revised the manuscript. SK discussed and suggested the experiment. QW processed the ICESat data. LC processed the MODIS data.
The authors declare that they have no conflict of interest.
Shuang Yi is supported by JSPS and the Alexander von Humboldt Foundation. Chunqiao Song is supported by the Strategic Priority Research Program of the Chinese Academy of Sciences and the National Key R&D Program of China.
This research has been supported by the JSPS KAKENHI grant (grant no. JP16F16328), the Alexander von Humboldt Foundation, the Strategic Priority Research Program of the Chinese Academy of Sciences (grant no. XDA23100102) and the National Key R&D Program of China (grant no. 2018YFD1100101, 2018YFD0900804).
This open-access publication was funded
by the University of Stuttgart.
This paper was edited by Bert Wouters and reviewed by Enrico Ciracì and four anonymous referees.
A, G., Wahr, J., and Zhong, S.: Computations of the viscoelastic response of a 3-D compressible Earth to surface loading: an application to Glacial Isostatic Adjustment in Antarctica and Canada, Geophys. J. Int., 192, 557–572, https://doi.org/10.1093/gji/ggs030, 2013.
Andermann, C., Longuevergne, L., Bonnet, S., Crave, A., Davy, P., and Gloaguen, R. : Impact of transient groundwater storage on the discharge of Himalayan rivers, Nat. Geosci., 5, 127–132, 2012.
Barnett, T. P., Adam, J. C., and Lettenmaier, D. P.: Potential impacts of a warming climate on water availability in snow-dominated regions, Nature, 438, 303–309, https://doi.org/10.1038/nature04141, 2005.
Biemans, H., Siderius, C., Lutz, A., Nepal, S., Ahmad, B., Hassan, T., von Bloh, W., Wijngaard, R., Wester, P., Shrestha, A., and Immerzeel, W.: Importance of snow and glacier meltwater for agriculture on the Indo-Gangetic Plain, Nat. Sustain., 2, 594–601, https://doi.org/10.1038/s41893-019-0305-3, 2019.
Björnsson, H. and Venegas, S.: A manual for EOF and SVD analyses of climatic data, CCGCR Report, 97, 112–134, McGill University, Canada, 1997.
Bolch, T., Kulkarni, A., Kaab, A., Huggel, C., Paul, F., Cogley, J. G., Frey, H., Kargel, J. S., Fujita, K., Scheel, M., Bajracharya, S., and Stoffel, M.: The State and Fate of Himalayan Glaciers, Science, 336, 310–314, https://doi.org/10.1126/science.1215828, 2012.
Bookhagen, B. and Burbank, D. W.: Toward a complete Himalayan hydrological budget: Spatiotemporal distribution of snowmelt and rainfall and their impact on river discharge, J. Geophys. Res., 115, F03019, https://doi.org/10.1029/2009jf001426, 2010.
Brun, F., Berthier, E., Wagnon, P., Kääb, A., and Treichler, D.: A spatially resolved estimate of High Mountain Asia glacier mass balances from 2000 to 2016, Nat. Geosci., 10, 668–673, https://doi.org/10.1038/ngeo2999, 2017.
Chen, J. L., Wilson, C. R., Li, J., and Zhang, Z.: Reducing leakage error in GRACE-observed long-term ice mass change: a case study in West Antarctica, J. Geodesys., 89, 925–940, https://doi.org/10.1007/s00190-015-0824-2, 2015.
Chen, X., Long, D., Hong, Y., Zeng, C., and Yan, D.: Improved modeling of snow and glacier melting by a progressive two-stage calibration strategy with GRACE and multisource data: How snow and glacier meltwater contributes to the runoff of the Upper Brahmaputra River basin?, Water Resour. Res., 53, 2431–2466, https://doi.org/10.1002/2016WR019656, 2017.
Cheng, M., Ries, J. C., and Tapley, B. D.: Variations of the Earth's figure axis from satellite laser ranging and GRACE, J. Geophys. Res., 116, B1, https://doi.org/10.1029/2010jb000850, 2011.
Cogley, J., Hock, R., Rasmussen, L., Arendt, A., Bauder, A., Braithwaite, R., and Nicholson, L.: Glossary of glacier mass balance and related terms, IHP-VII technical documents in hydrology, 86, UNESCO, Paris, , 2011.
Das, I. and Sarwade, R.: Snow depth estimation over north-western Indian Himalaya using AMSR-E, Int. J. Remote Sens., 29, 4237–4248, https://doi.org/10.1080/01431160701874595, 2008.
Dehecq, A., Gourmelen, N., Gardner, A. S., Brun, F., Goldberg, D., Nienow, P. W., and Trouvé, E.: Twenty-first century glacier slowdown driven by mass loss in High Mountain Asia, Nat. Geos., 12, 22–27, https://doi.org/10.1038/s41561-018-0271-9, 2018.
Dobslaw, H., Bergmann-Wolf, I., Dill, R., Poropat, L., and Flechtner, F.: AOD1B Product Description Document for Product Release 06 (Rev. 6.1, October 19, 2017), GFZ, Germany, 2017.
Farr, T. G., Rosen, P. A., Caro, E., Crippen, R., Duren, R., Hensley, S., and Roth, L.: The shuttle radar topography mission, Rev. Geophys., 45, RG2004, https://doi.org/10.1029/2005rg000183, 2007.
Gardelle, J., Berthier, E., Arnaud, Y., and Kääb, A.: Region-wide glacier mass balances over the Pamir-Karakoram-Himalaya during 1999–2011, The Cryosphere, 7, 1263–1286, https://doi.org/10.5194/tc-7-1263-2013, 2013.
Gardner, A. S., Moholdt, G., Cogley, J. G., Wouters, B., Arendt, A. A., Wahr, J., and Paul, F.: A Reconciled Estimate of Glacier Contributions to Sea Level Rise: 2003 to 2009, Science, 340, 852–857, https://doi.org/10.1126/science.1234532, 2013.
Hall, D., Salomonson, V., and Riggs, G.: MODIS/Terra snow cover daily L3 global 500 m grid, Version 5, Boulder, Colorado USA: National Snow and Ice Data Center, https://doi.org/10.5067/63NQASRDPDB0, 2006.
Huffman, G., Bolvin, D., Braithwaite, D., Hsu, K., Joyce, R., and Xie, P.: Tropical Rainfall Measuring Mission (TRMM) (2011), TRMM (TMPA/3B43) Rainfall Estimate L3 1 month V7, Greenbelt, MD, Goddard Earth Sciences Data and Information Services Center (GES DISC), https://doi.org/10.5067/TRMM/TMPA/MONTH/7, 2014.
Humphrey, V., Gudmundsson, L., and Seneviratne, S. I.: Assessing Global Water Storage Variability from GRACE: Trends, Seasonal Cycle, Subseasonal Anomalies and Extremes, Surv. Geophys., 37, 357–395, https://doi.org/10.1007/s10712-016-9367-1, 2016.
Huss, M.: Density assumptions for converting geodetic glacier volume change to mass change, The Cryosphere, 7, 877–887, https://doi.org/10.5194/tc-7-877-2013, 2013.
Huss, M., Bookhagen, B., Huggel, C., Jacobsen, D., Bradley, R. S., Clague, J. J., Vuille, M., Buytaert, W., Cayan, D., Greenwood, G., Mark, B., Milner, A., Weingartner, R., and Winder, M.: Toward mountains without permanent snow and ice, Earth's Future, 5, 418–435, https://doi.org/10.1002/2016EF000514, 2017.
Immerzeel, W. W., Van Beek, L. P., and Bierkens, M. F.: Climate change will affect the Asian water towers, Science, 328, 1382–1385, https://doi.org/10.1126/science.1183188, 2010.
Jacob, T., Wahr, J., Pfeffer, W., and Swenson, S.: Recent contributions of glaciers and ice caps to sea level rise, Nature, 482, 514–518, https://doi.org/10.1038/nature10847, 2012.
Jansson, P., Hock, R., and Schneider, T.: The concept of glacier storage: a review, J. Hydrol., 282, 116–129, https://doi.org/10.1016/S0022-1694(03)00258-0, 2003.
Kääb, A., Berthier, E., Nuth, C., Gardelle, J., and Arnaud, Y.: Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas, Nature, 488, 495–498, https://doi.org/10.1038/nature11324, 2012.
Kääb, A., Treichler, D., Nuth, C., and Berthier, E.: Brief Communication: Contending estimates of 2003–2008 glacier mass balance over the Pamir–Karakoram–Himalaya, The Cryosphere, 9, 557–564, https://doi.org/10.5194/tc-9-557-2015, 2015.
Kaser, G., Großhauser, M., and Marzeion, B.: Contribution potential of glaciers to water availability in different climate regimes, P. Natl. Acad. Sci. USA, 107, 20223–20227, https://doi.org/10.1073/pnas.1008162107, 2010.
Kusche, J., Schmidt, R., Petrovic, S., and Rietbroek, R.: Decorrelated GRACE time-variable gravity solutions by GFZ, and their validation using a hydrological model, J. Geodesy, 83, 903–913, https://doi.org/10.1007/s00190-009-0308-3, 2009.
Lutz, A. F., Immerzeel, W. W., Shrestha, A. B., and Bierkens, M. F. P.: Consistent increase in High Asia's runoff due to increasing glacier melt and precipitation, Nat. Clim. Change, 4, 587–592, https://doi.org/10.1038/Nclimate2237, 2014.
Matsuo, K. and Heki, K.: Time-variable ice loss in Asian high mountains from satellite gravimetry, Earth Planet. Sci. Lett., 290, 30–36, https://doi.org/10.1016/j.epsl.2009.11.053, 2010.
Ohmura, A.: Observed Mass Balance of Mountain Glaciers and Greenland Ice Sheet in the 20th Century and the Present Trends, Surv. Geophys., 32, 537–554, https://doi.org/10.1007/s10712-011-9124-4, 2011.
Ohno, H., Ohata, T., and Higuchi, K.: The influence of humidity on the ablation of continental-type glaciers, Ann. Glaciol., 16, 107–114, https://doi.org/10.3189/1992AoG16-1-107-114, 1992.
RGI Consortium: Randolph Glacier Inventory – A Dataset of Global Glacier Outlines: Version 6.0: Technical Report, Global Land Ice Measurements from Space, Colorado, USA, Digital Media, https://doi.org/10.7265/N5-RGI-60, 2017.
Rodell, M., Houser, P. R., Jambor, U., Gottschalck, J., Mitchell, K., Meng, C. J., Arsenault, K., Cosgrove, B., Radakovich, J., Bosilovich, M., Entin, J. K., Walker, J. P., Lohmann, D., and Toll, D.: The Global Land Data Assimilation System, B. Am. Meteorol. Soc., 85, 381–394, https://doi.org/10.1175/bams-85-3-381, 2004.
Sakai, A. and Fujita, K.: Contrasting glacier responses to recent climate change in high-mountain Asia, Sci. Rep., 7, 13717, https://doi.org/10.1038/s41598-017-14256-5, 2017.
Shamsudduha, M., Taylor, R., and Longuevergne, L.: Monitoring groundwater storage changes in the highly seasonal humid tropics: Validation of GRACE measurements in the Bengal Basin, Water Resour. Res., 48, W02508, https://doi.org/10.1029/2011WR010993, 2012.
Sun, W., Wang, Q., Li, H., Wang, Y., Okubo, S., Shao, D., Liu, D., and Fu, G.: Gravity and GPS measurements reveal mass loss beneath the Tibetan Plateau: Geodetic evidence of increasing crustal thickness, Geophys. Res. Lett., 36, L02303, https://doi.org/10.1029/2008gl036512, 2009.
Swenson, S. and Wahr, J.: Post-processing removal of correlated errors in GRACE data, Geophys. Res. Lett., 33, L08402, https://doi.org/10.1029/2005gl025285, 2006.
Swenson, S., Chambers, D., and Wahr, J.: Estimating geocenter variations from a combination of GRACE and ocean model output, J. Geophys. Res.-Solid Earth, 113, 1978–2012, https://doi.org/10.1029/2007JB005338, 2008.
Tanck, R. and Fazani, A.: Damming Tibet's Yarlung Tsangpo-Brahmaputra and other South Asian rivers, available at: http://tibetanplateau.blogspot.com/2010/05/damming-tibets-yarlung-tsangpo.html (last access: 5 May 2019), 2010.
Tapley, B. D., Bettadpur, S., Ries, J. C., Thompson, P. F., and Watkins, M. M.: GRACE measurements of mass variability in the Earth system, Science, 305, 503–505, https://doi.org/10.1126/science.1099192, 2004.
Treichler, D. and Kääb, A.: Snow depth from ICESat laser altimetry – A test study in southern Norway, Remote Sens. Environ., 191, 389–401, https://doi.org/10.1016/j.rse.2017.01.022, 2017.
Wang, Q., Yi, S., Chang, L., and Sun, W.: Large-Scale Seasonal Changes in Glacier Thickness Across High Mountain Asia, Geophys. Res. Lett., 44, 10427–10435, https://doi.org/10.1002/2016GL069985, 2017.
Wijngaard, R., Lutz, A., Nepal, S., Khanal, S., Pradhananga, S., Shrestha, A., and Immerzeel, W.: Future changes in hydro-climatic extremes in the Upper Indus, Ganges, and Brahmaputra River basins, PloS one, 12, e0190224, https://doi.org/10.1371/journal.pone.0190224, 2017.
Wouters, B., Chambers, D., and Schrama, E. J. O.: GRACE observes small-scale mass loss in Greenland, Geophys. Res. Lett., 35, L20501, https://doi.org/10.1029/2008gl034816, 2008.
Wu, G., Guan, Y., Liu, Y., Yan, J., and Mao, J.: Air–sea interaction and formation of the Asian summer monsoon onset vortex over the Bay of Bengal, Clim. Dynam., 38, 261–279, https://doi.org/10.1007/s00382-010-0978-9, 2011.
Yang, W., Yao, T., Guo, X., Zhu, M., Li, S., and Kattel, D. B.: Mass balance of a maritime glacier on the southeast Tibetan Plateau and its climatic sensitivity, J. Geophys. Res.-Atmos., 118, 9579–9594, https://doi.org/10.1002/jgrd.50760, 2013.
Yao, T., Thompson, L., Yang, W., Yu, W., Gao, Y., Guo, X., and Joswiak, D.: Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings, Nat. Clim. Change, 2, 663–667, https://doi.org/10.1038/nclimate1580, 2012.
Yi, S. and Sun, W.: Evaluation of glacier changes in high-mountain Asia based on 10 year GRACE RL05 models, J. Geophys. Res.-Sol. Earth, 119, 2504–2517, https://doi.org/10.1002/2013jb010860, 2014.
Yi, S., Sun, W., Feng, W., and Chen, J.: Anthropogenic and climate-driven water depletion in Asia, Geophys. Res. Lett., 43, 9061–9069, https://doi.org/10.1002/2016GL069985, 2016.
Zhang, L. L., Su, F. G., Yang, D. Q., Hao, Z. C., and Tong, K.: Discharge regime and simulation for the upstream of major rivers over Tibetan Plateau, J. Geophys. Res.-Atmos., 118, 8500–8518, https://doi.org/10.1002/jgrd.50665, 2013.






