On the Green's function emergence from interferometry of seismic wave fields generated in high-melt glaciers: implications for passive imaging and monitoring

Ambient noise seismology has revolutionized seismic characterization of the Earth's crust from local to global scales. The estimate of Green's function (GF) between two receivers, representing the impulse response of elastic media, can be reconstructed via cross-correlation of the ambient noise seismograms. A homogenized wave field illuminating the propagation medium in all directions is a prerequisite for obtaining an accurate GF. For seismic data recorded on glaciers, this condition imposes strong limitations on GF convergence because of minimal seismic scattering in homogeneous ice and limitations in network coverage. We address this difficulty by investigating three patterns of seismic wave fields: a favorable distribution of icequakes and noise sources recorded on a dense array of 98 sensors on Glacier d'Argentière (France), a dominant noise source constituted by a moulin within a smaller seismic array on the Greenland Ice Sheet, and crevasse-generated scattering at Gornergletscher (Switzerland). In Glacier d'Argentière, surface melt routing through englacial channels produces turbulent water flow, creating sustained ambient seismic sources and thus favorable conditions for GF estimates. Analysis of the cross-correlation functions reveals non-equally distributed noise sources outside and within the recording network. The dense sampling of sensors allows for spatial averaging and accurate GF estimates when stacked on lines of receivers. The averaged GFs contain high-frequency (>30 Hz) direct and refracted P waves in addition to the fundamental mode of dispersive Rayleigh waves above 1 Hz. From seismic velocity measurements, we invert bed properties and depth profiles and map seismic anisotropy, which is likely introduced by crevassing. In Greenland, we employ an advanced preprocessing scheme which includes match-field processing and eigenspectral equalization of the cross spectra to remove the moulin source signature and reduce the effect of inhomogeneous wave fields on the GFs. At Gornergletscher, cross-correlations of icequake coda waves show evidence for homogenized incident directions of the scattered wave field. Optimization of coda correlation windows via a Bayesian inversion based on the GF cross coherency and symmetry further promotes the GF estimate convergence. This study presents new processing schemes on suitable array geometries for passive seismic imaging and monitoring of glaciers and ice sheets.

1 Introduction

Passive seismic techniques have proven efficient to better understand and monitor glacier processes on a wide range of time and spatial scales. Improvements in portable instrumentation have allowed rapid deployments of seismic networks in remote terrain and harsh polar conditions (Podolskiy and Walter, 2016; Aster and Winberry, 2017). Studies on seismic source processes have revealed unprecedented details about englacial fracture propagation (e.g. Walter et al., 2009; Mikesell et al., 2012), basal processes (e.g. Winberry et al., 2013; Röösli et al., 2016a; Lipovsky et al., 2019), glacier hydrology (Bartholomaus et al., 2015; Gimbert et al., 2016), and iceberg calving (e.g. Walter et al., 2010; Bartholomaus et al., 2012; Sergeant et al., 2016, 2018).

The subsurface structure of ice sheets and glaciers has been characterized by analysis of seismic wave propagation in ice bodies. For example, Harland et al. (2013) and Smith et al. (2017) used records of basal seismicity to measure elastic anisotropy in two Antarctic ice streams. Lindner et al. (2019) identified crevasse-induced anisotropy in an Alpine glacier from velocity anomalies by analyzing icequake seismograms at seismic arrays. Walter et al. (2015) used transient seismic signals generated in moulins to compute frequency-dependent seismic velocities through matched-field processing and estimate the depth of the ice-to-bedrock transition beneath a seismic network deployed on the Greenland Ice Sheet (GIS).

At the same time, a new approach appeared in seismology which explores not only earthquakes but also ambient noise sources generated by climate and ocean activity (Ekström, 2001; Rhie and Romanowicz, 2004; Webb, 1998; Bonnefoy-Claudet et al., 2006). Shapiro and Campillo (2004) and Shapiro et al. (2005) pointed out the possibility of using continuous noise recordings to reconstruct propagating surface waves across a seismic array and to use them for crustal tomography in California. Other studies followed, shaping the analysis of ambient noise background into a powerful tool to constrain the elastic properties of the illuminated medium, making it possible to image the Earth's interior from regional (Yang et al., 2007; Lin et al., 2008) to local scales (e.g. Lin et al., 2013; Nakata et al., 2015) and monitor seismic fault (e.g. Brenguier et al., 2008b; Olivier et al., 2015) and volcanic processes (Sens-Schönfelder and Wegler, 2006; Brenguier et al., 2011), for example. Moreover, ambient noise studies have so far led to original observations such as thermal variations in the subsoil, spatiotemporal evolution of the water content, and stress changes along fault zones with applications to geomechanics, hydrology, and natural hazards (Larose et al., 2015).

For the cryosphere, few studies have successfully used oceanic ambient noise at permanent broadband stations deployed on the rocky margins of glaciers or up to 500 km away on polar ice sheets to monitor the subsurface processes. Mordret et al. (2016) and Toyokuni et al. (2018) tracked the strain evolution in the upper 5 km of the Earth's crust beneath the GIS due to seasonal loading and unloading of the overlaying melting ice mass. More recently, Zhan (2019) detected slowing down of surface wave velocities up to 2 % in the basal till layer of the largest North American glacier (Bering Glacier, 20 km wide) during a surge, likely due to the switch of the subglacial drainage from channelized to distributed.

The underlying seismic interferometry techniques used in ambient noise studies are rooted in the fact that the elastic impulse response between two receivers, Green's function (GF), can be approximated via cross-correlation of a diffuse wave field recorded at the two sites (Lobkis and Weaver, 2001; Campillo et al., 2014). Seismic interferometry consists in turning each of the two receivers into a virtual source and retrieving the estimated elastic response of the medium at the other receiver. Under specific assumptions on the source wave field (see below), the GF estimate is thus expected to be symmetric in its causal and acausal portions (referred to as “causal–acausal symmetry”).

In theory, the GF estimate is obtained in media capable of hosting an equipartitioned wave field, that is random modes of seismic propagation with the same amount of energy. In practice, the equipartition argument has limited applicability to the Earth because nonhomogeneously distributed sources, in the forms of ambient noise sources, earthquakes, and/or scatterers, prevent the ambient wave field from being equipartitioned across the entire seismic scale (Fichtner et al., 2017, and references therein). The GF estimation from inter-station correlation therefore usually relies on simplified approximations of diffusive wave fields which can be reached in (i) the presence of equally distributed sources around the recording network (Wapenaar, 2004; Gouédard et al., 2008b) and/or (ii) in strong-scattering settings as scatterers act like secondary seismic sources and likely homogenize the ambient wave field in all incident directions (e.g. Hennino et al., 2001; Malcolm et al., 2004; Larose et al., 2008). Even if the noise wave field is not generally diffuse (Mulargia, 2012), inhomogeneities in the Earth's crust and the generation of oceanic ambient noise all around Earth make ambient noise interferometry applications generally successful.

In glaciers, the commonly used oceanic ambient noise field lacks the high frequencies needed to generate GFs that contain useful information at the scale of the glacier. To target shallower glaciers and their bed, we must work with other sources such as nearby icequakes and flowing water which excite higher-frequency (>1 Hz) seismic modes (Sect. 2.1). In this context, the lack of seismic scattering in homogeneous ice (Podolskiy and Walter, 2016) renders the reconstruction of the GF from on-ice recordings challenging. Condition (i) can compensate for lack of condition (ii). However, microseismicity generated on glaciers is often confined to narrow regions such as crevasse margin zones (Roux et al., 2008; Mikesell et al., 2012) or other water-filled englacial conduits (Röösli et al., 2014; Walter et al., 2015; Preiswerk and Walter, 2018; Lindner et al., 2020). This often prevents the occurrence of homogeneous source distributions on glaciers. Nevertheless, the abundance of local seismicity indicates a considerable potential for glacier imaging and monitoring with interferometry.

Few attempts have been conducted on glaciers to obtain GF estimates from on-ice seismic recordings. Zhan et al. (2013) first calculated ambient noise cross-correlations on the Amery ice shelf (Antarctica) but could not compute accurate GF at frequencies below 5 Hz due to the low-velocity water layer below the floating ice shelf, which causes resonance effects and a significantly nondiffusive inhomogeneous noise field. Preiswerk and Walter (2018) successfully retrieved an accurate GF on two Alpine glaciers from the cross-correlation of high-frequency (≥2 Hz) ambient noise seismograms, generated by meltwater flow. However, due to localized noise sources in the drainage system that also change positions over the course of the melting season, they could not systematically obtain an accurate coherent GF when computed for different times, limiting the applications for glacier monitoring.

As an alternative to continuous ambient noise, Walter et al. (2015) used crevassing icequakes recorded during a 1-month seismic deployment at Gornergletscher (Switzerland). They recorded thousands of point source events which offered an idealized spatial source distribution around one pair of seismic sensors and could obtain accurate GF estimates. To overcome the situation of a skewed illumination pattern often arising from icequake locations, Lindner et al. (2018) used multidimensional deconvolution (Wapenaar et al., 2011; Weemstra et al., 2017) that relies on a contour of receivers enclosing the region of interest (see also Sect. 6.2). This technique proved to be efficient to suppress spurious arrivals in the cross-correlation function which emerge in the presence of heterogeneously distributed sources. However, this method was applied to active sources and synthetic seismograms, and its viability still needs to be addressed for passive recordings.

In this study, we provide a catalogue of methods to tackle the challenge of applying passive seismic interferometry to glaciers in the absence of significant scattering and/or an isotropic source distribution. After a review on glacier seismic sources (Sect. 2.1), we investigate the GF retrieval on three glacier settings with different patterns of seismic wave fields. In a first ideal case (Glacier d'Argentière in the French Alps, Sect. 3), we take advantage of a favorable distribution of noise sources and icequakes recorded on a dense array. In a second case (GIS, Sect. 4), a dominant persistent noise source constituted by a moulin prevents the accurate estimate of the GF across the array. We use a recently proposed scheme (Corciulo et al., 2012; Seydoux et al., 2017) that involves matched-field processing to remove the moulin signature and improve the GF estimates. In a third case (Gornergletscher in Swiss Alps, Sect. 5), the limited distribution of icequakes is overcome by the use of crevasse-generated scattered coda waves to obtain homogenized diffuse wave fields before conducting cross-correlations. In order to serve as a practical scheme for future studies, the three above sections are nearly independent from each other. They focus on the processing schemes to compute or improve the GF estimates. We refer the reader who is not familiar with ambient noise seismic processing to the appendix sections providing details on seismic detection methods, seismic array processing, and seismic velocity measurements. Finally, in light of our analysis, we discuss suitable array geometries and measurement types for future applications of passive seismic imaging and monitoring studies on glaciers.

2 Material and data

2.1 Glacier seismic sources

Glaciogenic seismic waves couple with the bulk Earth and can be recorded by seismometers deployed at local (Podolskiy and Walter, 2016) to global ranges (Ekström et al., 2003). In this study, we focus on three classes of local sources. For an exhaustive inventory of glacier seismicity and associated source mechanisms, we refer to the review papers of Podolskiy and Walter (2016) and Aster and Winberry (2017).

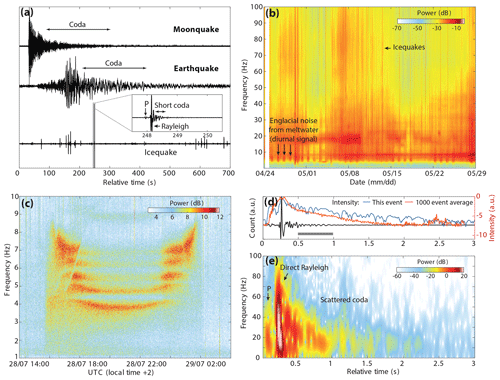
Figure 1 (a) Seismograms of a moonquake, regional earthquake, and typical Alpine glacier seismicity. Moonquake seismogram was recorded during the 1969–1977 Apollo passive seismic experiment (Nunn, 2017). Zoom on icequake waveform shows the lack of sustained coda in homogeneous ice when compared to other signals propagating in crustal rocks. (b) Spectrogram of 1 month of continuous recording at Glacier d'Argentière (French Alps) showing abundance of icequakes (5–100 Hz) and englacial noise (2–30 Hz) produced by turbulent meltwater flow. (c) Spectrogram for a 10 h long hydraulic tremor produced by the water moulin activity within the Greenland Ice Sheet network (Fig. 2b). (d) Seismic waveform and associated spectrogram (e) for one icequake recorded at Gornergletscher (Swiss Alps). Color lines in (d) are the signal intensity (see main text, Sect. 5.1) for this event in blue and averaged over 1000 events in orange (right y axis; note the logarithmic scale). The horizontal gray bar indicates the coda window which is used to generate the first estimations of Green's functions (Sect. 5.2).

Typically on Alpine glaciers and more generally in ablation zones, the most abundant class of recorded seismicity is related to brittle ice failure which leads to the formation of near-surface crevasses (e.g. Neave and Savage, 1970; Mikesell et al., 2012; Röösli et al., 2014; Podolskiy et al., 2019) and the generation of 10²–10³ daily recorded icequakes (Fig. 1a and b). Near-surface icequakes have local magnitudes of −1 to 1, and seismic waves propagate a few hundred meters before falling below the background noise level. Icequake waveforms have durations of 0.1–0.2 s and thus do not carry much energy at frequencies below 5 Hz (Fig. 1d and e). With its maximum amplitude on the vertical component, Rayleigh waves dominate the seismogram. In contrast, the prior P-wave arrival is substantially weaker and for distant events often below noise level. Rayleigh waves propagate along the surface and are not excited by a source at depth exceeding one wavelength (Deichmann et al., 2000). In addition, the crevasse zone is mostly confined to the surface (≤30 m) since ice-overburden pressure inhibits tensile fracturing at greater depths (Van der Veen, 1998). That is why such icequakes are usually considered to originate at shallow depth (Walter, 2009; Roux et al., 2010; Mikesell et al., 2012). The short duration and weak seismic coda after the Rayleigh wave arrival (compared to earthquake coda propagating in the crust, Fig. 1a; see also further details in Sect. 5.1) are the result of limited englacial scattering. This typically allows seismologists to approximate the glacier's seismic velocity model by a homogeneous ice layer on top of a rock half-space when locating events or modeling seismic waveforms (e.g. Walter et al., 2008, 2015).

From spring to the end of summer, another seismic source superimposes on icequake records and takes its origin in fluvial processes. Ice melting and glacier runoff create turbulent water flow at the ice surface that interacts with englacial and subglacial linked conduits. Gravity-driven transport of meltwater creates transient forces on the bulk of the Earth (e.g. Schmandt et al., 2013; Gimbert et al., 2014) and surrounding ice (Gimbert et al., 2016) that generate a mix of body and surface waves (Lindner et al., 2020; Vore et al., 2019). Meltwater flow noise is recorded continuously at frequencies of 1–20 Hz as shown in the 1-month spectrogram of ground velocity at Glacier d'Argentière (Fig. 1b). Seismic noise power shows diurnal variations that are correlated with higher discharge during daytime and reduced water pressure at night (Preiswerk and Walter, 2018; Nanni et al., 2019b).

Englacial and subglacial conduits can also generate acoustic (Gräff et al., 2019) and seismic wave resonances (Röösli et al., 2014) known as hydraulic tremors. In the presence of moulin, water flowing to the glacier base creates seismic tremors (Fig. 1c) which often dominate the ambient noise during peak melt hours. Frequency bands of either elevated or suppressed seismic energy reflect the geometry of the englacial conduit as it acts as a resonating semi-open pipe, modulated by the moulin water level (Röösli et al., 2016b).

Finally, in Alpine environments, seismic signatures of anthropogenic activity generally overlap with glacier ambient noise at frequencies >1 Hz. Whereas anthropogenic monochromatic sources can usually be distinguished by their temporal pattern (Preiswerk and Walter, 2018), separation of all active sources recorded on glacier seismograms can prove difficult. Nevertheless, locating the source regions through matched-field processing (Corciulo et al., 2012; Chmiel et al., 2015) can help to identify the noise source processes in glaciated environments (Sect. 4).

2.2 Study sites and seismic experiments

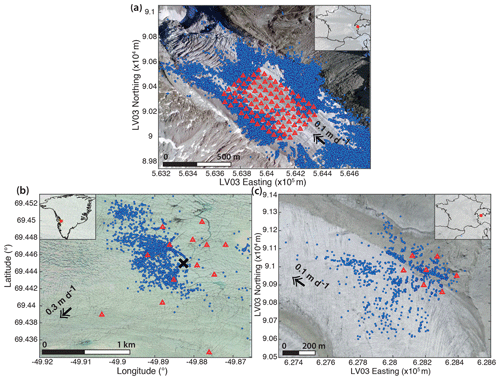
Figure 2 Icequake locations (blue dots) and seismic stations (red triangles) superimposed on aerial photographs of (a) Argentière (© IGN France), (b) the Greenland Ice Sheet (©  Google, Mixar Technologies), and (c) Gornergletscher (© swisstopo, SWISSIMAGE). The black arrows indicate ice flow direction. Black cross in (b) indicates the location of the moulin within the array.

We use seismic recordings from three seasonally deployed networks in the ablation zones of two temperate Alpine glaciers and of the GIS. Each of the acquired datasets presents different patterns of seismic wave fields corresponding to the three configurations investigated for GF estimate retrieval, as defined in the introduction. All networks recorded varying numbers of near-surface icequakes (blue dots in Fig. 2a–c). Different processing schemes were used to constitute the icequake catalogues and are detailed in Appendix A. In this study we only use vertical component data of ground velocity to generate vertical-to-vertical cross-correlation functions which primarily contain the Rayleigh wave fundamental mode (Shapiro and Campillo, 2004). Some of the datasets involve surface seismometers whose horizontal components are regularly shifted over the course of the melting season. Obtaining GF estimates from horizontal component data requires additional preprocessing to obtain accurate orientations of the seismic sensors.

2.2.1 Glacier d'Argentière array

The Argentière seismic array (Fig. 2a) was deployed in late April 2018 and recorded for 5 weeks. It consists of 98 three-component surface sensors regularly spaced on a grid with a 350 m×480 m aperture and a station-to-station spacing of ∼40 m for the along-flow profiles and ∼50 m for the across-flow profiles. This large N-array experiment used the technology of nodes (Fairfield Nodal ZLand 3C) that combine a geophone, digitizer, battery, data storage, and GPS in a single box (Hand, 2014) and allowed a rapid deployment within a few hours. ZLand geophones have a natural frequency of 5 Hz and recorded continuously at a sampling rate of 500 Hz. Besides seismic sensors, four on-ice GPS instruments were deployed. At the array site, the ice is 80–260 m thick (Hantz, 1981) and flows at an approximate rate of 0.1 m d⁻¹. The sensors were placed about 30 cm into the snow and accumulated about 4 m of downstream displacement at the end of the experiment. Because of snowmelt, we had to level and reorient the instruments twice during the experiment. A digital elevation model (DEM) for the glacier bed was obtained using 14 ground-penetrating radar tracks over the area covered by the seismic array, and a glacier surface DEM was acquired from a drone survey.

2.2.2 Greenland Ice Sheet array

The GIS network (Fig. 2b) was deployed 30 km north of the calving front of the Jakobshavn Isbræ from 2 July to 17 August 2011. The details of the study site and the seismic network can be found in Röösli et al. (2014), Ryser et al. (2014), and Andrews et al. (2014). We use seismic recordings from 13 stations: 12 seismometers (1 Hz Lennartz) installed on the surface or shallow boreholes (2–3 m deep), and one surface broadband seismometer (Trillium Compact 120 s corner period). Seismometers recorded continuously with a sampling frequency of 500 Hz. The array has a 1.8 km aperture. It is located around a prominent moulin with an average intake of 2.5 m³ s⁻¹ of meltwater. At the study site, the ice is approximately 600 m thick and flows at ∼0.3 m d⁻¹ (Röösli et al., 2016a).

2.2.3 Gornergletscher array

The Gornergletscher network (Fig. 2c) operated between 28 May and 22 July 2007. It consists of seven seismometers (six 8 Hz Geospace 11D and one 28 Hz Geospace 20D) installed in shallow boreholes (2–3 m deep). They recorded continuously with a sampling frequency of 1000 Hz. The array has a 320 m aperture. At the study site, the ice is approximately 160 m thick and flows at $\sim \mathrm{0.1}\mathrm{m}{\mathrm{d}}^{-\mathrm{1}}$ (Walter, 2009).

3 Passive interferometry at the Glacier d'Argentière dense array

We use a standardized processing scheme for computing GF estimates here. We either cross-correlate seismogram time windows, which encompass ballistic seismic waves of the icequake catalogue, or cross-correlate continuous seismograms as traditionally done in ambient noise studies. Prior to any calculation, seismic records are corrected for instrumental response and converted to ground velocity. Seismograms are then spectrally whitened between 1 and 50 Hz because of low instrumental sensitivity at lower frequency.

For icequake cross-correlation (ICC), we follow the method of Gouédard et al. (2008b) and Walter et al. (2015) on 11.1×10³ events. The length of the correlation window T is adjusted to the nature of seismic sources and the array aperture. Here we use T=0.5 s given the short icequake duration and the maximum station separation of 690 m. To avoid near-field source effects and to account for near-planar wave fronts, we select events that lie outside a circle centered at the midpoint between the two considered stations and with a radius equal to the inter-station distance (Fig. B4a). The plane wave approximation implies a sinusoidal dependence of the arrival times with respect to event azimuth (Fig. B4b). When stacking the individual ICC on all events, only the sources that lie in the stationary phase zones, i.e. aligned with the two-receiver direction, actually contribute to the GF (Gouédard et al., 2008b). The aperture of the stationary phase zones, also called “the endfire lobes” (Fig. B4a), depends on the considered seismic wavelength (Roux et al., 2004). In the case of anisotropic source distribution, the contribution of nonstationary sources eventually does not vanish and gives rise to spurious arrivals in the final GF estimate. Prior to stacking, we assign all cross-correlations to event azimuth bins of 5^∘ to attribute equal weights to all incident directions. To reduce eventual spurious arrivals, we compute the GF on selected sources in the endfire lobes whose aperture is calculated for maximum wavelengths corresponding to 3 Hz (Appendix B3).

For noise cross-correlation (NCC), we use a similar protocol as the one of Preiswerk and Walter (2018). To reduce the effects of teleseismic events or the strongest icequakes, we disregard the seismic amplitudes completely and consider 1-bit normalized seismograms (Bensen et al., 2007). By doing so, we attribute a similar weight to ambient noise and icequake source contributions to the GF. The traces are cross-correlated in nonoverlapping 30 min long windows. Resulting NCCs are stacked daily and then averaged over the 5 weeks of recording. We finally obtain a set of 4371 NCCs that corresponds to the GF estimates for all combinations of sensor pairs.

3.1 Green's function estimates

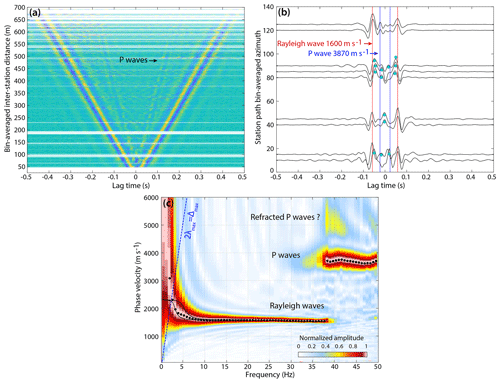
Figure 3 (a) Noise cross-correlations (NCCs) sorted by increasing inter-station distances at Glacier d'Argentière. For the representation, correlation functions are averaged in 1 m distance bins and band-pass filtered between 10 and 50 Hz to highlight the presence of high-frequency P waves. (b) Azimuthal dependence of GF estimates for pairs of stations 100 m apart. Accurate GF estimates are obtained at station paths roughly aligned with the glacier flow (azimuth $\sim \mathrm{120}{}^{\circ }$), indicating more noise sources likely located downstream and upstream of the array. For other station paths, we observe spurious arrivals (indicated by green dots) before the expected arrival times for Rayleigh (red bars) and P waves (blue bars) which primarily arise from non-distributed noise sources that lie outside the stationary phase zones of these stations (see main text). (c) Frequency–velocity diagram obtained from f-k (frequency–wavenumber) analysis of NCC in (a). The dispersion curve of phase velocity for Rayleigh waves and P waves is plotted as black dots. The dashed blue line shows the frequency-dependent resolution limit, given the maximum wavelength and sensor spacing ${\mathit{\lambda }}_{max}={\mathrm{\Delta }}_{max}/\mathrm{2}$. Black lines are theoretical dispersion curves for fundamental mode Rayleigh wave velocity computed for ice thickness of either 150 or 250 m with Geopsy software. We used the elastic parameters for the ice and bedrock as given in Preiswerk and Walter (2018, Sect. 6.1). The same figure for icequake cross-correlations is available in Appendix (Fig. B2).

Figure 3a shows the stacked section of NCCs averaged in 1 m binned distance intervals. Coherent Rayleigh waves with propagation velocity of 1600 m s⁻¹ are well reconstructed across the array. We also observe emergence of weak but faster waves identified at higher frequencies as P waves traveling in the ice.

Slight disparities in amplitudes of the causal and acausal parts of the GF estimates (positive versus negative times) are related to the noise source density and distribution. Higher acausal amplitudes observed at larger distances are evidence for a higher density of sources located downstream of the array, according to our cross-correlation definition. More sources downstream are likely generated by faster water flow running into subglacial conduits toward the glacier icefall (Gimbert et al., 2016; Nanni et al., 2019b). Looking closer at NCC for individual receiver pairs, we sometimes observe spurious arrivals around time 0 (marked as green dots in Fig. 3b), mostly at station pairs oriented perpendicular to the glacier flow (i.e. azimuth $\mathrm{0}{}^{\circ }\le \mathit{\varphi }\le \mathrm{50}{}^{\circ }$), indicating that dominant noise sources are located along the flow line. At other station pairs (i.e. azimuth $\mathit{\varphi }\sim \mathrm{90}{}^{\circ }$), the reconstructed arrival times are slightly faster than expected. This could be an effect of non-distributed noise sources and/or anisotropy introduced by englacial features (Sect. 3.3). This analysis shows that even if the noise sources are not equally distributed in space, averaging the NCC in regular distance intervals on a dense array deployment helps the GF estimate convergence.

The stacked section of ICCs (Fig. B2a) yields similar results to those of the NCC (Fig. 3a). The control of the icequake source aperture enables us to minimize the spurious arrivals which are observed on some NCC (Fig. 3b) and obtain more accurate Rayleigh wave travel times at most station paths (Fig. B2b). The differences in ICC and NCC support that NCCs are more sensitive to the noise sources rather than icequake sources. Icequake contributions certainly enable us to widen the spectral content of the NCC to frequencies higher than 20 Hz, as the most energetic ambient noise is recorded in the 1–20 Hz frequency band (Fig. 1b).

Seismic phases and their velocities can be identified on the frequency–velocity diagram (Fig. 3c, black dots) that is obtained from frequency–wavenumber (f-k) analysis of the NCC computed on a line of receivers (Appendix B1). As identified above, the correlation functions reconstruct P waves traveling in the ice well with an average velocity V_p=3870 m s⁻¹. We also observe weak intensity but fast seismic phases at frequencies above 35 Hz, which could correspond to refracted P waves traveling along the basal interface with a velocity around 5000 m s⁻¹.

Surface waves are dispersive, meaning that their velocity is frequency-dependent, with higher frequencies being sensitive to surface layers and conversely lower frequencies being sensitive to basal layers. Theoretical dispersion curves for Rayleigh wave fundamental mode are indicated as black solid lines in Fig. 3c. They correspond to a two-layer model with the top ice layer of thickness H=150 m and H=250 m over a semi-half-space representing the bedrock. The dashed blue line indicates the array resolution capability that corresponds to the maximum wavelength limit ${\mathit{\lambda }}_{max}={\mathrm{\Delta }}_{max}/\mathrm{2}$ (Wathelet et al., 2008), with Δ_max being the maximum sensor spacing. Reconstruction of Rayleigh waves and resolution of their phase velocities using f-k processing are differently sensitive for NCC and ICC at frequencies below 5 Hz (Fig. 3c versus Fig. B2c) as ICCs have limited energy at low frequency (Fig. 4a) due to the short and impulsive nature of icequake seismograms (Fig. 1d and e). Given the vertical sensitivity kernels for Rayleigh wave phase velocity (Fig. 4b) and the dispersion curves obtained from the cross-correlation sections (Figs. 3c and B2c), Rayleigh waves that are reconstructed with NCC are capable of sampling basal ice layers and bedrock while ICCs are more accurately sensitive to the ice surface. These results reflect the S-wave velocity dependence on depth.

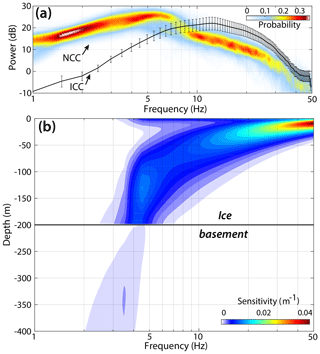
Figure 4 (a) Probability density function of noise cross-correlation (NCC) spectra (colors) and median average of icequake cross-correlation (ICC) spectra (black line). Note that raw data (i.e continuous noise or icequake waveforms) were spectrally whitened between 1 and 50 Hz prior to cross-correlation. Due to spectral content of englacial noise and icequakes, NCCs and ICCs have different depth sensitivity due to spectral response. (b) Vertical sensitivity kernels for phase velocities of the Rayleigh wave a fundamental mode for an ice thickness of 200 m over a semi-half-space representing the bedrock. The kernels were computed using the freely available code of Haney and Tsai (2017).

3.2 Dispersion curve inversion and glacier thickness estimation

Sensitivity of Rayleigh waves obtained on NCC to frequencies below 5 Hz enables us to explore the subsurface structure with inversions of velocity dispersion curves. Due to the general noise source locations up-flow and down-flow of the network, we limit our analysis to receiver pairs whose accurate GF could be obtained. We thus compute the dispersion curves on eight along-flow receiver lines which constitute the array (inset map in Fig. 5). For each line, we invert the 1-D ground profile which best matches seismic velocity measurements in the 3–20 Hz frequency range, using the neighborhood algorithm encoded in the Geopsy software (Wathelet, 2008).

Following Walter et al. (2015), we assume a two-layer medium consisting of ice and granite bedrock. This is a simplified approximation and does not include 2-D and 3-D effects and anisotropy introduced by englacial features (Sect. 3.3). The grid search boundaries for seismic velocity, ice thickness, and density are given in Table 1. We fix the seismic P-velocity in ice to 3870 m s⁻¹ as measured in Fig. 3c and couple all varying parameters to the S-wave velocity structure with the imposed condition of increasing velocity with depth.

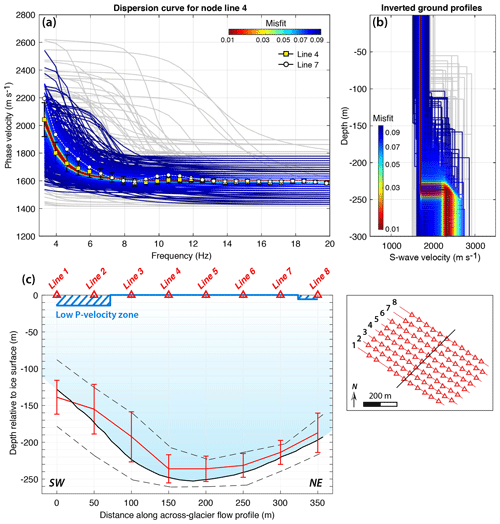
Figure 5 Inversion of glacier thickness using velocity dispersion curves of Rayleigh waves and the Geopsy neighborhood algorithm. Dispersion curve measurements are obtained from f-k analysis of noise cross-correlations on eight receiver lines whose geometry is described in the bottom-right panel. (a, b) Color-coded population of (a) dispersion curve fits and (b) S-wave velocity profiles for the node along-flow line labeled 4 in (c). Warmer colors correspond to smaller misfit, and gray lines correspond to models with misfit values higher than 0.1. In (a) the dispersion curve and uncertainties obtained from seismic measurements are overlaid in yellow squares. For comparison, the dispersion curve computed for the node line 7 and associated with a thinner ice layer is plotted in white dots. (c) Across-flow profile of (red line) ice thickness estimates from Rayleigh wave velocities obtained at eight along-flow node lines and (black line) average basal topography from a DEM. Dashed blue zones indicate the presence of a low P-velocity top layer from seismic inversions. Uncertainties in ice thickness estimates (red error bars) correspond to seismic inversion results which yield to a misfit lower than 1 standard deviation of misfit values from the 2500 best-fitting models. Black dashed lines indicate deviations from the glacier baseline around each node line due to longitudinal topography gradients.

Figure 5a and b show the inversion results for the receiver line at the center of the array labeled “4”. Velocity measurements are indicated by yellow squares, and dispersion curves corresponding to explored velocity models are in colors sorted by misfit values. Misfit values correspond here to the root-mean-square error on the dispersion curve residuals, normalized by the uncertainty average we obtained from the seismic data extraction (error bars in Fig. 5a). The inversion resolves the S-wave velocity in the ice layer well as all best matching models yield to $V_{\mathrm{s}}=\mathrm{1707}\mathrm{m}{\mathrm{s}}^{-\mathrm{1}}$ for misfit values below 0.05, meaning that the data dispersion curve is adjusted with an approximate error below 5 %. The best-fitting model gives a 236 m thick ice layer and bedrock S velocity of 2517 m s⁻¹. Walter et al. (2015) explored the sensitivity of the basal layer depth to the other model parameters and reported a trade-off leading to an increase in inverted ice thickness when increasing both ice and bedrock velocities. Here the ice thickness estimation is most influenced by the rock velocities as we notice that a 100 m s⁻¹ increase in basal S velocity results in an increase in ice thickness up to 15 m. These results are moreover influenced by larger uncertainties at lower frequencies (Fig. 5a), which comes from less redundant measurements at large distances. Furthermore, 3-D effects could lead to some errors in the depth inversion results which need to be further investigated.

From the eight receiver line inversions, we find average S-wave velocities of 1710 m s⁻¹ for the ice and 2570 m s⁻¹ for the granite and a P-wave velocity of 4850 m s⁻¹ in the basement, which is consistent with our measurement for refracted P waves in Fig. 3c. V_p∕V_s ratios are found to be 2.2 and 1.9 for ice and granite, giving Poisson's ratios of 0.37 and 0.3, respectively. For the receiver lines near the array edges (lines 1–3 and 8), the inversion yields to a low P-velocity surface layer of 15 and 7 m thickness, respectively, above thicker ice (dashed blue zone in Fig. 5c). In this thin top layer, the matching S velocity corresponds to the one for the ice (i.e. 1710 m s⁻¹). The V_p∕V_s ratio is around 1.6 and corresponds to a Poisson's ratio of 0.2. This is what is expected for snow, although only a ∼5 m snow cover was present in the area at the time of the experiment. This low-velocity surface layer could also at least be partially attributed to the presence of pronounced transversal crevasses (i.e. perpendicular to the receiver lines; see Sect. 3.3) near the array edges, which do not extend deeper than a few dozens of meters (Van der Veen, 1998) and can be modeled as a slow layer above faster ice (Lindner et al., 2019).

Inversion results for the ice thickness are plotted in red in Fig. 5c. Associated uncertainties (red error bars) are given by the models which fit the dispersion curves with misfit values below 1 standard deviation of the 2500 best-fitting models. The errors on the basal interface depth generally correspond to a maximum misfit value of 0.02. The black solid line shows the across-flow profile of the glacier baseline, which was extracted from the DEM of Glacier d'Argentière (Sect. 2.2.1) and averaged over the geophone positions. Results show that ambient noise interferometry determines the depth of the basal interface with a vertical resolution of 10 m, equivalent to ∼5 % accuracy relative to the average depth, as we are able to reproduce the transverse variations in the ice thickness. Differences in ice thickness values between our measurements and the DEM are generally less than 20 m (the DEM resolution), and the maximum error is 35 m for line 3.

Table 1 Parameter ranges and fixed parameters for grid search to invert the dispersion curves in Fig. 5 for ice thickness. Poisson's ratios of ice and granite were varied between 0.2 and 0.5. Poisson's ratio, ice thickness, and P-wave velocity V_p were coupled to the S-wave velocity V_s.

Errors and uncertainties on mapping the basal interface are primarily linked to bedrock velocities, as discussed above. Potentially, the bed properties can be refined using additional measurements from refracted P waves that should be reconstructed on NCC obtained on such a dense and large array and stacked over longer times. Ice thickness estimation is also affected by 2-D and 3-D effects as phase velocities are averaged here over multiple receiver pairs. The confidence interval we obtain for basal depth is of a similar order to the actual variations in glacier thickness along the receiver lines (black dashed lines). More accurate 3-D seismic models of the glacier subsurface could be obtained using additional station pairs as discussed in Sect. 6.

3.3 Azimuthal anisotropy from average phase velocities

Smith and Dahlen (1973) show that for a slightly anisotropic medium the velocity of surface waves varies in 2ϕ-azimuthal dependence according to

$$\begin{array}{}\text{(1)}& c\left(\mathit{\varphi }\right)=c_{\mathrm{0}}+A\cos \left[\mathrm{2}\right(\mathit{\varphi }-\mathit{\psi }\left)\right],\end{array}$$

where c₀ is the isotropic component of the phase velocity, A is the amplitude of anisotropy, and ψ defines the orientation of the anisotropic fast axis. On glaciers, azimuthal anisotropy can be induced by englacial crevasses, with fast direction for Rayleigh wave propagation being expected to orient parallel to the crack alignment (Lindner et al., 2019). Glacier and ice sheets are also represented as transversely isotropic media whose type of symmetry depends on the ice fabric (e.g. Diez and Eisen, 2015; Horgan et al., 2011; Smith et al., 2017; Picotti et al., 2015).

The dense array experiment of Glacier d'Argentière covers a wide range of azimuths ϕ defined by the orientation of the station pairs and allows us to investigate azimuthal variation in Rayleigh wave velocities at any given sensor. In order to cover a maximum range of ϕ-azimuth, we compute velocity dispersion curves for Rayleigh waves obtained for the correlation functions computed on icequake signals (ICCs), since accurate GF estimates from ambient noise are limited to station pair directions with azimuth ϕ roughly aligned with ice flow ($\mathit{\varphi }\sim \mathrm{120}{}^{\circ }$, Sect. 3.1). To measure phase velocities at different frequencies, we apply a slant-stack technique similar to that of Walter et al. (2015) to octave-wide frequency ranges by band-pass filtering the individual ICC, at each station pair (Appendix B3).

For each sensor position, we obtain c velocity measurements as a function of the ϕ-azimuth of the receiver pair that includes the target station. To reduce the effect of spatial averaging, we compute anisotropy parameters ψ and A considering subarrays of stations that lie within 250 m of the target point (inset map in Fig. 6a). ψ and A values are found at each station cell by fitting c(ϕ) with Eq. (1) using a Monte Carlo inversion scheme. Note that the formulation of Eq. (1) also gives rise to an additional 4ϕ dependence of velocities. Lindner et al. (2019) used a beam-forming approach on icequake records at 100 m aperture arrays and found that adding the 4ϕ component to describe the azimuthal variations in phase velocities induced by glacier crevasses yields similar ψ and A. We therefore neglect the 4ϕ term in the present analysis.

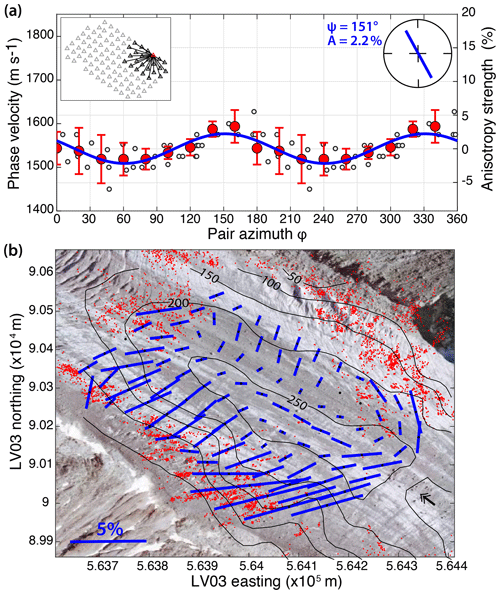
Figure 6 (a) Azimuthal variation in phase velocities measured at one node (red triangle in the inset map). White dots are the phase velocity measurements obtained for different azimuths ϕ that are defined by the station pair orientation. To avoid spatial averaging, we only consider subarrays of 250 m aperture around the target node at the center as described by black triangles in the inset map. Red dots are phase velocities averaged in 20^∘ azimuth bins. The thick blue curve is the best fit for the 2ϕ azimuthal variation in the averaged velocity measurements in red. Fast-axis angle and anisotropy strength are indicated in the top right corner circle. (b) Map of fast-axis direction and amplitude of anisotropy measured at 25 Hz, superimposed on an orthophotograph (© IGN France). Locations of icequakes active for 7 d are plotted in red dots to highlight the orientations of surface crevasses. Basal topography contour lines are indicated every 50 m. The black arrow indicates ice flow direction.

Anisotropy is observed to be more pronounced near the glacier margins (lines 1–2 and 8 as labeled in Fig. 5c), where the anisotropy strength varies between 2 % and 8 % (Fig. 6b). There, fast-axis directions of Rayleigh wave propagation coincide with the observed surface strike of the ice-marginal crevasses that are also responsible for the generation of icequakes indicated by red dots. At other locations, fast-axis directions indicate the presence of transversal crevasses (i.e. perpendicular to the ice flow) with weaker degrees of anisotropy up to 4 %. While the near-surface crevasses observed at the array edges result from shear stress from the margin of the glacier, the transversal crevasses are formed by longitudinal compressing stress from lateral extension of the ice away from the valley side walls, which is typical for glacier flow dynamics in ablating areas (Nye, 1952).

Alignment of the fast-axis directions with that of ice flow appears along the central lines of the glacier (receiver lines 4–5) with anisotropy degrees of 0.5 % to 1.5 %. This feature is only observed along the deepest part of the glacier where it flows over a basal depression. Results are here computed for seismic measurements at 25 Hz, and maps of anisotropy do not change significantly with frequency over the 15–30 Hz range. If we extend our analysis down to 7 Hz, we notice that the aligned-flow fast-axis pattern starts to become visible at 10 Hz. At frequencies lower than 10 Hz, the fast-axis generally tends to align perpendicular to the glacier flow because lateral topographic gradients introduce 3-D effects and nonphysical anisotropy. The results presented here are not punctual measurements but are rather averaged over the entire ice column. The vertical sensitivity kernels for Rayleigh waves (Fig. 4b) are not zero in the basal ice layers at the considered frequencies. The align-flow anisotropic pattern is likely attributed to a thin water-filled conduit at depth, as also suggested by locations of seismic hydraulic tremors at the study site (Nanni et al., 2019a).

Generally, we observe an increase in the degree of anisotropy with frequency, which is evident for a shallow anisotropic layer. Conversely, an increase in anisotropy strength at lower frequency would indicate a deeper anisotropic layer. At the Alpine plateau Glacier de la Plaine Morte, Lindner et al. (2019) find azimuthal anisotropy at frequencies of 15–30 Hz with strength up to 8 %. They also find that constraining the depth of the anisotropy layer is not straightforward as there exists a trade-off between its thickness and the degree of anisotropy. Without any further modeling effort, we refrain from further interpreting our results in terms of crevasse extent and depth of the anisotropic layer or any other cause for the observed patterns.

4 Matched-field processing of englacial ambient seismic noise

As pointed out earlier, localized englacial noise sources related to water drainage can prevent the reconstruction of stable GF estimates by introducing spurious arrivals (i.e. Walter, 2009; Zhan et al., 2013; Preiswerk and Walter, 2018). In this case, the workflow processing traditionally used in the NCC procedure as presented in Bensen et al. (2007) and Sect. 3 is not sufficient. Accordingly, we need to apply more advanced processing methods that can reduce the influence of localized sources and enhance a more isotropic distribution of the ambient sources around receiver pairs.

One of the approaches we apply here is matched-field processing (MFP) (Kuperman and Turek, 1997), which is an array processing technique allowing the location of low-amplitude sources. MFP is similar to traditional beam forming that is based on phase-delay measurements. MFP was used for location and separation of different noise sources in various applications, i.e., to monitor geyser activity (Cros et al., 2011; Vandemeulebrouck et al., 2013), in an exploration context (Chmiel et al., 2016), and in geothermal field (Wang et al., 2012) and fault zone (Gradon et al., 2019) event detection. MFP was also used by Walter et al. (2015) to measure phase velocities of moulin tremor signals on the GIS.

Moreover, joint use of MFP and the singular value decomposition (SVD) of the cross-spectral density matrix allows the separation of different noise source contributions, as in multi-rate adaptive beam forming (MRABF: Cox, 2000). The SVD approach was explored by Corciulo et al. (2012) to locate weak-amplitude subsurface sources, and Chmiel et al. (2015) used it for microseismic data denoising. Also, Seydoux et al. (2017) and Moreau et al. (2017) showed that the SVD-based approach improves the convergence of NCC towards the GF estimate. Here, we combine MFP and SVD in order to remove spurious arrivals in NCC caused by the moulin located within the GIS array and thus improve the GF estimate emergence.

4.1 Location of noise sources at the GIS via matched-field processing

Röösli et al. (2014) and Walter et al. (2015) documented the presence of hour-long tremor signals in GIS seismic records, typically starting in the afternoon hours. These events occurred on 29 d out of the 45 d total monitoring period. Signal intensity and duration depended on the days of observations, and the energy was mostly concentrated in the 2–10 Hz range within distinct frequency bands (Fig. 1b). Röösli et al. (2014) and Röösli et al. (2016b) showed a clear correlation between water level in the moulin and start and end times of the tremor; therefore the tremor signal is referred to as “moulin tremor”. Figure 1c shows a spectrogram of a moulin tremor lasting for 10 h on the night of 28–29 July 2011 and recorded at one station located 600 m away from the moulin. This signal is generated by the water resonance in the moulin, is coherent over the entire array, and dominates the ambient noise wave field during peak melt hours (Röösli et al., 2014; Walter et al., 2015).

We briefly summarize the basics of MFP, and the details of the method can be found in Cros et al. (2011), Walter et al. (2015), and Chmiel et al. (2016). MFP exploits the phase coherence of seismic signals recorded across an array. It is based on the match between the cross-spectral density matrix (CSDM) and a modeled GF. The CSDM captures the relative phase difference between the sensors, as it is the frequency-domain equivalent of the time-domain correlation of the recorded data. The CSDM is a square matrix with a size equivalent to the number (N=13 for the GIS array) of stations (N-by-N matrix). MFP is a forward propagation process. It places a “trial source” at each point of a search grid, computes the model-based GF on the receiver array, and then calculates the phase match between the frequency-domain-modeled GF and the Fourier transform of time-windowed data. The optimal noise source location is revealed by the grid points with maximum signal coherence across the array.

In order to calculate the MFP output, we use 24 h data of continuous recordings on 27 July which encompass the moulin tremor. We calculate a daily estimate of the CSDM by using 5 min long time segments in the frequency band between 2.5 and 6 Hz, which gives in total M=288 of segments for 1 d. This ensures a robust, full-rank estimation of the CSDM (M≫N). The modeled GFs are computed over the two horizontal spatial components (easting and northing) using a previously optimized Rayleigh wave velocity of c=1680 m s⁻¹ corresponding to the propagation of Rayleigh waves within the array obtained by Walter et al. (2015). The MFP output is averaged over 30 discrete frequencies in the 2.5–6 Hz range.

The lower frequency bound (2.5 Hz) ensures a higher rank regime of the seismic wave field, as defined in Seydoux et al. (2017). It means that the degree of freedom of the seismic wave field is higher than the number of stations. The degree of freedom of the seismic wave field is defined as a number of independent parameters that can be used to describe the wave field in the chosen basis of functions. This number depends on the analyzed frequency, slowness of the medium (inverse of velocity), and average inter-station spacing of the array (here 736 m). The higher frequency bound (6 Hz) ensures no spatial aliasing in the beam-former output, given the minimum sensor spacing of 156 m.

Figure 7a shows the grid search for MFP performed over easting and northing positions. In order to reveal the location of the source, we use the Bartlett processor (Baggeroer et al., 1993) to measure the match between the recorded and modeled wave field. The MFP output reveals two dominant noise sources: a well-constrained focal spot corresponding to the moulin position inside the GIS array and another source located north of the array. The latter source is revealed by a hyperbolic shape. This shape is related to a poor radial resolution of the beam former for sources located outside of an array. Walter et al. (2015) suggested that this dominant source might correspond to another moulin as satellite imagery shows the presence of several drainage features north of the array. Both noise source signals contribute to the NCC. However, while the source located outside of the array contributes to the stationary-phase zone (endfire lobes) of certain receiver pairs, the moulin located within the array will mostly cause spurious arrivals on NCC. In order to separate the contribution of these noise sources, we first perform SVD of the CSDM, and then we use a selection of eigenvectors and eigenspectral equalization (Seydoux et al., 2017) to improve the convergence of NCC towards an estimate of the GF.

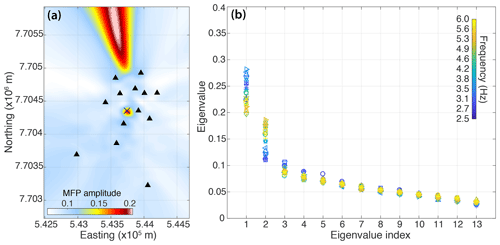
Figure 7 (a) Location of the dominant noise sources using MFP in the frequency band between 2.5 and 6 Hz (the MFP output is averaged over 30 discrete frequencies). The MFP was calculated using daily data recorded on 27 July at the 13 presented stations (black triangles). Blue cross indicates the moulin position. (b) Eigenvalue distribution of the CSDM for 30 discrete frequencies in the analyzed frequency band.

4.2 Green's function estimate from eigenspectral equalization

SVD is a decomposition of the CSDM that projects the maximum signal energy into independent coefficients (i.e. Moonen et al., 1992; Konda and Nakamura, 2009; Sadek, 2012). It allows the split of the recorded wave field into a set of linearly independent eigencomponents, each of them corresponding to the principal direction of incoming coherent energy and bearing its own seismic energy contribution:

$$\begin{array}{}\text{(2)}& K=US{V}^T=\sum _{i=\mathrm{1}}^N{K}_i=\sum _{i=\mathrm{1}}^N{U}_i{\mathrm{\Gamma }}_i{V}_i^T,\end{array}$$

where K is the CSDM, N is the number of receivers, U and V are unitary matrices containing the eigenvectors, and S is a diagonal matrix representing the eigenvalues Γ, and ^T denotes the transpose of the matrix. The total number of eigenvalues corresponds to the number N of receivers. The CSDM can be represented as the arithmetic mean of individual CSDMs (K_i), where each K_i is a CSDM corresponding to a given singular value Γ_i.

The SVD separates the wave field into dominant (coherent) and subdominant (incoherent) subspaces. It has been shown that the incoherent sources correspond to the smallest eigenvalues (Bienvenu and Kopp, 1980; Wax and Kailath, 1985; Gerstoft et al., 2012; Seydoux et al., 2016, 2017). Therefore, a common noise removal method consists of setting a threshold that distinguishes between coherent signal and noise and keeping only the index of eigenvectors that are above the threshold before reconstructing the CSDM (Moreau et al., 2017). The CSDM reconstruction consists of eigenspectral normalization (as explained in the following) and summing a selection of individual CSDMs (K_i). The “denoised” NCCs in the time domain are obtained with the inverse Fourier transform of the reconstructed CSDM.

Here, we follow the approach of Seydoux et al. (2016) for choosing the threshold. In the 2.5–6 Hz frequency band, the wave field is undersampled by the seismic array (which means that the typical radius of GIS seismic array is larger than half a wavelength of the analyzed Rayleigh waves). Seydoux et al. (2016) showed that in this case, the eigenvalue index cut-off threshold should be set to N∕2 in order to maximize the reconstruction of the CSDM. This means that we reject the last eigenvectors (from 7th to 13th) as they do not contain coherent phase information.

Figure 7b shows the eigenvalue distribution for 30 discrete frequencies in the analyzed frequency band. The first two eigenvalues correspond to the two dominant noise sources visible in Fig. 7b, and they show larger value variation with frequency in comparison with the rest of the distribution. This might be related to the change in the distribution of the dominant sources depending on the frequency related to the seismic signature of the hydraulic tremor and the distinctive frequency bands generated by the moulin activity (Fig. 1c). Moreover, the eigenvalue distribution decays steadily and does not vanish with high eigenvalue indexes. The latter confirms that the wave field is undersampled by the seismic array (see Seydoux et al., 2017, for details).

The CSDM can then be reconstructed by using only individual eigenvectors as in

$$\begin{array}{}\text{(3)}& \stackrel{\mathrm{̃}}{K_i}=U_i{V}_i^T.\end{array}$$

Note that we do not include the eigenvalues Γ in the CSDM reconstruction, which is equivalent to equalizing them to 1. That is why we refer to the reconstructed CSDM as “equalized” (Seydoux et al., 2016).

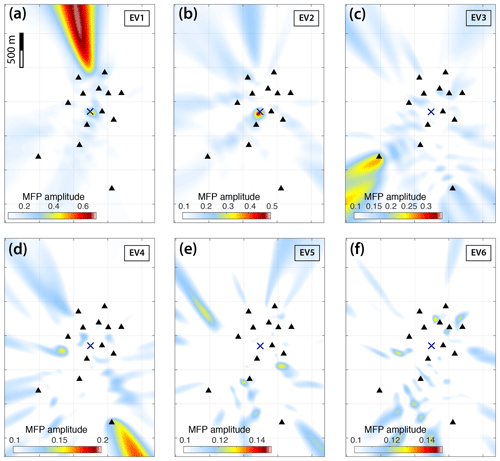
Figure 8 Reconstruction of the CSDM by using individual eigenvectors (EVs) that are related to different noise sources. Each plot shows MFP output computed using the reconstructed CSDM with individual eigenvectors as in Eq. (3). Each figure represents the MFP grid-search output calculated for the first eigenvectors: (a) 1, (b) 2, (c) 3, (d) 4, (e) 5, and (f) 6. The spatial coordinates are the same as in Fig. 7a. The blue cross indicates the moulin position.

Figure 8 shows the six individual equalized CSDMs $\stackrel{\mathrm{̃}}{K_i}$ reconstructed by using their associated eigenvector, each of them corresponding to the principal directions of incoming coherent energy that has been separated to point toward different ambient noise sources. Each plot represents MFP grid-search output computed on a reconstructed CSDM. Figure 8b shows that the second eigenvector corresponds to the moulin source located inside the array. However, we note that the first eigenvector also reveals a weaker focal spot corresponding to the moulin location. This indicates, similarly to the hydraulic tremor spectrum (Fig. 1c) and the singular value distribution (Fig. 7b), that the spatial distribution of dominant noise sources varies within the analyzed frequency band. Furthermore, higher eigenvectors do not reveal any strong noise sources localized within the array, and their MFP output points towards sources located outside of the array.

This MFP-based analysis of spatial noise source distribution allows us to select the eigenvectors of CSDM that contribute to noise sources located in the stationary phase zone (i.e. in the endfire lobes of each station path). We now reconstruct the NCC in the frequency band of 2.5–6 Hz with a step equivalent to the frequency sampling divided by the number of samples in the time window (here 0.0981 Hz, so 1019 individual frequencies in total). We perform the inverse Fourier transform of the equalized CSDM reconstructed using the first, third, fourth, fifth, and sixth eigenvectors.

Figure 9a and b compare the NCC before (in panel a) and after (in panel b) the eigenvector selection and eigenspectrum equalization procedure. The displayed NCCs are bin-averaged in fixed distance intervals (every 100 m) in order to improve the signal-to-noise ratio (SNR). The blue line shows the propagation of the Rayleigh waves with the velocity of 1680 m s⁻¹. In Fig. 9a we observe spurious arrivals (marked with green dots) that dominate the NCC together with a nonsymmetrical shape. On average, the CSDM equalization process (Fig. 9b) enhances the symmetry of NCC by 40 %. To quantify the symmetry of NCC, we used the correlation asymmetry as proposed in Ermert et al. (2015, Eq. 11).

Unfortunately, we notice that the equalization process reduces the overall SNR of the GF estimates and does not eliminate all spurious arrivals. This might be related to the imperfect separation of different noise sources which is likely influenced by the frequency variation in the moulin contribution. For example, we still keep some contribution of the central moulin in the first eigenvector. Moreover, by removing the second eigenvector we remove not only the seismic signature of the moulin, but also the contribution of coherent far-field sources.

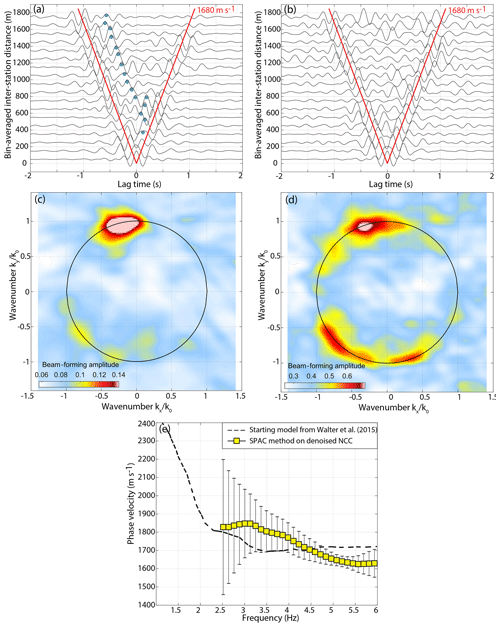
Figure 9 (a) Stacked sections of NCC in the frequency band from 2.5 to 6 Hz. The red line shows the propagation of the Rayleigh waves with velocity of 1680 m s⁻¹ (also in b). Spurious arrivals are marked with green dots. (b) Stacked sections of NCC reconstructed in the frequency band from 2.5 to 6 Hz from the CSDM eigenspectrum equalization. (c) Plane wave beam forming before the eigenspectrum separation and normalization and (d) afterwards. (e) Rayleigh wave phase velocity dispersion curves (yellow squares) calculated over the averaged seismic section in (d) with error bars indicating discrepancies in velocity measurements at different station paths. The dispersion curve is obtained with Aki's spectral method. The dashed black line is the dispersion curve obtained by Walter et al. (2015) with MFP.

To further assess the isotropy of the reconstructed noise field, we use the conventional plane wave beam former (e.g. Veen and Buckley, 1988). The plane wave beam-forming technique estimates the isotropy and coherence of the ambient seismic noise wave field with respect to the slowness and back azimuth. For the plane wave beam-forming calculation, we use the original (Fig. 9c) and the previously equalized CSDM (Fig. 9d). Figure 9c and d show the beam-forming output before (c) and after (d) the selection and equalization of eigenvectors. The wavenumbers k_x and k_y are normalized by the wavenumber k₀ corresponding to Rayleigh wave slowness of $s=\mathrm{1}/\mathrm{1680}\mathrm{s}{\mathrm{m}}^{-\mathrm{1}}$. A perfectly isotropic noise wave field consisting of Rayleigh waves would locate energy near the slowness circle of radius 1. After the removal of the second eigenvalue and the equalization of the strongest eigenvectors, we observe a more isotropic wave field, meaning other noise sources are enhanced. This quasi-circular shape reflects the energy that arrives from different azimuths. The difference in beam-former amplitude can be caused by the non-regular shape of the GIS array and different energy contributions of the ambient sources. The results show not only the strong source of noise coming from the north, but also energy incident from the southwest that might be related to oceanic ambient noise in the Labrador Sea (Sergeant et al., 2013) or other continuous noise generated by calving and ice-mélange dynamics in the proglacial fjord of Jakobshavn Isbræ (Amundson et al., 2010), one of Greenland's largest ice streams. Finally, it seems that not much seismic energy is incident from inland of the East GIS.

After the eigenspectrum equalization, we are able to extract a Rayleigh wave dispersion curve from the averaged seismic section obtained in Fig. 9b. For calculating the averaged dispersion curve we use a version of the Aki's spectral method (Aki, 1957) which consists of fitting a Bessel function to the real part of the cross-correlation spectrum. This method is referred to as spatial autocorrelation (SPAC) and is described in Appendix B2. The Rayleigh wave phase velocity dispersion curve averaged over all station measurements is shown in Fig. 9e with yellow squares and error bars representing the measurement discrepancies for individual NCCs. The dotted line presents an a priori Rayleigh velocity dispersion curve extracted from Walter et al. (2015). High discrepancies observed at lower frequencies mainly arise from the limited frequency band for computing the NCC (see the appendix method Sect. B). The slight differences between the two dispersion curves might be related to the different approaches used for phase velocity dispersion curve extraction (MFP in Walter et al. (2015) and SPAC in the current work). Moreover, Walter et al. (2015) worked on a wider frequency band and averaged their dispersion measurements over 46 d, and in our study we use only 1 d of data.

Several additional tests could be used to further improve the SNR of the NCC and their convergence to GF. For example, a similar procedure could be performed on other days, and the eigennormalized NCC could be stacked over a few days to increase the SNR. However, we verified that the index of eigenvectors corresponding to the moulin changes over days (the moulin can be located in the first, second, third, etc., eigenvector). This is the reason why it would be useful to find an automatic criterion for the eigenvalue selection based on the MFP output. However, this is beyond the scope of this paper. Another improvement could consist of azimuthal stacking the NCC according to the direction of the noise sources, although the GIS array does not have sufficient azimuthal and spatial coverage to implement this. Moreover, we could envisage calculating a projector based on the SVD (as in MRABF) only for the time period when the moulin is active and then project out the moulin signature from the continuous seismic data.

In summary, we conclude that the CSDM eigenspectrum equalization together with beam-forming-based selection of eigenvectors is a useful method to separate seismic sources in a glaciated environment. It can further improve the GF emergence from ambient seismic noise in the presence of strong, localized englacial noise sources for imaging applications.

5 Cross-correlation of icequake coda waves: a window-optimization approach

Contrary to ballistic waves, the likely diffuse coda arises from multiple seismic scattering (Aki and Chouet, 1975; Shapiro et al., 2000; Hennino et al., 2001) and is expected to contain all possible modes and propagation directions following an equipartition principle (Paul et al., 2005; Colombi et al., 2014). Scattered coda waves after an earthquake favor isotropy of the incident wave field, and then the GF estimates retrieval via the cross-correlation of a coda window at two sensors (Campillo and Paul, 2003; Malcolm et al., 2004; Paul et al., 2005; Gouédard et al., 2008b; Chaput et al., 2015a, b).

In the following, we explore the application of coda wave interferometry (CWI) on selected near-surface icequakes in Gornergletscher to estimate the GF which could not be obtained from traditional processing of icequake cross-correlations because of lacking sources in the stationary phase zones of the seismic array (Fig. 2c). The use of icequakes here is fundamentally different than in Sect. 3, in that the ballistic arrivals are specifically avoided (whereas in the other case, the ballistic component was the primary source of energy in the cross-correlation functions).

5.1 Icequake coda waves at Gornergletscher

The strongest 720 events chosen out of more than 24 000 icequakes detected at Gornergletscher exhibit a sustained coda with approximate duration of 1.5 s (Fig. 1d–e). The propagation regime of seismic waves can be identified by the evolution of the elastic intensity (“coda power spectrum”), the squared seismic amplitudes (color lines in Fig. 1d). Before the source energy has reached the receiver, the elastic intensity is equal to some background or ambient level. Once the source pulse arrives at the receiver, the intensity rises up and then begins to decay exponentially. This is the ballistic regime. After several mean-free times which are to be related to the scattering strength (De Rosny and Roux, 2001), the intensity begins to decay diffusively with time as multiple scattering slows the transport of energy out of the scan region (Malcolm et al., 2004). This is the diffusion regime and it is characterized by a linear decay of the coda intensity (Aki and Chouet, 1975). Eventually, intrinsic attenuation (anelastic loss) dominates and the energy falls to the noise level.

Figure 1d shows such linear decay of the coda power spectrum starting at ∼0.5 s, indicating that icequake seismogram signals contain enough scattered energy that may approach from a wide range of directions assuming that the scatterers are homogeneous around the network site (Chaput et al., 2015a). In the present study we do not investigate further the cause of wave scattering in glaciers and particularly in Gornergletscher, but we suggest a relation to the presence of conspicuous near-surface crevasses (Fig. 2c) and deeper fractures as intermediate-depth and basal fault planes have been reported at the study site (Walter et al., 2008, 2009, 2010), as well as topography gradients, reflections at the glacier margins, and/or rock and air inclusions.

5.2 Coda wave interferometry and Green's function estimate

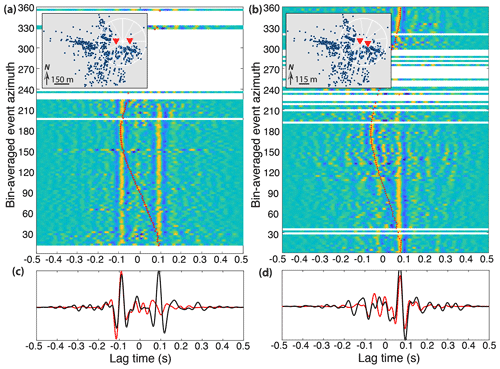
Figure 10 (a, b) Cross-correlation functions obtained at two station pairs from each source and plotted as a function of event azimuth relative to the station path, for a time window in the coda part. Rayleigh wave arrival times of correlation functions obtained for a time window which encompasses ballistic waves of icequake records are plotted in red dots. Stations, station separation, and source geometry are plotted in the inset maps. (c, d) Stack of the correlation functions obtained from icequake ballistic waves (red) and coda (black).

We first apply a standardized CWI processing scheme following Gouédard et al. (2008b). The cross-correlations are computed on 10–30 Hz spectrally whitened seismograms to reduce the influence of background noise. As a first guess, coda waves are arbitrarily time windowed around 0.5–1 s (gray horizontal bar in Fig. 1d) by looking at the decay of the waveform amplitudes. The first sample of the coda correlation window corresponds to the two-station average of the time when the seismogram envelope falls below 5 % of the ballistic wave maximum amplitudes. Because of the decrease in coda amplitude with time, we cannot perform a simple cross-correlation between the coda signals without strongly overweighing the earliest part of the coda. To avoid this problem, we follow Paul et al. (2005) by disregarding the amplitudes and considering 1-bit signals.

Figure 10a shows the individual coda wave cross-correlation functions (CWCCs) sorted by the azimuth of the source event relative to the station path. In contrast to conventional ICCs (correlations of icequake ballistic waves) whose computed arrival times (see also Fig. B4 and Sect. 3) are plotted in red, the coherent arrival times in the CWCC no longer depend on the event azimuth. The CWCCs correspond to stationary Rayleigh waves traveling between the two stations. The causal and acausal parts of the individual CWCCs tend to symmetrize as we are in the scattering regime. This results in a symmetric correlation stack (Fig. 10c), whereas only the acausal part of the GF is reconstructed from the ICC due to missing sources behind one of the two stations.

For the pair of closer stations (Fig. 10b), the reconstructed acausal times still depend on the source position while the CWCC causal times are stable with the event azimuth. The source position signature on one side of the correlation function could be an effect of heterogenous scatterers which cause single scattering and then skew the illumination pattern to one side of the receiver pair. Another explanation could be that the correlation window used here for CWI is still influenced by the incoming energy flux from ballistic waves, which then create an anisotropic incident wave field as we are in the presence of limited energy diffusion (Paul et al., 2005).

Focusing on a complex scattering medium at the glaciated Erebus volcano (Antarctica), Chaput et al. (2015b) showed that symmetric GF could be recovered when optimizing the icequake coda correlation window over the sources. In the case of a weak scattering medium such as glacial ice, the coda time window for the diffusion regime should notably depend on the distance of the scatterers to the recording seismic sensor. We therefore use a similar optimizing-window processing scheme for improving the GF convergence at each station pair.

The overall processing and technical details of coda window optimization are described in Chaput et al. (2015b). We refer to the method as MCMC processing as it involves a Markov chain Monte Carlo scheme. A Bayesian inversion determines the best coda window to generate a set of CWCCs that are the most coherent and symmetric across the source events. We first construct a matrix of CWCCs that are bin-averaged over N events and then iterate this correlation matrix by randomly shifting the coda window along a certain number M of random traces. At each iteration, a misfit function is constructed based on the coherency of the N-binned CWCC matrix and the causal–acausal symmetry of the CWCC stack. In the end, the best optimized models consisting of the cross-correlation matrices computed for different sets of coda windows are stored and used to generate an average stack of CWCCs, which is our final estimate of the GF.

MCMC processing involves several parameters that need to be tuned. As for traditional ICC processing, we need to define the frequency band of analysis (here 10–30 Hz) and the coda correlation window length T. Here we use T=0.5 s and we force the algorithm to shift the correlation window to no later than 1.5 s in order to stay within the icequake coda and to not correlate noise (see Fig. 1d). We use N=40 for event binning and M=10 for event trace selection, and we use up to 2×10⁴ iterations. We need to define the portion of the cross-correlation stack where we want to optimize the causal–acausal symmetry, the relative importance of the causal–acausal symmetry, and the CWCC matrix coherency that is used to optimize the misfit function (coefficient factors A and B in Chaput et al., 2015b, Eq. 2). We choose here to optimize the GF symmetry for both reconstructed ballistic and coda waves, i.e. at later times than expected for a Rayleigh wave propagating at a velocity of 1700 m s⁻¹, and we weight the symmetry and coherency evenly.

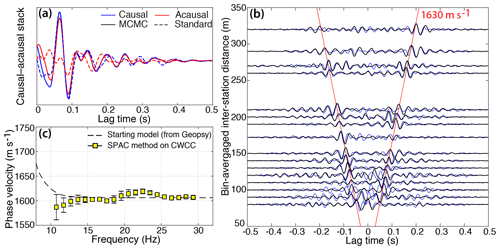
Figure 11 (a) Causal–acausal symmetry of the CWCC obtained at one station pair using standard coda interferometry processing as in Fig. 10d (dashed lines) and MCMC processing (solid lines). (b) Correlation gather sorted by increasing distance and averaged in 10 m intervals. Black and blue lines result from MCMC and standard processing, respectively. Red lines show the propagation of Rayleigh waves with the velocity of 1630 m s⁻¹. (c) Rayleigh wave phase velocity dispersion curve (yellow squares) averaged over measurements for all station pairs. Error bars indicate discrepancies in velocity measurements at different station paths. The dispersion curve is obtained with the Aki's spectral method. The dashed black line is the theoretical dispersion curve for a 160 m thick ice layer computed with Geopsy.

Figure 11a shows the MCMC optimization of the CWCC symmetry at the station pair already presented in Fig. 10d. Blue and red lines are the causal and acausal parts of the correlation stack, respectively. Solid and dashed lines are the resulting CWCCs obtained from MCMC processing and standard processing (i.e. first iteration of the MCMC inversion), respectively. While the ballistic Rayleigh waves could not be reconstructed in the acausal part of the correlation function using the first coda wave windowing, the MCMC output approaches the symmetrical GF as we see a Rayleigh wave propagation in both directions and also the emergence of a coherent coda in both parts of the correlation function. The MCMC inversion gives optimized coda windows in the range of 0.7–1.2 s for the majority of events, i.e. at later times than the initially used coda window. Enhanced symmetry of the CWCC computed in later time windows is consistent with the expectation of having a more isotropic diffuse wave field as all directions of propagation are closer to being equally represented after several mean free paths (Paul et al., 2005).

Figure 11b shows the final stack of CWCC gather sorted by increasing inter-station distance and averaged in 10 m binned intervals. For comparison, CWCCs computed with the standard processing are in blue. CWCCs are noisier than ICC obtained from correlations of icequake ballistic waves when computed on homogeneous source distributions (Gouédard et al., 2008b). Nevertheless, at most station pairs, the MCMC processing managed to extract Rayleigh waves with consistent travel times in both causal and acausal parts. We extract a dispersion curve of phase velocities averaged over the station components (Fig. 11c) using the SPAC method already used in Sect. 4.2 (Appendix B2). We find an average Rayleigh wave velocity of 1600 m s⁻¹, which is in the estimate range of what Walter et al. (2015) find at Gornergletscher using slant stacking of ICC arrival times (Appendix B3). Errors introduced at lower frequencies arise from the limited frequency band used for computing the CWCC and filtering effects (see the appendix method Sect. B).

5.3 Coda wave field isotropy and Green's function convergence

MCMC processing coherently increases the presence of energy at zero lag time (Fig. 11a and b). Such spurious arrival likely arises because scattered coda also contains a strong vertically trapped body wave that correlates at 0 across relatively close receivers, even if it is not part of the “true” GF. Obtained CWCCs may contain spurious arrivals and seismic modes that are not purely the result of an isotropic point-source GF estimate. We point out two reasons for this.

On the one hand, spurious arrivals at times of 0 or later could result from seismic reflections on the glacier bed beneath the stations, early aftershocks, or other noise sources if not in the stationary phase zones. A certain portion of the icequake coda may still be influenced by background noise especially at distant stations from the event source as the coda time window of one station may fall in the noise window of the further one.

On the other hand, spurious arrival contributions will not vanish in case of localized scatterers around the seismic array if the incident waves do not illuminate the scatterers with equal power from all directions because of limited source aperture (Snieder et al., 2008). This second argument is also supported by the observations of nonsymmetric CWCC. At some locations, there still exist differences in the amplitudes of the Rayleigh waves in the causal and acausal parts of the final GF estimate (Fig. 11a), meaning that the icequake coda is not entirely diffuse and may result from single reflections on preferred scatterers. Paul et al. (2005) could not obtain symmetric CWCC from regional earthquake coda seismograms and attribute this to the long-lasting anisotropy of the diffuse energy flux. Indeed, in weak (or homogeneous) media, the incident energy flux from earthquakes can still dominate the late coda, resulting in GF time asymmetry, provided the sources are located in the same distant region. The CWCC asymmetry is expected to disappear with an isotropic distribution of sources or scatterers around the seismic network. In the case of Gornergletscher icequakes, we still see the influence of the energy flux approaching from the direction of the source at a few station pairs and for some events as depicted in Fig. 10b, supporting the argument for single scattering rather than multiple scattering as the cause of icequake coda.

In general, CWI must be processed on carefully selected events which show sustained coda above the background noise. We try coda wave correlations on the Argentière node grid and notice an influence of the source position on the retrieved CWCC likely because we did not select strong enough signals with sustained coda that is coherent enough across the sensors. Similarly, GF convergence does not work for weak Gornergletscher icequakes. Moreover, the abundance of seismic sources in glaciers often pollutes coda wave seismograms. We often find the situation where ballistic body and surface waves generated by early aftershocks from repetitive and subsequent events (or bed reflections) arrive at the seismic sensor only a few milliseconds after the onset of the first event of interest and therefore fall in its coda window. This typically introduces anisotropic wave fields. The brief icequake coda duration, the interevent time distribution, and the weak scattering in glacial ice impose limitations of CWI on large arrays.

To conclude, even if limited, the extraction of GF from icequake coda waves allows imaging of a glacier subsurface between station pairs. In principle, this can be done even in cases when (skewed) distribution of icequake sources or sustained noise sources does not allow for GF estimation.

6 Discussion

The three methods proposed in this study could theoretically be applied to each one of the explored datasets but were not further tested here. The standard processing schemes proposed in Sect. 3 for computations of NCC and ICC successfully work on Glacier d'Argentière as we benefit from favorable seismic illumination patterns and redundancy of the measurements on the dense array. The need of spatial averaging of the correlation responses in regular distance intervals could potentially be overcome when (1) stacking the GF over a longer time range of typically weeks or months (e.g. Sabra et al., 2005; Larose et al., 2008) or (2) applying more advance processing schemes such as the one proposed for GIS and Gornergletscher studies, to overcome anisotropic source distribution effects.

Eigenspectral equalization of the cross-spectral matrix of ambient noise seismograms (Sect. 4) enables us to distinguish propagation directions of incoming seismic energy. This method improves the spatial homogenization of the incident wave field in order to reveal weaker sources that could eventually be used for extracting the GF at sensor pairs which initially lacked stationary phase contributions. The same technique could be applied to Glacier d'Argentière in order to improve the GF estimates which show spurious arrivals arising from the dominant sources near the glacier tongue (Fig. 3b). By doing so, we would improve our spatial coverage of seismic velocity measurements and could invert a more accurate 3-D model of the subsurface. The eigenspectral equalization method is particularly well suited for large sensor arrays. The geometry of the glacier discharge system (channelized versus distributed) is also the primary controlling factor for successful applications.

In the absence of distributed noise sources, the use of icequakes is a good alternative, especially in winter when the glacier freezes, preventing generation of coherent water flow noise. As icequakes propagate to a few hundred meters, ICC studies are well suited for medium-size arrays with an aperture typically of the order of 500 m. In the case of anisotropic distributions of icequakes which map the crevassed ice, GF estimates can be optimized with CWI and the coda-window optimization approach used in Sect. 5. CWI successfully works on the strongest selected events at Gornergletscher because we could record a coherent coda at adjacent sensors, with seismic amplitudes above the background noise level. CWI should be appropriate for smaller icequake datasets (here we employ the method on a loop of 700 events, i.e. less than 7 % of the icequake catalogue used in Argentière) and smaller size arrays to be able to record a coherent coda across the network (typically 250 m wide). Such arrays can be deployed in targeted regions where pervasive crevasses are present, i.e. typically near the glacier margins. As an example, CWI could help to estimate the GF at smaller subarrays at the edges of a larger array as in the configuration of the Glacier d'Argentière experiment.

In the following we discuss the type of array deployment, geometry, and measurements suitable for structural and monitoring studies using the GF obtained by either one of the processing methods described above.

6.1 Implications for glacier imaging

The performance of an array for imaging the structure at depth first relies on its geometry and secondly on the wave field characteristics as discussed in Sect. 3.1. Wathelet et al. (2008) recommend that the array diameter should be at least as large as the longest wavelength of interest (we conventionally take two to three wavelengths). The minimum station spacing for any direction should be less than half the shortest wavelength of interest to avoid spatial aliasing. To be able to sample the basal interface and target elastic parameters of sediments constituting the till layer or the bedrock, one should design suitable array geometry. For a glacier thickness of 200 m, we need an array aperture of at least 600 m to measure propagating surface waves with a one-wavelength cycle. For a 500 m thick glacier, we need sensors that are at least 1500 m apart, although prior knowledge on the basal interface allows us to better constrain the inversion of depth with lower-size arrays.

Seismic velocity measurements can additionally be complemented by other types of observations computed on the horizontal and vertical components of the GF, such as the horizontal-to-vertical (H∕V) ratio. Assuming a horizontally homogeneous medium, the resonance frequency of the H∕V ratio spectrum can be used to constrain the layered structure (Zhan et al., 2013) and the ice thickness (Picotti et al., 2017) or to investigate 3-D effects of the recorded wave field (Preiswerk et al., 2018). H∕V ratios and dispersion curves of surface wave velocities can be jointly inverted (Lin et al., 2014) for an even more accurate 3-D model of the glacier subsurface.

6.2 Implications for glacier monitoring

Repeated analysis of cross-correlations allows us to detect changes in the subsurface properties. Seismic velocity monitoring is usually performed in the coda part of the cross-correlation function through the application of CWI, as multiple scattered coda waves are less sensitive to the source distribution and travel larger distances, accumulating time delays (Hadziioannou et al., 2009). CWI enables us to detect relative velocity changes as small as 0.1 % (e.g. Sens-Schönfelder and Wegler, 2006; Brenguier et al., 2008a, b; Mainsant et al., 2012).

CWI computed on cross-correlation functions could lead to the monitoring of englacial crevasses, failure of calving icebergs, glacial lake outburst floods, break-off of hanging glaciers, surface mass balance, and bed conditions such as the evolution of the glacier hydraulic system and subglacial till properties. Such topics are currently investigated with active seismic experiments or through the spatiotemporal evolution of passive seismicity and associated source mechanisms (e.g. Walter et al., 2008; Bartholomaus et al., 2015; Preiswerk et al., 2016; Podolskiy et al., 2017; Lipovsky et al., 2019). Passive seismic monitoring of glaciers could lead to the detection and understanding of processes related to climate conditions, glacier hydraulics, and ice flow dynamics, which today are labor-intensive to investigate with active geophysical measurements.

Figure 12 (a) Source–receiver geometry used for the computation of icequake virtual-source responses through the application of MDD (c) to the cross-correlations in (b). In this particular case, a receiver contour (consisting of 32 regularly spaced receivers) and a single receiver between these receiver lines (green triangle) are illuminated by 4282 sources (i.e. icequakes) on either side of the receiver cavity. The receiver colored in red is here turned into a virtual source, whose response is recorded at the green receiver. Due to the reflecting boundary conditions and the receiver geometry, the emitted wave travels back and forth between the two receiver lines indicated with the black dashed lines. We obtain multiple reflections noted R_i (i indicates the number of virtual reflections), which are visible on the MDD correlation gather and averaged stack in (c). Virtual reflections R_i create an artificial coda after the ballistic Rayleigh wave reconstructed on the GF estimate. This coda is observed to be coherent through time (here we show cross-correlation stacks computed on a 2 d sliding window with an overlap of 1 d) and is suitable for CWI studies. Panel (b) is the same as (c) but for standard processing of icequake cross-correlations at the two sensors in green and red. Orthophotograph © Swisstopo, SWISSIMAGE.

Unfortunately, the weak ice scattering limits the emergence of a coherent coda in the correlation functions which appear to still be affected by the changing nature of primary ambient noise sources (Walter, 2009; Preiswerk and Walter, 2018). To overcome source effects and enhance the coda SNR, it is possible to design arrays for multidimensional deconvolution (MDD) of the time-averaged cross-correlations. Seismic interferometry by MDD measures the illumination pattern (e.g. Wapenaar et al., 2011; Weemstra et al., 2017) using recordings by a set of additional receivers along a contour which goes through the virtual source's location. MDD processing then enables us to remove the imprint of the (nonuniform) source distribution from the correlation responses and improves the quality of the retrieved GF. We follow Lindner et al. (2018) and use the outer receiver contour of the Glacier d'Argentière array (black triangles in Fig. 12a) as virtual boundaries for MDD of the icequake correlations computed at one pair of sensors and sorted for a 2 d window with 50 % overlap. MDD processing appears successful in retrieving accurate GF estimates which feature a coda that is coherent over time (Fig. 12c) and does not appear on more classical ICC as defined in Sect. 3 (Fig. 12b). The technique based on virtual reflectors allows us to create an artificial coda which consists of multiple reflections of the ballistic wave field trapped within the receiver contour. This approach is a promising candidate for a monitoring scheme of any changes in englacial seismic velocities even in the absence of scattering coda. Long-term installations directly on or in the ice have increased in recent years due to technological improvements (Aster and Winberry, 2017). MDD could be applied to glacier seismic sources recorded over timescales longer than a month, using borehole sensors which ensure a solid coupling to the ice.

7 Summary and concluding remarks

This study explores the application of seismic interferometry on on-ice recordings to extract the elastic response of the glacier subsurface beneath one array deployment. In contrast to ambient noise studies focusing on the Earth's crust, the GF retrieval from cross-correlations of glacier ambient seismicity is notoriously difficult due the limited spatial coverage of glacier point sources and the lack of seismic scattering in homogeneous ice. We investigate the GF emergence on three particular cases. We design processing schemes suitable for each configuration of seismic deployment, wave field characteristics, and glacier setting.

In Glacier d'Argentière (Sect. 3), cross-correlations of water flow ambient noise and icequake recordings result in accurate GF estimates as (1) we face the situation of a favorable source distribution, and (2) the large number of sensors and their dense spatial sampling allows us to stack redundant measurements on a line of receivers. The averaged GF estimate reconstructs P and dispersive Rayleigh waves propagating across the array well. Seismic velocity inversions enable us to conduct structural studies and map the englacial crevasses and the glacier bed with vertical resolution of ∼10 m.

On the GIS (Sect. 4), cross-correlations of ambient noise seismograms give rise to spurious arrivals which are not part of the true GF. MFP identifies a localized point source constituted by a moulin within the seismic array, out of the stationary phase zones of most of the receiver paths. Eigenspectral equalization of the cross-spectral matrix coupled to an adequate selection of its eigencomponents enables us to remove or at least attenuate the imprint of the moulin on the correlation functions. Such a technique allows the separation and weighting of the contributions of different noise sources shaping optimized conditions for GF convergence.

In Gornergletscher (Sect. 5), cross-correlations of icequake coda waves show evidence for a quasi-homogenized incident wave field as a result of seismic scattering by the crevassed ice. An optimization of the coda window based on the coherency and the causal–acausal symmetry of the cross-correlation functions is used to improve the GF convergence. CWI allows the retrieval of GFs at seismic arrays where icequakes are not recorded evenly around the study site.

The capability of extracting accurate seismic velocities on a line of receivers can be substantially improved when stacking the correlation functions on a large number of receiver pairs. However, MFP and CWI allow for new kinds of measurements on sparse seismic networks and enable the speedup of the GF convergence for non-idealized seismic illumination patterns which commonly arise in glacier settings.

Finally, the use of nodal sensor technology enables fast deployment of large N arrays suitable for seismic interferometry studies. This opens up new ways of characterizing and monitoring glacial systems using continuous passive seismic recordings.

Appendix A: Construction of icequake catalogues

There exist a wide range of seismic sources in glaciers as well as detection schemes (see  Podolskiy and Walter, 2016,  for a review on the methodology). The processing employed for icequake detections and localizations must be adapted to the type of network (number of sensors, sensor spacing, and array aperture) and to the type of the events of interest which involve various waveforms (e.g. Walter, 2009; Röösli et al., 2014; Podolskiy and Walter, 2016). Dispersive Rayleigh waves are well suited for investigating the glacier subsurface including the basal interface as they are primarily sensitive to the S-wave velocity structure and can sample depths up to approximately one-third of the wavelength. We then focus our study on one class of glacier seismic events, surface icequakes generated by ice crevassing. Another advantage of using such events is their high rate of time occurrence (∼10²–10³ recorded events per day) and their potentially wide spatial coverage, which is optimal for the application of seismic interferometry techniques (Walter et al., 2015). Here we introduce the methods used to compute the icequake catalogues at Gornergletscher (Sects. A1 and A2) and Glacier d'Argentière (Sect. A3).

A1 Icequake detection

Seismic waveforms of surface icequakes generally exhibit a first low-amplitude P wave followed by impulsive Rayleigh waves (Fig. 1a). Such events can be detected using a template matching on continuous seismograms (Mikesell et al., 2012). This cross-correlation method exploits the signal coherency with a reference waveform and can be used on single stations or across a network. Nevertheless, the most common and straightforward detection approach is to implement an amplitude threshold trigger.

The most broadly used algorithm in weak-motion seismology and on glaciers for detecting impulsive events (e.g. Walter, 2009; Canassy et al., 2012; Barruol et al., 2013) is the “trigger of the ratio of the short time average to the long time average” referred to as STA ∕ LTA (Allen, 1978). It continuously calculates the average values of the absolute amplitude of a seismic signal in two consecutive moving time windows. The short time window (STA) is sensitive to seismic events while the long time window (LTA) provides information about the temporal amplitude of seismic noise at the recording site. When the ratio of both exceeds a preset value at a single station or coherently across a network, an event is declared.

As icequakes usually propagate to distances of a few hundred meters before attenuating to the background noise level, the number of identified events varies with the network configuration and the minimum number of stations to require a trigger concurrently. For the Gornergletscher study, we work with events that have been detected by running a STA ∕ LTA trigger over 5–15 Hz band-pass-filtered continuous seismograms, using an STA window of 0.3 s (i.e. typical icequake duration) and an LTA window 10 times longer with a threshold value of 8. To declare an event, we require at least half of the network stations to trigger.

A2 Icequake location

The vast majority of icequakes recorded on glaciers are localized near crevasses that extend no deeper than ∼30 m (Walter et al., 2008; Lindner et al., 2019). To locate the events at Gornergletscher, we fix the source depth to the surface and invert for the epicenter distance following the automated approach of Roux et al. (2010) and Walter et al. (2015), also similar to that of Mikesell et al. (2012). This method employs cross-correlations to automatically measure differences in Rayleigh wave arrival times across the network.

To be able to record coherent icequake waveforms with high enough signal-to-noise ratios (SNR) at couples of sensors, the network aperture should be less than 1 km, or at least consist of several pairs of stations whose separation is shorter than the distance at which surface waves start to be strongly attenuated in the ice.

In the same spectral band that is used for event detection, icequake signals are first windowed around the Rayleigh wave and cross-correlated for each pair of stations to obtain time delays. Time delay measurements are then refined to subsample precision by fitting a quadratic function to the cross-correlation function centered on its discrete maximum. The best easting and northing coordinates of the source are concurrently inverted with the apparent propagation velocity to match the time delay catalogue for preselected pairs of stations. We only consider time shift measurements at pairs of stations whose cross-correlation maximum is above 0.8. This allows us to minimize complex source and/or propagation effects on seismic waveforms and the observed arrival times that can not be fit with the oversimplified velocity model.

The inversion process is an iterative procedure using a quasi-Newton scheme (Roux et al., 2010, Eq. 3). Reliability of icequake locations varies as a function of the events being inside or outside the network. Using a seismic network similar to the one of Gornergletscher used in the present study, Walter et al. (2015) estimated that in the azimuthal direction the error remains below 2^∘ for average apparent velocities in the range of 1600–1650 m s⁻¹.

A3 Array processing: matched-field processing using beam forming

A seismic network is called an array if the network aperture is shorter than the correlation radius of the signals, which is the maximum distance between stations at which time series are coherent, i.e. typically less than 1 km for glacier sources recorded by on-ice deployments (Podolskiy and Walter, 2016). A seismic array differs from a local network mainly by the techniques used for data analysis.

Dense sensor arrays have many advantages as the SNR can be improved by summing the individual recordings of the array stations. Compared to a single sensor or couples of sensors, array processing techniques, such as beam forming, allow for time domain stacking which constructively sums coherent signals over the sensors and cancels out incoherent random noise, enhancing the signal detection capability.

Continuous data are scanned through matched-field processing (MFP) which involves time domain beam forming (Kuperman and Turek, 1997). Beam forming uses the differential travel times of the plane wave front due to a specific apparent slowness (inverse of velocity) and back azimuth to individual array stations (Rost and Thomas, 2002). If the single-station recordings are appropriately shifted in time for a certain back azimuth and velocity, all signals with the matching back azimuth and slowness will sum constructively. MFP can be processed using a decomposition of seismic signals in frequency components. To be declared as an event and furthermore, with accurate location, the beam power of aligned seismic waveforms at a given frequency (i.e. the norm of the cross-spectral density matrix and the array response; see  Lindner et al., 2019, equation 3) must pass a preset trigger threshold. The final event location can be averaged from the beam-forming solutions obtained at several successive discrete frequencies (assuming that slowness and back azimuth are close to constant in the considered frequency band).

MFP was successfully used by Corciulo et al. (2012) to localize microseismic sources at the exploration scale using ambient-noise data. Moreover, recent studies focused on developing an automatic, optimization-based MFP approach that does not require grid search to localize thousands of weak seismic events in a complex fault zone (Gradon et al., 2019) and hydraulically fractured area (Chmiel et al., 2019).

The MFP method of Chmiel et al. (2019) was used on the Argentière array to detect and locate about 4000 events each day, with a beam-power threshold averaged over frequencies between 5 and 30 Hz set to 0.5. Locations of icequakes recorded over the 5-week deployment are presented in Fig. 2a. For computing the cross-correlation functions from icequake waveform described in Sect. 3, we restrict ourselves to 11 100 events (red stars in Fig. 12). Such events have been identified following Lindner et al. (2019) with a STA/LTA trigger on 8–16 Hz band-pass-filtered continuous seismograms (STA=0.3 s, LTA=3.6 s, trigger threshold =11 for events detected concurrently at the four corner stations of the array). Locations are the beam-forming solutions using a grid search over easting and northing positions in 25 m×25 m steps. All events with beam power lower than 0.5 were discarded.

Appendix B: Computation of phase velocity dispersion curves

Because dispersive surface waves of different frequencies propagate at different speeds, computation of seismic velocities generally involves Fourier analysis to decompose the wave into frequencies that compose it. One can distinguish two types of wave speeds.

The phase velocity c is the speed at which the phase of a wave propagates in space and is related to the angular frequency ω and the wavenumber k as

$$\begin{array}{}\text{(B1)}& c\left(\mathit{\omega }\right)={\displaystyle \frac{\mathit{\omega }}{k\left(\mathit{\omega }\right)}}.\end{array}$$

The angular frequency is related to the time periodicity of the signal of frequency f as ω=2πf. The ground displacement is also periodic in space over a distance equal to the wavelength λ that is used to describe how the wave oscillation repeats in space via the wavenumber $k=\mathrm{2}\mathit{\pi }/\mathit{\lambda }$.

If the harmonic waves of different frequencies propagate with different phase velocities, the velocity at which a wave group propagates differs from the phase velocity at which individual harmonic waves travel (Stein and Wysession, 2009). The group velocity u of a wave is the velocity with which the overall energy of the wave propagates through space. If the signal has energy over a wide range of frequencies, $u=\mathrm{d}\mathit{\omega }/\mathrm{d}k$ and the group velocity is related to the phase velocity as

$$\begin{array}{}\text{(B2)}& u\left(\mathit{\omega }\right)=c\left(\mathit{\omega }\right)+{\displaystyle \frac{\mathrm{d}c}{\mathrm{d}k}}.\end{array}$$

In ambient noise tomography, it is common to measure the group velocity of dispersive Rayleigh waves traveling in the Earth's crust and upper mantle (e.g. Shapiro et al., 2005; Mordret et al., 2013). Dispersion curves of group velocities are usually computed using the frequency time analysis (FTAN) of the noise cross-correlation time series (Levshin et al., 1992). FTAN employs a system of narrowband Gaussian filters, with varying central frequency, that do not introduce phase distortion and give a good resolution in the time–frequency domain. For each filter band the envelope of the inverse Fourier transform of the filtered signal is the energy carried by the central frequency component of the original signal. Since the arrival time is inversely proportional to group velocity, for a known distance, the maximum energy of the time–frequency diagram is obtained as a function of group velocity with frequency.

In glaciers, due to homogeneous ice, only weakly dispersive surface waves are recorded at on-ice seismometers. It is then difficult to use FTAN to measure Rayleigh wave group velocity dispersion. We choose here to compute the phase velocity dispersion curve for Rayleigh waves using different approaches. Obtaining the group velocity from the phase velocity is then straightforward while the reverse is not possible due to unknown additive constants which arise from the integration of the phase velocity over frequency (Eq. B2).

B1 Array processing: frequency–wavenumber analysis

Frequency–wavenumber analysis (f-k) was used to compute the velocity dispersion curves at Glacier d'Argentière (Sect. 3.1 and 3.2). The f-k analysis is a standard array processing for computing phase velocities from seismic time series recorded on a line of receivers (Capon, 1969). It enables the identification and separation of wave types and wave modes and also the design of appropriate f-k filters to remove any seismic energy in the original signal time series.

The most basic f-k processing employs a 2-D Fourier transform on both time and spatial components to construct the f-k diagram (Fig. B1b). We then need to select the dispersion curve of the phase of interest by picking the energy maxima of the 2-D Fourier transform output. The absolute value of the f-k space is then transformed into the velocity c(f) via Eq. (B1) (Fig. B1c).

There exist multiple array techniques for computing frequency–velocity diagrams using spectral analysis in time and space domains. Some of them are described in Rost and Thomas (2002) and Gouédard et al. (2008a) and referenced in Ohrnberger et al. (2004). Concerning the cross-correlation functions obtained at the Argentière array, we employ the phase-shift method of Park et al. (1998) which allows us to construct a frequency–velocity diagram where dispersion trends are identified from the pattern of energy accumulation in this space. Then, necessary dispersion curves are extracted by following the diagram amplitude trends (Figs. 3c and B2c).

The performance of an array for deriving phase velocity values in a wavenumber or frequency range depends on its geometry and on the wave field characteristics (i.e. frequency range and magnitude of seismic energy with respect to attenuation). The capability to resolve phase velocity at a given frequency depends on the array aperture (described by the array diameter Δ_max) and minimum sensor spacing (Δ_min) so that at least two wavelengths are sampled between adjacent receivers to avoid aliasing in the wavenumber domain (e.g. Wathelet et al., 2008). Phase velocities should then be computed for frequencies which satisfy ${\mathrm{\Delta }}_{min}\le n\mathit{\lambda }\le {\mathrm{\Delta }}_{max}$, with n usually taken as 2 or 3. This relationship depends on the expected phase velocity as $\mathit{\lambda }=c/f$.

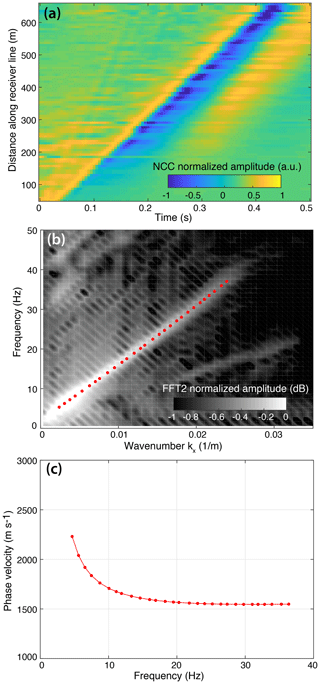
Figure B1 Computation of Rayleigh wave phase velocity from f-k analysis of the noise cross-correlation section obtained at the Argentière array (a). (b) Frequency–wavenumber diagram obtained from the 2-D Fourier transform of (a). Red dots show the peaks of energy maximum at each frequency and correspond to the Rayleigh wave fundamental mode. (c) Phase velocity dispersion curve obtained from the interpolated peaks in (b).

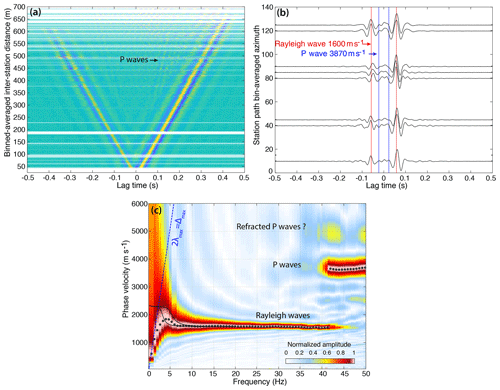
Figure B2 Same as Fig. 3 but for icequake cross-correlations (a) computed in Glacier d'Argentière. (b) GF estimates for pairs of stations 100 m apart and different orientations defined by the azimuth. (c) Frequency–velocity diagram obtained from f-k analysis of the correlation functions in (a) using the phase-shift method of Park et al. (1998). The extracted dispersion curve of Rayleigh and P waves is plotted in black dots.

B2 Aki's spectral method

This method was used to compute the Rayleigh wave velocity at the GIS and Gornergletscher arrays (Sects. 4.2 and 5.2). Whereas the f-k techniques are based on the assumption of a plane wave arriving at the array, Aki's spectral method (also referred to as the SPAC method;  Tsai and Moschetti, 2010) bases its theoretical foundation on the precondition of a scalar wave field which is stationary in both space and time. As detailed below, this technique does not require specific array geometries to compute phase velocities and can be used on single pairs of stations as long as one is in the presence of an isotropic incident wave field. Another advantage concerns the capability to resolve discrete frequencies on a potential wider range than what is possible using f-k methods as the Aki method produces robust and unbiased measurements at distances smaller than two wavelengths (Ekström et al., 2009). The major limit is set by the seismic wave field characteristics.

Aki (1957) states that the azimuthally averaged normalized cross spectrum S(Δ,ω₀) for a receiver separation Δ and frequency ω₀ varies as J₀, the zero-order Bessel function of the first kind

$$\begin{array}{}\text{(B3)}& S(\mathrm{\Delta },{\mathit{\omega }}_{\mathrm{0}})=J_{\mathrm{0}}\left({\displaystyle \frac{{\mathit{\omega }}_{\mathrm{0}}}{c\left({\mathit{\omega }}_{\mathrm{0}}\right)}}\mathrm{\Delta }\right).\end{array}$$

This relation suggests that the dispersion curve of phase velocities can be obtained from the fit of a J₀ Bessel function to the cross spectrum obtained on a loop of receivers of the same radius Δ, or also, as demonstrated by Cox (1973), to the cross spectrum obtained for a single station pair if computed on an azimuthally isotropic wave field.

Ekström et al. (2009) successfully obtain phase velocity estimates at discrete frequencies from ambient noise cross-correlations, by associating the zero crossing of the real part of the data cross spectrum with zeros of a Bessel function following Eq. (B3). Preiswerk and Walter (2018) and Lindner et al. (2018) both use this method to obtain dispersion curves of Rayleigh wave speeds from cross-correlations of on-ice seismic records.

Application of this method is presented in Fig. B3 for one cross-correlation function obtained at Argentière. Because of possible noise contained in the correlation time series, the cross spectrum is first smoothed to avoid any extra zero-crossing measurement. As there is a possibility of having missed one or several zero crossings (indicated by black squares in b), several dispersion curves are generated (black dashed lines in c). The correct one still needs to be identified by judging the plausibility of the results given the expected velocities of the propagation medium (Ekström et al., 2009).

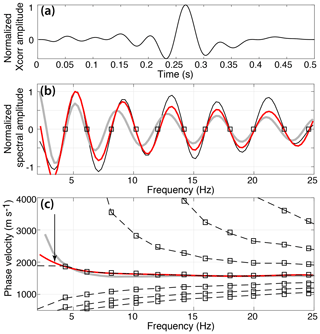
Figure B3 Computation of Rayleigh wave phase velocity using Aki's spectral method. (a) Symmetric icequake cross-correlation function obtained for one receiver pair in Glacier d'Argentière, with stations 450 m apart. (b) The real part of the spectrum of (a) is in black, and associated zero crossings are marked by squares. The gray line indicates the real part of the spectrum associated with an a priori phase velocity dispersion curve which serves as a starting model for the least-square fit (in red) of the observations. (c) Corresponding phase velocities estimated by zero crossings (black dashed lines) and least-square fit (red). The prior dispersion curve used for the Bessel fit is plotted in gray. The black arrow indicates the minimum frequency above which we can trust the velocity measurements and corresponds to approximately one wavelength.

The dispersion curve estimation can be refined by fitting the entire cross spectrum with a Bessel function, instead of fitting the zero crossings only. We develop an approach similar to that of Menke and Jin (2015), who employ a grid search to generate an initial estimate of the phase velocity that matches the observed cross spectrum and then use a generalized least-squares procedure to refine this initial estimate.

The prior dispersion curve has to be as close as possible to the measured dispersion curve to avoid cycle skipping during the fitting. In our procedure, we take as a starting model the average dispersion curve obtained from f-k analysis of the cross-correlation section computed at the Argentière array. For sparse network configuration (as in Greenland and Gornergletscher, i.e. Figs. 9d and 11c), we take the theoretical dispersion curve computed with Geopsy software and based on the prior knowledge we have on the subsurface. The dispersion curves are then modeled as polynomial functions to enforce their smoothness and to reduce the number of fitting parameters and help the convergence of the fitting process. The order of the polynomial can be varied. Usually a polynomial order of 5 is a good compromise between smoothness and complexity of the dispersion curve. We then use a least-square inversion procedure of the polynomial coefficients to estimate the dispersion curve which best reproduces the observed cross spectrum.

Figure B3 shows the output of this procedure which yields to the same dispersion curve (red line in panel c) as the most probable one computed by fitting the zero crossings. The overall-fitting method is particularly efficient for estimating more accurate phase velocities than with the zero-crossing fit, when considering correlation functions with low SNR (Menke and Jin, 2015). However it is particularly sensitive to the frequency range in which the least-square inversion is performed. When considering cross-correlation functions computed in narrow frequency bands as in Sects. 4 and 5, the method introduces strong side effects near the frequency corner limits due to filtering (Figs. 9d and 11c). The cross spectrum must then be fitted considering carefully selected frequency components.

In the example shown in Fig. B3, the cross-correlation function is computed for frequencies of 1–25 Hz. The Bessel fitting method is applied to frequencies above 2 Hz and enables us to widen the velocity estimates down to 3 Hz (that is the frequency at which the inter-station distance is approximately equal to one wavelength) when compared to the zero-crossing output.

B3 Slant-stack technique on discrete sources

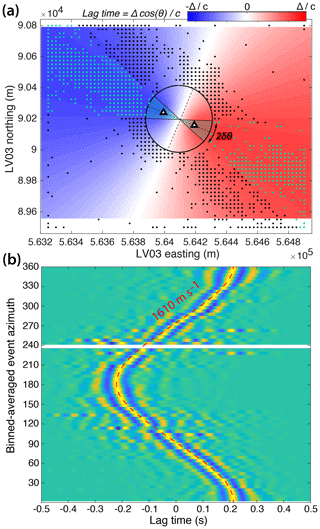
Figure B4 (a) Icequake locations (dots) in Glacier d'Argentière whose waveforms are cross-correlated at the two stations (triangles) to obtain (b). Green dots in (a) show the events that lie in the endfire lobes of aperture 2δθ (see main text). (b) The icequake cross-correlation functions (here averaged in 5^∘ azimuth bins) give coherent arrival times for Rayleigh waves traveling in the ice between the two stations, which are a function of the inter-station distance Δ and the event azimuth relative to the station path θ, as plotted in background colors in (a). The red dashed line shows the least-square fit of the arrival times with a sinusoidal function of phase velocity c=1610 m s⁻¹ for a central frequency of 15 Hz. Correlation functions are here filtered between 10 and 20 Hz.

This method employed by Walter et al. (2015) can only be applied to cross-correlation functions that are computed on discrete sources (i.e. icequakes). It was used to obtain the velocity from ICC at Glacier d'Argentière in Sect. 3.3. We here exploit the phase time difference in the arrival times of Rayleigh waves with respect to the source position, and we reproduce the azimuthal variations in phase times assuming a constant velocity.

The plane wave approximation implies a sinusoidal dependence of the arrival times which depend on the source azimuth and propagation velocity c as Δcos (θ)∕c with Δ the station separation and θ here defined as the source azimuth relative to the station pair axis (Fig. B4a and b). We call the endfire lobes the two areas aligned with the receiver direction, in which the phase of the correlation function is stationary with respect to azimuth. The angular aperture of the endfire lobes depends on the ratio between the seismic wavelength λ and the station separation as $\mathit{\delta }\mathit{\theta }=\sqrt{\mathit{\lambda }/\mathrm{\Delta }}$ (Roux et al., 2004; Gouédard et al., 2008b).

To measure seismic velocities at one station path and at different frequencies, we filter the individual correlation functions computed for each event to octave-wide frequency ranges. The lower frequency we can resolve is determined by the icequake spectral content and is most importantly related to the station separation as we require that at least two wavelengths are sampled. We then restrict the analysis to 15–30 Hz.

We assign all cross-correlations to event azimuth bins of 5^∘ to minimize the effects of location errors. For each trace, the arrival time of the Rayleigh wave is measured as the maximum of the correlation function computed at each frequency. We then invert the best sinusoid fit to the times of the maxima (in the least-square sense). The best solution gives the velocity estimate at the central frequency of the spectral band.

The velocity solution estimated by this method is naturally averaged over the azimuth range and can only be considered as the average velocity in the presence of strong azimuthal anisotropy which implies azimuthal variations in propagation velocities (Sect. 3.3). Nevertheless, the least-square solution fits very well the Rayleigh wave arrival times in the azimuth range of the stationary phase zones (Fig. B4b) and is then considered to represent the propagation medium between the two stations well.

To minimize the effects of location errors or low SNR of the correlation components, we perform a jackknife test on randomly selected events to fit the sinusoid. We require that the maximum of the cross-correlation stacked over bootstrap samples (i.e. selected correlation functions that have been shifted by the inverted arrival times prior to stacking) exceeds 0.7. We require that at least 10 azimuth bins including the endfire lobes are considered in the sinusoidal fit. The final velocity at each frequency is then averaged over 200 jackknife tests.