the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The 2018 North Greenland polynya observed by a newly introduced merged optical and passive microwave sea-ice concentration dataset
Gunnar Spreen
Christian Haas
Larysa Istomina
Frank Kauker
Dmitrii Murashkin
Observations of sea-ice concentration are available from satellites year-round and almost weather-independently using passive microwave radiometers at resolutions down to 5 km. Thermal infrared radiometers provide data with a resolution of 1 km but only under cloud-free conditions. We use the best of the two satellite measurements and merge thermal infrared and passive microwave sea-ice concentrations. This yields a merged sea-ice concentration product combining the gap-free spatial coverage of the passive microwave sea-ice concentration and the 1 km resolution of the thermal infrared sea-ice concentration. The benefit of the merged product is demonstrated by observations of a polynya which opened north of Greenland in February 2018. We find that the merged sea-ice concentration product resolves leads at sea-ice concentrations between 60 % and 90 %. They are not resolved by the coarser passive microwave sea-ice concentration product. The benefit of the merged product is most pronounced during the formation of the polynya. Next, the environmental conditions during the polynya event are analysed. The polynya was caused by unusual southerly winds during which the sea ice drifted northward instead of southward as usual. The daily displacement was 50 % stronger than normal. The polynya was associated with a warm-air intrusion caused by a high-pressure system over the Eurasian Arctic. Surface air temperatures were slightly below 0 ∘C and thus more than 20 ∘C higher than normal. Two estimates of thermodynamic sea-ice growth yield sea-ice thicknesses of 60 and 65 cm at the end of March in the area opened by the polynya. This differed from airborne sea-ice thickness measurements, indicating that sea-ice growth processes in the polynya are complicated by rafting and ridging. A sea-ice volume of 33 km3 was produced thermodynamically.
- Article
(9597 KB) - Full-text XML
- BibTeX
- EndNote
Arctic sea ice influences the climate system by radiating incident heat back into space and by regulating the ocean–atmosphere exchange of heat, humidity and momentum. The fraction of a given ocean area which is covered by sea ice is called sea-ice concentration (SIC). SIC is of high relevance for physics, biology and the safety of shipping routes. The summer sea-ice retreat observed since 2007 is a major driver of the Arctic amplification, the enhanced warming of the Arctic compared to the mid-latitudes (Dai et al., 2019). While the scientific community largely agrees that Arctic amplification changes the mid-latitude weather patterns, the exact mechanisms and pathways are subject to debate. A comprehensive literature synthesis is given in Vavrus (2018).
Arctic-wide SIC observations are available every second day by spaceborne passive microwave radiometers since 1979 and daily since 1987 (Tonboe et al., 2016). Passive microwave measurements do not require daylight and are only slightly affected by clouds. Therefore, they can provide data all year and under all weather conditions. The Advanced Microwave Scanning Radiometer 2 (AMSR2) has frequency channels between 6.9 and 89 GHz. The 89 GHz frequency channels are used in this study. The algorithm which we use is the ARTIST (Arctic Radiation and Turbulence Interaction STudy) Sea Ice algorithm (ASI) (Kaleschke et al., 2001; Spreen et al., 2008). The resolution of the 89 GHz channels of AMSR2 goes down to 3 km by 5 km in the instantaneous field of view. Thus, it is possible to retrieve SIC at 3.125 km grid spacing (Beitsch et al., 2014). The resolution of passive microwave sensors ranges from 40 to 50 km from the 19 and 37 GHz channels available since 1979 (Ivanova et al., 2014; Comiso, 1995; Markus and Cavalieri, 2000) to 5 km from the 89 GHz channels available since 2001 (Kaleschke et al., 2001; Spreen et al., 2008). The spatial and temporal coverage of passive microwave SIC and their year-round availability makes them valuable for climate research. However, the coarse resolution prevents accurate monitoring of the sea-ice edge, newly formed polynyas and leads. Polynyas are non-linearly shaped openings in the sea ice (WMO, 1970); leads are linear openings in the sea ice (Marcq and Weiss, 2012; Wernecke and Kaleschke, 2015) and are typically smaller than polynyas.
Thermal infrared data as acquired by the Advanced Very High Resolution Radiometer (AVHRR; since 1979), the Visible Infrared Imaging Radiometer Suite (VIIRS; since 2012) and the Moderate Resolution Imaging Spectroradiometer (MODIS; since 2000/2002) offer resolutions of 750 m (VIIRS) and 1 km (MODIS; AVHRR). An algorithm to derive SIC at 1 km resolution from MODIS thermal infrared measurements has been presented and evaluated by Drüe and Heinemann (2004, 2005). Compared to a typical AMSR2 5 km by 5 km grid cell, this allows 25 subpixel measurements and thus an enhanced potential to resolve leads.
Leads are not expected to show up as completely open water areas in the thermal infrared data since they refreeze rapidly, especially in winter. However, they still show up as reduced SIC while the sea ice is thin. They are responsible for more than 70 % of the upward ocean–atmosphere heat flux in the central Arctic during winter (Marcq and Weiss, 2012). According to Marcq and Weiss (2012), 1 % of the lead area fraction can change the surface air temperature by 3.5 ∘C; hence the thermal infrared SIC is quite sensitive to the presence of leads. In contrast, passive microwave measurements do not resolve narrow leads because of their coarse resolution. Also, 89 GHz measurements are insensitive to the sea-ice thickness for thicknesses above 10 cm (Heygster et al., 2014; Ivanova et al., 2015). While the high spatial resolution of thermal infrared measurements is a valuable benefit, they are only available in cloud-free locations and thus not suitable if one wants complete spatial coverage as is needed for long-term climate monitoring.
Synthetic Aperture Radar (SAR) data (Karvonen, 2014; Murashkin et al., 2018) have even higher spatial resolution, for example, Sentinel-1 A/B with about 90 m by 90 m in the Extra Wide swath mode used over the Arctic Ocean. Further, they penetrate clouds. If cloud cover is taken into account, there are more SAR data than thermal infrared. However, automated SIC retrieval from SAR measurements is difficult, although attempts have been undertaken, for example, in Karvonen (2014). Further, their availability and coverage are still limited by the duty cycle and the swath width; therefore complete daily Arctic-wide coverage is not guaranteed.
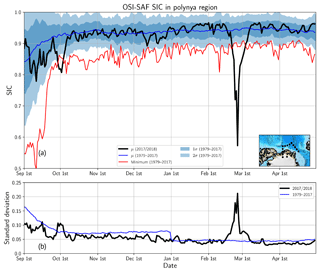
Figure 1(a) Mean OSI-SAF SIC (Lavergne et al., 2019) in the polynya region (indicated by the dashed box in the map in the lower right corner). The black line shows the mean SIC in 2018. The blue line shows the mean SIC between 1979 and 2017. The dark/light shades indicate the 1/2σ interval, respectively. The red line shows the minimal mean SIC between 1979 and 2017 for each day. (b) Time series of the standard deviation in the polynya region for 2018 (black). The blue line shows the mean of the standard deviations in the polynya region between 1979 and 2017.
For the first time this paper presents a merged product from AMSR2 passive microwave SIC and MODIS thermal infrared SIC at a spatial resolution of 1 km. This merged product benefits from both the high resolution of the MODIS thermal infrared data and the spatial coverage of the AMSR2 SIC. A Sentinel-1 SAR-based lead area fraction product (Murashkin et al., 2018) is used for comparison. The benefit of the merged SIC with respect to single-sensor passive microwave or thermal infrared SIC is demonstrated during the formation of a polynya which was observed between 14 February and 8 March 2018 north of Greenland (Fig. 1).
Polynyas typically last days to weeks, and most of them occur regularly (Morales-Maqueda et al., 2004). It can be argued whether a refrozen polynya which is covered by thin sea ice should be considered to be a polynya. An argument for referring to it as a polynya is that the heat flux is considerably higher for thin sea ice than for thick sea ice. Also, a refrozen polynya is often visible in SAR images because the sea ice grown thermodynamically under calm weather conditions has a smooth surface. On the other hand, passive microwave measurements retrieve it as fully sea-ice-covered as soon as the sea ice is thicker than about 10 cm or covered by frost flowers or snow (Heygster et al., 2014). In this paper, we refer to the polynya as opened as long as the merged SIC is below 100 %.
There are two types of polynyas: sensible and latent heat polynyas. Morales-Maqueda et al. (2004) describe both types of polynyas in detail. We continue with the description of latent heat polynyas since the one we investigate pertains to this type. Latent heat polynyas normally develop close to the coast due to offshore winds and/or ocean currents which cause divergent sea-ice motion. Sea ice is pushed away from the coast and new frazil/grease ice forms. The 10 major Arctic coastal polynyas produce roughly 130–840 km3 of sea ice per year (Tamura and Ohshima, 2011). Heat fluxes are typically between 300 and 500 W m−2 (Haid and Timmermann, 2013; Martin et al., 2004).
Polynyas form the basis for food webs by enabling photosynthesis and providing food for mammals, birds and humans alike (Smith et al., 1990; Morales-Maqueda et al., 2004; Schledermann, 1980). Preußer et al. (2016) report that polynyas between January and March have sizes between 400 and 43 600 km2. Many polynyas recur annually in the same places (Morales-Maqueda et al., 2004; Preußer et al., 2016), but the one we investigate does not appear frequently (Fig. 1).
The sea ice north of Greenland is one of the oldest and thickest in the entire Arctic (Vaughan et al., 2013). This sea ice was blown offshore in the course of days in February 2018, forming a coastal polynya which lasted from 14 February to 8 March, and spanned more than 60 000 km2 at its maximal extent. A recent study (Moore et al., 2018) uses the ASI-AMSR2 SIC mentioned above to show the polynya. We demonstrate the benefit of our higher-resolution merged SIC product when describing the formation of the polynya. Moore et al. (2018) identify a sudden stratospheric warming as the trigger of the polynya. We add to their work by investigating sea-ice drift data. We conclude by estimating the amount of sea ice which grew in the polynya and the amount of heat released to the atmosphere.
This paper is structured as follows: Sect. 2 describes the data used. Section 3 describes the merging procedure and the calculation of the thermal infrared MODIS SIC. Section 4 compares the SIC datasets and provides basic information about the polynya itself. Section 5 describes the local and large-scale 2 m air temperature, the surface air pressure and the sea-ice drift during the opening and refreezing of the polynya. Section 6 gives an estimate of the sea-ice growth and the heat release in the polynya. Section 7 discusses the results. Section 8 summarises the results and presents the conclusions. Section 9 lists directions for future research.
The following questions will be addressed and answered in this paper:
-
Does merging MODIS thermal infrared and AMSR2 passive microwave SIC allow additional insights about the formation of the polynya?
-
Was the polynya opened thermodynamically or dynamically, and how unusual were the environmental conditions?
-
How much sea ice grew in the polynya, and how much heat was released to the atmosphere?
This section describes the input data for the merged product (Sect. 2.1) and the data (Sect. 2.2) used to investigate reasons for and consequences of the polynya formation.
2.1 Input data to merged product
2.1.1 AMSR2 sea-ice concentration
The Global Change Observation Mission-Water Satellite 1 (GCOM-W1) carries the Advanced Microwave Scanning Radiometer 2 (AMSR2; https://suzaku.eorc.jaxa.jp/GCOM_W/w_amsr2/whats_amsr2.html, last access: 25 July 2019). Its orbit has an inclination of 98∘, and it crosses the Equator at 01:30 and 13:10 on its descending and ascending orbit, respectively. AMSR2 measures brightness temperatures at six microwave frequencies between 6.9 and 89 GHz. The 89 GHz brightness temperatures have the highest spatial resolution. It is 5 km by 5 km in the effective field of view. The ASI algorithm (Kaleschke et al., 2001; Spreen et al., 2008) derives SIC from these brightness temperatures. To get the smallest possible time lag to the MODIS data, we use swath data. Additionally, the swath data have a spatial resolution of 5 km by 5 km, while the grid spacing of the daily product is 6.25 km by 6.25 km. The daily product is publicly available at https://www.seaice.uni-bremen.de (last access: 25 July 2019). The swath data have been processed internally.
2.1.2 MODIS ice surface temperature
The Moderate Resolution Imaging Spectroradiometer (MODIS; https://modis.gsfc.nasa.gov/, last access: 25 July 2019) aboard NASA's Terra/Aqua satellites has provided data in the optical and thermal infrared spectrum since 2000 (Terra) and 2002 (Aqua), respectively. The Aqua satellite's orbit characteristics are similar to those of GCOM-W1. It has the same inclination and flies 4 min behind GCOM-W1. The Terra satellite's Equator crossing time is shifted by 45 min relative to Aqua. We therefore exclusively use the MYD29 ice surface temperature of MODIS Aqua and omit MODIS Terra data. The time lag between MODIS Aqua and AMSR2 is normally between 3 and 8 min since both satellites, Aqua and GCOM-W1, fly in the A-Train satellite constellation. The A-Train is a suite of satellites which follow each other closely on the same orbit. It was designed to obtain near-simultaneous Earth observation data from different measurements. The MYD29 ice surface temperature dataset was developed by NASA's Goddard Space Flight Center (Hall and Riggs., 2018) and is distributed by the National Snow and Ice Data Center (NSIDC) at https://nsidc.org/data/MYD29/versions/6 (last access: 25 July 2019). It has a spatial resolution of 1 km. The data are distributed as granules of 5 min length. For cloud screening, we use the MYD35_L2 cloud mask (Ackerman et al., 2017). A pixel is discarded if it is not labelled as “confident clear” or is over land or is at the coast or is labelled as “cirrus cloud” or “shadow”.
2.2 Additional data
2.2.1 OSI-SAF sea-ice concentration
For climatological reference, we use the OSI-450 SIC Climate Data Record product of the European Organisation for the Exploitation of Meteorological Satellites (EUMETSAT) Ocean and Sea Ice Application Facility (OSI-SAF) which is available for the period from 1979 to 2015 at http://osisaf.met.no/p/ice/ (last access: 25 July 2019) (Lavergne et al., 2019). It uses the coarse-resolution instruments SMMR (Scanning Multi-channel Microwave Radiometer), SSM/I (Special Sensor Microwave/Imager) and SSMIS (Special Sensor Microwave Imager/Sounder). The data are provided daily for the period since 1987 and every 2 d before. They are gridded to a Lambert azimuthal equal-area grid, also known as EASE grid 2.0, with a grid spacing of 25 km. For the years 2016–2018, the OSI-430-b SIC product (http://osisaf.met.no/p/ice/ice_conc_cdr_v2.html, last access: 25 July 2019) is used. The time series of both products is consistent at the transition (http://osisaf.met.no/docs/osisaf_cdop3_ss2_pum_sea-ice-conc-climate-data-record_v2p0.pdf, last access: 25 July 2019). For calculating the polynya area time series, we project all data to a north polar stereographic grid with the true latitude at 70∘ N (“NSIDC grid”; https://nsidc.org/data/polar-stereo/ps_grids.html, last access: 25 July 2019) with 12.5 km grid spacing. The average of all OSI-SAF SIC between 45∘ W/81∘ N and 5∘ W/85∘ N in geographic coordinates is used for the polynya area time series in Fig. 1. The polynya region is shown in the inset of Fig. 1. The climatology comprises the years from 1979 to 2017.
2.2.2 SAR sea-ice concentration
In addition to SIC, the lead area fraction is analysed. It is calculated as the fraction of leads in the area. Binary lead maps are produced by an automatic classification algorithm from Sentinel-1 C-band SAR data at 5.4 GHz (Murashkin et al., 2018). The lead classification algorithm analyses backscatter values and image texture of the surrounding area. Here leads are assumed to be areas of open water of an arbitrary shape. Therefore the polynya is expected to have a high lead area fraction. Sentinel-1 scenes taken in the Extra Wide swath mode with 40 m pixel size are used. Images taken within 1 d are combined in lead maps of the Arctic with 80 m resolution. Then the lead area fraction is calculated from these binary maps on a 800 m grid. Finally, the data are resampled to the NSIDC grid with 1 km grid spacing for comparison with the other SIC datasets. Sea-ice concentration is derived by inverting the lead area fraction:
where LAF is the lead area fraction. The product is called SAR SIC.
2.2.3 Sentinel mosaics
Since autumn 2014, the Technical University of Denmark has produced near-real-time mosaics of Sentinel-1 SAR data as they become available to the Copernicus Marine Environment Monitoring Service (CMEMS). The mosaics cover most of the potentially sea-ice-covered areas of the Northern Hemisphere and Southern Hemisphere, respectively. They consist of geometrically and radiometrically corrected data from Extra Wide swath and Interferometric Wide swath modes of both Sentinel-1A and Sentinel-1B. The radiometric correction includes a correction for the average incidence angle dependence of the sea-ice backscatter. The full mosaics are available at http://www.seaice.dk (last access: 25 July 2019).
2.2.4 Sea-ice drift, air temperature and air pressure
The OSI-405 low-resolution sea-ice drift product by EUMETSAT OSI-SAF (Lavergne et al., 2010) is used in this study. It has a grid spacing of 62.5 km, a temporal resolution of 2 d and is projected to the NSIDC grid. Sea-ice motion is first derived separately from ASCAT (Advanced Scatterometer) C-band backscatter, AMSR-E/AMSR2 37 GHz, SSM/I 85 GHz and SSMI/S 91 GHz brightness temperatures. Then, the single-sensor sea-ice drift vectors are merged by an optimal interpolation scheme. A comparison to other sea-ice drift datasets is given in Sumata et al. (2014).
We use 2 m temperature data from the weather station at Cape Morris Jesup operated by the Danish Meteorological Institute. They were sampled in 3 h intervals until 2015 and hourly since 2016. We average the values daily. Additionally, we use surface air pressure and 2 m air temperature at a spatial and temporal resolution of 0.25∘ and 1 d, respectively, from the ERA5 reanalysis (https://confluence.ecmwf.int/display/CKB/ERA5+data+documentation, ECMWF, 2015). The ERA5 reanalysis is run at the European Centre for Medium-Range Weather Forecasts (ECMWF). It is the fifth generation of reanalyses from ECMWF. Hourly reanalysis data of 2 m air temperature and 10 m wind are available in near-real time at a spatial resolution of 31 km (Hersbach and Dee, 2016).
2.2.5 Sea-ice growth from freezing degree days
To estimate thermodynamic sea-ice growth in the polynya, we employ an empirical equation described by Lebedev (1938):
where SIT is the sea-ice thickness in centimetres (cm), and FDD represents freezing degree days. Freezing degree days are the sum of air temperatures above and below freezing over a given time, where air temperatures below and above 0 ∘C count positively and negatively:
where n is the index of the respective day, ndays is the total number of days and is the daily mean air temperature of the respective day in degrees Celsius (∘C). We use the ERA5 2 m air temperature. We will compare sea-ice thickness from different sources. For a consistent comparison despite the very different grids, we introduce a grid-independent criterion for the polynya region: we consider only those grid cells in which the sea-ice concentration was below 50 % at least once during the polynya event. For the freezing degree days, we use the ERA5 sea-ice concentration. In addition to sea-ice thickness, we calculate the sea-ice volume produced by thermodynamic growth. For this, we multiply the sea-ice thickness by the fixed area of grid cells which were below 50 % SIC at least once while the polynya was open.
2.2.6 Passive microwave sea-ice thickness
Sea-ice thickness up to 50 cm can be derived from 1.4 GHz passive microwave measurements (Huntemann et al., 2014; Paţilea et al., 2019). We use the combined sea-ice thickness product of the Soil Moisture and Ocean Salinity (SMOS) and Soil Moisture Active/Passive (SMAP) radiometers to evaluate the sea-ice growth from the freezing degree days. The product is disseminated by the University of Bremen at https://seaice.uni-bremen.de (last access: 25 July 2019). It comprises both dynamic and thermodynamic growth. We need to ensure that we consider only those grid cells with thermodynamic sea-ice growth. Therefore, we apply the same criterion as described in Sect. 2.2.5. We select only grid cells in which the ASI-AMSR2 passive microwave sea-ice concentration was below 50 % at least once during the polynya event.
2.2.7 NAOSIM model
The North Atlantic Arctic Ocean Sea Ice Model (NAOSIM; Kauker et al., 2003) has been used to calculate the sea-ice growth and the vertical heat fluxes during the polynya event. No data have been assimilated. We want to avoid interpolating from the model grid to the NSIDC grid. For a consistent selection of grid cells with thermodynamic sea-ice growth, we select the model grid cells which had below 50 % SIC at least once during the polynya event, as described in Sect. 2.2.5, and perform the calculations on the model grid which is described in the next paragraph.
NAOSIM's ocean model is derived from version 2 of the Modular Ocean Model (MOM-2) of the Geophysical Fluid Dynamics Laboratory (GFDL). The version of NAOSIM used here has a horizontal grid spacing of 0.25∘ on a rotated spherical grid. The rotation maps the 30∘ W meridian onto the Equator and the North Pole onto 0∘ E. The ocean model is coupled to a sea-ice model with viscous–plastic rheology (Hibler, 1979). The thermodynamics are formulated as a zero-layer model following Semtner (1976). Freezing and melting are calculated by solving the energy budget equation for a single sea-ice layer with a snow layer and an ocean mixed layer according to Parkinson and Washington (1979). In contrast to the original formulation the energy flux through the sea ice is calculated by a probability density function for the distribution of sea-ice thickness based on airborne electromagnetic measurements (Castro-Morales et al., 2014). The sea-ice model's prognostic variables are sea-ice thickness, sea-ice concentration and snow depth. If atmospheric temperatures are below the freezing point, precipitation is added to the snow mass. The snow layer is advected jointly with the sea-ice layer. The surface heat flux is calculated using prescribed atmospheric data and sea surface temperature predicted by the ocean model. The sea-ice model is formulated on the ocean model grid and uses the same time step. The models are coupled following the procedure devised by Hibler and Bryan (1987).
In contrast to the version described by Kauker et al. (2003), the present version uses a modified atmospheric forcing dataset consisting of 10 m wind velocity, 2 m air temperature, 2 m specific humidity, total precipitation, and downward solar and thermal radiation. For the period from 1979 to 2010 the forcing is taken from the National Center for Environmental Prediction (NCEP) Climate Forecast System Reanalysis (NCEP-CFSR) (Saha et al., 2010) and for the period from 2011 onwards from the NCEP Climate Forecast System version 2 (CFSv2) (Saha et al., 2014).
The initial state of 1 January 1980 is taken from a hindcast from 1 January 1948 to 31 December 1979. For details about the initialisation, the interested reader is referred to Kauker et al. (2003). Recently the model parameters were optimised with the help of a genetic algorithm. For a detailed analysis of the optimisation we refer to Sumata et al. (2019a, b).
3.1 MODIS sea-ice concentration
To calculate the MODIS SIC, we adapt the approach used in Drüe and Heinemann (2004). They interpolate linearly between the ice surface temperature of a fully sea-ice-covered pixel (sea-ice tie point ISTI) and that of a fully water-covered pixel (water tie point ISTW):
where ISTobs is the observed ice surface temperature. ISTW is set to −1.8 ∘C, the freezing point of seawater. For ISTI, the local variability of the ice surface temperature has to be taken into account. MODIS granules normally have 2030 pixels by 1054 pixels. We crop them so that the dimensions are divisible by 48. Then a box of 48 pixels by 48 pixels, called one cell, is taken. The cell is divided into three by three subcells of 16 pixels by 16 pixels. The 25th percentile of each subcell is selected as the preliminary sea-ice tie point. The choice of the percentile does not have a significant impact on the final tie point (Lindsay and Rothrock, 1995). The sea-ice tie point for each pixel is then expressed as a linear function with two variables:
where a, b and c are coefficients determined by bilinear regression, and x and y are the x∕y coordinates of the respective pixel within the cell. Subcells are discarded if more than 70 % of the pixels are masked out by the cloud mask. Cells are discarded if they contain fewer than five valid subcells. Then, the next 48 pixel by 48 pixel box is processed. So far, we have strictly followed the approach by Drüe and Heinemann (2004). Then, in difference to them, we shift the box by only one pixel at a time and repeat the bilinear regression before shifting the box by the next pixel. Thus, there are 48 possible ISTI values per pixel. The mean of those values is selected as ISTI. Subsequently, each granule is projected to the NSIDC grid at 1 km grid spacing to be merged with the next closest AMSR2 swath. For one MODIS granule, there were on average 36 % cloud-free pixels. When considering all granules of one day, 80 % of the pixels were cloud-free at least once.
3.2 Merging
For each MODIS granule, the AMSR2 swath with the closest acquisition time is selected. On average, eight MODIS–AMSR2 matching overflights are available per day. AMSR2 SIC is given as a half-orbit starting either at the North Pole (descending orbit) or at the South Pole (ascending orbit). For a descending orbit, we take the time of the first measurement as acquisition time. For an ascending orbit, we take the time of the last measurement as acquisition time. For the MODIS SIC, we take the starting time of that granule as acquisition time. We use the MODIS–AMSR2 pair found in this way if it has at least 10 % of cloud-free overlap. For the merging, we split the MODIS SIC data into boxes of 5 km by 5 km, which roughly corresponds to one AMSR2 footprint. The MODIS and AMSR2 SIC in this 5 by 5 km box are called SICMODIS,5 km and SICAMSR2,5 km, respectively. Now, we calculate the difference between the two datasets, ΔSIC,5 km, for each box:
ΔSIC,5 km is now added to the MODIS SIC as shown in Eq. (7). This way, we preserve the mean of the AMSR2 SIC in this 5 km by 5 km box. In a last step, we use the AMSR2 data where no MODIS data are available:
where the indices i,j denote the position within the 5 km box. To get a smooth field, the box is then shifted by 1 km and the procedure is repeated, before the box is shifted again by 1 km. This way, each pixel is covered 25 times. The mean for each pixel is selected as the merged SIC value. This procedure preserves the AMSR2 mean within the 5 km by 5 km box, so that there are no sudden increases or decreases of SIC if no MODIS pixel is available. A similar procedure has been applied by Gao et al. (2010). If the AMSR2 SIC is 100 %, the merged SIC at single pixels can be above 100 %. We tolerate this because we want to preserve the mean SIC from AMSR2. Merged SIC above 100 % is set to 100 % in the end.
3.3 Open water extent
We want to show the benefits of the higher resolution of the merged SIC compared to the AMSR2 SIC. The mean SIC for both datasets is identical by definition. However, the higher resolution of the merged product results in sharper gradients, for example, at the edges of leads. To show this effect, we calculate the open water extent for both datasets. It is defined as the area covered by all pixels which have at least 15 % open water. Due to its higher spatial resolution, the merged SIC is expected to have a higher open water extent than the AMSR2 SIC. For meaningful comparison, we consider only those data points for which cloud-free MODIS data are available for the merging. Also, we constrain our analysis to scenes when at least 50 % of the pixels are cloud-free measurements. The open water extent is normalised by dividing it by the number of cloud-free pixels.
3.4 Airborne sea-ice thickness profiles
We use data of an airborne electromagnetic (AEM) sea-ice thickness survey carried out over the south-eastern region of the refrozen polynya on 30 and 31 March 2018, i.e. roughly 5 weeks after the polynya had begun to refreeze. Surveys were carried out with a DC-3/Basler BT67 aircraft (Haas et al., 2010) and were processed as described by Haas et al. (2009). AEM data have an accuracy of ±0.1 m over level ice but can underestimate the thickness of pressure ridge keels by up to 50 % due to the large footprint of the AEM measurement of up to 45 m over which an average sea-ice thickness estimate is retrieved. Accuracy was confirmed by a sufficiently large number of small open leads with sea-ice thickness of 0 m. AEM measurements obtain the total ice plus snow thickness. Visual observations during the flights showed that the snow on the young first-year ice of the polynya was less than 0.05 m thick and can be neglected for the purpose of this study. All measurements over small patches of multi-year ice embedded in the polynya have been removed from the dataset. The results therefore represent the thickness of 5-week-old first-year ice in those specific environmental conditions.
This section first compares the 2018 SIC in the polynya region to that of the entire satellite period (1979–today) in Sect. 4.1. Afterwards the advantage of the merged SIC over the other, single-sensor products is discussed and demonstrated in Sect. 4.2. Finally, the temporal evolution of the polynya is described in Sect. 4.3.
4.1 Climatological context
Figure 1 puts the polynya into a climatological context by comparing it to the OSI-SAF Climate Data Record (OSI-450) which goes back to 1979 (Lavergne et al., 2019). Since the Climate Data Record is only available for the period until 2015, we use the OSI-SAF Interim Climate Data Record (OSI-430-b) after 2015. The products are temporally consistent at the transition. We show the 1979–2017 mean SIC in the polynya region (box in the inset map) for each day between 1 September and 30 April. Normally, the mean SIC in the region north of Greenland is around 95 %, with a standard deviation of 3 % after the freeze-up period in September and October. The OSI-SAF SIC is capped at 100 %; thus the SIC average can only be below 100 % and must result in lower SIC than might have been the case. The climatological mean and the standard deviation do not change much between the beginning of November and the end of April. Except for a 10 % drop during the early freeze-up at the end of September, the 2017/2018 SIC stayed within 1 standard deviation of the climatological mean until mid-January. There was a 2-week period of SIC above the climatological mean in the second half of January. In mid-February, the polynya started opening rapidly. The mean SIC was at its minimum on 26 February, when it was close to 70 %. Previously, the lowest mean SIC at any day between 1 October and 30 April was 79 %. The time series of the minimal SIC shows that there were other periods during which the mean SIC was outside of the 2σ interval in particular years, for example once in mid-December 1986, once in early January 1984 and once in late March 1983 (single years not shown in Fig. 1). However, none of them reached the low extent of the 2017/2018 winter season. We also investigated the homogeneity of the sea-ice cover by calculating the mean spatial standard deviation in the polynya region (Fig. 1b). It was above 20 % in 2018, while it is normally close to 5 %. This underlines how strongly the normally homogeneously distributed sea-ice cover north of Greenland broke up during this exceptional event.
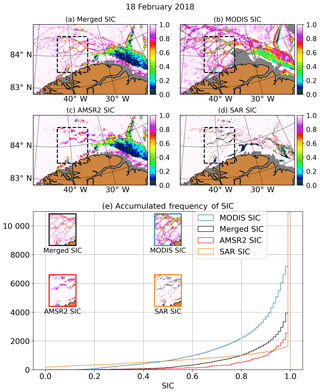
Figure 2SIC on 18 February 2018 observed with (a) merged, (b) MODIS, (c) AMSR2 and (d) SAR SIC. The acquisition times for MODIS–AMSR2 were 11:45 and 11:39 UTC, respectively. The dashed black box in panels (a)–(d) marks the region used in panel (e). (e) Cumulative histograms for the four datasets. The insets show the SIC distribution for the single datasets. Data points for which one of the products was not available were discarded for all products.
4.2 Sea-ice concentration comparison
The advantage of high-resolution SIC datasets and the differences between the single-sensor datasets are illustrated in this section. The AMSR2 SIC, MODIS SIC, merged SIC and SAR SIC are compared in Fig. 2a–d. West of the polynya, the MODIS SIC is lower than the AMSR2 SIC. The merged SIC preserves the AMSR2 mean and is thus higher than the MODIS SIC and spatially continuous if there are no MODIS data available. The benefit of including the MODIS data can be seen when looking at the leads which open west of the polynya: they are much more clearly resolved in the merged product. This is illustrated in the cumulative frequency distribution in Fig. 2e in more detail. The SAR SIC is the only product which shows 0 % SIC as it has the finest spatial resolution and is based on a binary product. Additionally, a lead covered by very thin, smooth sea ice would still be classified as “open water”. These leads show up as reduced SIC of around 20 % in MODIS SIC. The broader leads are also resolved by AMSR2 and show up as SIC between 70 % and 80 %. AMSR2 retrieves only few values in the range between 40 % and 60 %. The higher amount of SIC between 60 % and 80 % is where the merged SIC resolves leads which are too narrow to be retrieved by AMSR2. Over the polynya region, the MODIS SIC and the SAR SIC are higher than the AMSR2 SIC. While AMSR2 retrieves 0 % SIC at the onshore and 20 % at the offshore side of the polynya, MODIS retrieves 40 % SIC at the onshore and 80 % at the offshore side of the polynya. The gradient occurs because the newly formed sea ice is advected away from the coast and pushed towards the north-eastern boundary of the polynya. New sea ice forms and piles up at the offshore side of the polynya. Generally, the impact of thin sea ice on the different products can be described as follows: in the very early growth phase, the SAR SIC is close to 0 % as long as the sea ice is smooth. When the smooth sea-ice cover breaks up, the backscatter starts to increase, and the SAR SIC increases. Additionally, the algorithm was trained with small leads which have a flat surface (Murashkin et al., 2018). In the polynya area, which is larger, the water surface can be rougher and would therefore not be classified as lead. The MODIS SIC is low during the early growth phase but not 0 % because the surface air temperature is slightly below the freezing point as soon as there is a very thin layer of sea ice. Their sensitivity to sea-ice thickness decreases as the sea-ice thickness increases. The AMSR2 SIC is sensitive to sea-ice thicknesses up to 10 cm (Heygster et al., 2014). The merged SIC is less sensitive to sea-ice thickness than the MODIS SIC because it is tuned to preserve the AMSR2 SIC mean. However, because it also includes the MODIS information, it still has some sensitivity to sea-ice thickness above 10 cm. The different sensitivities to sea-ice thickness are further illustrated in the time series of the mean SIC in Fig. 3. Note that the mean of the AMSR2 SIC is not shown because it is equal to that of the merged SIC by definition (Sect. 3.2). The MODIS SIC is lower than the merged SIC while the polynya breaks up and after it has frozen over. This is because it is more sensitive to the sea-ice thickness, and thin sea ice is shown as reduced sea-ice concentration. During the peak of the polynya area, it is larger than the merged SIC. Here, it is more sensitive to freshly grown sea ice. Also, it is more sensitive to small sea-ice surface temperature variations because the range between the sea-ice tie point and the water tie point gets very small. The SAR SIC is also larger than the AMSR2 SIC during the peak of the polynya area. The reason is again that it is more sensitive to newly formed sea ice than the merged SIC. While recently formed sea ice is retrieved as low SIC by the merged SIC, it increases the backscatter as soon as it breaks up. Due to the drift within the polynya, it is expected that the sea-ice surface is not smooth but breaks up quickly. Additionally, as mentioned above, the algorithm was not trained to classify rough surfaces such as water. To further demonstrate the benefit of the higher resolution of the merged product compared to the AMSR2 SIC, we show the open water extent in Fig. 4. The open water extent is the area covered by all pixels which have at least 15 % open water. Consider a typical AMSR2 grid cell of 5 km by 5 km with an AMSR2 open water fraction of 10 %. Our 1 km resolution dataset allows the retrieval of 25 different open water fractions in this grid cell whose mean would still amount to 10 %. However, single cells may have an open water fraction above 15 %, so that the open water extent is expected to be higher for a dataset with higher resolution. A comparison of the time series shows that the difference between the two datasets is small most of the time. It is 2 %–3 % while the polynya is open and close to 1 % after it has been closed. The benefit is more apparent when comparing the datasets relative to each other, as shown in Fig. 4c. The normalised difference is largest during the very early opening phase and smaller towards the end of the opening phase.
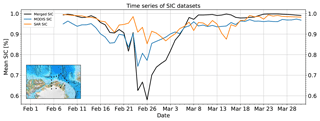
Figure 3Time series of the mean merged, MODIS and SAR SIC in the polynya region. The AMSR2 SIC is not shown because its mean is equal to the mean of the merged SIC by definition. Only points for which all datasets were available have been considered. The map on the lower left shows the region which was considered for the time series as dotted polygon.
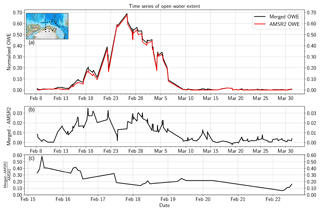
Figure 4Time series of the merged and AMSR2 open water extent. Panel (a) shows the open water extent for both datasets. It was normalised to the number of cloud-free pixels. Panel (b) shows the difference of the merged and the AMSR2 open water extent. Panel (c) shows the normalised difference of the two datasets during the opening phase. Note the different time span of panel (c). Only points for which MODIS data were available were considered for all three panels.
4.3 Polynya development
Having shown that the polynya was unprecedented in magnitude, and having demonstrated the benefit of our merged SIC product, we now focus on describing the temporal and spatial development of the polynya during the opening and refreezing. For this, we show maps before, during and after the polynya event in Fig. 5a–h, as well as a time series of the open water area from the merged product (Fig. 5i). First leads are already visible on 8 February, 6 d before the polynya actually starts to open. Also, the shear zone parallel to the coast where the polynya will break up later is already visible. This demonstrates the benefit of the merged product over the AMSR2 SIC, which would be too coarse to resolve these leads, as seen in Fig. 2. Starting on 14 February, the polynya area increases steadily until 22 February, when it already spans 30 000 km2. The polynya area decreases on 22 and 24 February. Apart from this, the polynya area increases strongly until it reaches its maximum extent on 26 February, when it spans more than 60 000 km2 (Fig. 5i). Afterwards, the area decreases almost linearly with time until the now refrozen polynya is not identified as open water anymore on 8 March. Note that the area of the opening is still visible as dark/new ice in the Sentinel-1 mosaic.
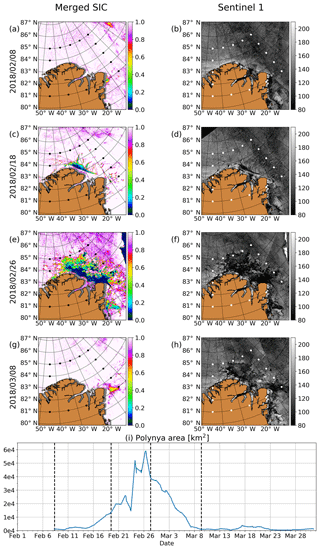
Figure 5(a, c, e, g) Merged SIC before, at the beginning, at the maximum and after the refreezing of the polynya. The MODIS–AMSR2 pairs were acquired at 07:50 and 07:44 on 8 February, at 11:45 and 11:39 on 18 February, at 09:15 and 09:11 on 26 February and at 11:30 and 11:28 on 8 March, respectively. All times are UTC. (b, d, f, h) Corresponding Sentinel-1A/B daily mosaics. The colour bar units are greyscale values. (i) Time series of the polynya area. The polynya area is calculated as the sum of the open water fraction (1 – merged SIC) in the map area, multiplied by the respective grid cell size. All available granules are shown. The acquisition times of panels (a), (c), (e) and (g) are marked by the vertical dashed lines.
There are areas (Fig. 5a,g) where leads and 100 % SIC are directly next to each other. This happens when there is no MODIS SIC available for the merging. In this case, the merged SIC is equal to the AMSR2 SIC which shows 100 % SIC for sea ice thicker than 10 cm.
In the next section, we investigate the driving mechanism behind the polynya and the environmental conditions throughout the event.
There are two possible reasons for the polynya: the sea ice could have drifted away, which would be typical of a latent heat polynya, or it could have melted, which would be typical of a sensible heat polynya. This section describes and analyses the 2 m air temperature and surface air pressure (Sect. 5.1) and the sea-ice drift pattern (Sect. 5.2) associated with the polynya.
5.1 Air temperature and surface air pressure
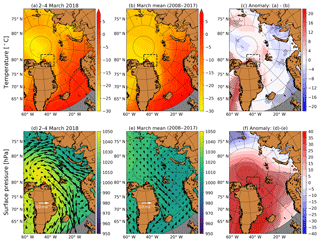
Local air temperatures (Fig. 6) at the autonomous weather station in Cape Morris Jesup in 2018 were above the 2010–2017 average from 15 February to 8 March. This is in line with the breaking up and refreezing of the polynya. The air temperature increased rapidly at the beginning of the polynya event. During the formation of the polynya, the air temperature varied by more than 10 ∘C from day to day and crossed the freezing point on 9 out of 10 d between 16 and 25 February. The air temperature decreased as soon as the polynya started to refreeze and reached the average value on 8 March. Above-average air temperatures during this time of the year have occurred before, for example in 2011 and 2013. However, those lasted only up to 5 d and not 10 d like during the event studied here. On a larger spatial scale, Figs. 7 and 8 show the air temperature and surface air pressure distribution during the formation phase (22 to 26 February) and the refreezing phase (2 to 4 March) of the polynya. During the formation, the air temperature was up to 20 ∘C and more than 2 standard deviations above average in the polynya region. This was not only a local phenomenon but was associated with a warm-air intrusion from the Atlantic Ocean which caused anomalously high air temperatures until beyond the North Pole (Fig. 7a). The surface air pressure distribution completes the picture: there was a high-pressure system over the Barents and Kara Sea which persisted until 26 February. The surface air pressure was 30–40 hPa above average, which is more than 2 standard deviations (Fig. 7f). This is the period when the polynya opening rate increased (Fig. 5i). The high-pressure system caused northward winds over the Greenland Sea which contributed to the opening of the polynya. Furthermore, it caused the advection of warm air from the mid-latitudes towards the Arctic region. A period of 10 d later, the atmospheric state had changed substantially (Fig. 8). The air temperature dropped down to the mean of the previous year. The surface air pressure was high over the Central Arctic and lower over the Eurasian Arctic. This caused southward winds which contributed to the closing of the polynya, together with the Transpolar Drift. Although the air temperature was far above average, it was not high enough to explain the polynya. It only crossed the freezing point for some hours but can not have melted the thick multi-year ice north of Greenland. We conclude that the sea ice must have been broken up by sea-ice drift. This is consistent with the study of Moore et al. (2018). They found that the thermodynamic sea-ice production was always positive, while the sea-ice motion caused the net loss of sea ice. The warm-air intrusion between 13 February and 3 March (Figs. 6 and 7) contributed to keeping the polynya open. The next section describes the sea-ice drift pattern throughout the polynya event.
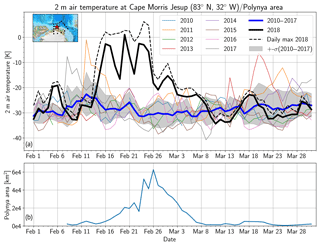
Figure 6(a) Daily average of 2 m air temperature data at the Danish Meteorological Institute's weather station at Cape Morris Jesup since 2010. The blue line shows the mean air temperature of the years 2010–2017, and the black line shows the air temperatures in 2018. The thin lines represent the single years. The shading indicates the standard deviation of the air temperatures in the years 2010–2017. The box and star in the map mark the region of the polynya event and the location of the Cape Morris Jesup station, respectively. (b) Time series of the polynya area are from Fig. 5 but with daily means instead of all granules.
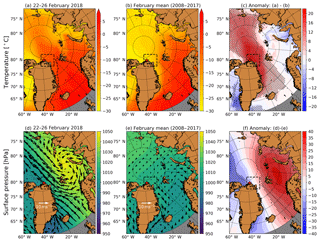
Figure 7(a) ERA5 2 m air temperature from 22 to 26 February 2018, together with the 0 ∘C isotherm. The box and star in the map mark the region of the polynya event and the location of the Cape Morris Jesup station, respectively. (b) February mean ERA5 2 m air temperature between 2008 and 2017. The 0 ∘C isotherm is shown as the dashed line. (c) Difference between panels (a) and (b). Black dots mark points where the air temperature in 2018 was more than 2 standard deviations above or below the 2008–2017 average. (d) ERA5 surface air pressure distribution from 22 to 26 February 2018. The black arrows give the ERA5 10 m wind. (e) Same as panel (d) but for the February mean surface air pressure between 2008 and 2017. (f) Difference between panels (d) and (e). Black dots mark points where the surface air pressure in 2018 was more than 2 standard deviations above or below the 2008–2017 average.
5.2 Sea-ice drift
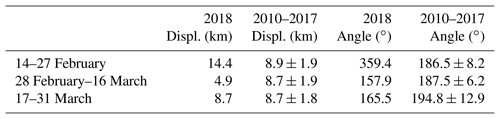
OSI-SAF sea-ice drift data between the opening of the polynya (14 February) and the end of our study period (31 March) are used to investigate the dynamic drivers of the polynya. In general, the Transpolar Drift exports the sea ice to the Atlantic Ocean via the Fram Strait. During the polynya event, however, this sea-ice drift pattern was reversed. Where there is normally southward flow, there was northward flow while the polynya opened (Fig. 9a, b). The sea-ice drift was not only in the opposite direction to usual but also stronger: the sea ice moved by more than 14 km d−1 over a period of almost 2 weeks. This is 50 % more than normal (Table 1). Afterwards, the sea-ice drift direction changed to normal conditions, i.e. south-east, and there was below-average displacement in the first half of March (Fig. 9c, d). During the second half of March, the sea-ice drift was about average (Fig. 9e, f). The mean sea-ice displacement and the sea-ice drift angle for 2018 and 2010–2017 are given in Table 1. The sea-ice drift angle is the orientation of the sea-ice drift towards north and is counted anticlockwise, so that a sea-ice drift angle of 90∘ means westward movement. Because of the south–south-western sea-ice drift direction, the sea ice was not completely exported towards the Fram Strait in the south-east direction. Instead, it partly returned to the polynya region. Here, it got rafted and ridged with the newly formed sea ice in the polynya. This matches the observation of strong south-western sea-ice drift between 16 and 20 March (Fig. 9g). We therefore expect a mix of thermodynamically grown flat sea ice and rough sea ice grown due to sea-ice deformation at the end of March.
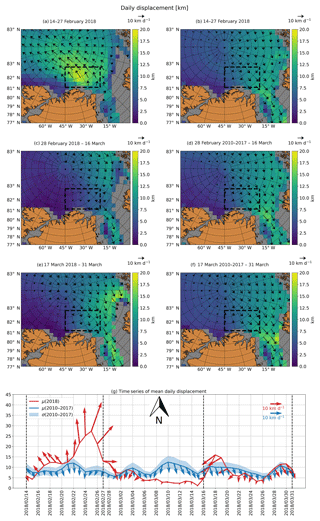
Figure 9Daily displacement based on the OSI-SAF drift product in the polynya region between 14 February and 31 March. The periods 14–27 February, 28 February–16 March and 17–31 March in 2018 are considered in panels (a), (c) and (e). The same periods, but for the mean between 2010 and 2017, are considered in panels (b), (d) and (f). The vectors in panels (a)–(f) show the mean sea-ice drift velocity in the corresponding periods, where velocity is defined as displacement per day. Panel (g) shows a time series of the displacement (lines), the standard error of the sea-ice drift between 2010 and 2017, defined as standard deviation divided by the square root of the number of years (blue shades) and the sea-ice drift velocity (vectors). The orientation is such that an upward-pointing vector points towards north. The arrows in the top right give the scale of the arrow length. Displacement and sea-ice drift velocity are the averages in the dashed black boxes in panels (a)–(f).
Table 1Mean daily displacement and sea-ice drift angle in the dashed box shown in Fig. 9a–f, calculated based on the OSI-SAF drift product. For the period 2010–2017, the standard error (defined as the standard deviation divided by the square root of the number of years) is given as well. The angles give the mean orientation of the sea-ice drift vectors towards north. The counting goes anticlockwise, so that a sea-ice drift angle of 0/90/180/270∘ corresponds purely to north-/west-/south-/eastward sea-ice drift, respectively.
The event can be summarised as follows: in February, the sea ice broke apart and was transported northwards. In the first half of March, the sea-ice drift was weak, and there was rapid thermodynamic sea-ice growth in the resulting open water of the polynya since air temperatures were almost 30 ∘C below the freezing point (Fig. 6). In the second half of March, parts of the sea ice which had moved northwards in February returned to the area, mainly during one event between 16 and 20 March, where the sea-ice drift was strong and directed towards south-west, i.e. towards the North Greenland coast.
This section is dedicated to the processes in the polynya: we estimate the amount of sea ice grown in the polynya and the heat released to the atmosphere. To estimate sea-ice growth, we calculate the accumulated thermodynamic sea-ice growth assuming calm, snow-free conditions. We employ the freezing degree day parameterisation of Lebedev (1938). The calculations start on 14 February, when the first leads were visible in the merged SIC product. This is compared to airborne electromagnetic (AEM) sea-ice thickness measurements taken on 30 and 31 March and to the simulations of thermodynamic growth by the NAOSIM model. Also, the estimates of thermodynamic growth are compared to the SMOS/SMAP sea-ice thickness product of the University of Bremen (Paţilea et al., 2019). For a consistent comparison despite the different grids, we define the polynya area as the area of all pixels which had less than 50 % SIC on the respective grid at least once during the event as described in Sect. 2.
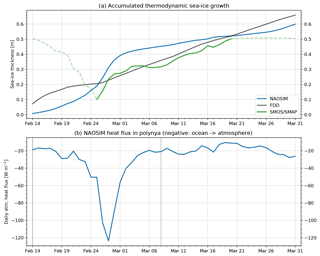
Figure 10(a) Accumulated thermodynamic sea-ice growth after 14 February modelled by NAOSIM and estimated using the freezing degree day parameterisation. The SMOS/SMAP passive microwave sea-ice thickness product of the University of Bremen is shown for comparison. Days before the refreezing started are marked by the faint dashed line. The same holds for the days after the algorithm reached its maximally retrievable sea-ice thickness. (b) Spatially averaged atmospheric heat flux, defined negative upward (blue line) during the polynya event (vertical dashed lines).
The accumulated sea-ice growth calculated from the freezing degree days increased strongly over the first days while the polynya opened and then slowed down (Fig. 10). This is expected because the heat flux decreases non-linearly with sea-ice thickness once the sea ice starts to grow. As air temperatures decreased, sea-ice growth increased until the accumulated sea-ice growth at the end of March was 65 cm. The accumulated sea-ice growth by NAOSIM increased slowly during the opening of the polynya. Then, it increased strongly from 25 February to 1 March. After that, the accumulated sea-ice growth increased slowly to 60 cm at the end of March. During the opening of the polynya, the SMOS/SMAP sea-ice thickness is dominated by dynamic processes. Also, the SMOS/SMAP algorithm assumes 100 % SIC (Paţilea et al., 2019; Huntemann et al., 2014), which is not the case here. In this phase, it can therefore not be compared to the estimates of pure thermodynamic growth. After the refreezing started, it evolved synchronously to the accumulated thermodynamic sea-ice growth from the freezing degree day parameterisation until both datasets showed sea-ice thicknesses of 50 cm. Since the SMOS/SMAP algorithm does not retrieve sea-ice thicknesses above 50 cm (Huntemann et al., 2014; Paţilea et al., 2019), we can not compare the two thermodynamic estimates to the SMOS/SMAP sea-ice thickness product after 20 March (Fig. 10).
In addition to sea-ice growth, we estimate the thermodynamically produced sea-ice volume by multiplying the accumulated growth rates from Fig. 10 by the maximum area covered by the polynya. For the maximum area, we again consider all points for which the sea-ice concentration dropped below 50 % at least once during the polynya event. The freezing degree day parameterisation yields a sea-ice volume of 33 km3, and NAOSIM yields a sea-ice volume of 15 km3. The lower sea-ice volume by NAOSIM is because the area of the polynya in the model was only half as big compared to the observations.
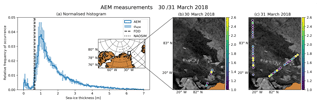
Figure 11AEM measurements of the thickness of young first-year ice formed in the polynya until the end of March. (a) Normalised histogram of the AEM measurements. The shades indicate the standard deviation of the three single flights. The black vertical line shows the mean sea-ice thickness calculated based on freezing degree days since 14 February. The dotted polygon shows the region of the polynya. The small black rectangle shows the region of the AEM flights. (b, c) AEM flights on 30 and 31 March. The dots show the AEM measurements, averaged every 5 km. The background shows a Sentinel-1 mosaic for the respective day.
Figure 11 compares the accumulated thermodynamic sea-ice growth to the sea-ice thicknesses measured by three AEM flights on 30 and 31 March. Their modal/mean value was 1 m/1.94±1.83 m with a smaller mode at 5 cm. The small mode is caused by refrozen leads covered with dark and light nilas which were observed visually during the flights. This explains the presence of classes of very thin sea ice adjacent to the open leads. The tail of the frequency distribution in Fig. 11 represents deformed sea ice rather than purely thermodynamically grown flat sea ice. We note that there is a difference of the main mode of the AEM measurements of 1.0 m which normally represents the thickness of the most abundant, thermodynamically grown sea ice (for example, Haas et al., 2010) and the 0.60 and 0.65 m obtained by the NAOSIM and FDD models, respectively. This difference can be due to insufficient heat flux assumptions in the models, in particular unrealistic ocean heat flux, or it can indicate that much of the level sea ice in the polynya was also formed by rafting, which could increase level sea-ice thickness much above the thermodynamically achievable thickness. However, the much larger mean AEM sea-ice thickness of 0.94 m above the modal sea-ice thickness demonstrates the importance of dynamic sea-ice growth by sea-ice convergence and compression as a result of the closing of the polynya. The heat released to the atmosphere calculated by the NAOSIM model (Fig. 10b) is closely coupled to the opening and closing of the polynya. It is negative, i.e. directed from the ocean to the atmosphere, throughout the entire event. The average/maximum daily heat flux was −40/−124 W m−2. The time-integrated heat flux was −866 W m−2.
Comparing the 2018 polynya north of Greenland to the climatology between 1979 and 2017, we find that the SIC in the polynya area during the peak period between 25 and 27 February was the lowest observed during any day between November and April since 1979. This confirms the findings of Moore et al. (2018) who showed that the mean February SIC 2018 was smaller than any mean February SIC between 1979 and 2018. We confirm and further strengthen the findings of Moore et al. (2018) as we include the entire winter season in our comparison. The 2018 winter polynya thus was a first-time event which had influence on the regional sea-ice production and ocean-to-atmosphere heat flux as will be discussed below. An event as strong as this never happened before during the satellite period. The 1979–2017 all-time minima curve accumulates all potential polynya events during that period. We identify clear but smaller polynya events like in 1986 in mid-December. Improved monitoring of these events is possible with the high-resolution, spatially continuous SIC dataset which we present in this paper.
By comparing the merged, MODIS and AMSR2 SIC, we find that AMSR2 SIC is higher than MODIS for high SIC. As the merged SIC preserves the AMSR2 SIC mean, this also holds for the merged SIC. The differences between the MODIS and the AMSR2 SIC arise because the algorithms have different sensitivities to sea-ice thickness: AMSR2 is based on the polarisation difference which is independent of the sea-ice thickness if the sea ice is thicker than 10 cm (Heygster et al., 2014). MODIS SIC is based on the local sea-ice surface temperature anomalies and assumes a bimodal sea-ice thickness distribution (Drüe and Heinemann, 2004). If the sea-ice thickness varies while the SIC is 100 %, the concentration of thin sea ice will thus be reported as reduced SIC. Within the 48 km by 48 km window used for the derivation of the sea-ice tie point, the sea-ice thickness is expected to vary. This is also the reason why the MODIS SIC is lower than the merged SIC before and after the maximal extension of the polynya (Fig. 3). The SIC underestimation is tolerated by Drüe and Heinemann (2004) because the algorithm was designed to derive the thermal surface conditions rather than the physical surface conditions, and the oceanic heat flux depends on sea-ice thickness. However, the SIC underestimation causes a discrepancy when compared to AMSR2 SIC. The described dependence of the MODIS SIC on sea-ice thickness and the fact that the SAR SIC also is close to 100 % let us conclude that the AMSR2 SIC is closer to the true SIC here. Thus we merge the AMSR2 SIC and MODIS SIC, keeping the AMSR2 SIC on a larger scale but adding the higher resolution of the MODIS SIC to resolve smaller leads and openings.
Comparing the histograms of the SIC datasets, we find that the leads west of the polynya tend to be smeared out by the AMSR2 SIC. This is caused by the lower spatial resolution of AMSR2 and not a deficiency of the algorithm. It illustrates that the merged SIC is better than AMSR2 or MODIS SIC alone. Using only MODIS SIC would mean an underestimation of the SIC in many cases, as described above, and would be limited to cloud-free scenes. Using only AMSR2 SIC would result in smearing out narrow leads. Also, refrozen leads which are covered by snow or sea ice which is thicker than 10 cm would not be identified. The merged product's magnitude is closer to the SAR SIC than the MODIS SIC, and at the same time it preserves most of the high-resolution spatial information of the MODIS data. The SAR SIC itself is well-suited as a reference product above the region west of the polynya due to its high spatial resolution. However, larger open water areas like the polynya itself can be misclassified due to, for example, wind roughening effects. Also, SAR data are only available locally. Thus, the merged SIC is the only product which combines high spatial resolution, spatial coverage and daily Arctic-wide coverage.
Over the polynya region, we find that the SAR and MODIS SIC are higher than the AMSR2 SIC. As the air temperatures were still below freezing, it is likely that sea-ice production started shortly after the opening. The wind and sea-ice drift patterns hindered the evolution of a homogeneous sea-ice cover, and the newly formed sea ice turned into grease ice. Under these circumstances, it may be that AMSR2 does not retrieve the grease ice. The grease ice would, however, change the backscatter signature so that the polynya is no longer recognised as such by the SAR SIC. Additionally, a rough water surface can be misinterpreted as ice by the SAR SIC algorithm as it was trained to retrieve small leads which generally have a smooth surface. The grease ice also shows up as increased MODIS SIC. Another reason for higher MODIS SIC is that the sea-ice tie point is derived based on the local sea-ice surface temperature anomaly. If the surrounding sea-ice surface temperature is only slightly below freezing, the range between the dynamic sea-ice tie point and the fixed water tie point gets small, and small sea-ice surface temperature variations cause high SIC variations. The described sensitivity of the MODIS and SAR SIC to very freshly grown sea-ice is also the reason why they are lower during the maximal extension of the polynya (Fig. 3). It may be that we underestimate the SIC here by tuning MODIS SIC to the AMSR2 SIC as we get SIC between 0 % and 20 %, although the actual concentration of grease ice is probably higher. We tolerate this as a trade-off because the approach allows better retrieval of higher SIC and a spatially continuous field. The advantage of the higher resolution of the merged SIC product was shown in Fig. 4. It was most pronounced during the early break-up and less pronounced towards the end of the opening phase. The reason is that small leads which are formed while the polynya breaks up are resolved by the merged product but not or only hardly by the AMSR2 SIC. This is caused partly by the higher resolution of the merged product and partly because the MODIS SIC can retrieve refrozen leads which are not retrieved by the AMSR2 SIC anymore.
Strictly speaking, a refrozen lead should not be visible in a SIC product, i.e. have a SIC of 100 % as soon as it refreezes. While the sea ice is thin (approximately thinner than 10 cm), a lead will likely be shown as reduced SIC in our merged product as the AMSR2 SIC is influenced by sea-ice thickness (Heygster et al., 2014; Wiebe et al., 2009). For new sea ice in leads, the brine on top of the ice and the thin sea-ice thickness influence the brightness temperatures measured by the passive microwave radiometer, which can lead to a reduced SIC retrieval. While the sea ice is growing, this effect gets reduced, and when the sea-ice thickness exceeds approximately 10 cm, the lead would appear as 100 % SIC in a pure AMSR2 SIC product. In our merged product, however, it may still appear as reduced SIC. This is due to the influence of thin sea ice on the MODIS SIC (Drüe and Heinemann, 2004), which is stronger than the influence on the AMSR2 SIC. In this case, we could set the SIC to 100 % to be fully consistent with the definition of SIC, but we decided to keep this additional lead information. The rationale for this is that for many applications and processes, for example, navigation or heat flux calculations, the presence of leads is highly relevant. We thus accept being slightly inconsistent with the definition of sea-ice concentration as a trade-off for conveying the lead information to the user. A step forward in future could be to add a flag to our product which tells the user that the AMSR2 SIC at the respective pixel is 100 %, meaning that the lead is already refrozen. This flag would also convey information about the sea-ice thickness: it would indicate that the sea ice is thick enough to be retrieved as 100 % SIC by AMSR2, i.e. thicker than approximately 10 cm but still thin enough to be retrieved as reduced SIC by MODIS.
Next, we look into the spatial and temporal evolution of the polynya and the environmental conditions. At its maximal extent, it spanned more than 60 000 km2. The mean size during the opening was 11 000 km2. This is slightly larger than the average size of 17 recurring Arctic polynyas reported by Preußer et al. (2016). They find sizes between 400 and 43 600 km2. The opening of the polynya was driven by anomalous sea-ice drift. It was directed northwards, while it is normally directed southwards. In addition, the sea-ice drift speed was 14 km d−1, which is 50 % stronger than in the 8 years before. Also, other studies (Kwok et al., 2013; Vaughan et al., 2013) find typical sea-ice drift speeds between 5 and 10 km d−1 in this region. During the second half of the opening period, the sea-ice drift anomaly was caused by a persistent high-pressure system above the Eurasian Arctic. The sea-ice drift pattern during the polynya event has also been analysed by Moore et al. (2018). They use data of the Pan-Arctic Ice Ocean Modeling and Assimilation System (PIOMAS; Zhang and Rothrock, 2003). We can only compare our findings indirectly because they look at the sea-ice thickness change due to sea-ice motion, while we look at the sea-ice drift directly. Still, the temporal evolution is consistent: they identify a first peak on 16 February and a second, stronger one on 23 and 24 February. In our sea-ice drift time series, the peaks are 1 to 2 d later. The event on 3 March during which the sea ice was partly returned to the polynya area is also visible in their data. Since their time series ends on 5 March, further comparison is not possible. We found that the surface air pressure distribution during February and March was coincident with the opening and closing of the polynya. Moore et al. (2018) identify the surface pressure distribution and the associated warm-air intrusion as a surface response to a sudden stratospheric warming which occurred in early February. The high-pressure system caused northward winds in the polynya area and increased the opening rate. The warm-air intrusion from the mid-latitudes featured air temperatures up to 20 ∘C above average, visible in both reanalysis data and local measurements. The heat released by the polynya contributed to the anomaly. Other studies (Graham et al., 2017; Woods and Caballero, 2016; Moore, 2016; Mewes and Jacobi, 2019) report that such winter warming events have occurred since the 1950s but did not last as long and were weaker than in recent years. Also, they were not related to polynyas. Even if the 2 m air temperatures in our case were exceptionally high, they were below or only slightly above the freezing point. The advected air temperature anomaly contributed to the polynya development only indirectly: it slowed down the sea-ice growth but did not prevent sea-ice growth totally and did not melt the sea ice. This is again consistent with the results of Moore et al. (2018) who show that the thermodynamic sea-ice production was always positive; i.e. no sea-ice melt occurred. After the air pressure distribution changed, the sea-ice drift was directed towards the Fram Strait as usual, and air temperatures were 20 ∘C below the freezing point. The polynya refroze and closed quickly.
We identify two periods of enhanced sea-ice drift directed towards the northern Greenland coast in the beginning and in the second half of March (Fig. 9). These closing events have caused deformation of the newly formed sea ice in the polynya. At the end of March, the polynya was covered by a mixture of second-year and multi-year ice from before the event, deformed newly grown young ice and flat new ice (Fig. 11). Our estimate of thermodynamic sea-ice growth (60 cm modelled by NAOSIM, 65 cm estimated by the freezing degree day parameterisation) for 31 March is thus likely an underestimation of the actual sea-ice thickness due to the sea-ice thickening by deformation. This is confirmed by comparing these estimates to AEM sea-ice thickness measurements at the end of March, which found a modal sea-ice thickness value of 1 m as well as a tail towards higher sea-ice thicknesses due to deformation.
The SMOS/SMAP algorithm assumes 100 % sea-ice concentration. This was not always the case during the event. In fact, our SIC curves in Fig. 3 show SIC down to 65 %. This contributes to the SMOS/SMAP sea-ice thickness decrease before 25 February. Especially for very thin sea ice, passive microwave retrievals of sea-ice thickness and sea-ice concentration are ambiguous, and it is hard to disentangle the influence of the two quantities on the signal (Ivanova et al., 2015; Heygster et al., 2014). A quantitative estimate of how much the lower sea-ice concentration influenced the sea-ice thickness retrieval would be beyond the scope of this paper. We note that the SMOS/SMAP sea-ice thickness during the opening and early refreezing is less reliable than at a later stage of refreezing. The SMOS/SMAP sea-ice thickness is only valid up to a sea-ice thickness of 50 cm (Huntemann et al., 2014; Paţilea et al., 2019). Therefore, we can only compare the SMOS/SMAP sea-ice thickness to the other products between 25 February, when the refreezing starts, and 20 March, when the SMOS/SMAP sea-ice thickness reaches 50 cm. The agreement between the freezing degree day parameterisation, the SMOS/SMAP sea-ice thickness and the NAOSIM sea-ice thickness in this period is good. For SMOS/SMAP and the freezing day parameterisation, this is partly because the SMOS/SMAP algorithm was trained using this parameterisation (Huntemann et al., 2014; Paţilea et al., 2019). The influence of the warm-air intrusion on the quality of the sea-ice thickness retrieval was probably negligible. The air temperature was only above 0 ∘C during the opening of the polynya. During the refreezing phase which we analyse here, the air temperature was below 0 ∘C and therefore did not influence the sea-ice thickness retrieval.
By comparing the estimates of the thermodynamically produced sea-ice volume, we find a discrepancy between the freezing degree day parameterisation (33 km3) and the NAOSIM model (15 km3). The discrepancy is because the polynya in the model is only half as large as in the observations. A similar finding was presented in Moore et al. (2018), who find that the polynya in the PIOMAS model was significantly smaller than in the observations. Since our observations agree well with the outline of the polynya in the SAR images, we conclude that 33 km3 is the better estimate. Preußer et al. (2016) give January–March accumulated sea-ice production rates of 52 km3 on average for 17 Arctic coastal polynyas. According to Tamura and Ohshima (2011), the 10 major coastal polynyas in the Arctic produce between 130 and 840 km3 per year. Total winter-accumulated sea-ice production in Arctic polynyas has been estimated to be between 1811 km3 (Preußer et al., 2016) and 2940 km3 (Tamura and Ohshima, 2011). However, given that normally sea-ice production north of Greenland is negligible and that the 2018 polynya was only open for 3 weeks while the values of Preußer et al. (2016)/Tamura and Ohshima (2011) are given for 3 months/an entire year, the event is still remarkable on a regional scale. Finally, we estimate a mean/maximum heat flux of −40/−124 W m−2 during the time when the polynya was opened. This is small compared to the heat fluxes given by Morales-Maqueda et al. (2004). They report mean heat fluxes between −38 and −105 W m−2. We attribute this to the warm-air intrusion. When the polynya was opening, the air temperatures were around −10 ∘C, so that the heat flux was comparably small. When the air temperatures decreased to −30 ∘C, the polynya had already started to refreeze, which dampened the heat flux.
This paper uses a new SIC product at 1 km resolution from merged passive microwave (AMSR2) and thermal infrared (MODIS) data. The product comprises the high spatial resolution of the thermal infrared data and the spatial coverage of the passive microwave data. Its benefit is demonstrated by means of the polynya which opened north of Greenland in winter 2018. We show that the merged product detects more leads than the passive microwave data and at the same time allows continuous monitoring of the event.
The polynya opened in the second half of February. The open water area expanded over 12 d, reached its maximal extent of more than 60 000 km2 on 26 February and decreased linearly until it closed on 8 March. The closing was due to fast refreezing after the warm-air intrusion abated. Additionally, there was dynamic closing by southward sea-ice drift. The merged SIC shows closed sea-ice cover after 8 March. Nonetheless, the area of freshly grown sea ice is still distinguishable in SAR images on 31 March.
The evolution is driven by the sea-ice drift in the polynya region. The sea-ice drift was directed northwards instead of the usually dominating southward direction during the polynya opening. Furthermore, it was 50 % stronger than usual. The sea-ice drift was weak during the first half of March, allowing for undisturbed thermodynamic growth of new sea ice. Two convergent events at the end of February and mid-March brought back sea ice which was exported from the polynya area during the formation. Therefore, there is a mixture of flat, thermodynamically grown and rough sea ice grown due to sea-ice dynamics at the end of March.
Temperatures during the opening of the polynya were more than 20 ∘C above average. This was caused partly by a high-pressure system above the Kara Sea which brought in warm air from the Atlantic. However, the air temperatures still remained below freezing. They were not high enough to melt the sea ice but slowed down the refreezing process. Only locally did the daily maximum air temperature exceed the freezing point several times but not long and strong enough to cause substantial melting. The polynya also contributed to this air temperature anomaly due to the heat released from the ocean to the atmosphere.
The questions which we raised in the beginning can be answered as follows:
-
Does merging MODIS thermal infrared and AMSR2 passive microwave SIC allow additional insights about the formation of the polynya?
Before the opening of the polynya, leads were visible in the merged, high-resolution SIC product which would have been smeared out by the AMSR2 SIC due to the coarse resolution. Generally, the merged SIC showed more SIC values between 60 % and 90 % than the AMSR2 SIC, indicative of the leads which are identified due to the higher resolution. Over regions with 100 % SIC, an underestimation of the merged SIC compared to the AMSR2 SIC may occur, which we tolerate as a trade-off for the possibility to resolve more leads. The benefit of the merged SIC is most pronounced during the opening of the polynya.
-
Was the polynya opened thermodynamically or dynamically, and how unusual were the environmental conditions?
The polynya was opened by an anomalous sea-ice drift event in the end of February, which confirms the findings of Moore et al. (2018). The sea-ice drift was directed northwards for 12 d, while it is normally directed southwards. Also, it was 50 % stronger than usual. A high-pressure system over the Eurasian Arctic kept the polynya open. It was accompanied by local air temperatures more than 20 ∘C above average, caused partly by advection due to the high-pressure system and partly by heat release from the opening polynya. Although the air temperature was exceptionally high, it was not high enough to melt the sea ice. Events like this have occurred before but not with the same magnitude. They are expected to occur more frequently in future due to the expected thinning of the sea-ice cover.
-
How much sea ice grew in the polynya, and how much heat was released to the atmosphere?
Two estimates of thermodynamic sea-ice growth show accumulated growth of 60 cm (NAOSIM model) and 65 cm (freezing degree day parameterisation) on 31 March, i.e. much lower than the modal AEM thickness of 1.0 m. This could indicate that thermodynamic ice growth was strongly underestimated by the models, despite the fact that we have observed a thin snow cover which would have reduced ice growth but was not considered by the freezing degree day parameterisation. On the other hand, the larger observed modal sea-ice thickness could also have been due to rafting which would double the resulting sea-ice thickness compared to the level sea-ice thickness of the undeformed ice at the time of deformation. However, the much larger mean AEM sea-ice thickness of 0.94 m more than the modal sea-ice thickness shows that deformation played a strong role for ice growth in addition to thermodynamic growth considered by the models. According to the freezing degree day parameterisation, a volume of 33 km3 of sea ice was produced. The modelled heat release from the ocean to the atmosphere was on average 40 W m−2 while the polynya was open.
The merged SIC product is presented here for the first time. The benefit over single-sensor SIC is demonstrated. However, more validation is needed and planned in future work. This could be done by using, for example, high-resolution optical data from the European Union Copernicus Sentinel-2 or the US Landsat satellite. Also, other methods for merging SIC should be tested and compared to the method presented here. For example, Dasgupta and Qu (2006) use a wavelet-based approach to merge MODIS and AMSR-E data for vegetation moisture retrieval, and Ricker et al. (2017) use an optimal interpolation scheme to merge CryoSat-2 and SMOS (Soil Moisture and Ocean Salinity) sea-ice thicknesses. In principle, their approaches should also be applicable for merging SIC. The combination of passive microwave and thermal infrared data is not expected to work in summer as both of them can not distinguish melt ponds from open water and thus underestimate the summer SIC. Data in the visible wavelength range provide the possibility to detect melt ponds separately (Rösel et al., 2012). Including them in the merging procedure could thus improve the product's performance in summer. Higher resolution can also be achieved by including SAR data as suggested by Karvonen (2014).
At the moment, potential atmospheric effects on the AMSR2 sea-ice concentration over sea ice are not considered. Work on correcting these effects is currently undertaken (Lu et al., 2018). It is planned to include this in the future development of our product.
We found that events like this have occurred before north of Greenland. Future research could focus on investigating when, where and how often such events occurred and how strong they were. A polynya was observed in the same spot in August 2018. It could be investigated whether the event described here preconditioned the event in August 2018.
The freeze-up period could also be analysed in more detail. We show that the modal sea-ice thickness at the end of March can be approximately reproduced by rather simple approaches neglecting dynamic processes. More research could clarify how much flat and how much rough sea ice there was at the end of March and how the remaining discrepancy between our two estimates and the AEM sea-ice thickness of 35 cm can be explained.
The code and data needed for reproducing the figures are available upon request from Valentin Ludwig (vludwig@uni-bremen.de). Frank Kauker (frank.kauker@awi.de) may be contacted for the NAOSIM model code and output. Dmitrii Murashkin (murashkin@uni-bremen.de) may be contacted for the binary Sentinel-1 lead maps. Valentin Ludwig may be contacted for the AEM sea-ice thickness data as well as for the AMSR2, MODIS and merged SIC code and data. The merged SIC product will be publically available at https://www.seaice.uni-bremen.de in near future. MODIS Ice Surface Temperature data were provided by the National Snow and Ice Data Center (NSIDC) at https://nsidc.org/data/MYD29/versions/6. MODIS geolocation (MYD03) and cloud mask data (MYD35_L2) were provided by the Level-1 and Atmosphere Archive and Distribution System (LAADS) Distributed Active Archive Center (DAAC) at https://ladsweb.modaps.eosdis.nasa.gov/archive/allData/61/. Copernicus Sentinel data are available at https://scihub.copernicus.eu/. ERA5 data were obtained from Copernicus Climate Change Service (2017). The OSI-450 (SIC 1979–2015), OSI-430-b (SIC 2015–2018) and OSI-405 (sea-ice drift) data were provided by EUMETSAT OSI SAF at http://osisaf.met.no/p/ice/. Station data from Cape Morris Jesup were obtained at https://rp5.ru/Weather_in_Cape_Morris_Jesup. The Sentinel-1 SAR mosaics were provided by http://www.seaice.dk. SMOS/SMAP sea-ice thickness data are available at https://seaice.uni-bremen.de/thin-ice-thickness/. All URLs were last accessed on 22 July 2019.
The authors declare that they have no conflict of interest.
This study was supported by the Institutional Strategy of the University of Bremen, funded by the German Excellence Initiative, and by the Deutsche Forschungsgemeinschaft (DFG) through the International Research Training Group IRTG 1904 ArcTrain. We thank the editor, Chris Derksen, for editing the paper. We thank Thomas Lavergne and one anonymous reviewer for reviewing our paper. Their comments greatly helped to improve content, structure and clarity of the paper. We sincerely thank Leif Toudal Pedersen for his constructive and useful comments on this manuscript and for the provision of the SAR mosaics. We thank Cătălin Paţilea for the fruitful discussion about the SMOS/SMAP sea-ice thickness. We thank Stefan Hendricks and Jan Rohde for the contribution in acquisition and processing of the AEM data. We thank JAXA (https://global.jaxa.jp/, last access: 22 July 2019) for the provision of AMSR2 brightness temperatures used for the calculation of the AMSR2 SIC. We thank the Danish Meteorological Institute for operating the Cape Morris Jesup weather station and sharing the data.
This research has been supported by the Deutsche Forschungsgemeinschaft (grant no. GRK1904) and a Junior
Research Group in the framework of the Institutional Strategy of the University of Bremen (funded by the German Excellence Initiative).
The article processing charges for this open-access publication were covered by the University of Bremen.
This paper was edited by Chris Derksen and reviewed by Thomas Lavergne and one anonymous referee.
Ackerman, S., Frey, R., Strabala, K., Liu, Y., Gumley, L., Baum, B., and Menzel, P.: MODIS Atmosphere L2 Cloud Mask Product. NASA MODIS Adaptive Processing System, Goddard Space Flight Center, USA, https://doi.org/10.5067/MODIS/MOD35_L2.061, 2017. a
Beitsch, A., Kaleschke, L., and Kern, S.: Investigating High-Resolution AMSR2 Sea Ice Concentrations during the February 2013 Fracture Event in the Beaufort Sea, Remote Sensing, 6, 3841–3856, https://doi.org/10.3390/rs6053841, 2014. a
Castro-Morales, K., Kauker, F., Losch, M., Hendricks, S., Riemann-Campe, K., and Gerdes, R.: Sensitivity of simulated Arctic sea ice to realistic ice thickness distributions and snow parameterizations, J. Geophys. Res.-Oceans, 119, 559–571, https://doi.org/10.1002/2013JC009342, 2014. a
Copernicus Climate Change Service: (C3S): ERA5: Fifth generation of ECMWF atmospheric reanalyses of the global climate. Copernicus Climate Change Service Climate Data Store (CDS), available at: https://archive.org/details/nasa_techdoc_19960016967 (last access: 29 July 2019), 2017. a
Comiso, J. C.: SSM/I sea ice concentrations using the bootstrap algorithm, vol. 1380, National Aeronautics and Space Administration, Goddard Space Flight Center (GSFC), Greenbelt, Maryland, 1995. a
Dai, A., Luo, D., Song, M., and Liu, J.: Arctic amplification is caused by sea-ice loss under increasing CO2, Nat. Commun., 10, 121, https://doi.org/10.1038/s41467-018-07954-9, 2019. a
Dasgupta, S. and Qu, J. J.: Combining MODIS and AMSR-E-based vegetation moisture retrievals for improved fire risk monitoring, in: Remote Sensing and Modeling of Ecosystems for Sustainability III, International Society for Optics and Photonics, vol. 6298, 62981B, https://doi.org/10.1117/12.681147, 2006. a
Drüe, C. and Heinemann, G.: High-resolution maps of the sea-ice concentration from MODIS satellite data, Geophys. Res. Lett., 31, L20403, https://doi.org/10.1029/2004GL020808, 2004. a, b, c, d, e, f
Drüe, C. and Heinemann, G.: Accuracy assessment of sea-ice concentrations from MODIS using in-situ measurements, Remote Sens. Environ., 95, 139–149, 2005. a
European Centre for Medium-Range Weather Forecasts (ECMWF): https://confluence.ecmwf.int/display/CKB/ERA5+data+documentation (last access: 26 July 2019), 2015. a
Gao, Y., Xie, H., Lu, N., Yao, T., and Liang, T.: Toward advanced daily cloud-free snow cover and snow water equivalent products from Terra–Aqua MODIS and Aqua AMSR-E measurements, J. Hydrol., 385, 23–35, https://doi.org/10.1016/j.jhydrol.2010.01.022, 2010. a
Graham, R. M., Cohen, L., Petty, A. A., Boisvert, L. N., Rinke, A., Hudson, S. R., Nicolaus, M., and Granskog, M. A.: Increasing frequency and duration of Arctic winter warming events, Geophys. Res. Lett., 44, 6974–6983, https://doi.org/10.1002/2017GL073395, 2017. a
Haas, C., Lobach, J., Hendricks, S., Rabenstein, L., and Pfaffling, A.: Helicopter-borne measurements of sea ice thickness, using a small and lightweight, digital EM system, J. Appl. Geophys., 67, 234–241, https://doi.org/10.1016/j.jappgeo.2008.05.005, 2009. a
Haas, C., Hendricks, S., Eicken, H., and Herber, A.: Synoptic airborne thickness surveys reveal state of Arctic sea ice cover, Geophys. Res. Lett., 37, L09501, https://doi.org/10.1029/2010GL042652, 2010. a, b
Haid, V. and Timmermann, R.: Simulated heat flux and sea ice production at coastal polynyas in the southwestern Weddell Sea, J. Geophys. Res.-Oceans, 118, 2640–2652, https://doi.org/10.1002/jgrc.20133, 2013. a
Hall, D. and Riggs., G.: MODIS/Aqua Sea Ice Extent 5-Min L2 Swath 1km, Version 6.[20180214-20180308], https://doi.org/10.5067/MODIS/MOD29.006, 2018. a
Hersbach, H. and Dee, D.: ERA-5 reanalysis is in production, ECMWF newsletter, p. 7, available at: https://www.ecmwf.int/en/newsletter/147/news/era5-reanalysis-production (last access: 25 July 2019), 2016. a
Heygster, G., Huntemann, M., Ivanova, N., Saldo, R., and Pedersen, L. T.: Response of passive microwave sea ice concentration algorithms to thin ice, in: Geoscience and Remote Sensing Symposium (IGARSS), 2014 IEEE International, 3618–3621, IEEE, 13–18 July 2014, Québec City, Canada, 2014. a, b, c, d, e, f
Hibler, W.: A dynamic thermodynamic sea ice model, J. Geophys. Res., 9, 815–846, 1979. a
Hibler, W. I. and Bryan, K.: A diagnostic ice-ocean model, J. Phys. Oceanogr., 17, 987–1015, 1987. a
Huntemann, M., Heygster, G., Kaleschke, L., Krumpen, T., Mäkynen, M., and Drusch, M.: Empirical sea ice thickness retrieval during the freeze-up period from SMOS high incident angle observations, The Cryosphere, 8, 439–451, https://doi.org/10.5194/tc-8-439-2014, 2014. a, b, c, d, e
Ivanova, N., Johannessen, O. M., Pedersen, L. T., and Tonboe, R. T.: Retrieval of Arctic Sea Ice Parameters by Satellite Passive Microwave Sensors: A Comparison of Eleven Sea Ice Concentration Algorithms, IEEE T. Geosci. Remote, 52, 7233–7246, https://doi.org/10.1109/TGRS.2014.2310136, 2014. a
Ivanova, N., Pedersen, L. T., Tonboe, R. T., Kern, S., Heygster, G., Lavergne, T., Sørensen, A., Saldo, R., Dybkjær, G., Brucker, L., and Shokr, M.: Inter-comparison and evaluation of sea ice algorithms: towards further identification of challenges and optimal approach using passive microwave observations, The Cryosphere, 9, 1797–1817, https://doi.org/10.5194/tc-9-1797-2015, 2015. a, b
Kaleschke, L., Lüpkes, C., Vihma, T., Haarpaintner, J., Borchert, A., Hartmann, J., and Heygster, G.: SSM/I sea ice remote sensing for mesoscale ocean-atmosphere interaction analysis, Can. J. Remote Sens., 5, 526–537, 2001. a, b, c
Karvonen, J.: A sea ice concentration estimation algorithm utilizing radiometer and SAR data, The Cryosphere, 8, 1639–1650, https://doi.org/10.5194/tc-8-1639-2014, 2014. a, b, c
Kauker, F., Gerdes, R., Karcher, M., Köberle, C., and Lieser, J.: Variability of Arctic and North Atlantic sea ice: A combined analysis of model results and observations from 1978 to 2001, J. Geophys. Res.-Oceans, 108, 3182, https://doi.org/10.1029/2002JC001573, 2003. a, b, c
Kwok, R., Spreen, G., and Pang, S.: Arctic sea ice circulation and drift speed: Decadal trends and ocean currents, J. Geophys. Res.-Oceans, 118, 2408–2425, https://doi.org/10.1002/jgrc.20191, 2013. a
Lavergne, T., Eastwood, S., Teffah, Z., Schyberg, H., and Breivik, L.-A.: Sea ice motion from low-resolution satellite sensors: An alternative method and its validation in the Arctic, J. Geophys. Res.-Oceans, 115, C10032, https://doi.org/10.1029/2009JC005958, 2010. a
Lavergne, T., Sørensen, A. M., Kern, S., Tonboe, R., Notz, D., Aaboe, S., Bell, L., Dybkjær, G., Eastwood, S., Gabarro, C., Heygster, G., Killie, M. A., Brandt Kreiner, M., Lavelle, J., Saldo, R., Sandven, S., and Pedersen, L. T.: Version 2 of the EUMETSAT OSI SAF and ESA CCI sea-ice concentration climate data records, The Cryosphere, 13, 49–78, https://doi.org/10.5194/tc-13-49-2019, 2019. a, b, c
Lebedev, V.: Rost l'da v arkticheskikh rekakh i moriakh v zavisimosti ot otritsatel'nykh temperatur vozdu kha, Problemy arktiki, 5–6, 9–25, 1938. a, b
Lindsay, R. W. and Rothrock, D. A.: Arctic sea ice leads from advanced very high resolution radiometer images, J. Geophys. Res.-Oceans, 100, 4533–4544, https://doi.org/10.1029/94JC02393, 1995. a
Lu, J., Heygster, G., and Spreen, G.: Atmospheric Correction of Sea Ice Concentration Retrieval for 89 GHz AMSR-E Observations, IEEE J. Sel. Top. Appl., 11, 1–16, https://doi.org/10.1109/JSTARS.2018.2805193, 2018. a
Marcq, S. and Weiss, J.: Influence of sea ice lead-width distribution on turbulent heat transfer between the ocean and the atmosphere, The Cryosphere, 6, 143–156, https://doi.org/10.5194/tc-6-143-2012, 2012. a, b, c
Markus, T. and Cavalieri, D. J.: An Enhancement of the NASA Team Sea Ice Algorithm, IEEE T. Geosci. Remote, 38, 1387–1398, 2000. a
Martin, S., Robert, D., Ronald, K., and Benjamin, H.: Estimation of the thin ice thickness and heat flux for the Chukchi Sea Alaskan coast polynya from Special Sensor Microwave/Imager data, 1990–2001, J. Geophys. Res.-Oceans, 109, C10012, https://doi.org/10.1029/2004JC002428, 2004. a
Mewes, D. and Jacobi, C.: Heat transport pathways into the Arctic and their connections to surface air temperatures, Atmos. Chem. Phys., 19, 3927–3937, https://doi.org/10.5194/acp-19-3927-2019, 2019. a
Moore, G.: The December 2015 North Pole Warming Event and the Increasing Occurrence of Such Events, Sci. Rep., 6, 39084, https://doi.org/10.1038/srep39084, 2016. a
Moore, G. W. K., Schweiger, A., Zhang, J., and Steele, M.: What Caused the Remarkable February 2018 North Greenland Polynya?, Geophys. Res. Lett., 45, 13342–13350, https://doi.org/10.1029/2018GL080902, 2018. a, b, c, d, e, f, g, h, i, j
Morales-Maqueda, M. A., Willmott, A. J., and Biggs, N. R. T.: Polynya Dynamics: a Review of Observations and Modeling, Rev. Geophys., 42, RG1004, https://doi.org/10.1029/2002RG000116, 2004. a, b, c, d, e
Murashkin, D., Spreen, G., Huntemann, M., and Dierking, W.: Method for detection of leads from Sentinel-1 SAR images, Ann. Glaciol., 59, 1–-13, https://doi.org/10.1017/aog.2018.6, 2018. a, b, c, d
Parkinson, C. L. and Washington, W. M.: A large-scale numerical model of sea ice, J. Geophys. Res., 84, 311–337, 1979. a
Paţilea, C., Heygster, G., Huntemann, M., and Spreen, G.: Combined SMAP–SMOS thin sea ice thickness retrieval, The Cryosphere, 13, 675–691, https://doi.org/10.5194/tc-13-675-2019, 2019. a, b, c, d, e, f
Preußer, A., Heinemann, G., Willmes, S., and Paul, S.: Circumpolar polynya regions and ice production in the Arctic: results from MODIS thermal infrared imagery from 2002/2003 to 2014/2015 with a regional focus on the Laptev Sea, The Cryosphere, 10, 3021–3042, https://doi.org/10.5194/tc-10-3021-2016, 2016. a, b, c, d, e, f
Ricker, R., Hendricks, S., Kaleschke, L., Tian-Kunze, X., King, J., and Haas, C.: A weekly Arctic sea-ice thickness data record from merged CryoSat-2 and SMOS satellite data, The Cryosphere, 11, 1607–1623, https://doi.org/10.5194/tc-11-1607-2017, 2017. a
Rösel, A., Kaleschke, L., and Birnbaum, G.: Melt ponds on Arctic sea ice determined from MODIS satellite data using an artificial neural network, The Cryosphere, 6, 431–446, https://doi.org/10.5194/tc-6-431-2012, 2012. a
Saha, S., Moorthi, S., Wu, X., Wang, J., Nadiga, S., Tripp, P., Behringer, D., Hou, Y., Chuang, H., Iredell, M., Ek, M., Meng, J., Yang, R., Peña Mendez, M., van den Dool, H., Zhang, Q., Wang, W., Chen, M., and Becker, E.: The NCEP Climate Forecast System Reanalysis, B. Am. Meteorol. Soc., 91, 1015–1057, https://doi.org/10.1175/2010BAMS3001.1, 2010. a
Saha, S., Moorthi, S., Pan, H., Wu, X., Wang, J., Nadiga, S., Tripp, P., Kistler, R., Woollen, J., Behringer, D., Liu, H., Stokes, D., Grumbine, R., Gayno, G., Wang, J., Hou, Y., Chuang, H., Juang, H., Sela, J., Iredell, M., Treadon, R., Kleist, D., Van Delst, P., Keyser, D., Derber, J., Ek, M., Meng, J., Wei, H., Yang, R., Lord, S., van den Dool, H., Kumar, A., Wang, W., Long, C., Chelliah, M., Xue, Y., Huang, B., Schemm, J., Ebisuzaki, W., Lin, R., Xie, P., Chen, M., Zhou, S., Higgins, W., Zou, C., Liu, Q., Chen, Y., Han, Y., Cucurull, L., Reynolds, R., Rutledge, G., and Goldberg: The NCEP Climate Forecast System Version 2, J. Climate, 27, 2185–2208, https://doi.org/10.1175/JCLI-D-12-00823.1, 2014. a
Schledermann, P.: Polynyas and Prehistoric Settlement Patterns, Arctic, 33, 292–302, 1980. a
Semtner, A.: A Model for the Thermodynamic Growth of Sea Ice in Numerical Investigations of Climate, J. Phys. Oceanogr., 6, 379–389, 1976. a
Smith, S. D., Muench, R. D., and Pease, C. H.: Polynyas and leads: An overview of physical processes and environment, J. Geophys. Res.-Oceans, 95, 9461–9479, https://doi.org/10.1029/JC095iC06p09461, 1990. a
Spreen, G., Kaleschke, L., and Heygster, G.: Sea ice remote sensing using AMSR-E 89-GHz channels, J. Geophys. Res.-Oceans, 113, C02S03, https://doi.org/10.1029/2005JC003384, 2008. a, b, c
Sumata, H., Lavergne, T., Girard-Ardhuin, F., Kimura, N., Tschudi, M. A., Kauker, F., Karcher, M., and Gerdes, R.: An intercomparison of Arctic ice drift products to deduce uncertainty estimates, J. Geophys. Res.-Oceans, 119, 4887–4921, https://doi.org/10.1002/2013JC009724, 2014. a
Sumata, H., Kauker, F., Karcher, M., and Gerdes, R.: Simultaneous Parameter Optimization of an Arctic Sea Ice–Ocean Model by a Genetic Algorithm, Mon. Weather Rev., 147, 1899–1926, https://doi.org/10.1175/MWR-D-18-0360.1, 2019a. a
Sumata, H., Kauker, F., Karcher, M., and Gerdes, R.: Covariance of optimal parameters of an Arctic sea ice-ocean model, Mon. Weather Rev., 147, 2579–2602, https://doi.org/10.1175/MWR-D-18-0375.1, 2019b. a
Tamura, T. and Ohshima, K. I.: Mapping of sea ice production in the Arctic coastal polynyas, J. Geophys. Res.-Oceans, 116, C07030, https://doi.org/10.1029/2010JC006586, 2011. a, b, c, d
Tonboe, R. T., Eastwood, S., Lavergne, T., Sørensen, A. M., Rathmann, N., Dybkjær, G., Pedersen, L. T., Høyer, J. L., and Kern, S.: The EUMETSAT sea ice concentration climate data record, The Cryosphere, 10, 2275–2290, https://doi.org/10.5194/tc-10-2275-2016, 2016. a
Vaughan, D., Comiso, J., Allison, I., Carrasco, J., Kaser, G., Kwok, R., Mote, P., Murray, T., Paul, F., Ren, J., Rignot, E., Solomina, O., Steffen, K., and Zhang, T.: Observations: Cryosphere, in: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Changeedited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, UK and New York, NY, USA, 2013. a, b
Vavrus, S. J.: The Influence of Arctic Amplification on Mid-latitude Weather and Climate, Current Climate Change Reports, 4, 238–249, https://doi.org/10.1007/s40641-018-0105-2, 2018. a
Wernecke, A. and Kaleschke, L.: Lead detection in Arctic sea ice from CryoSat-2: quality assessment, lead area fraction and width distribution, The Cryosphere, 9, 1955–1968, https://doi.org/10.5194/tc-9-1955-2015, 2015. a
Wiebe, H., Heygster, G., and Markus, T.: Comparison of the ASI ice concentration algorithm with Landsat-7 ETM+ and SAR imagery, IEEE T. Geosci. Remote, 47, 3008–3015, 2009. a
WMO: WMO sea-ice nomenclature: Terminology, codes and illustrated glossary, Tech. rep., Secretariat of the World Meteorological Organization, Geneva, Switzerland, 1970. a
Woods, C. and Caballero, R.: The role of moist intrusions in winter Arctic warming and sea ice decline, J. Climate, 12, 4473–4485, https://doi.org/10.1175/JCLI-D-15-0773.1, 2016. a
Zhang, J. and Rothrock, D. A.: Modeling Global Sea Ice with a Thickness and Enthalpy Distribution Model in Generalized Curvilinear Coordinates, Mon. Weather Rev., 131, 845–861, https://doi.org/10.1175/1520-0493(2003)131<0845:MGSIWA>2.0.CO;2, 2003. a