the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Converting snow depth to snow water equivalent using climatological variables
David F. Hill
Elizabeth A. Burakowski
Ryan L. Crumley
Julia Keon
J. Michelle Hu
Anthony A. Arendt
Katreen Wikstrom Jones
Gabriel J. Wolken
We present a simple method that allows snow depth measurements to be converted to snow water equivalent (SWE) estimates. These estimates are useful to individuals interested in water resources, ecological function, and avalanche forecasting. They can also be assimilated into models to help improve predictions of total water volumes over large regions. The conversion of depth to SWE is particularly valuable since snow depth measurements are far more numerous than costlier and more complex SWE measurements. Our model regresses SWE against snow depth (h), day of water year (DOY) and climatological (30-year normal) values for winter (December, January, February) precipitation (PPTWT), and the difference (TD) between mean temperature of the warmest month and mean temperature of the coldest month, producing a power-law relationship. Relying on climatological normals rather than weather data for a given year allows our model to be applied at measurement sites lacking a weather station. Separate equations are obtained for the accumulation and the ablation phases of the snowpack. The model is validated against a large database of snow pillow measurements and yields a bias in SWE of less than 2 mm and a root-mean-squared error (RMSE) in SWE of less than 60 mm. The model is additionally validated against two completely independent sets of data: one from western North America and one from the northeastern United States. Finally, the results are compared with three other models for bulk density that have varying degrees of complexity and that were built in multiple geographic regions. The results show that the model described in this paper has the best performance for the validation data sets.
- Article
(5427 KB) - Full-text XML
- BibTeX
- EndNote
In many parts of the world, snow plays a leading-order role in the hydrological cycle (USACE, 1956; Mote et al., 2018). Accurate information about the spatial and temporal distribution of snow water equivalent (SWE) is useful to many stakeholders (water resource planners, avalanche forecasters, aquatic ecologists, etc.), but can be time consuming and expensive to obtain.
Snow pillows (Beaumont, 1965) are a well-established tool for measuring SWE at fixed locations. Figure 1 provides a conceptual sketch of the variation in SWE with time over a typical water year. A comparatively long accumulation phase is followed by a short ablation phase. While simple in operation, snow pillows are relatively large in size and they need to be installed prior to the onset of the season's snowfall. This limits their ability to be rapidly or opportunistically deployed. Additionally, snow pillow installations tend to require vehicular access, limiting their locations to relatively simple topography. Finally, snow pillow sites are not representative of the lowest or highest elevation bands within mountainous regions (Molotch and Bales, 2006). In the western United States (USA), the Natural Resources Conservation Service (NRCS) operates a large network of snow telemetry (SNOTEL) sites, featuring snow pillows. The NRCS also operates the smaller Soil Climate Analysis Network (SCAN), which provides the only, and very limited, snow pillow SWE measurements in the eastern United States.
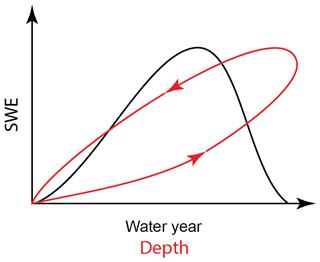
Figure 1Conceptual sketch of the evolution of snow water equivalent (SWE) over the course of a water year (black line). Also shown is the evolution of SWE with snowpack depth over a water year (red line). Note the hysteresis loop due to the densification of the snowpack.
SWE can also be measured manually, using a snow coring device that measures the weight of a known volume of snow to determine snow density (Church, 1933). These measurements are often one-off measurements, or in the case of “snow courses” they are repeated weekly or monthly as a transect of measurements at a given location. The simplicity and portability of coring devices expand the range over which measurements can be collected, but it can be challenging to apply these methods to deep snowpacks due to the limited length of standard coring devices. Note that there are numerous different styles of coring devices, including the Adirondack sampler and the Mt. Rose or Federal sampler (Church and Marr, 1937). The NRCS operates a large network of snow course sites (USDA, 2011) in the western United States.
There are a number of issues that affect the accuracy of both snow pillow and snow coring measurements. With coring measurements, if the coring device is not carefully extracted, a portion of the core may fall out of the device. Or, snow may become compressed in the coring device during insertion. These effects have led to varying conclusions, with some studies (e.g., Sturm et al., 2010) showing a low SWE bias and other studies (e.g., Goodison, 1978) showing a high SWE bias. As noted by Johnson et al. (2015) a good rule of thumb is that coring devices are accurate to around ±10 %. Also, studies comparing different styles of snow samplers report statistically different results, suggesting that SWE measurements are sensitive to the design of the specific coring device, such as the presence of holes or slots, the device material, etc. (Beaumont and Work, 1963; Dixon and Boon, 2012). With snow pillows, some studies (e.g., Goodison et al., 1981) note that ice bridging can lead to low biases in measured SWE, with the snow surrounding the pillow partly supporting the snow over the pillow. Other studies (Johnson and Marks, 2004; Dressler et al., 2006; Johnson et al., 2015) note a more complex situation with SWE underreported at times, but overreported at other times. Note that when snow pillow data are evaluated, they are most commonly compared to coring measurements at the same location.
All methods of measuring SWE are challenged by the fact that SWE is a depth-integrated property of a snowpack. This is why the snowpack must be weighed, in the case of a snow pillow, or a core must be extracted from the surface to the ground. This measurement complexity makes it difficult to obtain SWE information with the spatial and temporal resolution desired for watershed-scale studies. Other snowpack properties, such as the depth h, are much easier to measure. For example, using a graduated device such as a meterstick or an avalanche probe to measure the depth takes only seconds. Automating depth measurements at a fixed location can easily be done using low-cost ultrasonic devices (Goodison et al., 1984; Ryan et al., 2008). High-spatial-resolution measurements of snowpack depth are commonly made with lidar. One example of this is the Airborne Snow Observatory program (ASO; Painter et al., 2016). The comparatively high expense of airborne lidar surveys typically limits measurements geographically (to a few basins) and temporally (weekly to monthly interval).
Given the relative ease in obtaining depth measurements, it is common to use h as a proxy for SWE. Figure 1 shows a conceptual sketch of the variation in SWE with h over a typical water year. Noting the arrows on the curve, we see that SWE is multivalued for each h. This is due to the fact that the snowpack increases in density throughout the water year, producing a hysteresis loop in the curve. A large body of literature exists on the topic of how to convert h to SWE. It is beyond the scope of this paper to provide a full review of these “bulk density equations”, where the density is given by . Instead, we refer readers to the useful comparative review by Avanzi et al. (2015). Here, we prefer to discuss a limited number of previous studies that illustrate the spectrum of methodologies and complexities that can be used to determine ρb or SWE.
Many studies express ρb as an increasing function (often linear) of h. In some cases (e.g., Lundberg et al., 2006) a second equation is added where ρb attains a constant value when a threshold h is exceeded. A single linear equation captures the process of densification of the snowpack during the accumulation phase, but performs poorly during the ablation phase, where depths are decreasing but densities continue to increase or approach a constant value.
Other approaches choose to parameterize ρb in terms of time, rather than h. Pistocchi (2016) provides a single equation while Mizukami and Perica (2008) provide two sets of equations, one set each for early and late seasons. Each set contains four equations, each of which is applicable to a particular “cluster” of stations. This clustering was driven by observed densification characteristics and the resulting clusters are relatively spatially discontinuous. Jonas et al. (2009) take the idea of region- (or cluster-) specific equations and extend it further to provide coefficients that depend on time and elevation as well. They use a simple linear equation for ρb in terms of h and the slope and intercept of the equation are given as monthly values, with three elevation bins for each month (36 pairs of coefficients). There is an additional contribution to the intercept (or “offset”) which is region-specific (one of seven regions).
These classifications, whether based on region, elevation, or season, are valuable since they acknowledge that all snow is not equal. McKay and Findlay (1971) discuss the controls that climate and vegetation exert on snow density, and Sturm et al. (2010) address this directly by developing a snow density equation where the coefficients depend upon the “snow class” (five classes). Sturm et al. (1995) explain the decision tree, based on temperature, precipitation, and wind speed, that leads to the classification. The temperature metric is the “cooling degree month” calculated during winter months only. Similarly, only precipitation falling during winter months was used in the classification. Finally, given the challenges in obtaining high-quality, high-spatial-resolution wind information, vegetation classification was used as a proxy. Using climatological values (rather than values for a given year), Sturm et al. (1995) were able to develop a global map of snow classification.
There are many other formulations for snow density that increase in complexity and data requirements. Meloysund et al. (2007) express ρb in terms of sub-daily measurements of relative humidity, wind characteristics, air pressure, and rainfall, as well as h and estimates of solar exposure (“sun hours”). McCreight and Small (2014) use daily snow depth measurements to develop their regression equation. They demonstrate improved performance over both Sturm et al. (2010) and Jonas et al. (2009). However, a key difference between the McCreight and Small (2014) model and the others listed above is that the former cannot be applied to a single snow depth measurement. Instead, it requires a continuous time series of depth measurements at a fixed location. Further increases in complexity are found in energy-balance snowpack models (SnowModel, Liston and Elder, 2006; VIC, Liang et al., 1994; DHSVM, Wigmosta et al., 1994, others), many of which use multilayer models to capture the vertical structure of the snowpack. While the particular details vary, these models generally require high-temporal-resolution time series of many meteorological variables as input.
Despite the development of multilayer energy-balance snow models, there is still a demonstrated need for bulk density formulations and for vertically integrated data products like SWE. Pagano et al. (2009) review the advantages and disadvantages of energy-balance models and statistical models and describe how the NRCS uses SWE (from SNOTEL stations) and accumulated precipitation in their statistical models to make daily water supply forecasts. If SWE information is desired at a location that does not have a SNOTEL station, and is not part of a modeling effort, then bulk density equations and depth measurements are an excellent choice.
The present paper seeks to generalize the ideas of Mizukami and Perica (2008), Jonas et al. (2009), and Sturm et al. (2010). Specifically, our goal is to regress physical and environmental variables directly into the equations. In this way, environmental variability is handled in a continuous fashion rather than in a discrete way (model coefficients based on classes). The main motivation for this comes from evidence (e.g., Fig. 3 of Alford, 1967) that density can vary significantly over short distances on a given day. Bulk density equations that rely solely on time completely miss this variability and equations that have coarse (model coefficients varying over either vertical bins or horizontal grids) spatial resolution may not fully capture it either.
Our approach is most similar to Mizukami and Perica (2008), Jonas et al. (2009), and Sturm et al. (2010) in that a minimum of information is needed for the calculations; we intentionally avoid approaches like Meloysund et al. (2007) and McCreight and Small (2014). This is because our interests are in converting h measurements to SWE estimates in areas lacking weather instrumentation. The following sections introduce the numerous data sets that were used in this study, outline the regression model adopted, and assess the performance of the model.
2.1 Data
2.1.1 Snow depth and snow water equivalent
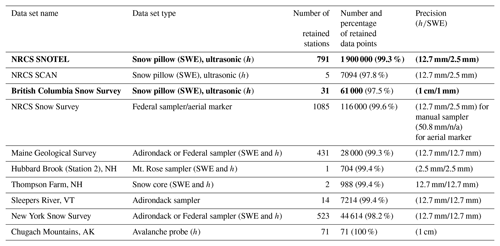
In this section, we list sources of 1970–present snow data utilized for this study (Table 1). With regards to snow coring devices, we refer to them using the terminology preferred in the references describing the data sets.
USA NRCS snow telemetry and soil climate analysis networks
SNOTEL (Serreze et al., 1999; Dressler et al., 2006) and SCAN (Schaefer et al., 2007) stations in the contiguous United States (CONUS) and Alaska typically record sub-daily observations of h, SWE, and a variety of weather variables (Fig. 2a). The periods of record are variable, but the vast majority of stations have a period of record in excess of 30 years. For this study, data from all SNOTEL sites in CONUS and Alaska and northeastern US SCAN sites (Fig. 2b) were obtained with the exception of sites whose period of record data were unavailable online. Only stations with both SWE and h data were retained.
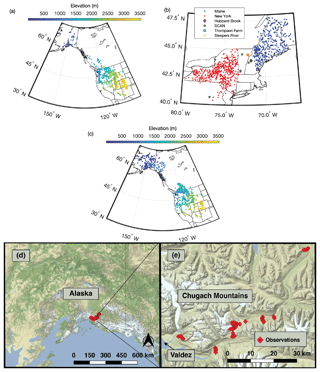
Figure 2Distribution of measurement locations used in this study. (a) Western US and Canada snow pillow locations, with colors indicating station elevation in meters. (b) Northeastern United States snow pillow and snow course locations, with stations colored according to data source. (c) Western North America snow course and aerial marker locations, with colors indicating station elevation in meters. (d, e) Measurement sites in the Chugach Mountains, south-central Alaska.
Canada (British Columbia) snow survey data
Goodison et al. (1987) note that Canada has no national digital archive of snow observations from the many independent agencies that collect snow data and that snow data are instead managed provincially. The quantity and availability of the data vary considerably among the provinces. The Water Management Branch of the British Columbia (BC) Ministry of the Environment manages a comparatively dense network of Automated Snow Weather Stations (ASWSs) that measure SWE, h, accumulated precipitation, and other weather variables (Fig. 2a). For this study, data from all British Columbia ASWS sites were initially obtained. As with the NRCS stations, only ASWS stations with both SWE and h data were retained.
USA NRCS snow course/aerial marker data
The snow survey program (USDA, 2008) dates to the 1930s and includes a large number of snow course and aerial marker sites (Fig. 2c) in western North America. While the measurement frequency is variable, it is most commonly monthly. To generate a data set for this study, data were extracted using the National Water and Climate Center Report Generator 2.0. This allows filtering by time period, elevation band, and other elements. All sites with data between 1980 and 2018 were included (Fig. 2c).
Northeastern US data
In addition to the data from the SCAN sites, snow data for this project from the northeastern United States come from two networks and three research sites (Fig. 2b). The Maine Cooperative Snow Survey (MCSS, 2018) network includes h and SWE data collected by the Maine Geological Survey, the United States Geological Survey, and numerous private contributors and contractors. MCSS snow data are collected using the standard Federal or Adirondack snow sampling tubes typically on a weekly to biweekly (every other week) schedule throughout the winter and spring, 1951–present. The New York Snow Survey network data were obtained from the National Oceanic and Atmospheric Administration's Northeast Regional Climate Center at Cornell University (NYSS, 2018). Similar to the MCSS, NYSS data are collected using standard Federal or Adirondack snow sampling tubes on weekly to biweekly schedules, 1938–present.
The Sleepers River, Vermont Research Watershed in Danville, Vermont (Shanley and Chalmers, 1999), is a USGS site that includes 15 stations with long-term weekly records of h and SWE collected using Adirondack snow tubes. Most of the periods of record are 1981–present, with a few stations going back to the 1960s. The sites include topographically flat openings in conifer stands, old fields with shrub and grass, a hayfield, a pasture, and openings in mixed softwood–hardwood forests. The Hubbard Brook Experiment Forest (Campbell et al., 2010) has collected weekly snow observations at the Station 2 rain gauge site, 1959–present. Measurement protocol collects 10 samples 2 m apart along a 20 m transect in a hardwood forest opening about 1∕4 ha in size. At each sample location along the transect, h and SWE are measured using a Mt. Rose snow tube and the 10 samples are averaged for each transect. Finally, the Thompson Farm Research site includes a mixed hardwood forest site and an open pasture site (Burakowski et al., 2013, 2015). Daily (from 2011 to 2018), at each site, a snow core is extracted with an aluminum tube and weighed (tube + snow) using a digital hanging scale. The net weight of the snow is combined with the depth and the tube diameter to determine ρb, similar to a Federal or Adirondack sampler.
Chugach Mountains (Alaska) data
In the spring of 2018, we conducted 3 weeks of fieldwork in the Chugach Mountains in coastal Alaska, near the city of Valdez (Fig. 2d–e). We measured h using an avalanche probe at 71 sites along elevational transects during March, April, and May. The elevational transects ranged between 250 and 1100 m (net change along transect) and were accessible by ski and snowshoe travel. At each site, we measured h in eight locations within the surrounding 10 m2, resulting in a total of 550+ snow depth measurements. These 71 sites were scattered across eight regions in order to capture spatial gradients that exist in the Chugach Mountains as the wetter, more dense maritime snow near the coast gradually changes to drier, less dense snow on the interior side.
Data preprocessing
Figure 3 demonstrates that it is not uncommon for automated snow pillow measurements to become noisy or nonphysical, at times reporting large depths when there is no SWE reported. This is different from instances when physically plausible but very low densities might be reported; say in response to early season dry, light snowfalls. It was therefore desirable to apply some objective, uniform procedure to each station's data set in order to remove clear outlier points, while minimizing the removal of valid data points. We recognize that there is no accepted standardized method for cleaning bivariate SWE–h data sets. While Serreze et al. (1999) offer a procedure for SNOTEL data in their appendix, it is relevant only for precipitation and SWE values, not h. Given the strong correlation between h and SWE, we instead choose to use common outlier detection techniques for bivariate data.
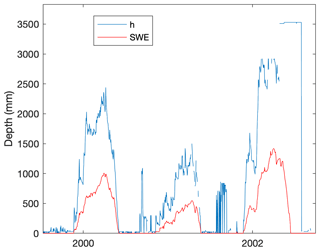
Figure 3Sample time series of SWE and h from the Rex River (WA) SNOTEL station. Observations of h at times when SWE is zero are likely spurious.
The Mahalanobis distance (MD; De Maesschalck et al., 2000) quantifies how far a point lies from the mean of a bivariate distribution. The distances are in terms of the number of standard deviations along the respective principal component axes of the distribution. For highly correlated bivariate data, the MD can be qualitatively thought of as a measure of how far a given point deviates from an ellipse enclosing the bulk of the data. One problem is that the MD is based on the statistical properties of the bivariate data (mean, covariance) and these properties can be adversely affected by outlier values. Therefore, it has been suggested (e.g., Leys et al., 2018) that a “robust” MD (RMD) be calculated. The RMD is essentially the MD calculated based on statistical properties of the distribution unaffected by the outliers. This can be done using the minimum covariance determinant (MCD) method as first introduced by Rousseeuw (1984).
Once RMDs have been calculated for a bivariate data set, there is the question of how large an RMD must be in order for the data point to be considered an outlier. For bivariate normal data, the distribution of the square of the RMD is χ2 (Gnanadesikan and Kettenring, 1972), with p (the dimension of the data set) degrees of freedom. So, a rule for identifying outliers could be implemented by selecting as a threshold some arbitrary quantile (say 0.99) of . For the current study, a threshold quantile of 0.999 was determined to be an appropriate compromise in terms of removing obvious outlier points, yet retaining physically plausible results.
A scatter plot of SWE vs. h for the SNOTEL data set from CONUS and AK reveals many nonphysical points, mostly when a very large h is reported for a very low SWE (Fig. 4a). Approximately 0.7 % of the original data points were removed in the preprocessing described above, creating a more physically plausible scatter plot (Fig. 4b). Note that the outlier detection process was applied to each station individually. The distribution of day of year (DOY) values of removed data points was broad, with a mean of 160 and a standard deviation of 65. Note that the DOY origin is 1 October. The same procedure was applied to the BC snow pillow, NRCS snow course, and northeastern US data sets as well (not shown). Table 1 summarizes useful information about the numerous data sets described above and indicates the final number of data points retained for each. We acknowledge that our process inevitably removes some valid data points, but, as a small percentage of an already small 0.7 % removal rate, we judged this to be acceptable.
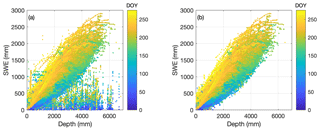
Figure 4Scatter plot of SWE vs. h for the complete SNOTEL data set before (a) and after (b) removing data points, following the method described in the section Chugach Mountains (Alaska) data. Symbols are colored by day of water year (DOY; 1 October is the origin).
2.1.2 Climatological variables
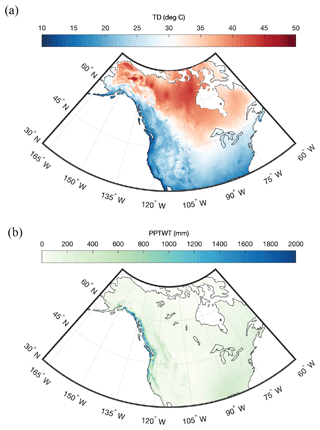
The 30-year climate normals at 1 km resolution for North America were obtained from the ClimateNA project (Wang et al., 2016). This project provides grids for minimum, maximum, and mean temperature, and total precipitation for a given month. These grids are based on the PRISM normals (Daly et al., 1994) and are available for the periods 1961–1990 and 1981–2010. For this study, the more recent climatology was used. The ClimateNA project also provides a wide array of derived bioclimatic variables, such as precipitation as snow (PAS), frost-free period (FFP), mean annual relative humidity (RH), and others. Wang et al. (2012) summarize these additional variables and how they are derived. Figure 5 shows gridded maps of winter (sum of December, January, February) precipitation (PPTWT) and the temperature difference (TD) between the mean temperature of the warmest month and the mean temperature of the coldest month. The latter variable (TD) is a measure of continentality.
2.2 Regression model
In order to demonstrate the varying degrees of influence of explanatory variables, several regression models were constructed. In each case, the model was built by randomly selecting 50 % of the paired SWE–h measurements from the aggregated CONUS, AK, and BC snow pillow data sets, excluding the SCAN data. The model was then validated by applying it to the remaining 50 % of the data set and comparing the modeled SWE to the observed SWE for those points. We constructed a second version of the regression models by randomly selecting 50 % of the snow pillow stations and using all of the data from those stations. The model was then validated by applying it to the data from the remaining 50 % of the stations. These two methods provided identical results, likely due to the very large sample size (N) of our data set. In all cases, the p values from the linear regression were 0, again due to the large sample size. Additional validation was performed with the northeastern US data sets (SCAN snow pillow and various snow coring data sets) and the NRCS snow course/aerial marker data set, which were completely left out of the model building process.
2.2.1 One-equation model
The simplest equation, and one that is supported by the strong correlation seen in the portions of Fig. 3 when SWE is present, is one that expresses SWE as a function of h. A linear model is attractive in terms of simplicity, but this limits the snowpack to a constant density. An alternative is to express SWE as a power law, i.e.,
This equation can be log-transformed into
which immediately allows for simple linear regression methods to be applied. With both h and SWE expressed in millimeters, the obtained coefficients are . Information on the performance of the model will be deferred until the results section.
2.2.2 Two-equation model
Recall from Figs. 1 and 4 that there is a hysteresis loop in the SWE–h relationship. During the accumulation phase, snow densities are relatively low. During the ablation phase, the densities are relatively high. So, the same snowpack depth is associated with two different SWEs, depending upon the time of year. The regression equation given above does not resolve this difference. This can be addressed by developing two separate regression equations, one for the accumulation (acc) phase and one for the ablation (abl) phase. This approach takes the form of
where DOY is the number of days from the start of the water-year, and DOY* is the critical or dividing day of water year separating the two phases. Put another way, DOY* is the day of peak SWE. Interannual variability results in a range of DOY* values for a given site. Additionally, some sites, particularly the SCAN sites in the northeastern United States, demonstrate multi-peak SWE profiles in some years. To reduce model complexity, however, we investigated the use of a simple climatological (long-term average) value of DOY* at each site. For each snow pillow station, the average DOY* was computed over the period of record of that station. Analysis of all of the stations revealed that this average DOY* was relatively well correlated with the climatological mean April maximum temperature (the average of the daily maximums recorded in April; R2=0.7). However, subsequent regression analysis demonstrated that the SWE estimates were relatively insensitive to DOY* and the best results were actually obtained when DOY* was uniformly set to 180 for all stations. Again, with both SWE and h in millimeters, the regression coefficients turn out to be and
As these two equations are discontinuous at DOY*, they are blended smoothly together to produce the final two-equation model.
The coefficient 0.01 in the tanh function controls the width of the blending window and was selected to minimize the root-mean-square error of the model estimates.
2.2.3 Two-equation model with climate parameters
A final model was constructed by incorporating climatological variables. Again, the emphasis in this study is on methods that can be implemented at locations lacking the time series of weather variables that might be available at a weather or SNOTEL station. Climatological normals are unable to account for interannual variability, but they do preserve the high spatial gradients in climate that can lead to spatial gradients in snowpack characteristics. Stepwise linear regression was used to determine which variables to include in the regression. The initial list of potential variables included was
where z is the elevation (m), PPTWT is the winter (sum of December, January, February) precipitation (mm), PAS is mean annual precipitation as snow (mm), TWT is the winter (December, January, February) mean temperature (∘C), TD is the difference between the mean temperature of the warmest month and the mean temperature of the coldest month (∘C), DOY is the day of water year, and RH is the relative humidity (%). In the stepwise regression, explanatory variables were accepted only if they improved the adjusted R2 value by 0.001. The result of the regression yielded
or, in log-transformed format,
indicating that only snow depth, winter precipitation, temperature difference, and day of water year were relevant. Manual tests of model construction with other variables included confirmed that Eqs. (7)–(8) yielded the best results. These two SWE estimates for the individual (acc and abl) phases of the snowpack were then blended with Eq. (5) to produce a single equation for SWE spanning the entire water year. The obtained regression coefficients were and , b3,b4) . The physical interpretation of these coefficients is straightforward. For example, both a2 and b2 are greater than zero. So, for two locations with equal h, DOY, and TD, the location with greater PPTWT will have a greater SWE and therefore density. These locations are typically maritime climates with wetter, denser snow. In contrast, both a3 and b3 are less than zero. Therefore, for two locations with equal h, DOY, and PPTWT, the location with greater TD (a more continental climate) will have a lower density, which is again an expected result. These trends are similar in concept to Sturm et al. (2010), whose discrete snow classes (based on climate classes) indicate which snow will densify more rapidly.
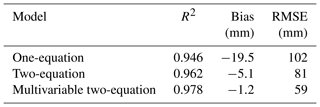
A comparison of the three regression models (one-equation model, Eq. 2; two-equation model, Eqs. 3–5; multivariable two-equation model, Eqs. 5, 7–8) is provided in Fig. 6. The left column shows scatter plots of modeled SWE to observed SWE for the validation data set with the 1:1 line shown in black. Figure 6a, c, and e show distributions of the model residuals. The vertical lines in Fig. 6b, d, and f show the mean error, or model bias. Visually, it is clear that the one-equation model performs relatively poorly with a large negative bias. This large negative bias is partially overcome by the two-equation model (Fig. 6c, d). The cloud of points is closer to the 1:1 line and the vertical black line indicating the mean error is closer to zero. In Fig. 6e, f, we see that the multivariable two-equation model yields the best result by far. The residuals are now evenly distributed with a small bias. Several metrics of performance for the three models, including R2 (Pearson coefficient), bias, and root-mean-square error (RMSE), are provided in Table 2. Figure 7 shows the distribution of model residuals for the multivariable two-equation model as a function of DOY.
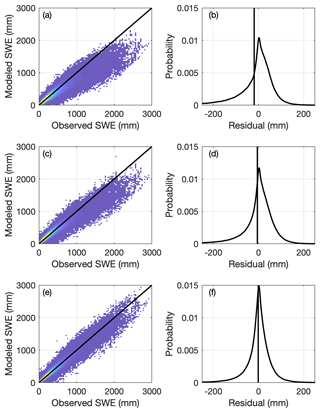
Figure 6Two-dimensional histograms (heat maps; a, c, e) of modeled vs. observed SWE and probability density functions (b, d, f) of the residuals for three simple models applied to the CONUS, AK, and BC snow pillow data. Warmer colors in the heat maps indicate greater density of points. The vertical lines in (b, d, f) indicate the location of the mean residual, or bias. (a, b) One-equation model (Sect. 2.2.1). (c, d) Two-equation model (Sect. 2.2.2). (e, f) Multivariable two-equation model (Sect. 2.2.3).
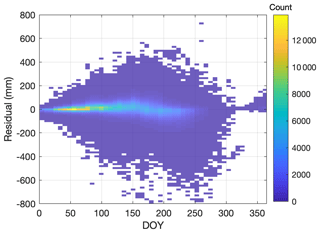
Figure 7Heat map of SWE residuals as a function of DOY for the application of the multivariable two-equation model to the western North America snow pillow validation data set.
It is useful to also consider the model errors in a nondimensional way. Therefore, an RMSE was computed at each station location and normalized by the winter precipitation (PPTWT) at that location. Figure 8 shows the probability density function of these normalized errors. The average RMSE is approximately 15 % of PPTWT with most values falling into the range of 5 %–30 %. The spatial distribution of these normalized errors is shown in Fig. 9. For the SNOTEL stations, it appears there is a slight regional trend, in terms of stations in continental climates (Rockies) having larger relative errors than stations in maritime climates (Cascades). The British Columbia stations also show higher relative errors.
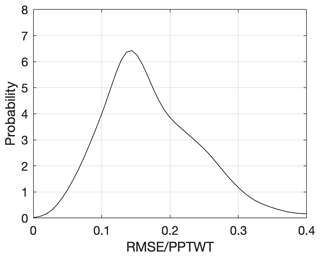
Figure 8Probability density function of snow pillow station root-mean-square error (RMSE) normalized by station winter precipitation (PPTWT) for the application of the multivariable two-equation model to the western North America snow pillow validation data set.
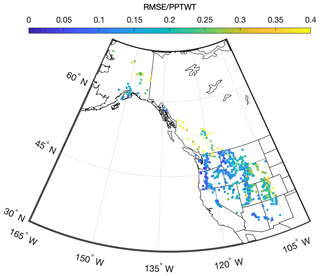
Figure 9Spatial distribution of snow pillow station root-mean-square error (RMSE) normalized by station winter precipitation (PPTWT) for the application of the multivariable two-equation model to the western North America snow pillow validation data set.
3.1 Results for snow classes
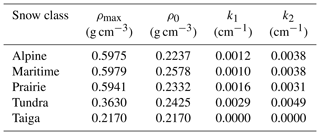
A key objective of this study is to regress climatological information in a continuous rather than a discrete way. The work by Sturm et al. (2010) therefore provides a valuable point of comparison. In that study, the authors developed the following equation for density ρb:
where ρ0 is the initial density, ρmax is the maximum or “final” density (end of water year), k1 and k2 are coefficients, and DOY in this case begins on 1 January. This means that their DOY for 1 October is −92. The coefficients vary with snow class and the values determined by Sturm et al. (2010) are shown in Table 3.
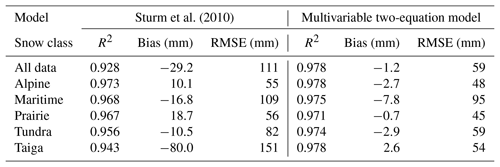
To make a comparison, the snow class for each SNOTEL and British Columbia snow survey (rows 1 and 3 of Table 1) site was determined using a 1 km snow class grid (Sturm et al., 2010). The aggregated data set from these stations was made up of 27 % alpine, 14 % maritime, 10 % prairie, 11 % tundra, and 38 % taiga data points. Equation (11) was then used to estimate snow density (and then SWE) for every point in the validation data set described in Sect. 2.2. Figure 10 compares the SWE estimates from the Sturm model and from the current multivariable, two-equation model (Eqs. 5, 7–8). The upper left panel of Fig. 10 shows all of the data, and the remaining panels show the results for each snow class. In all cases, the current model provides better estimates (narrower cloud of points; closer to the 1:1 line). Plots of the residuals by snow class are provided in Fig. 11, giving an indication of the bias of each model for each snow class. Summaries of the model performance, broken out by snow class, are given in Table 4. The current model has smaller biases and RMSEs for each snow class.
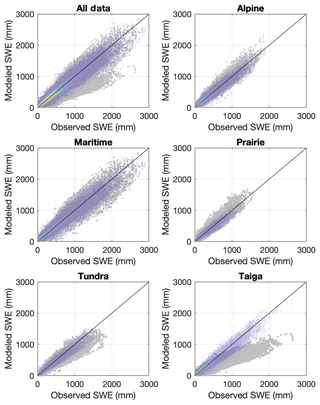
Figure 10Comparison of the multivariable, two-equation model of the current study with the model of Sturm et al. (2010), applied to the western North America snow pillow validation data set. The subpanels show modeled SWE vs. observed SWE for all of the data binned together, as well as for the data broken out by the snow classes identified by Sturm et al. (1995). The gray symbols show the Sturm result and the transparent heat maps (warmer colors indicate greater density of points) show the current result.
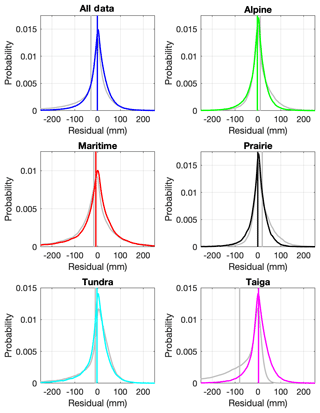
Figure 11Comparison of the multivariable, two-equation model of the current study with the model of Sturm et al. (2010), applied to the western North America snow pillow validation data set. The panels show probability density functions of the residuals of the model fits for all of the data binned together, as well as for the data broken out by the snow classes identified by Sturm et al. (1995). The gray lines show the Sturm result and the colored lines show the current result. The vertical lines show the mean error, or the model bias, for both the Sturm and current results.
3.2 Comparison to Pistocchi (2016)
In order to provide an additional comparison, the simple model of Pistocchi (2016) was also applied to the validation data set. His model calculates the bulk density as
where ρ0 has a value of 200 kg m−3 and K has a value of 1 kg m−3. The DOY for this model has its origin at 1 November. Application of this model to the validation data set yields a bias of 55 mm and an RMSE of 94 mm. These results are comparable to the Sturm et al. (2010) model, with a larger bias but smaller RMSE.
3.3 Comparison to Jonas et al. (2009)
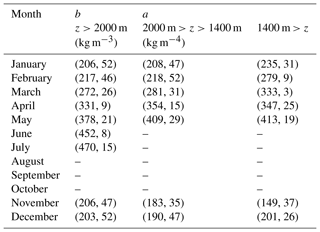
A final point of comparison can be provided by the model of Jonas et al. (2009). The full version of that model contains region-specific offset parameters that are not relevant to North America, so the following partial version of the model is used (their Eq. 4):
where h is in m and the parameters (a, b) vary with elevation and month as given by Table 5. Note that coefficients are not given for every month. Application of the Jonas et al. (2009) model to the snow pillow data set yields a bias of −5 mm and an RMSE of 69 mm. These results are not directly comparable to those of the current model (Table 2, row 3) since the Jonas et al. (2009) model is unable to compute results for several months of the year. To make a direct comparison to the current model, it is necessary to first remove those data points (about 5 %). When this is done, the current model yields a bias of −0.3 mm and an RMSE of 59 mm.
3.4 Results for northeastern United States
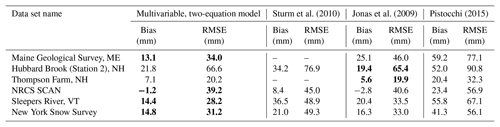
The regression equations in this study were developed using a large collection of snow pillow sites in CONUS, AK, and BC. The snow pillow sites are limited to locations west of approximately 105∘ W (Fig. 2a). By design, the data sets from the northeastern United States were left as an entirely independent validation set. These northeastern sites are geographically distant from the training data sets, subject to a very different climate, largely use different methods (snow coring, with the exception of the SCAN network), and are generally at much lower elevations than the western sites, providing an interesting opportunity to test how robust the current model is.
Figure 12 graphically summarizes the data sets and the performance of the multivariable two-equation model of the current study. The RMSE values are comparable to those found for the western stations, but, given the comparatively thinner snowpacks in the northeast, represent a larger relative error (Table 6). The bias of the model is consistently positive, in contrast to the western stations where the bias was negligible. Note that Table 6 also includes results from the application of the other three models discussed. Sturm et al. (2010) cannot be applied to several of the data sets since their available 1 km snow class data set cuts off at −71.6∘ longitude. The current model and the Jonas et al. (2009) model perform better than the other two models, with the current model generally outperforming the Jonas et al. (2009) model. The two data sets where the Jonas et al. (2009) model has a slightly better performance are the two smallest data sets (less than 1000 measurements; see Table 1).
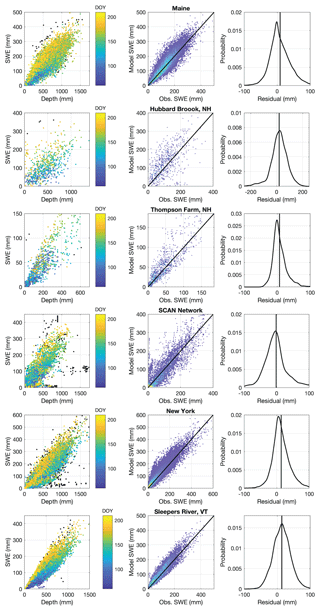
Figure 12Results from application of the multivariable, two-equation model to numerous northeastern US data sets. The left column shows the SWE–h data for each data set. Note that the black symbols are points removed during the data preprocessing stage. The remaining symbols are colored by DOY. The middle column plots heat maps of the model estimates of SWE against the observations of SWE with the 1:1 line included. Warmer colors indicate higher density of points. The right column shows probability density functions of the model residuals, with the vertical line indicating the mean error, or bias. Individual rows correspond to individual data sets and are labeled.
3.5 Results for NRCS snow course/aerial marker data
The NRCS snow course and aerial marker data were also left out of the model building process so they provide an additional and completely independent comparison of the various models considered. Recall that these data come from snow course (coring measurements) and aerial surveys, which are different measurement methods than the snow pillows, which provided the data for construction of the current regression model. Figure 13 shows the aggregated snow course/aerial marker data set, along with the performance of the multivariable two-equation model of the current study. Table 7 summarizes the results and demonstrates that the current model has the best performance.
Table 7Performance metrics for various models applied to the NRCS snow course and aerial marker data set. Bold font is used to highlight the model with the best performance.

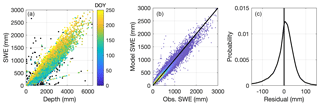
Figure 13Results from application of the multivariable, two-equation model to the NRCS snow course/aerial marker data set. Panel (a) shows the SWE–h data. Note that the black symbols are points removed during the data preprocessing stage. The remaining symbols are colored by DOY. Panel (b) shows a heat map of the model estimates of SWE against the observations of SWE with the 1:1 line included. Warmer colors indicate higher densities of points. Panel (c) shows the probability density function of the model residuals, with the vertical line indicating the mean error, or bias.
The results presented in this study show that the regression equation described by Eqs. (5), (7)–(8) is an improvement (lower bias and RMSE) over other widely used bulk density equations. The key advantage is that the current method regresses in relevant parameters directly, rather than using discrete bins (for snow class, elevation, month of year, etc.), each with its own set of model coefficients. The comparison (Figs. 10–11; Table 4) to the model of Sturm et al. (2010) reveals a peculiar behavior of that model for the taiga snow class, with a large negative bias in the Sturm estimates. Inspection of the coefficients provided for that class (Table 3) shows that the model simply predicts that for all conditions.
When our multivariable two-equation model, developed solely from western North American data, is applied to northeastern US locations, it produces SWE estimates with smaller RMSE values and larger biases than the western stations. When comparing the SWE–h scatter plots of the SNOTEL data (Fig. 4b) to those of the east coast data sets (left column; Fig. 12), it is clear that the northeast data generally have more scatter. This is confirmed by computing the correlation coefficients between SWE and h for each data set. It is unclear if this disparity in correlation is related to measurement methodology or is instead a signal-to-noise ratio issue. Comparing Figs. 4 and 12 shows the considerable difference in snowpack depth between the western and northeastern data sets. When the western data set is filtered to include only measurement pairs where h<1.5 m, the correlation coefficient is reduced to a value consistent with the northeast data sets. This suggests that the performance of the current (or other) regression model is not as good at shallow snowpack depths. This is also suggested upon examination of the time series of observed for a given season at a snow pillow site. Very early in the season, when the depths are small, the density curve has a lot of variability. Later in the season, when depths are greater, the density curve becomes much smoother. Very late in the season, when depths are low again, the density curve becomes highly variable again.
Measurement precision and accuracy affect the construction and use of a regression model. Upon inspection of the snow pillow data, it was observed that the precision of the depth measurements was approximately 25 mm and that of the SWE measurements was approximately 2.5 mm. To test the sensitivity of the model coefficients to the measurement precision, the depth values in the training data set were randomly perturbed by ±25 mm and the SWE values were randomly perturbed by ±2.5 mm and the regression coefficients were recomputed. This process was repeated numerous times and the mean values of the perturbed coefficients were obtained. These adjusted coefficients were then used to recompute the SWE values for the validation data set and the bias and RMSE were found to be −10.5 and 72.7 mm. This represents a roughly 10 % increase in RMSE, but a considerable increase in bias magnitude (see Table 4 for the original values). This sensitivity of the regression analysis to measurement precision underscores the need to have high-precision measurements for the training data set. Regarding accuracy, random and systematic errors in the paired SWE–h data used to construct the regression model will lead to uncertainties in SWE values predicted by the model. As noted in the introduction, snow pillow errors in SWE estimates do not follow a simple pattern. Additionally, they are complicated by the fact that the errors are often computed by comparing snow pillow data to coring data, which itself is subject to error. Lacking quantitative information on the distribution of snow pillow errors, we are unable to quantify the uncertainty in the SWE estimates.
Another important consideration has to do with the uncertainty of depth measurements that the model is applied to. For context, one application of this study is to crowd-sourced, opportunistic snow depth measurements from programs like the Community Snow Observations (CSO; Hill et al., 2018) project. In the CSO program, backcountry recreational users submit depth measurements, typically taken with an avalanche probe, using a smartphone in the field. The measurements are then converted to SWE estimates, which are assimilated into snowpack models. These depth measurements are “any time, any place” in contrast to repeated measurements from the same location, like snow pillows or snow courses. Most avalanche probes have centimeter-scale graduated markings, so measurement precision is not a major issue. A larger problem is the considerable variability in snowpack depth that can exist over short (meter-scale) distances. The variability of the Chugach avalanche probe measurements was assessed by taking the standard deviation of eight depth measurements per site. The average of this standard deviation over the sites was 22 cm and the average coefficient of variation (standard deviation normalized by the mean) over the sites was 15 %. This variability is a function of the surface roughness of the underlying terrain, and also a function of wind redistribution of snow. Propagating this uncertainty through the regression equations yields a slightly higher (16 %) uncertainty in the SWE estimates. CSO participants can do three things to ensure that their recorded depth measurements are as representative as possible. First, avoid measurements in areas of significant wind scour or deposition. Second, avoid measurements in terrain likely to have significant surface roughness (rocks, fallen logs, etc.). Third, take several measurements and average them.
Expansion of CSO measurements in areas lacking SWE measurements can increase our understanding of the extreme spatial variability in snow distribution and the inherent uncertainties associated with modeling SWE in these regions. It could also prove useful for estimating watershed-scale SWE in regions like the northeastern United States, which is currently limited to five automated SCAN sites with historical SWE measurements for only the past 2 decades. Additionally, historical snow depth measurements are more widely available in the Global Historical Climatology Network (GHCN-Daily; Menne et al., 2012), with several records extending back to the late 1800s. While many of the GHCN stations are confined to lower elevations with shallower snow depths, the broader network of quality-controlled snow depth data paired with daily GHCN temperature and precipitation measurements could potentially be used to reconstruct SWE in the eastern United States given additional model development and refinement.
We have developed a new, easy-to-use method for converting snow depth measurements to snow water equivalent estimates. The key difference between our approach and previous approaches is that we directly regress in climatological variables in a continuous fashion, rather than a discrete one. Given the abundance of freely available climatological norms, a depth measurement tagged with coordinates (latitude and longitude) and a time stamp is easily and immediately converted into SWE.
We developed this model with data from paired SWE–h measurements from the western United States and British Columbia. The model was tested against entirely independent data (primarily snow course, some snow pillow) from the northeastern United States and was found to perform well, albeit with larger biases and root-mean-squared errors. The model was tested against other well-known regression equations and was found to perform better. The model was also tested against a large data set of independent snow course and aerial marker measurements from western North America. For this second independent test, the current model outperformed the other models considered.
This model is not a replacement for more sophisticated snow models that evolve the snowpack based on high-frequency (e.g., daily or sub-daily) weather data inputs. The intended purpose of this model is to constrain SWE estimates in circumstances where snow depth is known, but weather variables are not, a common issue in sparsely instrumented areas in North America.
Numerous online data sets were used for this project and were obtained from the following locations:
-
NRCS Snow Telemetry, https://www.wcc.nrcs.usda.gov/snow/SNOTEL-wedata.html (last access: 1 August 2018);
-
NRCS Soil Climate Analysis Network, https://www.wcc.nrcs.usda.gov/scan/ (last access: 15 September 2018);
-
British Columbia Automated Snow Weather Stations, https://www2.gov.bc.ca/gov/content/environment/air-land-water/water/water-science-data/water-data-tools/snow-survey-data/automated-snow-weather-station-data (last access: 1 October 2018);
-
Maine Cooperative Snow Survey, https://mgs-maine.opendata.arcgis.com/datasets/maine-snow-survey-data (last access: 15 October 2018);
-
New York Snow Survey, http://www.nrcc.cornell.edu/regional/snowsurvey/snowsurvey.html (last access: 15 October 2018);
-
Sleepers River Research Watershed, snow data not available online; request data from contact at https://nh.water.usgs.gov/project/sleepers/index.htm (last access: 30 October 2018);
-
Hubbard Brook Experimental Forest, https://hubbardbrook.org/d/hubbard-brook-data-catalog (last access: 30 October 2018);
-
Climatological Data, https://adaptwest.databasin.org/pages/adaptwest-climatena (last access: 1 June 2019);
-
NRCS snow course/aerial marker data, https://wcc.sc.egov.usda.gov/reportGenerator/ (last access: 1 June 2019).
-
A MATLAB function for calculating SWE based on the results is this paper has been made publicly available at GitHub (https://github.com/communitysnowobs/snowdensity).
JK contributed (acquisition, formatting, preliminary analysis) the Alaska and British Columbia data, JMH contributed the SNOTEL data, EAB and JK contributed the northeastern USA data, DFH contributed the western USA snow course/aerial marker data, RLC contributed the Chugach data. All authors contributed to the conception and direction of this study and to writing and editing of the manuscript. DFH conducted the regression analysis and was the principal author of the manuscript.
The authors declare that they have no conflict of interest.
We thank Matthew Sturm, Adam Winstral, and the third anonymous referee for their careful and thoughtful reviews of this paper.
This research has been supported by NASA (grant no. NNX17AG67A), CUAHSI (Pathfinder Fellowship grant), and the NSF (grant no. MSB-ECA 1802726).
This paper was edited by Jürg Schweizer and reviewed by Matthew Sturm, Adam Winstral, and one anonymous referee.
Alford, D.: Density variations in alpine snow, J. Glaciol., 6, 495–503, https://doi.org/10.3189/S0022143000019717, 1967.
Avanzi, F., De Michele, C., and Ghezzi, A.: On the performances of empirical regressions for the estimation of bulk snow density, Geogr. Fis. Din. Quat., 38, 105–112, https://doi.org/10.4461/GFDQ.2015.38.10, 2015.
Beaumont, R.: Mt. Hood pressure pillow snow gage, J. Appl. Meteorol., 4, 626–631, https://doi.org/10.1175/1520-0450(1965)004<0626:MHPPSG>2.0.CO;2, 1965.
Beaumont, R. and Work, R.: Snow sampling results from three samplers, Hydrolog. Sci. J., 8, 74–78, https://doi.org/10.1080/02626666309493359, 1963.
Burakowski, E. A., Wake, C. P., Stampone, M., and Dibb, J.: Putting the Capital “A” in CoCoRAHS: An Experimental Program to Measure Albedo using the Community Collaborative Rain Hail and Snow (CoCoRaHS) Network, Hydrol. Process., 27, 3024–3034, https://doi.org/10.1002/hyp.9825, 2013.
Burakowski, E. A., Ollinger, S., Lepine, L., Schaaf, C. B., Wang, Z., Dibb, J. E., Hollinger, D. Y., Kim, J.-H., Erb, A., and Martin, M. E.: Spatial scaling of reflectance and surface albedo over a mixed-use, temperate forest landscape during snow-covered periods, Remote Sens. Environ., 158, 465–477, https://doi.org/10.1016/j.rse.2014.11.023, 2015.
Campbell, J., Ollinger, S., Flerchinger, G., Wicklein, H., Hayhoe, K., and Bailey, A.: Past and projected future changes in snowpack and soil frost at the Hubbard Brook Experimental Forest, New Hampshire, USA, Hydrol. Process., 24, 2465–2480, https://doi.org/10.1002/hyp.7666, 2010.
Church, J. E.: Snow surveying: its principles and possibilities, Geogr. Rev., 23, 529–563, https://doi.org/10.2307/209242, 1933.
Church, J. E. and Marr, J. C.: Further improvement of snow-survey apparatus, T. Am. Geophys. Un., 18, 607–617, https://doi.org/10.1029/TR018i002p00607, 1937.
Daly, C., Neilson, R., and Phillips, D.: A statistical-topographic model for mapping climatological precipitation over mountainous terrain, J. Appl. Meteorol., 33, 140–158, https://doi.org/10.1175/1520-0450(1994)033<0140:ASTMFM>2.0.CO;2, 1994.
De Maesschalck, R., Jouan-Rimbaud, D., and Massart, D.: The Mahalanobis distance, Chemometr. Intell. Lab., 50, 1–18, https://doi.org/10.1016/S0169-7439(99)00047-7, 2000.
Dixon, D. and Boon, S.: Comparison of the SnowHydro sampler with existing snow tube designs, Hydrol. Process., 26, 2555–2562, https://doi.org/10.1002/hyp.9317, 2012.
Dressler, K., Fassnacht, S., and Bales, R.: A comparison of snow telemetry and snow course measurements in the Colorado River basin, J. Hydrometeorol., 7, 705–712, https://doi.org/10.1175/JHM506.1, 2006.
Gnanadesikan, R. and Kettenring, J.: Robust estimates, residuals, and outlier detection with multiresponse data, Biometrics, 28, 81–124, https://doi.org/10.2307/2528963, 1972.
Goodison, B.: Accuracy of snow samplers for measuring shallow snowpacks: An update, Proceedings of the 35th Annual Eastern Snow Conference, Hanover, NH, 36–49, 2–3 February 1978.
Goodison, B., Ferguson, H., and McKay, G.: Measurement and data analysis. The Handbook of Snow: Principles, Processes, Management, and Use, edited by: Gray, D. and Male, D., The Blackburn Press, Caldwell, NJ, USA, 191–274, 1981.
Goodison, B., Wilson, B., Wu., K, and Metcalfe, J.: An inexpensive remote snow-depth gauge: An assessment, Proceedings of the 52nd Annual Western Snow Conference, Sun Valley, ID, 188–191, 17–19 April 1984.
Goodison, B., Glynn, J., Harvey, K., and Slater, J.: Snow Surveying in Canada: A Perspective, Can. Water Resour. J., 12, 27–42, https://doi.org/10.4296/cwrj1202027, 1987.
Hill, D. F., Wolken, G. J., Wikstrom Jones, K., Crumley, R., and Arendt, A.: Crowdsourcing snow depth data with citizen scientists, Eos, 99, https://doi.org/10.1029/2018EO108991, 2018.
Johnson, J. and Marks, D.: The detection and correction of snow water equivalent pressure sensor errors, Hydrol. Process., 18, 3513–3525, https://doi.org/10.1002/hyp.5795, 2004.
Johnson, J., Gelvin, A., Duvoy, P., Schaefer G., Poole, G., and Horton, G.: Performance characteristics of a new electronic snow water equivalent sensor in different climates, Hydrol. Process., 29, 1418–1433, https://doi.org/10.1002/hyp.10211, 2015.
Jonas, T., Marty, C., and Magnusson, M.: Estimating the snow water equivalent from snow depth measurements, J. Hydrol., 378, 161–167, https://doi.org/10.1016/j.jhydrol.2009.09.021, 2009.
Leys, C., Klein, O., Dominicy, Y., and Ley, C.: Detecting multivariate outliers: use a robust variant of the Mahalanobis distance, J. Exp. Soc. Psychol., 74, 150–156, https://doi.org/10.1016/j.jesp.2017.09.011, 2018.
Liang, X., Lettermaier, D., Wood, E., and Burges, S.: A simple hydrologically based model of land surface water and energy fluxes for general circulation models, J. Geophys. Res., 99, 14415–14428, https://doi.org/10.1029/94JD00483, 1994.
Liston, G. and Elder, K.: A distributed snow evolution modeling system (SnowModel), J. Hydrometerol., 7, 1259–1276, https://doi.org/10.1175/JHM548.1, 2006.
Lundberg, A., Richardson-Naslund, C., and Andersson, C.: Snow density variations: consequences for ground penetrating radar, Hydrol. Process., 20, 1483–1495, https://doi.org/10.1002/hyp.5944, 2006.
McCreight, J. L. and Small, E. E.: Modeling bulk density and snow water equivalent using daily snow depth observations, The Cryosphere, 8, 521–536, https://doi.org/10.5194/tc-8-521-2014, 2014.
McKay, G. and Findlay, B.: Variation of snow resources with climate and vegetation in Canada, Proceedings of the 39th Western Snow Conference, Billings, MT, 17–26, 20–22 April 1971.
MCSS (Maine Cooperative Snow Survey): Maine Cooperative Snow Survey Dataset, Maine Geological Survey, available at: https://www.maine.gov/dacf/mgs/hazards/snow_survey/, last access: 15 October 2018.
Meloysund, V., Leira, B., Hoiseth, K., and Liso, K.: Predicting snow density using meterological data, Meteorol. Appl., 14, 413–423, https://doi.org/10.1002/met.40, 2007.
Menne, M. J., Durre, I., Vose, R. S., Gleason, B. E., and Houston, T. G.: An overview of the Global Historical Climatology Network-Daily Database, J. Atmos. Ocean. Tech., 29, 97–910, https://doi.org/10.1175/JTECH-D-11-00103.1, 2012.
Mizukami, N. and Perica, S.: Spatiotemporal characteristics of snowpack density in the mountainous regions of the western United States, J. Hydrometeorol., 9, 1416–1426, https://doi.org/10.1175/2008JHM981.1, 2008.
Molotch, N. P. and Bales, R. C.: SNOTEL representativeness in the Rio Grande headwaters on the basis of physiographics and remotely sensed snow cover persistence, Hydrol. Process., 20, 723–739, https://doi.org/10.1002/hyp.6128, 2006.
Mote, P., Li, S., Letternaier, D., Xiao, M., and Engel, R.: Dramatic declines in snowpack in the western US, npj Climate and Atmospheric Science, 1, 1–6, https://doi.org/10.1038/s41612-018-0012-1, 2018.
NYSS (New York Snow Survey), NOAA, Northeast Regional Climate Center, Cornell University, NY, USA, 2018.
Pagano, T., Garen, D., Perkins, T., and Pasteris, P.: Daily updating of operational statistical seasonal water supply forecasts for the western U.S., J. Am. Water Resour. As., 45, 767–778, https://doi.org/10.1111/j.1752-1688.2009.00321.x, 2009.
Painter, T., Berisford, D., Boardman, J., Bormann, K., Deems, J., Gehrke, F., Hedrick, A., Joyce, M., Laidlaw, R., Marks, D., Mattmann, C., Mcgurk, B., Ramirez, P., Richardson, M., Skiles, S., Seidel, F., and Winstral, A.: The Airborne Snow Observatory: fusion of scanning lidar, imaging spectrometer, and physically-based modeling for mapping snow water equivalent and snow albedo, Remote Sens. Environ., 184, 139–152, https://doi.org/10.1016/j.rse.2016.06.018, 2016.
Pistocchi, A.: Simple estimation of snow density in an Alpine region, Journal of Hydrology: Regional Studies, 6, 82–89, https://doi.org/10.1016/j.ejrh.2016.03.004, 2016.
Rousseeuw, P.: Least Median of Squares Regression, J. Am. Stat. Assoc., 79, 871–880, https://doi.org/10.1080/01621459.1984.10477105, 1984.
Ryan, W., Doesken, N., and Fassnacht, S.: Evaluation of Ultrasonic Snow Depth Sensors for U.S. Snow Measurements, J. Atmos. Ocean. Tech., 25, 667–684, https://doi.org/10.1175/2007JTECHA947.1, 2008.
Schaefer, G., Cosh, M., and Jackson, T.: The USDA Natural Resources Conservation Service Soil Climate Analysis Network (SCAN), J. Atmos. Ocean. Tech., 24, 2073–2077, https://doi.org/10.1175/2007JTECHA930.1, 2007.
Serreze, M., Clark, M., Armstrong, R., McGinnis, D., and Pulwarty, R.: Characteristics of the western United States snowpack from snowpack telemetry (SNOTEL) data, Water Resour. Res., 35, 2145–2160, https://doi.org/10.1029/1999WR900090, 1999.
Shanley, J. and Chalmers, A.: The effect of frozen soil on snowmelt runoff at Sleepers River, Vermont, Hydrol. Process., 13, 1843–1857, https://doi.org/10.1002/(SICI)1099-1085(199909)13:12/13<1843::AID-HYP879>3.0.CO;2-G, 1999.
Sturm, M., Holmgren, J., and Liston, G.: A seasonal snow cover classification system for local to global applications, J. Climate, 8, 1261–1283, https://doi.org/10.1175/1520-0442(1995)008<1261:ASSCCS>2.0.CO;2, 1995.
Sturm, M., Taras, B., Liston, G. E., Derksen, C., Jonas, T., and Lea, J.: Estimating snow water equivalent using snow depth data and climate classes, J. Hydrometeorol., 11, 1380–1394, https://doi.org/10.1175/2010JHM1202.1, 2010.
USACE (U.S. Army Corps of Engineers): Snow hydrology: Summary report of the snow investigations of the North Pacific Division, North Pacific Division, Corps of Engineers, US Army, Portland, OR, USA, 437 pp., 1956.
USDA (U.S. Department of Agriculture): The History of Snow Survey and Water Supply Forecasting, Interviews With U.S. Department of Agriculture Pioneers, edited By: Helms, D., Phillips, S., and Reich, P., Natural Resources Conservation Service, U.S. Department of Agriculture, Natural Resources Conservation Service, Washington D.C., USA, 2008.
USDA (U.S. Department of Agriculture): Snow Survey and Water Supply Forecasting. National Engineering Handbook Part 622, Water and Climate Center, Natural Resources Conservation Service, 2011.
Wang, T., Hamann, A., Spittlehouse, D. L., and Murdock, T.: ClimateWNA - High-Resolution Spatial Climate Data for Western North America, J. Appl. Meteorol. Clim., 51, 16–29, https://doi.org/10.1175/JAMC-D-11-043.1, 2012.
Wang, T., Hamann, A., Spittlehouse, D. L., and Carroll, C: Locally downscaled and spatially customizable climate data for historical and future periods for North America, PLoS One, 11, e0156720, https://doi.org/10.1371/journal.pone.0156720, 2016.
Wigmosta, M. S., Vail, L., and Lettenmaier, D.: A distributed hydrology-vegetation model for complex terrain, Water Resour. Res., 30, 1665–1679, https://doi.org/10.1029/94WR00436, 1994.