NHM–SMAP: spatially and temporally high-resolution nonhydrostatic atmospheric model coupled with detailed snow process model for Greenland Ice Sheet

To improve surface mass balance (SMB) estimates for the Greenland Ice Sheet (GrIS), we developed a 5 km resolution regional climate model combining the Japan Meteorological Agency Non-Hydrostatic atmospheric Model and the Snow Metamorphism and Albedo Process model (NHM–SMAP) with an output interval of 1 h, forced by the Japanese 55-year reanalysis (JRA-55). We used in situ data to evaluate NHM–SMAP in the GrIS during the 2011–2014 mass balance years. We investigated two options for the lower boundary conditions of the atmosphere: an offline configuration using snow, firn, and ice albedo, surface temperature data from JRA-55, and an online configuration using values from SMAP. The online configuration improved model performance in simulating 2 m air temperature, suggesting that the surface analysis provided by JRA-55 is inadequate for the GrIS and that SMAP results can better simulate physical conditions of snow/firn/ice. It also reproduced the measured features of the GrIS climate, diurnal variations, and even a strong mesoscale wind event. In particular, it successfully reproduced the temporal evolution of the GrIS surface melt area extent as well as the record melt event around 12 July 2012, at which time the simulated melt area extent reached 92.4 %. Sensitivity tests showed that the choice of calculation schemes for vertical water movement in snow and firn has an effect as great as 200 Gt year⁻¹ in the GrIS-wide accumulated SMB estimates; a scheme based on the Richards equation provided the best performance.

1 Introduction

In the Greenland Ice Sheet (GrIS), the second largest terrestrial ice sheet, a significant loss of ice mass has been occurring since the early 1990s (e.g., Rignot et al., 2008; van den Broeke et al., 2009, 2016; Hanna et al., 2013). Changes in the ice sheet mass (mass balance, MB) are controlled by surface mass balance (SMB) and ice discharge across the grounding line (D), i.e., MB = SMB − D. The SMB component is related mainly to meteorological conditions and denotes the sum of mass fluxes towards the ice surface (precipitation) and away from it (runoff, sublimation, and evaporation). The Intergovernmental Panel on Climate Change's Fifth Assessment Report (IPCC AR5) (Vaughan et al., 2013) pointed out that SMB has decreased and discharge has increased at almost the same rates since the early 1990s (van den Broeke et al., 2009), accounting for the accelerated mass loss (Rignot et al., 2011). However, more recently the situation has changed drastically as mass loss has continued to increase. Enderlin et al. (2014) attributed 84 % of the increase in the GrIS mass loss after 2009 to increased surface runoff, which highlights the growing importance of SMB (see also Andersen et al., 2015; van den Broeke et al., 2016). Therefore, today, in situ measurements are of rising importance for monitoring changes in SMB as well as surface meteorological conditions.

Much effort has gone into monitoring surface weather conditions and SMB on the GrIS with in situ measurements. Steffen and Box (2001) established the Greenland Climate Network (GC-Net), consisting of 18 surface automated weather stations (AWSs), distributed mainly in the accumulation area. Ahlstrøm et al. (2008) built another AWS network as part of the Programme for Monitoring of the Greenland Ice Sheet (PROMICE), with stations distributed mainly in the ablation area. Van den Broeke et al. (2008) constructed an AWS network in the K-transect, a stake array along the 67^∘ N parallel in the south-western GrIS. Aoki et al. (2014a) installed two AWSs, SIGMA-A, and SIGMA-B (Snow Impurity and Glacial Microbe effects on abrupt warming in the Arctic), which are currently operating in the northwestern GrIS. Regarding in situ SMB measurements, Machguth et al. (2016) compiled a large number of historical stake measurement data with a unified format, although the observations do not cover the entire GrIS. To fill geographic gaps, climate models have been developed that are constrained and calibrated by these in situ measurements. Once the validity of these models is confirmed on the basis of the in situ data, output from the models can be used for analysis of ongoing environmental changes around the entire GrIS. These models also enable us to perform present and future climate simulations for the GrIS, including the effects of ice mass loss on global sea level rise (e.g., Rignot et al., 2011).

Several physically based regional climate models (RCMs) (e.g., MAR: Fettweis, 2007; RACMO2: Noël et al., 2015; Polar MM5: Box, 2013; and HIRHAM5: Langen et al., 2015) and statistically downscaled meteorological reanalysis data (Hanna et al., 2005, 2011; Wilton et al., 2017) have been applied to the GrIS that have been found to be reliable in terms of reproducing current climate conditions (e.g., Fettweis et al., 2017; Hanna et al., 2011; Box, 2013; Fausto et al., 2016; van den Broeke et al., 2016) and simulating realistic future climate change (e.g., Franco et al., 2013). Nevertheless, considerable discrepancies can be found among the SMB components simulated by these models (Vernon et al., 2013), and uncertainties in the calculated SMBs are large compared to the uncertainties in ice discharge (Enderlin et al., 2014; van den Broeke et al., 2016). Regarding this situation, van den Broeke et al. (2016) pointed out that advances are imperative in two areas: improving the physics of SMB models and enhancing their horizontal resolution. For the first area, the authors noted that current models poorly represent the effects of snow/firn/ice darkening, vertical and horizontal flow of meltwater in firn or over ice lenses, and the effect of liquid water clouds on the surface energy balance as well as the resulting melt. Regarding the second area, the authors argued the necessity of statistical and dynamical downscaling from RCM outputs.

In the present study, we constructed a high-resolution polar RCM called Non-Hydrostatic atmospheric Model–Snow Metamorphism and Albedo Process (NHM–SMAP), composed of atmospheric and snowpack models developed by the Meteorological Research Institute, Japan. We employed the Japan Meteorological Agency (JMA)'s operational nonhydrostatic atmospheric model JMA-NHM (Saito et al., 2006), with a high horizontal resolution of 5 km for dynamical downscaling. In general, a nonhydrostatic atmospheric model can be run at much higher horizontal resolution (less than 10 km, the limit of validity of the hydrostatic approximation) than a hydrostatic atmospheric model. Accordingly, a high-resolution nonhydrostatic atmospheric model has the advantage of simulating detailed mesoscale cloud structures, unlike a traditional hydrostatic atmospheric model. In light of the recent evolution of supercomputers, it is inevitable to perform dynamical downscaling with a very high horizontal resolution, which allows us to explicitly consider effects of complex terrain like the GrIS margin on the atmospheric field. We also utilized the detailed physical snowpack model SMAP (Niwano et al., 2012, 2014), which features a physically based snow albedo model (Aoki et al., 2011) and a realistic vertical water movement scheme based on the Richards equation (Richards, 1931; Yamaguchi et al., 2012). Combining high-resolution detailed atmospheric and snow models is a computational challenge that has limited previous efforts of this type (e.g., Brun et al., 2011; Vionnet et al., 2014). The purpose of this study was to assess the performance of the NHM–SMAP polar RCM in reproducing current GrIS atmospheric and snow/firn/ice conditions by utilizing in situ measurements. The chosen study period, September 2011 to August 2014, includes the record surface melt event that occurred during summer 2012 (Nghiem et al., 2012; Tedesco et al., 2013; Hanna et al., 2014). Using the data, NHM–SMAP was evaluated from various aspects, for which 1 h interval model output data were employed. Typical output data from this kind of RCM have a temporal resolution of 6 h to 1 day (Cullather et al., 2016). Therefore, this study was an attempt to take advantage of both short-term detailed weather forecast models and long-term computationally stable climate models. The success of our attempt may make model output data from NHM–SMAP valuable for assessing not only long-term climate change in the GrIS but also detailed diurnal variations of the meteorological, snow, firn, and ice conditions in the GrIS.

The purposes of this paper are to describe the NHM–SMAP polar RCM and to demonstrate its capacity to reproduce current GrIS atmospheric and snow/firn/ice conditions by utilizing in situ measurements. Section 2 of this paper describes the NHM–SMAP model in detail, and the in situ measurement data for surface meteorology and SMB we used in this study are introduced in Sect. 3. Section 4 presents the results of our validation analysis and discusses their implications for the future direction of NHM–SMAP's applications. Finally, in Sect. 5 we summarize our conclusions.

2 Model descriptions

2.1 Atmospheric model JMA-NHM

JMA-NHM employs flux form equations in spherical curvilinear orthogonal coordinates as the governing basic equations. Saito et al. (2006) demonstrated that JMA-NHM outperforms the JMA's previous hydrostatic regional model in predictions of synoptic meteorological fields and quantitative forecasts of precipitation. Although JMA-NHM is used mainly for operational daily weather forecasts around Japan, the model can also be used for long-term climate simulations (Murata et al., 2015). Recently, JMA-NHM was applied to support a field expedition in the GrIS (Hashimoto et al., 2017), and the model setting used on that occasion was used in this study. A double-moment bulk cloud microphysics scheme was used to predict both the mixing ratio and the concentration of solid hydrometeors (cloud ice, snow, and graupel), and a single-moment scheme was used to predict the mixing ratio of liquid hydrometeors (cloud water and rain). In addition, ice crystal formation in the atmosphere was simulated by using an up-to-date formulation that depends on temperature. Following Hashimoto et al. (2007), we did not employ the ice-saturation adjustment scheme and the cumulus parameterization used in the original configuration. The turbulence closure boundary layer scheme was formulated following the improved Mellor–Yamada level 3 (Nakanishi and Niino, 2006). For atmospheric radiation, the transfer function in longwave radiation was computed by a random model developed by Goody (1952), and shortwave radiation was computed by diagnosing the transfer function following Briegleb (1992).

2.2 Physical snowpack model SMAP

The multilayered physical snowpack model SMAP was developed for the seasonal snowy areas of Japan by Niwano et al. (2012, 2014). SMAP calculates the temporal evolution of broadband snow albedos in the UV-visible, near-infrared, and shortwave spectra as well as the internal physical parameters of snowpack such as temperature, density, grain size, and grain shape. Because the model incorporates the physically based snow albedo model (PBSAM) developed by Aoki et al. (2011), in principle it can explicitly assess the effects of snow grain size and impurity concentration (black carbon and dust) on snow albedo. SMAP calculates vertical water movement in snow and firn by employing the detailed Richards equation (Richards, 1931; Yamaguchi et al., 2012). SMAP is also equipped with a bucket scheme to calculate vertical water movement in snow and firn, in which liquid water exceeding the maximum prescribed water content descends to the adjacent lower layer (Niwano et al., 2012). Because a bucket scheme is used in most existing polar RCMs (Reijmer et al., 2012), we investigated whether the Richards equation scheme improves the GrIS SMB (see Sect. 4.7).

Niwano et al. (2015) applied SMAP to the SIGMA-A site (Aoki et al., 2014b), on the northwestern GrIS and demonstrated that when forced by the measured surface meteorological data, the model reproduced the temporal evolution of the physical conditions in near-surface snow (Yamaguchi et al., 2014) during the record surface melt event of summer 2012 (Nghiem et al., 2012; Tedesco et al., 2013; Hanna et al., 2014). The authors modified the original model settings only for the effective thermal conductivity of snow and the surface roughness length for momentum. In this study, we started with the same model settings described by Niwano et al. (2015). Because this was the first attempt to perform year-round regional simulations of the GrIS with SMAP, we were obliged to make adjustments for three snow/firn/ice physical processes: new snow density (density of falling snow), ice albedo, and effects of drifting snow.

2.2.1 New snow density

Previous studies have suggested that new snow density in the polar region exceeds 300 kg m⁻³ (Greuell and Konzelmann, 1994; Lenaerts et al., 2012a), whereas new snow density in midlatitudes is typically around 100 kg m⁻³ (e.g., Niwano et al., 2012). For this study, we used the following parameterization for new snow density developed by Lenaerts et al. (2012a) in Antarctica:

$$\begin{array}{}\text{(1)}& {\mathit{\rho }}_{\mathrm{new}}=A+B{T}_{\mathrm{sfc}}+C{U}_{\mathrm{10}\mathrm{m}},\end{array}$$

where ρ_new is the new snow density (kg m⁻³), T_sfc is the surface temperature (K), U_10 m is the 10 m wind speed (m s⁻¹), and the coefficients were set at A=97.5 kg m⁻³, B=0.77 kg m⁻³ K⁻¹, and C=4.49 kg s⁻¹ m⁻⁴. As an additional condition, the minimum and maximum values of ρ_new were set at 300 and 350 kg m⁻³ following Lenaerts et al. (2012a).

2.2.2 Ice albedo

Although the PBSAM snow albedo component in SMAP allows us to simulate snow albedo realistically, its present version cannot be applied to an ice surface because the optically equivalent grain size of high-density ice, an important input parameter, cannot be defined and calculated by SMAP. In this study, we calculated the albedos of snow and firn with the PBSAM snow albedo component, defining firn as snow with density between 400 and 830 kg m⁻³ following Cuffey and Paterson (2010). The albedo of ice was calculated by a linear equation as a function of density and ranged from 0.55 for a surface density of 830 kg m⁻³, the typical albedo of clean firn (Cuffey and Paterson, 2010), to 0.45 for a surface density of 917 kg m⁻³, taken from the MAR model setting as explained by Alexander et al. (2014).

2.2.3 Effects of drifting snow

Sublimation of drifting snow is an important contributor to the GrIS SMB (Lenaerts et al., 2012b). In SMAP, the drifting snow condition is diagnosed on the basis of a mobility index M_O, which describes the potential for snow erosion of a given snow layer, and a driftability index S_I. Following Vionnet et al. (2012), M_O is calculated by

$$\begin{array}{ll}\text{(2)}& {\displaystyle }& {\displaystyle }{M}_{\mathrm{O}}={\displaystyle }& {\displaystyle }\left\{\begin{array}{ll}\mathrm{0.34}\left(\mathrm{0.75}d-\mathrm{0.5}s+\mathrm{0.5}\right)& \mathrm{for}\mathrm{dendritic}\mathrm{case}\\ +\mathrm{0.66}F\left(\mathit{\rho }\right)& \\ \mathrm{0.34}\left(-\mathrm{0.583}{g}_{\mathrm{s}}-\mathrm{0.833}s\right.& \mathrm{for}\mathrm{non}-\mathrm{dendritic}\mathrm{case}\\ \left.+\mathrm{0.833}\right)+\mathrm{0.66}F\left(\mathit{\rho }\right)& \end{array}\right.,\end{array}$$

where d is dendricity, s is sphericity, ρ is snow density, and g_s is geometric snow grain size (mm). Here d describes the remaining portion of the original snow grains in a snow layer, and s is the ratio of rounded versus angular snow grains (Brun et al., 1992). These two parameters are calculated by SMAP as explained by Niwano et al. (2012). F as an empirical function of density is written as

$$\begin{array}{}\text{(3)}& F\left(\mathit{\rho }\right)=\left[\mathrm{1.25}-\mathrm{0.0042}\left(max(\mathrm{50},\mathit{\rho })-\mathrm{50}\right)\right].\end{array}$$

Using M_O, S_I is diagnosed from the equation proposed by Guyomarc'h and Merindol (1998):

$$\begin{array}{}\text{(4)}& S_{\mathrm{I}}=-\mathrm{2.868}{e}^{-\mathrm{0.085}U}+\mathrm{1}+M_{\mathrm{O}},\end{array}$$

where U is the 2 m wind speed (m s⁻¹), and the value of U when S_I becomes 0 indicates the threshold wind speed U_t for the occurrence of drifting snow. Once the onset of the drifting snow condition is simulated by SMAP, the drifting snow sublimation rate F_s (kg m⁻² s⁻¹) at 2 m above the surface is calculated following Gordon et al. (2006):

$$\begin{array}{}\text{(5)}& F_{\mathrm{s}}=D{\left({\displaystyle \frac{T_{\mathrm{0}}}{T_{\mathrm{a}}}}\right)}^{\mathit{\gamma }}{U}_{\mathrm{t}}{\mathit{\rho }}_{\mathrm{a}}{q}_{\mathrm{si}}\left(\mathrm{1}-R_{\mathrm{Hi}}\right){\left({\displaystyle \frac{U}{U_{\mathrm{t}}}}\right)}^E,\end{array}$$

where T_a is air temperature (K), T₀ is 273.15 K, ρ_a is air density (kg m⁻³), q_si is saturation-specific humidity with respect to ice at temperature T_a (kg kg⁻¹), and R_Hi is relative humidity with respect to ice. The dimensionless constants are D=0.0018, γ=4, and E=3.6. In NHM–SMAP, surface mass loss due to drifting snow sublimation is assumed by Eq. (5); however, it is not used to moisten the boundary layer in the current version, because an interaction between the atmosphere and the snow/firn/ice surface is performed through the medium of albedo and surface temperature as mentioned later in Sect. 2.3.4.

Although it is ideal to calculate the erosion of drifting snow (redistribution of near-surface snow caused by drifting snow), tracking changes in physical conditions of snow particles (prognostic variables of SMAP, namely, snow grain size, grain shape, density, and so on) during a drifting snow event and redistributing them in an updated surface field demands substantial computational costs. Therefore, the current version of NHM–SMAP neglects this process, which implies that simulated SMB is not closed locally. Lenaerts et al. (2012b) reported that the contribution of drifting snow erosion to SMB is negligible on the GrIS; however, it is locally important, especially in areas where topographic features induce strong divergence or convergence in the wind field.

2.3 NHM–SMAP coupling simulation procedure

2.3.1 Model domain and ice sheet mask

The 5 km horizontal resolution JMA-NHM outputs hourly values of surface meteorological properties including precipitation (snow and rain are discriminated internally), 2 m air temperature, 2 m relative humidity with respect to water, 2 m and 10 m wind speed, surface pressure, downward shortwave and longwave radiant fluxes, and cloud fraction in the calculation domain shown in Fig. 1. The model domain consists of 450 × 550 horizontal grid cells, with each cell characterized as land, sea, snow and ice, or sea ice. At present, the abovementioned domain setting faces a limitation imposed by practical computational costs in the supercomputer of the Meteorological Research Institute (Fujitsu PRIMEHPC FX100 and PRIMERGY CX2550M1). The ice sheet mask for the GrIS, which is constant in time, was based on Bamber et al. (2001) and updated by Shimada et al. (2016) on the basis of 2000 to 2014 MODIS satellite images. As a result, the modeled area of the GrIS and peripheral glaciers was 1.807×10⁶ km², which agrees well with the estimate of 1.801 ± 0.016 × 10⁶ km² by Kargel et al. (2012). The GrIS surface elevation was taken from Bamber et al. (2001). In the Canadian Arctic Archipelago, considerations for details in the ice sheet mask were nod given in the present study, because we focused the GrIS SMB. Therefore, there is room for improvement in the modeled ice sheet mask, which is a future issue for NHM–SMAP.

2.3.2 Dynamical downscaling of atmospheric field from reanalysis data with JMA-NHM

We performed our high-resolution atmospheric calculation by using the dynamical downscaling approach. The model atmosphere used by JMA-NHM in this study had a top height of about 22 km and included 50 grid cells in the vertical direction based on terrain-following coordinates. The vertical grid spacing increased with altitude from 40 m near the surface to 886 m at the top of the atmosphere. We used JRA-55 (Kobayashi et al., 2015) for the upper, lower, and lateral boundary conditions of the atmosphere. The horizontal resolution of JRA-55 is TL319 (∼ 55 km). Simmons and Poli (2015) reported that the near-surface and lower-tropospheric warming of the Arctic over the past 35 years is well reproduced by JRA-55, very much like the European Centre for Medium-Range Weather Forecasts (ECMWF) Interim reanalysis (ERA-Interim) data (Dee et al., 2011). Surface physical properties, including albedo and temperature of land, sea, and sea ice, were taken from JRA-55 as the bottom boundary conditions of the atmosphere. As for those surface physical properties of snow and ice, two options were possible: it was provided by JRA-55 or SMAP (see Sect. 2.3.4).

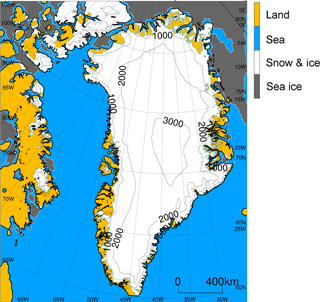
Figure 1 Model domain of NHM–SMAP used in this study showing surface types (colors). The sea ice pattern is depicted for 1 July 2012, and it changes from day to day. Contours on ice sheets and ice caps indicate surface elevation (contour interval 1000 m).

Although it is possible for JMA-NHM to perform long-term climate simulations in “climate simulation mode”, where the atmosphere is initialized only at the beginning of the simulation period (Murata et al., 2015), in this study we used the “weather forecast mode”, initializing the atmospheric profile every day by referring to JRA-55. The purpose of this approach was to prevent large deviations between the JRA-55 and NHM–SMAP atmospheric fields. Therefore, every day a 30 h long simulation was carried out, starting from 18:00 UTC of the previous day, and the model outputs of the last 24 h were employed after discarding output from the initial 6 h spinup period. This is the same procedure developed by Hashimoto et al. (2017) for producing daily weather forecasts for the GrIS.

2.3.3 SMAP calculation forced by results from JMA-NHM

We used SMAP, forced by the calculated surface meteorological data from the JMA-NHM, to simulate the temporal evolution of the top 30 m of snow, firn, and ice from September 2011 to August 2014. The thickness of snow/firn/ice is always set to constant (30 m) in the model during the calculation. In case snow accumulation or ablation is simulated, the thickness of the bottom model layer is modified accordingly. The initial top 30 m of snow/firn/ice physical conditions for the entire GrIS on 1 September 2011 were prepared by performing a 30-year spinup of the NHM–SMAP model. Before starting the model spinup, the initial profiles for snow/firn/ice physical conditions in the GrIS were given following the procedure presented by Lefebre et al. (2005), and properties for snow/firn microstructure (e.g., optically equivalent grain size and grain shape) were given from the firn core analysis at SIGMA-A (Yamaguchi et al., 2014) in the GrIS. From the initial condition, surface atmospheric conditions from September 2010 to August 2011 simulated by JMA-NHM forced by JRA-55 were used to drive SMAP for 30 times cyclically. We restricted the number of vertical model layers in the snow/firn/ice to 40 to limit computational costs. The vertical grid spacing increased from 1 cm at the surface to around 10 m at the bottom. We assumed zero heat flux at 30 m depth. For mass flux, runoff was calculated when meltwater or rain reached impermeable ice (density higher than 830 kg m⁻³) and saturated the layer above the impermeable ice. A slush layer was not allowed to form, and the runoff mass was removed from the GrIS instantaneously. When water reached 30 m depth and could not be retained, it was forced to run off immediately; however, this situation was quite rare during the study period.

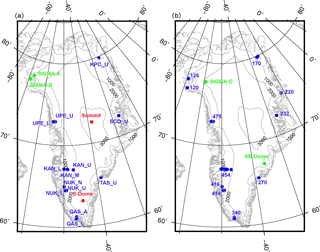
Figure 2 Locations of observation sites for (a) surface meteorology and (b) SMB. Green circles indicate SIGMA and Japanese sites, red circles denote GC-Net sites, and blue circles represent PROMICE sites. Contours on ice sheets and ice caps indicate surface elevation (contour interval 1000 m). All sites are listed in Tables 1 and 2. Site numbers in (b) identify specific glaciers and make up the first part of the PROMICE IDs listed in Table 2.

Although the PBSAM component of the model allowed us to explicitly consider the effects of snow impurities such as black carbon and dust, the relevant data were not available at high temporal resolution for the study period; therefore, we assumed a pure snow condition. Aoki et al. (2014b) examined published concentrations of black carbon in near-surface snow in the GrIS and noted that most were less than several parts per billion in weight (ppbw). Reducing the albedo of snow by 0.01 requires 40 ppbw of black carbon in new snow and 10 ppbw in old melting snow (Warren and Wiscombe, 1980). We concluded that the measured concentrations of black carbon in the GrIS would not reduce albedo in snow, except possibly in old melting snow. Therefore, the pure snow assumption is probably reasonable in the accumulation area of the GrIS. However, recent darkening of the GrIS (Shimada et al., 2016; Tedesco et al., 2016) has commanded attention. This effect is discussed in Sect. 4.4 and 4.7.

2.3.4 Interaction between the atmosphere and snow/firn/ice

In this study, we examined two configurations of the NHM–SMAP coupled model for the lower boundary condition of the atmosphere, using snow/firn/ice albedo and surface temperature from JRA-55 or from SMAP (Sect. 2.3.2). The online configuration (SMAP) allowed us to simulate the interaction between the atmosphere and the surface, whereas the offline configuration (JRA-55) treated only the one-way supply of energy and mass from the atmosphere. Bellaire et al. (2017) used the data obtained at GC-Net stations to demonstrate that the offline version yields sufficiently accurate input data for the detailed snow process model SNOWPACK (Lehning et al., 2002) to reproduce the measured near-surface snow density profiles at GC-Net stations.

2.3.5 Surface mass balance

Using NHM–SMAP, we calculated SMB, in meters of water equivalent (m w.e.), using the equation

$$\begin{array}{}\text{(6)}& \mathrm{SMB}=P-{\mathrm{SU}}_{\mathrm{s}}-{\mathrm{SU}}_{\mathrm{ds}}-\mathrm{RU},\end{array}$$

where P is precipitation, SU_s is sublimation or evaporation from the surface, SU_ds is sublimation from drifting snow particles, and RU is runoff. As mentioned in Sect. 2.2.3, we neglected drifting snow erosion to reduce computational costs.

3 Observational data

3.1 Surface meteorology and surface melt area extent

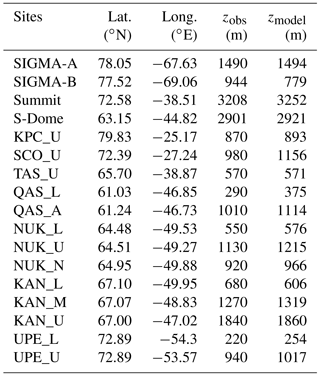
To validate NHM–SMAP, we employed hourly surface meteorological data obtained with the AWSs from the SIGMA (Aoki et al., 2014a; Niwano et al., 2015), GC-Net (Steffen and Box, 2001; Box and Rinke, 2003), and PROMICE (Ahlstrøm et al., 2008; van As et al., 2012) projects, as listed in Table 1 and shown in Fig. 2a. The properties we sought to validate were 2 m air temperature, 2 m water vapor pressure, surface pressure, 10 m wind speed, downward shortwave and longwave radiant fluxes, snow/firn/ice surface temperatures, surface albedo, and snow surface height change. Our selection of AWSs was based on the availability of high-quality data in adequate quantities during the study period and the elevation difference between the AWS site and the topographic model in NHM–SMAP (Sect. 2.3.1). To compare the in situ measurements and the NHM–SMAP results, we used modeled data for the grid cell nearest to each AWS. Differences in elevation were not corrected in NHM–SMAP, although elevation differences greater than 200 m were not allowed. From GC-Net stations, only 2 m air temperature, surface pressure, 10 m wind speed, and downward shortwave radiant flux were taken. From PROMICE stations, all the properties except for surface height change were acquired, and SIGMA stations provided all the properties. Because the sensor heights changed over time depending on accumulation and ablation, we calculated the 2 m air temperature, 2 m water vapor pressure, and 10 m wind speed from the measurements by using the flux profile calculation module of SMAP (Niwano et al., 2012). Erroneous values were rejected after visual inspection, and temporal gaps left by the rejected data were not filled by interpolation.

Table 1 Locations of observation sites for surface meteorology, including surface elevations measured on site (z_obs) and specified in NHM–SMAP (z_model).

For the extent of the surface melt area in the GrIS, we used the daily composite of satellite data developed by Mote (2007, 2014). This data set, which was created from measurements by the Special Sensor Microwave Imager/Sounder (SSMIS), offers a daily record of surface and near-surface melting on the GrIS with 25 km horizontal resolution. Hanna et al. (2014) utilized this data set to evaluate recent changes in the GrIS melt area.

3.2 Surface mass balance

The SMB of the GrIS calculated by NHM–SMAP for the study period was evaluated by using data provided by PROMICE (Machguth et al., 2016) as well as ice core data from the SIGMA-D (Matoba et al., 2015) and SE Dome (Iizuka et al., 2015) drilling sites (Table 2 and Fig. 2b). Most of the PROMICE stations are in the ablation area, whereas SIGMA-D and SE Dome are in the accumulation area. Recently, SMB data from PROMICE were used for the validations of MAR (Fettweis et al., 2017), and the 1 km horizontal resolution GrIS SMB product statistically downscaled from the daily output of RACMO2.3 (Noël et al., 2016) and ERA-Interim (Wilton et al., 2017). The validation sites were selected on the same basis as AWSs: data availability and an elevation difference less than 200 m between the site and the model. By employing the provided information for measurement periods at each site, the NHM–SMAP calculated SMB for each exact corresponding period were retrieved.

Table 2 Locations of observation sites for SMB, including the official ID for PROMICE sites and surface elevations measured on site (z_obs) and specified in NHM–SMAP (z_model).

4 Model validation results and discussion

In this section we present validation results of the 5 km resolution hourly NHM–SMAP output for the GrIS using in situ data obtained from September 2011 to August 2014. We include detailed information for mean error (ME; the average of the difference between simulated and observed values), root mean square error (RMSE), and the coefficient of determination (R²) to assess the model performance (see Table 3; and Tables S1–S8, in the Supplement). Section 4.1 to 4.5 refer to hourly data from measurements and model simulations unless otherwise specified. Dates and times are expressed in UTC.

4.1 2 m air temperature, 2 m water vapor pressure, and surface pressure

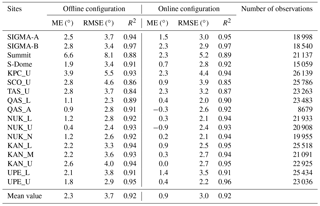
Table 3 lists the model performance for 2 m air temperature during the study period at each AWS depicted in Fig. 2a. Average ME and RMSE at all sites were improved for the online simulation by 1.4 ^∘C (p<0.01) and 0.7 ^∘C (p<0.1), respectively. Notable overestimates by the model (ME reached 6.6 ^∘C at Summit, for example) were corrected in the online configuration (ME was within 2.3 ^∘C at all sites). These results suggest that the surface analysis provided by JRA-55 is of inadequate quality in the GrIS and that SMAP improves the results through the use of more realistic snow/firn/ice physical conditions. This result in turn suggests that making every day an atmospheric spinup period (6 h; Sect. 2.3.2) longer than 6 h can improve the performance of NHM–SMAP. Finding an appropriate spinup period in the GrIS is a future issue to be dealt with. The following discussion focuses on results from the online simulation.

Figure 3a displays a year of observed and modeled 2 m air temperature at SIGMA-A, from 1 September 2013 to 31 August 2014. The observed seasonal cycle was well reproduced by NHM–SMAP (R²=0.95; Table 3); however, overestimation of the model was especially evident during winter (November to March), when measured 2 m air temperature sometimes reached below −30 ^∘C; this characteristic was found at all sites. The scatter plot of measurements versus model simulations for the whole study period at SIGMA-A (Fig. 3b) also displays this tendency. A possible reason for this discrepancy is that JRA-55 overestimates the surface temperature. The JMA Climate Prediction Division (CPD), which operationally develops JRA-55 data, recognizes that JRA-55 tends to overestimate winter surface air temperature in the polar region owing to inadequate treatment of energy exchanges between the atmosphere and the snow/firn/ice surface, especially under very stable atmospheric conditions: a failure that also affects the reproducibility of the surface inversion layer and results in underestimation of the lower tropospheric temperature (Shinya Kobayashi, personal communication, 2017). Further investigation of this issue would require conducting further NHM–SMAP simulations forced by other reanalysis data sets like ERA-Interim, as done by Fettweis et al. (2017), which was beyond the scope of this study. At the same time, extending the atmospheric spinup period discussed above can also resolve the issue, because simulation results are expected to be less susceptible to a parent reanalysis data.

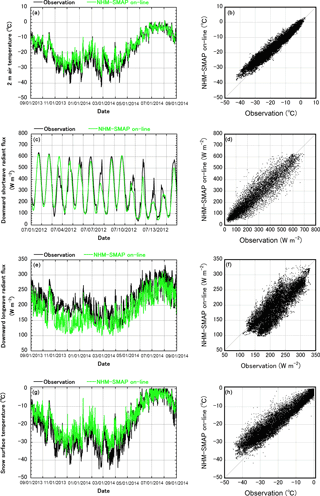
Figure 3 Model validation of hourly (a, b) 2 m air temperature, (c, d) downward shortwave radiant flux, (e, f) downward longwave radiant flux, and (g, h) snow surface temperature at SIGMA-A. Target periods for the time series on the left are (a, e, g) 1 September 2013 to 31 August 2014 and (c) 1–14 July 2012. Data for the scatter plots on the right are from the whole study period, 1 September 2011 to 31 August 2014.

Table 3 Model performance in simulating hourly 2 m air temperature at each AWS on the GrIS (locations in Fig. 1). ME is mean error (average of the difference between simulated and observed values), RMSE is root mean square error, and R² is coefficient of determination.

Tables S1 and S2 indicate statistics for the model performance in terms of 2 m water vapor pressure and surface pressure. To summarize, R² for both parameters was acceptably high (more than 0.84), and ME and RMSE were reasonable. Relatively large biases and RMSE as well as relatively low R² were found for 2 m water vapor pressure at sites TAS_U, QAS_L, and QAS_U. This result suggests that NHM–SMAP forced by JRA-55 cannot adequately reproduce absolute water content in the southeastern GrIS. According to Hanna et al. (2006), the southeastern GrIS is characterized by high accumulation rates attributed to prevailing easterly winds, frequent cyclogenesis in and around Fram Strait, and relatively high moisture availability when source air originates over a warm ocean. Stations TAS_U, QAS_L, and QAS_U are very close to the margin of our model domain (Fig. 1). Therefore, the use of a larger model domain that includes all of Svalbard may improve model results by resolving frequent cyclone activity in and around Fram Strait. Surface pressure was well simulated by NHM–SMAP, because R² was very close to 1.0 except for Summit. Even at Summit, ME and RMSE were still reasonable when they were compared with those obtained at other sites (Table S2). The reason why R² at Summit was relatively low should be investigated in the future. The slightly larger ME and RMSE for surface pressure found at SIGMA-B, SCO_U, QAS_L, QAS_A, and NUK_U can be attributed to relatively large elevation differences between the actual topography and the topographic model (−165, 176, 85, 104, and 85 m, respectively), as indicated in Table S2.

4.2 10 m wind speed

Orr et al. (2005) and Moore et al. (2016) pointed out that topographic flow distortion commonly induces high-speed low-level winds in the southern GrIS including tip jets, barrier winds, and katabatic flows. They also noted that an atmospheric model of Greenland would need a horizontal resolution of about 15 km to characterize the impact of topography on the regional wind field and climate; however, even at this resolution, features of the wind field would be under-resolved. Therefore, we investigated the reproducibility of a strong wind event observed at the TAS_U site (Fig. 2a) during the study period, when a maximum 10 m wind speed of 46.9 m s⁻¹ was recorded at 17:00 UTC on 27 April 2013. A comparison of measured and simulated data (Fig. 4a) shows that the 5 km resolution NHM–SMAP successfully reproduced the strong wind event but underestimated its maximum wind speed by about 5 m s⁻¹. In the figure, 10 m wind speed from the parent JRA-55 reanalysis with a horizontal resolution of TL319 (∼ 55 km) is depicted. Clearly, JRA-55 could not reproduce the strong wind event and the advantage of a high-resolution nonhydrostatic atmospheric model is successfully demonstrated. A comparison of measured and modeled 10 m wind speeds at TAS_U during the whole study period indicates that the model tended to underestimate high wind speeds (> 30 m s⁻¹) but overestimated relatively low wind speeds, resulting in ME, RMSE, and R² of 2.5 m s⁻¹, 4.3 m s⁻¹, and 0.68, respectively (Fig. 4b). At other sites, absolute values for ME and RMSE were smaller than those at TAS_U, and R² ranged widely between 0.13 (SCO_U) and 0.78 (KAN_U) (Table S3).

These results confirm that it is difficult for atmospheric models to reproduce surface wind fields in the southern GrIS. This problem may be solved by updating the boundary layer scheme (Sect. 2.1) and increasing the horizontal resolution. In addition, a simple treatment of the surface roughness length for momentum (Niwano et al., 2015) may also affect surface wind speed estimates, as suggested by Amory et al. (2015). NHM–SMAP can provide synoptic weather data during strong wind events. Figure 4c, depicting the estimated surface wind speed field at 17:00 UTC on 27 April 2013, shows that strong wind speeds were simulated near the southeastern margin of the GrIS. This surface strong wind event corresponds to the Køge Bugt Fjord katabatic flow reported by Moore et al. (2016).

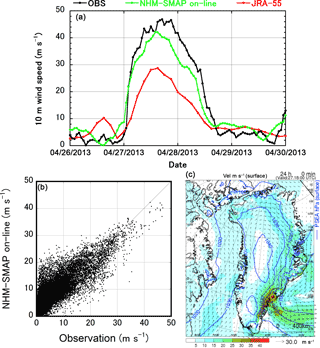
Figure 4 Model evaluation of hourly 10 m wind speed at TAS_U. (a) Time series of observed and simulated 10 m wind speed at TAS_U from 26 to 29 April 2013. Three-hourly interval 10 m wind speed from JRA-55 is depicted. (b) Scatter plot of observed and simulated 10 m wind speed at TAS_U during the study period. (c) Surface synoptic weather map for the model region at 17:00 UTC on 27 April 2013 simulated by NHM–SMAP, showing surface wind speed (color), surface wind vector (arrows), and sea level pressure (contours, at 10 hPa intervals). Yellow circle indicates the position of TAS_U.

4.3 Downward shortwave and longwave radiant fluxes

The downward shortwave and longwave radiant fluxes are important elements of the GrIS surface energy balance. During 30 June to 14 July 2012, Niwano et al. (2015) visited SIGMA-A (Fig. 2a) and witnessed the record surface melt event (Nghiem et al., 2012; Tedesco et al., 2013; Hanna et al., 2014). They reported mainly clear-sky conditions until 9 July and cloudy conditions with occasional heavy rainfall after 10 July. NHM–SMAP successfully reproduced the observed temporal evolution and diurnal variation of downward shortwave radiant flux at SIGMA-A from 1 to 15 July; however, it tended to underestimate slightly when clouds appeared (Fig. 3c). This tendency was typical during the whole study period, as shown by Fig. 3d and the ME value of −13.5 W m⁻² listed in Table S4, although the signs of ME differ from place to place. RMSE ranged from 56.0 W m⁻² (KPC_U) to 127.3 W m⁻² (KAN_L) and was close to values reported by Ohtake et al. (2013) when the operational version of JMA-NHM was validated using hourly data from Japan, and relatively accurate RMSEs were obtained in the northern GrIS (Table S4). The underestimation in cloudy conditions may arise from effects in the cloud radiation scheme or in the reproducibility of cloud amounts and types by the model.

Although the tendencies of ME for downward shortwave radiant flux vary from place to place, ME for the downward longwave radiant flux had a similar tendency across the GrIS, ranging from −25.1 W m⁻² at SIGMA-A to −10.8 W m⁻² at KAN_M (Table S5). Underestimates of downward longwave radiant fluxes at SIGMA-A were especially large during winter (November to January when observed values reached less than about 200 W m⁻²) in the record from 1 September 2013 to 31 August 2014 (Fig. 3e) and over the whole study period (Fig. 3f). This characteristic was also found at other sites. One possible reason for this discrepancy is that the parent JRA-55 underestimates lower tropospheric temperatures, especially during winter (see Sect. 4.1). In addition, uncertainty in the winter cloud amount, low-level liquid clouds (Bennartz et al., 2013), and thin clouds (Cox et al., 2014) may affect the results. Improving the model would require detailed in situ measurements of cloud amount, cloud type, and atmospheric profiles as well as intercomparisons with satellite remote sensing data like that of Van Tricht et al. (2016). A model intercomparison like that done by Inoue et al. (2006) would also aid a deeper understanding of the limitations of current polar RCMs. On the other hand, observation data for downward longwave radiant flux can also have errors, especially during the winter period due to riming, which may act to increase measured values. In SIGMA-A, measured 2 m air temperature often decreased to about −40 ^∘C during the 2013–2014 winter (Fig. 3a). Although such reductions in 2 m air temperature during March and April 2014 were followed by significant reductions in downward longwave radiant flux (Fig. 3e), they did not synchronize in December 2013 and January 2014. These results suggest that observed downward longwave radiant flux, especially during December 2013 and January 2014, were affected by riming and forced to increase. A reliable quality control technique for automatic downward longwave radiant flux measurements in the polar region should be developed in the future to perform not only model validation accurately but also climate monitoring.

4.4 Snow/firn/ice surface temperature and albedo

We assessed the surface energy balance of the GrIS simulated by NHM–SMAP in terms of surface temperature and albedo. Measured and simulated snow surface temperature at SIGMA-A from 1 September 2013 to 31 August 2014 agreed well, especially from May to October; however, overestimates were obvious at temperatures below about −20 ^∘C (Fig. 3g), much like the pattern for 2 m temperature (Sect. 4.1). As listed in Table S6, the model overestimated surface temperature at all sites except NUK_U, where 2 m temperature was also underestimated (Table 3). Therefore, the temporal evolution of simulated surface and 2 m temperatures followed the same pattern. Both ME and RMSE for surface temperature were slightly larger than those for 2 m temperature (Table 3); however, they are reasonable because they were almost the same as those obtained in Japan (Niwano et al., 2014). It is difficult to ascertain which physical process affected the model tendency because that would require us to investigate the complicated atmosphere–snow/firn/ice coupled system simulated by NHM–SMAP. One possible cause of the model's overestimation of surface temperature is overestimation of the surface wind speeds when they are relatively low (see Sect. 4.2), which acts to heat the surface through increases in sensible heat flux. Of course, overestimation of 2 m temperature by the model (see Sect. 4.1) especially during winter (November to March) may also contribute to the error. For a deeper insight, each physical scheme related to this problem should be investigated by standalone tests utilizing detailed in situ measurements.

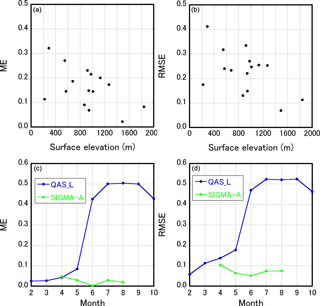
Figure 5 Evaluation of the hourly snow/firn/ice albedo simulated at each AWS (Fig. 1 and Table S7). (a) Mean error (ME) and (b) root mean square error (RMSE) as a function of surface elevation. (c) Monthly changes in ME and (d) monthly changes in RMSE for simulated snow/firn/ice albedo at QAS_L (blue line) and SIGMA-A (green line) during months in which the sun appears at each site.

NHM–SMAP could not adequately reproduce surface albedo. The model tended to overestimate surface albedo, especially in the ablation area (Fig. 5a). Similarly, the RMSE increased at lower surface elevations (Fig. 5b). The model performance was best at SIGMA-A, in the accumulation area, and worst at QAS_L in the ablation area, the most southerly station in this study (Table S7). ME and RMSE at these two stations during months of the study period when the sun appeared (Fig. 5c and d) show that model performance was uniformly good at SIGMA-A, covered with snow throughout the year, but both ME and RMSE suddenly increased after June at QAS_L. These results imply that our version of NHM–SMAP has difficulty simulating high-density firn and ice. Alexander et al. (2014) and Fettweis et al. (2017) reported that this is also the case for the MAR model. Tedesco et al. (2016) argued that the discrepancy between measured firn/ice albedo trends and trends modeled by MAR can be explained by the absence in MAR of processes associated with light-absorbing impurities. The dark microbe-rich sediment called cryoconite significantly reduces the surface albedo in the ablation area (Takeuchi et al., 2014; Shimada et al., 2016). Therefore, future models should consider this process as well as the possibility that NHM–SMAP overestimates snowfall during the summer period. In any case, it is necessary to conduct in situ measurements in the ablation area to confirm what is happening in reality.

Figure 6 Time series of observed and simulated hourly snow surface height with respect to 1 September. (a) SIGMA-A, 2012–2013; (b) SIGMA-A, 2013–2014; (c) SIGMA-B, 2012–2013; (d) SIGMA-B, 2013–2014.

4.5 Snow surface height

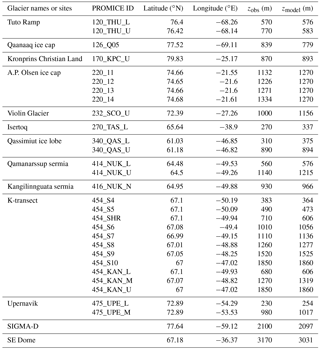
If a polar RCM can calculate changes in surface height realistically, it can be used to partition volume changes supported by satellite altimetry observations into mass changes related to SMB and ice dynamics (Kuipers Munneke et al., 2015). Therefore, we compared the modeled changes in hourly snow surface height with in situ measurements obtained at SIGMA-A and SIGMA-B. Because the SIGMA AWSs started operation in the summer of 2012 (Aoki et al., 2014a), comparisons were performed for the 2012–2013 and 2013–2014 mass balance years (September to August). On the whole, the model captured the trend of measured changes, but underestimations were apparent for both sites and years (Fig. 6). At SIGMA-A, ME, and RMSE were −0.19 and 0.21 m for 2012–2013 and −0.13 and 0.17 m for 2013–2014. At SIGMA-B, ME and RMSE were −0.24 and 0.26 m for 2012–2013 and −0.04 and 0.12 m for 2013–2014. These scores are still acceptable in comparison to the SMAP validation results for seasonal snowpack in Japan (Niwano et al., 2014). As discussed in Sect. 4.7, SMB at the SIGMA-D site, located near SIGMA-A and SIGMA-B, is well reproduced by the model. Therefore, the underestimation can be attributed mainly to overestimation of simulated snow density, as mentioned in Sect. 4.4. Schemes for new snow density and the viscosity coefficient of snow in the polar region may need to be upgraded by performing detailed laboratory experiments.

4.6 Melt area extent

The area of surface melt in the GrIS was extensive in the summer of 2012, setting a new record on 12 July 2012 (Nghiem et al., 2012; Tedesco et al., 2013; Hanna et al., 2014). At present, the melt area extent in the GrIS is commonly diagnosed from satellite data (Mote, 2007, 2014; Nghiem et al., 2012; Hall et al., 2013). A polar RCM that can simulate the melt area extent realistically would enable us to investigate atmospheric and snow/firn/ice physical factors controlling the melt area extent within the same RCM framework, as was done by Fettweis et al. (2011). We compared the simulated daily melt area extent with the data of Mote (2007, 2014) during 2012 and 2013.

The daily melt area extent simulated by NHM–SMAP was diagnosed from hourly snow/firn/ice surface temperature data and water content profiles. First, the daily maximum surface temperature was extracted at each grid point. If the value reached 0 ^∘C and the top model layer contained water at the time when the maximum surface temperature was recorded, we considered the grid point to have experienced surface melt. Figure 7 shows that the simulated results matched the data well (R² was 0.97 and 0.94 for 2012 and 2013, respectively), and NHM–SMAP successfully reproduced the record melt event around 12 July 2012, at which time the simulated melt area extent reached 92.4 %. The following year was relatively cold, as suggested by the maximum observed melt area extent of 44 %, and the model successfully replicated the satellite-derived results. It appears that NHM–SMAP can reliably and consistently simulate surface melt extent in the GrIS. Figure S1, which shows observed and simulated total numbers of surface melt days in 2012, supports this argument.

4.7 Surface mass balance

We evaluated the simulated SMB for the GrIS by using the PROMICE stake measurements and the ice core data obtained at SIGMA-D and SE Dome (Table 2 and Fig. 2b). During the study period, 55 measurements were available, and comparison results are presented in Fig. 8. In addition, simulated SMB data from MAR v3.5.2 forced by JRA-55 (Fettweis et al., 2017) were employed as reference information. The geographic patterns of accumulation and ablation simulated for the 2011–2012, 2012–2013, and 2013–2014 mass balance years by NHM–SMAP are depicted in Fig. S2.

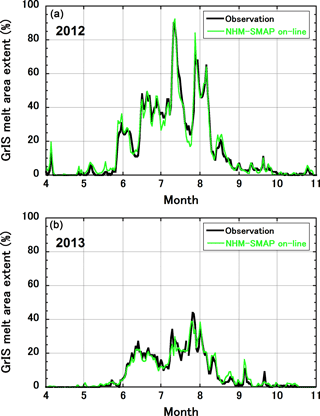
Figure 7 Time series of observed and simulated daily GrIS melt area extent for (a) 2012 and (b) 2013. Observation data are from Mote (2014).

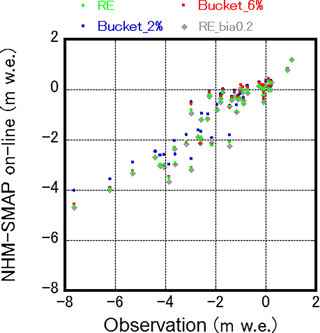
Figure 8 Scatter plot of observed and simulated SMBs during the study period. Observation data are from stake measurements compiled by PROMICE and ice core measurements from SIGMA-D and SE Dome. RE indicates the default setting for vertical water movement in snow and firn based on the Richards equation; Bucket_6 % and Bucket_2 % are alternative settings based on simple bucket schemes with irreducible water contents of 6 and 2 % of the pore volume; RE_bia0.2 is another alternative setting, where bare ice albedo is set to 0.2, while the other configuration is the same as RE.

The default version of NHM–SMAP employs the Richards equation to calculate vertical water movement in snow and firn. However, most polar RCMs employ a simpler scheme in which the maximum amount of water retained against gravity (irreducible water content) controls the vertical water movement (Reijmer et al., 2012). The irreducible water content is typically set at 2 % or 6 % of the pore volume, depending on the chosen modeling strategy. The lower of these values can induce more rapid transport of water towards lower layers, mimicking the piping process. To examine the adequacy of the Richards equation for GrIS SMB estimates, we performed sensitivity tests in which the Richards equation scheme was replaced by bucket schemes with irreducible water contents of 2 and 6 %. The tests employed only the standalone SMAP simulations forced by the atmospheric field calculated by the online version of NHM–SMAP, which implies that interaction between the atmosphere and the snow/firn/ice was not considered. In the sensitivity tests, profiles for snow/firn/ice physical conditions were reset at the beginning of the 2011–2012, 2012–2013, and 2013–2014 mass balance years by referring to the simulation data from the online version of NHM–SMAP. It means that feedbacks, which have a timescale of more than a year, are not considered. In the accumulation area where the observed SMB was positive, the simulated SMB agreed well with measurements during the study period regardless of the choice of vertical water movement scheme; however, the model did not capture large mass losses in which observed SMB reached values lower than −4 m water equivalent (m w.e.). The model tended to overestimate SMB in the lower part of the ablation area. In the default simulation, ME, RMSE, and R² were 0.75 m w.e., 1.07 m w.e., and 0.86, respectively. With the bucket scheme, these scores worsened slightly, to 0.82 m w.e., 1.12 m w.e., and 0.85 for the case of 6 % irreducible water content and to 0.95 m w.e., 1.26 m w.e., and 0.85 for the case of 2 % irreducible water content. The Richards equation generally allows more water retention than the bucket scheme (Yamaguchi et al., 2012), which may result in higher near-surface density. In turn, more impermeable ice can form near the surface and induce runoff from the near-surface layer. On the other hand, lower irreducible water content forces rapid transport of water towards lower layers as expected, which acts to prevent the formation of ice layers and thus surface mass loss. To confirm the discussion, the GrIS-area-integrated daily melt and refreeze rates were investigated (Fig. 9). In the figure, results for the 2011–2012 mass balance year are shown, whereas results for other mass balance years are depicted in Fig. S3. During the 2011–2012 mass balance year, simulated daily melt rates were almost the same among the results from Richards equation scheme and two bucket schemes (Fig. 9a); however, refreeze rates from the control Richards equation scheme were much lower compared to other results (Fig. 9b), which is evidence for the abovementioned more impermeable ice in the results from Richards equation scheme. The same characteristics could be found in other mass balance years (Fig. S3).

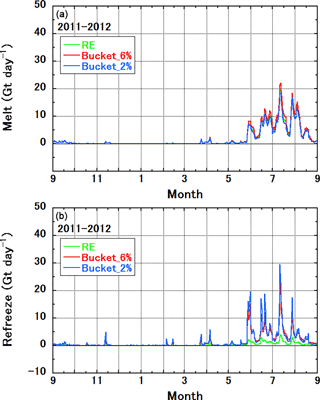
Figure 9 Sensitivity to the choice of vertical water movement scheme of the simulated top 30 m integrated (a) melt and (b) refreeze rates for the GrIS during the 2011–2012 mass balance year. RE indicates the default setting for vertical water movement in snow and firn based on the Richards equation; Bucket_6 % and Bucket_2 % are alternative settings based on simple bucket schemes with irreducible water contents of 6 and 2 % of the pore volume.

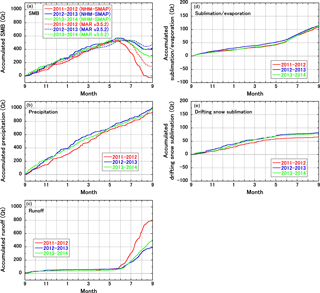
Figure 10 Seasonal evolution of accumulated (a) SMB, (b) precipitation, (c) runoff, (d) sublimation and evaporation from the surface, and (e) drifting snow sublimation over the GrIS with respect to 1 September during the periods 2011–2012 (red), 2012–2013 (blue), and 2013–2014 (green). Note that the vertical scale differs between the left and right columns. All results are from the default setting for vertical water movement in snow and firn based on the Richards equation. Only for SMB, data from MAR v3.5.2 forced by JRA-55 are displayed.

Although the Richards equation scheme contributed to improved SMB estimates by NHM–SMAP, the model still produced significant overestimates, especially in the ablation area. Deviations between the measurements and the default model simulation results became larger where the measured SMB was smaller. As presented in Sect. 4.1, the online version of NHM–SMAP successfully reproduced 2 m air temperature at SIGMA-A during summer. Because surface mass loss during the summer is affected by near-surface (2 m) temperature, model performance in terms of simulating JJA 2 m air temperature at each AWS on the GrIS were re-examined (Table S8). As indicated in the table, significant or systematic errors were not found, and obtained ME and RMSE were around −0.2 and 2.1 ^∘C, respectively. Therefore, a possible cause is overestimation of surface albedo by NHM–SMAP, especially in the ablation area (Sect. 4.4). According to the PROMICE data in the ablation area, ice albedo often decreases to around 0.2 during summer. Therefore, additional model sensitivity tests, in which ice albedo is set to 0.2, were performed. Obtained results indicate that simulated SMB did not change significantly compared to the control Richards equation setting (Fig. 8), suggesting that overestimation of surface albedo by NHM–SMAP can be attributed mainly to overestimates of snowfall as pointed out in Sect. 4.4. In addition, it is possible that even at 5 km resolution, NHM–SMAP cannot resolve the complex topography in the ablation area. Recently, Noël et al. (2016) demonstrated that statistical downscaling of individual SMB components from 11 km resolution RACMO2.3 to a 1 km ice mask and topography (Howat et al., 2014) can improve SMB estimates owing to the correction of modeled surface elevations. Moreover, Wilton et al. (2017) showed generally favorable results from a 1 km statistical downscaling of reanalysis data, with results generally comparing well with MAR and RACMO RCM output. On the other hand, MAR v3.5.2 with a horizontal resolution of 20 km is generally able to resolve the ablation zone well (Fettweis et al., 2017). A possible cause of this success can be attributed to the introduction of a subgrid mask, which is not employed by NHM–SMAP. It appears that statistical downscaling or further dynamical downscaling or introduction of the subgrid mask is inevitable that more realistic SMB estimates are obtained.

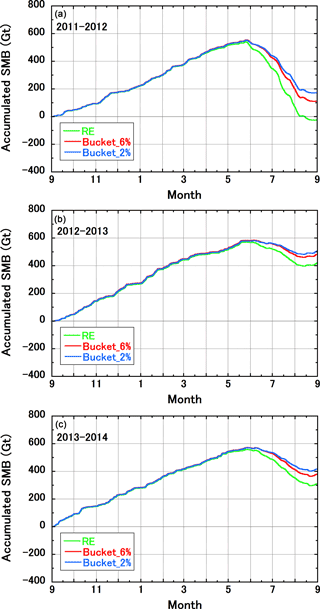
Figure 11 Sensitivity to the choice of vertical water movement scheme of the simulated SMB for the GrIS during the (a) 2011–2012, (b) 2012–2013, and (c) 2013–2014 mass balance years. RE indicates the default setting for vertical water movement in snow and firn based on the Richards equation; Bucket_6 % and Bucket_2 % are alternative settings based on simple bucket schemes with irreducible water contents of 6 and 2 % of the pore volume.

Using the SMB estimates from NHM–SMAP, we calculated the temporal evolution of accumulated SMB over the entire GrIS during the 2011–2012, 2012–2013, and 2013–2014 mass balance years. We set the area of the GrIS and peripheral glaciers at 1.807×10⁶ km², as explained in Sect. 2.3.1. The 2011–2012 and 2012–2013 mass balance years present a strong contrast as warm and cold years, respectively. According to simulation results by MAR v3.5.2 forced by JRA-55 (Fettweis et al., 2017), which uses the bucket schemes with an irreducible water content of 8 %, the GrIS SMB during the 2011–2012 mass balance year was relatively low (147 Gt year⁻¹), then increased greatly in 2012–2013 (473 Gt year⁻¹) and decreased slightly in 2013–2014 (403 Gt year⁻¹). Our model, which tends to simulate lower SMB compared to MAR v3.5.2, produced a similar sequence in those years, with accumulated SMBs at the end of each mass balance year of −23, 420, and 312 Gt year⁻¹ (Fig. 10a). In each of these years, the differences in these estimates emerged after the beginning of June.

Figure 10b–e show the accumulated totals of each SMB component in Eq. (6) for the same three mass balance years. They make it clear that the differences in the yearly estimates can be attributed almost entirely to the differences in runoff amounts (Fig. 10c), the differences in P, SU_s, and SU_ds being relatively small. As mentioned, NHM–SMAP overestimated SMB especially in the ablation area, which implies that the runoff amount is still underestimated. Future studies should upgrade the model physics in the ways mentioned above, then clarify how much the current version overestimates SMB across the entire GrIS. At the same time, it is imperative to validate the simulations of each SMB component in Eq. (6). In a comparison of SMB components from four reanalysis data sets and the MAR model, Cullather et al. (2016) found that large variations exist for all of the SMB components.

In light of the importance of the runoff amounts for our SMB estimates, we again investigated the sensitivity of our SMB simulations to the three different vertical water movement schemes. The results clearly showed that the vertical water movement scheme made a notable difference to our GrIS-wide SMB estimates: for the relatively warm 2011–2012 mass balance year, the accumulated SMBs were −23, 113, and 174 Gt year⁻¹ for the default setting and the bucket schemes with irreducible water contents of 6 and 2 %, respectively (Fig. 11a). Even in the other two relatively cold years, the SMB estimates deviated by as much as 100 Gt year⁻¹ (Fig. 11b and c). Clearly, the percolation and retention of water in snow and firn plays an important role in estimates of the present-day SMB for the GrIS.

5 Summary and conclusions

We developed the NHM–SMAP polar RCM, with 5 km resolution and hourly output, to reduce uncertainties in SMB estimates for the GrIS. Combining JMA's operational nonhydrostatic atmospheric model JMA-NHM and the multilayered physical snowpack model SMAP is an attempt to take advantage of both short-term detailed weather forecast models and long-term computationally stable climate models. The model, forced by the latest Japanese reanalysis data JRA-55, was evaluated in the GrIS during the 2011–2014 mass balance years using in situ data from the SIGMA, GC-Net, and PROMICE AWS networks, PROMICE SMB data, and ice core data from SIGMA-D and SE Dome.

We first tested two options for the lower boundary conditions of the atmosphere. The offline configuration used values for snow/firn/ice albedo and surface temperature from JRA-55, and the online configuration used values from SMAP calculations. The online version improved the model performance for 2 m air temperature, suggesting that the surface analysis provided by JRA-55 is of inadequate quality, at least for the GrIS, and that SMAP simulates more realistic snow/firn/ice physical conditions. Therefore, we continued our investigation using only the online version of NHM–SMAP.

Although the online version of NHM–SMAP reproduced a realistic history of 2 m air temperature, it produced slight overestimates, especially during winter. A possible cause is overestimation by JRA-55 of surface temperatures in the parent data. JRA-55 overestimates surface air temperature in the polar region and underestimates lower tropospheric air temperature, apparently from deficient treatment of energy exchanges between the atmosphere and the snow/firn/ice surface, especially under very stable atmospheric conditions. A confirmation of this reasoning would require NHM–SMAP simulations forced by other reanalysis data sets. At the same time, extending the atmospheric spinup period (6 h) can also resolve the issue, because simulation results are expected to be less susceptible to a parent reanalysis data. Regarding 2 m water vapor pressure, NHM–SMAP did not adequately reproduce absolute water content in the southeastern GrIS, and expanding the model domain to include all of Svalbard, where frequent cyclogenesis accompanies prevailing easterly winds, might improve this result. Surface pressure was realistically simulated. As for 10 m wind speeds, NHM–SMAP successfully reproduced a Køge Bugt Fjord katabatic flow event observed at station TAS_U on 27 April 2013. Downward shortwave and longwave radiant fluxes, which are important contributors for the GrIS surface energy balance, were also reproduced adequately. Although our RMSEs for downward shortwave radiant flux were almost the same as those reported for Japan with the operational version of JMA-NHM, NHM–SMAP produced greater underestimates when clouds were present. Possible causes of the error include the cloud radiation scheme and the reproducibility of cloud amount and cloud type. For downward longwave radiant flux, the model produced underestimates, especially during winter (November to January). A possible reason is underestimation of lower tropospheric temperature (especially during winter) by JRA-55, and results may also be affected by inadequate reproducibility of the winter cloud amount, low-level liquid clouds, and thin clouds. On the other hand, observation data for downward longwave radiant flux can also have errors, especially during the winter period due to riming, which might affect the evaluation. Detailed in situ measurements for cloud amount, type, and atmospheric profiles would be required to improve model performance for downward radiant fluxes.

We assessed the simulated surface energy balance in the GrIS in terms of surface temperature and albedo. The model generally overestimated surface temperatures of snow/firn/ice, although our ME and RMSE values were close to those obtained in Japan. A possible cause of this overestimate is overestimation of the surface wind speeds when they are relatively low, which acts to heat the surface through increases in sensible heat flux. In addition, overestimation of 2 m temperature by the model especially during winter (November to March) also may contribute to the error. The model overestimated the snow/firn/ice albedo, particularly in the ablation area, where both ME and RMSE suddenly increased after June. It was attributed to an overestimation of snowfall. Because surface temperature and albedo were reasonably well reproduced in the accumulation area, the model successfully simulated the GrIS melt area extent, including the record surface melt event during the warm summer of 2012 and the relatively cold year 2013.

In our assessment of the model's simulation of SMB, the ME, RMSE, and R² values during the study period were fairly good (0.75 m w.e., 1.07 m w.e., and 0.86, respectively). We performed additional sensitivity tests in which the Richards equation scheme that calculates vertical water movement in snow and firn was replaced by simple bucket schemes with irreducible water contents of 2 and 6 %, demonstrating that the realistic Richards equation scheme contributed to the improvement in SMB estimates. However, the model still produced significant overestimates, especially in the ablation area. Improving this would require developing a realistic albedo model for high-density firn and ice. Resolving overestimation of snowfall by the model is also necessary. Moreover, statistical downscaling or further dynamical downscaling to a higher spatial resolution than used here, e.g., 1 km (Noël et al., 2016; Wilton et al., 2017) or the introduction of the subgrid mask (Fettweis et al., 2017) may inevitably be required to improve the SMB estimates. The estimates of accumulated SMB for the entire GrIS were also affected by the choice of vertical water movement scheme, which resulted in differences as great as 200 Gt year⁻¹ in our estimates. The process chosen to simulate water percolation and retention in snow and firn thus plays an important role in estimating SMB for the present-day GrIS.