the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Seasonal monitoring of melt and accumulation within the deep percolation zone of the Greenland Ice Sheet and comparison with simulations of regional climate modeling
Olaf Eisen
Michael MacFerrin
Marco Tedesco
Xavier Fettweis
Increasing melt over the Greenland Ice Sheet (GrIS) recorded over the past several years has resulted in significant changes of the percolation regime of the ice sheet. It remains unclear whether Greenland's percolation zone will act as a meltwater buffer in the near future through gradually filling all pore space or if near-surface refreezing causes the formation of impermeable layers, which provoke lateral runoff. Homogeneous ice layers within perennial firn, as well as near-surface ice layers of several meter thickness have been observed in firn cores. Because firn coring is a destructive method, deriving stratigraphic changes in firn and allocation of summer melt events is challenging. To overcome this deficit and provide continuous data for model evaluations on snow and firn density, temporal changes in liquid water content and depths of water infiltration, we installed an upward-looking radar system (upGPR) 3.4 m below the snow surface in May 2016 close to Camp Raven (66.4779∘ N, 46.2856∘ W) at 2120 m a.s.l. The radar is capable of quasi-continuously monitoring changes in snow and firn stratigraphy, which occur above the antennas. For summer 2016, we observed four major melt events, which routed liquid water into various depths beneath the surface. The last event in mid-August resulted in the deepest percolation down to about 2.3 m beneath the surface. Comparisons with simulations from the regional climate model MAR are in very good agreement in terms of seasonal changes in accumulation and timing of onset of melt. However, neither bulk density of near-surface layers nor the amounts of liquid water and percolation depths predicted by MAR correspond with upGPR data. Radar data and records of a nearby thermistor string, in contrast, matched very well for both timing and depth of temperature changes and observed water percolations. All four melt events transferred a cumulative mass of 56 kg m−2 into firn beneath the summer surface of 2015. We find that continuous observations of liquid water content, percolation depths and rates for the seasonal mass fluxes are sufficiently accurate to provide valuable information for validation of model approaches and help to develop a better understanding of liquid water retention and percolation in perennial firn.
- Article
(7884 KB) - Full-text XML
- BibTeX
- EndNote
The Greenland Ice Sheet (GrIS) has been affected by changes in environmental conditions over recent decades, which resulted in persistent negative mass balances all over the ice sheet (Sasgen et al., 2012). Mass loss of the ice sheet, determined by methods relying on satellite data, has increased by a factor of four within the last two decades, from 51 ± 65 Gt per year (1992–2001) to 211 ± 37 Gt per year in 2002–2011 (Hanna et al., 2013; Shepherd et al., 2012). Negative trends in annual surface mass balances (SMBs) over the same time period are attributed to an increase in surface melt and runoff (Vaughan et al., 2013). van den Broeke et al. (2016) attributed 61 % of the recent mass loss to a decrease in SMB and only 39 % to an increase in solid ice discharge. Since melt conditions are expected to continue to increase (Huybrechts et al., 2011; Vizcaíno et al., 2010) and being amplified especially in northern latitudes (Meehl et al., 2012), the determination of melt and refreezing, and mass redistribution through liquid water are of utmost importance for density and firn temperature estimations in accumulation areas of polar regions (Gascon et al., 2014). Moreover, increased surface melt influences entire glacier systems including glacier velocities and basal motion (Meierbachtol et al., 2013). Single snow and firn parameters such as density and temperature have a major effect on the storage capacity of melt water with the consequence that understanding and monitoring of these parameters is necessary for correct predictions of SMB and, thus, on sea-level rise through melt of polar ice sheets (Gardner et al., 2013; Hanna et al., 2008). Liquid water infiltration into snow and firn and retention therein are major components of uncertainties in current SMB measurements and projections (Vernon et al., 2013) because observations are lacking (Harper et al., 2012).
For percolation regimes, it remains unclear whether meltwater is stored and refreezes within the firnpack and gradually fills up all pore space or whether near-surface refreezing causes the formation of massive ice lenses (Machguth et al., 2016). Such thick ice lenses block water infiltration and thus force lateral runoff. Both homogeneous ice layers within perennial firn (Harper et al., 2012), as well as near-surface ice layers of several meter thickness have been observed in firn cores (Machguth et al., 2016). However, the formation process of neither of them in real time has been monitored before. Machguth et al. (2016) state that it is essential to understand feedback mechanisms in firn to predict future GrIS mass balances. Taking firn cores is a destructive sampling technique and thus hampers monitoring and derivation of quantification of changes in parameters. It remains nondistinctive whether differences in between annual cores are attributed to spatial variability or temporal evolution.
Recently, near-surface firn layers (upper tens of meters) have been exposed to enhanced effects from mass loss, firn compaction and refreezing. Although records for the maximum extent in area of surficial melt on the GrIS were broken in 2005 (Hanna et al., 2008), 2007 (Tedesco et al., 2008), 2010 (Tedesco et al., 2011) and 2012 (Tedesco et al., 2013), for none of these record years are direct determinations in firn of percolation depths and quantification of the amount of melt available. Information on melt usually just exist for the area extent of surficial melt over the GrIS (Abdalati and Steffen, 2001) from remote sensing data.
Coverage of in situ observations in space and time is insufficient to produce detailed maps for seasonal mass balance (van den Broeke et al., 2017). Hence, regional climate models are used to reproduce the contemporary and previous SMB (Fettweis et al., 2017; Noël et al., 2017) and to predict future mass changes. Apart from several existing automatic weather stations (AWSs) being unevenly distributed over the GrIS, no temporal continuous observations exist to validate the results of such models. However, AWS provide only limited information about changes in snowpack and firnpack parameters. No direct data for percolation, snow, firn density and mass transfers are available from atmospheric data. Data on refreezing within snow and firn can only be derived indirectly from temperature data (Steger et al., 2017a). However, the quantification of surface water, in combination with accumulation and monitoring of liquid water percolation and blocking capabilities of ice layers, has been defined as very valuable by an expert elicitation and recent model intercomparison (Steger et al., 2017b; van As et al., 2016). Temperature records in snow and firn (Humphrey et al., 2012) only indicate the depth of percolating meltwater but cannot provide information on mass fluxes and bulk liquid water content.
Upward-looking ground penetrating radar systems (upGPRs) (Heilig et al., 2009, 2010) proved to provide reliable data on bulk snow height and density, liquid water infiltration, volumetric liquid water content (θw) as well as total accumulation (SWE) in seasonal snow (Heilig et al., 2015; Mitterer et al., 2011; Schmid et al., 2014). For this study, we installed an upGPR in perennial firn within the deep percolation zone of the GrIS. Such instrumentation is capable of providing new insights in the temporal evolution of ice layer formation, liquid water percolation and of monitoring differences in summer melt for various melt seasons. On a longer term perspective, upGPR might be capable of monitoring processes and changes which lead to establishment of either impermeable ice slabs or the progressive fill-up of pore space above the system. To estimate the reliability of radar-derived parameters, we compare determined percolation depths with changes in temperature records and analyze monitored changes in thickness of the snow and firn column above the antennas with results of ultrasonic transducers located within a distance of less than 2 km (MacFerrin et al., 2015; Steffen et al., 1996). In addition, to validate performance of MAR at a point scale, we investigate discrepancies in accumulation, near surface densities, percolation depths and bulk liquid water content between simulations and radar data. The presented data have a large potential to demonstrate current short comings in model approaches and supports understanding of short-term changes in snow and firn of near-surface layers. Such data will help to improve understanding of liquid water retention by quantification of surface water in combination with accumulation and monitoring liquid water percolation and blocking capabilities of ice layers.
2.1 Test site, instrumentation and data processing
We installed an upGPR system within the perennial firn regime of the GrIS at the research site Dye-2 (Coordinates: 66.4779∘ N, 46.2856∘ W) next to Camp Raven, in April 2016 (Fig. 1). The radar system consists of an IDS (Ingegneria dei Sistemi, Pisa, Italy) FastWave control unit with dual frequency 600/1600 MHz antennas. The whole aperture is powered by six 50 Ah batteries and two 60 W solar panels (Fig. 1b). We buried the radar antennas in a box approximately 4.5 m beneath the surface in April 2016. To enable observation of undisturbed snow and firn, we further excavated an additional 2 m cave sideways and fixed the antenna box at this position. The upGPR system is programmed to conduct measurements periodically at three different intervals: during summer time (15 April–14 August) every 30 min during the day (09:00–21:00 h) and every 1 h for nocturnal measurements; after 14 August until 14 October and from 1 March until 14 April every 3 h and from 15 October until end of February, we only record one measurement per day at 12:00 h. All times are given in local winter time (UTC −3 h). From 16 October 2016 until our next visit in April 2017, the radar stopped working due to technical problems. For analysis, we defined the start of upGPR measurements as 1 May 2016, when the installation pit was filled in and had had time to settle for 2 days.
Radar data were processed as described in Schmid et al. (2014). Snow surfaces in the resulting radargrams for both frequencies were determined using the “semi-automated picking algorithm” (Schmid et al., 2014). All reflectors were automatically picked at the maximum amplitude per positive half cycle or minimum amplitude per negative half cycle, depending on the phase sequence of the respective reflector. However, for the same reflector, we consistently chose the same half cycle. The resulting radargram of the 1600 MHz system was used to pick the snow surface and the 600 MHz signal to determine the two-way travel time (TWT with mathematical symbol τ) to the target reflector. However, for periods with large amounts of melt affecting the snowpack and firnpack, the reflection from the snow surface for the 1600 MHz antennas diminished. We then also used the 600 MHz signal to pick surfaces for such periods and vice versa used higher frequency signal to determine the distance of the target reflector for some radar records. For all displayed radargrams, we generated a wave speed model for electromagnetic waves derived from core densities to convert measured TWT to height above the upGPR antennas. Since we only have density data available for May when we visited the site, the wave speed model is not updated during the season and certainly incorrect for radar reflections affected by liquid water. These inaccuracies have no influence on data analysis as will be shown in the discussion. The model is just used for visualization.
Two firn cores down to the depth of the radar antennas were drilled in 2016 and used for the installation of the target reflector (Fig. 1). Core data were processed in 5 cm steps for average densities and stratigraphy was visually inspected on a 1 cm resolution. In May 2017, we drilled only one core down to 5.5 m depth in close proximity to the radar antennas but outside of the estimated footprint of the antennas (about 8 m away from the center of the antennas). Data were processed again with 5 cm resolution in density and 1 cm resolution in stratigraphy.
In 2016, in addition to the radar we also installed a thermistor string about 4 m away from the solar panel mast of the radar system (Fig. 1b). Thermistors were deployed at depths of 0.4 to 5.4 m every meter and additionally at 7.4 and at 9.4 m depth beneath the snow surface of 1 May 2016.

Figure 1Sketch and image of the radar arrangement for Dye 2. (a) Sketch of the installations above and beneath the snow surface. ρi indicate the density of specific snow layers, Ls indicates the whole firn and snow column above the antennas and dA, d indicate distances. (b) Image of the above snow installations at the research site Dye-2. The inset displays the location of the upGPR for the southern half of Greenland. The color coding for the inset map represents 250 m contour lines with the digital elevation model generated from Howat et al. (2014). TS in (b) represents the location of the thermistor string.
2.2 Determination of bulk snow and firn parameters above the radar antennas
The bulk layer (Ls) above the antennas (Fig. 1) has a layer thickness , with i the individual layer from one horizon to the next layer above. Correspondingly, the bulk mass (bs) is the sum of the mass of all layers: bs=Σbi. To derive snow and firn parameters for Li, we use the target reflector at a fixed height above the surface similar to Heilig et al. (2015). With the known distance between target and antennas (d), the surface pick in measured TWT and the known relative dielectric permittivity of air (εa), we can simply calculate for the height of the target above the snow surface (dA). Since the target posts are drilled to the same depth as the radar antennas (Fig. 1a), we expect compaction of the radar and the target to be approximately equal. As a consequence, d remains constant. From simple subtraction, we obtain the bulk thickness of the snow and firn layer above the antennas . The retrieval of bulk firnpack parameters above the antennas relies on previously published assumptions and equations (Heilig et al., 2009, 2010, 2015; Schmid et al., 2014): we used the three phase mixing formula postulated by, for example, Roth et al. (1990) or Wilhelms (2005) with the exponent β=0.5 and the assumption of only three contributing volume fractions (air, ice and water: ). For cold conditions with snow and firn temperatures below 0 ∘C (θw=0), the bulk density above the antennas can easily be determined. In contrast to conditions in seasonal snow described by Heilig et al. (2015), melting snow and firn on cold ice sheets can rapidly refreeze due to the underlying cold content. As a consequence, the assumption of a constant ice volume fraction after initial melt is invalid for ice sheets. Hence, melt and dry periods have to be treated differently. The resolution of the thermistor string with a 1 m spacing and the first thermistor at 0.4 m depth is not adequate to identify first occurrences of melt above the antennas. We use radar data instead for identification and timing of melt periods. Surficial melt produces strong changes in dielectric permittivity and, consequently, has an effect on radar response. The appearances of multiples or ringing in the radargram above the snow surface indicate those effects (Fig. 2). This allowed for the determination of periods when melt is present. For such periods, we assume that (i) no lateral flow transported mass downslope (slope angle below 0.5∘); (ii) wind erosion after surficial wetting is not effective; (iii) evaporation and sublimation effects are negligible for wet snow surfaces; and (iv) no mass transfer from Ls to layers below is possible as long as percolation did not reach the location of the antennas. Those four assumptions lead to the fact that a decrease in height of Ls is compensated by a corresponding increase in wet snow density (ρs), since the total mass (bs) cannot diminish:
To reduce the effects of single outliers and uncertainties in the surface and target picks, we averaged the 37 radar measurements per day and analyzed subsequently for diurnal differences during melting periods. For calculating diurnal changes in ρs, we use Eq. (1) and determine the differences () from day i to i+1 in :
with the new snow density estimate ρn=120 kg m−3 being slightly larger than for Alpine sites (Schmid et al., 2014).
In a second step, we set the obtained average values per day of ρs to be equal for each diurnal radar measurement. Since ρs in Eq. (2) describes the wet snow density, it is impossible to discriminate for individual volume fractions. Hence, we use the empirical equation of Denoth (1994):
with , , c3=18.7, c4=45, ρs with units [kg m−3] and εs as the relative dielectric permittivity of snow to solve for θw.
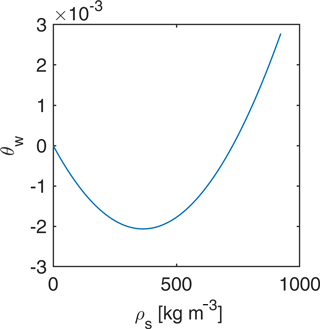
We checked the reliability of the application of the three phase mixing formulation to gather snow density from defined relative dielectric permittivity ranges for snow and ice ( in increments of 0.01) and applied the received values in Eq. (3). In case the three phase mixing formulation and the empirically determined equations were compatible, we would receive a volumetric liquid water content of constantly θw=0. Figure 3 displays the estimated discrepancy in θw values. In order to correct for the observed discrepancies, we applied a quadratic correction on the resulting θw of Eq. (3): (again with ρs in [kg m−3]).
2.3 Seasonal mass fluxes
Mass fluxes from snow above the previous summer horizon into firn are hereinafter defined as seasonal mass fluxes (SMFs with mathematical symbol F). Determination of SMF requires more iterations but can be accomplished with the applied setup as well. Two more layer definitions were necessary to prepare SMF analysis. First, we had to define a reference horizon, below which no temporal changes in stratigraphy are observable (Fig. 2, yellow line). Consequently, the total mass of the layer between the top of the antennas and the reference horizon did not change within the observation period. From the known height of the reference horizon and corresponding layer thickness (), determined from core data, and the calculated ρs,x, we could then continuously calculate the amount of mass of the reference layer (bx), which results in the following:
The second horizon necessary to determine SMF is the previous summer surface. The assignment of the 2015 summer horizon is possible for both radar frequencies over the entire observation period (Fig. 2, white line). We chose to refer to the 600 MHz data (Fig. 2b), since both the surface reflection and the summer 2015 horizon are more predominant and persistent for this antenna configuration. It is possible that either the data processing or slightly different environmental conditions influenced radar acquisitions with the consequence that peaks in amplitude shifted by ±1 sample. During dry snow periods when no compaction of the layer between the reference horizon and the summer 2015 horizon (L15,x) was identifiable, we used the most frequently occurring TWT for both horizons to minimize effects of shifted peaks. To calculate the mass changes (b15) occurring within the snow layer above the previous summer surface (L15), we had to determine the mass flux (F15,x) into L15,x due to percolating melt water. To solve for b15, we simply subtracted b15,x together with the seasonal mass flux from the mass balance of the reference layer:
in Eq. (5) was simply determined using the recorded core data. We assumed that remained constant over the entire observation period. It is certainly questionable whether this assumption is reasonable as will be discussed later. However, from measured TWT and , we could then calculate ρ15,x during periods with dry firn. The third term in Eq. (5), F15,x corresponds to the gravitational liquid water content of L15,x, which can easily be converted from θw if the imaged radar volume is known. We used the same approach as described by Heilig et al. (2015). To assess the imaged radar volume for this layer, we applied the known radiation characteristics of the radar system. Refraction occurring at density transitions was neglected, since permittivity differences are small and consequently refraction ineffectual. However, for each event with percolating water reaching L15,x, the three phase mixing formula is underdetermined (Heilig et al., 2015). Hence, to solve for θw, we used the same assumption as Heilig et al. (2015) that θi remains constant after initial percolation into L15,x. This precondition will be discussed in the following as well.
2.4 Regional climate model MAR
Here we use the versions 3.7 and 3.8 of the regional climate model MAR, especially developed for simulating the GrIS surface mass balance. MARv3.7 is run at a resolution of 20 km and is forced by reanalysis NCEP1 (National Centers for Environmental Prediction, resolution of 2.5∘) over 1948–2016. MARv3.8 is run at a resolution of 15 km and forced by reanalysis ERA-Interim (ECMWF Interim Re-Analysis, resolution of approximately 0.75∘) over 1979–2016. Both reanalyses and the MAR model are described in detail in Fettweis et al. (2017). In respect to MARv3.5 used in Fettweis et al. (2017), the main improvements of MARv3.7 and MARv3.8 – apart from regular bugs corrections – are the increase in cloud life, partly correcting the cloudiness underrepresentation (and, hence, the infrared energy flux) as well as the excess of inland precipitation found in Fettweis et al. (2017). The differences between MARv3.7 and MARv3.8 are mainly improvements in computing efficiency without significant modifications in the physics. The MAR snow model is based on an older version of the snow model Crocus (Brun et al., 1989) using the “bucket approach” as water transport scheme discussed in D'Amboise et al. (2017). MAR is forced every 6 h by either NCEP1 or ERA-Interim reanalysis data. We decided to use daily outputs for comparisons.
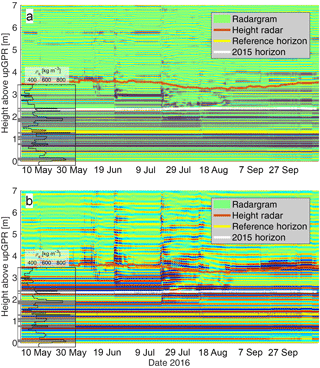
Figure 2Comparison of dual frequency upGPR data with firn core records gathered for the beginning of May 2016. (a) Reflection responses for the 1600 MHz are compared with density and stratigraphy from one firn core with corresponding depth scale. (b) Reflection responses for the 600 MHz are compared with density and stratigraphy from one firn core with corresponding depth scale. Occurrences of ice lenses at specific depths are indicated through gray shaded horizontal areas within the boxes. In addition, we display the determined height of the snowpack and firnpack above the antennas (brown line), the height of the reference horizon (yellow line) and the reflection response corresponding to the summer surface of the previous summer (2015 – white line).
For the remaining part of this study, we will consistently use “height above the radar antennas” as coordinates for specific horizons and events. All MAR outputs for depths beneath the surface and recorded temperature data are converted to match the radar data. This was performed by subtracting simulated depths beneath the surface from bulk layer thickness of Ls measured by the FirnCover ultrasonic transducer (MacFerrin et al., 2015).
3.1 Radar reflection response and corresponding firn core data
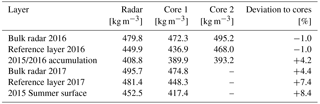
All major density steps and ice lenses identified in the cores can be related to radar reflection events (Fig. 2a and b). Starting from the bottom, each ice lens corresponds to an amplitude increase in the radargrams. Since we buried the top of the antenna box within the significant ice crust at a 0.1 m height, only the decrease in density of that crust produced a reflection response (Fig. 2b). The next ice lens at 0.8 m height produced a strong reflection for both frequencies, while the double lens right above at 1.0 m only results in a significant signal amplitude increase in the 1600 MHz radargram (Fig. 2a). In firn, the vertical resolution of the 600 MHz antennas is roughly 17.7 cm and for the 1600 MHz antennas 6.6 cm (Daniels, 2004). Destructive interferences diminish reflections appearing within shorter distance than the respective wavelength. However, the lens at 1.3 m appears again in both radargrams as a strong reflection. This reflection is marked as reference horizon. At about 2.0 m height, we identified another significant ice lens with densities exceeding 800 kg m−3. While for the 1600 MHz array (Fig. 2a), it is possible to track this horizon over the entire time period in the radargram, the reflection signal disappears in the 600 MHz data after the last liquid water percolations by mid-August (Fig. 2b).
The summer 2015 melt produced a remarkable double crust just below the recent snow accumulation at about 2.3 m above the antennas. Both radargrams in Fig. 2 show a clear reflection signal for this horizon. The 600 MHz data allow following this reflection throughout the whole summer season until fall 2016 (Fig. 2b).
Concerning the surface reflection, different behavior for both antennas could be observed as well. The 1600 MHz radargram (Fig. 2a) is incapable of producing a clear surface signal after strong melt affected the snowpack. In contrast, the 600 MHz data still show a clear surface signature. Such occurrences are in agreement with upGPR radargrams observed in seasonal snow (Schmid et al., 2014). The use of a dual-frequency system is beneficial for such events. We still received a strong surface signal even after mid-July for the 600 MHz array (Fig. 2b).
3.2 Validation of radar derived parameters
The calculated layer thickness of the snow and firn column above the antennas was compared with data from two ultrasonic depth rangers. One of the ultrasonic transducers is located at a distance of about 60 m to the upGPR location being part of the FirnCover station (MacFerrin et al., 2015) and the other ultrasonic data were measured about 1 km west at the GCnet station (Steffen et al., 1996). Fig. 4 displays all three curves. In perennial firn ultrasonic depth rangers measure only the distance of the instruments to the snow surface. Since no snow free conditions can be used to recalibrate the measurements, we adjusted both stations to match the height of the snow and firn column during installation for the start of upGPR measurements. Differences in between ultrasonic data and upGPR determined are 5.1 cm in comparison to GCnet data and 4.3 cm to results of the FirnCover station in root mean square deviation (RMS) over almost six months of observations.
Density values determined by radar could only be validated through available firn cores, which were drilled during time of visits. Table 1 displays density differences of core data and radar derived values for several different radar reflections, which could be attributed to distinctive layers in cores. As a third data set of validation, we can use the height of the target above the snow surface (dA, Fig. 1). In May 2016 this height was measured manually to 1.80–1.86 m, due to surface roughness. In May 2017, we had to raise the target and measured dA to 2.69–2.70 m. Radar determined dA equal to 1.79 m in 2016 and 2.68 m in 2017 for the same date as the manual measurements.
3.3 Observed temporal changes in snow and firn
In Fig. 5, determined changes in snow and firn from upGPR (Fig. 5a. extent of percolation, and Fig. 5c. changes in SWE, brown line and volumetric liquid water content, blue line) are compared with temperature data derived from the installed thermistor string (Fig. 5b). The radargram was additionally processed by horizontal filtering. All reflectors remaining constant over the observation period were thus removed. Such filtering enhances visibility of abrupt changes in stratigraphy such as those provoked by water percolation (Fig. 5a). In Fig. 5b, temperature data are interpolated for the upper four thermistors with the blue line on top indicating the snow surface. Isotherms for every 1 K are presented as black lines.
For the bulk snow and firn above the antennas, we observed two early peaks in melt in June causing percolation to reach down to 2.9 m height in early June and down to 1.8 m on 23 June. After a period of refreezing conditions from early July until mid-July, the strong melt event on 19 July caused deep percolation to a height of approximately 1.5 m with derived bulk θw approaching 1 vol %. Melt conditions lasted until early August when the next increase in melt caused the determined θw to exceed 1 vol % and water percolation to reach about 1 m above the antennas. After this peak, we observed rapid refreezing with fully refrozen snow and firn by early September.
Table 2 illustrates dates of local minimum for percolation above the radar antennas determined from the radargram and height above the antennas of the −1 ∘C isotherm. This isotherm was determined by linearly interpolating recorded snow temperatures. In general, radar-observed percolation matches well the temperature progression. Almost all liquid water occurrences in the radar data at the snow surface or below (indicated in the radargram by distinct multiples or ringing above the surface up to 7 m in air) correspond to heat waves penetrating into deeper layers of snow and firn. While the first stronger melt event by early June did not affect temperature records significantly, the next melt event for this season showed a clear signal in temperature data as well. The delay in temperature response by about five days in Table 2 is a consequence of the simple search for local minimum in height of the −1 ∘C isotherm. The primary decrease in height of that isotherm already occurred on 23 June at 21:00 h and consequently was delayed only by 20 h in comparison to upGPR results. However, the minimum height within the melt period of the isotherm was reached four days later. The strongest dips in water percolation for mid-July and early August 2016 match by 2–4 h for radar and thermistor string.
The measurements of percolation depths differ more significantly. The first percolation event, recorded by temperature data, are a mismatch with radar observed percolations by 1 m. However, the much stronger events in June and August show a coincidence of radar and temperature observations of 10–70 cm. Actual temperature records for the same day showed a maximum of −0.2 ∘C at a height of 1.0 m at 17:00 h (Fig. 5b). The given accuracy of the deployed thermistors is in the range of ±0.25 ∘C. Even though the minimum in height of percolation for the radar was detected four hours later (Table 2), we detected percolation reaching a height of approximately 1.1 m in the radar data at 17:30 h the same day. Concerning determined θw data in Fig. 5c, it seems that any strong gradient in derived θw corresponds well with the timing of percolation of the warming signal for the temperature records.
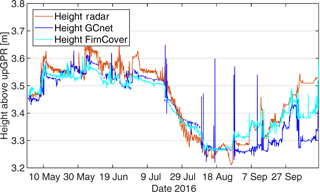
Figure 4Comparison of derived thickness from radar of the snow and firn column above the antennas with changes in snow depth recorded by two different ultrasonic rangers.
Since all contributing volume fractions of the overlying snowpack and firnpack are determined, we can simply calculate for accumulation mass in the water equivalent as well. The bulk SWE over the antennas is presented in Fig. 5c (brown line). During wet snow conditions, the determined SWE remained stable or only slightly increased. Only after 1 September and before 1 June remarkable increases in snow accumulation were determined.
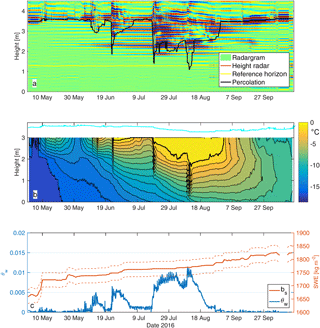
Figure 5(a) Radargram of the observed six month time period in 2016 with display of water percolation. (b) Recorded and interpolated snow and firn temperatures with 1 ∘C contour interval for the upper four thermistors of the installed thermistor chain. The bold contour line displays the −1 ∘C isotherm. The cyan line in (b) represents the snow surface measured by the FirnCover ultrasonic transducer. (c) Derived bulk volumetric liquid water contents above the antennas (blue line, left axis) in comparison to radar data of changes in total mass in snow water equivalent (SWE) for the same layer (brown line, right axis). The dashed lines in (c) represent the uncertainty of SWE arising from the error in density and layer thickness determinations.
3.4 Seasonal mass transfer
We could clearly identify a strong mass transfer from snow into firn below the 2015 summer surface (Fig. 6a and b). At least three melt events routed liquid water beneath this summer horizon (Figs. 2a, b, 5a and b), which was located at about 2.4 m above the antennas for May 2016. In total, we determined a mass flux of 56 kg m−2 from snow into firn (Fig. 6b). The three major percolation events occurred after mid-June and before mid-August. While the first event produced an outflow of roughly 6 kg m−2 water mass from the snow layer in three individual routing events within three hours, the percolations in July and August routed 27 and 23.5 kg m−2, respectively (Fig. 6b). L15,x experienced a volumetric liquid water content of up to almost 1 vol % at 10 August 2016, 18:00 h (Fig. 6a, blue line). At that day, both the thermistor data and radar observations obtain the maximum depth in percolation (Table 2). The timing of all three data sets is within three hours difference.
The mass balance estimates for early May 2016 (b15) derived from the radar exceeds conventionally measured SWE values for the snow layer by roughly 100 kg m−2 (upGPR b15=438 kg m−2; b15 measured in the pit above the antennas: 335 kg m−2).
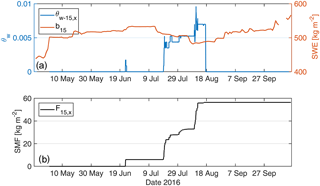
Figure 6(a) Mass balance estimates for the snow layer above the summer horizon 2015 (brown line, right axis) and changes in θw of the layer between the summer horizon of 2015 and the reference horizon (blue line, left axis). (b) Seasonal mass flux (SMF) that has percolated through the 2015 summer horizon into firn below.
3.5 Comparison of radar derived snow parameters with simulations from MAR
We use MAR outputs with a daily temporal resolution and two different forcings, which generate grid cells of 20 km (NCEP1) and 15 km (ERA-Interim), respectively. The radar, in contrast, provided point data on changes in total accumulation of up to every 30 min together with data on volumetric liquid water content, percolation and bulk density (Figs. 5, 6). To quantify offsets of individual parameters, we averaged radar data to diurnal outputs to match the temporal resolution of MAR simulations.
The comparison of seasonal changes in accumulation in between simulation results and radar data (Fig. 7) shows high agreement for both data sets. Uncertainty in radar determined SWE derives from the error in total height of snow (±4.3 cm, Sect. 3.2) and the uncertainty in density estimates (±1 %, Table 1) in an error propagation. Apart from the beginning of the time series in May, changes in SWE simulated in MAR with both forcings match radar observations very accurately. To assess the similarity between simulations and radar data, we calculate the Nash–Sutcliffe efficiency value (NSE) (Nash and Sutcliffe, 1970). NSE values of 1 indicate a perfect fit of the model with the data, while a NSE of 0 shows that the model fit is as good as simply the average value of the data. NSE for MAR NCEP1 simulations is at 0.75 and below 0 for ERA-Interim driven simulations for the whole data series. While NCEP1 driven simulations gradually approach changes determined from upGPR data over time, MAR with ERA-Interim forcing remain parallel to the radar line almost over the entire time series. We assume that the strong rise in SWE for upGPR data at 10 and 11 May 2016 is attributed to additional drifting caused by a shelter, which we created for digging the radar pit. Hence, deleting only the data point of 11 May (Δ bs=35 kg m−2) from analysis lead to NSE values for MAR-NCEP1 of 0.53 and MAR-ERA of 0.95. Consequently, the temporal progression of changes in SWE is simulated in MAR with very high agreement to radar data using ERA-Interim forcings and acceptably well with NCEP1 forcing (Fig. 7). However, the simulated significant increase in accumulation (by MAR-NCEP1) at 10 August is not reproducible by radar observations and distinctly smaller for ERA-Interim forced MAR.
Table 2Dates and minimum infiltration heights above the antennas for local minima in percolation of both, the upGPR data and thermistor records. We used the interpolated −1 ∘C isotherm for percolation minima of the thermistor data.

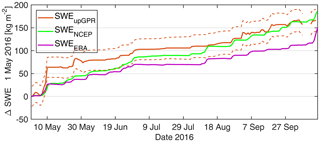
Figure 7Seasonal changes in accumulation in respect to 1 May 2016. We compare upGPR derived changes in SWE (brown line with uncertainty range indicated by dashed lines) with simulated variations by MAR for both forcings (green line – NCEP1 forcing; purple line – ERA-Interim forcing).
For θw and bulk snow density above the reference horizon much more distinct differences in between simulations and radar determinations appear (Fig. 8a and b). Bulk density over the entire observation period is highly overestimated by MARv3.7 with NCEP1 forcing and significantly underestimated by MARv3.8 with ERA-Interim forcing for this specific location. Bulk density values of the NCEP1 forced simulation are exaggerating field data within the full observation period. While simulations overestimate ρx in the beginning by only 20 kg m−3, at the peak of the melt season, differences of almost 100 kg m−3 are commonly present (Fig. 8a). RMS deviations to upGPR derived ρx for MAR forced by NCEP1 reach 71.4 kg m−3. RMS values determined for ERA-Interim forced MAR simulations result in 51.2 kg m−3, which is only slightly better and still represents a deviation of roughly 10 % in comparison to mean ρx. Here, MAR models bulk density of the upper 2 m constantly too low.
MAR simulations with both forcings tend to exaggerate melt at Dye-2. This is especially the case for MAR being forced by NCEP1 reanalysis. For instance, the first spike in simulated θw for mid-May does not have an equivalent in radar data at all. Here, MAR simulations exaggerate the amount of melt and the duration. Documented changes in snow temperature (Fig. 5b) do not indicate such strong melt occurrences either. The subsequent simulated θw peaks correspond in timing but not in amplitude for MAR-NCEP1, while ERA-Interim forced MAR matches the amplitude but refreezes earlier. For the melting period lasting from 23 June until 3 July timing of the melt event agrees with radar derived data. Here, ERA-Interim forcing leads to a stronger overestimation in amplitude than NCEP1. Such occurrences are the opposite of the subsequent melt event starting at 19 July. While MAR-ERA data agree well in θw amplitude with radar, MAR-NCEP1 overestimates maximum θw by almost a factor of three. In consequence, refreezing is delayed for MAR-NCEP1 by 27 days. Since MAR-ERA misses the strong peak in melt (10 August), refreezing is simulated already for 15 August 2016 and thereby 18 days earlier than radar data indicates (Fig. 5b). Temporal offsets in between diurnal average values of θw≥0.3 vol % for the upGPR and NCEP1 forced simulations are always within maximum one day for the initiation of melt. However, duration of the periods with θw≥0.3 vol % differ by three days in mid-June and 31 days in late August/September 2016. For MAR-ERA, onset of melt reaching θw=0.3 vol % is delayed by three days in mid-June and otherwise within ±1 day. Refreezing of snow and firn to values below 0.3 vol % is usually predicted within an accuracy of ±1 day as well with the exception of mid-August, when MAR-ERA simulates a drop below the 0.3 vol % range 15 days too early.
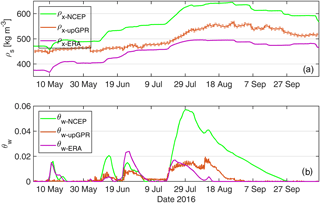
Figure 8(a) Seasonal changes in bulk density (ρx) for layer Lx simulated by MAR with NCEP1 and ERA-Interim forcing compared with ρx derived from upGPR data (brown line with uncertainty range). (b) Seasonal changes in θw for the same layer Lx simulated by MAR with forcing NCEP1 and ERA-Interim compared with θw values from radar data (brown line). For bulk density in (a) as well as bulk liquid water content in (b) upGPR data has a temporal resolution of 30 min maximum, while MAR has daily values as output.
Simulations of percolation depths for both model forcings are highly diverse and mainly disagree with upGPR determined data (Fig. 9). Temporal agreement for the onset of melt is high for MAR-NCEP1 and upGPR percolation but percolation depths and timing of refreezing do not agree. For MAR-ERA, percolation depths are mostly underestimated over the course of the season and the strong melt in August is not captured, which leads to an earliness of refreezing. Both percolation simulations exceed radar determined percolations significantly for the first melt event in mid-May, which is in agreement with bulk θw predictions. For the following melt occurrences at mid-June, offsets in maximum percolation are rather small. Radar data reveal a height of infiltrating liquid water down to 2.85 m above the antennas, MAR-NCEP1 down to 2.82 m and MAR-ERA down to 3.07 m. Here, MAR-ERA has a slight delay in timing of water infiltration. The following melt event, lasting from late June to early July, results in much larger offsets of percolation depths. Deviations to radar data are at −1.08 m (MAR-NCEP1) and −0.76 m (MAR-ERA). For the major melt event (19 July–mid August), MAR-NCEP1 exceeds maximum percolation as observed by radar by at least +0.81 m and MAR-ERA underestimates water infiltration by −1.27 m. Such percolation offsets are in agreement with θw over- (MAR-NCEP1) and underestimation (MAR-ERA) as shown in Fig. 8. For both simulations, the speed of percolation is significantly underestimated for the onset of melt, when compared with upGPR data.
For the time period in between 3 August until 8 August, we observed refreezing conditions at the bottom of the percolation (Figs. 5a, 9). However, MAR-NCEP1 simulates a stable percolation front with refreezing being simulated at the snow surface (Fig. 9). ERA-Interim forced simulation correctly predicts refreezing from the bottom.
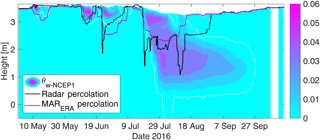
Figure 9Simulated percolation depths compared with upGPR derived percolation (black line). The color bar presents volumetric liquid water content from MAR-NCEP1 with 1 vol % contour interval. The thin white line delineates interpolated water content below 0.1 vol % as approximate of the borders of the simulated wetting front.
4.1 Reliability of radar derived snowpack and firnpack parameters
It is important to mention that the used wave speed model becomes incorrect when liquid water infiltrates snow and firn. Liquid water decelerates radar wave propagation significantly and, consequently, distance to reflections above the infiltration increase in measured TWT. However, snow pits and firn cores at the site can only be obtained when the instruments are visited once a year. For data analysis only measured TWT is used and, consequently, presented heights are not relevant. Still we consider a presentation of heights, even though they are partly incorrect after certain time periods, as being more intuitive and more supportive for readability. Percolation depths are unaffected from erroneous TWT conversions as they indicate the maximum height of dry snow and firn. In contrast to the ice lens at about 2 m height, the 2015 horizon and the snow surface, all layers below the reference layer (Fig. 2a and b) are basically unaffected by melt events and consequently do not show variations in TWT.
In Sect. 2.2, we described four assumptions required to enable data derivation for wet snow conditions: (i) no lateral flow transported mass downslope; (ii) wind erosion after surficial wetting is negligible; (iii) evaporation and sublimation effects are negligible for wet snow surfaces as well and (iv) no mass loss above the antennas is possible as long as percolation did not reach antenna height. Assumption (i) and (iv) induce each other and, hence, are discussed together. Lv et al. (2013) conclude that lateral redistribution of soil moisture is sensitive to slope angle. Here, we observed an area with an almost planar surface (< 0.5∘ slope angle). Consequently, lateral redistribution of liquid mass is considered negligible. Considering liquid water percolation, we recorded changes in firnpack stratigraphy every 30 min during daytime. For none of the records was water infiltration past the radar antennas identifiable. There is a slight chance that small amounts of water percolated in between two radar measurements below the depth of the antennas and refroze before the next radar scan. However, such infiltration would cause a release of latent heat at such depth during refreezing, which is not documented in the temperature data (Fig. 5b). Wind erosion of wet surfaces is assumed to have a negligible effect, since cohesion forces and bonds among grains are much stronger than for loose new snow (Li and Pomeroy, 1997). For the proof of assumption (iii), we used MAR outputs and quantified the effect of sublimation and evaporation during melting surfaces. For the time period in between 19 July and 19 August 2016, when strong melt affected the snow and firn at Dye-2 (Fig. 5), MAR calculates an effect of evaporation being at 5 % of simulated SMB. Such an effect remains within the given uncertainty for radar derived SWE. However, MAR uses assumptions as well to estimate sublimation and evaporation. According to our knowledge, no experimental setup within the deep percolation zone of the GrIS exists to provide a more rigorous proof for assumption (iii).
Due to the fact that independent snow and firn temperature records of ∘C match percolation observed by radar very accurately and due to the high agreement between seasonal changes in SWE simulated with MAR and radar determined SWE development, we have strong reasons to trust results derived from radar data. In addition, calculated above the antennas is in close agreement with two time series of ultrasonic depth rangers. An error of 4–5 cm (< 1.5 % for a 3.4 m thick snowpack and firnpack) is below an observed uncertainty between manual measurements and snow depth sensors for a much smaller spatial offset in seasonal snow (Schmid et al., 2014). For the presented data, conventionally measured bulk densities for specific layers agreed within ±1 % with radar derived densities for May 2016. In 2016, we had the opportunity to drill cores less than 2 m from the center of the radar antennas. Overestimation of bulk density of radar data in May 2017 cannot be directly attributed to increased uncertainties in radar derived parameters. Due to the fact that we did not want to influence snow and firn within the footprint of the radar antennas, we had to drill the core in 2017 about 8 m away from the center of the target reflector. Spatial variability in stratigraphy and caused difficulties in relating layers to radar reflectors and contributed to offsets for specific layer densities. The height of the target reflector above the snow surface could be determined with very high accuracies as well. Offsets in radar derived mass balance data (b15) of about 100 kg m−2 to manual observations can be attributed to difficulties in picking the reflection event seasonal snow above the summer horizon of 2015 in the radargram. Snow pits are usually just dug down to a remarkable crust, which is hardly penetrable with a shovel. The reflection response at this specific density gradient is masked by signal interferences with the reflection generated at the lower border of this crust, which represents the melt horizon of summer 2015. Correspondingly, including the observed ice lenses into SWE calculation of the pits results in a mass of 426 kg m−2 for early May. This reduces the offset to values obtained from upGPR to only 2.8 %.
The assumption of a fixed layer thickness in Sect. 2.3 for L15,x is based on the fact that during cold and dry conditions the TWT for both determined horizons remain at the same sample number within ±1 sample uncertainty. In addition, it is important to consider the respective firn layer to be part of a closed system. Neither evaporation, sublimation nor erosion can transfer mass. Due to rather small temperature gradients in perennial firn (here, approximately 3 K m−1 at maximum; Fig. 5b), water vapor transport mechanisms are small and consequently negligible. We presume that only compaction with a corresponding increase in ρs influence the measured TWT for dry conditions. Theoretically, it is possible that compaction is happening but the measured TWT remains constant. For instance, such conditions could be the case for the period until 19 June 2016 (Fig. 2). The numerical approximation for a fixed TWT with varying ρs values ranging from 200–900 kg m−3 results in , with the strain s in meter and ρs in kg m−3. From this approximation it follows that a density increase for the observed layer of kg m−3 would only allow a compaction of about 3.7 cm for the reflector remaining at the same distance in TWT. For an observation period of one year, we observed maximum density increases of less than 30 kg m−3 per layer (Table 1). Thus, the fixed layer thickness is a reasonable assumption for possible densification rates of that layer.
In addition, we assume the ice volume fraction to remain constant for the time period after water reached the respective layer and before refreezing is completed. Such an assumption is conceptually wrong in cold firn. Percolating water will refreeze and through the release of latent heat gradually increase the temperature of this layer. However, a gradual increase in θi is difficult to estimate from the given temperature resolution of the thermistor data. Consequently, we overestimate θw after initial percolation. However, only further increases in θw result in further increases in the amount of F15,x within the layer. Since F15,x remains stable after the first percolation event reaching L15,x (23 June) and after the third event (10 August), we expect the named overestimation to being of relevance only for the period in between 19 July and 10 August. As a consequence, for this time period of gradual warming (see Fig. 5b), the assumption of θi= const might lead to an overestimation of less than 10 kg m−2 for F15,x.
4.2 Changes in seasonal snow and firn for the melt season 2016
For the summer season 2016, we observed several major changes in snow and firn parameters. According to the radar records, a maximum volumetric liquid water content of θw≤2 vol % was observed for snow and firn above the reference layer (approximately 2 m beneath the snow surface). A maximum percolation depth throughout the season of 1.0 m height above the antennas, which corresponds to 2.3 m below the surface was recorded for 10 August. Deep percolation down to 10 m and more as proposed by Machguth et al. (2016) for the here observed elevation range was not observed for the melt season in 2016. In terms of spatial extent of melt at the surface, this melt season is considered as above average (tenth in the 38-year satellite records) (NSIDC, 2016). All melt events together routed about 60 kg m−2 of mass into firn beneath the previous summer surface of 2015. This corresponds to roughly 40 % of liquid water, which were transferred into deeper layers, while about 60 % were retained against gravitational forces within the seasonal snow layer. Steger et al. (2017a) model an average retention over the entire GrIS of 47 % with values reaching up to 75 % in the southeast of Greenland where rates of snow accumulation are largest. We did not observe major stratigraphic changes along the previous summer surface after the melt season 2016 as proposed by Pfeffer and Humphrey (1998); neither within the radargrams of both frequencies nor in the firn core of May 2017. However, a distinct increase in accumulation for the layer above the reference horizon and below summer 2015 was recorded from May 2016 ( kg m−2) to May 2017 ( kg m−2) of kg m−2. This confirms the recorded mass transfer, despite of radar determined mass transfer being ∼ 12 % larger. Spatial inhomogeneities and inaccuracies in both measurement methods (uncertainty through use of θi= const, difficulties in layer attribution within firn cores) certainly contribute to this offset. Although, one should be very cautious of direct comparisons between annual firn cores, especially for individual layers, a general trend of mass increase could be confirmed by this core data. However, it is obvious that small scale changes appeared within the course of the melting period in 2016. In the layer bonded by the summer 2015 and the reference horizon, remarkable changes in reflection structure occur after percolation. Especially, the 600 MHz signal was influenced. A new reflector appeared right below the summer 2015 horizon and the reflection previously attributed to the significant ice lens at about 2 m height diminished with refreezing firn.
Concerning the mass balance of the snow layer above the summer horizon 2015 (b15) at Dye-2, we found an increase in accumulation of 84.4 kg m−2 for the time period of May until 30 September 2016. The simulated SMB in MAR resulted in 151 kg m−2 for the same time span with a simulated mass loss of only 7 kg m−2. Subtracting the mass flux of kg m−2 of mass would result in an overestimation in MAR of b15 in comparison with radar data of roughly 12 %. This is in agreement with results presented by e.g., Heilig et al. (2015) that model accuracies benefit from in situ data. For assessment of mass balance rates at Dye-2 without runoff and lateral redistributions at the current stage, it is of no relevance whether mass is transferred into firn beneath or remains within the seasonal accumulation layer. However, concerning lower elevation sites at the transition between accumulation and ablation area, the accurate assessment of residual water and outflow is critical for estimates on mass balances (Charalampidis et al., 2015). The same appears for the formation of near surface layers of low permeability (Machguth et al., 2016). Only monitoring and accurate determination of liquid mass being transferred into firn enables correct simulation of ice layer formations and future development.
4.3 Reliability of model simulations in comparison with upGPR data
Generally, regional climate model outputs are not compared with data from single point measurements and validation on time spans of days to several months is not common (Fettweis et al., 2017). It remains questionable whether such comparisons are fruitful or not, keeping in mind that the modeled snowpack is representing a mean state over an area of 20×20 km2 (15×15 km2). However, since conventional instrumentations such as lysimeters to measure snowpack outflow or snow pillows to determine changes in SWE are not applicable in perennial firn, upGPR offers an unique possibility to validate – on a temporally continuous basis – simulated snow and firn parameters with measurements and determine reliability of model results. Hence, we tested the performance of MAR on its upper end of accuracy.
In general, the performance of MAR with both forcings is very good especially for the timing of melt onset and simulated changes in SWE. After removal of one data point supposedly influenced by drifting, the agreement of seasonal SWE changes of upGPR data and simulations reach up to 0.95 in NSE values for the ERA-Interim forcing. Such NSE values indicate an almost perfect fit of simulation data. The temporal offset of melt simulated by MAR with respect to upGPR and thermistor results is mostly below one day, which is the temporal resolution of the model outputs. Such accurate performance of a regional climate model is encouraging since the model is not run with input data from the AWS nearby but forced at its lateral boundaries with atmospheric fields with a typical resolution of 100 km. As a consequence, the downsampling of MAR seems to be reasonably accurate. It should be remembered that we compare point measurements of specific parameters with an average snowpack over 20×20 km2 (15×15 km2) in area, which likely partially explains discrepancies.
Significant offsets between simulations and radar observations exist for the calculation of bulk density of the upper 2 m in snow and firn, which reach an offset of up to +100 kg m−3. In addition θw is overestimated for each melt event up to a factor of three in comparison to values derived for the upGPR. The general exaggeration of melt in the percolation zone by regional climate models has been described previously for another model as well (Noël et al., 2015). As a consequence of overestimation of density and θw for MAR run by NCEP1 forcing, water percolates too deep and refreezing is strongly delayed. The irreducible liquid water content of snow and firn is related to porosity (Schneider and Jansson, 2004). Snow and firn of higher density have less potential to retain liquid water and thus percolation is overreached. However, MAR forced by ERA-Interim has a tendency to exaggerate bulk volumetric liquid water content as well but with a lower amplitude. For two out of four melt events during the summer 2016, MAR-ERA predictions of θw are in agreement with radar data over a few days. However, MAR forced by ERA-Interim misses the peak of melt and percolation in August 2016 almost completely. For the moment when upGPR data obtain the highest percolation depths, MAR-ERA simulates refreezing in snow and firn. Here, problems with the reanalysis forcing might occur, which lead to a distinct underrepresentation of melt. Simulation of liquid water infiltration and percolation depths are coupled with the amount of melt being produced at the surface and the applied water transport scheme. The here used simple bucket approach is not capable of reproducing water infiltration as observed by radar and temperature data. Deviations of simulation results for percolation depths are rather erratic. This surveillance is in agreement with previous comparisons in seasonal snow (Wever et al., 2015). The bucket approach is not capable of predicting heterogeneous infiltration and consequently, percolation is delayed at each onset of strong melt events but once melt has started is routing liquid water too fast in deeper snow (Wever et al., 2015). This study displays a very similar behavior of the bucket scheme to perennial firn as well. However, in contrast to seasonal snow, the cold content in firn forces refreezing from the bottom of water percolation as long as latent heat release is absorbed by the cold content of the surrounding firn. Hence, the typical water infiltration pattern of sharp dips in height as documented by radar and temperature data (i.e., Fig. 5) is not reproduced in the model independent of used forcings. In addition, without adequate climate forcing, melt cannot be predicted in a correct manner. Neither of the two applied forcings for MAR enable correct prediction of full snowpack refreezing. Hence, we conclude that a model capable in modeling heterogeneous flow is required to assess water infiltration, retention and refreezing correctly.
As stated above, predicting individual parameters of the SMB for a point location of the GrIS is beyond the scope of regional climate modeling. Here, we used two different versions of MAR with two different resolutions. This already explains a large fraction of the observed discrepancies for the analyzed parameters density and melt. Since models are usually tuned to accurately reproduce SMB data, individual parameters such as bulk density or bulk liquid water content may result in variable offsets from in-situ data for different climate forcings. In addition, the initial conditions for summer 2016 for both ERA-Interim and NCEP1 are not exactly equal, which causes the model to adjust differently for the individual parameters. Next, clouds have a large impact on the energy balance of the percolation zone of the GrIS. Due to the positive feedback of melt and albedo, small differences in the timing of melt and the amount result in significant offsets for the used forcings. However, upGPR data can help to identify misconceptions in regional climate modeling and, consequently, support further improvements in simulations of temporal changes in snowpack and firnpacks.
This study investigated temporal changes of liquid water content, density and SWE in snow and the upper few meters of perennial firn within the deep percolation zone of the GrIS. Over the entire melt season in 2016, liquid water infiltrations reached a minimum height above the radar antennas of 1 m, which corresponds to 2.26 m beneath the snow surface. The volumetric liquid water content does not exceed 2 vol % for the upper approximate 2 m beneath the snow surface. It is obvious from radar data that liquid mass has been routed out of the snow layer into firn beneath. We obtain a seasonal mass flux of 56 kg m−2 for the six months observation period in 2016. The applied instrumentation enable quasi-continuous monitoring of changes in mass for specific layers as well. For the bulk layer above the antennas, we derive a change in mass of +157 kg m−2.
We compare results derived from upGPR data with MAR run by two different reanalysis forcings and modeling a mean snowpack and firnpack over an area of 20×20 km2 (15×15 km2 respectively). In general, the performance of MAR with both forcings is very good, especially for the timing of melt onset and simulated temporal changes in SWE. However, prediction of layer density and bulk liquid water content is inaccurate for both reanalysis. ERA-Interim forced MAR is slightly decreasing the offset in density and significantly improving the performance for simulation of bulk θw. This study demonstrates that for correct assessment of infiltration depths and timing of refreezing, a more sophisticated water transport scheme than the bucket approach is required.
On a long-term perspective the installation of upGPR antennas at such a location might provide observation data on the transition from porous firn into either the formation of impermeable ice slabs or the gradual filling of the pore space above. Since the spatial melt extent in 2016 over the GrIS derived from remote sensing data was among the ten largest of the last 38 years, we do not expect percolation to reach beneath the height of the antennas apart from very exceptional years such as 2012. This possibly will enable monitoring of melt, mass fluxes and accumulation at this site for the next years to come.
All parameters derived from upGPR data are available from the lead author upon request, together with raw radar data. The MARv3.8 outputs, generated by Xavier Fettweis (University of Liège) and used here can be found under ftp://ftp.climato.be/fettweis/MARv3.8/Greenland/ (last access: 18 May 2018 created by Xavier Fettweis).
The authors declare that they have no conflict of interest.
This article is part of the special issue “Mass balance of the Greenland Ice Sheet”. It is not associated with a conference.
Achim Heilig was supported by DFG grant (HE 7501/1-1). Computational
resources for running MAR have been provided by the Consortium des
Équipements de Calcul Intensif (CÉCI), funded by the Fonds de la
Recherche Scientifique de Belgique (F.R.S.–FNRS) under grant no. 2.5020.11
and the Tier-1 supercomputer (Zenobe) of the Fédération
Wallonie-Bruxelles infrastructure funded by the Walloon Region under the
grant agreement no. 1117545. Michael MacFerrin was supported by the National
Aeronautics and Space Administration (NASA) grant NNX15AC62G. Marco Tedesco
would like to acknowledge NSF award PLR #1604058 and NASA award
#NNX17AH04G. We acknowledge support in logistics and preparation of
the field campaigns from Kathy Young and staff from Polar Field Services. In
addition, we would like to thank Silver Williams and Drew Abbott for swapping and
mailing SD cards at the end of each summer. Lino Schmid and Matthias Siebers
supported software preparations and Torsten Sponholtz helped with instrument
preparations. Field assistance by Bastian Gerling, Leander Gambal, Samira Samimi, Shawn
Marshall, Max Stevens, Baptiste Vandecrux, Jonathan Kingslake, Clement Miege and Frederico Covi is
acknowledged.
Edited by: Edward Hanna
Reviewed by: two anonymous referees
Abdalati, W. and Steffen, K.: Greenland Ice Sheet melt extent: 1979–1999, J. Geophys. Res.-Atmos., 106, 33983–33988, https://doi.org/10.1029/2001JD900181, 2001. a
Brun, E., Martin, E., Simon, V., Gendre, C., and Coleou, C.: An energy and mass model of snowcover suitable for operational avalanche forecasting, J. Glaciol., 35, 333–342, 1989. a
Charalampidis, C., van As, D., Box, J. E., van den Broeke, M. R., Colgan, W. T., Doyle, S. H., Hubbard, A. L., MacFerrin, M., Machguth, H., and Smeets, C. J. P. P.: Changing surface–atmosphere energy exchange and refreezing capacity of the lower accumulation area, West Greenland, The Cryosphere, 9, 2163–2181, https://doi.org/10.5194/tc-9-2163-2015, 2015 a
D'Amboise, C. J. L., Müller, K., Oxarango, L., Morin, S., and Schuler, T. V.: Implementation of a physically based water percolation routine in the Crocus/SURFEX (V7.3) snowpack model, Geosci. Model Dev., 10, 3547–3566, https://doi.org/10.5194/gmd-10-3547-2017, 2017. a
Daniels, D.: Ground Penetrating Radar, The Institution of Electrical Engineers, London, UK, 2nd Edn., 2004. a
Denoth, A.: An electronic device for long-term snow wetness recording, Ann. Glaciol., 19, 104–106, 1994. a
Fettweis, X., Box, J. E., Agosta, C., Amory, C., Kittel, C., Lang, C., van As, D., Machguth, H., and Gallée, H.: Reconstructions of the 1900–2015 Greenland ice sheet surface mass balance using the regional climate MAR model, The Cryosphere, 11, 1015–1033, https://doi.org/10.5194/tc-11-1015-2017, 2017. a, b, c, d, e
Gardner, A. S., Moholdt, G., Cogley, J. G., Wouters, B., Arendt, A. A., Wahr, J., Berthier, E., Hock, R., Pfeffer, W. T., Kaser, G., Ligtenberg, S. R. M., Bolch, T., Sharp, M. J., Hagen, J. O., van den Broeke, M. R., and Paul, F.: A reconciled estimate of glacier contributions to sea level rise: 2003 to 2009, Science, 340, 852–857, https://doi.org/10.1126/science.1234532, 2013. a
Gascon, G., Sharp, M., Burgess, D., Bezeau, P., Bush, A. B., Morin, S., and Lafaysse, M.: How well is firn densification represented by a physically based multilayer model? Model evaluation for Devon Ice Cap, Nunavut, Canada, J. Glaciol., 60, 694–704, https://doi.org/10.3189/2014JoG13J209, 2014. a
Hanna, E., Huybrechts, P., Steffen, K., Cappelen, J., Huff, R., Shuman, C., Irvine-Fynn, T., Wise, S., and Griffiths, M.: Increased Runoff from Melt from the Greenland Ice Sheet: A Response to Global Warming, J. Climate, 21, 331–341, https://doi.org/10.1175/2007JCLI1964.1, 2008. a, b
Hanna, E., Navarro, F. J., Pattyn, F., Domingues, C. M., Fettweis, X., Ivins, E. R., Nicholls, R. J., Ritz, C., Smith, B., Tulaczyk, S., Whitehouse, P. L., and Zwally, H. J.: Ice-sheet mass balance and climate change, Nature, 498, 51–59, https://doi.org/10.1038/nature12238, 2013. a
Harper, J., Humphrey, N., Pfeffer, W. T., Brown, J., and Fettweis, X.: Greenland ice-sheet contribution to sea-level rise buffered by meltwater storage in firn, Nature, 491, 240–243, https://doi.org/10.1038/nature11566, 2012. a, b
Heilig, A., Schneebeli, M., and Eisen, O.: Upward-looking Ground-Penetrating Radar for monitoring snowpack stratigraphy, Cold Reg. Sci. Technol., 59, 152–162, https://doi.org/10.1016/j.coldregions.2009.07.008, 2009. a, b
Heilig, A., Eisen, O., and Schneebeli, M.: Temporal Observations of a Seasonal Snowpack using Upward-Looking GPR, Hydrol. Process., 24, 3133–3145, https://doi.org/10.1002/hyp.7749, 2010. a, b
Heilig, A., Mitterer, C., Schmid, L., Wever, N., Schweizer, J., Marshall, H.-P., and Eisen, O.: Seasonal and diurnal cycles of liquid water in snow-Measurements and modeling, J. Geophys. Res.-Earth, 120, 2139–2154, https://doi.org/10.1002/2015JF003593, 2015. a, b, c, d, e, f, g, h
Howat, I. M., Negrete, A., and Smith, B. E.: The Greenland Ice Mapping Project (GIMP) land classification and surface elevation data sets, The Cryosphere, 8, 1509–1518, https://doi.org/10.5194/tc-8-1509-2014, 2014. a
Humphrey, N. F., Harper, J. T., and Pfeffer, W. T.: Thermal tracking of meltwater retention in Greenland's accumulation area, J. Geophys. Res., 117, F01010, https://doi.org/10.1029/2011JF002083, 2012. a
Huybrechts, P., Goelzer, H., Janssens, I., Driesschaert, E., Fichefet, T., Goosse, H., and Loutre, M.-F.: Response of the Greenland and Antarctic Ice Sheets to Multi-Millennial Greenhouse Warming in the Earth System Model of Intermediate Complexity LOVECLIM, Surv. Geophys., 32, 397–416, https://doi.org/10.1007/s10712-011-9131-5, 2011. a
Li, L. and Pomeroy, J. W.: Estimates of Threshold Wind Speeds for Snow Transport Using Meteorological Data, J. Appl. Meteorol., 36, 205–213, https://doi.org/10.1175/1520-0450(1997)036<0205:EOTWSF>2.0.CO;2, 1997. a
Lv, M., Hao, Z., Liu, Z., and Yu, Z.: Conditions for lateral downslope unsaturated flow and effects of slope angle on soil moisture movement, J. Hydrol., 486, 321–333, https://doi.org/10.1016/j.jhydrol.2013.02.013, 2013. a
MacFerrin, M., Stevens, C., Waddington, E., and Abdalati, W.: The FirnCover Project – Real-time Monitoring of Greenland's Firn Compaction in a Changing Climate, in: AGU Fall Meeting, San Francisco, CA, USA, 2015. a, b, c
Machguth, H., MacFerrin, M., van As, D., Box, J. E., Charalampidis, C., Colgan, W., Fausto, R. S., Meijer, H. A. J., Mosley-Thompson, E., and van de Wal, R. S. W.: Greenland meltwater storage in firn limited by near-surface ice formation, Nat. Clim. Change, 6, 390–393, https://doi.org/10.1038/NCLIMATE2899, 2016. a, b, c, d, e
Meehl, G. A., Washington, W. M., Arblaster, J. M., Hu, A., Teng, H., Tebaldi, C., Sanderson, B. N., Lamarque, J.-F., Conley, A., Strand, W. G., and White, J. B.: Climate System Response to External Forcings and Climate Change Projections in CCSM4, J. Climate, 25, 3661–3683, https://doi.org/10.1175/jcli-d-11-00240.1, 2012. a
Meierbachtol, T., Harper, J., and Humphrey, N.: Basal drainage system response to increasing surface melt on the Greenland ice sheet, Science, 341, 777–779, https://doi.org/10.1126/science.1235905, 2013. a
Mitterer, C., Heilig, A., Schweizer, J., and Eisen, O.: Upward-looking ground-penetrating radar for measuring wet-snow properties, Cold Reg. Sci. Technol., 69, 129–138, 2011. a
Nash, J. and Sutcliffe, J.: River flow forecasting through conceptual models part I – A discussion of principles, J. Hydrol., 10, 282–290, 1970. a
Noël, B., van de Berg, W. J., van Meijgaard, E., Kuipers Munneke, P., van de Wal, R. S. W., and van den Broeke, M. R.: Evaluation of the updated regional climate model RACMO2.3: summer snowfall impact on the Greenland Ice Sheet, The Cryosphere, 9, 1831–1844, https://doi.org/10.5194/tc-9-1831-2015, 2015. a
Noël, B., van de Berg, W. J., van Wessem, J. M., van Meijgaard, E., van As, D., Lenaerts, J. T. M., Lhermitte, S., Kuipers Munneke, P., Smeets, C. J. P. P., van Ulft, L. H., van de Wal, R. S. W., and van den Broeke, M. R.: Modelling the climate and surface mass balance of polar ice sheets using RACMO2 – Part 1: Greenland (1958–2016), The Cryosphere, 12, 811–831, https://doi.org/10.5194/tc-12-811-2018, 2018. a
NSIDC: Greenland Ice Sheet Today, available at: http://nsidc.org/greenland-today/2016/10/2016-melt-season-in-review/ (last access: 6 December 2017), 2016. a
Pfeffer, W. T. and Humphrey, N. F.: Formation of ice layers by infiltration and refreezing of meltwater, Ann. Glaciol., 26, 83–91, https://doi.org/10.1017/S0260305500014610, 1998. a
Roth, K., Schulin, R., Flüler, H., and Attinger, W.: Calibration of Time Domain Reflectrometry for Water Content Measurement Using a Composite Dielectric Approach, Water Resour. Res., 26, 226–273, 1990. a
Sasgen, I., van den Broeke, Michiel, Bamber, J. L., Rignot, E., Sørensen, L. S., Wouters, B., Martinec, Z., Velicogna, I., and Simonsen, S. B.: Timing and origin of recent regional ice-mass loss in Greenland, Earth Planet. Sc. Lett., 333–334, 293–303, https://doi.org/10.1016/j.epsl.2012.03.033, 2012. a
Schmid, L., Heilig, A., Mitterer, C., Schweizer, J., Maurer, H., Okorn, R., and Eisen, O.: Continuous snowpack monitoring using upward-looking ground-penetrating radar technology, J. Glaciol., 60, 509–525, https://doi.org/10.3189/2014JoG13J084, 2014. a, b, c, d, e, f, g
Schneider, T. and Jansson, P.: Internal accumulation in firn and its significance for the mass balance of Storglaciären, Sweden, J. Glaciol., 50, 25–34, 2004. a
Shepherd, A., Ivins, E. R., A, G., Barletta, V. R., Bentley, M. J., Bettadpur, S., Briggs, K. H., Bromwich, D. H., Forsberg, R., Galin, N., Horwath, M., Jacobs, S., Joughin, I., King, M. A., Lenaerts, J. T. M., Li, J., Ligtenberg, S. R. M., Luckman, A., Luthcke, S. B., McMillan, M., Meister, R., Milne, G., Mouginot, J., Muir, A., Nicolas, J. P., Paden, J., Payne, A. J., Pritchard, H., Rignot, E., Rott, H., Sørensen, L. S., Scambos, T. A., Scheuchl, B., Schrama, E. J. O., Smith, B., Sundal, A. V., van Angelen, J. H., van de Berg, W. J., van den Broeke, M. R., Vaughan, D. G., Velicogna, I., Wahr, J., Whitehouse, P. L., Wingham, D. J., Yi, D., Young, D., and Zwally, H. J.: A reconciled estimate of ice-sheet mass balance, Science, 338, 1183–1189, https://doi.org/10.1126/science.1228102, 2012. a
Steffen, K., Box, J. E., and Abdalati, W.: Greenland Climate Network: GC – Net, in: Special Report on Glaciers, Ice Sheets and Volcanoes, trib. to M. Meier, edited by: Colbeck, S. C. and CRREL, 96–27, 98–103, 1996. a, b
Steger, C. R., Reijmer, C. H., and van den Broeke, M. R.: The modelled liquid water balance of the Greenland Ice Sheet, The Cryosphere, 11, 2507–2526, https://doi.org/10.5194/tc-11-2507-2017, 2017a. a, b
Steger, C. R., Reijmer, C. H., van den Broeke, M. R., Wever, N., Forster, R. R., Koenig, L. S., Kuipers Munneke, P., Lehning, M., Lhermitte, S., Ligtenberg, S. R. M., Miège, C., and Noël, B. P. Y.: Firn Meltwater Retention on the Greenland Ice Sheet: A Model Comparison, Front. Earth Sci., 5, F03011, https://doi.org/10.3389/feart.2017.00003, 2017b. a
Tedesco, M., Serreze, M., and Fettweis, X.: Diagnosing the extreme surface melt event over southwestern Greenland in 2007, The Cryosphere, 2, 159–166, https://doi.org/10.5194/tc-2-159-2008, 2008. a
Tedesco, M., Fettweis, X., van den Broeke, M. R., van de Wal, R. S. W., Smeets, C. J. P. P., van de Berg, W. J., Serreze, M. C., and Box, J. E.: The role of albedo and accumulation in the 2010 melting record in Greenland, Environ. Res. Lett., 6, 014005, https://doi.org/10.1088/1748-9326/6/1/014005, 2011. a
Tedesco, M., Fettweis, X., Mote, T., Wahr, J., Alexander, P., Box, J. E., and Wouters, B.: Evidence and analysis of 2012 Greenland records from spaceborne observations, a regional climate model and reanalysis data, The Cryosphere, 7, 615–630, https://doi.org/10.5194/tc-7-615-2013, 2013. a
van As, D., Box, J. E., and Fausto, R. S.: Challenges of Quantifying Meltwater Retention in Snow and Firn: An Expert Elicitation, Front. Earth Sci., 4, F03011, https://doi.org/10.3389/feart.2016.00101, 2016. a
van den Broeke, M., Box, J., Fettweis, X., Hanna, E., Noël, B., Tedesco, M., van As, D., van de Berg, W. J., and van Kampenhout, L.: Greenland Ice Sheet Surface Mass Loss: Recent Developments in Observation and Modeling, Current Climate Change Reports, 8, 2293, https://doi.org/10.1007/s40641-017-0084-8, 2017. a
van den Broeke, M. R., Enderlin, E. M., Howat, I. M., Kuipers Munneke, P., Noël, B. P. Y., van de Berg, W. J., van Meijgaard, E., and Wouters, B.: On the recent contribution of the Greenland ice sheet to sea level change, The Cryosphere, 10, 1933–1946, https://doi.org/10.5194/tc-10-1933-2016, 2016. a
Vaughan, D., Comiso, J., Allison, I., Carrasco, J., Kaser, G., Kwok, R., Mote, P., Murray, T., Paul, F., Ren, J., Rignot, E., Solomina, O., Steffen, K., and Zhang, T.: Observations: Cryosphere, chap. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 317–382, 2013. a
Vernon, C. L., Bamber, J. L., Box, J. E., van den Broeke, M. R., Fettweis, X., Hanna, E., and Huybrechts, P.: Surface mass balance model intercomparison for the Greenland ice sheet, The Cryosphere, 7, 599–614, https://doi.org/10.5194/tc-7-599-2013, 2013. a
Vizcaíno, M., Mikolajewicz, U., Jungclaus, J., and Schurgers, G.: Climate modification by future ice sheet changes and consequences for ice sheet mass balance, Clim. Dynam., 34, 301–324, https://doi.org/10.1007/s00382-009-0591-y, 2010. a
Wever, N., Schmid, L., Heilig, A., Eisen, O., Fierz, C., and Lehning, M.: Verification of the multi-layer SNOWPACK model with different water transport schemes, The Cryosphere, 9, 2271–2293, https://doi.org/10.5194/tc-9-2271-2015, 2015. a, b
Wilhelms, F.: Explaining the dielectric properties of firn as a density-and-conductivity mixed permittivity (DECOMP), Geophys. Res. Lett., 32, L16501, https://doi.org/10.1029/2005GL022808, 2005. a