Simulating the roles of crevasse routing of surface water and basal friction on the surge evolution of Basin 3, Austfonna ice cap

The marine-terminating outlet in Basin 3, Austfonna ice cap, has been accelerating since the mid-1990s. Stepwise multi-annual acceleration associated with seasonal summer speed-up events was observed before the outlet entered the basin-wide surge in autumn 2012. We used multiple numerical models to explore hydrologic activation mechanisms for the surge behaviour. A continuum ice dynamic model was used to invert basal friction coefficient distributions using the control method and observed surface velocity data between April 2012 and July 2014. This has provided input to a discrete element model capable of simulating individual crevasses, with the aim of finding locations where meltwater entered the glacier during the summer and reached the bed. The possible flow paths of surface meltwater reaching the glacier bed as well as those of meltwater produced at the bed were calculated according to the gradient of the hydraulic potential.

The inverted friction coefficients show the “unplugging” of the stagnant ice front and expansion of low-friction regions before the surge reached its peak velocity in January 2013. Crevasse distribution reflects the basal friction pattern to a high degree. The meltwater reaches the bed through the crevasses located above the margins of the subglacial valley and the basal melt that is generated mainly by frictional heating flows either to the fast-flowing units or potentially accumulates in an overdeepened region. Based on these results, the mechanisms facilitated by basal meltwater production, crevasse opening and the routing of meltwater to the bed are discussed for the surge in Basin 3.

1 Introduction

The Austfonna ice cap, located on Nordaustlandet in the Svalbard archipelago, is the largest ice mass in the Eurasian Arctic in terms of area (7800 km²) (Moholdt and Kääb, 2012). Basin 3 is one of its south-eastern basins containing a marine-terminating outlet glacier. The glacier is marine-grounded to as much as 150 m below sea level and is known to have surged around 1850–1870 (Dowdeswell et al., 1986).

The northern flow unit of the outlet glacier has experienced long-term acceleration since the mid-1990s (Dowdeswell et al., 1986) along with stepwise interannual accelerations since 2008. These short-lived summer speed-up events occurred during the surface melt season (Dunse et al., 2015). The southern corner of Basin 3 accelerated to about 290 m a⁻¹ in spring 2008 but had decelerated again by spring 2011 (Gladstone et al., 2014). However, high velocities were again observed in the same area during spring 2012, which subsequently gradually increased to ∼ 1800 m a⁻¹ after the summer melt season and before a basin-wide surge took place in autumn 2012 (Dunse et al., 2015). The surge reached its peak in January 2013 with a maximum velocity of ∼ 6500 m a⁻¹.

The 130–140-year-long quiescent phase of Basin 3 is similar to other Svalbard glaciers, but the two-decade-long accelerating phase of the northern flow unit exceeds those of other glaciers such as the 7–11 years of Monacobreen (Strozzi et al., 2002). The stepwise multi-annual acceleration observed since 2008, associated with seasonal summer speed-up events, is also distinguishable from other surging glaciers in Svalbard. Similar melt season speed-up events have been observed in Greenland, and they provide evidence for rapid, large-scale, dynamic responses of the ice sheet to climate warming (Sundal et al., 2011; van de Wal et al., 2008; Zwally et al., 2002). Sundal et al. (2011) pointed out that a simple model of basal lubrication alone could not simulate the fast-flowing manner of the glaciers on Greenland ice sheet, and that an improved understanding of subglacial drainage would be essential in model studies that capture ice dynamic responses to climate warming. This applies also to the surge in Basin 3, which requires a mechanism involving both thermal and hydrologic changes to explain the interannual and seasonal accelerations (e.g. Dunse et al., 2015; Gladstone et al., 2014).

The glacier in Basin 3 (recently named Storisstraumen) is polythermal, with a maximum ice thickness of 567 m, which is sufficient to raise internal ice temperatures to the pressure melting point (pmp) (Dunse et al., 2011). Where the ice is thinner, closer to the margins, the ice is probably frozen to the bed except under fast-flowing outlets. In principle the surge of polythermal glaciers can be explained by a soft-bed mechanism with some constraints for the initiation, such as the unfreezing of the cold bed by the evolution of the thermal regime or by the input of meltwater from englacial channels (Clark, 1976; Lingle and Fatland, 2003; Robin, 1955).

Gladstone et al. (2014) suggested soft-bed sliding mechanisms involving feedbacks in the hydrological system at the ice–till interface. They respond to the penetration of surface melt and explain the summer speed-up events that have been observed since 2008. Surface meltwater can penetrate cold and polythermal glacier ice in High Arctic glaciers and the Greenland ice sheet through moulins and fractures that cut down all the way to the glacier bed (e.g. Benn et al., 2009; Copland et al., 2003; van de Wal et al., 2008; Zwally et al., 2002). Water-filled crevasses can penetrate to the glacier bed regardless of ice thickness or crevasse spacing, as long as the tensile stress acting normal to the crevasse exceeds about 100 kPa (Boon and Sharp, 2003; van der Veen, 1998). Bougamont et al. (2014) investigated the sensitivity of the basal hydrology system in the Russell glacier catchment to the volume of surface melt delivered to the bed and found that increases in surface melt volumes lead to faster summer flow.

Dunse et al. (2015) has suggested a hydrothermodynamic feedback whereby summer meltwater penetrating to the bed is not considered a purely external forcing to the system: meltwater penetrating crevasses to reach the bed enhances basal processes such as lubrication and sediment deformation, resulting in enhanced ice flow and potentially an increase in extensional stress, which may in turn cause increased crevasse formation over a larger area, routing more ice down to the bed.

These earlier studies highlight the importance of time-evolving basal temperature and friction, which are strongly influenced by the evolution of a basal hydrology system. The basal hydrology system can be fed both by in situ melting and by surface meltwater, and has the capacity to not only directly cause sliding but also to alter the thermal regime and hence deformational flow.

Previous crevasse modelling studies simulate the formation of fractures as a continuous process. They treat the development of cracks on a macroscopic scale by either using simplified parameterisation of fracturing effects via variables such as depth of crevasse (Cook et al., 2014; Nick et al., 2010, 2013; Weertman, 1973) or using continuous damage mechanics (CDM), which simulates the continuous process from micro-scale cracks to macro-scale crevasses (Albrecht and Levermann, 2014; Bassis and Ma, 2015; Borstad et al., 2012, 2016; Krug et al., 2014). In this study we take a different approach and apply a discrete element model (Åström et al., 2013, 2014) capable of simulating crevasse formation as a microscopic-scale discrete process in addition to the continuum ice dynamics models. The discrete element model (HiDEM) is used to determine the locations of the crevasses penetrating though the full thickness of the glacier whereby surface water may reach the bed.

In Sect. 2 we present the observational data used to set up the simulation. In Sect. 3 we present the methodology. We used a continuum ice dynamic model to invert the basal friction fields from approximately monthly observations of ice surface velocities between April 2012 and July 2014. These basal friction fields then were input as boundary conditions for basal sliding in our discrete element model, which simulates crevasse distribution in the lower part of Basin 3 at particular points in time. We also converted a satellite image of crevasse distribution to a cartographic map using Radon transform and simplified line integral convolution to validate our modelled crevasse distribution results. In Sect. 4.1 we first investigate the evolution of the basal conditions in Basin 3 during and after the peak of the surge. In Sect. 4.2 we present the modelled crevasse distributions before and after maximum surge velocity and validated the latter with crevasse maps derived from satellite imagery. In Sect. 4.3 we locate the crevasses that reach the bed, calculate basal melt rates and estimate the flow path of the basal water. In Sect. 5 we discuss the mechanisms facilitated by basal meltwater production, surface meltwater and crevasse opening for the surge that occurred in Basin 3. In Sect. 6 we summarise the key findings of the study and present conclusions.

2 Observations

2.1 Surface and bedrock topography data

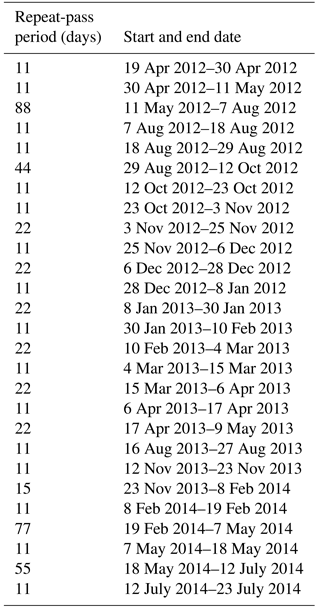
Bedrock elevation (Dunse, 2011) was derived by pointwise subtracting the measured ice thickness from a 250 m resolution map of surface elevation that was published by the Norwegian Polar Institute (NPI) in 1998 and InSAR data of Austfonna acquired in the years 1995–1996 (Unwin and Wingham, 1997). The ice thickness used for generating bedrock elevation was based on airborne radio echo sounding (RES; Dowdeswell et al., 1986) supplemented with two RES data sets from 2008 (Vasilenko et al., 2009). Marine bathymetry data (2 km horizontal resolution) were from the International Bathymetry Chart of the Arctic Ocean, version 2.0 (Jakobsson et al., 2008). Bathymetry and inland bedrock elevation were combined by using an interactive gridding scheme to eliminate the mismatch along the southern and north-western coastline (Dunse, 2011). We assumed that bedrock elevation did not have any significant changes over decadal timescales and used it with a set of updated surface elevation data. The surface elevation was derived from Cryosat altimetry data acquired during July 2010–December 2012 (McMillan et al., 2014). McMillan et al. (2014) grouped measurements acquired over a succession of orbit cycles that are within 2–5 km².

We point out several bed topography features (Fig. 1b) that are important to the investigation here. The subglacial hill located at roughly 700 km E and 8850 km N rises to about 250 m above sea level. A corresponding but smaller-magnitude bedrock maximum exists on the opposite side of Basin 3, approx. 15–20 km south-west of the hill. A subglacial valley runs between these bedrock maxima, marked SV in Fig. 1b, and extends several tens of kilometres upstream and downstream. The minimum bedrock height for Basin 3 is within an overdeepening in the lower part of the valley, marked OD on Fig. 1b. The importance of these features is discussed in more detail in Sects. 4 and 5.

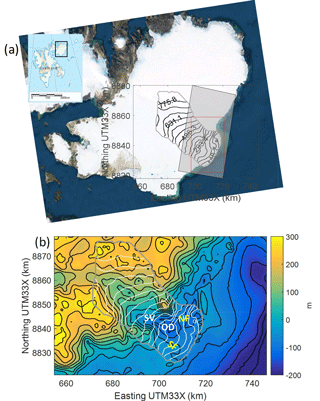
Figure 1 Surface and bedrock topography of Basin 3, Austfonna. (a) Surface elevation contours with solid black lines (with ∼ 48.2 m interval), on top of a satellite image of Nordaustlandet from TerraColor^® Global Satellite Imagery (http://www.terracolor.net/). The grey transparent box shows the coverage of the TerraSAR-X scene (30 April 2012). The model domain of HiDEM is outlined with a red box. The insert at the upper-left corner shows the ice cap's location within the Svalbard archipelago. (b) Bedrock topography is colour-coded, contoured with black solid line with a ∼ 37.1 m interval and superimposed by surface elevation contours (white solid line with ∼ 48.2 m interval). The grey solid line outlines Basin 3 and the model domain of Elmer/Ice in both panels. “SV” marks the subglacial valley that runs between two bedrock maxima in the north-east and south-west and extends several tens of kilometres upstream and downstream. “OD” marks the minimum bedrock height for Basin 3 and is within an overdeepening in the lower part of the valley. “NF” marks the downstream area of the northern flow unit of the glacier, which runs from upstream of the valley and exits from the northern terminus. The alignment of these labels roughly indicates the flow direction. Similarly, “SF” marks the downstream area of the southern flow unit.

2.2 Surface velocity data

We used velocity time series maps (April 2012–July 2014) generated from TerraSAR-X (TSX) satellite synthetic aperture radar (SAR) scenes (Table 1; Schellenberger et al., 2017) as the input surface velocity data for basal friction coefficient inversion. These maps were based on original 2 m resolution TSX scenes provided by the German Aerospace Center (DLR), covering only the lower part of Basin 3 (Fig. 1a). To generate the final velocity maps for the times between two successive TSX images, which were geocoded using a DEM of Austfonna (Moholdt and Kääb, 2012), we needed to use displacement maps. The displacement maps between two consecutive acquisitions were determined using a cross-correlation of the intensity images (Strozzi et al., 2002).

Table 1 TerraSAR-X acquisitions of Basin 3 and repeat-pass periods.

The coverage of the TSX velocity was smaller than the model domain used by our ice dynamic model (Fig. 1a). Therefore we stitched the TSX data on top of two background velocity fields with larger coverage depending on the acquisition time. The TSX time series maps derived during 19 April 2012–28 December 2012 were stitched with a velocity snapshot from ERS-2 (European Remote Sensing Satellite 2) SAR observations acquired from March to April 2011 (Gladstone et al., 2014; Schäfer et al., 2014), and the TSX time series maps derived after 28 December 2012 were stitched with a velocity snapshot from Landsat 8 imagery acquired in April 2013. We then applied a row-wise recalculation of the velocity value for the grid points on the model mesh that were upstream from the TSX velocity map coverage (Fig. 1a) to create a smoother transition from the TSX velocity map to the background velocity map. The recalculation was carried out by weighting the background velocity data and TSX velocity data according to the distance between the column indices of the targeting grid point and the column indices of the first grid point that had values from the TSX velocity map on the same row.

The velocity recalculated for the upstream area was simply to avoid numerical instability that might appear at the boundary between the TSX and background velocities. So as not to bias the distribution calculation of the crevasses, we confined the discrete element model domain to a smaller region close to the ice front, which was fully covered by TSX velocity map and far away from this transition zone (Fig. 1a).

3 Methodology

3.1 Basal friction inversion in the ice flow model

The continuum ice dynamic model we used is Elmer/Ice, an open-source finite-element model for computational glaciology. In this study, the simulations with Elmer/Ice were carried out by considering a gravity-driven flow of incompressible and non-linearly viscous ice flowing over a rigid bed. Some of the governing equations are presented below. More details can be found in Gagliardini et al. (2013).

The ice flow was computed by solving the unaltered full Stokes equations, which express the conservation of linear momentum,

$$\begin{array}{}\text{(1)}& \mathrm{\nabla }\cdot \mathit{\sigma }+{\mathit{\rho }}_{\text{i}}\mathit{g}=\mathrm{\nabla }\cdot \mathit{\tau }-\mathrm{\nabla }p+{\mathit{\rho }}_{\text{i}}\mathit{g}=\mathrm{0},\end{array}$$

and the mass conservation for an incompressible fluid,

$$\begin{array}{}\text{(2)}& \mathrm{\nabla }\cdot \mathit{u}=\text{tr}\left(\dot{\mathit{\epsilon }}\right)=\mathrm{0},\end{array}$$

in which ρ_i is the ice density, $\mathit{g}=(\mathrm{0},\mathrm{0},-g)$ the gravity vector, $\mathit{u}=(u,v,w)$ the ice velocity vector, $\mathit{\sigma }=\mathit{\tau }-p\mathbf{I}$ the Cauchy stress tensor with $p=-\text{tr}\left(\mathit{\sigma }\right)/\mathrm{3}$ the isotropic pressure, τ the deviatoric stress tensor, I the identity matrix and $\dot{\mathit{\epsilon }}$ the strain-rate tensor.

The constitutive relation for ice rheology is given by Glen's flow law (Glen, 1955):

$$\begin{array}{}\text{(3)}& \mathit{\tau }=\mathrm{2}\mathit{\mu }\dot{\mathit{\epsilon }},\end{array}$$

where the effective viscosity μ is defined as

$$\begin{array}{}\text{(4)}& \mathit{\mu }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(\text{EA}{)}^{-}{\displaystyle \frac{\mathrm{1}}{n}}{\dot{\mathit{\epsilon }}}_{\text{e}}^{\frac{\mathrm{1}-n}{n}},\end{array}$$

in which n=3 is the Glen's flow law exponent, ${\dot{\mathit{\epsilon }}}_{\text{e}}^{\mathrm{2}}=\text{tr}\left({\dot{\mathit{\epsilon }}}^{\mathrm{2}}\right)/\mathrm{2}$ is the square of the second invariant of the strain rate tensor, E is the enhancement factor. A is the rate factor calculated via Arrhenius law:

$$\begin{array}{}\text{(5)}& {\displaystyle }& {\displaystyle }A=A_{\mathrm{0}}\exp \left(-{\displaystyle \frac{Q}{{\text{RT}}^{\prime }}}\right)\text{(6)}& {\displaystyle }& {\displaystyle }{T}^{\prime }=T+\mathit{\beta }p,\end{array}$$

where A₀ is the pre-exponential constant, Q is the activation energy, R=8.321 J mol⁻¹ K⁻¹ is the universal gas constant and T^′ is the temperature relative to pressure melting.

The upper surface, $Z_{\text{s}}(x,y,z)$, evolved with time in transient simulations through an advection equation:

$$\begin{array}{}\text{(7)}& {\displaystyle \frac{\partial Z_{\text{s}}}{\partial t}}+u_{\text{s}}{\displaystyle \frac{\partial \left(Z_{\text{s}}\right)}{\partial x}}+v_{\text{s}}{\displaystyle \frac{\partial \left(Z_{\text{s}}\right)}{\partial y}}-w_{\text{s}}=M_{\text{s}},\end{array}$$

where $(u_{\text{s}},v_{\text{s}},w_{\text{s}})$ is the surface velocity vector obtained from the Stokes solution, and M_S is the meteoric accumulation/ablation rate at the glacier surface.

For all the simulations carried out in this study a linear relation linking basal shear stress, τ_b, to basal velocity, ${\mathit{u}}_{\text{b}}=(u_{\text{b}},v_{\text{b}},w_{\text{b}})$, was applied:

$$\begin{array}{}\text{(8)}& {\mathit{\tau }}_{\text{b}}=-C{\mathit{u}}_{\text{b}},\end{array}$$

in which C=10^α is the basal friction coefficient.

We performed inverse modelling of basal friction coefficient distributions from all the surface velocity observation snapshots using Elmer/Ice based on the control method (MacAyeal, 1993; Morlighem et al., 2010) implemented in Elmer/Ice by Gillet-Chaulet et al. (2012). The inverse modelling determined the spatial distribution of the exponent, α, of the basal friction coefficient, C, by minimising the mismatch between modelled and observed surface velocity as defined by a cost function:

$$\begin{array}{}\text{(9)}& J_o={\int }_{{\mathrm{\Gamma }}_{\text{s}}}{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\left(\left|{\mathit{u}}_{\text{mod}}\right|-\mathrm{|}{\mathit{u}}_{\text{obs}}\mathrm{|}\right)}^{\mathrm{2}}d\mathrm{\Gamma },\end{array}$$

where $\left|{\stackrel{\mathrm{‾}}{u}}_{\text{mod}}\right|$ and $\left|u_{\text{obs}}\right|$ are the magnitudes of the modelled and observed horizontal surface velocities. The mismatch in the direction of the velocity components is ignored and only a match of the velocity magnitude is optimised.

A Tikhonov regularisation term penalising the spatial first derivatives of α was used to avoid overfitting:

$$\begin{array}{}\text{(10)}& J_{\text{reg}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\underset{{\mathrm{\Gamma }}_{\text{b}}}{\int }{\left({\displaystyle \frac{\partial \mathit{\alpha }}{\partial x}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{\partial \mathit{\alpha }}{\partial y}}\right)}^{\mathrm{2}}d\mathrm{\Gamma },\end{array}$$

such that the total cost function is now written as

$$\begin{array}{}\text{(11)}& J_{\text{tot}}=J_{\mathrm{0}}+\mathit{\lambda }{J}_{\text{reg}},\end{array}$$

where λ is a positive ad-hoc parameter. We adopted the same procedure as in Gillet-Chaulet et al. (2012) to find the optimal λ value.

As introduced in Sect. 1, ideally, a soft-bed sliding mechanism needs to be presented in the simulation to be able to capture the surging behaviour. However, as the main goal of this study is only to find a model approach to locate the surface meltwater input sources, a linear basal sliding relation solved with an inverted parameter (C), which reflects the observation quite well (Fig. 2) is good enough to serve this purpose.

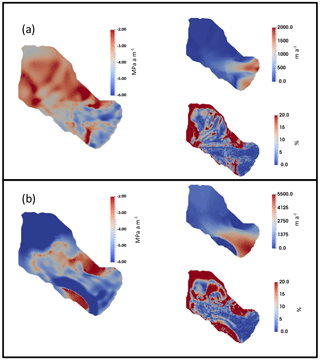
Figure 2 Basal friction coefficient inverted from surface velocity data in (a) 18–29 August 2012 (C_pre) and (b) 16–27 August 2013 (C_post). Both panels display a basal friction coefficient shown on the left, surface velocity data after post-processing (Sect. 2.2) shown on the upper right and the relative difference between observed and modelled surface velocity magnitude shown on the lower right.

The temperature distribution was calculated according to the general balance equation of internal energy written as

$$\begin{array}{}\text{(12)}& {\mathit{\rho }}_{\text{i}}{c}_{\text{v}}\left({\displaystyle \frac{\partial T}{\partial t}}+\mathit{u}\cdot \mathrm{\nabla }T\right)=\mathrm{\nabla }\cdot \left(\mathit{\kappa }\mathrm{\nabla }T\right)+\dot{\mathit{ϵ}}:\mathit{\sigma },\end{array}$$

where κ=κ(T) and c_v=c_v(T) are the heat conductivity and specific heat of ice, respectively. $\dot{\mathit{ϵ}}:\mathit{\sigma }$ represents the amount of energy produced by ice deformation. The upper value of the temperature T is constrained by the pressure melting point T_m of ice.

The Dirichlet boundary condition at the upper surface was prescribed as

$$\begin{array}{}\text{(13)}& T_{\text{surf}}=T_{\text{sea}}+\mathrm{\Gamma }{z}_{\text{s}},\end{array}$$

where T_surf is the surface ice temperature, $T_{\text{sea}}=-\mathrm{7.68}$ ^∘C is the mean annual air temperature at sea level estimated from two weather stations on Austfonna during 2004 and 2008 (Schuler et al., 2014) and four weather stations on Vestfonna during 2008 and 2009 (Möller et al., 2011), and Γ = 0.004 K m⁻¹ is the lapse rate (Schuler et al., 2007).

An initial guess of the ice temperature, T_init, was given by

$$\begin{array}{}\text{(14)}& T_{\text{init}}=T_{\text{surf}}+{\displaystyle \frac{q_{\text{geo}}}{\mathit{\kappa }}}d,\end{array}$$

where q_geo=40.0 mW m⁻² is the geothermal heat flux (Dunse et al., 2011) and d is the distance from the upper surface.

Spatially varied ice temperature (T) snapshots in the flow solution were accommodated using an iterative process which includes four parts: (i) invert C_invert for the first time with either an initial guess of C_init and T_init or the previously inverted C_prev and T_prev; (ii) carry out a steady-state simulation only for thermodynamics to calculate T_invert using the velocities obtained from the inversion; (iii) do the inversion again using C_invert and T_invert derived from the previous simulations; (iv) repeat the iteration until the differences in C_invert and T_invert between the two successive iterations fall below a given threshold. More details about the interactive process can be found in Gong et al. (2016).

All the thermodynamic-coupled inversions were done in chronological order with a transient simulation after each inversion to evolve the geometry for the next inversion. A month of geometry evolution was started, with the C field being inverted from the first velocity map acquired during that month to evolve the glacial geometry for 30 days with a temporal resolution of half a day and mean 1990–2000 surface mass budget (SMB) forcing from the regional climate model HIRHAM 5 (Christensen et al., 2007). In the case of acquisition time gaps (Table 1; mostly after August 2013) transient simulations were carried out for the length of the gap with the latest C distribution and a temporal resolution of 1 day.

All simulations were computed on an unstructured mesh over Basin 3 and generated with the open-source software GMSH (Geuzaine and Remacle, 2009). The element size of the mesh increased from ∼ 150 m at the glacier terminus to 2500 m at the back of the basin. The 2-D mesh was then vertically extruded between the interpolated bedrock and surface elevation into 10 equally spaced terrain-following layers to form a 3-D mesh.

A fixed calving front criterion was adopted in all the simulations in this study due to the lack of ice thickness information corresponding to the observed calving front positions after 2011. The criterion assumed that the calving front was always grounded with a positive height above floatation, which reflected the observation at the terminus in Basin 3. As the near-frontal region was not confined between lateral walls we would not expect a significant impact of different calving front positions on longitudinal stress gradients upstream; i.e. the migration of the calving front would have less of an impact on the basal shear stress distribution in the upstream area than on the uncertainties brought by the observed ice velocity or the lack of ice thickness information at the calving front. The fixed calving front criterion would not distort the basal shear stress calculation at the ice terminus either, as the basal resistance there was already low in 2012. However, as the ice front in the simulation did not migrate, the calving flux might be biased.

3.2 Crevasse distribution calculation by a discrete element model

HiDEM is a model for fracture formation and dynamics. In HiDEM, an ice body is divided into discrete particles connected by massless beams. The version of HiDEM used here is purely elastic rather than viscoelastic (Åström et al., 2013). The elastic version is sufficient for the purpose of locating fractures governed by glacier geometry and basal friction. If the initial state of a model glacier is out of elastic equilibrium, deformation within the ice will appear as a result of Newtonian dynamics.

The explicit scheme for simulating the Newtonian dynamics and the elastic modulus can be found in Riikilä et al. (2015). We use a Young's modulus Y=2.0 GPa and a Poisson ratio ν≈0.3 for the modelled ice here. The modelled ice fractures if the stress on a beam exceeds a fracture stress criterion (stretching or bending). The fracture stress is ∼ 1 MPa.

All the simulations in this study were carried out with 30 m spatial resolution (the particles are uniformly shaped and initially uniformly spaced). We used a time step length of 10⁻⁴ s and ran a simulation until the glacier began to approach an equilibrium state. Compared to viscous flow, elastic deformation and fracturing processes are very rapid, and a typical simulation covers about ∼ 10 min of glacier dynamics. At the end of a simulation, a crevasse field has formed. HiDEM reflects the instantaneous stress field calculated for the time of the input boundary conditions without consideration of any pre-existing damage or advection. Further details on the model, including sensitivity of the chosen parameters to the model results are discussed in Åström et al. (2013, 2014) and Riikilä et al. (2015). All parameters were set beforehand.

The simulations were set up with input data from marine bathymetry, bedrock topography, C field, and the surface topography. We selected two C snapshots inverted from velocity data observed in 18–29 August 2012 (C_pre) and 16–27 August 2013 (C_post) (Fig. 2) as a boundary condition for basal sliding in HiDEM. Those dates were chosen to model the crevasse distribution after the summer melt season before and after the peak in surge velocities observed in January 2013. The computations were carried out on an HPC cluster typically using 500 computing cores for a few hours.

3.3 Crevasse map

We created a crevasse map from satellite imagery to validate our modelled crevasse distribution. The map was generated from a Landsat 8 image acquired on 4 August 2013 using the Radon transform technique (Petrou and Kadyrov, 2004; Toft and Sørensen, 1996). We experimented with crevasse maps created from various different satellite sensors (Landsat 7, Landsat 8, ASTER, Sentinel-2), but here we used only the Landsat 8 scene, which combines good spatial coverage with high radiometric quality.

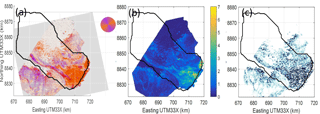
Figure 3 The crevasse maps created from Radon transform. (a) The orientation of crevasses indicated by a colour wheel, in which the strength of the signal controls the saturation. (b) The highest responding orientation from the Radon transform ($\stackrel{\mathrm{̃}}{s}\left(\mathit{\theta }\right))$ with the colour bar indicating the intensity. (c) The cartographic map indicating both the orientation and intensity of the two strongest responding orientations. Basin 3 is outlined by a black solid line.

The Radon transform has been demonstrated to be efficient in detecting along-flow features (Roberts et al., 2013), but can also be used for complex flow patterns, like the one in Basin 3 which has a wide range of crevasse orientations. The advantages of the Radon transform over other detecting methods are that crevasse patterns can be extracted where edge detectors methods (Bhardwaj et al., 2015; Wesche et al., 2013) would fail, and also that it is more robust than frequency-domain methods (Sangwine and Thornton, 1998) in detecting crevasses from incomplete coverage due to clouds, image borders or the calving front.

In this study we followed a similar approach to Roberts et al. (2013), but used a more robust implementation and a different post-processing procedure. Firstly, the satellite image was pre-processed with a Laplacian filter to prioritise the high frequencies, e.g. to sharpen the edges of surface features. We performed the Radon transform, R(p,θ) on 300 m × 300 m subsets of the satellite image, and project the image intensity I(x,y) along lines with tangent vectors oriented at θ to the x axis and offset by a perpendicular distance, p, from the origin (Toft and Sørensen, 1996):

$$\begin{array}{ll}{\displaystyle }R\left(p,\mathit{\theta }\right)=& {\displaystyle }\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}I\left(x,y\right)\mathit{\delta }\left(-x\text{sin}\mathit{\theta }+y\text{cos}\mathit{\theta }-p\right)\\ \text{(15)}& {\displaystyle }& {\displaystyle }\text{d}x\text{d}y,\end{array}$$

where the 2-D integration is restricted by the Dirac delta function, $\mathit{\delta }(-x\text{sin}\mathit{\theta }+y\text{cos}\mathit{\theta }-p)$, to the appropriate straight line in the x–y plane. The range of the transform coordinates is a half circle ($\mathrm{0}\le \mathit{\theta }<\mathit{\pi })$ and p is the spatial integral ranging over the domain of the subset of the image. The result of the transform was a 2-D feature space at different azimuthal orientations (θ). To capture both small and big crevasses, we resampled the image intensity I(x,y) in each 300 m × 300 m image subset with a resolution of 2 pixels and again implemented a weighted Radon transform function, where a mask over the subset was used to remove features like image borders, clouds, ocean etc. The resulting Radon transformation of a subset was again a 2-D subset. Then, the standard deviation at each orientation was used to extract the response for elongated texture:

$$\begin{array}{}\text{(16)}& s\left(\mathit{\theta }\right)=\sqrt{{\displaystyle \frac{\sum _{i=-P}^P{\left(R\left(i,\mathit{\theta }\right)-\stackrel{\mathrm{‾}}{R}\left(\mathit{\theta }\right)\right)}^{\mathrm{2}}}{N+\mathrm{1}}}}\end{array}$$

Here the overbar denotes the mean and N denotes the number of steps within the domain of p. Finally, a running median filter with a spacing of two (Δ=1^∘) was used to remove noise:

$$\begin{array}{}\text{(17)}& \stackrel{\mathrm{̃}}{s}\left(\mathit{\theta }\right)=\text{median}\left\{s\left(\mathit{\theta }-\mathrm{\Delta }\right),\mathrm{\cdots },s(\mathit{\theta }+\mathrm{\Delta }))\right\}.\end{array}$$

The results of the procedure were maps showing the dominating azimuthal orientations (θ) of the crevasse clusters (Fig. 3a) and their response ($\stackrel{\mathrm{̃}}{s}\left(\mathit{\theta }\right))$ (Fig. 3b) in each 300 m × 300 m window. We wish to compare the simulated crevasse pattern from HiDEM with these results from the observation. To identify crevasse zones and their alignment in the satellite images we processed an empty image array for each 300 m × 300 m window with randomly seeded high-intensity values. Then, a simplified line integral convolution was applied to add each element of the image to its local neighbours, weighted by a kernel. The kernel had an elongated shape. The orientation of the shape was dependent on θ at the underlying position. The response of the kernel (the intensities within) was dependent on $\stackrel{\mathrm{̃}}{s}\left(\mathit{\theta }\right)$ extracted from the underlying position. The resulting image is shown in Fig. 3c and was used in a visual comparison with the modelled crevasse distribution as well as by using the statistical Kappa method.

4 Results

4.1 Basal friction evolution

Figure 2 shows that the relative errors between the modelled and observed surface velocity magnitudes during both 18–29 August 2012 and 16–27 August 2013 are the lowest over the fast-flowing region (< 5 %; Fig. 2), which are mostly moving by basal sliding. The root-mean-square difference of the modelled surface velocity magnitude fields in the TXS data covered region (Fig. 1) for these two time periods are 65.0 and 190.9 m a⁻¹. As we are mostly interested in the ice dynamics of the fast-flowing area, these errors are acceptable for the crevasse formation simulations.

Figure 4 shows the friction pattern of the region that is fully covered by TSX velocity observations between April 2012 and July 2014, spanning the period of the Basin 3 peak surge velocities in January 2013. To make the pattern of the C distribution clearer we plotted the common logarithm of C (log₁₀ (C)). Figure 4a shows a clear expansion of low-friction area (log₁₀ (C) ≤ −3.5), both inland and to the frontal region in the southern basin before the glacier enters the peak of the surge.

In 2011 the low-friction patches in the central and southern basins were disconnected from the inland region and lay behind a stagnant terminus. Before May 2012, the enlarged low-friction area in both northern and southern glacier termini did not expand across the flat glacier bed in between them, which might impose some topographic restriction to the expansion of the fast flow. After the summer melt season (August 2012), the stagnant frontal region shrank to the glacial terminus, which might have thinned to reach a condition close to floatation (McMillan et al., 2014). During this period the low-friction area underneath the southern part expanded further inland and became connected to the northern low-friction area. In January 2013 the glacier reached its maximum flow speed and the low-friction area also expanded across the entire width of the basin near the calving front with a few particularly deep minima (log₁₀ (C) ≤ −5.5; almost vanishing friction) in the south (Fig. 4b).

After January 2013 the basal friction pattern in northern basin remained almost stable. The almost vanishing friction area (log₁₀ (C) ≤ −5.5) in the southern frontal region gradually shrank back inland, away from the terminus.

4.2 Crevasse distribution and validation

All the fractures calculated by HiDEM are wider than 0.055 m, and we regard them as crevasses in this study. The fractures marked with black dots (Fig. 5b, in both the upper-left and lower-left corners of the domain) are generated by boundary effects due to the limited domain. Although they might be deep enough to cut through the full depth of the ice we regard them as artificial crevasses. They are irrelevant to the water routing and surge processes we focus on in this paper, thus are excluded from the comparison in this section and the water routing calculation in Sect. 4.3.

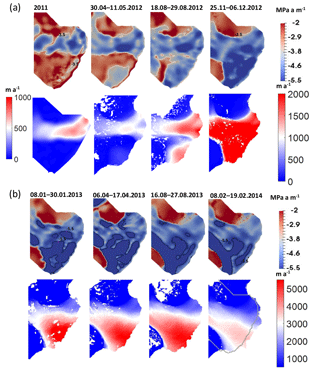
Figure 4 The evolution of the basal friction coefficient (C), with the corresponding observed speeds plotted below, shown for the model domain of HiDEM: (a) log₁₀(C), overlain with white contour lines showing log${}_{\mathrm{10}}\left(C\right)=-\mathrm{3.5}$ (low friction), from the time before the peak of the surge; (b) log₁₀(C), overlain with black contour lines showing log${}_{\mathrm{10}}\left(C\right)=-\mathrm{5.5}$ (almost vanishing friction), from the time period at and after the peak of the surge. The speed in 2011 was acquired from ERS-2 SAR imagery (colour bar on the left). The rest of the speed snapshots were from TSX SAR (colour bar on the right). The grey solid line outlines the Basin 3 boundary.

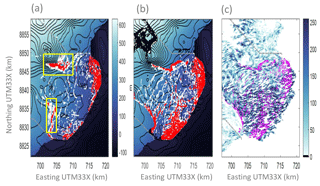
Figure 5 Crevasse distribution from HiDEM on (a) August 2012 and (b) August 2013 and (c) satellite observation. The colour of the underlying image in (a) and (b) shows the surface elevation of the glacier. Bedrock topography contours are shown in black with a ∼ 23.7 m interval. All the dots in both (a) and (b), regardless of the colour, indicate the modelled crevasse distribution from HiDEM. The red dots mark the cut-through crevasses. The red dots in the yellow boxes in (a) are the ones referred to as cut-through crevasses above the subglacial valley margins and are used for calculating the flow paths of the surface melt reaching the bed. The black dots in (b) (upper-left and lower-left corners) mark crevasses produced due to boundary effects in the model (Sect. 4.2). They are eliminated from the crevasse map. The rest of the crevasses are marked with white dots and are mostly shallow crevasses, hence irrelevant to water routing. The cartographic representation of the observed crevasse orientation on 8 August 2013 is shown in (c) (colour-coded with detecting intensity in the background). The magenta colour shows the area where modelled and observed crevasse match. The basin side boundary is outlined with a grey dashed line in all the subplots.

The crevasse map created by the Radon transform shows a highly crevassed glacial lower region, which comprise sections with crevasses of different orientation (Fig. 3). Transverse crevasses that are almost perpendicular to the flow direction can be found in both northern and southern flow units (Fig. 1b), reflecting large longitudinal tensile stress after dramatic acceleration. However, the detection intensity of the crevasse in the northern flow unit is rather weak. The terminus between the northern and middle flow units has a mixture of crevasses with orientations perpendicular to each other, indicating the expansion and merging of the two flow units. Marginal crevasses can be found above the subglacial valley (Fig. 1b) margins parallel to the local flow direction, reflecting lateral shear stresses and longitudinal compressive stress caused by the presence of the valley margins.

The modelled crevasse distribution reflects the broad features of the basal friction pattern (Fig. 5b). A high crevasse density is generated in areas with large tensile stress caused by extending flow on the lower part of Basin 3 as well as at shear margins between low- and high-friction areas. The orientation of the modelled crevasses in August 2013 above the subglacial valley margins agrees with the representation map of the observation (Fig. 5c). However, the orientations of most of the modelled crevasses in the middle-upper area have a ∼ 60^∘ mismatch with the satellite image (Fig. 5c) and the modelled crevasse density at the frontal area of the southern and northern flow units are larger than those in the observationally derived map.

Although the visual comparison between the two maps shows a general agreement (Fig. 5c), estimations of statistical quality of the simulated crevasse field with the observationally derived map are necessary. We calculated the Kappa coefficient (K) (Wang et al., 2016) to quantify the agreement, but this is not trivial as almost any two maps will be significantly different, with large sample sizes (> 62 483) (Monserud and Leemans, 1992). We achieve moderate agreement (Cohen, 1960), (K = 0.45) when resampling the two maps with a 1.5 × 1.5 km smoothing window and substantial agreement (K = 0.71) with a 4.6 × 4.6 km smoothing window. When including the artificial crevasses (defined at the beginning of the section) the agreement is only fair (K $\sim =$ 0.30) for both resampling windows. A variety of reasons can explain the resolution dependency of the results of the Kappa method: the ice dynamics model cannot advect crevasses; hence many crevasses in the image that in reality were created further upstream were simply not present in the simulation. Crevasse densities are very variable, and the observationally derived map is not a perfect representation of reality.

To investigate the crevasse distribution after the summer melt season in 2012, we used C_pre and the corresponding geometry within HiDEM. The configuration produced more crevasses in the frontal region of the northern flow unit than in the southern flow unit and almost no crevasses over the frontal region of the central flow unit (Fig. 5a). Crevasses also appeared at the margins of the subglacial valley.

By looking at the overall crevasse distributions in August 2012 and August 2013 (Fig. 5a and b), together with their corresponding C distributions (Fig. 4), we noticed that the outline of the densely crevassed region more or less follows the outline of the low-friction region, indicating the governing role of basal friction on crevasse formation. This was also shown by the fact that there were more crevasses formed in the southern and middle frontal areas in August 2013 than in August 2012 as the bed was more “slippery” in August 2013 (Fig. 4). The confining effects of the bed rock topography to the fast flow, basal friction and crevasse distribution also became more visible in the later stage of the surge: the modelled crevasses at the subglacial valley sides indicated a sharper boundary in August 2013 than in August 2012.

4.3 Surface and basal water sources

We defined “cut-through crevasses” as crevasses that penetrate through two-thirds of the ice depth and assume that they could cut through the full depth of ice if filled with water and potentially route the surface meltwater into the basal hydrology system vertically.

We selected the cut-through crevasses in August 2012 and August 2013 (red dots in Fig. 5a and b). In August 2012 most of the crevasses in the frontal area cut deep enough into the ice and very likely represented future calving locations for the terminus during its advance. Most of the crevasses located between the northern and southern fast-flowing regions were shallow surface crevasses. Many crevasses above the margins of the subglacial valley could reach the bed and potentially route the surface meltwater from upstream to the bed. By August 2013 more cut-through crevasses had been developed in the lower southern and central basins compared with August 2012 as velocity gradients significantly increased after the basin-wide acceleration. There were more cut-through crevasses present above the shear margin but almost no cut-through crevasses above the overdeepened area.

Using the locations of cut-through crevasses above the margins of the subglacial valley that could potentially route the surface meltwater down to the bed in August 2012, we calculated the subglacial water flow path according to the gradient of the hydraulic potential (Fig. 6a). The hydraulic potential (h) was calculated as below:

$$\begin{array}{}\text{(18)}& h=\left(z_{\text{s}}-z_{\text{b}}\right){\displaystyle \frac{{\mathit{\rho }}_{\text{i}}}{{\mathit{\rho }}_{\text{w}}}}+z_{\text{b}},\end{array}$$

in which z_s and z_b are surface and bedrock elevation, and ρ_i = 910 kg m⁻³ and ρ_w=1000 kg m⁻³ are the density of ice and water.

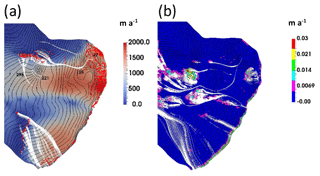
Figure 6 The flow paths of different water sources derived from the results in August 2012. (a) The white lines indicate the path of the surface meltwater after entering the glacier bed via cut-through crevasses (red dots) according to hydraulic potential. The modelled basal velocity magnitude is colour-coded in the background. (b) The white lines indicate the water path of the basal meltwater from locations with in situ melt rates above 0.005 m a⁻¹. The coloured contour lines indicate the value of the basal melt rate. The black contour lines in both (a) and (b) indicate isovalues of the hydraulic potential with a ∼ 10 m interval.

The flow paths are generated by being integrated through the vector field that follows the steepest descent in h using the fourth-order Runge–Kutta method.

The surface meltwater entering the bed in the north was predicted to either flow directly to the terminus or stop at the subglacial overdeepened area (Sect. 2.1; Fig. 6a). The surface meltwater entering the bed from the south was routed directly towards the terminus at the southern corner of the glacier, suggesting that surface melt contributed to the dramatic acceleration of the southern part of Basin 3 after the summer melt season in 2012.

In addition to the basal water supplied via the crevasse system, we also estimated the basal melt rate (Fig. 6b) for the temperate base area of the glacier. Within Elmer/Ice we computed the energy balance at the bed from estimated geothermal heat flux, strain heating and basal friction heating (Gong et al., 2016). Relatively high basal melt rates (> 0.005 m a⁻¹) appeared at the side walls of the subglacial valley around the overdeepened area, mainly caused by frictional heating. The basal meltwater followed similar flow patterns of the surface meltwater that reached the bed.

5 Discussion

Previous studies of the surge in Basin 3 (Dunse et al., 2012, 2015; Gladstone et al., 2014) revealed an atypical surge activation phase with multi-decadal acceleration superimposed, for at least 6 years, by short-lived, abrupt seasonal speed-up events that were clearly related to summer melt, which could not be explained solely by the thermal switch mechanism (Murray et al., 2003) typical of polythermal surging glaciers in Svalbard.

We used the discrete element model, HiDEM (Åström et al., 2014), to locate crevasses. In general the modelled crevasse distribution in August 2013 matches the crevasse map derived from satellite observation. However, there is a mismatch of the orientation in the middle-upper area (Fig. 5c). It may be because HiDEM only simulates the ad-hoc formation but not the advection of crevasses; thus no crevasse formation history can be inferred from the model. The inclusion of crevasse advection could be implemented in a two-way coupling of HiDEM with a continuum model accounting for damage transport in future studies. The mismatch of the crevasse density (Fig. 5c) at the northern and southern frontal areas could be caused by a mismatch in the ice front position between reality and the model. Although in reality the ice front advanced for several kilometres after the full surge, it was kept in a fixed position in Elmer/Ice (Sect. 3.1). The shape and steepness of the ice front are likely to affect the behaviour of the discrete element model. However, as they are concentrated at the terminus of the glacier, these crevasses are less likely to affect the basal hydrology system on a larger scale.

We then selected the modelled crevasses in August 2012 that might penetrate the ice far enough to act as routing paths from the glacier surface to the bed. In this study we focused on the cut-through crevasses that formed above the margins of the subglacial valley because the basal flow pattern of the surface melt entering through those crevasses was indicative of potential subglacial water routing and hydrology.

We cannot directly simulate or quantify the effects of the surface meltwater or basal meltwater on the surge development due to the lack of a basal effective pressure-dependent sliding relation. However, based on our results we can still present arguments to emphasise the role of crevasses, summer melt and the basal hydrology system in the seasonal speed-up events.

Firstly, our calculation of the flow paths of both surface melt entering through the crevasses and basal meltwater production suggest the potential for a direct lubricating effect acting beneath the northern and southern fast-flow units. Figure 6 shows that water entering through the crevasses downstream from the subglacial hill (the flow paths in the northern half of Fig. 6a) will flow through the area where the northern fast ice flow unit has developed. The water accessing the bed at the southern part of the basin travels directly towards the terminus at the southern corner of the glaciated system, which has dramatically accelerated during the melt season in 2012.

Secondly, some of the basal water flow paths presented in Fig. 6a and b terminate under a plateau in the hydraulic potential, which occurs in the overdeepened region (see also Fig. 1b). Given the very low gradients of our calculated hydraulic potential in this region and the presence of a local hydraulic potential minimum slightly downstream of the overdeepening, basal water would likely have low flow speeds and possibly even accumulate in the overdeepened bedrock region over time. This may have impacted the surge development in Basin 3. Also, given that the lowest basal resistance during most of 2012 (Fig. 4a) was immediately downstream of the overdeepening area in the northern flow unit, the outflow of accumulated water likely enhanced the surge activation here. If seasonal surface ice accumulates here and drains over a longer period, this may explain prolonged high ice velocities after the melt season has ended.

The temporary speed-up of the southern flow unit in 2008 (Gladstone et al., 2014) could have been triggered by an influx of basal water that was not repeated again until the basin-wide surge was initiated. An outburst of basal water that accumulated in the overdeepened bedrock region could provide one mechanism for this to occur. A ridge in hydraulic potential divides the northern and southern flow units in August 2012 (Fig. 6a). An anomalously high inflow of surface meltwater could have caused this ridge to be flooded if regular drainage channels were of insufficient capacity. We are unable to say how likely this is without a time series of surface melt data including the 2007 and 2008 seasons, but such an event could cause a temporary speed-up in the southern flow unit.

Englacial channels which may cause a redistribution of water within the hydrologic system (Fountain and Walder, 1998) are not directly considered in the current study. We assume that direct transfer of surface run-off via cut-through crevasses exceeds the englacial water transport at Basin 3.

Lastly, we look at the role of basal meltwater in the activation of the southern flow unit. Basal meltwater from further upstream in the northern flow unit can drain toward the southern unit (Fig. 6b; prior to the basin-wide surge, nearly all of the ice drained toward the northern flow unit). If this basal meltwater accumulated upstream due to the lower part of the glacier being below pressure melting point, the accumulated basal meltwater could have caused the speed-up once basal temperatures reached melting point under the southern corner and the hydrologic system extended beneath the southern flow unit. Also, basal meltwater generated locally in the overdeepened area (Fig. 6b) may not have been able to drain completely in one season; thus it could be accumulated locally. However, whether the basal meltwater can eventually burst out from the overdeepening area and contribute to the seasonal speed-up events or refreeze locally also depends on the development of the hydrology system and the thermal regime.

Although we lack either simulated or observed surface melt volumes for summer 2012, we would expect that the surface melt is much larger than basal melt. The run-off output from the HIRHAM5 regional climate model in 1995 (Ruth Mottram, Danish Meteorological Institute, personal communication, 2014; 1995 was not a year with high surface melt) at the location of the cut-through crevasses was at least 10 time larger than the basal melt rate in either 1995 or 2012. The volume of surface melt observed at weather stations located in south-western Basin 3 after the summer of 2004 was also at least 10 times larger (Schuler et al., 2007). Considering the seasonal timings and magnitudes of speed-up events, and the feedback between the surface meltwater input and hydraulic warming at the bed, it is clear that surface melt, when it can penetrate to the bed, causes a much greater impact on sliding and ice dynamics than the basal meltwater.

Then, we also discuss the role of the crevasse formation in the long-term acceleration. These are initiated as a consequence of extensional flow resulting from changes in the basal thermal structure in an early post-quiescent phase and act as the triggering and enhancing factor in the annual hydrothermodynamic feedback proposed by Dunse et al. (2015). While Dunse et al. (2015) are unspecific as to the cause of hydrothermodynamic initiation zone in the long-term glacier acceleration, we propose that the basal meltwater resulting from the gradual thickening of ice (raising basal temperatures) during the quiescent phase could sufficiently enhance flow speeds to initiate cut-through crevassing. The basal temperature distribution inversely calculated from the glacier geometry and velocity (Gong et al., 2016) showed a partially temperate bed in 1995 and expansion of the temperate region from 1995 to 2011, which is consistent with the presence of water at the bed. Given that basal meltwater fluxes are likely to be at least an order of magnitude lower than surface meltwater or run-off fluxes, it probably has a relatively small influence on glacier sliding. We suggest that water at the bed, which is likely to be primarily routed toward the northern rather than the southern flow unit due to topographic constraints (Fig. 6b), caused the speed-up from the quiescent phase during the last part of the 20th century and early 21st century.

This would require two key developments from quiescent to surge phase. Firstly, the initiation of sliding after ice thickening provided sufficient insulation for the bed to reach pressure melting temperature and generate meltwater. This could have occurred during the early 1990s. Then, at some point before August 2012, extensional flow due to sliding became sufficient to cause cut-through crevasses, leading to further acceleration and the surge onset due to the annual hydrothermodynamic feedback. We have demonstrated that cut-through crevasses are likely to be present just prior to the surge in Basin 3, and that surface meltwater can flow along the paths corresponding to the regions of observed fast flow.

It is not clear at which point the hydrothermodynamic feedback cut in, though it is likely to have first occurred in the northern flow unit, due to this unit's earlier acceleration. We suggest that the hydrothermodynamic feedback cut into the southern unit in 2011 or early 2012 due to crevasses penetrating near the southern margin (Fig. 5a), rapidly causing the basin-wide surge.

Direct verification of the long-term evolution of the surge active phase discussed above cannot be provided without quantification of the water reaching the bed and a basal sliding relation engaging the basal effective pressure. However, our approach and results can throw some light on future studies of coupled ice dynamic–thermodynamic–hydrology simulations.

6 Conclusions

We have forced the discrete element model HiDEM with outputs from the continuum ice dynamic model Elmer/Ice to study the crevasse distribution during the surge in Basin 3, the Austfonna ice cap in the period 2012–2013. Our continuum to discrete multimodel approach provides simulated locations where cut-through crevasses allow the surface meltwater to be routed to the bed. We have demonstrated that automatic crevasse detection through Radon transform may be used to validate simulated crevasse distribution from our continuum–discrete modelling approach. With the future addition of a basal hydrology model, the current study constitutes a step towards a fully coupled ice-dynamic englacial–basal hydrology modelling system in which both input locations of input surface water and basal meltwater generation are represented.

Our results support the hydrothermodynamic feedback to summer melt proposed by Dunse et al. (2015) to explain the seasonal speed-up in Basin 3 and the initiation of the acceleration of the southern flow unit in 2012. The calculated flow paths of the basal water according to hydraulic potential indicate either a direct enhancement to the ice flow through basal lubrication or a lagging mechanism through the outflow of accumulated water in the overdeepened area.

We propose that basal meltwater production caused the speed up from the quiescent phase of Basin 3 during the last part of the 20th century and early 21st century. Then, the hydrothermodynamic feedback initiated during 2011 or early 2012 caused the activation of the southern flow unit and the expansion of the surge across the entire basin. The quantification of the roles and mechanisms involving basal meltwater production, the surface meltwater and crevasse opening for the surge discussed in this study need to be further improved by coupling basal hydrology with the thermal regime evolution and surface mass and energy balance.

This publication also contains Matlab^® codes for generating crevasse maps from satellite images (Sect. 3.3) as a supplement.