Sediment transport capacity response to variations in water discharge in pressurized subglacial channels

Sediment transport capacity in both subaerial and subglacial channels depends on the shear stress exerted across the channel bottom, which varies with water velocity and channel width. In fully subaerial channels, water discharge variations are accommodated by flow depth and width changes along with water velocity. However, in subglacial channels, water is pressurized by the ice above, and they grow in response to the frictional heating of the water flowing through them. As a result, rapid changes in water discharge mainly result in velocity variations, as the channel geometry evolves slowly. Here, we present formulations of sediment transport capacity in different channel types and apply subglacial and subaerial hydraulics models to hydrographs from an Alpine glacier and a catchment of the Greenland Ice Sheet. Numerical experiments show that changing channel size results in sediment transport capacity peaking before the maximum water discharge. This hysteresis causes a highly variable relationship between sediment and water discharge in a transport-limited subglacial system. The results also indicate that high subglacial sediment transport capacities can occur across a wide range of water discharges. Reducing water discharge variability by smoothing lessens the hysteresis effects, in some cases to the point where a covarying relationship between water discharge and sediment transport capacity can be approached, similar to subaerial systems. A second set of numerical experiments shows that subglacial sediment transport is highly non-linear with respect to water discharge, creating more variability in sediment transport capacity. Yet, the results and formulations of subglacial sediment transport capacity show that its variability can approach that of subaerial systems when subglacial channel size is in equilibrium with water discharge. The implications of these findings help to evaluate sediment discharge from glaciers with different hydro-climatic forcings and to establish sources of variability in sediment export–water discharge relationships. These findings can improve the interpretation of sediment discharge records in glacierized catchments.

1 Introduction

Changes in glacier dynamics and hydrology have motivated numerous recent studies on sediment transport processes in cold regions (e.g. Li et al., 2022; Vergara et al., 2022; Zhang et al., 2022). Increases in sediment transport have been observed in Greenland (Bendixen et al., 2017), the European Alps (Costa et al., 2018), the Himalayas (Li et al., 2021), and the Andes (Vergara et al., 2022). To accurately explain the observed changes in sediment transport in glacierized catchments, the processes controlling sediment discharge and its variations with water discharge need to be examined (e.g. Riihimaki et al., 2005; Swift et al., 2005).

Glacier abrasion and quarrying sculpt landscapes and create sediment that is transported fluvially over periods of millennia or longer (cf. Hallet, 1979; Iverson, 2012; Ugelvig et al., 2018). Pressurized subglacial water can transport this sediment from underneath glaciers (Walder and Fowler, 1994; Creyts et al., 2013; Beaud et al., 2018; Delaney et al., 2019) if it is reachable by the water.

In a transport-limited regime, sediment discharge is controlled by sediment transport capacity, which is defined as the amount of sediment the water can carry. In both subglacial and subaerial channels, sediment transport capacity depends on the shear stress between water and the sediment it flows over (Shields, 1936; Meyer-Peter and Müller, 1948; Engelund and Hansen, 1967) as well as the width of the channel bottom w over which sediment mobilizes. The shear stress τ responds to the velocity of water v flowing through the channel so that

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }\mathit{\tau }\propto v^{\mathrm{2}}.\end{array}$$

The mean velocity of the water flowing through a channel is

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }v={\displaystyle \frac{Q}{S}},\end{array}$$

where Q is water discharge, and S is the channel's wetted area.

In subaerial channels operating with open channel flow, S evolves with changing water discharge Q, by changing both the channel width and the water depth (Leopold and Maddock, 1953). The change in water depth results in a proportional increase in water velocity, and the shear stress τ increases according to Eq. (1).

However, the response of water velocity to changing water discharge in subglacial channels differs from that in subaerial ones. The size of subglacial channels is controlled by two opposing processes: channel opening due to frictional heating from water flow on the one hand, and creep closure due to ice flow on the other (Röthlisberger, 1972). As a result, the subglacial channel size evolves relatively slowly over days, whereas water discharge can vary more quickly over hours (e.g. Iken and Bindschadler, 1986; Andrews et al., 2014; Nanni et al., 2020). Therefore, subglacial water flow behaves more like pipe flow over short periods (hours or days), and changes in water discharge Q are mainly accommodated by changing water velocity v (Eq. 2 and Fig. 1; Alley et al., 1997).

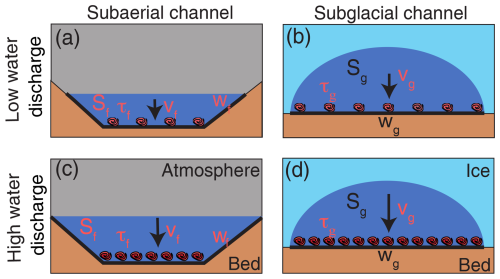
Figure 1 Sketch of the different responses of subglacial and subaerial channels to increased water discharge over short time scales. Variables in black remain constant with short variations in water discharge, whereas variables in colour change. Arrow length denotes water velocity magnitudes in the subglacial (subaerial) v_g (v_f) channels. S_g (S_f) represents the wetted area in the subglacial (subaerial) channels. The subglacial channel width w_g remains unchanged, while the subaerial channel width w_f evolves with water discharge. Subglacial (subaerial) shear stress τ_g (τ_f) is responsible for the mobilization of sediment.

Because of the above, sediment mobilization in subaerial and subglacial channels responds differently to changing water discharge. These differences are implicitly included in a range of models quantifying sediment transport in both subglacial and subaerial channels (e.g. Walder and Fowler, 1994; Alley et al., 1997; Tucker and Slingerland, 1997; Creyts et al., 2013; Beaud et al., 2018; Delaney et al., 2019; Hewitt and Creyts, 2019; Wickert and Schildgen, 2019). To date, several modelling frameworks have examined subglacial sediment transport with evolving channel size (Creyts et al., 2013; Beaud et al., 2018; Delaney et al., 2019; Hewitt and Creyts, 2019). However, these works minimally discuss the impact of different hydrological regimes on sediment transport capacity underneath glaciers in the context of interpreting sediment transport records. The few explicit parameterizations of subglacial sediment transport capacity with respect to water discharge assume fixed channel size (Alley et al., 1997). These formulations demonstrate that subglacial sediment transport capacity has a strongly non-linear response to water discharge. Yet, continually evolving channel size can impact variations in sediment transport capacity. Understanding these processes is imperative for establishing the effect of hydro-climatic conditions on subglacial sediment dynamics, especially as sediment discharge capacity controls the mobilization and deposition of sediment. This makes it a fundamental aspect of subglacial sediment evacuation, especially over short timescales.

Despite the different physical processes in subaerial and subglacial systems, observed water discharge and sediment export are often compared in contemporary glacierized catchments (e.g. Willis et al., 1996; Hodson et al., 1998; Pearce et al., 2003; Richards and Moore, 2003; Swift et al., 2005, 2021; Chu et al., 2009, 2012; Tedstone and Arnold, 2012; Overeem et al., 2017; Delaney et al., 2018; Lu et al., 2022; Andresen et al., 2024). Many of these studies discuss the disparity between water discharge and sediment export, especially given the role of sediment availability or production. Yet, a variable relationship between water discharge and sediment export can be expected in glaciers with evolving conduit size in a transport-limited regime. The response of sediment transport capacity to water discharge variations may affect the interpretation of sediment transport records in these glacierized catchments (e.g. Ganti et al., 2016; Mancini et al., 2023; Núñez Ferreira et al., 2025). This relationship must be clarified, as sediment dynamics change in glacierized regions along with changing hydrology (e.g. Brunner et al., 2019), which can increase the variability of water discharge (Lane and Nienow, 2019) and occurrence of extreme glacier melt (e.g. Overeem et al., 2015; Cremona et al., 2023), which may drive high magnitude sediment transport events.

This paper has two objectives: (1) to establish the hydrological conditions where sediment transport capacity co-varies with water discharge in subglacial systems, and (2) to evaluate the variability of sediment transport capacity in subglacial channels with evolving channel size and different hydrographs compared to subaerial ones. We use numerical models to examine sediment transport capacity in both subglacial channels that evolve in size and subaerial channels that remain fixed. They are applied to proglacial hydrological records from an Alpine glacier in Switzerland (Fieschergletscher) and a land-terminating glacier in Greenland (Leverett Glacier). We also run a model ensemble to evaluate the sediment transport capacity variability in subglacial channels compared to subaerial channels. Lastly, we present algebraic formulations of the sediment transport capacity response to water discharge in subaerial, steady-state R-channel, and pipe flow conditions. These formulations extend the relationships presented in Alley et al. (1997) and illustrate sediment transport capacity behaviour under different channel assumptions. The paper then discusses the implications of variability in sediment transport capacity from glaciers and the interpretation of sediment transport records.

2 Study sites and data

The water discharge data is from Alpine and ice sheet settings collected downstream of the glacier and assumes no water storage in the proglacial area. The Alpine site (labelled ALPINE) is Fieschergletscher in the Swiss Alps (46°29^′07^′′ N, 8°08^′03^′′ E). The water discharge data used here was collected at a 1 min interval from 24 May 2014 to 10 October 2014 (Fig. 2a; Felix et al., 2022).

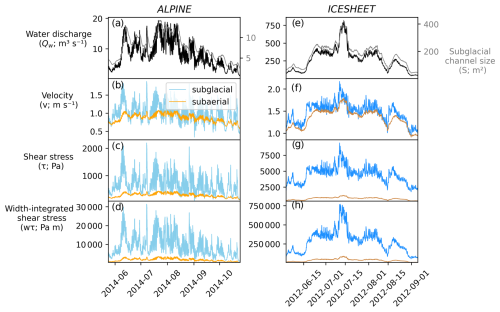
Figure 2 Model outputs from simulations using the hydrographs in panels (a) and (e) for the scenarios ALPINE (a–d) and ICESHEET (e–h). Black (grey) lines in (a) and (e) represent the subglacial water discharge (channel size). Blue (orange) lines represent outputs from the subglacial (subaerial) channel. Data are shown at 15 min intervals. Arrows highlight cases where variables peak in the subglacial channel before the subaerial one.

The Leverett Glacier in Greenland (labelled ICESHEET) serves as the ice sheet setting. Water discharge was measured roughly 2 km downstream from the terminus (67°03^′5^′′ N, 50°12^′59^′′ W), at a 5 min time interval from 28 May 2012 to 8 August 2012 (Fig. 2b; Tedstone et al., 2013).

3 Methods

The two models described in the following sections (Sects. 3.1 and 3.2) represent relationships amongst water discharge, water velocity, and channel geometry in both subaerial and subglacial channels (Table 1). Both models use the measured discharge to calculate water velocity, shear stress, and width-integrated shear stress, upon which both suspended sediment and bedload transport depend (Fig. 1; Shields, 1936). The choice to evaluate results in terms of shear stress omits the need to select a sediment transport relationship and a grain-size parameter (e.g. Shields, 1936; Meyer-Peter and Müller, 1948).

Table 1 Variables, parameters, and constants. Where two values are given, the first refers to ALPINE, a scenario from Fieschergletscher, and the second to a glacier marginal to the ICESHEET, a scenario from Leverett Glacier. A second line refers to the range of values examined in the parameter search.

3.1 Subglacial channel model

The subglacial channel model accounts for the channel geometry and water velocity to evaluate the shear stress of water flowing across sediments underneath a glacier. We use a lumped hydraulics model from Werder et al. (2010), which is based upon that of Clarke (1996).

Here, it is assumed that the water is transported through a subglacial channel (Fig. 1; Röthlisberger, 1972) beneath a glacier with channel length l, with a flat bed and a mean ice thickness of h_ice. The channel size grows from melt due to frictional heating from water flow and closes due to ice creep. The formulation here does not consider the englacial storage of water. The evolution of subglacial channel size S_g is given as

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle \frac{\partial S_g}{\partial t}}=C_{\mathrm{1}}{\displaystyle \frac{Q\mathrm{\Delta }h}{l}}-C_{\mathrm{2}}{\left(h_{\mathrm{o}}-\stackrel{\mathrm{‾}}{h}\right)}^n{S}_g,\end{array}$$

where t is time, $C_{\mathrm{1}}=(\mathrm{1}-{\mathit{\rho }}_{\mathrm{w}}{c}_p{c}_t)\frac{{\mathit{\rho }}_{\mathrm{w}}g}{{\mathit{\rho }}_{\mathrm{i}}L}$ and $C_{\mathrm{2}}=\mathrm{2}A(\frac{{\mathit{\rho }}_{\mathrm{w}}g}{n}{)}^n$ are constants (values in Table 1), g is the acceleration due to gravity, Q is water discharge, $\stackrel{\mathrm{‾}}{h}=\frac{\mathrm{1}}{\mathrm{2}}(h+h_{\mathrm{p}})$ is the mean hydraulic head in the channel, with h_p being the proglacial hydraulic head equal to zero, l, $h_{\mathrm{o}}=\frac{{\mathit{\rho }}_{\mathrm{i}}}{{\mathit{\rho }}_{\mathrm{w}}}{h}_{\text{ice}}$ is the mean ice overburden pressure expressed in metre water equivalent, (ρ_w is density of water, and ρ_i is density of ice), and n is Glen's n (usually n=3; Glen, 1955). The first term on the equation's right side represents the channel opening due to frictional heating, while the following term represents the channel closure from ice deformation.

Following the Darcy–Weisbach equation, the head drop Δh is

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }\mathrm{\Delta }h=l{\displaystyle \frac{\mathrm{1}}{\mathrm{2}g}}{f}_{\mathrm{i}}{\displaystyle \frac{v_g^{\mathrm{2}}}{D_{\mathrm{h}}}},\end{array}$$

where f_r is a friction factor, D_h is the hydraulic diameter, l is the channel length, and $v_g=\frac{Q}{S_g}$ is the water velocity. The hydraulic diameter D_h is converted to wetted area S_g with

$$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle }{S}_g={\displaystyle \frac{D_{\mathrm{h}}^{\mathrm{2}}}{\mathrm{2}}}{\displaystyle \frac{{\left(\frac{\mathit{\beta }}{\mathrm{2}}+\sin \frac{\mathit{\beta }}{\mathrm{2}}\right)}^{\mathrm{2}}}{\mathit{\beta }-\sin \mathit{\beta }}},\end{array}$$

where β is the central angle of the circular segment that comprises the channel (the Hooke angle, Hooke et al., 1990). β=π corresponds to a semi-circular channel, and smaller values of β result in shallow, wide channels. This completes the subglacial hydraulic model that is described by the state variables S_g and Δh.

The shear stress, τ_g, between the water and the channel bed results from the Darcy–Weisbach formulation:

$$\begin{array}{}\text{(6)}& {\displaystyle }{\displaystyle }{\mathit{\tau }}_g={\displaystyle \frac{\mathrm{1}}{\mathrm{8}}}{f}_r{\mathit{\rho }}_{\mathrm{w}}{v}_g^{\mathrm{2}},\end{array}$$

where $v_g=\frac{Q}{S_g}$ is the water velocity. The width of the channel floor w_g is represented as

$$\begin{array}{}\text{(7)}& {\displaystyle }{\displaystyle }{w}_g=\mathrm{2}\sin {\displaystyle \frac{\mathit{\beta }}{\mathrm{2}}}\sqrt{{\displaystyle \frac{\mathrm{2}{S}_g}{\mathit{\beta }-\sin \mathit{\beta }}}}.\end{array}$$

This value establishes the integrated shear stress across the channel w_gτ_g.

3.2 Subaerial channel model

The hydraulics parameterization presented in Tucker and Slingerland (1997) is implemented to represent the subaerial channel. This model uses mass conservation and the Darcy–Weisbach relationship and assumes that the channel is sufficiently wide compared to its depth. This latter assumption means that the hydraulic radius is well approximated by the flow depth. Therefore, the resulting shear stress τ_f at the river bed is

$$\begin{array}{}\text{(8)}& {\displaystyle }{\displaystyle }{\mathit{\tau }}_f={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{w}}{g}^{\frac{\mathrm{2}}{\mathrm{3}}}{f}_f^{\frac{\mathrm{1}}{\mathrm{3}}}}{\mathrm{2}}}({\displaystyle \frac{Q}{w_f}}{)}^{\frac{\mathrm{2}}{\mathrm{3}}}\mathrm{\nabla }{z}_{\mathrm{c}}^{\frac{\mathrm{2}}{\mathrm{3}}},\end{array}$$

where ∇z_c is the channel slope, and f_f is the friction factor for subaerial channels (Tucker and Slingerland, 1997). Channel width w_f is

$$\begin{array}{}\text{(9)}& {\displaystyle }{\displaystyle }{w}_f=k{Q}^{\mathit{\alpha }},\end{array}$$

where k is a constant and $\mathit{\alpha }=\frac{\mathrm{1}}{\mathrm{3}}$ is a commonly chosen exponent (Leopold and Maddock, 1953). Also, following the Darcy–Weisbach relationship, subaerial water velocity, v_f, is given as

$$\begin{array}{}\text{(10)}& {\displaystyle }{\displaystyle }{v}_f=\sqrt{{\displaystyle \frac{\mathrm{8}{\mathit{\tau }}_f}{f_f{\mathit{\rho }}_{\mathrm{w}}}}}.\end{array}$$

As mentioned above, the width-integrated shear stress is w_fτ_f.

3.3 Implementation

Proglacial discharge records from the Fieschergletscher (scenario ALPINE) and Leverett Glacier (scenario ICESHEET) are used as inputs for the models above. The model outputs represent generalizable sediment transport characteristics from these hydrographs, rather than actual hydraulic conditions. To generalize these scenarios, ALPINE is exemplified by relatively thin ice (h_ice=225 m; Grab et al., 2021), low water discharge ($\sim \mathrm{10}{\mathrm{m}}^{\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$), and high diurnal variability in water discharge, as seen at Fieschergletscher (Fig. 2a). ICESHEET is exemplified by thick ice (h_ice=700 m; Morlighem et al., 2017), high water discharge ($\sim \mathrm{300}{\mathrm{m}}^{\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$), and low diurnal variability in water discharge, as observed at Leverett Glacier (Fig. 2e). We note that the subglacial results apply to pressurized subglacial channels and not depressurized ones that can occur underneath glacier termini (Perolo et al., 2018).

In the first experiment, the models are applied to a reference test case for each glacier. These experiments assume a subglacial channel with $\mathit{\beta }=\frac{\mathit{\pi }}{\mathrm{6}}$ and a subaerial channel with $\mathit{\alpha }=\frac{\mathrm{1}}{\mathrm{3}}$ and slope of 0.02 (Table 1). Both friction factors f_r and f_f are tuned so that reasonable water velocities (∼ 1–1.5 m s⁻¹; Werder et al., 2010; Chandler et al., 2013) occur for both ALPINE and ICESHEET.

To test the covariance between sediment transport capacity and water discharge, model outputs are compared to water discharge from the glaciers using Spearman rank correlation. This metric accounts for the ordering of values but not their magnitude. Rank correlation reduces the impact of the non-linear relationship between sediment transport capacity and hydrology. Note that this subaerial channel model is purely algebraic, whereas the subglacial model comprises a differential equation for the evolution of S_g. Thus, the channel size in the subaerial model has no history dependence on the discharge Q_w, whereas the subglacial one does (Eq. 3). Therefore, rank correlation is 1 between water discharge and sediment transport capacity in subaerial systems or subglacial systems where channel size S_g evolves more slowly than water discharge.

The second experiment aims to characterize the variability in sediment discharge capacity in subglacial channels relative to subaerial ones across a range of channel slopes and shapes and friction factors. Additionally, we examine the effects of differing water discharge smoothing periods from 15 min up to 15 d. The results below present water velocity (v_g, v_f), shear stress (τ_g, τ_f), and width-integrated shear stress (w_gτ_g, w_fτ_f) from the subglacial and subaerial models. For brevity, these values are referred together as “model outputs” in the text. To evaluate variability, we subtract the model outputs from their daily averages. This creates a time series that is detrended from the seasonal variations in the model outputs and has an approximately normal distribution. We then present the variability in the model output by taking the standard deviation of this detrended time series.

The effects of channel shape, gradient, and roughness are established by running the model with random parameter values across a range of channel slope and geometry factors (β, ∇z_c, and α) and friction factors (f_r and f_f; see Table 1 for value range). Runs with parameter combinations are accepted if their mean subglacial water velocity over the season lies between 0.5 and 2 m s⁻¹ or if subaerial water velocity lies between 0.3 and 1.2 m s⁻¹ (e.g. Werder et al., 2010; Magnusson et al., 2012; Chandler et al., 2013). To be accepted, subglacial model runs must experience a flotation fraction ($\frac{\mathrm{\Delta }h}{\mathrm{2}{h}_{\mathrm{o}}}$) of above 1.2 for less than 2.5 % of the run. A model spinup dictates the initial condition of cross-sectional area S_g. The spinup consists of applying the maximum observed water discharge of the first 4 d of the study period to the model until there is no change in the channel area S_g.

The routine runs until 100 different parameter combinations for each water discharge smoothing period are accepted with the conditions described above. To test the effects of variability in water discharge, it is smoothed using a moving average over periods ranging from 15 min to 15 d.

4 Results

4.1 Timing and covariance of subaerial and subglacial sediment transport capacity variations

The first numerical experiment aims to quantify the timing and covariance of the subglacial model outputs with respect to water discharge in response to different seasonal evolutions and peaks (Fig. 2). Variable relationships between model outputs and water discharge emerge for the subaerial and subglacial cases as channel size evolves (Fig. 2a and e). Because subaerial channels have no history dependence, each water discharge value in the subaerial channel produces a unique water velocity, shear stress, and width-integrated shear stress (Sect. 3.1). This characteristic results in a perfect rank correlation between the variables and water discharge (Fig. 3). An inconsistent relationship between the subglacial model outputs and water discharge persists across the range of parameters examined in the ensemble runs (Sect. 4.2; Fig. S15 in the Supplement).

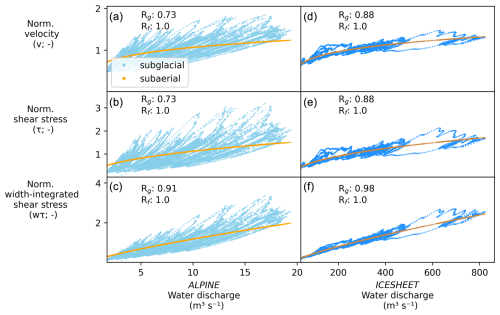
Figure 3 Relationships between water discharge and normalized velocity, shear stress, and width-integrated shear stress for ALPINE (a–c) and ICESHEET (d–f). Variables on the x axis have been normalized to mean values. R_g (R_f) shows the Spearman rank correlations for the subglacial (subaerial) outputs. Plots are shown with discharge and model outputs at 15 min intervals.

Peaks in subaerial model outputs occur coincident with peaks in water discharge (Fig. 2). In the subglacial channel, peaks in model outputs generally occur when water discharge increases but before the maximum water discharge. As the water discharge stabilizes at its peak, channel growth continues (Fig. 2a and e), causing water velocity and other model outputs to decrease from their peak values (Fig. 2b–d and f–h). Subglacial sediment transport capacity is greatest on the hydrograph's rising limb, relative to the falling limb, creating a hysteresis effect.

The history dependence on channel size in subglacial channels means that different sediment transport characteristics, such as velocity, occur across a large range of water discharges. For instance, in subglacial channels in ALPINE, high water velocity values and shear stresses can occur from a low water discharge ($\sim \mathrm{4}{\mathrm{m}}^{\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$) to the maximum water discharge at over 17 m³ s⁻¹ (Fig. 3a). In ICESHEET, water velocities close to the seasonal mean value can occur at water discharges between roughly 150 and 310 m³ s⁻¹. The subglacial channel's evolving width can counteract some of these effects. Width-integrated shear stress generally increases with water discharge, with greater rank correlation than with water velocity or shear stress (ALPINE, Fig. 3a–c). Yet, even width-integrated shear stress can vary substantially relative to water discharge. The highest values of width-integrated shear stress occur at water discharge values ranging from roughly 11 m³ s⁻¹ to over 17 m³ s⁻¹. The variability in width-integrated shear stress is less pronounced in the ICESHEET scenario, where the hydrograph has less diurnal variability (Fig. 3c and f).

Water discharge and sediment transport characteristics correlate better in ICESHEET, which has lower diurnal variations in water discharge compared to ALPINE. To evaluate the impact of water discharge variability, we smoothed the two hydrographs across different periods and evaluated the Spearman rank correlation between sediment transport characteristics and water discharge. We assume that a higher rank correlation indicates a reduced amount of hysteresis and behaviour more similar to subaerial channels (Fig. 3).

Smoothing water discharge over periods longer than one day causes a substantial increase in rank correlation (Fig. 4), removing diurnal variations (Figs. S1–S14). Even with the variations removed, correlations in sediment transport characteristics in ICESHEET remain higher than in ALPINE, which has more water discharge variations even when smoothed (Figs. S1–S14).

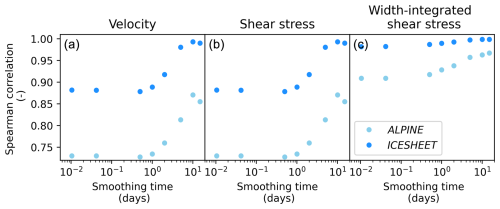
Figure 4 Spearman rank correlation between water discharge over a smoothing period and sediment transport characteristics (a) water velocity, (b) shear stress, (c) width-integrated shear stress. We assume that higher correlation scores approach subaerial behaviour. Hydrographs for the different smoothing periods are shown in the Supplement.

4.2 Variability in sediment transport capacity across a range of channel shapes, slopes, and friction values

The second numerical experiment aims to compare the variability between the subglacial and subaerial sediment transport capacities. To do this, model outputs from both systems are forced with a range of channel shapes, friction factors, and water discharge variability. This is accomplished by applying a range of parameter values to models representing the different hydrological regimes and examining the variability in model outputs (Sect. 3.3).

Across the range of parameters examined, variability in all model outputs (i.e. velocity, shear stress, and width-integrated shear stress) remains higher in the subglacial system than the subaerial one for both ALPINE and ICESHEET (Fig. 5). In some cases, the subglacial model outputs' variability is a magnitude larger than that of their subaerial counterparts. Variability in both subglacial and subaerial outputs decreases with smoothing times longer than approximately 1–5 d (Fig. 5). These smoothing timescales remove diurnal variations in water discharge, thereby reducing variability in model outputs. The velocity variability in ICESHEET, with smaller relative water discharge variations, is substantially smaller than that in ALPINE (Fig. 5a and d). Variations in ICESHEET shear stress are comparable to that in ALPINE due to the effects of evolving shear stress with subglacial conduit size (Eqs. 3 and 12). The much greater water flux and thus subglacial channel size in ICESHEET drives the larger width-integrated shear stress variations (Fig. 2c and f).

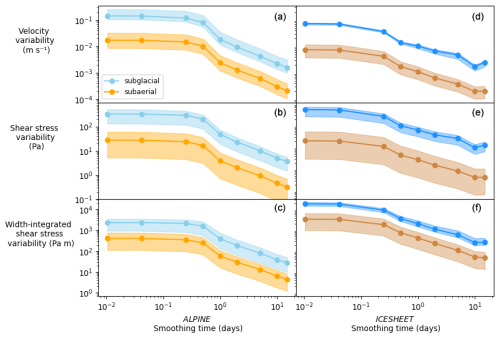
Figure 5 Standard deviation of detrended model outputs for different smoothing times with different subglacial and subaerial channel shapes and friction factors. Shaded areas denote the range of standard deviations from the accepted 100 parameter combinations (Sect. 3.3). Solid lines denote the mean value of standard deviations. Markers show smoothing periods (15 min, 1, 6, 12 h, 1, 2, 5, 10, and 15 d).

Greater subglacial friction factors f_i result in greater variability in the shear stress and width-integrated shear stress in the ALPINE case (Fig. 6). Low values of f_i result in slower growth rates in subglacial channels (Eqs. 3 and 4). Higher values of f_i allow faster channel growth that accommodates increases in water discharge, reducing velocity variability. Smaller values of channel factor β create low and broad channels, where the channel width grows more quickly in response to water discharge increases than a semi-circular channel with β=π (Eq. 4).

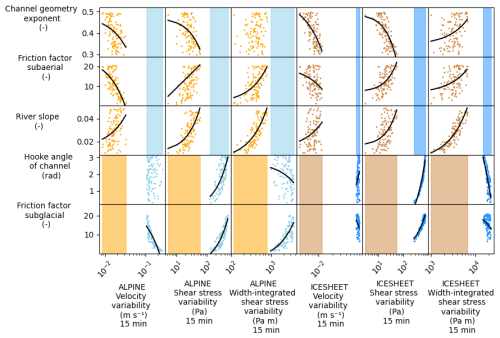
Figure 6 Parameter values compared to variability in model outputs. Plots on the left (orange, light blue) correspond to the ALPINE case. Plots on the right (brown, dark blue) correspond to the ICESHEET case. Outputs are shown using 15 min smoothing time. Linear trends are denoted in black if they are significant at p≥0.01. To compare the range of model outputs for the subaerial and subglacial cases, shaded areas show the range of model outputs that are independent of the parameter values.

Smaller values of subaerial channel shape factor α, or a channel cross-section shape closer to a slot canyon, result in greater variability in subaerial velocity and shear stress that can approach the variability of subglacial values (Fig. 6). Steeper subaerial channel slopes ∇z_c result in greater variability in both shear stress and width-integrated shear stress, but it only approaches the subglacial channel's variability in the ALPINE case (Fig. 6). Greater values of subaerial friction factors f_p result in greater variability of shear stress and width-integrated shear stress. Yet, subaerial values do not exceed the variability of subglacial channels. We note that these parameter values span a commonly accepted range. Therefore, we do not anticipate a scenario where variability in the subaerial system would exceed that in the subglacial system with these two hydrologic forcings.

4.3 Sediment transport scaling in different channel types

The numerical experiments in the previous sections consider the size evolution of subglacial channels and demonstrate that for these hydrographs, subglacial sediment transport variability is greater than its subaerial counterpart (Sect. 4.2). Additionally, the results demonstrate the impact of water discharge variability on sediment transport capacity. Here, we discuss and compare the sediment transport behaviour of different channel types as they respond to water discharge, channel shape, and hydraulic gradient, extending the formulations presented in Alley et al. (1997).

The channel types examined include

1. pipe flow (i.e. R-channels of fixed size that do not adjust their size to discharge conditions; Fig. 7a) – this scenario could represent ALPINE with minimal discharge smoothing and high water fluctuations compared to channel size (i.e. Fig. 2a–d);

2. subaerial channels (Fig. 7c);

3. steady-state R-channels (Röthlisberger, 1972, Fig. 7d), where water discharge is in equilibrium with channel size – this scenario could be approached with a large amount of discharge smoothing (i.e. Fig. 4) or hydrographs with minimal variations.

These formulations do not allow us to evaluate the non-steady-state R-channels presented above (Sect. 3.1, Fig. 7b). The sediment transport capacity is calculated for a given water discharge and hydraulic gradient using three different sediment transport capacity formulas: Meyer-Peter and Müller (MPM; Meyer-Peter and Müller, 1948), Engelund and Hansen (EH; Engelund and Hansen, 1967), and Bagnold (Bagnold, 1980); additionally, width-integrated shear stress is assessed, instead of sediment transport, as above.

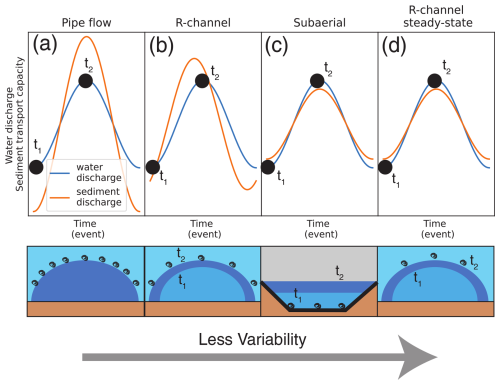
Figure 7 Response of sediment transport capacity (orange line) and channel size (bottom row) to a water discharge event (blue line) under different channel conditions. (a) Pipe flow with fixed channel size described in Sect. 4.3. (b) R-channel described in Sect. 3.1. (c) Subaerial channel described in Sect. 3.2. (d) Steady-state R-channel (channel size evolves in equilibrium with water discharge) described in Sect. 4.3. Note axes are not to scale. t₁ (t₂) represents low (high) water discharge.

Sediment discharge is given by the MPM, EH, and Bagnold formulations as

$$\begin{array}{}\text{(11)}& {\displaystyle }{\displaystyle }{Q}_s\propto w{\mathit{\tau }}^{\mathrm{3}/\mathrm{2}},Q_s\propto w{\mathit{\tau }}^{\mathrm{5}/\mathrm{2}},Q_s\propto w{\left({\displaystyle \frac{\mathrm{\Omega }}{w}}\right)}^{\mathrm{3}/\mathrm{2}}{H}^{-\mathrm{2}/\mathrm{3}},\end{array}$$

respectively, for sediment transport conditions well above the threshold of sediment motion.

We use the Darcy–Weisbach equation to evaluate shear stress

$$\begin{array}{}\text{(12)}& {\displaystyle }{\displaystyle }\mathrm{\Psi }\propto f{\displaystyle \frac{Q^{\mathrm{2}}}{D_{\mathrm{h}}{S}^{\mathrm{2}}}},\end{array}$$

with $\mathrm{\Psi }=\mathrm{\Delta }h/l$ the head gradient and friction factor f. The shear stress and stream power are, respectively,

$$\begin{array}{}\text{(13)}& {\displaystyle }{\displaystyle }\mathit{\tau }\propto f{v}^{\mathrm{2}}=f{\left({\displaystyle \frac{Q}{S}}\right)}^{\mathrm{2}},\mathrm{\Omega }\propto \mathrm{\Psi }Q.\end{array}$$

As in Sect. 3.2, the subaerial channel is assumed to have a width w much greater than its depth H, such that D_h≈4H, and to have a constant head gradient (Ψ) given by the topography. Further, it is assumed that its width can be approximated by a relation w∝Q^α (Eq. 9) with $\mathit{\alpha }\in [\mathrm{0},\mathrm{1}]$. End members α=0 or α=1 correspond to a subaerial channel of constant width (a slot canyon) or depth (no natural equivalent), respectively. For a steady-state R-channel, it is assumed that Ψ is constant (approximated by the gradient of the Shreve, 1972, potential) and that S adjusts in steady state with Ψ and Q. Note that in the R-channel model used above (Sect. 3.1), Eq. (3) calculates Ψ from the time-evolving S_g via the Darcy–Weisbach equation  (4), and thus no Shreve approximation is then needed. Pipe flow–like conditions occur when an R-channel is subjected to rapid discharge variations such that the channel cannot adjust its size. Such a case could occur during diurnal variations in the ALPINE case, where water discharge changes rapidly with respect to channel size. In this case, it is assumed that the cross-sectional area S is fixed, and Ψ adjusts to the specified Q. For both steady-state R-channel and pipe flow, it is assumed that $D_{\mathrm{h}}\propto S^{\mathrm{1}/\mathrm{2}}$.

With these assumptions, the Darcy–Weisbach equation (12) can be solved for the not-fixed quantity: H for a subaerial channel, S for a R-channel, and Ψ for pipe flow. Then, using Eq. (13), the shear stress and stream power can be calculated. These results are summarized in Table 2. The results of the 12 combinations of shear stress and sediment transport capacity are presented in Table 3 and also in Table S1 in the Supplement, where the fractions in the exponents are approximately given by decimal numbers for ease of comparison.

Table 2 Relations among hydraulic variables for the three different channel types: subaerial channels, R-channels, and pipe flow. The Darcy–Weisbach equation is abbreviated as “D–W” and stream power as “Stream p.”.

Table 3 Sediment transport proxy (wτ) and rates for the three considered different transport formulas: MPM (Meyer-Peter and Müller, 1948), EH (Engelund and Hansen, 1967), and Bagnold (Bagnold, 1980).

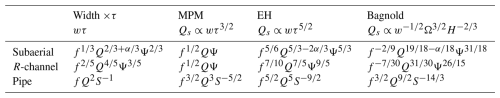
Table 3 shows the scaling of the proxy wτ as well as the Q_s in the MPM, EH, and Bagnold sediment transport formulas with respect to Q, Ψ, or S for the three different channel types and α values. Sediment transport in pipe flow scales much more severely with discharge (Table 3), as the exponent on Q is between 3 and 5, compared to the other two channel types, where that exponent is at most $\frac{\mathrm{5}}{\mathrm{3}}$. Remarkably, the Bagnold formula has a negative exponent for f in all but the pipe flow channel type. The total transport formula EH gives a slightly stronger dependence on all variables due to the larger exponent on τ of $\frac{\mathrm{5}}{\mathrm{2}}$ vs. $\frac{\mathrm{3}}{\mathrm{2}}$ for the MPM (Eq. 11). However, the sediment transport response in pipe flow for the Bagnold case is close to that of EH. Conversely, the sediment transport proxies w_g τ_g and w_f τ_f used previously scale only with Q² for pipe flow, whereas the sediment transport capacity scales with at least Q³. The exponent for the width scaling α only impacts the relationship between sediment transport and water discharge in the EH relation in any meaningful way. However, for the value of α around $\frac{\mathrm{1}}{\mathrm{3}}$ (a value appropriate for most streams), the exponent on Q for EH is only slightly greater in than the other transport relations.

The sediment discharge capacity in the steady-state R-channel scales very similarly to the subaerial channel case for all relations and virtually identically for the $\mathit{\alpha }=\frac{\mathrm{1}}{\mathrm{3}}$ case (Table 3). However, the head gradients Ψ are likely higher for comparable Q in an ice-sheet marginal or alpine glacier setting than in a subaerial channel (Alley et al., 1997). Thus, sediment transport capacity is likely higher in a steady-state R-channel.

5 Experiment limitations

Several aspects of the models and experiment design make the comparison of the subaerial and subglacial systems difficult. The lumped nature of the models means that they operate independently of the upstream drainage network. Additionally, we omit analysis of suspended sediment discharge records due to their dependence on sediment supply to capture variations in sediment discharge in addition to sediment transport capacity (e.g. Delaney et al., 2019). In reality, processes such as sediment access are often important in controlling sediment export in glacierized catchments (e.g. Herman et al., 2015; Vergara et al., 2022). Furthermore, meltwater can be distributed to flow through several adjacent conduits impacting the sediment transport capacity in each (e.g. Werder et al., 2013; Hewitt and Creyts, 2019; Delaney et al., 2023). The lumped models used here isolate the relationship between water discharge and sediment transport capacity in subglacial and subaerial systems. However, they neglect more complex, yet important, spatially distributed processes.

Different hydraulic gradients control the velocity and sediment transport capacity in the subglacial and subaerial cases (Sects. 3.1 and 3.2). The subglacial one is generally much steeper (Alley et al., 1997). This results in shear stress and width-integrated shear stress across the channel bed being much greater in subglacial channels, which in turn control sediment transport capacity (Fig. 2). The parameters' range tested in Sect. 4.2 covers a likely span of viable shear stresses in both subglacial and subaerial channels. The greater sediment transport capacity in subglacial channels implies that the sediment grain size underneath subglacial channels is likely larger than in subaerial channels, as smaller clasts would be evacuated. Note, however, that the mean water velocities are similar in both channel types.

The channel width and size variations in the subglacial channels presented here also occur in subaerial channels in response to water discharge (Phillips and Jerolmack, 2016), likely over decadal timescales or in response to individual extreme events (e.g. Slater and Singer, 2013; Dean and Schmidt, 2013). These timescales are likely considerably longer than the continuous changes in the subglacial channel's response time of days. Furthermore, observations from subaerial systems can show a co-varying relationship between water discharge and sediment transport over time (e.g. Schmidt and Morche, 2006; Pitlick et al., 2021). Even so, if channel width changes occur in subaerial channels, then the values of α in Eq. (9) could change over time. α must be less than 1, and even this would cause the exponent on Q in the w_g τ_g relationships to remain substantially lower that of pipe flow (Sect. 4.3, Tables 2 and 3).

Width-integrated shear stress is examined in the two numerical experiments as it does not have a dependence on grain size, unlike sediment transport relationships (Meyer-Peter and Müller, 1948, Sect. 4.3). This makes comparison between the two systems simpler. Preferential transport of smaller sediment clasts and the input of upstream sediment influence sediment transport capacity as grain size distribution changes (e.g. Gomez, 1983). These processes are only beginning to be evaluated underneath glaciers (Aitken et al., 2024), but they can be important in subaerial systems. Subglacial sorting processes could be an additional source of variability in sediment export from glaciers with respect to water discharge, especially for bedload transport.

6 Discussion

6.1 Interpreting sediment transport records from glacierized catchments with respect to water discharge

A variable relationship between subglacial sediment transport capacity and water discharge occurs due to hysteresis in subglacial channel size (Fig. 3). This hysteresis can limit water discharge as an indicator of sediment discharge capacity in these systems, especially when water discharge is highly variable and out of equilibrium with subglacial channel size. As a result, characteristics such as bankfull or effective water discharge, which link geomorphic work to hydro-climatic conditions, may have limited meaning in evaluating subglacial sediment transport (Wolman and Miller, 1960; Lenzi et al., 2006). A glacier's sediment transport capacity is impacted by the ice thickness controlling the channel closure rate and the glacier's surface slope in addition to water discharge and sediment size (Fig. 5, Sect. 3.1; Röthlisberger, 1972; Gimbert et al., 2016; Stevens et al., 2022; Walder and Fowler, 1994; Núñez Ferreira et al., 2025). This multitude of processes contrasts many subaerial channels, where transport capacity typically responds to water discharge, sediment size, channel shape, and hydraulic gradient. The last of these parameters can remain relatively stable over years or longer (Sect. 3.2; e.g. Tucker and Slingerland, 1997). Strong correlations between water discharge and sediment export in glacier systems could indicate the role of other processes, such as increased sediment access (Zhang et al., 2022). Furthermore, the observed correlation between water discharge and sediment discharge far downstream likely largely represents subaerial transport processes, especially with respect to bedload (Mancini et al., 2023).

Clockwise hysteresis loops between sediment concentration and water discharge in subaerial channels suggest that sediment availability is reduced over the event scale (Williams, 1989). These loops are often observed in glacierized catchments and are used to suggest limited access to subglacial sediment (e.g. Collins, 1979; Willis et al., 1996; Richards and Moore, 2003; Stott and Mount, 2007; Delaney et al., 2018). The results here suggest that clockwise hysteresis could also be expected in transport-limited regimes in many subglacial environments. Here, the smaller channel size on the rising limb would result in greater sediment transport capacity and sediment mobilization (Fig. 7b). The subsequently larger channel size would reduce sediment transport capacity for an equivalent water discharge on the falling limb, creating clockwise hysteresis.

The co-varying relationship between sediment transport capacity and water discharge in subaerial conditions could be noticeable ∼20 km downstream of the Leverett site. A strong correlation persists between sediment plume size and the Watson River's water discharge into the Kangerlussuaq fjord (Fig. 7c; Chu et al., 2009; McGrath et al., 2010). In contrast, in marine-terminating glacier catchments, a less consistent relationship may occur between water discharge or melt extent and sediment plume size (Chu et al., 2012; Tedstone and Arnold, 2012). Here, ocean water pressurizes subglacial channels at the ice front (e.g. How et al., 2017), so the observed reduced correlation could result from the inconsistent relationship between subglacial sediment transport capacity and water discharge (Figs. 3 and 7b).

Water discharge measurements at sub-daily timescales could severely limit the ability of a subglacial sediment transport model to capture specific events. The decreased model output variability beyond 1–5 d of smoothing could result in water discharge appearing to be in equilibrium with the subglacial channel when they are in fact not (Fig. 5). Over this period, water discharge variations could lead to a stronger relationship with sediment transport capacity (Fig. 7d and Sect. 4.3). Particularly, if water discharge changes slowly with respect to the subglacial channel size, then it will covary with sediment transport capacity (Fig. 7d). Such a strong relationship would not represent the impact of actual shorter-term fluctuations in water discharge.

6.2 Increased variability in sediment transport capacity in subglacial systems

The greater variations in shear stress in subglacial channels than in subaerial channels may cause even greater variations in sediment transport capacity in subglacial channels than our numerical results suggest (Fig. 5). In sediment transport capacity relationships, such as in Meyer-Peter and Müller (1948) or Engelund and Hansen (1967), shear stress is scaled to the power of $\frac{\mathrm{3}}{\mathrm{2}}$ or $\frac{\mathrm{5}}{\mathrm{2}}$, respectively (e.g. Sect. 4.3). The exponent greater than 1 magnifies sediment discharge variability beyond the variable sediment transport parameters described in Fig. 5 and Table 3.

R-channels rarely operate in a steady state with variations in water discharge, especially during severe rain or melt, where meltwater input timescales are too short for the channel to reach a steady state (Figs. 2 and 3). In such cases of high water discharge variability, channels can behave more like a pipe of fixed cross-section. Here, the cross-section responds to a characteristic discharge, but variations in water discharge deviate substantially from the flow conditions responsible for the channel size (i.e. diurnal water discharge variations in the ALPINE case – see Fig. 3; e.g. Gimbert et al., 2016). Thus, fluctuations in discharge on short timescales (to the order of a day; Fig. 5) have the potential to cause conditions with very high sediment transport capacities. Alternatively, at low water discharges, these channels could become depressurized and transition to subaerial flow, resulting in sediment deposition (Perolo et al., 2018). These variations in sediment transport capacity are far larger than those in subaerial channels (Alley et al., 1997). Note, however, that pipe flow assumptions would cause sediment discharge capacity to covary with water discharge, as is not the case in normal R-channels (Figs. 3 and 7a and b). Covariance also occurs for steady-state R-channels (Sect. 4.1; Fig. 7d).

Greater variations in subglacial sediment transport capacity could cause a supply-limited regime at many glaciers due to their high sediment transport capacity under assumed pressurized flow conditions (Alley et al., 1997). In subglacial systems, sediment's critical shear stress, or the threshold at which sediment mobilization occurs, can be reached more frequently and across many water discharges, compared to subaerial systems (Fig. 3). This result suggests that sediment export here is especially sensitive to observed changes in water discharge variability (Lane and Nienow, 2019). Sediment exhaustion through repeatedly crossing the mobilization threshold may explain the stronger dependence of sediment discharge from the Greenland Ice Sheet on the glaciers' basal shear stress, a proxy for bedrock erosion, rather than glacier melt (Overeem et al., 2017). More generally, the same process could also explain the strong dependence of sediment discharge on sediment production from glacial sliding, which is dependent on the basal shear stress of the glacier (Herman et al., 2015; Koppes et al., 2015). In addition to greater variability, the larger sediment transport capacity in subglacial systems compared to subaerial ones (Fig. 2) could cause sediment deposition at the glacier margin in the transition from pressurized to open channel flow (Perolo et al., 2018; Mancini et al., 2023; Delaney et al., 2024).

At glaciers with abundant bed sediment, in a transport-limited regime, the great variability in subglacial sediment transport capacity may make it difficult to link sediment discharge to hydrology, especially when peak events occur (Cowan et al., 1988; Delaney et al., 2018; Lu et al., 2022). The results here suggest that different channel sizes with the same hydrology forcing can result in very different sediment transport capacities, making it challenging to establish the effects of individual extreme precipitation or melt events without establishing the antecedent state of the subglacial drainage system.

Catchments with reduced water discharge variability may experience less variability in sediment transport capacity, as shown by the ALPINE and ICESHEET model outputs. Indeed, the more decoupled and variable relationship between model outputs and water discharge in ALPINE results from the relatively larger discharge variations on sub-daily to weekly timescales (Fig. 3). This occurs because the subglacial channel's size evolves slowly compared to variations in water discharge (Fig. 7b). High water discharge variability in ALPINE may cause width-integrated shear stress to approach Q², assuming pipe flow conditions, where the water discharge varies largely compared to channel size (Fig. 7; Sect. 4.3; cf. Alley et al., 1997). Conversely, the reduced relative variability in water discharge in ICESHEET is a result of the larger catchment areas and longer travel times of the water (e.g. van As et al., 2017). The stronger correlation between water discharge and width-integrated shear stress in ICESHEET may result in the subglacial channel's size remaining closer to equilibrium due to the smaller variations in water discharge (Fig. 7d). In this case, the exponent on water discharge for shear stress is likely substantially lesser than wτ∝Q² but greater than the wτ∝Q^⅘ that occurs in a steady-state R-channel (see Sect. 4.3). As a result, there is a stronger relationship between subglacial model outputs and water discharge in ICESHEET (Fig. 3) and less variability in model outputs in the ICESHEET case (Fig. 5).

7 Conclusions

The sediment transport capacity of both subglacial and subaerial channels is driven by channel width and the shear stress exerted by the flowing water, which is proportional to flow velocity squared. Subaerial channels immediately alter both their width and water velocity in response to changing water discharge. In contrast, pressurized subglacial channels largely accommodate rapidly changing water discharge by altering water velocity, while their size only responds to changes in discharge over longer timescales, typically, several days. Thus, sediment transport capacity is more sensitive to changes in water discharge in subglacial channels compared to subaerial ones.

The paper's first objective is to establish the conditions where water discharge covaries with subglacial sediment transport capacity. In subglacial channels, peak water velocity and sediment transport capacity occur before peak water discharge during a discharge event in hydrographs from an alpine and an ice sheet catchment, due to evolving channel size. In subaerial channels, the timing of peak sediment transport capacity and water discharge coincide. The results suggest that, even in a transport-limited subglacial system, a variable relationship exists between water and subglacial sediment discharge. Water discharge variations in representative Greenland Ice Sheet and Alpine catchments are substantial enough to cause this inconsistent relationship, even when these water discharge records are smoothed. This variable relationship presents a challenge in linking hydro-climatic conditions or events to sediment export from glaciers. Water discharge and sediment transport capacity covariance could be possible when water discharge varies at a slower rate than subglacial channel size, such as in Antarctica, which has minimal surface melt input. The results also suggest that water discharge records averaged over periods longer than 12 h from alpine and ice sheet hydrographs substantially impact subglacial sediment transport capacity characteristics.

The paper's second objective is to evaluate the relative variability in sediment transport capacity between subglacial and subaerial channels. The results demonstrate that sediment transport capacity variability is higher in pressurized subglacial channels that are out of equilibrium with water discharge than subaerial channels. Increased variability occurs even in environments where water discharge has relatively small diurnal variations, as in the ICESHEET case. Yet, elevated variability is especially strong with greater water discharge variations, as in the ALPINE case. Further evaluation is needed to establish the influence of high variability on sediment transport capacity in evaluating hydro-climatic signals from sediment records. Greater variability in sediment transport capacity may also lead to sediment exhaustion by subglacial water repeatedly crossing the mobilization threshold across a range of water discharges.

Limited observations of the subglacial environment hinders our ability to quantify processes such as the shape of subglacial channels and the response time of subglacial channels to water discharge variations. The poor constraints on subglacial sediment size and sorting processes make it difficult to link shear stress to sediment transport capacity. New methods are emerging to quantify these processes (Jenkin et al., 2023; Núñez Ferreira et al., 2025), furthering our understanding of the response of sediment transport capacity to water discharge forcing in subglacial environments.

This study calls for the explicit consideration of evolving channel size when examining the relationship between sediment transport and hydro-climatic conditions in glacierized catchments, especially ones with high water discharge variability.