Creep enhancement and sliding in a temperate, hard-bedded alpine glacier

Glacier internal deformation is usually described by Glen's flow law using two material parameters: the creep factor (A) and the flow law exponent (n). However, the values of these parameters and their spatial and temporal variability are rather uncertain due to the difficulty in quantifying internal strain and stress fields at natural scales. In this study, we combine 1-year-long continuous measurements of borehole inclinometry and surface velocity with three-dimensional full-Stokes ice flow modeling to infer ice rheologies and sliding velocities for the ablation zone of the Argentière Glacier, a temperate glacier in the French Alps. We demonstrate that the observed deformation rate profile has limited sensitivity to the flow law exponent (n) and instead mainly reflects an increase in the creep factor (A) with depth, with A departing from its surface value by up to a factor of 2.5 below 160 m depth. We interpret this creep factor enhancement as an effect of increasing interstitial water content with depth (from 0 % to 1.3 %), which results in an average value of A=148 MPa⁻³ a⁻¹. We further observe that internal ice deformation exhibits seasonal variability similar to that concerning surface velocity, indicating that the local basal sliding velocity exhibits no significant seasonal variation. We suggest that these changes in deformation rate are due to variations in the stress field, driven by contrasting changes in subglacial hydrology conditions between the sides and center of the glacier. Our study provides further evidence that borehole inclinometry, combined with full-Stokes flow modeling, allows for the constraining of both ice rheology and basal friction at scales that cannot be inferred from surface velocity measurements alone.

1 Introduction

Glacier dynamics depend on both internal deformation and basal sliding. Given the scarcity of direct observations of ice rheology and basal sliding speed at natural scales, ice flow models commonly use inverse methods to estimate the material parameters that best fit surface velocities (e.g., Arthern and Gudmundsson, 2010; Fürst et al., 2015; Mosbeux et al., 2016). However, the problem is largely undetermined due to limited knowledge of ice thicknesses, and it does not allow for the identification of model weaknesses as model errors are compensated for by material parameter adjustments. Independent and accurate estimates of ice material parameters, as well as subglacial basal-friction changes, are key to better representing glacier dynamics in models, particularly the fraction of surface velocities due to basal sliding versus that due to internal ice deformation.

Ice deformation is commonly assumed to follow Glen's flow law (Glen, 1955), with the creep parameter (A) being primarily dependent on ice temperature (Barnes et al., 1971; Weertman, 1983). This dependency has been studied extensively in both the laboratory and the field (Cuffey and Paterson, 2010) and can be reasonably well accounted for in models given a temperature profile. Typical values for ice viscosity and exponents for temperate glaciers and ice caps correspond to A≈75 MPa⁻³ a⁻¹ and n=3, respectively (Cuffey and Paterson, 2010). The applicability of these values for describing glacier dynamics at natural scales, however, is still quite uncertain, mainly due to other controls coming into play, such as ice texture (orientation and microstructure) (Barnes et al., 1971; Goldsby and Kohlstedt, 2001; Chauve et al., 2024), impurities (Jones and Glen, 1969), and water content (Lliboutry and Duval, 1985; Duval, 1977). These controls are challenging to evaluate as they may vary quite extensively in time and space depending on stress and deformation conditions (Chauve et al., 2024; Rathmann and Lilien, 2022). This is especially true under temperate-ice conditions, which are hard to study in the laboratory, where water content is not only difficult to control but also hard to characterize in the field, requiring the drilling of ice cores or indirect geophysical measurements, which are often difficult to interpret. Geophysical methods include ground-penetrating radar observations (Young et al., 2021; Ogier et al., 2023), seismic tomography (Benjumea et al., 2003; Endres et al., 2009), and surface nuclear magnetic resonance (Legchenko et al., 2014). However, the first method is mainly sensitive to integrated water content, and its spatial variations are poorly retrieved. Analysis of seismic and radar wave velocities provides relevant information on relative changes in water content but remains more uncertain in absolute terms (Murray et al., 2007). We note that the recent use of fiber optics in boreholes provides accurate measurements of variations in seismic velocity with depth and might be a promising method for the in situ characterization of temperate-ice properties, although until now, it has mostly been applied to cold-ice settings (Fichtner et al., 2023; Booth et al., 2020). As temperate-ice deformation is expected to primarily control ice dynamics, including on ice sheets such as the Greenland Ice Sheet, where most of the deformation is concentrated in its basal temperate layer (Law et al., 2023), it is crucial to study it specifically.

Basal sliding on hard beds is also known to be a function of ice deformation as it is enhanced near the bed, thus involving the same sources of uncertainty as presented above, with the added complexity that subglacial hydrology also affects it. Water pockets, commonly referred to as cavities, can form on the lee side of bedrock bumps, reducing the apparent bed roughness, facilitating creep, and thus enhancing basal sliding (Lliboutry, 1959, 1968). Subglacial channels can also form under sufficient turbulent-induced melt, causing the opposite effect of reducing basal sliding by lowering the basal water pressure (Röthlisberger, 1972; Schoof, 2010). Ultimately, the resultant effect of subglacial hydrology on overall glacier dynamics depends on the type of subglacial hydrology system at play at any given time and location. Of fundamental importance is the ability to evaluate the spatiotemporal evolution of basal sliding to improve our representation of the evolution of subglacial hydrology and its link to overall glacier dynamics in glacier and ice sheet models.

Borehole inclinometry is a unique means for investigating ice deformation and basal sliding simultaneously and can be achieved either by measuring changes in borehole orientation through repeated surveys (e.g., Perutz, 1949; Shreve and Sharp, 1970; Raymond, 1971; Hooke, 1973; Hooke and Hanson, 1986; Hooke et al., 1992; Harper et al., 2001; Marshall et al., 2002; Chandler et al., 2008) or through continuous englacial tiltmeter recordings (e.g., Gudmundsson et al., 1999; Lüthi et al., 2002; Willis et al., 2003; Amundson et al., 2006; Ryser et al., 2014; Keller and Blatter, 2012; Doyle et al., 2018; Lee et al., 2019; Maier et al., 2019, 2021). These observations provide deformation rate profiles that allow for in situ estimates of ice rheology and basal velocity, as well as their respective temporal variations, with basal velocity determined by integrating the deformation rate profile with depth and subtracting it from the surface velocity (Hooke et al., 1992; Maier et al., 2021). However, a major challenge in evaluating ice rheology based on these observations is the retrieval of stress fields against which deformation rates can be compared. Since stress variations with depth along the borehole cannot be measured, they must be estimated independently using a modeling approach, which, depending on model assumptions or prescribed boundary conditions, can introduce large uncertainties into the derived creep factor or flow exponent, especially with respect to valley glaciers (e.g., Harper et al., 2001; Chandler et al., 2008), where the highly three-dimensional geometry necessitates an evaluation of the full stress tensor. Even on large ice caps, strong spatial variations in the measured deformation rate between different boreholes have been shown to reflect a complex stress field influenced by spatial variability in bed friction (Ryser et al., 2014). This, together with variations in ice temperature, complicates the accurate assessment of ice rheology. This stress field complexity can also influence the temporal variations observed in deformation rates, due to either flow over changing bed topography (Maier et al., 2019) or hydrologically driven temporal changes in basal-drag patterns (Hooke et al., 1992; Willis et al., 2003).

In this paper, we infer internal rheological parameters and reconstruct basal velocity over time by combining continuous borehole inclinometry observations with full-Stokes three-dimensional modeling of the stress field throughout an entire melting season. The study focuses on the Argentière Glacier (temperate ice), located in the French Alps, which has been intensively monitored for several decades (e.g., with regard to mass balance, surface velocity and topography, sliding velocity, and bedrock geometry) and provides a unique and well-constrained environment for a natural-scale study of ice deformation. We first describe the study site and the measurement methods. We then analyze our observations in terms of material parameters using the flow model and, finally, provide the observed time series of both deformation and basal velocities. With this methodology, we identify a depth dependency of ice viscosity, which we attribute to changes in interstitial water content, as well as temporal changes in ice deformation, which we argue are due to subglacial-hydrology-driven changes in basal-friction conditions. These novel observations contribute to a better understanding of the complex interplay between basal sliding and internal ice deformation while providing constraints on ice rheology in a natural setting.

2 Field site and instrumentation

2.1 The Argentière Glacier

The Argentière Glacier is a temperate glacier located in the Mont Blanc range of the French Alps (45°10^′ N, 6°10^′ E). The glacier rests on hard bedrock (Vivian and Bocquet, 1973) and extends for 9 km within an altitude range of 1600 to 3400 m, separated by an icefall at 2300 m. Glacier dynamics have been continuously monitored since the 1970s, particularly with regard to their basal sliding velocities, thanks to direct access to the glacier bed ∼700 m downstream of the drilling site (Vincent and Moreau, 2016; Gimbert et al., 2021a; Gilbert et al., 2022). Measurements are conducted using a cavitometer installed in a natural ice cavity, which records sliding velocities at a 30 min resolution. Surface velocities exhibit seasonal variability, with the lowest velocities observed in fall (October–November) and sustained high velocities observed during summer (June–August) (Vincent et al., 2022). The glacier also benefits from subglacial-runoff monitoring conducted by the power company Electricité d'Emosson SA, along with continuous records of yearly surface mass balance, topography, and velocity from the GLACIOCLIM monitoring program (https://glacioclim.osug.fr/, last access: 15 January 2025). Several campaigns of ground-penetrating radar measurements have also provided a good understanding of basal topography (Rabatel et al., 2018; Gimbert et al., 2021b), further extended by seismic investigations (Sergeant et al., 2020).

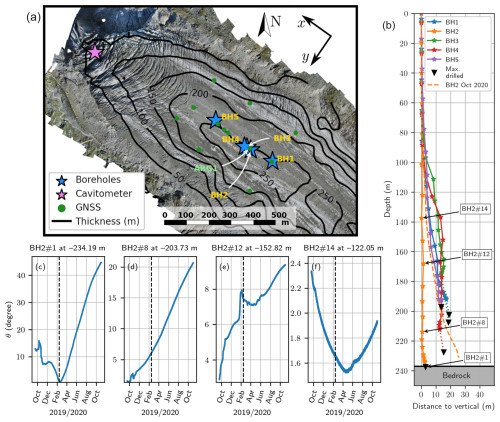
Figure 1 (a) Map of the ablation area of the Argentière Glacier (EPSG:27572 projection), showing ice thickness (black contours) and instrument locations. (b) The estimated initial shape, drilled depth (black triangles), and instrumented depth (with each star representing a tiltmeter) of the five boreholes. The dashed orange line represents the estimated shape of BH2 at the end of the tilt record. (c–f) Tilt (θ) recorded at four example inclinometers at BH2 (as labeled in panel b). The dashed vertical lines indicate 15 February 2020, the starting date of our analysis, when all sensors at BH2 had stabilized. GNSS: Global Navigation Satellite System.

2.2 Borehole deformation instrumentation

Drilling operations took place between 12 and 14 September 2019. The drilling sites are located in the central part of the ablation area at an elevation of 2380 m, where the ice thickness along the center flow line is about 230–250 m and the bedrock forms an overdeepening, where most of the boreholes are located (Fig. 1a and Table 1). We used a custom-built hot water drill operating at 70 °C to drill boreholes 10 cm in diameter at an average speed of 60 m h⁻¹. The positions of the final completed and instrumented boreholes (BH1, BH2, BH3, BH4, and BH5) are indicated by the blue dots in Fig. 1a.

The deformation rate sensors, which we refer to as tiltmeters, consist of a high-end triaxial gravity sensor (SCL3300, Murata) and a triaxial magnetic sensor (LSM303, STMicroelectronics). The gravity sensors are used to determine the tilt (θ), the angle with respect to the vertical, with an estimated accuracy of 0.01°. Lab calibrations have shown that tilt readings above 45° become increasingly unreliable. The magnetic sensors do not provide reliable absolute measures of orientation relative to north because they are very sensitive to parasitic magnetic fields. The tiltmeters are grouped in chains of 20 and are more densely concentrated toward the bottom of the glacier (Fig. 1b). For each borehole (i), we refer to each tiltmeter (j) using the format BHi#j, starting with a j value of 1 for the deepest tiltmeter. All sensors acquired data every 30 min, but high-frequency noise was removed by smoothing the data using an exponential filter with a 1 d time window.

We estimate the initial shape of the boreholes using tilt and azimuth data averaged over the first month of the record (15 September to 15 October 2019). The estimated shape is used to correct for borehole and sensor depth errors resulting from the boreholes not being perfectly vertical. Although the actual shapes are three-dimensional, uncertainties in the azimuth measurements lead us to restrict our analysis of borehole shape to the estimated horizontal distance between each inclinometer and a vertical line starting at the surface (Fig. 1b). In Fig. 1b, we also show the final shape attained by the BH2 borehole before the chain of tiltmeters broke in October 2020.

Table 1 Summary of the borehole instrumentation and depths after installation. The instrumented depth corresponds to the depth of the deepest sensor. The bedrock depth was previously estimated using ground-penetrating radar measurements (Rabatel et al., 2018; Sergeant et al., 2020).

Tiltmeter array performance varied across boreholes. Sensor arrays at BH1 and BH5 stopped working after a few days and provided no useful data. At BH2, BH3, and BH4, all sensors recorded data for more than a year until late October 2020. However, both BH3 and BH4 exhibit a tortuous shape in their deeper sections, suggesting problems during drilling that subsequently affected the quality of the measurements. We provide a summary of borehole and sensor-corrected depths in Table 1. Since BH2 reaches the bed and provides good data quality, which we attribute to the nearly vertical shape of the borehole, most of the results presented in this paper are based solely on BH2.

The tilt time series for each sensor in the three boreholes – BH2, BH3, and BH4 – can be found in Sect. S1 in the Supplement. Tilt data recorded during the first few months are affected by insufficient mechanical coupling between the tiltmeters and the ice, resulting in unstable signals until steady tilt occurs, which we interpret as the point at which the tiltmeters become well coupled to the ice (Fig. 1c–f). The duration of the transition between unstable and steady tilt change varies from sensor to sensor, ranging from about 2 months for deeper sensors, where borehole closure from creep is faster, to about 6 months for shallower sensors, where borehole closure from creep takes longer. At BH2, most tiltmeters became fully coupled by 15 February 2020 – that is, 5 months after installation (see Sect. S1). We thus start our analysis from this point. Certain sensors reached a minimum tilt after installation, either shortly after installation (e.g., BH2#8) or long after (e.g., BH2#1 and BH2#14, with the minimum occurring in September 2019), indicating that they initially tilted against the flow.

2.3 Surface motion instrumentation

Five Global Navigation Satellite System (GNSS) stations were deployed in the ablation zone of the Argentière Glacier in February 2019, with an additional seven installed in February 2020. We employ multi-frequency Leica GR25 receivers and Leica AS10 antennas, which continuously record GNSS signals at a 1 Hz sampling interval. This GNSS receiver network (green dots in Fig. 1) covers the borehole sites, with the ARG1 station located ∼30 m from BH2. See Togaibekov et al. (2024) for more details.

3 Methods

3.1 GNSS processing

GNSS signals are processed using a static approach with a double-difference processing technique and linear, ionosphere-free combination-phase observables (Bock et al., 1986), incorporated into the software packages GAMIT and GLOBK (Herring et al., 2018). Daily GNSS position time series are then converted into horizontal velocities, which are used in this study. We empirically determined a velocity error of 0.9 m a⁻¹ using a stationary GNSS station located on bedrock approximately 500 m away from the survey network, which is exposed to a similar multi-path scattering environment as the stations on the glacier.

3.2 Calculating internal-deformation rates from tiltmeter observations

We use a three-dimensional reference system with x as the main along-flow direction and z as the upward vertical, with its origin at the surface (see Fig. 1a and b). Velocities in the x, y, and z directions are denoted by u, v, and w, respectively. Assuming that the temporal evolution of the tilt (θ) occurs entirely in the along-flow direction, the changes in θ are controlled by the horizontal shear strain ($\mathrm{d}u/\mathrm{d}z$), as well as the compressive strain ($\mathrm{d}u/\mathrm{d}x$) and extensive strain ($\mathrm{d}w/\mathrm{d}z$) (Keller and Blatter, 2012). To detect the potential effect of compressive/extensive strain, we fit the tilt curves recorded at each BH2 inclinometer using the analytical model from Keller and Blatter (2012) (see Sect. S2). We find that the best data fit can always be obtained by neglecting $\mathrm{d}u/\mathrm{d}x$ and $\mathrm{d}w/\mathrm{d}z$, except with respect to the two deepest sensors (BH2#1 and BH2#2), where a better fit is obtained with nonzero compressive strain. For these deepest sensors, neglecting compressive strain leads to an overestimation of $\mathrm{d}u/\mathrm{d}z$ by about 30 % at BH2#1 and 20 % at BH2#2. The presence of significant compressive strain near the glacier bed is likely related to a local effect of bed roughness, as shown by the local evaluation of strain over a rough bed presented in Sect. 5.1. Hereafter, we refer to this layer as the basal boundary layer. Within this layer, the derived $\mathrm{d}u/\mathrm{d}z$ values are expected to be strongly biased and are thus ignored in the ice rheology interpretation.

With the hypothesis that $\mathrm{d}u/\mathrm{d}z$ dominates the flow gradient outside of the boundary layer, the internal-deformation rate ($\mathrm{d}u/\mathrm{d}z$) from the temporal evolution of the tilt (θ) is computed as follows (Lüthi et al., 2002; Ryser et al., 2014; Doyle et al., 2018; Maier et al., 2019):

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{d}u}{\mathrm{d}z}}={\displaystyle \frac{\mathrm{1}}{\mathrm{d}t}}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}z}}\approx {\displaystyle \frac{\mathrm{1}}{\mathrm{\Delta }t}}\mathrm{\Delta }\tan \left(\mathit{\theta }\right),\end{array}$$

where Δt is a given time period and Δtan (θ) is the change in the tangent of the tilt during that time period. In our particular implementation, we calculate the least-squares linear approximation of tan (θ) as a function of time for each time period (Δt), set to 1 d, meaning the regression coefficient directly yields $\mathrm{d}u/\mathrm{d}z$. The estimated maximum uncertainty for the daily averaged deformation rate is, for most of the sensors, lower than 0.1 a⁻¹ (see Sect. S3).

3.3 Computation of time series of surface, internal, and basal velocity

As it is not always possible to directly interpolate the surface velocities obtained at borehole locations from the GNSS network due to data gaps, we construct a continuous time series of the surface velocities recorded at the GNSS station close to the boreholes by filling gaps using a linear model traditionally employed to derive continuous surface mass balances from sparse data on alpine glaciers (Lliboutry, 1974; Vincent et al., 2017). In this linear model, we assume similar temporal variability in surface velocity across the stations, meaning that the surface velocity at each GNSS station (i) can be expressed as

$$\begin{array}{}\text{(2)}& u_{\mathrm{s}i}\left(t\right)={\mathit{\alpha }}_i+\mathit{\beta }\left(t\right),\end{array}$$

where α_i is the average surface velocity at the station (i) over the measurement period and β(t) represents the temporal variability, which is assumed to be identical for all stations and satisfies $\sum \mathit{\beta }\left(t\right)=\mathrm{0}$. We first solve the system of equations by finding the values of α_i and β(t) that best approximate the observations while satisfying $\sum \mathit{\beta }\left(t\right)=\mathrm{0}$. We then compute the residuals between the modeled and observed velocities, along with their standard deviation (s_res) values, and classify as outliers all observations with residuals greater than 3s_res. We then solve the system again, excluding these outliers, to obtain the final values of α_i and β(t). The residuals between the observed and reconstructed velocities follow a normal distribution centered around 0, which validates the initial assumption (Sect. S4). The surface velocity time series $u_{\mathrm{s}}={\mathit{\alpha }}_{\mathrm{ARG}\mathrm{1}}+\mathit{\beta }\left(t\right)$ (s_res=3.2 m a⁻¹) is thus used to fill the gaps at the ARG1 station, which is the closest station to BH2, as seen in Fig. 1.

The internal velocities are computed by integrating the deformation rate over depth as follows:

$$\begin{array}{}\text{(3)}& u_{\mathrm{d}}(z,t)=\underset{z_{\mathrm{bed}}}{\overset{z}{\int }}{\displaystyle \frac{\mathrm{d}u}{\mathrm{d}z}}(z,t)\mathrm{d}z,\end{array}$$

where z_bed is the bedrock elevation (expressed in meters). Finally, the basal velocity, u_b(t), is computed as the difference between the reconstructed surface velocity, u_s(t), and the integrated deformation rate over the entire ice thickness, u_d(t). The time series are computed from the daily averaged deformation rate at a daily resolution.

3.4 Quantifying the parameters of Glen's flow law

In addition to deformation measurements, the study of ice rheology requires knowledge of the stress field within the ice, which is evaluated in this study using numerical modeling. We use the three-dimensional, full-Stokes finite-element model Elmer/Ice (Gagliardini et al., 2013) to solve the equation of conservation of momentum for a given glacier geometry and ice rheology. The glacier geometry is prescribed based on bedrock topography and surface topography measurements derived from Pleiades satellite imagery obtained on 25 August 2019 (Beraud et al., 2022). The ice rheology is described by Glen's flow law:

$$\begin{array}{}\text{(4)}& {\dot{\mathit{\epsilon }}}_{ij}=A{\mathit{\tau }}_{\mathrm{e}}^{n-\mathrm{1}}{\mathit{\tau }}_{ij},\end{array}$$

where ${\dot{\mathit{\epsilon }}}_{ij}$ and τ_ij are the components of the strain rate tensor (a⁻¹) and the deviatoric stress tensor (MPa), respectively; A is the creep factor (MPa⁻ⁿ a⁻¹); ${\mathit{\tau }}_{\mathrm{e}}=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}{\mathit{\tau }}_{ij}{\mathit{\tau }}_{ij}}$ is the effective stress (MPa); and n is an exponent. We assume a stress-free upper surface boundary condition and a basal boundary condition as defined by the Weertman friction law (Weertman, 1957),

$$\begin{array}{}\text{(5)}& A_{\mathrm{s}}{\mathit{\tau }}_{\mathrm{b}}^m=u_{\mathrm{b}},\end{array}$$

where τ_b is the basal shear stress (MPa), m is an exponent setting the nonlinearity of the law and is taken to be 3 (Gilbert et al., 2023), A_s is the sliding coefficient at the bed (m a⁻¹ MPa^−m), and u_b is the sliding velocity (m a⁻¹). We use values of A_s for m=3 as inferred by Gilbert et al. (2023) from surface velocity inversion measurements. To avoid stress anomalies caused by uncertainties in the ice thickness, we relax the surface topography for 1 year using surface mass balance forcing from Gilbert et al. (2023) before extracting the deformation rate and stress tensor from the model.

We run several simulations to test the sensitivity of the deformation rate profile to different values of A and n. We run a set of simulations with n=3, 4, or 5 and a constant, uniform creep factor (A). The value of A for each n value is chosen such that the numerically calculated total deformation velocity at the location of BH2 matches the observed value. To minimize the potential effect of temporal changes in basal friction on the stress field (Hooke et al., 1992; Willis et al., 2003), we use an averaged deformation rate profile that was recorded during the last month of the time series (1 to 31 October 2020), when basal friction was least affected by subglacial hydrology and the inclinometers were well coupled to the ice. We run another set of simulations using n=3 and a depth-dependent creep factor, A=A(z), ensuring that the computed $\mathrm{d}u/\mathrm{d}z$ profile matches the observed one. We infer A(z) using Glen's flow law (Eq. 4), based on the observed mean $\mathrm{d}u/\mathrm{d}z$ value at BH2 and the stress tensor computed from the Elmer/Ice simulation, such that

$$\begin{array}{}\text{(6)}& A\left(z\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{d}u}{\mathrm{d}z}}{\mathit{\tau }}_{E,\mathrm{num}}^{-\mathrm{2}}{\mathit{\tau }}_{xz,\mathrm{num}}^{-\mathrm{1}}.\end{array}$$

We then approximate A(z) using a piecewise linear function, A_fit(z). Since changing the creep factor slightly modifies the overall stress balance, we repeatedly run the numerical model, updating the A_fit(z) value inferred from the numerical solution of the previous iteration during each iteration, until the modeled stress field converges. The depth-dependent creep factor, A_fit(z), determined at BH2 is applied uniformly over the entire domain by normalizing it with depth and applying this normalization everywhere.

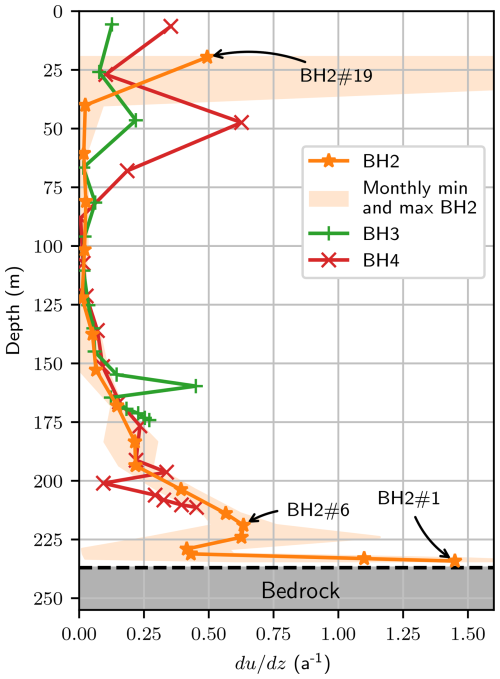
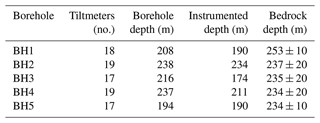
Figure 2 Average measured deformation rate profiles at BH2, BH3, and BH4, along with the monthly minima and maxima for BH2. The continuous lines show the average measured deformation rate profile for each borehole for the period between 15 February and 15 October 2020, and the shaded region represents the range between the monthly averaged minimum and maximum deformation rate values (shown only for BH2). Each symbol represents a tiltmeter.

4 Results

4.1 Observed mean deformation rate profiles

In Fig. 2, we show the average deformation rate profiles computed from tilt measurements (see Sect. 3.2 (Methods)) at BH2, BH3, and BH4 between 15 February and 15 October 2020. The orange-shaded region represents the range associated with the monthly averaged deformation rate ($\mathrm{d}u/\mathrm{d}z$) for BH2. The retrieved profiles show a similar depth-increasing deformation rate, with only a few outliers, associated with the high deformation rate at $\sim -\mathrm{160}$ m at BH3 and the low deformation rate at $\sim -\mathrm{200}$ m at BH4. These outliers are likely measurement artifacts, as evident in the raw data (see Sect. S1; BH3#6 and BH4#5). Only BH2 reached the bed (see Fig. 1b and Table 1), and it also generally shows lower measurement noise, likely due to better ice coupling (see Sect. S1). For both of these reasons, from now on, we only focus on the deformation rate profile recorded at BH2, which we divide into three parts.

The upper part (uppermost 120 m) of the deformation rate profile at BH2 shows a low shear deformation rate (≈0.02 a⁻¹), except at BH2#19, which exhibits very noisy records and is thus disregarded from our analysis (see Sect. S1). The middle part, from −120 m to −219 m (BH2#6), is characterized by much higher deformation rates, which increase nonlinearly toward the bed, ranging from less than 0.02 a⁻¹ at −120 m to a local maximum of 0.63 a⁻¹ at −219 m. Below −219 m begins the section we refer to as the boundary layer, which includes a 40 % decrease in deformation rates over the first 10 m below −219 m, followed by more than a 3-fold increase in $\mathrm{d}u/\mathrm{d}z$ from −230 to −235 m, where the deformation rate reaches a maximum of 1.5 a⁻¹.

Figure 3 (a) Modeled shear stress (τ_xz), (b) effective stress (τ_e), (c) deformation rate ($\mathrm{d}u/\mathrm{d}z$), and (d) shear stress (τ_xy) along a transversal cross section at the BH2 location. The inclinometers from BH2 are indicated by red dots.

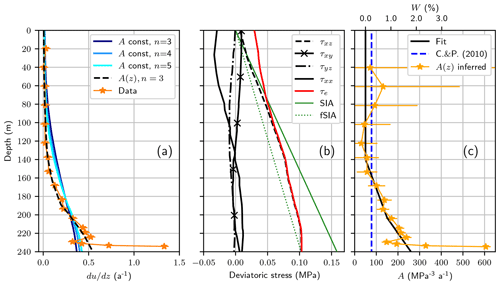
Figure 4 (a) Observed and modeled deformation profiles for BH2, using a uniform creep factor with n=3, n=4, and n=5, as well as a depth-variable creep factor (A=A(z)) with n=3. (b) Vertical profiles of different modeled stress components (negative values correspond to compressive stress). The shallow-ice approximation solution, without (SIA) and with (fSIA) a shape factor, is provided for comparison (dotted and solid green lines, respectively). (c) An inferred creep factor calculated using the measured deformation rate and modeled effective stress at BH2, based on Eq. (6) (bottom horizontal axis). The corresponding water content, according to Duval (1977), is shown along the top horizontal axis. The dashed blue line marks the value of A proposed by Cuffey and Paterson (2010) (C. & P. (2010) in the figure). Note that “const” stands for constant.

4.2 Ice flow model

Ice flow as predicted by our model is mainly dominated by along-flow shear (τ_xz) and lateral shear (τ_xy) (Fig. 3). Lateral shear is significant on the sides of the glacier, where it greatly affects the effective stress (τ_e) and, consequently, the deformation rate (Fig. 3). However, along the centerline near BH2, the magnitude of τ_xy is very small (<0.02 MPa) compared to that of along-flow shear (τ_xz) (>0.08 MPa, where most deformation occurs), meaning our measurements are mainly influenced by τ_xz. We find that other components of the stress tensor are small compared to τ_xz (<10 %), except near the surface, where they can be of a similar amplitude (see Sect. S5). The modeled flow gradient tensor components ($\mathrm{d}u/\mathrm{d}x$ and $\mathrm{d}w/\mathrm{d}z$) are very small (see Sect. S5), which suggests that the use of Eq. (1) to calculate $\mathrm{d}u/\mathrm{d}z$ is appropriate (see Sect. 3.2). We also find that the stress tensor is rather insensitive to the choice of rheological parameters and is mainly controlled by glacier geometry (Sect. S5). Comparing our results with a simplified plane-strain model, commonly referred to as the shallow-ice approximation (SIA), we show that shear stress estimated using the SIA is overestimated (see Fig. 4b), leading to an incorrect quantification of the rheological parameters. Following Nye (1965), the use of the shape factor f=0.646 in the SIA formulation accounts for the effect of the parabolic valley shape (considering a half-width-to-thickness ratio of 2, a reasonable approximation of the Argentière Glacier cross section at the study site; see Sect. S6). Applying this correction improves the stress representation obtained using the SIA, but large discrepancies remain (see the dotted green line in Fig. 4b), with the corrected SIA underestimating the effective stress along most of the profile, except at the bottom, where the basal shear stress matches that of the full-Stokes model.

We find that simulations with a constant creep factor (A) and a varying Glen flow law exponent (n=3, 4, or 5) yield deformation rate profiles exhibiting much lower nonlinearity with depth than that observed (see Fig. 4a). The use of a constant creep factor thus cannot explain the observed profile, regardless of the value of n, which turns out to be poorly constrained in this context due to stresses not varying strongly with depth (Fig. 4b). To remain consistent with the commonly used value of n and infer a relevant creep factor for ice flow modeling in general, we thus assume n=3 and quantify A by following the method described in Sect. 3.2 (Fig. 4c).

Using a linear piecewise approximation of A (black line in Fig. 4c), the simulation provides a good match with observations (Fig. 4a), except for the deformation rates recovered in the boundary layer, which are poorly reproduced by the numerical model. This discrepancy is likely due to the bed topography being too low in resolution to capture stress variations near unresolved local bed irregularities, as well as to our observed $\mathrm{d}u/\mathrm{d}z$ values potentially being strongly biased as a result of the neglect of compressive/extensive strains in the present analysis, which are likely significant within the boundary layer (see Sect. 3.2). For this reason, we consider the values of A inferred from the boundary layer to not be relevant. In Fig. 4c, we see that the inferred creep factor, A(z), in the upper half of the glacier is compatible with the value proposed by Cuffey and Paterson (2010) for temperate ice but increases by up to a factor of ∼4 from −140 m down to the top of the boundary layer (−219 m). We discuss this depth-increasing creep factor in Sect. 5.2.

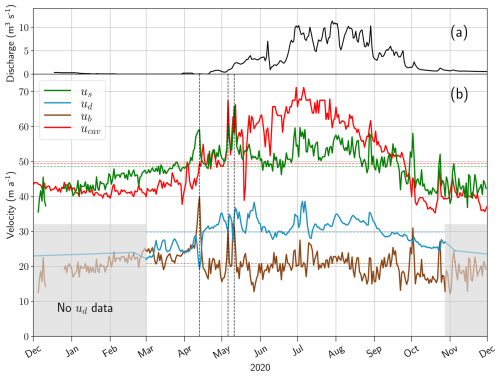
Figure 5 Computed time series of daily subglacial discharge (a) and velocities (b) at the Argentière Glacier. Panel (b) shows the surface velocity computed with the linear model for the GNSS station ARG1 (u_s), the deformation velocity at BH2 (u_d), the inferred basal velocity at BH2 (u_b), and the sliding velocity at the cavitometer (u_cav). The horizontal dashed lines correspond to the average velocities over the studied period. In the shaded areas, an estimate of the sliding velocity (brown line) is shown, assuming a linear trend in the deformation velocity (blue line). The vertical dashed lines indicate speed-up events, which are referred to in the text.

4.3 Temporal evolution of velocities

On a seasonal timescale, the surface velocity exhibits an annual cycle, with a gradual increase between December and May, a period of stagnation until mid-September, and a decrease until December (Fig. 5). The period of stagnation coincides with the melting period, as indicated by the observed high discharges. Surprisingly, however, the deformation velocity also shows seasonal variation, with a phase and amplitude similar to those of the surface velocity. As a result, basal velocity remains roughly constant throughout the year. This is in contrast to in situ observations of basal velocity at the cavitometer, where sliding velocities show strong seasonal variability, marked by the highest sliding speeds in July and the lowest in February and March (Fig. 5b; see also Gimbert et al., 2021a). These results are further discussed in Sect. 5.3.

On shorter timescales, the relationships between surface, deformation, and sliding velocities are different from those observed at the seasonal timescale. Peaks in surface velocity that occur at the beginning of the melt season (Togaibekov et al., 2024) coincide with a decrease in deformation velocity and a strong increase in sliding velocity (highlighted as vertical dashed lines in Fig. 5). These peaks are also visible at the cavitometer, particularly during the May events. At the end of the melt season (October), peaks in surface velocities are also mainly explained by changes in sliding speed but do not necessarily coincide with a decrease in deformation velocity, as observed for the early-melt-season peaks.

To better understand the origin of temporal changes in deformation velocities, we investigate the extent to which these changes occur in proportion to changes in $\mathrm{d}u/\mathrm{d}z$ with depth. For this, we define s_n as the standard deviation of the monthly averaged values of $\mathrm{d}u/\mathrm{d}z$, normalized by $\mathrm{d}u/\mathrm{d}z$ values averaged between 15 February and 15 October 2020. We show that s_n is consistently on the order of 20 %, with no preferential localization in any specific section of the ice column (Fig. 6b). A more detailed analysis of $\mathrm{d}u/\mathrm{d}z$ variations at each sensor shows that most of these variations exhibit a similar seasonal cycle, with maximum deformation occurring in summer (see Sect. S7). Temporal variations in $\mathrm{d}u/\mathrm{d}z$ at any given depth thus generally occur in proportion to the long-term average value of $\mathrm{d}u/\mathrm{d}z$. Only four sensors (BH2#6, BH2#11, BH2#12, and BH2#14) significantly depart from this general picture, either by exhibiting a different phasing (BH2#6, BH2#12, and BH2#14) or by showing a different amplitude (BH2#11) (Fig. S17), which may be due to poor coupling with the ice (the noise levels for BH2#12 and BH2#14 are particularly high).

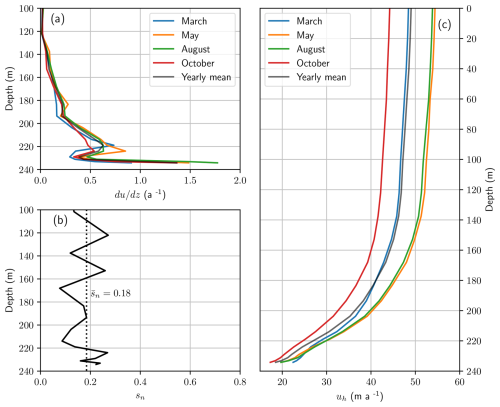
Figure 6 (a) Observed monthly and yearly $\mathrm{d}u/\mathrm{d}z$ profiles for four periods (see legend). (b) Standard deviation of the monthly averaged $\mathrm{d}u/\mathrm{d}z$ profile, normalized by the $\mathrm{d}u/\mathrm{d}z$ value averaged between 15 February and 15 October 2020. (c) Observed monthly and yearly horizontal-velocity (u_h) profiles for four periods (see legend).

5 Discussion

5.1 Identification and interpretation of the boundary layer

The shape of the deformation rate profile and the retrieved values of $\mathrm{d}u/\mathrm{d}z$ close to the bed suggest intense deformation due to local stress concentrations around bedrock irregularities within the boundary layer (Maier et al., 2019; Weertman, 1957; Gudmundsson, 1997a). We qualitatively explored the viability of this explanation with a simulation of tilt evolution close to the bed, using the deformation rates provided by Gudmundsson (1997b) and the model of tilt evolution for a given velocity field provided by Gudmundsson et al. (1999), as explained in Sect. S8. In Fig. S18, we show that significant rates of compressive or extensive horizontal strain ($\mathrm{d}u/\mathrm{d}x$) localize close to the bed and dominate the flow gradient in a boundary layer with a thickness equal to ∼6 times the vertical amplitude of the bedrock bump. We find that under the hypothesis of Eq. (1), and using synthetic tilt time series produced from the estimated strain rates, the inferred apparent $\mathrm{d}u/\mathrm{d}z$ values have a zigzag shape similar to that observed in Fig. 2. This suggests that the zigzag shape in the reconstructed $\mathrm{d}u/\mathrm{d}z$ values is an artifact resulting from neglecting $\mathrm{d}u/\mathrm{d}x$ rather than a real variation in $\mathrm{d}u/\mathrm{d}z$. A comparison between our reconstructed $\mathrm{d}u/\mathrm{d}z$ values from the tilt data and the inferred apparent $\mathrm{d}u/\mathrm{d}z$ values using the models of Gudmundsson (1997b) and Gudmundsson et al. (1999) suggests that we drilled on the summit of a bedrock bump with a vertical amplitude of ∼2 m.

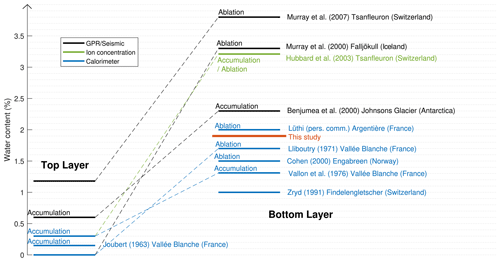
Figure 7 Synthesis of water content measurements taken in temperate glaciers, with a distinction made between the top layer (close to the surface) and the bottom layer (close to the bedrock). The colors indicate the methods (ground-penetrating radar (GPR)/seismic methods, calorimeter measurements, and ion concentrations). Note that “pers. comm.” stands for personal communication.

5.2 Interpretation of the depth-increasing creep factor

The Argentière Glacier is fully temperate – i.e., ice lies at the pressure melting point throughout the entire ice column, meaning that the observed increase in the creep factor with depth must result from factors other than changing temperature. We test the hypothesis that the depth increase in the creep factor is due to an associated increase in interstitial water content (W) by linking these two quantities using the formula proposed by Duval (1977). Adapting the formulation from Duval (1977) by considering A=50 MPa⁻³ a⁻¹ as a reference value when W=0 (i.e., assuming no water content in the upper half of the glacier), we obtain

$$\begin{array}{}\text{(7)}& W={\displaystyle \frac{\mathrm{1}}{\mathrm{2.34}}}\left({\displaystyle \frac{A}{\mathrm{50}}}-\mathrm{1}\right),\end{array}$$

where W is expressed as a percentage and A in terms of MPa⁻³ a⁻¹. The inferred water content values are shown along the top horizontal axis of Fig. 4c. Discarding the negative values as artifacts of our chosen parametrization of the Duval (1977) model, we find that the expected water content above −219 m ranges between 0 % and 1.3 %, increasing toward the bed. Below this depth, the deformation profile is likely influenced by enhanced stress and underestimated velocity gradients due to local basal roughness and cannot be interpreted in terms of an enhanced creep factor (see Sect. 5.1). These values of W and this type of spatial distribution are comparable to those observed for temperate ice (see Fig. 7). The depth-increasing creep factor is thus compatible with the effect of depth-increasing water content.

Our suggestion of increased water content with depth might seem to contradict the findings of Lliboutry and Duval (1985), who reported no relationship between W and depth based on their analysis of an ice core obtained from the Argentière Glacier at a location close to our boreholes (Hantz and Lliboutry, 1983). However, the researchers who performed the measurements considered them unreliable as the water content was primarily correlated with the air temperature at which the measurements were taken at the glacier surface, with higher temperatures increasing ice core melt and thus artificially increasing the measured water content (Michel Vallon, personal communication). For these reasons, we do not include the results from Lliboutry and Duval (1985) in Fig. 7, although they have previously appeared in other compilations of observations of interstitial water content (e.g., Pettersson et al., 2004; Cuffey and Paterson, 2010). We also note that the absolute values of water content, as inferred using the relationship proposed by Duval (1977), may be associated with high uncertainty since this empirical relationship was derived in the laboratory by shearing temperate ice in tertiary creep with a water content of up to 0.8 % and has not been validated for higher water content values. Recently, Adams et al. (2021) found in similar experiments that ice viscosity under secondary creep is not sensitive to water content when W>0.6 %. However, we do not expect these results to apply to the present case since tertiary creep is expected under the significant cumulative deformations of the Argentière Glacier (Lliboutry and Duval, 1985; Budd and Jacka, 1989).

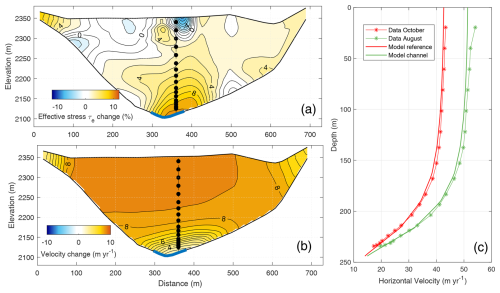
Figure 8 Modeled changes in effective stress (a) and horizontal velocity (b) resulting from nonuniform variations in basal friction. We assume that, during the melting period, friction increases in the central part (thick blue line in panels a and b) and decreases elsewhere due to channelized efficient drainage in the central line contrasting with the inefficient cavity network elsewhere. The inclinometers for BH2 are indicated by black dots in panels (a) and (b). Panel (c) compares the observed velocity profiles at BH2 for August and October with the modeled velocity profiles with nonuniform (channel) and uniform (reference) basal friction.

Although water content is our best identified candidate for explaining the increase in the creep factor with depth, we note that other factors might also be at play, such as depth-decreasing grain sizes due to the increased rate of mechanical work (Behn et al., 2021) or depth-increasing ice anisotropy due to increased shearing (Cuffey and Paterson, 2010; Montagnat and Duval, 2004). The role of these factors would need to be specifically analyzed by quantifying the evolution of grain size and ice texture with depth at the measurement site in order to determine whether their respective influences on ice viscosity can be discarded.

5.3 Temporal changes in deformation velocity

We show that deformation velocity varies seasonally by ∼30 % (Fig. 5). Using Glen's flow law with n=3, this implies either a stress change of ∼9 % or a change in the creep factor of ∼30 %, of which the latter would require the water content to be multiplied by 1.6 throughout the entire ice column. Although microcracking in response to changes in surface melting and subglacial water pressure can provide significant amounts of water at depth (Gajek et al., 2021), the extent to which this mechanism could alter interstitial water content at the source of the ice softening remains unknown. In addition, an increase in microcracking at depth during summer is inconsistent with the observed decrease in basal water pressure. Aside from microcracking, a 30 % increase in deformation heat ($\approx +\mathrm{3}\times {\mathrm{10}}^{-\mathrm{4}}$ W m⁻³) would produce an excess water content of only ∼0.17 % over 1 month (the time frame within which the deformation change occurs), which would have a much smaller effect on the creep factor than what was observed. Finally, with regard to the stress variation hypothesis, a 9 % stress change cannot be explained by the seasonal evolution of ice thickness, which is at its maximum in May and decreases until October (Vincent et al., 2022), making it out of phase with the observed deformation rate. Furthermore, the amplitude of the thickness change at the BH2 site is about 6 m (Vincent et al., 2022), which represents only a 2 % stress change.

The hypothesis that we find most plausible for explaining the seasonal variability in deformation rates observed at BH2 is that it arises from changes in stress distribution due to nonuniform spatial changes in basal drag during the melting season, as previously suggested in Hooke et al. (1992) and Willis et al. (2003). The loss of drag in response to meltwater input in areas surrounding the observation site may locally increase stress through stress transfer in the form of lateral shear. This may be caused by differences in subglacial hydrological conditions between the glacier's centerline and its sides. The lack of change in basal velocity during summer at BH2 (Fig. 5), despite increases in deformation velocity and stress, suggests that basal friction also increased in the central part of the glacier to accommodate more stress while remaining at a constant velocity. This may have resulted from the development of efficient drainage in the central part of the glacier, as previously identified from seismic observations (Nanni et al., 2021). This efficient drainage reduces water pressure and thus promotes high friction along the central line, while the sides remain dominated by higher-pressure, inefficient drainage, promoting lower basal friction. To investigate this hypothesis, we perform a complementary numerical simulation in which friction is increased around a central ∼50 m wide area (assumed to be affected by efficient drainage) and decreased elsewhere (see Fig. 8a and b). We find that, relative to the reference state from October 2020, a 20 % decrease in A_s in the central part of the glacier, combined with an increase of 70 % in A_s elsewhere, is sufficient for producing the stress change needed to explain the enhanced internal deformation observed in summer (Fig. 8c). Such a contrast in A_s (i.e., a factor of 2.1) is compatible with that expected when cavitation does or does not occur (Gimbert et al., 2021a; Gilbert et al., 2022; Maier et al., 2022). This view is also consistent with the findings of Vincent et al. (2022), which show that bed separation by means of cavitation increases between January and July, with greater amplitudes along the glacier margin than along the midline. This leads to an increase in basal sliding during this period, as observed in our data (Figs. 5 and 6c). An evolving drag contrast between the center and sides of the glacier would also explain why strong peaks in surface velocity are associated with a decrease in deformation velocity during the early melt season. Early water input into the not-yet-developed efficient drainage system along the centerline of the glacier may lead to pressurization of the central channel, reducing drag along the centerline relative to the sides of the glacier. This effect may be less pronounced in fall because the channels are still of significant size after summer, and this would explain why the decrease in deformation velocity during surface velocity peaks is observed not in fall but only in spring (Fig. 5).

6 Conclusions

Using borehole inclinometry, we were able to reconstruct the deformation profile along the central line of the ablation area of the Argentière Glacier and its evolution over 8 months, including the entire melt season. We quantified the Glen flow law creep factor by combining our observations with modeling of the local stress field using a three-dimensional full-Stokes ice flow model, which appears to be different from what the SIA would predict, making its use inappropriate at our study site. We show that surface values (above 100 m depth) of the creep factor are consistent with the standard value for temperate ice (Cuffey and Paterson, 2010) but increase progressively from below this depth up to 200 MPa⁻³ a⁻¹. We interpret the depth-increasing creep factor as being associated with an increase in water content from 0 % to 1.3 %, which are reasonable values given previous in situ water content measurements found in the literature (Fig. 7). We also find seasonally evolving deformation rates, with higher deformation rates occurring during the melt season, meaning that the local deformation velocity explains most of the evolution of the surface velocity on a seasonal timescale. We show that this variability is due to changes in stress distribution within the ice body in response to the evolving contrast in basal drag between the centerline and the rest of the glacier during the melt season. We interpret the difference in drag at the center of the glacier as the effect of efficient drainage developing at the deepest point of the subglacial valley.

This study demonstrates the significant value of using borehole inclinometry to infer ice rheology and local changes in basal friction that cannot be detected through surface velocity observations. The data obtained provide rare insights into how subglacial hydrology, basal friction, and surface velocity are interconnected.