Spectral induced polarization survey for the estimation of hydrogeological parameters in an active rock glacier

Degrading permafrost in rock glaciers has been reported from several sites in the European Alps. Changes in ground temperature and ice content are expected to affect the hydrogeological properties of rock glaciers and in turn modify the runoff regime and groundwater recharge in high-mountain environments. In this study, we investigate the use of an emerging geophysical method in permafrost studies to understand the hydrogeological properties of the active Gran Sometta rock glacier, which consists of a two-lobe tongue (a white and a black) whose lobes differ in their geologies. We present the application of spectral induced polarization (SIP) imaging, a method that provides quasi-continuous spatial information about the electrical conductivity and polarization of the subsurface, which are linked to hydrogeological properties. To quantify the water content and the hydraulic conductivity from SIP imaging results, we used the petrophysical dynamic stern layer model. The SIP results show a continuously frozen layer at 4–6 m depth along both lobes which hinders the infiltration of water, leading to a quick flow through the active layer. To evaluate our results, we conducted tracer experiments monitored with time-lapse electrical conductivity imaging, which confirms the hydraulic barrier associated with the frozen layer and allows the pore water velocity to be quantified (∼ 10⁻² m s⁻¹). Below the frozen layer, both lobes have distinct water content and hydraulic conductivity. We observed a higher water content in the black lobe, which moves faster than the white lobe, supporting the hypothesis that the water content at the shear horizon affects the rock glacier velocity. Our study demonstrates that the SIP method is able to provide valuable information for the hydrogeological characterization of rock glaciers.

1 Introduction

The European Alps are undergoing drastic changes due to climate change (Beniston et al., 2018) such as retreating glaciers, the degradation of permafrost or the loss of ground ice (e.g., Biskaborn et al., 2019). The loss of ground ice has been linked to rockfalls and slope instability (e.g., Krautblatter et al., 2013; Haeberli et al., 2017) posing a threat to infrastructure and human life not only in high-mountain environments but also in downstream areas. Active rock glaciers, which consist of frozen rocks, sediments and large amounts of ground ice, move downslope, resulting in surface deformation (e.g., Haeberli, 1985; Barsch, 1996). Accordingly, they can play an important role in the storage of frozen and liquid water (Jones et al., 2018; Wagner et al., 2021). Rock glaciers are more resilient towards the increase in air temperatures, compared to glaciers, as they are protected by a top layer of large blocks and air-filled voids with low thermal conductivity (Haeberli et al., 2006; Giardino et al., 2011; Amschwand et al., 2024). Due to the higher resilience of subsurface ice towards increasing air temperatures compared to glacier ice, future predictions expect a change in the hydrological regime in mountainous areas with a shift from glacially dominated hydrological systems to periglacially dominated systems (e.g., Haeberli et al., 2017), which has a particular impact on areas which are supplied by water from high-mountain environments (e.g., Brighenti et al., 2019).

Water, coming from snowmelt, rainfall, groundwater and ice meltwater, commonly percolates through intact rock glaciers as supra-permafrost flow in the active layer along the top of an ice-rich core, which is assumed to be quasi-impervious (e.g., Giardino et al., 2011; Buchli et al., 2013; Winkler et al., 2016; Krainer et al., 2007; Jones et al., 2019). The supra-permafrost flow, also called quickflow, takes place in the active layer, which is characterized by coarse-grained materials and high hydraulic conductivity (reported pore water velocity values between 10⁻³ and 10⁻² m s⁻¹) (e.g., Krainer and Mostler, 2002; Buchli et al., 2013; Winkler et al., 2016; Harrington et al., 2018; Del Siro et al., 2023). Due to their high hydraulic conductivities, rock glaciers release water from heavy rainfalls quickly, and they increase flood peaks when compared to catchments without rock glaciers (Geiger et al., 2014; Pourrier et al., 2014). Within rock glaciers, the ice-rich cores might be considered quasi-impermeable as they hinder the infiltration of water from rainfall or snowmelt. In contrast, groundwater can move underneath the frozen layer as sub-permafrost flow (also called baseflow) through fine-grained sediments (e.g., Arenson et al., 2002; Krainer et al., 2015) with lower hydraulic conductivity than the supra-permafrost layer (Winkler et al., 2016; Rogger et al., 2017). In degraded rock glaciers with only discontinuous ice layers, also rainwater and snow meltwater can percolate into deeper areas where it accumulates, leading to an increased storage capacity in the fine-grained section of the rock glacier (Pourrier et al., 2014; Winkler et al., 2016).

The monitoring of rock glacier kinematics during the last decades in the European Alps revealed an overall acceleration in the downslope movement (e.g., Delaloye et al., 2010; Wirz et al., 2014; Kellerer-Pirklbauer et al., 2024), which was first related to warming ice and liquid water in the frozen material due to increasing air temperatures (e.g., Kääb et al., 2007; Roer et al., 2008). Recent studies focus on processes in the shear horizon underneath the ice-rich layer because most of the deformation (60 %–90 %) occurs there (Arenson et al., 2002; Cicoira et al., 2021). They demonstrate that rock glacier movement is primarily dominated by the liquid water content around the shear horizon (Wirz et al., 2016; Cicoira et al., 2019), where groundwater can accumulate (Kenner et al., 2017; Buchli et al., 2018). Water accumulated within the rock glacier increases the pore water pressure and decreases the frictional resistance, leading to deformation (Cicoira et al., 2019; Kenner et al., 2017). Ikeda et al. (2008) and Cicoira et al. (2021) demonstrated that in degrading rock glaciers increasing subsurface temperatures and fast deformation can lead to the creation of hollow spaces in the frozen layer acting as water flow paths. Water from precipitation and snowmelt can slowly percolate from the unfrozen active layer through such channels down to the shear horizon on the bottom of the rock glacier.

Commonly, the internal structure of rock glaciers is investigated by either boreholes or geophysical measurements. While boreholes can provide direct information about the subsurface, e.g., in terms of ice and water content, they only provide punctual information. Hence, borehole data need to be interpolated to resolve spatial variations in the internal structure, which may bias the interpretation of the data, as those parameters can vary largely in rock glaciers (e.g., Krainer et al., 2015). Moreover, core drillings in rock glaciers are rare (e.g., Noetzli et al., 2021), and drilling in a given position is possible only once, thus not being suited for the monitoring of the ice and water content.

Phillips et al. (2023) installed a cross-borehole electrical resistivity tomography (ERT) monitoring on an active rock glacier. ERT is a geophysical method that allows the variations in the electrical resistivity (ρ) of the materials to be resolved (see Binley and Slater, 2020, for further details), in this case between the two boreholes. Due to the link between ρ and temperature, ERT has been used to discriminate between frozen and unfrozen materials (e.g., Kneisel et al., 2008; Mollaret et al., 2019). The ERT results can also be expressed in terms of the electrical conductivity σ (with $\mathit{\sigma }=\mathrm{1}/\mathit{\rho }$), which is more intuitive when used to estimate hydraulic conductivity, for instance. While initial studies assume that current can only flow through the unfrozen water filling the pores (electrolytic conductivity), quantitative interpretation of the ERT imaging results need to account for surface conductivity, which is the current flowing at the fluid–ice (or fluid–grain) interface (Stillmann et al., 2010; Maierhofer et al., 2022, 2024). The application of an external electrical field not only triggers the accumulation of charges in the electrical double layer (EDL) (surface conductivity) but also leads to a polarization effect (e.g., Vinegar and Waxman, 1984). Several studies have shown a direct relation between the surface conductivity and the polarization at low frequencies (<10 kHz) (e.g., Revil, 2013a; Weller et al., 2013), which allows the contribution of surface conductivity to the total electrical conductivity to be considered.

The induced polarization (IP) method measures both the electrical conductivity and polarization (i.e., capacitive) properties of the subsurface at low frequencies (<10 kHz), either in the time domain (TDIP) or in the frequency domain (FDIP) at one single frequency (single-frequency IP) or over a broad range of frequencies (spectral IP) (for a review of the method, see Binley and Slater, 2020). Recently, induced polarization has been used for an improved discrimination of ice-rich areas from bedrock (e.g., Maierhofer et al., 2022) due to the high surface charge, and in turn high polarization signature, of ice (Stillman et al., 2010). Yet, to the best of our knowledge, no study examined the potential of spectral induced polarization (SIP) data for the estimation of water content and hydraulic conductivity in a rock glacier or other alpine permafrost landforms.

Hydrogeological information of rock glaciers is critical to fully understand the parameters controlling their deformation and movement. Hence, the objective of this study is to understand the hydrogeological properties of the active rock glacier Gran Sometta in the Italian Alps. We evaluate the potential of SIP imaging results for the estimation of hydrogeological parameters, namely the hydraulic conductivity and the water content. The SIP results are validated by two tracer experiments, where the distribution and flow of a saltwater injection were monitored by repeated 3D ERT images, permitting the direct estimation of the pore water velocity in the rock glacier. Additionally, we investigate the link between the hydro-geophysical results and spatial variations in deformation rates of the Gran Sometta rock glacier to demonstrate the relevance of geophysical investigations in understanding the main drivers of rock glacier movement in the European Alps.

2 Material and methods

2.1 Study area

The Gran Sometta rock glacier is tongue-shaped and located in the Valtournenche valley (Aosta valley) in the western European Alps (see Fig. 1) at an elevation between 2630 and 2770 m. The rock glacier has a total length of 400 m, a width of 150–300 m and a thickness of 20–30 m, estimated from the height of the front (Bearzot et al., 2022). At the surface, the rock glacier mainly consists of pebbles and angular blocks originating from the rock walls of the Gran Sometta peak. In the central area, longitudinal ridges dominate the structure of the morphology, while in the front part there are transversal furrows. The upper (southern) part of the rock glacier was covered by a glacier during the Little Ice Age (LIA), which still has effects on the distribution of ice content (see detailed descriptions of the rock glacier in Bearzot et al., 2022 and 2023).

The rock glacier can be split into two main lobes (see Fig. 1), which are called the white lobe (eastern part) and the black lobe (western part), as the former is mainly composed of light-colored dolomitic marbles and the latter of dark-colored carbonate–silicate schists. Apart from the color, the lobes differ in their internal structure and their kinematics (Bearzot et al., 2022). ERT results presented by Bearzot et al. (2022) revealed a continuous ice-rich layer with a thickness of 20 m approximately in the black lobe, while in the white lobe there are more spatial variations in the ice content, possibly related to the influence of the coverage of an LIA glacier. The rock masses in these areas possibly warmed up during the LIA due to the thermal isolation of the ice cover (Bearzot et al., 2022). Kinematic investigations of Bearzot et al. (2022) for the period 2013–2020 show that the black lobe moves faster (∼ 1 m yr⁻¹) than the white lobe (∼ 0.5 m yr⁻¹), which has been linked to the different internal structure and the steeper topography of the black lobe.

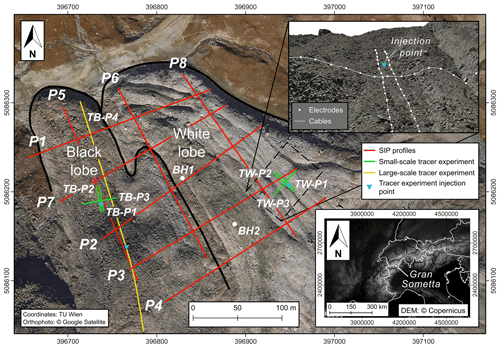
Figure 1 Map of the Gran Sometta rock glacier, which consists of two lobes: the black lobe in the west and the white lobe in the east. The SIP profiles P1–P8 are indicated by red lines, while profiles of the small-scale tracer experiments are indicated by green lines. The large-scale tracer profile is presented by a yellow line, and the positions of two boreholes (BH1 and BH2) are displayed by white dots. To the lower right is a map of the Alps with the position of the Gran Sometta rock glacier. A 3D visualization of the area of the tracer experiment on the white lobe (TW) is given in the upper right area. Electrodes are presented by white dots and cables by white lines. Orthophoto: © Google Satellite; digital elevation model: © Copernicus.

2.2 The spectral induced polarization (SIP) method and the complex conductivity

IP measurements are considered an extension of the ERT method and provide the conductive (electrical conductivity) and capacitive properties (polarization) of the subsurface (for an overview, see Binley and Slater, 2020). When working in the FDIP, as in this study, an alternating current at a given angular frequency ω (in the range between 1 mHz and 10 kHz) is injected via two electrodes and the resulting voltage is measured between two additional electrodes. The ratio between the voltage and the injected current gives a complex-valued transfer impedance Z^∗(ω) consisting of a magnitude $\left|Z^{\ast }\right(\mathit{\omega }\left)\right|$ and a phase shift φ(ω) between the voltage and the current.

$$\begin{array}{}\text{(1)}& Z^{\ast }\left(\mathit{\omega }\right)=\left|Z^{\ast }\right(\mathit{\omega }\left)\right|e^{i\mathit{\phi }\left(\mathit{\omega }\right)}\end{array}$$

FDIP measurements can be conducted at one single frequency (single-frequency IP) or at several frequencies, which is the spectral induced polarization (SIP) method. Data at multiple frequencies provide additional information about the frequency dependence of the electrical properties as different materials with different textural properties polarize at different length scales (see Binley et al., 2005; Revil and Florsch, 2010). Such information is essential for a reliable estimation of hydrogeological properties, as, for example, the hydraulic conductivity (see Sect. 2.4).

Equal to ERT, a small separation between current and potential dipole favors high resolution, while increasing their separation helps to reach deeper areas of investigation, yet at costs of decreasing the signal-to-noise ratio. At the field scale, combinations through tens of electrodes can be used to resolve for vertical and horizontal variations in the complex-valued electrical conductivity σ^∗ or its inverse, the complex resistivity ρ^∗.

The complex conductivity is used to represent both electrical properties of the subsurface: the electrical conduction (real part, σ^′) and the capacitive property (imaginary part, σ^′′). The σ^∗ can also be represented by its magnitude $\left|{\mathit{\sigma }}^{\ast }\right|$ and phase angle φ(ω):

$$\begin{array}{}\text{(2)}& {\mathit{\sigma }}^{\ast }\left(\mathit{\omega }\right)={\mathit{\sigma }}^{\prime }\left(\mathit{\omega }\right)+i{\mathit{\sigma }}^{\prime \prime }\left(\mathit{\omega }\right)=\left|{\mathit{\sigma }}^{\ast }\right(\mathit{\omega }\left)\right|e^{i\mathit{\phi }\left(\mathit{\omega }\right)}.\end{array}$$

In areas free of metallic materials $\left|{\mathit{\sigma }}^{\ast }\right|$ is approximately equal to σ^′ because φ(ω) is relatively low (typically below 100 mrad) (Kemna et al., 2004).

Current can be conducted through the subsurface via three mechanisms: matrix conductivity, electrolytic conductivity and surface conductivity (see Eq. 3). (1) The matrix conductivity σ_m refers to the current conduction through the solid (i.e., grains and matrix). This mechanism is negligible at sites without electronic conductors and semi-conductors like metallic minerals, such as in rock glaciers. (2) The electrolytic conductivity σ_el (Eq. 4) is conduction through the pore fluid. It is dominated by the porosity ϕ, the cementation exponent m (which can be also expressed by the formation factor $F={\mathit{\varphi }}^{-m}$), the saturation S_w, the saturation exponent n and the fluid conductivity σ_f (see Archie, 1942). (3) The surface conductivity ${\mathit{\sigma }}_{\mathrm{s}}^{\prime }$ takes place in the EDL at the interface between solid particles and the pore fluid. This conduction mechanism is controlled by the surface area and surface charge of particles and is frequency-dependent (e.g., Waxman and Smits, 1968).

$$\begin{array}{}\text{(3)}& {\displaystyle }{\mathit{\sigma }}^{\prime }\left(\mathit{\omega }\right)={\mathit{\sigma }}_{\mathrm{m}}+{\mathit{\sigma }}_{\mathrm{el}}+{\mathit{\sigma }}_{\mathrm{s}}^{\prime }\left(\mathit{\omega }\right)\text{(4)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{el}}=S_{\mathrm{w}}^n{F}^{-\mathrm{1}}{\mathit{\sigma }}_{\mathrm{f}}\end{array}$$

The imaginary component of the complex conductivity is only dependent on the imaginary component of the surface conductivity because the pore water is assumed to be non-polarizable at frequencies below 10 kHz:

$$\begin{array}{}\text{(5)}& {\mathit{\sigma }}^{\prime \prime }\left(\mathit{\omega }\right)={{\mathit{\sigma }}^{\prime }}_{\mathrm{s}}^{\prime }\left(\mathit{\omega }\right).\end{array}$$

In the absence of electronically conductive materials, the polarization is primarily related to the surface area and the surface charge of the particles (Vinegar and Waxman, 1984; Leroy et al., 2008; Revil and Florsch, 2010).

2.3 SIP field measurements, data processing and inversion

In October 2022, we collected SIP data along eight lines (P1 to P8) on the Gran Sometta rock glacier (see Table 1). P5, P6 and P8 are longitudinal lines, and P1, P2, P3, P4 and P7 are transversal to the flow direction of the rock glacier (see Fig. 1). Different line orientations allow data of quadrupoles to be collected with different dipole orientations, which provides a good coverage of the subsurface electrical properties in all directions (see, e.g., Chambers et al., 2002; Moser et al., 2023). For each line of electrodes, we used 32 stainless-steel electrodes with a separation of 7.5 m. We collected data using dipole–dipole (DD) normal and DD reciprocal (electrodes used for current and voltage dipole interchanged) configurations for analysis of data error (see, e.g., LaBrecque et al., 1996). We also collected data using a multiple-gradient (MG) configuration, which is related to higher signal-to-noise ratio than DD. While DD data were collected with a dipole length of 4 times the electrode spacing (i.e., skip-3), MG readings were used with a voltage dipole using a skip-0, skip-1, skip-2 and skip-3 configuration, as well as the current dipoles wrapping the eight potential dipoles. Due to the lower number of independent current injections, with the MG configuration we collected data in a frequency range of 0.1–225 Hz, and with the DD configuration we used a frequency range of 0.5–225 Hz due to time constraints in the field. For the data acquisition, we used the eight-channel device DAS-1 (data acquisition system, from MPT-IRIS Inc.), which was connected to stainless-steel electrodes via coaxial cables (COAX10, designed at TU Wien; see Flores Orozco et al., 2021). The isolation of coaxial cables allows us to avoid electromagnetic (EM) coupling due to cross-talk between the cables, as demonstrated by Flores Orozco et al. (2013 and 2021) and (in alpine permafrost) by Maierhofer et al. (2022).

The SIP data were processed in four steps. (1) We calculated the geometric factors k_num as the ratio between numerically modeled transfer resistances of a homogeneous synthetic model and the resistivity of the homogeneous model. Impedance magnitudes $\left|Z^{\ast }\right|$ were multiplied with k_num to derive the apparent resistivities $\left|{\mathit{\rho }}_{\mathrm{a}}^{\ast }\right|$. Readings with negative apparent resistivity (inconsistent polarity between k_num and the measured transfer resistance) were deleted as erroneous readings. (2) All readings with an absolute misfit between normal and reciprocal above 2 times the standard deviation of the normal–reciprocal misfit for the entire dataset, as well as those readings with a relative normal–reciprocal misfit (above 5 % in the case of |Z^∗| and 50 % in the case of φ) were removed, similar to the filtering protocol of Flores Orozco et al. (2019). (3) Additionally, outliers in the readings of apparent resistivity $\left|{\mathit{\rho }}_{\mathrm{a}}^{\ast }\right|$, defined as those below 10³ Ωm and above 10⁵ Ωm, as well as positive impedance-phase values (φ), were removed. The apparent resistivity thresholds were defined based on a histogram analysis, where large gaps at the margin of the data distribution were identified as thresholds, resulting in approximately five to six removed quadrupoles per electrode line. Steps 1 to 3 were conducted separately for each frequency. (4) Similar to Moser et al. (2023), readings which were removed during steps 1 to 3 at at least one frequency were removed at all frequencies to keep the same quadrupoles for the inversion of data collected at all frequencies, aiming at having consistent sensitivity in the inverted images (Flores Orozco et al., 2013). After applying filtering steps 1–4, 731 of 1792 quadrupoles remained in the case of the MG configuration and 359 of 4416 in the case of the DD configuration. Considering the high density of measurements collected with the MG configuration designed in our study, the number of filtered measurements has just a minimal effect on the coverage and resolution of our datasets, as demonstrated, for instance, in the pseudosection (in terms of $\left|{\mathit{\rho }}_{\mathrm{a}}^{\ast }\right|$) presented in the Appendix (see Fig. A1). From now on, for all multi-frequency analyses, we only consider MG data because of the larger range of frequencies used for the data collection with the MG configuration (0.1–225 Hz) than with the DD configuration (0.5–225 Hz).

We inverted the data collected at each frequency independently using the ResIPy code (Blanchy et al., 2020), which calls the cR3t 3D complex resistivity inversion algorithm (for details see Binley and Slater, 2020). cR3t is a smoothness-constrained algorithm based on complex calculus, which iteratively solves for a 3D complex conductivity model. The 3D model is represented by a finite element mesh, which is created in Gmsh (Geuzaine and Remacle, 2009). The mesh is based on tetrahedral elements, whose sizes increase with increasing distance from the electrodes, and it incorporates the topography through a digital terrain model.

The inversion algorithm fits the data under the consideration of an error model to a certain level of confidence (Binley and Kemna, 2005), which is here represented by the error-weighted root mean square error (RMSE) between the data and the forward solution of the inverse model. The error model consists of a relative magnitude error, which for our measurements was estimated at 10 %, as well as an absolute phase error, which in our measurements was estimated at 7 mrad (at 0.1 Hz) and increased to 43 mrad (at 25 Hz) due to the increasing contamination of EM coupling with increasing frequency in the data (e.g., Binley et al., 2005). All inversions converged and resulted in an error-weighted RMSE value equal or close to 1.

Table 1 Overview of electrical measurements.

2.4 Deriving hydraulic conductivity from SIP measurements

The polarization (capacitive property) provides information about textural properties of the subsurface, which control the ability of water to flow, i.e., its hydraulic properties (see Binley and Slater, 2020). According to the Kozeny–Carman equation, geometric parameters, i.e., the hydraulic radius and the tortuosity, are dominating the hydraulic conductivity of the subsurface (Carman, 1939; Kozeny, 1927). These parameters can be derived from IP and SIP measurements, as the tortuosity is linked to the electrolytic conductivity and the hydraulic radius is related to the surface conductivity (for a review see Slater, 2007). Using only electrical conductivity and neglecting surface conductivity in the estimation of hydraulic conductivity bears the risk of overestimating the hydraulic properties, as the contribution to current conduction through the EDL is incorrectly assumed to be through a higher porosity and charge transfer across the electrolyte filling the pores. On the one hand, in relatively coarse-grained materials such as sands and gravels, the electrolytic conductivity dominates over the surface conductivity. In such media the hydraulic conductivity increases with increasing porosity, which in turn increases the electrolytic conductivity, resulting in a positive correlation between electrical and hydraulic conductivity (e.g., Frohlich et al., 1996). On the other hand, in relatively fine-grained materials (clays and fine silts), the surface conductivity dominates over the electrolytic conductivity. In such media the hydraulic conductivity decreases with increasing clay content as the pores are less connected, hindering water flow, which in turn increases the surface conductivity and results in a negative correlation between electrical and hydraulic conductivity (e.g., Urish et al., 1981).

Several studies have demonstrated an improvement in the hydraulic conductivity estimation when considering the frequency dependence of the polarization because the frequency dependence is particularly linked to different length scales of the pore space (e.g., Binley et al., 2005; Revil et al., 2015). Thus, SIP measurements permit an improved estimation of the hydraulic properties, as observed from laboratory (e.g., Revil and Florsch, 2010; Slater et al., 2014; Weller et al., 2015) and field-scale investigations (e.g., Hördt et al., 2009; Benoit et al., 2019; Flores Orozco et al., 2022). However, investigations in different environments demonstrate that there is no universal model linking SIP parameters and hydraulic conductivity, and thus every model applied in the field needs to be carefully evaluated (see Slater, 2007).

2.5 The relation between complex conductivity and hydrogeological parameters

The volumetric water content θ of porous media is directly linked to the electrical conductivity σ^′ via F, S_w and n (see Eq. 4), which allows θ to be estimated based on σ^′. However, as described above, σ^′ is related not only to σ_el but also to ${\mathit{\sigma }}_{\mathrm{s}}^{\prime }$ (see Eq. 3). To take ${\mathit{\sigma }}_{\mathrm{s}}^{\prime }$ into account, in this study we use the dynamic stern layer model (DSLM; Revil, 2013a, b), which provides the following equations for the instantaneous (high-frequency) conductivity σ_∞ and the direct-current (low-frequency) conductivity σ₀, where the first term represents the frequency-independent σ_el and the second term the frequency-dependent ${\mathit{\sigma }}_{\mathrm{s}}^{\prime }$:

$$\begin{array}{}\text{(6)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{\infty }}={\mathit{\theta }}^m{\mathit{\sigma }}_{\mathrm{f}}+{\mathit{\theta }}^{m-\mathrm{1}}{\mathit{\rho }}_{\mathrm{g}}B\mathrm{CEC},\text{(7)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{0}}={\mathit{\theta }}^m{\mathit{\sigma }}_{\mathrm{f}}+{\mathit{\theta }}^{m-\mathrm{1}}{\mathit{\rho }}_{\mathrm{g}}(B-\mathit{\lambda })\mathrm{CEC},\end{array}$$

where ρ_g is the grain density (kg m⁻³), B is the apparent mobility of the counterions for surface conduction (m² s⁻¹ V⁻¹), and λ is the apparent mobility of the counterions for the polarization (m² s⁻¹ V⁻¹). CEC is the cation exchange capacity (C kg⁻¹), which is directly linked with the clay content (Mao et al., 2016) and the normalized chargeability M_n, which is the difference between σ_∞ and σ₀ but can also be calculated by the difference between the conductivity at a high frequency f₂ and the conductivity at a low frequency f₁.

$$\begin{array}{}\text{(8)}& M_{\mathrm{n}}={\mathit{\sigma }}_{\mathrm{\infty }}-{\mathit{\sigma }}_{\mathrm{0}}={\mathit{\theta }}^{m-\mathrm{1}}{\mathit{\rho }}_{\mathrm{g}}\mathit{\lambda }\mathrm{CEC}\end{array}$$

In the case of a broad distribution of grain sizes, the spectrum of the conductivity phase angle is rather flat and can be roughly described by a constant phase angle model, the so-called Drake's model (Van Voorhis et al., 1973). If such a model is applicable, M_n is linearly related to σ^′′ (at the geometric mean frequency between f₁ and f₂) by the factor α, as demonstrated by laboratory and field investigations (see Revil et al., 2017c, 2021):

$$\begin{array}{}\text{(9)}& {\displaystyle }{\mathit{\sigma }}^{\prime \prime }=-{\displaystyle \frac{M_{\mathrm{n}}}{\mathit{\alpha }}},\text{(10)}& {\displaystyle }\mathit{\alpha }={\displaystyle \frac{\mathrm{2}}{\mathit{\pi }}}\ln \left(A\right).\end{array}$$

Here A is the number of decades between f₁ and f₂ (Revil et al., 2017c):

$$\begin{array}{}\text{(11)}& A={\log }_{\mathrm{10}}\left({\displaystyle \frac{f_{\mathrm{2}}}{f_{\mathrm{1}}}}\right).\end{array}$$

We used the difference between the conductivity real part at 25 and 0.1 Hz of the MG inverse model for the calculation of M_n as proposed by Revil et al. (2021). In contrast to Revil et al. (2021), the linear relation between M_n and σ^′′ is weak (see Fig. 2c) with a large contrast between the predicted and the estimated slope α (10.11 and 3.37). This discrepancy is due to the strong increase in φ and the nonlinear increase in $\left|{\mathit{\sigma }}^{\ast }\right|$ at frequencies above 2.5 Hz as presented in Fig. 2a (here marked as “high-frequency range”), and it therefore does not fulfill the conditions of the DSLM. Above 2.5 Hz, the surface conductivity is controlled by the accumulation and polarization of charges within the EDL not only at the grain–fluid interface, but also at the ice–water interface as observed by Stillman et al. (2010). The contribution of ice to the polarization at high frequencies is not considered in the DSLM (Coperey et al., 2019); thus, we decided to calculate M_n based on the conductivity resolved at 0.1 and 2.5 Hz (in Fig. 2a marked as “low-frequency range”). As presented in Fig. 2b, such an analysis results in a stronger correlation between M_n and σ^′′ with similar predicted and estimated values for α (2.06 and 1.91).

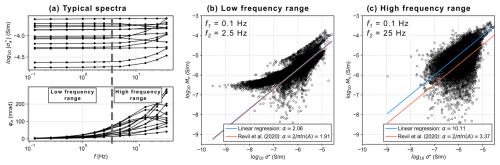
Figure 2 (a) Typical spectra of the apparent conductivity magnitude and phase shift of the Gran Sometta rock glacier. Panels (b) and (c) present the relation between the normalized chargeability, calculated from a low frequency f₁ and a high frequency f₂, and the imaginary part of the complex conductivity at the geometric mean frequency between f₁ and f₂ for the low- (b) and high-frequency range (c). The blue line indicates a linear regression, while the red line represents the theoretical relation (Revil et al., 2020). The data shown here were collected with an MG configuration along P1–P8.

If we combine Eqs. (6) and (8), we can formulate expressions for θ and CEC (Revil et al., 2020):

$$\begin{array}{}\text{(12)}& {\displaystyle }\mathit{\theta }={\left[{\displaystyle \frac{\mathrm{1}}{{\mathit{\sigma }}_{\mathrm{f}}}}\left({\mathit{\sigma }}_{\mathrm{\infty }}-{\displaystyle \frac{M_{\mathrm{n}}}{R}}\right)\right]}^{\mathrm{1}/m},\text{(13)}& {\displaystyle }\mathrm{CEC}={\displaystyle \frac{M_{\mathrm{n}}}{{\mathit{\theta }}^{m-\mathrm{1}}{\mathit{\rho }}_{\mathrm{g}}\mathit{\lambda }}},\end{array}$$

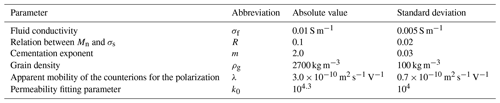
where R is the ratio between λ and B. Laboratory investigations have shown that R is a dimensionless constant value in a range of 0.1 ± 0.02 (Revil et al., 2017a, b, c). To determine σ_f for Eq. (12), we measured σ_f at the spring of the white and black lobes, which is in a range of 0.02–0.03 S m⁻¹. The water stored within the rock glacier increases σ_f over time because of its contact with subsurface materials, like rocks and sediments. Therefore, σ_f of the water stored in the rock glacier is lower than the water released at the rock glacier springs. To take into account the increase in the fluid conductivity of the water stored in the rock glacier over time, we used a value of 0.01 S m⁻¹. For m we used 2, as used by Coperey et al. (2019), and for ρ_g we used the mean grain density of green schist, dolomite and marble (2700 kg m⁻³).

Soueid Ahmed et al. (2020) further developed the DSLM for the estimation of the permeability k (m²) in unsaturated media based on θ, CEC and the fitting parameter k₀.

$$\begin{array}{}\text{(14)}& k\approx {\displaystyle \frac{k_{\mathrm{0}}{\mathit{\theta }}^{\mathrm{6}}}{{\left({\mathit{\rho }}_{\mathrm{g}}\mathrm{CEC}\right)}^{\mathrm{2}}}}\end{array}$$

θ and CEC were calculated by Eqs. (12) and (13), and for k₀ we used a value of 10^4.3 as estimated in the laboratory by Soueid Ahmed et al. (2020). In a next step, we converted k into the hydraulic conductivity K (m s⁻¹) by the following equation:

$$\begin{array}{}\text{(15)}& K={\displaystyle \frac{g\mathit{\delta }}{\mathit{\mu }}}k,\end{array}$$

where we used reference values for the gravitational acceleration g (g=9.81 m s⁻²) and for the groundwater dynamic viscosity μ ($\mathit{\mu }=\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{3}}$ kg m⁻¹ s⁻¹). For the density of the fluid δ, we assumed 1000 kg m⁻³. K can be converted into the pore water velocity v_p under the consideration of the porosity ϕ, where we used a mean value of 40 % (as used as an approximate value in other rock glacier studies, e.g., Hauck et al., 2011; Halla et al., 2021) and the hydraulic gradient $\frac{\mathrm{\Delta }H}{\mathrm{\Delta }L}$. The hydraulic gradient is the ratio between the difference in height ΔH and the horizontal distance ΔL between two points, which we estimated from a digital elevation model:

$$\begin{array}{}\text{(16)}& v_{\mathrm{p}}={\displaystyle \frac{K}{\mathit{\varphi }}}{\displaystyle \frac{\mathrm{\Delta }H}{\mathrm{\Delta }L}}.\end{array}$$

2.6 Resistivity tracer experiment

Several studies have demonstrated the value of monitoring saltwater tracer tests by time-lapse ERT to investigate hydraulic connections between different geological units or to directly estimate hydraulic conductivity of the subsurface (e.g., Kemna et al., 2002; Singha and Gorelick, 2005; Cassiani et al., 2006; Perri et al., 2012) because the bulk electrical conductivity is sensitive to saltwater due to its high fluid conductivity. We carried out three water amendments into the subsurface, two small tracer tests and one large test, identified in such a way by the volume of water injected and the geometry of the ERT arrays for monitoring. One of the small tracer tests was conducted in the white lobe (tracer test white lobe, TW) in October 2022 and the second one in the black lobe (tracer test black lobe, TB) in August 2023 (see Table 1 and location in Fig. 1). The small tracer tests aimed at investigating the dispersion properties of water in the rock glacier, particularly to estimate the hydraulic conductivity in the active layer. For each small tracer experiment, we injected 70 L of saltwater in 4.5 min (29 g NaCl L⁻¹; σ_f=41.5 mS cm⁻¹ at the white lobe and σ_f=51.5 mS cm⁻¹ at the black lobe; the discrepancy in σ_f is most likely related to the difference in the water temperature: 10 and 19 °C). We conducted resistivity measurements (498 quadrupoles) every 2 min and 10 s along three lines for 3 h and 20 min (see Fig. 1) in the frequency domain at 7 Hz with a stacking of 2 (see Table 1). We decided upon 7 Hz instead of a lower frequency to decrease the measurement time, thus increasing the temporal resolution of the ERT monitoring. Test measurements at 7 Hz (data not shown) showed similar data quality compared to lower frequencies (1 Hz). The ERT setup consists of two parallel lines per lobe (profile TW-P1 and TW-P2 and profile TB-P1 and TB-P2), which are longitudinal to the rock glacier flow direction and include 16 electrodes per line, and one transversal profile per lobe (TW-P3 and TB-P3) consisting of 20 electrodes, which crosses TW-P1 and TW-P2, as well as TB-P1 and TB-P2, 4 m downgradient from the injection point (see Fig. 1). For all time steps, we used a DD skip-1 protocol with inline (current and voltage dipole in one line) and crossline (current and voltage dipole in two different lines) quadrupoles along TW-P1 and TW-P2 as well as TB-P1 and TB-P2 and DD skip-1 inline measurements along TW-P3 and TB-P3. One full SIP measurement (0.5–225 Hz) was conducted before the start of the tracer injection, and the 7 Hz data were used as the baseline dataset (time step 0) for the ERT monitoring. After 24 min, we repeated the tracer experiment with the same protocol to validate the results of injection 1.

The large tracer experiment aimed at investigating larger paths for water conduction and was performed in August 2023. To this end, we injected 425 L saltwater (σ_f=51.5 mS m⁻¹) over 6 min on the black lobe (see Fig. 1). We repeated ERT measurements every 15 min along a 355 m long 2D profile (TB-P4 in Fig. 1) with an electrode separation of 5 m. ERT measurements were carried out with a DD schedule in the time domain with a pulse length of 250 ms. Apart from the ERT monitoring, we measured the fluid conductivity (1 min sampling interval) at the rock glacier springs in the front over 3 d during the tracer tests in the black lobe, but we did not identify any changes related to the arrival of the tracer. The application of discrete sampling methods within the boreholes was impossible because the boreholes are used for temperature monitoring and are not suited for the extraction of water samples.

In the processing of the ERT data collected during the tracer tests, we removed measurements with an incorrect polarity in all time steps and kept only those quadrupoles which were found in all time steps to invert for imaging results with similar sensitivity, analogously to the step followed for the comparison of inversion results for different frequencies in the SIP data. For the small-scale tracer experiments, we inverted the time-lapse data of the two parallel electrode lines (TW-P1 and TW-P2 as well as TB-P1 and TB-P2) three-dimensionally in ResIPy (Blanchy et al., 2020), with a time-lapse background constrained (TLBC) inversion under the consideration of a relative error of 10 %. We used the TLBC approach because the comparison with results of a time-lapse difference (TLD) approach and the independent (IDP) inversion of all time steps showed that in areas where we expected no changes over time, we revealed fewer changes in the resistivity images of the TLBC approach than in the images of the IDP (in agreement with Wilkinson et al., 2022) and TLD inversion (data not shown here). Data collected along the profiles perpendicular to the parallel lines (TW-P3 in the white lobe and TB-P3 in the black lobe) were not considered in the inversion as we did not observe any saltwater movement perpendicular to the elevation gradient (data not shown here). For the large-scale tracer experiment, we also decided upon the TLBC inversion approach, as we observed smoother changes in the conductivity over time than with the IDP and TLD approach.

2.7 Kinematic analysis to evaluate surface deformation

The surface of the Gran Sometta rock glacier is regularly monitored by UAV surveys. They are carried out every year at the end of August to produce an orthomosaic and a digital surface model (DSM) of the rock glacier which is used to understand surface deformation (results from the period 2016–2019 were published in Bearzot et al., 2022). Technical details about the UAV campaigns can be found in Table 2. The images collected are processed using a structure-from-motion (SfM) workflow implemented in the commercial software Agisoft Metashape. A network of 23 painted targets were used as ground control points (12) and check points (11). The RMSE value for each survey is shown in Table 2 (XY error). The horizontal displacements were calculated for the periods 2020–2023 and 2022–2023 using the positions of blocks detected through photointerpretation on orthomosaics with a resolution of 2 cm per pixel. The spatial distribution of the rock features was defined using a square grid of 20 × 20 m. The position of the most representative targets for each year was defined manually, and the horizontal displacement of the chosen points was calculated using the QGIS plugin “PointsToPaths”.

Table 2 Technical details of the UAV surveys.

3 Results

3.1 Electrical properties of the Gran Sometta rock glacier

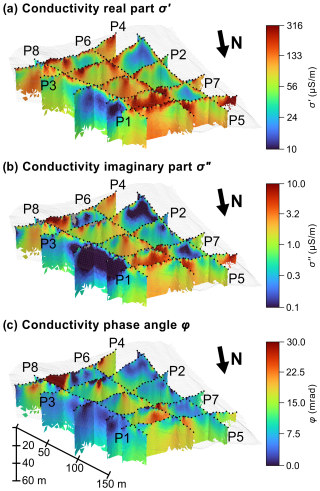
The 3D inverse model of data collected with MG and DD configurations at 0.5 Hz is shown in Fig. 3. The inversion results are presented in terms of the conductivity real part σ^′, the conductivity imaginary part σ^′′ and the phase φ of the complex conductivity, and they are visualized by slices cut through the 3D model vertically along the electrode lines. Along the longitudinal profiles P8 (white lobe) and P5 (black lobe) we can identify three main layers: the top layer is, in comparison to the generally highly resistive media in mountain permafrost, conductive (σ^′>56 µS m⁻¹, or by its inverse, the resistivity ρ<17 857 Ωm) and polarizable (σ^′′>0.3 µS m⁻¹) with a thickness of 4–6 m. The second layer along the white and the black lobes is 20–30 m thick, resistive (σ^′<56  µS m⁻¹, i.e., with a resistivity ρ>17 857 Ωm) and less polarizable (σ^′′<0.3 µS m⁻¹). Below this resistive and less polarizable layer, there are again materials with relatively high σ^′ and σ^′′. While the electrical properties along P5 and P8 are horizontally layered with a relatively continuous resistive and polarizable layer, we can observe higher spatial variability in the center of the rock glacier, at the position where both the white and the black lobes intersect. Such an area is covered by all profiles apart from P5 and P8 and can be characterized by maximum values in σ^′ and σ^′′ in all layers.

Figure 3 Slices of the 3D inverse model along the profiles at 0.5 Hz in terms of (a) real part, (b) imaginary part and (c) phase angle of the complex conductivity. The north direction is given by a black arrow. The positions of electrodes are indicated by black dots.

3.2 Estimation of hydrogeological parameters based on IP data

The results for θ and K based on the DSLM are presented in Fig. 4 as slices parallel to the surface, at a depth of 4 and 20 m, as resolved from the 3D inversion. In the Appendix (Fig. C1) we added the same slices in terms of σ^′ at 0.1 Hz and M_n. The water content is in a range of 0 %–15 % (see Fig. 4a and b) and the hydraulic conductivity in a range of 10⁻⁷ to 10⁻³ m s⁻¹. Minimum values of both parameters (θ<5 % and K<10⁻⁶ m s⁻¹) occur along P5 and P8 at a depth of 20 m, most likely because in this area most of the water is permanently frozen, hindering water flow and leading to a low σ^′ and low σ^′′ at 0.5 Hz, as shown in Fig. 3. We can observe higher θ and K values in the 4 m depth slice (K up to 10^−4.5 m s⁻¹ and θ up to 10 %), which is unfrozen. Maximum θ values (up to 15 %) can be observed in the western part of the white lobe (center of the rock glacier), not only in the uppermost layer close to the surface (4 m depth slice) where the rock glacier thaws during summer, but also at a depth of 20 m.

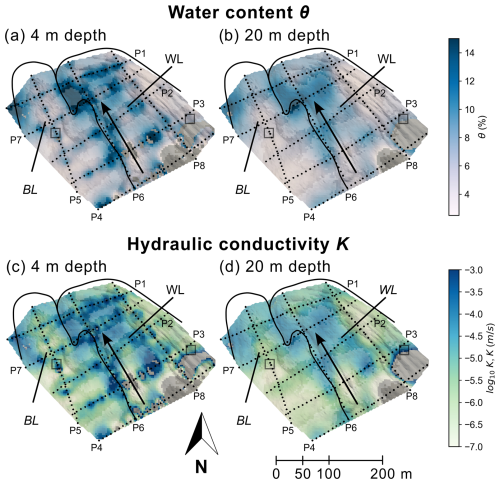
Figure 4 Water content (a and b) and hydraulic conductivity (c and d) visualized as slices parallel to the surface at two different depths. The edges of the black lobe (BL) and white lobe (WL) are indicated by black lines. Low-sensitivity areas are displayed transparently, and the positions of electrodes are presented by black dots. Additionally, the direction of topography is indicated by a black arrow and the positions of tracer experiments by gray squares.

3.3 Tracer experiments

Figure 5 presents the 3D inversion results of the small-scale tracer experiments at the white lobe (left) and the black lobe (right). The baseline (time step 0) σ^′ is visualized as slices along the two parallel electrode lines for the white lobe in Fig. 5a and for the black lobe in Fig. 5g. In the former, Fig. 5a reveals two layers: an upper relatively conductive layer (${\mathit{\sigma }}^{\prime }>\mathrm{56}$ µS m⁻¹) and a lower continuous resistive layer (${\mathit{\sigma }}^{\prime }<\mathrm{56}$ µS m⁻¹). The interface between both layers is at a depth of approximately 4 m, where also borehole temperature data show the interface between an unfrozen active layer and an underlying frozen layer (4–6 m; see Fig. B1). Therefore, we assume that the upper conductive layer is the active layer and the lower resistive layer the frozen layer. The σ^′ baseline slices on the black lobe show the two layers as well, but we can observe that the contrast between the upper conductive and the lower resistive layers is weaker and the depth of the interface varies along the parallel profiles. The comparison of Fig. 5a and g reveals that the black lobe is related to slightly higher electrical conductivity in the upper layer, although we observed similar θ values in the active layer of the black and white lobe (see Fig. 4a).

Time-lapse conductivity changes (Δσ^′) after the saltwater injection in the center between the monitoring lines are presented in Fig. 5b–f (white lobe) and h–l (black lobe). Blue-colored voxels present a Δσ^′ of $\ge +\mathrm{40}$ % (white lobe) and $\ge +\mathrm{20}$ % (black lobe) compared to the baseline σ^′. Different thresholds (20 % and 40 %) were used because in the white lobe maximum values of Δσ^′ were in a range of +200 % and in the black around +50 %. In the white lobe, during and directly after the injection, a conductive anomaly (Δσ^′>40 %) propagates from the injection point downwards nearly perpendicular to the gravitational field. After reaching the interface between the active and the frozen layer, the anomaly starts to move through the active layer parallel to the interface. In the black lobe, we can also observe a change in conductivity starting from the injection point, but the value is smaller (∼ 20 %–30 %, with maxima around 50 %). The conductive anomaly percolates nearly vertically from the injection point, similar to the movement in the white lobe directly after the injection, yet the conductive plume stops at a distance of 2–3 m below the injection point and no movement downslope is observed, in contrast to the lateral movement observed in the white lobe.

The TLBC inversion results of the large-scale tracer experiment on the black lobe are visualized in Fig. D1. The results show a Δσ^′ anomaly moving from the injection point downslope along the surface. In comparison to the small-scale tracer tests, the Δσ^′ plume is much smaller (∼ 5 % compared to ∼ 20 % and ∼ 40 %, respectively) most likely due to the different sensitivity associated with the larger electrode separation used in the large-scale tracer experiment (5 m vs. 2 m). In the images, the smaller Δσ^′ values in the downslope vicinity of the injection point highlight conductivity changes associated with inversion artifacts, as can be observed particularly in the area above the injection point, where we do not expect big changes over time.

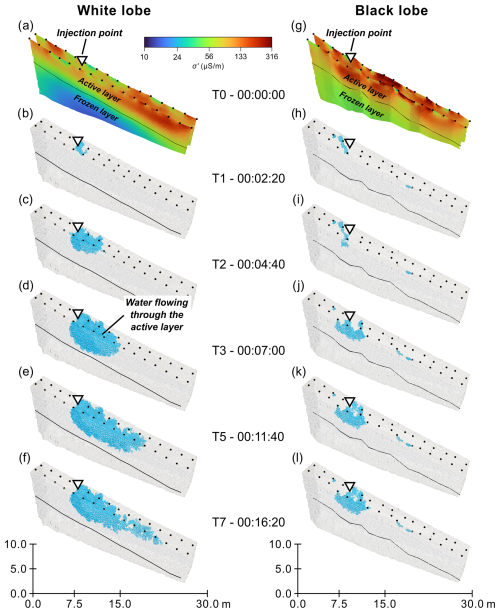
Figure 5 Slices presenting the real part of the complex conductivity along the electrode lines at the baseline for the white lobe (a) and the black lobe (g). The black line indicates the interface between the active layer and the frozen layer, determined and interpreted by the gradient in the electrical conductivity model. Panels (b) to (f) and (h) to (l) represent the change in the conductivity with time after the injection of a salt tracer. Blue areas show a conductivity increase above 40 % in the case of the white lobe and above 20 % in the case of the black lobe. The position of the tracer injection is indicated by a triangle, while the positions of electrodes are indicated by black dots. A scale was added at the bottom.

3.4 Rock glacier movement

Figure 6 presents the direction and magnitude of the horizontal displacement of 161 rocks on the surface of the Gran Sometta rock glacier between August 2022 and August 2023 as determined from the kinematic analysis of the UAV images (see Sect. 2.7). The kinematic changes in the rock glacier surface over the longer time span (2020–2023) are presented in Fig. E1 (Appendix). Most parts of the rock glacier moved to the northwest due to the aspect of the surface topography except for a few points at the lateral boundaries of the rock glacier lobes. Over the whole area under investigation, the displacements are between 0 and 2 m per year, with a higher range of values on the black lobe (1–1.5 m yr⁻¹) than on the white lobe (0–0.5 m yr⁻¹). Maximum values can be observed on the southern part of the black lobe (>1.5 m yr⁻¹), while the minimum displacements (<0.25 m yr⁻¹) were measured on the front and eastern part of the white lobe.

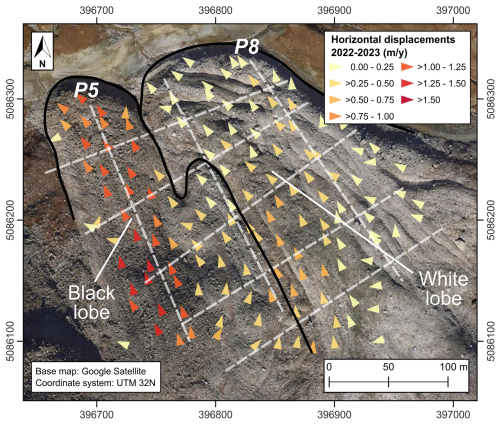
Figure 6 Horizontal displacements of the Gran Sometta rock glacier between 2022 and 2023. The direction of the arrows presents the direction of the rock glacier movement, while the color displays the velocity of the rock glacier (in m yr⁻¹). The positions of the SIP profiles are indicated by dashed white lines, while the front edge of the rock glacier and the border between the black and the white lobe are presented by a black line. Orthophoto: © Google Satellite.

4 Discussion

4.1 Identifying hydraulic units in the Gran Sometta rock glacier

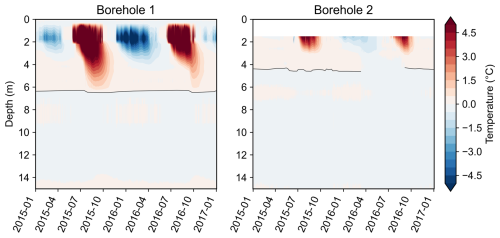
Based on the complex conductivity results presented in Fig. 3 we identified three layers along the white and the black lobes. The relatively conductive uppermost layer, in comparison with the underlying second layer, is related to the active layer with a thickness of 4–6 m, in this case associated with unfrozen sediments and rocks (as described in Bearzot et al., 2022). No direct validation data of active layer thickness for the measurements in 2022 and 2023 are available because boreholes with temperature sensors in the Gran Sometta rock glacier were destroyed in 2018. However, the active layer thickness estimation is in a similar range as the value determined from the boreholes (6 m in borehole 1 and 4 m in borehole 2) during 2015–2016 (see Fig. B1). We expect an active layer thickness in 2022 still in a range between 4 and 6 m as rock glaciers are more resilient towards increasing air temperatures compared to other permafrost features (e.g., Pruessner et al., 2021). The second layer is more resistive than the uppermost layer, corresponding to the frozen materials with a thickness of 20–30 m, in agreement with results from Bearzot et al. (2022). At a depth of 20–30 m the conductivity increases again, which indicates the lower bound of the permafrost or a decreased ice content.

In this study, we applied the model proposed by Soueid Ahmed et al. (2020) (explained in Sect. 2.4; see Eq. 13), based on the DSLM developed by Revil (2013a, b), to estimate K on the Gran Sometta rock glacier. The results show a contrast in K values between the unfrozen active layer (K up to 10⁻³ m s⁻¹) and the frozen layer (K down to 10⁻⁷ m s⁻¹). Such a contrast in K values is in agreement with results of the tracer test in the white lobe. We assume that the conductive anomalies changing their position observed in the tracer experiments are due to the saltwater plume moving through the subsurface (see Fig. 5). The time-lapse inversion images in the white lobe suggest that, after a nearly vertical flow in the uppermost 3 m, the injected water was blocked by a resistive layer, associated with a frozen ice-rich layer. This layer might hinder the infiltration of most of the water into deeper areas along the tracer test site on the white lobe, which leads to a nearly parallel flow to the interface between the frozen layer and the active layer.

In the small-scale experiment in the black lobe (see Fig. 5), the injected water spreads a few meters around the injection point but did not move further downslope. Compared to the tracer test area on the white lobe, we observed bigger blocks on the black lobe with huge pores and a poor hydraulic connection. We suggest that we did not inject enough water (70 L per injection) to hydraulically connect such big pores; thus, the water might have been run through the uppermost hollow spaces, split up in different holes and stopped there. Additionally, the conditions during the tracer experiment in the black lobe in August 2023 were drier than during the tracer test in the white lobe in October 2022, which also leads to a lower hydraulic connection between pores. The saltwater injected in the large-scale tracer experiment in the black lobe has been successfully tracked in the inversion images (see Fig. D1), but the results need to be considered carefully due to time-lapse inversion artifacts observed along the profile. The images reveal a similar water flow to that observed in the small-scale tracer experiment in the white lobe with a nearly parallel flow to the surface through the active layer.

The water flow resolved with electrical images described above is in agreement with the assumption that frozen areas in active rock glaciers act as impermeable layers hindering water flow (e.g., Krainer and Mostler, 2002; Giardino et al., 2011; Winkler et al., 2016; Del Siro et al., 2023). Commonly, the dispersion of a tracer is monitored through chemical analyses of samples from several sampling points, e.g., boreholes or springs. Krainer and Mostler (2002), e.g., conducted hydrological tracer experiments on rock glaciers in Austria, where the time between the tracer injection and the arrival time at the rock glacier spring allows a mean pore water velocity to be measured, which resulted in relatively large flow velocities. Given that frozen materials are rather poor hydraulic conductors (e.g., Burt and Williams, 1976) and the active layer mainly consists of large blocks with huge pores with a high hydraulic conductivity, the authors suggested that the water does not percolate into the frozen layer but flows through the active layer. While sampling provides highly accurate and reliable data, such information gives only discrete information about the tracer flow and can fail if the tracer escapes from the sampling points (Cassiani et al., 2006). Coupling tracer experiments with time-lapse ERT monitoring overcomes this limitation as the method provides continuous images of the subsurface over time, which can be used to describe the movement and the dispersion of the fluid (e.g., Camporese et al., 2011). Recently, Pavoni et al. (2023) conducted a tracer experiment in the inactive Sadole rock glacier, where they tracked the position of a salt tracer by 2D ERT monitoring over a distance of 40 m. They reported that most of the water did not percolate into the frozen area but moved through the active layer.

Bearzot et al. (2022) injected a tracer fluid in the black lobe of the Gran Sometta rock glacier and measured the arrival time at the spring located at a distance of around 270 m downgradient. The arrival of the tracer was identified by changes in the chemical composition of the spring water, and estimations of the pore water velocity were conducted through the distance between the injection point and the spring position divided by the elapsed time. Their analyses in the black lobe resolved a pore water velocity of around 10⁻³ m s⁻¹, but they only monitored the chemical composition of the spring water during the night, which might have led to an underestimation of the pore water velocity. The value is smaller than the pore water velocities estimated by Krainer and Mostler (2002) ($v_{\mathrm{p}}\sim {\mathrm{10}}^{-\mathrm{2}}$) for three rock glaciers in Austria but still suggests that the water mainly flowed through the active layer.

4.2 Hydraulic conductivity estimation based on tracer experiments

The Δσ^′ anomalies detected in Fig. 5 in the white and black lobes are moving from the injection point downslope directly after the time of the injection. Therefore, we assume that the increase in σ^′ (Δσ^′ anomaly) is related to the injected saltwater, which moves through the active layer of the rock glacier. Changes in σ^′ over time (after the injection of the tracer) allows the velocity of the water moving through the subsurface to be estimated, as presented in Fig. 7a for the white lobe. For the small tracer experiment in the black lobe we did not conduct such an analysis because the conductive anomaly associated with the injected saltwater stopped 2–3 m below the injection point.

Singha and Gorelick (2005) and Camporese et al. (2011) demonstrated that the timing of the peak arrival is a reliable parameter for K estimations because it is relatively unaffected by inversion artifacts. Hence, we used the time of the maximum conductivity concentration in 18 voxels to estimate the arrival time of the saltwater in the given voxels. Skipping the inversion and estimating K based on raw data can lead to incorrect interpretations, considering that the raw data do not contain information about the spatial position of the saltwater plume (Camporese et al., 2011). As presented in Fig. 7a and c, the time t of the maximum Δσ^′, also called arrival time T_a, increases with increasing distance from the injection position as the tracer moves from the injection point downslope through interconnected pores in the active layer. Additionally, we can observe that the slope of T_a and Δσ^′ is not constant over a distance of 0–23 m from the injection position but reveals a contrast between the nearest voxels and voxels which are further away from the injection position. This contrast reflects the two different flow characteristics identified in Fig. 5: an initial nearly vertical flow (from now on called stage 1, S1) followed by a flow parallel to the interface between the active layer and the frozen layer (from now on called stage 2, S2).

The pore water velocity v_p, which was estimated by the slope between T_a and the distance from the injection point, is presented in Fig. 7c. Due to the different slopes observed in Fig. 7a we fit two linear regression models per tracer injection, one for S1 and one for S2, resulting in a v_p of 10.9 cm s⁻¹ (injection 1) and 5.9 cm s⁻¹ (injection 2) for S1 (mean value: 8.4 cm s⁻¹) and a v_p of 2.0 cm s⁻¹ (injection 1) and 2.7 cm s⁻¹ (injection 2) for S2 (mean value: 2.35 cm s⁻¹). The contrast in v_p between S1 and S2 is mainly related to the difference in the hydraulic gradient, while the discrepancy in v_p between injection 1 and injection 2 is related to a difference in the matrix potential. When we injected saltwater for the second time the subsurface materials were already wet from the previous injection (higher θ). The higher water content during the second injection leads to a lower absolute matrix potential and in turn to higher K and v_p values (e.g., Van Genuchten, 1980).

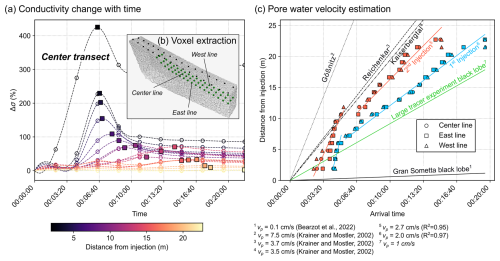
Figure 7 (a) Change in the conductivity (in %) with time relative to the baseline for different voxels (positions are presented in b) along the center line of the tracer path in the active layer during the small-scale tracer experiment in the white lobe. The distance of the voxels from the injection position is presented by the line color, and the maximum change in conductivity for each voxel is visualized by a square symbol. Panel (c) shows the time of the maximum change in conductivity for each voxel in relation to the distance from the injection point. The slope of a linear regression (in blue for injection 1, in red for injection 2) gives the pore water velocity. Pore water velocities of other studies are visualized by the black lines for a comparison. The estimated pore water velocity in the large-scale tracer experiment on the black lobe is added in green.

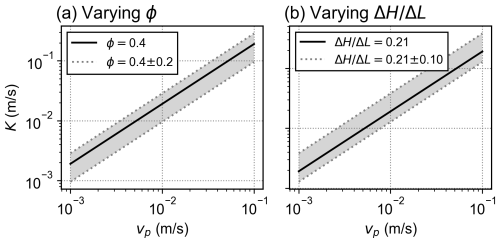
Multiplying the mean values of v_p for S1 and S2 by the reciprocal of the hydraulic gradient (0.57 for S1 and 4.77 for S2) and an assumed mean porosity of 40 % (as used in other rock glacier studies, e.g., Hauck et al., 2011; Halla et al., 2021) allows us to estimate the hydraulic conductivity, which results in K values of $\mathrm{1.9}\times {\mathrm{10}}^{-\mathrm{2}}$ m s⁻¹ (S1) and 4.5 × 10⁻² m s⁻¹ (S2). The difference in the values resolved for the two stages is related to vertical changes in the water content in the active layer of the rock glacier. While the uppermost rocks in the active layer (S1) are relatively dry, the material at the interface between the frozen layer and the active layer (S2) can be assumed to be more humid, leading to the slight increase in K in S2. The hydraulic gradient used in S1 was derived from the slope of the water path in Fig. 5, while the hydraulic gradient in S2 was derived from the topography gradient because the tracer experiment images (see Fig. 5) suggest that in S2 the water flowed along a frozen layer nearly parallel to the surface. Changing the porosity or the hydraulic gradient in a range between ±50 % of the absolute value only slightly affects the estimation of K (see Fig. G1 in the Appendix) as the range of values for v_p and K can extend over several orders of magnitudes.

The large-scale tracer experiment on the black lobe permitted the computation of the pore water velocity (see Fig. D1 in the Appendix), resolving for values around 1 cm s⁻¹ (see green line in Fig. 7c), which is half of the v_p estimated for the white lobe, but it needs to be considered carefully due to time-lapse inversion artifacts (as described in Sect. 3.3). This lower pore water velocity found in the black lobe compared to the white lobe would explain the difference in water movement observed in the small-scale tracer experiments conducted on the white and the black lobes. However, the v_p value estimated by Bearzot et al. (2022) for the black lobe (based on the analysis of water samples at the rock glacier spring after the injection of a tracer fluid) is 1 order of magnitude lower than the value derived from our tracer experiment (10⁻³ m s⁻¹ vs. 10⁻² m s⁻¹). This discrepancy can be related to the difference in the covered flow path. While our ERT monitoring covered a steep area with a maximum length of only 30 m, Bearzot et al. (2022) investigated the flow over a distance of 270 m, covering also flat areas. Accordingly, the study area of Bearzot et al. (2022) might result in the averaged values from high pore water velocity in the steep areas (covered in our study) and the low pore water velocity in the flatter areas not investigated with our tracer test.

In Fig. 7c, we also compare v_p estimations in our study with results from other rock glaciers based on hydrological tracer experiments. The v_p results for the Gößnitz, Reichenkar and Kaiserbergtal rock glaciers (located in the eastern Alps) reveal v_p values varying between 3.5 and 7.5 × 10⁻² m s⁻¹ (Krainer and Mostler, 2002). Those values are of the same order of magnitude as the value estimated for the white lobe in the small-scale tracer experiment and the value estimated for the black lobe in the large-scale tracer experiment. Variations in v_p between different rock glaciers can be related to different slope angles, geologies, active layer depths and ice content.

4.3 Uncertainty of hydrogeological properties estimated from multi-frequency electrical conductivity

In Fig. 4 we presented maps of θ and K estimated from multi-frequency electrical conductivity data. Comparing the K values from the tracer experiment in the white lobe with the results of K estimations for the active layer based on the analysis of the multi-frequency conductivity data (see Fig. 4c) reveals a discrepancy of 2 orders of magnitude (10⁻² m s⁻¹ vs. 10⁻⁴ m s⁻¹). To understand this discrepancy, it is useful to quantify the uncertainty in the estimated hydrogeological parameters from the geophysical imaging results. The petrophysical model to resolve θ and K from multi-frequency conductivity data requires different parameters, which are assumed to be constant across the entire rock glacier, namely the fluid conductivity (σ_f=0.01 S m⁻¹), the cementation exponent (m=2), the grain density (2700 kg m⁻³), the dimensionless parameter R (0.1) which relates M_n to σ_s and the fitting parameter k₀ (10^4.3).

To investigate the uncertainty of θ and K, we (1) visualized the sensitivity of the parameters and their standard deviations used in Eqs. (12)–(14) to the resulting hydrogeological parameter (see Fig. 8) and (2) applied the error propagation law to Eqs. (12)–(14). The equations used for the analysis regarding the error propagation and standard deviations of all parameters are given in Appendix F. The resulting values of θ due to variations in the assumed values of σ_f, R and m (in an interval of ±1 standard deviation) reveal that θ is primarily sensitive to σ_f (25.0 % relative standard deviation, RSD) and m (17.0 % RSD) and less sensitive to R (3.6 % RSD), as presented in Fig. 8a–c. According to our analysis, the uncertainty of the parameters σ_f, R and m results in an RSD of 30.5 % for θ. The different sensitivities of the parameters highlight the need for an accurate estimation of particularly σ_f and m to derive a highly reliable water content.

In Fig. 8d–g we visualized the range of K considering ±1 standard deviation of θ, ρ_g, CEC and k₀. The parameters δ, g, and μ were fixed because we assume no strong deviation in these parameters. The strongest effect on K can be observed for θ (with a large RSD of 183 %), followed by CEC (103 % RSD) and k₀ (50 % RSD), while the sensitivity of ρ_g is low (7.4 % RSD), resulting in a total RSD of 216 %. To obtain a more reliable hydraulic conductivity estimation, reducing the uncertainty of the water content and the CEC via more accurate information on σ_f and m is necessary. Additionally, there is a lack of information on the actual uncertainty and applicability of using a value of 10^4.3 for the parameter k₀ (see Soueid Ahmed et al., 2020). Here, we used half of the value as standard deviation to investigate its sensitivity regarding the estimation of K.

The uncertainty in our results due to the non-uniqueness of the inversion itself and due to the imaging resolution related to the electrode spacing is not considered in the analysis above. In this study, we used an electrode separation of 7.5 m, which reduces the resolving capability of the electrical properties in the uppermost layer. An electrode spacing of 7.5 m was chosen as a compromise between a large depth of investigation (needed to cover the area below the permafrost) and a high resolution to resolve the active layer thickness, as well as to collect data over a large part of the rock glacier in a reduced time. Estimating the uncertainty of the inverse model is challenging (see list of approaches in Binley and Slater, 2020) because the inversion is an underdetermined problem and therefore beyond the scope of this paper. Additional uncertainty is due to the calculation of M_n in our study, as we used a relatively small frequency window (0.1–2.5 Hz), which increases the risk of overlooking polarization effects at higher frequencies (f>2.5 Hz), apart from ice polarization.

Accordingly, while our study reveals that the use of the DSLM might provide relevant information about the hydrogeological features and their connectivity, a quantitative estimation of hydrogeological parameters, particularly of the hydraulic conductivity, might still require some calibration for its application. Future studies might consider approaches to estimate the uncertainty of the geophysical parameters and a more accurate estimation of σ_f, m and k₀.

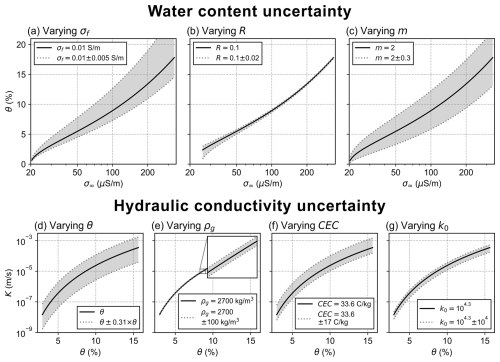
Figure 8 Uncertainty analysis of the hydrogeological parameters θ (a–c) and K (d–g). The black line symbolizes θ and K, respectively, in relation to the absolute values, while the gray area, delimited by dotted lines, shows the range of θ and K using ±1 standard deviation (68 % confidence interval) of the parameters used in Eqs. (12)–(14). The range of values used in (a)–(c) for σ_∞ and θ was chosen based on the minimum and maximum of σ_∞ and θ in the 4 and 20 m depth slices (see Fig. 4). While we used a constant value for the tested parameters in panels (a)–(c) and (e)–(g), we varied θ according to the values given in Fig. 4a and b and used a mean fractional standard deviation of 0.31, derived from error propagation for θ.

4.4 The large variability in water content and hydraulic conductivity at the Gran Sometta rock glacier

Results of the estimation of hydrogeological properties (θ and K) have shown a high spatial variability with depth and laterally across the rock glacier (see Fig. 4). We can observe high θ values (up to 15 %) in the active layer, where rain and snowmelt can accumulate on top of the frozen layer. At a depth of 20 m, the rock glacier is frozen in several areas, resulting in a low amount of liquid water, which hinders vertical water flow to deeper areas. Laterally, local maxima of θ can be found along furrows, particularly longitudinal furrows, while local minima can be found in ridges. Such a spatial pattern suggests that water from snowmelt or rainfall flows nearly vertically through the active layer, as described by S1 in the small-scale tracer experiments, until it reaches the interface between the active layer and the frozen layer. After that, in S2 the water moves along the interface downhill in the direction of the steepest slope, either in the flow direction of the rock glacier or into a nearby depression zone (see, e.g., Halla et al., 2021), which are the most shaded areas on the rock glacier with low evaporation rates.

The longitudinal furrows act as preferential flow paths transferring water from areas above to the front part of the rock glacier (Halla et al., 2021), as the furrows are related to high hydraulic conductivity ($K>{\mathrm{10}}^{-\mathrm{4.5}}$) (see Fig. 4c). After flowing through the furrows, water mainly accumulates in the western front part of the white lobe and can percolate into deeper areas (20 m depth) because there is no continuously frozen horizontal layer in such an area. The complex conductivity results have revealed that the internal structure of the western frontal part of the white lobe is different compared to the eastern part of the white lobe and the black lobe. There is no continuous layer of low conductivity, associated with frozen materials, which might be related to a high ice degradation rate allowing water to infiltrate into deeper areas, where we observed high θ values at a depth of 20 m and which in turn accelerates the degradation process (Ikeda et al., 2008).

4.5 Role of water content in the spatial variability in rock glacier movement

Several studies working on the kinematics of rock glaciers have revealed an overall acceleration of rock glacier movement during the last decades (e.g., Delaloye et al., 2010; Marcer et al., 2021; Kellerer-Pirklbauer et al., 2024). In some studies, variations in rock glacier velocities were related to the topography (e.g., Müller et al., 2016; Bodin et al., 2018), the ice content (e.g., Kääb et al., 2007) or the thermal state (e.g., Bearzot et al., 2022) because, e.g., topographical variations and ground surface temperatures can be measured directly. Recent studies discuss the role of water content (e.g., Kenner et al., 2019), with a particular focus on the amount of liquid water in the shear horizon (e.g., Cicoira et al., 2019), where most of the deformation takes place (Arenson et al., 2002). However, due to the limited access, direct measurements of the water content in the shear horizon are challenging. Phillips et al. (2023) installed piezometers and an ERT monitoring instrument in boreholes on a rock glacier in Switzerland that penetrate until reaching the upper boundary of the shear horizon, permitting a direct investigation of the shear plane. They reported a link between high water content and increased rock glacier velocity for two seasons (Bast et al., 2024).

Kinematic analyses on the Gran Sometta rock glacier have shown a contrast in surface velocities between the white and the black lobes, with higher values on the black lobe (∼ 1–1.5 m yr⁻¹) than on the white lobe (0–0.5 m yr⁻¹) (see Figs. 7 and D1). This contrast is in agreement with kinematic results of similar analyses published by Bearzot et al. (2022) for the period 2016–2019 (∼ 1.2 m yr⁻¹ for the black lobe and ∼ 0.4 m yr⁻¹ for the white lobe). Bearzot et al. (2022) related the spatial flow patterns to the internal structure and the contrast in topography as the black lobe is steeper (∼ 21° slope angle) than the white lobe (∼ 11° slope angle). This suggestion is consistent with other rock glacier studies, which showed a strong link between slope angle and surface velocity (e.g., Müller et al., 2016; Cicoira et al., 2021).

The geophysically based estimation of the hydrogeological properties along both lobes in this study (see Fig. 9) allows the relation between the water content and the spatial variations in rock glacier velocity to be investigated. Figure 9c and g show that in the frozen layer most of the water is frozen in both lobes (θ<5 %), leading to a low electrical conductivity (see Fig. 9a). Below this low-electrical-conductivity layer, we observe a layer of increased electrical conductivities associated with increased water content. In this area, higher θ is found for the black lobe (up to 10 %) than for the white lobe (around 5 %). Our results might indicate that water accumulates in the shear horizon of the black lobe at a profile distance above 100 m in the southern direction, with higher K values (>10⁻⁵ m s⁻¹) above the 100 m profile distance than downslope (<10⁻⁶ m s⁻¹) (see Fig. 9d, h). The lower K values may be due to a larger content of fine-grained sediments, as also suggested by the higher electrical conductivity and normalized chargeability values (Fig. 9a, b). Such a low K area might reduce the velocity of water flow coming from uphill leading to an increase in pore water pressure, which would in turn increase the potential of deformation in the shear horizon and can, together with the slope angle, accelerate the rock glacier movement. This observation is similar to the one reported by Kenner et al. (2017) at the Ritigraben rock glacier, where borehole data revealed a wet area below the frozen layer at the depth of the shear horizon. Kenner et al. (2019) argue that the idea of water content as a driving force for rock glacier kinematics is not a contradiction to the correlations between temperature and rock glacier velocity variations (Kääb et al., 2007; Roer et al., 2008); rather the water content can act as the link between temperature and kinematic changes.

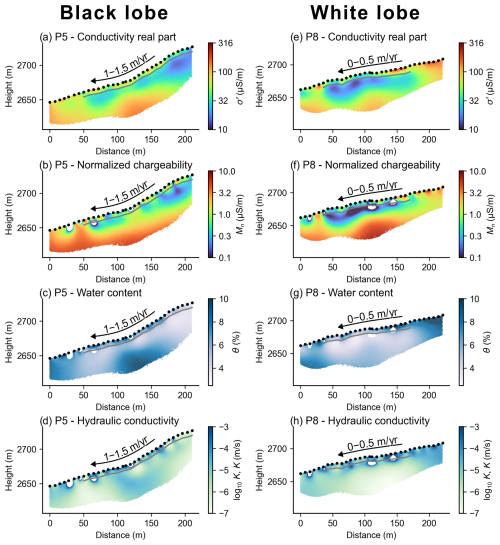
Figure 9 Panels (a) and (e) show the real part of the complex conductivity, (b) and (f) the normalized chargeability, (c) and (g) the water content, and (d) and (h) the hydraulic conductivity along P5 (left) and P8 (right). Pixels where the normalized chargeability results in negative values are blanked. The positions of electrodes are indicated by black dots, and the interface between the active layer and the frozen layer is presented by a gray line. The rock glacier flow direction of each lobe is presented by a black arrow including its mean velocity.

5 Conclusions

In this study, we investigated the hydrogeological properties of the active Gran Sometta rock glacier in the Italian Alps by SIP mapping. Electrical conductivity and normalized chargeability data were used within the DSLM model to directly estimate the spatial water content and hydraulic conductivity distribution within the rock glacier. To validate the estimation of both parameters, we conducted tracer experiments where we injected saltwater and tracked the change in electrical conductivity in the subsurface by ERT monitoring. Both methods reveal similar hydraulic units: an upper non-frozen layer with high hydraulic conductivity and a lower frozen layer with low hydraulic conductivity. However, in the absolute values there is a discrepancy of 2 orders of magnitude between the hydraulic conductivity estimated within the DSLM and the tracer experiment, which is mainly related to the decreased resolution of the SIP mapping in the uppermost layer due to a large electrode spacing and the large uncertainty of the parameters used to estimate K. We observed that uncertainties in K estimations using the DSLM are strongly sensitive to the water content, which is in turn primarily sensitive to the fluid conductivity and the cementation exponent defined for the use of the petrophysical model.

The Gran Sometta rock glacier can be divided into three different areas characterized by their hydrogeological properties. As revealed by complex conductivity images, the internal structure of the black lobe and the eastern part of the white lobe is similar with an active layer of around 4–6 m thickness and a continuously frozen layer beneath, which is in agreement with borehole temperature data. The hydraulic conductivity and water content estimations based on the DSLM have shown that in both areas the frozen layer acts as a hydraulic barrier hindering water flow into deeper areas. Most of the water coming from rainfall or snowmelt flows rapidly through the active layer with hydraulic conductivities in a range of 10⁻² m s⁻¹, with slightly higher values in the white lobe than in the black lobe, as revealed by the tracer tests. Contrary to this, in the western front part of the white lobe, ice content is low, and a continuously frozen horizontal layer is missing, leading to water penetration into deeper areas where water accumulates in fine-grained sediments.

Additional analyses of the hydrogeological properties in the area below the poorly electrically conductive ice-rich layer have shown a higher water content in the black lobe (up to 10 %) than in the white lobe (around 5 %). As kinematic analyses have revealed that the black lobe moves 3 times faster than the white lobe, such a contrast in water content suggests that water accumulated close to the shear horizon decreases the frictional resistance and in turn might accelerate the rock glacier velocity.

Our study shows that the SIP method is a valuable tool to describe and quantify hydraulic conductivity and water content in rock glaciers. Not only does such information help in the understanding of the hydrological cycle in rock-glaciated alpine catchments, but it should also be considered in the analysis of spatial patterns in rock glacier movement.

Appendix A: 3D pseudosection

The 3D pseudosection of the apparent resistivity data after filtering along P1–P8 is shown in Fig. A1.

Figure A1 The 3D visualization of the data along P1–P8 after the filtering procedure. The data are presented in terms of the apparent resistivity ($\left|{\mathit{\rho }}_{\mathrm{a}}^{\ast }\right|$). Electrode positions are visualized as black dots.

Appendix B: Borehole temperatures

Temperature data from two boreholes in the Gran Sometta rock glacier are presented in Fig. B1. The active layer depth (ALD), which is the depth down to which the material thaws at least once per year, is ∼ 6 and ∼ 4 m in boreholes 1 and 2, respectively. The temperature data in borehole 1 shows that between 4 and 6 m depth the material does not freeze during winter, which suggests the existence of a supra-permafrost talik. Taliks have been observed several times in the European Alps (e.g., Zenklusen Mutter and Phillips, 2012; Luethi et al., 2017) and are assumed to be an indicator of permafrost degradation, but they have not yet been investigated in detail. However, such information has not been reported at the Gran Sometta rock glacier. Nonetheless, as the temperature in the talik is close to the freezing point, we cannot exclude any calibration error in the temperature sensors, which could also lead to such a temperature pattern.

Figure B1 Temperature data at two boreholes (borehole BH1 and borehole BH2) on the Gran Sometta rock glacier. The active layer depth is displayed by a gray line. Date format is year-month.

Appendix C: Conductivity real part and normalized chargeability maps

Figure C1 shows σ^′ and M_n used for the calculation of θ and K at a depth of 4 and 20 m.

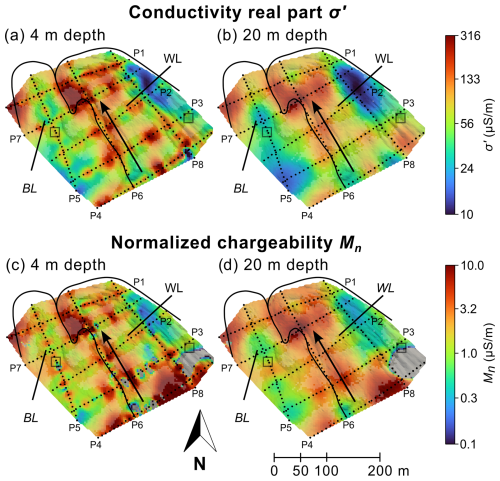
Figure C1 Conductivity real part (a and b) and normalized chargeability (c and d) visualized as slices parallel to the surface at two different depths. The edges of the black lobe (BL) and white lobe (WL) are indicated by black lines. Low-sensitivity areas are displayed transparently, and the positions of electrodes are presented by black dots. Additionally, the direction of topography is indicated by a black arrow and the positions of tracer experiments by gray squares. The normalized chargeability refers to the difference between the bulk electrical conductivity at high and low frequencies (2.5 and 0.1 Hz in our study, respectively), as presented in Eq. (8).

Appendix D: Large-scale tracer experiment on the black lobe

Results of the large-scale tracer experiment on the black lobe are presented in Fig. D1.

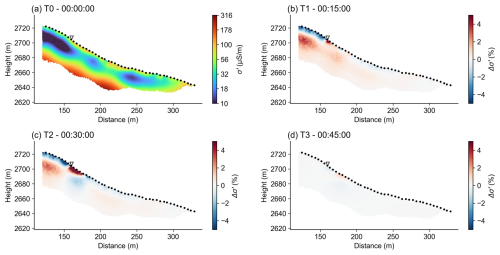
Figure D1 The 2D conductivity inversion results of the baseline data for the large-scale tracer profile in the black lobe (a). Panels (b) to (d) present the change in conductivity relative to the previous time step in percentages (linear scale). The position of the tracer injection, at the surface, is indicated by a triangle, while the positions of electrodes are indicated by black dots.

Appendix E: Horizontal rock glacier movement 2020–2023

While we presented the horizontal rock glacier movement for the period 2022–2023 in Fig. 6, we show the mean velocity for a longer period (2020–2023) in Fig. E1.

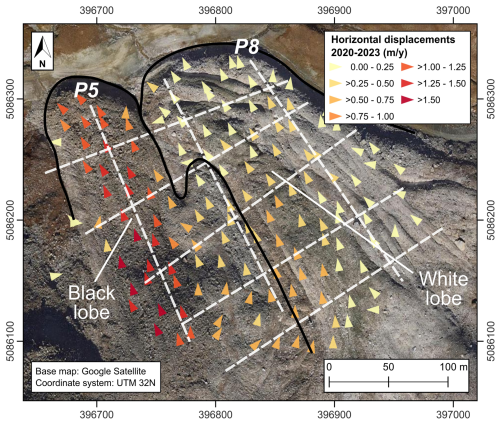
Figure E1 Horizontal displacements of the Gran Sometta rock glacier between 2020 and 2023. The direction of the arrows presents the direction of the rock glacier movement, while the color displays the velocity of the rock glacier (in m yr⁻¹). The positions of the SIP profiles are indicated by dashed white lines, while the front edge of the rock glacier and the border between the black and the white lobe are presented by a black line. Orthophoto: © Google Satellite.

Appendix F: Uncertainty of θ and K based on multi-frequency conductivity data

We estimated the standard deviation s of θ and K by applying the error propagation law:

$$\begin{array}{}\text{(F1)}& s_f=\sqrt{\sum _{i=\mathrm{1}}^n{\left({\displaystyle \frac{\partial f}{\partial x_i}}{s}_{x_i}\right)}^{\mathrm{2}}},\end{array}$$

where s_f is the standard deviation of the parameter f, $s_{x_i}$ is the standard deviation of the parameter x_i, and i is the parameter number. For s_θ the partial derivatives are as follows.

$$\begin{array}{}\text{(F2)}& {\displaystyle \frac{\partial \mathit{\theta }}{\partial {\mathit{\sigma }}_{\mathrm{f}}}}=-{\displaystyle \frac{{\left[\frac{\mathrm{1}}{{\mathit{\sigma }}_{\mathrm{f}}}\left({\mathit{\sigma }}_{\mathrm{\infty }}-\frac{M_{\mathrm{n}}}{R}\right)\right]}^{\frac{\mathrm{1}}{m}}}{{\mathit{\sigma }}_{\mathrm{f}}m}}\text{(F3)}& {\displaystyle \frac{\partial \mathit{\theta }}{\partial R}}={\displaystyle \frac{M_{\mathrm{n}}{\left[\frac{\mathrm{1}}{{\mathit{\sigma }}_{\mathrm{f}}}\left({\mathit{\sigma }}_{\mathrm{\infty }}-\frac{M_{\mathrm{n}}}{R}\right)\right]}^{\frac{\mathrm{1}}{m}-\mathrm{1}}}{{\mathit{\sigma }}_{\mathrm{f}}m{R}^{\mathrm{2}}}}\text{(F4)}& {\displaystyle \frac{\partial \mathit{\theta }}{\partial m}}=-{\displaystyle \frac{{\left[\frac{\mathrm{1}}{{\mathit{\sigma }}_{\mathrm{f}}}\left({\mathit{\sigma }}_{\mathrm{\infty }}-\frac{M_{\mathrm{n}}}{R}\right)\right]}^{\frac{\mathrm{1}}{m}}{\log }_{\mathrm{10}}\left[\frac{\mathrm{1}}{{\mathit{\sigma }}_{\mathrm{f}}}\left({\mathit{\sigma }}_{\mathrm{\infty }}-\frac{M_{\mathrm{n}}}{R}\right)\right]}{m^{\mathrm{2}}}}\end{array}$$

The derivatives for the CEC are as follows.

$$\begin{array}{}\text{(F5)}& {\displaystyle \frac{\partial \mathrm{CEC}}{\partial \mathit{\theta }}}=-{\displaystyle \frac{M_{\mathrm{n}}\left(m-\mathrm{1}\right){\mathit{\theta }}^{-m}}{{\mathit{\rho }}_{\mathrm{g}}\mathit{\lambda }}}\text{(F6)}& {\displaystyle \frac{\partial \mathrm{CEC}}{\partial m}}=-{\displaystyle \frac{M_{\mathrm{n}}{\mathit{\theta }}^{\mathrm{1}-m}{\log }_{\mathrm{10}}\mathit{\theta }}{{\mathit{\rho }}_{\mathrm{g}}\mathit{\lambda }}}\text{(F7)}& {\displaystyle \frac{\partial \mathrm{CEC}}{\partial {\mathit{\rho }}_{\mathrm{g}}}}=-{\displaystyle \frac{M_{\mathrm{n}}{\mathit{\theta }}^{\mathrm{1}-m}}{{\mathit{\rho }}_{\mathrm{g}}^{\mathrm{2}}\mathit{\lambda }}}\text{(F8)}& {\displaystyle \frac{\partial \mathrm{CEC}}{\partial \mathit{\lambda }}}=-{\displaystyle \frac{M_{\mathrm{n}}{\mathit{\theta }}^{\mathrm{1}-m}}{{\mathit{\rho }}_{\mathrm{g}}{\mathit{\lambda }}^{\mathrm{2}}}}\end{array}$$

The derivatives for K are as follows.

$$\begin{array}{}\text{(F9)}& {\displaystyle \frac{\partial K}{\partial k_{\mathrm{0}}}}={\displaystyle \frac{{\mathit{\theta }}^{\mathrm{6}}}{{\mathit{\rho }}_{\mathrm{g}}^{\mathrm{2}}{\mathrm{CEC}}^{\mathrm{2}}}}{\displaystyle \frac{g\mathit{\delta }}{\mathit{\mu }}}\text{(F10)}& {\displaystyle \frac{\partial K}{\partial \mathit{\theta }}}={\displaystyle \frac{\mathrm{6}{k}_{\mathrm{0}}{\mathit{\theta }}^{\mathrm{5}}}{{\mathit{\rho }}_{\mathrm{g}}^{\mathrm{2}}{\mathrm{CEC}}^{\mathrm{2}}}}{\displaystyle \frac{g\mathit{\delta }}{\mathit{\mu }}}\text{(F11)}& {\displaystyle \frac{\partial K}{\partial {\mathit{\rho }}_{\mathrm{g}}}}=-{\displaystyle \frac{\mathrm{2}{k}_{\mathrm{0}}{\mathit{\theta }}^{\mathrm{6}}}{{\mathit{\rho }}_{\mathrm{g}}^{\mathrm{3}}{\mathrm{CEC}}^{\mathrm{2}}}}{\displaystyle \frac{g\mathit{\delta }}{\mathit{\mu }}}\text{(F12)}& {\displaystyle \frac{\partial K}{\partial \mathrm{CEC}}}=-{\displaystyle \frac{\mathrm{2}{k}_{\mathrm{0}}{\mathit{\theta }}^{\mathrm{6}}}{{\mathit{\rho }}_{\mathrm{g}}^{\mathrm{2}}{\mathrm{CEC}}^{\mathrm{3}}}}{\displaystyle \frac{g\mathit{\delta }}{\mathit{\mu }}}\end{array}$$

We used the values and standard deviations from Table F1 for the parameters used above.

Table F1 Parameters used for the estimation of θ and K, including absolute values and standard deviations used for the error propagation.

Appendix G: Uncertainty of K based on tracer experiments

To investigate the sensitivity of the parameters ϕ and $\frac{\mathrm{\Delta }H}{\mathrm{\Delta }L}$ to the estimation of K based on v_p, measurements are presented in Fig. G1.

Figure G1 Effects of changing ϕ (a) and $\frac{\mathrm{\Delta }H}{\mathrm{\Delta }L}$ (b) on K. The black line symbolizes θ using ϕ=0.4 and $\frac{\mathrm{\Delta }H}{\mathrm{\Delta }L}=\mathrm{0.21}$, while the gray area delimited by dashed lines shows the range of θ using ±50 % of the values.