Impact assessment of snow thickness, sea ice density and water density in CryoSat-2-derived sea ice thickness

Sea ice thickness is an essential climate variable, which is often derived from satellite altimetry freeboard estimates, e.g., by CryoSat-2. In order to convert freeboard to sea ice thickness, assumptions are needed for snow thickness, snow density, sea ice density and water density. These parameters are difficult to observe when co-located in time and space with the satellite-derived freeboard measurements. For this reason, most available CryoSat-2 sea ice thickness products rely on climatologies based on outdated observations and empirical values. Model- and observation-based alternatives to sea ice density and snow thickness values have been suggested in recent years, but their combined influence on the freeboard to sea ice thickness conversion has not been analyzed.

This study evaluates model-based spatially varying snow thickness, sea ice density and water density with in situ observations and the associated parameters used in the classical CryoSat-2 sea ice thickness production. The observations used for the comparison are a snow thickness product from Ku- and Ka-band radar, sea ice density observations from airborne campaigns and ice core measurements as well as water density from a large variety of observation platforms included in the World Ocean Atlas. Furthermore, this study calculates the mean sea ice thickness differences resulting from substituting the parameters used in a classical CryoSat-2 sea ice thickness product with model-based values. The evaluation shows that the model-derived snow thickness, sea ice density and water density compare better to observations than the associated parameters used in the CryoSat-2 sea ice thickness product. The parameters were compared to the weekly CryoSat-2 sea ice thickness (SIT) product from the Alfred Wegener Institute, which uses similar values for snow thickness, sea ice density and water density to other available CryoSat-2 SIT products. Furthermore, we find that the model-based snow thickness and sea ice density separately lead to the largest sea ice thickness differences but that, to some extent, their differences cancel out when both parameters are used in combination.

For the water density, we find the average and maximum sea ice thickness difference to be small in comparison to the sea ice thickness differences introduced by the snow thickness and sea ice density, but this is not negligible, as currently stated in most studies. We find that the origin of the assumption that water density is negligible in the freeboard to sea ice thickness conversion originates from a study investigating the seasonal Arctic sea ice density variability, not taking into account the spacial variability. Based on our findings, we recommend using either a water density climatology or an uncertainty value of 2.6 kg m⁻³ instead of the commonly used value of 0 to 0.5 kg m⁻³ in CryoSat-2 freeboard to sea ice thickness conversion.

1 Introduction

Observing sea ice thickness (SIT) on an Arctic-wide scale was impossible before the satellite era. Laxon et al. (2003) published the first study that calculated SIT from freeboard (FB) observations derived from satellite radar altimetry. They based the derivation on an assumption of hydrostatic balance and estimates of the mass of snow and ice. Equation (1) is often used to derive SIT from radar FB, following similar assumptions (Tilling et al., 2018).

$$\begin{array}{}\text{(1)}& \mathrm{SIT}={\displaystyle \frac{({\mathrm{FB}}_{\mathrm{r}}+\mathrm{0.25}\times H_{\mathrm{s}}){\mathit{\rho }}_{\mathrm{w}}}{({\mathit{\rho }}_{\mathrm{w}}-{\mathit{\rho }}_{\mathrm{i}})}}+{\displaystyle \frac{H_{\mathrm{s}}{\mathit{\rho }}_{\mathrm{s}}}{({\mathit{\rho }}_{\mathrm{w}}-{\mathit{\rho }}_{\mathrm{i}})}}\end{array}$$

FB_r is the radar freeboard, H_s is the snow thickness, ρ_s is the snow density, ρ_i is the ice density and ρ_w is the water density. These variables are difficult to observe at the same location and time as satellite-derived FB estimates. For this reason, most current CryoSat-2-based SIT products use, with adaptations of snow thickness and sea ice density estimates, the approach introduced by Laxon et al. (2003), which was based on using climatologies and empirical values.

The first of these adaptations was introduced by Alexandrov et al. (2010) for the sea ice density. While Laxon et al. (2003) used a constant sea ice density, Alexandrov et al. (2010) allowed the sea ice density to differentiate between multiyear ice (MYI) and first-year ice (FYI). The second adaptation was introduced into the snow thickness. Laxon et al. (2003) used values from Warren et al. (1999), which form the Warren climatology or simply W99. The W99 climatology is based on observations in the central Arctic collected during the time period 1954–1991 on primarily MYI (Warren et al., 1999). Since then, the Arctic sea ice cover has had dramatic changes towards a larger coverage of FYI (Maslanik et al., 2011). In line with this, Kurtz and Farrell (2011) pointed out that the W99 snow thickness is biased towards snow on thick ice, i.e., MYI, and that the snow thickness should be reduced on the thinner FYI. Different approaches have since then been used to modify the W99 snow thickness over FYI. For example, Tilling et al. (2018) and Guerreiro et al. (2017) reduced the snow thickness from W99 by 50 % on FYI, whereas, e.g., Hendricks et al. (2021) used auxiliary satellite products to estimate the snow thickness over FYI. The approach of differentiating the snow thickness and sea ice density based on satellite-derived ice types will be referred to here as the classical approach.

The snow thickness and sea ice density values used in the classical approach have been much discussed in recent years. According to Kern et al. (2015), these are the variables with the largest impact on the conversion from FB to SIT. Mallett et al. (2021b) showed that inclusion of seasonal variability in the snow thickness product used in the FB-to-SIT conversion can lead to a faster decline of up to 100 % in the sea ice of the marginal seas. For this analysis, they used the SnowModel-LG (Liston et al., 2020) forced by ERA5 (Hersbach et al., 2020) to simulate the seasonal variability. Later, Landy et al. (2022) used the same snow model in their FB-to-SIT conversion, and finally Fiedler et al. (2022) used the modeled snow thickness in their sea ice thickness assimilation. However, both Landy et al. (2022) and Fiedler et al. (2022) used the bimodal sea ice densities introduced by Alexandrov et al. (2010).

Alternative approaches to derive sea ice density for FB-to-SIT conversion have been explored by, e.g., Jutila et al. (2022a) and Ji et al. (2021). Ji et al. (2021) showed that sea ice densities from a climatology derived from sea ice density observations from 2011 to 2015 improved SIT estimates in the Beaufort Sea compared to using the fixed values from Alexandrov et al. (2010). However, the observations used in this climatology are sparse, with significantly more observations close to the validation site in the Beaufort Sea, which means that more validation is needed before relying on the derived method. Jutila et al. (2022a) used airborne observations to derive bulk sea ice densities and found that sea ice in the Arctic has become denser since Alexandrov et al. (2010). They also derived a negative exponential relationship between the bulk density and the FB but acknowledged that more research is needed in order to use this relationship in FB-to-SIT retrievals. Based on the study by Jutila et al. (2022a), Hendricks et al. (2021) recognized that the Alexandrov et al. (2010) sea ice densities in their SIT product were probably biased low but that a change in one variable should go hand in hand with a review of the other variables, which might be biased too. Changing only one of the variables in Eq. (1) could introduce a significant bias.

A multivariable evaluation has to our knowledge not been carried out to date. One challenge with such an approach is the lack of available Arctic-wide sea ice density observations. Even though Jutila et al. (2022a) suggested a method to derive sea ice density from FB, they acknowledged that the method was not mature enough to be used routinely in FB-to-SIT conversion for the entire Arctic. Sievers et al. (2023) introduced a new FB assimilation method, including a FB-to-SIT conversion in which snow thickness, sea ice density and water density model values were used to derive SIT from FB. The values from this modeling approach allow for an Arctic-wide comparison to the classically used values of snow thickness, sea ice density and water density, as they are available at similar temporal and spatial resolutions to the typically used satellite-derived FB values.

The model values from Sievers et al. (2023) include Arctic-wide varying water densities, which are typically assumed to be constant in the classical FB-to-SIT conversion: see Laxon et al. (2003), Alexandrov et al. (2010), Tilling et al. (2018), Guerreiro et al. (2017) and Kurtz et al. (2013). Most of these studies cite Laxon et al. (2003) or Alexandrov et al. (2010) as their water density source. Alexandrov et al. (2010) stated that the surface water density only varied by 2 kg m⁻³ throughout the Arctic, which is not reflected in our model results. Laxon et al. (2003) used the water density from Wadhams et al. (1992) that changed with the season but not in space. It is known that the surface (upper 1 to 10 m) salinity varies throughout the Arctic (Zweng et al., 2019) and that this governs the density. Wadhams et al. (1992) also emphasized that water density could have a significant influence on the FB-to-SIT conversion but has since not gotten much attention, which means that it might be time to revise the assumption that water density can be considered constant.

This study aims to analyze how, on average, the geographical variability of sea ice density, snow thickness and water density influences the derived SIT. First, we compare the modeled and classical approach values for sea ice density, snow thickness and water density to in situ observations. Since in this study we find that the model sea ice density from Sievers et al. (2023) is not variable enough, we introduce an improved model-derived sea ice density. A detailed derivation of the improved model sea ice density is added in the Appendix. Secondly, the impact of using the different snow thickness, sea ice density and water density values in the FB-to-SIT conversion is evaluated. For this, the SIT difference resulting from each parameter is calculated separately, together with the combined impact on the SIT.

The snow thickness, sea ice density and water density values from the classical approach are taken from Hendricks et al. (2021) in this study. This dataset was chosen because it provides all the variables used to derive SIT from FB. Sallila et al. (2019) compared different CryoSat-2-derived SIT products, also listing their approach to deriving sea ice density and snow thickness. Their analysis showed that the publicly available SIT products derived using the classical approach use similar values for snow thickness and sea ice density, and hence it can be assumed that the Hendricks et al. (2021) dataset provides a good representation of the typical values used.

As mentioned above, observations on similar timescales and spatial scales to the CryoSat-2 observations are currently unavailable for snow thickness, sea ice density and water density. Therefore, different methods for the validation of each of the parameters were introduced. They are presented in Sect. 2.4. The variable with the closest temporal and spatial coverage to CryoSat-2 FB is the snow thickness. For the comparison in Sect. 3.1, we decided to utilize the radar-based snow product (Garnier et al., 2021) due to its independence from both the model snow thickness and the snow thickness used in Hendricks et al. (2021). Since we compare 10-year averages in the SIT comparison, we chose to compare the surface water density to the World Ocean Atlas climatology from 2018 (Zweng et al., 2019) in Sect. 3.3. Most in situ observations that could have been used instead are included in the climatology. The sea ice density observations are the most sparse, which is why we included two datasets for the sea ice density observation comparison in Sect. 3.2: the airborne observation from Jutila et al. (2022a) and the ice-core-based observations from Oggier et al. (2023a, b).

2 Data and methods

2.1 Model setup

The model system is a coupled ocean and sea ice model, which is described in Sievers et al. (2023). The ocean model is the Nucleus for European Modelling of the Ocean (NEMO v4.2; Madec et al., 2017), and it closely follows the tuning from Hordoir et al. (2022). NEMO is a numerical ocean model. It was coupled to CICE v6.2 (Hunke et al., 2021a), which models the growth, melt, movement and state of the sea ice. The model setup used in this study will be called C6N4 in the following.

In CICE, snow ice formation is applied and melt ponds are included. The CICE surface water density (at 0.5 m depth) is calculated from sea surface salinity following Feltham et al. (2006). The coupling is performed every time step, and both the ocean and ice components are run with a 600 s time step and on a 10 km × 10 km grid. The analyzed model ran from 1 January 2010 to 31 December 2020 and was initialized using a 15-year spinup simulation.

The atmospheric forcing applied is ERA5 (Hersbach et al., 2020) with a frequency of 3 h. The snow thickness is calculated by CICE based on the snow forcing from ERA5. We found that the atmospheric boundary layer scheme and the atmospheric drag formulation impacts the snow thickness. This study uses the CICE default atmospheric boundary layer and the form drag formulation from Tsamados et al. (2014).

The sea ice density parameterization requires temporally evolving sea ice salinity, which is only available in the mushy thermodynamics (Turner et al., 2013). Two sea ice density parameterizations are investigated. The sea ice density originally used in the Sievers et al. (2023) C6N4 model is shown in Eq. (2):

$$\begin{array}{}\text{(2)}& {\mathit{\rho }}_{\mathrm{i}}=a_{\mathrm{b}}\times {\mathit{\rho }}_{\mathrm{b}}+(\mathrm{1.0}-a_{\mathrm{b}})\times {\mathit{\rho }}_{\mathrm{fresh}},\end{array}$$

where a_b is the fraction of brine contained in sea ice and ρ_b is the density of the brine, following Assur (1958). ρ_fresh is the sea ice density excluding brine and is set to 882 kg m⁻³ in C6N4. The second model approach for calculating the sea ice density, here called C6N4_J21, is achieved by letting ρ_fresh depend on the model variable FYI area fraction (FYI_frac):

$$\begin{array}{}\text{(3)}& {\mathit{\rho }}_{\mathrm{fresh}}={\mathit{\rho }}_{\mathrm{myi}}\times (\mathrm{1}.-{\mathrm{FYI}}_{\mathrm{frac}})+{\mathit{\rho }}_{\mathrm{fyi}}\times {\mathrm{FYI}}_{\mathrm{frac}},\end{array}$$

where ρ_myi=890 kg m⁻³ is the sea ice density of MYI and ρ_fyi=907 kg m⁻³ is the sea ice density of FYI, in both cases excluding brine. The values for ρ_myi and ρ_fyi were determined using least-square-fit analysis of data from Jutila et al. (2022a). Since the sea ice density is only a diagnostic variable, it has no impact on the snow thickness and water density, which are the same as in C6N4. More details on the derivation of ρ_myi and ρ_fyi are listed in the Appendix.

2.2 Snow thickness, sea ice density and water density from the classical approach

The weekly gridded along-track CryoSat-2-derived SIT data product version 2.4 developed at the Alfred Wegener Institute (AWI) (Hendricks et al., 2021) includes all the values used in Eq. (1) to derive the SIT from the radar FB at the corresponding location. It also only differs in minor details from other CryoSat-2 FB-derived SIT datasets (Sallila et al., 2019), which is why it is used here as a representation of the classical FB-to-SIT approach.

The sea ice density values used are 916.7 ± 35.7 kg m⁻³ for FYI and 882.0 ± 23.0 kg m⁻³ for MYI, following Alexandrov et al. (2010). The ice type data are from the Ocean and Sea Ice Satellite Application Facility (OSISAF) daily ice type product OSI-403-d (OSI SAF, 2017). The snow thickness is a combination of the W99 snow climatology and a product that uses the Advanced Microwave Scanning Radiometer 2 (AMSR2) in the marginal seas. The snow thickness products are weighted depending on their location. In the central Arctic extending to the Russian, Greenlandic and Canadian coasts, the W99 climatology dominates. In the marginal seas of the Canadian Archipelago, the Fram Strait, the Barents Sea and the Bering Sea, the AMSR2 snow thickness dominates. Following Kurtz and Farrell (2011), they reduce the W99 snow thickness by 50 % over FYI. The value used for the water density is 1024 kg m⁻³, and its uncertainties are neglected. The data come with the Equal-Area Scalable Earth Grid version 2 (EASE2-Grid) at 25 km resolution. For model comparison, the data were bilinearly interpolated to the model grid. In the following text, this dataset will be referred to as CS2_AWI.

2.3 Validation data

2.3.1 Snow thickness

To validate the snow thickness, the altimeter-based snow thickness product (ASD) published by Garnier et al. (2021) from the Laboratoire d'Etudes en Géophysique et Océanographie Spatiales (LEGOS) was used. The ASD product is based on the assumption of different penetration depths of different radar wavelengths. It is derived by subtracting the SARAL/Altika Ka-band and CryoSat-2 Ku-band radar height measurements from one another. It is available on a monthly basis on a 12.5 km grid.

In recent years, multiple efforts have been made to derive new Arctic winter snow thickness products. These efforts comprise microwave-based snow thickness products (Rostosky et al., 2018), radar-based snow thickness products (Garnier et al., 2021; Lawrence et al., 2018) and model-based approaches (Liston et al., 2020; Petty et al., 2018). We utilized the radar-based snow product (Garnier et al., 2021), due to its independence from the CryoSat-2 snow thickness including W99 and the microwave-based (Rostosky et al., 2018) snow product, together with its more realistic seasonal cycle compared to Lawrence et al. (2018). Garnier et al. (2021) found that the ASD data product compares better to NASA Operation IceBridge airborne snow thickness observations than both the W99 climatology and the AMSR2-based data product. The ASD data product covers the Arctic up to 81.5° N, which sets the limit for the comparison in Sect. 3.1.

2.3.2 Sea ice density

Airborne observations (Jutila et al., 2022a) of sea ice bulk densities are used as the baseline for sea ice densities. The densities were calculated based on Archimedes' principle, following

$$\begin{array}{}\text{(4)}& {\mathit{\rho }}_{\mathrm{i}}={\mathit{\rho }}_{\mathrm{w}}(\mathrm{1}-{\displaystyle \frac{H_{\mathrm{fs}}}{h_{\mathrm{tot}}-H_{\mathrm{s}}}})+({\mathit{\rho }}_{\mathrm{w}}-{\mathit{\rho }}_{\mathrm{s}}){\displaystyle \frac{H_{\mathrm{s}}}{H_{\mathrm{tot}}-H_{\mathrm{s}}}}.\end{array}$$

ρ_w equals 1024 kg m⁻³, and ρ_s equals 300 kg m⁻³. The values for H_s (snow thickness), H_tot (total snow and ice thickness) and H_fs (snow freeboard) are based on airborne observations at the beginning of April 2017 and April 2019. The locations of the field campaign in 2017 are marked in Fig. 1 with blue dots and stars and with red dots and stars for the 2019 campaign. H_s was measured with a snow radar (Jutila et al., 2022b), h_tot was measured with an electromagnetic induction sounding instrument also called EM-Bird (Haas et al., 2009) and H_fs was measured with a near-infrared, line-scanning Riegl VQ-580 airborne laser scanner. More details about each of the measurements can be found in Jutila et al. (2022a). The resulting data include an error estimate that was used to filter the data. No values with errors larger than 30 kg m⁻³ were used.

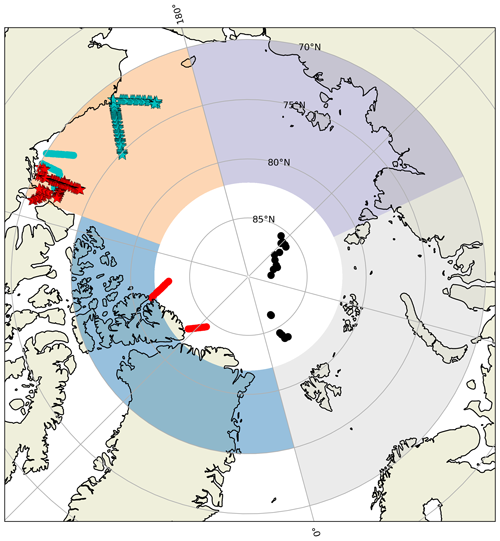
Figure 1 The map shows the locations of the observations from the IceBird campaigns in April 2017 (turquoise stars and dots) and April 2019 (red stars and dots), together with the four areas considered in Fig. 2. The stars and dots indicate the grouping of the data discussed in Sect. 3.2. The blue region is the Canadian Arctic, the orange region the Beaufort Sea, the purple region the Russian Arctic East and the gray region the Russian Arctic West. The black dots indicate the locations of the MOSAiC sea ice density measurements shown in Fig. 4.

A second sea ice density dataset, used for comparison, was obtained primarily in the central Arctic (Fig. 1, black dots). This dataset was collected during the Multidisciplinary drifting Observatory for the Study of Arctic Climate (MOSAiC) expedition, where the sea ice density from FYI and second-year-ice cores was obtained (Oggier et al., 2023a, b). The sea ice density values were calculated using the method of hydrostatic weighing. For this method, the mass of the ice core was measured in both air and an unspecified liquid (Oggier et al., 2023a, b). The locations of the coring sites were interpolated to the model grid using the nearest-neighbor method. The times at which the measurements were taken range from October 2019 to August 2020.

2.3.3 Water density

The surface water density was calculated from the salinity of the World Ocean Atlas (WOA) 2018 dataset described in Zweng et al. (2019). The WOA consists of quality-controlled observations interpolated to a standardized depth grid. This is the largest freely available gridded dataset of oceanographic observations (Garcia et al., 2018). The dataset used in this study is the 0.25° dataset spanning the years 1955 to 2017 and the averaged monthly subsets for October to March. The density was calculated following the saltwater density calculation from Feltham et al. (2006) utilizing only the surface values from the WOA.

2.4 Validation methods

Reference observations of ice conditions in the Arctic are sparsely distributed in both time and geographic coverage. The reference measurements included in this study have different spatial and temporal resolutions, and thus different methods have been used to validate the model and CS2_AWI values of snow thickness, sea ice density and water density. Where the latter two are compared using conventional methods such as the root-mean-square difference (RMSD), the snow thickness and SIT comparison methods need a more detailed description, which is included in Sects. 2.4.1 and 2.5.

2.4.1 Snow thickness

The snow thickness datasets from C6N4, CS2_AWI and ASD have different spatial and temporal resolutions. The C6N4 data are provided on an Arctic-wide 10 × 10 km grid at a weekly frequency, the CS2_AWI data include approximately 100 orbit passes per week gridded on a 25 × 25 km EASE2 grid covering up to 88° N and the ASD data are provided at a monthly frequency on a 12.5 km EASE2 grid, covering only up to 81.5° N. To ensure a fair comparison, probability density functions (PDFs) of each month's snow data were calculated for each of the three datasets. The data were divided into four regions covered by all three datasets (Fig. 1), which enables the discussion of regional differences. The area under the PDF is always 1, allowing a direct comparison of datasets with different resolutions. To evaluate how well the model and CS2_AWI data agree with the ASD data, a measure called “disagreement” (Dis) is introduced here:

$$\begin{array}{}\text{(5)}& \mathrm{Dis}=\int {\mathrm{PDF}}_{\mathrm{ASD}}+\int {\mathrm{PDF}}_{\mathrm{model}}-\int {\mathrm{PDF}}_{\mathrm{overlap}},\end{array}$$

where PDF_ASD is the PDF of the ASD dataset, PDF_model is the PDF of the model and PDF_overlap is the area where the two PDFs overlap. For the disagreement between ASD and CS2_AWI, PDF_model would be substituted by PDF_CS2 in Eq. (5). If both curves perfectly overlap Dis = 0 and if there is no overlap between the curves Dis = 2, Dis is dimensionless.

2.5 SIT comparison

One objective of this study was to evaluate SIT differences resulting from using different sea ice density, snow thickness and water density values in the production of CS2_AWI and C6N4 data. To evaluate this, first the CS2_AWI data were bilinearly interpolated onto the model grid and the model data were averaged to weekly means to match the temporal resolution of the CS2_AWI data. Following this, all grid points covered by fewer than 50 satellite overpasses in the CS2_AWI dataset from 1 January 2010 to 31 December 2020 were discarded, and only grid points and time steps covered by both the CS2_AWI data product and C6N4 were kept for further analysis. In the second step, where grid cells fulfilled the abovementioned criteria, the mean snow thickness, sea ice density and water density values for the model and CS2_AWI data were calculated, followed by their differences as a model – CS2_AWI – resulting in Δρ_i, ΔH_s and Δρ_w. Finally, the average snow thickness, sea ice density and water density for each grid cell fulfilling the abovementioned criteria were calculated from all the model and CS2_AWI values, represented in the following by $\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}}$, $\stackrel{\mathrm{‾}}{H_{\mathrm{s}}}$ and $\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}$. The mean difference and mean values are used to determine the mean SIT difference when calculating the SIT. For the SIT differences resulting from snow thickness ($\mathrm{\Delta }{\mathrm{SIT}}_{H_{\mathrm{s}}}$), sea ice density ($\mathrm{\Delta }{\mathrm{SIT}}_{{\mathit{\rho }}_{\mathrm{i}}}$) and water density ($\mathrm{\Delta }{\mathrm{SIT}}_{{\mathit{\rho }}_{\mathrm{w}}}$), the following equations were used:

$$\begin{array}{}\text{(6)}& {\displaystyle }\begin{array}{rl}\mathrm{\Delta }{\mathrm{SIT}}_{H_{\mathrm{s}}}& =\left({\displaystyle \frac{\mathrm{FB}\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}}{(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}-\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}})}}+{\displaystyle \frac{(\stackrel{\mathrm{‾}}{H_{\mathrm{s}}}+\mathrm{\Delta }{H}_{\mathrm{s}}){\mathit{\rho }}_{\mathrm{s}}}{(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}-\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}})}}\right)\\ & -\left({\displaystyle \frac{\mathrm{FB}\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}}{(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}-\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}})}}+{\displaystyle \frac{\stackrel{\mathrm{‾}}{H_{\mathrm{s}}}{\mathit{\rho }}_{\mathrm{s}}}{(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}-\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}})}}\right),\end{array}\text{(7)}& {\displaystyle }\begin{array}{rl}\mathrm{\Delta }{\mathrm{SIT}}_{{\mathit{\rho }}_{\mathrm{i}}}& =\left({\displaystyle \frac{\mathrm{FB}\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}}{(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}-(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathrm{i}}\left)\right)}}+{\displaystyle \frac{\stackrel{\mathrm{‾}}{H_{\mathrm{s}}}{\mathit{\rho }}_{\mathrm{s}}}{(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}-(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathrm{i}}\left)\right)}}\right)\\ & -\left({\displaystyle \frac{\mathrm{FB}\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}}{(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}-\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}})}}+{\displaystyle \frac{\stackrel{\mathrm{‾}}{H_{\mathrm{s}}}{\mathit{\rho }}_{\mathrm{s}}}{(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}-\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}})}}\right),\end{array}\text{(8)}& {\displaystyle }\begin{array}{rl}\mathrm{\Delta }{\mathrm{SIT}}_{{\mathit{\rho }}_{\mathrm{w}}}& =\left({\displaystyle \frac{\mathrm{FB}(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathrm{w}})}{\left(\right(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathrm{w}})-\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}})}}+{\displaystyle \frac{\stackrel{\mathrm{‾}}{H_{\mathrm{s}}}{\mathit{\rho }}_{\mathrm{s}}}{\left(\right(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathrm{w}})-\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}})}}\right)\\ & -\left({\displaystyle \frac{\mathrm{FB}\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}}{(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}-\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}})}}+{\displaystyle \frac{\stackrel{\mathrm{‾}}{H_{\mathrm{s}}}{\mathit{\rho }}_{\mathrm{s}}}{(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}-\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}})}}\right).\end{array}\end{array}$$

For the combined SIT difference, this was

$$\begin{array}{}\text{(9)}& \begin{array}{rl}\mathrm{\Delta }\mathrm{SIT}& =\left({\displaystyle \frac{\mathrm{FB}(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathrm{w}})}{\left(\right(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathrm{w}})-(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathrm{i}}\left)\right)}}\right.\\ & \left.+{\displaystyle \frac{(\stackrel{\mathrm{‾}}{H_{\mathrm{s}}}+\mathrm{\Delta }{H}_{\mathrm{s}}){\mathit{\rho }}_{\mathrm{s}}}{\left(\right(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathrm{w}})-(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathrm{i}}\left)\right)}}\right)\\ & -\left({\displaystyle \frac{\mathrm{FB}\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}}{(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}-\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}})}}+{\displaystyle \frac{\stackrel{\mathrm{‾}}{H_{\mathrm{s}}}{\mathit{\rho }}_{\mathrm{s}}}{(\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{w}}}-\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathrm{i}}})}}\right).\end{array}\end{array}$$

The mean FB values are calculated from CS2_AWI data only, and the ρ_s values are equal in both datasets.

3 Results

The results are split into two sections. In Sect. 3.1, 3.2 and 3.3 the snow thickness, sea ice density and water density from C6N4 and CS2_AWI data are compared to observations for validation. In Sect. 3.4, the differences in SIT resulting from the 10-year mean snow thickness, sea ice density and water density values of the two datasets are analyzed, first for each parameter in isolation and finally for all three combined.

3.1 Snow thickness

The PDFs of the snow thicknesses from C6N4, CS2_AWI and ASD are displayed in Fig. 2 for the months November to March.

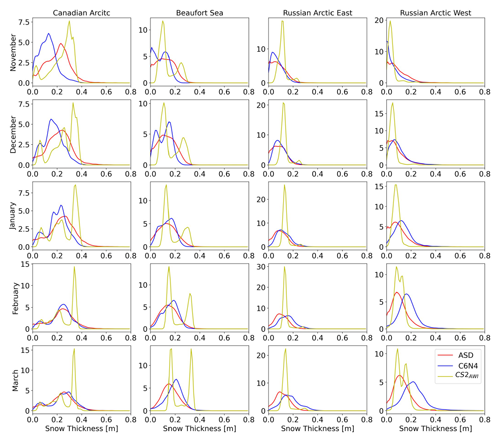
Figure 2 Probability density functions (PDFs) for snow thickness in the regions defined in Fig. 1, where all three datasets exist.

Compared to the CS2_AWI and ASD snow thicknesses, the C6N4 values are thinner in November and have their largest accumulation over winter. The CS2_AWI snow thickness PDFs show two or even three distinct peaks due to the thinner snow cover over FYI and the thicker snow cover over MYI. In the Canadian Arctic, three peaks are visible. This is due to the diverse snow conditions in the Canadian Archipelago, northern Baffin Bay and Fram Strait that are all included within the region (Fig. 1). Overall, the PDFs in Fig. 2 show that the snow cover of C6N4 is in better agreement with the ASD snow thickness compared to the agreement of the CS2_AWI and the ASD. To quantify this, the disagreement between the CS2_AWI and the ASD PDFs and the disagreement between the C6N4 and the ASD PDFs were calculated and are displayed in Table 1.

Table 1 Overview of the disagreement between the PDFs in Fig. 2 using the ASD observations as a reference. The disagreement is based on Eq. (5), and it ranges from 0 to 2, where 0 is best.

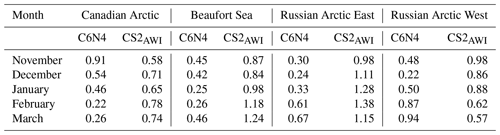
Overall, the disagreement between C6N4 and the ASD is lower than the disagreement between the ASD and CS2_AWI. The C6N4 snow thickness is in best agreement with the ASD data in the Beaufort Sea and the Russian Arctic East. The large disagreement in the Beaufort Sea (Fig. 2) is caused by the presence of the large peak indicating thick MYI snow (∼ 0.3–0.4 m) in the CS2_AWI data, which is not reflected in the ASD dataset or the C6N4 data. It is only in November in the Canadian Arctic and in February and March in the Russian Arctic West that the CS2_AWI data match better with the ASD data when compared to C6N4.

3.2 Sea ice density

The relation between the sea ice density retrievals from the IceBird measurements of Jutila et al. (2022a) and the C6N4, C6N4_J21 and CS2_AWI data is displayed in Fig. 3. According to Jutila et al. (2022a), the observations from 2017 were only obtained over the FYI locations, while the 2019 observations cover both MYI and FYI. To distinguish between the datasets from 2017 and 2019, they are shown here in two separate panels. All IceBird measurements originating from the same day and grid cell were averaged to one value. Grid cells with fewer than 10 IceBird measurements were excluded (0.9 % of the data) from the analysis. The RMSDs between the IceBird, CS2_AWI, IceBird and C6N4/C6N4_J21 data are listed separately in Table 2 for each year.

In both 2017 and 2019, there appears to be clustering of the modeled data and the CS2_AWI data in Fig. 3. The flight tracks of the IceBird campaigns in both years (Fig. 1) are in two different locations. The clustering is a result of the different representations of sea ice densities in C6N4 and the CS2_AWI data in the different locations. The locations are marked by stars and dots in Fig. 1. The large stars and dots in Fig. 3 show the average values for the two regions of each year.

Comparing C6N4 and C6N4_J21 with the IceBird observations in Fig. 3, C6N4_J21 appears to be in better agreement with the IceBird observations than C6N4. From the RMSD in Table 2, it is also clear that the C6N4_J21 sea ice densities are in closer agreement with the observations than C6N4. For 2019, both the eastern and western average values (large red stars and dots in Fig. 3b) from C6N4_J21 compare especially well to the IceBird values, which was to be expected, since the 2019 values were used to derive the C6N4_J21 sea ice density. In 2017, the C6N4_J21 sea ice density also compares better to the IceBird values than the C6N4 sea ice density, but the 2017 C6N4_J21 RMSD is 4 kg m⁻³ higher than in 2019. Especially in the western Beaufort Sea (large red star in Fig. 3a), the values have not improved as much as in 2019 or compared to the 2017 eastern Beaufort Sea values (large red dot in Fig. 3a).

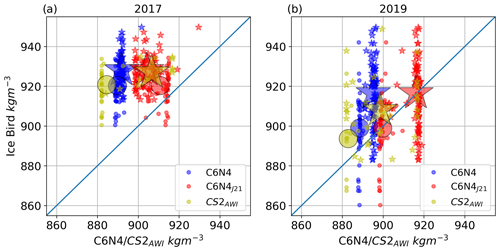
Figure 3 The IceBird sea ice density plotted against the CS2_AWI, C6N4 and C6N4_J21 sea ice densities for the 2017 and 2019 campaigns. The stars and dots represent the averaged western and eastern observation sites, as defined in Fig. 1.

The close agreement between the averaged sea ice density from C6N4_J21 and the IceBird data in 2019, together with the fact that the 2019 IceBird data were used to derive the sea ice density parameterization in C6N4_J21, calls for a comparison with independent reference observations. Such a comparison has been made between the sea-ice-core-based sea ice density measured by the MOSAiC expedition and the C4N6 and C4N6_J21 model-based estimates. All the MOSAiC density measurements and density estimates are plotted against time in Fig. 4, and the resulting RMSDs are listed in Table 3. From Fig. 4 and Table 3, it is clear that the C6N4_J21 sea ice densities are in closer agreement with the observations than the C6N4 values, supporting the findings of the IceBird comparison. Figure 4 also shows that both model estimates result in overall lower sea ice density values, with a slight seasonality of decreasing density over the winter that is not reflected in the observations. Since this is visible in both C6N4_J21 and the C6N4 sea ice density, the reason for this seasonality must be linked to the sea ice brine content, since this is the only factor varying the C6N4 sea ice density. The best agreement between the C6N4_J21 and MOSAiC observations is in April, which is also the month in which the observations (Jutila et al., 2022a) used to derive ρ_myi and ρ_fyi in Eq. (3) were collected.

Table 2 RMSDs between C6N4, C6N4_J21, CS2_AWI and the IceBird sea ice density. The values in parentheses indicate the model values when only considering the data points covered by all three datasets.

In the 2019 plot (Fig. 3b), the mean IceBird values (large stars and dots on the y axis) differ significantly between the CS2_AWI (yellow) and model data (blue and red). This is due to the different number of data points covered by the observation and CS2_AWI data and the observation and C6N4 data. To compare the CS2_AWI and the model values, only data points should be taken into account which are covered by all three datasets. This reduces the comparison data significantly. For comparison, the CS2_AWI data only coincide with ∼ 40 observation points, while the model coincides with 130–140 observation points, depending on the year. To compare the CS2_AWI data with the modeled sea ice density and the observations, the RMSD was calculated for all data points covering all three datasets. The RMSDs are listed in the parentheses in Tables 2 and 3. Overall, the RMSDs between the C6N4_J21 and the IceBird data are lower than the ones between CS2_AWI and the IceBird data. For the MOSAiC data, the C6N4_J21 RMSD is also lower than the CS2_AWI RMSD but is not as significant as in the IceBird data comparison.

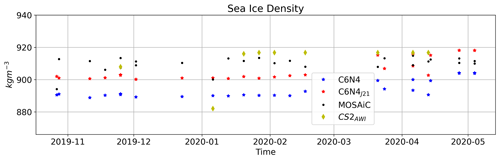
Figure 4 C6N4, C6N4_J21 and CS2_AWI sea ice density estimates and MOSAiC FYI and SYI core sea ice densities.

While the CS2_AWI data were biased low in comparison to the IceBird data in Fig. 3, the CS2_AWI data are biased high in comparison to the MOSAiC data (Fig. 4). Most of the CS2_AWI data points here are classified as FYI, and many of the observations are also taken on a FYI ice flow (Oggier et al., 2023a). Jutila et al. (2022a) concluded that the sea ice density values following Alexandrov et al. (2010) are biased low for both FYI and MYI. The results displayed in Fig. 4 suggest that this might not be the case for the FYI values everywhere in the Arctic.

Table 3 RMSDs between the MOSAiC sea ice density observations and the model and CS2_AWI values. The values in parentheses indicate the results for model values in locations where only CS2_AWI data exist (yellow rhombuses in Fig. 4).

3.3 Water density

To evaluate the model and CS2_AWI surface water densities, the model's 10-year mean and the CS2_AWI approach using a single value of 1024 kg m⁻³ were compared to the WOA climatology, which is based on observations. The water 10-year mean densities of WOA, CS2_AWI and the C6N4 simulation are displayed for November to March in Fig. 5.

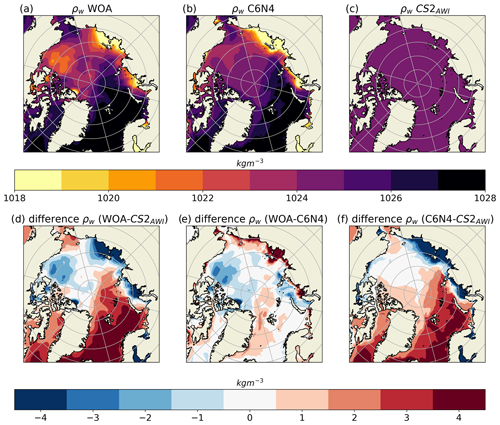
Figure 5 From left to right: maps of the WOA, C6N4 and CS2_AWI water densities (a–c) and difference maps of the WOA − CS2_AWI, WOA − C6N4 and CS2_AWI − C6N4 water densities (d–f).

Overall, a pattern of dense water in the Atlantic sector, low-density water in the Russian shelf area and a negative density gradient from the Fram Strait towards the Beaufort Sea is present in both the model and the WOA density maps. The WOA − C6N4 surface water density difference (Fig. 5e) reveals areas with the highest differences located in the Russian shelf area. The WOA − CS2_AWI surface water density differences (Fig. 5d) also show the largest differences here, but they have opposite signs to WOA − C6N4. The model simulated lower densities than the WOA suggests, and the CS2_AWI value is higher than the WOA's. In the rest of the Arctic, the WOA − C6N4 and WOA − CS2_AWI differences have similar signs but locally have different magnitudes. In the Beaufort Sea, both the WOA − C6N4 and WOA − CS2_AWI differences have about the same magnitude, and in the Atlantic sector the WOA − CS2_AWI difference is larger than the WOA − C6N4 difference. In the Lincoln Sea, a strong negative anomaly is shown in both differences. Apart from this, the WOA − CS2_AWI difference is lower here than the WOA − C6N4 difference. Overall, C6N4 is in better agreement with the WOA, except in the Lincoln Sea. C6N4 shows less variability when compared to the WOA data. The standard deviation (SD) between the C6N4 and WOA water densities for the entire Arctic is 1.6 kg m⁻³, and the SD between the WOA and CS2_AWI water densities is 2.1 kg m⁻³.

3.4 Sea ice thickness difference analysis

The individual influences of sea ice density, snow thickness and water density on the FB-to-SIT conversion are displayed in Fig. 6.

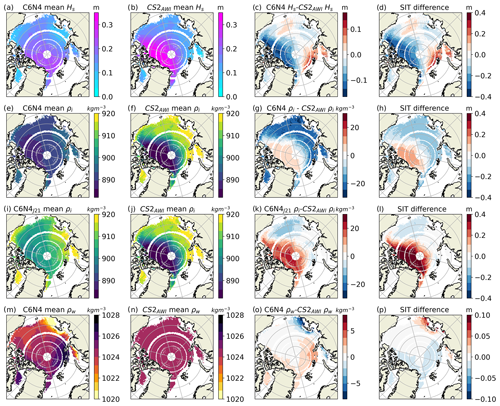
Figure 6 The rows show, from top to bottom, the snow thickness, the C6N4 sea ice density, the C6N4_J21 sea ice density and the water density. Each column shows, from left to right, the 10-year model mean, the 10-year CS2_AWI mean, their differences and the resulting SIT differences of the respective parameters. Be aware of the different color scales of the SIT differences in panels (p) and (o).

Both the snow thickness differences between C6N4 and CS2_AWI (Fig. 6c) and the sea ice density differences between C6N4_J21 and CS2_AWI (Fig. 6k) result in significant SIT differences, as seen in Fig. 6d and l, respectively. The largest SIT difference results from the sea ice density differences between C6N4_J21 and CS2_AWI. On average, this amounts to 0.14 m but reaches a maximum value of 1.16 m (Table 4) close to the northern coast of Greenland. The water density results in the lowest SIT difference (on average 0.01 m), but the maximum value of 0.33 m is not negligible.

Table 4 Maximum (D_max) and root-mean-square difference (RMSD) of the SIT differences calculated by the 10-year mean model and the CS2_AWI differences for snow thickness, sea ice density, water density and all three combined.

Figure 6 also shows that the impacts of the specific variables on the SIT differences are not necessarily mapped one to one for all the parameters. The snow thickness differences in Fig. 6c for example translate almost one to one into the resulting SIT differences in Fig. 6d. For example, both in the Lincoln Sea and north of Svalbard, a H_s anomaly of about 0.1 m translates into a SIT anomaly of about 0.2 m. This is not the case for the sea ice density, which is particularly visible when comparing Fig. 6g and h. In this case, the sea ice density anomaly in the Lincoln Sea of about 5 kg m⁻³ causes the same SIT anomaly in the Lincoln Sea as the sea ice density anomaly of about −20 kg m⁻³ on the East Siberian Shelf.

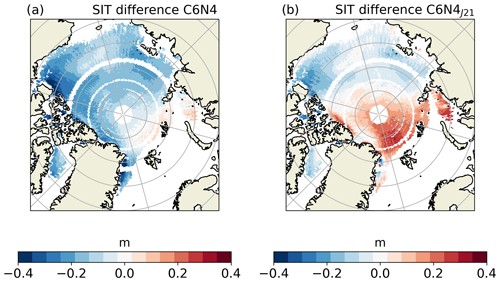
Figure 7 SIT differences resulting from all variable combined differences. Panel (a) shows the SIT differences using C6N4, and panel (b) uses the C6N4_J21 sea ice density.

The influences of all the combined differences are shown in Fig. 7 for the two different cases using C6N4 (Fig. 7a) and C6N4_J21 (Fig. 7b), respectively. Both plots show differences of up to 0.4 m but with opposite signs and in different locations, indicating that the change in the sea ice density from C6N4 to C6N4_J21 has a significant impact on the FB-to-SIT conversion. The largest SIT difference between the C6N4 data and the CS2_AWI data is located in the eastern Beaufort Sea and is mainly caused by lower snow thickness and sea ice density in the C6N4 data (Fig. 6c and g). The largest difference between the C6N4_J21 data and the CS2_AWI data is located north of Svalbard and is mainly caused by higher snow thickness and sea ice density in the model (Fig. 6c and k).

3.4.1 Water-density-derived SIT differences

To evaluate whether the differences in water density between the WOA and the model and between the WOA and the CS2_AWI data lead to significant differences in SIT, we calculated the SIT differences using different water density differences (Δρ_w) as input for Eq. (8). The results are presented in Fig. 8. For Fig. 8a, Δρ_w was calculated from mean values of WOA–CS2_AWI and for Fig. 8b from WOA–C6N4. Both SIT difference plots show maximum values in the Lincoln Sea. These maxima are caused by an anomalous low surface salinity in the WOA data. The observation density in this area is sparse, and the climatology might be biased to a certain year with an anomalously low salinity here. For further analysis, this region is excluded.

The SIT difference calculated from the WOA–CS2_AWI density has a more widespread variation than is the case for the one calculated from WOA–C6N4, including regions with both positive and negative biases. Since the CS2_AWI water density is constant, this was to be expected. Both the C6N4 and CS2_AWI water densities lead to thicker ice in the Beaufort Sea and thinner ice in the Fram Strait and Greenland Sea, with the bias towards thinner ice being less pronounced in the C6N4 comparison. In the Russian shelf region, the CS2_AWI data lead to thicker ice and the C6N4 data to no difference, except for a small area of thinner ice west of the Anzhu Islands.

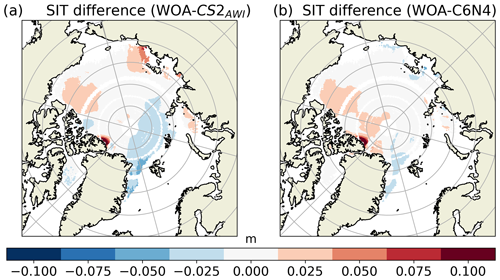
Figure 8 SIT differences resulting from varying Eq. (5) using the difference between the WOA–CS2_AWI (a) and WOA–C6N4 (b) water densities.

The RMSD between WOA and CS2_AWI amounts to 0.02 m and that between WOA and C6N4 to a 0.01 m SIT difference with maxima of 0.13 m for the CS2_AWI data and 0.16 m for the C6N4 data.

4 Discussion

4.1 Snow thickness

The snow thicknesses of C6N4, CS2_AWI and ASD are compared in Fig. 2 and Table 1. The best agreement is found between the C6N4 and ASD snow thicknesses, whereas the CS2_AWI snow thickness is in general too thick. The CS2_AWI snow thickness consists of a combination of two snow products, i.e., the W99 climatology and the AMSR2 snow thickness. The areas included in this study primarily use the W99 climatology, except for the marginal seas of the Greenland Sea, the Barents Sea and the Baffin Bay. Here, the snow thickness was derived from microwave data (Hendricks et al., 2021). The snow thickness comparison in Fig. 2 does not include any snow observations in the central Arctic, as the ASD snow product only covers up to 81.5° N. Zhou et al. (2021) compared eight different snow thickness products to W99 and found that W99 was significantly thicker than any of them. This is in good agreement with our results. The PDFs in Fig. 2 show that the C6N4 snow thickness, when compared to the ASD snow thickness product, is overall thinner in the beginning of winter and thicker by the end of winter. The snow is thinner in the beginning of winter in C6N4, because most of the snow in the model is melted away during the summer. There are three possible reasons for the thicker snow by the end of winter. First, C6N4 does not include snow densification, which is the process where wind and temperature reduce the volume over time without changing the mass (Liston et al., 2020). When C6N4 is run with FB assimilation, the value of 0.25 in Eq. (1) is substituted with a term depending on the snow density, which densifies over winter according to a linear function introduced by Mallett et al. (2021a). This snow densification term is only used during the assimilation and does not influence the snow thickness anywhere else in the model (Sievers et al., 2023). To avoid overestimation of the C6N4 snow thickness in late winter, the densification used in the assimilation following Mallett et al. (2021a) could be applied to scale the snow thickness. The second reason for the difference in snow thickness in late winter could be that the Ku-band radar, which is used to determine the snow–ice interface in the ASD product, does not penetrate the entire snowpack (Willatt et al., 2011; Kwok, 2014; Ricker et al., 2015; King et al., 2018). In situ observations that can be used to evaluate the Arctic-wide snow thickness products are limited in time and space, and thus a consistent validation of this will remain a challenge. A third reason that may bias the C6N4 snow thickness is regional biases in the snowfall from ERA5, which could be overestimated in certain regions. Stroeve et al. (2020) compared two snow model runs forced with ERA5 and NASA's Modern-Era Retrospective analysis for Research and Applications, version 2 (MERRA-2) (Gelaro et al., 2017). They found that the modeled snow thicknesses from both atmospheric forcing datasets are thicker compared to W99 in a similar region slightly further west. They attributed this difference to a storm that brought more snow into the region in the year they evaluated, but they also mentioned that the snowfall rate might have changed in recent decades due to changes in the atmospheric circulation as a result of the decreased summer sea ice extent (Stroeve et al., 2011). The in situ observations from the MOSAiC expedition can provide some insight into the evaluation of at least one winter season. Wagner et al. (2022) compared snowfall rates during the MOSAiC expedition to ERA5 (the atmospheric forcing C6N4 and C6N4_J21) and found good agreement between the observed and ERA5 snowfall rates. C6N4 is forced by ERA5 snowfall. Furthermore, Kwok et al. (2020) found that snow thickness estimates from the combined CryoSat-2 and IceSat data compare well with reconstructed snowfall from ERA5. However, they also used the CryoSat-2 radar measurements, which might lead to underestimation of snow thickness, as mentioned above. All of these studies (Stroeve et al., 2011; Zhou et al., 2021; Wagner et al., 2022; Kwok et al., 2020) support the thicker modeled snow in the Russian Arctic West area as being more realistic than both the ASD product and the CS2_AWI snow thickness.

Overall, Table 1 shows that the snow thickness from C6N4 agrees better with the ASD data product than the CS2_AWI snow thickness. A few exceptions are found in the Canadian Arctic and the Russian Arctic West for specific months, where the CS2_AWI and ASD snow products agree better. In the Russian Arctic West, the C6N4 snow thickness increasingly disagrees with the ASD snow thickness in the late winter months. As mentioned above, this could be a result of either the Ku-band radar not penetrating the entire snowpack or the snow in C6N4 not including snow densification. The in situ measurements on which King et al. (2018) based their findings, i.e., that the Ku-band radar does not penetrate the entire snowpack, were taken north of Svalbard, in a region of ours called the Russian Arctic West (Fig. 1). In November in the Canadian Arctic, the difference most likely came from the overestimation of summer snowmelt in C6N4. This region is typically covered by ice that has survived several winters. The snow thickness from the snow model in Stroeve et al. (2020) supports the snow thickness of about 0.20–0.25 m from the ASD product in November in the Canadian Arctic. Overall, we conclude that there is enough evidence that the C6N4 snow thickness is more realistic than the CS2_AWI data snow thickness.

4.2 Sea ice density

According to Fig. 3, the C6N4 sea ice density is too low and has too little spatial variability compared to the airborne IceBird observations. Figure 4 also shows that the C6N4 sea ice density is too low when compared to the MOSAiC observations. The 10-year mean C6N4 sea ice density in Fig. 6e shows that similarly low values are calculated for the entire Arctic. In fact, all the observations are denser than the C6N4 sea ice density. The formula used to calculate the sea ice density (Eq. 2) accounts for the amount of brine but not the fact that the number of enclosed air bubbles in the ice changes during the melt season, leading to lower sea ice density in MYI (Timco and Frederking, 1996). The C6N4 value for ρ_fresh is 882 kg m⁻³, which reflects a typical density for MYI (Alexandrov et al., 2010) and explains the comparable low sea ice density in the C6N4 run.

The C6N4_J21 sea ice density parameterization varies for ρ_fresh, depending on the FYI area fraction in each grid cell. Based on the RMSD, the resulting sea ice density is in better agreement with the IceBird data. This was expected, as ρ_fyi and ρ_myi from Eq. (3) were fitted to the 2019 IceBird data. This is also closer to the MOSAiC observations (Fig. 4), which are independent of the IceBird data sea ice density observations. This shows that, overall, the C6N4_J21 density parametrization performs better than the simpler approach used in C6N4.

The 2017 averaged values (Fig. 3a) show that the eastern Beaufort Sea (dots) ice is denser than in the western Beaufort Sea (stars). This is reflected in the C6N4 and CS2_AWI data but not in the C6N4_J21 data, where the opposite is the case. Jutila et al. (2022a) stated that the 2017 data consist exclusively of FYI. C6N4_J21 and CS2_AWI however also include MYI data, just in different locations: CS2_AWI mostly in the western Beaufort Sea and C6N4_J21 mostly in the eastern Beaufort Sea. The denser western Beaufort Sea values in C6N4 must be caused by the brine content, since no destination of MYI and FYI is included in this simulation. The lower C6N4_J21 densities in the western Beaufort Sea (stars in Fig. 3a) indicate that the model here falsely models MYI. The 10-year mean sea ice density in Fig. 6i indicates that, on average, the model simulates more MYI in this region. Since the observations only cover 1 year, no conclusion can be drawn about whether the model in general simulates too much MYI in the western Beaufort Sea. The wrongly modeled MYI in C6N4_J21 seems to stem from too much MYI exported into the western Beaufort Gyre. Hunke (2014) found that the drag parameterization from Tsamados et al. (2014) increases the MYI export into this region. This drag parameterization is also the one used in the presented model setup. This means that the drag parameterization is one of the first model settings that should be examined to determine the reason for the excessive MYI export into the western Beaufort Gyre. In the CS2_AWI data (Fig. 3a, yellow stars and dots), the majority of the eastern Beaufort Sea values were classified as MYI, but some western Beaufort Sea values are too. The results in Fig. 3 show that both CS2_AWI and C6N4_J21 assume MYI, whereas the observations only suggest FYI. In the CS2_AWI data, this classification is based on passive microwave ice type data. Our results suggest that the classification is not reliable. Another study evaluating different satellite sea ice type datasets came to the same conclusion (Ye et al., 2023). It found that the ice type data used in the CS2_AWI FB-to-SIT conversion have a MYI area bias of up to −0.54 × 10⁶ km² and a FYI area bias of up to 0.60 × 10⁶ km². More accurate classification of MYI and FYI would influence both the snow thickness and sea ice density, which are also the parameters found to be most important in the FB-to-SIT conversion.

Comparing the RMSDs of the C6N4_J21 and CS2_AWI sea ice densities shows that, overall, the C6N4_J21 densities are in better agreement with observations than the CS2_AWI densities (compare the values in parentheses in Tables 2 and 3). As discussed above, for 2017 the reason for the overly low sea ice density values is FYI, which is classified as MYI. However, other studies have also suggested that the Alexandrov et al. (2010) values in general are too low (Ji et al., 2021; Jutila et al., 2022a). Ji et al. (2021) did not specify whether it is both the values for MYI and FYI that are biased low according to their results. However, Jutila et al. (2022a) found that the MYI and FYI values from Alexandrov et al. (2010) are both biased low. Figure 4 however suggests that the CS2_AWI FYI sea ice densities are actually slightly higher than the MOSAiC observations. There are two distinct differences between the IceBird observations and the MOSAiC observations: the location and the observation method. The physical conditions under which ice is formed vary throughout the Arctic. This might lead to differences in density, which is however only speculation and will need further investigation. Timco and Frederking (1996) reviewed sea ice density observation methods and found that the method used to obtain the IceBird observations is the least reliable and the method used to obtain the MOSAiC observations is the most reliable. This is also reflected in the uncertainties associated with the Jutila et al. (2022a) observations, which on average are above 20 kg m⁻³. Based on the large spread of the Jutila et al. (2022a) observations, we can assume that the errors are random and that the comparison still allows conclusions to be drawn based on the averaged values as indicated by the large dots and stars in Fig. 3, e.g., that the model and CS2_AWI values were too low in 2017.

One disadvantage of the MYI and FYI methods used to derive the CS2_AWI sea ice densities is illustrated by the outlier in January 2020 in Fig. 4. The observations were made of FYI and second-year ice (SYI), but CS2_AWI assigned this ice to MYI. A study evaluating different satellite ice type products found that the ice type product used in the CS2_AWI data has a −0.54 × 10⁶ km² bias for MYI area and a 0.60 × 10⁶ km² bias for FYI area (Ye et al., 2023).

The sea ice density that is derived for C6N4_J21 is rather simple, which imposes at least three limitations. The first limitation is that the model tracks the FYI area as a fraction of the grid cell area. To estimate the bulk sea ice density, the volumes of MYI and FYI are needed. The calculation of the volume assumes that the ice thickness is the same for FYI and MYI, which introduces a bias towards too large a volume of FYI. Secondly, the FYI area is defined as the ice area formed since the previous September. This means that, every September, all the remaining ice is classified as MYI, including ice younger than 1 year. This results in a jump in sea ice density that is nonphysical. The physical explanation for the lower densities in summer is the inclusion of air bubbles where brine has washed out (Timco and Frederking, 1996). This happens gradually throughout the melt season and not as a jump in September. With these limitations in mind, we recommend only using the sea ice density parameterization derived here during the ice growth season. Thirdly, the observation method and time are limited. Timco and Frederking (1996) reviewed different methods to derive the sea ice density and found the method used in Jutila et al. (2022a) to be the least reliable. This might explain some of the variability shown in Fig. 3. Another limitation of the observations is that they are only available in April, but the parameterization was derived for the entire winter. Figure 4 shows that the C6N4_J21 sea ice density indeed agrees best with the MOSAiC observations in April. The April model values in Fig. 4 are however also more variable than in the winter months, and further observation comparisons have to be made to come to a final conclusion.

4.3 Water density

Following the WOA (Fig. 5), the general pattern of dense water on the Atlantic side of the Arctic and lighter water in the Russian shelf area and the Beaufort Sea is replicated by C6N4. However, this spatial water density gradient is less pronounced in C6N4. In particular, the Beaufort Sea surface water is lighter, and in the Fram Strait region it is denser in the WOA. The CS2_AWI water density is represented by a single value with no spatial variations.

Evaluating the C6N4 mixed-layer depth (MLD), we found that it is overall too deep, similar to the MLD in Hordoir et al. (2022), whose mixing parameterizations were closely followed in our model setup. This overestimated MLD is a result of enhanced mixing, which also explains the overly high Beaufort Sea water densities, which are a result of the low-density surface water becoming mixed with denser subsurface water. The largest differences between the WOA climatology and the C6N4 data are found in the Laptev Sea. The Laptev Sea surface salinity is highly dependent on river runoff and atmospherically forced transport of the river runoff to different locations each year (Janout et al., 2020). A climatology like the WOA will not reflect this interannual variability, whereas an ocean model potentially could. In most regions of the Arctic, there are fewer than 50 water density observations on a 1°×1° grid for a period covering 150 years (Zweng et al., 2018). Even though the WOA climatology compiles a large part of all the existing oceanographic observations (Zweng et al., 2018), one has to keep in mind that the coverage is extremely sparse. Keeping all these limitations in mind, C6N4 compares better to the WOA dataset than the constant value used in the CS2_AWI dataset. In areas like the Laptev Sea, where the surface salinity is subject to large interannual variability due to wind forcing, models could be even more suited than climatologies. When using modeled surface density, a thorough analysis of the region's freshwater distribution should be carried out.

The C6N4 water density was calculated following Feltham et al. (2006), who only calculated the density depending on the salinity. This is currently the default in CICE. For consistency, the WOA water density was calculated following a similar approach by Feltham et al. (2006). The oceanographic standard would have been to use the salinity- and temperature-dependent Thermodynamic Equation Of Seawater - 2010 (TEOS-10) (IOC et al., 2015). We tested whether using TEOS-10 had any impact on the results in the SIT difference or the overall SD calculation between the CS2_AWI and WOA data, and we found this not to be the case.

4.4 Evaluation of sea ice thickness differences

Currently available SIT products (Hendricks et al., 2021; Tilling et al., 2018; Guerreiro et al., 2017; Kurtz et al., 2013) use similar approaches to the CS2_AWI data product to derive their sea ice density, snow thickness and water density. Differences mainly accrue in the snow thickness reduction over FYI or the satellite data product used to derive the ice type (Sallila et al., 2019). Since the values are similar, the CS2_AWI data can in the following discussion be used as a general representation of the classical approach for CryoSat-2 SIT data. The above discussion of C6N4, C6N4_J21, CS2_AWI and observations for snow thickness, sea ice density and water density shows that all the model variables compare better to observations than the values used in CS2_AWI.

The largest SIT differences (Fig. 6b and Table 4) result from the snow thickness differences and the C6N4_J21 sea ice density differences. The snow and sea ice density that influences the SIT calculation has been discussed by other studies (Zygmuntowska et al., 2014; Kern et al., 2015; Ji et al., 2021; Jutila et al., 2022a; Mallett et al., 2021a). Kern et al. (2015) found that both snow thickness and sea ice density contribute equally to the SIT uncertainty, while Zygmuntowska et al. (2014) found that snow contributed 70 % and sea ice density 30 %–35 %. Even though this study does not analyze the exact contribution from each parameter as a percentage, we find that the sea ice density differences on average influence the sea ice thickness more than the snow thickness (RMSD in Table 4), where the values from the classical approach are substituted with the modeled values.

The differences in SIT are compared variable by variable in Fig. 6d, h, l and p, and the combined SIT differences are shown in Fig. 7b. The single-value SIT differences in Fig. 6 result in higher SIT differences than the combined ones in Fig. 7b. This is due to the opposite signs in the SIT differences of snow and sea ice density (Fig. 6d and l) canceling each other out in the combined SIT difference. Here, our results show that only substituting W99 snow thickness, or only the Alexandrov et al. (2010) sea ice density, introduces biases.

The effects of varying the water density on the SIT are normally neglected (Alexandrov et al., 2010; Kurtz et al., 2013; Guerreiro et al., 2017; Tilling et al., 2018; Hendricks et al., 2021). The SIT difference analysis between C6N4 and CS2_AWI suggests that the water density can lead to a difference of up to 0.33 m with a RMSD of 0.01 m, which is little in comparison to the SIT differences initiated by snow thickness and sea ice density but is still not negligible in certain areas. The SIT RMSD between WOA and CS2_AWI amounts to 0.02 m, and for the WOA − C6N4 difference it is 0.01 m. The average value shows that, in general, the C6N4 value results in a lower SIT difference, which is also shown in Fig. 8. The maximum though is higher for the WOA − C6N4 difference. The higher maximum value could be due to the nature of the WOA climatology. This maximum is located close to the Lena River delta. As discussed above, this is a region with high interannual sea surface salinity variability (Janout et al., 2020; Zhuk and Kubryakov, 2021) and low observational convergence (Zweng et al., 2018). As also mentioned above, an analysis of the interannual variability of the sea surface salinity of C6N4 in this area is needed to draw any final conclusion about its ability to model the right location of river discharge.

All existing SIT data products that use the hydrostatic balance equation to derive SIT either neglect the error contribution from water density (Kurtz et al., 2013; Tilling et al., 2018; Hendricks et al., 2021) or use a value of 0.5 kg m⁻³ (Guerreiro et al., 2017) as the uncertainty with reference to Alexandrov et al. (2010) or Laxon et al. (2003). Alexandrov et al. (2010) referred to three data sources (Gorshkov, 1980; Pavlov and Stanovoy, 1998; Timokhov and Tanis, 1997) for their assumptions, which were not accessible to us, and Laxon et al. (2003) referred to Wadhams et al. (1992). Wadhams et al. (1992) evaluated the seasonal variability of the Arctic surface water density and found that it varies by about 0.5 kg m⁻³, but they did not take the spatial variability into account. Figure 5 shows that the WOA water density varies by up to 10 kg m⁻³ in space. Our results show that using a climatology like the WOA or a model value would give more realistic water density estimates than the commonly used single value. If a single value is used for the water density in Eq. (1), the spatial variability should be accounted for in the uncertainty estimate. We suggest, in this case, using 2.6 kg m⁻³ calculated as the sum of the SDs between the WOA and CS2_AWI density of 2.1 and 0.5 kg m⁻³ to account for the seasonal variability, as suggested by Wadhams et al. (1992). Figure 8 shows that using a variable water density can improve the SIT, which is why we suggest that data products deriving SIT using the hydrostatic balance equation should use a data product like the WOA climatology. As discussed above, the WOA climatology is also associated with its own uncertainties, but these are still smaller than those related to a single value of water density.

Even though the model values were found to be closer to the validation data, our analysis indicates that more work should be invested in validation of the ocean component. In particular, the migration of river discharge should be validated. Furthermore, we found that the mixing seems to be too strong, which results in too deep a mixed layer. Furthermore, the ice transport in the Beaufort Sea should be investigated. Our results show that MYI is present where observations indicate only FYI in the Beaufort Sea. The drag parameterization seems to be a good first subject of interest to improve this.

The analysis focused on 10-year mean values. One additional benefit of using model values would be to include the interannual variability. This could lead to significantly higher SIT differences compared to the ones found in this study.

5 Conclusions

The aims of this study were as follows. (1) Evaluate whether sea ice model values, as used in Sievers et al. (2023) (C6N4), can replace the commonly used W99 snow thickness, the Alexandrov et al. (2010) sea ice density and the Arctic-wide constant water density values in the classically satellite-derived FB-to-SIT conversion. (2) Evaluate how much changing the snow thickness, sea ice density and water density would impact the SIT difference for each variable, separately and combined.

We found that the C6N4 snow thickness and water density compare better to the observations than the CS2_AWI values but that the C6N4 sea ice density does not. Therefore, this study introduced an improved sea ice density parameterization (Eq. 3), C6N4_J21, which we find compares better to the observations by Jutila et al. (2022a), Oggier et al. (2023a) and Oggier et al. (2023b) than the Alexandrov et al. (2010) sea-ice-type-based densities used in the CS2_AWI approach.

Analyzing the SIT differences resulting from the snow thickness, sea ice density and water density separately, we find that the snow thickness and sea ice density differences between CS2_AWI and C6N4_J21 lead to the largest SIT differences. The areas with the largest differences for both values are located north of Greenland and Canada and have opposite signs. In the combined SIT difference (Fig. 7b), their effects cancel out. The combined SIT difference analysis shows that only substituting snow thickness, or sea ice density, introduces a bias. This underlines the value of the derived C6N4_J21 sea ice density, which can easily be combined with approaches to substituting the snow thickness with model values, as done for example by Landy et al. (2022) and Fiedler et al. (2022).

In contrast to other studies (Kurtz et al., 2013; Tilling et al., 2018; Hendricks et al., 2021), we find that the uncertainty introduced by water density is not negligible but on average leads to a 0.02 m difference in the SIT-to-FB conversion and can in extreme cases lead to a difference of up to 0.13 m in SIT, comparing the CS2_AWI constant value and WOA values. To our knowledge, all publicly available CryoSat-2 SIT products assume a water density uncertainty of 0 to 0.5 kg m⁻³, which is based on assumptions only taking into account the seasonal variability of water density (Wadhams et al., 1992) but not the spatial variability. We suggest changing the sea ice density uncertainty to 2.6 kg m⁻³ to account for both the seasonal and spatial variations or using water density values from climatologies like the WOA or, as in this study, ocean model values. The value of 2.6 kg m⁻³ is derived from the SD between the CS2_AWI constant value and the WOA.

Appendix A: Deriving the C6N4_J21 sea ice density

C6N4 sea ice density varies only by the amount of brine enclosed in the ice (Eq. 2). The analysis in Sect. 3.2 shows that the resulting sea ice density is not variable enough (Fig. 3) and is too low (Fig. 4). The value of ρ_fresh in Eq. (2) represents, at 882 kg m⁻³, typical MYI values. Enclosed air bubbles are the main reason for older ice being less dense than newly formed ice (Timco and Frederking, 1996). The sea ice model is not capable of simulating enclosed air bubbles, so we need an alternative method to derive ρ_fresh, e.g., by using MYI and FYI volumes per grid cell following the classical approach. Also, FYI and MYI volumes are not calculated by the model. However, the model does calculate the percentage of the FYI area coverage per grid cell (FYI_frac), where FYI_frac is defined as the area fraction of ice formed since last September. Equation (3) was introduced to substitute the constant ρ_fresh value of 882 kg m⁻³ in Eq. (2), with the ρ_myi and ρ_fyi values weighted by FYI_frac. Here we use the sea ice density observations from Jutila et al. (2022a) to minimize the root-mean-square error (RMSE) between observation and model values for different ρ_myi and ρ_fyi:

$$\begin{array}{}\text{(A1)}& {\mathit{\rho }}_{\mathrm{i},\mathrm{RMSE}}=\sqrt{\sum _{i=\mathrm{1}}^n{\displaystyle \frac{({\mathit{\rho }}_{\mathrm{i},\mathrm{model}}-{\mathit{\rho }}_{\mathrm{i},\mathrm{J}\mathrm{21}}{)}^{\mathrm{2}}}{n}}},\end{array}$$

where ρ_i,model was calculated following

$$\begin{array}{}\text{(A2)}& \begin{array}{rl}{\mathit{\rho }}_{i_{\mathrm{model}}}& =a_{\mathrm{b}}\times {\mathit{\rho }}_{\mathrm{b}}+(\mathrm{1}.-a_{\mathrm{b}})\times ({\mathit{\rho }}_{\mathrm{myi}}\times (\mathrm{1}.-{\mathrm{FYI}}_{\mathrm{frac}})\\ & +{\mathit{\rho }}_{\mathrm{fyi}}\times {\mathrm{FYI}}_{\mathrm{frac}}).\end{array}\end{array}$$

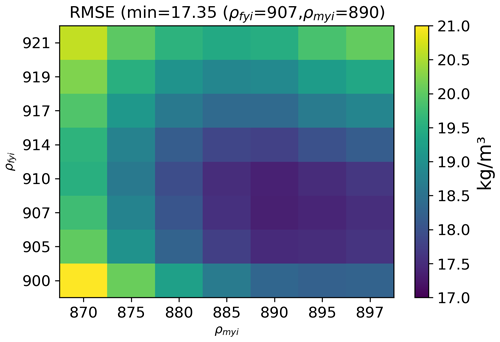
Similarly to the ρ_b in Eq. (2), ρ_b is the model-calculated sea-ice-enclosed brine density and a_b is the percentage of brine in the total ice volume. The sea ice density values for ρ_myi and ρ_fyi used as input to estimate the RMSE matrix are

$$\begin{array}{rl}& {\mathit{\rho }}_{\mathrm{myi}}=[\mathrm{870},\mathrm{875},\mathrm{880},\mathrm{885},\mathrm{890},\mathrm{895},\mathrm{897}],\\ & {\mathit{\rho }}_{\mathrm{fyi}}=[\mathrm{900},\mathrm{905},\mathrm{907},\mathrm{910},\mathrm{914},\mathrm{917},\mathrm{919},\mathrm{921}].\end{array}$$

The values for ρ_myi and ρ_fyi were chosen under the following assumptions: (a) MYI is typically less dense than FYI due to the presence of enclosed air bubbles in MYI (Timco and Frederking, 1996). (b) Taking into consideration that the observed values from the literature (Jutila et al., 2022a; Alexandrov et al., 2010; Timco and Frederking, 1996) and (c) the densities for MYI and FYI need to lie within the observed ranges, excluding extreme outliers, the resulting value will reflect a bulk value for an area of 10 km².

The 2019 observations from Jutila et al. (2022a) were used for this calculation because they include similar FYI and MYI values from the same source. The observations were interpolated to the model grid using the nearest-neighbor method, and all values on the same day and in the same grid cell were averaged. All observation values with an associated error larger than 30 kg m⁻³ were excluded from the analysis. The considered observations have an average error of 22.62 kg m⁻³.

The RMSE matrix between the observations and model values, using all combinations of ρ_myi and ρ_fyi, are visualized in Fig. A1. The lowest RMSEs were found for ρ_myi=890 kg m⁻³ and ρ_fyi=907 kg m⁻³, indicated by the darkest blue area in Fig. A1. We use these densities for MYI and FYI as input for ρ_myi and ρ_fyi in the C6N4_J21 sea ice density in Eq. (3).

Figure A1 Error matrix of the calculated sea ice density RMSE following Eq. (A1) for all the tested ρ_myi and ρ_fyi values.