A fast and simplified subglacial hydrological model for the Antarctic Ice Sheet and outlet glaciers

We present a novel and computationally efficient subglacial hydrological model that represents in a simplified way both hard- and soft-bed rheologies, as well as an automatic switch between efficient and inefficient subglacial discharge, designed for the Antarctic Ice Sheet. The subglacial model is dynamically linked to a regularized Coulomb friction law, allowing for a coupled evolution of the ice sheet on decadal to centennial timescales. It does not explicitly simulate the details of water conduits at the local scale and assumes that subglacial hydrology is in quasi-static equilibrium with the ice sheet, which makes the computations very fast. The hydrological model is tested on an idealized marine ice sheet and subsequently applied to the drainage basin of Thwaites Glacier, West Antarctica, that is composed of a heterogeneous (hard/soft) bed. We find that accounting for subglacial hydrology in the sliding law accelerates the grounding-line retreat of Thwaites Glacier under present-day climatic conditions. Highest retreat rates are obtained for hard-bed configurations and/or inefficient drainage systems. We show that the sensitivity is particularly driven by large gradients in effective pressure, more so than the value of effective pressure itself, in the vicinity of the grounding line. Therefore, we advocate for a better understanding of the subglacial system with respect to both the spatial and temporal variability in effective pressure and the rheological conditions/properties of the bed.

1 Introduction

Due to the ubiquitous and permanent ice cover, subglacial environments in Antarctica are hard to observe. The lack of direct observations results in major uncertainties in ice dynamical behavior, especially since the ice–bed interface is one of the main boundary layers that influence the overall dynamics of the ice sheet. In ice sheet models, basal processes are generally translated in a basal sliding law that, for the sake of simplicity, is largely parameterized. However, recent studies have shown that the level of plasticity of basal sliding, which mainly depends on the bed rheology, is a highly controlling factor in terms of mass change in the Antarctic Ice Sheet (Brondex et al., 2019; Bulthuis et al., 2019; Sun et al., 2020; Kazmierczak et al., 2022). The rheology of the bed broadly covers two categories, i.e., (i) hard beds, composed of bedrock and whose rigidity is greater than the ice and also considered non-deformable, and (ii) soft beds, or a subglacial till cover, whose rigidity is lower than the ice and which can easily be deformed (Muto et al., 2019). The rheology is further influenced by the presence of subglacial water, which is present underneath more than 50 % of the ice sheet due to the thick ice cover (Robin et al., 1968; Smith et al., 2009; Pattyn, 2010). The spatial organization of the subglacial drainage system remains poorly known, although recent attempts led to improvements regarding the modeling of subglacial water flow (Livingstone et al., 2013; Willis et al., 2016; Dow et al., 2022; Dow, 2022a; Hager et al., 2022).

The nature of drainage systems and their tendency to organize into channels depend on subglacial water flow, as well as bed rheology. The morphology of subglacial water drainage systems influences basal sliding by modifying the basal boundary conditions (Hewitt, 2011). Furthermore, within drainage systems, water flow and water pressure also vary greatly. Physically, the presence of subglacial water directly influences basal sliding by lubricating the bedrock or by weakening the till strength. Budd et al. (1979) proposed linking subglacial water to basal sliding through the effective pressure (which is the ice overburden pressure; i.e., the downward pressure due to the weight of overlying ice minus the subglacial water pressure). The link between basal sliding and subglacial hydrology through the effective pressure is used in most glacier and ice sheet studies (Pattyn, 1996; Hoffman and Price, 2014; Beyer et al., 2018; Gagliardini and Werder, 2018). Other approaches are the use of subglacial water thickness (Weertman and Birchfield, 1982; Budd and Jenssen, 1987; Alley et al., 1989; Johnson and Fastook, 2002) or subglacial water flux (Pattyn et al., 2005; Goeller et al., 2013) as a control on basal sliding. In this study, we consider basal sliding a function of effective pressure at the base of the ice sheet.

Generally, bed areas characterized by a low effective pressure correspond to regions of faster ice flow (Iken and Bindschadler, 1986; Iverson et al., 1999) and consequently may become more sensitive (react much faster and/or exhibit more ice change) to climate forcing (Kazmierczak et al., 2022). However, the effective pressure at the base of the ice sheet is difficult to determine as it depends on bed rheology, the presence and distribution of subglacial water, the distribution of subglacial till and its thickness, etc. Furthermore, subglacial processes occur on timescales that can be as small as a few hours (e.g., Clarke, 2005). Such timescales are several orders of magnitude smaller than the typical response times of glaciers and ice sheets, which are at least of the order of years. This discrepancy hampers numerical coupling between subglacial hydrology and the ice dynamical response. Another limiting factor is the spatial resolution on which these processes occur, hence the computational demand it entails. For instance, state-of-the-art hydrological models such as GlaDS (Werder et al., 2013) are – due to their high spatial and temporal resolution – extremely computationally demanding, and their applications to evolving ice sheets are often limited to the initialization of the ice sheet system (e.g., McArthur et al., 2023; Pelle et al., 2023). Although there have been recent attempts to reduce their computational cost using data-driven methods (Verjans and Robel, 2024), physics-based approaches have not yet been widely explored to achieve this goal.

In this paper, we propose a simplified model of the complex subglacial system that allows us to dynamically link subglacial hydrology to basal sliding for various bed types (hard and soft). The model considers different spatially and temporally varying subglacial water drainage systems. Their morphologies depend both on the subglacial water flux (distributed or channelized) and the rheology of the bed. The approach allows us to evaluate the impact of the subglacial hydrological system and its evolution on the ice sheet response in a hard- and a soft-bed environment in large-scale models and with reasonable computational times. By large-scale models, we mean models that have a spatial grid size that is orders of magnitude larger than that of the hydrological system. The model also allows us to deal with mixed beds composed of zones of different rigidity.

In Sect. 2, we describe the hydrological model and its implementation. We first evaluate our model for an idealized marine ice sheet in Sect. 3 to evaluate the implementation and robustness of the method. Subsequently, we apply our methodology to Thwaites Glacier, West Antarctica (Sect. 4), generally characterized by a heterogeneous bed composed of soft- and hard-bed zones (Joughin et al., 2009; Schroeder et al., 2014; Muto et al., 2019). We discuss the impact of the dynamic subglacial hydrology linked to basal sliding, as well as the limitations of the model, in Sect. 5. Finally, we conclude on the relevance of our findings in Sect. 6.

2 Model description

2.1 Ice flow model

We employ the Kori-ULB ice flow model (previously called f.ETISh; Pattyn, 2017; Seroussi et al., 2019, 2020; Sun et al., 2020; Coulon et al., 2024), which is a vertically integrated and thermomechanically coupled hybrid ice sheet/ice shelf model. It combines the shallow-ice approximation for ice deformation with the shallow-shelf approximation for basal sliding in a way that is similar to Winkelmann et al. (2011). To account for sliding on both a hard and soft bed (Cuffey and Paterson, 2010; Beaud et al., 2022), we employ a regularized Coulomb friction law (Joughin et al., 2019; Zoet and Iverson, 2020). Such a law allows for a smooth transition between a power law behavior at low velocity and a plastic Coulomb behavior at high velocity and takes the following form:

$$\begin{array}{}\text{(1)}& {\mathit{\tau }}_{\mathrm{b}}=CN{\left({\displaystyle \frac{\Vert {\mathit{v}}_{\mathrm{b}}\Vert }{\Vert {\mathit{v}}_{\mathrm{b}}\Vert +v_{\mathrm{0}}}}\right)}^{\frac{\mathrm{1}}{m}}{\displaystyle \frac{{\mathit{v}}_{\mathrm{b}}}{\Vert {\mathit{v}}_{\mathrm{b}}\Vert }},\end{array}$$

where τ_b is the basal shear or friction stress, N is the effective pressure, C is a friction coefficient limiting the shear stress to a maximum plastic value C N, and v_b is the basal sliding velocity. The velocity threshold v₀ is a parameter that controls the onset of plasticity in the friction law. Values of m=3 and v₀=300 m a⁻¹ are taken as in Joughin et al. (2019). A complete list of symbols, and their corresponding values and units, can be found in Appendix A.

2.2 Hydrological model

Subglacial water in Antarctica essentially stems from basal melting of areas of the ice sheet that are at the pressure melting point (Pattyn et al., 2005; Pattyn, 2010; Beyer et al., 2018; Dow et al., 2022), due to dissipative phenomena at the ice–bedrock interface. It is absent when the basal ice is at a temperature below the pressure melting point (Pattyn, 2010; Livingstone et al., 2013). Limited surface water infiltration towards the bed has been observed in Antarctica, contrary to the Greenland ice sheet (Bell et al., 2018). The presence of subglacial water will lead to a reduction in the contact between the ice and the subglacial substrate; i.e., it will decrease the value of the effective pressure $N=p_{\mathrm{o}}-p_{\mathrm{w}}$, with p_o as the ice overburden pressure and p_w as the subglacial water pressure. It is generally assumed that the ice overburden pressure is cryostatic, so that p_o=ρ_igh, where ρ_i is the ice density, g is the gravitational acceleration, and h is the ice thickness. For a given ice sheet geometry, the effective pressure is therefore fully characterized by the subglacial water pressure.

Alternatively, one can consider a description based on potentials. Introducing the hydraulic potential $\mathit{\varphi }={\mathit{\rho }}_{\mathrm{w}}gb+p_{\mathrm{w}}$ and the geometric potential ${\mathit{\varphi }}_{\mathrm{0}}={\mathit{\rho }}_{\mathrm{i}}gh+{\mathit{\rho }}_{\mathrm{w}}gb$, with ρ_w being the density of freshwater and b the bedrock elevation with respect to the local sea level height, the effective pressure is then the difference between both (i.e., $N={\mathit{\varphi }}_{\mathrm{0}}-\mathit{\varphi }$). The rationale behind this description is that water flows from regions where the hydraulic potential is high to regions where the potential is low (Shreve, 1972).

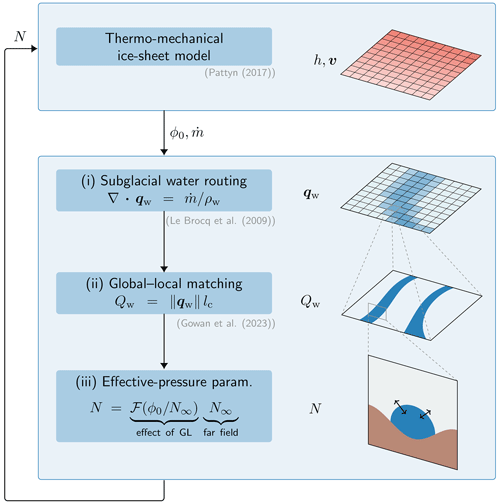
Figure 1 Flowchart of the dynamical linkage between the ice sheet and the subglacial hydrology. At each time step, the ice sheet model provides the basal melt rate $\dot{m}$ and the geometrical potential ϕ₀. Based on these, the effective pressure is computed in three steps: (i) the globally distributed subglacial water flux q_w is computed according to Le Brocq et al. (2009); (ii) a connection between both the global and local (conduit) scale is obtained by specifying the distance l_c between the conduits (Gowan et al., 2023), yielding a volumetric water flux Q_w in each conduit; and (iii) the effective pressure N is computed for each conduit via a parameterization, where $\mathcal{F}({\mathit{\varphi }}_{\mathrm{0}}/N_{\mathrm{\infty }})=\text{erf}\left[\right(\sqrt{\mathit{\pi }}/\mathrm{2}){\mathit{\varphi }}_{\mathrm{0}}/N_{\mathrm{\infty }}]$ serves as a correction factor for the impact of the grounding line (GL), and where N_∞ is the effective pressure far upstream of the grounding line. This effective pressure is then used by the large-scale ice sheet model and is the same for all conduits that belong to the same grid cell.

In this paper, we attempt to model together efficient and inefficient water flow over both hard and soft beds. Generally, efficient systems transport large water fluxes and are characterized by localized channelized flow, while inefficient systems take the form of distributed water flow. We define two spatial scales: a global scale, which is the same as the one used for the ice sheet model and that is typically of the order of kilometers, and a local scale, associated with a water conduit, which is much smaller than the global one (observations suggest that channels are meters to at most a few hundreds meters wide that maximal width being reached close to the grounding line; Drews et al., 2017). The computation of the water flow is done at the global scale, while the computation of the effective pressure is done at the local scale. For the latter, we consider a single element of the hydrological system, which we refer generically to as “conduit”. The term conduit is used for localized drainage systems (such as cavities, channels, and canals), as opposed to diffuse drainage systems (such as continuous films and diffuse water flow within sediments). This applies to efficient flow (channel or canal) or to elements of an inefficient system (cavity or patchy film between clasts) applicable to both a hard or a soft bed. In particular, we do not use “conduit” as a synonym for “channel”, as a conduit can correspond to other types of hydrological elements. Such an approach can be seen as a sub-grid parameterization of the effective pressure; a similar procedure was described in Gowan et al. (2023). The idea of unifying both inefficient and efficient water flow has been previously explored in Arnold and Sharp (2002), in Schoof (2010), and in Sommers et al. (2018). Our approach is shown schematically in Fig. 1 and described in detail in the following subsections.

2.2.1 Simplifying assumptions

Our model is constructed from multiple approximations that simplify the physics describing subglacial hydrology. It differs from recent studies aiming to develop high-resolution models, such as GlaDS (Werder et al., 2013), SHAKTI (Sommers et al., 2018), CUAS (Beyer et al., 2018), and the subglacial hydrology components within PISM (Bueler and van Pelt, 2015) and MALI (Hoffman et al., 2018). These models typically take the form of a series of coupled partial differential equations that are computationally challenging to solve. Furthermore, these models involve a large number of parameters, with many being poorly constrained. Finally, due to their high spatial and temporal resolution they are often computationally demanding. The latter may limit their application to drainage basins or single glaciers on timescales of a few years. By contrast, our model is computationally cheap, with the computational time associated with the subglacial hydrology calculation representing only a small fraction of the computational time associated with the ice sheet model. This allows us to study the impact of subglacial hydrology on ice dynamics on a large scale and at a limited computational cost, while at the same time keeping the essential features of complex subglacial hydrology models.

The key simplifying assumptions are given by the following:

1. There is limited temporal melt variability so that the hydrological system is in a quasi-static equilibrium with respect to the ice sheet geometry. Therefore, changes in ice geometry will be the main driver for changes in subglacial water variability (both spatial and temporal).

2. A few kilometers upstream of the grounding line, the hydraulic gradient is approximated by the geometrical gradient.

3. The drainage density, that is, the number of conduits per grid cell, is uniform.

4. The effective pressure distribution is not calculated at the sub-grid (local) level.

The first assumption is based on several studies of subglacial hydrology in Antarctica (Le Brocq et al., 2009; Pattyn, 2010; Kazmierczak et al., 2022), among others, that demonstrate that – contrary to the Greenland ice sheet – there is limited surface meltwater infiltration. Hence, changes in hydrology are primarily due to changes in ice geometry. Since the timescales associated with water flow are much smaller than those associated with ice flow, subglacial hydrology automatically adapts to any change in ice geometry and reaches the associated equilibrium. The second assumption is motivated by a scaling analysis through an estimation of the dimensionless ratio $\mathit{\eta }:=\left[\mathrm{\nabla }N\right]/\left[\mathrm{\nabla }{\mathit{\varphi }}_{\mathrm{0}}\right]$, where [∇N] is the scale of the spatial gradients for the effective pressure, and [∇ϕ₀] is the characteristic scale for the geometric potential gradient. For the former, we take $\left[\mathrm{\nabla }N\right]=\left[N\right]/\left[x\right]$, with [N]=1 MPa and [x]=10³ km. For the latter, we take $\left[\mathrm{\nabla }{\mathit{\varphi }}_{\mathrm{0}}\right]=\mathrm{5}\times {\mathrm{10}}^{-\mathrm{2}}$ MPa km⁻¹, which is a plausible value for ice sheets (Hewitt, 2011). This results in $\mathit{\eta }=\mathrm{2}\times {\mathrm{10}}^{-\mathrm{2}}\ll \mathrm{1}$, suggesting that $\Vert \mathrm{\nabla }N\Vert \ll \Vert \mathrm{\nabla }{\mathit{\varphi }}_{\mathrm{0}}\Vert$ and ∇ϕ≈∇ϕ₀. We further note that profiles obtained with a high-resolution subglacial hydrology model suggest that ∇ϕ and ∇ϕ₀ have a correlation of at least ∼ 80 % for a region that is several kilometers upstream of the grounding line (see Sect. S1 in the Supplement). Finally, the third and fourth assumptions follow from our modeling approach, where we do not describe the effective pressure at the sub-grid scale, and where we assume the same number of conduits in each grid cell, similar to Gowan et al. (2023). However, the effective pressure within a channel may well differ from its value away from the channel, which is something that is not taken into account. Consequently, these last assumptions are the most likely to be debatable.

2.2.2 Subglacial water routing

Let us denote by Ω the grounded ice sheet domain where subglacial water is routed. This domain evolves over time according to both internal conditions (e.g., changes in ice velocity) and external conditions (e.g., changes in sub-shelf melt). Its boundary is partitioned into non-overlapping subsets Γ_d and Γ_gl, representing the divides of the considered basin and the grounding line, respectively. The subglacial water flux, q_w (m² s⁻¹), is determined from a mass balance equation that takes the form of a steady-state continuity equation:

$$\begin{array}{}\text{(2a)}& {\displaystyle }\mathrm{\nabla }\cdot {\mathit{q}}_{\mathrm{w}}={\displaystyle \frac{\dot{m}}{{\mathit{\rho }}_{\mathrm{w}}}},\text{in }\mathrm{\Omega },\text{(2b)}& {\displaystyle }{\mathit{q}}_{\mathrm{w}}\cdot \mathit{n}=\mathrm{0},\text{on }{\mathrm{\Gamma }}_{\mathrm{d}},\end{array}$$

in which ∇ is the horizontal spatial gradient, n is the outward normal to the boundary Γ_d, and $\dot{m}$ is the melt rate ($\mathrm{kg}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$). The latter is computed from the energy balance within the ice sheet and includes effects of geothermal heat flux, frictional heating due to the motion of both ice and subglacial water, and thermal conduction, i.e.,

$$\begin{array}{}\text{(3)}& \dot{m}={\displaystyle \frac{G+{\mathit{\tau }}_{\mathrm{b}}\cdot {\mathit{v}}_{\mathrm{b}}-q_{\mathrm{T}}}{{\mathcal{L}}_{\mathrm{w}}}}+{\dot{m}}_{\mathrm{w}},\end{array}$$

where G is the geothermal heat flux, q_T is the thermal conduction flux, ℒ_w is the latent heat for ice, and ${\dot{m}}_{\mathrm{w}}=\mathrm{|}{\mathit{q}}_{\mathrm{w}}\cdot \mathrm{\nabla }\mathit{\varphi }\mathrm{|}/{\mathcal{L}}_{\mathrm{w}}$ is the water melt rate due to the dissipated energy from the subglacial water conduits. However, we do not include this last term in the computation of the subglacial water in our simulations as it was found to be negligible compared to the other terms. Note that by writing the system of Eq. (2), we have assumed that the subglacial water system is in a steady state with respect to a given ice sheet geometry. As previously mentioned, we justify this assumption by the observation that the timescales associated with subglacial water flow are much smaller than the ones associated with ice flow. By construction, this inhibits oscillations in the coupled system formed by the ice sheet and the subglacial hydrology, which are known to exist for ice streams on timescales of thousands of years (Robel et al., 2013) and well beyond the timescales considered here.

Equation (2) is solved at the global scale, using the water routing of Le Brocq et al. (2009) to compute the water flux based on the geometric potential gradient ∇ϕ₀. As the subglacial water flux q_w is in fact proportional to ∇ϕ instead of ∇ϕ₀, we should use the potential gradient ∇ϕ itself. Nonetheless, in view of the assumption that ∇ϕ≈∇ϕ₀ over most of the domain, we choose not to do so as this allows us to decouple the water routing solver from the effective pressure calculation.

2.2.3 Subglacial effective pressure

The distributed water flux q_w needs to be converted to the local volumetric water flux Q_w (m³ s⁻¹) within the water conduits. Since the distance between the conduits is given by l_c, it follows that there are $\mathrm{\Delta }x/l_{\mathrm{c}}$ conduits within each square grid cell of size Δx×Δx of the ice sheet mesh. Hence, the local water flux is given by (Gowan et al., 2023)

$$\begin{array}{}\text{(4)}& Q_{\mathrm{w}}={\displaystyle \frac{\Vert {\mathit{q}}_{\mathrm{w}}\Vert \mathrm{\Delta }x}{\mathrm{\Delta }x/l_{\mathrm{c}}}}=\Vert {\mathit{q}}_{\mathrm{w}}\Vert l_{\mathrm{c}}.\end{array}$$

We take l_c = 10 km, which is similar to the value considered in Gowan et al. (2023) based on observations of distances between eskers formed under the Laurentide Ice Sheet (Storrar et al., 2014). However, we acknowledge that this distance is likely to be a function of the drainage system but leave this to be investigated in future work.

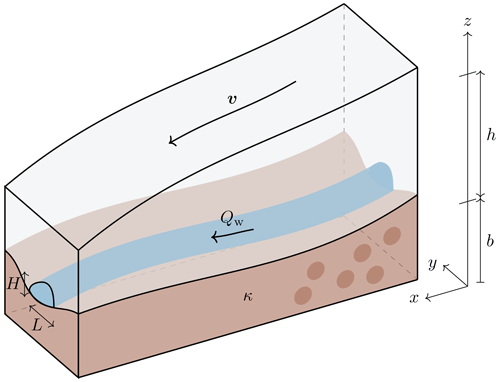
Figure 2 Schematic representation of a conduit (of a channel here) in the subglacial hydrological system, characterized by a cross-sectional width L and thickness H and by a water flux Q_w. The ice sheet has a thickness h, is moving at a velocity v, and overlays the bedrock whose upper surface is located at z=b. The bedrock type is parameterized by κ, with κ=1 corresponding to a soft bed, κ=0 corresponding to a hard bed, and $\mathrm{0}<\mathit{\kappa }<\mathrm{1}$ corresponding to a mixed bed.

While the water mass balance is defined at the global scale, conduits must evolve at the local scale, which requires water flow to be resolved at this scale, irrespective of whether it is associated with a distributed or a localized flow pattern, similar to what is done in Arnold and Sharp (2002), Schoof (2010), and Gowan et al. (2023). Let us denote by S the cross-section area in a conduit, with characteristic width and thickness L and H (Fig. 2), so that S=HL. The equations governing the geometry of the conduits and the flow of water within them in a quasi-static regime are given by the following:

$$\begin{array}{}\text{(5a)}& {\displaystyle }{Q}_{\mathrm{w}}=K{S}^{\mathit{\alpha }}\Vert \mathrm{\nabla }\mathit{\varphi }{\Vert }^{\mathit{\beta }-\mathrm{1}},\text{in }\mathrm{\Omega },\text{(5b)}& {\displaystyle }\Vert {\mathit{v}}_{\mathrm{b}}\Vert h_{\mathrm{b}}+{\displaystyle \frac{Q_{\mathrm{w}}\Vert \mathrm{\nabla }\mathit{\varphi }\Vert }{{\mathit{\rho }}_{\mathrm{i}}{\mathcal{L}}_{\mathrm{w}}}}=\mathrm{2}{n}^{-n}A{L}^{\mathrm{2}}\mathrm{|}N{\mathrm{|}}^{n-\mathrm{1}}N,\text{in }\mathrm{\Omega },\text{(5c)}& {\displaystyle }N=\mathrm{0},\text{on }{\mathrm{\Gamma }}_{\text{gl}},\end{array}$$

where h_b is the characteristic height of bed obstacles, and A and n are the viscosity parameters in Glen's flow law (Glen, 1955; Paterson, 1994), respectively. The first equation is a Darcy–Weisbach constitutive equation for the water flow, with K as the conductivity coefficient and α and β as exponents. Following Schoof (2010), we assume a turbulent flow, with $\mathit{\alpha }=\mathrm{5}/\mathrm{4}$, $\mathit{\beta }=\mathrm{3}/\mathrm{2}$, and $K=(\mathrm{2}/\mathit{\pi }{)}^{\mathrm{1}/\mathrm{4}}\sqrt{(\mathit{\pi }+\mathrm{2})/\left({\mathit{\rho }}_{\mathrm{w}}f\right)}$, where f is a friction coefficient (e.g., Clarke, 1996). The choice of a turbulent flow is justified for large water fluxes, which is the case for converging subglacial channels near the grounding line. Other choices have been considered for subglacial hydrology in the literature; we refer to Hewitt (2011) and Werder et al. (2013) for laminar parameterizations and to Hill et al. (2023) for a discussion of the transition between laminar and turbulent flow and their range of validity. The second equation describes the equilibrium between opening and closure rates of the conduits, assuming that the hydrological system is at equilibrium. In general, opening and closing of subglacial water systems are due to various mechanisms, depending on the drainage system and bed type involved. These mechanisms include, amongst others, melt of the subglacial conduit walls, sliding over bed protrusions, erosion of sediments, regelation, creep of ice, and creep of sediments (Hewitt, 2011; Bueler and van Pelt, 2015). Here, we consider opening rates associated with sliding over bed obstacles, melting of the conduit walls, and a closure rate due to ice creep (Nye, 1953). The bed obstacles correspond to bed protrusions if the bed is hard and to clasts if the bed is soft, and our model treats these cases in the same way. Note that the first type of opening rate is associated with an inefficient drainage system, while the second one is associated with an efficient one. Finally, the third equation comes from the equality between the subglacial water pressure and the seawater pressure at the grounding line (Drews et al., 2017), which holds because we are considering marine-terminated ice sheets.

The above model (Eq. 5) is similar to the one that was used by Schoof (2010) to describe both linked-cavity systems (i.e., inefficient systems) and channels (i.e., efficient systems). Linked cavities have first been described by Kamb (1987), following earlier theoretical developments related to sliding with cavitation (Lliboutry, 1968, 1979; Kamb, 1970; Iken, 1981; Fowler, 1986, 1987). For larger water fluxes, the flow in cavities localizes into channels, and the system becomes efficient, forming so-called R channels (Röthlisberger, 1972), defined as semi-circular tunnels formed within the ice of the glacier. Such conduits allow water to flow rapidly and more efficiently (Kamb et al., 1985; Iken et al., 1993; Hubbard et al., 1995; Lappegard et al., 2006).

Our model is also analogous to those that describe ice flow over soft beds. In a soft-bed system, water can infiltrate the till and weaken its strength, hence increasing basal motion. In Antarctica, till properties indicate a low porosity and hydraulic conductivity, obstructing the water circulation in the till itself and leading to water saturation (Tulaczyk et al., 2000a, b). Indeed, as the drainage rate from the till towards a subglacial aquifer is much smaller than the basal melt rate, subglacial till is supposed to be water-saturated (Bueler and van Pelt, 2015; Kazmierczak et al., 2022). Water that cannot infiltrate the till will take the form of a water film that flows around clasts higher than the water thickness (Creyts and Schoof, 2009; Kyrke-Smith et al., 2014). For large subglacial water fluxes, the film becomes unstable and conduits form a channelized network (Walder, 1982). For ice sheets, efficient conduits on a soft bed take the form of canals, which are incised in the till. They are typically much wider and shallower compared to hard-bed channels (Walder and Fowler, 1994). These different types of drainage systems, following (Eq. 5), are schematized in Fig. 3. Despite the qualitative differences between soft- and hard-bed hydrology, the governing equations are quite similar and mainly differ in their geometry, i.e., how width L and thickness H of the conduits are related to their cross-sectional area S.

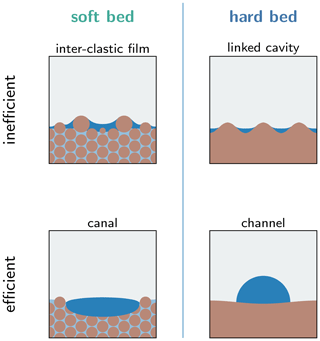
Figure 3 Schematic representation of the different types of drainage systems considered in this study, namely efficient and inefficient drainage systems on soft and hard beds.

To compute the effective pressure within each conduit, we combine the Darcy–Weisbach equation (Eq. 5a) with the opening–closing equation (Eq. 5b). This allows us to eliminate S and obtain an equation for N only. However, the resulting equation takes the form of a non-linear differential equation, which is not easy to solve. The complexity stems from the fact that ∇ϕ depends on N through $\mathrm{\nabla }\mathit{\varphi }=\mathrm{\nabla }{\mathit{\varphi }}_{\mathrm{0}}-\mathrm{\nabla }N$. However, given our second simplifying assumption, we have ∇ϕ≈∇ϕ₀ outside the vicinity of the grounding line. We then obtain algebraic equations for the effective pressure and the cross-sectional area far from the grounding line, N_∞ and S_∞, as follows:

$$\begin{array}{}\text{(6a)}& {\displaystyle }{N}_{\mathrm{\infty }}& {\displaystyle }={\left[{\left({\displaystyle \frac{H\left(S_{\mathrm{\infty }}\right)}{S_{\mathrm{\infty }}}}\right)}^{\mathrm{2}}{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{i}}{\mathcal{L}}_{\mathrm{w}}\Vert {\mathit{v}}_{\mathrm{b}}\Vert h_{\mathrm{b}}+Q_{\mathrm{w}}\Vert \mathrm{\nabla }{\mathit{\varphi }}_{\mathrm{0}}\Vert }{\mathrm{2}{n}^{-n}{\mathit{\rho }}_{\mathrm{i}}{\mathcal{L}}_{\mathrm{w}}A{S}_{\mathrm{\infty }}}}\right]}^{\frac{\mathrm{1}}{n}},\text{(6b)}& {\displaystyle }{S}_{\mathrm{\infty }}& {\displaystyle }=K^{-\frac{\mathrm{1}}{\mathit{\alpha }}}\Vert \mathrm{\nabla }{\mathit{\varphi }}_{\mathrm{0}}{\Vert }^{\frac{\mathrm{1}-\mathit{\beta }}{\mathit{\alpha }}}{Q}_{\mathrm{w}}^{\frac{\mathrm{1}}{\mathit{\alpha }}}.\end{array}$$

Here, we have written $H\left(S\right)/S$ instead of $\mathrm{1}/L$ to emphasize that N_∞ depends on the way that H depends on S, which is a function of the bed type.

The assumption that ∇ϕ is approximately equal to ∇ϕ₀ breaks down close to the grounding line because N must reach a zero value there for water to be connected to the ocean (see Eq. 5c). Hence, the effective pressure decreases significantly in that area, leading to strong gradients in N. A boundary layer analysis actually reveals that N≈ϕ₀ close to the grounding line, suggesting that the effective pressure can be approximated over the whole domain by

$$\begin{array}{}\text{(7)}& N=\text{erf}\left[{\displaystyle \frac{\sqrt{\mathit{\pi }}}{\mathrm{2}}}{\displaystyle \frac{{\mathit{\varphi }}_{\mathrm{0}}}{N_{\mathrm{\infty }}}}\right]N_{\mathrm{\infty }},\end{array}$$

where erf(x) is the Gauss error function (see Appendix B for more details). This approximation has been verified by comparing it with numerical solutions of the differential equation for the effective pressure. This equation reveals that the assumption that N≈N_∞ becomes valid when ϕ₀ becomes of the order of N_∞, which for Thwaites Glacier is typically a few kilometers from the grounding line.

2.2.4 Bed rheology

One element that is lacking from the equations describing conduits is the definition of their geometry, e.g., through a relation between their thicknesses and their cross-sectional areas, H=H(S). For “hard-bed” systems, we follow Schoof (2010) by assuming that $L=H=\sqrt{S}$; i.e., we consider conduits that are equally wide and thick, even though we acknowledge that the theory of linked cavities by Kamb (1987) was initially developed in the context of shallow cavities. For “soft-bed” systems, the geometry of conduits is more challenging. For small subglacial water fluxes, water takes the form of a patchy film. When the film gets thicker due to an increased water flux, its height will exceed the thickness of the smallest clasts, so that the film will be flowing in between larger clasts that are separated by a larger distance (Kyrke-Smith and Fowler, 2014; Kyrke-Smith et al., 2014). This means that L increases with H. The relation between both depends on the spatial distribution of the clasts, as well as their thickness (Creyts and Schoof, 2009). Here, we assume $L\sim \sqrt{S}$, which is not implausible, as this corresponds to the parameterization used for cavities on a hard bed. However, a soft bed is qualitatively different from a hard bed, as the till can be deformed. To take into account this difference, we introduce a factor F_till, defined as

$$\begin{array}{}\text{(8)}& L=F_{\text{till}}\sqrt{S}.\end{array}$$

This deformation factor depends on the difference between ice and till viscosity, as well as the till thickness, and increases with the ability of the till to deform, provided it is sufficiently thick. For a factor F_till>1, the effective pressure is lower compared to hard-bed systems (Beaud et al., 2022). For this reason, we here consider F_till=1.1. For larger subglacial water fluxes, water flow channelizes into canals for which we prescribe a thickness H=H₀. Here, we take H₀ = 0.1 m as prescribed in Walder and Fowler (1994) for a sand/silt sediment type located under an ice sheet. For both inefficient and efficient cases, we then set

$$\begin{array}{}\text{(9)}& H\left(S\right)=H_{\mathrm{0}}+\left(\sqrt{S}/F_{\text{till}}-H_{\mathrm{0}}\right)\exp (-Q_{\mathrm{w}}/Q_{\mathrm{c}}),\end{array}$$

with Q_c as a critical water flux value. Then $H\approx \sqrt{S}/F_{\text{till}}$ if Q_w≪Q_c, and H≈H₀ if Q_w≫Q_c. In our simulations, we take Q_c = 1 m³ s⁻¹, which corresponds to the scale of the water flux considered in Walder and Fowler (1994).

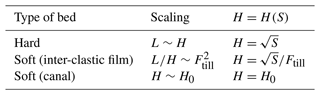
Finally, a “mixed bed” is composed of regions of various stiffness. We define the state of the bed through a spatial field κ=κ(x) that describes the proportion of the hard (κ=0) and soft (κ=1) bed. An intermediate value of $\mathrm{0}<\mathit{\kappa }<\mathrm{1}$ corresponds to a variation in the till thickness or stiffness, granting it possesses intermediate rigidity compared to those attributed to the hard and soft cases. For a mixed bed, the conduit–evolution relation is the same as the one used for the hard and soft cases, where we set $H=(\mathrm{1}-\mathit{\kappa })H_{\text{hard}}+\mathit{\kappa }{H}_{\text{soft}}$, with H_hard (respectively H_soft), which is the thickness associated with a hard (respectively soft) bed. A mixed-bed system is therefore able to cover the case of linked cavities, channels, inter-clastic films, and canals, depending on the value of κ and of the subglacial water flow intensity. A summary of the differences between these cases can be found in Table 1.

The dependence of the far-field effective pressure N_∞ with respect to the magnitude of the conduit water flux Q_w is shown in Fig. 4 for hard- and soft-bed systems. It clearly shows that the effective pressure decreases with water flux for inefficient systems. For efficient systems, hard- and soft-bed systems differ, where channels lead to an increase in the effective pressure, contrary to canals. Note that this last distinction can be explained as follows. For large flux values, the opening–closing relation (Eq. 5b) essentially becomes a balance between the opening due to melt, which is proportional to the water flux, and ice creep. Therefore, if the flux further increases, the ice creep term must also increase. For channels, the factor L² in the ice creep term of (Eq. 5b) increases with the water flux but at an insufficient rate; hence, the effective pressure factor must also increase. By contrast, canals, because of their shallower form, are such that this factor increases at a much faster rate. As a consequence, the effective pressure must decrease in that case.

Table 1 Scaling for the geometry of the conduits of the hydrology system.

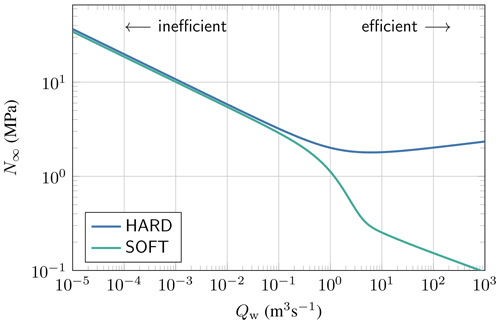
Figure 4 Relation between the value of the effective pressure N_∞ far from the grounding line and the magnitude of the conduit water flux Q_w for hard (in blue) and soft (in green) beds. The curves correspond to Eq. (6a) coupled with the geometric relations shown in Table 1. The physical parameters are the ones displayed in Appendix A, with $A=\mathrm{2.4}\times {\mathrm{10}}^{-\mathrm{24}}$ ${\mathrm{Pa}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$, $\Vert {\mathit{v}}_{\mathrm{b}}\Vert =\mathrm{0.5}\times {\mathrm{10}}^{-\mathrm{5}}$ m s⁻¹, and $\Vert \mathrm{\nabla }{\mathit{\varphi }}_{\mathrm{0}}\Vert =\mathrm{100}$ Pa m⁻¹.

Besides soft, hard, and mixed beds, we also consider entirely efficient and inefficient drainage systems to gauge the sensitivity of both separately, independent of the subglacial water flux. By default, our model is such that the subglacial system naturally transitions from one to another, depending on the subglacial water flux. This transition happens because the melting term, which is proportional to the water flux, becomes dominant over the sliding term on the left-hand side of (Eq. 5b) as the water flux increases. By removing the opening term associated with the sliding over obstacles, $\Vert {\mathit{v}}_{\mathrm{b}}\Vert h_{\mathrm{b}}$, from Eqs. (5b) and (6a), it is possible to force the model to produce an entirely efficient drainage system. In this case, we also set Q_c=∞, which guarantees that the conduit geometry is the one of an inefficient system for soft beds. Similarly, to force an entirely inefficient system, the efficient component, $Q_{\mathrm{w}}\Vert \mathrm{\nabla }\mathit{\varphi }\Vert /{\mathit{\rho }}_{\mathrm{i}}{\mathcal{L}}_{\mathrm{w}}$, can be removed from Eq. (5b), together with the condition that Q_c=0.

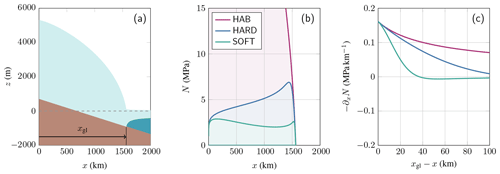
Figure 5 Initial state for the experiments on idealized conditions based on the MISMIP geometry (Pattyn et al., 2012). (a) The initial MISMIP steady-state ice sheet geometry; x_gl corresponds to the distance to the grounding line. (b) Flow band profiles of the subglacial effective pressure for HAB (in purple), HARD (in blue), and SOFT (in green) hydrological models. (c) Gradient of the subglacial effective pressure near the grounding line for HAB (in purple), HARD (in blue), and SOFT (in green) hydrological models.

3 Idealized experiments

3.1 Experimental setup

As a first test of the hydrological model, we consider a flow band geometry for a marine ice sheet taken from the benchmark projects MISMIP and MISMIP3d (Pattyn et al., 2012, 2013) and which consists of a linearly downward-sloping bed towards the ocean (Fig. 5a). On this bed topography, a marine ice sheet is developed with a spatial resolution of 500 m, following the setup described in the EXP1 of the MISMIP experiments (Pattyn et al., 2012, see Fig. 5a). The steady state obtained with these conditions is considered to be the “reference state”.

In our experiments, we use a regularized Coulomb friction law combined with hydrological models, while the reference state from the MISMIP setup has been obtained with a Weertman friction law. To guarantee that the thickness and velocity fields obtained in the reference state are still compatible with a steady state, we modify the friction coefficient at each position, following the method of Brondex et al. (2017, 2019). In practice, an iterative nudging method is used so that the basal friction matches the basal friction obtained in the reference state. Here, the subglacial hydrologies are generated with a uniform basal melt rate underneath the grounded ice sheet of $\dot{m}/{\mathit{\rho }}_{\mathrm{w}}=\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$ m a⁻¹, which corresponds to the mean basal melt rate of the Antarctic Ice Sheet (Pattyn, 2010). By construction, this method yields initial states that are steady states and in which both the geometry and the velocity field are identical for each type of hydrology, allowing a direct comparison between them. The initial ice sheet effective pressure profiles are shown in Fig. 5b.

We consider a uniform hard and soft bed and compare these to an experiment in which (i) the effective pressure is determined according to the HAB model (for “height above buoyancy”), which assumes a perfect connection with the ocean, and (ii) basal sliding being independent of subglacial pressure or bed rheology (NON). The effective pressure in the HAB model is therefore simply defined by

$$\begin{array}{}\text{(10)}& N={\mathit{\rho }}_{\mathrm{i}}gh-{\mathit{\rho }}_{\mathrm{s}}gmax(\mathrm{0},-b),\end{array}$$

where ρ_s is the density of seawater. It is the most common parameterization of N used Tsai et al. (e.g., 2015).

For all models, the effective pressure is high in the interior and decreases towards the grounding line, where it becomes zero by definition. For the HAB model, the horizontal gradient of the effective pressure is the highest, mainly governed by the geometry of the bedrock and surface slopes. For HARD and SOFT, representing the hard-bed and soft-bed systems, respectively, the effective pressure varies due to variations in both the subglacial water flux and the cross-sectional size of the conduits, according to Eq. (6a) (Fig. 5b).

Besides, we also compare the impact of the drainage efficiency by comparing the cases where only efficient (eff) or inefficient (ineff) systems are allowed to develop. Note that, by default, the switch between both systems (efficient/inefficient) is determined based on the subglacial water flux magnitude.

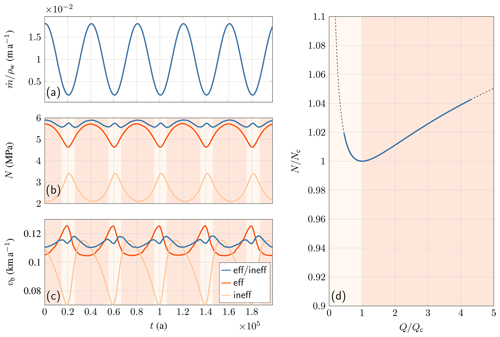
Figure 6 (a) Forcing of the MISMIP geometry with a sinusoidal variation in subglacial meltwater for a hard-bed system. (b) Response to the forcing in effective pressure and (c) basal sliding velocity (blue – efficient/inefficient; red – entirely efficient; beige – entirely inefficient). (d) Relationship between subglacial water flux and effective pressure for both the efficient/inefficient drainage system. The dashed line corresponds to Eq. (6a), and N_c and Q_c are critical values for a hard-bed system, as defined in Schoof (2010). The light pink (respectively dark pink) areas correspond to regions in which the efficient/inefficient system is an inefficient (respectively efficient) regime.

3.2 Results: the efficient to inefficient switch

A first experiment aims at understanding the switch between efficient and inefficient drainage systems. We force the MISMIP flow band setup with a sinusoidal variation in subglacial meltwater that is then routed across a hard bed (Fig. 6a). The response in effective pressure and sliding velocity does not simply follow the same sinusoidal pattern, but the ice velocity accelerates and decelerates as a function of whether the system evolves into an efficient or inefficient drainage system (Fig. 6b and c). Sudden speedups correspond to sudden drops in the effective pressure and occur when either the amount of meltwater diminishes or increases. Note that these sudden changes do not appear if the model is entirely efficient or entirely inefficient. Similar characteristics of the subglacial hard-bed system have been described by Schoof (2010) and are shown in Fig. 6d. Although our model is a relatively crude parameterization of the subglacial system, the intrinsic instability related to the switch between efficient and inefficient drainage systems is captured.

3.3 Results: perturbation experiment

For each hydrological model, the initial steady state is perturbed by instantaneously reducing the net mass accumulation rate to 0.2 m a⁻¹. The ice sheet is then allowed to evolve for a period of 20 000 years with a time step of 5 years, eventually reaching a (near-) steady state. The hydrological model is updated at each time step (see also Appendix C). The first series of experiments consists of comparing the response of the different models (NON, HAB, HARD, and SOFT), as well as the fully efficient (eff) and fully inefficient (ineff) cases for HARD and SOFT models, to this perturbation. The reduction in surface accumulation generally leads to a slowdown of the ice velocity, as well as a smaller ice sheet. This reduction also results in a slight grounding-line retreat (NON in Fig. 7). However, linking basal sliding to any of the hydrological models that are a function of effective pressure at the base of the ice sheet, leads to a significant grounding-line retreat and overall grounded mass loss (Fig. 7). Of all subglacial models, HAB is the most sensitive to the forcing, i.e., leading to the highest mass loss after forcing. Several factors may be responsible for this, as has been shown in Fig. 5c; it is not only that the effective pressure is low near or at the grounding line but also that the effective pressure gradient upstream of the grounding line is the highest for the HAB model. The fact that the sensitivity of grounding-line retreat increases with increasing gradient in effective pressure near the grounding line is shown in Fig. 5c. While this gradient is equally high near the grounding line for all model configurations, it drops quite quickly with distance from the grounding line for soft-bed systems, resulting in a minimal grounding-line retreat. Since by definition the NON model, representing the solution independent of effective pressure, has a zero gradient in effective pressure, it therefore leads to the least grounding-line retreat due to forcing compared to the other hydrological models, as shown hereunder.

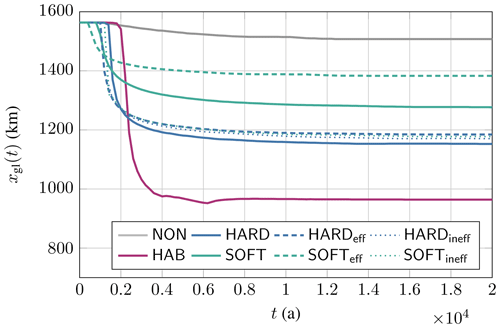
Figure 7 Grounding-line evolution after a sudden reduction in surface accumulation rate for the MISMIP setup for NON (in grey), HAB (in purple), HARD (in blue), SOFT (in green), HARD efficient (dashed blue line), HARD inefficient (dotted blue line), SOFT efficient (dashed green line), and SOFT inefficient (dotted green line) hydrological models.

4 Application to Thwaites Glacier

4.1 Experimental setup

For Thwaites Glacier, necessary input data are the present-day ice sheet surface and bed geometry from BedMachine v2 (Morlighem et al., 2019), surface mass balance and temperature from RACMO2.3p2 (van Wessem et al., 2018), and a prescribed field for the geothermal heat flux (Shapiro and Ritzwoller, 2004). All datasets were resampled at a spatial resolution of 2 km. The simulations are performed at that spatial resolution and with a time step of 0.05 years.

Similar to the idealized experiments, a reference state is obtained with a Weertman friction law. To obtain this state, the basal friction field is iteratively adapted to obtain a steady-state ice sheet with grounded ice thickness as close as possible to the observed thickness using a nudging method (Pollard and DeConto, 2012; Pattyn, 2017; Coulon et al., 2024). For the floating ice shelves, the sub-shelf melt/accretion is adjusted to keep the ice thickness comparable to observed (Coulon et al., 2024). In a second step, the initial friction field corresponding to a given hydrological model is obtained with the same method as explained for the idealized experiments. Initial bedrock and surface topographies, as well as the ice velocity field, can be found in Sect. S2, the friction coefficient fields after initialization in Sect. S3, and the effective pressure values for HAB, HARD, and SOFT in Sect. S4. To evaluate the model drift of this initialization, the model is run forward in time according to the different hydrological models, leading to a mass change after 100 years corresponding to 1–2 mm sea level rise. Thanks to this small model drift, the control run does not have to be subtracted from the forcing runs, as was the case in Kazmierczak et al. (2022). It also demonstrates the improvements that have been made in terms of model initialization (Coulon et al., 2024).

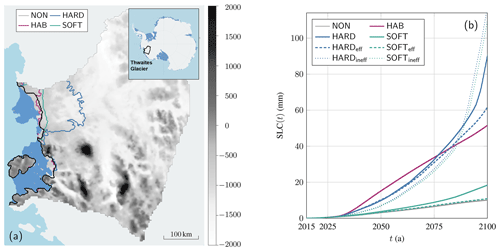
Figure 8 Effect of the subglacial hydrological models in the Thwaites Glacier setup. Present-day climate conditions (atmospheric and oceanic) are applied from 2015 to 2100. (a) Grounding-line positions of Thwaites Glacier (bedrock elevation (m) in the background) in 2100 under constant present-day climate conditions (atmospheric and oceanic) for the NON (black), HAB (purple), HARD (blue), and SOFT (green) models. The inset in the upper-right corner shows the position of Thwaites Glacier within Antarctica. (b) Sea level contribution from Thwaites Glacier from 2015 to 2100 under constant present-day climate conditions (atmospheric and oceanic) for the NON (grey), HAB (purple), HARD (blue), SOFT (green), HARD efficient (dashed blue line), HARD inefficient (dotted blue line), SOFT efficient (dashed green line), and SOFT inefficient (dotted green line).

All simulations start from this initial steady state, corresponding to the 2015 conditions. We then run the model forward until 2100, under present-day climate conditions (atmospheric and oceanic). Sub-shelf melt rates are calculated by the PICO model (Reese et al., 2018) with an effective heat exchange velocity value of $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{5}}$ m s⁻¹, which gives a realistic melt pattern for present-day ocean temperatures and salinity. Since these dynamic melt rates replace the optimized basal melting/accretion field, the ice sheet system is no longer in steady state, and the grounding line reacts to the applied oceanic forcing by a small retreat over the course of this century (reference experiment NON in Fig. 8a). Note that the mass loss for the NON experiment results in sea level rise on the order of 10 mm by 2100, which is an order of magnitude larger than the model drift (∼ 1 mm).

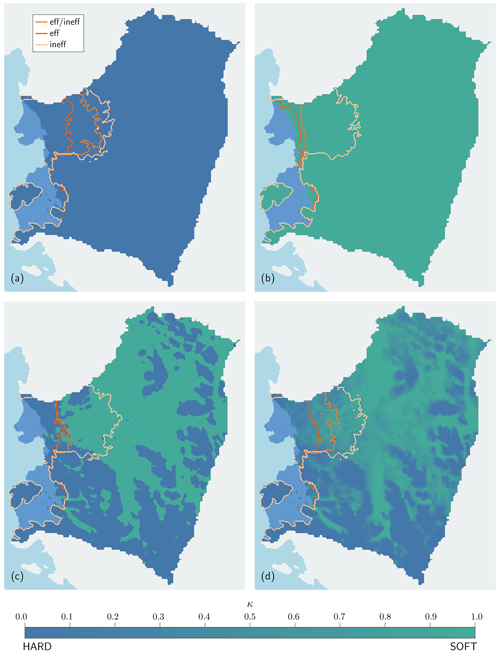
Figure 9 Grounding-line positions of Thwaites Glacier in 2100 under constant present-day climate conditions (atmospheric and oceanic) for the subglacial model (inefficient and efficient, entirely efficient, and entirely inefficient) on (a) a uniform homogeneous hard bed; (b) a uniform homogeneous soft bed; (c) a heterogeneous uniform bed, with a sharp transition; and (d) a heterogeneous bed, with a transition zone of mixed bed.

This simulation under present-day forcing conditions is repeated for the different subglacial hydrological models HAB, HARD, and SOFT. Akin to this, the spatial variability in the HARD and SOFT bed models is assessed by considering heterogeneous and/or mixed beds for Thwaites Glacier (Muto et al., 2019; Alley et al., 2022). By heterogeneous we mean that the spatial field is composed of soft- and hard-bed portions, while for a mixed bed, we consider that a particular grid cell is composed of a mix of hard and soft bed or $\mathrm{0}<\mathit{\kappa }<\mathrm{1}$. We can therefore have different cases, namely homogeneous uniform (the whole bed domain with either κ=0 or κ=1) or mixed (the whole bed domain with a constant value $\mathrm{0}<\mathit{\kappa }<\mathrm{1}$), as well as heterogeneous uniform (the domain composed of portions of hard bed and soft bed) and mixed ($\mathrm{0}\le \mathit{\kappa }\le \mathrm{1}$). For the heterogeneous uniform beds, Joughin et al. (2009) and Muto et al. (2019) suggest that soft beds are mainly found in subglacial depressions and hard beds generally on topographic highs, allowing us to make the separation between both based on the subglacial topography, with the soft layer occupying the deeper basins. In a first experiment, we set the transition between soft and hard bed at a bedrock elevation of 1000 m below sea level (Fig. 9c). In a second experiment, a transition zone is considered (heterogeneous mixed), where κ is linearly varied between a depth of 500 and 1500 m below sea level (Fig. 9d). We tested the influence of the nature of the drainage system itself by applying only inefficient, efficient, or both drainage systems for the different bed types described above.

4.2 Results: subglacial hydrology on homogeneous beds

As mentioned above, even under present-day atmospheric and oceanic forcing, the reference experiment NON leads to a slight retreat of the grounding line over the period 2015–2100 that continues thereafter. This is in line with large-scale model experiments (Coulon et al., 2024) showing that Thwaites Glacier may collapse (i.e., that it will continue to retreat even if the forcing is completely stopped) under present-day climatic conditions on timescales of several centuries.

The same retreat behavior is observed for the experiment including subglacial hydrology. However, in all cases, subglacial hydrology accelerates the retreat of the grounding line by 2100 (Fig. 8a). For instance, by 2100, we observe a sea level contribution of around 50 mm for HAB, 95 mm for HARD, and 20 mm for SOFT, while only 10 mm for NON (Fig. 8b). It is important to note that for all the subglacial models a collapse of Thwaites Glacier is engaged under present-day climate forcing conditions. However, only the hard-bed model (HARD) results in a collapse in shorter than 100 years. Not all major mass losses coincide with a distinct grounding-line retreat as the HAB model exhibits significant thinning of the ice for a modest grounding-line retreat compared to the other subglacial models.

The efficiency of subglacial drainage is tested for both a uniform homogeneous soft and hard bed (Fig. 9a and b). As demonstrated in the idealized experiments, it is also possible to force the drainage to be efficient (eff) or inefficient (ineff). The results corroborate the previous experiment, namely that for a hard bed, a large amount of ice is lost by 2100 compared to the soft bed. The only exception is that a similar amount of (high) mass loss is observed for the inefficient drainage systems both for soft and hard beds (Fig. 9a and b).

4.3 Results: subglacial hydrology on heterogeneous beds

Figure 9c and d show the grounding-line positions for a heterogeneous bed, where the subglacial basins of Thwaites Glacier are considered to be soft bed and the topographic high hard bed. As previously mentioned, the limit between both is set at a depth of 1000 m below the present-day sea level. A peculiarity of this setting is that the present-day grounding line is situated on a hard bed and that the soft bed region is only reached further inland. In the first experiment (Fig. 9c), the transition between both bed rheologies is sharp (uniform heterogeneous); in the second experiment (Fig. 9d), there is a transition zone (mixed heterogeneous). Despite the hard-bed conditions in the present-day grounding zone, a larger mass loss by 2100 is observed for the mixed case. Similar to the previous experiment, the largest mass loss is observed for inefficient drainage, irrespective of the bed rheology.

The results on mixed heterogeneous bed experiments show that the nature of the bed near the grounding line determines the sensitivity of the glacier. With a sharp transition, the motion of the grounding line over the hard-to-soft bed system will lead to a stabilization effect delaying grounding-line retreat. Such stabilization is less pronounced for a mixed bed, where hard-bed physics also play a role in the transition zone. Similar results are presented in Sect. S4, with the hard- and soft-bed zone locations exchanged.

5 Discussion

We have developed a novel and unified subglacial hydrological model that incorporates efficient and inefficient drainage and that applies to both soft and hard beds. It represents different discharge types, ranging from channels and canals to cavities. While the model is a simplification compared to higher-resolution hydrological models, it seems to capture the main characteristics of subglacial flow and incorporates the feedbacks associated with basal sliding and the ice dynamical response.

In this section, we first discuss the influence of the hydrological model and the bed type. We then describe the hydrological feedback that may explain the increased sensitivity of the ice sheet due to subglacial hydrology. Finally, we comment on the limitations of the model and suggest improvements to our model.

5.1 Influence of subglacial conditions

Our experimental results show that subglacial hydrology and the rheology of the bed (soft, hard, and its related spatial variability) have a major impact on the dynamics of marine ice sheets and the West Antarctic Ice Sheet in particular. Taking into account subglacial hydrology systematically leads to a higher ice sheet sensitivity for a given climate forcing. This is mainly due to the reduction in the effective pressure near the grounding line, which migrates upstream with a retreating grounding line.

Traditionally, large-scale ice sheet models tend to calculate effective pressure at the base of the ice sheet using the HAB parameterization, based on the height above flotation. This model assumes that seawater infiltrates at the grounding line, increasing the water pressure and reducing the effective pressure in the grounding zone. This leads to significant increases in basal sliding near the grounding line. The idealized experiments clearly demonstrate that this model leads to the highest mass loss after a perturbation and probably overestimates the contribution of ice sheets to climate forcing.

However, in more complex settings, such as Thwaites Glacier, the HAB model remains sensitive but also allows the grounding line to stabilize during its retreat on subglacial ridges. These bed peaks are known to have a strong impact on grounding-line dynamics, and their influence on ice sheet stability is the subject of recent research (Robel et al., 2022a).

Results of our simplified hydrological model show that sliding over a hard bedrock (HARD) leads to the largest reduction in the grounded domain and the highest sea level contribution for a given forcing, while sliding over a soft bed (SOFT) yields the smallest grounding-line retreat and sea level contribution (Fig. 8). In terms of drainage efficiency, the concentration of water flow in efficient conduits, especially in canals but also for channels, slows down the retreat of the grounding line, which aligns with one of the conclusions of Schoof (2010). This can be explained by a higher basal friction, due to the higher effective pressure in hard bed channels (Hager et al., 2022), and by the lower effective pressure variation in canals, leading to a reduced impact of subglacial hydrology on the basal friction field. It is interesting to note that in the case of hard beds, our effective pressure results are similar to those obtained by Hager et al. (2022) with the MALI model (Hoffman et al., 2018), using a subglacial drainage model built on cavities and channels.

Besides the hard bed, inefficient systems also lead to the highest mass loss of Thwaites Glacier over this century. We observe that the largest mass loss occurs when the effective pressure gradient is large towards the grounding line and less so when effective pressure is low, such as in canals (Fig. 8b; see the video supplement). This observation aligns with the work of Iken (1981), specifying that the highest velocities are not observed where effective pressures is lowest but rather when cavities enlarge due to an increase in subglacial water pressure. Therefore, inefficient systems on both soft and hard beds show very similar results consistent with the representation of the considered drainage systems. Such systems are quite similar to bumps in the hard system that correspond to the clasts in the soft system. However, the lower effective pressure in the soft-bed system, associated with the deformation of saturated till, slows down grounding-line retreat.

In general, a soft bed near the grounding line slows down its retreat under climatic forcing. However, transitions between bed types also influence the speed of the grounding-line retreat. A binary switch from hard to soft is more likely to stabilize the grounding-line position than a smooth transition. Moreover, taking the total proportion between soft and hard beds and applying it uniformly across the entire domain does not allow the capturing of the variation introduced by the spatial variability in bed rheology and the associated drainage system.

5.2 Hydrological feedback

The increased sensitivity observed with hydrological models can be explained by a positive feedback between grounding-line migration and the reduction in basal friction at or near the grounding line. Formally, frictional stress τ_b can be split into two components, namely ${\stackrel{\mathrm{̃}}{\mathit{\tau }}}_{\mathrm{b}}$, which is the value of the friction stress with the initial effective pressure field, and $\mathrm{\Delta }{\stackrel{\mathrm{̃}}{\mathit{\tau }}}_{\mathrm{b}}$, which is the deviation with respect to this value:

$$\begin{array}{}\text{(11)}& {\mathit{\tau }}_{\mathrm{b}}={\stackrel{\mathrm{̃}}{\mathit{\tau }}}_{\mathrm{b}}+\mathrm{\Delta }{\stackrel{\mathrm{̃}}{\mathit{\tau }}}_{\mathrm{b}},\end{array}$$

where

$$\begin{array}{}\text{(12a)}& {\displaystyle }{\stackrel{\mathrm{̃}}{\mathit{\tau }}}_{\mathrm{b}}\left(t\right)& {\displaystyle }=C{N}_{\mathrm{0}}{\left({\displaystyle \frac{\Vert {\mathit{v}}_{\mathrm{b}}\Vert }{\Vert {\mathit{v}}_{\mathrm{b}}\Vert +v_{\mathrm{0}}}}\right)}^{\frac{\mathrm{1}}{m}}{\displaystyle \frac{{\mathit{v}}_{\mathrm{b}}}{\Vert {\mathit{v}}_{\mathrm{b}}\Vert }},\text{(12b)}& {\displaystyle }\mathrm{\Delta }{\stackrel{\mathrm{̃}}{\mathit{\tau }}}_{\mathrm{b}}\left(t\right)& {\displaystyle }=C\left[N\left(t\right)-N_{\mathrm{0}}\right]{\left({\displaystyle \frac{\Vert {\mathit{v}}_{\mathrm{b}}\Vert }{\Vert {\mathit{v}}_{\mathrm{b}}\Vert +v_{\mathrm{0}}}}\right)}^{\frac{\mathrm{1}}{m}}{\displaystyle \frac{{\mathit{v}}_{\mathrm{b}}}{\Vert {\mathit{v}}_{\mathrm{b}}\Vert }},\end{array}$$

and where $N_{\mathrm{0}}=N(t=\mathrm{0})$ is the effective pressure for the initial state. Because of the initialization procedure, ${\stackrel{\mathrm{̃}}{\mathit{\tau }}}_{\mathrm{b}}$ is initially the same for every hydrological model. In particular, it is also equal to the absence of subglacial hydrology (NON). Therefore, $\mathrm{\Delta }{\stackrel{\mathrm{̃}}{\mathit{\tau }}}_{\mathrm{b}}$ stems from the evolution of the subglacial system and its influence on basal friction. In other words, $\mathrm{\Delta }{\stackrel{\mathrm{̃}}{\mathit{\tau }}}_{\mathrm{b}}$ is associated with the spatial and temporal evolution of the effective pressure.

Due to the evolution of subglacial hydrology in time, an instability mechanism may appear near the grounding line, as the effective pressure is always low, and the gradient of the effective pressure is the largest (Fig. 5). The zone of low effective pressure migrates with a migrating grounding line. Such migration obviously does not take place when the subglacial hydrological field is kept constant or when subglacial hydrology is not linked to basal sliding (or not considered; NON). For a retreating grounding line, such linkage actually amplifies grounding-line retreat, as the friction stress close to the grounding line is also reduced following this retreat, leading to a positive feedback mechanism. This reduction in τ_b stems from a reduction in ${\stackrel{\mathrm{̃}}{\mathit{\tau }}}_{\mathrm{b}}$ but most importantly from a large value in the magnitude of $\mathrm{\Delta }{\stackrel{\mathrm{̃}}{\mathit{\tau }}}_{\mathrm{b}}$, which is typically negative. This essentially explains the distinction between the HAB and the HARD/SOFT models. The HAB model is purely local as it depends on the geometry of the ice sheet at the position where the effective pressure is evaluated. By contrast, the HARD/SOFT models also depend on the subglacial water flux and on the distance with respect to the grounding line. This distinction allows for a perturbation near the grounding line to “propagate” upstream for the latter models. As this is not the case for HAB models, it potentially enables the grounding line to stabilize near a ridge, for instance. This distinction can be observed in the Video supplement.

The qualitative assessment can be quantified in the case of a flowline, according to the shallow-shelf approximation. Following previous work (Weertman, 1974; Schoof, 2007a, 2012), a steady-state marine ice sheet is unstable if

$$\begin{array}{}\text{(13)}& {\partial }_{s}q-a<\mathrm{0},\end{array}$$

in which q is the flux at the grounding line, s is a coordinate parameterizing the position along the ice sheet, and a is the net mass accumulation rate. For a large class of friction laws (Schoof, 2007b; Tsai et al., 2015; Gregov et al., 2023), the flux at the grounding line can be approximated as

$$\begin{array}{}\text{(14)}& q=q_{\mathrm{0}}{C}^{-\frac{\mathrm{1}}{m+\mathrm{1}}}{\left[-({\mathit{\rho }}_{\mathrm{w}}/{\mathit{\rho }}_{\mathrm{i}})b\right]}^r,\end{array}$$

where $q_{\mathrm{0}},r>\mathrm{0}$. It follows that for a uniform friction coefficient, a steady-state position on an up-sloping (retrograde) bed is always unstable, i.e.,

$$\begin{array}{}\text{(15)}& {\partial }_{s}q-a=-rq({\mathit{\rho }}_{\mathrm{w}}/{\mathit{\rho }}_{\mathrm{i}}){\left[-({\mathit{\rho }}_{\mathrm{w}}/{\mathit{\rho }}_{\mathrm{i}})b\right]}^{-\mathrm{1}}{\partial }_{s}b-a<\mathrm{0}.\end{array}$$

However, an ice sheet on a downward-sloping bed can be stable. For a spatially variable friction coefficient C=C(s), the instability condition becomes

$$\begin{array}{}\text{(16)}& -{\displaystyle \frac{q{C}^{-\mathrm{1}}{\partial }_{s}C}{m+\mathrm{1}}}-rq({\mathit{\rho }}_{\mathrm{w}}/{\mathit{\rho }}_{\mathrm{i}}){\left[-({\mathit{\rho }}_{\mathrm{w}}/{\mathit{\rho }}_{\mathrm{i}})b\right]}^{-\mathrm{1}}{\partial }_{s}b-a<\mathrm{0}.\end{array}$$

This inequality can be achieved more easily for a downward-sloping (prograde) bed compared to Eq. (15). Indeed, if ∂_sC is positive and large at the grounding line, then the left-hand side of Eq. (16) is reduced, and the instability condition is easier to fulfill. The initialization produces this condition for the HAB, HARD, and SOFT models, contrary to the NON case, where C(s) has to increase considerably close to the grounding line to compensate for the vanishing effective pressure in order to obtain a frictional stress similar to the one obtained by the absence of hydrology. Overall, this implies that the ice sheet is less stable, and therefore exhibits a higher sensitivity to external forcings. This instability was explored in greater details with a similar model in Lu and Kingslake (2023).

5.3 Model limitations

Although our simulations for hard, soft, and mixed beds allow us to better assess the variability in the response of ice sheets to a climate forcing, there remain some limitations. Our subglacial hydrology models do not include variations in drainage density or of effective pressure below the resolution of the ice sheet discretization. This is a clear limitation, as we have shown that the spatial variability plays an important role in the numerical experiments. From a physical perspective, improvements could be made to the representation of physical processes. For example, till water pressure is omitted in the soft bed model, and till deformation is only crudely parameterized. Water flow within the till and exchanges with the neighboring area (especially in the case of a variation in ice thickness) could well modify subglacial water flow and therefore ice sheet dynamics (Robel et al., 2023). Recent studies have also shown that seawater intrusion may impact grounding-line dynamics through modifying the subglacial hydrology, hence increasing the instability (Robel et al., 2022b; Bradley and Hewitt, 2024). This also suggests that the grounding line should be considered a grounding zone that allows for such intrusion, in agreement with recent observations (Rignot et al., 2024). Furthermore, erosion, deposition, and sedimentary transport processes that are not taken into account could play a role in the variability in the effective pressure at the base of the ice sheet (Ng, 2000; Hewitt and Creyts, 2019; Stevens et al., 2022). Finally, even if our results remain qualitatively valid if the parameter settings are modified (see Appendix D), the latter could be subject to more scrutiny, ideally within a probabilistic framework (Bulthuis et al., 2019; Verjans et al., 2022; Coulon et al., 2024). This analysis could then be used to quantify the uncertainties in the projections obtained in the simulations.

6 Conclusions

We developed a novel and simplified model of subglacial hydrology that applies to both soft and hard beds, thereby representing both efficient and inefficient discharge types. The hydrological model is dynamically linked to an ice sheet model (Kori-ULB) via a regularized Coulomb friction law. Despite its relative simplicity, our model allows us to obtain results that agree with multiple previous studies. Our experiments are in agreement with Kazmierczak et al. (2022), showing that the type of subglacial hydrology modulates the basal sliding and that considering subglacial hydrology enhances the ice sheet response to sliding. Our tests on the spatial and temporal variability in bed rheology also show that a soft-bed system in the grounding zone tends to stabilize a grounding line more easily compared to other bed rheologies. By investigating various drainage efficiencies, our results concur with those of Schoof (2010) by showing that a channelization leads to ice deceleration, as well as grounding-line stabilization. The switch between efficient and inefficient drainage has clearly been shown in our experiments where subglacial water input has been varied. Moreover, our results agree with Iken (1981) by the fact that the highest sliding is not occurring at the highest subglacial water pressure but rather where basal cavities are growing (i.e., when the basal water pressure is increasing downstream). Furthermore, we obtain the largest response in grounding-line retreat for those subglacial conditions where the gradient in effective pressure is the largest and not where its value is the lowest. Therefore, highly saturated grounding zones on soft beds seem to be less responsive than hard-bed systems, where such large gradients in the vicinity of the grounding line occur. While our results for Thwaites Glacier for a hard bed are qualitatively similar to those of Hager et al. (2022), the ability of model to reproduce such results could be studied in more detail.

Overall, our study also emphasizes the necessity for more accurate data and observations of the bed rheology of the Antarctic Ice Sheet at different spatial scales (Parizek et al., 2013; Koellner et al., 2019; Muto et al., 2019; Alley et al., 2022; Li et al., 2022; Aitken et al., 2023). Similarly, the observation of efficient and inefficient subglacial water drainage systems and a connection with numerical results is required (Schroeder et al., 2014; Hager et al., 2022; Dow, 2022b).

Appendix A: List of symbols

List of symbols used for the model (Greek alphabet)

Symbol	Description	Units	Value
α	Exponent in Darcy–Weisbach relation	–	$\mathrm{5}/\mathrm{4}$
β	Exponent in Darcy–Weisbach relation	–	$\mathrm{3}/\mathrm{2}$
Γd	Boundary of the basin	–	–
Γgl	Grounding line	–	–
κ	Indicator of the heterogenous content of the bed	–	–
ρi	Density of ice	kg m−3	9.17×103
ρs	Density of seawater	kg m−3	1.03×103
ρw	Density of freshwater	kg m−3	1.00×103
τb	Basal shear stress	Pa	-
ϕ	Hydraulic potential	Pa	–
ϕ0	Geometric potential	Pa	–
Ω	Grounded ice domain	–	–

List of symbols used for the model (Latin alphabet)

Symbol	Description	Units	Value
A	Viscosity parameter in Glen's flow law	${\mathrm{Pa}}^{-\mathrm{n}}{\mathrm{s}}^{-\mathrm{1}}$	–
b	Bedrock elevation	m	–
C	Friction coefficient	–	–
f	Friction coefficient for a turbulent flow	–	0.10
Ftill	Factor for the conduits geometry in a till	–	1.10
g	Gravitational acceleration	m s−2	9.81
G	Geothermal heat flux	W m−2	–
h	Ice thickness	m	–
hb	Thickness of obstacles	m	0.10
H	Thickness of conduits	m	–
Hhard	Thickness of conduits over a hard bed	m	–
Hsoft	Thickness of conduits over a soft bed	m	–
H0	Thickness of canals	m	0.10
K	Conductivity coefficient in Darcy–Weisbach relation	${\mathrm{kg}}^{\mathrm{1}-\mathit{\beta }}{\mathrm{m}}^{\mathrm{2}\mathit{\beta }-\mathrm{2}\mathit{\alpha }+\mathrm{1}}{\mathrm{s}}^{\mathrm{2}\mathit{\beta }-\mathrm{3}}$	–
L	Width of conduits	m	–
lc	Distance between conduits	m	1.00×104
ℒw	Latent heat of fusion of water	J kg−1	3.35×105
m	Power law exponent	–	3.00
$\dot{m}$	Melt rate	$\mathrm{kg}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$	–
${\dot{m}}_{\mathrm{w}}$	Melt rate associated with the subglacial water flow	$\mathrm{kg}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$	–
n	Exponent in Glen's flow law	–	3.00
n	Normal vector to a boundary	–	–
N	Effective pressure	Pa	–
N∞	Far-field effective pressure	Pa	–
qw	Subglacial water flux	m2 s−1	–
qT	Thermal conduction flux	W m−2	–
Qw	Volumetric water flux in a conduit	m3 s−1	–
Qc	Critical water flux in a conduit	m3 s−1	1.00
S	Cross-sectional area of conduits	m2	–
S∞	Far-field cross-sectional area of conduits	m2	–
v	Ice velocity	m s−1	–
vb	Basal ice velocity	m s−1	–
v0	Velocity threshold in the friction law	m s−1	$\mathrm{9.51}\times {\mathrm{10}}^{-\mathrm{6}}$
x	Position	m	–

Appendix B: The effective pressure near the grounding line: a boundary layer analysis

In this section, we apply a boundary layer analysis of the hydrology system close to the grounding line and derive an approximate expression of the effective pressure in the area.

B1 Problem statement

We consider a streamline of subglacial water parameterized by a parameter $s\in [\mathrm{0},s_{\text{gl}}]$, where s=s_gl corresponds to the grounding-line position. All the parameters are fixed, and the magnitude of the geometric potential gradient, $\mathrm{\Psi }=\Vert \mathrm{\nabla }{\mathit{\varphi }}_{\mathrm{0}}\Vert$, is assumed to be constant and known. The governing equations of the hydrology system are then expressed as

$$\begin{array}{}\text{(B1a)}& {\displaystyle }N={\mathit{\varphi }}_{\mathrm{0}}-\mathit{\varphi },\text{(B1b)}& {\displaystyle }{\partial }_{t}S+{\partial }_s{Q}_{\mathrm{w}}={\displaystyle \frac{\dot{M}}{{\mathit{\rho }}_{\mathrm{w}}}},\text{(B1c)}& {\displaystyle }{Q}_{\mathrm{w}}=-K{S}^{\mathit{\alpha }}\mathrm{|}{\partial }_s\mathit{\varphi }{\mathrm{|}}^{\mathit{\beta }-\mathrm{2}}{\partial }_s\mathit{\varphi },\text{(B1d)}& {\displaystyle }{\partial }_{t}S=\Vert {\mathit{v}}_{\mathrm{b}}\Vert h_{\mathrm{b}}+{\displaystyle \frac{\mathrm{|}{Q}_{\mathrm{w}}{\partial }_s\mathit{\varphi }\mathrm{|}}{{\mathit{\rho }}_{\mathrm{i}}{\mathcal{L}}_{\mathrm{w}}}}-\mathrm{2}{n}^{-n}A{L}^{\mathrm{2}}\mathrm{|}N{\mathrm{|}}^{n-\mathrm{1}}N,\end{array}$$

where $\dot{M}$ is the net melt rate, associated with the amount of water that reaches the conduit. For the boundary conditions, we require a zero-water flux at the ice divide, i.e., Q_w=0 at s=0, and a continuity of the subglacial water pressure with the ocean water, i.e., N=0 at s=s_gl. We consider hard beds for which $L\left(S\right)=\sqrt{S}$. For canals, $L\left(S\right)=S/H_{\mathrm{0}}$, the derivation and results are quite similar.

B2 Dimensionless equations

We first make the problem and the unknown values dimensionless. We therefore write

$$\begin{array}{}\text{(B2)}& \begin{array}{rl}& \widehat{s}={\displaystyle \frac{s}{\left[s\right]}},\widehat{t}={\displaystyle \frac{t}{\left[t\right]}},\widehat{\mathit{\varphi }}={\displaystyle \frac{\mathit{\varphi }}{\left[\mathit{\varphi }\right]}},\widehat{N}={\displaystyle \frac{N}{\left[N\right]}},\\ & {\widehat{Q}}_{\mathrm{w}}={\displaystyle \frac{Q_{\mathrm{w}}}{\left[Q_{\mathrm{w}}\right]}},\widehat{S}={\displaystyle \frac{S}{\left[S\right]}}.\end{array}\end{array}$$

The scales are chosen as follows. First, we set [s]=s_gl, and [ϕ]=Ψ[s]. We further choose [t] to be a timescale associated with ice flow. The other scales, [N], [Q_w], and [S], are chosen such that

$$\begin{array}{}\text{(B3)}& \begin{array}{rl}& {\displaystyle \frac{\left[Q_{\mathrm{w}}\right]}{\left[s\right]}}={\displaystyle \frac{\dot{M}}{{\mathit{\rho }}_{\mathrm{w}}}},\left[Q_{\mathrm{w}}\right]=K[S{]}^{\mathit{\alpha }}{\mathrm{\Psi }}^{\mathit{\beta }-\mathrm{1}},\\ & {\displaystyle \frac{\mathrm{1}}{{\mathit{\rho }}_{\mathrm{i}}{\mathcal{L}}_{\mathrm{w}}}}\left[Q_{\mathrm{w}}\right]\mathrm{\Psi }=\mathrm{2}{n}^{-n}A\left[S\right][N{]}^n.\end{array}\end{array}$$

This leads to the following dimensionless formulation of the problem:

$$\begin{array}{}\text{(B4a)}& {\displaystyle }\mathit{\eta }\widehat{N}=-\widehat{s}-\widehat{\mathit{\varphi }},\text{(B4b)}& {\displaystyle }{\mathit{\tau }}_{\mathrm{1}}{\partial }_{\widehat{t}}\widehat{S}+{\partial }_{\widehat{s}}{\widehat{Q}}_{\mathrm{w}}=\mathrm{1},\text{(B4c)}& {\displaystyle }{\widehat{Q}}_{\mathrm{w}}=-{\widehat{S}}^{\mathit{\alpha }}\mathrm{|}{\partial }_{\widehat{s}}\widehat{\mathit{\varphi }}{\mathrm{|}}^{\mathit{\beta }-\mathrm{2}}{\partial }_{\widehat{s}}\widehat{\mathit{\varphi }},\text{(B4d)}& {\displaystyle }{\mathit{\tau }}_{\mathrm{2}}{\partial }_{\widehat{t}}\widehat{S}=\mathit{\nu }+\mathrm{|}{\widehat{Q}}_{\mathrm{w}}{\partial }_{\widehat{s}}\widehat{\mathit{\varphi }}\mathrm{|}-\widehat{S}\mathrm{|}\widehat{N}{\mathrm{|}}^{n-\mathrm{1}}\widehat{N},\end{array}$$

for $\mathrm{0}<\widehat{s}<\mathrm{1}$, with boundary conditions ${\widehat{Q}}_{\mathrm{w}}(\widehat{s}=\mathrm{0})=\mathrm{0}$ and $\widehat{N}(\widehat{s}=\mathrm{1})=\mathrm{0}$. The following four dimensionless ratios appear:

$$\begin{array}{}\text{(B5)}& \begin{array}{rl}& \mathit{\eta }:={\displaystyle \frac{\left[N\right]/\left[s\right]}{\mathrm{\Psi }}},\mathit{\nu }:={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{i}}{\mathcal{L}}_{\mathrm{w}}\Vert {\mathit{v}}_{\mathrm{b}}\Vert h_{\mathrm{b}}}{\left[Q_{\mathrm{w}}\right]\mathrm{\Psi }}},\\ & {\mathit{\tau }}_{\mathrm{1}}:={\displaystyle \frac{\left[S\right]\left[s\right]}{\left[t\right]\left[Q_{\mathrm{w}}\right]}},{\mathit{\tau }}_{\mathrm{2}}:={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{i}}{\mathcal{L}}_{\mathrm{w}}\left[S\right]\left[s\right]}{\left[t\right]\left[Q_{\mathrm{w}}\right]\left[\mathit{\varphi }\right]}}.\end{array}\end{array}$$

The first ratio compares the magnitude of the spatial variation in N with respect to the geometric potential gradient Ψ. It thus follows that if η≪1, then ${\partial }_s\mathit{\varphi }\approx \mathrm{\Psi }$, while for η≫1, ${\partial }_s\mathit{\varphi }\approx -{\partial }_{s}N$. The second parameter compares the two possible terms that lead to an opening of the cavities or of the channels: it compares the opening due to sliding over bumps of the bedrock and the melt of the conduit boundaries. The two last ratios compare the characteristic times related to changes in the water flux and in the channel thickness with respect to the characteristic time of ice flow. In particular, if ${\mathit{\tau }}_{\mathrm{1}},{\mathit{\tau }}_{\mathrm{2}}\ll \mathrm{1}$, which we anticipate, then the time dependency disappears from the problem, and the hydrological system is in a steady state.

In what follows, we drop the hats on the dimensionless variables to simplify the notations.

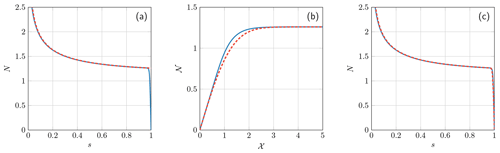
Figure B1 Inner, outer, and composite solutions of the dimensionless problem for $\mathit{\eta }={\mathrm{10}}^{-\mathrm{2}}$ and ν=1. (a) The outer solution is the numerical solution to the system of Eq. (B4a) (continuous line) and the leading-order solution (Eq. B6) to the outer problem (dashed line). (b) The inner solution is the numerical solution to Eq. (B8) (continuous line) and the approximate solution (Eq. B9) (dashed line). (c) The composite solution is the numerical solution to the system of Eq. (B4a) (continuous line) and the composite solution (Eq. B10) (dashed line).

B3 Outer solution

For commonly used parameters, we obtain $\mathit{\eta },{\mathit{\tau }}_{\mathrm{1}},{\mathit{\tau }}_{\mathrm{2}}\ll \mathrm{1}$, and ν∼1. This suggests treating η, τ₁, and τ₂ as small parameters of the problem. The leading-order solution is then given by

$$\begin{array}{}\text{(B6)}& Q_{\mathrm{w}}=s,S=s^{\frac{\mathrm{1}}{\mathit{\alpha }}},\mathit{\varphi }=-s,N=s^{-\frac{\mathrm{1}}{n\mathit{\alpha }}}(\mathit{\nu }+s{)}^{\frac{\mathrm{1}}{n}}.\end{array}$$

This effective pressure has originally been obtained by Schoof (2010). It is defined such that $N(s=\mathrm{1})={\mathit{\nu }}^{\mathrm{1}/n}$, so the Dirichlet boundary condition at the grounding line is not fulfilled. This suggests that a boundary layer exists close to the grounding line in which N quickly decreases to reach a zero value (Fig. B1a). We therefore refer to the leading-order solution (Eq. B6) as the outer solution, and the inner solution, associated with the boundary layer, must be found to obtain an acceptable expression of the effective pressure.

B4 Inner solution

We first eliminate Q_w and S from the dimensionless system of Eq. (B4) to get the following equation for N only:

$$\begin{array}{}\text{(B7)}& \mathit{\nu }+s\mathrm{|}\mathrm{1}+\mathit{\eta }{\partial }_{s}N\mathrm{|}=s^{\frac{\mathrm{1}}{\mathit{\alpha }}}\mathrm{|}\mathrm{1}+\mathit{\eta }{\partial }_{s}N{\mathrm{|}}^{\frac{\mathrm{1}-\mathit{\beta }}{\mathit{\alpha }}}\mathrm{|}N{\mathrm{|}}^{n-\mathrm{1}}N,\end{array}$$

for $\mathrm{0}<s<\mathrm{1}$ and with $N(s=\mathrm{1})=\mathrm{0}$. The boundary layer at the grounding line suggests the introduction of a scaling in which ∂_sN becomes of the order of 𝒪(1). We therefore introduce $\mathcal{X}={\mathit{\eta }}^{-\mathrm{1}}(\mathrm{1}-s)$ and rename 𝒩=N. Then, at the leading order,

$$\begin{array}{}\text{(B8)}& \mathit{\nu }\mathrm{|}\mathrm{1}-{\partial }_{\mathcal{X}}\mathcal{N}{\mathrm{|}}^{\frac{\mathit{\beta }-\mathrm{1}}{\mathit{\alpha }}}+\mathrm{|}\mathrm{1}-{\partial }_{\mathcal{X}}\mathcal{N}{\mathrm{|}}^{\frac{\mathit{\beta }+\mathit{\alpha }-\mathrm{1}}{\mathit{\alpha }}}=\mathrm{|}\mathcal{N}{\mathrm{|}}^{n-\mathrm{1}}\mathcal{N},\end{array}$$

for 𝒳>0 and with $\mathcal{N}(\mathcal{X}=\mathrm{0})=\mathrm{0}$. Because the inner solution must join the outer solution, we also have the compatibility condition $\mathcal{N}\to (\mathit{\nu }+\mathrm{1}{)}^{\frac{\mathrm{1}}{n}}$ as $\mathcal{X}\to +\mathrm{\infty }$. Finding the solution of this leading-order problem is not trivial because of its non-linearity. Nonetheless, we approximate it by an expression $\stackrel{\mathrm{̃}}{\mathcal{N}}$. We require that this approximate has the correct behavior over the boundaries of the boundary layer; that is, $\stackrel{\mathrm{̃}}{\mathcal{N}}\sim \mathcal{X}$ as 𝒳→0 and $\stackrel{\mathrm{̃}}{\mathcal{N}}\sim (\mathit{\nu }+\mathrm{1}{)}^{\frac{\mathrm{1}}{n}}$ as $\mathcal{X}\to +\mathrm{\infty }$. We find that the following expression is a good approximation of 𝒩 for ν≲1 (see Fig. B1b):

$$\begin{array}{}\text{(B9)}& \stackrel{\mathrm{̃}}{\mathcal{N}}=\text{erf}\left[{\displaystyle \frac{\sqrt{\mathit{\pi }}}{\mathrm{2}}}{\displaystyle \frac{\mathcal{X}}{(\mathit{\nu }+\mathrm{1}{)}^{\frac{\mathrm{1}}{n}}}}\right](\mathit{\nu }+\mathrm{1}{)}^{\frac{\mathrm{1}}{n}},\end{array}$$

where $\text{erf}\left(x\right)=\left(\mathrm{2}\mathit{\pi }{)}^{-\mathrm{1}/\mathrm{2}}{\int }_{\mathrm{0}}^x\exp \right(-t^{\mathrm{2}})\mathrm{d}t$ is the Gauss error function.

B5 Composite solution

The composite solution, which is valid over the whole domain, is obtained by summing the inner and outer solutions and subtracting the overlap in the matching area. This leads to the following expression:

$$\begin{array}{}\text{(B10)}& \begin{array}{rl}N\left(s\right)=& \text{erf}\left[{\displaystyle \frac{\sqrt{\mathit{\pi }}}{\mathrm{2}}}{\displaystyle \frac{{\mathit{\eta }}^{-\mathrm{1}}(\mathrm{1}-s)}{(\mathit{\nu }+\mathrm{1}{)}^{\frac{\mathrm{1}}{n}}}}\right](\mathit{\nu }+\mathrm{1}{)}^{\frac{\mathrm{1}}{n}}\\ & +s^{-\frac{\mathrm{1}}{n\mathit{\alpha }}}(\mathit{\nu }+s{)}^{\frac{\mathrm{1}}{n}}-(\mathit{\nu }+\mathrm{1}{)}^{\frac{\mathrm{1}}{n}}.\end{array}\end{array}$$

It is possible to go back to the original variables to obtain the expression of the effective pressure as a function of the original parameters. To do so, we introduce

$$\begin{array}{}\text{(B11)}& N_{\mathrm{\infty }}\left(s\right)={\left[{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{i}}{\mathcal{L}}_{\mathrm{w}}\Vert {\mathit{v}}_{\mathrm{b}}\Vert h_{\mathrm{b}}+\left({\mathit{\rho }}_{\mathrm{w}}^{-\mathrm{1}}\dot{M}s\right)\mathrm{\Psi }}{\mathrm{2}{n}^{-n}{\mathit{\rho }}_{\mathrm{i}}{\mathcal{L}}_{\mathrm{w}}A({\mathit{\rho }}_{\mathrm{w}}^{-\mathrm{1}}\dot{M}s{)}^{\frac{\mathrm{1}}{\mathit{\alpha }}}{K}^{-\frac{\mathrm{1}}{\mathit{\alpha }}}{\mathrm{\Psi }}^{\frac{\mathrm{1}-\mathit{\beta }}{\mathit{\alpha }}}}}\right]}^{\frac{\mathrm{1}}{n}},\end{array}$$

which is the outer solution written in its dimensional form. The effective pressure is then given by

$$\begin{array}{}\text{(B12)}& \begin{array}{rl}N\left(s\right)=& \text{erf}\left[{\displaystyle \frac{\sqrt{\mathit{\pi }}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{\Psi }{s}_{\text{gl}}}{N_{\mathrm{\infty }}\left(s_{\text{gl}}\right)}}\left(\mathrm{1}-{\displaystyle \frac{s}{s_{\text{gl}}}}\right)\right]N_{\mathrm{\infty }}\left(s_{\text{gl}}\right)\\ & +N_{\mathrm{\infty }}\left(s\right)-N_{\mathrm{\infty }}\left(s_{\text{gl}}\right).\end{array}\end{array}$$

Because N_∞ does not change much over the boundary layer, the previous expression can be replaced by

$$\begin{array}{}\text{(B13a)}& {\displaystyle }N\left(s\right)& {\displaystyle }=\text{erf}\left[{\displaystyle \frac{\sqrt{\mathit{\pi }}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{\Psi }{s}_{\text{gl}}}{N_{\mathrm{\infty }}\left(s\right)}}\left(\mathrm{1}-{\displaystyle \frac{s}{s_{\text{gl}}}}\right)\right]N_{\mathrm{\infty }}\left(s\right),\text{(B13b)}& {\displaystyle }& {\displaystyle }=\text{erf}\left[{\displaystyle \frac{\sqrt{\mathit{\pi }}}{\mathrm{2}}}{\displaystyle \frac{{\mathit{\varphi }}_{\mathrm{0}}\left(s\right)}{N_{\mathrm{\infty }}\left(s\right)}}\right]N_{\mathrm{\infty }}\left(s\right).\end{array}$$

This composite solution closely matches the numerical solution to the problem (Fig. B1c).

Appendix C: Effect of the coupling frequency between the hydrological and ice sheet models

Here, we investigate the effect of the coupling frequency between the hydrological and the ice sheet models. We show results for both MISMIP and Thwaites Glacier setups and show that the hydrological model must be updated at a frequency that is at least of the same order of magnitude as the updated frequency of the ice sheet model. As a consequence, no subglacial hydrology model, no matter how complex, can improve ice sheet simulations involving the grounding-line motion if it is not updated at a sufficiently high frequency. In particular, considering a hydrological model during the initialization of an ice sheet model but not during a forward simulation is virtually useless as the impact of the hydrological model is then almost nonexistent.

C1 MISMIP

Figure C1a shows the grounding-line position after the same forcing as the one that was considered in Sect. 3 for various update frequencies of the hydrological model. If the hydrology model is not regularly updated, then the results resemble the no-subglacial-hydrology case NON. This last case is evidently not affected by the chosen time steps. A higher sensitivity of the subglacial hydrological model also requires higher update frequency rates.

C2 Thwaites Glacier

We can make the same observations in Fig. C1b as those made for the MISMIP configuration. A difference remains in the timescales considered for the two studies and in the fact that HAB does not exhibit the largest sensitivity.

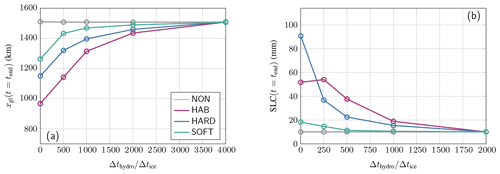
Figure C1 The effect of the coupling frequency between the hydrological and ice sheet models shows the grounding-line position after the forcing as a function of the ratio between the time step Δt_hydro of the hydrological model and the time step Δt_ice of the ice sheet model. Practically, we fix the ice sheet time step and increase the time step of the hydrological model to obtain several values for $\mathrm{\Delta }{t}_{\text{hydro}}/\mathrm{\Delta }{t}_{\text{ice}}$. (a) The MISMIP configuration shows the grounding-line position after the forcing. (b) The Thwaites Glacier configuration shows the sea level contribution after the forcing.

Appendix D: Influence of the unconstrained parameters of the hydrological model

We performed a sensitivity analysis of the least constrained parameters of our model, i.e., l_c, Q_c, and F_till (Fig. D1). It can be observed that l_c has only a limited effect for hard beds, while it has a more pronounced impact for soft beds. From Eq. (4), a change in l_c results in a change in the water flux Q_w, which will be important if water flow transitions from an efficient to an inefficient flow (or the reverse). However, for hard beds, the entirely efficient or inefficient cases yield similar results (Fig. 8b). On the contrary, for soft beds, the difference between the entirely efficient or inefficient cases is more pronounced (Fig. 8b), and it follows that there is a stronger dependence with respect to l_c. For Q_c and F_till, the impact is limited. Finally, it can be noted that the spread in the results increases over a time.

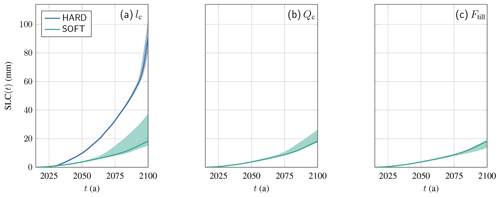
Figure D1 Sensitivity analysis of the results with respect to the parameters l_c, Q_c, and F_till. The setup is the same as the one described in the forcing experiments over Thwaites Glacier (Sect. 4.2; subglacial hydrology on homogeneous beds), except that different values of these parameters are chosen. The shaded areas correspond to the ranges $l_{\mathrm{c}}\in [\mathrm{5},\mathrm{15}]$ km, $Q_{\mathrm{c}}\in [\mathrm{0.5},\mathrm{1.5}]$ m³ s⁻¹, and $F_{\text{till}}\in [\mathrm{1},\mathrm{2}]$, and the lines correspond to the nominal values considered in the original experiment.