Impacts of differing melt regimes on satellite radar waveforms and elevation retrievals

Geodetic surface mass balance calculations rely on satellite radar altimeters such as CryoSat-2 to understand elevation and volumetric changes of the Greenland Ice Sheet (GrIS). However, the impact of varying GrIS shallow subsurface stratigraphic conditions on level 2 CryoSat-2 elevation products is poorly understood. We investigate the reliability of the Offset Center Of Gravity (OCOG) and University College London Land-Ice (ULI) elevation retracking algorithms through the analysis of (and comparison with) level 1B waveform-derived leading-edge width (LeW). We generate a 2010 to 2021 LeW time series using temporal clustering and Bayesian model averaging, and we compare them with level 2 OCOG and ULI elevation time series. We perform this workflow at Summit Station, North Greenland Eemian Ice Drilling (NEEM) Camp, and Raven Camp, chosen to represent the upper and lower bounds of the dry-snow zone and percolation zone. We note that melting event, snowpack recovery, and potentially anomalous snow accumulation and high-speed wind signatures are evident in Summit Station's LeW time series. We find that level 1B LeW has a significant inverse relationship with the ULI level 2 elevations at NEEM Camp and Summit Station and likely with the entire dry-snow zone. The ULI retracked level 2 elevations at Raven Camp (and likely the entire percolation zone) have no clear elevation bias associated with significant melt events. The OCOG retracked level 2 elevations showed no significant association with LeW at any site. Future work is needed to understand the impacts of GrIS high-speed wind events and snow accumulation on elevation products.

1 Introduction

1.1 Climatological significance

The Greenland Ice Sheet (GrIS) contains 6–7 m of global sea-rise equivalent of ice (Cuffey and Marshall, 2000) and is predicted to contribute between 30–170 mm to sea-level rise by 2100 (Shepherd et al., 2019). GrIS elevation and mass balance products need to be accurate, given its climatological significance in the face of warming temperatures. A valuable tool in developing such products is ESA's CryoSat-2 radar altimeter, SIRAL (Wingham et al., 2006). Unlike NASA's ICESat-2 laser elevation instrument ATLAS, SIRAL can penetrate the GrIS shallow subsurface (Neumann et al., 2019; Nilsson et al., 2015; Simonsen and Sørensen, 2017; Vermeer et al., 2022). CryoSat-2 elevation retrievals can be influenced by local and regional effects of surface melting and snowpack processes, as noted around North Greenland Eemian Drilling (NEEM) Camp (or simply NEEM) from 2011 to 2014 (Nilsson et al., 2015). However, the impact of melt on radar waveforms and thus surface elevation retrievals is not uniform across the ice sheet.

As anthropogenic climate change accelerates GrIS surface melt (Sellevold and Vizcaíno, 2020) and increases interannual variability in surface mass balance (Fyke et al., 2014), melt-induced CryoSat-2-derived elevation biases are likely to increase in significance. Therefore, the relationship between these elevation biases and changing shallow subsurface GrIS dynamics needs to be fully understood. Here, we analyze changes in the shallow subsurface and their influence on retracked elevations from 2010–2021 in the dry-snow and percolation zones (Benson, 1996; Nghiem et al., 2001, 2012; Polashenski et al., 2014; Rizzoli et al., 2017).

1.2 Retrackers

Researchers can choose from two land–ice retracking algorithms when deriving elevations from SIRAL waveforms (Fig. 1) within the GrIS low-resolution-mode (LRM) zone: Offset Center of Gravity (OCOG) and University College London Land-Ice (ULI) elevation (European Space Agency, 2019a, b).

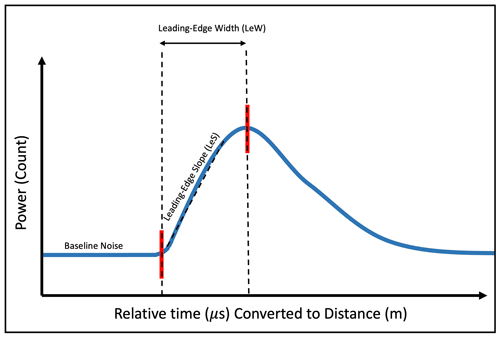
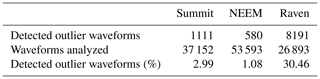
Figure 1 Idealized CryoSat-2 radar waveform (modified from Simonsen and Sørensen, 2017). The leading-edge width (LeW) is defined as the time or distance it takes for the returning radar waveform to reach peak amplitude from baseline, and the leading-edge slope (LeS) is defined as the slope of the waveform during the bins corresponding to the LeW. LeW and LeS have an inverse relationship when the waveform's peak amplitude remains constant.

1.2.1 OCOG retracker

The OCOG algorithm is an empirical threshold retracker which locates the leading-edge (LE) of a waveform based on the shape of the overall waveform. The OCOG retracker first calculates the amplitude of the waveform (Eq. 1; European Space Agency, 2019a), where Φ(i) is the corresponding power at bin n₁ to n₂.

$$\begin{array}{}\text{(1)}& A_{\text{OCOG}}=\sqrt{{\displaystyle \frac{{\sum }_{i=n_{\mathrm{1}}}^{n_{\mathrm{2}}}{\mathrm{\Phi }}^{\mathrm{4}}\left(i\right)}{{\sum }_{i=n_{\mathrm{1}}}^{n_{\mathrm{2}}}{\mathrm{\Phi }}^{\mathrm{2}}\left(i\right)}}}\end{array}$$

The OCOG retracker then locates the range bin i_OCOG (and therefore the derived range) of the corresponding retracked point to when the power crosses an empirically derived threshold of amplitude A. The SIRAL instrument uses a threshold of 30 % (European Space Agency, 2019a).

1.2.2 ULI retracker

Although the OCOG retracker empirically relies on the overall shape of the observed waveform to derive a retracked position, the ULI retracker applies parametric model fitting to the initial OCOG retracker to estimate ranges (European Space Agency, 2019a). The ULI specifically fits a Brown model (Brown, 1977) adapted to the CryoSat-2 instrument (European Space Agency, 2019b). The ULI retracker used in SIRAL determines the retracked point by multiplying the fitted model's peak power located at the end of the LE by an empirically derived threshold.

The ULI retracker's smoothed Brown model (Fig. 2, with the subtraction of the added noise term) is defined as amplitude A multiplied by wave w (Eq. 2; European Space Agency, 2019a).

$$\begin{array}{}\text{(2)}& M(t{)}_{\text{Brown}}=A\cdot w(t)\end{array}$$

Amplitude A (Eq. 3; European Space Agency, 2019a) contains P_T (peak transmitted power; European Space Agency, 2019a), K₁ (first-order approximation of the mispointing angle handling term, Eq. 4), ξ (mispointing angle), γ (antenna beamwidth parameter, Eq. 5), σ (standard deviation of the point response (σ_P) and significant wave height (SWH) (σ_H) function, Eq. 6), and T (time constant, Eq. 7; European Space Agency, 2019a).

$$\begin{array}{}\text{(3)}& A=P_{\mathrm{T}}T\exp \left[{\displaystyle \frac{-\mathrm{4}}{\mathit{\gamma }}}{\sin }^{\mathrm{2}}\mathit{\xi }\right]\exp \left[{\displaystyle \frac{(k_{\mathrm{1}}\mathit{\sigma }{)}^{\mathrm{2}}}{\mathrm{2}}}\right]\end{array}$$

The first-order approximation of the mispointing angle term (Eq. 4) contains ξ, c (speed of light), and h (estimated height of the SIRAL instrument above mean sea level (MSL) subtracted by the determined range accounting for any bias; European Space Agency, 2019a).

$$\begin{array}{}\text{(4)}& k_{\mathrm{1}}={\displaystyle \frac{\mathrm{4}c}{\mathit{\gamma }h}}\left[\cos \left(\mathrm{2}\mathit{\xi }\right)-{\displaystyle \frac{\mathrm{1}}{\mathit{\gamma }}}{\sin }^{\mathrm{2}}\left(\mathrm{2}\mathit{\xi }\right)\right]\end{array}$$

γ (Eq. 7) contains Θ_Major and Θ_Minor: the along- and across-antenna beamwidths (European Space Agency, 2019a).

$$\begin{array}{}\text{(5)}& {\displaystyle }\mathit{\gamma }=\left({\displaystyle \frac{\mathrm{2}}{\ln \left(\mathrm{2}\right)}}\right){\sin }^{\mathrm{2}}\left(\left\{{\displaystyle \frac{\mathrm{2}}{\left[\frac{\mathrm{1}}{{\mathrm{\Theta }}_{\text{Major}}}+\frac{\mathrm{1}}{{\mathrm{\Theta }}_{\text{Minor}}}\right]}}\right\}/\mathrm{2}\right),\text{(6)}& {\displaystyle }\mathit{\sigma }=\sqrt{({\mathit{\sigma }}_{\mathrm{P}}{)}^{\mathrm{2}}+({\mathit{\sigma }}_{\mathrm{H}}{)}^{\mathrm{2}}},\text{(7)}& {\displaystyle }T={\mathit{\sigma }}_{\mathrm{P}}\sqrt{\mathrm{2}\mathit{\pi }}.\end{array}$$

σ_P (Eq. 8; MacArthur, 1978, as cited in Amarouche et al., 2004) includes P_L (compressed pulse length), and σ_H (Eq. 9; Stewart, 1985, as cited in Garcia et al., 2014) includes SWH and c.

$$\begin{array}{}\text{(8)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{P}}\cong \mathrm{0.513}{P}_{\mathrm{L}},\text{(9)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{H}}={\displaystyle \frac{\text{SWH}}{\mathrm{2}c}}.\end{array}$$

First-order approximation of waveform w₁ (Eq. 10) includes the addition of t (time subtracted from the wave epoch; European Space Agency, 2019a).

$$\begin{array}{}\text{(10)}& w_{\mathrm{1}}(t,k_{\mathrm{1}})={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\exp [-k_{\mathrm{1}}(t\left)\right]\left\{\mathrm{1}+\text{erf}\left[{\displaystyle \frac{\left(t\right)}{\mathit{\sigma }\sqrt{\mathrm{2}}}}-{\displaystyle \frac{k_{\mathrm{1}}\mathit{\sigma }}{\sqrt{\mathrm{2}}}}\right]\right\}\end{array}$$

SWH in the ULI retracker's Brown model is inversely related to the LeS and positively related to the LeW (Fig. 2; Brown, 1977; Hayne, 1980; Schlembach et al., 2020). As such, we rewrite σ_H (Eq. 9) to show the Brown model as a function of the LeW (Eq. 11).

$$\begin{array}{}\text{(11)}& {\mathit{\sigma }}_{\mathrm{H}}={\displaystyle \frac{f\left(\text{LeW}\right)}{\mathrm{2}c}}\end{array}$$

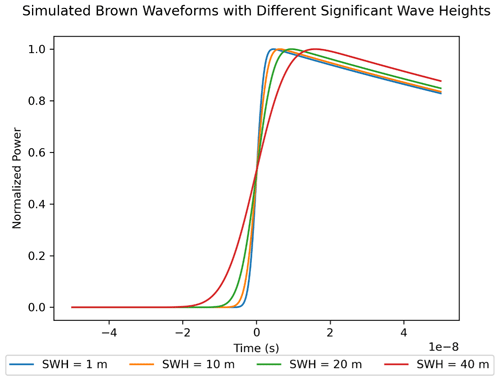
Figure 2 Smoothed Brown waveforms (Eqs. 2–11; European Space Agency, 2019a) with different significant wave height (SWH) values. P_L=3.125 ns, P_T=25 W, Θ_Major=1.060°, Θ_Minor=1.992° (European Space Agency, 2019b), h=3246.6 m (Hawley et al., 2020), and ξ=0.1° (University College London, 2024). There is an inverse relationship between LeW and LeS and a positive relationship between LeW and SWH, highlighting that the Brown model is a function of the LeW.

1.2.3 Effect of non-constant LeW on retracker performance

It has been shown that the 2012 melting event created a level 2 elevation bias of 89 ± 49 cm at NEEM by artificially decreasing the waveform's LeW and radar penetration depth following the creation of a more specular melt layer (Nilsson et al., 2015). While a large-scale melting event decreased the surface roughness within the altimeter's footprint (Nilsson et al., 2015) and surface roughness is a contributor to the LeW (Ashcraft and Long, 2005; Legrésy and Rémy, 1997), it was not found to be a potential long-lasting cause of elevation bias (Nilsson et al., 2015).

These results indicate that retrackers are not immune to melt-induced changes within the shallow subsurface, raising questions about the long-term performance of the CryoSat-2 level 2 OCOG and ULI LRM retrackers, given that the LRM zone does not contain a monolithic melt regime (Benson, 1996; Nghiem et al., 2001, 2012; Polashenski et al., 2014; Rizzoli et al., 2017). While the choice of retracker may seem inconsequential, ULI's Brown model reliance on LeW (Sect. 1.2.2), which itself can change based on the surface conditions of the targeted surface (Ashcraft and Long, 2005; Legrésy and Rémy, 1997; Nghiem et al., 2001; Nilsson et al., 2015; Simonsen and Sørensen, 2017), may cause elevation inconsistencies if applied uniformly across different melt regimes. This study addresses these resulting questions through the creation of a framework to calculate and evaluate level 1B baseline D LeW and level 2 elevation time series at any given location on the GrIS within CryoSat-2's LRM zone (Ronan et al., 2024), and we hypothesize that the OCOG retracker should generate a truer elevation trend regardless of shallow GrIS subsurface changes, given its relative independence from the waveform's LeW (Sect. 1.2.1; Ferraro and Swift, 1995).

2 Methodology

This study applies the aforementioned framework (Ronan et al., 2024) for NEEM and Summit Station (or simply Summit) in the dry-snow zone and Raven Camp (or simply Raven) in the percolation zone (Fig. 3; Benson, 1996; Nghiem et al., 2001, 2012; Polashenski et al., 2014; Rizzoli et al., 2017). These well-studied locations were chosen to investigate retracker performance and waveform characteristics within different melt regimes.

Figure 3 Study sites, elevation (Howat et al., 2015), and mean annual snowmelt (Noël et al., 2019) within the LRM boundary. Raven (located within the percolation zone) experiences 3 orders of magnitude more melt than Summit (located within the dry-snow zone) and 2 orders of magnitude more melt than NEEM (located within the dry-snow zone) (Noël et al., 2019). Mean annual snowmelt is derived from 1958 to 2019 RACMO2.3p2 time series (Noël et al., 2019).

2.1 Defining a region of interest

The framework begins by ingesting level 1B waveforms collected within a predesignated radius for each location, assuming homogeneity within the shallow subsurface. Unlike the decision to use a 25 km buffer around NEEM in Nilsson et al. (2015), this study uses a buffer with a radius of 20 km around each study site to estimate level 1B metrics and level 2 elevations.

2.2 Data preparation

2.2.1 Level 2 elevations

Assuming that the true elevation is not constant throughout the 20 km circular buffer area (Helm et al., 2014) and that none of the CryoSat-2 tracks directly overlap the field site, we employ a least-squares-fit algorithm to generate a 3D elevation plane ($Z_{\text{Surface}}=C_{\mathrm{1}}X+C_{\mathrm{2}}Y+C_{\mathrm{0}}$) for any given month; then we predict the elevation of the specified site along with its 95 % confidence interval (CI). This value and the average date of all points used are included in the level 2 elevation time series. A 1-month aggregation period is used to allow for a robust multiple linear regression (MLR).

2.2.2 Level 1B LeW

All level 1B waveforms are clipped to remove remnants of the preceding waveform, and range bins are converted to range (m) (European Space Agency, 2019b), centralized around the beginning of the LE. To estimate the location of the true peak and minimize the interference of inconsistencies within the waveform itself, the waveform is smoothed using a Savitzky–Golay filter (we empirically chose the parameters of window length (17) and order (second)). This study defines the waveform's LeW as the resulting range (m) of the smoothed peak (Fig. 4).

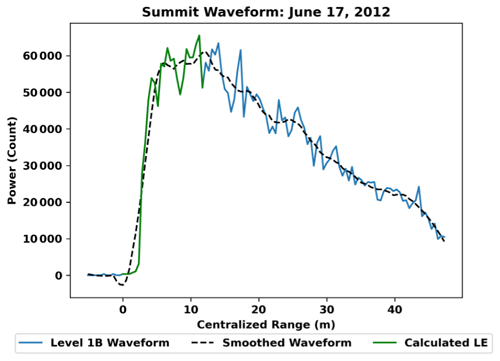
Figure 4 Visual representation of the LeW methodology. A Savitzky–Golay filter (window length of 17 and second-order approximation) is applied to the waveform, and the range of the resulting peak is defined as the LeW.

As individual level 1B LeW values corresponding to returning waveforms within a 20 km buffer are assumed to be consistent (Sect. 2.1), we employ a simple metric average of values within the radius to create a time series. Points that fall within a calendar week of each other are aggregated and averaged. This resulting averaged LeW and the averaged date of all points used are included in the level 1B metric time series. A 1 calendar week aggregation period for the LeW is used instead of the month used for the level 2 elevations as there is no need to maximize the number of tracks for an additional MLR step (Sect. 2.2.1).

2.3 Trend analysis and comparison

We employ the Bayesian Estimator for Abrupt Seasonality and Trend (BEAST) algorithm (Zhao et al., 2019) to derive trends within the mean clustered level 1B LeWs and level 2 elevation time series and to serve as a visual aid in analysis. The temporal resolution of the time series proves difficult when analyzing the possible impact from glaciologically significant processes; GrIS melting events occur in the span of days (Nghiem et al., 2012), whereas the clustered time series have a data point approximately every month (even in the case of level 1B LeW, with a weekly clustering period). This low temporal resolution and irregularity makes the decision to use certain trend-calculating models challenging, which the BEAST algorithm avoids by using Bayesian inference and model averaging (Zhao et al., 2013, 2019). We used a window length of $\mathrm{1}/\mathrm{8}$ of a year with the BEAST algorithm, which is a compromise between the ability to resolve seasonal trends and the unintentional introduction of artifacts.

To account for the difference in aggregation period between level 1B LeW (weekly) and level 2 elevations (monthly) (Sects. 2.2.1 and 2.2.2) and to allow for separate correlation analyses between the two time series, level 1 LeW values are interpolated in time to the same dates as the clustered level 2 elevations.

2.4 Outliers

Anomalous waveforms, defined as waveforms that significantly deviate from ideal (Fig. 1), were removed before the clustering phase (Sect. 2.2.2; Sect. 1 in the Supplement). In the case of Summit and Raven, a cluster outlier was removed from the level 2 elevation time series for containing elevations greater than or equal to 6 standard deviations from the mean of the remaining clusters in the time series. We note that the methodology used to filter outlier waveforms relies on an empirical understanding of ideal radar waveforms and simple thresholding rather than a deterministic algorithm. Given the wide variety of level 1B LEs and its underlying characteristics, more research is needed to develop a more encompassing methodology. The numbers of anomalous waveforms detected at Summit and NEEM are small in comparison to the total number of waveforms within the 20 km buffer throughout the entire temporal range (Table 1). At Raven, however, we detect >30 % of the total waveforms as anomalous.

Table 1 Outliers removed during the analytical process.

Raven's high percentage of outliers can be attributed to its large LeW and to its increased likelihood of erroneously including a second waveform before being clipped. The likely explanation of Raven's increased LeW is grounded in the fact that Raven is in a melt-dominated glaciological regime (Benson, 1996; Noël et al., 2019). An increased amount of accumulation in southwest Greenland (Noël et al., 2019) paired with more melt periods per season can potentially create many subsurface ice layers in the snowpack, also resulting in a higher LeW (see Sect. 4.2.2 for more information).

3 Results

3.1 NEEM Camp

LeW at NEEM increases negligibly from 2010.62 to 2012.5 (decimal year) by 1.99 % (6.97 to 7.12 m) (Fig. 5a). From 2012.5 to 2012.62, the LeW abruptly decreased by 46.6 % to 4.43 m, and then it steadily increased back to 6.20 m (33.4 %) and slightly decreases again to 5.67 m (−9 %) in 2012.62 (Fig. 5a). The LeW at NEEM is inversely related to ULI retracked level 2 elevations (two-tailed test (TTT), α=0.05, $r=-\mathrm{0.53}$, p<0.0001) (Fig. 5a and b) and not significantly correlated with the OCOG retracked level 2 elevations (TTT, α=0.05, r=0.03, p=0.81084) (Fig. 5a and c). It is noted that the elevation derived from the OCOG retracker at NEEM is, on average, ∼1 m higher than corresponding elevations from the ULI retracker (Fig. 5b and c).

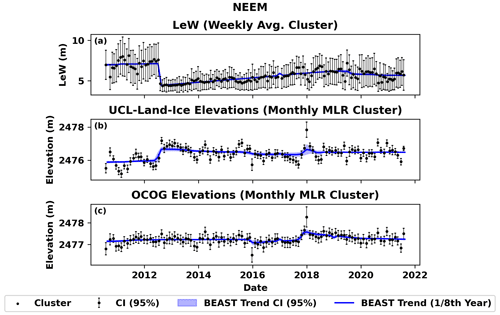
Figure 5 (a) Level 1B LeW, (b) ULI level 2, and (c) OCOG retracked elevations at NEEM. The LeW at NEEM is inversely related to ULI retracked level 2 elevations (TTT, α=0.05, $r=-\mathrm{0.53}$, p<0.0001) (a, b) and not significantly correlated to the OCOG retracked level 2 elevations (TTT, α=0.05, r=0.03, p=0.81084) (a, c). OCOG-derived elevations are, on average, ∼1 m higher than corresponding elevations from the ULI retracker (b, c).

3.2 Summit Station

From 2012.38 to 2012.5, the LeW abruptly decreased by 49.2 % to 5.15 m, and then it steadily increased to 8.36 m in 2018.99 (Fig. 6a). The LeW ultimately decreased down to 7.22 m in 2019.58 (−15.8 %) and recovered back to 7.92 m in 2021.62 (Fig. 6a). ULI retracked elevation trends contain an abrupt increase in July 2012, followed by a linear decrease in elevation until approx. 2018. LeW at Summit increased from 2010.5 to 2012.38 by 36.1 % (5.91 to 8.52 m) (Fig. 6a). The LeW at Summit Station is inversely related to ULI retracked level 2 elevations (TTT, α=0.05, $r=-\mathrm{0.71}$, p<0.0001) (Fig. 6a and b) and not significantly correlated to the OCOG retracked level 2 elevations (TTT, α=0.05, $r=-\mathrm{0.06}$, p=0.59046) (Fig. 6a and c). It is noted that the elevation derived from the OCOG retracker at Summit Station is, on average, ∼2 m higher than corresponding elevations from the ULI retracker (Fig. 6b and c).

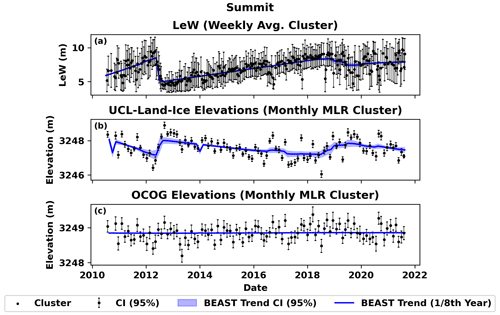
Figure 6 (a) Level 1B LeW, (b) ULI level 2, and (c) OCOG retracked elevations at Summit Station. The LeW is inversely related to ULI retracked level 2 elevations (TTT, α=0.05, $r=-\mathrm{0.71}$, p<0.0001) (a, b) and not significantly correlated to the OCOG retracked level 2 elevations (TTT, α=0.05, $r=-\mathrm{0.06}$, p=0.59046) (a, c). OCOG-derived elevations are, on average, ∼2 m higher than corresponding elevations from the ULI retracker (b, c). One outlier cluster (13 September 2010) was removed from the level 2 elevation time series (b, c).

3.3 Raven Camp

Unlike NEEM Camp and Summit Station, where there are significant changes in LeW over time (Figs. 5a and 6a), the LeW time series at Raven Camp remains constant (Fig. 7a). We note that the average LeW at Raven is a full 2 m wider than the largest LeW cluster at Summit (Figs. 6a and 7a; see Sect. 4.2.2 for more information). In addition, the LeW time series from Summit and NEEM show a single, large, and abrupt LeW decrease during the July 2012 melt event (Figs. 5a and 6a), but no such abrupt change is found in the corresponding LeW time series at Raven Camp (Fig. 7a) Finally, the elevation estimates from the two retrackers at Raven Camp follow a different pattern than at Summit Station: the variability of elevations derived from the ULI retracker is comparable to that of OCOG, and their means are comparable to each other (Fig. 7b and c). Unlike at Summit (Fig. 6b), the ULI retracker shows no significant trends during the study period (Fig. 7b) or noticeable bias associated with the LeW (TTT, α=0.05, $r=-\mathrm{0.02}$, p=0.82634) (Fig. 7b and c). The OCOG retracker behaves the same as at Summit, with no noticeable bias associated with the LeW (TTT, α=0.05, $r=-\mathrm{0.071}$, p=0.48564) (Fig. 7a and c).

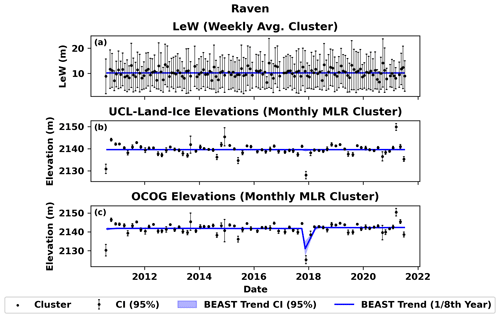
Figure 7 (a) Level 1B LeW, (b) ULI level 2, and (c) OCOG retracked elevations at Raven Camp. The ULI retracker shows no significant trends during the study period (c) or noticeable bias associated with the LeW (TTT, α=0.05, $r=-\mathrm{0.02}$, p=0.82634) (b, c). OCOG-derived elevations have no noticeable bias associated with the LeW (TTT, α=0.05, $r=-\mathrm{0.071}$, p=0.48564) (a, c). One outlier cluster (24 August 2021) was removed from the level 2 elevation time series (b, c).

4 Discussion

4.1 Dry-snow zone elevations

This study asserts that large changes in dry-snow zone level 2 ULI elevations are artifacts of a changing LeW, which in turn are caused by inter- and intra-seasonal changes in the shallow subsurface. Previous research has demonstrated that when corrected for downslope advection and seasonal variations, the surface elevation from at least 2008 to 2018 at Summit Station increased at an average rate of 0.019 m a⁻¹ (p≪0.001) (Hawley et al., 2020). Given this near-constant trend at Summit Station and concurrence with Nilsson et al. (2015), the ∼2 m elevation variation calculated in this study using the ULI elevations at NEEM and Summit (Figs. 5b and 6b) is unlikely to represent actual elevation change and is likely an artifact of the waveform's changing LeW. Kuipers Munneke et al. (2015) corroborate this conclusion as they indicate that the range of surface elevation change within the time frame is 1 order of magnitude smaller than the elevation changes indicated by the ULI retracker. Unlike OCOG-derived elevations, which remain statistically uncorrelated with the LeW at NEEM and Summit Station (Figs. 5c and 6c), ULI-derived elevations are found to have an inverse relationship with the LeW (Figs. 5b and 6b; Sects. 3.1 and 3.2).

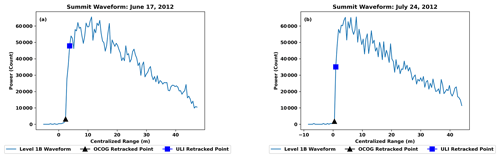
Figure 8 Plot containing representative waveforms within a 20 km radius of Summit Station (a) before and (b) after the 2012 melting event (July 2012). Between these two waveforms where the LeW decreases from 12.18 m (a) to 3.75 m (b), the retracked elevation difference between the OCOG and ULI retrackers Δ(h_OCOG−h_ULI) decreases from 1.21 m (a) to 0.50 m (b). Such waveforms serve as a visual interpretation of how the OCOG retracked point remains earlier in the waveform than with the ULI retracker, indicating a higher h_OCOG (Figs. 5c and 6c). As the LeW decreases, h_ULI approaches h_OCOG.

Such a relationship can be explained through the inner mechanics of the ULI retracker itself; a decreased LeW will result in an increased LeS and decreased noise floor, which, when ingested into the Brown model (Eqs. 2–11; Fig. 2), will find a retracked point in the waveform earlier, which ultimately decreases the calculated time of flight of the radar signal and results in an artificially high surface elevation. Given the OCOG-derived elevations are ∼1 m higher than in the ULI algorithm at NEEM and Summit (Figs. 5a and 6a), we assess that the OCOG behaves as a low-threshold retracker (Fig. 8). The OCOG algorithm places the retracked points earlier in the waveform, which results in a decreased time of flight of the radar signal. As such, OCOG-derived elevations escape most artifacts from a changing LeW that hinder the ULI retracker (Figs. 5, 6, and 8).

4.2 LeW

4.2.1 Summit and NEEM

Consistent with Nilsson et al. (2015), we also note significant drops in the LeW at NEEM (−46.6 %) and Summit (−49.2 %), corresponding to the July 2012 melting event. We assert that an influx of refrozen meltwater during the 2012 melting event on the surface and in the immediate shallow subsurface resulted in a more specular surface and reduction in radar waveform penetration depth (Nilsson et al., 2015), which significantly increased the surface-to-volume scattering ratio. Such a dramatic increase in this ratio results in a sharp decrease in a waveform's LeW. As the melting event subsides and more climatologically average weather conditions return, the LeW increases as the melt layer is buried, and the surface-to-volume scattering ratio moves back towards pre-melt values. We see that the LeW at Summit has a higher recovery rate than NEEM, which can be explained by Summit's higher average snow accumulation rates (Noël et al., 2019).

This study also notes a second abrupt decrease in LeW at Summit in winter 2019 and NEEM in winter 2020, with no reported melting event. This may be due to a period of elevated surface wind speeds that, through wind packing, created wind slabs and crusts (Sommer, 2018; Sommer et al., 2018) and/or removed an upper layer of the loosely layered snowpack. Wind slabs and crusts would result in a decreased LeW through the same mechanism as the melting crust generated from the 2012 melting event.

4.2.2 Raven

Although NEEM and Summit within the dry-snow zone experience shallow subsurface changes, resulting in LeW changes and therefore changes in ULI-derived elevations, no such processes are observed at Raven Camp. Raven experiences 3 orders of magnitude more melt than at Summit and 2 orders of magnitude more melt per year than at NEEM (Noël et al., 2019), and as such, Raven's shallow subsurface contains vastly more melt layers. We assess that these melt layers keep Raven's LeW high (∼2 m higher in Raven than in NEEM or Summit) through the decrease in penetration depth and keep the volume to surface scattering ratio low. Such a low ratio minimizes the effect of snow accumulation and high-profile melt crusts (and perhaps wind slabs and crusts) on the LeW signal.

Given the inverse relationship between the ULI trend and LeW at Summit and NEEM (Figs. 5 and 6), the explanation behind such a relationship (Eqs. 2–11; Fig. 2; Brown, 1977; Hayne, 1980; Schlembach et al., 2020), and the constant ULI trend at Raven (Fig. 7b), we are confident that our outlier methodology (Sect. 2.4; Sect. S1 in the Supplement) does not selectively produce an artificially flat LeW trend at Raven (Fig. 7a).

5 Conclusion

We analyzed 10-year trends in level 2 OCOG and ULI retracked GrIS surface elevations, as well as level 1B LeW from 2010 to 2021. We assess that abrupt first-order LeW changes within the dry-snow zone are a function of large-scale melting events and perhaps wind-packing events, whereas second-order trends are a function of snowpack recovery. We provide supporting evidence for the assertion by Nilsson et al. (2015) that climatological events impact elevations derived from CryoSat-2's SIRAL instrument. We find that the ULI retracker becomes biased within the dry-snow zone during periods of intense melt, changing snowpack, and potential wind events. This is apparent in changes in the level 1B LeW, which result in a changing position of the retracked point in the Brown model. We find that there is no noticeable ULI retracker bias within the percolation zone during periods of intense melt, changing snowpack, or potential wind events.

The results from this study indicate that future satellite radar altimeters covering the GrIS dry-snow zone must take climatologically significant events (such as melting events, potential high-speed wind events, or snow accumulation patterns) into consideration when analyzing elevations derived from model retracking algorithms. Our study also indicates that empirically derived retrackers such as OCOG are preferable across the GrIS LRM zone over their model retracking counterpart, ULI.