the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Unravelling the sources of uncertainty in glacier runoff projections in the Patagonian Andes (40–56° S)
Rodrigo Aguayo
Fabien Maussion
Lilian Schuster
Marius Schaefer
Alexis Caro
Patrick Schmitt
Jonathan Mackay
Lizz Ultee
Jorge Leon-Muñoz
Mauricio Aguayo
Glaciers are retreating globally and are projected to continue to lose mass in the coming decades, directly affecting downstream ecosystems through changes in glacier runoff. Estimating the future evolution of glacier runoff involves several sources of data uncertainty, which to date have not been comprehensively assessed on a regional scale. In this study, we used the Open Global Glacier Model (OGGM) to estimate the evolution of each glacier (with area > 1 km2) in the Patagonian Andes (40–56° S). As sources of uncertainty, we used different glacier inventories (n = 2), ice thickness datasets (n = 2), historical climate datasets (n = 4), general circulation models (GCMs; n = 10), emission scenarios (Shared Socioeconomic Pathways, SSPs; n = 4) and bias correction methods (BCMs; n = 3) to generate 1920 possible scenarios over the period of 1980–2099. In each scenario, glacier runoff and melt time series were characterised by 10 glacio-hydrological signatures (i.e. metrics). We used the permutation feature importance of random forest regression models to assess the relative importance of each source of uncertainty on the signatures of each catchment. Considering all scenarios, 34 % ± 13 % (mean ± 1 standard deviation) of the glacier area has already peaked in terms of glacier melt (the year 2020), and 68 % ± 21 % of the glacier area will lose more than 50 % of its volume this century. Considering the glacier melt signatures, the future sources of uncertainty (GCMs, SSPs and BCMs) were the main source in only 17 % ± 21 % of the total glacier area. In contrast, the reference climate was the main source in 69 % ± 22 % of the glacier area, highlighting the impact of calibration choices on baseline conditions, model parameters and the initial starting geometry for future projections. The results provide a basis for prioritising future efforts (e.g. the improvement of reference climate characterisation) to reduce glacio-hydrological modelling gaps in poorly instrumented regions such as the Patagonian Andes.
- Article
(9841 KB) - Full-text XML
-
Supplement
(8743 KB) - BibTeX
- EndNote
Glaciers are retreating worldwide (Hugonnet et al., 2021) and are projected to continue to lose mass (Marzeion et al., 2020). Recent projections by Rounce et al. (2023) indicate that glaciers will lose 26 ± 6 % (+1.5 °C) to 41 ± 11 % (+4 °C) of their present mass by 2100 (median ± 95 % confidence interval), contributing between 90 ± 26 and 154 ± 44 mm to sea-level rise. The rapid glacier shrinkage has led to cascading effects on downstream systems (Huss et al., 2017; Milner et al., 2017), affecting the availability and quality of water resources (IPCC, 2022) and causing changes in the ecological (Cauvy-Fraunié and Dangles, 2019) and socio-economic (Rasul and Molden, 2019) aspects of downstream environments.
One of the most important impacts of glaciers on downstream systems is the contribution of meltwater to streamflow (Huss and Hock, 2018), which is essential for irrigation, industry, domestic use, hydropower and ecosystems (Immerzeel et al., 2020; Viviroli et al., 2020). However, as glaciers continue to shrink, the reliability and quantity of this water reserve becomes increasingly uncertain, potentially increasing drought stress (Kaser et al., 2010; Pritchard, 2019; Van Tiel et al., 2021, 2023). Ultee et al. (2022) showed globally that accounting for glacier runoff reduces simulated drought frequency and severity, even in basins with low glacier cover (< 2 %). The buffering effect is higher in moderately glaciated arid regions such as the Central Andes and is projected to increase through the 21st century. In this region, glaciers have provided an important drought mitigation capacity during the current mega drought (Ayala et al., 2020; McCarthy et al., 2022), which is unprecedented in recent centuries according to dendrochronological studies (Garreaud et al., 2017; Morales et al., 2020).
Recent global estimates suggest that Andean glaciers are likely to be one of the largest per-unit-area contributors to sea-level rise, with a sea-level-equivalent (SLE) contribution of 0.057 ± 0.006 mm SLE yr−1 (−20.7 ± 2.1 Gt yr−1) representing 7.7 % of the global ice mass loss between 2000 and 2019 (mean ± 95 % confidence interval; Hugonnet et al., 2021). Glaciers in the Patagonian Andes (40–56° S) account for 96 % of the total ice loss in the Southern Andes (25–56° S; Braun et al., 2019), which has accelerated in recent decades (Davies and Glasser, 2012; Dussaillant et al., 2019). Due to the high precipitation levels in the Patagonian Andes (Aguayo et al., 2024a), the relative contribution of glaciers to regional water supply is generally low, with glacier runoff serving as a flow buffer during dry periods rather than a major source of streamflow (Ruiz et al., 2022). Nevertheless, recent studies have reported increased river flows in catchments with important glacierised areas (Masiokas et al., 2019; Van Wyk de Vries et al., 2023), with a growing number of rivers showing significant trends (p < 0.01) in the last decade (e.g. Santa Cruz River; Pasquini et al., 2021).
Despite advances in glacier research, modelling efforts in the Patagonian Andes remain constrained by limited data for calibration and validation. For example, to circumvent the limited ground-based atmospheric data, many modelling studies have used dynamic/statistical downscaling methods based on global climate reanalyses (Table S1 in the Supplement). However, the different approaches and data sources have overestimated the precipitation, according to numerical simulations of regional moisture fluxes (Sauter, 2020). Despite the severe lack of data on melt patterns and snow accumulation in the upper plateaus of the Patagonian ice fields (Bravo et al., 2019a, b), most regional modelling efforts have focused on this region (Table S1). In this area, glacier modelling has generally relied on energy balance approaches based on downscaled reanalysis data. Only two studies have modelled the regional hydrological contribution of the Patagonian glaciers. Using the SnowModel (1979–2014), Mernild et al. (2017) estimated a mean specific runoff of 6240 and 6700 mm yr−1 for the Southern Patagonian Ice Field (SPI) and Northern Patagonian Ice Field (NPI), respectively. More recently, Caro et al. (2024) used the Open Global Glacier Model (OGGM) to compare the hydrological response of Andean catchments between 2000–2009 and 2010–2019. In the Patagonian Andes, an increase in glacier melt was found, ranging from 6 % to 14 % depending on the zone. Although recent modelling efforts have benefited from the increased availability of geodetic mass balances to calibrate and validate surface mass balance models (Table S1), important sources of uncertainty in the future evolution of Patagonian glaciers remain.
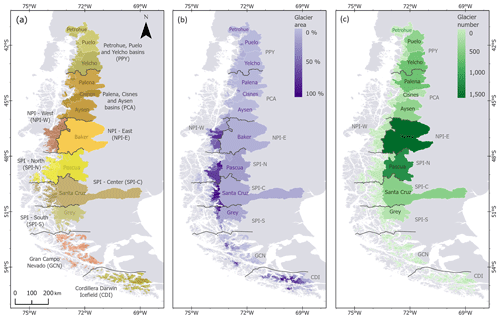
Figure 1Study area. (a) Hydrological zones (n = 9) for the 847 catchments. The names in grey correspond to the names of the main catchments (area > 5000 km2) in the study area, which account for 68 % of the total catchment area. (b) Glacier area for each catchment. (c) Number of glaciers in RGI6 per catchment.
There are several sources of uncertainty in the modelling chain of glacier projections. At the global scale, results from the Glacier Model Intercomparison Project Phase 2 (GlacierMIP2) showed that the emission scenario is the largest source of uncertainty by the end of the century, but the uncertainty from the glacier models, which use different data sources and calibration setups, is the largest source until 2050 (Marzeion et al., 2020). Locally, several studies have shown that individual choices during model initialisation and calibration, such as the historical climate (Compagno et al., 2021; Watanabe et al., 2019), the glacier inventory (Li et al., 2022), the ice thickness (Gabbi et al., 2012) and the downscaling strategy (Schuster et al., 2023), have an impact on glacier evolution. However, few studies have compared the influence of multiple components of the modelling chain on projected glacio-hydrological changes, and those that have been conducted are typically local (basin-specific), limiting the broader applicability of their conclusions. For instance, Huss et al. (2014) found that winter snow accumulation and the glacier retreat model have the greatest influence on the glacier runoff projections in the Findelengletscher basin (Switzerland), while the downscaling strategy, calibration data quality and the surface mass balance model are of secondary importance. Mackay et al. (2019) used hydrological signatures, which are quantitative metrics that describe the dynamic properties of hydrological time series (McMillan, 2021), to measure changes in the hydrology of the Virkisá basin (southern Iceland). They found that the main sources of uncertainty were global circulation models and emission scenarios, but for certain hydrological signatures, the most important source was the representation of glacio-hydrological processes. Overall, adding additional data (e.g. snow cover area, glacier mass change) to the calibration of glacio-hydrological processes has proven to be more important than increasing the complexity of the model (Van Tiel et al., 2020).
In this study, we investigated the importance of six sources of data uncertainty in 10 glacio-hydrological signatures (i.e. metrics) that characterise the evolution of glacier runoff. The sources of uncertainty were glacier inventories (n = 2), ice thickness datasets (n = 2), historical climates (n = 4), global circulation models (n = 10), emission scenarios (n = 4) and bias correction methods (n = 3). The resulting 1920 scenarios were simulated using the Open Global Glacier Model (OGGM) to project the evolution of each glacier (area > 1 km2) in the Patagonian Andes (40–56° S) over the period of 1980–2099. Finally, the importance of each source of data uncertainty was measured using the permutation feature importance of random forest regression models.
Our study area comprises the Patagonian Andes (40–56° S; Fig. 1), where the seasonal melting of glaciers is essential for the long-term sustainability of the local ecosystems and coastal human populations (Iriarte et al., 2014). Glaciers in the Patagonian Andes cover an extensive area of 25 886 km2, which represents 82 % of the total glacierised area of the Andes at the time of the inventory (∼ the year 2000; RGI Consortium, 2017). This region includes the Patagonian ice fields, which form the largest freshwater reservoir in the Southern Hemisphere outside of Antarctica, with a total area of 17 195 km2 in 2011 (Davies and Glasser, 2012) and an estimated ice volume of 4756 ± 923 km3 (Millan et al., 2019).
To better analyse the spatial variability in hydrological dynamics and to provide a framework for aggregating projected glacio-hydrological changes, the glaciers in the study area were grouped into catchments, which were then aggregated into nine hydrological zones (Fig. 1). This catchment-scale aggregation is consistent with ongoing efforts to integrate global glacier simulations into hydrological models (Hanus et al., 2024; Pesci et al., 2023; Wiersma et al., 2022), which often operate at the catchment or river scale.
We delimited all catchments in the study area using 3 arcsec NASA digital elevation model (NASADEM) data (NASA JPL, 2020), with each catchment representing an independent river system reaching the sea. From these, we selected 847 glacierised catchments, each with at least one glacier and a glacier area greater than 0.1 %. The 0.1 % glacier area threshold was selected as a conservative threshold for the drought buffering effect (see Fig. 3 in Ultee et al., 2022). These catchments were divided into nine hydrological zones based on the spatial patterns of precipitation and temperature, which have previously shown a strong ability to explain recent spatial variability in glacier change (Caro et al., 2021). The northern area (∼ 41–46° S; Fig. 1) is characterised by two zones that aggregate large catchments with a low glacier area: Petrohue, Puelo and Yelcho (PPY) basins and Palena, Cisnes and Aysen (PCA) basins. The Northern Patagonian Ice Field (NPI; ∼ 46–48° S) was divided into two zones according to its main aspect (NPI-E and NPI-W). The eastern side (NPI-E) coincides with the location of the Baker River basin, one of the catchments with the largest glacier area in the study area and the focus of regional (Dussaillant et al., 2019) and global (Huss and Hock, 2018) glacio-hydrological studies. The Southern Patagonian Ice Field (SPI; ∼ 48–52° S) was divided latitudinally according to the main catchments on the eastern side (Pascua in SPI-N, Santa Cruz in SPI-C and Grey in SPI-S). Finally, the southern area was divided into the Gran Campo Nevado (GCN; ∼ 52–54° S) and the Cordillera Darwin ice fields (CDI; < ∼ 54° S), which host many small catchments. In contrast to the rest of the area, both southern zones receive uniform precipitation throughout the year, with no clear seasonality.
3.1 The Open Global Glacier Model (OGGM)
We used the Open Global Glacier Model v1.5.4 (OGGM, Maussion et al., 2019), an open-source model that couples a surface mass balance model with a model of glacier dynamics, to simulate the individual evolution of glaciers. The model has been used in global studies (Marzeion et al., 2020; Rounce et al., 2023; Zekollari et al., 2024) and hydrological studies (e.g. Caro et al., 2024; Hanus et al., 2024; Pesci et al., 2023; Zhao et al., 2023). The climatic mass balance model is based on an adapted version of the temperature index model used by Marzeion et al. (2012). In this approach, the monthly mass balance (Bi) at elevation z is calculated as
where Pf is a precipitation factor used to account for measurement biases in mountainous topography, to further downscale precipitation to the glacier resolution and to account for missing processes (e.g. debris cover, firn densification, avalanches) not explicitly included in the mass balance. and Ti are the monthly solid precipitation and air temperature, μ∗ is the temperature sensitivity of the glacier, and Tmelt is the monthly mean air temperature above which ice melt is assumed to occur. The climate variables are obtained from the nearest grid point of the climate gridded product (see Sect. 3.2.1). For temperature, this is adjusted to the glacier surface elevation using a constant lapse rate of −6.5 °C km−1, a value that is commonly used (see local examples in Table S1). Positive-degree months () and solid precipitation are calculated using the default thresholds for melting (Tmelt = −1 °C) and accumulation (Tsolid = 0 °C and Tliquid = 2 °C). When the temperature is between Tsolid and Tliquid, the solid precipitation varies linearly between 100 % and 0 % at the lower and upper limits, respectively. The contributions of positive-degree months and solid precipitation are combined to calculate the monthly mass balance, which is used to update the glacier geometry annually.
Gridded glacier geometry is obtained by overlaying glacier inventory outlines and NASADEM elevation data (NASA JPL, 2020) on a regular grid. The resolution of the grid varies with the glacier size, ranging from 10 to 200 m. Glaciers are then segmented into elevation bands, each of which covers an elevation difference of 30 m, following the algorithm described in Werder et al. (2020). The ice dynamics flowline model of OGGM relies on a depth-integrated ice velocity u (m s−1), utilising the shallow ice approximation (SIA):
where A is the ice creep parameter (), n is the exponent of Glen's flow law (n = 3), h is the local ice thickness (m), ρ is the ice density (900 kg m−3), g is the gravitational acceleration (9.81 m s−2) and α is the surface slope computed numerically along the flowline (following Eqs. 3 and 4 of Maussion et al., 2019). With this velocity, the flux of ice along the glacier is explicitly computed.
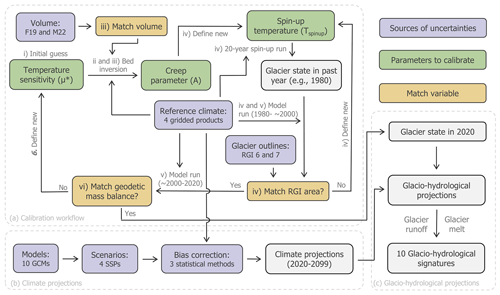
Figure 2Methodological framework. (a) Open Global Glacier Model (OGGM) dynamic calibration workflow. Roman numerals refer to the calibration steps in Sect. 3.1. (b) Climate projections. (c) Glacio-hydrological projections. GCMs are general circulation models, SSPs are Shared Socioeconomic Pathways, F19 and M22 are thicknesses estimated from Farinotti et al. (2019) and Millan et al. (2022), and RGI is the Randolph Glacier Inventory.
In this study, we set the precipitation factor (Pf) to 1.0 to assess the influence of different reference climates on the evolution of each glacier (Fig. 2), assuming that the estimated precipitation from the different products corresponds to the “true” values. Frontal ablation of marine-terminating and lake-terminating glaciers was not explicitly simulated. However, Malles et al. (2023) recently showed that the mass-balance model (through different temperature sensitivities) implicitly accounts for the effect of frontal ablation when calibrated against the Hugonnet et al. (2021) observations, resulting in relatively small changes in the projections. Not considering frontal ablation is an acknowledged shortcoming of our study and should be further investigated in future studies.
The calibration of each glacier consisted of a newly developed iterative process that involves three parameters: the temperature sensitivity (μ∗; Eq. 1), the composite ice creep parameter (A; encapsulating basal sliding and ice deformation, Eq. 2) and finally, the spin-up temperature (Tspin-up; used to find a historical glacier state). The calibration procedure, shown in Fig. 2, unfolds through the following steps.
- i.
We defined the initial value of μ∗ (Eq. 1) by matching the modelled specific mass balance with the geodetic mass balance of Hugonnet et al. (2021). This is calculated using the period of 2000–2020, the reference climate and the static surface geometry, which refers to the outline obtained from the Randolph Glacier Inventory (RGI; see next section).
- ii.
For the snapshot inversion in the next step, we need to determine the apparent mass balance. The apparent mass balance is defined as the climatic mass balance plus any changes in thickness due to ice flow and is always zero when integrated over the entire glacier (see Farinotti et al., 2009). By assuming that the glacier is in equilibrium at the time of the static surface geometry (i.e. no dynamic thickness changes), we calculate the apparent mass balance by first determining the specific mass balance using the static surface geometry and the reference climate from the geodetic mass balance period (2000–2020). We then adjust this mass balance profile vertically so that when integrated over the entire glacier, it equals zero. This method follows the equilibrium assumption described in Maussion et al. (2019).
- iii.
We used the derived apparent mass balance for an inversion for the underlying glacier bed. Throughout this inversion, parameter A (Eq. 2) is defined such that the resulting inversion glacier volume matches the estimates for each hydrological zone defined in Fig. 1. The inversion method follows Maussion et al. (2019) when the sliding parameter is set to 0.
- iv.
The next step is to find a glacier state in the past (the first attempt is 1980) from which a dynamic glacier run to the RGI date (approximately the year 2000) results in the given RGI area. To define different glacier states in the past, the temperature spin-up Tspin-up (the first guess is −1 °C) is added to the reference climate, and we define a mean mass balance using the perturbed reference climate between 1980 and the RGI date. With this mean mass balance a 20-year dynamic model run is conducted, and the resulting glacier state defines the 1980 extent. How consecutive guesses of Tspin-up are found is described in Appendix A. If the resulting glacier is too large even when we start from an ice-free initial glacier state in the past or if the resulting glacier is too small and the algorithm grows the glacier outside the domain, a shorter spin-up period is tried two times (starting in 1985 or 1990). If the spin-up period is shortened, a fixed geometry volume is calculated by going backwards to 1980, using the calculated mass change on the constant surface geometry (assuming a bulk density of 900 kg m−3). This is done to have a continuous volume time series for all glaciers. We only move on if this step has successfully found a proper past glacier state to match the RGI area within 1 km2 or 1 % of the total area, whichever is smaller.
- v.
We initiated a dynamic simulation from 1980 to 2020, using the reference climate inputs and starting from the glacier state inferred in the previous step.
- vi.
Finally, the geodetic mass balance resulting from the dynamic simulation was calculated and compared with the observed values from Hugonnet et al. (2021). If the difference between these values was within the defined uncertainty (± 250 ), the calibration/initialisation workflow was terminated and the resulting glacier in 2020 and the parameters μ∗ and A were used as inputs for the projection runs. If not, a new μ∗ was defined (Appendix A) and the process was started again from the beginning.
3.2 Sources of uncertainty
The historical conditions involved in the calibration process considered the geometry obtained from the glacier inventories, the volume obtained from ice thickness datasets and the reference climate dataset (Sect. 3.2.1). The historical conditions were used to project the future evolution given by different general circulation models (GCMs), future scenarios and bias correction methods (Sect. 3.2.2 and 3.2.3).
3.2.1 Historical conditions
-
Glacier geometry. The geometry, represented by the glacier outlines, was obtained from RGI6 (Randolph Glacier Inventory – Version 6; RGI Consortium, 2017) and RGI7 (RGI Consortium, 2023). In the latest version, RGI7 integrates the national inventories of Chile (Barcaza et al., 2017) and Argentina (Zalazar et al., 2020). Previous assessments of the complete RGI region (20–56° S) have shown that both datasets (RGI6 and RGI7) show similar areas across different latitudes (−3 % of total area relative to RGI6; Zalazar et al., 2020). Nevertheless, the national inventories included in RGI7 showed a higher number of glaciers (Δn = 8493) and area (Δ = 651 km2) for the smallest glaciers (< 0.5 km2) and differences of less than 7 % in the Patagonian ice fields compared to RGI6.
-
Ice volume. Individual volumes for each glacier were derived from the thickness estimated from Farinotti et al. (2019) and Millan et al. (2022) (hereafter F19 and M22, respectively). F19 is a consensus estimate from five models that use principles of ice flow dynamics to infer ice thickness from surface properties. In contrast, M22 uses glacier flow mapping to reconcile the spatial distribution of ice masses with glacier dynamics, morphology and ice divides. In the Southern Andes, Hock et al. (2023) reported that M22 had 13 % more total ice volume than F19. Considering that the two volume data sources do not have complete coverage of all glaciers in RGI6 (100 % and 98.2 % of the area for F19 and M22, respectively) and RGI7 (99.1 % and 96.4 % of the area for F19 and M22, respectively), we used volume-area scaling (VAS, Hock et al., 2023) to complete the coverage. In this approach, we calculated the VAS parameters for each hydrological zone (defined in Fig. 1) and volume data source separately.
-
Reference historical climate. We used monthly precipitation and air temperature time series (period of 1980–2019) from ERA5 (0.25°; Hersbach et al., 2020) and three gauge-corrected alternatives that use ERA5 in the bias correction process (CR2MET v2.5, MSWEP v2.8/MSWX and PMET v1.0). CR2MET v2.5 (0.05°; Boisier, 2023) is the current national reference for hydrometeorological studies in Chile and is based on a statistical downscaling technique that uses ERA5, meteorological records, satellite land surface temperature and topographic descriptors. MSWEP v2.8 (0.1°; Beck et al., 2019) is a global precipitation product that merges gauges, satellites and reanalysis data and has outperformed other state-of-the-art precipitation products over Chile (Zambrano-Bigiarini, 2018). Precipitation from MSWEP v2.8 was complemented with air temperature from MSWX (0.1°; Beck et al., 2022), a bias-corrected meteorological product compatible with MSWEP. Finally, PMET v1.0 (Aguayo et al., 2024a) was developed for western Patagonia using statistical bias correction procedures, spatial regression models (random forest) and hydrological methods (Budyko framework) to correct the underestimation of precipitation reported in areas with pronounced elevation gradients and significant snowfall. In an earlier study, PMET outperformed ERA5, CR2MET and MSWEP in terms of hydrological modelling performance (Aguayo et al., 2024a).
3.2.2 Climate projections
Climate projections of monthly precipitation and air temperature (the period of 2020–2099) were obtained from 10 GCMs (Table S2 in the Supplement) of the Coupled Model Intercomparison Project 6 (CMIP6; Eyring et al., 2016). Previous hydrological studies have suggested that 10 GCMs can ensure that the median of all possible combinations produces similar uncertainty components as the entire ensemble (Wang et al., 2020). Considering only GCMs with at least one output in all emission scenarios, the selection of the 10 GCMs was based on the recommendations of Hausfather et al. (2022), who suggest focusing on a subset of GCMs that are most consistent with the assessed warming projections of the Sixth Assessment Report (AR6). In this case, the selected GCMs have a transient climate response (TCR; temperature change at the time of CO2 doubling) that lies in the “likely” range of 1.4–2.2 °C (Table S2), which is a good approximation of the assessed warming (Tokarska et al., 2020). Considering that future scenarios are the main source of uncertainty at the end of the century in the Southern Andes (Marzeion et al., 2020), we used four different Shared Socioeconomic Pathways (SSPs; O'Neill et al., 2016): SSP1-2.6, SSP2-4.5, SSP3-7.0 and SSP5-8.5. Each GCM was initially resampled to 1.0° using a bilinear filter, and only the standard model realisation was considered (r1i1p1f1 in all cases).
3.2.3 Bias correction method
Three statistical bias correction methods were evaluated to assess their impact on the glacier projections. The objective of bias correction is to minimise the systematic error in the climate projections obtained from general circulation models (Sect. 3.2.2) using the reference climate used in the calibration process (Sect. 3.2.1). The selected methods were mean and variance scaling (MVA; Chen et al., 2011), quantile delta mapping (QDM; Cannon et al., 2015) and multivariate bias correction with N-dimensional probability density function transformation (MBCn; Cannon, 2018). The MVA approach is commonly used in GlacierMIP2, as it guarantees that the bias-corrected time series has the same mean and variance as the reference time series in the reference period. QDM is a univariate hybrid method that combines quantile-based delta change and bias correction methods, aiming to adjust the entire distribution of the climate variable rather than just the mean and variance. Finally, MBCn is a multivariate bias correction that corrects biases in multiple variables simultaneously by transforming the joint probability distribution of these variables (in our case, precipitation and temperature), addressing inter-variable dependencies in addition to individual biases. The bias correction parameters of all methods were calculated on a monthly basis to account for the seasonality of GCM biases. Following the protocol of the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP3b; Lange, 2021), the reference period was 1980–2015 for all correction methods. Climate outputs based on the QDM and MBCn approaches were obtained using the xclim package v0.4 (Logan et al., 2022).
3.3 Comparative analysis of sources of uncertainty
Taking all glaciers into account, each source of data uncertainty was analysed to quantify the difference between the alternatives. For area and volume, we calculated the relative and absolute differences for each catchment and hydrological zone defined in Fig. 1. To calculate these differences, we aggregated glacier area and volume for a given catchment by selecting all glaciers with a terminus location within that catchment. It is assumed that if the inventory outlines are correct, all the water flowing out of the glacier will flow via its terminus. In addition, we compared the acquisition dates of the glacier geometries for both inventories. To assess the influence of the reference climate on the glacier mass balance, we calculated the solid precipitation and positive-degree-day sum in addition to precipitation and temperature. To isolate the effect of the spatial resolution, temperature from ERA5 and MSWEP/MSWX was downscaled to 0.05° using the same lapse rate used by OGGM (−6.5 °C km−1). Precipitation was not downscaled. Similarly, the solid precipitation and positive-degree-day sum were calculated using the thresholds indicated in Sect. 3.1 (Tmelt = −1 °C, Tsolid = 0 °C and Tliquid = 2 °C). Specifically, we calculated and compared annual means for each variable, catchment and product for the reference period (1980–2015) using only the glacierised grid cells.
The climate projections were another source of uncertainty. To assess the impact of the raw climate projections, we calculated the relative change between the reference period (1980–2015) and the future period (2070–2099) for each GCM and SSP. In addition, we calculated the model agreement for precipitation following Iturbide et al. (2021), who defined a high model agreement as being when more than 80 % of the GCMs agree on the sign of the change. Finally, to assess the individual impact of each climate uncertainty source, we estimated the future climate uncertainty, which we defined as the standard deviation across different reference climates (n = 4), GCMs (n = 4), SSPs (n = 4) and bias correction methods (n = 4), resulting in 480 possible combinations. Specifically, we calculated the standard deviation based on the long-term annual mean of each variable, catchment and alternative. Analogously to the reference climate, we calculated the annual mean for the future period (2070–2099) using only the glacierised grid cells.
3.4 Glacio-hydrological runs
We used the OGGM model to estimate the evolution of all glaciers with an area > 1 km2 in the Patagonian Andes (40–56° S) over the period of 1980–2099. This corresponds to 2034 and 1837 glaciers that accumulate 99.0 % and 98.5 % of the total volume estimated by Millan et al. (2022) for RGI6 and RGI7, respectively. For each glacier, we evaluated 16 scenarios generated by the historical conditions (Sect. 3.2.1). These scenarios were used to project the future evolution given by different GCMs, future scenarios and bias correction methods, resulting in 120 future scenarios for each historical simulation (a total of 1920 potential scenarios; Fig. 2). We additionally ran 16 simulations for 80 years with a pseudo-random climate based on the historical climate (30 years) around the year 2000 (i.e. the commitment run).
For all 1920 scenarios, we extracted the annual glacier area, volume and specific mass balance of each modelled glacier. To assess the hydrological contribution, we additionally extracted glacier runoff that corresponds to all water originating from the initially glacierised area (i.e. the year 1980 here; Huss and Hock, 2018). In this approach, OGGM calculates the glacier runoff from the sum of on- and off-glacier melt and on- and off-glacier liquid precipitation. To disaggregate the impact of projected precipitation changes, we also extracted the melt on the glacier (hereafter glacier melt), which is the sum of ice melt and seasonal snowmelt on the glacier (Fig. 2c). As in the comparative analysis (Sect. 3.3), the time series were initially aggregated at the catchment scale according to the location of the glacier terminus.
Table 1Glacio-hydrological signatures used to characterise the glacier runoff and melt time series of each catchment. The regime characteristics correspond to the initial categories proposed by Richter et al. (1996).
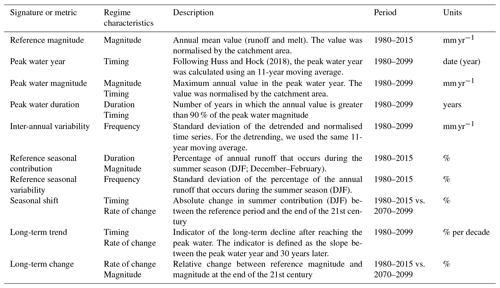
Glacier runoff and melt were characterised by 10 glacio-hydrological signatures (i.e. metrics) to describe the hydrological dynamic properties of each catchment (Table 1). The set of signatures was selected to cover the different categories proposed by Richter et al. (1996): magnitude, timing, frequency, duration and rate of change. Poff et al. (1997) used these categories to characterise the hydrological regime and proposed that these components fully describe the streamflow characteristics that are important to the aquatic ecosystem. However, our analysis of glacier runoff should not be considered downstream streamflow because our simulations considered only the initially glacierised area and did not include the interaction with other hydrological fluxes (e.g. evaporation and infiltration).
3.5 Hydrological importance of sources of uncertainty
We build random forest (RF) regression models based on the six sources of uncertainty to predict the glacio-hydrological signatures of each catchment (Table 1). For this analysis, we selected 329 catchments with at least one glacier (area > 1 km2) in both inventories. RF regression models generate predictions using an adaptation of Leo Breiman's random forest algorithm, a supervised machine learning method (Breiman, 2001; Svetnik et al., 2003). We used the permutation feature importance to assess the influence of each source (Breiman, 2001). This technique measures the change in model performance (in this case, the root-mean-square error; RMSE) after the values of a single model feature have been permuted (also known as shuffled). First, the baseline performance of the model is established using all features. Then, each feature is shuffled one at a time, breaking its link with the target variable, and the performance is recalculated. A significant increase in the RMSE after shuffling indicates the importance of the feature, as its removal degrades the performance of the model. This process is repeated for all features, allowing the relative importance to be assessed based on their impact on model performance. This method has been successfully used as a sensitivity analysis tool in several studies (e.g. Bennett et al., 2022; Schmidt et al., 2020). For each catchment and signature, the training set was selected to be 90 % of the full dataset of scenarios, and the remaining 10 % was used to measure the permutation importance. The importance of each feature (in this case, categorical predictors) was represented as the percentage of the average change in the RMSE over 30 experiments of shuffling one feature. For all RF models, we used 500 regression trees as an ensemble, with each tree having a minimum leaf size of five. For each split, two variables were randomly selected as candidates. The complete procedure was performed using scikit-learn v1.3.0 (Pedregosa et al., 2011).
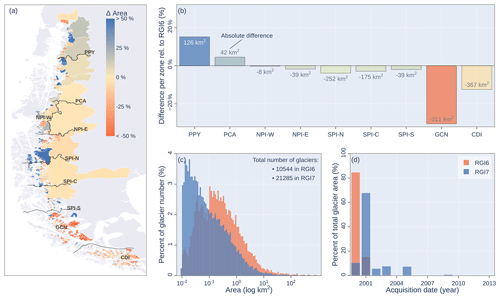
Figure 3Comparison between Randolph Glacier Inventory (RGI) versions 6 and 7. Difference in area (a) per catchment and (b) per hydrological zone considering RGI6 as reference. The solid black lines correspond to the division between the hydrological zones defined in Fig. 1. The text in (b) indicates the absolute differences in area (RGI7 − RGI6). (c) Distribution of glacier area. (d) Percent of glacier area per year of acquisition.
4.1 Analysis of sources of uncertainty
4.1.1 Historical conditions
The incorporation of national inventories in RGI7 resulted in important differences compared to RGI6 (Fig. 3). The total number of glaciers increased from 10 544 in RGI6 to 21 285 in RGI7. Relative to this, RGI6 showed a higher number of glaciers with an area greater than 1.0 km2, but RGI7 has considerably more smaller glaciers (< 1.0 km2). The total glacier area decreased by 4.0 % in RGI7 (Δ = 1024 km2), with important regional differences (Fig. 3a and b). The northern area between the Puelo and Aysen catchments (PPY and PCA) showed increases ranging from 4 % to 15 % relative to RGI6 (Fig. 3b). In contrast, the area located south of the SPI (GCN and CDI) showed decreases with values as low as −31 % (Fig. 3b). These regional differences may be due to several factors, including improved outlines and corrections from local inventories and differences in acquisition dates (Fig. 3d). For example, 84.7 % of the glacier area in RGI6 has an acquisition date in 2000, while 67.8 % of the glacier area in RGI7 has an acquisition date in 2001.
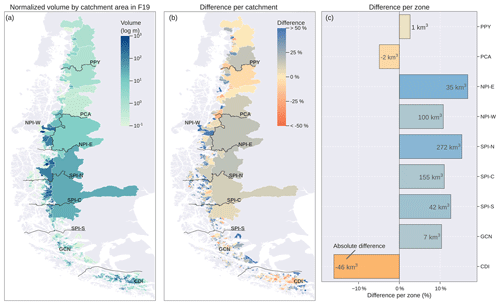
Figure 4Volume comparison between Millan et al. (2022) (M22) and Farinotti et al. (2019) (F19) based on RGI6. (a) Volume normalised by the catchment area from F19 (in log scale). Percentage difference between M22 and F19 per (b) catchment and (c) hydrological zone considering F19 as the reference. The solid black lines correspond to the divisions between the hydrological zones defined in Fig. 1. The text in (c) indicates the absolute difference in volume (M22 − F19).
Ice volume was another source of uncertainty analysed in this study (Fig. 4). According to the F19 dataset, the hydrological zones comprising the SPI have an ice volume of 3526 km3, representing 68.8 % of the study area. Conversely, the PPY, PCA, GCN and CDI zones accounted for only 8.9 % of the total ice volume. Based on RGI6, 26.6 % of the glacier area had a normalised volume (ice volume divided by catchment area) of less than 1.0 m (Fig. 4a). The M22 dataset showed more ice volume than the F19 dataset in 81.7 % of the total glacier area (overall volume difference of 11.1 %; Fig. 4b), mainly in the Patagonian ice fields (Fig. 4c). In this area, the NPI and SPI zones showed increases of 135 and 469 km3 (relative to F19), respectively. Only the PCA and CDI zones showed the opposite change, where the M22 dataset shows a lower total ice volume (Fig. 4c).
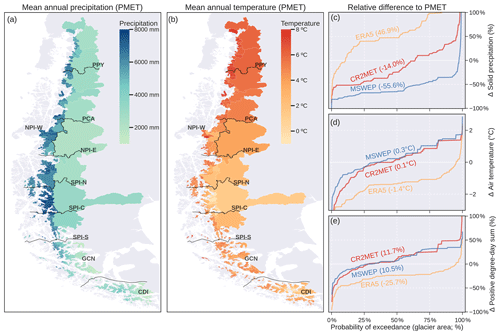
Figure 5Historical reference climate in terms of annual precipitation (a) and temperature (b) according to the PMET dataset. Long-term averages (1980–2015) were calculated using only the glacierised grid cells of each catchment. The grey names in (a) and (b) correspond to the names of the main catchments, while the solid black lines correspond to the divisions between the hydrological zones defined in Fig. 1. Differences between PMET and CR2MET, ERA5, and MSWEP/MSWX are sorted by glacier area for solid precipitation (c), temperature (d) and positive-degree-day sum (e). The values in parentheses indicate the glacier area-weighted means.
The historical climate of the glaciers of the Southern Andes showed an important spatial climate diversity according to the PMET dataset, with annual mean precipitation varying between 1000 and 8000 mm yr−1 (Fig. 5a; 1980–2015). The spatial pattern of precipitation showed a clear difference between the western (> 4000 mm yr−1) and the eastern (< 2000 mm yr−1) side of the Andes (Fig. 5a). Mean precipitation was greater than 4000 mm yr−1 over 51.5 % of the glacier area, and 95.0 % of the glacier area showed a mean temperature above 0 °C (Fig. 5b). The four climate products used to model the historical evolution of the glaciers showed important differences in precipitation and temperature (Fig. 5c–e). In relation to PMET, ERA5 and MSWEP showed total differences in solid precipitation of 46.9 % and −55.6 % (glacier area-weighted mean; Fig. 5c), respectively. The relative differences in temperature were mostly less than 1 °C, except for ERA5, which showed a cold bias (Fig. 5d). These differences resulted in discrepancies of less than 25 % for the positive-degree-day sum (Fig. 5e).
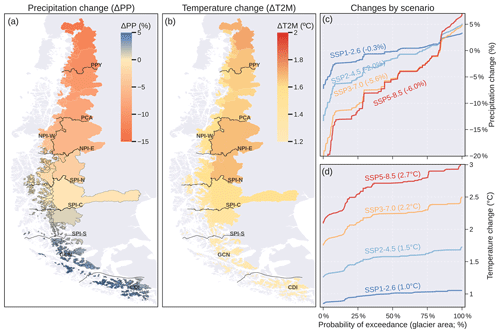
Figure 6Multi-model means (n = 10) of future precipitation (a) and temperature change (b) considering the SSP 2-4.5 scenario (1980–2015 vs. 2070–2099). Means were calculated using only the glacierised grid cells of each catchment. The catchments with black outlines indicate low model agreement, where less than 80 % of the models agree on the sign of the change. The solid black lines indicate the divisions between the hydrological zones defined in Fig. 1. Differences by scenario for precipitation (c) and temperature (d). The values in parentheses indicate the glacier area-weighted means.
4.1.2 Climate projections
The climate projections for the end of the century (2070–2099) showed clear latitudinal patterns (Fig. 6a and b). Overall, the northern area was characterised by a warmer and drier future climate, while the southern area showed a slight increase in precipitation accompanied by a slight increase in temperature. The GCMs showed high model agreement in all zones (> 80 % of the models agree on the sign of the change), except in the SPI and GCN zones (Fig. 6a). The climate projections for the catchments varied according to the SSP scenario. Under the SSP1-2.6 scenario, 54 % of the glacier area is projected to experience a decline in precipitation (Fig. 6c). This percentage increases to 83 % under the SSP5-8.5 scenario. For temperature, the glacier area-weighted warming varies from 1.0 °C in SSP1-2.6 to 2.7 °C in SSP5-8.5 (Fig. 6d).
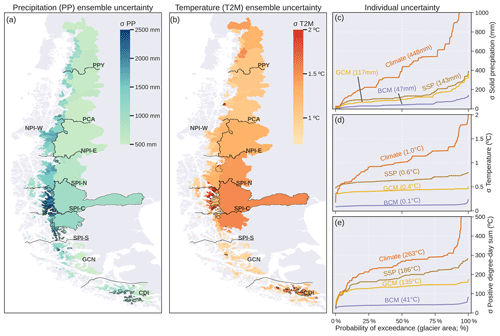
Figure 7Future climate uncertainty (standard deviation; σ) in mean annual precipitation (a) and temperature (b) obtained from the complete ensemble (2070–2099; n = 480). The catchments with a coefficient of variation greater than 40 % have black outlines. Means were calculated using only the glacierised grid cells of each catchment. The solid black lines indicate the divisions between the hydrological zones defined in Fig. 1. Individual uncertainty (in terms of glacier area) in solid precipitation (c), temperature (d) and positive-degree-day sum (e) across different reference climates, emission scenarios (SSPs), general circulation models (GCMs) and bias correction methods (BCMs). The values in parentheses indicate the glacier area-weighted means.
4.1.3 Future climate uncertainty
The standard deviation of the mean annual precipitation in the long term (2070–2099) was greater than 1000 mm in 68 % of the glacier area (Fig. 7a). Similarly, the standard deviation of the temperature was greater than 1.0 °C in 89 % of the glacier area (Fig. 7b). The precipitation showed greater variability (expressed as coefficient of variation) in the glaciers located on the western side of the Southern Andes (Fig. 7a). On the other hand, the greater variability in temperature was concentrated in the SPI-C and CDI zones (Fig. 7b). For all variables, the reference climate was the most important source of uncertainty (Fig. 7c–e). The difference between SSPs and GCMs was more pronounced for temperature and the positive-degree-day sum (Fig. 7d and e) than for solid precipitation (Fig. 7c). The different bias correction methods (BCMs) converged to similar values with no important differences between them.
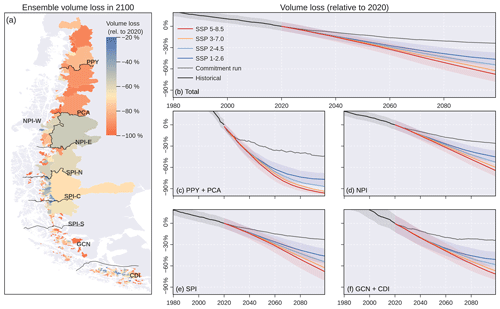
Figure 8Glacier volume loss relative to 2020. (a) Mean volume loss in 2100 derived from the full ensemble (n = 1920). Volume loss for the sum of all catchments (b), the northern area including PPY and PCA (c), the Northern Patagonian Ice Field (d), the Southern Patagonian Ice Field (e), and the southern area including GCN and CDI (f). The solid line represents the mean for each scenario, while the uncertainty bands represent ± 1 standard deviation (shown only for the historical, SSP 1-2.6 and SSP 5-8.5 scenarios for visualisation purposes). Volume, area and specific mass balance by hydrological zone are shown in Fig. S1. The commitment run considers a pseudo-random climate based on the period of 1985–2015.
4.2 Glacio-hydrological projections
Projections from OGGM indicate that the glacier volume loss of recent decades will continue (Fig. 8). Considering the full set of SSP scenarios (n = 1920), 68 % ± 21 % (mean ± 1 standard deviation) of the total glacier area will lose more than 50 % of its current (the year 2020) volume by the end of the century (Fig. 8a). The results indicate variable ice loss depending on model choices. Considering the prolongation of historical climate conditions (commitment run), 24 % ± 6 % of the total glacier ice is committed to melt in the long term (the year 2099 in Fig. 8b). Aggregating the time series by the emission scenario (n = 480 per SSP), the volume loss varied from 46 ± 9 % in SSP1-2.6 to 67 ± 11 % in SSP5-8.5, with clear spatial differences (Fig. 8c–f). In the northern region (PPY and PCA), the projected loss is exacerbated by the precipitation projections (Fig. 5) and the low ice volume (Fig. 4), resulting in percentage losses exceeding 70 % under all scenarios (Fig. 8c). Under the high-emissions scenario (SSP 5-8.5), the percentage losses in NPI, SPI and the southern area (GCN and CDI) are projected to be 64 % ± 8 %, 68 % ± 12 % and 71 % ± 7 %, respectively (Fig. 8d–f). The confidence intervals for volume and area in the reference period (Fig. S1 in the Supplement) are consistent with the differences found between the glacier inventories (Fig. 3) and ice thickness datasets (Fig. 4). Similar to the ice volume projections, the mean specific mass balance diverges strongly depending on the emission scenarios (Fig. S1).
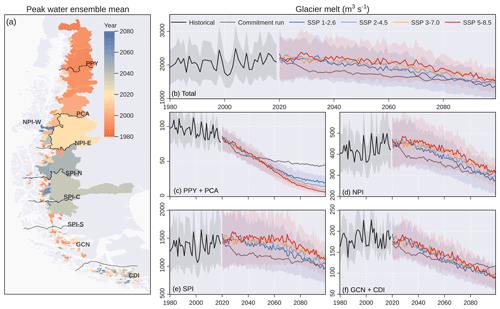
Figure 9Glacier melt projections for the Patagonian Andes. (a) Peak water year obtained from the complete ensemble (n = 1920). Glacier melt evolution for the sum of all catchments (b), the northern area including PPY and PCA (c), the Northern Patagonian Ice Field (d), the Southern Patagonian Ice Field (e), and the southern area including GCN and CDI (f). The solid line represents the mean for each scenario, while the uncertainty bands represent ± 1 standard deviation (shown only for the historical, SSP 1-2.6 and SSP 5-8.5 scenarios for visualisation purposes). Glacier runoff and melt and the ratio between the two, disaggregated by hydrological zone, are shown in Fig. S2. The commitment run considers a pseudo-random climate based on the period of 1985–2015. For visualisation purposes, the commitment run was smoothed using a 10-year moving average.
The volume loss drives changes in the hydrological contribution of glaciers in the Patagonian Andes (Fig. 9). Considering the full set of SSP scenarios (n = 1920), 34 % ± 13 % of the glacier area has already peaked in terms of glacier melt (the year 2020; Fig. 9a). The total glacier melt for the study domain in the reference period (1980–2015) was 2051 ± 537 m3 s−1 (Fig. 9b). For this total, the northern area (PPY and PCA), NPI, SPI and the southern area (CGN and CDI) contributed 4.6 %, 20.5 %, 66.0 % and 8.8 % (Fig. 9c–f), respectively. The projected trajectories of glacier melt varied slightly among emissions scenarios (n = 480 per SSP), and the projections and their uncertainties tended to converge towards the end of the century (Fig. 9b). For example, the mean glacier melt in 2070–2099 varies from 1555 ± 372 m3 s−1 in SSP 1-2.6 to 1784 ± 369 m3 s−1 in SSP 5-8.5 for the whole region. While most hydrological zones are projected to experience a steady decrease in glacier melt, the SPI zones show slightly diverging trajectories in their mid-century meltwater contribution depending on the emission scenario (Fig. 9e). To the south of SPI, the slight increase in precipitation projections (Fig. 6) buffers the decrease in glacier melt, maintaining the contribution of glacier runoff. In all hydrological zones, the ratio between glacier runoff and melt is close to 60 % in the reference period and decreases to 40 % towards the end of the century (Fig. S2 in the Supplement).
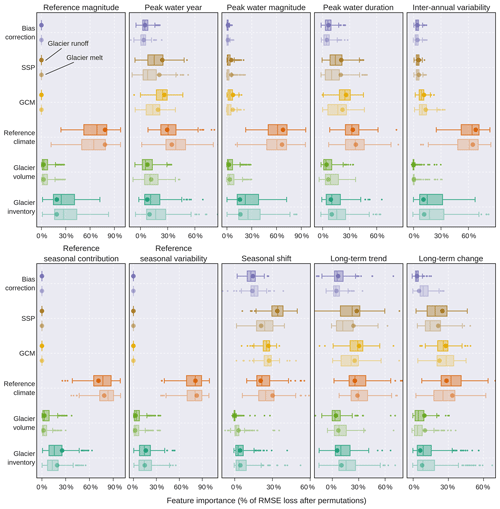
Figure 10The importance of each source of uncertainty for the glacio-hydrological signatures (Table 1) obtained from the glacier runoff (dark colours) and melt (light colours). The importance of each source is represented as the percentage of the average change in the root-mean-square error (RMSE), with high values indicating greater importance. Each boxplot aggregates the results obtained from the permutation feature importance using 329 catchments (Sect. 3.5). The circles correspond to the glacier area-weighted means. Note that each panel has a different range.
4.3 Hydrological importance of sources of uncertainty
The glacio-hydrological signature was represented by 10 metrics that characterise the hydrological regime of each catchment (Table 1). Regardless of the variable (glacier runoff or melt), the permutation feature importance of RF models showed that the differences between the historical reference climates contributed most to the total uncertainty (Fig. 10). This was especially clear for the reference magnitude, peak water magnitude, inter-annual variability, and reference seasonal contribution and variability metrics, where the reference climate explained more than 50 % of the total RMSE loss after the permutations. Considering glacier melt only, the accumulated RMSE loss of the historical sources of uncertainty (glacier inventory, glacier volume and reference climate) was greater than that of the future sources (GCM, SSP and BCM) in eight signatures (only five for glacier runoff), including the peak water metrics. In the long-term (trend and change signatures), the historical sources accumulated RMSE losses similar to those of the future sources. In these cases, the selection of the reference climate or GCM was as important as the emission scenario (SSP). The selection of glacier inventory was more important than the ice thickness dataset for most metrics, while the importance of the bias correction method (BCM) was significant (median > 10 %) only for the reference seasonal shift (Fig. 10). As expected, the relative importance of future sources was 0 % for all metrics calculated from the reference period (Table 1).
No clear spatial patterns were detected in the main source of uncertainty (i.e. the variable that accumulated the most RMSE loss; Figs. S3 and S4 in the Supplement). Considering the glacier melt signatures (Fig. S3), the future sources of uncertainty were the main source in only 17 % ± 21 % (mean ± 1 standard deviation) of the total glacier area. In contrast, the reference climate was the main source of uncertainty in 69 % ± 22 % of the glacier area. In comparison to the glacier runoff signatures, the importance of the reference climate decreases to 58 % ± 31 % of the glacier area (Fig. S4).
5.1 Hydrological response of Patagonian glaciers to climate change
The primary objective of glacio-hydrological modelling studies has been to assess the future impacts of climate change (Van Tiel et al., 2020), and therefore GCM and SSP choices have commonly been part of the uncertainty analysis of previous modelling efforts. For the first time, this study incorporated four additional sources of uncertainty (both historical and future) to generate 1920 possible future evolution scenarios in the Patagonian Andes.
As expected, volume loss showed a strong dependence on the emission scenario, with total projected losses ranging from 48 ± 9 % in SSP1-2.6 to 69 ± 10 % in SSP5-8.5 (Fig. 8b). Despite the dependence of the specific mass balance () on the emission scenarios (Fig. S1), the ice melt component of runoff (m3 s−1) did not show a clear dependence on the emission scenario (Fig. 9). This is because, although higher-emission scenarios lead to increased melt rates, the overall glacier area decreases significantly throughout the century (Fig. S1). As the glacier area shrinks, the potential for meltwater generation is reduced, which offsets the increased melt rates under higher emissions. This results in a relatively consistent glacier melt across different emission scenarios. Only a few hydrological zones showed clear differences in their mid-century meltwater contributions between SSP scenarios, such as NPI-W and SPI-N. This is partly explained by the fact that 30 % ± 13 % of the glacier area has already peaked in terms of glacier melt (the year 2020; Fig. 9a). The uncertainty in the glacier melt component is lower than that of the total glacier runoff (Fig. S2) because the latter also includes the liquid precipitation and off-glacier snowmelt components, which are determined more by the reference climate than by model parameters (Fig. 7).
Although glacio-hydrological studies are scarce in the Patagonian Andes, the Baker River basin (NPI-E in Fig. 1; 7.2 % of glacier area) provides a point of comparison with previous studies. Our study revealed a slight increase in glacier runoff (3 % per decade) between 1980 and 2015. This finding is consistent with previous studies by Dussaillant et al. (2019), who observed a similar trend from 2001 to 2017 using ASTER stereo images and stream gauges, and Caro et al. (2024), who reported a 10 % increase in glacier melt from 2000 to 2019 using the OGGM model (Table S1). In a longer time frame, Huss and Hock (2018) found that the peak water of the Baker River has already occurred or will occur in the coming years regardless of the emission scenario (2015 ± 18 and 2020 ± 16 for RCP2.6 and RCP8.5, respectively), which is in agreement with our results indicating that the glacier runoff may have peaked in 2021 (± 15 years), considering all scenarios.
5.2 Hydrological importance of data uncertainty
All 10 glacio-hydrological metrics across the catchments show a considerable uncertainty to modelling choices (Fig. 10). Previous studies have shown that accurate estimates of glacier outlines (Li et al., 2022) and initial ice volumes (Gabbi et al., 2012) have played a pivotal role in ensuring reliable projections of volume and runoff. In our study, despite the larger relative differences in glacier volume than in glacier area (11.1 % vs. 4.0 % of overall difference; Figs. 3 and 4), the selection of glacier inventory was more important than the volume data source for most glacio-hydrological metrics (Fig. 10). The importance of these glacier attributes was only superseded by the choice of the climate in the historical period (Fig. 10). Our uncertainty analysis showed that the reference climate was the most important source in 69 % ± 22 % of the glacier area for glacier melt (Fig. S3) and 58 % ± 31 % of the glacier area for glacier runoff (Fig. S4). The importance of the reference climate lies in its role in establishing baseline conditions against which future changes can be assessed. The reference climate influences temperature and precipitation patterns, which directly shape the seasonal response of glaciers, affecting both melt and accumulation processes. In addition, the choice of reference climate affects parameter calibration, which in turn affects the sensitivity of the model to climate change. For instance, Fig. S5 in the Supplement shows that the temperature sensitivity parameter varies significantly with reference climate, more so than other factors such as glacier geometry and thickness. This highlights how specific combinations of model parameters and reference climate can lead to different outcomes in terms of glacier runoff and melt response.
Despite the large variability in climate, geography and glacier characteristics in the Patagonian Andes, only a few regions showed a low sensitivity to the reference climate. This is partly explained by the fact that some climate products showed overall relative differences of almost 50 % in solid precipitation (Fig. 5), which dominates glacier runoff and melt evolution. For the long-term trend in glacier melt (Fig. S3), the GCMs and SSPs were the main sources of uncertainty in the Patagonian ice fields (SPI, NPI and CDI), areas characterised by mostly neutral precipitation projections (Fig. 6) and the presence of high ice volumes (Fig. 4). The greater importance of the GCMs and SSPs was also observed in the northern area (PPY and PCA) for the long-term change in glacier melt. When considering glacier runoff (Fig. S4), which includes liquid precipitation as glaciers retreat, the importance of the SSP scenario increases in several metrics, such as seasonal shift and long-term change.
5.3 Influence of model calibration
The calibration of large-scale glacier model parameters is usually glacier specific and varies according to the glacier model and the available data (for an extensive overview, refer to Zekollari et al., 2022). For example, in the Global Glacier Evolution Model (GloGEM; Huss and Hock, 2015), the calibration follows a sequential approach where glaciological observations are matched by adjusting a precipitation factor, then a melt factor and finally a temperature bias parameter within predefined ranges. This type of procedure strongly adjusts the forcing climate data to match the expected values from the combination of a mass balance model and observations, which likely explains why Compagno et al. (2021) found that the choice of the reference climate leads to differences of only 7 % in the remaining ice volume by 2100 in Scandinavia and Iceland. However, in High Mountain Asia and using another methodology, Watanabe et al. (2019) found that the differences between the reference climate introduced uncertainties of about 15 % into projected changes in glacier volume.
Considering the scaling effect of the precipitation factor on glacier runoff (Schuster et al., 2023; Wimberly et al., 2024), our study, in turn, chooses not to correct the historical climate dataset (i.e. maintaining Pf = 1), and therefore the historical climate uncertainty is incorporated into the model calibration and then into the projections. This approach recognises the inherent variability in precipitation estimates and aims to capture the range of potential “true” precipitation values. In particular, certain regional climate datasets used in our analysis, such as PMET and CR2MET, are already subject to bias correction procedures to address the potential underestimation of precipitation in high-mountain areas. Thus, by incorporating historical climate uncertainty, our methodology aims to provide a robust framework for glacier runoff projections. Alternatively, future studies could use ensemble meteorological datasets (e.g. Tang et al., 2022) to incorporate uncertainty into their assessments.
In recent years, the calibration workflow of large-scale glacier models has evolved to incorporate model parameter uncertainty as a significant source of uncertainty. For example, the Python Glacier Evolution Model (PyGEM) uses Bayesian inference to calibrate the three parameters of each glacier based on Markov chain Monte Carlo (MCMC) methods (Rounce et al., 2020, 2023). Interestingly, when comparing the mean projected volume loss disaggregated by hydrological zone and SSP scenario with the Rounce et al. (2023) projections, the difference compared to our study was only 4.4 % (RMSE; Fig. S6 in the Supplement). This suggests a remarkable consistency in projected glacier evolution despite potential differences in the sources of uncertainty considered between the studies.
5.4 Limitations and potential implications
There are several sources of uncertainty that were not considered in this study, such as downscaling strategies (e.g. temperature lapse rates), observation uncertainty, the use of frontal ablation parameterisation schemes, the surface mass balance model (e.g. degree day vs. energy balance) and the ice-flow model itself. These are acknowledged shortcomings of our study and should be investigated further. For example, using the OGGM model, Schuster et al. (2023) showed that the use of spatially and seasonally variable lapse rates has the most systematic influence on glacier projections with smaller glacier volumes by the end of the century compared to the constant option. The geodetic mass balance used in the dynamic calibration process is another source of uncertainty. While Hugonnet et al. (2021) obtained a specific mass balance of −720 ± 70 for the complete RGI region (2000–2019), Braun et al. (2019) and Dussaillant et al. (2019) estimated values of −640 ± 20 (2000–2015) and −720 ± 220 (2000–2018), respectively. Minowa et al. (2021) estimated that frontal ablation was −24.1 ± 1.7 Gt yr−1 (2000–2019), representing 34 ± 6 % of total ablation. The study of calving glaciers adds a layer of complexity, as additional processes require potential parameterisations and adjustments, which are also subject to uncertainty (Van Tiel et al., 2020). Using the OGGM model, Malles et al. (2023) found that the global mean sea-level rise contribution at the end of this century is reduced by ∼ 9 % when marine frontal processes were considered in Northern Hemisphere glaciers. Surface mass balance models can also play an important role in glacier evolution, but the lack of data hinders the assessment of the added value of more model complexity (e.g. Temme et al., 2023; Schuster et al., 2023; Huss and Hock, 2015).
The use of ground-based observations can help to reduce the overall uncertainty. For example, the use of observations of ice thickness, such as those based on ground-penetrating radar or airborne surveys, can help to select a better dataset for the study area. However, these observations are spatially and temporally scarce in the Patagonian Andes (e.g. Millan et al., 2019). Furthermore, the generation of large-scale ice thickness datasets requires the compilation of numerous datasets derived from different acquisition dates, which hinders regional validation (Hock et al., 2023). The reference climate can also be assessed using ground-based data. However, the current scarcity, poor quality control protocols, and lack of continuity and reliability of meteorological stations are very important limitations on properly understand atmospheric processes at high elevations (Condom et al., 2020; Masiokas et al., 2020). Recent studies have attempted to narrow the ranges of uncertainty using, for example, regional estimates of moisture flux (Sauter, 2020) and catchment hydrological balance (Aguayo et al., 2024a). Future sources of uncertainty could potentially be reduced using a GCM screening approach. Using Chile as a case study, Gateño et al. (2024) recently proposed an approach that goes beyond bias-related metrics to include metrics related to the ability of GCMs to reproduce the teleconnection responses that can affect regional climate variability and trends. Out of the 10 selected GCMs in our study, 4 are included in the screening recommendation of Gateño et al. (2024) (more details in Table S2).
The implications of our study extend far beyond the Patagonian Andes and resonate with global concerns about the effects of climate change on the hydrological cycle in high-mountain regions. These regions very often face challenges in constraining climate estimates due to a low density of meteorological stations (e.g. Beck et al., 2020). These limitations have led to substantial modelling uncertainties in the hydrological cycle (Tang et al., 2023), which can be projected into the future in climate change impact studies (Tarek et al., 2021). Our study is the first to assess the influence of the reference climate on the evolution of glacier runoff, resulting in differences from previous studies (Fig. 10). In the Southern Andes, the Glacier Model Intercomparison Project Phase 2 (GlacierMIP2) showed that the uncertainty in the emission scenario is the largest source of the specific mass balance rate (Marzeion et al., 2020). Similarly, Mackay et al. (2019) found that the emission scenarios were also the dominant source of projections of streamflow during the melt season in Iceland, contributing up to 65 % of the total projected uncertainty. In our study, the relatively greater influence of the future sources was limited to the long-term metrics, where the selection of the emission scenario or the GCM was as important as the reference climate (Fig. 10). This underscores that future glacio-hydrological projections are strongly shaped by modellers' choices, which should be guided by a systematic review of local datasets to adequately justify modelling choices. In addition, further research into the mechanisms driving the observed differences in precipitation and temperature and their implications for glacier runoff dynamics could provide valuable insights into the broader hydrological response of glaciated regions to changing climate conditions.
In this study, we investigated the importance of six sources of data uncertainty associated with model choices in 10 glacio-hydrological signatures covering the necessary categories to characterise the glacio-hydrological regime of each catchment. For this purpose, we used the Open Global Glacier Model (OGGM) to project the potential change in the hydrological contribution of each glacier (area > 1 km2; 2034 glaciers in RGI6) in the Patagonian Andes (40–56° S) under 1920 potential scenarios. Based on these projections, we used the permutation importance of random forest regression models to calculate the relative importance of each source of data uncertainty. Our main findings are as follows.
-
The sources of data uncertainty showed relative differences of varying magnitudes. The importance of the selection of glacier inventory and ice thickness source was masked by the reference climate. While the glacier inventory and ice thickness source showed overall differences close to 10 %, the different climate alternatives showed differences of more than 50 % for solid precipitation, for example. Among all contributors to future climate uncertainty (2070–2099), the reference climate was also the most important source for all variables, followed by the SSP, the GCM and finally the bias correction method used.
-
The volume loss of glaciers varies significantly by emission scenario, ranging from 46 ± 9 % in SSP1-2.6 to 67 ± 11 % in SSP5-8.5. However, while the specific mass balance is influenced by emission scenarios, glacier melt does not show a clear dependence due to changes in glacier area over time. Uncertainty in glacier melt is reduced compared to glacier runoff due to the smaller influence of the reference climate, which mainly influences glacier runoff through past-climate-dependent liquid precipitation.
-
For eight glacio-hydrological signatures obtained from the glacier melt evolution, the uncertainty from historical sources exceeded that from future sources, underscoring the critical role of modeller decisions during the calibration process. Considering all glacier melt signatures, the reference climate was the main source of uncertainty in 69 % ± 22 % of the glacier area. For long-term metrics (trend and change), factors not typically considered in regional studies, such as the selection of GCMs and reference climate, were as important as emission scenarios. This emphasises the need to consider historical climate variability and modeller decisions as integral components of uncertainty analysis, rather than limiting the focus to future sources of uncertainty alone.
Our results shed light on the evolution of glacier runoff in the Patagonian Andes and provide new insights into the impacts of data uncertainty. To our knowledge, the present study is the first large-scale assessment of the impact of multiple sources of data uncertainty (both historical and future) from a perspective beyond future glacier volume loss. In order to proceed with adaptation plans for the long-term sustainability of local ecosystems, future studies should address sources of uncertainty not considered in this study (e.g. parameterisation of frontal ablation, climate downscaling, and surface mass balance and ice-flow models) and extend the scope from glaciers to downstream hydrology (e.g. groundwater recharge, evaporation, snowmelt). Downstream hydrology can play a critical role in the seasonal and interannual water release during dry seasons (Drenkhan et al., 2022), attenuating the consequences of glacier shrinkage (e.g. Somers et al., 2019). Finally, we hope that our rigorous uncertainty quantification helps to prioritise future efforts (e.g. reference climate) to reduce glacio-hydrological modelling gaps in the Patagonian Andes.
At the beginning, a first guess of the control variable (Tspin-up or μ∗) is used and evaluated. If the mismatch between model and observation happens to be close enough, the algorithm stops. Otherwise, the second guess depends on the calculated first-guess mismatch. For example, if the first resulting area is smaller (larger) than the one searched, the second temperature spin-up will be colder (warmer). This is because a colder (warmer) temperature leads to a larger (smaller) initial glacier state. The same idea is used for matching the geodetic mass balance. If the second guess is still unsuccessful, the previous value pairs (control variable, mismatch) are used for all subsequent guesses to determine the next guess. This is done by fitting a stepwise linear function to these pairs and then setting the mismatch to 0 to obtain the next guess (this method is similar to the one described in appendix A of Zekollari et al., 2019).
The complete code repository can be found at https://doi.org/10.5281/zenodo.14177951 (Aguayo, 2024).
The glacier outlines from RGI6 and RGI7 were downloaded from https://doi.org/10.7265/4m1f-gd79 (RGI Consortium, 2017) and https://doi.org/10.5067/F6JMOVY5NAVZ (RGI Consortium, 2023). NASADEM was downloaded from https://doi.org/10.5067/MEaSUREs/NASADEM/NASADEM_HGT.001 (NASA JPL, 2020). Ice thicknesses datasets were downloaded from https://doi.org/10.6096/1007 (Millan et al., 2021) and https://doi.org/10.3929/ethz-b-000315707 (Farinotti, 2019). PMET v1.0 was downloaded from https://doi.org/10.5281/zenodo.7992761 (Aguayo et al., 2023). CR2MET v2.5 was downloaded from https://doi.org/10.5281/zenodo.7529682 (Boisier, 2023). ERA5 was downloaded from https://doi.org/10.24381/cds.f17050d7 (Hersbach et al., 2023). Access to the MSWEP precipitation dataset is provided through the GloH2O website (https://www.gloh2o.org/mswep/, Beck et al., 2019). CMIP6 data were downloaded using the intake-esm data cataloging utility (Banihirwe et al., 2023) https://doi.org/10.5281/zenodo.3491062. The complete set of results provided in this study is available at https://doi.org/10.5281/zenodo.11353065 (Aguayo et al., 2024b). The data package includes detailed information on the catchments studied, historical glacier conditions, future climate drivers and impacts, and glacio-hydrological signatures at the catchment scale.
The supplement related to this article is available online at: https://doi.org/10.5194/tc-18-5383-2024-supplement.
This study was conceptualised and designed by RA, FM and LS. RA collected the data and performed the modelling and core data analysis. PS implemented and developed the dynamic calibration algorithm. MS, AC, JLM, MA, JM and LU contributed to the analysis and discussion of the results and drafting of the paper. All authors revised the paper, provided feedback, and contributed to the preparation of the figures and tables. All authors approved the final version of the paper.
The contact author has declared that none of the authors has any competing interests.
Jonathan Mackay publishes with the permission of the executive director of the British Geological Survey (UKRI). This text reflects only the author's view, and the agency is not responsible for any use that may be made of the information it contains.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
Rodrigo Aguayo would like to acknowledge the support of the Open Global Glacier Model (OGGM) community for their valuable assistance, collaboration and commitment to open science.
Rodrigo Aguayo was supported by the National Agency for Research and Development (ANID) PFCHA/DOCTORADO NACIONAL/2019 – 21190544 and by the European Research Council (ERC) under the European Union's Horizon Framework research and innovation programme (grant agreement no. 101115565; ICE3 project). Lilian Schuster's contribution was funded by her DOC Fellowship from the Austrian Academy of Sciences, Department of Atmospheric and Cryospheric Sciences, University of Innsbruck (grant no. 25928). Lilian Schuster, Patrick Schmitt and Fabien Maussion's contributions were funded by the European Union's Horizon 2020 research and innovation programme under grant agreement no. 101003687. Jonathan Mackay's contribution was funded by the Natural Environment Research Council (NERC) MCNC Grant TerraFirma NE/W004895/1. Jorge Leon-Muñoz received financial support from National Agency for Research and Development (grant nos. FONDAP-INCAR 1522A0004 and FONDECYT-REGULAR grant 1221102).
This paper was edited by Johannes J. Fürst and reviewed by three anonymous referees.
Aguayo, R.: rodaguayo/Glacier_Uncertainties: v1.0.1 (v1.0.1), Zenodo [software], https://doi.org/10.5281/zenodo.14177951, 2024.
Aguayo, R., León-Muñoz, J., Aguayo, M., Baez-Villanueva, O., Zambrano-Bigiarini, M., Fernández, A., and Jacques-Coper, M.: PatagoniaMet: A multi-source hydrometeorological dataset for Western Patagonia (v1.0), Zenodo [data set], https://doi.org/10.5281/zenodo.7992761, 2023.
Aguayo, R., León-Muñoz, J., Aguayo, M., Baez-Villanueva, O. M., Zambrano-Bigiarini, M., Fernández, A., and Jacques-Coper, M.: PatagoniaMet: A multi-source hydrometeorological dataset for Western Patagonia, Sci. Data, 11, 6, https://doi.org/10.1038/s41597-023-02828-2, 2024a.
Aguayo, R., Maussion, F., Schuster, L., Schaefer, M., Caro, A., Schmitt, P., Mackay, J., Ultee, L., Leon-Muñoz, J., and Aguayo, M.: Glacier runoff projections and their multiple sources of uncertainty in the Patagonian Andes (40–56° S), v1.1, Zenodo [data set], https://doi.org/10.5281/zenodo.11353065, 2024b.
Ayala, Á., Farías-Barahona, D., Huss, M., Pellicciotti, F., McPhee, J., and Farinotti, D.: Glacier runoff variations since 1955 in the Maipo River basin, in the semiarid Andes of central Chile, The Cryosphere, 14, 2005–2027, https://doi.org/10.5194/tc-14-2005-2020, 2020.
Banihirwe, A., Long, M., Grover, M., bonnland, Kent, J., Bourgault, P., Squire, D., Busecke, J., Spring, A., Schulz, H., Paul, K., RondeauG, and Kölling, T.: intake/intake-esm: v2023.11.10, Zenodo [software], https://doi.org/10.5281/zenodo.10103723, 2023.
Barcaza, G., Nussbaumer, S. U., Tapia, G., Valdés, J., García, J.-L., Videla, Y., Albornoz, A., and Arias, V.: Glacier inventory and recent glacier variations in the Andes of Chile, South America, Ann. Glaciol., 58, 166–180, https://doi.org/10.1017/aog.2017.28, 2017.
Beck, H. E., Wood, E. F., Pan, M., Fisher, C. K., Miralles, D. G., van Dijk, A. I. J. M., McVicar, T. R., and Adler, R. F.: MSWEP V2 Global 3-Hourly 0.1° Precipitation: Methodology and Quantitative Assessment, B. Am. Meteorol. Soc., 100, 473–500, https://doi.org/10.1175/BAMS-D-17-0138.1, 2019 (data available at: https://www.gloh2o.org/mswep/, last access: 20 November 2024).
Beck, H. E., Wood, E. F., McVicar, T. R., Zambrano-Bigiarini, M., Alvarez-Garreton, C., Baez-Villanueva, O. M., Sheffield, J., and Karger, D. N.: Bias correction of global high-resolution precipitation climatologies using streamflow observations from 9372 catchments, J. Climate, 33, 1299–1315, https://doi.org/10.1175/JCLI-D-19-0332.1, 2020.
Beck, H. E., van Dijk, A. I. J. M., Larraondo, P. R., McVicar, T. R., Pan, M., Dutra, E., and Miralles, D. G.: MSWX: Global 3-Hourly 0.1° Bias-Corrected Meteorological Data Including Near-Real-Time Updates and Forecast Ensembles, B. Am. Meteorol. Soc., 103, E710–E732, https://doi.org/10.1175/BAMS-D-21-0145.1, 2022.
Bennett, K. E., Miller, G., Busey, R., Chen, M., Lathrop, E. R., Dann, J. B., Nutt, M., Crumley, R., Dillard, S. L., Dafflon, B., Kumar, J., Bolton, W. R., Wilson, C. J., Iversen, C. M., and Wullschleger, S. D.: Spatial patterns of snow distribution in the sub-Arctic, The Cryosphere, 16, 3269–3293, https://doi.org/10.5194/tc-16-3269-2022, 2022.
Boisier, J. P.: CR2MET: A high-resolution precipitation and temperature dataset for the period 1960–2021 in continental Chile, (v2.5), Zenodo [data set], https://doi.org/10.5281/zenodo.7529682, 2023.
Braun, M. H., Malz, P., Sommer, C., Farías-Barahona, D., Sauter, T., Casassa, G., Soruco, A., Skvarca, P., and Seehaus, T. C.: Constraining glacier elevation and mass changes in South America, Nat. Clim. Change, 9, 130–136, https://doi.org/10.1038/s41558-018-0375-7, 2019.
Bravo, C., Quincey, D. J., Ross, A. N., Rivera, A., Brock, B., Miles, E., and Silva, A.: Air Temperature Characteristics, Distribution, and Impact on Modeled Ablation for the South Patagonia Icefield, J. Geophys. Res.-Atmos., 124, 907–925, https://doi.org/10.1029/2018JD028857, 2019a.
Bravo, C., Bozkurt, D., Gonzalez-Reyes, Á., Quincey, D. J., Ross, A. N., Farías-Barahona, D., and Rojas, M.: Assessing Snow Accumulation Patterns and Changes on the Patagonian Icefields, Frontiers in Environmental Science, 7, 1–18, https://doi.org/10.3389/fenvs.2019.00030, 2019b.
Breiman, L.: Random Forests, Mach. Learn., 45, 5–32, https://doi.org/10.1023/A:1010933404324, 2001.
Cannon, A. J.: Multivariate quantile mapping bias correction: an N-dimensional probability density function transform for climate model simulations of multiple variables, Clim. Dynam., 50, 31–49, https://doi.org/10.1007/s00382-017-3580-6, 2018.
Cannon, A. J., Sobie, S. R., and Murdock, T. Q.: Bias correction of GCM precipitation by quantile mapping: How well do methods preserve changes in quantiles and extremes?, J. Climate, 28, 6938–6959, https://doi.org/10.1175/JCLI-D-14-00754.1, 2015.
Caro, A., Condom, T., and Rabatel, A.: Climatic and Morphometric Explanatory Variables of Glacier Changes in the Andes (8–55° S): New Insights From Machine Learning Approaches, Front. Earth Sci., 9, 713011, https://doi.org/10.3389/feart.2021.713011, 2021.
Caro, A., Condom, T., Rabatel, A., Champollion, N., García, N., and Saavedra, F.: Hydrological response of Andean catchments to recent glacier mass loss, The Cryosphere, 18, 2487–2507, https://doi.org/10.5194/tc-18-2487-2024, 2024.
Cauvy-Fraunié, S. and Dangles, O.: A global synthesis of biodiversity responses to glacier retreat, Nat. Ecol. Evol., 3, 1675–1685, https://doi.org/10.1038/s41559-019-1042-8, 2019.
Chen, J., Brissette, F. P., and Leconte, R.: Uncertainty of downscaling method in quantifying the impact of climate change on hydrology, J. Hydrol., 401, 190–202, https://doi.org/10.1016/j.jhydrol.2011.02.020, 2011.
Compagno, L., Zekollari, H., Huss, M., and Farinotti, D.: Limited impact of climate forcing products on future glacier evolution in Scandinavia and Iceland, J. Glaciol., 67, 727–743, https://doi.org/10.1017/jog.2021.24, 2021.
Condom, T., Martínez, R., Pabón, J. D., Costa, F., Pineda, L., Nieto, J. J., López, F., and Villacis, M.: Climatological and Hydrological Observations for the South American Andes: In situ Stations, Satellite, and Reanalysis Data Sets, Front. Earth Sci., 8, 1–20, https://doi.org/10.3389/feart.2020.00092, 2020.
Davies, B. J. and Glasser, N. F.: Accelerating shrinkage of Patagonian glaciers from the Little Ice Age (∼ AD 1870) to 2011, J. Glaciol., 58, 1063–1084, https://doi.org/10.3189/2012JoG12J026, 2012.
Drenkhan, F., Buytaert, W., Mackay, J. D., Barrand, N. E., Hannah, D. M., and Huggel, C.: Looking beyond glaciers to understand mountain water security, Nat. Sustain., 6, 130–138, https://doi.org/10.1038/s41893-022-00996-4, 2022.
Dussaillant, I., Berthier, E., Brun, F., Masiokas, M., Hugonnet, R., Favier, V., Rabatel, A., Pitte, P., and Ruiz, L.: Two decades of glacier mass loss along the Andes, Nat. Geosci., 12, 802–808, https://doi.org/10.1038/s41561-019-0432-5, 2019.
Eyring, V., Bony, S., Meehl, G. A., Senior, C. A., Stevens, B., Stouffer, R. J., and Taylor, K. E.: Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization, Geosci. Model Dev., 9, 1937–1958, https://doi.org/10.5194/gmd-9-1937-2016, 2016.
Farinotti, D.: A consensus estimate for the ice thickness distribution of all glaciers on Earth – dataset, ETH Zürich [data set], https://doi.org/10.3929/ethz-b-000315707, 2019.
Farinotti, D., Huss, M., Bauder, A., Funk, M., and Truffer, M.: A method to estimate the ice volume and ice-thickness distribution of alpine glaciers, J. Glaciol., 55, 422–430, https://doi.org/10.3189/002214309788816759, 2009.
Farinotti, D., Huss, M., Fürst, J. J., Landmann, J., Machguth, H., Maussion, F., and Pandit, A.: A consensus estimate for the ice thickness distribution of all glaciers on Earth, Nat. Geosci., 12, 168–173, https://doi.org/10.1038/s41561-019-0300-3, 2019.
Gabbi, J., Farinotti, D., Bauder, A., and Maurer, H.: Ice volume distribution and implications on runoff projections in a glacierized catchment, Hydrol. Earth Syst. Sci., 16, 4543–4556, https://doi.org/10.5194/hess-16-4543-2012, 2012.
Garreaud, R. D., Alvarez-Garreton, C., Barichivich, J., Boisier, J. P., Christie, D., Galleguillos, M., LeQuesne, C., McPhee, J., and Zambrano-Bigiarini, M.: The 2010–2015 megadrought in central Chile: impacts on regional hydroclimate and vegetation, Hydrol. Earth Syst. Sci., 21, 6307–6327, https://doi.org/10.5194/hess-21-6307-2017, 2017.
Gateño, F., Mendoza, P. A., Vásquez, N., Lagos-Zúñiga, M., Jiménez, H., Jerez, C., Vargas, X., Rubio-Álvarez, E., and Montserrat, S.: Screening CMIP6 models for Chile based on past performance and code genealogy, Climatic Change, 177, 87, https://doi.org/10.1007/s10584-024-03742-1, 2024.
Hanus, S., Schuster, L., Burek, P., Maussion, F., Wada, Y., and Viviroli, D.: Coupling a large-scale glacier and hydrological model (OGGM v1.5.3 and CWatM V1.08) – towards an improved representation of mountain water resources in global assessments, Geosci. Model Dev., 17, 5123–5144, https://doi.org/10.5194/gmd-17-5123-2024, 2024.
Hausfather, Z., Marvel, K., Schmidt, G. A., Nielsen-Gammon, J. W., and Zelinka, M.: Climate simulations: recognize the `hot model' problem, Nature, 605, 26–29, https://doi.org/10.1038/d41586-022-01192-2, 2022.
Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz-Sabater, J., Nicolas, J., Peubey, C., Radu, R., Schepers, D., Simmons, A., Soci, C., Abdalla, S., Abellan, X., Balsamo, G., Bechtold, P., Biavati, G., Bidlot, J., Bonavita, M., De Chiara, G., Dahlgren, P., Dee, D., Diamantakis, M., Dragani, R., Flemming, J., Forbes, R., Fuentes, M., Geer, A., Haimberger, L., Healy, S., Hogan, R. J., Hólm, E., Janisková, M., Keeley, S., Laloyaux, P., Lopez, P., Lupu, C., Radnoti, G., de Rosnay, P., Rozum, I., Vamborg, F., Villaume, S., and Thépaut, J.-N.: The ERA5 global reanalysis, Q. J. Roy. Meteor. Soc., 146, 1999–2049, https://doi.org/10.1002/qj.3803, 2020.
Hersbach, H., Bell, B., Berrisford, P., Biavati, G., Horányi, A., Muñoz Sabater, J., Nicolas, J., Peubey, C., Radu, R., Rozum, I., Schepers, D., Simmons, A., Soci, C., Dee, D., and Thépaut, J.-N.: ERA5 monthly averaged data on single levels from 1940 to present, Copernicus Climate Change Service (C3S) Climate Data Store (CDS) [data set], https://doi.org/10.24381/cds.f17050d7, 2023.
Hock, R., Maussion, F., Marzeion, B., and Nowicki, S.: What is the global glacier ice volume outside the ice sheets?, J. Glaciol., 69, 204–210, https://doi.org/10.1017/jog.2023.1, 2023.
Hugonnet, R., McNabb, R., Berthier, E., Menounos, B., Nuth, C., Girod, L., Farinotti, D., Huss, M., Dussaillant, I., Brun, F., and Kääb, A.: Accelerated global glacier mass loss in the early twenty-first century, Nature, 592, 726–731, https://doi.org/10.1038/s41586-021-03436-z, 2021.
Huss, M. and Hock, R.: A new model for global glacier change and sea-level rise, Front. Earth Sci., 3, 1–22, https://doi.org/10.3389/feart.2015.00054, 2015.
Huss, M. and Hock, R.: Global-scale hydrological response to future glacier mass loss, Nat. Clim. Change, 8, 135–140, https://doi.org/10.1038/s41558-017-0049-x, 2018.
Huss, M., Zemp, M., Joerg, P. C., and Salzmann, N.: High uncertainty in 21st century runoff projections from glacierized basins, J. Hydrol., 510, 35–48, https://doi.org/10.1016/j.jhydrol.2013.12.017, 2014.
Huss, M., Bookhagen, B., Huggel, C., Jacobsen, D., Bradley, R. S., Clague, J. j., Vuille, M., Buytaert, W., Cayan, D. R., Greenwood, G., Mark, B. G., Milner, A. M., Weingartner, R., and Winder, M.: Toward mountains without permanent snow and ice, Earths Future, 5, 418–435, https://doi.org/10.1002/2016EF000514, 2017.
Immerzeel, W. W., Lutz, A. F., Andrade, M., Bahl, A., Biemans, H., Bolch, T., Hyde, S., Brumby, S., Davies, B. J., Elmore, A. C., Emmer, A., Feng, M., Fernández, A., Haritashya, U., Kargel, J. S., Koppes, M., Kraaijenbrink, P. D. A., Kulkarni, A. V., Mayewski, P. A., Nepal, S., Pacheco, P., Painter, T. H., Pellicciotti, F., Rajaram, H., Rupper, S., Sinisalo, A., Shrestha, A. B., Viviroli, D., Wada, Y., Xiao, C., Yao, T., and Baillie, J. E. M.: Importance and vulnerability of the world's water towers, Nature, 577, 364–369, https://doi.org/10.1038/s41586-019-1822-y, 2020.
Intergovernmental Panel on Climate Change (IPCC): High Mountain Areas, in: The Ocean and Cryosphere in a Changing Climate: Special Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, 2022, 131–202, 2022.
Iriarte, J. L., Pantoja, S., and Daneri, G.: Oceanographic Processes in Chilean Fjords of Patagonia: From small to large-scale studies, Prog. Oceanogr., 129, 1–7, https://doi.org/10.1016/j.pocean.2014.10.004, 2014.
Iturbide, M., Fernández, J., Gutiérrez, J. M., Bedia, J., Cimadevilla, E., Díez-Sierra, J., Manzanas, R., Casanueva, A., Baño-Medina, J., Milovac, J., Herrera, S., Cofiño, A. S., San Martín, D., García-Díez, M., Hauser, M., Huard, D., and Yelekci, Ö.: Repository supporting the implementation of FAIR principles in the IPCC-WGI Atlas, Zenodo [data set], https://doi.org/10.5281/ZENODO.3691645, 2021.
Kaser, G., Großhauser, M., and Marzeion, B.: Contribution potential of glaciers to water availability in different climate regimes, P. Natl. Acad. Sci. USA, 107, 20223–20227, https://doi.org/10.1073/pnas.1008162107, 2010.
Lange, S.: ISIMIP3 bias adjustment fact sheet, https://www.isimip.org/documents/413/ISIMIP3b_bias_adjustment_fact_sheet_Gnsz7CO.pdf (last access: 18 November 2024), 2021.
Li, F., Maussion, F., Wu, G., Chen, W., Yu, Z., Li, Y., and Liu, G.: Influence of glacier inventories on ice thickness estimates and future glacier change projections in the Tian Shan range, Central Asia, J. Glaciol., 69, 266–280, https://doi.org/10.1017/jog.2022.60, 2022.
Logan, T., Aoun, A., Bourgault, P., Dupuis, É., Huard, D., Lavoie, J., Rondeau-Genesse, G., Smith, T. J., Alegre, R., Barnes, C., Biner, S., Caron, D., Ehbrecht, C., Fyke, J., Keel, T., Labonté, M.-P., Lierhammer, L., Low, J.-F., Quinn, J., Roy, P., Squire, D., Stephens, A., Tanguy, M., and Whelan, C.: Ouranosinc/xclim: v0.39.0, Zenodo [code], https://doi.org/10.5281/zenodo.7274811, 2022.
Mackay, J. D., Barrand, N. E., Hannah, D. M., Krause, S., Jackson, C. R., Everest, J., Aðalgeirsdóttir, G., and Black, A. R.: Future evolution and uncertainty of river flow regime change in a deglaciating river basin, Hydrol. Earth Syst. Sci., 23, 1833–1865, https://doi.org/10.5194/hess-23-1833-2019, 2019.
Malles, J., Maussion, F., Ultee, L., Kochtitzky, W., Copland, L., and Marzeion, B.: Exploring the impact of a frontal ablation parameterization on projected 21st-century mass change for Northern Hemisphere glaciers, J. Glaciol., 69, 1317–1332, https://doi.org/10.1017/jog.2023.19, 2023.
Marzeion, B., Jarosch, A. H., and Hofer, M.: Past and future sea-level change from the surface mass balance of glaciers, The Cryosphere, 6, 1295–1322, https://doi.org/10.5194/tc-6-1295-2012, 2012.
Marzeion, B., Hock, R., Anderson, B., Bliss, A., Champollion, N., Fujita, K., Huss, M., Immerzeel, W. W., Kraaijenbrink, P., Malles, J., Maussion, F., Radić, V., Rounce, D. R., Sakai, A., Shannon, S., van de Wal, R., and Zekollari, H.: Partitioning the Uncertainty of Ensemble Projections of Global Glacier Mass Change, Earth's Future. 8, e2019EF001470, https://doi.org/10.1029/2019EF001470, 2020.
Masiokas, M., Rabatel, A., Rivera, A., Ruiz, L., Pitte, P., Ceballos, J. L., Barcaza, G., Soruco, A., and Bown, F.: A review of the current state and recent changes of the Andean cryosphere, Front. Earth Sci., 8, 99, https://doi.org/10.3389/FEART.2020.00099, 2020.
Masiokas, M. H., Cara, L., Villalba, R., Pitte, P., Luckman, B. H., Toum, E., Christie, D. A., Le Quesne, C., and Mauget, S.: Streamflow variations across the Andes (18°–55° S) during the instrumental era, Sci. Rep.-UK, 9, 17879, https://doi.org/10.1038/s41598-019-53981-x, 2019.
Maussion, F., Butenko, A., Champollion, N., Dusch, M., Eis, J., Fourteau, K., Gregor, P., Jarosch, A. H., Landmann, J., Oesterle, F., Recinos, B., Rothenpieler, T., Vlug, A., Wild, C. T., and Marzeion, B.: The Open Global Glacier Model (OGGM) v1.1, Geosci. Model Dev., 12, 909–931, https://doi.org/10.5194/gmd-12-909-2019, 2019.
McCarthy, M., Meier, F., Fatichi, S., Stocker, B. D., Shaw, T. E., Miles, E., Dussaillant, I., and Pellicciotti, F.: Glacier Contributions to River Discharge During the Current Chilean Megadrought, Earths Future, 10, e2022EF002852, https://doi.org/10.1029/2022EF002852, 2022.
McMillan, H. K.: A review of hydrologic signatures and their applications, WIREs Water, 8, e1499, https://doi.org/10.1002/wat2.1499, 2021.
Mernild, S. H., Liston, G. E., Hiemstra, C., and Wilson, R.: The Andes Cordillera. Part III: glacier surface mass balance and contribution to sea level rise (1979–2014), Int. J. Climatol., 37, 3154–3174, https://doi.org/10.1002/joc.4907, 2017.
Millan, R., Rignot, E., Rivera, A., Martineau, V., Mouginot, J., Zamora, R., Uribe, J., Lenzano, G., De Fleurian, B., Li, X., Gim, Y., and Kirchner, D.: Ice Thickness and Bed Elevation of the Northern and Southern Patagonian Icefields, Geophys. Res. Lett., 46, 6626–6635, https://doi.org/10.1029/2019GL082485, 2019.
Millan, R., Mouginot, J., and Rabatel, A.: Global mapping of surface ice flow velocity and ice thickness of glaciers around the world from Millan et al. (2022), Theia [data set], https://doi.org/10.6096/1007, 2021.
Millan, R., Mouginot, J., Rabatel, A., and Morlighem, M.: Ice velocity and thickness of the world's glaciers, Nat. Geosci., 15, 124–129, https://doi.org/10.1038/s41561-021-00885-z, 2022.
Milner, A. M., Khamis, K., Battin, T. J., Brittain, J. E., Barrand, N. E., Füreder, L., Cauvy-Fraunié, S., Gíslason, G. M., Jacobsen, D., Hannah, D. M., Hodson, A. J., Hood, E., Lencioni, V., Ólafsson, J. S., Robinson, C. T., Tranter, M., and Brown, L. E.: Glacier shrinkage driving global changes in downstream systems, P. Natl. Acad. Sci. USA, 114, 9770–9778, https://doi.org/10.1073/pnas.1619807114, 2017.
Minowa, M., Schaefer, M., Sugiyama, S., Sakakibara, D., and Skvarca, P.: Frontal ablation and mass loss of the Patagonian icefields, Earth Planet. Sc. Lett., 561, 116811, https://doi.org/10.1016/j.epsl.2021.116811, 2021.
Morales, M. S., Cook, E. R., Barichivich, J., Christie, D. A., Villalba, R., LeQuesne, C., Srur, A. M., Ferrero, M. E., González-Reyes, Á., Couvreux, F., Matskovsky, V., Aravena, J. C., Lara, A., Mundo, I. A., Rojas, F., Prieto, M. R., Smerdon, J. E., Bianchi, L. O., Masiokas, M. H., Urrutia-Jalabert, R., Rodriguez-Catón, M., Muñoz, A. A., Rojas-Badilla, M., Alvarez, C., Lopez, L., Luckman, B. H., Lister, D., Harris, I., Jones, P. D., Williams, A. P., Velazquez, G., Aliste, D., Aguilera-Betti, I., Marcotti, E., Flores, F., Muñoz, T., Cuq, E., and Boninsegna, J. A.: Six hundred years of South American tree rings reveal an increase in severe hydroclimatic events since mid-20th century, P. Natl. Acad. Sci. USA, 117, 16816–16823, https://doi.org/10.1073/pnas.2002411117, 2020.
NASA JPL: NASADEM Merged DEM Global 1 arc second V001, NASA EOSDIS Land Processes Distributed Active Archive Center [data set], https://doi.org/10.5067/MEaSUREs/NASADEM/NASADEM_HGT.001, 2020.
O'Neill, B. C., Tebaldi, C., van Vuuren, D. P., Eyring, V., Friedlingstein, P., Hurtt, G., Knutti, R., Kriegler, E., Lamarque, J.-F., Lowe, J., Meehl, G. A., Moss, R., Riahi, K., and Sanderson, B. M.: The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6, Geosci. Model Dev., 9, 3461–3482, https://doi.org/10.5194/gmd-9-3461-2016, 2016.
Pasquini, A. I., Cosentino, N. J., and Depetris, P. J.: The Main Hydrological Features of Patagonia's Santa Cruz River: An Updated Assessment, in: Environmental Assessment of Patagonia's Water Resources, edited by: Torres, A. I. and Campodonico, V. A., Environmental Earth Sciences, Springer, Cham, https://doi.org/10.1007/978-3-030-89676-8_9, 2021.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., Vanderplas, J., Passos, A., Cournapeau, D., Brucher, M., Perrot, M., and Duchesnay, É.: Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 12, 2825–2830, 2011.
Pesci, M. H., Schulte Overberg, P., Bosshard, T., and Förster, K.: From global glacier modeling to catchment hydrology: bridging the gap with the WaSiM-OGGM coupling scheme, Frontiers in Water, 5, 296344, https://doi.org/10.3389/frwa.2023.1296344, 2023.
Poff, N. L., Allan, J. D., Bain, M. B., Karr, J. R., Prestegaard, K. L., Richter, B. D., Sparks, R. E., and Stromberg, J. C.: The Natural Flow Regime, BioScience, 47, 769–784, https://doi.org/10.2307/1313099, 1997.
Pritchard, H. D.: Asia's shrinking glaciers protect large populations from drought stress, Nature, 569, 649–654, https://doi.org/10.1038/s41586-019-1240-1, 2019.
Rasul, G. and Molden, D.: The Global Social and Economic Consequences of Mountain Cryospheric Change, Frontiers in Environmental Science, 7, 91, https://doi.org/10.3389/fenvs.2019.00091, 2019.
RGI Consortium: Randolph Glacier Inventory – A Dataset of Global Glacier Outlines, Version 6, National Snow and Ice Data Center [data set], https://doi.org/10.7265/4m1f-gd79, 2017.
RGI Consortium: Randolph Glacier Inventory – A Dataset of Global Glacier Outlines, NSIDC-0770, Version 7, National Snow and Ice Data Center [data set], https://doi.org/10.5067/F6JMOVY5NAVZ, 2023.
Richter, B. D., Baumgartner, J. V., Powell, J., and Braun, D. P.: A Method for Assessing Hydrologic Alteration within Ecosystems, Conserv. Biol., 10, 1163–1174, https://doi.org/10.1046/j.1523-1739.1996.10041163.x, 1996.
Rounce, D. R., Khurana, T., Short, M. B., Hock, R., Shean, D. E., and Brinkerhoff, D. J.: Quantifying parameter uncertainty in a large-scale glacier evolution model using Bayesian inference: application to High Mountain Asia, J. Glaciol., 66, 175–187, https://doi.org/10.1017/jog.2019.91, 2020.
Rounce, D. R., Hock, R., Maussion, F., Hugonnet, R., Kochtitzky, W., Huss, M., Berthier, E., Brinkerhoff, D., Compagno, L., Copland, L., Farinotti, D., Menounos, B., and McNabb, R. W.: Global glacier change in the 21st century: Every increase in temperature matters, Science, 379, 78–83, https://doi.org/10.1126/science.abo1324, 2023.
Ruiz, L., Pitte, P., Rivera, A., Schaefer, M., and Masiokas, M. H.: Current State and Recent Changes of Glaciers in the Patagonian Andes (∼ 37° S to 55° S), in: Freshwaters and Wetlands of Patagonia: Ecosystems and Socioecological Aspects, edited by: Mataloni, G. and Quintana, R. D., Springer International Publishing, Cham, 59–91, https://doi.org/10.1007/978-3-031-10027-7_4, 2022.
Sauter, T.: Revisiting extreme precipitation amounts over southern South America and implications for the Patagonian Icefields, Hydrol. Earth Syst. Sci., 24, 2003–2016, https://doi.org/10.5194/hess-24-2003-2020, 2020.
Schmidt, L., Heße, F., Attinger, S., and Kumar, R.: Challenges in Applying Machine Learning Models for Hydrological Inference: A Case Study for Flooding Events Across Germany, Water Resour. Res., 56, e2019WR025924, https://doi.org/10.1029/2019WR025924, 2020.
Schuster, L., Rounce, D. R., and Maussion, F.: Glacier projections sensitivity to temperature-index model choices and calibration strategies, Ann. Glaciol., 1–16, https://doi.org/10.1017/aog.2023.57, 2023.
Somers, L. D., McKenzie, J. M., Mark, B. G., Lagos, P., Ng, G. C., Wickert, A. D., Yarleque, C., Baraër, M., and Silva, Y.: Groundwater Buffers Decreasing Glacier Melt in an Andean Watershed—But Not Forever, Geophys. Res. Lett., 46, 13016–13026, https://doi.org/10.1029/2019GL084730, 2019.
Svetnik, V., Liaw, A., Tong, C., Culberson, J. C., Sheridan, R. P., and Feuston, B. P.: Random Forest: A Classification and Regression Tool for Compound Classification and QSAR Modeling, J. Chem. Inf. Comp. Sci., 43, 1947–1958, https://doi.org/10.1021/ci034160g, 2003.
Tang, G., Clark, M. P., and Papalexiou, S. M.: EM-Earth: The Ensemble Meteorological Dataset for Planet Earth, B. Am. Meteorol. Soc., 103, E996–E1018, https://doi.org/10.1175/BAMS-D-21-0106.1, 2022.
Tang, G., Clark, M. P., Knoben, W. J. M., Liu, H., Gharari, S., Arnal, L., Beck, H. E., Wood, A. W., Newman, A. J., and Papalexiou, S. M.: The Impact of Meteorological Forcing Uncertainty on Hydrological Modeling: A Global Analysis of Cryosphere Basins, Water Resour. Res., 59, e2022WR033767, https://doi.org/10.1029/2022WR033767, 2023.
Tarek, M., Brissette, F., and Arsenault, R.: Uncertainty of gridded precipitation and temperature reference datasets in climate change impact studies, Hydrol. Earth Syst. Sci., 25, 3331–3350, https://doi.org/10.5194/hess-25-3331-2021, 2021.
Temme, F., Farías-Barahona, D., Seehaus, T., Jaña, R., Arigony-Neto, J., Gonzalez, I., Arndt, A., Sauter, T., Schneider, C., and Fürst, J. J.: Strategies for regional modeling of surface mass balance at the Monte Sarmiento Massif, Tierra del Fuego, The Cryosphere, 17, 2343–2365, https://doi.org/10.5194/tc-17-2343-2023, 2023.
Tokarska, K. B., Stolpe, M. B., Sippel, S., Fischer, E. M., Smith, C. J., Lehner, F., and Knutti, R.: Past warming trend constrains future warming in CMIP6 models, Science Advances, 6, eaaz9549, https://doi.org/10.1126/sciadv.aaz9549, 2020.
Ultee, L., Coats, S., and Mackay, J.: Glacial runoff buffers droughts through the 21st century, Earth Syst. Dynam., 13, 935–959, https://doi.org/10.5194/esd-13-935-2022, 2022.
Van Tiel, M., Stahl, K., Freudiger, D., and Seibert, J.: Glacio–hydrological model calibration and evaluation, WIREs Water, 7, e1483, https://doi.org/10.1002/wat2.1483, 2020.
Van Tiel, M., Van Loon, A. F., Seibert, J., and Stahl, K.: Hydrological response to warm and dry weather: do glaciers compensate?, Hydrol. Earth Syst. Sci., 25, 3245–3265, https://doi.org/10.5194/hess-25-3245-2021, 2021.
Van Tiel, M., Weiler, M., Freudiger, D., Moretti, G., Kohn, I., Gerlinger, K., and Stahl, K.: Melting Alpine Water Towers Aggravate Downstream Low Flows: A Stress-Test Storyline Approach, Earths Future, 11, e2022EF003408, https://doi.org/10.1029/2022EF003408, 2023.
Van Wyk de Vries, M., Romero, M., Penprase, S. B., Ng, G.-H. C., and Wickert, A. D.: Increasing rate of 21st century volume loss of the Patagonian Icefields measured from proglacial river discharge, J. Glaciol., 69, 1187–1202, https://doi.org/10.1017/jog.2023.9, 2023.
Viviroli, D., Kummu, M., Meybeck, M., Kallio, M., and Wada, Y.: Increasing dependence of lowland populations on mountain water resources, Nat. Sustain., 3, 917–928, https://doi.org/10.1038/s41893-020-0559-9, 2020.
Wang, H., Chen, J., Xu, C., Zhang, J., and Chen, H.: A Framework to Quantify the Uncertainty Contribution of GCMs Over Multiple Sources in Hydrological Impacts of Climate Change, Earth's Future, 8, e2020EF001602, https://doi.org/10.1029/2020EF001602, 2020.
Watanabe, M., Yanagawa, A., Watanabe, S., Hirabayashi, Y., and Kanae, S.: Quantifying the range of future glacier mass change projections caused by differences among observed past-climate datasets, Clim. Dynam., 53, 2425–2435, https://doi.org/10.1007/s00382-019-04868-0, 2019.
Werder, M. A., Huss, M., Paul, F., Dehecq, A., and Farinotti, D.: A Bayesian ice thickness estimation model for large-scale applications, J. Glaciol., 66, 137–152, https://doi.org/10.1017/jog.2019.93, 2020.
Wiersma, P., Aerts, J., Zekollari, H., Hrachowitz, M., Drost, N., Huss, M., Sutanudjaja, E. H., and Hut, R.: Coupling a global glacier model to a global hydrological model prevents underestimation of glacier runoff, Hydrol. Earth Syst. Sci., 26, 5971–5986, https://doi.org/10.5194/hess-26-5971-2022, 2022.
Wimberly, F., Ultee, L., Schuster, L., Huss, M., Rounce, D. R., Maussion, F., Coats, S., Mackay, J., and Holmgren, E.: Inter-model differences in 21st Century Glacier Runoff for the World's Major River Basins, EGUsphere [preprint], https://doi.org/10.5194/egusphere-2024-1778, 2024.
Zalazar, L., Ferri, L., Castro, M., Gargantini, H., Gimenez, M., Pitte, P., Ruiz, L., Masiokas, M., Costa, G., and Villalba, R.: Spatial distribution and characteristics of Andean ice masses in Argentina: results from the first National Glacier Inventory, J. Glaciol., 66, 938–949, https://doi.org/10.1017/jog.2020.55, 2020.
Zambrano-Bigiarini, M.: Temporal and spatial evaluation of long-term satellite-based precipitation products across the complex topographical and climatic gradients of Chile, Proc. SPIE 10782, Remote Sensing and Modeling of the Atmosphere, Oceans, and Interactions VII, 1078202, 23 October 2018, https://doi.org/10.1117/12.2513645, 2018.
Zekollari, H., Huss, M., and Farinotti, D.: Modelling the future evolution of glaciers in the European Alps under the EURO-CORDEX RCM ensemble, The Cryosphere, 13, 1125–1146, https://doi.org/10.5194/tc-13-1125-2019, 2019.
Zekollari, H., Huss, M., Farinotti, D., and Lhermitte, S.: Ice-Dynamical Glacier Evolution Modeling—A Review, Rev. Geophys., 60, e2021RG000754, https://doi.org/10.1029/2021RG000754, 2022.
Zekollari, H., Huss, M., Schuster, L., Maussion, F., Rounce, D. R., Aguayo, R., Champollion, N., Compagno, L., Hugonnet, R., Marzeion, B., Mojtabavi, S., and Farinotti, D.: 21st century global glacier evolution under CMIP6 scenarios and the role of glacier-specific observations, EGUsphere [preprint], https://doi.org/10.5194/egusphere-2024-1013, 2024.
Zhao, H., Su, B., Lei, H., Zhang, T., and Xiao, C.: A new projection for glacier mass and runoff changes over High Mountain Asia, Sci. Bull.., 68, 43–47, https://doi.org/10.1016/j.scib.2022.12.004, 2023.





