Improved snow property retrievals by solving for topography in the inversion of at-sensor radiance measurements

Accurately modelling optical snow properties like snow albedo and specific surface area (SSA) are essential for monitoring the cryosphere in a changing climate and are parameters that inform hydrologic and climate models. These snow surface properties can be modelled from spaceborne imaging spectroscopy measurements but rely on digital elevation models (DEMs) of relatively coarse spatial scales (e.g. Copernicus at 30 m), which degrade accuracy due to errors in derived products such as slope and aspect. In addition, snow deposition and redistribution can change the apparent topography, and thereby static DEMs may not be considered coincident with the imaging spectroscopy dataset. Testing in three different snow climates (tundra, maritime, alpine), we established a new method that simultaneously solves snow, atmospheric, and terrain parameters, enabling a solution that is more unified across sensors and introduces fewer sources of uncertainty. We leveraged imaging spectroscopy data from Airborne Visible Infrared Imaging Spectrometer-Next Generation (AVIRIS-NG) and PRecursore IperSpettrale della Missione Applicativa (PRISMA) (collected within 1 h) to validate this method and showed a 25 % increase in performance for the radiance-based method over the static method when estimating SSA. This concept can be implemented in missions such as Surface Biology and Geology (SBG), the Environmental Mapping and Analysis Program (EnMap), and the Copernicus Hyperspectral Imaging Mission for the Environment (CHIME).

1 Introduction

Accurately mapping snow surface properties is essential for seasonal snow zones in a changing climate, especially in regions where seasonal snowpack is expected to change dramatically in the coming decades (Siirila-Woodburn et al., 2021). For example, snow albedo plays a crucial role in melting of the snowpack during the ablation season (Wang et al., 2020), with changes in snow albedo directly affecting the amount of absorbed solar radiation and therefore the amount of snow that is melted off. Throughout the winter season, snow albedo fluctuates due in part to grain size (Seidel et al., 2016) and light-absorbing particles (LAPS; Kaspari et al., 2015; McKenzie, 2020; Skiles and Painter, 2017). With a limited number of in situ snow stations around the globe and the snow surface constantly undergoing metamorphism across space and time, satellite imagery represents the best potential for spatially and temporally complete mapping of snow properties. Accurately retrieving snow albedo and other snow surface properties from satellite imagery is paramount, especially in a rapidly changing climate (Malmros et al., 2018).

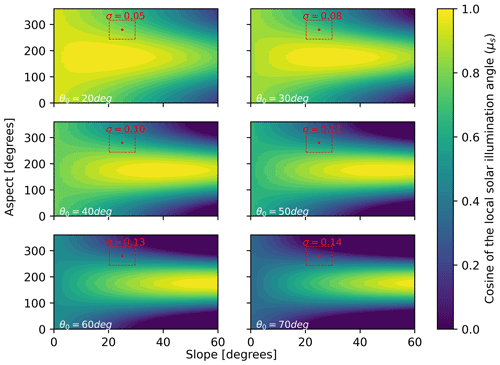
Figure 1 Cosine of local illumination angles (μ_s) as a function of slope (x axis) and aspect (y axis) incremented by 1°, illustrating the problem at higher latitude, and/or winter acquisitions, where standard deviation (σ) of μ_s increases monotonically with solar zenith angles (θ₀). Aspect is shown here measured clockwise from north (with north containing a discontinuity at 360°). For this illustration ϕ₀ is fixed at a value of 175°. The red dots represent the example point at a slope of 25° ±4.73 and an aspect of 280° ±36.3 and are bordered by their uncertainty and the resulting σ.

Retrieval of snow properties from satellite remote sensing relies on digital elevation models (DEMs) to correct for local terrain effects (Bair et al., 2021, 2022; Dozier et al., 2022). In a previous study, researchers found global DEM products to have “blunders and errors” when compared to airborne lidar, particularly in derived slope and aspect, which cause severe errors in calculated cosine of local solar illumination angles (μ_s) (Dozier et al., 2022). They found errors in μ_s ranging from 0.048 to 0.117 (dimensionless) across several sites for Copernicus global DEMs caused by errors in slope and aspect. The μ_s term is a function (Eq. 1) of slope angle (S), slope azimuth angle or aspect (A), solar zenith angle (θ₀), and solar azimuth angle (ϕ₀), with the last two being well constrained:

$$\begin{array}{}\text{(1)}& {\mathit{\mu }}_{\mathrm{s}}=max[\mathrm{0},\cos \left({\mathit{\theta }}_{\mathrm{0}}\left)\cos \right(S\right)+\sin \left({\mathit{\theta }}_{\mathrm{0}}\right)\sin \left(S\right)\cos ({\mathit{\varphi }}_{\mathrm{0}}-A\left)\right].\end{array}$$

Because θ₀ and ϕ₀ are calculable with low errors, the biggest contributions to errors in μ_s stem from slope and aspect. Errors in μ_s increase monotonically with increasing θ₀ (e.g. sunset has high θ₀, as does solar noon in high-latitude winters). This phenomenon can be explained by plotting Eq. (1) for various θ₀ (Fig. 1). Put simply, at higher θ₀ there is a higher standard deviation in μ_s surrounding a known slope and aspect (with some temporally consistent uncertainty), increasing the probability and magnitude of such an error. If one were to compute standard deviations of μ_s across varying θ₀, one would arrive at similar errors of μ_s to those presented in Dozier et al. (2022). For clarity, in Fig. 1 we have highlighted an example case with slope of 25° ±4.73 and aspect of 280° ±36.3. Example uncertainties for this exercise can be found in Table 2 of Dozier et al. (2022).

Recent work has shown μ_s can be modelled using an optimal estimation framework given the top-of-atmosphere (TOA) radiance observed from imaging spectroscopy (Carmon et al., 2023). The authors solve for surface, atmospheric, and topographic state variables simultaneously in their model. This works physically because the partition of direct to diffuse light introduces a shape and magnitude effect on the TOA radiance spectra. However, retrieving snow optical properties is sensitive to directional reflectance, which is significantly influenced by the viewing geometry and surface roughness (Bair et al., 2022), leading to possible shortcomings in this method specifically for snow-covered pixels. To address this and expand upon this framework, we present a new method to account for terrain in snow-covered areas. Our method was tested on pixels with greater than 75 % snow cover in three different snow climates (tundra, maritime, and alpine) with spaceborne imaging spectroscopy with the aim to reduce error in derived snow properties by optimally solving for topography. The spaceborne results are validated against high-confidence airborne spectrometer data. This work directly contributes to snow property retrievals in steep terrain and/or at times of high solar zenith angles for satellite imaging spectroscopy missions such as Surface Biology and Geology (SBG) (Cawse-Nicholson et al., 2021), the Copernicus Hyperspectral Imaging Mission for the Environment (CHIME) (Celesti et al., 2022), and EnMap (Guanter et al., 2015).

Figure 2 PRISMA true-colour images for Toolik on 21 March 2021 (a), the San Juan Mountains on 29 April 2021 (b), and Mount Shasta on 28 February 2021 (c). Four coincident AVIRIS-NG flight lines (F1–F4) are shown in cyan over the San Juan Mountains.

2 Methods

2.1 Study area

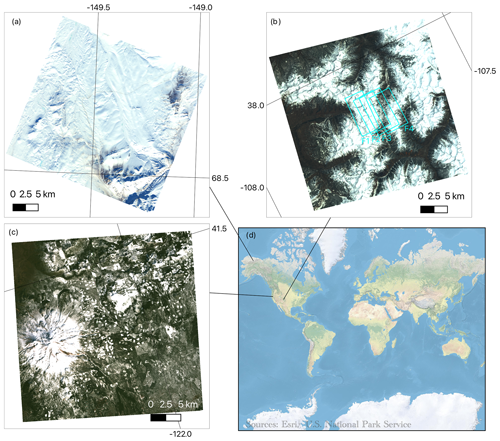
For our study, we used PRecursore IperSpettrale della Missione Applicativa (PRISMA) imagery over three sites capturing different snow climates and solar zenith angles: the San Juan Mountains (Colorado, USA, 29 April 2021, θ₀=27°), Mount Shasta (California, USA, 28 February 2021, θ₀=52°), and the Toolik area (Alaska, USA, 21 March 2021, θ₀=68°) (Fig. 2). The San Juan Mountains location is considered a high alpine site located in the interior continental USA with an elevation range of 2208–4129 m. The Mount Shasta site is a maritime snow climate along the western coast of the USA with an elevation range of 750–4232 m. The Toolik site (elevation range = 504–1748 m) is a high-latitude tundra site, being mostly flat but with steep sections along the Brooks Range (along the southern part of the image). PRISMA, launched by the Italian Space Agency (ASI) and beginning operation on 22 March 2019, is a spaceborne imaging spectroscopy mission collecting radiance at 30 m spatial resolution across 239 bands spanning 400–2500 nm at a spectral resolution better than 12 nm across the visible near infrared and shortwave infrared (Cogliati et al., 2021).

To validate our method, we used four existing Airborne Visible Infrared Imaging Spectrometer-Next Generation (AVIRIS-NG) flight lines over the San Juan Mountains from 29 April 2021 (flying 1 h after PRISMA acquisition). AVIRIS-NG collects radiance measurements at variable spatial resolution (depending on the flight altitude) across 425 bands spanning 380–2510 nm in 5 nm intervals (Green et al., 2023). For this flight, data were collected at 4 m spatial resolution. We downloaded AVIRIS-NG apparent reflectance from National Snow and Ice Data Center (NSIDC) and observation geometry data from NASA Search Earth Data (Skiles and Vuyovich, 2023).

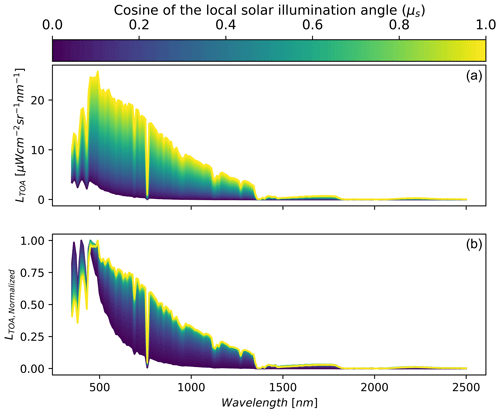
Figure 3 Synthetic data showing the change in magnitude (a) and shape (b) of top-of-atmosphere radiance (L_TOA) with respect to changing local solar illumination angle (μ_s) for fixed snow surface state variables modelled with AART and fixed atmospheric state variables modelled with libRadtran (viewing geometry was fixed as well). State variables and solar and view geometry were based on a PRISMA acquisition over southern Idaho on 8 December 2022. Panel (b) shows normalized radiance with respect to peak TOA radiance across wavelengths to highlight the change in shape.

2.2 Modelling surface, atmosphere, and topography from PRISMA

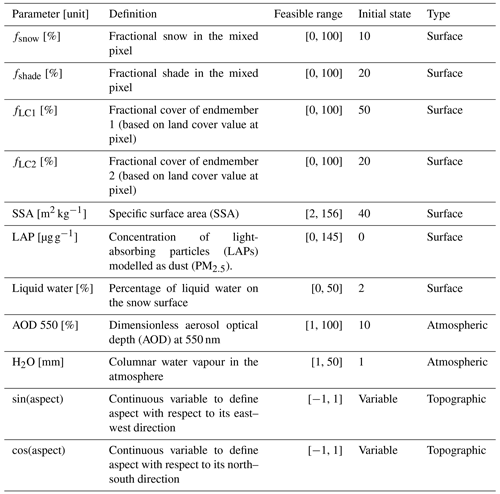
The algorithmic improvements build off a workflow that estimates snow properties given PRISMA TOA radiance, titled Global Optical Snow properties via High-speed Algorithm using K-means (GOSHAWK) (Wilder et al., 2024). In short, our method uses the analytic asymptotic radiative transfer model (AART) (Kokhanovsky and Zege, 2004) coupled with libRadtran (Mayer and Kylling, 2005; Emde et al., 2016) to invert snow surface and atmospheric properties (Bohn et al., 2021; Dalcin and Fang, 2021) and fractional covers of mixed pixels under varied lighting conditions using non-linear numerical optimization (Bair et al., 2021). The parameters solved for in the optimization routine include fractional covers, specific surface area (SSA), light-absorbing particle concentration (modelled as dust), liquid water percentage, dimensionless aerosol optical depth at 550 nm, and columnar water vapour in the atmosphere. Here, we expand upon the algorithm considering recent work showing the capacity to estimate μ_s from TOA radiance (Carmon et al., 2023; Bohn et al., 2024). This idea is demonstrated in Fig. 3 using fixed snow properties via AART and fixed atmosphere properties via libRadtran across the range of plausible μ_s (i.e. 0 to 1). Like the findings in Carmon et al. (2023), Fig. 3 shows that μ_s controls both the spectral shape and magnitude of observed TOA radiance with the effect varying across wavelengths. The greatest shape effect can be seen in the visible spectrum (roughly 400–700 nm) due to the magnitude of the diffuse irradiance. In combination with the magnitude and shape shift, this parameter becomes solvable during optimization due to its strong separability – especially when considering the entire spectrum data from a hyperspectral remote sensing source such as PRISMA. It is important to note that μ_s impacts both the AART estimation of snow reflectance and libRadtran estimation of incoming solar irradiance.

However, if we were only to optimize μ_s, the other key terms, local viewer zenith angle (μ_v) and local phase angle (ξ) in the AART formulation for bidirectional reflectance of snow (Eq. 2) (Kokhanovsky and Zege, 2004; Kokhanovsky et al., 2021a), would remain constant from the available DEM (i.e. μ_s, μ_v, ξ are all derived from DEMs),

$$\begin{array}{}\text{(2)}& r_{\mathrm{snow}}\left({\mathit{\mu }}_{\mathrm{s}},{\mathit{\mu }}_{\mathrm{v}},\mathit{\xi },\mathit{\lambda }\right)=r\left({\mathit{\mu }}_{\mathrm{s}},{\mathit{\mu }}_{\mathrm{v}},\mathit{\xi }\right)a_{\mathrm{snow}}(\mathit{\lambda }{)}^{\mathrm{f}},\end{array}$$

where r is the reflection function of a semi-infinite non-absorbing snow layer (Tedesco and Kokhanovsky, 2007), α_snow is the spherical albedo (plane albedo can be computed using Eq. (26) in Kokhanovsky et al., 2021a), f is the escape function (Kokhanovsky et al., 2021a), and r_snow is the bidirectional reflectance of snow. Keeping other terms (μ_v and ξ) the same is problematic because snow reflectance is poorly approximated as a non-Lambertian surface (Leroux and Fily, 1988), and the outcome will be greatly influenced by μ_v and ξ. Therefore, to incorporate solving for μ_s, μ_v, and ξ from TOA radiance into the algorithm, we instead elect to optimally solve for cos(aspect) and sin(aspect) (Table 1).

Table 1 Parameter space and initial vectors used in numerical optimization for PRISMA data.

Aspect can be solved during optimization by using the atan2 function. We chose to use this method because sin(aspect) and cos(aspect) are continuously differentiable and are therefore suited for numerical optimization methods, whereas aspect is discontinuous at north (using the convention of 0 and 360° as north). We then can use this optimal aspect to estimate μ_s (Eq. 1), μ_v, and ξ. This directly impacts Eqs. (2) and (3) (formulation of incoming solar energy in the model) (Picard et al., 2020),

$$\begin{array}{}\text{(3)}& \begin{array}{rl}E\left(\mathit{\lambda }\right)& =\mathit{\psi }{\mathit{\mu }}_{\mathrm{s}}E{\left(\mathit{\lambda }\right)}_{\mathrm{dir}}+V_{\mathrm{\Omega }}E{\left(\mathit{\lambda }\right)}_{\mathrm{diff}}\\ & +\left[\left(\mathrm{1}+{\displaystyle \frac{\cos \left(S\right)}{\mathrm{2}}}-V_{\mathrm{\Omega }}\right)r{\left(\mathit{\lambda }\right)}_{\mathrm{surf}}E{\left(\mathit{\lambda }\right)}_{\mathrm{diff}}\right]\end{array},\end{array}$$

where E is total incoming irradiance; ψ is binary shade or no shade; E_dir and E_diff are the direct and diffuse irradiance, respectively; V_Ω is the sky view factor (Dozier, 2022); and r_surf is the reflectance of nearby terrain (which is assumed to be equal to the pixel itself). The term E is solved within our non-linear numerical optimization method as described in Wilder et al. (2024). This was modelled incorrectly in Wilder et al. (2024); however, this was corrected in this paper where only diffuse irradiance is used in the third term in Eq. (3). In addition, adding the two extra parameters (sin(aspect) and cos(aspect)) into our updated optimization scheme did not change our run time significantly. Caution is advised against solving for slope and aspect in the inversion due to the non-unique solution space (Fig. 1); however, only considering aspect ensures unique solutions, i.e. μ_s, μ_v, and ξ. We chose aspect because of its greater impact on determining partition of direct and diffuse illumination and as it has been found to be more impactful to errors associated with snow property retrieval (Donahue et al., 2023). Also, in this study we used an estimate of total ozone column as input for creating the libRadtran lookup table specific for each image. We used the average weekly ozone over the bounds of the image from the Sentinel-5P NRTI O3: Near Real-Time Ozone dataset. This approach is an improvement over Wilder et al. (2024), where ozone was fixed at 300 DU.

2.3 Estimating snow properties from AVIRIS-NG for validation

Due to the fine signal-to-noise ratio and spatial resolution of AVIRIS-NG, we treated the dataset as the ground reference. It also captured a similar spectral range to PRISMA, which made it a suitable comparison dataset. The main assumption here is that AVIRIS-NG pixels at 4 m are relatively homogenous and are either snow or no snow, which may not always be the case. This could be a potential source of uncertainty in our analysis. To select snow-covered pixels, we solved for NDSI (normalized difference snow index) using bands at 600 and 1500 nm. We limited our retrieval of snow properties for NDSI greater than or equal to 0.90 (Painter et al., 2013). A common approach to retrieve snow grain size from pure snow pixels is to apply the scaled band area algorithm (Nolin and Dozier, 2000); however, it is recognized that the large presence of liquid water is a limitation. The maximum air temperature of 10.8 °C on the day of the image at the San Juan Mountains site indicated that elevated liquid water at the surface was probable (Center for Snow and Avalanche Studies, 2023). Additionally, reflectance spectra appeared to be shifted along the x axis (wavelength) due to the presence of liquid water. Therefore, we used constrained non-linear numerical optimization to model apparent snow reflectance with AART by allowing fractional snow, fractional shade, liquid water, and SSA to vary. We did not include rock or forest endmembers in this formulation, assuming the 4 m pixels are relatively homogenous as previously stated. Topographic incident angles were held constant based on the 4 m resolution DEM provided by AVIRIS-NG. We minimized the root-mean-square difference (RMSD) between observed apparent and modelled apparent snow reflectance from AART wavelengths in the range 1000–1250 nm. This range has high ice absorption and limited impacts from atmospheric interference and LAP (Miller et al., 2016). The presence of liquid water was included in our analysis by means of the composite refractive index of water and ice (Donahue et al., 2022; Hale and Querry,1973; Warren and Brandt, 2008). We assumed similar grain shape assumptions for both PRISMA and AVIRIS-NG, and we also assumed that if there is a bias due to this it should be consistent between the two datasets in our analysis.

2.4 Comparing modelled snow properties

The algorithm was used in two different modes: (1) static topography based on the Copernicus DEM (from hereon called “static”) and (2) solved topography based on the algorithm updates (from hereon called “radiance”). To compare the accuracy of PRISMA-derived SSA and liquid water, we resampled the AVIRIS-NG optical property results (SSA and liquid water content (LWC)) to match the PRISMA resolution (30 m) and extent by using bilinear interpolation. We then sampled all valid pixels where PRISMA and AVIRIS-NG had snow. We then computed Pearson correlation coefficient (r), mean bias, and RMSD for the radiance and static methods (with respect to AVIRIS-NG). Finally, we used Copernicus-derived slope and aspect maps to determine where the largest errors were occurring on the landscape to compare with the theoretical basis presented in Fig. 1. We do this by using the mean absolute difference with respect to μ_s. We expected to see higher differences in north-facing aspects (i.e. μ_s approaches 0) and where θ₀ was higher. To test the interaction with θ₀ more fully, we extended the analysis to Mount Shasta, CA, and Toolik, AK, where no in situ data existed. We compared the modelled properties between the radiance and static methods to assess how these assumptions impacted results for these types of data at 30 m scale.

2.5 Comparing DEM and radiance derived μ_s

To ensure the resulting radiance-derived μ_s values were valid, we downloaded the best available validation data sources for comparison. For the San Juan and Shasta sites, we collected DEM products at 1 m spatial resolution and collected a 5 m spatial resolution DEM for the Toolik site (U.S. Geological Survey, 2019, 2022). We then computed slope, aspect, solar zenith angle, and solar azimuth angle for all pixels to compute μ_s at the native resolution (Eq. 1). We then used bilinear interpolation to resample the 1 and 5 m products to 30 m to exactly match the extents and resolution of our PRISMA images. We would like to acknowledge that while these are the best freely available datasets for our images, they still do not capture the true “snow-on” topography and instead are a representation of the “snow-free” surface. We compared matching pixels to determine the RMSD, r, and mean bias. Pixels that were marked as shadow from ray tracing were excluded from this comparison.

3 Results

3.1 Validation using AVIRIS-NG data over the San Juan Mountains

Over the area of the flight lines, AVIRIS-NG estimated mean SSA = 18.0±8.3 m² kg⁻¹, the PRISMA radiance method estimated mean SSA = 19.6±5.8 m² kg⁻¹, and the PRISMA static method estimated mean SSA = 22.0±12.1 m² kg⁻¹. When comparing the SSA performance over each pixel to the AVIRIS-NG flight lines (Fig. 4) we found the PRISMA radiance method (r=0.43; RMSD = 8.0 m² kg⁻¹; bias $=+\mathrm{1.7}$ m² kg⁻¹; n=36 412) performed slightly better than the static method (r=0.23; RMSD = 13.6 m² kg⁻¹; bias $=+\mathrm{4.0}$ m² kg⁻¹; n=36 412) for SSA.

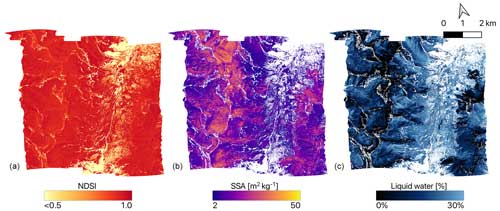
Figure 4 Snow properties computed from AVIRIS-NG (4 m spatial resolution) on 29 April 2021 including NDSI (a), SSA (b), and LWC (c) for the San Juan Mountains site.

There was not a significant improvement in liquid water estimation between radiance (r=0.67; RMSD = 10 %; bias $=-\mathrm{8}$ %; n=36 412) and static (r=0.67; RMSD = 10 %; bias $=-\mathrm{9}$ %; n=36 412). Furthermore, it appeared that there was a consistent liquid water bias of 8 % to 9 %, hinting that more melt had occurred during the AVIRIS-NG flights. As previously noted, the temperatures were well above 0 °C during the overpass of AVIRIS-NG and occurred roughly 1 h later in the day compared to the PRISMA acquisition. This most likely explains the higher liquid water and lower SSA observed by AVIRIS-NG. We further tested this by masking out areas where AVIRIS-NG liquid water content was greater than 0.1 % to establish areas where low amounts of melt occurred between the two acquisitions. We found that performance of PRISMA static (RMSD = 14.2 m² kg⁻¹; rRMSD = 49 %; n=181) and radiance (RMSD = 6.9 m² kg⁻¹; rRMSD = 23 %; n=181) methods were more accurate for these areas. The radiance method performed slightly better, suggesting a modest 25 % improvement in accuracy for SSA over the static method when considering pixels that were less impacted by melt.

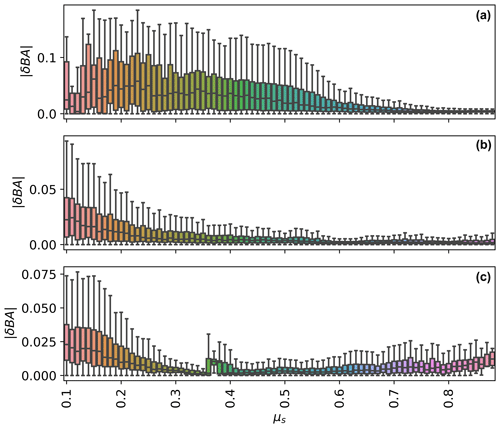
Additionally, comparing all pixels we found improvement from radiance occurred mostly on steep, north-facing aspects (e.g. when μ_s approached 0). We found the absolute residual increased as μ_s approached zero for the static method ($r=-\mathrm{0.47}$; p<0.01), while this relationship was diminished nearly by a factor of 5 for the radiance method ($r=-\mathrm{0.10}$; p<0.01) (Fig. 5a). These errors were caused by incorrect terrain information in the inversion, where inversion error increased proportionately in the static method (Fig. 5b).

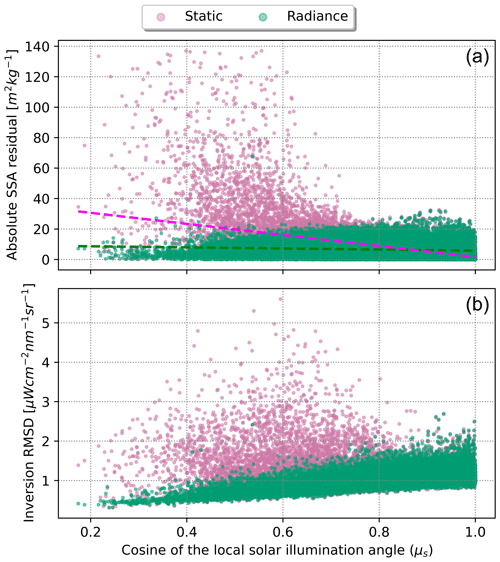
Figure 5 Absolute difference in modelled SSA when compared to AVIRIS-NG for radiance method (green) and static method (pink) with respect to μ_s (a) and the resulting RMSD from the inversion from PRISMA with respect to μ_s (b). Error in the static method increases significantly when μ_s approached zero ($r=-\mathrm{0.47}$; p<0.01); however, the difference was less noticeable in the radiance method ($r=-\mathrm{0.10}$; p<0.01).

Table 2 Image-wide statistics comparing derived properties between the two methods (static vs. radiance) processing the PRISMA imagery for all three sites.

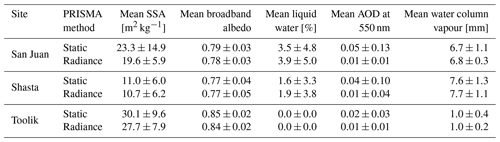
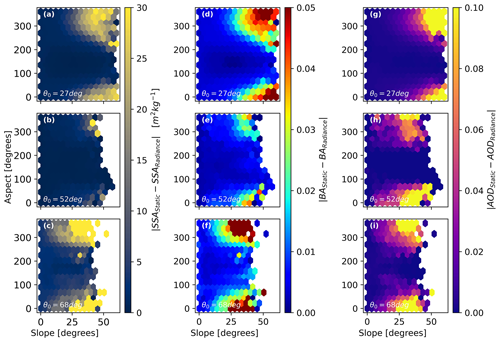
Figure 6 Two-dimensional histogram plots showing absolute difference in SSA (a–c), broadband albedo (d–f), and AOD (g–i) with respect to slope and aspect across the entire dataset. In this figure absolute difference is calculated as |static − radiance|. This is shown for the San Juan Mountains site (a, d, g), Shasta site (b, e, h), and Toolik site (c, f, i). The average solar zenith angle (θ₀) is shown for reference in each panel.

3.2 Comparing radiance and static methods between sites

On average across each of the images, radiance and static methods provided similar retrieved parameters within less than 1 standard deviation (Table 2). In general, this means there is not a significant difference at the 30 m scale for computing parameters such as SSA and broadband albedo (BA) when considering the entire image. Interestingly, when terrain is fixed, the static model compensated for incorrect illumination by increasing the aerosol optical depth (thereby reducing the amount of direct solar radiation). Investigating the errors more closely, we found much larger differences in retrieved properties where μ_s approached 0 (Fig. 6). The difference in distributions matched closely to the theoretical demonstration (Fig. 1) and is most likely associated with the standard error of slope and aspect from the Copernicus DEM given the illumination conditions. This result also demonstrates that the difference between the two methods had the biggest impact for images where θ₀ was high, resulting in potentially inaccurate retrievals that impact both surface and atmospheric state variables on relatively mild slopes.

Putting this into spatial context (Fig. 7), the San Juan site had 37 % of pixels (135.3 km²) with an absolute difference in BA $\left(\right|\mathit{\delta }\text{BA}\left|\right)\mathit{>=}\mathrm{0.01}$ % and 14 % pixels (49.9 km²) with $\left|\mathit{\delta }\text{BA}\right|\mathit{>=}\mathrm{0.02}$. The Shasta site had 30 % of pixels (16.7 km²) with $\left|\mathit{\delta }\text{BA}\right|\mathit{>=}\mathrm{0.01}$ % and 9 % pixels (5.1 km²) with $\left|\mathit{\delta }\text{BA}\right|\mathit{>=}\mathrm{0.02}$. The Toolik site had 40 % of pixels (325.3 km²) with $\left|\mathit{\delta }\text{BA}\right|\mathit{>=}\mathrm{0.01}$ % and 8 % pixels (66.6 km²) with $\left|\mathit{\delta }\text{BA}\right|\mathit{>=}\mathrm{0.02}$.

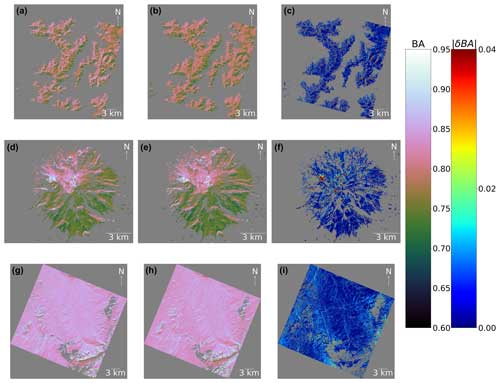
Figure 7 Modelled broadband snow albedo (BA) for the San Juan Mountains site (a–c), Shasta Mountain site (d–f), and Toolik site (g–i). The left column represents BA from the static method, the middle column represents BA from the radiance method, and the right column represents the absolute difference in BA ($\left|\mathit{\delta }\text{BA}\right|$). The dark grey colour symbolizes data that are not a value.

Median $\left|\mathit{\delta }\text{BA}\right|$ for all sites with respect to μ_s generally increased as μ_s approached zero (Fig. 8). For example, for the San Juan site, median $\left|\mathit{\delta }\text{BA}\right|$ ranged from 0.03 to 0.00 across μ_s. For the Shasta and Toolik sites, median $\left|\mathit{\delta }\text{BA}\right|$ ranged from 0.02 to 0.00 across μ_s. This relation was non-linear and depended on the site and illumination conditions. This analysis demonstrates the levels of uncertainty potentially left in for retrievals relying on static, non-coincident DEMs. This quantitatively shows the improvements to snow broadband albedo at 30 m scale by using radiance-based approach to be relatively small for well-lit slopes – on the order 0 %–1 %. In contrast, shaded slopes may have errors in snow broadband albedo on the order of 1 %–3 %. Interestingly, for the Toolik site $\left|\mathit{\delta }\text{BA}\right|$ also increased as μ_s approached one.

Figure 8 Modelled absolute difference in broadband albedo ($\left|\mathit{\delta }\text{BA}\right|=|{\text{BA}}_{\mathrm{Static}}-{\text{BA}}_{\mathrm{Radiance}}|$) for San Juan (a), Shasta (b), and Toolik (c). Note that these boxplots were created by rounding μ_s to the nearest hundredth place.

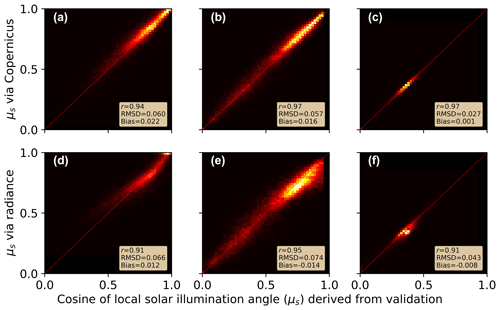
3.3 Comparing DEM and radiance derived μ_s

At the 30 m pixel scale, Copernicus DEM-derived μ_s had similar overall performance to radiance-derived μ_s (Fig. 9), with Copernicus DEM-derived μ_s having slightly higher performance. For example, for the San Juan site, RMSD only varied by 0.006 between the two methods. Similarly, the r for Copernicus-derived μ_s was 0.94, while the radiance-derived μ_s was slightly lower at 0.91. This similar overall performance was common amongst the three sites. We found the average bias for radiance-derived μ_s was generally closer to zero (±0.01) and did not show a strong negative or positive direction.

Figure 9 Comparing μ_s at 30 m pixel scale derived from radiance and Copernicus against high-resolution DEM for the San Juan site (a, d), Shasta site (b, e), and Toolik site (c, f).

4 Discussion

4.1 Radiance-derived DEMs may replace coincident DEMs and contain information related to surface roughness

Derivative slope and aspect maps are prone to errors at 30 m spatial resolutions (Dozier et al., 2022). This is relevant for derived snow products from upcoming missions such as SBG and CHIME, which will rely on topographic information to calculate optical properties like snow albedo. These errors can be inherent to the DEM itself or a product of spatial and/or temporal misalignments (Carmon et al., 2023). Our modelled $\left|\mathit{\delta }\text{BA}\right|$ with respect to the non-coincident DEM was similar to work by Donahue et al. (2023), who found slightly higher uncertainties of broadband albedo (ranging from −10 % to 10 %) for their investigation of Place Glacier, British Columbia, Canada. With the surface and roughness undergoing dramatic change on glaciers throughout a given season, using this radiance-based approach may be especially impactful for improving estimates over glaciers.

Snow surface roughness has long been a challenging issue in modelling snow properties from space where the solar incidence angle at high spatial resolution for snow-on DEM is not well known (Bair et al., 2022). Previous research found radiance-derived μ_s from airborne imaging spectroscopy showed a negative bias and postulated this could be due to within-pixel topography, shadows, and surface roughness (Carmon et al., 2023). Since a bi-directional reflectance function (BRDF) model was not used in their study, it then would be plausible for the optimal μ_s to compensate for these effects. Interestingly, when using a BRDF model in our study (i.e. AART) and solving for aspect optimally (therefore informing μ_s, μ_v, and ξ), we did not find a strong negative or positive bias. However, we did not take surface roughness measurements, and therefore we do not know to what extent this impacted our study. Within-pixel shadows, textures, and surface roughness remain difficult to validate, and we were unable to achieve this in our study. Future work interested in further understanding this radiance-based approach may investigate how such approaches interact with micro-scale topography through ground measurements such as terrestrial and airborne lidar.

4.2 Next steps in possibly improving this radiance-based approach

While we solved for a few terrain parameters in this study, we did not entirely remove the use of the DEM from the radiance method. The elevation from global DEMs has a much higher confidence than its derivative products (Dozier et al., 2022). Therefore, we used these values to inform our atmospheric routine, as well as our shadow-casting ray-tracing module (Wilder et al., 2024). Additionally, we used the method presented in Dozier (2022) for estimating the sky view factor (V_Ω) based on nearby terrain and the pixel itself. This factor could potentially be problematic but was cited as being not as impactful as μ_s in propagating error (Dozier et al., 2022). Therefore, we elected to use V_Ω derived from the static Copernicus DEM. However, this could be an area for future improvement, especially in very steep terrain where V_Ω becomes small. It is not advised to attempt to add V_Ω directly into the optimization routine presented in this study, as it is a function of pixel slope and aspect, and therefore altering V_Ω and aspect together would create invalid solutions. Finally, we used a static value for slope derived from Copernicus DEM. The slope influences the μ_s term, but also influences the passive radiation from nearby slopes. Ultimately, we concluded that aspect had the largest impact on changing μ_s (Fig. 1), as well as large RMSD reported in previous work (Dozier et al., 2022; Donahue et al., 2023), and thus this was the focus of our study. Caution is advised in including both slope and aspect together, as non-unique solution space for μ_s may cause the optimization outputs to become invalid. In summary, elevation, V_Ω, and slope remain static in our current implementation. Future work may explore other algorithmic choices to further remove or improve static DEM parameters.

Another consideration for improving this method is the inclusion of total column ozone into the optimization. Previous research has been able to use TOA snow reflectance data to retrieve reliable estimates of ozone (Kokhanovsky et al., 2021b). In our paper, we elected for a simpler approach to first investigate the impacts of including terrain in the optimization. In this paper we input a fixed ozone for the entire image based on coincident Sentinel-5 measurements. However, it should be stated that ozone impacts a similar spectral range to μ_s (Fig. 10). It therefore may be beneficial to include ozone in the atmospheric lookup table (e.g. MODTRAN, libRadtran) to enable optimization of ozone as well. This may be beneficial in building more realistic radiance-based methods.

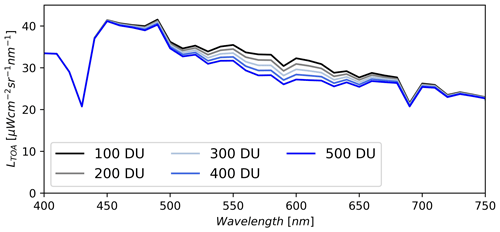
Figure 10 Synthetic data showing the change in magnitude of top-of-atmosphere radiance (L_TOA) with respect to changing total column ozone for fixed snow surface state variables modelled with AART and other fixed atmospheric state variables modelled with libRadtran. Reference data are based on the PRISMA image taken over southern Colorado. Note that values of total column ozone are shown in Dobson units (DU).

Finally, future studies should investigate including improvements to BRDF models of snow (Mei et al., 2022). For example, recent work by Kokhanovsky et al. (2024) has proposed the use of a two-layer model which may be especially useful for vertically heterogenous snowpacks. Their method has been tested using EnMAP data and may easily be transferable to other sensors. The current AART method we used in our paper does not account for these layers, and instead assumes an optically thick, homogenous snowpack. To validate both AART, the new layered approach, and future BRDF models, snow pit (i.e. vertical profile) measurements of SSA (e.g. Meloche et al., 2023) become essential in ensuring models accurately account for diverse layering of snow.

4.3 Big-picture implications of the radiance-based approach

This research responds to the objectives stated in Thriving on our changing planet: A decadal strategy for Earth observation from space to improve biogeophysical modelling at scales driven by topography (National Academies of Science, Engineering, and Medicine, 2018), enabling more accurate snow property retrievals in the cryosphere under challenging illumination conditions. Our presented work on solving terrain where DEM data are not available or reliable may serve to accelerate improvements to satellite remote sensing tools to monitor and model at both regional and global scales (Sturm et al., 2017) at a critical juncture in time where northern latitudes are changing quickly under a warming climate. This includes Earth's glaciers, where radiance-based methods may have the largest improvements over static approaches. Our research is complemented by other recent works that show promise in including terrain in the inversions (Bohn et al., 2024, 2023; Bair et al., 2024; Carmon et al., 2023).

We recommend additional coincident AVIRIS-NG flights with spaceborne imaging spectroscopy datasets to further this work. As we have shown for the San Juan Mountains site, on particularly warm days images that are separated by longer than 1 h may exhibit drastically different SSA and liquid water content. As shown in this paper, this creates an issue when trying to validate improvements to retrieval algorithms.

5 Conclusion

In this study we used existing PRISMA L1 TOA imagery to demonstrate the improvements in modelling snow optical properties when explicitly modelling the terrain in the inversion. This would especially be true for areas where the surface undergoes rapid change such as glaciers. This new method is especially useful for steep mountain terrain and/or high latitudes where illumination conditions are suboptimal. The θ₀ (solar zenith angle) was relatively low for the San Juan Mountains site in our study and thus represents a lower bound of the improvement in accuracy one could expect. This disparity was demonstrated further for the Mount Shasta and Toolik sites when θ₀ was larger (i.e. a greater difference in retrieved properties due to more challenging solar and sensor geometry). Even for the relatively flat Toolik site, we showed that correctly accounting for incidence angles can impact snow properties when θ₀ is large. Future work may look to build from this radiance-based approach to enable better quantification of snow properties at scales impacted by topography.