Control of the temperature signal in Antarctic proxies by snowfall dynamics

Antarctica, the coldest and driest continent, is home to the largest ice sheet, whose mass is predominantly recharged by snowfall. A common feature of polar regions is the warming associated with snowfall, as moist oceanic air and cloud cover increase the surface temperature. Consequently, snow that accumulates on the ice sheet is deposited under unusually warm conditions. Here we use a polar-oriented regional atmospheric model to study the statistical difference between average and snowfall-weighted temperatures. During snowfall, the warm anomaly scales with snowfall amount, with the strongest sensitivity occurring at low-accumulation sites. Heavier snowfall in winter helps to decrease the annual snowfall-weighted temperature, but this effect is overwritten by the event-scale warming associated with precipitating atmospheric systems, which particularly contrast with the extremely cold conditions that occur in winter. Consequently, the seasonal range of snowfall-weighted temperature is reduced by 20 %. On the other hand, the annual snowfall-weighted temperature shows 80 % more interannual variability than the annual temperature due to the irregularity of snowfall occurrence and its associated temperature anomaly. Disturbances of the apparent annual temperature cycle and interannual variability have important consequences for the interpretation of water isotopes in precipitation, which are deposited with snowfall and commonly used for paleotemperature reconstructions from ice cores.

1 Introduction

Antarctica is the coldest and driest continent on earth and almost entirely covered by ice. The surface temperature remains below freezing year-round over most of the continent, allowing the snow to accumulate and form the ice sheet, which is recharged primarily by snowfall. Precipitating atmospheric systems in polar regions are known to increase the surface temperature (Uotila et al., 2011). This is because atmospheric perturbations and clouds strongly disturb the surface energy balance: while short-wave radiation is reduced during overcast weather, the absorption of snow-emitted long-wave radiation and downward radiation from the cloud base cause the net radiative heat flux to warm the surface (Nardino and Georgiadis, 2003; Van Den Broeke et al., 2006). Snow that accumulates on the Antarctic ice sheet is mostly deposited under cloudy conditions, except in the higher parts of the Antarctic Plateau, where clear-sky precipitation forms a large part of the total ice accumulation (Stenni et al., 2016; Fujita and Abe, 2006; Bromwich, 1988). Even for clear-sky precipitation, despite the absence of clouds, a vapour-rich atmosphere emits more long-wave radiation and warms the surface (Gallée and Gorodetskaya, 2010; Genthon et al., 2013). Atmospheric perturbations can increase the surface wind speed (Argentini et al., 2014; Vignon et al., 2017; Baas et al., 2019). This weakens or breaks the surface temperature inversion as increased turbulent mixing incorporates warmer air from the upper temperature inversion layer (Hirasawa et al., 2000; Vignon et al., 2019; Heinemann et al., 2019). In addition to modifying the local energy balance, synoptic systems effectively transport heat inland in Antarctica (Carleton and Whalley, 1988; Giovinetto et al., 1992). Large atmospheric perturbations thus modify the heat flux and surface temperature (Uotila et al., 2011), causing occasional surface warming exceeding 10 ^∘C (Ganeshan et al., 2022). Atmospheric rivers, which are extreme water vapour fluxes associated with some cyclones, are also associated with intense warming, particularly in winter (Wille et al., 2021). Consequently, days with snow or ice accumulation in Antarctica are warmer than average.

Knowledge of the temperature variability in Antarctica strongly relies on paleoclimate studies to extend the time period beyond the observation period of the satellite era (Jones et al., 2016). Among various temperature proxies, stable water isotopes in ice are the most used in paleoclimate studies in Antarctica (Stenni et al., 2017) due to the widely available base material and a good understanding of the fractionation processes associated with precipitation formation (Markle and Steig, 2022). Due to Rayleigh distillation during the transport of moisture to cold regions, water isotopes reflect the condensation temperature of precipitation (Dansgaard, 1964). However, the relationship between the average temperature at a location and isotopes in the snow is altered by the deposition dynamics of snowfall-borne water isotopes (Werner et al., 2000; Persson et al., 2011; Casado et al., 2020), post-deposition processes such as ablation–redeposition and sublimation–condensation cycles (Steen-Larsen et al., 2014; Touzeau et al., 2016; Stenni et al., 2016; Münch et al., 2017; Hughes et al., 2021), and the difference between the condensation and surface temperatures (Buizert et al., 2021; Liu et al., 2023). Water isotope measurements characterize the ice deposited during snowfall events, so δ¹⁸O (following the δ notation as in Dansgaard, 1964) is thought to better correlate with the snowfall-weighted temperature than the average temperature (Stenni et al., 2016; Fujita and Abe, 2006), as shown in isotope-enabled models (Sturm et al., 2010). Differences between the snowfall-weighted temperature and average temperature remain poorly described. Characterizing these differences will thus help us to understand the signal recorded in water isotopes and quantify the effects of precipitation intermittency on Antarctic ice cores (Masson-Delmotte et al., 2011).

In Antarctica, the top 10 % of the daily precipitation events at a location can generate most of the annual accumulation amount and interannual variability (Turner et al., 2019). Consequently, these events control the temperature signal imprinted in the isotopic composition of the deposited snow. The few days when most of the snow is accumulated may not represent average conditions because they are associated with temperature increases and may occur anytime in the year, causing aliasing of the seasonal signal due to irregular sampling. Quantifying the temperature changes associated with snowfall could highlight key mechanisms for the interpretation of water isotopes in snow and ice, and it can ultimately improve water-isotope-based temperature reconstructions. Although the different heat transport mechanisms are relatively well understood and included in current atmospheric models, a climatology of the warming associated with snowfall events has not been made so far.

The covariance of precipitation and temperature at synoptic and seasonal scales was shown to affect the isotope–temperature slope by changing the temperature that can effectively be recorded in an ice core (Sime et al., 2008). Changes in recordable temperature may be linked to precipitation changes rather than temperature changes (Krinner et al., 2006). In addition, the intermittency of precipitation induces isotopic variability unrelated to the temperature, which is especially important at the interannual scale for the low-accumulation East Antarctic Plateau (Casado et al., 2020). Spatial and temporal changes in snowfall intermittency impact the recordable temperature (Sime et al., 2008), which is partly responsible for the spatial and temporal variations in isotope–temperature slope values (Sime et al., 2009a, b; Klein et al., 2019). Sub-sampling the temperature signal by snowfall affects the recordable temperature in water isotopes, but the extent of this effect and its variability among the variety of precipitation regimes in the entire Antarctic continent have been poorly characterized. Although post-deposition effects can further modify isotope–temperature slopes after deposition (Sime et al., 2011; Casado et al., 2018), understanding the temperature changes (which are related to the snow precipitation) at the time of deposition at different timescales and locations can help us to explain some of the spatial and temporal diversity of the slopes.

Here, we study the surface temperature changes associated with snowfall, aiming to understand the signal that a precipitation-based proxy would carry at the time of its deposition. Using the polar-oriented regional atmospheric model MAR, which has been extensively evaluated for its representation of the Antarctic surface mass balance (Agosta et al., 2019) and temperature (Kittel et al., 2021), we compute snowfall-weighted statistics to evaluate the average bias and interannual variability of temperature across Antarctica for the period 1979–2020. We focus our analysis on the quantification of the temperature anomaly, defined as the difference from the daily climate normal temperature, and suggest possible effects on water isotopes.

2 Methods

2.1 Regional atmospheric model

We use the polar-oriented regional atmospheric model MAR version 3.12 to assess the variability of snowfall and temperature in Antarctica. Version 3.11 of this model has shown good performance when representing the surface mass balance (defined as the total precipitation minus sublimation and runoff; Agosta et al., 2019), temperature (Kittel et al., 2021), and cloud (Kittel et al., 2022) variability. The version used here (3.12) differs mainly in the temperature transition of rainfall to snowfall (both can now co-occur in the model) and the correction of the snowpack temperature (Antwerpen et al., 2022) as well as albedo tuning for the dense Antarctic snow. The simulation domain is on an Antarctic polar stereographic projection (EPSG:3031) with a horizontal resolution of 35×35 km. The MAR model is nudged to ERA5, the latest re-analysis product of the European Center for Medium-Range Weather Forecasts, which gives the most accurate representation of both temperature and surface mass balance in Antarctica among climate re-analyses (Gossart et al., 2019). The use of the MAR regional model provides further detail in the near-surface atmospheric layers and spatial scale compared to ERA5. The simulation used in this study covers the period 1979–2020 (42 years). There is a notable lack of direct snowfall observations in the low-accumulation regions of Antarctica, which hinders our ability to directly evaluate the model for this parameter. The modelled surface mass balance can be evaluated against the observed accumulation, but this includes several processes, ranging from snowfall to snow drift, the evaporation of falling snow, and evaporation–condensation on the snow surface, each of which comes with its own uncertainties. We evaluate the performance of MARv3.12 in representing the temperature and surface mass balance in Figs. A1–A4.

2.2 Temperature averaging, temperature difference, and temperature anomaly: definitions and notation

Although the temperature recorded in water isotopes is imprinted at the condensation level (Jouzel and Merlivat, 1984), we chose to use the 2 m air temperature for simplicity because condensation levels change both spatially and temporally. Studies using water isotopes usually bypass condensation to surface temperature changes by directly calibrating the isotope–temperature slope with the 2 m temperature in most cases (e.g. Jouzel et al., 2007; Stenni et al., 2017) or applying a ratio of temperature changes that would be amplified at the surface (e.g. Jouzel et al., 2003). If we used the condensation-level temperature, the difference from the climate normal would depend on the level of precipitation formation that is vertically spread on the atmospheric column, making the comparison more complex. With the condensation temperature, we would expect weaker seasonal cycles because winter surface cooling is amplified by a strong inversion, but the long-term temperature variability may not change much, as implied by deglaciation simulations (Liu et al., 2023). Choosing the 2 m temperature also enables comparison with available observations, and this is the level considered in many paleotemperature reconstructions.

In this study, we use the average temperature calculated with the arithmetic mean,

$$\begin{array}{}\text{(1)}& T={\displaystyle \frac{{\sum }_{\mathrm{day}=\mathrm{1}}^{n_{\mathrm{days}}}{T}_{\mathrm{day}}}{n_{\mathrm{days}}}},\end{array}$$

and the snowfall-weighted temperature, defined as the weighted average of the temperature with the daily snowfall rate as the weighting coefficient:

$$\begin{array}{}\text{(2)}& T_{\mathrm{w}}={\displaystyle \frac{{\sum }_{\mathrm{day}=\mathrm{1}}^{n_{\mathrm{days}}}{T}_{\mathrm{day}}\times {\text{SF}}_{\mathrm{day}}}{{\sum }_{\mathrm{day}=\mathrm{1}}^{n_{\mathrm{days}}}{\text{SF}}_{\text{day}}}}.\end{array}$$

In both cases, T_day refers to the temperature on a given day, and SF_day is the snowfall on the same day. Temperature averages can be computed for the entire study period (n_days=15 341), a year (n_days=366), or on a given day of year (n_days=42, used for the climate normals $\stackrel{\mathrm{‾}}{T}$ and $\stackrel{\mathrm{‾}}{T_{\mathrm{w}}}$). We define the climate normal temperature for each model grid cell as the average for the same day of year across the 42 years, and we subsequently apply a 30 d rolling mean to smooth the signal.

To quantify the difference in temperature associated with snowfall, we define the snowfall-weighted temperature difference as

$$\begin{array}{}\text{(3)}& \mathrm{\Delta }T=T_{\mathrm{w}}-T.\end{array}$$

This metric was previously described as “precipitation-weighted biasing” in Sime et al. (2008), but we choose not to call it a bias to avoid confusion with the modelling temperature bias, which refers to the difference between the modelled and observed temperatures here.

Decomposition of the daily temperature T_day into the climate normal temperature on that day (${\stackrel{\mathrm{‾}}{T}}_{\mathrm{day}}$) and the daily anomaly with respect to the climate normal (${T^{\prime }}_{\mathrm{day}}$) allows us to separate the seasonal and non-seasonal effects of snowfall weighting:

$$\begin{array}{}\text{(4)}& {\displaystyle }\begin{array}{rl}\mathrm{\Delta }T& ={\displaystyle \frac{\sum _{\mathrm{day}=\mathrm{1}}^{n_{\mathrm{days}}}\left({\stackrel{\mathrm{‾}}{T}}_{\mathrm{day}}+T_{\mathrm{day}}^{\prime }\right)\times {\text{SF}}_{\mathrm{day}}}{\sum _{\mathrm{day}=\mathrm{1}}^{n_{\mathrm{days}}}{\text{SF}}_{\mathrm{day}}}}\\ & -{\displaystyle \frac{\sum _{\mathrm{day}=\mathrm{1}}^{n_{\mathrm{days}}}\left({\stackrel{\mathrm{‾}}{T}}_{\mathrm{day}}+T_{\mathrm{day}}^{\prime }\right)}{n_{\mathrm{days}}}}\end{array}\text{(5)}& {\displaystyle }\begin{array}{rl}\mathrm{\Delta }T& =+\underset{\text{seasonal}}{\underbrace{{\displaystyle \frac{\sum _{\mathrm{day}=\mathrm{1}}^{n_{\mathrm{days}}}{\stackrel{\mathrm{‾}}{T}}_{\mathrm{day}}\times {\text{SF}}_{\mathrm{day}}}{\sum _{\mathrm{day}=\mathrm{1}}^{n_{\mathrm{days}}}{\text{SF}}_{\mathrm{day}}}}-{\displaystyle \frac{\sum _{\mathrm{day}=\mathrm{1}}^{n_{\mathrm{days}}}{\stackrel{\mathrm{‾}}{T}}_{\mathrm{day}}}{n_{\mathrm{days}}}}}}\\ & +\underset{\text{non-seasonal}}{\underbrace{{\displaystyle \frac{\sum _{\mathrm{day}=\mathrm{1}}^{n_{\mathrm{days}}}{T}_{\mathrm{day}}^{\prime }\times {\text{SF}}_{\mathrm{day}}}{\sum _{\mathrm{day}=\mathrm{1}}^{n_{\mathrm{days}}}{\text{SF}}_{\mathrm{day}}}}-{\displaystyle \frac{\sum _{\mathrm{day}=\mathrm{1}}^{n_{\mathrm{days}}}{T}_{\mathrm{day}}^{\prime }}{\underset{=\mathrm{0}}{\underbrace{n_{\mathrm{days}}}}}}}}.\end{array}\end{array}$$

A summary of the abbreviations used is given in Table 1.

Table 1 Abbreviations used in this study.

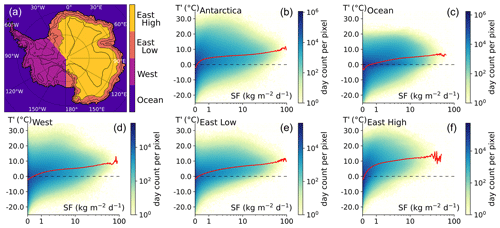
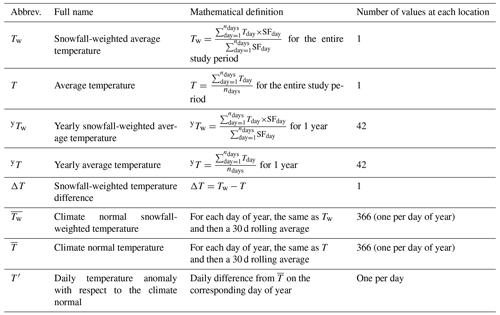
Figure 1 Scatter heatmaps of the daily temperature anomaly with respect to the climate normal as a function of daily snowfall for different major regions of Antarctica for the period 1979–2020. The temperature anomaly T^′ is defined as the difference between the daily 2 m temperature and the climate normal $\stackrel{\mathrm{‾}}{T}$ (the temperature on the average seasonal cycle for this day; see Sect. 2) on the corresponding model cell for each day. Scatter heatmaps are represented for each region defined in (a), with the heatmap for Antarctica (b) regrouping every point on the surface of the Antarctic ice sheet (including ice shelves). Ocean (c) is the remaining model domain in the Southern Ocean. Antarctica is further subdivided into west (d), for longitudes between 180 and 40^∘ W; east low (e), for longitudes between 40^∘ W and 180^∘ E and elevations below 2000 m; and east high (f), for longitudes between 40^∘ W and 180^∘ E and elevations above 2000 m. For heatmaps (b–f), the red line represents the average temperature anomaly given the snowfall rate, dashed lines highlight $T^{\prime }=\mathrm{0}$ (no anomaly), the x axis scales with log₁₀(1 + snowfall), and the scatter density is the number of days in each pixel-sized bin after projection onto the logarithmic snowfall scale.

3 Results and discussion

3.1 Average temperature during snowfall

The temperature during snowfall is statistically higher than the average temperature on the same day, as shown by the mostly positive temperature anomalies (Fig. 1). Despite a wide distribution of temperature anomalies at any given snowfall rate, the average temperature anomaly increases with snowfall. Over Antarctica, there is a +5 ^∘C increase between snowfall rates of 0 (no snowfall) to 1 kg m⁻² d⁻¹, and a gradual increase of another +5 ^∘C as snowfall rates increase from 1 up to 100 kg m⁻² d⁻¹. Conversely, days without snowfall are 2 ^∘C cooler than average. For major regions of Antarctica, similar patterns are modelled, with negative temperature anomalies on days without snowfall and increasing temperature anomalies of up to +10 ^∘C for snowfall exceeding 50 kg m⁻² d⁻¹. The main difference for East Antarctic high elevations (Fig. 1f) is that the temperature anomalies reach the +5 ^∘C threshold for snowfall rates of less than 1 kg m⁻² d⁻¹.

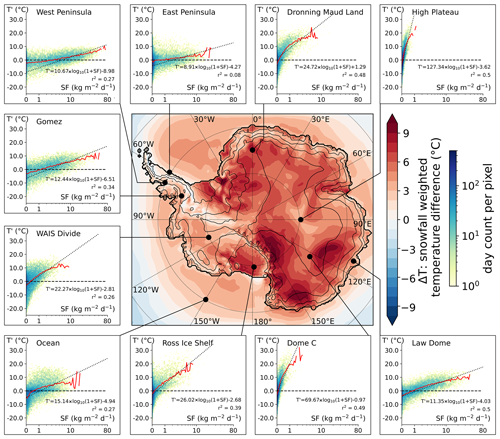
Figure 2 Map of snowfall-weighted 2 m temperature differences (ΔT), and scatter heatmaps of site-specific temperature anomalies (T^′) against snowfall rates (SF). Thick black lines indicate the extent of the Antarctic continent (including ice shelves). Thin lines show the 100, 1000, 2000, and 3000 m elevation contours. Black dots show the locations of 10 selected locations where the scatter density heatmap of temperature anomaly with respect to climate normal is shown in an inset (as in Fig. 1, but for a single model cell). Dotted lines represent linear trends computed for each inset on the log₁₀(1 + SF) scale using snowfall-weighting coefficients (following the regression method described in Servettaz et al., 2020). Days without snowfall or with extremely low snowfall rates (below 0.05 kg m⁻² d⁻¹) were excluded from the trend computation. All trends are significant (p value <0.01). T^′: temperature anomaly with respect to climate normal; SF: snowfall.

The positive anomaly associated with snowfall affects all of the Antarctic continent, although with varying intensity, as shown by the map of differences between the snowfall-weighted temperature and average temperature (denoted ΔT, Fig. 2; abbreviations listed in Table 1). Over the entire Antarctic continent and ice shelves, ΔT averages 5.4 ^∘C. While coastal regions and West Antarctica show ΔT values of 0 to 5 ^∘C, the East Antarctic Plateau and ice shelves reach ΔT values of up to 10 ^∘C. Interestingly, ΔT is highest in large topographical depressions such as the Recovery (20^∘ W, 80^∘ S), Aurora (115^∘ E, 75^∘ S), and Wilkes (150^∘ E, 70^∘ S) basins or the Byrd glacier catchment inland of the Transantarctic Mountains (150^∘ E, 80^∘ S). On the other hand, over steep slopes and ridges, the snowfall-weighted temperature is relatively close to the average temperature. Note that hoar frost is computed separately from snowfall in the model and occurs in cold conditions (Schlosser et al., 2016). Therefore, ice accumulated by hoar frost can mitigate the warm conditions associated with snowfall, but this is not depicted by ΔT, which accounts only for snowfall. Another modelling study by Sime et al. (2008) showed ΔT values of up to 10 ^∘C in East Antarctica and lower values of about 5 ^∘C in West Antarctica for the present day, consistent with the results presented here. Our results mostly differ in the coastal regions, which may relate to the increased resolution used in this study or differences in modelling the physical processes of the katabatic-affected Antarctic slopes. In this work we focus on the quantitative temperature increase, but the degradation of the climatic signal due to the loss of correlation induced by precipitation intermittency has been treated in similar studies (Sime et al., 2011; Casado et al., 2020).

Table 2 Values of the temperature anomaly (T^′) for snowfall rates higher than 1 kg m⁻² d⁻¹. Locations of sites are shown in Fig. 2. For each site, the average (arithmetic) and quantiles for different percentages are shown.

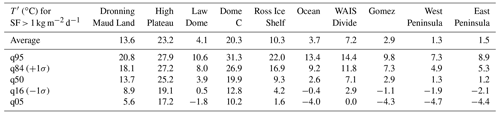
To better understand the temperature anomaly associated with snowfall at the Antarctic scale, we analyse 10 sites where the impact of extreme precipitation events on the total accumulation has previously been discussed (Turner et al., 2019), and we show the temperature–snowfall relationship at these locations (insets in Fig. 2). There are strong differences between sites located near the coast (Law Dome, East and West Peninsula, Gomez) compared to high-elevation sites on the East Antarctic Plateau (High Plateau, Dronning Maud Land, Dome C): high-elevation sites are characterized by low snowfall rates, but events causing a snowfall larger than 1 kg m⁻² d⁻¹ are accompanied by a temperature increase of more than 10 ^∘C on average, and commonly up to 20 ^∘C (Table 2). These high-elevation sites with low snowfall and large temperature anomalies are responsible for the sharp increase in temperature associated with low snowfall rates (Fig. 1f). Most locations reach temperature anomalies close to 10 ^∘C at their respective maximum snowfalls (WAIS Divide, Gomez, Law Dome), except for sites where dry warming usually occurs, driven by foehn (East Peninsula) or katabatic adiabatic compression (coastal slopes). Each site shows an increasing temperature trend with snowfall rate, with steeper slopes for sites with low accumulation (Fig. 2). Overall, days with snowfall are statistically warmer than average conditions, and they are increasingly so for higher snowfall rates at a given location.

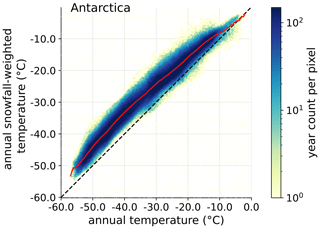
Figure 3 Scatter heatmap of annual snowfall-weighted temperature (T_w) as a function of annual temperature (T) for every model point on the surface of the Antarctic ice sheet (including ice shelves). The continuous red line represents the average snowfall-weighted temperature given the annual temperature. The dashed line highlights the 1:1 line.

The analysis of yearly snowfall-weighted temperature (^yT_w) and “true” yearly temperature (^yT, Fig. 3) further supports that the effect of snowfall weighting is not constant and may depend on local parameters including the temperature, but also probably the precipitation regimes. Importantly, ^yT_w is not linearly related with ^yT, suggesting that changes in the annual temperature are not matched by proportional changes in the snowfall-weighted temperature. This relationship may also change depending on whether we average annually or at other time resolutions. Besides, any given ^yT is matched with a large distribution of ^yT_w, which means that snowfall weighting induces variability in the temperature.

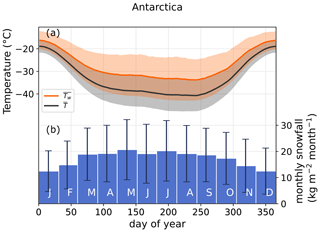
Figure 4 Seasonal cycles of temperature and snowfall averaged over Antarctica. (a) Climate normals of temperature ($\stackrel{\mathrm{‾}}{T}$) and snowfall-weighted temperature ($\stackrel{\mathrm{‾}}{T_{\mathrm{w}}}$). Shading indicates the 1σ standard deviation. (b) Monthly snowfall, with the 1σ standard deviation indicated by error bars. All modelled points on the Antarctic continent, including ice shelves, are included in both panels. Climate normal temperatures were computed as the arithmetic (for $\stackrel{\mathrm{‾}}{T}$) or snowfall-weighted (for $\stackrel{\mathrm{‾}}{T_{\mathrm{w}}}$) average for the same day of year across the 1979–2020 period and then smoothed with a 30 d rolling mean (see Sect. 2).

3.2 Variability of the temperature during snowfall

Snowfall events, in particular large precipitation events, are an important source of variability in the Antarctic climate (Turner et al., 2019). As there is a clear link between snowfall intensity and the temperature anomaly, the variability of snowfall translates into a variability of temperature. We first investigate the seasonality of temperature anomalies associated with snowfall (Fig. 4) by considering the climate normal snowfall-weighted temperature ($\stackrel{\mathrm{‾}}{T_{\mathrm{w}}}$, see Sect. 2 for details on computation) and the climate normal temperature ($\stackrel{\mathrm{‾}}{T}$). $\stackrel{\mathrm{‾}}{T_{\mathrm{w}}}$ differs from $\stackrel{\mathrm{‾}}{T}$ by 3 ^∘C in summer and up to 8 ^∘C in winter on average on the Antarctic ice sheet. The larger difference in winter results from the attenuation of near-surface temperature inversion during the passage of precipitating atmospheric systems. Indeed, $\stackrel{\mathrm{‾}}{T}$ reaches extremely low temperatures in winter, driven by the strong surface radiative cooling (Connolley, 1996; Hudson and Brandt, 2005; Genthon et al., 2021). While it contributes to large variability in winter temperatures compared to the summer season (Ricaud et al., 2017), snowfall consistently occurs under warm conditions. The seasonal amplitude of $\stackrel{\mathrm{‾}}{T_{\mathrm{w}}}$ is thus 20 % lower than that of $\stackrel{\mathrm{‾}}{T}$ on average in Antarctica (Fig. 5). The reduction in seasonal amplitude occurs consistently over the Antarctic continent and is strongest on coastal slopes.

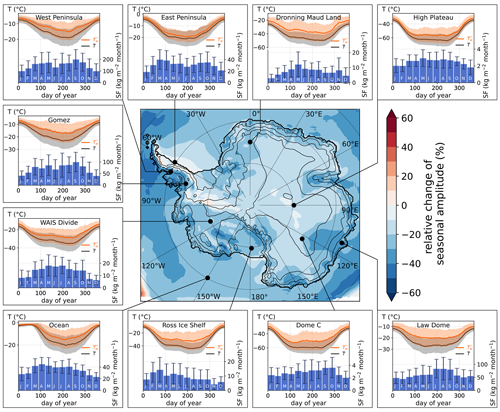
Figure 5 Map of the relative change in seasonal amplitude, defined as the ratio of standard deviations $r_{\mathrm{SD}}=\left(\frac{\mathrm{SD}\left(\stackrel{\mathrm{‾}}{T_{\mathrm{w}}}\right)}{\mathrm{SD}\left(\stackrel{\mathrm{‾}}{T}\right)}-\mathrm{1}\right)\times \mathrm{100}$ for each model cell, where SD is the standard deviation. Insets show seasonal cycles of temperature and snowfall for a selection of 10 sites in Antarctica. For each site, climate normals are shown for temperature ($\stackrel{\mathrm{‾}}{T}$), snowfall-weighted temperature ($\stackrel{\mathrm{‾}}{T_{\mathrm{w}}}$), and monthly snowfall, similarly to Fig. 4. Climate normal temperatures were computed as the arithmetic (for $\stackrel{\mathrm{‾}}{T}$) or snowfall-weighted (for $\stackrel{\mathrm{‾}}{T_{\mathrm{w}}}$) average for the same day of year across the 1979–2020 period and then smoothed with a 30 d rolling mean.

In winter, cyclogenesis is slightly higher (Uotila et al., 2011) and atmospheric blocking is more frequent (Wille et al., 2021; Scarchilli et al., 2011), increasing the probability of poleward moisture transport and Antarctic snowfall. This results in higher snowfall in the winter months at the Antarctic scale (Fig. 4b) and causes the snowfall-weighted temperature to be influenced more by the winter season, when the snowfall-related warming is the strongest.

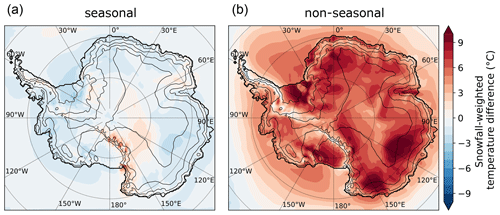
Figure 6 Seasonal and non-seasonal effects of snowfall weighting on the temperature difference (ΔT). (a) The seasonal effect on the temperature difference reflects the temperature changes induced by snowfall seasonality. (b) Non-seasonal effects of snowfall weighting, revealing the influence of snowfall-event-related warming. Summing both maps results in the map shown in Fig. 2 (see Sect. 2).

We decompose the contributions of the seasonal distribution of snowfall (Fig. 6a) and the event-related daily temperature anomaly (Fig. 6b) to ΔT. As most of Antarctica receives more snowfall in winter (Palerme et al., 2017), the difference induced by seasonality averages −0.7 ^∘C over the ice sheet but rarely exceeds −3 ^∘C. On the contrary, snowfall-event-related warming causes a difference of +6.1 ^∘C and dominates the difference between snowfall-weighted and all-day temperatures. These results are also in good agreement with the frequency decomposition of Sime et al. (2008), who showed that most of the ΔT signal was in the synoptic signal, comparable to the daily anomaly of the temperature used here. Although the seasonal signal is mostly negative in Fig. 6a, we note weakly positive ΔT in Victoria Land, where Sime et al. (2008) also found positive ΔT for their seasonally band-passed signal. The extent of this positive region is greater in Sime et al. (2008), extending well within continental East Antarctica, but this may be related to the discrepancy in modelled seasonal precipitation for the dry East Antarctic plateau, with the summer precipitation maximum causing positive ΔT in Sime et al. (2008) as opposed to the winter maximum causing negative ΔT here (Figs. 5 and 6, High Plateau site). In another study using the same method, Masson-Delmotte et al. (2011) find much stronger ΔT over the East Antarctic plateau, which is linked to seasonal effects on temperature. However, this difference is likely to have emerged from the ERA40 re-analysis used, which was documented as having a lack of winter precipitation and cyclone intensity in winter in the driest regions of Antarctica (Bromwich et al., 2007; Marshall, 2009), which leads to unrealistically large seasonal effects of precipitation weighting.

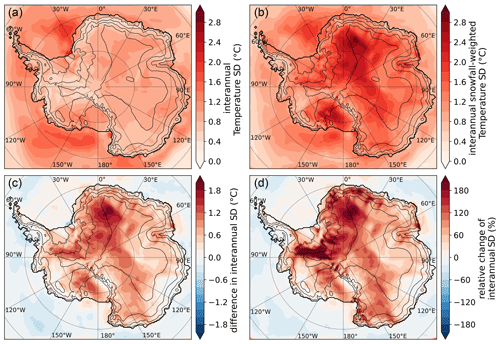
Figure 7 Maps of the change in the interannual standard deviation of temperature induced by snowfall weighting. (a) Standard deviation of the yearly averaged temperature SD(^yT). (b) Standard deviation of the annually snowfall-weighted temperature SD(^yT_w). (c) Difference in standard deviations SD(^yT_w)−SD(^yT). (d) Relative change in standard deviation, given by $r_{\mathrm{SD}}=\left(\frac{\mathrm{SD}{(}^{\mathrm{y}}{T}_{\mathrm{w}})}{\mathrm{SD}{(}^{\mathrm{y}}T)}-\mathrm{1}\right)\times \mathrm{100}$. For all definitions, SD is the standard deviation and ^yT_w and ^yT are the yearly snowfall-weighted temperature and yearly average temperature, respectively. Thick black lines indicate the extent of the Antarctic continent (including ice shelves). Thin lines show the 100, 1000, 2000, and 3000 m elevation contours.

The dampened seasonal amplitude of the snowfall-weighted temperature results from averaging across 42 years, smoothing out interannual variability. While the yearly averaged temperature (^yT) is relatively stable over time (Fig. 7a), the interannual snowfall is highly variable, especially for the winter season (Casado et al., 2020; Turner et al., 2019). This causes the yearly snowfall-weighted temperature (^yT_w) to vary significantly from one year to another, with the standard deviation increased by +80 % on average over the ice sheet compared to ^yT (Fig. 7d). The variability is especially increased in Dronning Maud Land and the eastern part of West Antarctica facing the Ronne Ice Shelf, where the interannual variability of ^yT_w can be 200 % larger than the variability of ^yT. Previous studies highlighted that the large variability of winter temperatures causes the winter season to be dominant in the interannual temperature variability, as a warm year is usually due to a warm winter, which is often accompanied by one or multiple snowfall events in winter (Persson et al., 2011; Casado et al., 2020; Servettaz et al., 2020). Despite the reduced seasonality of the snowfall-weighted temperature and the tendency to oversample warm winters, its interannual variability is increased. In other words, the temperature averaged equally over all days of a year is more stable than the temperature taken during snowfall only. This is because of the sporadic nature of snowfall, which causes the temperature to be subsampled on a limited number of days (Fujita and Abe, 2006; Turner et al., 2019) at random times of the year and with a temperature bias which depends on precipitation intensity. On the interannual scale, the variability of yearly averaged temperature is thus enhanced when weighting with snowfall.

3.3 Implications for water isotopes

Water isotopes are used in Antarctic paleoclimate studies as a proxy for temperature due to the relationship between air temperature at condensation and the isotopic ratio in precipitation (Stenni et al., 2017; Dansgaard, 1964). Ice cores retrieve material accumulated over time onto the ice sheet, where the ice mass contribution depends on the snowfall. Therefore, snowfall-weighted temperatures provide an analogue to the isotopes we can expect to measure in an ice core. We thus discuss how the temperature during snowfall may affect δ¹⁸O at the time of snow deposition, prior to post-deposition effects that occur later and further modify snow isotopes. Although we mainly discuss water isotopes due to their preponderance in paleotemperature studies in Antarctica, these effects would theoretically apply to any snowfall-dependent temperature proxy.

Water isotopes in snow are deposited under warmer-than-normal conditions (Fig. 2), which leads to a higher-than-expected δ¹⁸O. Some climatic information is lost for δ¹⁸O as cold days are not recorded or they are recorded with lower weight. Previous works suggested that δ¹⁸O could be seasonally biased due to the annual cycle of snowfall (Markle and Steig, 2022; Werner et al., 2000; Persson et al., 2011), but here we show that the temperature increase associated with precipitation events is clearly the main factor controlling the snowfall-weighted temperature in Antarctica. The variety of ΔT values across modern Antarctica suggest that it depends on precipitation regimes and the amplitude of temperature change during precipitation at a given site. The stability of ΔT over time is thus decisive for temperature reconstructions based on isotopes because temporal changes in ΔT could accompany temperature and precipitation changes and hinder the δ¹⁸O-based reconstructions. Here, the short study period does not allow us to evaluate temporal changes in ΔT, but such changes may be responsible for modifications of δ¹⁸O–temperature slopes at longer timescales, as was suggested for the glacial-interglacial range (Buizert et al., 2021). Previous studies also highlighted that, despite being weaker than non-seasonal effects in absolute value, seasonal effects on ΔT are more likely to vary with climate as the seasonality of precipitation changes (Sime et al., 2008) in response to sea ice and moisture source changes (Holloway et al., 2016). Given the spatial variability of ΔT, we advise against the use of spatial gradients to define isotope–temperature slopes for temporal reconstructions.

Moreover, the reduced annual cycle of $\stackrel{\mathrm{‾}}{T_{\mathrm{w}}}$ relative to $\stackrel{\mathrm{‾}}{T}$ may reflect an annual cycle of δ¹⁸O with attenuated amplitude, which can explain why the seasonal δ¹⁸O–temperature slope appears to be lower in precipitation δ¹⁸O studies than in simple isotopic models (Casado et al., 2018). On the other hand, averaging temperature and isotopes yearly to define the δ¹⁸O–temperature slope may increase the slope value because of the higher interannual variability of δ¹⁸O induced by the irregularity of the snowfall distribution, similarly to the snowfall-weighted temperature. Links were found between Antarctic temperature and large-scale atmospheric circulation patterns in the Southern Hemisphere such as the Southern Annular Mode (abbreviated to SAM, Marshall and Thompson, 2016), which possibly influence the δ¹⁸O (Abram et al., 2014; Kino et al., 2021). Nevertheless, we did not find any significant correlation between the SAM and the yearly or monthly snowfall-weighted temperature difference. Detecting possible links between the SAM, or other climate modes, and the precipitation-weighted temperature (or δ¹⁸O) would require a more detailed investigation and may be explored in a different study.

Slopes of snowfall-weighted δ¹⁸O of precipitation against snowfall-weighted temperature have previously been suggested (Fujita and Abe, 2006; Sturm et al., 2010; Servettaz et al., 2020). The precipitation-weighted δ¹⁸O makes physical sense because it mimics the ice core signal (omitting the post-deposition effects), but paleoclimate reconstructions seek the temperature rather than the snowfall-weighted temperature. This work highlights the critical importance of event-related warming for the temperature during snowfall, as it reduces the seasonal amplitude, while the irregular snowfall distribution enhances the interannual variability of the temperature possibly recorded in water isotopes. This explains, at least partly, the higher interannual variability of precipitation-weighted δ¹⁸O, which causes an increased δ¹⁸O–temperature slope across most of Antarctica at the interannual scale compared to the seasonal scale (Goursaud et al., 2018), and low correlations between modelled δ¹⁸O and temperature at the annual scale (Münch et al., 2021). Simulation of δ¹⁸O signals that would be recorded in Antarctic Peninsula ice cores also revealed that the interannual variability in δ¹⁸O may show a poor correlation to temperature variability, even in high-accumulation regions (Sime et al., 2009a). Non-linearities in the snowfall-weighted temperature as the temperature and climate change (Fig. 3) may be responsible for the non-linear responses of isotopes to temperature and the underestimation of the temperature maximum in warm periods through increased winter precipitation (Sime et al., 2009b).

Understanding the effect of snowfall weighting on the average temperature at ice coring sites will help us to reconstruct paleotemperatures more accurately. Depending on the targeted time frame for temperature reconstruction from isotopes, be it seasonal (Jones et al., 2023) or pluriannual (Stenni et al., 2017), the reconstructed temperature range may be lessened or increased. Moreover, using slopes that are variable over time would result in better temperature quantification because the slope depends on the temperature range and the location (Sime et al., 2009b) and may vary over time (Klein et al., 2019).

Quantifying the local effect of snowfall weighting on the temperature range can help refine the temperature–isotope slopes for more accurate estimation, and it should be done for different settings ranging from glacial to warmer-than-present interglacial climates. Future temperature reconstructions could consider proceeding in two steps: (1) determine the snowfall-weighted temperature from water isotopes, for which the correlation is generally good and can be determined by Rayleigh-type models (e.g. Markle and Steig, 2022), and then (2) determine the average (non-weighted) temperature through the site-calibrated T_w–T slope, calculated for the matching temporal resolution (similarly to Fig. 3, but here we only show the ^yT_w–^yT slope computed with yearly averages and include all of Antarctica), while accounting for the difference in temperature between the condensation level and surface, often dictated by inversion strength. Greater snowfall-weighted temperature differences at low-accumulation sites suggest that changes in snowfall regimes could impact the temperature difference and thus bias the reconstructions from isotopes. Further work is necessary to fully understand how changes in snowfall dynamics may influence temperature reconstructions from isotopes, which may be facilitated by atmospheric models equipped with isotopes.

4 Conclusions

We evaluated the temperature during snowfall in Antarctica using the regional atmospheric climate model MAR. Positive temperature anomalies usually accompany snowfalls, and the anomalies tend to increase with snowfall rate at any given site. The slope of the temperature increase as a function of snowfall rate is strongest at sites with low accumulation, so even locations with low snowfall rates experience a strong snowfall-weighted temperature difference. Over the Antarctic continent, this difference averages 5.4 ^∘C. Temperature anomalies are typically strongest in winter, which leads to a 20 %-reduced amplitude of the seasonal cycle of temperature during snowfall. Larger temperature anomalies during winter also offset the slightly higher seasonal contribution of winter precipitation, which would reduce the snowfall-weighted temperature by 0.7 ^∘C. Year-to-year irregularities in snowfall distribution contribute to the random subsampling of temperature and increase the interannual variability of the snowfall-weighted temperature, making it 80 % more variable. Under the assumption that water isotopes reflect the snowfall-weighted temperature, these biases will transfer to the isotopic signal in ice cores, which may explain the necessity to adjust isotope–temperature slope values depending on the time frame of the reconstruction. Non-linearities in the snowfall-weighted temperature compared to the site temperature confirm previous results which indicated that using linear isotope–temperature slopes may lead to overestimated temperature decreases in cold periods and underestimated temperature increases in warm periods. While we focused on the 1979–2020 period in this study, potential changes in precipitation regimes at longer timescales may be associated with changes in the snowfall-weighted biases, and these deserve attention in future studies aimed at adjusting the isotope–temperature slopes accordingly to achieve quantitatively accurate paleotemperature reconstructions.

Appendix A: Evaluation of MAR performance

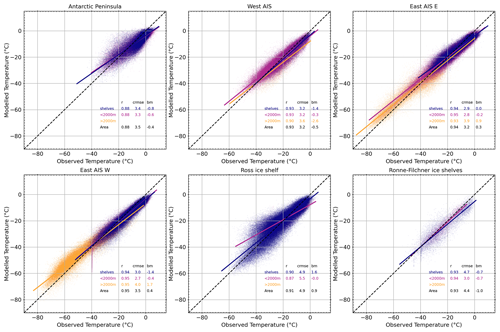
Figure A1 Evaluation of the model performance in representing temperature. Scatterplots and linear regressions of modelled (MAR v3.12) vs. observed temperature (from a compilation of automatic weather stations and other measurements; Mottram et al., 2021) for different regions (as in Kittel et al., 2021). Slopes that are slightly lower than 1 indicate that the natural range of temperature variability is greater than what the model can achieve, although the difference is minor. The residual mean square error (RMSE) measures the scattering of modelled temperatures around the observed temperature, and the bias mean (BM) measures the average difference from the observed temperature. Both give an estimation of imprecision of the model.

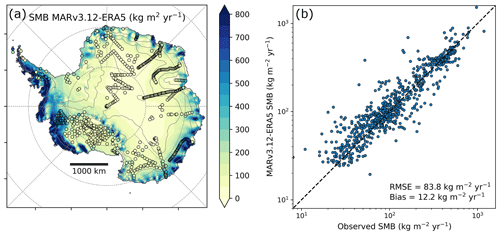
Figure A2 Evaluation of the model performance in representing surface mass balance. (a) Map of surface mass balance (SMB), defined as precipitation minus evaporation and runoff in MARv2.13, compared to accumulation observations (Wang et al., 2016) represented as colour dots. (b) Log-scale scatterplot of modelled SMB vs. accumulation observations. The modelled SMB is higher than the observations by a bias of 12.2 kg m⁻² yr⁻¹.

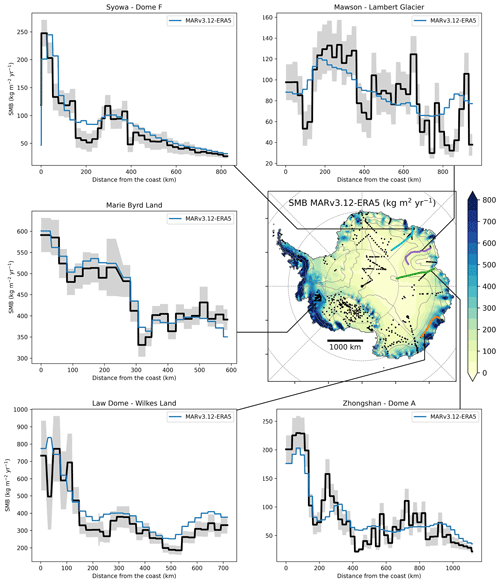
Figure A3 Evaluation of the surface mass balance model performance along transects. The surface mass balance (SMB), defined as precipitation minus evaporation and runoff in MARv2.13, is compared to observations (Wang et al., 2016) along five transects represented by coloured lines on the map. MAR tends to slightly overestimate the SMB at high-elevation sites and to underestimate the variability of small-scale changes. This could be attributed to unresolved drifting snow transport in MAR due to a coarser than real topography (Agosta et al., 2019). Despite these flaws, the modelled SMB follows the observed spatial trends in accumulation remarkably well.

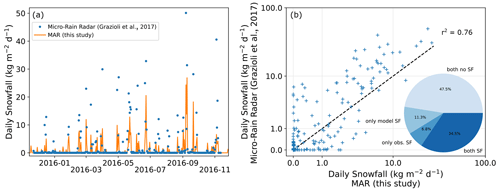
Figure A4 Evaluation of the ability of MAR to match the snowfall timing observed with micro-rain radar at Dumont D'Urville station (66^∘ S, 140^∘ E; Grazioli et al., 2017). Micro-rain radar data indicate snow passing through the atmospheric layer 300 m above the surface, while the modelled snowfall is shown for the surface only, where some of the snow may have sublimated. (a) Time series of modelled and observed snowfall for the year 2016. (b) Scatterplot of observed vs. modelled snowfall. The pie chart indicates the percentage of days with matching or mismatching snowfall in the model and observations, with discrepancies noted for about 18 % of the days in total.