Exploring the potential of thermal infrared remote sensing to improve a snowpack model through an observing system simulation experiment

The assimilation of data from Earth observation satellites into numerical models is considered to be the path forward to estimate snow cover distribution in mountain catchments, providing accurate information on the mountainous snow water equivalent (SWE). The land surface temperature (LST) can be observed from space, but its potential to improve SWE simulations remains underexplored. This is likely due to the insufficient temporal or spatial resolution offered by the current thermal infrared (TIR) missions. However, three planned missions will provide global-scale TIR data at much higher spatiotemporal resolution in the coming years.

To investigate the value of TIR data to improve SWE estimation, we developed a synthetic data assimilation (DA) experiment at five snow-dominated sites covering a latitudinal gradient in the Northern Hemisphere. We generated synthetic true LST and SWE series by forcing an energy balance snowpack model with the ERA5-Land reanalysis. We used this synthetic true LST to recover the synthetic true SWE from a degraded version of ERA5-Land. We defined different observation scenarios to emulate the revisiting times of Landsat 8 (16 d) and the Thermal infraRed Imaging Satellite for High-resolution Natural resource Assessment (TRISHNA) (3 d) while accounting for cloud cover. We replicated the experiments 100 times at each experimental site to assess the robustness of the assimilation process with respect to cloud cover under both revisiting scenarios. We performed the assimilation using two different approaches: a sequential scheme (particle filter) and a smoother (particle batch smoother).

The results show that LST DA using the smoother reduced the normalized root mean square error (nRMSE) of the SWE simulations from 61 % (open loop) to 17 % and 13 % for 16 d revisit and 3 d revisit respectively in the absence of clouds. We found similar but higher nRMSE values by removing observations due to cloud cover but with a substantial increase in the standard deviation of the nRMSE of the replicates, highlighting the importance of revisiting times in the stability of the assimilation performance. The smoother largely outperformed the particle filter algorithm, suggesting that the capability of a smoother to propagate the information along the season is key to exploit LST information for snow modelling. Finally, we have compared the benefit of assimilating LST with synthetic observations of fractional snow cover area (FSCA). LST DA performed better than FSCA DA in all the study sites, suggesting that the information provided by LST is not limited to the duration of the snow season. These results suggest that the LST data assimilation has an underappreciated potential to improve snowpack simulations and highlight the value of upcoming TIR missions to advance snow hydrology.

1 Introduction

The seasonal snowpack plays a key role in many ecological and hydrological processes worldwide (Barnett et al., 2005). Due to its high albedo and insulating capabilities, the extensive snow-covered area of the Northern Hemisphere influences the Earth climate system (Henderson et al., 2018). In mountain regions, the seasonal snowpack is also an important source of runoff during the summer when the water demand peaks. Hence, accurate knowledge of the snowpack conditions has an important economic value (Sturm et al., 2017). The snow cover is also a source of natural hazards such as floods caused by rain-on-snow events or snow avalanches, events that are expected to increase due to the impacts of climate warming (Ballesteros-Cánovas et al., 2018; Musselman et al., 2018).

Despite its importance, monitoring the snowpack remains challenging for both scientists and water management agencies. The variable nature of the snowpack makes it challenging to deploy and maintain dense enough ground-based monitoring networks (Kinar and Pomeroy, 2015). Therefore, snow hydrologists have developed methods to take advantage of satellite remote sensing since the beginning of the Landsat programme (Rango and Martinec, 1979). Yet, the application of remote sensing in snow hydrology remains hindered by the lack of direct observations of the snow water equivalent (SWE) in mountain regions (Dozier et al., 2016).

Numerical models allow for simulating many snowpack state variables, including the SWE. However, their accuracy is primarily constrained by the large uncertainty in the meteorological forcing (Raleigh et al., 2015). Recent studies have suggested that data assimilation (DA) of remotely sensed products is the path forward to estimate the spatial distribution of relevant snowpack characteristics (Aalstad et al., 2018; Charrois et al., 2016; Cortés and Margulis, 2017; Margulis et al., 2016; Smyth et al., 2020; Stigter et al., 2017). Using DA techniques it is possible to fuse model simulations and multiple remote sensing datasets to improve the snowpack simulations. In particular, the snow cover area has been assimilated in many case studies due to its widespread availability (e.g. Baba et al., 2018; Alonso-González et al., 2021). Yet, the extent of the snow cover provides no direct information on the internal state of the snowpack and is blind to snowpack changes when the pixel is fully snow covered (De Lannoy et al., 2012).

The ice surface temperature (IST) is a key state variable for simulating the snowpack evolution. Physically based snowpack models solve the energy balance equation iteratively along the time dimension, estimating the IST at each time step of the model (Essery, 2015; Liston and Elder, 2006). It is also a key parameter to estimate the emitted energy as outgoing long-wave radiation. The estimation of the IST allows for detecting the occurrence of surface melting events, as when the IST reaches 0 ^∘C all the added energy is converted to melt. Thus, assimilating IST may provide key information about the timing of the melting events. Also, the assimilation of the land surface temperature (LST) (i.e. the temperature of the Earth surface independently of if it is snow covered) may improve the snowpack simulations by different mechanisms. The IST is physically bound to the melting point temperature, while once the snow melts, the LST can exceed 0 ^∘C. Thus the assimilation of the LST may indirectly provide information about the snow cover area too. Also, it should be possible to improve the snow simulations by retrieving thermal information when there is no sunlight, like during the nighttime or during the polar night at high latitudes. A previous study has shown that IST DA could potentially improve the surface ice mass balance simulations of the Greenland ice sheet (Navari et al., 2016), fusing synthetic IST estimations with the CROCUS snow model. On the other hand, previous research has suggested few improvements in the SWE simulations after assimilating LST simulations retrieved from the Meteosat Second Generation (MSG) (∼6 km spatial resolution) in the Alps (Piazzi et al., 2019). However, the coarse resolution of the LST products of MSG prevents its use in complex terrain. Also, the rapid variation in LST at hourly timescales can make it difficult to assimilate this variable using particle filters as done by Piazzi et al. (2018) and could be addressed using different algorithms. Thus, more research is needed to assess the potential of high-resolution LST DA.

The thermal imagery already available only offers coarse resolution for the snow applications over complex terrain (MODIS, Sentinel-3) or long revisiting times (Landsat). This has probably prevented the study of the impact of LST DA, although recent research has suggested that LST can provide useful information to retrieve internal snowpack properties (Colombo et al., 2019), a capability that can be exploited from satellites (Colombo et al., 2023). The availability of high-spatiotemporal-resolution LST products will be improved in the short term with the appearance of new satellites, such as the French–Indian mission Thermal infraRed Imaging Satellite for High-resolution Natural resource Assessment (TRISHNA) (Lagouarde et al., 2018). TRISHNA is expected to provide surface temperature measurements at 60 m spatial resolutions every 3 d at the Equator, with an increasing revisiting time towards the poles. Also, given the agenda of the space agencies, high-resolution thermal infrared retrievals will be readily accessible in the near future, including the Copernicus Land Surface Temperature Monitoring (LSTM) (Koetz et al., 2018), which will offer similar observations to TRISHNA but with improved spectral, spatial and temporal resolutions, and the Surface Biology and Geology (SBG) satellite (Cawse-Nicholson et al., 2021) from NASA, which will provide similar high-resolution thermal infrared (TIR) images of the surface of the Earth. The combination of these three missions may eventually provide close to bi-daily (day- and nighttime) high-resolution thermal infrared observations of the Earth surface. In this context the objectives of this work are (i) to test the potential of the LST to improve the snowpack simulations and (ii) to explore the effect of increasing the temporal resolution of the observations.

A convenient approach to emulate future remote sensing observations is to use an observing system simulation experiment (OSSE). For example, Navari et al. (2016) assessed the feasibility of integrating ice surface temperatures in a regional climate model estimate of the Greenland ice sheet surface mass balance through an OSSE. Synthetic experiments were also used to explore the potential of data assimilation techniques in improving the snowpack simulations (Clark et al., 2006; Revuelto et al., 2021; Smyth et al., 2019).

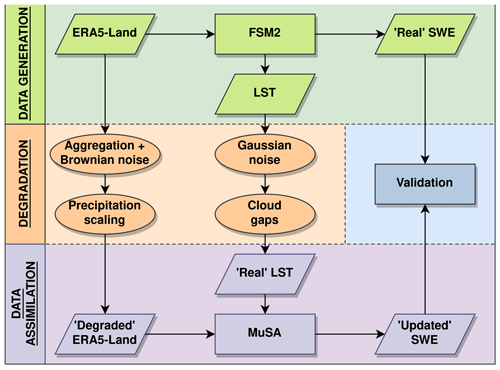
Here, we designed an OSSE to evaluate the benefit of future remote sensing LST to simulate seasonal SWE. In this experiment, synthetic LST and SWE data were generated in several climatic regions. Synthetic LST data were assimilated into a snowpack model under different cloud cover scenarios and with different satellite revisit times. The benefit of assimilating LST was studied by comparing the posterior (after assimilation) SWE to the synthetic SWE.

2 Data and methods

2.1 Synthetic observations

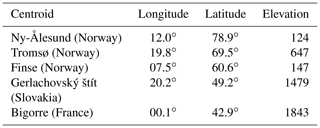
We selected five sites in snow-dominated regions of Europe, spanning 40^∘ latitude from the Pyrenees mountains to the Svalbard archipelago. The sites were chosen approximately every 10^∘ latitude to sample different climatic influences. The southern sites (Gerlachovský štít, Bigorre) are located in mountain regions (Tatra, Pyrenees), Finse is located on an elevated plateau (Hardangervidda), and Tromsø and Ny-Ålesund are in the polar circle. Gerlachovský štít is in eastern Europe, and its climate is influenced by its continental characteristics; Tromsø and Ny-Ålesund exhibit obvious polar climates, and Bigorre shows a montane climate with Mediterranean influences.

Table 1 Geographical coordinates and elevation (m a.s.l.) of the ERA5-Land centroids used in the study.

We used ERA5-Land surface reanalysis data (∼9 km spatial resolution) (Muñoz-Sabater et al., 2021) to force the Flexible Snow Model (FSM2) (Essery, 2015) over 4 consecutive hydrological years from 1 September 2017 to 31 August 2021. From this simulation, we retrieved the SWE and LST time series, which were used as the synthetic truth. The LST was exported at 13:00 local time, corresponding to the foreseen TRISHNA overpass time. To mimic observational noise, we added to the LST time series a Gaussian noise with a mean of 0 and a standard deviation of 1.5 K. This standard deviation was chosen as an intermediate value between the reported root mean square error (RMSE) obtained by the comparison of Landsat 8 with in situ measurements of the snow surface temperature (RMSE =2.0 K) (Robledano et al., 2022) and the expected performance of LST products delivered by the TRISHNA mission.

The synthetic true LST time series were downsampled with a period of 16 and 3 d to emulate revisit times of Landsat 8 and TRISHNA respectively. We simulated the impact of cloud cover on data availability by further removing values in the synthetic LST time series at random dates selected from a uniform distribution. We defined four different cloud cover scenarios with probabilities of 0 %, 25 %, 50 % and 75 %. Following the same strategy we generated synthetic fractional snow cover area (FSCA) true observations to be assimilated. The synthetic FSCA observations were degraded by adding random Gaussian noise with a mean of 0 and a standard deviation of 0.17 based on Aalstad et al. (2020).

Figure 1 Main workflow of the OSSE.

For each site, we created a new degraded meteorological forcing to run FSM2. First we averaged the ERA5-Land data from the nearest nine cells (i.e. resampling the spatial resolution from 10 to 30 km approximately). Then, we added autocorrelated Brownian noise in 12 h time windows (the data assimilation window of ERA5) using the standard deviation of the variable itself (Supplement Fig. S1). We further perturbed the precipitation field after aggregation, dividing the precipitation by 2. This strong perturbation was chosen to emulate precipitation biases that are typically found in global reanalyses and large-scale precipitation products (Beck et al., 2019), potentially leading to a large underestimation of SWE in mountain regions (Wrzesien et al., 2019). A similar value has already been used in previous snow data assimilation experiments (Deschamps-Berger et al., 2022).

2.2 Data assimilation experiments

The degraded meteorological forcing and synthetic LST were used to feed the Multiple Snow Data Assimilation System (MuSA). MuSA is an open-source ensemble-based data assimilation toolbox built around FSM2 (Alonso-González et al., 2022). We used the same initial conditions to run FSM2 within MuSA (soil temperature profile, initial LST and absence of snow); therefore we did not perform a spin-up. To emulate the differences between the reality and modelling pipeline, we used a simplified parameterization scheme of FSM2 in MuSA (Table 2). The assimilation experiments were done using a particle batch smoother (PBS) (Margulis et al., 2015) and a particle filter (PF). Smoother algorithms are typically used to develop reanalyses, as all time series of information are available, whereas filtering is used for operational forecasting where future observations with respect to the analysis step are not available (Largeron et al., 2020). A rigorous description of the algorithms, the underlying theory and implementation details can be found in Alonso-González et al. (2022).

We performed a final experiment in which we assimilated fractional snow cover area (FSCA) using a PBS. This experiment has been performed using exactly the same set-up as for the assimilation of LST. This includes running the simulations over the same geographical areas, using the same forcing and cloud cover scenarios, as well as using a different FSM2 parameterization to generate the synthetic truth and MuSA. Using exactly the same set-up allows for a simple comparison between the performance of assimilating LST and FSCA.

Table 2 FSM2 configuration chosen (and configuration number) to generate the synthetic truth and simulations.

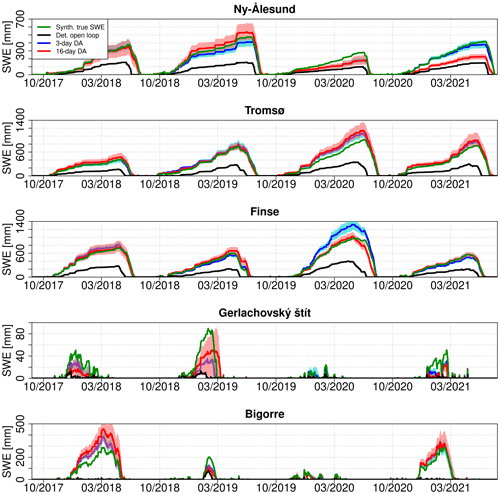
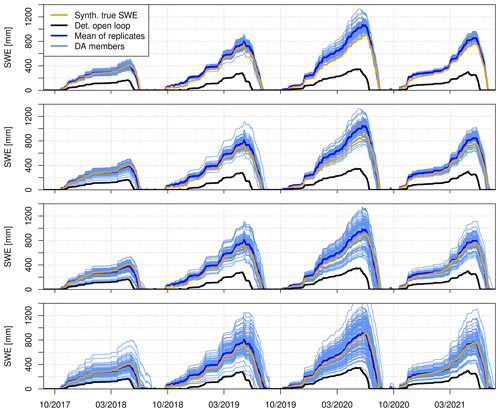
Figure 2 Comparison of hourly time series of synthetic true SWE with the open-loop simulations and the posterior SWE after assimilating LST with a revisit time of 16 or 3 d (0 % cloud cover scenario) using the PBS. Here, the posterior SWE is the average of the 100 replicates, and the shaded areas represent the 95th to 5th quantile range.

The prior ensemble of FSM2 simulations was composed of 300 particles that were generated by perturbing the air temperature (additive perturbation) and the precipitation (multiplicative perturbation). The perturbations were time invariant and were randomly drawn from a normal distribution of mean μ=0 and standard deviation σ=2 (temperature) and a log-normal distribution with mean μ=0.45 and standard deviation σ=0.8 of the underlying normal distribution (precipitation). These parameters were chosen to cover the expected differences between the “true” forcing and the degraded forcing (Fig. S2) and were obtained by preliminary trial-and-error tests. Both PF and PBS are very prone to collapse. Although there are uncertainties in other variables, keeping a limited number of dimensions helps to prevent the collapse of the ensembles. In addition, not correcting for the other variables introduces errors into the simulations, which also helps to prevent the collapse of the ensembles. The observation errors prescribed for the synthetic true observations were the same as those defined to generate the degradation Gaussian noise.

The PF performs the analysis sequentially, i.e. each time an observation occurs, and the PBS is a smoother; hence it assimilates all the available observations in a single time window, propagating information from the observations forward and backward in time. Here the assimilation time window was defined as a hydrological year (i.e. one snow season). In both the PF and PBS, prior weights of ensemble members (particles) are updated based on the likelihood, i.e. a measure of the distance between the predictions of each particle and the observations. The posterior weights are then used to estimate posterior statistics from the ensemble, typically its weighted mean and weighted standard deviation. In the case of the PF, we used the bootstrap resampling algorithm to eliminate particles with low weights and to replicate particles with high weights by sampling with replacement randomly from the probability distribution of the updated weights. To prevent the filter from collapsing (all the weight is shared by a few particles and eventually just one particle), new perturbation parameters were drawn from a normal approximation of the posterior from the previous analysis step at each new analysis step, instead of resampling both the states of the model and the parameters.

2.3 Evaluation of the experiments

For each site and each cloud cover scenario, we ran MuSA and generated a posterior SWE. However, the output of MuSA is stochastic due to the random generation of the forcing perturbation parameters. Also, the position of the gaps in the different cloud cover scenarios and the Gaussian and Brownian noises added to the observations and forcing respectively are random. Therefore, to increase the statistical robustness of our results, we repeated each assimilation experiment 100 times, drawing new gaps and noise for each replicate of the experiment. This created an ensemble of posterior SWE, which was compared to the synthetic true SWE.

In total, for a given site, MuSA was run 2400 times (100 replicates ×4 cloud cover scenarios ×2 revisit times ×3 DA experiments). This corresponds to 720 000 FSM2 runs (300 particles by MuSA run), summing up to 3 600 000 FSM2 runs considering the five study areas, which is equivalent to simulating the snowpack over a period of 14 400 000 years. To compare the performance of data assimilation, in every site regardless of the absolute magnitude of the SWE, we used the normalized RMSE (nRMSE) as a performance score:

$$\mathrm{nRMSE}={\displaystyle \frac{\sqrt{\frac{\mathrm{1}}{n}{\sum }_{i=\mathrm{1}}^n{\left({\mathrm{Pred}}_i-{\mathrm{Ref}}_i\right)}^{\mathrm{2}}}}{\stackrel{\mathrm{‾}}{\mathrm{Ref}}}},$$

where n is the number of samples, Pred the predicted values and Ref the reference SWE values.

Figure 3 Comparison of hourly time series of synthetic true SWE with the open-loop simulation, the 100 replicates of posterior SWE after assimilating LST with a revisit time of 3 d, varying cloud cover scenarios and the average of the experiments in Tromsø.

3 Results

As expected, the degradation of the ERA5-Land meteorological forcing had a large impact on the open-loop SWE simulations (Figs. 2 and S3, S4 and S5). In comparison with the synthetic true SWE, the average normalized RMSE (nRMSE) was 61 % (after removing the summertime months of July and August). The degradation of the ERA5-Land data caused an overall reduction in the simulated SWE, leading to a shorter snow season at all sites (Fig. 2). However, the LST assimilation with the PBS substantially improved the SWE simulations (Fig. 2). This improvement was evident during both revisit times, although the 3 d revisit scenario (nRMSE =13 %) outperformed the 16 d revisit scenario (nRMSE =17 %).

The posterior SWE series in Fig. 2 were averaged from an ensemble of 100 replicates under clear-sky conditions. The uncertainty in the replicates is mostly caused by the different random noises in the observations (see Sect. 2 “Data and methods”). Figure 3 shows every posterior SWE realization in the case of the Tromsø site under different cloud cover scenarios when assimilating LST at 3 d resolution. This figure shows that the spread of the replicates increased with the cloud cover probability. The standard deviation of the obtained nRMSE values over each cloud cover scenario ranged from 4 % to 10 % in this particular case.

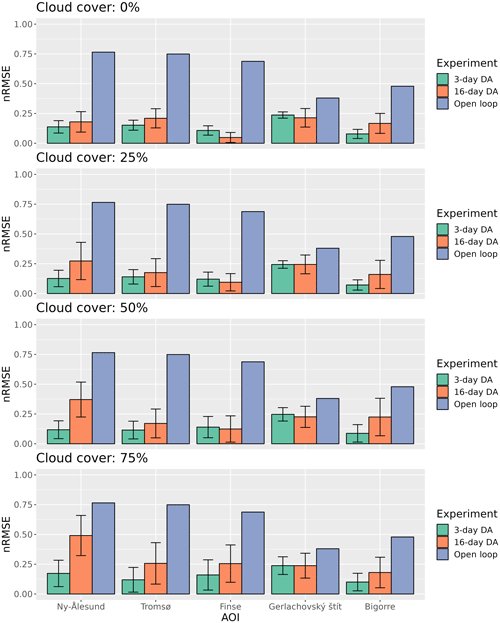
Figure 4 Normalized root mean square error (nRMSE) of the posterior SWE after assimilating LST using the PBS compared with the synthetic true SWE for each experiment. The bars indicate the mean nRMSE, while the error bars indicate the standard deviation in the 100 replicates.

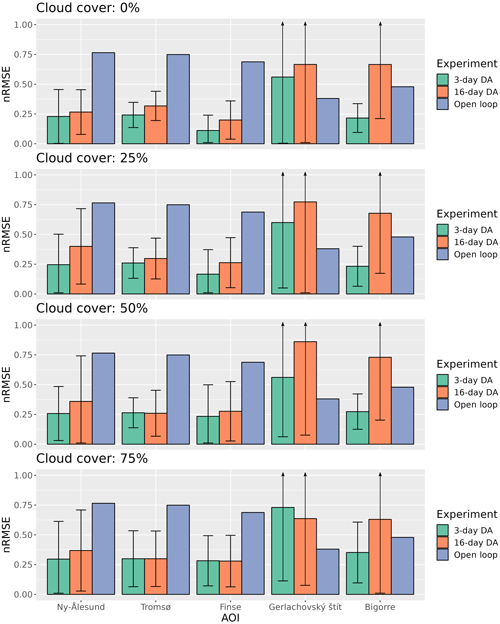
Figure 5 Normalized root mean square error (nRMSE) of the posterior SWE after assimilating FSCA using the PBS compared with the synthetic true SWE for each experiment. The bars indicate the mean nRMSE, while the error bars indicate the standard deviation in the 100 replicates.

Figure 4 summarizes the results of the PBS from all experiments under every cloud cover and revisit scenario. In all cases, the data assimilation significantly reduces the nRMSE in comparison with the open-loop simulations. In most situations the nRMSE is always higher for the 16 d revisit compared to the 3 d revisit, but the difference was more pronounced under the 50 % and 75 % cloud cover scenarios. In addition, the standard deviation of the nRMSE of the 100 replicates is higher for the 16 d compared to the 3 d revisit scenarios. Both the averaged nRMSE and the standard deviations increase with the cloud cover, with an average nRMSE for all the sites ranging between 13 % and 16 % in the case of the 3 d revisit experiments and 17 % and 28 % for the 16 d revisit experiments. The results indicate a comparatively lower reduction in SWE nRMSE when FSCA is assimilated compared to LST assimilation ranging between 27 % and 39 % in the case of the 3 d revisit experiments and 41 % and 45 % for the 16 d revisit experiments (Fig. 5), being comparable to results obtained in previous studies assimilating real observations (Aalstad et al., 2018) and thus confirming the robustness of the OSSE design. Furthermore, the greater dispersion of nRMSE values suggests an increased sensitivity to cloud distribution in the case of FSCA compared to LST.

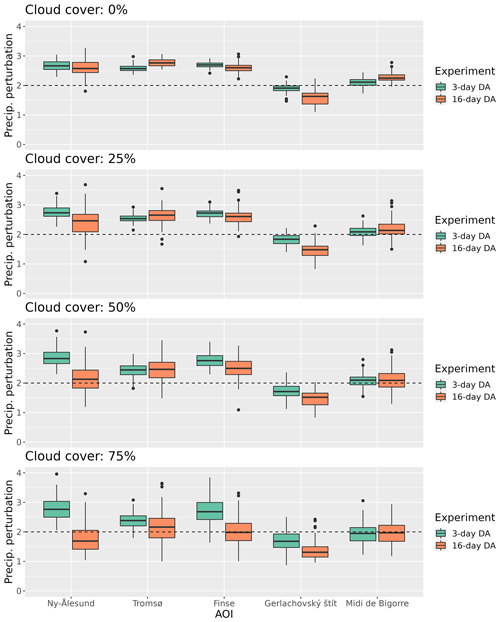
Figure 6 Boxplots showing the distribution of the posterior precipitation perturbation parameter for each experiment estimated by the PBS. The dashed line indicates the true perturbation that was applied to the forcing.

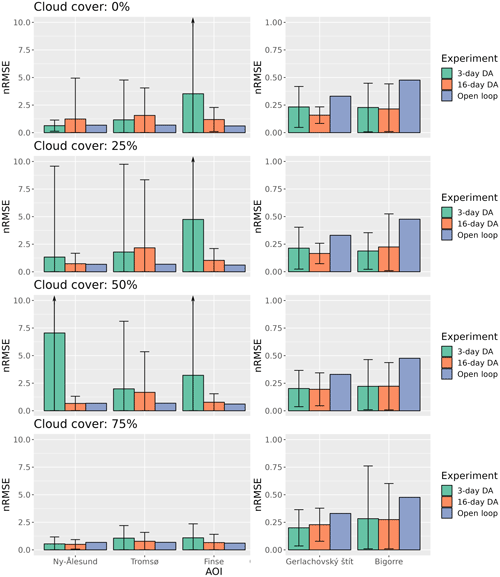
Figure 7 Normalized root mean square error (nRMSE) of the posterior SWE after assimilating LST from the PF compared with the synthetic true SWE for each experiment. The bars indicate the mean nRMSE, while the error bars indicate the standard deviation in the 100 replicates.

Figure 6 shows the distribution of the mean of the posterior precipitation perturbation parameters obtained from the 100 data assimilation runs using the PBS. It demonstrates that the assimilation of LST reduces the error in the precipitation forcing, since the posterior parameter distributions approximate the actual multiplicative perturbation factor of 2 to compensate for the 0.5 scaling factor used to degrade the input precipitation. However, the difference between the true precipitation and the degraded precipitation should not exactly be equal to the scaling factor of 2 due to the perturbation strategy used, the fact that we do not correct all forcing variables and the differences between the FSM2 configurations (Sect. 2) as well as the fact that other components of the forcing were also degraded and were not included in the simulation to induce errors in FSM2. As observed in Fig. 4, the standard deviation of the posterior perturbation parameters of the replicates increases when comparing the 3 d with the 16 d revisit scenarios and with the cloud cover probability.

Whereas the above results show that the PBS algorithm clearly improved the SWE simulation, it was not the case with the PF. Figure 7 summarizes the results of the same experiments shown in Fig. 4 but using the PF instead of the PBS. In this case the improvement in the average nRMSE of the posterior simulations is not as obvious with respect to the open loop as in the PBS experiments. Although in the medium-latitude cases the nRMSE shows a moderate improvement compared with the open loop on average, several runs among the 100 replicates had a higher nRMSE than the open-loop run. The revisit or cloud cover scenarios had no clear effect on the nRMSE. The results in the high-latitude areas yielded a higher nRMSE standard deviation than in the medium-latitude regions. This is a consequence of the very cold conditions in these high-latitude areas, causing some particles to become glaciers due to the perturbed forcing (non-zero SWE at the end of the hydrological year).

4 Discussion

Navari et al. (2016) showed the potential of IST data assimilation to improve the surface mass balance of the Greenland ice sheet in a regional climate simulation with an ensemble batch smoother. Our study also suggests that the assimilation of LST can improve seasonal snow simulations in sites with different climate contexts. With the PBS, the improvement was substantial independently of the site; i.e. the climatic context did not exhibit an obvious influence on the results. However, our results with the PF also support the conclusions of Piazzi et al. (2019), who did not obtain obvious improvements in the posterior SWE simulations after assimilating LST using an ensemble Kalman filter. Therefore, our study provides an explanation of the contrasting performances found by Navari et al. (2016) and Piazzi et al. (2019). While Navari et al. (2016) used smoothers, Piazzi et al. (2019) used a filter. A filter updates the simulations sequentially, while smoothers update the whole season in a batch. This in-batch assimilation allows for the propagation of the information of the observations backward in the simulation time. Also, the performance of the LST data assimilation reported by Piazzi et al. (2019) was probably hampered by the coarse resolution of the MSG LST products that were used to update snowpack simulations at the point scale. In the specific case of the LST, considering the observations of the whole snow season in a batch may be key to have a positive impact on the posterior SWE. The trajectory of the LST in seasonal-snow-dominated regions exhibits a characteristic pattern, as the physical bounds of the IST are different from the LST. Once the snow melts, the LST can rise above the water melting point, and therefore the trajectory of the LST may be a good indicator of the length of the snow season. However, this should not be the only reason, as Navari et al.'s (2016) experiments were developed over the Greenland ice sheet where there is a permanent ice cover. During the melting season the IST is fixed to the melting point temperature, providing information on the duration of the melting period. The occurrence of wintertime melt events should also be visible in the TIR domain. The LST assimilation outperformed the FSCA assimilation in all study areas in our experiments. This also suggests that LST may provide more information than FSCA. In addition, the lower dispersion of nRMSE values suggests that LST may be more resilient to cloud cover distribution than FSCA. The information of the whole seasonal trajectory of the LST is propagated to the posterior by using a smoother but not by using a filter. This is highlighted at the high-latitude study areas, where the polar conditions made snowmelt impossible at the end of the hydrological year for some of the replicates (Fig. S2), leading to very high nRMSE using the PF (Fig. 7). These results suggest that the LST may be less beneficial to snowmelt forecasting applications, where the use of filters is more extended, to update the model as new observations arise, but it should be regarded as valuable information to improve snow reanalyses which aim to reconstruct snow cover climatologies.

Our results also suggest that even the currently available thermal infrared estimations of the LST from Landsat missions have the potential to significantly improve SWE simulations despite a revisit time of 16 d. The emulated revisiting times of both Landsat and TRISHNA are the expected values at the Equator and can be lower in other latitudes. Here we did not study the effect of the spatial resolution but hypothesized that high resolution (i.e. Landsat-like) is needed for snow cover simulations in the studied regions. Landsat TIR images have a 100 m resolution, which makes them suitable to sample the slope scale in mountain terrain, hence resulting in homogeneous conditions in the energy balance budget (Baba et al., 2019). Despite the low revisiting times of the Landsat mission, Landsat TIR imagery may be useful to improve SWE simulations using a smoother data assimilation algorithm, an approach that to our knowledge has not been explored yet. More research should be carried out on this topic, especially in the context of joint assimilation experiments where more than one variable is assimilated.

Nevertheless, the change in revisit from 3 to 16 d in our experiments translated into a higher posterior nRMSE. Therefore, we expect significant progress with TRISHNA observations, not to mention the enhanced spatial resolution (approximately 60 m). The benefit of the 3 d revisit was particularly evident under 50 % to 75 % cloud cover. This should be considered, as previous global estimates of the cloud cover suggest values closer to our highest-cloud-cover scenario (Wylie et al., 2005). For instance, cloud cover probability in MODIS products reached 60 % in the Alps and 50 % in the Pyrenees (Gascoin et al., 2015; Parajka and Blöschl, 2008).

In any case, under both revisit scenarios, the cloud cover decreased the precision of the replicates of the posterior SWE, i.e. the variability between repeated experiments, but the average was only marginally affected. In other words, the cloud cover reduced the robustness of the data assimilation, but even regions with a persistent cloud cover could benefit from LST assimilation. The different replicates of each experiment exhibited different results, with a variance that increased with the number of gaps introduced into the synthetic LST observations, suggesting that not all the combinations of observations are equally informative. This was also obvious regarding the posterior precipitation perturbation parameters, as the standard deviation of the different replicates increased with the percentage of cloud cover.

Despite the promising potential of the LST to improve SWE simulation, some limitations of the current study inherent to the synthetic nature of the OSSE should be taken into consideration. The synthetic nature of the experiment could lead to an overestimation of the value of LST assimilation. This effect is mitigated in our experiment as typically done in OSSEs by (i) the degradation of all forcing variables, while only temperature and precipitation were corrected, and (ii) the different FSM2 parameterizations used to create the synthetic truth. The simulation of the cloud cover scenarios was generated by selecting random dates from a uniform distribution. However, in some regions the cloud cover exhibits marked seasonal patterns (Sudmanns et al., 2020) that may pose a challenge to updating the snowpack simulations even with smoothers if cloud cover is more frequent during key periods in the snow season. Also, the surface temperature observation in complex terrain may differ from the simulated temperature due to intra-pixel variability as a consequence of variable snow and/or mixed-pixel conditions (Robledano et al., 2022; Lundquist et al., 2018). But this issue is greatly limited by the expected increase in resolution. In light of the results of this work, the next step is to conduct experiments using real remote sensing observations, although the general lack of data may complicate the interpretation of the results.

5 Conclusions

The motivation for the study of LST data assimilation is the upcoming launch of high-resolution thermal infrared spatial missions with an improved revisit time and resolution in the next few years. We implemented a synthetic data assimilation experiment to study the potential of LST in improving SWE simulations along a latitudinal gradient in the Northern Hemisphere. The methodology was based on the generation of synthetic LST estimations and true SWE estimates, as well as a prior ensemble of SWE simulations generated by forcing FSM2 with degraded meteorological fields. The MuSA snow data assimilation software was used to generate SWE posterior time series using the particle batch smoother and particle filter algorithms to be compared with synthetic true SWE.

The results suggest that the assimilation of LST has great potential to improve seasonal snowpack simulations across all the tested sites. Gap-free LST series improved the average nRMSE of the open-loop simulations from 61 % to 17 % and 13 % for the 16 d and 3 d revisiting times respectively. However, a lower revisit frequency caused an increase in the variance of the nRMSE when the runs were replicated 100 times, showing that the performance of the assimilation would depend on cloud cover scenarios. This conclusion was more evident with high-cloud-cover scenarios, highlighting the importance of the revisit time in thermal infrared remote sensing to reduce the uncertainty in the updated SWE.

The type of data assimilation was also key to explain the role of LST in improving SWE simulations. The particle batch smoother strongly improved the simulations, whereas the particle filter was much less effective and could even cause a degradation of the simulations. This effect could be interpreted as a consequence of the strong seasonal signal of the LST, which reflects the duration of the snow season. But the lower performance shown by the FSCA assimilation suggests that the LST assimilation provides more than just information on snow duration.

Overall, our results encourage a more systematic use of the current LST products within snow data assimilation studies, especially if the objective is to perform a snow reanalysis, which can benefit from observations acquired over an entire snow season.