Brief communication: Is vertical shear in an ice shelf (still) negligible?

Vertical shear is recognized today as a key component of the stress balance of ice shelves. However, the first ice shelf models were built on the neglect of vertical shear. Partly due to its historical treatment, it remains common to discuss vertical shear as though it were still considered negligible in ice shelf models. Here, we offer a historical perspective on the changing treatment of vertical shear over time, and we emphasize the term's non-negligibility in current ice shelf modeling. We illustrate our discussion in the simplest context of an analytic, isothermal, shallow-ice-shelf model.

1 Introduction

Analytic models of floating ice shelves date back to at least 1957, when Johannes Weertman derived expressions for the tension and velocity gradients within a uniform-thickness ice shelf (Weertman, 1957). Weertman found that, for a shelf with uniform surface elevation h=h_T; uniform density ρ; and no lateral flow, the depth-averaged longitudinal deviatoric tension, $\stackrel{\mathrm{‾}}{{\mathit{\tau }}_{xx}}$, could be calculated via

$$\begin{array}{}\text{(1)}& \stackrel{\mathrm{‾}}{{\mathit{\tau }}_{xx}}={\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}\mathit{\rho }g{h}_T.\end{array}$$

Using a depth-averaged constitutive relation, expressions of this form permit the calculation of strain rates and velocities. Nearly 2 decades later, Thomas (1973) set out to generalize Weertman's expression for shelves of nonuniform thickness. Using the same underlying assumptions as Weertman but imposing no restrictions on the surface elevation h=h(x), Thomas obtained an expression nearly identical to Weertman's, wherein the depth-averaged deviatoric tension is

$$\begin{array}{}\text{(2)}& \stackrel{\mathrm{‾}}{{\mathit{\tau }}_{xx}}={\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}\mathit{\rho }gh.\end{array}$$

By Thomas' analysis, Weertman's solution is valid regardless of how h varies along a shelf. Thomas’ expression remains the generally accepted description of a nonuniform-thickness shelf in longitudinal extension, and it is routinely cited or independently derived in the literature (Sanderson, 1979; Cuffey and Paterson, 2010; Gudmundsson, 2013; Oerlemans, 2021; Millstein et al., 2022). However, though Eq. (2) has persisted, the formulation of this model has quietly undergone a conceptual shift over the decades. This conceptual shift relates to the role of vertical shear in ice shelves – a topic which is sometimes incompletely communicated today, and on which we seek to provide clarification.

2 The conceptual evolution of Thomas' model

In originally deriving the nonuniform-thickness model of Eq. (2), Thomas' “sole restriction [was] that of zero shear stresses in vertical planes.” The neglect of vertical shear stress, τ_xz, was universal in the formulation of ice shelf models at the time (Weertman, 1957; Thomas, 1973; Robin, 1975; Sanderson, 1979). However, it was understood by some authors to be theoretically suspect. In a seminal paper titled “Is Vertical Shear in an Ice Shelf Negligible?”, Sanderson and Doake (1979) argued that vertical shear is fundamentally linked with the thickness gradient of an ice shelf and that, strictly speaking, vertical shear “cannot be precisely zero” except in the case of uniform thickness. This observation did not challenge the practical utility of Eq. (2) (Sanderson and Doake, 1979, found vertical shear to be small enough that its neglect was, in fact, justified, answering their own titular question in the affirmative), but it highlighted a relationship that had been missed in Thomas' analysis.

The formulation of Thomas' model evolved with the development of the shallow-shelf approximation (SSA) (Morland, 1987; MacAyeal, 1989; Schoof and Hindmarsh, 2010). The SSA, besides empowering a leap forward in computational glaciology, was accompanied by two key theoretical advances in ice shelf modeling: how the neglect of terms is justified and which terms are neglected.

The SSA is built on the fundamental assumption that the thickness-to-length aspect ratio, ϵ, of an ice shelf is small (this is the “shallowness” of the SSA). With ϵ≪1, larger powers of the aspect ratio attain smaller values. In contemporary terminology, an “nth-order approximation” is obtained by neglecting any term appearing as a coefficient of ϵⁿ⁺¹ after nondimensionalization (i.e., setting those terms to zero in the approximate model, with the understanding that they are not exactly zero in real life). This dimensional-analysis approach to excluding terms adds quantitative rigour to the approach of Sanderson and Doake (1979), for whom negligibility was more qualitatively assessed. As we sketch out in the next section and contrary to the postulates of the first ice shelf modelers, dimensional analysis does not lead to the wholesale neglect of vertical shear from shallow-shelf models. Using the SSA as a starting point to derive an analytic model for a longitudinally extending ice shelf, Thomas' Eq. (2) results, albeit without the assumption of vanishing vertical shear. This is the modern approach to deriving Eq. (2).

However, the inclusion of vertical shear stress in the present-day interpretation of Thomas' model may somewhat clash with intuition, not least because the vertical shear term does not actually appear anywhere in Eq. (2). Even in literature postdating the development of the SSA, it is common to encounter language which, to a novice glaciologist, might seem to imply that vertical shear is still discarded entirely from shallow-ice-shelf models.¹ This potential misstep is the primary motivation for the present paper. In the sections below, we briefly illustrate (a) that dimensional analysis does not entail the neglect of vertical shear from the stress balance of even a zero-order shallow-ice-shelf model and (b) that, despite the term's absence in Eq. (2), the vertical shear stress of an ice shelf can be directly calculated. For compactness, we present this discussion in the simplest context of an isothermal, unconfined ice shelf in one horizontal dimension (as depicted in Fig. 1).

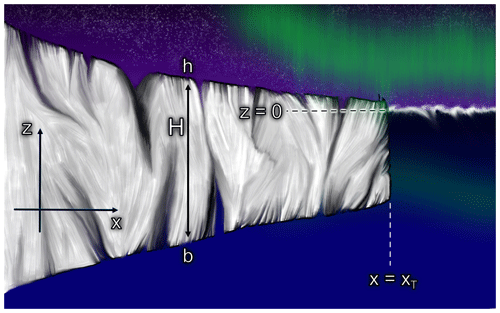
Figure 1 An ice shelf cross-section alongside a visual description of several geometric parameters commonly used to describe ice shelf dynamics. H, h, and b represent the thickness, surface elevation, and basal elevation of the shelf. z=0 is the waterline, and x=x_T is the terminus. People on terminus for scale.

3 Pre-construction: which terms are neglected from shallow-ice-shelf models by dimensional analysis?

The typical balance of momentum for a 2D ice shelf cross-section, in x and z, can be expressed as

$$\begin{array}{}\text{(3a)}& {\displaystyle \frac{\partial }{\partial x}}{\mathit{\tau }}_{xx}+{\displaystyle \frac{\partial }{\partial z}}{\mathit{\tau }}_{xz}={\displaystyle \frac{\partial }{\partial x}}P,\text{(3b)}& {\displaystyle \frac{\partial }{\partial x}}{\mathit{\tau }}_{xz}+{\displaystyle \frac{\partial }{\partial z}}{\mathit{\tau }}_{zz}={\displaystyle \frac{\partial }{\partial z}}P,\end{array}$$

where each τ_ij term is a deviatoric stress and P is pressure. Both historically and today, simplification of these equations has typically been carried out by neglecting the “bridging term” ($\frac{\partial }{\partial x}{\mathit{\tau }}_{xz}$ of Eq. 3b). Possibly in an effort to maintain internal consistency, the pioneering authors discussed above tended to additionally neglect all other appearances of τ_xz, including the second term of Eq. (3a).

In contrast to their approach and with asterisks denoting appropriately scaled parameters, Eq. (3a)–(3b) can be nondimensionalized as in Weis et al. (1999) (see also MacAyeal, 1989, or Schoof and Hindmarsh, 2010) to become

$$\begin{array}{}\text{(4a)}& {\displaystyle \frac{\partial }{\partial x^{*}}}{\mathit{\tau }}_{xx}^{*}+{\displaystyle \frac{\partial }{\partial z^{*}}}{\mathit{\tau }}_{xz}^{*}={\displaystyle \frac{\partial }{\partial x^{*}}}{P}^{*},\text{(4b)}& {\displaystyle }{\mathit{ϵ}}^{\mathrm{2}}{\displaystyle \frac{\partial }{\partial x^{*}}}{\mathit{\tau }}_{xz}^{*}+{\displaystyle \frac{\partial }{\partial z^{*}}}{\mathit{\tau }}_{zz}^{*}={\displaystyle \frac{\partial }{\partial z^{*}}}{P}^{*}.\end{array}$$

By this approach, in the zeroth- and first-order approximations, the bridging term in Eq. (4b) will be neglected as a coefficient of ϵ² (i.e., omitted for the purpose of further simplification), in agreement with Weertman, Thomas, and others. However, the vertical shear term in Eq. (4a) is retained, as it represents a coefficient of ϵ⁰. Thus, dimensional analysis provides an internally consistent means of neglecting $\frac{\partial }{\partial x}{\mathit{\tau }}_{xz}$ while retaining $\frac{\partial }{\partial z}{\mathit{\tau }}_{xz}$.

4 Constructing the simplest shallow-shelf model

Following the workflow presented in Sect. 5.2 of Greve and Blatter (2009), the neglect of $\frac{\partial }{\partial x}{\mathit{\tau }}_{xz}$ in Eq. (4b) yields the modified x-momentum equation shown below (where we have omitted asterisks for readability).

$$\begin{array}{}\text{(5)}& \mathrm{2}{\displaystyle \frac{\partial }{\partial x}}{\mathit{\tau }}_{xx}+{\displaystyle \frac{\partial }{\partial z}}{\mathit{\tau }}_{xz}=\mathit{\rho }g{\displaystyle \frac{\partial }{\partial x}}h\end{array}$$

Although the most general shallow-shelf models are constructed by depth-integrating equations of the above form (resulting in, for example, Eq. 6.55 of Greve and Blatter, 2009), we can provide an even simpler solution for an isothermal shelf, for which viscosity is depth invariant, and, consequently, τ_xx is depth invariant and equal to its depth-averaged value, $\stackrel{\mathrm{‾}}{{\mathit{\tau }}_{xx}}$. It can be verified, by direct substitution (see also Schoof and Hindmarsh, 2010), that Eq. (5) is solved by the system

$$\begin{array}{}\text{(6a)}& {\displaystyle }{\mathit{\tau }}_{xx}={\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}\mathit{\rho }gh,\text{(6b)}& {\displaystyle }{\mathit{\tau }}_{xz}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathit{\rho }gz{\displaystyle \frac{\partial }{\partial x}}h,\end{array}$$

where Eq. (6a) is simply the isothermal case of Thomas' Eq. (2), and Eq. (6b) is the (nonzero!) vertical shear stress which must accompany that solution. In fact, if we had set τ_xz to 0, Eq. (6a) would not actually solve Eq. (5), unless we additionally assumed that $\frac{\partial }{\partial x}h=\mathrm{0}$. This observation succinctly illustrates the work of Sanderson and Doake (1979): τ_xz=0 only to the extent that a shelf has uniform thickness.

5 Concluding remarks

In discussions of shallow-ice-shelf models, it is fairly common to hear vertical shear spoken of as “zero”, “neglected”, or otherwise unimportant. While this certainly was an approximation made by early ice shelf modelers, this language is at odds with current modeling practice. Indeed, as first shown by Sanderson and Doake (1979) in “Is Vertical Shear in an Ice Shelf Negligible?”, nonzero vertical shear stress is a fundamental requirement of a nonuniform-thickness ice shelf. With dimensional analysis now enabling modelers to more rigorously define negligibility, the present-day answer to their question is a resounding “no”.