the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Formation of glacier tables caused by differential ice melting: field observation and modelling
Marceau Hénot
Vincent J. Langlois
Jérémy Vessaire
Nicolas Plihon
Nicolas Taberlet
Glacier tables are structures frequently encountered on temperate glaciers. They consist of a rock supported by a narrow ice foot which forms through differential melting of the ice. In this article, we investigate their formation by following their dynamics on the Mer de Glace (the Alps, France). We report field measurements of four specific glacier tables over the course of several days, as well as snapshot measurements of a field of 80 tables performed on a given day. We develop a simple model accounting for the various mechanisms of the heat transfer on the glacier using local meteorological data, which displays a quantitative agreement with the field measurements. We show that the formation of glacier tables is controlled by the global heat flux received by the rocks, which causes the ice underneath to melt at a rate proportional to the one of the surrounding ice. Under large rocks the ice ablation rate is reduced compared to bare ice, leading to the formation of glacier tables. This thermal insulation effect is due to the warmer surface temperature of rocks compared to the ice, which affects the net long-wave and turbulent fluxes. While the short-wave radiation, which is the main source of heat, is slightly more absorbed by the rocks than the ice, it plays an indirect role in the insulation by inducing a thermal gradient across the rocks which warms them. Under a critical size, however, rocks can enhance ice melting and consequently sink into the ice surface. This happens when the insulation effect is too weak to compensate for a geometrical amplification effect: the external heat fluxes are received on a larger surface than the contact area with the ice. We identified the main parameters controlling the ability of a rock to form a glacier table: the rock thickness, its aspect ratio, and the ratio between the averaged turbulent and short-wave heat fluxes.
- Article
(4951 KB) - Full-text XML
-
Supplement
(2609 KB) - BibTeX
- EndNote
A wide variety of spectacular shapes and patterns formed through differential ablation can be found in nature: surface patterns known as rillenkarren result from the dissolution of soluble rocks (Cohen et al., 2016, 2020; Claudin et al., 2017; Guérin et al., 2020), tafoni are cavernous rock domes dug by salt crystallization during wetting–drying cycles (Huinink et al., 2004), scallops and sharp pinnacles are created by convective flows (Huang et al., 2020; Weady et al., 2022), mushroom rocks undergo erosion of their base by strong particle-laden winds (Mashaal et al., 2020), and hoodoos consist of a hard stone protecting a narrow column of sedimentary rock from rain-induced erosion (Young and Young, 1992; Bruthans et al., 2014; Turkington and Paradise, 2005).
On ice and snow surfaces, similar structures can be found: slender snow blades known as penitentes (Mangold, 2011; Bergeron et al., 2006; Claudin et al., 2015), as well as blue ice ripples observed in Antarctica (Bintanja et al., 2001) and on Mars (Bordiec et al., 2020), are caused by sublimation; suncups are bowl-shaped depressions found at the surface of a snow patch (Rhodes et al., 1987; Betterton, 2001; Mitchell and Tiedje, 2010); scallops are regularly spaced patterns of surface indentations at the ice–water or ice–air interface (Bushuk et al., 2019); ice sails (or pyramids) are larger bare-ice structures that form on debris-covered glaciers (Evatt et al., 2017; Fowler and Mayer, 2017); Zen stones found on frozen lakes are pebbles resting on a delicate ice pedestal protected from sun-induced sublimation (Taberlet and Plihon, 2021); and glacier tables (see Fig. 1c) form when a foot of ice resists melting due mostly to thermal insulation provided by a large rock (Agassiz, 1840; Bouillette, 1933, 1934; Smiraglia and Diolaiuti, 2011; Hénot et al., 2021).
On a temperate glacier, the ice ablation rate is influenced by the presence of debris on its surface. Indeed, a dense debris layer covering an ice surface can, when thin enough (less than 0.5 cm), enhance the ice melting compared to a bare-ice surface or, if thick enough, act as an insulation layer and reduce the melting rate (Östrem, 1959). The insulation effect is well captured by complex energy balance models which use meteorological data as input parameters (Reid and Brock, 2010; Collier et al., 2014) and more recently by enhanced temperature index models (Carenzo et al., 2016; Moeller et al., 2016). The melt amplification effect for thin debris layers has been explained by its patchiness (Reid and Brock, 2010) or by its porosity to airflow (Evatt et al., 2015). At a more local scale, patches of dirt or ashes on a glacier are known to lead to the formation of ice structures known as dirt cones, which consist of ice cones covered with a centimetric layer of dirt (Swithinbank, 1950; Krenek, 1958; Drewry, 1972; Betterton, 2001).
Glacier tables (see Fig. 1c) are structures frequently encountered on the levelled part of temperate glaciers (Agassiz, 1840). They typically consist of a metre-sized rock supported by a column (or foot) of ice. They form over the course of a few days to a few weeks at the end of the spring, from May to June, and may progressively disappear during the summer. Very large tables however, whose size can reach 10 m, can last for several years (Bouillette, 1933, 1934). Glacier tables form because the ablation rate of the ice is lower under the rock than at the air–ice interface. When the ice foot becomes too thin, the table falls, usually on its south side. The ice foot progressively disappears, and the rock can potentially form another table if it is not too late in the season. Similarly to what is known for debris layers, smaller rocks tend not to form tables but can instead increase the melting rate and gradually sink into the ice, creating narrow and deep holes which can reach up to 15 cm in depth (McIntyre, 1984). In a previous work (Hénot et al., 2021), artificial glacier tables were reproduced experimentally in a lab-controlled environment (constant temperature, humidity, absence of wind), at a centimetric scale. The study focused on the initial behaviour of pattern formation using cylindrical “rocks” of various sizes, the aspect ratio and materials, initially resting on a flat ice surface. Although this small-scale study under controlled conditions allowed one to understand the physical mechanisms that could play a role in glacier table formation, it did not encompass the complexity of the energy balance on a natural glacier, in particular the effects of the direct solar irradiation and of the wind.
In this article, we report field observations made on the Mer de Glace (French Alps) of the formation dynamics of glacier tables monitored over the course of a few days, as well as a systematic measurement of already-formed tables on a given day. The Mer de Glace is a temperate glacier, meaning that the ice temperature is always given by the melting temperature of water: Tice=273 K. We use local meteorological data to fit the ice ablation rate and characterize the heat transfer mechanisms at the surface of the glacier. We then develop a 1D conduction model taking into account the effect of the solar irradiation as well as sensible and long-wave heat fluxes, which is in excellent agreement with the field measurements and which illustrates the synergistic effect between solar irradiation and sensible flux responsible for glacier table formation.
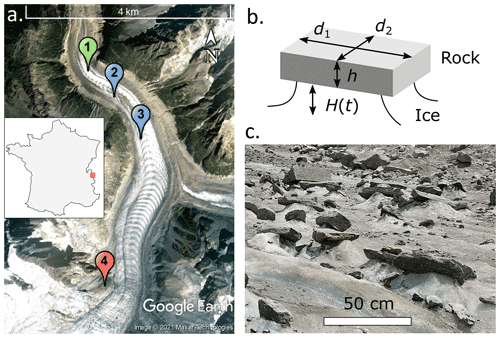
Figure 2(a) Map of the Mer de Glace in the French Alps (Google Earth image © 2021 Maxar Technologies) locating the measurement site of 3 June 2021 (1), the time-lapse observation sites of June 2021 (2) and June 2019 (3), and the Requin AWS (4). (b) The 3D schematics of a typical glacier table defining the height H(t) of the ice foot and the average thickness h and widths d1 and d2 of the rock. (c) Picture of a portion of the glacier taken in June 2021 showing natural glacier tables, from which the data shown in Fig. 3 were obtained.
2.1 Location and definitions
In this article, we report two sets of observations made on the Mer de Glace: a time-resolved camera recording of the formation and evolution of four glacier tables and a field observation of 80 glacier tables.
The lower part of the Mer de Glace (below a 2100 m altitude) is largely covered with granitic debris, with sizes ranging from submillimetric up to several metres. In the following, their dimensions are characterized by their thickness h and their larger and smaller widths d1 and d2 (see Fig. 2b). We define an effective width of the rock , whose expression will be justified in Sect. 3.2, and the aspect ratio . The vertical distance from the bottom of a rock to the surface of the ice far from it is denoted H. This quantity is either positive if the rock forms a table, in which case it corresponds to the height of the ice foot, or negative if the rock sinks into the ice surface, in which case it corresponds to the depth of the hole.
2.2 Time evolution of four large tables
Time-lapse images were obtained using an autonomous solar-powered camera (Enlaps Tikee) placed on three 1.5 m long wood rods set into the ice. Pictures (4608 px×3456 px) were taken every 30 min between 05:00 and 22:00 (LT, UTC+2) over 5 to 7 d until the camera fell on the ice due to the melting around the supporting rods. The movements of the device were corrected by tracking two fixed points on the background of the images. The positions of the top of the rocks were then manually pointed onto each image. The formation of glacier tables created by four granite rocks of various shapes and dimensions was recorded in two time periods: A (7–14 June 2019) and B (4–9 June 2021), situated at locations 3 and 2 respectively on the map of Fig. 2a, as summarized in Table 1. Rocks 1, 2 and 4 were moved on clean, flat ice, in front of the camera, the day before the recording started in order to provide a controlled initial state in which the rocks are lying on a horizontal ice surface (H=0; see Fig. 1a). Rock 3 was already standing on an ice foot, approximately 1 m high, at the beginning of period B (see the Supplement). The evolution of the vertical position of these rocks is plotted in Fig. 4a and b. The position of the ice surface was followed using a scaling rod, embedded into the ice and located approximately 2 m away from the rocks.
The surface temperature of rock 4 was measured every 5 min during period B using thermocouples and a homemade battery-powered device (Arduino MKR ZERO and EVAL-CN0391-ARDZ Shield). The wind speed ua, air temperature Ta, air specific humidity qa and solar radiative flux Φ were measured at the Requin automatic weather station (AWS) (see Nadeau et al., 2009, who use identical devices, for a detailed description), at zm=5 m above ground (located at 45.8846∘ N, 06.9297∘ E; see marker 4 in Fig. 2a), 600 m higher than and 3 km away from the measurement site. The time resolution was 1 h in 2019 and 15 min in 2021. During a 2-week time period in July 2021, we also measured the air temperature at location 2, 3 m above the glacier surface (see the Supplement), which was systematically 2.5 ∘C higher than the AWS data. In the rest of the article, we use the AWS data, to which an offset was added: ∘C. We do not expect the measured solar flux and the wind speed to be significantly affected by the distance from the measurement site. The incoming long-wave radiation coming from the atmosphere QLW atm ↓ was obtained from the S2M (SAFRAN–SURFEX/ISBA–Crocus–MEPRA) reanalysis, which combines information from numerical weather prediction models and in situ meteorological observation to estimate massif-averaged meteorological data with a 1 h time resolution (Vernay et al., 2022a) (the parameters used to compute the meteorological data in this study are the closest available that are representative of the real field, i.e. massif 3, 2100 m altitude, 20∘ slope facing north). The meteorological data are displayed in Fig. 4c–l.
2.3 An 800 m2 field comprising 80 glacier tables
On 3 June 2021, we systematically measured, in an area of 10 m×80 m located at point 1 in Fig. 2a, the dimensions of granite rocks (thickness and widths) as well as either the height of the ice foot supporting them (H>0) or the depth of penetration in the ice (H<0). The data of H are plotted in Fig. 3 as a function of the thickness h and the widths d1 and d2 of the rocks.
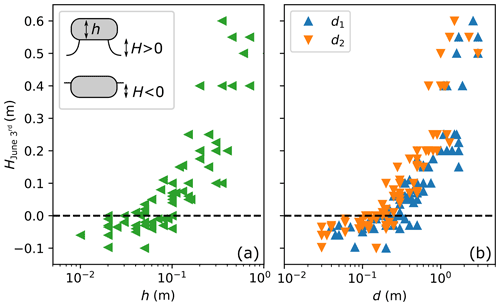
Figure 3Raw data of the observation made at location 1 (see Fig. 2a) on 3 June 2021: height of the ice foot (H>0) or of the penetration depth of the rock in the ice (H<0) as a function of the rock thickness h (a) and widths d1 and d2 (b). On the date of these observations the rocks were still standing on their ice feet and the maximum heights had presumably not been reached yet.
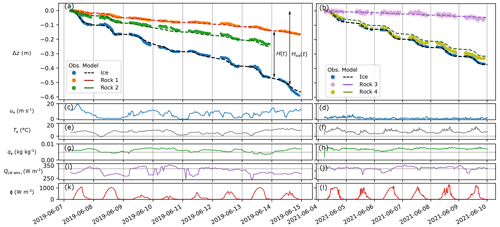
Figure 4(a, b) Vertical position of the ice surface (blue markers) and of rocks 1 to 4 (coloured markers; see Table 1). The dashed black line corresponds to the model for ice ablation (see Sect. 3.1). The coloured solid lines correspond to the model for rocks (see Sect. 3.2). These models use meteorological data measured at the Requin AWS as input: wind speed ua (c, d), air temperature Ta (e, f), air specific humidity qa (g, h) and solar radiation Φ (k, l) as well as the long-wave radiation coming from the atmosphere QLW atm ↓ obtained from the S2M reanalysis (i, j). The dotted lines correspond to the ice surface values. The date format is year-month-day.
3.1 Energy balance at the ice surface
In the following, we characterize the heat flux balance on the glacier surface by linking the ablated ice thickness to local meteorological data in the same way as it has previously been carried out in the literature (Hock, 2005; Conway and Cullen, 2013; Fitzpatrick et al., 2017). The net incident heat flux causing the glacier surface to melt with an open environment can be expressed as
where and are the net short-wave and long-wave radiative fluxes, and are the turbulent heat fluxes corresponding to sensible and latent heat respectively, and is the flux associated with rain. The short-wave radiation (when neglecting the reflected radiation by the surrounding terrain) is given by , where αice is the ice albedo and Φ is the incoming solar radiative flux (direct and diffuse) given by the meteorological S2M reanalysis model. The net long-wave flux comes from a balance between the radiation received by the ice from the atmosphere and the radiation emitted by the ice at temperature Tice. Assuming an emissivity equal to unity 1, , where , is the Stefan–Boltzmann constant. This leads to . The long wave flux received from the atmosphere is given by the meteorological S2M reanalysis model. The turbulent fluxes transmitted to a surface are assumed to be proportional to the wind velocity ua:
where ρa=0.98 kg m−3 is the air density at atmospheric pressure at a 2100 m altitude patm=785 hPa, cp=1004 is the specific heat capacity of air, ℒv=2.48 MJ kg−1 is the latent heat of evaporation for water, and and are the air temperature and specific humidity respectively at the height zm above the surface. Assuming saturation near the melting ice surface, the specific humidity is qsurface=qice and is given by , where pvap(Tice)=611 Pa is the vapour pressure of water at temperature Tice (here and in the following, pvap(T) values are obtained following the ITS-90 formula for water; Hardy, 1998). The exchange coefficients CH and CE are assumed to be identical and are given by the simplest form found classically in the literature assuming a neutral atmospheric stability (Conway and Cullen, 2013):
where k=0.41 is the von Kármán constant and z0 is a roughness length characterizing the surface (assumed to be equal for the momentum, temperature and vapour pressure). This length is denoted as z0 ice for the ice surface. There was no precipitation and thus no associated heat flux on the glacier during the duration of our study (). As the incoming heat flux directly causes the ice to melt, the vertical position of the ice surface zice(t) and the total ablated thickness of ice since t=0, Hice(t), are given by
where ℒfus=303 MJ m−3 is the volumetric enthalpy of fusion for ice. This model relies on meteorological data and has two adjustable parameters: the ice surface roughness z0 ice and its albedo αice. These adjustable parameters will be determined from the model fit to the ice ablation rate measured away from the glacier tables in Sect. 4.1.
3.2 Glacier table formation model
In Hénot et al. (2021), an analytical model was developed in order to explain the formation of artificial glacier tables made of cylindrical caps in a controlled environment, in which the heat transfer (natural convection of air and infrared radiation from the enclosure) was modelled through an effective heat exchange coefficient. In the following, we adapt this model to the non-symmetrical geometry of the rocks and we take into account the more complex energy balance of the glacier. Here we only attempt to describe the vertical motion of the rock with respect to the ice surface and we do not consider the lateral melt of the ice foot in this model, but this is briefly discussed in Sect. 5.2.
For the sake of simplicity, the following main assumptions are made in the model: (1) the rocks are considered cuboids (see Fig. 2b). The area Abase of contact with the ice is considered constant during the table formation, although it evidently varies over time. Yet, as discussed in the Supplement, this has little effect on the total heat transfer. The top and bottom areas are thus , and the side area is . (2) The surface temperature of the rock is assumed to be homogeneous and is denoted as Trock, allowing the development of a 1D thermal conduction model. (3) The thermal process is assumed to be quasi-static, meaning that all transient thermal effects are neglected. The validity of this assumption is discussed in the Supplement.
The energy balance of a rock, taking into account its 3D structure, is summarized in the schematic of Fig. 5a. The short-wave radiative flux is received by the rock on a surface 〈Asun〉. This area should depend on the shape and orientation of the rock with respect to the course of the sun, but for the sake of simplicity in the following it is simply assumed to be equal to the rock base surface area 〈Asun〉=Abase (the validity of this assumption is discussed in the Supplement). The long-wave flux coming from the atmosphere QLW atm ↓ is also assumed to be received only on the top surface of area Abase, but the rock also receives a long-wave flux on its side denoted as QLW env ↓. Strictly speaking, this quantity depends on the emissivity, surface temperature and view factor of all surfaces (ice, other rocks, terrain) seen from the rock sides (Lienhard, 2019) and thus cannot be simply estimated. In the following it will be kept as an adjustable parameter. The rock also emits a long-wave flux from its external surface (top and side). The sensible and latent fluxes are received from the air on the external surface of the rock (of area Abase+Aside). Finally a flux Qrock→ice is transferred to the ice through the contact area Abase.
The quasi-static assumption implies that the flux balance is verified at each time t:
The net short-wave flux is where αrock=0.18 is the albedo of the granite rock (measured by Watson, 1971; see the Supplement). The granite emissivity is taken as equal to 1 (Michalski et al., 2004), leading to . The turbulent fluxes are computed according to an equation similar to Eq. (3), for which the surface terms are those relative to the rock; i.e. Tsurface=Trock, and z0=z0 rock. If QE>0, water from the air condenses on the rock surface, which justifies the value of qsurface (corresponding to 100 % humidity at the temperature Trock). However, QE<0 would correspond to evaporation and would be limited by the quantity of water present on the rock surface. In the following QE is thus forced to 0 if QE<0.
The heat flux transmitted from the rock to the ice underneath can be estimated using a 1D conduction model as
where λ is the thermal conductivity of granite (measured in a previous work – Hénot et al., 2021 – as λ=2.8 , which is in agreement with the literature; Cho et al., 2009) and d1D is a length scale for the conduction process in the rock. It was postulated and verified experimentally (see Fig. 5 of Hénot et al., 2021) that this length could be estimated by , where Vrock is the volume of the rock and η=2.5 is a numerical prefactor adjusted from the lab experiments. This expression justifies the definition of deff.
From Eqs. (6) and (7) and using the measured meteorological data (Φ(t), QLW atm ↓(t), ua(t), Ta(t) and qa(t)) as input, the rock surface temperature Trock(t) can be computed at each time t by solving numerically non-linear Eq. (6). The flux Qrock→ice(t) reaching the ice can then be computed. When positive, this leads to ice melting under the rock, lowering the altitude of the bottom of the rock zrock:
The height of the ice foot supporting the rock is . The time origin corresponds to the rock lying at the surface of the ice (). Note that at this stage, there are two adjustable parameters in the table formation model: QLW env ↓ and z0 rock (αrock and η are taken from the literature). However, the roughness size z0 in the turbulent coefficient is not clearly defined (Hock, 2005), but the resulting model is not very sensitive to its value. Thus in the following, z0 rock will be taken as equal to that of the ice z0 ice.
4.1 Ice melting
The dashed black lines in Fig. 4a and b correspond to the model described in Sect. 3.1 with parameters αice=0.30 and z0=0.34 mm adjusted on the concatenated data of periods A and B (see the Supplement for a discussion on the sensitivity). The agreement between the model and the field measurements is good: the error on zice(t) stays below 3 cm (except at the end of period A when the movement of the camera increases the uncertainty in the measurements). The value of the adjusted ice albedo corresponds to what is reported in the literature for aged surface glacier ice, at the beginning of summer (Brock et al., 2000). The value of the roughness length z0 also falls in the range previously reported (10−4–10−2 m) (Brock et al., 2006; Conway and Cullen, 2013). Figure 5 shows (in white) the time-averaged values of , and , as well as the total flux reaching the ice surface, Qopen env→ice, for both time periods. The short-wave flux varies weakly between periods A and B (from 150 to 200 W m−2), and the net long-wave flux is comparatively small (−20 to 3 W m−2). The total turbulent flux strongly differs between periods A and B. It decreases from 120 W m−2 (which represents 50 % of the total flux) in period A to 25 W m−2 (10 % of the total flux) in period B. This is due to the drastic difference in mean wind speed, from 6.5 m s−1 during period A to 1.0 m s−1 during period B, which explains the difference in the ice ablation rate (of the order of 8 cm d−1 in period A and 5.5 cm d−1 in period B).
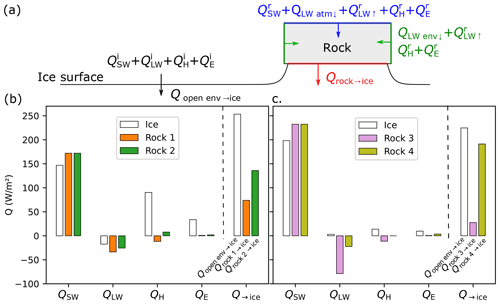
Figure 5(a) Schematics of the heat fluxes considered in the models for the ice surface melting (left) and glacier table formation. The colours denote the surfaces on which the fluxes are received. (b, c) Distribution of the heat fluxes averaged over the duration of observation as predicted by the time-resolved model for the ice surface (white) and for the four rocks studied (coloured).
4.2 Table formation
Rocks 1 and 2 formed glacier tables over the course of approximately a week (see Fig. 4a and b), after which they fell off the ice pedestal. Rock 3 was initially sitting on an ice foot, which grew bigger, while rock 4, although exhibiting dimensions close to those of rock 2 went down almost at the same rate as the bare-ice surface and did not form any significant glacier table (see the Supplement for pictures). The integration of the flux given by the model is shown in solid lines in Fig. 4a and b. The best agreement with the observed data was obtained for a value of the adjustable parameter W m−2. This corresponds to the long-wave flux emitted by a surface with emissivity 1 at a temperature 278.3 K, which seems reasonable as the physical meaning of this quantity is the mean temperature of the environment seen by the sides of the rocks (ice surface, others rocks and terrain surrounding the glacier). The agreement between the measurements and the model prediction is overall good for rocks 1 to 3. The model overestimates slightly the ability to form a table of rock 4, but the error (integrated over 6 d) stays under 3 cm for total ice ablation of 37 cm. Figure 6 shows the measured temperature of the top surface of rock 4 (solid line) as well as the value of Trock(t) predicted by the model. The two curves qualitatively display the same behaviour. The mean temperature is slightly overestimated by the model on average (by 2 ∘C), but the typical minimum (0–3 ∘C) and maximum (22–24 ∘C) daily temperature remain close.
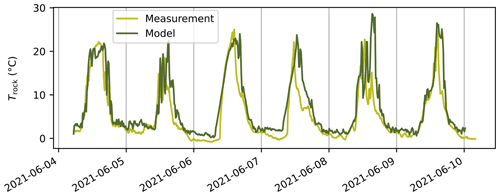
Figure 6Temperature Trock of the top surface of rock 4 measured using a thermocouple (light green) and predicted by the model using the meteorological data of period B (dark line). The date format is year-month-day.
Figure 5 shows for each rock (in colour) the surface- and time-averaged radiative and turbulent flux computed from the model as well as the resulting heat flux transmitted to the ice underneath. The short-wave flux received on the top surface of the rocks is 17 % higher than the one received by the ice due to the difference in albedo. However the net long-wave and turbulent fluxes are significantly reduced due to the fact that on average the rocks' surface temperature 〈Trock〉 are higher than Tice. For rocks 1 to 4, the averaged surface temperatures predicted were 8.2, 6.3, 13.0 and 7.2 ∘C respectively. The turbulent flux reduction is more important during period A than during period B due to the higher mean wind speed. Note that this effect is geometrically amplified (by a factor 1+4β) as these negative fluxes are integrated over the external surface of the rocks, which is larger than the base surface in contact with ice (this is especially true for rock 4, which has the largest aspect ratio). For all the rocks studied, the predicted flux causing ice to melt under the rocks was on average reduced compared to the flux received by the ice surface (from −15 % for rock 4 to −88 % for rock 3), leading to the formation of tables. Note that this amplification effect can also, depending of the shape and size of the rocks, have the opposite consequence of causing a rock to sink into the ice surface, as will be shown in Sect. 5.2.
Figure 7a shows, for each rock, the height of the ice foot, , as a function of the ablated ice thickness, . On average these quantities appear to be proportional. The slope corresponds to a dimensionless growth rate of the glacier table, denoted as : a unity slope would correspond to no melt under the rock (the ice foot height would then correspond exactly to the ablated ice thickness); conversely a zero slope would correspond to a rock descending at the same rate as the ice surface around it and thus never forming a glacier table. The solid lines in Fig. 7a correspond to linear adjustments. The deduced slopes are plotted for each rock in Fig. 7b as a function of their thickness h (markers). The value predicted by the model is plotted in the same figure for periods A (dashed lines) and B (solid lines) for the values of β corresponding to the four rocks as a function of the thickness of the rock. Moving along a line thus corresponds to a change in scale but not in shape of the rocks. The dimensionless growth rates of the tables are accurately predicted by the model. It is visible that independently of the rock shape and time period, a small enough rock would not form a table and instead sink into the ice surface ().
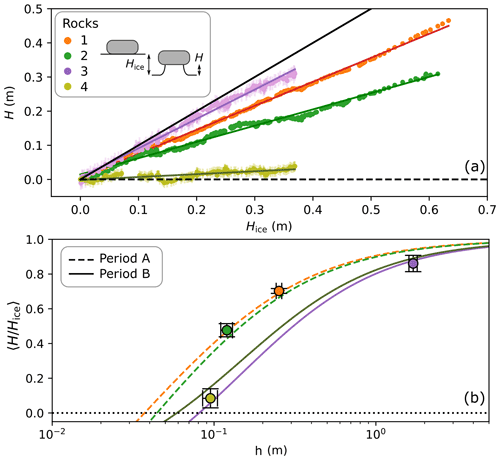
Figure 7(a) Evolution of the height H of the ice foot under rocks 1–4 as a function of the ablated ice thickness Hice. The coloured lines correspond to linear adjustments of the data. The solid black line has a slope of 1. (b) The mean ratio of the height H of the ice foot under a rock and of the total ablated ice thickness Hice since the beginning of the table formation, as a function of the thickness h of the rock. The markers correspond to the slopes of (a) for each rock. The lines correspond to the application of the model for the meteorological values measured in period A (dashed lines) and B (solid lines) and the aspect ratio β of each rock given in Table 1.
4.3 Analysis of the 80 glacier tables field
In Fig. 3, showing the height of the ice structure formed by 80 rocks 8 d after the melt of the snow layer, is it visible that a critical size exists (4–10 cm in thickness and 9–13 cm in width) above which rocks tend to form glacier tables. The larger the rock, the greater its ability to protect the ice underneath from melting and, assuming all tables started their formation at the same time, the higher the ice foot. Below this critical size, however, the rocks have a tendency to sink into the ice surface. Having successfully modelled the evolution of the four larger glacier tables, the model presented in Sect. 3.2 can be applied to the data obtained on a given day for a field comprising 80 rocks.
The snow layer covering that part of the glacier finished melting on 26 May, leaving the ice exposed. The meteorological data of the time period C (from 26 May until 3 June), alongside the previously adjusted parameters αice and z0, allow us to compute the thickness of ablated ice m during this period (see Fig. S5 in the Supplement). The observed values of H are plotted in Fig. 8a as a function of the ones predicted by the model for each rock, assuming that the structure formation started on 26 May (H26 May=0). The rocks that have sunk into the ice surface (H<0) are shown in blue. For those, the prediction of the model is, as expected, not accurate. Indeed, a rock that has penetrated into the ice has a greater contact surface area with the ice and a smaller external surface open to the atmosphere than what is taken into account in the model. It is thus cooler, and its (negative) dimensionless growth rate is smaller (in absolute terms) than that given by the model, as observed. The rocks that have formed glacier tables (H>0) are shown in red. The threshold between rocks forming or not forming a table (the point (0,0) in the graph) is well predicted by the model. For the smaller structures (H<0.3 m), the height of the ice foot is also well predicted (with an error smaller than 5 cm). Note that this required no new adjustable parameter and this prediction is the result of a model integrated over 8 d in a time period different from A and B, during which the parameters of the model were adjusted. For ice feet taller than 0.3 m, however, the prediction of the model is not good. For some H>Hice, and the assumption H26 May=0 is thus obviously not valid. We infer that larger rocks emerged from the snow layer before 26 May and started to form a table earlier.
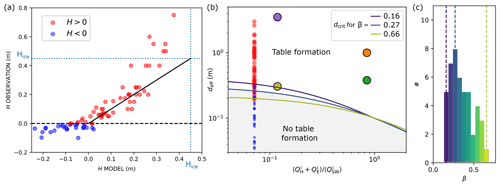
Figure 8(a) Observation versus model for the distance H between the bottom of rocks and the ice surface for the data measured on 3 June 2021 (see Fig. 3). The data are represented in red if a table is observed (H>0) and in blue otherwise. The solid black line has a slope of 1, and the dotted lines correspond to the ablated ice thickness Hice since the melting of the snow layer (see the Supplement). (b) Diagram of the ability of a rock to form a table as a function of its typical width deff and the ratio . The solid lines correspond, for three values of the aspect ratio β, to the delimitation predicted by the model with averaged meteorological data, between a rock forming a table and a rock sinking into the ice surface. The small circles correspond to the data of (a) with the same colour code. The larger circles correspond to rocks 1–4. (c) Distribution of the aspect ratio β of the rocks close to the transition between the two regimes ( m). The vertical dashed lines correspond to the limits plotted in (b) with the same colour code.
5.1 Critical diameter
The critical diameter, corresponding to the transition between the two regimes described in the previous section (the rock sinks into the ice or forms a table), is denoted as dcrit. We chose to consider a critical width instead of a critical thickness as the transition seems sharper when considering this quantity in Fig. 3. This is reminiscent of the results obtained in a controlled environment in the absence of solar radiation, for which the transition occurred for a critical diameter of the cylinders, independently of their aspect ratio (Hénot et al., 2021).
From our model, given a set of meteorological data and an aspect ratio β, a critical width dcrit can be computed. In the following, unlike what has been done until now, typical time-averaged meteorological data (〈Φ〉=210 W m−2, W m−2, 〈Ta〉=7 ∘C, 〈qa〉=0.0058 kg kg−1 and 〈ua〉 ranging from 0 to 20 m s−1) will be used as inputs (we have checked that this pre-averaging of the input data affects the output of the model by less than a few percent). Figure 8b shows a diagram of the ability of a rock to form a table as a function of its effective width deff (which in practice can be replaced by the mean width) and the ratio , which is a quantity proportional to 〈ua〉 and whose relevance will be discussed in the next paragraph. The four monitored rocks as well as the field data from the 80 rocks found in the 800 m2 field are plotted in this diagram. The distribution of aspect ratio β of rocks (46 of them) close to the transition (defined by m) is plotted in Fig. 8c. The bounding values (β=0.16 and β=0.66) as well as the value corresponding to the maximum of the distribution (β=0.27) are used to plot, in Fig. 8b, the values of dcrit predicted by the model. This threshold, which depends slightly on β, shows a good agreement with the transition visible in the field data. This diagram illustrates the sensitivity of the glacier table formation to the meteorological conditions and especially the mean wind speed: deff is divided by 2 between time periods A and B.
5.2 Physical discussion
A rock forms a glacier table when the heat flux reaching the ice underneath is reduced compared to that received by the bare-ice surface around it. If, on the contrary, this heat flux is amplified, the rock will sink into the ice surface. Depending on the rock size, both phenomena are observed on temperate glaciers. During summer, the main source of heat flux causing the ice to melt is the short-wave radiation coming from the sun. Due to the lower albedo of the rock, this flux is slightly amplified compared to what is received by a similar area of bare ice and thus does not directly favour the formation of glacier tables. However this induces a heat flux across the thickness of the rock that elevates its surface temperature Trock (the bottom surface staying at Tice) and strongly affects the net infrared radiation and turbulent fluxes. As can be seen in Fig. 5, the sign of the sensible flux can even change (if , the wind warms the ice surface but cools the rock) and induces a negative net short-wave flux (the rock flux lost being proportional to ). At the end, if the rock is large enough (so that its surface temperature can rise enough), all these combined effects lead to the formation of a glacier table. As illustrated by the difference between periods A and B, the wind intensity can vary significantly at the surface of the glacier. The sensible flux being one motor of glacier table formation (with emitted long-wave radiation), this affects the critical size dcrit. The ratio used on the abscissa in Fig. 8b demonstrates this effect. When this ratio is small (<0.1), the structure formation is controlled by the long-wave emission of the rock, while a large value (>1) would correspond to a regime dominated by the effect of sensible flux. Note that at this point, a 1D model with d1D=h and no geometrical amplification would have achieved the same result. However, the 3D structure has its importance: the heat transfer with the environment (short-wave and turbulent) that cools the rock is exchanged on a surface area with is much larger than the base area of a rock. In our model we considered the total external surface of the rock, which is larger by a factor of 1+4β typically of the order of 2–3 than Abase. As detailed in the Supplement, a 1D model would, in order to verify Eq. (6), significantly overestimate Trock (by 150 ∘C during sunlight for rock 3, which is not a physically acceptable value). This 3D effect also explains the influence of the rock shape on its ability to form a table.
The formation of glacier tables in the natural environment of a temperate glacier results from a more complex energy balance than the idealized lab-controlled study conducted previously (Hénot et al., 2021) while the main physical ingredient stays the same: the greater temperature of the rock surface, compared to the ice, reduces the incoming heat flux and thus the melt rate under the rock. In the absence of solar radiation, the threshold controlling the ability of a rock to form a table was determined by a trade-off between this effect and a geometrical amplification effect: a rock can act as a fin in amplifying the incoming heat flux, leading to a higher melt rate under the rock than for bare ice. While this effect also plays a role in natural conditions, the threshold is also significantly affected by the direct solar radiation that has two opposite effects: on the one hand, due to lower albedo, a higher flux is received by a rock than a bare-ice surface, but, on the other hand, the temperature gradient induced by the solar flux across a rock elevates its temperature, enhancing the cooling effect due to turbulent and long-wave flux. The first effect dominates for small rocks, while the latter dominates for larger rocks.
While the heat transfer across the rock controls the formation dynamics, the end of life of glacier tables and in particular the maximum height reached by ice feet will likely result from lateral melting of the ice column. This process is expected to be affected by the rock shape and size that would prevent radiative melting due to shading effects, leaving only turbulent flux and long-wave balance. Note also that when the ice pedestal becomes very slender, a heavy rock could also cause the ice column to creep.
We studied the formation of four glacier tables over the course of a week, and we measured the characteristics of 80 glacier tables on the Mer de Glace (Alps). We developed a simple model taking into account the infrared and solar radiation and turbulent heat flux received by a rock and by the glacier ice surface using local meteorological data, allowing us to quantitatively reproduce the glacier table formation dynamics and to identify the physical effects at its origin. The table formation is controlled by the ice melting under the rocks, and the ice foot growth rate is proportional to the ice ablation rate at the glacier surface. The size of the rocks is a determinant factor governing table formation: the bigger the rock, the higher and faster the ice foot supporting it will grow. Under a critical size, rocks show the opposite behaviour of sinking into the ice surface. The ability of a rock to form a table is controlled by the balance between two opposing effects: a thermal insulation effect, which depends strongly on the rock size, and a geometrical amplification effect linked to the fact that the external surface on which the rock receives an external heat flux is larger than its contact area with the ice. This second effect becomes dominant only for rocks smaller than a few tens of centimetres. The insulation effect originates from the warmer temperature of the rock surface compared to the ice, which reduces, even sometimes changing the sign of, the net long-wave and turbulent flux, ultimately reducing the heat available for ice melting under the rock. While a rock receives a slightly larger net short-wave flux (the main source of heat at the glacier surface) than ice because of the difference in albedo, this effect is too weak to compensate for the insulation effect for large rocks. The solar radiation, by inducing a strong thermal gradient across the thickness of the rock, raises the rock surface temperature, which also contributes to the insulation effect. To summarize, we identified three main parameters controlling the dimensionless growth rate of the ice foot that characterize the ability of a rock to form a table: the rock thickness h; its aspect ratio β; and the ratio , which depends on the meteorological conditions. When this ratio is higher than ≈0.1 (i.e. in windy periods), the turbulent heat exchange lowers the critical diameter dcrit (by up to 50 %), which facilitates glacier table formation. We did not consider in this study the lateral melting of the ice pedestal and the end of life of the structures, but this could be the subject of future work.
The graphical user interface (GUI) developed to extract the data from the raw images is available at https://doi.org/10.5281/zenodo.6683570 (Hénot, 2022). Python script files used to generate the figures are available upon request to the corresponding author.
The S2M data used in this work provided by Météo-France CNRS, CNRM Centre d'Etudes de la Neige, through AERIS, are available at https://doi.org/10.25326/37#v2020.2 (Vernay et al., 2022b). All other data used in this work are available upon request to the corresponding author for non-commercial research use.
The supplement related to this article is available online at: https://doi.org/10.5194/tc-16-2617-2022-supplement.
MH, VL, JV, NP and NT conceived the study and performed the fieldwork. MH performed the data analysis, developed the model and drafted the manuscript. All authors contributed to the data interpretation, discussion of the results and writing of the manuscript.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors acknowledge technical support and useful scientific discussion with Marine Vicet and Thierry Dauxois. The S2M data are provided by Météo-France CNRS, CNRM Centre d'Etudes de la Neige, through AERIS.
This research has been supported by the Fédération de Recherche André-Marie Ampère and Laboratoire de Physique at ENS de Lyon.
This paper was edited by Chris R. Stokes and reviewed by Adrien Gilbert and two anonymous referees.
Agassiz, L.: Études sur les glaciers, Gent & Gassman, Neuchâtel, LCCN (Librairy of congress catalog), https://lccn.loc.gov/12008544 (last access: 23 June 2022), 1840. a, b
Bergeron, V., Berger, C., and Betterton, M. D.: Controlled Irradiative Formation of Penitentes, Phys. Rev. Lett., 96, 098502, https://doi.org/10.1103/physrevlett.96.098502, 2006. a
Betterton, M. D.: Theory of structure formation in snowfields motivated by penitentes, suncups, and dirt cones, Phys. Rev. E, 63, 056129, https://doi.org/10.1103/PhysRevE.63.056129, 2001. a, b
Bintanja, R., Reijmer, C. H., and Hulscher, S. J. M. H.: Detailed observations of the rippled surface of Antarctic blue-ice areas, J. Glaciol., 47, 387–396, https://doi.org/10.3189/172756501781832106, 2001. a
Bordiec, M., Carpy, S., Bourgeois, O., Herny, C., Massé, M., Perret, L., Claudin, P., Pochat, S., and Douté, S.: Sublimation waves: Geomorphic markers of interactions between icy planetary surfaces and winds, Earth-Sci. Rev., 211, 103350, https://doi.org/10.1016/j.earscirev.2020.103350, 2020. a
Bouillette, E.: Une Superbe Table des Glaciers, L'Astronomie, 47, 201–202, 1933. a, b
Bouillette, E.: La fin d'une table des glaciers, L'Astronomie, 48, 89–91, 1934. a, b
Brock, B. W., Willis, I. C., and Sharp, M. J.: Measurement and parameterization of albedo variations at Haut Glacier d'Arolla, Switzerland, J. Glaciol., 46, 675–688, https://doi.org/10.3189/172756500781832675, 2000. a
Brock, B. W., Willis, I. C., and Sharp, M. J.: Measurement and parameterization of aerodynamic roughness length variations at Haut Glacier d'Arolla, Switzerland, J. Glaciol., 52, 281–297, https://doi.org/10.3189/172756506781828746, 2006. a
Bruthans, J., Soukup, J., Vaculikova, J., Filippi, M., Schweigstillova, J., Mayo, A. L., Masin, D., Kletetschka, G., and Rihosek, J.: Sandstone landforms shaped by negative feedback between stress and erosion, Nat. Geosci., 7, 597–601, https://doi.org/10.1038/ngeo2209, 2014. a
Bushuk, M., Holland, D. M., Stanton, T. P., Stern, A., and Gray, C.: Ice scallops: a laboratory investigation of the ice–water interface, J. Fluid Mech., 873, 942–976, https://doi.org/10.1017/jfm.2019.398, 2019. a
Carenzo, M., Pellicciotti, F., Mabillard, J., Reid, T., and Brock, B. W.: An enhanced temperature index model for debris-covered glaciers accounting for thickness effect, Adv. Water Resour., 94, 457–469, https://doi.org/10.1016/j.advwatres.2016.05.001, 2016. a
Cho, W., Kwon, S., and Choi, J.: The thermal conductivity for granite with various water contents, Eng. Geol., 107, 167–171, https://doi.org/10.1016/j.enggeo.2009.05.012, 2009. a
Claudin, P., Jarry, H., Vignoles, G., Plapp, M., and Andreotti, B.: Physical processes causing the formation of penitentes, Phys. Rev. E, 92, 033015, https://doi.org/10.1103/physreve.92.033015, 2015. a
Claudin, P., Durán, O., and Andreotti, B.: Dissolution instability and roughening transition, J. Fluid Mech., 832, R2, https://doi.org/10.1017/jfm.2017.711, 2017. a
Cohen, C., Berhanu, M., Derr, J., and du Pont, S. C.: Erosion patterns on dissolving and melting bodies, Physical Review Fluids, 1, 050508, https://doi.org/10.1103/PhysRevFluids.1.050508, 2016. a
Cohen, C., Berhanu, M., Derr, J., and Du Pont, S. C.: Buoyancy-driven dissolution of inclined blocks: Erosion rate and pattern formation, Physical Review Fluids, 5, 053802, https://doi.org/10.1103/PhysRevFluids.5.053802, 2020. a
Collier, E., Nicholson, L. I., Brock, B. W., Maussion, F., Essery, R., and Bush, A. B. G.: Representing moisture fluxes and phase changes in glacier debris cover using a reservoir approach, The Cryosphere, 8, 1429–1444, https://doi.org/10.5194/tc-8-1429-2014, 2014. a
Conway, J. and Cullen, N.: Constraining turbulent heat flux parameterization over a temperate maritime glacier in New Zealand, Ann. Glaciol., 54, 41–51, https://doi.org/10.3189/2013AoG63A604, 2013. a, b, c
Drewry, D. J.: A Quantitative Assessment of Dirt-Cone Dynamics, J. Glaciol., 11, 431–446, https://doi.org/10.3189/S0022143000022383, 1972. a
Evatt, G., Mayer, C., Mallinson, A., Abrahams, I., Heil, M., and Nicholson, L.: The secret life of ice sails, J. Glaciol., 63, 1049–1062, https://doi.org/10.1017/jog.2017.72, 2017. a
Evatt, G. W., Abrahams, I. D., Heil, M., Mayer, C., Kingslake, J., Mitchell, S. L., Fowler, A. C., and Clark, C. D.: Glacial melt under a porous debris layer, J. Glaciol., 61, 825–836, https://doi.org/10.3189/2015JoG14J235, 2015. a
Fitzpatrick, N., Radić, V., and Menounos, B.: Surface Energy Balance Closure and Turbulent Flux Parameterization on a Mid-Latitude Mountain Glacier, Purcell Mountains, Canada, Front. Earth Sci., 5, 67, https://doi.org/10.3389/feart.2017.00067, 2017. a
Fowler, A. C. and Mayer, C.: The formation of ice sails, Geophys. Astro. Fluid, 111, 411–428, https://doi.org/10.1080/03091929.2017.1370092, 2017. a
Guérin, A., Derr, J., Du Pont, S. C., and Berhanu, M.: Streamwise dissolution patterns created by a flowing water film, Phys. Rev. Lett., 125, 194502, https://doi.org/10.1103/PhysRevLett.125.194502, 2020. a
Hardy, B.: ITS-90 Formulations for Vapor Pressure, Frost point Temperature, Dew point Temperature, and Enhancement Factors in the range −100 to +100 C”, Papers and Abstracts of the Third International Symposium on Humidity and Moisture, Teddington, London, England, April 1998, https://api.semanticscholar.org/CorpusID:98492826 (last access: 23 June 2022), 214–222, 1998. a
Hénot, M.: Pointing interface, Zenodo [code], https://doi.org/10.5281/zenodo.6683570, 2022. a
Hénot, M., Plihon, N., and Taberlet, N.: Onset of Glacier Tables, Phys. Rev. Lett., 127, 108501, https://doi.org/10.1103/PhysRevLett.127.108501, 2021. a, b, c, d, e, f, g
Hock, R.: Glacier melt: a review of processes and their modelling, Progress in Physical Geography: Earth and Environment, 29, 362–391, https://doi.org/10.1191/0309133305pp453ra, 2005. a, b
Huang, J. M., Tong, J., Shelley, M., and Ristroph, L.: Ultra-sharp pinnacles sculpted by natural convective dissolution, P. Natl. Acad. Sci. USA, 117, 23339–23344, https://doi.org/10.1073/pnas.2001524117, 2020. a
Huinink, H. P., Pel, L., and Kopinga, K.: Simulating the growth of tafoni, Earth Surf. Proc. Land., 29, 1225–1233, https://doi.org/10.1002/esp.1087, 2004. a
Krenek, L. O.: The Formation of Dirt Cones on Mount Ruapehu, New Zealand, J. Glaciol., 3, 312–315, https://doi.org/10.3189/S0022143000023984, 1958. a
Lienhard, J. H.: A Heat Transfert Textbook, Phlogiston Press, 411–428, ISBN 9780486837352, 2019. a
Mangold, N.: Ice sublimation as a geomorphic process: A planetary perspective, Geomorphology, 126, 1–17, https://doi.org/10.1016/j.geomorph.2010.11.009, 2011. a
Mashaal, N. M., Sallam, E. S., and Khater, T. M.: Mushroom rock, inselberg, and butte desert landforms (Gebel Qatrani, Egypt): evidence of wind erosion, Int. J. Earth Sci., 109, 1975–1976, https://doi.org/10.1007/s00531-020-01883-z, 2020. a
McIntyre, N. F.: Cryoconite hole thermodynamics, Can. J. Earth Sci., 21, 152–156, https://doi.org/10.1139/e84-016, 1984. a
Michalski, J., Reynolds, S., Sharp, T., and Christensen, P.: Thermal infrared analysis of weathered granitic rock compositions in the Sacaton Mountains, Arizona: Implications for petrologic classifications from thermal infrared remote-sensing data, J. Geophys. Res.-Planet., 109, E03007, https://doi.org/10.1029/2003JE002197, 2004. a
Mitchell, K. A. and Tiedje, T.: Growth and fluctuations of suncups on alpine snowpacks, J. Geophys. Res., 115, F04039, https://doi.org/10.1029/2010JF001724, 2010. a
Moeller, R., Moeller, M., Kukla, P. A., and Schneider, C.: Impact of supraglacial deposits of tephra from Grímsvötn volcano, Iceland, on glacier ablation, J. Glaciol., 62, 933–943, https://doi.org/10.1017/jog.2016.82, 2016. a
Nadeau, D. F., Brutsaert, W., Parlange, M., Bou-Zeid, E., Barrenetxea, G., Couach, O., Boldi, M.-O., Selker, J. S., and Vetterli, M.: Estimation of urban sensible heat flux using a dense wireless network of observations, Environ. Fluid Mech., 9, 635–653, https://doi.org/10.1007/s10652-009-9150-7, 2009. a
Östrem, G.: Ice Melting under a Thin Layer of Moraine, and the Existence of Ice Cores in Moraine Ridges, Geogr. Ann., 41, 228–230, http://www.jstor.org/stable/4626805, 1959. a
Reid, T. D. and Brock, B. W.: An energy-balance model for debris-covered glaciers including heat conduction through the debris layer, J. Glaciol., 56, 903–916, https://doi.org/10.3189/002214310794457218, 2010. a, b
Rhodes, J. J., Armstrong, R. L., and Warren, S. G.: Mode of Formation of “Ablation Hollows” Controlled by Dirt Content of Snow, J. Glaciol., 33, 135–139, https://doi.org/10.3189/S0022143000008601, 1987. a
Smiraglia, C. and Diolaiuti, G.: Encyclopedia of Snow, Ice and Glaciers, Chap. Epiglacial Morphology, Springer, 262–267, ISBN 978-90-481-2641-5, 2011. a
Swithinbank, C.: The origin of dirt cones on glaciers, J. Glaciol., 1, 461–465, https://doi.org/10.3189/S0022143000012880, 1950. a
Taberlet, N. and Plihon, N.: Sublimation-driven morphogenesis of Zen stones on ice surfaces, P. Natl. Acad. Sci. USA, 118, e2109107118, https://doi.org/10.1073/pnas.2109107118, 2021. a
Turkington, A. V. and Paradise, T. R.: Sandstone weathering: a century of research and innovation, Geomorphology, 67, 229–253, https://doi.org/10.1016/j.geomorph.2004.09.028, 2005. a
Vernay, M., Lafaysse, M., Monteiro, D., Hagenmuller, P., Nheili, R., Samacoïts, R., Verfaillie, D., and Morin, S.: The S2M meteorological and snow cover reanalysis over the French mountainous areas: description and evaluation (1958–2021), Earth Syst. Sci. Data, 14, 1707–1733, https://doi.org/10.5194/essd-14-1707-2022, 2022a. a
Vernay, M., Lafaysse, M., Hagenmuller, P., Nheili, R., Verfaillie, D., and Morin, S.: The S2M meteorological and snow cover reanalysis in the French mountainous areas (1958–present), AERIS [data set], https://doi.org/10.25326/37#v2020.2, 2022b. a
Watson, R. D.: Spectral reflectance and photometric properties of selected rocks, Remote Sens. Environ., 2, 95–100, https://doi.org/10.1016/0034-4257(71)90082-4, 1971. a
Weady, S., Tong, J., Zidovska, A., and Ristroph, L.: Anomalous Convective Flows Carve Pinnacles and Scallops in Melting Ice, Phys. Rev. Lett., 128, 044502, https://doi.org/10.1103/PhysRevLett.128.044502, 2022. a
Young, R. and Young, A.: Sandstone Landforms, Lecture Notes in Physics, Springer-Verlag, ISBN 9780387539461, https://books.google.fr/books?id=Da8rvwEACAAJ (last access: 1 June 2022), 1992. a







