the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Stabilizing effect of mélange buttressing on the marine ice-cliff instability of the West Antarctic Ice Sheet
Tanja Schlemm
Johannes Feldmann
Ricarda Winkelmann
Anders Levermann
Owing to global warming and particularly high regional ocean warming, both Thwaites and Pine Island Glaciers in the Amundsen region of the Antarctic Ice Sheet could lose their buttressing ice shelves over time. We analyse the possible consequences using the parallel ice sheet model (PISM), applying a simple cliff-calving parameterization and an ice mélange-buttressing model. We find that the instantaneous loss of ice-shelf buttressing, due to enforced ice-shelf melting, initiates grounding-line retreat and triggers marine ice sheet instability (MISI). As a consequence, the grounding line progresses into the interior of the West Antarctic Ice Sheet and leads to a sea level contribution of 0.6 m within 100 a. By subjecting the exposed ice cliffs to cliff calving using our simplified parameterization, we also analyse marine ice cliff instability (MICI). In our simulations it can double or even triple the sea level contribution depending on the only loosely constrained parameter that determines the maximum cliff-calving rate. The speed of MICI depends on this upper bound of the calving rate, which is given by the ice mélange buttressing the glacier. However, stabilization of MICI may occur for geometric reasons. Because the embayment geometry changes as MICI advances into the interior of the ice sheet, the upper bound on calving rates is reduced and the progress of MICI is slowed down. Although we cannot claim that our simulations bear relevant quantitative estimates of the effect of ice-mélange buttressing on MICI, the mechanism has the potential to stop the instability. Further research is needed to evaluate its role for the past and future evolution of the Antarctic Ice Sheet.
- Article
(12405 KB) - Full-text XML
- BibTeX
- EndNote
Ice loss from the Greenland and Antarctic Ice Sheets is contributing increasingly to global sea level rise (Rignot et al., 2014; Shepherd et al., 2018b; WCRP Global Sea Level Budget Group, 2018). Ice sheets gain mass through accumulation of snowfall. Whether they contribute to sea level changes depends on how much this mass gain is offset or overcompensated for by mass losses due to surface and basal melting as well as iceberg calving. Ice sheets in both Greenland and Antarctica are currently losing ice (Enderlin et al., 2014; Shepherd et al., 2018b; Mouginot et al., 2019; Larour et al., 2019; Bell and Seroussi, 2020). Estimating the additional future mass loss of these ice sheets is critical for future sea level projections (Church et al., 2013; Ritz et al., 2015; DeConto and Pollard, 2016; Mengel et al., 2016; Kopp et al., 2017; Slangen et al., 2017; Golledge et al., 2019; Levermann et al., 2020; Edwards et al., 2021). Uncertainties in modelling the physics of the Antarctic Ice Sheet (AIS) lead to large uncertainties in sea level projections (Noble et al., 2020; Pattyn and Morlighem, 2020).
One such uncertainty is the potential collapse and the calving of large ice cliffs after the ice shelves buttressing them have disintegrated. The concept of cliff calving was motivated by an analysis of depth-averaged stresses near an ice cliff, which showed that ice cliffs exceeding an ice thickness stability limit are inherently unstable (Bassis and Walker, 2011). Cliff calving could lead to uncontrolled ice retreat: grounding-line retreat caused by cliff calving may expose even higher ice cliffs further inland, which in turn are more susceptible to collapse, resulting in self-reinforcing ice retreat. This is referred to as Marine Ice Cliff Instability (MICI) (DeConto and Pollard, 2016).
A study by DeConto and Pollard (2016) found that the AIS could contribute up to 1 m of sea level rise within a century, if cliff calving is taken into account. This is substantially more than all other projections that do not include MICI. However, this study has been criticized as over-estimating sea level contribution (Edwards et al., 2019) owing to a lack of observationally constrained models of the cliff-calving process. DeConto and Pollard (2016) parameterized cliff calving with a step-like function that is zero for ice cliffs below the stability limit and ramps up rapidly to an upper limit for all ice cliffs exceeding the stability limit. We revisit the question of MICI in the AIS using a more complex parameterization of cliff calving, which is based on the shear failure of an ice cliff and gives the cliff-calving rate as an exponential function of ice thickness and water depth (Schlemm and Levermann, 2019). A recent, more detailed modelling study of ice cliff failure, incorporating different structural failure modes as well as surface lowering due to viscous deformation, supports the findings that calving rates increase exponentially with ice thickness (Crawford et al., 2021). In our model, we further assume that calved icebergs form an ice mélange that buttresses the ice cliffs, providing an upper bound on calving rates (Schlemm and Levermann, 2021).
We consider the Amundsen region of the West Antarctic Ice Sheet (WAIS) as the likely initiator of MICI. Iceberg plough marks on the seafloor indicate that large full thickness icebergs calved from Pine Island Glacier and that MICI was active in this area during the last deglaciation (Wise et al., 2017). Additionally, the WAIS is grounded largely on bedrock below sea level and is therefore vulnerable to both the marine ice sheet instability (MISI) and MICI. MISI is caused by grounding-line retreat on a retrograde bed: retreat into deeper bed regions increases the flux across the grounding line and therefore accelerates grounding-line retreat, resulting in self-reinforcing ice loss (Mercer, 1978; Schoof, 2007; Favier et al., 2014). Observations show that MISI is possibly already underway in the Amundsen region (Joughin et al., 2014; Mouginot et al., 2014; Rignot et al., 2014). Once MISI is initiated, the entire WAIS could collapse on a millennial time scale, resulting in a sea- level rise of 3 m (Feldmann and Levermann, 2015). With the addition of cliff calving (MICI), the WAIS collapse would occur much more rapidly.
The breakup of ice shelves is a necessary precondition for the calving of exposed ice cliffs and thus for the onset of MICI. Hydrofracturing, in which the deepening of ice crevasses due to extensive surface meltwater leads to the catastrophic failure of an entire ice shelf, has been proposed by DeConto and Pollard (2016) as the main mechanism for ice-shelf breakup and the consequent exposure of ice cliffs.
In 2002, the Larsen B Ice Shelf on the Antarctic Peninsula collapsed within a week after having thinned in previous years owing to high summer melt rates (Rack and Rott, 2004; Glasser and Scambos, 2008). As a result of the ice-shelf collapse, glaciers flowing into the shelf have permanently accelerated (Scambos et al., 2004; Berthier et al., 2012). These are small glaciers with little impact on the overall Antarctic mass balance. Based on the observation of numerous surface meltwater ponds prior to ice-shelf collapse, it has been suggested that hydrofracturing owing to intense surface melting was the primary cause of this sudden collapse (MacAyeal et al., 2003). However, anomalously large surface melt rates are required for an ice shelf to break up as rapidly as the Larsen B Ice Shelf did (Robel and Banwell, 2019). Thus, hydrofracturing would probably not be the main mechanism leading to ice-shelf failure in the Amundsen region: even under the RCP 8.5 scenario, surface meltwater production on the Pine Island Ice Shelf is projected to remain far below a threshold of 300 mm a−1 at the end of the century (Trusel et al., 2015). This threshold is equivalent to current surface meltwater production on the remaining Larsen C Ice Shelf and less than half of the pre-collapse surface meltwater production on the Larsen B Ice Shelf (Trusel et al., 2015). Therefore, it is unlikely that the ice shelves in the Amundsen region will fail owing to hydrofracturing.
Nevertheless, it is likely that the ice shelves in the Amundsen region will break apart under persisting global warming conditions. The Amundsen Sea is warming (Shepherd et al., 2004, 2018a), leading to increased basal melting of ice shelves. This is already causing thinning and grounding-line retreat in all the glaciers in the Amundsen region (MacGregor et al., 2012; Mouginot et al., 2014; Milillo et al., 2019).
The destabilizing effect of basal melt on ice shelves can be further amplified by basal and surface crevasses: satellite observations show a trend of widespread surface rifting at the shear margins of all glaciers in the Amundsen region (MacGregor et al., 2012) as well as an increase in rifts originating from basal crevasses in the centre of the Pine Island Ice Shelf (Jeong et al., 2016). Ocean warming may be the cause of the observed expansion of basal crevasses (Jeong et al., 2016). Rifting and crevassing accelerates grounding-line retreat: damage feedback modelling showed that a basal melt rate of 20 m a−1 combined with a 20-m-deep surface crevasse in the shear zone at the grounding line causes a faster grounding-line retreat than a basal melt rate of 100 m a−1 on an undamaged shelf (Lhermitte et al., 2020).
In addition, calving front retreat of small ice shelves may be self-reinforcing: a linear elastic fracture mechanics model of calving at Thwaites Glacier showed a positive feedback, i.e. if calving results in a shorter ice shelf, this shorter ice shelf is more likely to calve (Yu et al., 2017). It is also possible that weakened buttressing due to ice-shelf thinning at Pine Island and Thwaites Glaciers could amplify the development of damage in their shear zones. Lhermitte et al. (2020) suggest that this damage feedback might predispose the ice shelves at Pine Island and Thwaites Glaciers to disintegration. This would remove buttressing from glaciers terminating in the Amundsen Sea and expose large ice cliffs, triggering MISI and MICI.
We perform a series of simulations using the parallel ice sheet model (PISM) in a regional setup of the WAIS, where we initiate MISI and MICI by removing the ice shelves in the Amundsen region. The ice sheet model and calving parameterizations are described in more detail in Sect. 2. We present the resulting sea-level contributions in Sect. 3. In Sect. 4, we discuss how the strength of mélange buttressing changes with grounding-line retreat and show that as a result MICI slows down as it progresses.
2.1 Mélange-buttressed cliff calving
2.1.1 Model description
The model for mélange-buttressed cliff calving consists of two parts: cliff-calving parameterization (Schlemm and Levermann, 2019) and mélange-buttressing parameterization (Schlemm and Levermann, 2021).
For the ice cliffs, i.e. grounded ice sheet at the coast, we use a cliff-calving relation based on shear failure of an ice cliff (Schlemm and Levermann, 2019). If the difference between ice thickness and water depths lies below a water depth-dependent threshold (≈100 m), the cliff is assumed to be stable. For larger ice cliffs, the calving rate grows exponentially with ice thickness and water depth. This assumed exponential relation and the fact that in many regions in West Antarctica the bed topography is down-sloping inland, can lead to very large calving rates (>30 km a−1, see Fig. 1a).
In addition to the recently discussed stabilizing effect of dynamic thinning (Bassis et al., 2021; Golledge and Lowry, 2021), a mélange of icebergs and sea ice, may have a stabilizing effect on MICI. Here we apply a very simple mélange-buttressing parameterization (Schlemm and Levermann, 2021): larger calving rates lead to the production of more icebergs, which together with sea ice form a stiff ice mélange. This mélange buttresses the ice cliff, thereby stabilizing it. As a result of this negative feedback between calving rate and mélange buttressing, there is an upper limit to the calving rate, Cmax (see Fig. 1b). This threshold, derived in Schlemm and Levermann (2021), is a function of embayment geometry and mélange properties,
where the mélange length is denoted by Lem, the mélange width at the calving front by Wcf, the mélange exit width by Wex and the average mélange width by Wem (see Fig. 2). γ is the fraction of the ice thickness H beyond which calving is completely suppressed, and uex is the exit velocity, with which mélange drifts out of the embayment. Finally, the internal friction of the mélange, μ0, has values between 0.1 and 1 (Amundson and Burton, 2018), and the linearization parameters are given by b0=1.17 and b1=1.11.
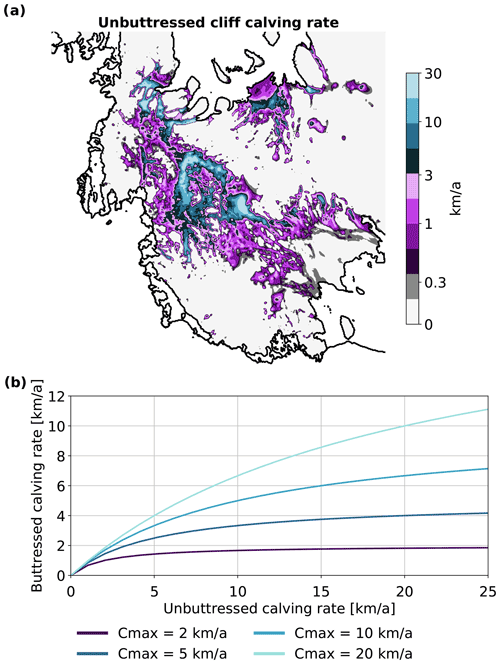
Figure 1(a) Potential unbuttressed cliff-calving rates in the WAIS. For this estimate we assume the ice cliff to be at flotation thickness, making the calving rate a function of bed topography. In the case of very fast grounding-line retreat, the ice cliff may not have thinned to flotation and calving rates may be larger. (b) The mélange-buttressed calving rates as a function of the unbuttressed calving rates for the values of Cmax considered in this study.
2.1.2 Uncertainties in the model parameters
The scaling parameter in the cliff-calving parameterization, C0, is poorly constrained because it depends on the time scale of shear failure and there are no experimental or observational studies on this for ice (Schlemm and Levermann, 2019). However, in the mélange-buttressed case, Cmax plays a much larger role in determining the overall calving rate, so the uncertainty of C0 is not a major concern (Schlemm and Levermann, 2021).
In the mélange-buttressing parameterization, we chose μ0=0.3 and γ=0.2 as in Schlemm and Levermann (2021). Cmax depends linearly on the embayment exit velocity uex (see Eq. 1). Therefore, constraining its range is important for estimating Cmax: maximum mélange flow speeds observed in front of Greenland glaciers are 30–50 m d−1 ≈ 10–18 km a−1 (Amundson and Burton, 2018). The velocities of icebergs drifting in the Weddel Sea in Antarctica are within the range 9–15 km d−1 ≈ 3000–5500 km a−1 (Schodlok et al., 2006). We assume that the mélange exit velocity lies within the range covered by these observations. The value of Cmax then depends solely on the embayment geometry (Fig. 2).
2.1.3 Mélange buttressing depends on embayment geometry
In order to estimate Cmax for a given grounding-line configuration, we assume that the entire embayment is filled with mélange. Note that the calving rate would be larger if the embayment were initially free of mélange. However, as the mélange parameterization cannot evolve the mélange margin, we must assume its position. The evolution of the mélange thickness can be modelled, though: when the entire embayment is filled with a very thin, spread-out mélange, the calving rate is high and many icebergs are produced. As a result, the mélange thickness grows rapidly and reaches its equilibrium thickness within a few years (Schlemm and Levermann, 2021). Therefore, it can be assumed that within a few years after the onset of calving, the entire embayment is filled with mélange.
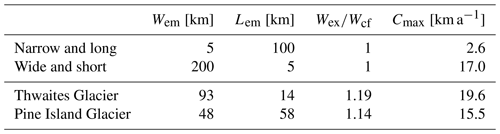
We estimate the width of the mélange exit, Wex, and the length of the calving front, Wcf, by measuring the embayment manually. The average mélange width, Wem, is calculated as the average of Wex and Wcf. The mélange length, Lem, is calculated as the average distance between the embayment exit and the calving front (the resulting trapezoids are shown in Fig. 11b). Table 1 shows estimates of Cmax for Thwaites and Pine Island Glaciers as well as for two extreme cases of mélange geometry: a narrow and long mélange strongly buttresses the calving front, resulting in a small Cmax, while a wide and short mélange provides little buttressing at the calving front, resulting in a large Cmax.
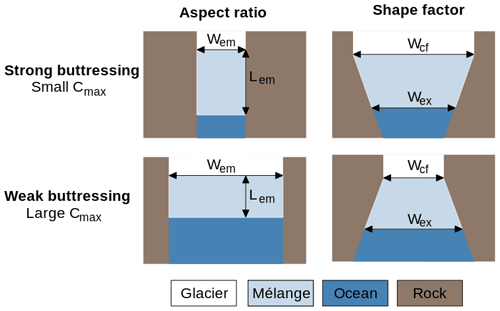
Figure 2Illustration of how embayment geometry determines buttressing strength in Eq. (1): aspect ratio and shape factor determine the strength of mélange buttressing.
Table 1Upper bounds on calving rates given by Eq. (1) with μ0=0.3, γ=0.2 and uex=100 km a−1. We first consider two extremes of a narrow and long as well as a wide and short buttressing mélange, while assuming a rectangular mélange geometry with constant mélange width, . For Thwaites and Pine Island Glaciers, we assume mélange geometry similar to the current ice shelf. The smaller the upper bound Cmax, the stronger the buttressing effect caused by the ice mélange.
2.2 PISM
2.2.1 Model description
We carry out regional simulations of the WAIS with PISM (Bueler and Brown, 2009; Winkelmann et al., 2011) at a horizontal resolution of 4 km and a minimum vertical resolution of 7 m. At this resolution, the reversibility of the grounding line is similar to that of higher-order models (Feldmann et al., 2014). The model setup is similar to the one used and described in Feldmann et al. (2019).
PISM is a thermomechanically coupled model based on the Glen–-Paterson–-Budd–-Lliboutry–-Duval flow law (Aschwanden et al., 2012). It uses a superposition of the shallow ice approximation (Hutter, 1983) and the shallow shelf approximation (Morland, 1987; MacAyeal, 1989), allowing for a smooth transition between different ice-sheet flow regimes. Basal friction is calculated using a non-linear Weertman-type sliding law with a sliding exponent of combined with a Mohr-Coulomb model for plastic till (Bueler and van Pelt, 2015) that accounts for the effect of evolving ice thickness and the associated change in overburden pressure on the basal till. The till friction angle is parameterized with bed elevation (see Martin et al., 2011, Eqs. 8–12). This friction scheme ensures a continuous transition from quasi–non-slip regimes in elevated regions to the marine areas where basal resistance is low. The grounding-line position is free to evolve using hydrostatic equilibrium. Grounding-line movement has been evaluated in the model intercomparison projects MISMIP3d (Pattyn et al., 2013; Feldmann et al., 2014) and MISMIP+ (Cornford et al., 2020). Basal friction at the grounding line is interpolated according to a sub-grid, linear interpolation of the grounding-line position (Feldmann et al., 2014).
2.2.2 Breakup of ice shelves
In our simulations, we assume that in the near future the ice shelves in the Amundsen region will break apart and will not be able to regenerate. This is a very strong assumption and is implemented in PISM with what we call a ”floatkill” mechanism, which removes all floating ice in the Amundsen region at each time step. The ice front, which is now identical to the grounding line, is free to evolve. For the remaining ice shelves, mainly the Ross and Ronne–Filchner ice shelves, but also small ice shelves along the Antarctic Peninsula, the so-called eigencalving parameterization is applied (Levermann et al., 2012).
2.2.3 Mélange-buttressed cliff calving
Mélange-buttressed cliff calving is applied to ice cliffs, i.e. grounded ice sheet at the coast. Similar to the floatkill parameterization, it is not applied to the entire model domain, but only to the coast of the Amundsen region and the interior of the WAIS. The shaded region in Fig. 5 shows the region where the floatkill parameterization and mélange-buttressed cliff calving are not applied. This implementation prevents MISI and MICI from starting in other regions of the AIS, such as the Antarctic Peninsula.
2.3 MISI and MICI in the WAIS with PISM
2.3.1 Boundary conditions
Basal melt rates under ice shelves are calculated using the Potsdam Ice-shelf Cavity mOdel (PICO) (Reese et al., 2018a), where ocean conditions are determined by mean values over the observational period 1975–2012 (Schmidtko et al., 2014). The surface mass balance and ice surface temperature are averaged from RACMO2.3p2 1986–2005 (van Wessem et al., 2018). The model domain includes the West Antarctic Ice Sheet, the Antarctic Peninsula and parts of the East Antarctic Ice Sheet, in particular, the drainage basins towards the Ross and Ronne–Filchner ice shelves (Zwally et al., 2012). The bed topography and initial ice configuration were taken from Bedmap2 (Fretwell et al., 2013). For more details see Feldmann et al. (2019), where the same setup was used.
2.3.2 Initialization and experiments
The ice sheet was spun up into thermal equilibrium with fixed bed and ice geometry for 100 000 model years (Feldmann et al., 2019). A further 10-year run with evolving ice geometry was performed to remove short-lived floating regions in the WAIS (such as in the middle of Smith Glacier, west of Thwaites Glacier). Five types of experiments were carried out:
- REF:
a reference simulation with the current-day atmosphere and ocean conditions held constant (see Sect. 2.3.1)
- BMT:
the “basal melt experiment” is a melt experiment with current-day atmospheric conditions and the melt rate in the Amundsen Basin set to 200 m a−1. This assumed basal melt rate is higher than the current and projected average melt rates of the Amundsen region ice shelves (Naughten et al., 2018). However, close to the grounding line of Thwaites Glacier, basal melt rates of up to 200 m a−1 were found (Milillo et al., 2019). In the melt experiment, this rate was applied to the whole of the ice shelves in the Amundsen region. The ice front is free to evolve.
- FLK:
the floatkill-parameterization experiment with current- day atmospheric and ocean conditions, in which all floating ice in the Amundsen Basin and the interior of the WAIS was removed. The grounding line is now the ice front and is free to evolve.
- CC#:
four cliff-calving experiments, which were performed in the same way as the floatkill-parameterization experiment, with the addition of exposing grounded glacier margins to cliff calving with different upper limits. The upper bound range is km a−1 (CC2, CC5, CC10, CC20).
- CCA#:
five adaptive cliff-calving experiments, where the upper bound Cmax was updated every 5 model years for the new embayment geometry. The mélange exit velocity range is km a−1 (CCA10, CCA50, CCA100, CCA200, CCA1000).
Each experiment was run for 100 a. Some experiments (FLK, CC2, CC5, CC10, CCA10, CCA50, CCA100, CCA200) were extended until they reached a retreat comparable with the fastest cliff-calving experiment (CC20).
2.4 Seasonal mélange freezing with the stand-alone mélange model
Finally, we investigated whether mélange freezing can stop MICI after its onset. Mélange freezing and thereby stopping of calving has been observed in Greenland glaciers in the winter season (Medrzycka et al., 2016). In the summer season, the sea ice in the mélange breaks up, the mélange becomes mobile, and calving sets in again.
The mélange-buttressing parameterization can model melting of mélange as a loss of mélange volume and therefore mélange-buttressing strength. However it cannot explicitly model mélange freezing. We used the exit velocity as a tool to simulate mélange freezing: in the steady-state model of mélange buttressing (see Sect. 2.1), calving is completely suppressed if no mélange leaves the embayment exit (, according to Eq. 1). However, starting with a very thin mélange and solving the non-steady-state equations of the mélange-buttressing model as described in Schlemm and Levermann (2021), calving is allowed until the mélange thickness has reached its steady-state value.
We started from a very thin mélange (10 m) and modelled seasonality with a time-dependent mélange exit velocity of the form
with a winter minimum of uwinter=0, a summer maximum of usummer=2u0 and an average of u0.
The mélange geometry was assumed to be rectangular with W=30 km, L=60 km, the initial mélange thickness at the calving front was d0=10m and the unbuttressed calving rate was C0=5 km a−1.
3.1 MISI discharge caused by floatkill is similar to that caused by basal melt
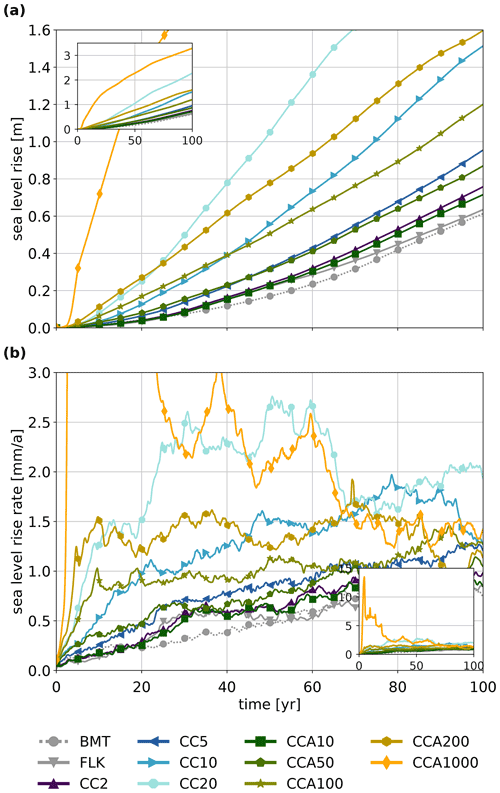
In our setup, the two MISI experiments (FLK and BMT) contribute about 0.6 m of sea-level rise within 100 a (see Fig. 3 and Table 2). This corresponds to the upper limit of the sea-level contribution from the Amundsen sector found in LARMIP-2 (Levermann et al., 2020), where a basal melt anomaly of up to 16 m a−1 was applied to currently observed melt rates. It is at the upper end of the 16 models that participated in LARMIP-2, but is not the highest.
The sea-level contributions resulting from the FLK and BMT experiments are very similar. This agrees with results from the ABUMIP intercomparison study (Sun et al., 2020), which showed that Antarctic-wide ice loss due to large basal melt rates is comparable with ice loss due to the floatkill parameterization.
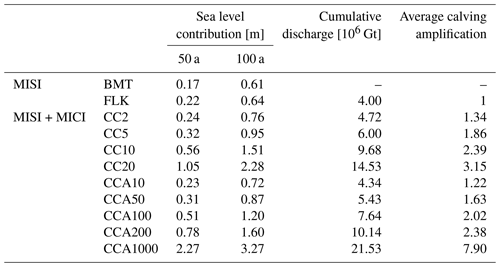
Table 2Sea- level contribution after 50 and 100 a is computed as the difference to the REF simulation. Cumulative calving discharge from the Amundsen region is given after 100 a. Average calving amplification is calculated as fraction between overall calving discharge (including cliff calving) and calving discharge only due to the floatkill parameterization.
3.2 MICI discharge is controlled by an upper bound on calving rates
When comparing the speed of the instabilities, we use two measures: the sea- level contribution and the calving discharge. In the experiments with cliff calving (CC# and CCA#), MISI and MICI occur simultaneously. Therefore, the sea-level contribution in these experiments is caused by both instabilities. Calving discharge is a better parameter to compare the contribution of MISI and MICI in each experiment because the discharge caused by the floatkill mechanism and the discharge caused by cliff calving are reported separately.
For the two lowest upper bounds on cliff calving (CC2 and CC5), MICI contributes a factor of up to 1.5 in addition to sea-level rise from the MISI experiments. For larger upper bounds, MICI can more than double (CC10) or even triple (CC20) the sea-level contribution compared with the MISI experiments (FLK, BMT). The sea-level contributions of the first four adaptive experiments (CCA10, CCA50, CCA100, CCA200) are similar to those of the first three cliff-calving experiments (CC2, CC5, CC10). The adaptive experiment with the largest exit velocity (CCA1000) has more than five times the sea-level contribution of the MISI experiments (FLK and BMT) (see Fig. 3 and Table 2).
Ice-retreat rates increase with time, with sea-level rates for the FLK and CC2 experiments reaching about 1 mm a−1 after 100 a, whereas the CC20 experiment reaches its maximum sea-level rate of 2.5 mm a−1 as early as after 50 a. The sea-level rate of the CC20 experiment decreases after 60 a of runtime because the grounding-line retreat along the Pine Island Glacier towards the Ronne Ice Shelf has reached the boundary of the inner WAIS region, beyond which cliff calving and the floatkill parameterization are not applied (see Fig. 5). In the adaptive experiments (CCA10, CCA50, CCA100, CCA200), the sea-level rise rate increases initially and then levels off. This corresponds to the reduction of the adaptive upper bound on calving rates (see Table 3 and Fig. 6). In the CCA1000 experiment, the sea-level rise rate initially goes up to 13 mm a−1 and decreases sharply after 20 a when the retreat along the Pine Island Glacier reaches the boundary of the inner WAIS region where cliff calving and floatkill parameterization are applied. The sea-level rate decreases again after 45 a when the retreat reaches bedrock above sea level and after 65 a when it reaches the boundary of the inner WAIS region close to the Siple coast (see Fig. 5).
Calving is the main cause of sea-level rise: for experiments CC2, CC5, CCA10 and CCA50 the cumulative calving discharge is only slightly larger than for the FLK experiments; for experiments CC10 and CCA100 as well as CC20 and CCA200 the calving discharge doubles and triples, respectively. The slowdown of the CC20 experiment after 60 a is also visible in the reduced calving discharge. Similar to the sea-level rise rate, the calving discharge of the adaptive experiments (CCA10, CCA50, CCA100, CCA200) increases initially and then levels off (see Fig. 4 and Table 2).
For each cliff-calving experiment (CC# and CCA#), PISM reports ice discharge due to the floatkill mechanism and due to cliff calving separately. We use this to calculate the calving amplification as the ratio between the total calving discharge and the discharge only due to floatkill (Table 2). It reveals a doubling or tripling in the calving discharge for the highest values of Cmax, similar to the increase in the sea-level contributions mentioned above.
The cliff-calving experiments with a small upper bound (CC2, CCA10) show only a modestly faster ice retreat than the floatkill experiment. This is because PISM uses a subgrid scheme for the ice margin, involving partially filled cells that are not affected by either the ice dynamics or the floatkill mechanism (Albrecht et al., 2011). Cliff calving with a small value of Cmax can prevent partially filled cells from filling up and thus reduce the ice loss due to the floatkill parameterization. This may result in a slightly lower overall calving discharge than floatkill with no cliff calving. Cliff calving with a large value of Cmax is much more likely to completely remove partially filled cells, so the floatkill parameterization mechanism is not hindered in this case. This issue depends on the resolution of the domain: previously unpublished sensitivity tests in a channel setup showed that for a resolution of x km, this problem occurs for calving rates smaller than x km a−1.
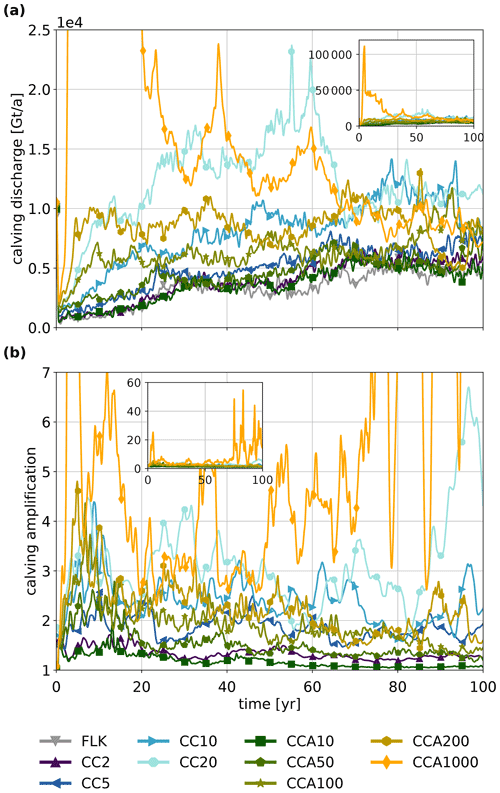
Figure 4(a) Overall calving discharge from the Amundsen region. PISM uses a subgrid scheme at the ice margin with partially filled cells (Albrecht et al., 2011). At each time step, calving removes some of the ice in such a cell, whereas floatkill removes whole cells if they float. This removed ice volume is summed up in the calving discharge variable. (b) The calving amplification calculated as the fraction between overall calving discharge and calving discharge due to the floatkill parameterization only. Note that no calving amplification has been calculated for the floatkill-only experiment because no cliff calving takes place. The calving amplification of the CC20 and the CCA1000 experiments increases toward the end of the simulation time because parts of the grounding line have reached the margin of the inner WAIS region, beyond which cliff calving and the floatkill mechanism are not applied.
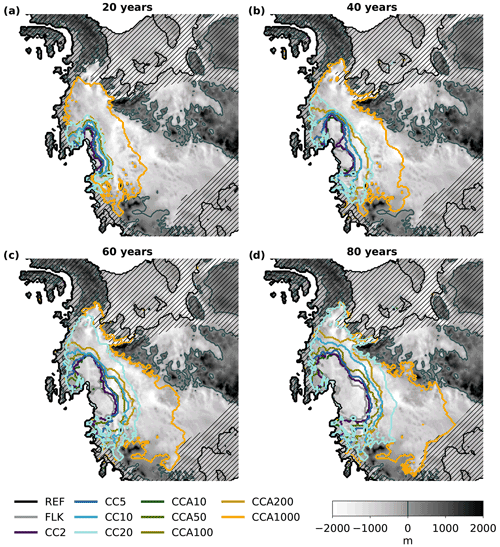
Figure 5Maps of grounding-line retreat in the WAIS, underlaid with the bed topography. In the shaded region, neither the floatkill parameterization nor cliff calving is applied (see Sect. 2.2.3). Grounding-line retreat of CCA1000, the fastest experiment, halts when it reaches bed topography above sea level (in which case cliff calving is no longer applied) or the margin of the interior Amundsen region domain (beyond which neither floatkill nor cliff calving is applied).
3.3 Mélange buttressing increases as MICI progresses, slowing MICI speed
In the adaptive cliff-calving experiments (CCA#), mélange-buttressing strength depends on the embayment geometry (see Eq. 1 and Fig. 2). Because the calving front becomes longer and its distance to the embayment exit increases, the upper bound on calving rate decreases with grounding-line retreat into the Amundsen Basin. The development of the upper bound with simulation time is given in Table 3. In Fig. 6, the upper bound is shown as a function of the sea-level contribution of the corresponding embayment geometry. Initially, Thwaites and Pine Island Glaciers have separate embayments with different values for Cmax. After some time, depending on the mélange exit velocity, the embayments merge, leading to one value of Cmax for the whole Amundsen Basin. As the grounding-line retreats deeper into the Amundsen Basin, Cmax decreases to about one third of its initial value. The relation between calving rate and sea-level contribution can be fitted with:
with the average of the initial upper bounds for Thwaites and Pine Island Glaciers.
As MICI progresses and the grounding-line retreats, the area covered by ice mélange grows, which increases the strength of mélange buttressing. This in turn lowers the upper limit on calving rates and slows further progression of MICI. Thus, as a consequence of mélange buttressing, MICI cannot be arbitrarily fast and even decelerates as it progresses.
Table 3Upper bound on calving rates for the adaptive cliff-calving experiments (CCA#) in km a−1. Where two values are given, the first is for Thwaites Glacier and the second for Pine Island Glacier. Where only one value is given, both glaciers share one embayment.
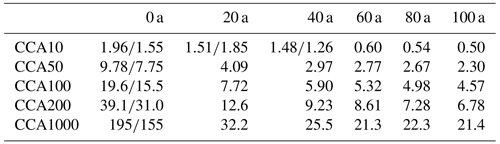
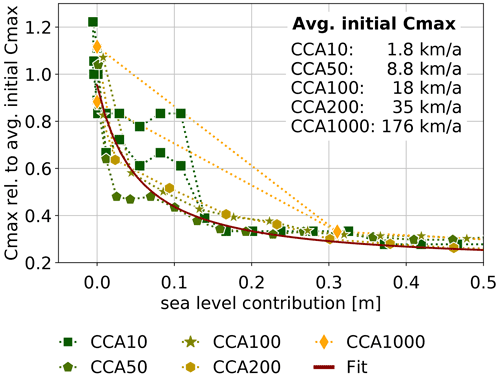
Figure 6The upper bound on calving rates, Cmax of the adaptive cliff-calving experiments (CCA#) as a function of the sea-level contribution of the corresponding embayment geometry. Initially, Thwaites and Pine Island Glaciers have separate embayments, which merge after several model years. The upper bound decreases with sea-level contribution and with the corresponding simulation time (see Table 3).
3.4 Bed topography controls the rate of grounding-line retreat
The grounding-line retreat initially follows the main flow directions of Pine Island and Thwaites Glaciers, but after some time (depending on Cmax) it involves the entire interior of the WAIS (see Fig. 5). The retreat reaches the Ronne Basin earlier than the Ross Basin. The CC20 experiment reaches the Ronne Ice Shelf after 70 a of runtime, where the retreat ends as no further floatkill parameterization and cliff calving are allowed there. The retreat towards the Ross Ice Shelf continues. The experiments with smaller Cmax as well as the FLK experiment take longer to reach the Ronne Ice Shelf, with the FLK experiment being the slowest, arriving there after 150 a (not shown here).
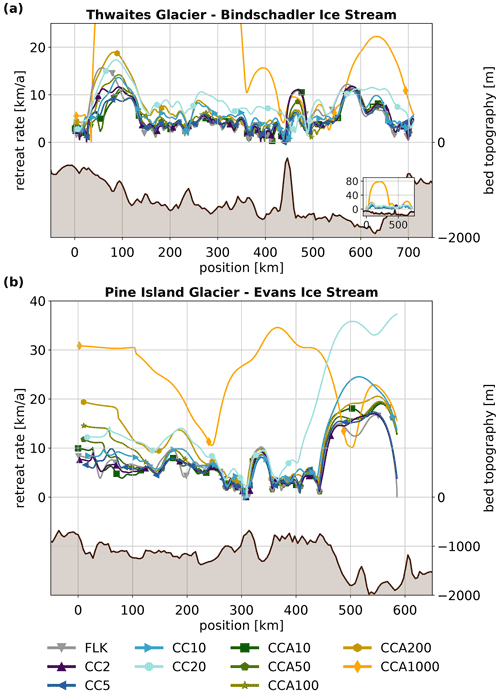
We examine the retreat along two flowlines, leading from Thwaites Glacier across to the Ross Ice Shelf and from Pine Island Glacier across to the Ronne Ice Shelf, respectively (see Fig. 7). These are the same 2-dimensional experiments discussed in the rest of the paper, except that they are analysed along the trajectory of the flowlines. As the ice divides are free to move, it may be that their lateral movement changes the actual flowline, i.e. the main direction of the ice flow. This has not been taken into account.
Both glaciers have retrograde beds, with Thwaites Glacier having a steeper slope than Pine Island Glacier. After the flowlines cross the initial ice divide, the bed topography changes: the retreating grounding line of Thwaites Glacier meets the Bindschadler Ice Stream, which has a rather shallow and slightly prograde bed topography (in the direction of grounding-line retreat). In contrast, the retreating grounding line of Pine Island Glacier reaches the Evans Ice Stream, which has a deep bed depression. Figure 8 shows the retreat of the grounding line and ice divide along these flowlines over time. For Thwaites Glacier, all experiments show some inertia to the retreat initially, which is followed by rapid retreat along the first 150 km of the flowline. Retreat then levels off, with experiments with larger Cmax showing faster retreat. Pine Island Glacier shows steady initial retreat over the first 300 km, after which the retreat stalls for 25 to 50 a, depending on the experiment. This is followed by a rapid retreat that is stopped only when the grounding line reaches the Ronne Ice Shelf, where no further retreat is possible. As the grounding-line retreats, so does the ice divide, but with a considerable delay.
An explanation for this retreat pattern can be found by a more detailed analysis that compares the grounding-line retreat rates with the slope of the bed topography (see Fig. 9). Grounding-line retreat along Thwaites flow line is rapid at first, with retreat rates up to 18 km a−1 (depending on Cmax) along a steep retrograde bed, and slows down once the grounding line reaches a more even bed topography segment beginning at 150 km. In this segment, retreat rates fluctuate below 10 km a−1. Ridges in the bed topography at 220 and 430 km cause stagnation of grounding-line retreat on the upslope, followed by acceleration on the downslope. A steady retrograde slope between 500 and 630 km causes grounding-line retreat rates to increase up to 10 km a−1. The steep prograde slope between 630 and 700 km causes the retreat to slow down significantly.
The retreat along the Pine Island flow line has a steady rate between 5 and 15 km a−1 for the first 300 km until the grounding line approaches a bathymetric ridge, where the retreat slows temporarily. A short 20-km-long depression following this ridge causes an acceleration of up to 10 km a−1, followed by a slowdown as the bed rises again. Grounding-line retreat accelerates sharply up to values between 15 and 33 km a−1 once it reaches a steep bed depression beneath the Evans Ice Stream, which begins at 450 km.
The CCA1000 experiment has much larger calving rates than the other experiments (see Table 3) and therefore also much larger retreat rates. Its retreat depends more on the mélange buttressing than the bed topography.
We expect bed topography to control grounding-line retreat for two reasons: analytical calculations in a depth-averaged flowline model show that the flux across the grounding-line scales superlinearly with ice thickness (Schoof, 2007). The cliff-calving rate also scales superlinearly with ice thickness (Schlemm and Levermann, 2019). Assuming that the glacier terminus is at flotation, this means that there should also be a relationship between the grounding-line retreat rate and the bed depth.
However, a correlation analysis using the Spearman correlation coefficient of determination between the grounding-line retreat rate and bed topography shows only a minimal correlation for Pine Island Glacier and no correlation at all for Thwaites Glacier (see Table 4). There are two main reasons for this: first, we analyse flow along a 1-dimensional flowline embedded in a more complex 2-dimensional flow. The retreat of the grounding line in neighbouring flowlines, where the bed topography can be different, may drag on the grounding line and either accelerate or decelerate it, in comparison to the result of the 1-dimensional analysis. In addition, the analysed flowlines may not lie exactly along the flow direction, especially in the vicinity of bed-topography disturbances that are only a few grid cells in size. Second, ice flow has inertia, which means that the grounding line takes some time to accelerate when it reaches a steep retrograde bed. Inertia can also drive it over bumps in the bed that would be expected to slow it down, especially in the case of large Cmax.
In summary, we find no clear statistical correlation between the bed topography and the grounding-line retreat rate. Nevertheless, we observe an acceleration of the grounding line when the bed is retrograde and a deceleration when it is prograde. In addition, bathymetric ridges temporarily halt grounding-line retreat. So we can conclude that bed topography is a major control of the rate of grounding-line retreat.
Table 4Spearman correlation coefficients of determination between bed depth and grounding-line retreat rate.
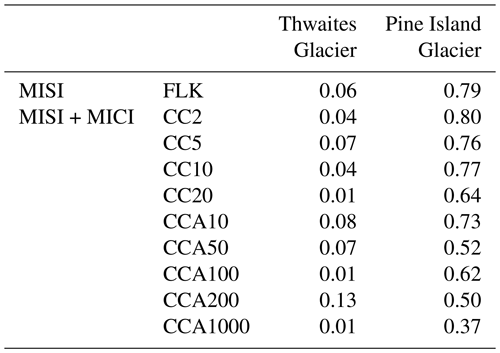
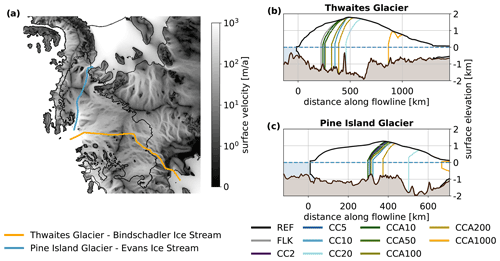
Figure 7(a) Map of flowlines from Pine Island Glacier through Evans ice stream to the Ronne Ice Shelf and from Thwaites Glacier through the Bindschadler Ice Stream to the Ross Ice Shelf. (b, c) Bed topography and ice surface profiles after 60 a runtime for Thwaites Glacier and Pine Island Glacier respectively. The distance along the flowline has its zero at the initial grounding-line position. Note that for Pine Island Glacier, the reference run also shows some grounding-line retreat.
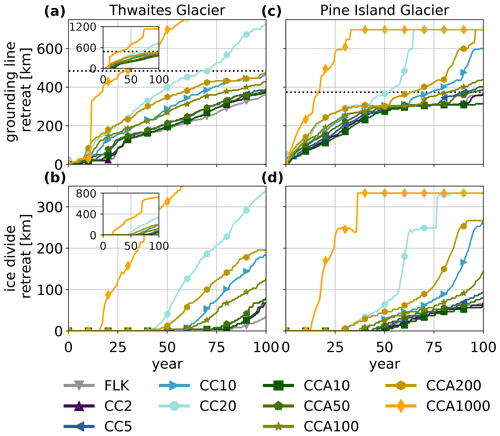
Figure 8Grounding-line retreat (a, c) and ice-divide retreat (b, d) along the flowlines in Thwaites (a, b) and Pine Island Glaciers (c, d) as a function of simulated time. The dotted line shows the initial ice-divide position.
3.5 Winter freezing of mélange is not sufficient to stop MICI
Assuming that no mélange exits the embayment, mélange buildup can prevent calving almost completely within 10 a (see Fig. 10a, grey lines). Also, assuming a seasonal exit velocity leads to seasonal variations in the strength of mélange buttressing (see Fig. 10, orange and blue lines): after an initial equilibration period, mélange volume and backstress decrease in the summer and the calving rate increases, whereas in the winter mélange volume and backstress increase and the calving rate decreases. The minimum and maximum mélange properties fluctuate around the equilibrium value calculated by using the averaged exit velocity u0. Contrary to observations, in this simplified mélange parameterization, winter freezing of mélange is not sufficient to stop calving. The reason is that the equilibration of the mélange is too slow and takes several years rather than months or weeks.
Studies explicitly analysing the influence of the mélange backpressure on the stress balance of the glacier terminus focus on the force per unit width exerted by the mélange at the calving front (Amundson et al., 2010; Todd and Christoffersen, 2014; Crawford et al., 2021). Therefore, the force per unit width was calculated as a diagnostic variable. A mélange backpressure of 6.66×106 N m−1 is sufficient to prevent cliff calving of an ice cliff with H=1000 m (Crawford et al., 2021). In our solution of the non-steady-state equation, a similar force per unit width was found when calving is suppressed (see Fig. 10c, grey lines after >5 a).
In conclusion, assuming that no mélange is lost by drifting off at the mélange exit, a very thick and strong mélange is built up within a period of several years, which completely prevents further calving and would thus stop the progression of MICI. However, this is only likely to happen in the winter season and would therefore halt MICI only temporarily.
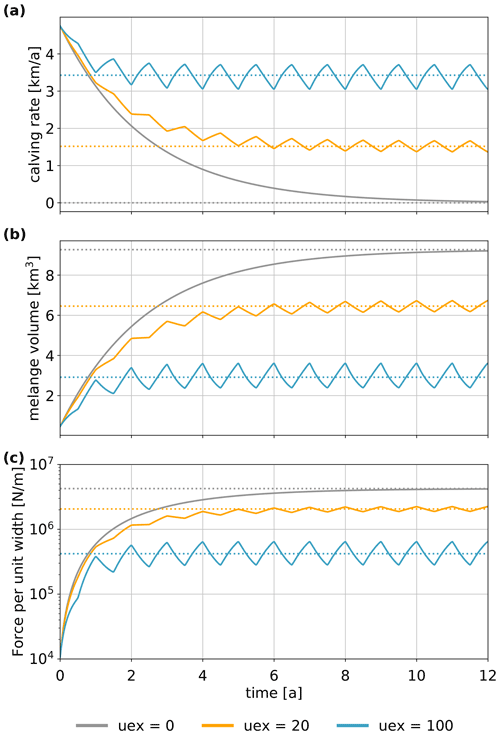
Figure 10Evolution of the buttressed calving rate (a), the mélange volume (b), and the force per unit width at the calving front (c) in the case of no mélange exiting the embayment (uex=0, grey lines) and for a seasonal variation in mélange exit velocity (orange and blue lines). The dotted lines show the corresponding equilibrium solution. For an equilibrated ice mélange, if no mélange exits the embayment (uex=0), calving is completely suppressed (Cmax=0). However, in the time-dependent case and starting with a thin initial mélange, calving is possible for some years. Seasonal variations in the exit velocity lead to seasonal variations of the mélange-buttressing strength.
In this section we discuss our results in the light of mechanisms and conditions that may be important in limiting the speed of MICI evolution, including the influence of mélange properties, climatic variations, and the ice or bed geometry.
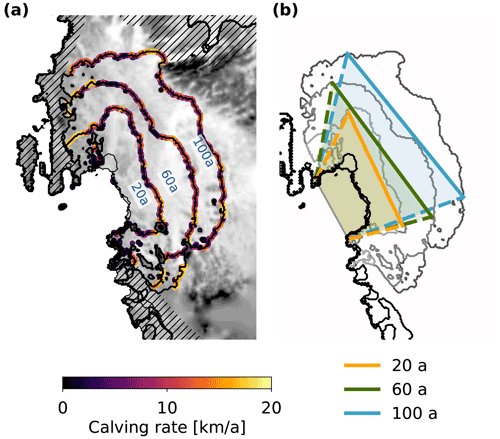
Figure 11(a) Different grounding-line configurations of the adaptive cliff-calving experiment CCA100 with unbuttressed calving rates. (b) Idealized embayment geometry derived from the grounding lines.
4.1 Limitations of the idealized mélange-buttressing parameterization
Owing to its reliance on an idealized geometry, the mélange parameterization has several limitations when applied to realistic embayment geometries (see Fig. 11a and b):
-
The conversion of the realistic geometry into the idealized geometry is not unique: it is difficult to specify exactly where each parameter of the idealized geometry should be measured.
-
The mélange parameterization assumes a constant calving rate along the entire length of the calving front. This may be valid when considering a single glacier, but is no longer the case when several glaciers calve into the same embayment.
-
On the west side of the Amundsen embayment, ice resting on bedrock above sea-level forms pinning points that provide additional support to the ice mélange. This effect is neglected in the parameterization.
-
The mélange margin cannot be inferred from the model and must therefore be provided as an external parameter.
-
Mélange freezing cannot be modelled explicitly and has been modelled using the mélange exit velocity. This allows mélange buildup, but its effect takes too long to transmit to the calving front (several years).
To get a better understanding of how mélange buttressing impacts calving rates in a realistic setup, it would be beneficial to use a spatially resolved mélange model. It should be able to handle realistic embayment geometries, including pinning points, as well as spatially resolved calving rates, and have a criterion for where mélange stops being mélange, which would enable it to model the mélange margin (see for example Pollard et al., 2018). However, such a model introduces additional mélange parameters, which are difficult to constrain.
4.2 The role of ice shelves for MICI
Understanding the processes by which ice shelves fracture rapidly and disintegrate is still ongoing work (Yu et al., 2017; Robel and Banwell, 2019; Lhermitte et al., 2020) and difficult to implement in an ice-sheet model.
One way of removing ice shelves is by highly elevated basal melting. In PISM, this approach leaves small ice-shelf remnants that are only a few grid cells in size. The resulting buttressing loss induces MISI. However, because we assume that cliff calving only occurs at exposed, grounded ice cliffs, the ice-shelf remnants prevent the onset of MICI. This is in contrast to the implementation in Pollard et al. (2015): they assumed that a small ice-shelf remnant with vanishing buttressing strength does not prevent cliff calving, basing their reasoning on the Schoof flux across the grounding line (Schoof, 2007) and depth-averaged stresses in the vicinity of the ice cliff (Bassis and Walker, 2011). However, the Schoof flux may not be applicable beyond a flowline setup (Reese et al., 2018b). Additionally, a small ice shelf may impact the stress balance at the ice cliff in a 3d setup. Therefore, we assume that cliff calving only occurs at exposed grounded ice cliffs.
In our model setup, we remove all floating ice in the Amundsen Basin and inner WAIS. This floatkill parameterization mechanism eliminates all existing ice shelves at once in the first-time step and prevents re-growth of ice shelves during the retreat. The removal of ice shelves initiates both MISI and MICI.
Two questions of vital importance for the onset and progress of MICI need further research:
-
Under which conditions do ice shelves collapse completely? As ice-shelf collapse is the prerequisite for the onset of MICI, the answer to this question determines when and if at all MICI will play a role in the future of the Antarctic Ice Sheet. There has been a lot of observational and theoretical work on hydrofracturing (MacAyeal et al., 2003; Robel and Banwell, 2019) as well as rifting and crevassing (Borstad et al., 2012; Jeong et al., 2016; Lhermitte et al., 2020), but so far it is impossible to predict under which environmental and internal conditions a specific ice shelf will collapse.
-
Can ice shelves regrow after MICI has set in? If ice shelves can regrow after cliff calving has begun, this could stop MICI after its onset by buttressing the ice cliffs and preventing further cliff calving. However, if ice shelves cannot regrow, then MICI will continue mostly unhindered, because mélange buttressing can only slow the progress of MICI, but not stop it. Viscous deformation could prevent the formation of unstable ice cliffs (Clerc et al., 2019; Bassis et al., 2021) and allow ice shelves to regrow, whereas a mixed-mode behaviour of viscous deformation and fracture (Crawford et al., 2021) would make ice-shelf regrowth unlikely.
4.3 Influence of regional climatic conditions on the progress of MICI
So far there are few observations of cliff-calving glaciers. The retreat of Sermeq Kujalleq, also known as Jakobshavn Glacier (Bjørk et al., 2015), in Greenland since 1998 (Joughin et al., 2008) was regarded as an indication that Sermeq Kujalleq may be at the beginning of a cliff-calving regime (Bassis and Walker, 2011; DeConto and Pollard, 2016; Schlemm and Levermann, 2019). However, since 2016, Sermeq Kujalleq has re-advanced as a result of regional ocean cooling (Khazendar et al., 2019). The cooling of the Fjord water has led to a decrease in frontal melt (Khazendar et al., 2019) as well as increased mélange buttressing at the glacier terminus (Joughin et al., 2020), thereby stopping its retreat. This suggests that changes in regional climatic conditions may slow or prevent grounding-line retreat caused by cliff calving.
4.4 Slowdown of MICI at bathymetric ridges
During the last deglaciation, MICI was probably active for approximately 1000 a in the Amundsen region of the WAIS and then stopped, when the grounding line re-stabilized on a prominent bathymetric ridge (Wise et al., 2017). This is an indication that MICI can be stopped after its onset by features of the bed topography. However, our simulations show only temporary halts in grounding-line retreat at bathymetric ridges in the interior of the WAIS (see Fig. 9).
We performed PISM simulations of the WAIS to investigate the potential speeds of the two marine instabilities, MISI and MICI. We choose the Amundsen region as the starting point of the instabilities because observations show that MISI is possibly already in progress there. Owing to ocean warming and increased crevassing, glaciers in the Amundsen region may lose their ice shelves in the future, which would set MICI in motion. We applied a floatkill parameterization to remove the ice shelves in the Amundsen region, a cliff-calving parameterization depending on ice thickness, and a mélange-buttressing parameterization, which limits calving rates.
We found that MISI, whether forced by the floatkill parameterization or by high subshelf melt rates, has the potential to contribute 0.6 m of sea- level rise within 100 a. The sea-level potential of MICI depends on the upper limit of calving: if the cliff-calving rate is limited below 2 km a−1 or 5 km a−1, MICI has a smaller contribution to sea-level rise than MISI. If the upper limit is 10 km a−1 or 20 km a−1, MICI doubles or even triples the sea-level contribution of MISI.
We also showed that grounding-line retreat is regulated by bed topography for both MISI and MICI. Although there is no clear statistical correlation between the retreat rate and the bed depth, we observe an accelerated retreat of the grounding line on retrograde beds and a slowdown on prograde beds.
Finally, we investigated how the upper limit for calving from mélange buttressing depends on the embayment geometry and the mélange exit velocity. Seasonal effects cause mélange build-up, which slows the progress of MICI temporarily under winter conditions. We also showed that as MICI progresses and the grounding-line retreats, the calving front becomes longer whereas the width of the embayment exit remains the same. This leads to an increase in mélange buttressing, a decrease in the upper bound on calving rates, and consequently a slowdown in the progress of MICI. It is unlikely that mélange alone can completely stop MICI, but it could provide enough buttressing to enable ice-shelf regrowth, which would then stop further MICI progress.
Future research is needed to gain a better understanding of the conditions under which MICI kicks off and to further constrain its potential sea-level contribution.
The applied mélange parameterization assumes an idealized geometry and is therefore of limited applicability when extended to realistic embayment geometries. A spatially resolved mélange model might be a better choice. However, such a model would require more parameters describing mélange properties, which are difficult to constrain.
Two important unresolved questions about ice-shelf collapse are beyond the scope of this study. First, under which conditions do ice shelves collapse? This determines the onset of MICI and is therefore crucially important in constraining at what degree of warming MICI becomes a concern. Second, can ice shelves regrow after MICI has started? This seems to be the only way to stop MICI. These two important questions control if and when MICI sets in and if it can be not only slowed down but stopped completely after its onset.
The PISM code used for these simulations is available at https://doi.org/10.5281/zenodo.6325006 (Schlemm and PISM authors, 2022). The model output data and Python scripts for running the experiments and generating the figures shown in the paper are stored in a band archive at the Potsdam Institute for Climate Impact Research and indexed in a metadata archive; they are available upon request.
TS and AL designed the study with input from RW. JF created the regional setup of the WAIS and performed the spinup. TS performed the simulations, analysed the model results, and wrote the paper. All authors commented on the paper.
The contact author has declared that neither they nor their co-authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This paper is supported by the European Union's Horizon 2020 research and innovation programme under grant agreement no. 869304 (PROTECT). This paper is supported by the European Union's Horizon 2020 research and innovation programme under grant agreement no. 820575 (TiPACCs). Johannes Feldmann and Ricarda Winkelmann acknowledge support by the Deutsche Forschungsgemeinschaft (DFG) through grants WI4556/4-1 and WI4556/6-1. RW is grateful for support by the European Union's Horizon 2020 research and innovation programme under grant agreements no. 820575 (TiPACCs) and no. 869304 (PROTECT), and by the PalMod project (FKZ: 01LP1925D), supported by the German Federal Ministry of Education and Research (BMBF) as a Research for Sustainability initiative (FONA). Tanja Schlemm acknowledges support by the Heinrich Böll Stiftung.
This research has been supported by the Heinrich Böll Stiftung.
The publication of this article was funded by the Open Access Fund of the Leibniz Association.
This paper was edited by Ginny Catania and reviewed by Lizz Ultee and two anonymous referees.
Albrecht, T., Martin, M., Haseloff, M., Winkelmann, R., and Levermann, A.: Parameterization for subgrid-scale motion of ice-shelf calving fronts, The Cryosphere, 5, 35–44, https://doi.org/10.5194/tc-5-35-2011, 2011. a, b
Amundson, J. M. and Burton, J. C.: Quasi-Static Granular Flow of Ice Mélange, J. Geophys. Res.-Earth, 123, 2243–2257, https://doi.org/10.1029/2018JF004685, 2018. a, b
Amundson, J. M., Fahnestock, M., Truffer, M., Brown, J., Lüthi, M. P., and Motyka, R. J.: Ice mélange dynamics and implications for terminus stability, Jakobshavn Isbræ, Greenland, J. Geophys. Res.-Earth, 115, F01005, https://doi.org/10.1029/2009JF001405, 2010. a
Aschwanden, A., Bueler, E., Khroulev, C., and Blatter, H.: An enthalpy formulation for glaciers and ice sheets, J. Glaciol., 58, 441–457, https://doi.org/10.3189/2012JoG11J088, 2012. a
Bassis, J. N. and Walker, C. C.: Upper and lower limits on the stability of calving glaciers from the yield strength envelope of ice, P. Roy. Soc. Lond. A, 468, 913–931, https://doi.org/10.1098/rspa.2011.0422, 2011. a, b, c
Bassis, J. N., Berg, B., Crawford, A. J., and Benn, D. I.: Transition to marine ice cliff instability controlled by ice thickness gradients and velocity, Science, 372, 1342–1344, https://doi.org/10.1126/science.abf6271, 2021. a, b
Bell, R. E. and Seroussi, H.: History, mass loss, structure, and dynamic behavior of the Antarctic Ice Sheet, Science, 367, 1321–1325, https://doi.org/10.1126/science.aaz5489, 2020. a
Berthier, E., Scambos, T. A., and Shuman, C. A.: Mass loss of Larsen B tributary glaciers (Antarctic Peninsula) unabated since 2002, Geophys. Res. Lett., 39, L13501, https://doi.org/10.1029/2012GL051755, 2012. a
Bjørk, A. A., Kruse, L. M., and Michaelsen, P. B.: Brief communication: Getting Greenland's glaciers right – a new data set of all official Greenlandic glacier names, The Cryosphere, 9, 2215–2218, https://doi.org/10.5194/tc-9-2215-2015, 2015. a
Borstad, C. P., Khazendar, A., Larour, E., Morlighem, M., Rignot, E., Schodlok, M. P., and Seroussi, H.: A damage mechanics assessment of the Larsen B ice shelf prior to collapse: Toward a physically-based calving law, Geophys. Res. Lett., 39, l18502, https://doi.org/10.1029/2012GL053317, 2012. a
Bueler, E. and Brown, J.: Shallow shelf approximation as a “sliding law” in a thermomechanically coupled ice sheet model, J. Geophys. Res.-Earth, 114, F03008, https://doi.org/10.1029/2008JF001179, 2009. a
Bueler, E. and van Pelt, W.: Mass-conserving subglacial hydrology in the Parallel Ice Sheet Model version 0.6, Geosci. Model Dev., 8, 1613–1635, https://doi.org/10.5194/gmd-8-1613-2015, 2015. a
Church, J. A., Clark, P. U., Cazenave, A., Gregory, J. M., Jevrejeva, S., Levermann, A., Merrifield, M. A., Milne, G. A., Nerem, R. S., Nunn, P. D., Payne, A. J., Pfeffer, W. T., Stammer, D., and Unnikrishnan, A. S.: Sea-Level Rise by 2100, Science, 342, 1445–1445, https://doi.org/10.1126/science.342.6165.1445-a, 2013. a
Clerc, F., Minchew, B. M., and Behn, M. D.: Marine Ice Cliff Instability Mitigated by Slow Removal of Ice Shelves, Geophys. Res. Lett., 46, 12108–12116, https://doi.org/10.1029/2019GL084183, 2019. a
Cornford, S. L., Seroussi, H., Asay-Davis, X. S., Gudmundsson, G. H., Arthern, R., Borstad, C., Christmann, J., Dias dos Santos, T., Feldmann, J., Goldberg, D., Hoffman, M. J., Humbert, A., Kleiner, T., Leguy, G., Lipscomb, W. H., Merino, N., Durand, G., Morlighem, M., Pollard, D., Rückamp, M., Williams, C. R., and Yu, H.: Results of the third Marine Ice Sheet Model Intercomparison Project (MISMIP+), The Cryosphere, 14, 2283–2301, https://doi.org/10.5194/tc-14-2283-2020, 2020. a
Crawford, A. J., Benn, D. I., Todd, J., Åström, J. A., Bassis, J. N., and Zwinger, T.: Marine ice-cliff instability modeling shows mixed-mode ice-cliff failure and yields calving rate parameterization, Nat. Commun., 12, 2701, https://doi.org/10.1038/s41467-021-23070-7, 2021. a, b, c, d
DeConto, R. M. and Pollard, D.: Contribution of Antarctica to past and future sea-level rise, Nature, 531, 591–597, https://doi.org/10.1038/nature17145, 2016. a, b, c, d, e, f
Edwards, T. L., Brandon, M. A., Durand, G., Edwards, N. R., Golledge, N. R., Holden, P. B., Nias, I. J., Payne, A. J., Ritz, C., and Wernecke, A.: Revisiting Antarctic ice loss due to marine ice-cliff instability, Nature, 566, 58–64, https://doi.org/10.1038/s41586-019-0901-4, 2019. a
Edwards, T. L., Nowicki, S., Marzeion, B., Hock, R., Goelzer, H., Seroussi, H., Jourdain, N. C., Slater, D. A., Turner, F. E., Smith, C. J., McKenna, C. M., Simon, E., Abe-Ouchi, A., Gregory, J. M., Larour, E., Lipscomb, W. H., Payne, A. J., Shepherd, A., Agosta, C., Alexander, P., Albrecht, T., Anderson, B., Asay-Davis, X., Aschwanden, A., Barthel, A., Bliss, A., Calov, R., Chambers, C., Champollion, N., Choi, Y., Cullather, R., Cuzzone, J., Dumas, C., Felikson, D., Fettweis, X., Fujita, K., Galton-Fenzi, B. K., Gladstone, R., Golledge, N. R., Greve, R., Hattermann, T., Hoffman, M. J., Humbert, A., Huss, M., Huybrechts, P., Immerzeel, W., Kleiner, T., Kraaijenbrink, P., Le clec’h, S., Lee, V., Leguy, G. R., Little, C. M., Lowry, D. P., Malles, J.-H., Martin, D. F., Maussion, F., Morlighem, M., O’Neill, J. F., Nias, I., Pattyn, F., Pelle, T., Price, S. F., Quiquet, A., Radić, V., Reese, R., Rounce, D. R., Rückamp, M., Sakai, A., Shafer, C., Schlegel, N.-J., Shannon, S., Smith, R. S., Straneo, F., Sun, S., Tarasov, L., Trusel, L. D., Van Breedam, J., van de Wal, R., van den Broeke, M., Winkelmann, R., Zekollari, H., Zhao, C., Zhang, T., and Zwinger, T.: Projected land ice contributions to twenty-first-century sea level rise, Nature, 593, 74–82, https://doi.org/10.1038/s41586-021-03302-y, 2021. a
Enderlin, E. M., Howat, I. M., Jeong, S., Noh, M.-J., Angelen, J. H., and Broeke, M. R.: An improved mass budget for the Greenland ice sheet, Geophys. Res. Lett., 41, 866–872, https://doi.org/10.1002/2013GL059010, 2014. a
Favier, L., Durand, G., Cornford, S. L., Gudmundsson, G. H., Gagliardini, O., Gillet-Chaulet, F., Zwinger, T., Payne, A. J., and Le Brocq, A. M.: Retreat of Pine Island Glacier controlled by marine ice-sheet instability, Nat. Clim. Change, 4, 117–121, https://doi.org/10.1038/nclimate2094, 2014. a
Feldmann, J. and Levermann, A.: Collapse of the West Antarctic Ice Sheet after local destabilization of the Amundsen Basin, P. Natl. Acad. Sci. USA, 112, 14191–14196, https://doi.org/10.1073/pnas.1512482112, 2015. a
Feldmann, J., Albrecht, T., Khroulev, C., Pattyn, F., and Levermann, A.: Resolution-dependent performance of grounding line motion in a shallow model compared with a full-Stokes model according to the MISMIP3d intercomparison, J. Glaciol., 60, 353–360, https://doi.org/10.3189/2014JoG13J093, 2014. a, b, c
Feldmann, J., Levermann, A., and Mengel, M.: Stabilizing the West Antarctic Ice Sheet by surface mass deposition, Sci. Adv., 5, eaaw4132, https://doi.org/10.1126/sciadv.aaw4132, 2019. a, b, c
Fretwell, P., Pritchard, H. D., Vaughan, D. G., Bamber, J. L., Barrand, N. E., Bell, R., Bianchi, C., Bingham, R. G., Blankenship, D. D., Casassa, G., Catania, G., Callens, D., Conway, H., Cook, A. J., Corr, H. F. J., Damaske, D., Damm, V., Ferraccioli, F., Forsberg, R., Fujita, S., Gim, Y., Gogineni, P., Griggs, J. A., Hindmarsh, R. C. A., Holmlund, P., Holt, J. W., Jacobel, R. W., Jenkins, A., Jokat, W., Jordan, T., King, E. C., Kohler, J., Krabill, W., Riger-Kusk, M., Langley, K. A., Leitchenkov, G., Leuschen, C., Luyendyk, B. P., Matsuoka, K., Mouginot, J., Nitsche, F. O., Nogi, Y., Nost, O. A., Popov, S. V., Rignot, E., Rippin, D. M., Rivera, A., Roberts, J., Ross, N., Siegert, M. J., Smith, A. M., Steinhage, D., Studinger, M., Sun, B., Tinto, B. K., Welch, B. C., Wilson, D., Young, D. A., Xiangbin, C., and Zirizzotti, A.: Bedmap2: improved ice bed, surface and thickness datasets for Antarctica, The Cryosphere, 7, 375–393, https://doi.org/10.5194/tc-7-375-2013, 2013. a
Glasser, N. and Scambos, T.: A structural glaciological analysis of the 2002 Larsen B ice-shelf collapse, J. Glaciol., 54, 3–16, https://doi.org/10.3189/002214308784409017, 2008. a
Golledge, N. R. and Lowry, D. P.: Is the marine ice cliff hypothesis collapsing?, Science, 372, 1266–1267, https://doi.org/10.1126/science.abj3266, 2021. a
Golledge, N. R., Keller, E. D., Gomez, N., Naughten, K. A., Bernales, J., Trusel, L. D., and Edwards, T. L.: Global environmental consequences of twenty-first-century ice-sheet melt, Nature, 566, 65–72, https://doi.org/10.1038/s41586-019-0889-9, 2019. a
Hutter, K.: Theoretical Glaciology, D. Reidel Publishing Company/Terra Scientific Publishing Company, https://doi.org/10.1007/978-94-015-1167-4, 1983. a
Jeong, S., Howat, I. M., and Bassis, J. N.: Accelerated ice shelf rifting and retreat at Pine Island Glacier, West Antarctica, Geophys. Res. Lett., 43, 11720–11725, https://doi.org/10.1002/2016GL071360, 2016. a, b, c
Joughin, I., Howat, I. M., Fahnestock, M., Smith, B., Krabill, W., Alley, R. B., Stern, H., and Truffer, M.: Continued evolution of Jakobshavn Isbrae following its rapid speedup, J. Geophys. Res.-Earth, 113, F04006, https://doi.org/10.1029/2008JF001023, f04006, 2008. a
Joughin, I., Smith, B. E., and Medley, B.: Marine Ice Sheet Collapse Potentially Under Way for the Thwaites Glacier Basin, West Antarctica, Science, 344, 735–738, https://doi.org/10.1126/science.1249055, 2014. a
Joughin, I., Shean, D. E., Smith, B. E., and Floricioiu, D.: A decade of variability on Jakobshavn Isbræ: ocean temperatures pace speed through influence on mélange rigidity, The Cryosphere, 14, 211–227, https://doi.org/10.5194/tc-14-211-2020, 2020. a
Khazendar, A., Fenty, I. G., Carroll, D., Gardner, A., Lee, C. M., Fukumori, I., Wang, O., Zhang, H., Seroussi, H., Moller, D., Noël, B. P. Y., van den Broeke, M. R., Dinardo, S., and Willis, J.: Interruption of two decades of Jakobshavn Isbrae acceleration and thinning as regional ocean cools, Nature Geoscience, 12, 277–283, https://doi.org/10.1038/s41561-019-0329-3, 2019. a, b
Kopp, R. E., DeConto, R. M., Bader, D. A., Hay, C. C., Horton, R. M., Kulp, S., Oppenheimer, M., Pollard, D., and Strauss, B. H.: Evolving Understanding of Antarctic Ice-Sheet Physics and Ambiguity in Probabilistic Sea-Level Projections, Earth's Future, 5, 1217–1233, https://doi.org/10.1002/2017EF000663, 2017. a
Larour, E., Seroussi, H., Adhikari, S., Ivins, E., Caron, L., Morlighem, M., and Schlegel, N.: Slowdown in Antarctic mass loss from solid Earth and sea-level feedbacks, Science, 364, eaav7908, https://doi.org/10.1126/science.aav7908, 2019. a
Levermann, A., Albrecht, T., Winkelmann, R., Martin, M. A., Haseloff, M., and Joughin, I.: Kinematic first-order calving law implies potential for abrupt ice-shelf retreat, The Cryosphere, 6, 273–286, https://doi.org/10.5194/tc-6-273-2012, 2012. a
Levermann, A., Winkelmann, R., Albrecht, T., Goelzer, H., Golledge, N. R., Greve, R., Huybrechts, P., Jordan, J., Leguy, G., Martin, D., Morlighem, M., Pattyn, F., Pollard, D., Quiquet, A., Rodehacke, C., Seroussi, H., Sutter, J., Zhang, T., Van Breedam, J., Calov, R., DeConto, R., Dumas, C., Garbe, J., Gudmundsson, G. H., Hoffman, M. J., Humbert, A., Kleiner, T., Lipscomb, W. H., Meinshausen, M., Ng, E., Nowicki, S. M. J., Perego, M., Price, S. F., Saito, F., Schlegel, N.-J., Sun, S., and van de Wal, R. S. W.: Projecting Antarctica's contribution to future sea level rise from basal ice shelf melt using linear response functions of 16 ice sheet models (LARMIP-2), Earth Syst. Dynam., 11, 35–76, https://doi.org/10.5194/esd-11-35-2020, 2020. a, b
Lhermitte, S., Sun, S., Shuman, C., Wouters, B., Pattyn, F., Wuite, J., Berthier, E., and Nagler, T.: Damage accelerates ice shelf instability and mass loss in Amundsen Sea Embayment, P. Natl. Acad. Sci. USA, 117, 24735–24741, https://doi.org/10.1073/pnas.1912890117, 2020. a, b, c, d
MacAyeal, D. R.: Large-scale ice flow over a viscous basal sediment: Theory and application to ice stream B, Antarctica, J. Geophys. Res.-Sol. Ea., 94, 4071–4087, https://doi.org/10.1029/JB094iB04p04071, 1989. a
MacAyeal, D. R., Scambos, T. A., Hulbe, C. L., and Fahnestock, M. A.: Catastrophic ice-shelf break-up by an ice-shelf-fragment-capsize mechanism, J. Glaciol., 49, 22–36, https://doi.org/10.3189/172756503781830863, 2003. a, b
MacGregor, J. A., Catania, G. A., Markowski, M. S., and Andrews, A. G.: Widespread rifting and retreat of ice-shelf margins in the eastern Amundsen Sea Embayment between 1972 and 2011, J. Glaciol., 58, 458–466, https://doi.org/10.3189/2012JoG11J262, 2012. a, b
Martin, M. A., Winkelmann, R., Haseloff, M., Albrecht, T., Bueler, E., Khroulev, C., and Levermann, A.: The Potsdam Parallel Ice Sheet Model (PISM-PIK) – Part 2: Dynamic equilibrium simulation of the Antarctic ice sheet, The Cryosphere, 5, 727–740, https://doi.org/10.5194/tc-5-727-2011, 2011. a
Medrzycka, D., Benn, D. I., Box, J. E., Copland, L., and Balog, J.: Calving Behavior at Rink Isbræ, West Greenland, from Time-Lapse Photos, Arct. Antarct. Alp. Res., 48, 263–277, https://doi.org/10.1657/aaar0015-059, 2016. a
Mengel, M., Feldmann, J., and Levermann, A.: Linear sea-level response to abrupt ocean warming of major West Antarctic ice basin, Nat. Clim. Change, 6, 71–74, https://doi.org/10.1038/nclimate2808, 2016. a
Mercer, J. H.: West Antarctic ice sheet and CO2 greenhouse effect: a threat of disaster, Nature, 271, 321–325, https://doi.org/10.1038/271321a0, 1978. a
Milillo, P., Rignot, E., Rizzoli, P., Scheuchl, B., Mouginot, J., Bueso-Bello, J., and Prats-Iraola, P.: Heterogeneous retreat and ice melt of Thwaites Glacier, West Antarctica, Sci. Adv., 5, aau3433, https://doi.org/10.1126/sciadv.aau3433, 2019. a, b
Morland, L. W.: Unconfined Ice-Shelf Flow, in: Dynamics of the West Antarctic Ice Sheet, edited by: Van der Veen, C. J. and Oerlemans, J., Springer Netherlands, Dordrecht, 99–116, https://doi.org/10.1007/978-94-009-3745-1_6, 1987. a
Mouginot, J., Rignot, E., and Scheuchl, B.: Sustained increase in ice discharge from the Amundsen Sea Embayment, West Antarctica, from 1973 to 2013, Geophys. Res. Lett., 41, 1576–1584, https://doi.org/10.1002/2013GL059069, 2014. a, b
Mouginot, J., Rignot, E., Bjørk, A. A., van den Broeke, M., Millan, R., Morlighem, M., Noël, B., Scheuchl, B., and Wood, M.: Forty-six years of Greenland Ice Sheet mass balance from 1972 to 2018, P. Natl. Acad. Sci. USA, 116, 9239–9244, https://doi.org/10.1073/pnas.1904242116, 2019. a
Naughten, K. A., Meissner, K. J., Galton-Fenzi, B. K., England, M. H., Timmermann, R., and Hellmer, H. H.: Future projections of Antarctic ice shelf melting based on CMIP5 scenarios, J. Clim., 31, 5243–5261, 2018. a
Noble, T. L., Rohling, E. J., Aitken, A. R. A., Bostock, H. C., Chase, Z., Gomez, N., Jong, L. M., King, M. A., Mackintosh, A. N., McCormack, F. S., McKay, R. M., Menviel, L., Phipps, S. J., Weber, M. E., Fogwill, C. J., Gayen, B., Golledge, N. R., Gwyther, D. E., Hogg, A. M., Martos, Y. M., Pena-Molino, B., Roberts, J., van de Flierdt, T., and Williams, T.: The Sensitivity of the Antarctic Ice Sheet to a Changing Climate: Past, Present, and Future, Rev. Geophys., 58, e2019RG000663, https://doi.org/10.1029/2019RG000663, 2020. a
Pattyn, F. and Morlighem, M.: The uncertain future of the Antarctic Ice Sheet, Science, 367, 1331–1335, https://doi.org/10.1126/science.aaz5487, 2020. a
Pattyn, F., Perichon, L., Durand, G., Favier, L., Gagliardini, O., Hindmarsh, R. C., Zwinger, T., Albrecht, T., Cornford, S., Docquier, D., Fürst, J. J., Goldberg, D., Gudmundsson, G. H., Humbert, A., Hütten, M., Huybrechts, P., Jouvet, G., Kleiner, T., Larour, E., Martin, D., Morlighem, M., Payne, A. J., Pollard, D., Rückamp, M., Rybak, O., Seroussi, H., Thoma, M., and Wilkens, N.: Grounding-line migration in plan-view marine ice-sheet models: results of the ice2sea MISMIP3d intercomparison, J. Glaciol., 59, 410–422, https://doi.org/10.3189/2013JoG12J129, 2013. a
Pollard, D., DeConto, R. M., and Alley, R. B.: Potential Antarctic Ice Sheet retreat driven by hydrofracturing and ice cliff failure, Earth Planet. Sc. Lett., 412, 112–121, https://doi.org/10.1016/j.epsl.2014.12.035, 2015. a
Pollard, D., DeConto, R. M., and Alley, R. B.: A continuum model (PSUMEL1) of ice mélange and its role during retreat of the Antarctic Ice Sheet, Geosci. Model Dev., 11, 5149–5172, https://doi.org/10.5194/gmd-11-5149-2018, 2018. a
Rack, W. and Rott, H.: Pattern of retreat and disintegration of the Larsen B ice shelf, Antarctic Peninsula, Ann. Glaciol., 39, 505–510, https://doi.org/10.3189/172756404781814005, 2004. a
Reese, R., Albrecht, T., Mengel, M., Asay-Davis, X., and Winkelmann, R.: Antarctic sub-shelf melt rates via PICO, The Cryosphere, 12, 1969–1985, https://doi.org/10.5194/tc-12-1969-2018, 2018a. a
Reese, R., Winkelmann, R., and Gudmundsson, G. H.: Grounding-line flux formula applied as a flux condition in numerical simulations fails for buttressed Antarctic ice streams, The Cryosphere, 12, 3229–3242, https://doi.org/10.5194/tc-12-3229-2018, 2018b. a
Rignot, E., Mouginot, J., Morlighem, M., Seroussi, H., and Scheuchl, B.: Widespread, rapid grounding line retreat of Pine Island, Thwaites, Smith, and Kohler glaciers, West Antarctica, from 1992 to 2011, Geophys. Res. Lett., 41, 3502–3509, https://doi.org/10.1002/2014GL060140, 2014. a, b
Ritz, C., Edwards, T. L., Durand, G., Payne, A. J., Peyaud, V., and Hindmarsh, R. C. A.: Potential sea-level rise from Antarctic ice-sheet instability constrained by observations, Nature, 528, 115–118, https://doi.org/10.1038/nature16147, 2015. a
Robel, A. A. and Banwell, A. F.: A Speed Limit on Ice Shelf Collapse Through Hydrofracture, Geophys. Res. Lett., 46, 12092–12100, https://doi.org/10.1029/2019GL084397, 2019. a, b, c
Scambos, T. A., Bohlander, J. A., Shuman, C. A., and Skvarca, P.: Glacier acceleration and thinning after ice shelf collapse in the Larsen B embayment, Antarctica, Geophys. Res. Lett., 31, L18402, https://doi.org/10.1029/2004GL020670, l18402, 2004. a
Schlemm, T. and Levermann, A.: A simple stress-based cliff-calving law, The Cryosphere, 13, 2475–2488, https://doi.org/10.5194/tc-13-2475-2019, 2019. a, b, c, d, e, f
Schlemm, T. and Levermann, A.: A simple parametrization of mélange buttressing for calving glaciers, The Cryosphere, 15, 531–545, https://doi.org/10.5194/tc-15-531-2021, 2021. a, b, c, d, e, f, g, h
Schlemm, T. and PISM authors: PISM for MICI: PISM version as used in Schlemm et al. The Cryosphere publication, Zenodo [data set], https://doi.org/10.5281/zenodo.6325006, 2022. a
Schmidtko, S., Heywood, K. J., Thompson, A. F., and Aoki, S.: Multidecadal warming of Antarctic waters, Science, 346, 1227–1231, https://doi.org/10.1126/science.1256117, 2014. a
Schodlok, M. P., Hellmer, H. H., Rohardt, G., and Fahrbach, E.: Weddell Sea iceberg drift: Five years of observations, J. Geophys. Res.-Ocean., 111, C06018, https://doi.org/10.1029/2004JC002661, 2006. a
Schoof, C.: Ice sheet grounding line dynamics: Steady states, stability, and hysteresis, J. Geophys. Res.-Earth, 112, F03S28, https://doi.org/10.1029/2006JF000664, f03S28, 2007. a, b, c
Shepherd, A., Wingham, D., and Rignot, E.: Warm ocean is eroding West Antarctic Ice Sheet, Geophys. Res. Lett., 31, L23402, https://doi.org/10.1029/2004GL021106, l23402, 2004. a
Shepherd, A., Fricker, H. A., and Farrell, S. L.: Trends and connections across the Antarctic cryosphere, Nature, 558, 223–232, https://doi.org/10.1038/s41586-018-0171-6, 2018a. a
Shepherd, A., Ivins, E., Rignot, E., Smith, B., van den Broeke, M., Velicogna, I., Whitehouse, P., Briggs, K., Joughin, I., Krinner, G., Nowicki, S., Payne, T., Scambos, T., Schlegel, N., Geruo, A., Agosta, C., Ahlstrøm, A., Babonis, G., Barletta, V., Blazquez, A., Bonin, J., Csatho, B., Cullather, R., Felikson, D., Fettweis, X., Forsberg, R., Gallee, H., Gardner, A., Gilbert, L., Groh, A., Gunter, B., Hanna, E., Harig, C., Helm, V., Horvath, A., Horwath, M., Khan, S., Kjeldsen, K. K., Konrad, H., Langen, P., Lecavalier, B., Loomis, B., Luthcke, S., McMillan, M., Melini, D., Mernild, S., Mohajerani, Y., Moore, P., Mouginot, J., Moyano, G., Muir, A., Nagler, T., Nield, G., Nilsson, J., Noel, B., Otosaka, I., Pattle, M. E., Peltier, W. R., Pie, N., Rietbroek, R., Rott, H., Sandberg-Sørensen, L., Sasgen, I., Save, H., Scheuchl, B., Schrama, E., Schröder, L., Seo, K.-W., Simonsen, S., Slater, T., Spada, G., Sutterley, T., Talpe, M., Tarasov, L., van de Berg, W. J., van der Wal, W., van Wessem, M., Vishwakarma, B. D., Wiese, D., Wouters, B., and the IMBIE team: Mass balance of the Antarctic Ice Sheet from 1992 to 2017, Nature, 558, 219–222, https://doi.org/10.1038/s41586-018-0179-y, 2018b. a, b
Slangen, A. B. A., Adloff, F., Jevrejeva, S., Leclercq, P. W., Marzeion, B., Wada, Y., and Winkelmann, R.: A Review of Recent Updates of Sea-Level Projections at Global and Regional Scales, Springer International Publishing, Cham, 395–416, https://doi.org/10.1007/978-3-319-56490-6_17, 2017. a
Sun, S., Pattyn, F., Simon, E. G., Albrecht, T., Cornford, S., Calov, R., Dumas, C., Gillet-Chaulet, F., Goelzer, H., Golledge, N. R., Greve, R., Hoffman, M. J., Humbert, A., Kazmierczak, E., Kleiner, T., Leguy, G. R., Lipscomb, W. H., Martin, D., Morlighem, M., Nowicki, S., Pollard, D., Price, S., Quiquet, A., Seroussi, H., Schlemm, T., Sutter, J., van de Wal, R. S. W., Winkelmann, R., and Zhang, T.: Antarctic ice sheet response to sudden and sustained ice-shelf collapse (ABUMIP), J. Glaciol., 66, 891–904, https://doi.org/10.1017/jog.2020.67, 2020. a
Todd, J. and Christoffersen, P.: Are seasonal calving dynamics forced by buttressing from ice mélange or undercutting by melting? Outcomes from full-Stokes simulations of Store Glacier, West Greenland, The Cryosphere, 8, 2353–2365, https://doi.org/10.5194/tc-8-2353-2014, 2014. a
Trusel, L. D., Frey, K. E., Das, S. B., Karnauskas, K. B., Kuipers Munneke, P., van Meijgaard, E., and van den Broeke, M. R.: Divergent trajectories of Antarctic surface melt under two twenty-first-century climate scenarios, Nat. Geosci., 8, 927–932, https://doi.org/10.1038/ngeo2563, 2015. a, b
van Wessem, J. M., van de Berg, W. J., Noël, B. P. Y., van Meijgaard, E., Amory, C., Birnbaum, G., Jakobs, C. L., Krüger, K., Lenaerts, J. T. M., Lhermitte, S., Ligtenberg, S. R. M., Medley, B., Reijmer, C. H., van Tricht, K., Trusel, L. D., van Ulft, L. H., Wouters, B., Wuite, J., and van den Broeke, M. R.: Modelling the climate and surface mass balance of polar ice sheets using RACMO2 – Part 2: Antarctica (1979–2016), The Cryosphere, 12, 1479–1498, https://doi.org/10.5194/tc-12-1479-2018, 2018. a
WCRP Global Sea Level Budget Group: Global sea-level budget 1993–present, Earth Syst. Sci. Data, 10, 1551–1590, https://doi.org/10.5194/essd-10-1551-2018, 2018. a
Winkelmann, R., Martin, M. A., Haseloff, M., Albrecht, T., Bueler, E., Khroulev, C., and Levermann, A.: The Potsdam Parallel Ice Sheet Model (PISM-PIK) – Part 1: Model description, The Cryosphere, 5, 715–726, https://doi.org/10.5194/tc-5-715-2011, 2011. a
Wise, M. G., Dowdeswell, J. A., Jakobsson, M., and Larter, R. D.: Evidence of marine ice-cliff instability in Pine Island Bay from iceberg-keel plough marks, Nature, 550, 506–510, https://doi.org/10.1038/nature24458, 2017. a, b
Yu, H., Rignot, E., Morlighem, M., and Seroussi, H.: Iceberg calving of Thwaites Glacier, West Antarctica: full-Stokes modeling combined with linear elastic fracture mechanics, The Cryosphere, 11, 1283–1296, https://doi.org/10.5194/tc-11-1283-2017, 2017. a, b
Zwally, H. J., Giovinetto, M. B., Beckley, M. A., and Sab, J. L.: Antarctic and Greenland Drainage Systems, https://earth.gsfc.nasa.gov/cryo/data/polar-altimetry/antarctic-and-greenland-drainage-systems (last access: 15 May 2022), 2012. a