the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The cooling signature of basal crevasses in a hard-bedded region of the Greenland Ice Sheet
Ian E. McDowell
Neil F. Humphrey
Joel T. Harper
Toby W. Meierbachtol
Temperature sensors installed in a grid of nine full-depth boreholes drilled in the southwestern ablation zone of the Greenland Ice Sheet recorded cooling in discrete sections of ice over time within the lowest third of the ice column in most boreholes. Rates of temperature change outpace cooling expected from vertical conduction alone. Additionally, observed temperature profiles deviate significantly from the site-average thermal profile that is shaped by all thermomechanical processes upstream. These deviations imply recent, localized changes to the basal thermal state in the boreholes. Although numerous heat sources exist to add energy and warm ice as it moves from the central divide towards the margin such as strain heat from internal deformation, latent heat from refreezing meltwater, and the conduction of geothermal heat across the ice–bedrock interface, identifying heat sinks proves more difficult. After eliminating possible mechanisms that could cause cooling, we find that the observed cooling is a manifestation of previous warming in near-basal ice. Thermal decay after latent heat is released from freezing water in basal crevasses is the most likely mechanism resulting in the transient evolution of temperature and the vertical thermal structure observed at our site. We argue basal crevasses are a viable englacial heat source in the basal ice of Greenland's ablation zone and may have a controlling influence on the temperature structure of the near-basal ice.
- Article
(3337 KB) - Full-text XML
-
Supplement
(263 KB) - BibTeX
- EndNote
Rates of ice deformation and the onset of basal sliding are regulated by the thermal regime of ice sheets (Hooke, 1981; Weertman, 1957), which makes ice temperature an important physical variable to be measured in the field and modeled to determine current and future ice motion. As ice moves from the central divide towards the margins, heat is conducted into the ice column from the surface and basal boundaries and is introduced through sources such as energy released by internal deformation and refreezing of meltwater (Cuffey and Paterson, 2010).
Mechanisms of heat transfer and heat sources in Greenland's ablation zone have been investigated by comparing sparsely collected temperature profiles to output from thermomechanical models (e.g., Iken et al., 1993; Funk et al., 1994; Lüthi et al., 2002; Harrington et al., 2015; Lüthi et al., 2015; Poinar et al., 2017). When attempting to replicate the vertical temperature structure, models consistently produced ice temperatures that are lower than collected temperatures. Previous modeling and observational studies highlight the appreciable influence of refreezing meltwater as a source of latent heat in Greenland's ablation zone (e.g., Phillips et al., 2013; Harrington et al., 2015; Lüthi et al., 2015; Poinar et al., 2017; Seguinot et al., 2020; Thomsen et al., 1991). Outside of Greenland, observations of englacial warming from latent heat sources have been demonstrated as early as the 1970s (Jarvis and Clarke, 1974).
Here we investigate heat transfer processes using an extensive dataset collected from over 300 temperature sensors emplaced in a grid of nine full-depth boreholes in southwestern Greenland. Our data provided sub-daily continuous records of ice temperature over a 2–3-year period, longer than many similar temperature time series datasets. The high temporal and spatial resolution allowed us to examine how the vertical thermal structure evolves in both time and space during the study period. Our continuous record of englacial temperatures enabled us to identify dominant drivers of heat flow at our field location.
2.1 Field site
Nine boreholes were drilled in the southwestern portion of the Greenland Ice Sheet in a sector that discharges in the land-terminating outlet glacier, Issunguata Sermia. The field site was located approximately 33 km from the margin and had a surface elevation of 980 m above sea level with ice depth ranging from 640 to 680 m. The dimensions of the borehole grid were approximately 250 m N–S and 500 m E–W. Figure 1 shows the layout of the instrumented field site.
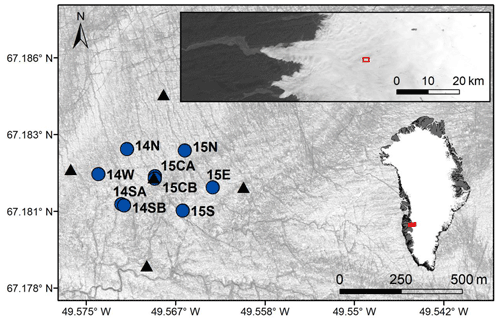
Figure 1Map of the field location showing the layout of the nine boreholes (blue dots) and the five GPS stations (black triangles). Borehole nomenclature is determined by the year that they were drilled and the direction from the center borehole and GPS station. The boreholes are located ∼ 33 km from the margin of Issunguata Sermia outlet glacier shown in a Landsat 8 image taken in July 2014 in the upper right inset. The location in southwestern Greenland is shown in the lower inset, and boreholes are plotted on a WorldView-2 image from July 2012 (© DigitalGlobe, Inc. 2011).
Borehole experiments conducted immediately after drilling indicated the ice rests on bedrock with perhaps a veneer of sand and gravel approximately a decimeter thick (Harper et al., 2017). The subglacial drainage system was indicative of one overlying bedrock and governed by hard-bedded physics (Harper et al., 2017). Mean annual air temperature measured at the site was −10.5 ∘C, and ablation rates were 2–3 m yr−1 (Hills et al., 2018). Ice moved to the west (266∘) at ∼ 100 m yr−1, and inclinometry-derived deformation rates showed that basal sliding comprised ∼ 96 % of ice motion, with internal deformation contributing the remaining 4 % (Maier et al., 2019). Airborne radar measurements indicated that the bed elevation increases slightly from east to west across the site such that the ice flowed up a minor reverse bed slope (Paden et al., 2014).
2.2 Data collection
A hot water drill was used to melt boreholes ∼ 10 cm in diameter through the full depth of the ice column. Cat-5 cables instrumented with TMP102 temperature sensors with 12-bit analog-to-digital converters were installed in the boreholes after drilling and logged with a custom data logger at the surface. Each temperature sensor was controlled by a separate downhole microprocessor that ensured the sensor was powered only as minimally required to obtain a reading. The paired microprocessor handled all digital communications, power control, and data processing to minimize errors caused by self-heating. Sensors were spaced every 10 m in the lowest 150 m of the ice column and every 20 m for the remainder of the depth. The uncalibrated accuracy of the sensors was 0.5 ∘C, and the resolution was 0.0625 ∘C. We performed a freezing-point calibration prior to complete borehole freeze-up using a Clausius–Clapeyron gradient of ∘C Pa−1 (Cuffey and Paterson, 2010). However, due to uncertainty in the Clausius–Clapeyron slope given dissolved air and impurities within the ice and the ambient pressure at the time of calibration, we are confident in the sensors' accuracy to approximately 0.5 ∘C. Data loggers at the ice surface recorded temperature readings every 4 h between the date the borehole was drilled in either July 2014 or July 2015 and the end of the data collection period in July 2017. Each temperature measurement that the sensor records was an average of 64 temperature readings, which was then registered at the nearest resolution step of the sensor.
Our data allowed us to examine both the vertical temperature field within the ice column and the temporal changes in temperature. The temperature of a hot-water-drilled borehole decays towards the ambient ice temperature over time. After 1 year <0.1 % difference remains between the borehole temperature and ambient ice temperatures. For ambient ice temperatures below −1 ∘C, this is well below sensor resolution and does not affect our observational data. Additionally, regressing equation 24 in Humphrey and Echelmeyer (1990) between 1 and 3 years after borehole closure results in a rate of residual cooling on the order of 10−4 ∘C yr−1. To avoid any potential contamination of both the static and temporal trends of the sensor temperature data from the thermal disturbance of installation, we disregarded temperatures recorded in the first year after drilling in our analysis. To display a snapshot of the ambient vertical temperature field with minimal effects of the thermal disturbance from hot water drilling, we report temperatures collected 1 year after boreholes are drilled (Humphrey and Echelmeyer, 1990; Supplement).
We also neglected the first year of measured temperatures in the temporal records of temperature change to eliminate the drilling disturbance. After this time, the measurements of temperature in the environment isolated from electrical noise resulted in a time series of temperature changes that is mostly noise-free and at the absolute limit of the sensor's resolution. The data were cleaned of the few readings recording more than ±2 resolution steps from the preceding and succeeding measurements, since extreme jumps were likely caused by digital transmission errors between the sensor and data logger at the surface. Although englacial temperatures likely vary smoothly over time, the digital representation from sensor data shows temperatures changing over time in a stair-stepping pattern. Since the temporal temperature variations are small in relation to the sensor resolution, the dataset is highly characterized by this stepped behavior (Fig. S1).
We determined the rate of temperature change recorded by a sensor using a least-squares regression of the data recorded over time. Often the first and last digital steps of this record had fewer entries recorded due to the restrictions of the sampling window. Linearly regressing our stepped data to determine the rate of change of temperature required careful treatment to prevent a biased estimate from truncated observation periods. Assuming that temperature change is close to linear with time, we expected that with a longer record, the sensor would record approximately the same number of readings at each resolution step. Short data lengths occurring at either the beginning or end of the records were likely truncated by the restricted time period of our study. To correct for our restricted sampling time, we padded the first and last steps in our data to match the length of a fully recorded resolution step. This was performed by copying the required length of data from a full resolution step and pre- or post-appending it to the truncated data, while equating the temperatures. This procedure is illustrated in Fig. S2, which also shows the difference in derived rates of temperature change over time (Supplement).
The vertical temperature field collected from the nine boreholes 1 year after temperature sensors were installed contains a cold central core with temperatures increasing towards the surface and the bed (Fig. 2). Two boreholes were only instrumented with temperature sensors in the lowest half of the ice column. Temperatures are lowest in approximately the middle of the ice column, ranging from ∼ −12 to −10 ∘C, and increase to ∼ −11 to −4.5 ∘C at the surface. Temperatures also increase towards the bed, reaching temperatures that range from approximately −0.9 to −0.5 ∘C. To establish a depth reference for sensor comparison, and since we are most interested in near-basal ice temperatures, we have plotted temperature profiles with respect to height above the bed.
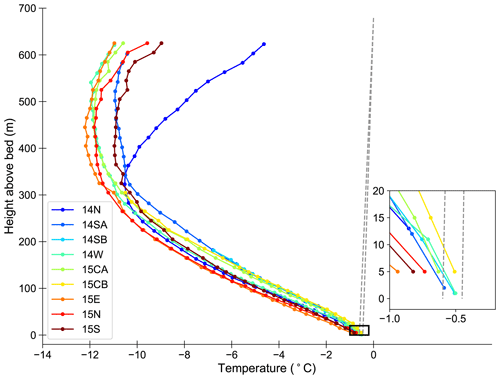
Figure 2Temperature profiles for each borehole plotted with respect to each sensor's height above the bed. Sensor locations are marked with points, and temperatures between sensors are linearly interpolated. Dashed lines indicate the range of pressure melting temperatures given the various Clausius–Clapeyron gradients presented in Cuffey and Paterson (2010). The black box indicates the extent of the inset showing temperatures in the lowest 20 m.
Rates of temperature change are generally a function of position in the ice column (Fig. 3). We captured a clear cooling signature in the lowest third of the ice column in most boreholes, with some boreholes warming or cooling in locations outside of this region. Most boreholes cool at a rate of a few hundredths of a degree Celsius per year in the lowest portion of the ice column. Only five full-depth profiles are shown, as temperature sensors in boreholes 15N and 14W failed for most of the study period. Boreholes 15CB and 14SB were only instrumented in the lowest portion of the ice column.
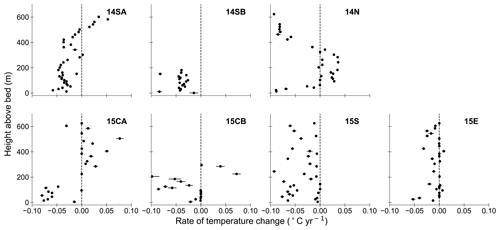
Figure 3Rates of temperature changes for each borehole plotted against each sensor's height above the bed. Boreholes drilled in 2014 show trends between July 2015 and July 2017, while temperature trends in boreholes drilled in 2015 represent temperature changes observed between July 2016 and July 2017. Error bars indicate 2 standard errors from the mean rate, determined by the linear regression.
While the observed temporal temperature changes are small, we believe the trends are a real signal and not an artifact of sensor drift or random noise. Analog-to-digital systems can exhibit both noise and drift over time; however, the expected magnitude of drift or aging is approximately an order of magnitude less than our observed trends. In addition, the coherence and lack of obvious bias in the data gives us confidence. We observe coherent sections of ice that cool (the bottom of 14SA, 14N, and 15CA) while other portions warm (top of 15CA and 14SA). Additionally, borehole pairs 14SA, 14SB and 15CA, 15CB are located within 10 m of each other and show similar rates and extent of cooling over time, establishing repeatability and viability of our measurements and methods.
We focus on observed basal cooling, since cooling of ice near the bed is enigmatic. Multiple heat sources are available to warm ice as it flows from the interior towards the margins. Heat sinks, however, are not obvious, other than vertical thermal conduction from the relatively warm ice at the bed into the cold central core. We proceed by investigating the potential causes of cooling in the lower part of the ice column.
4.1 Diffusive cooling driven by the observed static temperature field
We compare the magnitude of observed cooling over time to the temporal temperature changes that would be produced from purely vertical thermal diffusion given the shapes of our collected temperature profiles. We use the 1-D thermal diffusion equation in the vertical dimension:
where T is temperature, and t is time; κ, ρ, and C are respectively the thermal diffusivity, density, and specific heat capacity of ice. Table S1 contains the constants used in this study. We set the source or sink term, Q, to zero, assuming only thermal diffusion occurs for the following calculations. The spatial second derivative is derived from our observed temperature profile. The temperature data have small amounts of noise as well as calibration offsets between sensors. Derivatives of real data, with any noise or error, tend to amplify the noise. To reduce noise levels and focus on the large-scale characteristics, we smooth the profiles using a fifth-degree polynomial. We choose a fifth-degree polynomial because it smooths over sharp kinks within the profile from calibration errors while maintaining the original curvature, particularly the negative concavity of the temperature profiles observed near the bed. The full-depth observed rates of temperature change in Fig. 3 are also smoothed using a fifth-degree polynomial to facilitate comparison between the changes in temperature expected from collected profiles.
Comparison of our data and expected temperature changes from the analytical diffusion equation (Eq. 1) indicates the curvatures in our temperature profiles cannot produce the observed temporal changes of temperature over time through diffusive vertical heat flow alone. To illustrate the discrepancies between calculated temperature changes caused by vertical thermal diffusion and the observed temporal temperature change, we calculate the additional sources or sinks of heat required throughout the ice column to sustain the observed temperature change through time. Figure 4 presents a vertical distribution of the required Q from the thermal diffusion calculations to produce the recorded temperature changes. Although there is considerable variability, all boreholes require additional heat sinks within portions of the lowest half of the ice column, demonstrating that cooling near the bed cannot result from vertical thermal conduction alone.
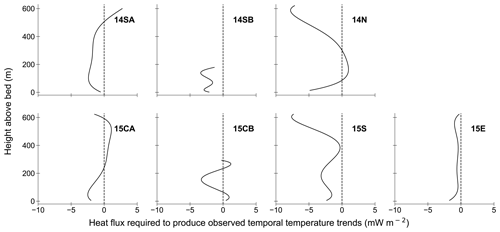
Figure 4Additional heat fluxes required to maintain observed rates of temperature change if the collected static temperature profiles evolve through vertical thermal conduction over time. The dashed line indicates the switch between a required heat source or sink.
In addition, we also highlight regions of the temperature profiles that are not only warming or cooling anomalously, but that may be warmer or cooler than would be expected given the average vertical temperature field at our site. The shape of the site-averaged temperature profile results from ice integrating changes in boundary conditions and all upstream thermomechanical processes. Any deviation from this averaged profile within each collected temperature profile will highlight thermal regions that reflect changes either to the local boundary conditions or to heat sources or sinks. These changes must have occurred recently for sensors within the closely spaced boreholes to capture temperature fields that do not match the average vertical temperature field at the site.
Discrepancies between each collected profile and the site-average temperature profile are shown in Fig. 5. Generally, there are positive deviations within the lowest portion of the ice column where there is a clear signal of cooling in boreholes 14SA, 14SB, 14N, 15CA, and 15CB, showing temperatures in the lowest portion of these boreholes are higher than those in the site-average profile and cool over time. Encouragingly for this analysis, the temperatures in the upper half of the 14N and 15CA profiles are warmer than the site-average profile, and cooling occurs over time. While the pattern of temporal temperature change in boreholes 15S and 15E is not as clear, 15E is colder throughout the full-ice depth than the mean thermal profile, but this borehole is also where sensors record the most warming throughout the profile. Spatially, the southeast portion of our field site does not have a cooling signature in relatively warm ice near the bed, which is evident throughout the other boreholes that have time series of temperature measurements.
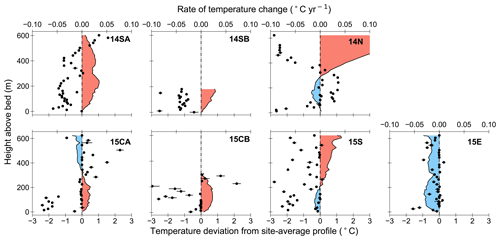
Figure 5Rates of temperature change for each borehole (black dots) plotted with temperature deviations within each borehole from the site-average temperature profile. Red shaded regions indicate that the collected static profile is warmer than the site-average profile, and blue shaded regions show the static profile is colder than the site-average profile. Error bars on the calculated rates are the same as in Fig. 3.
4.2 Possible heat sinks
Pervasive cooling in the lowest portion of boreholes where ice is warmer than the site-average profile in some, but not all, of our borehole data is enigmatic, since multiple heat sources exist near the bed, but identifying heat sinks is problematic. In addition, the non-uniform nature of cooling near the bed requires explanation. We discuss several possible heat sinks below.
4.2.1 Melting in basal temperate ice
Ice near the bed at our field site is at the calculated pressure melting temperature (Fig. 2). Some melting can occur in this temperate ice as the pressure field varies due to ice flow, and transient increases in pressure decrease the melting point. Melting may contribute to cooling near the bed as heat is needed for the phase change. However, ice only reaches the pressure melting temperature in the lowest ∼ 5–10 m at our site, with an even smaller temperate layer upstream. This process cannot explain cooling outside of this small area near the bed.
4.2.2 Basal refreezing from a thinning ice column
The ice sheet thins slightly along flow at our field site; the bed elevation increases while the surface elevation remains relatively constant. With a lower ice overburden pressure, the pressure melting temperature increases (Cuffey and Paterson, 2010). Any interstitial water present in the ice would then be colder than the new melting temperature and would refreeze. Lüthi et al. (2002) estimated the water content of the temperate layer of ice near the bed of Jakobshavn Isbræ has a moisture content of ∼ 1 %. However, refreezing releases latent heat into the surrounding ice, resulting in warming rather than cooling. Because the temperate layer is confined adjacent to the bed, this process would also be localized.
4.2.3 Downward advection of the cold central core
All full-depth temperature profiles display a characteristic cold central core (Fig. 2). Vertical compression caused by longitudinal and transverse extension or basal melting could shift the cold ice downwards, causing temperatures in the lowest 100 m to decrease. Our sensors would fail to detect this cooling because they are mechanically coupled to the same package of ice through time after the borehole freezes. The sensors move with the ice and continue to record temperature of the same section of ice through time.
Alternatively, vertically compressing ice would steepen thermal gradients and facilitate higher rates of heat flow into the cold core. With an average surface vertical strain rate of −0.0043 yr−1 at our site (Maier et al., 2019), the change in the temperature gradient would result in temperature changes orders of magnitude lower than observed.
4.2.4 Long-term changes in boundary conditions
Variations in the boundary temperatures will propagate into the interior of the ice column. Here we address several of the most likely boundary temperature changes to assess how they could affect the temporal evolution of the ice at our site.
The Little Ice Age in Greenland occurred approximately 500–200 years ago, and surface temperatures were ∼ 0.5 ∘C colder than present (Dahl-Jensen et al., 1998). Scaling the e-folding time and length-scale of 1-D thermal diffusion described in Eq. (1) is useful for examining the thermal influence of a heat source and is approximated based on the exponential behavior of the solution to the partial-differential equation. The length, δ, at which surface temperatures have significantly decayed is proportional to the square root of thermal diffusivity (κ) and time (t):
The length scale for changes in surface temperatures during the Little Ice Age 500 years ago is ∼ 130 m, which suggests hardly any thermal signature from the surface boundary exists below ∼ 400 m depth.
Equation (2) also provides an estimate of the timescale of diffusion, illustrating changes in ice temperature from the end of the last interglacial period would have diffused away through the entire ice column after ∼ 12 000 years.
The most significant thermal change to the basal boundary is the transition from frozen to temperate, which occurs upstream of our site. This change introduces a warmer basal boundary relatively recently in terms of the ice flow; however, this would create a region of colder ice near the bed that is being warmed by conduction from the warm bed, not cooled as we observe.
4.2.5 Changes in ice motion
The interior ice sheet, which is frozen to the bed, moves largely by internal deformation and accumulates dissipated heat near the bed where strain rates are highest. Ice at our site moves primarily by basal sliding (Maier et al., 2019) and this strain heat source is negligible, although frictional heating still exists at the base. Downstream from the region where this transition from deformation to sliding occurs, the ice near the bed would lose the strain-derived thermal energy and would cool as the heat diffused upward into the cold core. Although the location of the upstream transition from a frozen to thawed bed conducive to basal sliding is not precisely known, it is on the order of 200 km up-glacier from our field site (MacGregor et al., 2016), which translates to several thousand years for ice flow. Any heat anomalies would have decayed using Eq. (2). Additionally, we have shown that the shape of the temperature profiles that would result from previously accumulated strain heat near the base will not produce the magnitude of observed cooling from vertical thermal conduction alone. An additional heat sink must be required.
Although the frozen-to-sliding transition is probably the largest change to the strain heating term, analysis by Meierbachtol et al. (2016) shows a strong change in the basal shear stress regime approximately 75 km upstream of our site, where the basal shear stress decreases down-flow by a factor of 2. Again Eq. (2) illustrates that the thermal impact is negligible at our site, especially since the bulk of the strain, and therefore strain heating, occurs close to the basal boundary, which forms a fixed boundary condition at a short length scale for heat flow. However, this analysis indicates that variations in the basal boundary stress state can cause minor heating or cooling if strain, and therefore dissipated heat, is removed or reduced. We cannot completely eliminate this process, since basal conditions are not well known.
4.3 Thermal decay from basal crevasses
With the lack of obvious heat sinks, we investigate the possibility that the observed cooling in the lower depths of the ice occurs as thermal decay after latent heat is released from freezing water. Temporally and spatially uniform heating by refreezing of disseminated water would not lead to our observations, since horizontal thermal diffusion would not occur in laterally extensive sections of isothermal ice. However, widely spatially separated transient heating events, such as dispersed basal crevasses or moulins, only warm ice locally, leaving significant regions of colder, unheated ice to facilitate horizontal diffusion. Heat flow along horizontal temperature gradients allows the warmed ice to cool back to ambient temperature. Since heat would flow horizontally, not vertically, the temperature changes would not be revealed by our vertical thermal diffusion calculations governed by the shape of the temperature profiles.
A similar pattern of cooling in ice warmer than the site-average thermal profile is found in the upper portion of 14N (Fig. 4). Hills et al. (2017) discussed the thermal anomaly exhibited in borehole 14N; the authors recognized the relatively high temperatures of ice in the upper portion of the borehole when compared to others in the grid (Fig. 2) and noticed that temperature sensors recorded decreasing temperatures over time. Hills et al. (2017) attributed this localized thermal anomaly to a refrozen crevasse that was observed on the ice surface nearby. The lowest 100 m of ice in boreholes 14SA, 14N, and 15CA exhibits nearly identical thermal characteristics to the uppermost portion of 14N: ice is warmer than the site-average profile and it cools through time.
Basal crevasses can have a thermal influence on discrete but large regions of ice. Because these fractures are distinct features, the fact that we do not see a clear cooling signature in relatively warm ice throughout the base of the ice column at our site is not surprising. Slight warming in cold ice in borehole 15E and no clear signal in borehole 15S provide evidence that the ice is being affected by a thermal process that is not distributed in nature.
Multiple fractures can open similar to crevasses at the surface, and their growth is likely vertically restricted above the bed due to the cold, stiff central core of the ice column which reduces fracture propagation. Therefore, these features only affect the lower portion of the ice column. Additionally, basal crevasses likely are not simple planar features; strong deformational gradients near the bed can alter their shape and cause them to intersect more recently formed crevasses. Although basal crevasses may be more complex than an en echelon arrangement of vertical fractures, for simple modeling we focus on the thermal disturbance by basal crevasses that allow the influx of a plane of water from the bed up into the cold ice. The refreezing of this injected water releases heat into the surrounding ice. Accurately modeling the thermal disturbance created by a basal crevasse is hampered by our lack of knowledge of these features within grounded glaciers and ice sheets, since they have only been directly observed under mountain glaciers (Harper et al., 2010). Extensive basal crevasse fields have been identified based on strong hyperbolic reflections in radar surveys near the base of floating ice shelves (e.g., Jezek and Bentley, 1983; McGrath et al., 2012; Luckman et al., 2012) and in ice streams that were once a part of relict ice shelves (Catania et al., 2005). However, the base environment of ice shelves is different than that of grounded glaciers and ice sheets, with conditions characterized by deviatoric tensile stresses and basal water pressures at ice overburden pressure that are conducive for basal crevasse formation (Weertman, 1980), while tidal flexing at the grounding line also contributes to the formation and spacing of basal crevasses within floating ice (Jezek and Bentley, 1983).
We do not attempt detailed modeling of the thermal disturbance of basal crevasses at our field site, but we can approximate the thermal disturbance created by a single or by multiple basal crevasses to compare with our data. One-dimensional thermal modeling in ice surrounding a crevasse requires knowledge of the width of the crevasse and the presence of other nearby crevasses, since closely spaced water-filled crevasses greatly reduce the refreezing rate (Jarvis and Clarke, 1974). In addition, even the refreezing problem is complicated by the Stefan boundary condition as the thickness of the crevasse is reduced by refreezing (Carslaw and Jaeger, 1959). We are interested in the thermal behavior of ice in the region of a basal crevasse at times much longer than the crevasse remained open, so we model the crevasse as an instantaneous planar heat source, considering only the total latent heat released during the refreezing. We examine the thermal disturbance at a long timescale in the half-space adjacent to the crevasse using an analytic solution presented by Carslaw and Jaeger (1959):
Here T is temperature; l is the linear distance away from the heat source; t is the time that has passed since the heat was released; Q is the amount of heat released per unit area of the plane; and ρ, C, and κ are respectively the density, specific heat capacity, and thermal diffusivity of ice.
We assume a crevasse thickness of 1 m, matching the upper limit of previously observed basal crevasse widths (Harper et al., 2010). The release of heat initiates a wave of thermal energy propagating away from the source (Fig. 6a). The diffusion of the warming front causes ice temperature to increase before cooling asymptotically back to the ambient ice temperature (Fig. 6b). After the crevasse refreezes, the remaining period of warming is short compared to the timescale of cooling; thus the likelihood of temperature sensors installed in a previously crevassed area recording warming is low. To compare this theoretical result with our data, we average the rates of cooling observed in the lowest 100 m of the boreholes and show the range of these averages in Fig. 6c. The theoretical curves depend strongly on the original size of the crevasse and on the distance away from the crevasse; however, we have chosen values that show that this process can produce rates of cooling of the same magnitude as observed in the borehole array.
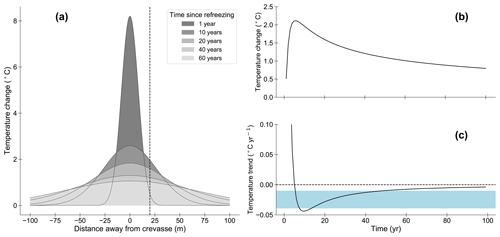
Figure 6(a) Modeled changes in temperature after a crevasse 1 m wide refreezes. Darker colors show earlier times. Dashed line indicates a distance 20 m from the crevasse, for which temperatures and temporal rates of temperature change are shown in (b) and (c). (b) Changes in temperature over time 20 m away from the basal crevasse. (c) Corresponding rates of temperature change for (b). The blue shaded region shows the range of averaged rates of cooling in the lowest 100 m of the boreholes.
It is tempting to estimate the time since water-filled basal crevasses were formed using our extensive temperature data. However, such an attempt is under-constrained since similar thermal signatures could be produced by many crevasse geometries and arrangements in time and space. Instead we examine the same crevassing scenario above as a baseline to investigate the amount of time elapsed since refreezing to produce observed cooling rates given various distances between boreholes and hypothetical crevasses. Equation (3) is solved for a range of time and linear distances from the heat source, and rates of temperature change over time are calculated. Equivalent rates of cooling could be produced from the dissipation of thermal energy released by a refrozen crevasse after approximately 20–30 years if the boreholes directly intersect the crevasse. The time elapsed is less if the boreholes do not intersect the refrozen crevasse. Although speculative, it is interesting that using a timescale of 10–30 years, assuming an ice velocity of 100 m yr−1, the ice currently at our field site would have been 1–3 km up-glacier, which is a location of current surface crevasses and a significant change in slope.
Basal water pressures at or above ice overburden pressure promote the growth of basal crevasses tens of meters above the bed (van der Veen, 1998). Longitudinal extension further facilitates crevassing at distances over 100 m above the bed (van der Veen, 1998). Subglacial water pressures in Greenland's ablation zone have consistently been measured at or near ice overburden pressure (e.g., Iken et al., 1993; Meierbachtol et al., 2013; Andrews et al., 2014; Ryser et al., 2014; van de Wal et al., 2015; Doyle et al., 2018) and have peaked at ∼ 1.15 times the ice overburden pressure at our field location (Wright et al., 2016). Longitudinal extension, while not temporally or spatially prevalent, may result from ice flow over uneven bed topography or spatial changes in basal friction. Additionally, observed stick–slip behavior and hydraulic jacking from rapid delivery of surface meltwater through passive seismic surveys could provide another mechanism for basal crevasse formation (Moore et al., 2013).
It is unlikely that a single basal crevasse is responsible for the cooling that we observe at the field site. More plausibly, the ice at our field site was fractured by multiple crevasses up-glacier. We cannot precisely determine the number or spacing of crevasses; however, a 1-D modeling analysis shows that three 1 m thick refrozen crevasses would lead to dispersed cooling over a large area of the bed after 20–30 years (Supplement). The 1-D temperature field evolution illustrates the warming that occurs due to the release of latent heat immediately as the crevasse completely refreezes, followed by dispersed cooling surrounding the crevasses over time (Fig. 7). Given negative heat fluxes are required in the lowest portion of all boreholes (Fig. 4) to create observed cooling, thermal energy likely diffuses away from our field site in three dimensions, which would result in cooling that we have not captured in our vertical 1-D diffusion calculations. It is plausible that boreholes intersect these regions of ice that have been thermally altered by basal crevassing.
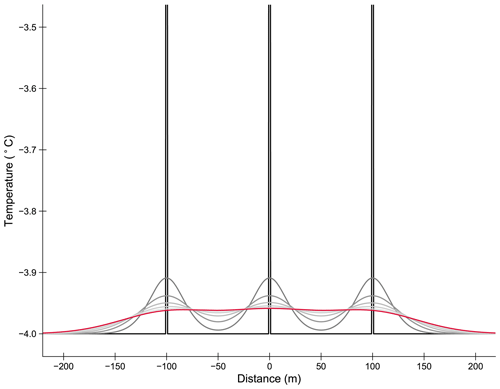
Figure 7Evolution of a synthetic 1-D temperature field from basal crevasses spaced 100 m apart. Temperatures are plotted every 5 years, and older temperature fields are shaded darker shades of grey. The red line shows the temperature field 30 years after refreezing. Distinct crevasses can cause cooling over large regions of the bed.
Moulins are unlikely to create the observed thermal observations. While the internal architecture of moulins is likely complex, as a simple model, we conceptualize moulins as linear pipes that release thermal energy from the surface to the bed because of how these features are manifested at the surface. Cooling in relatively warm ice is not observed throughout the entire ice column in each borehole, which we would expect to see from a linear heat source extending over the full ice depth. Moulins have been shown to migrate horizontally with depth (Holmund, 1988), which could possibly avoid this objection; however, numerous moulins would be needed to generate the cooling we observe in multiple boreholes. In the ablation zone surrounding Issunguata Sermia, active moulins have a mean density of 0.1 per square kilometer (Smith et al., 2015), and Catania and Neumann (2010) found relict moulins to be spaced ∼ 1 km apart, which suggests that it is unlikely that multiple moulins have thermally altered the instrumented block of ice with a surface area of ∼ 0.125 km2.
The existence of basal crevasses has not been widely considered outside of alpine or tidally influenced settings; however, these features likely impact the bulk water storage, basal water flow, and ice rheology in Greenland's ablation zone. Harrington et al. (2015) examined full-depth ice temperature data collected in boreholes at a site down-glacier, but on the same flow line as this study, and found temperate layer growth could not be reproduced by thermal modeling incorporating strain heat and longitudinal compression. The authors suggest basal crevasses allow latent heat to be released well above the bed and create the thick temperate layer.
The lack of a thick basal temperate layer indicates the transient thermal influence of basal crevasses. Ice viscosity is highly temperature dependent; thus basal crevasses could create regions of enhanced deformation, although previous observations in Greenland have shown that deformation rates in temperate ice are often lower than theory predicts (e.g., Ryser et al., 2014; Doyle et al., 2018; Maier et al., 2019). In addition, water content in basal temperate ice also influences rates of glacial ice deformation. A previous study at the down-glacier site found a higher water content in the basal temperate ice layer revealed by ground-based radar than is used in modeling studies (Brown et al., 2017). While unable to detect macro-spaces for bulk water storage in the radargrams, the authors speculated that basal crevasses provide macro-spaces for water storage based on the thermal evidence from Harrington et al. (2015), which results in the high water content observed.
Although basal crevasses have only been directly observed in alpine settings, their existence under the Greenland Ice Sheet has strong implications for the basal hydrology. Basal crevasses have been observed creating englacial water flow above the bed (Harper et al., 2010) and even allowing complex three-dimensional crossing water flow paths (Huzurbazar and Humphrey, 2008). These features have the potential to modulate subglacial discharge and efficiently transfer water through the subglacial drainage system.
Temperature measurements that began 1 year after sensor installation in nine boreholes and span 2–3 years show that ice cools in the lowest portion of the ice column, with all boreholes displaying cooling within the lowest third of the ice column. The main thermal sink is conduction of heat from this region up into the cold central core of the ice. Vertical diffusion calculations show this cooling to be insufficient to explain our data. In addition, the lowest section of ice in some boreholes is warmer than the mean thermal profile at our field site, which suggests relatively recent and localized changes to the boundary conditions or near-basal heat sources. The observed cooling regions of the boreholes are often the same regions of ice that are warmer than the site-average profile.
After eliminating various potential heat sinks, we conclude the observed thermal anomalies are created by the cooling of basal ice that has been previously warmed by basal crevassing occurring upstream of our observation site. Latent heat released by refrozen basal crevasses locally warms ice near the bed, but the effects are distributed as thermal energy propagates outwards, resulting in dispersed cooling at rates of the same magnitude as our observations. Our results provide additional thermal evidence for the existence of basal crevasses in Greenland's ablation zone, which has strong relevance for the temperature-dependent rheology of the basal ice and intriguing implications for the complexity of the basal hydrologic system.
Temperature measurements used in this paper are available at https://doi.org/10.15786/20.500.11919/7147 (McDowell et al., 2020)
The supplement related to this article is available online at: https://doi.org/10.5194/tc-15-897-2021-supplement.
NFH, JTH, and TWM designed the field study and installed temperature sensors. IEM performed the analysis and wrote the manuscript with contributions from all co-authors.
The authors declare that they have no conflict of interest.
We thank Megan Thompson-Munson for her helpful discussions throughout this project. We are grateful to Martin Lüthi and Samuel Doyle for their reviews that significantly improved the quality of this paper and to Ginny Catania, who served as the scientific editor.
This research has been supported by the National Science Foundation, Office of Polar Programs (grant nos. 1203451 and 0909495).
This paper was edited by Ginny Catania and reviewed by Martin Lüthi and Samuel Doyle.
Andrews, L. C., Catania, G. A., Hoffman, M. J., Gulley, J. D., Lüthi, M. P., Ryser, C., Hawley, R. L., and Neumann, T. A.: Direct observations of evolving subglacial drainage beneath the Greenland Ice Sheet, Nature, 514, 80–83, https://doi.org/10.1038/nature13796, 2014.
Brown, J., Harper, J., and Humphrey, N.: Liquid water content in ice estimated through a full-depth ground radar profile and borehole measurements in western Greenland, The Cryosphere, 11, 669–679, https://doi.org/10.5194/tc-11-669-2017, 2017.
Carslaw, H. S. and Jaeger, J. C.: Conduction of Heat in Solids, 2nd edition, Clarendon Press, Oxford, England, 1959.
Catania, G. A. and Neumann, T. A.: Persistent englacial drainage features in the Greenland Ice Sheet, Geophys. Res. Lett., 37, L02501, https://doi.org/10.1029/2009GL041108, 2010.
Catania, G. A., Conway, H., Raymond, C. F., and Scambos, T. A.: Surface morphology and internal layer stratigraphy in the downstream end of Kamb Ice Stream, West Antarctica, J. Glaciol., 51, 423–431, https://doi.org/10.3189/172756505781829142, 2005.
Cuffey, K. M. and Paterson, W. S. B.: The Physics of Glaciers, Academic Press, Burlington, Massachusetts, USA, 2010.
Dahl-Jensen, D., Mosegaard, K., Gundestrup, N., Clow, G. D., Johnsen, S. J., Hansen, A. W., and Balling, N.: Past Temperatures Directly from the Greenland Ice Sheet, Science, 282, 268–271, https://doi.org/10.1126/science.282.5387.268, 1998.
Doyle, S. H., Hubbard, B., Christoffersen, P., Young, T. J., Hofstede, C., Bougamont, M., Box, J. E., and Hubbard, A.: Physical conditions of fast glacier flow: 1. measurements from boreholes drilled to the bed of Store Glacier, West Greenland, J. Geophys. Res.-Earth, 123, 324–348, https://doi.org/10.1002/2017JF004529, 2018.
Funk, M., Echelmeyer, K., and Iken, A.: Mechanisms of fast flow in Jakobshavns Isbræ, West Greenland: Part II. Modeling of englacial temperatures, J. Glaciol., 40, 569–585, https://doi.org/10.3189/S0022143000012466, 1994.
Harper, J. T., Bradford, J. H., Humphrey, N. F., and Meierbachtol, T. W.: Vertical extension of the subglacial drainage system into basal crevasses, Nature, 467, 579–582, https://doi.org/10.1038/nature09398, 2010.
Harper, J. T., Humphrey, N. F., Meierbachtol, T. W., Graly, J. A., and Fischer, U. H.: Borehole measurements indicate hard bed conditions, Kangerlussuaq sector, western Greenland Ice Sheet, J. Geophys. Res.-Earth, 122, 1605–1618, https://doi.org/10.1002/2017JF004201, 2017.
Harrington, J. A., Humphrey, N. F., and Harper, J. T.: Temperature distribution and thermal anomalies along a flowline of the Greenland ice sheet, Ann. Glaciol., 56, 98–104, https://doi.org/10.3189/2015AoG70A945, 2015.
Hills, B. H., Harper, J. T., Humphrey, N. F., and Meierbachtol, T. W.: Measured horizontal temperature gradients constrain heat transfer mechanisms in Greenland ice, Geophys. Res. Lett., 44, 9778–9785, https://doi.org/10.1002/2017GL074917, 2017.
Hills, B. H., Harper, J. T., Meierbachtol, T. W., Johnson, J. V., Humphrey, N. F., and Wright, P. J.: Processes influencing heat transfer in the near-surface ice of Greenland's ablation zone, The Cryosphere, 12, 3215–3227, https://doi.org/10.5194/tc-12-3215-2018, 2018.
Holmund, P.: Internal geometry and evolution of moulins, Storglaciaren, Sweden, J. Glaciol., 34, 242–248, https://doi.org/10.3189/S0022143000032305, 1988.
Hooke, R. L.: Flow law for polycrystalline ice in glaciers: comparison of theoretical predictions, laboratory data, and field measurements, Rev. Geophys. Space. Ge., 19, 664–672, https://doi.org/10.1029/RG019i004p00664, 1981.
Humphrey, N. and Echelmeyer, K.: Hot-water drilling and bore-hole closure in cold ice, J. Glaciol., 36, 287–298, https://doi.org/10.3189/002214390793701354, 1990.
Huzurbazar, S. and Humphrey, N. F.: Functional clustering of time series: An insight into length scales in subglacial water flow, Water Resour. Res., 44, W11420, https://doi.org/10.1029/2007WR006612, 2008.
Iken, A., Echelmeyer, K., Harrison, W., and Funk, M.: Mechanisms of fast flow in Jakobshavns Isbrae, West Greenland: Part I. Measurements of temperature and water level in deep boreholes, J. Glaciol., 39, 15–25, https://doi.org/10.3189/S0022143000015689, 1993.
Jarvis, G. T. and Clarke, G. K. C.: Thermal effects of crevassing on Steele Glacier, Yukon Territory, Canada, J. Glaciol., 13, 243–254, https://doi.org/10.3189/S0022143000023054, 1974.
Jezek, K. C. and Bentley, C. R.: Field Studies of Bottom Crevasses in the Ross Ice Shelf, Antarctica, J. Glaciol., 29, 118–126, https://doi.org/10.3189/S0022143000005189, 1983.
Luckman, A., Jansen, D., Kulessa, B., King, E. C., Sammonds, P., and Benn, D. I.: Basal crevasses in Larsen C Ice Shelf and implications for their global abundance, The Cryosphere, 6, 113–123, https://doi.org/10.5194/tc-6-113-2012, 2012.
Lüthi, M., Funk, M., Iken, A., Gogineni, S., and Truffer, M.: Mechanisms of fast flow in Jakobshavn Isbrae, West Greenland: Part III. Measurements of ice deformation, temperature and cross-borehole conductivity in boreholes to the bedrock, J. Glaciol., 48, 369–385, https://doi.org/10.3189/172756502781831322, 2002.
Lüthi, M. P., Ryser, C., Andrews, L. C., Catania, G. A., Funk, M., Hawley, R. L., Hoffman, M. J., and Neumann, T. A.: Heat sources within the Greenland Ice Sheet: dissipation, temperate paleo-firn and cryo-hydrologic warming, The Cryosphere, 9, 245–253, https://doi.org/10.5194/tc-9-245-2015, 2015.
MacGregor, J. A., Fahnestock, M. A., Catania, G. A., Aschwanden, A., Clow, G. D., Colgan, W. T., Gogineni, S. P., Morlighem, M., Nowicki, S. M. J., Paden, J. D., Price, S. F., and Seroussi, H.: A synthesis of the basal thermal state of the Greenland Ice Sheet, J. Geophys. Res.-Earth, 121, 1328–1350, https://doi.org/10.1002/2015JF003803, 2016.
Maier, N., Humphrey, N., Harper, J., and Meierbachtol, T.: Sliding dominates slow-flowing margin regions, Greenland Ice Sheet, Sci. Adv., 5, eaaw5406, https://doi.org/10.1126/sciadv.aaw5406, 2019.
McDowell, I., Humphrey, N., Harper, J., and Meierbachtol T.: Full-depth ice temperature measurements from southwestern Greenland's ablation zone, 2015–2017, Mountain Scholar Dataset, https://doi.org/10.15786/20.500.11919/7147, 2020.
McGrath, D., Steffen, K., Scambos, T., Rajaram, H., Casassa, G., and Lagos, J. L. R.: Basal crevasses and associated surface crevassing on the Larsen C ice shelf, Antarctica, and their role in ice-shelf instability, Ann. Glaciol., 53, 10–18, https://doi.org/10.3189/2012AoG60A005, 2012.
Meierbachtol, T., Harper, J., and Humphrey, N.: Basal drainage system response to increasing surface melt on the Greenland Ice Sheet, Science, 341, 777–779, https://doi.org/10.1126/science.1235905, 2013.
Meierbachtol, T., Harper, J., and Johnson, J.: Force balance along Isunnguata Sermia, West Greenland, Front. Earth Sci., 4, 87, https://doi.org/10.3389/feart.2016.00087, 2016.
Moore, P. L., Winberry, J. P., Iverson, N. R., Christianson, K. A., Anandakrishnan, S., Jackson, M., Mathison, M. E., and Cohen, D.: Glacier slip and seismicity induced by surface melt, Geology, 41, 1247–1250, https://doi.org/10.1130/G34760.1, 2013.
Paden, J., Li, J., Leuschen, C., Rodriguez-Morales, F., and Hale, R.: IceBridge MCoRDS L1B Geolocated Radar Echo Strength Profiles, Version 2, NASA National Snow and Ice Data Center Distributed Active Archive Center, https://doi.org/10.5067/90S1XZRBAX5N, 2014.
Phillips, T., Rajaram, H., Colgan, W., Steffen, K., and Abdalati, W.: Evaluation of cryo-hydrologic warming as an explanation for increased ice velocities in the wet snow zone, Sermeq Avannarleq, West Greenland, J. Geophys. Res.-Earth Surf., 118, 1241–1256, https://doi.org/10.1002/jgrf.20079, 2013.
Poinar, K., Joughin, I., Lenaerts, J. T. M., and Van Den Broeke, M. R.: Englacial latent-heat transfer has limited influence on seaward ice flux in western Greenland, J. Glaciol., 63, 1–16, https://doi.org/10.1017/jog.2016.103, 2017.
Ryser, C., Lüthi, M. P., Andrews, L. C., Catania, G. A., Funk, M., Hawley, R., Hoffman, M., and Neumann, T. A.: Caterpillar-like ice motion in the ablation zone of the Greenland ice sheet, J. Geophys. Res.-Earth, 119, 2258–2271, https://doi.org/10.1002/2013JF003067, 2014.
Ryser, C., Lüthi, M. P., Andrews, L. C., Hoffman, M. J., Catania, G. A., Hawley, R. L., Neumann, T. A., and Kristensen, S. S.: Sustained high basal motion of the Greenland ice sheet revealed by borehole deformation, J. Glaciol., 60, 647–660, https://doi.org/10.3189/2014JoG13J196, 2014.
Seguinot, J., Funk, M., Bauder, A., Wyder, T., Senn, C., and Sugiyama, S.: Englacial warming indicates deep crevassing in Bowdoin Glacier, Greenland, Front. Earth Sci., 8, 65, https://doi.org/10.3389/feart.2020.00065, 2020.
Smith, L. C., Chu, V. W., Yang, K., Gleason, C. J., Pitcher, L. H., Rennermalm, A. K., Legleiter, C. J., Behar, A. E., Overstreet, B. T., Moustafa, S. E., Tedesco, M., Forster, R. R., LeWinter, A. L., Finnegan, D. C., Sheng, Y., and Balog, J.: Efficient meltwater drainage through supraglacial streams and rivers on the southwest Greenland ice sheet, P. Natl. Acad. Sci. USA, 112, 1001–1006, https://doi.org/10.1073/pnas.1413024112, 2015.
Thomsen, H. H., Olesen, O., Braithwaite, R. J., and Boggild, C.: Ice drilling and mass balance at Pakitsoq, Jakobshavn, central West Greenland, Report 152, Grønlands Geologiske Undersøgelse, Copenhagen, Denmark, 80–84, 1991.
van der Veen, C. J.: Fracture mechanics approach to penetration of bottom crevasses on glaciers, Cold Reg. Sci. Technol., 27, 213–223, https://doi.org/10.1016/S0165-232X(98)00006-8, 1998.
van de Wal, R. S. W., Smeets, C. J. P. P., Boot, W., Stoffelen, M., van Kampen, R., Doyle, S. H., Wilhelms, F., van den Broeke, M. R., Reijmer, C. H., Oerlemans, J., and Hubbard, A.: Self-regulation of ice flow varies across the ablation area in south-west Greenland, The Cryosphere, 9, 603–611, https://doi.org/10.5194/tc-9-603-2015, 2015.
Weertman, J.: On the sliding of glaciers, J. Glaciol., 3, 33–38, https://doi.org/10.3189/S0022143000024709, 1957.
Weertman, J.: Bottom crevasses, J. Glaciol., 25, 185–188, https://doi.org/10.3189/S0022143000010418, 1980.
Wright, P. J., Harper, J. T., Humphrey, N. F., and Meierbachtol, T. W.: Measured basal water pressure variability of the western Greenland Ice Sheet: Implications for hydraulic potential, J. Geophys. Res.-Earth, 121, 1134–1147, https://doi.org/10.1002/2016JF003819, 2016.





