the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Local-scale variability of seasonal mean and extreme values of in situ snow depth and snowfall measurements
Michael Begert
Stefan Brönnimann
Christoph Marty
Daily measurements of snow depth and snowfall can vary strongly over short distances. However, it is not clear if there is a seasonal dependence in these variations and how they impact common snow climate indicators based on mean values, as well as estimated return levels of extreme events based on maximum values. To analyse the impacts of local-scale variations we compiled a unique set of parallel snow measurements from the Swiss Alps consisting of 30 station pairs with up to 77 years of parallel data. Station pairs are usually located in the same villages (or within 3 km horizontal and 150 m vertical distances). Investigated snow climate indicators include average snow depth, maximum snow depth, sum of new snow, days with snow on the ground, days with snowfall, and snow onset and disappearance dates, which are calculated for various seasons (December to February (DJF), November to April (NDJFMA), and March to April (MA)). We computed relative and absolute error metrics for all these indicators at each station pair to demonstrate the potential variability. We found the largest relative inter-pair differences for all indicators in spring (MA) and the smallest in DJF. Furthermore, there is hardly any difference between DJF and NDJFMA, which show median variations of less than 5 % for all indicators. Local-scale variability ranges between less than 24 % (DJF) and less than 43 % (MA) for all indicators and 75 % of all station pairs. The highest percentage (90 %) of station pairs with variability of less than 15 % is observed for days with snow on the ground. The lowest percentage (30 %) of station pairs with variability of less than 15 % is observed for average snow depth. Median differences of snow disappearance dates are rather small (3 d) and similar to the ones found for snow onset dates (2 d). An analysis of potential sunshine duration could not explain the higher variabilities in spring. To analyse the impact of local-scale variations on the estimation of extreme events, 50-year return levels were quantified for maximum snow depth and maximum 3 d new snow sum, which are often used for avalanche prevention measures. The found return levels are within each other's 95 % confidence intervals for all (but three) station pairs, revealing no striking differences. The findings serve as an important basis for our understanding of variabilities of commonly used snow indicators and extremal indices. Knowledge about such variabilities in combination with break-detection methods is the groundwork in view of any homogenization efforts regarding snow time series.
- Article
(1304 KB) - Full-text XML
- BibTeX
- EndNote
Snow, in all its forms, is of great social and environmental importance. Implications can be found in many fields as diverse as ecology, climatology, hydrology, tourism, and natural hazards. All measurements of snow cover are dependent on the local characteristics of the site: i.e. exposure to wind or solar radiation. Furthermore, nearby buildings or trees may have an impact on the measured snow quantities. In an ideal world this would not matter, as basic guidelines (e.g. World Meteorological Organization, 2018) recommend measuring snow in a flat, not-wind-exposed measurement field, which is at least at the same distance from a building or tree as the height of the obstacle. In reality, manual measurement locations sometimes do not fulfil these basic requirements for many reasons, such as the availability of suitable terrain and observers or easy access to the site. Due to this fact, the variability of the measured snow quantities on the 1 km scale (i.e. next to an open field) may be smaller than the variability on the 10 m scale (e.g. south or north of a house). In theory, this bias introduced by sometimes-not-ideal measuring locations that may be season dependent as we hypothesize that the wind impact is mostly relevant during the accumulation season (availability of loose snow) and the solar impact during the ablation season (more available melt energy). The knowledge about such a possible seasonally dependent bias is important, as it helps to understand existing inhomogeneities. Furthermore, this information is invaluable in view of homogenization efforts of snow data series.
Moreover, climatological applications and studies usually focus either on the meteorological winter DJF (Scherrer and Appenzeller, 2006) or on the 6 months NDJFMA (Marcolini et al., 2017). However, winter in the Alps is not simply restricted to these 3 or 6 months. In contrast, for many ecological and hydrological applications, the melting spring snow cover is the main interest (Brown and Robinson, 2011; Livensperger et al., 2016; Zampieri et al., 2015) and for some applications even the onset of the snow cover (Roland et al., 2021). We therefore analyse the variations of important and commonly used snow climate indicators for seasonal effects. Additionally, snow onset and disappearance dates are introduced, as they are important for snow phenology, which is especially crucial for ecological purposes (Vorkauf et al., 2021).
Using and extending the data set of parallel time series introduced by Buchmann et al. (2021a) in the available number of stations, months, and years enables the investigation of the impact of the above-mentioned bias introduced by sometimes-not-ideal measuring locations, hereafter referred to as “local bias” or variability. Investigating snow onset and disappearance dates, as well as extreme value analyses, we strive to answer the following questions.
-
Is the behaviour of the local bias a function of time series length (Sect. 4.1); i.e. are relative percentage deviations dependent on the length of parallel series?
-
Is there any seasonal dependence of the local bias? To what extent do the various seasons contribute to variations observed in indicators derived from parallel snow series (Sect. 4.2)? To further explore the effects at the beginning and end of the snow season, snow onset and disappearance dates are used to put the seasonal variations into context and to test the hypothesis that the beginning and especially the end of a snow season are most sensitive to the local bias for snow climate indicators (Sect. 4.3 and 4.4).
-
What is the impact of the local bias on return levels based on a commonly calculated return period of extreme events? Such values and their uncertainties are often used to answer engineering questions for prevention measures (Sect. 4.5).
The paper is organized as follows: Sect. 2 introduces the data set, Sect. 3 covers the statistical methods used for the analyses, results are presented and discussed in Sect. 4, and conclusions are drawn in Sect. 5.
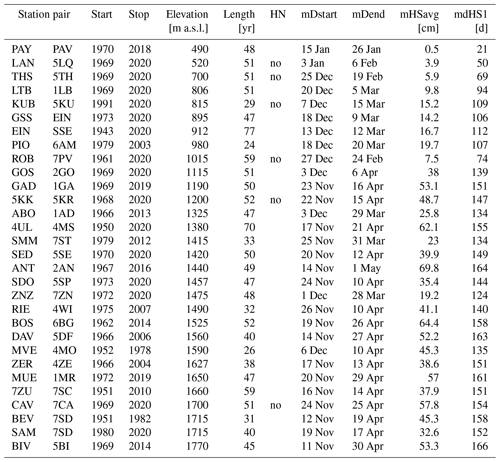
Our data consist of daily manually measured snow depth (HS) and height of new snow (HN) maintained by two separate institutions in Switzerland: Institute for Snow and Avalanche Research (SLF) and the Federal Office for Meteorology and Climatology (MeteoSwiss). HS measurements are taken from a fixed graduated stake, and HN measurements are taken from a board on top of the previous day's snow cover every morning at 06:00 UTC at least between November and April (for details refer to Haberkorn, 2019, and Buchmann et al., 2021a). To obtain parallel series, station pairs were constructed by combining stations into pairs which are located within a distance of 3 km horizontally and 150 m vertically of each other. The mean horizontal (vertical) distance in the data set is 1 km (50 m). Most, but not all, pairs consist of one SLF and one MeteoSwiss station. The so-defined set consists of 30 (24 for HN) station pairs between 490 and 1770 m a.s.l. with complete data between October and May (September and June in extreme cases). The set includes one station pair with 77 years of parallel data (1944–2020) and 10 station pairs with more than 50 years of parallel data, and it incorporates a total of 1338 station years, covering the time period from 1944 to 2020. However, not all station pairs cover the same length. Table A1 shows the various available time periods for each station pair. Six station pairs are excluded from all calculations involving HN due to irregular measurement procedures in the past, manifested by clusters of cases where HN equals HS minus HS from the previous day, thus neglecting the settling of the snow pack.
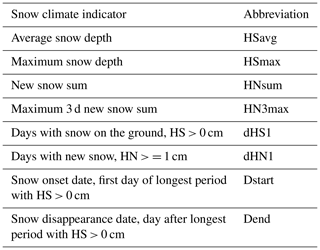
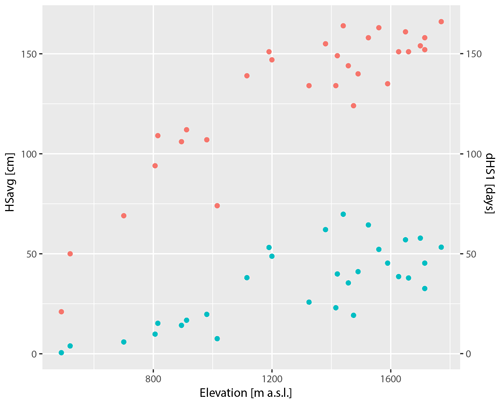
For our analyses, we focused on derived snow climate indicators as seasonal values. The main variables are defined in Table 1: average snow depth (HSavg); maximum snow depth (HSmax); sum of new snow (HNsum); maximum 3 d new snow sum (HN3max); days with snow on the ground, defined by HS of at least 1 cm (dHS1); and days with snowfall of at least 1 cm (dHN1). Figure A1 gives a quantitative impression of the data set by depicting elevation and mean values for HSavg and dHS1.
Availability and quality of the corresponding metadata records (coordinates, observer) are an issue. Although we managed to compile complete metadata records, there is no guarantee that these are always precise and correct. Theoretically, the exact locations of the snow measurements are known; however, until about two decades ago, only approximate coordinates were recorded. The main reason is the general lack of awareness for the importance as to where the snow measurements are actually conducted. Further, in the case of some MeteoSwiss sites, the coordinates refer to the main meteorological measurements and the snow measurements may have been conducted on a slightly different spot. Also, sometimes decades have passed between station visits, thus resulting in missing information.
Potential sunshine duration is obtained with the help of Swisstopo's digital elevation model DHM25, which has an accuracy in Alpine terrain of 5–8 m.
To be able to compare and quantify the differences of the various snow climate indicators, we use relative percentage differences (RPDs), calculated according to Eq. (1) for each indicator (i) and station pair (X–Y), with the number of years denoted by n and k indicating the actual year. These RPDs are expressed as seasonal mean values for DJF, NDJFMA, and MA or monthly mean values. A potential influence of observational length on RPD is investigated by plotting the number of available parallel years against mean RPD for each indicator and station pair in the data set.
Absolute differences (absD) are calculated accordingly (see Eq. 2).
To be able to capture all onset and disappearance dates, we defined the current hydrological year as the period from 1 September of the previous year to 31 August of the current year, as it is often used in snow hydrological modelling (e.g. Liston and Elder, 2006; Seibert and Vis, 2012).
There are various definitions for snow onset (Dstart) and disappearance dates (Dend) depending on the application in hand, e.g. Foster (1989), Kirdyanov et al. (2003), Peng et al. (2013), Stone et al. (2002), and Klein et al. (2016). However, as none of them suits our purpose and for sake of simplicity, we defined them as the first day (Dstart) and day after the last day (Dend) of the longest period with continuous snow cover. For the purposes in this study, we additionally allowed gaps of up to 3 consecutive days with no snow cover during the season. The chosen gap length allows the inclusion of full seasons in case they were fragmented in the middle of the winter by a maximum of 3 d without snow. Such an approach corresponds much more to the experience of the biotic world than just using the duration of the longest continuous snow cover.
In order to assess the impact of the local-scale differences on the long-term temporal changes of snow onset and disappearance dates Theil–Sen linear slopes (Sen, 1968; Theil, 1950) are calculated for each station pair. For each station we calculated absolute changes (AC) defined as the difference between the fitted value at the end and the fitted value at the beginning of the time series.
To further investigate the potential impact of the beginning and end of the snow season on local bias, median differences of daily snow depth measurements for each station pair are calculated, separately for the first (accumulation) and last (ablation) 60 d periods of the hydrological year.
To investigate a potential influence of the local bias on the differences in snow disappearance dates, we compared them to the difference in potential MA sunshine duration hours (Sdur) for a selection of station pairs with good quality metadata. Sdur are obtained as daily values with the help of a digital elevation model and geographical information system (GIS) software. This calculation depends on the accuracy of the coordinates of the measurement sites.
To analyse the impact of the local bias on potential extreme events based on the annual maximum 3 d new snow sum HN3max (e.g. Bocchiola et al., 2008) and annual maximum snow depth HSmax (e.g. Marty and Blanchet, 2012), return levels for fixed (50-year) return periods are calculated for each station and indicator using the R package extRemes and standard settings (GEV, estimation method MLE, and 95 % confidence intervals). For three station pairs (CAV, KUB, ZER), Gumbel instead of GEV is used due to bad model fit. The analysis is based on data for NDJFMA.
4.1 Time series length and relative percentage differences
To investigate a possible relationship of relative percentage differences (RPDs) with time series length, we plotted the mean RPD (season NDJFMA) against the length of the underlying parallel time series for each indicator (Fig. 1). Here we found no clear pattern. RPDs are between 10 % and 50 % for all station pairs and indicators. The values are in line with findings from Buchmann et al. (2021a) for a 25-year common period. However, the variations within each indicator show some visual differences, with average snow depth (HSavg) having the largest (20 %) and days with snow on the ground (dHS1) the smallest (8 %) variations. Outliers are caused by the same station pairs for all indicators. For a majority of station pairs, all HN variables show RPDs smaller than 20 %. There is no difference between the shorter and the longer time series. This suggests that the lengths of the time series have no effect on the RPD values. This further implies that time series of different lengths can be compared and compiled into one data set for the purpose of this study. Moreover, this highlights the possible large differences among the various station pairs involved.
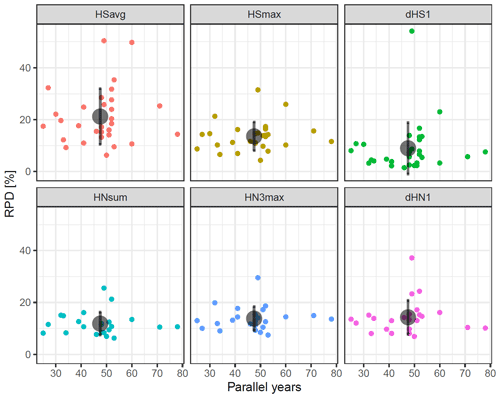
Figure 1Relative percentage differences (RPDs) as a function of number of parallel years for six snow climate indicators. Black dots and error bars indicate mean and standard deviations. The variables are defined in Table 1. Snow depth (HS) and snowfall (HN) indicators are based on 30 and 24 station pairs, respectively.
The absence of any clear relationship between observational length and RPD (Fig. 1) justifies the combined use of station pairs with varying lengths. However, it could be possible that the overall variations are too large to disentangle the signal of possible breaks from the noise.
4.2 Seasonal influence
To explore the effects of various seasons on the snow climate indicators, we calculated RPD and absolute differences (absD) for three commonly used seasons: winter (DJF), spring (MA), and the 6 months November to April (NDJFMA), as well as for each individual month. Figure 2 summarizes the results. Here we found that RPD for DJF and NDJFMA are similar (difference never exceeds 5 %). However, the main differences are visible in the MA period, which shows the largest RPD values for all indicators (Fig. 2 panel a).
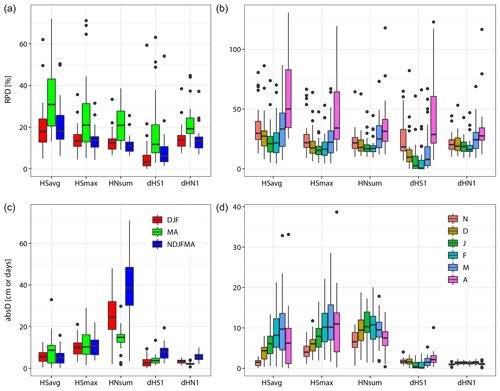
Figure 2Shown are relative percentage deviations (RPD) and absolute differences (absD) for five snow climate indicators. Depicted are (a, b) three seasons from December to February (DJF, red), March–April (MA, green), and November to April (NDJFMA, blue) and (c, d) all months individually. Snow depth (HS) and snowfall (HN) indicators are based on 30 and 24 station pairs, respectively. The variables are defined in Table 1.
Furthermore, dHS1 has the lowest median RPD for all seasons, whereas HSavg is the one with the largest median RPD for all three seasons. Overall median RPD values for NDJFMA are between 7 % and 18 % and correspond to findings in Buchmann et al. (2021a). Figure 2 (panel b) further reveals that the largest relative variations occur early (November) and late (MA) in the season and the patterns look similar for all indicators.
However, the picture looks somewhat different when we look at absD (Fig. 2 panels c and d). Here we see that the largest median differences are not found in the same seasons for all indicators. Figure 2 (panel d) reveals that absD for HSavg and maximum snow depth (HSmax) seem to be largest in March and smallest in November, whereas for the sum of new snow (HNsum), the largest absD values are found in January and February and the smallest values in November and April. The daily snow depth values are generally largest in March and lowest in November, thus explaining the pattern of absD for HSavg and HSmax. The same applies to HNsum; the largest monthly snowfall sums are observed in January and February, whereas November and April are months with usually the smallest snowfall sums. dHS1 shows the largest absD at the beginning and end of the snow season (first and last 2 months) likely due to larger differences in thermal conditions (ground and local air temperature) in these transition months. dHN1, in contrast, shows fewer monthly differences than the rest, because the number of snowfall events is only marginally dependent on local measurement conditions.
These monthly patterns transform to indicator-dependent seasonal absD patterns (Fig. 2 panel c). The different seasons reveal much smaller variations compared to RPD. For NDJFMA, absD varies between 5 and 10 cm or 5 and 8 d for all indicators with the exception of HNsum. Due to the cumulating nature of the snowfall sum, the indicator HNsum always shows the largest absD values, which increases with the number of included months (NDJFMA). The same is true for the other snowfall count indicator, dHN1, but on a much lower level. Additional information of absD allows us to put the RPD into context. The lower absD values for dHS1 during DJF are no surprise, as the ground tends to be snow-covered for almost all station pairs during this period; hence the difference only applies to cases where the snow cover is quite low (a couple of centimetres). NDJFMA shows the highest absD value for dHS1 because this period contains the beginning and end of the season.
These findings imply that the higher RPD values in the MA period for all indicators are mainly caused by smaller absolute values in this period. The only exceptions are HSavg and HSmax, which also show high absD values in the MA period. This indicates that the local bias is indeed larger for snow depth during MA.
To further test the seasonal influence from a more general point of view, we just looked at the snow depth evolution, comprising of accumulation and ablation for each station pair irrespective of the actual season. The two station pairs below 700 m a.s.l. were excluded from this analysis due to median winter seasons shorter than 60 d. We calculated the climatology of the daily snow depth differences for each station pair. We then constructed the difference series as the combination of the first (and last) 60 d for each station pair. The median of all these difference series is the thick black line in Fig. 3. These two periods stand for accumulation (first 60 d) and ablation (last 60 d). The 60 d period is an empirical value. Here we found that the differences and variabilities observed in the first period seem to be smaller than in the last period (Fig. 3). This suggests that the ablation period shows more variation than the accumulation period, which corroborates the pattern found in the absD analysis.
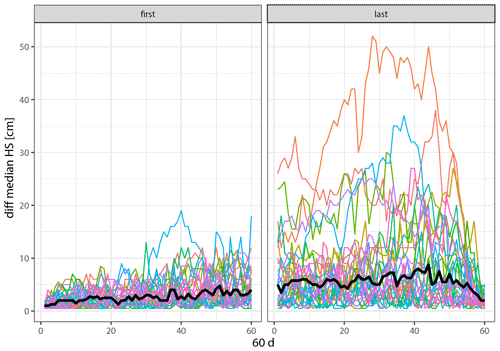
Figure 3Median daily absolute differences in snow depth for each station pair for the first and last 60 d of each snow season. The bold line highlights the median of all station pairs.
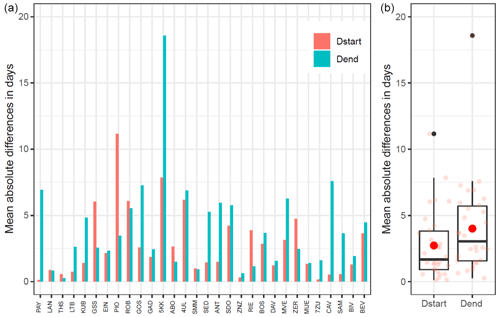
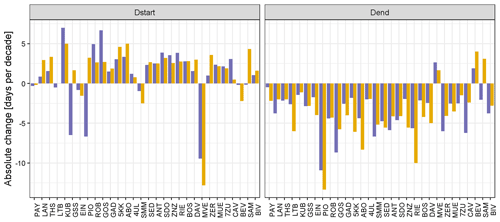
Figure 4(a) Mean absolute differences in onset (Dstart) and disappearance (Dend) dates for all station pairs. The station pairs are ordered from left to right according to their elevation. (b) Variations of mean absolute differences of Dstart and Dend for all station pairs and available years. The light red dots mark the actual values, and the bold red dot indicates the mean.
4.3 Snow onset and disappearance dates
To further investigate the larger impact of the local bias towards the end of the snow season compared to the beginning, differences between station pairs in mean snow onset (Dstart) and snow disappearance dates (Dend) are analysed. Figure 4 (left) highlights the computed absolute differences for Dstart and Dend. We found that for 20 out of 30 station pairs, differences of Dend are larger than differences of Dstart. In contrast to the general impression that Dstart should be the same for parallel stations, our data show the differences of several days are not uncommon, which could be caused by the different thermal conditions of the ground of the measurement field. Figure 4 (right) depicts the mean inter-pair differences for Dstart and Dend. The median values over all station pairs are 2 d for snow onset and 3 d for snow disappearance dates. This corroborates the previous findings of Fig. 3 that spring (ablation) shows larger variations than autumn (accumulation), with PIO, ZER, GSS, and RIE being the exceptions. We found that for 75 % of the station pairs, Dstart varies between 0 and 4 d, whereas Dend shows slightly larger differences (0 to 6 d). A possible explanation for the large differences associated with station 5KK is discussed in Sect. 4.6.
Additionally, we use absolute temporal changes of snow onset and disappearance dates, expressed as days per decade, as yet another indicator to test the variability within the station pairs. For this purpose, the temporal change in days for Dstart and Dend is calculated for each station pair (Fig. 5). The pairs are aligned from low (left) to high (right) elevation. Here we see that for a majority of station pairs, the direction of changes for Dstart and Dend is the same, and Dstart tends to be associated with positive (later) and Dend with negative (earlier) values.
Although inter-pair differences occur more pronounced and more frequently during the decline phase (spring) compared to the accumulation period (Fig. 3), the actual end of the snow season (snow disappearance date) does not show these larger variations (Fig. 4). Dend appears to be a rather stable indicator, varying for 50 % of the station pairs on average between 2 and 6 d. In contrast to what is observed in the much more complex topography on the catchment scale, this is a good result as the relative changes derived from trend analysis of station (point) data from flat measurement fields can also be transferred to the catchment scale, even though the absolute values may be different (Grünewald and Lehning, 2015).
Our values of temporal changes in Dstart and Dend (Fig. 5) correspond to values obtained by Klein et al. (2016). Although the definition of Dstart and Dend are different and also the time periods are not exactly the same, the absolute changes in Dstart and Dend are mostly similar for the few stations analysed by both studies. This suggests that the absolute changes of Dstart and Dend are in general quite robust.
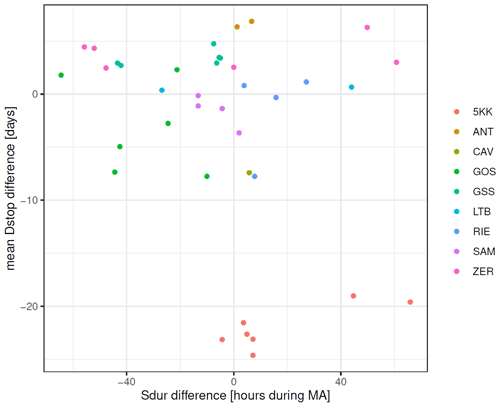
Figure 6Relationship between differences in snow disappearance dates (Dend) and differences in potential sunshine durations (Sdur) for the months March and April (MA), calculated for a selection of station pairs with manually checked coordinates during different time periods.
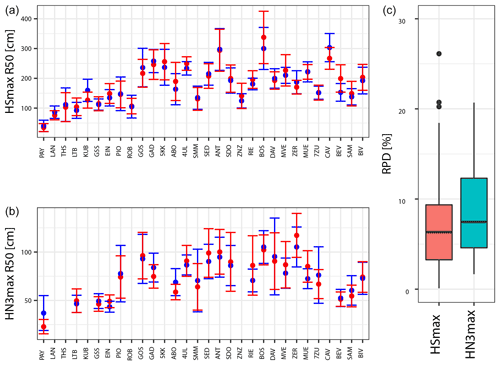
Figure 7Return levels for seasonal maximum snow depth (HSmax) (top left) and maximum 3 d new snow sum (HN3max) (bottom left) for 50-year return periods. MeteoSwiss (SLF) stations are coloured red (blue). The error bars indicate the 95 % confidence intervals. Station pairs are ordered from left to right from low to high elevation. Relative percentage differences (RPDs) of return levels for HSmax and HN3max are depicted on the right.
4.4 Influence of potential sunshine duration on snow disappearance dates
When looking for a possible explanation for the inter-pair differences in Dend with available local-scale variables, we compared them to differences in potential sunshine durations. Figure 6 displays the relationship of differences in Dend and differences in potential sunshine duration during March and April for a selection of station pairs. The largest difference in a station pair (64 h during MA) amounts to approximately 1 h per day. Mean and standard deviations of all unpaired combinations of this subset are −5 and 124 h. Here we found no relationship between potential sunshine duration and differences in Dend. As outlined in Sect. 2, our metadata is not perfect, and although we limited this analysis to a selection of measurement sites with reliable coordinates, the influence of local-scale obstacles cannot be detected with such an approach. As the accuracy is true for the 50 m scale, but not for 10 m, the conundrum in front or behind a house still remains. An example is given in Sect. 4.6.
4.5 Extreme value analyses
To test whether estimated extreme events based on annual maximum values of snow depth and snowfall differ significantly within station pairs, return levels for two indicators, HSmax and HN3max, are calculated for a 50-year return period using the NDJFMA season (Fig. 7). Inter-pair differences of the 50-year return levels are small (7 %–8 % for both indicators). We found that the return levels of the individual stations are usually within the 95 % confidence intervals, indicated by error bars in Fig. 7. This suggests that in spite of obvious differences, in terms of return levels for 50-year return periods, the station pair values are similar or at least within each other's 95 % confidence intervals.
The relative differences of return levels for HSmax and HN3max are less than 30 % for all station pairs and less than 15 % for 75 % of the station pairs. For all but three station pairs these values are within each other's 95 % confidence intervals, which may be useful for applications where there is normally only a single time series available. On the other hand, the analysis clearly proves that just taking the return value of one station, without considering the estimation uncertainty, drastically limits the validity of the results.
4.6 Metadata, possible explanations, and limitations
To illustrate and explain the issues associated with metadata, we focus on the station pair Klosters (5KR, 5KK). Concerning metadata, at a first glance, no striking difference is visible between the two stations. Elevation and surroundings are similar. One station is situated at a train station and the other next to a power station. However, when looking closer, it is revealed that the one at the train station is located on a first-floor roof deck cutting. The second one sits just 5 m to the east of a high turbine house (with corresponding shading) at the power station. Both sites are affected by their surroundings, and corresponding exposure to wind, solar radiation, and temperature is definitely different. Such differences are difficult or impossible to detect if the coordinates or metadata are not accurate.
Even though potential sunshine durations can vary on a local scale, especially in mountainous areas, the influence on specific stations is virtually impossible to determine. The influence of a tree or house in close proximity to a station (not only regarding sunshine duration) remains an important but unaccountable factor, especially because the exact location of the snow measurement stake in the past is often not known. It is therefore not possible to attribute any local factors in the first place. For example, a measurement field in front of a south-facing wall is influenced completely differently than a station located behind said wall on the north-facing side. These limitations inhibit the simple use of terrain indicators to explain the variations. Furthermore, the influence of the observer on the snow onset or disappearance date cannot go unnoticed. Officially, the ground ought to be declared snow-free if at least 50 % of the measurement field is snow-free. However, as simple as the instruction may sound, the interpretation can vary and may easily account for a difference of a couple of days. Unfortunately, that remains impossible to prove.
Ideally, station metadata would include the exact coordinates of the snow stake and panoramic pictures of its surroundings. Also, regular visits to sites and observers would be beneficial. As our focus is solely on parallel measurements, the scalability to higher elevations is limited by the fact that there are no stations above 1800 m a.s.l. Therefore, any scalability attempts would involve a lot of speculation.
We presented the first assessment of seasonal local-scale variability of common extremal indices and snow climate indicators based on a unique data set of long-term parallel snow measurements.
Our term variability or local bias is only valid for the parallel analysis (two point measurements). But even so, the results give an indication of possible variations for various indices.
Regarding common snow climate indicators, the results revealed relatively small median differences for the majority of the station pairs and indicators. However, spring months (MA) have the highest relative differences (16 %–30 %) and show more inter-pair variation (8 %–43 %) for all indicators than DJF (2 %–24 %) or NDJFMA (3 %–25 %). Relative differences for these two seasons varied between 3 % (days with snow on the ground) and 20 % (average snow depth) for all indicators, whereas average snow depth also demonstrated the largest spread of all indicators. Average snow depth also revealed in absolute terms the highest local bias (ca. 10 cm) in spring. Additionally, inter-pair median differences of the snow disappearance date (per definition a proxy for spring) displayed again more variation and higher absolute values than the snow onset date. However, the differences between the local bias of the snow disappearance date (2 d) and the snow onset date (3 d) are small; nevertheless, there is considerable variation for some station pairs.
As the station pairs are constructed with stations that are on average located within 1 km, the variations are most likely down to local-scale influences. This suggests that seasonal differences are likely caused by local bias, which in isolated cases can have large effects and that local bias is probably amplified in MA (and November), likely because of the larger impact of radiation (and thus temperature). However, insufficient metadata prohibits further analyses on the influence of local-scale factors. But being able to quantify season-dependent biases is important in itself, as it increases our knowledge about existing inhomogeneities, especially in view of homogenization efforts of snow data series. The larger differences found in spring may be an indication to preferably search for inhomogeneities (breaks) in these months or to determine correction factors separately for the ablation season.
The analysis of estimated 50-year return periods based on annual extreme values demonstrates that the return levels for HSmax and HN3max, for the large majority of station pairs, are within each other's 95 % confidence intervals, corroborating that the knowledge of considering the uncertainty in return level estimation is indispensable.
Generally, local bias is often small and negligible for many applications, at least for the large majority of the stations.
The problem is that stations exhibiting local bias are not easily detectable in the record without the availability of parallel measurements.
Therefore, a larger number of neighbouring stations are needed to find such problematic stations and to be able to develop stable homogenization procedures. Assuming the same problem also exists in other parts of the world implies that the current number of available long-term snow measurement sites should at least be maintained.
Table A1Station pairs, available parallel periods, mean elevation, and number of parallel years. HN indicates whether a station pair was used for HN analyses. mDstart and mDend are mean onset and disappearance dates, mHSavg indicates the mean average snow depth, and mdHS1 indicates the mean number of days with snow on the ground. Station indicators starting with a number refer to SLF stations, and station indicators without a number refer to MeteoSwiss stations.
The basis for all our analyses, the indicator data set, is available from EnviDat: https://doi.org/10.16904/envidat.218 (Buchmann et al., 2021b).
CM, MiB, and MoB designed the outline with input from SB. MoB performed the analyses and wrote the draft. The revised manuscript was written by MoB with inputs from all authors. CM supervised the work.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Johannes Aschauer (SLF) for his valuable work in sorting out the metadata mess and contribution to the data set. We thank Francesco Issota (MeteoSwiss) for providing the sunshine duration (Sdur) data set and Wolfgang Schöner and Gernot Resch for valuable discussions. Our thanks go to Craig Smith and Kay Helfricht and one anonymous referee, whose valuable comments helped to improve the manuscript.
This research has been supported by the Schweizerischer Nationalfonds zur Förderung der Wissenschaftlichen Forschung (grant no. 175920).
This paper was edited by Ketil Isaksen and reviewed by Craig Smith, Kay Helfricht, and one anonymous referee.
Bocchiola, D., Bianchi Janetti, E., Gorni, E., Marty, C., and Sovilla, B.: Regional evaluation of three day snow depth for avalanche hazard mapping in Switzerland, Nat. Hazards Earth Syst. Sci., 8, 685–705, https://doi.org/10.5194/nhess-8-685-2008, 2008.
Brown, R. D. and Robinson, D. A.: Northern Hemisphere spring snow cover variability and change over 1922–2010 including an assessment of uncertainty, The Cryosphere, 5, 219–229, https://doi.org/10.5194/tc-5-219-2011, 2011.
Buchmann, M., Begert, M., Brönnimann, S., and Marty, C.: Evaluating the robustness of snow climate indicators using a unique set of parallel snow measurement series, Int. J. Climatol., 41 E2553–E2563, https://doi.org/10.1002/joc.6863, 2021a.
Buchmann, M., Aschauer, J., Begert, M., and Marty, C.: Snow climate indicators derived from parallel manual snow measurements, EnviDat [data set], https://doi.org/10.16904/envidat.218, 2021b.
Foster, J. L.: The Significance of the Date of Snow Disappearance on the Arctic Tundra as a Possible Indicator of Climate Change, Arct. Alp. Res., 21, 60–70, https://doi.org/10.2307/1551517, 1989.
Grünewald, T. and Lehning, M.: Are flat-field snow depth measurements representative? A comparison of selected index sites with areal snow depth measurements at the small catchment scale, Hydrol. Process., 29, 1717–1728, https://doi.org/10.1002/hyp.10295, 2015.
Haberkorn, A.: European Snow Booklet – an Inventory of Snow Measurements in Europe, EnviDat, https://doi.org/10.16904/envidat.59, 2019.
Kirdyanov, A., Hughes, M., Vaganov, E., Schweingruber, F., and Silkin, P.: The importance of early summer temperature and date of snow melt for tree growth in the Siberian Subarctic, Trees, 17, 61–69, https://doi.org/10.1007/s00468-002-0209-z, 2003.
Klein, G., Vitasse, Y., Rixen, C., Marty, C., and Rebetez, M.: Shorter snow cover duration since 1970 in the Swiss Alps due to earlier snowmelt more than to later snow onset, Clim. Change, 139, 637–649, https://doi.org/10.1007/s10584-016-1806-y, 2016.
Liston, G. E. and Elder, K.: A Meteorological Distribution System for High-Resolution Terrestrial Modeling (MicroMet), J. Hydrometeorol., 7, 217–234, https://doi.org/10.1175/JHM486.1, 2006.
Livensperger, C., Steltzer, H., Darrouzet-Nardi, A., Sullivan, P. F., Wallenstein, M., and Weintraub, M. N.: Earlier snowmelt and warming lead to earlier but not necessarily more plant growth, AoB Plants, 8, plw021, https://doi.org/10.1093/aobpla/plw021, 2016.
Marcolini, G., Bellin, A., Disse, M., and Chiogna, G.: Variability in snow depth time series in the Adige catchment, J. Hydrol. Reg. Stud., 13, 240–254, https://doi.org/10.1016/j.ejrh.2017.08.007, 2017.
Marty, C. and Blanchet, J.: Long-term changes in annual maximum snow depth and snowfall in Switzerland based on extreme value statistics, Clim. Change, 111, 705–721, https://doi.org/10.1007/s10584-011-0159-9, 2012.
Peng, S., Piao, S., Ciais, P., Friedlingstein, P., Zhou, L., and Wang, T.: Change in snow phenology and its potential feedback to temperature in the Northern Hemisphere over the last three decades, Environ. Res. Lett., 8, 014008, https://doi.org/10.1088/1748-9326/8/1/014008, 2013.
Roland, J., Filazzola, A., and Matter, S. F.: Spatial variation in early-winter snow cover determines local dynamics in a network of alpine butterfly populations, Ecography, 44, 334–343, https://doi.org/10.1111/ecog.05407, 2021.
Scherrer, S. C. and Appenzeller, C.: Swiss Alpine snow pack variability: major patterns and links to local climate and large-scale flow, Clim. Res., 32, 187–199, https://doi.org/10.3354/cr032187, 2006.
Seibert, J. and Vis, M. J. P.: Teaching hydrological modeling with a user-friendly catchment-runoff-model software package, Hydrol. Earth Syst. Sci., 16, 3315–3325, https://doi.org/10.5194/hess-16-3315-2012, 2012.
Sen, P. K.: Estimates of the regression coefficient based on Kendall's tau, J. Am. Stat. Assoc., 63, 1379–1389, 1968.
Stone, R. S., Dutton, E. G., Harris, J. M., and Longenecker, D.: Earlier spring snowmelt in northern Alaska as an indicator of climate change, J. Geophys. Res.-Atmos., 107, ACL 10-1–ACL 10-13, https://doi.org/10.1029/2000JD000286, 2002.
Theil, H.: A rank-invariant method of linear and polynomial regression analysis, Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen Series A, 53, 386–392, 1950.
Vorkauf, M., Marty, C., Kahmen, A., and Hiltbrunner, E.: Past and future snowmelt trends in the Swiss Alps: the role of temperature and snowpack, Clim. Change, 165, 44, https://doi.org/10.1007/s10584-021-03027-x, 2021.
World Meteorological Organization: World Meteorological Organization, and Organisation Météorologique Mondiale: Guide to meteorological instruments and methods of observation, WMO, Geneva, 2018.
Zampieri, M., Scoccimarro, E., Gualdi, S., and Navarra, A.: Observed shift towards earlier spring discharge in the main Alpine rivers, Sci. Total Environ., 503–504, 222–232, https://doi.org/10.1016/j.scitotenv.2014.06.036, 2015.