Behavior of saline ice under cyclic flexural loading

New systematic experiments reveal that the flexural strength of saline S2 columnar-grained ice loaded normal to the columns can be increased upon cyclic loading by about a factor of 1.5. The experiments were conducted using reversed cyclic loading over ranges of frequencies from 0.1 to 0.6 Hz and at a temperature of −10 ^∘C on saline ice of two salinities: 3.0 ± 0.9 and 5.9 ± 0.6 ‰. Acoustic emission hit rate during cycling increases with an increase in stress amplitude of cycling. Flexural strength of saline ice of 3.0 ± 0.9 ‰ salinity appears to increase linearly with increasing stress amplitude, similar to the behavior of laboratory-grown freshwater ice (Murdza et al., 2020b) and to the behavior of lake ice (Murdza et al., 2021). The flexural strength of saline ice of 5.9 ± 0.6 ‰ depends on the vertical location of the sample within the thickness of an ice puck; i.e., the strength of the upper layers, which have a lower brine content, was found to be as high as 3 times that of lower layers. The fatigue life of saline ice is erratic. Cyclic strengthening is attributed to the development of an internal back stress that opposes the applied stress and possibly originates from dislocation pileups.

1 Introduction

Fatigue of materials is a subject of practical importance in engineering and has been widely studied (Bathias and Pineau, 2013; Broek, 1986; Schijve, 2009; Suresh, 1998). Fatigue refers to changes in material properties resulting from cyclic loading. Fatigue strength of crystalline materials is typically controlled by microcrack initiation and subsequent growth that leads to failure.

It is not surprising that fatigue appears to play an important role in sea ice mechanics. For example, the Arctic and Antarctic floating ice covers and ice shelves are subjected to cyclic loading from ocean swells that can penetrate deeply into an ice pack and potentially result in the breakup of the ice cover (Squire, 2007). Such events, where under the action of surface waves a floating ice cover exhibited sudden breakup into smaller pieces, have been repeatedly witnessed and described (Shackleton, 1982; Liu et al., 1988; Prinsenberg and Peterson, 2011; Asplin et al., 2012; Collins et al., 2015; Kohout et al., 2016; Hwang et al., 2017). Ice cover breakup leads to a decline in albedo (Pistone et al., 2014; Zhang et al., 2019) and to the acceleration of melting. Also, smaller ice floes attenuate ocean waves less effectively than does the parent solid ice cover, thereby endangering coastal zones to erosion. Given the retreat of the sea ice cover and the attendant increase in oceanic fetch, larger waves are expected to develop; correspondingly, the remaining ice cover is expected to be subjected to episodes of greater cyclic loading. The potential for fatigue failure is thus increasing.

Cyclic loading may also play an important role in other scenarios. For instance, during ice–structure interactions (Jordaan, 2001; Hendrikse and Metrikine, 2016; O'Rourke et al., 2016; Jordaan et al., 2008) the structure itself, such as a lighthouse, may be weakened or damaged to a degree that depends on the strength of the ice. Other examples are runways and roads that are built by freezing water on cold oceans, rivers, and lakes and subsequently subject to cyclic loading. Therefore, it is important to understand the behavior of ice under cyclic loading.

Currently, the effects of cyclic loading on the physical and mechanical properties of sea ice and on the susceptibility of the material to fatigue are poorly constrained. Tabata and Nohguchi (1980) conducted experiments on sea ice sampled from Lake Saroma, Hokkaido, Japan, and from Utqiaġvik, Alaska. They loaded the ice cyclically under uniaxial compression between two specified stress levels under a variety of combinations of strain rate (from 10⁻⁵ to 10⁻² s⁻¹), temperature (from −2 to −24 ^∘C) and orientation (horizontal and vertical). They found that with a decrease in average stress and with a decrease in amplitude, the time to failure increases; and by lowering the temperature, the time to failure and the number of cycles also increases.

Other evidence of the weakening of sea ice under wave-driven in situ cyclic loading is discussed by Haskell et al. (1996), Bond and Langhorne (1997), Langhorne et al. (1998, 1999, 2001). In these works the authors obtained an S–N fatigue curve (S, upper peak stress of cycling; N, number of cycles imposed to failure), typical of curves obtained from engineering materials, i.e., for lower stress amplitude more cycles are needed for failure. The authors stated that the endurance limit, that is the stress amplitude below which the sea ice can withstand an unlimited number of cycles, is approximately one-half the failure stress of non-cycled ice.

The constitutive behavior of saline ice under cyclic loading was also investigated previously (Cole, 1995, 1998; Cole et al., 1998, 2002; Cole and Dempsey, 2004; Cole and Durell, 1995; Dempsey et al., 2003; Wei et al., 2020); specifically, inelastic deformation of sea ice was explored and interpreted in terms of a dislocation-based mechanism. In these works the authors investigated the effect of temperature (from −5 to −50 ^∘C), microstructure (total porosity varied from 14 to 104 ppt), cyclic stress amplitude (from 0.04 to 0.8 MPa), loading frequency (from 10⁻³ to 1 Hz), and dry isothermal vs floating specimens on the response of the ice. However, the strength of ice after it had been cycled was not measured.

Nothing more (to our knowledge) has been reported on the fatigue of sea ice. The topic is absent from a critical review by Squire (2007) and from two recent books on ice (Schulson and Duval, 2009; Weeks, 2010).

The behavior summarized above indicating the weakening of ice under cyclic loading, obtained from experiments conducted on saline and sea ice, might possibly account for the sudden breakup of natural ice covers. However, this behavior appears in conflict with the behavior of freshwater ice under cyclic loading (Cole, 1990; Gupta et al., 1998; Iliescu et al., 2017; Iliescu and Schulson, 2002; Murdza et al., 2019, 2020b, a). In those experiments, it was discovered that the ice flexural strength increases upon repetitive loading, followed by the recovery of the cyclic-induced increment in strength to the original non-cycled strength upon post-cycling annealing. This difference in the behavior of the two kinds of ice could perhaps be attributed to the presence of defects in sea/saline ice, such as brine pockets , brine channels and non-penetrating microcracks. Such defects serve as stress concentrators, thereby lessening the need to nucleate cracks to the degree that fatigue life may be governed primarily by crack propagation. The strengthening of ice is of more than scientific interest, reflected, perhaps in an interesting comment of an arctic engineer who reported that builders of ice roads never trust the ice until it had been “worked in” (Masterson, 2018).

Therefore, given that limited information about the behavior of sea/saline ice under cyclic loading and given the discrepancy in behavior of fresh and sea/saline ice, we conducted a study under controlled conditions in the laboratory on the flexural behavior of saline ice. In this paper, we describe the experiments in which beams of S2 columnar-grained saline ice of two salinities (3.0 ± 0.9 and 5.9 ± 0.6 ‰) were subjected at −10 ^∘C to four-point, reverse cycling at ∼ 0.1–0.6 Hz and then, after several hundred or more cycles, were bent to failure, provided the beams did not break during cycling. We chose the rate of cycling to simulate the vibration frequency of a natural sea ice cover (Collins et al., 2015).

2 Experimental procedure

2.1 Ice growth and characterization

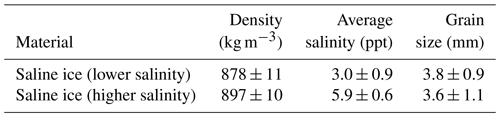
We studied saline ice of two meltwater salinities: 3.0 ± 0.9 and 5.9 ± 0.6 ppt, where ± sign indicates standard deviation. We produced the ice in the laboratory in an 800 L circular polycarbonate tank in the manner described previously (Golding et al., 2014). Briefly, solutions containing 17.5 ± 0.2 ppt and 35 ± 0.2 ppt (parts per thousand, or ‰) of the commercial product “Instant Ocean” salt mixture were prepared and then frozen unidirectionally downward over a period of about 7 d by using a top-placed cold plate maintained at a temperature $T=-\mathrm{20}$ ± 0.1 ^∘C. Before bringing the cold plate into contact with the salt-water solution, the top surface of the solution was seeded with freshwater ice fragments of ∼ 0.3–1 mm in diameter. This procedure produced pucks ∼ 1 m in diameter and ∼ 0.3 m thick. For practical considerations, the bottom, skeletal layer of ice of about 7–10 cm was discarded as it was slushy and weak; we also believe that the skeletal layer does not play a significant role in supporting load. The top layer of ice of a few centimeters was also discarded because it was seeded and its grain size was considerably smaller and its microstructure thus different from the rest of the ice puck. Meltwater salinity was measured using a calibrated YSI Pro30 conductivity and salinity probe.

Table 1 Physical properties of as-grown saline ice.

Figure 1 Photographs of a vertically oriented (a) and a horizontally oriented (b) thin section (∼ 1 mm) of columnar-grained, saline ice of lower salinity (3.0 ± 0.9 ppt) as viewed between crossed-polarized filters; photographs of a vertically oriented (c) and a horizontally oriented (d) thin section of saline ice of higher salinity (5.9 ± 0.6 ppt).

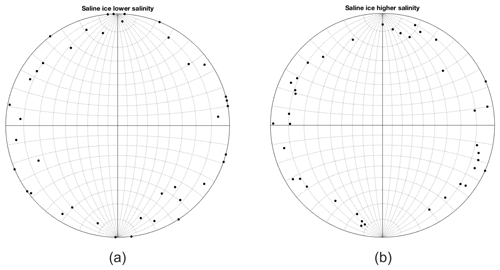
Figure 2 Stereographic projection plots of crystal c-axis {0001} orientations in saline ice of lower (3.0 ± 0.9 ppt) salinity (a) and saline ice of higher (5.9 ± 0.6 ppt) salinity (b).

Figure 1 shows the microstructure of the ice. Table 1 lists its density and the average grain size of the test specimens described below. Figure 2 shows stereographic projections of the orientation of the crystallographic c axes. The ice is characterized by columnar-shaped grains whose growth texture is marked by c axes confined within about 15^∘ of the horizontal plane of the parent ice puck and randomly oriented within that plane. In other words, the ice is termed S2, after Michel and Ramseier (1971), and is similar to natural first-year sea ice (for comparison, see Fig. 3.7 of Schulson and Duval, 2009). The grain size noted above is the average diameter of the columnar-shaped grains, ranging from about 2 to 7 mm in Fig. 1.

Figure 3 Photographs of saline ice samples of lower salinity (3.0 ± 0.9 ppt) from the top (a) and bottom (b) of an ice block and saline ice samples of higher salinity (5.9 ± 0.6 ppt) from the top (c) and bottom (d) of an ice block. The concentration of whitish features along the width of a sample in (d) is shown inside circles, which is a predominant place for a crack to initiate. The columnar grains run in and out of the images. Scale bars: 20 mm.

Figure 4 Photograph of a sample from the bottom of an ice block of higher salinity (5.9 ± 0.6 ppt) before cycling (a) and after (b) failure. Note a crack that propagated along whitish features in the area in (a) depicted by the circle. Scale bars: 20 mm.

2.2 Growth features

The ice contained both sub-millimeter-sized brine pockets and supra-millimeter-sized drainage channels, reminiscent of natural sea ice. Figures 3 and 4 show examples. The ice of lower salinity (3.0 ± 0.9 ppt) had fewer defects of both kinds. Some of the ice of higher salinity (5.9 ± 0.6 ppt) possessed channels whose size was almost as large as the grain diameter. The defects scattered light to the degree that in bulk form the ice had an overall opaque appearance. When observed in thin section (∼ 1 mm) the ice exhibited to the naked eye distinct linear whitish features which we took to be sets of interconnected brine pockets that could possibly be filled with very fine-grained ice. The ice of higher salinity possessed more of these features, especially near the bottom of the parent puck (which was the last part to solidify). Our sense is that these features served as stress concentrators, particularly ones that traversed the width of the test specimen (described below), thereby weakening the ice. Indeed, as will become apparent, samples obtained from near the bottom of a puck of higher salinity (5.9 ± 0.6 ppt) had relatively low flexural strength.

Because the ice of both salinities exhibited a different appearance from the top and bottom of the parent puck, in preparing test specimens for flexing we distinguished them by their position (depth from top surface) within the ice puck from which they were prepared, Table 2.

Table 2 Flexural strength of non-cycled saline ice at −10 ^∘C and a displacement rate of 0.1 mm s⁻¹.

2.3 Sample preparation and test setup

Once the ice had been grown, it was cut into blocks of dimensions ∼ $\mathrm{10}\times \mathrm{30}\times \mathrm{20}$ cm³, where the longest and the shortest dimensions are in the horizontal plane of the original ice puck, perpendicular to the direction of growth. The blocks were stored in a cooler (at −10 ± 0.5 ^∘C) on their side (such that columnar-shaped grains were oriented horizontally) to reduce brine drainage for periods of time of about 1–10 weeks.

Specimens for flexing were manufactured from the ice blocks in the form of thin beams of dimensions h∼ 16 mm in thickness (parallel to the long axis of the grains), b∼ 85 mm in width, and l∼ 300 mm in length. The test specimens were allowed to equilibrate to the test temperature of −10 ± 0.5 ^∘C for at least 24 h before testing.

A detailed description of the specimens' preparation and loading can be found elsewhere (Iliescu et al., 2017; Murdza et al., 2018, 2019, 2020b). To summarize, the ice beams were flexed up and down under four-point loading under constant displacement rate using a servo-hydraulic loading system (MTS model 810.14) to which we attached a custom-built four-point loading frame, Fig. 5. The hydraulic actuator was driven up and down under displacement control with the load limited in both directions. A load cell, calibrated for both tension and compression, and a linear variable differential transformer (LVDT) gauge were used for measurements of load and displacement of the upper surface of the ice beam during cycling.

Acoustic emissions were recorded during cycling using a PCI-2 18-bit A/D system; its frequency response was 3 kHz–3 MHz and its minimum acoustic emission (AE) amplitude detection threshold was set to 45 dB. We used a micro 30STC sensor (9.5 mm diameter, 11 mm thickness), which was attached to the top surface of an ice beam with a rubber band. Vacuum grease was used as the coupling agent between the sensor and the ice surface.

The experiments were performed in a cold room at a temperature of −10 ^∘C and at an outer-fiber center-point displacement rate of 0.1 mm s⁻¹ (or outer-fiber strain rate of about $\mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹). This displacement rate resulted in an outer-fiber stress rate in the range from ∼ 0.3 to 0.5 MPa s⁻¹, outer-fiber stress amplitude in the range from 0.35 to 1.2 MPa, outer-fiber strain amplitude in the range from ∼ 1 to $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{4}}$, and frequencies in the range from 0.1 to 0.6 Hz (i.e., periods from ∼ 10 to 1.5 s). The period, as already noted, is similar to the period of ocean swells (Collins et al., 2015). The major outer-fiber stress σ_f was calculated from the relationship (the loading span is one-half of the support span)

$$\begin{array}{}\text{(1)}& {\mathit{\sigma }}_{\text{f}}={\displaystyle \frac{\mathrm{3}PL}{\mathrm{4}b{h}^{\mathrm{2}}}},\end{array}$$

where P is the applied load and L is the distance between the outer pair of loading cylinders (shown in Fig. 5b) and is set by the geometry of the apparatus to be L=254 mm.

We used two different loading procedures, as we did earlier in our study of S2 freshwater ice. Type I loading was a completely reversed stress cycle with constant stress amplitude and mean stress of zero. Type II was similar to Type I but incorporated an increasing multi-level (or step-level) stress amplitude. This second type of loading essentially consisted of several Type I steps of increasing stress amplitudes. In the present study for stress amplitudes below 0.7 MPa, we used Type I loading. To cycle ice samples at stress amplitudes above 0.7 MPa, we first pre-conditioned specimens through step-loading the Type II procedure at progressively higher stress amplitude levels; i.e., we cycled specimens for ∼ 300 times at each of the following stress amplitudes: 0.7, 0.75, 0.8, 0.85 MPa, and so on either until failure occurred or until a specific value of stress amplitude set by the operator (see Iliescu et al., 2017, and Murdza et al., 2018, for details). To change stress amplitude the loading was stopped for ∼ 15 s to change settings. After pre-conditioning, the specimens were cyclically loaded according to Type I loading at least 300 times and generally for ∼ 2000 times, since no change in strength was observed beyond a few hundred cycles (see below).

Figure 5 Photograph (a) and sketch (b) of the four-point bending apparatus connected to an MTS hydraulic testing system (Iliescu et al., 2017; Murdza et al., 2020b). The upper part is attached to the frame of the machine while the mobile middle part is attached through a fatigue-rated load cell to the piston. The apparatus is made from an aluminum alloy; the loading cylinders are made from stainless steel.

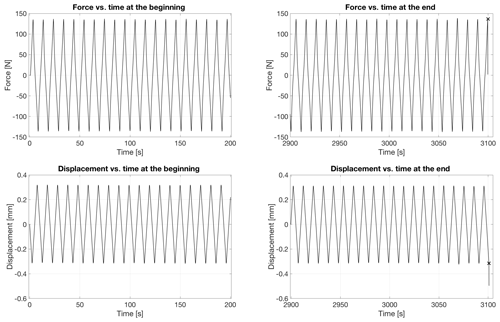
Figure 6 Curves of force/load and displacement vs. time for periods of 200 s near the beginning and near the end of cycling before fatigue failure occurred. Marker symbol “x” denotes a moment of specimen failure. Force of ∼ 135 N corresponds to ∼ 1.2 MPa.

Figure 6 shows measurements of load and of displacement versus time at the beginning and near the end of cycling before specimen failure of a lower-salinity specimen (3.0 ± 0.9 ppt). The measurements detected no softening. According to Bažant et al. (1984) softening is a decline of stress at increasing strain or, in our case, an increase in strain during cycling at constant stress amplitude during the tests. The absence of detectable softening during cycling of the saline ice is reminiscent of the absence of softening during the cycling of freshwater ice (Iliescu et al., 2017; Murdza et al., 2020b).

3 Results and observations

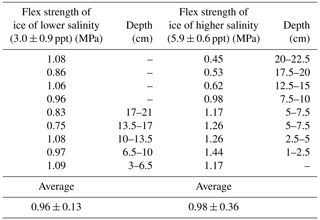
3.1 Flexural strength of non-cycled ice

The flexural strength of non-cycled saline ice of both salinities was measured at −10 ^∘C and at a nominal outer-fiber center-point displacement of 0.1 mm s⁻¹. The results are listed in Table 2. Failure more often occurred at random locations between the two inner loading cylinders and less often either below or slightly outside the loading cylinders. The reason for the latter location was the presence prior to testing of a significant concentration of whitish features at loading cylinders which served as stress concentrators and along which the failure ultimately occurred (similar to Fig. 4). The average and standard deviation of the measured flexural strength of saline ice of lower salinity (3.0 ± 0.9 ppt) are 0.96 ± 0.13 MPa. The strength of the lower-salinity ice did not correlate systematically with the depth of the parent puck from which ice beams were prepared. The measured strength compares favorably with the value of 0.85 ± 0.20 MPa reported by Timco and O'Brien (1994) for sea ice of similar salinity, as can be seen in Fig. 7. Brine volume fraction ν_b was calculated according to Frankenstein and Garner (1967):

$$\begin{array}{}\text{(2)}& {\mathit{\nu }}_{\text{b}}=\mathrm{0.001}\times S\left({\displaystyle \frac{\mathrm{49.185}}{\left|T\right|}}+\mathrm{0.532}\right),\end{array}$$

where T is temperature in degrees Celsius between −0.5 and −22.9 ^∘C, and S is meltwater salinity (in parts per thousand) of the ice.

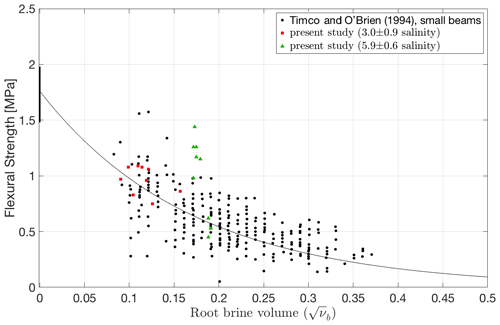
Figure 7 Flexural strength of saline ice as a function of root brine volume for the ice grown in the present study and for data from Timco and O'Brien (1994) for comparison.

The average and standard deviation of the measured flexural strength of saline ice of higher salinity (5.9 ± 0.6 ppt) are 0.98 ± 0.36 MPa. The measured values (Fig. 7) deviate slightly towards higher values compared to the data of Timco and O'Brien (1994), although scatter is significantly greater than the scatter in the strength of the ice of lower salinity (3.0 ± 0.9 ppt). This may be explained by the greater degree of interconnectivity of brine pockets at the bottom of an ice puck (discussed above and shown in Figs. 3 and 4). Indeed, the flexural strength of the higher-salinity specimens appears to depend on the depth of ice from which beams were prepared, Table 2. This result shows how much the strength of ice is sensitive to flaws and defects. Given that larger bodies usually contain larger defects, the flexural strength of sea ice on the medium and large scales, in the field (Karulina et al., 2013, 2019; Murdza et al., 2016) for instance, is expected to be lower than on the smaller scale of the present experiments.

We also compare our measurements of flexural strength with the tensile strength of sea ice. For this purpose, and as we did in our previous work on freshwater ice (Iliescu et al., 2017; Murdza et al., 2020b), flexural strength is divided by 1.7 (Ashby and Jones, 2012). This factor reflects the fact that the volume of the material which is subjected to the highest stress in bending is smaller than in uniaxial tension; thus, the largest defect which governs the failure may not be near the surface of a bent specimen. Upon dividing the flexural strength of the non-cycled saline ice of lower salinity by 1.7, we found the average across-column tensile strength from our experiments to be 0.96 ± 0.13 MPa $/$ 1.7 = 0.56 ± 0.08 MPa. This value compares favorably with the values 0.56 ± 0.06 MPa and 0.63 ± 0.12 MPa reported by Richter-Menge and Jones (1993) for the tensile strength of columnar-grained first-year sea ice of 4.1 ± 0.3 ppt salinity loaded uniaxially across the columns at a temperature of −10 ^∘C and strain rates of 10⁻⁵ and 10⁻³ s⁻¹. Recall that in the present experiments the outer-fiber strain rate was about $\mathrm{1.4}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹, which is within the range reported by Richter-Menge and Jones (1993). This agreement between direct and indirect measurements of tensile strength lends confidence that our lab-grown saline ice is a reasonably faithful analogue of natural sea ice.

Figure 8 Flexural strength and the corresponding number of cycles imposed for saline ice of lower salinity (3.0 ± 0.9) ppt cycled at 0.35 MPa outer-fiber stress amplitude at −10 ^∘C and 0.1 mm s⁻¹ outer-fiber center-point displacement rate.

3.2 Flexural strength versus number of reversed cycles under constant low stress amplitude

To determine whether there is a relationship between flexural strength and number of cycles imposed under a constant low stress amplitude, we performed via Type I loading a series of experiments on saline ice of lower salinity (3.0 ± 0.9 ppt) at −10 ^∘C at an outer-fiber center-point displacement rate of 0.1 mm s⁻¹ at a low stress amplitude of 0.35 MPa, i.e., at an amplitude less than one-half the flexural strength of non-cycled ice. Figure 8 shows the results. The number of cycles varied from about 100 to 14 000. The average strength and standard deviation of all data from Fig. 8 are 0.96 ± 0.23 MPa. As noted above, the strength and standard deviation of non-cycled ice are 0.96 ± 0.13 MPa. In other words, no strengthening was detected upon cycling up to 14 000 times at a stress amplitude of 0.35 MPa. For freshwater ice (Murdza et al., 2020b), we found that once the number of cycles at a given low stress amplitude exceeded 300, the number of cycles had no significant effect on the flexural strength, implying that a kind of saturation of strength developed. Given that result and the new results for saline ice, we followed the practice in the present study of cycling more than 300 times, often as many as 2000 times, before bending the ice to failure.

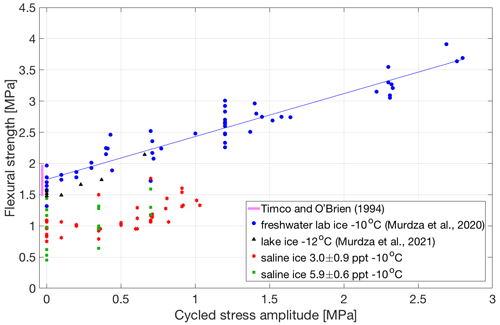
Figure 9 Flexural strength of freshwater ice and saline ice of lower (3.0 ± 0.9 ppt) and of higher (5.9 ± 0.6 ppt) salinity as a function of reverse-cycled stress amplitude. Freshwater ice laboratory and lake data are taken from Murdza et al. (2020b, 2021). Red five-pointed stars and green squares represent tests performed on saline ice of lower and higher salinities, respectively, at 0.1 mm s⁻¹ and −10 ^∘C. During all depicted tests the ice did not fail during cycling and was broken by applying one unidirectional displacement until failure occurred.

3.3 Flexural strength versus stress amplitude

The flexural strength increases with stress amplitude. Figure 9 shows measurements obtained from saline ice of both salinities cycled at −10 ^∘C at an outer-fiber displacement rate of 0.1 mm s⁻¹. For comparison, data from laboratory grown freshwater ice (Murdza et al., 2020b) of S2 character and from lake ice of the same character (Murdza et al., 2020a, 2021) are also shown. The relationship between the flexural strength, ${\mathit{\sigma }}_{{\text{f}}_c}$, and cycled stress amplitude, σ_a, for saline ice appears to be a linear one and, within experimental scatter, to have essentially the same sensitivity to stress amplitude as freshwater ice, namely

$$\begin{array}{}\text{(3)}& {\mathit{\sigma }}_{{\text{f}}_c}={\mathit{\sigma }}_{{\text{f}}_{\mathrm{0}}}+k{\mathit{\sigma }}_{\text{a}},\end{array}$$

where k=0.68 is a constant. For freshwater ice the non-cycled flexural strength is ${\mathit{\sigma }}_{{\text{f}}_{\mathrm{0}}}=\mathrm{1.75}$ MPa compared with ${\mathit{\sigma }}_{{\text{f}}_{\mathrm{0}}}=$ 0.96 MPa for the saline ice. There is, perhaps, in Fig. 9 a hint that for saline ice there is a threshold of about 0.4 MPa that must be exceeded to detect strengthening. Interestingly, this apparent threshold is similar in magnitude to the stress that marks the onset of significant AE activity under cyclic loading of sea ice cores (Cole and Dempsey, 2006). Although saline ice is weaker than freshwater ice, it appears that upon cycling its strength increases at the same rate as freshwater ice.

Although the rate of strengthening with stress amplitude appears to be the same for saline ice and freshwater ice, the maximum increase in strength in the case of saline ice of lower salinity (3.0 ± 0.9 ppt) is significantly lower. We were able to strengthen saline ice by about 50 % of the non-cycled strength compared with about 100 % for freshwater ice (Murdza et al., 2020b). Another point is that we almost were not able to cycle specimens at stress amplitudes greater than the flexural strength of non-cycled material, whereas in the case of freshwater ice we were able to cycle at stress amplitudes significantly greater than flexural strength of non-cycled ice. Indeed, the maximum cycled stress amplitude we were able to reach in the case of saline ice of lower salinity (3.0 ± 0.9 ppt) during all tests was 1.1 MPa, which is not statistically different from the non-cycled flexural strength of 0.96 ± 0.13 MPa.

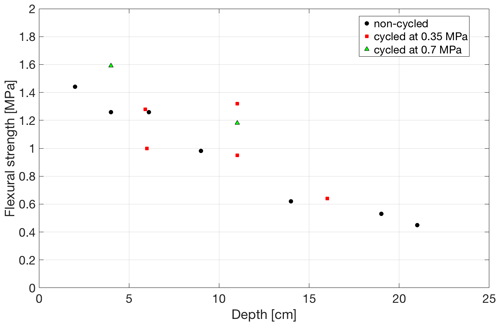
Figure 10 Flexural strength as a function of position of saline ice samples of higher salinity (5.9 ± 0.6 ppt) for different cyclic amplitudes. The imposed number of cycles for specimens cycled at 0.35 and 0.7 MPa is ∼ 2000.

For saline ice of lower salinity (3.0 ± 0.9 ppt), there is no evidence that the flexural strength of both non-cycled and cycled ice is significantly affected by the depth of ice from which ice beams were harvested. For saline ice of higher salinity (5.9 ± 0.6 ppt), however, the flexural strength of both non-cycled and cycled ice appears to depend on the depth of ice from which beams were prepared, Fig. 10. Indeed, the flexural strength of specimens from the bottom and from the top of an ice puck of higher salinity (5.9 ± 0.6 ppt) differs by a factor of ∼ 3 (∼ 0.4 MPa vs. ∼ 1.4 MPa).

3.4 Fatigue behavior

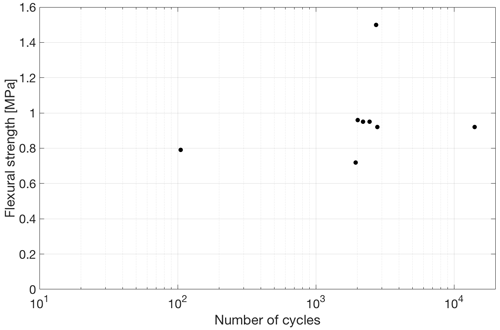
Although the specimens from which the data in Fig. 9 were obtained did not fail during cycling, other specimens cycled under similar conditions did fail while being cycled. Results from such tests (on saline ice of lower salinity (3.0 ± 0.9 ppt) at −10 ^∘C and 0.1 mm s⁻¹ outer-fiber displacement rate) allowed us to construct a S–N fatigue curve, shown in Fig. 11. The number of cycles here is the number of cycles to failure during cycling at the last stress amplitude level and not the total number of cycles. At most the S–N curve showed only a weak systematic dependence of the number of cycles to failure on stress amplitude. Indeed, for the same stress amplitude of ∼ 0.9 MPa, fatigue failure occurred after as few as < 10 cycles and after as many as a few thousand cycles. Statistical analyses to test the hypothesis that the slope in Fig. 11 is zero resulted in a p value equal ∼ 0.06. Therefore, there is only a marginally significant effect of number of cycles on the stress at which failure occurred. We attribute this variability in fatigue life to the variability in microstructure from specimen to specimen.

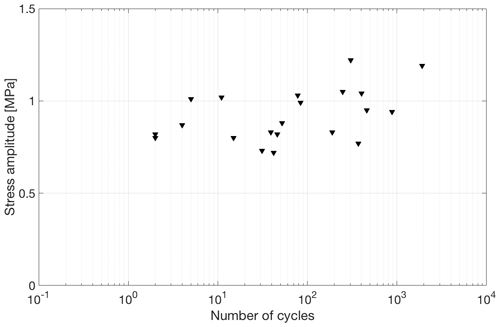
Figure 11 Stress amplitude as a function of the number of cycles to fatigue fracture for saline ice of lower salinity (3.0 ± 0.9 ppt) tested at −10 ^∘C and 0.1 mm s⁻¹ outer-fiber center-point displacement rate.

That said, a note of caution is appropriate. The data in Fig. 11 should not be viewed as fatigue data in the usual sense, i.e., in the way such data are viewed when obtained from other materials (e.g., metals and alloys) that exhibit classical fatigue behavior. In those cases, before cycling, all specimens are assumed to have the same thermal–mechanical history. That was not the case here for the saline ice, as most of the samples were pre-conditioned according to the Type II procedure before they were cycled at the last stress level where they failed while cycling. In other words, in order to get fatigue failure, we were increasing stress amplitude by small increments of ∼ 0.05 MPa and allowed a sufficient number of cycles at each stress level (∼ 500–1000) before we reached a fatigue failure.

The question to address here is why we did not obtain a classical S–N curve. We suggest that the classical mechanism of fatigue, i.e., accumulation of damage, is not in play in our tests, and some other process is controlling fatigue life.

3.5 Microstructural observations of samples after fatigue failure

In an attempt to reveal deformation damage in the form of microcracks, we examined using thin-section optical microscopy (up to 50× magnification) the microstructure of specimens of the lower-salinity ice (3.0 ± 0.9 ppt) after they had failed during cycling, i.e., failed in fatigue. Three thin sections were prepared from four specimens in order to ensure a greater probability of observing microcracks growing from brine pockets or brine channels, should they be present. The plane of the thin section was parallel to the long axis of the columnar grains and parallel to the direction of the greater normal stress. This plane was taken as the best plane to observe possible cracks. Thin sections were observed using non-polarized light. We found no evidence of microcracks starting from brine pockets or from other defects. In fact, we found no microcracks at all. It appears, therefore, that slow crack growth is not a significant contribution to the fatigue life of the beams of the laboratory-grown saline ice that we studied.

Figure 12 Acoustic emissions (hits) against time for saline ice of lower salinity (3.0 ± 0.9 ppt), cycled at a stress amplitude of 0.5 MPa at −10 ^∘C at an outer-fiber displacement rate of 0.1 mm s⁻¹.

3.6 Acoustic emissions

Acoustic emissions (AE) during repetitive loading of ice have been previously recorded and analyzed in laboratory and in situ (Langhorne and Haskell, 1996; Cole and Dempsey, 2006, 2004; Lishman et al., 2020; Murdza et al., 2020b). Langhorne and Haskell (1996) suggested that the emissions originate either from dislocation breakaway or from microcracking associated with dislocation motion.

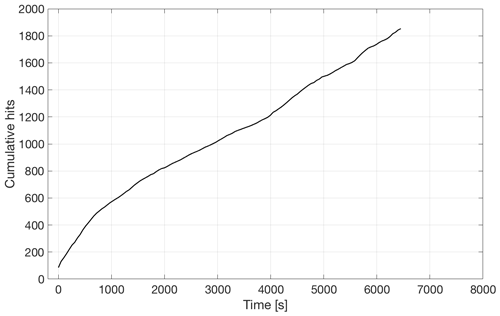
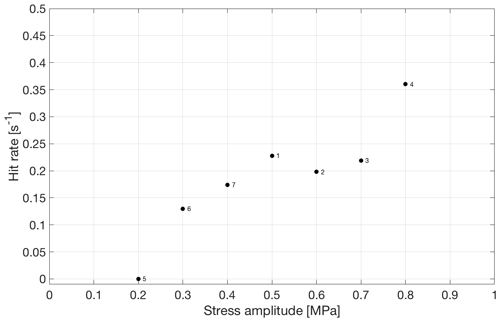
In contrast to freshwater ice, where no sound was detected until failure (Murdza et al., 2020b), continuous emission was detected while cycling at constant stress amplitude. Figure 12 shows the cumulative acoustic emissions, or “hits”, as a function of time for ice that was cycled reversely at a constant stress amplitude of 0.5 MPa. As can be seen, the hit rate (or hits per unit time), which is the slope of the curve in Fig. 12, is about the same for the duration of the experiment.

Interestingly, the hit rate depends on stress amplitude during cycling. Figure 13 shows this behavior. The greater the stress amplitude, the greater the hit rate. However, during cycling below about 0.2 MPa no hits were detected.

Figure 13 also indicates that the hit rate is independent of the sequence of different stress amplitudes. The numbers in Fig. 13 show the order of cycling at different stress amplitudes; i.e., firstly we cycled ice at higher stress amplitudes (0.5–0.8 MPa) and then at lower stress amplitudes (0.2–0.4 MPa). The results showed an increase in the hit rate as stress amplitude increases, regardless of the sequence of cycling.

Figure 13 Hit rate as a function of cycled stress amplitude for saline ice sample of lower salinity (3.0 ± 0.9 ppt). Numbers show the order of cycling at different stress amplitudes.

4 Discussion

The results obtained from the experiments described in this paper show that the flexural strength of saline ice can be increased upon reversed cyclic loading. Therefore, the same set of questions as for the freshwater ice should be addressed here. What governs the flexural strength of saline ice? Does crack propagation or crack nucleation control the tensile strength? First of all, to understand the behavior of saline ice, it is important to recognize that flexural strength in the present experiments is governed by the tensile strength, although greater by a factor of about 1.7 (Ashby and Jones, 2012). Secondly, the apparent absence of remnant microcracks within the two parts of broken samples (Sect. 3.5) indicates that crack nucleation controls the flexural strength, just as it appears to do for freshwater ice. Indeed, this seems reasonable given the fact that freshwater ice comprises ∼ 95 % by volume of the saline ice we studied. Within the freshwater component, there is almost no solubility of salts (Weeks and Ackley, 1986). The remainder of the saline ice is a mixture of air and brine. As was shown earlier, the microstructure of saline ice that we grew is closely similar to the microstructure of sea ice. Pores lower the saline ice strength (Sammis and Ashby, 1986). However, the behavior of S2 saline ice under cyclic loading is essentially the same as the behavior of S2 freshwater ice (Murdza et al., 2020b); i.e., its strength increases at the same rate as freshwater ice upon cycling under a given amplitude of the outer-fiber stress. Hence, it is reasonable to assume that the strengthening mechanism for the saline ice is similar to that for the freshwater ice. In our earlier work (Murdza et al., 2020b) we proposed that strengthening might be due to the development of an internal back stress that originates from either dislocation pileups or grain boundary sliding. However, one reviewer suggested the possibility of a different strengthening mechanism. Due to the inherent weakness of the saline ice microstructure, the microstructural stress relief may occur through localized damage via microcracking mentioned above. More research, however, is needed to examine this hypothesis.

The maximum degree of strengthening in the case of saline ice is significantly lower than that for the freshwater ice, although the slopes of the two data sets (rate of strength increase with increasing cyclic amplitude) in Fig. 9 are nearly equivalent. That difference may be explained by the structure of saline ice which limits maximum possible strengthening. Given the significantly greater number of stress concentrators in saline ice, such as brine pockets and channels, the propensity for failure during cycling is greater in saline ice (Sammis and Ashby, 1986), thereby limiting the development of the back stress. Indeed, in the present study failure of specimens during cycling occurred more frequently than in the study on freshwater ice (Murdza et al., 2020b).

Flexural experiments conducted on saline ice of higher salinity (5.9 ± 0.6 ppt) showed the importance of brine features. Samples that were manufactured from the bottom of the ice puck were characterized by more frequent whitish interconnected features (taken to be interconnected brine pockets) that often were the path for easy crack propagation. Often samples were so weak that they failed before testing simply by handling. Interestingly, there were no interconnected features in samples prepared from the top of an ice puck, which resulted in a difference of more than a factor of 3 in strength between samples from top and bottom. Samples produced from saline ice of lower salinity (3.0 ± 0.9 ppt) also had whitish features; however, these features were spread more uniformly (on a macroscopic scale) across the sample, resulting in little difference in strength between the bottom and top samples.

It is worth noting again that a significantly greater fraction of saline ice samples failed in fatigue while pre-conditioning compared with freshwater ice. This may be explained by the fact that freshwater ice was essentially free from pores, brine pockets, and other defects. Based on this observation, it appears that crack growth is not a significant contribution to the fatigue life of saline ice under the conditions of our experiments.

On the origin of the acoustic emissions, there are at least four possible sources of the noise detected. One is from microcracking. We imagine that microcracks form in regions of mechanical weakness which results in accumulation of damage that we detected via the AE method. Specifically, the whitish brine drainage features discussed above in the test specimens constitute regions of high porosity and thus provide favorable sites for the concentration of such damage. Failure may occur when one of these sites can no longer support the applied stress and a microcrack emerges from the damage zone and propagates. It is possible that newly formed microcracks are stable until a critical length is reached (Cannon et al., 1990; Schulson et al., 1991), at which point the crack growth ensues. The reason that microcracks were not observed under the optical microscope may be because they filled up with liquid brine upon formation, which results in a loss of contrast. A second possible explanation for the acoustic emissions is the motion and friction of very fine particles of ice which may have been entrapped inside brine drainage features, as mentioned above. A third possibility is microcracking along grain boundaries due to grain boundary sliding (Elvin and Shyam Sunder, 1996; Goldsby and Kohlstedt, 1997; Mulmule and Dempsey, 1997; Schulson et al., 1997; Weiss and Schulson, 2000). A fourth possible explanation consistent with the non-history dependence of the hit rate (Fig. 13) is a kind of water-hammer effect in which brine entrapped within pockets impacts the wall, first in one direction and then another. None of these possibilities can be evaluated based upon the limits of the present observations. We refrain, therefore, from further speculation on this point.

Returning to the observations noted in the Introduction, and to the results obtained from imposed in situ cyclic loading experiments on sea ice beams by Bond and Langhorne (1997), Haskell et al. (1996), and Langhorne et al. (1998, 1999), the question is as follows: why does ice fail in the field under wave action and under imposed cyclic loading, but strengthen upon cycling in our experiments in the laboratory? Although we do not know the process through which the ice sheet failed in the field, we expect that there are many micro- and macrocracks in natural sea ice. Indeed, thermally induced tensile stresses can induce thermal cracking in floating ice sheets (Evans and Untersteiner, 1971). Therefore, our sense is that the difference in ice behavior under cyclic loading in situ in the field (Bond and Langhorne, 1997; Langhorne et al., 1998) and in the laboratory in the present study is due to other types of defects other than brine channels and pockets that are generated in the field as a result of thermomechanical history of ice.

5 Conclusions

From new, systematic experiments on the flexural strength of sub-meter-sized beams of S2 columnar-grained saline ice stressed principally across the columns through reversed cyclic loading at a temperature of −10 ^∘C and frequencies in the range from 0.1 to 0.6 Hz, the following is concluded.

• i.

  The flexural strength of saline ice can be increased upon reversed cyclic loading by as much as a factor of 1.5.

• ii.

  The flexural strength of ice subsequent to cycling scales linearly with the amplitude of the outer-fiber stress.

• iii.

  The fatigue life of saline ice is erratic and does not obey classical S–N behavior.

• iv.

  Crack growth is not a significant contribution to the fatigue life of saline ice.

• v.

  There is high variability in structure and strength through the thickness of a saline ice puck of higher salinity (5.9 ± 0.6 ppt).

• vi.

  Given the lack of definitive proof of the underlying failure mechanism in saline ice, the increase in flexural strength of freshwater ice and saline ice attributable to pre-failure load cycling is roughly equivalent.

• vii.

  Acoustic emission hit rate during cycling at a constant stress amplitude is about constant.

• viii.

  Acoustic emission hit rate during cycling increases with an increase in stress amplitude of cycling.