Deciphering the evolution of the Bleis Marscha rock glacier (Val d'Err, eastern Switzerland) with cosmogenic nuclide exposure dating, aerial image correlation, and finite element modeling

We constrain the Holocene development of the active Bleis Marscha rock glacier (Err–Julier area, eastern Swiss Alps) with 15 cosmogenic nuclide exposure ages (¹⁰Be, ³⁶Cl), horizontal surface creep rate quantification by correlating two orthophotos from 2003 and 2012, and finite element modeling. We used the latter to separate the control on surface movement exerted by topography and material properties. Bleis Marscha is a stack of three overriding lobes whose formation phases are separated by time gaps expressed morphologically as over-steepened terrain steps and kinematically as a sharp downslope decrease in surface movement. The three discrete formation phases appear to be correlated to major Holocene climate shifts: Early Holocene low-elevation lobes (∼8.9–8.0 ka, after the Younger Dryas), Middle Holocene lobe (∼5.2–4.8 ka, after the Middle Holocene warm period), and Late Holocene high-elevation lobes (active since ∼2.8 ka, intermittently coexisting with oscillating Bleis Marscha cirque glacierets). The formation phases appear to be controlled in the source area by the climate-sensitive accumulation of an ice-debris mixture in proportions susceptible to rock glacier creep. The ongoing cohesive movement of the older generations requires ice at a depth which is possibly as old as its Early–Middle Holocene debris mantle. Permafrost degradation is attenuated by “thermal filtering” of the coarse debris boulder mantle and implies that the dynamics of the Bleis Marscha lobes that once formed persisted over millennia are less sensitive to climate. The cosmogenic radionuclide inventories of boulders on a moving rock glacier ideally record time since deposition on the rock glacier root but are stochastically altered by boulder instabilities and erosional processes. This work contributes to deciphering the long-term development and the past to quasi-present climate sensitivity of rock glaciers.

1 Introduction

Active rock glaciers are defined as “lobate or tongue-shaped bodies of perennially frozen unconsolidated material supersaturated with interstitial ice and ice lenses that move downslope or downvalley by creep as a consequence of the deformation of ice contained in them and which are, thus, features of cohesive flow” (Barsch, 1996). Their active phase and development are conditioned by ice preservation, permafrost conditions (Haeberli et al., 2006), and debris supply (Kenner and Magnusson, 2017).

In our current warming climate (Hock et al., 2019), active rock glaciers as the “visible expression of mountain permafrost” (Barsch, 1996) receive considerable attention. Their surface kinematics is considered to be diagnostic of the thermal state of mountain permafrost (Delaloye et al., 2018), which is otherwise not directly observable. Rock glaciers are thought to store significant water resources (Jones et al., 2019) and to become more significant in the deglaciating mountains (Haeberli et al., 2017; Knight et al., 2019).

In the literature, different views on the climate sensitivity of rock glaciers are proposed. One concept is that rock glaciers respond in a delayed fashion to current warming because of the high thermal inertia of the ice-rich core and the thermal decoupling from climate by the insulating effect of the boulder mantle (active layer) (e.g., Haeberli et al., 2017; Anderson et al., 2018) via the “thermal semi-conductor” effect (Harris and Pedersen, 1998; Humlum, 1998; Hanson and Hoelzle, 2004). The ground cooling effect of a coarse debris mantle (Schneider et al., 2012; Wicky and Hauck, 2017) favors a large negative thermal offset and more resilient permafrost conditions even at mean annual ground temperatures close to 0 ^∘C (Kellerer-Pirklbauer, 2019). Furthermore, the creep of millennia-old rock glaciers is tied to the ice supersaturation of the debris and hence to the preservation of ice over their entire lifetime (Barsch, 1996; Haeberli et al., 2003).

Another concept is the synchronous, rapid response to warming based on kinematic rock glacier monitoring. Many rock glaciers across the Alps show a common behavior of surface creep rates with (sub-)seasonal fluctuations (Delaloye et al., 2010). These decennial to annual changes in surface creep rates respond within months to changing summer air temperature, snow cover timing (Noetzli et al., 2019), and water in the shear layer (Cicoira et al., 2019). Rock glacier formation can occur within centuries (Humlum, 1996) or under very specific topo-climatic conditions even within decades (Scotti et al., 2017). Debris pulses or “surge packages” (Kenner et al., 2014), as well as significant acceleration and destabilization (Marcer et al., 2019) up to sudden collapse (Bodin et al., 2016), are reported.

The response of rock glaciers to external forcing such as air temperature, precipitation, snow cover, weathering intensity, debris supply, and interactions with glaciers (e.g., pushing ice, altered thermal conditions by insulation, glacial debris sources) are insufficiently understood. Furthermore, their external response is difficult to disentangle from internal thermomechanical and topographic feedbacks. Historical records are sparse and too short compared to typical rock glacier lifetimes, activity phases, and response periods. To resolve long-term effects on rock glacier development (Kenner and Magnusson, 2017) and to put the present-day morphology reflecting the lifelong dynamic history of active rock glaciers and (relict) rock glacier deposits in a climate-sensitivity context (Frauenfelder and Kääb, 2000), their activity phases need to be placed in a chronological framework. Cosmogenic radionuclide concentrations record all periods of exposure of the rock surface to cosmic rays. In principle, they are a suitable tool for deriving numerical exposure ages for boulders on the landform surface (Ivy-Ochs and Kober, 2008). The technique has been applied to (relict) rock glacier deposits or related periglacial landforms, e.g., by Ivy-Ochs et al. (2009), Böhlert et al. (2011a, b), Moran et al. (2016), Denn et al. (2017), and Steinemann et al. (2020). Relict and active rock glacier deposits in Iceland were exposure dated by Fernández-Fernández et al. (2020).

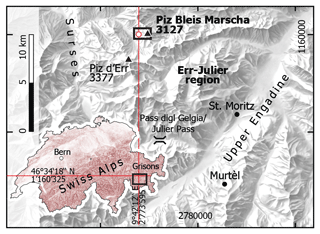
Figure 1 Location of the Bleis Marscha rock glacier to the west below Piz Bleis Marscha in the Err–Julier region, eastern Swiss Alps. The rectangle shows the area covered by the geomorphological map (Fig. 3). Inset map: location and extent (black rectangle) of the Err–Julier regional map within Switzerland and the coordinates of the lowermost front of the Bleis Marscha rock glacier (maps reproduced with the authorization of the Swiss Federal Office of Topography, swisstopo).

In this study, our focus is on the Bleis Marscha rock glacier located in the Err–Julier area, eastern Swiss Alps (Fig. 1). Previous relative dating studies based on Schmidt-hammer rebound values, as well as the thickness and chemical composition of weathering rinds, suggest a development through the entire Holocene (Frauenfelder et al., 2001, 2005; Laustela et al., 2003). We exposure dated 15 boulders along a longitudinal transect from the lowermost front up to the transition towards the talus with the cosmogenic radionuclides ¹⁰Be and ³⁶Cl. To our knowledge, this is the first study that exposure dates boulders on an active, presently moving rock glacier lobe in the Alps. The exposure ages are interpreted in light of field observations, modern surface creep rate quantification through image correlation, and numerical finite element modeling to unveil periods of activity and the development of the Bleis Marscha rock glacier. This work contributes to deciphering the long-term development and the past to quasi-present climate sensitivity of rock glaciers

2 Study site

The studied Bleis Marscha rock glacier (WGS 84: 46^∘34^′18^′′ N, 9^∘42^′12^′′ E; CH1903+/LV95: 2773595, 1160326) lies on the eastern slope of the upper Val d'Err, a side valley of the Surses (Oberhalbstein) in the Err–Julier area, Grisons, eastern Swiss Alps (Fig. 1). The rock glacier originates in a north-northwest-oriented cirque of Piz Bleis Marscha (3127 m a.s.l.).

The Err–Julier area lies in the rain shadow of the Lepontine, Bernese, and Glarus Alps resulting in a dry-cold, continental-type climate. Frauenfelder et al. (2001) report low mean annual precipitation (MAP) of 900–1000 mm a⁻¹ (1971–1990), a regional lapse rate of 0.55 ^∘C/100 m, and a mean annual 0 ^∘C isotherm at ca. 2180 m a.s.l. Val d'Err is a high valley with the valley floor at an elevation above 2000 m a.s.l. and surrounding peaks rising to over 3000 m a.s.l. The present-day lower limit of permafrost occurrence is roughly at 2400 m a.s.l. (Gruber et al., 2006; Boeckli et al., 2012; Kenner et al., 2019).

The north-northwest- to south-southeast-oriented valley lies in a tectonically complex zone between the Upper Penninic Platta nappe overlain by the Lower Austroalpine Err nappe. The debris-supplying headwalls (in the Tschirpen unit of the Err nappe) are composed of post-Variscan granitoids and Permo-Triassic to Lower Cretaceous sediments (mostly slate and carbonates), separated by a thrust fault outcropping subhorizontally along the cirque walls (Cornelius, 1932; Frauenfelder et al., 2005).

During the Last Glacial Maximum (LGM) around 24 ka (Ivy-Ochs, 2015), the area was covered up to an elevation of ∼2800 m a.s.l. by ice flowing northwards from the nearby Engadine ice dome (Inn–Danube river catchment) into the Rhine glacier system (Bini et al., 2009). Prominent presumed late-glacial (Egesen) moraines along the valley flanks (Schlosser, 1990; Frauenfelder et al., 2001) suggest that the upper Val d'Err, including our study site, was likely last occupied by a glacier during the Egesen stadial (12.9–11.7 ka; Ivy-Ochs, 2015). The Bleis Marscha cirque was occupied by a glacieret during the Little Ice Age (LIA) and up until recently (Dufour, 1853; Frauenfelder et al., 2001).

3 Material and methods

The morphology of rock glaciers, in which process and form are intrinsically linked via deformation by creep, largely preserves the cumulative deformation history over the lifetime of the landform (Frauenfelder and Kääb, 2000). The concept of rock glacier formation and the conveyor-belt-like advance mechanism form the theoretical groundwork on how surface boulders move compared to the rock glacier as a whole (outlined in Sect. 5.1–5.2). The subdivision in geomorphologically defined units of the polymorphic (sensu Frauenfelder and Kääb, 2000) Bleis Marscha rock glacier, assisted by an estimate of modern surface creep rates from aerial image correlation, provides a framework for the discussion and interpretation of the exposure ages. Topographic maps, aerial photographs, digital elevation models (DEMs), geomorphological field mapping, surface exposure dating, and finite element (FE) modeling form the data basis to reconstruct the Bleis Marscha development. Surface exposure ages of 15 boulders of the rock glacier deposit were determined with the cosmogenic radionuclides ¹⁰Be and ³⁶Cl. FE modeling separates the control of topography (e.g., surface slope) and material properties (e.g., ice content at depth) on the surface movement.

3.1 Field work and landform analysis

Field mapping was performed in August 2017, focusing on Quaternary geology and geomorphology. Fieldwork was carried out at the scale of 1:5000 following standard geomorphological mapping procedures as outlined in Chandler et al. (2018). Details of the landform and sediments of various sectors of the rock glacier were characterized, in concert with digital elevation model (DEM) analysis, to subdivide Bleis Marscha into different lobes. Especially distinguishing were lichen coverage (leading to pale vs. dark appearance of the blocks) and general freshness of the blocks, the location of ridges and furrows, and the presence of steep steps on the rock glacier, as well as the dominant size and rounding of blocks. Crosscutting relationships with talus and rockfall deposits, moraines, and the past location of the cirque glacier were also examined based on historical maps. Landform interpretation was supported by aerial and DEM data on an iPad with the Garafa GIS Pro application accessed in the field. Photos taken in the field and locations of boulders sampled for cosmogenic nuclide exposure dating were thus automatically georeferenced. Orthorectified aerial images (0.25×0.25 m resolution) and the high-resolution DEM swissALTI3D provided by the Swiss Federal Office of Topography (swisstopo) served for topographic analysis and visualization. The DEM, derived from aerial images acquired in 2016, is gridded on 2×2 m cells and has an accuracy of ±1–3 m (1σ level, all three dimensions) for areas above 2000 m a.s.l. Extraction of swath profiles and morphometric calculations were carried out with the MATLAB toolbox TopoToolbox 2 (Schwanghart and Scherler, 2014) and the open-source software QGIS.

3.2 ¹⁰Be and ³⁶Cl exposure dating

Boulders suitable for exposure dating are large (>1.5 m side length) and in a stable position; suitable rock surfaces do not show signs of fast weathering or spalling. A total of 15 boulders on the rock glacier surface were sampled with hammer, chisel, and battery-powered saw according to the guidelines of Ivy-Ochs and Kober (2008) and field observations. Topographic shielding, dip, and dip direction of sampled surfaces were measured using a compass and clinometer. The samples (∼0.5 kg of rock material each) were collected close to the central flow line from the lowermost front up to the high-elevation active lobes, preferentially on ridges to minimize topographic and snow shielding (Böhlert et al., 2011b) and towards the frontal upper edge of each morphologically identified lobe (Haeberli et al., 2003; Steinemann et al., 2020). A total of 14 samples were Err Granodiorite (for quartz, ¹⁰Be; Table 1); only one Main Dolomite boulder for ³⁶Cl met the sampling criteria (Table 2).

Table 1 The ¹⁰Be sample information of the Bleis Marscha rock glacier boulders (Err Granodiorite) with location, sample information, blank-corrected AMS ¹⁰Be concentration, and calculated exposure age.

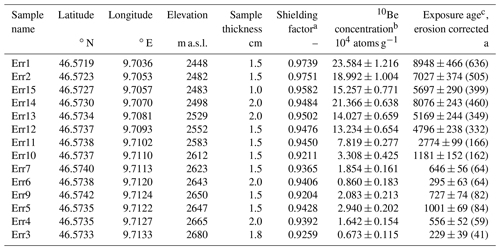
^a Shielding correction includes the topographic shielding due to surrounding landscape and the dip of the sampled surface.
^b AMS measurement errors are at 1σ level and include the AMS analytical uncertainties and the error of the subtracted blank. Measured ratios were measured against the in-house standard S2007N which is calibrated to 07KNSTD.
^c  Exposure age errors are internal errors (uncertainties represent 1σ confidence range comprising AMS counting errors and errors based on the normalization to blanks and standards). External errors are given in parentheses. Erosion correction for a surface erosion rate of 1 mm kyr⁻¹.

Table 2 The ³⁶Cl sample information of the Bleis Marscha rock glacier boulder (Main Dolomite) with location, sample information, blank-corrected AMS ³⁶Cl concentration, and calculated exposure age.

^a Concentration measured against ${}^{\mathrm{36}}\mathrm{Cl}/\mathrm{Cl}$ standard K382/4N (Christl et al., 2013; Vockenhuber et al., 2019).
^b Sample ratio corrected for laboratory blank of $(\mathrm{2.5}\pm \mathrm{0.4})\times {\mathrm{10}}^{-\mathrm{15}}$ ${}^{\mathrm{36}}\mathrm{Cl}{/}^{\mathrm{35}}\mathrm{Cl}$.
^c Production rates as in Alfimov and Ivy-Ochs (2009) and references therein. Erosion correction for a surface erosion rate of 5 mm kyr⁻¹ (karst weathering/corrosion).

The ¹⁰Be sample preparation followed Kronig et al. (2018). The ratio of ${}^{\mathrm{10}}\mathrm{Be}{/}^{\mathrm{9}}\mathrm{Be}$ is measured with the 600 kV Tandy at the ETH Zurich accelerator mass spectrometry (AMS) facility (Christl et al., 2013). The in-house standard S2007N, which is calibrated against the 07KNSTD, was used. For ³⁶Cl extraction from the dolomite sample (Err8), the method of isotope dilution was employed (Ivy-Ochs et al., 2004). Concentrations of major and trace elements were measured by ICP-MS (inductively coupled plasma mass spectrometry) at Actlabs (Ontario, Canada) (Table 3). AMS measurements were conducted with the 6 MV Tandem accelerator (Synal et al., 1997; Vockenhuber et al., 2019) of the Laboratory of Ion Beam Physics (LIP), ETH Zurich.

Table 3 Elemental composition of the dolomite sample Err8.

The ¹⁰Be surface exposure ages were calculated from the blank-corrected data (long-time laboratory blank of ${}^{\mathrm{10}}\mathrm{Be}{/}^{\mathrm{9}}\mathrm{Be}=(\mathrm{3.2}\pm \mathrm{1.4})\times {\mathrm{10}}^{-\mathrm{15}}$) using the CRONUS-Earth online calculator (Balco et al., 2008) with the northeastern North America (NENA) ¹⁰Be production rate of 3.87±0.19 atoms g⁻¹ a⁻¹ and the scaling model by Lal (1991) and Stone (2000). The shielding parameters were calculated with the “online calculators formerly known as the CRONUS-Earth online calculators” (Balco et al., 2008; http://hess.ess.washington.edu/math, last access: 22 April 2021). The NENA production rate has been shown to be well applicable for the Alpine area (Claude et al., 2014). The ³⁶Cl surface exposure age was computed with a LIP in-house-developed MATLAB program based on the equations and constants given in Alfimov and Ivy-Ochs (2009, and references therein). The ³⁶Cl production in dolomite is dominated by the spallation of Ca, muon interactions with Ca, and low-energy neutron capture reflecting the high natural Cl concentration (Err8: 49.6±0.1 ppm; Table 2). The following production rates were used: 48.8±3.4 ³⁶Cl atoms g⁻¹ a⁻¹ for spallation in Ca and 5.3±1.0 ³⁶Cl atoms g⁻¹ a⁻¹ for muon capture in Ca at the rock surface. A neutron capture rate of 760±150 neutrons g${}_{\mathrm{air}}^{-\mathrm{1}}$ (Alfimov and Ivy-Ochs, 2009) was implemented. We used the Lal and Stone scaling of the production rates to the site latitude, longitude, and elevation (Balco et al., 2008).

We report and discuss exposure ages with an erosion rate of 1 mm kyr⁻¹ for the crystalline samples (¹⁰Be) and 5 mm kyr⁻¹ for the dolomite sample (³⁶Cl). Snow-cover corrections are omitted as such corrections would increase the exposure ages by only a few percent (by 6 % for 50 cm of snow during 6 months of a year). The reported errors are at the 1σ level including analytical uncertainties of the AMS measurements and the blank correction (internal errors).

3.3 Estimation of modern surface creep rates

We quantify the horizontal surface creep rate with the cross-correlation of orientation images (Fitch et al., 2002) derived from two ortho-images with the MATLAB tool ImGRAFT (Messerli and Grinsted, 2015). The orthophoto mosaic swissimage 25 cm is a composite of orthorectified digital color aerial photographs, provided by the Swiss Federal Office of Topography (swisstopo). Ground resolution is given as 0.25 m and positional accuracy as ±0.25 m.

The orientation correlation method developed by Fitch et al. (2002) is a feature-based method of translatory image matching that correlates the orientation of the image intensity gradients. Orientation images are normalized and invariant to pixel brightness, making the method more robust and less susceptible to different illumination in the images. We derived the orientation images from the R band of the RGB images.

The post-processing steps are noise filtering to remove erroneous matches and smoothing to attenuate small-scale and thus likely short-lived creep rate variations. A minimum correlation coefficient of 0.6 and a conservative signal-to-noise ratio threshold of 6 sufficed to remove incoherent and poor-quality displacement vectors. The optimal template size of 51×51 pixels was found using a procedure based on Debella-Gilo and Kääb (2012). The search window size of 211×211 pixels was defined with the recommendations of Messerli and Grinsted (2015). The modal displacement of the presumably stable adjacent off-rock glacier areas defined the significance level, which is the threshold below which any measured displacement is not distinguishable from immobility.

3.4 Finite element modeling

The surface movement of a rock glacier integrates the overall vertical deformation profile (e.g., Müller et al., 2016). An appropriate flow law – a mathematical formulation of the governing deformation process – allows us in principle to infer from (known, observable) surface properties (e.g., surface deformation) to (unknown) effective material parameters and structures at depth.

The first-order deformation of rock glaciers is governed by gravity-driven steady-state creep of its ice-bonded interior (Müller et al., 2016). In the case of ice supersaturation, the deformable (excess) ice leads to stress transfer in space and time and thus to a cohesive surface creep rate pattern, a diagnostic feature of active rock glaciers. Creep of permafrost can be approximately described by Glen's flow law for polycrystalline ice (Haeberli et al., 2006), establishing a constitutive power-law relationship between shear stresses τ (Pa) and shear strain rates $\dot{\mathit{\epsilon }}$ (s⁻¹). To illustrate the problem, consider the surface speed u_s (m s⁻¹) of an infinite, parallel-sided slab calculated with Glen's flow law,

$$\begin{array}{}\text{(1)}& u_{\mathrm{s}}={\displaystyle \frac{\mathrm{2}A}{n+\mathrm{1}}}(\mathit{\rho }g\sin \overline{\mathit{\alpha }}{)}^n{H}^{n+\mathrm{1}},\end{array}$$

with flow rate factor A (Pa⁻ⁿ s⁻¹) related to dynamic viscosity $\mathit{\mu }:=\frac{\mathit{\tau }}{\mathrm{2}\dot{\mathit{\epsilon }}}=(\mathrm{2}A{\mathit{\tau }}^{n-\mathrm{1}}{)}^{-\mathrm{1}}$ (Pa s), stress exponent n (–), density ρ (kg m⁻³), average surface slope $\overline{\mathit{\alpha }}$ (^∘), thickness H (m), and gravitational acceleration g (9.81 m s⁻²). However, Eq. (1) is underdetermined, and no unique solution exists. A simultaneous determination of material properties (density, viscosity) and structure (thickness) is not possible. This inverse problem requires regularization to become solvable; i.e., all but one of these parameters need to be estimated independently.

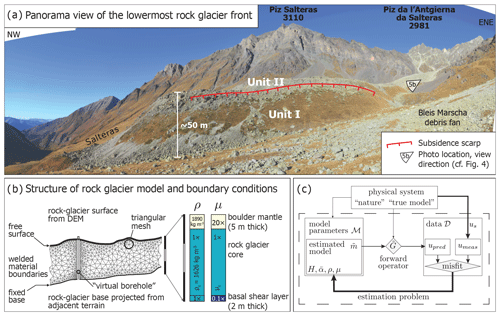
Figure 2 (a) Side view of the lowermost front, rising 30–50 m above the Salteras trough shoulder (see Fig. 4 for photo location and view direction). A stabilized, grassy sidewall extends upstream beneath younger lobes. The southernmost fringe is subsiding possibly due to ice loss. (b) Finite element (FE) model setup, triangular mesh (Shewchuk, 1996), boundary conditions, and prescribed ratios of density ρ and dynamic viscosity μ (profiles). The surface boundary is the well-constrained elevation along a longitudinal profile, extracted from the DEM as a swath profile with TopoToolbox. The a priori prescribed density and viscosity ratios create the characteristic mechanical layering of rock glaciers with a stiff, high-viscosity boulder mantle, deformable core, and weak, low-viscosity basal layer. (c) Inverse problem structure with the model parameters $\stackrel{\mathrm{̃}}{m}$ that are linked to the observable data u_s via the discrete forward operator $\stackrel{\mathrm{̃}}{G}$, the FE model. The model predicts a synthetic surface velocity u_pred from the mechanical parameters that control the rock glacier creep: thickness H, average surface slope $\overline{\mathit{\alpha }}$, density ρ, and dynamic viscosity μ. A combination of parameter values for $(H,\overline{\mathit{\alpha }},\mathit{\rho },\mathit{\mu })$ that produces synthetic surface velocities u_pred whose misfit to the observed data u_meas is equal to or smaller than the measurement uncertainties is one solution to the inverse problem. Starting from an initial guess, the rock glacier model $\stackrel{\mathrm{̃}}{m}=(H,\overline{\mathit{\alpha }},\mathit{\rho },\mathit{\mu })$ is iteratively refined until a solution is found (estimation problem).

The rock glacier model is mechanically described by the model parameters H, $\overline{\mathit{\alpha }}$, ρ, and μ. We invert for effective dynamic viscosity μ from known surface slope $\overline{\mathit{\alpha }}$ and surface speed u_s. We regularize the inverse problem by a priori prescribing density ρ and thickness H, parameters that can be reasonably well estimated from the literature knowledge and field observations (Fig. 2a). In the absence of any Bleis Marscha rheological borehole data to constrain the power-law exponent n of the effective viscous flow law, we proceed by a forward operator that implements the simplest temperature-independent (isothermal) linear viscous (Newtonian) material (n=1). The system of force-balance and constitutive equations are solved numerically in two dimensions along the central flow line with the numerical FE code presented in Frehner et al. (2015).

Direct evidence from over-steepened rock glacier fronts, borehole deformation measurements (Arenson et al., 2002), and indirect geophysical investigations (Springman et al., 2012) suggests a pronounced thermomechanical layering of rock glaciers. A robust finding is that the deforming part can be divided into a sequence of three layers: surface boulder mantle, rock glacier core, and shear layer (Haeberli et al., 2006; Frehner et al., 2015; Cicoira et al., 2021). (1) The seasonally frozen ice-free or ice-poor surface layer consists of a matrix-poor, clast-supported framework of large, interlocked boulders (∼ active layer). Discrete movements of blocks in the boulder mantle are negligible compared to the total surface movement (but not with respect of inventories of cosmogenic nuclides; see Sect. 5.2). Deformation is accommodated by the ice-bearing interior that comprises the rock glacier core and the basal shear layer. (2) The ice-rich rock glacier core consists of a perennially frozen mixture of ice, debris, and fine material. (3) A fine-grained shear layer a few meters thick concentrates 60 %–90 % of the total displacement. Its higher deformation susceptibility, arising from the weakening effect of liquid water at grain boundaries, is in our model accounted for by a lower viscosity. Boulder mantle, core, and shear layer lie on an immobile substratum of debris or bedrock.

Over-steepened terrain steps, exposing the uppermost few meters of the stratigraphy, show the coarse boulder mantle over the finer-grained rock glacier core (see field observations in Sect. 4.1). Although no borehole deformation data are available for Bleis Marscha to confirm the presence of a shear layer, it is very likely that this typical rock glacier feature (Arenson et al., 2002) does exist there. We approximate the deforming part of the rock glacier as a three-layer system consisting of a 5 m thick boulder mantle, 30–40 m thick core, and a 3 m thick low-viscosity basal shear layer. The (variable) total thickness is estimated as follows. The model top boundary is the rock glacier surface given by the DEM, implemented as a free surface (Fig. 2b). The bottom boundary is defined by a fixed, no-slip boundary to the immobile substratum. Its elevation is projected from the adjacent terrain at the rock glacier front where the rock glacier rises from the Salteras trough shoulder (Fig. 2a; cf. Kääb and Reichmuth, 2005; Scapozza et al., 2014) and parallel to the average rock glacier surface in the upper stretches. All layers including the boulder mantle effectively obey a viscous flow law and are separated by no-slip boundaries (dynamically coupled, “welded”) (Arenson et al., 2002; Springman et al., 2012; Frehner et al., 2015).

We estimate the density of the rock glacier materials as the weighted average of the density of its constituents (Müller et al., 2016), namely debris (Err Granodiorite, ρ_debris=2700 kg m⁻³), ice (ρ_ice=910 kg m⁻³), and air (ρ_air=1 kg m⁻³). For the approximately void-free rock glacier core with 60 vol % ice, we obtain ρ_c=1626 kg m⁻³, and for the boulder mantle with 30 vol % air ρ_m=1890 kg m⁻³ (Barsch, 1996; Fig. 2b). The effect of water on density is insignificant. The prescribed viscosity ratios between the different layers are rock glacier core to high-viscosity boulder mantle 1:20 (estimated from dominant wavelength of furrow-and-ridge microtopography; see back-of-the-envelope calculation below; Fig. 2b) and core to low-viscosity basal shear layer 10:1 (conservative assumption from the literature; Cicoira et al., 2021, and references therein). To estimate the effective viscosity ratio R between the rock glacier mantle and core, we use an analytical formula based on buckle-folding theory that we apply to the furrow-and-ridge microtopography on units I–II (see Sect. 4.1; equation modified for one-sided support from Biot, 1961; cf. Frehner et al., 2015):

$$\begin{array}{}\text{(2)}& R:={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{m}}}{{\mathit{\mu }}_{\mathrm{c}}}}={\displaystyle \frac{\mathrm{3}}{\mathrm{8}}}{\left[{\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{d}}}{\mathit{\pi }{h}_{\mathrm{m}}}}\right]}^{\mathrm{3}}.\end{array}$$

The viscosity ratio R can be calculated from the dominant wavelength λ_d and rock glacier mantle thickness h_m. Inserting λ_d=50 m and h_m=4 m (estimates from field observations), we roughly estimate R=24.

The susceptibility for steady-state creep of debris-ice mixtures depends on debris-ice proportions (specifically the degree of ice supersaturation, i.e., the ice volume exceeding the pore volume), fabric, particle size, temperature, and water content (Moore, 2014). Since the influence of each parameter is difficult to disentangle and the material properties and composition are not known at this level of detail, we absorb these contributions by the effective viscosity, μ, and estimate it by solving the inverse problem. We depart from an initial rock glacier model with a uniform viscosity of pure ice for the entire rock glacier core, ${\mathit{\mu }}_{\mathrm{c}}^{\mathrm{0}}=\mathrm{2}\times {\mathrm{10}}^{\mathrm{13}}$ Pa s, as an initial guess. Next, we compute synthetic surface velocity data by means of the discretized forward operator, carried out by the numerical FE code (Fig. 2c). The synthetic data predicted by the current model are visually compared to the measured data, the orthophoto-derived surface creep rates. For rock glacier parts where the misfit between synthetic and measured data exceeds the data uncertainty, the viscosity is either increased if synthetic velocities were too high compared to measured values (u_pred>u_meas) or decreased in the opposite case (u_pred<u_meas, estimation problem). The obtained rock glacier viscosity distribution, $\stackrel{\mathrm{̃}}{m}$, that plausibly explains the measured surface creep rates, u_meas, within their uncertainty is one solution to the inverse problem.

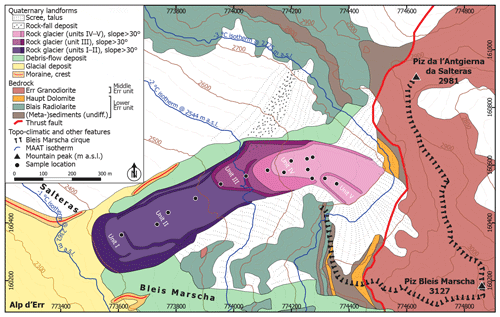
Figure 3 Quaternary features and main lithologies in the Bleis Marscha cirque. Bedrock map modified from Cornelius (1932). A subhorizontal thrust separates the crystalline Middle Err unit from the sedimentary Lower Err unit. Present-day mean annual air temperature (MAAT) isotherms are drawn according to Frauenfelder et al. (2001).

4 Results and interpretation

4.1 Geomorphology of Bleis Marscha

The Bleis Marscha rock glacier is a tongue-shaped multi-unit or polymorphic (sensu Frauenfelder and Kääb, 2000) talus rock glacier at an elevation range of 2400–2700 m a.s.l. (Fig. 3). With a length of 1100 m, a width of 150–200 m, a surface area of $\sim \mathrm{2.4}\times {\mathrm{10}}^{\mathrm{5}}$ m², and a source area of $\sim \mathrm{3.1}\times {\mathrm{10}}^{\mathrm{5}}$ m², it ranks among the largest rock glaciers in the Err–Julier area. Based on an assumed mean thickness of 30–40 m, we estimate a total volume of ∼ (7–10) × 10⁶ m³.

The rock glacier boulder mantle consists of three main rock types, each with its source in different parts of the cirque headwall (Fig. 3; Cornelius, 1932): prevalently weathering-resistant Err Granodiorite, followed by Blais Radiolarite and tectonically fractured Main Dolomite. Weathering-prone lithologies such as rauhwacke (cellular dolomite), conglomerate, limestone, and shales occur only in lenses or thin seams in the headwall and are only rarely found on the rock glacier surface. Block volumes are typically between 0.5–50 m³. Average block diameter is 1–2 m, exceptionally with >10 m edge length. The size of the largest blocks increases downstream towards the lowermost front. Downstream, the rock glacier rises over and is disconnected from the surrounding terrain.

Observations such as overall debris color reflecting differences in freshness of the sediment (weathering of the Err Granodiorite and lichen coverage), degree of soil development, and internal steep frontal terrain steps (slope angle >30^∘) allows us to subdivide the complex rock glacier into five different morphological units (Fig. 3) sensu Barsch (1996). These are labeled unit I (the lowest elevation, frontal part) to unit V (the highest elevation lobe). We interpret over-steepened terrain steps as marking internal boundaries in the rock glacier related to overriding of lower lobes by higher lobes. The lower lobes must originally have been connected to the talus slopes in the Bleis Marscha cirque, the only source of Err Granodiorite, as testified by the dominance of Err Granodiorite (>80 vol %) increasing towards the lowermost rock glacier front. In theory then, the lower lobes in part underlie the overriding higher lobes. Along its lower part (units I–II), the rock glacier lies on a till-mantled bedrock step (trough shoulder) known as Salteras. Schlosser (1990) mapped a right-lateral moraine near the trough shoulder break in slope (Fig. 3) and interpreted it as belonging to the Egesen stadial. The moraines and the rock glacier are nowhere in contact.

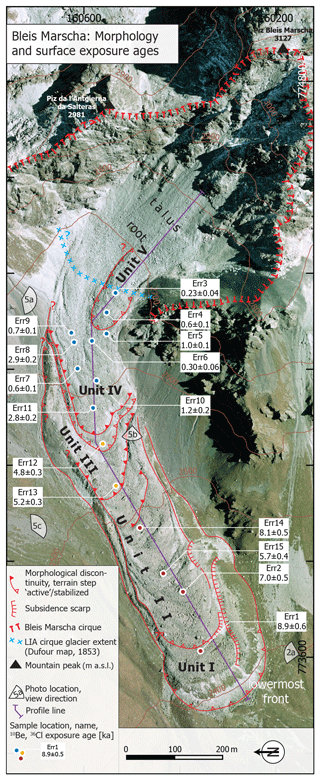
Figure 4 Plan view of morphological domains on a 2003 orthophoto showing the morphological discontinuities (inner fronts and terrain steps, slope breaks), sampling locations, and exposure ages (in ka; uncertainties are 1σ external errors; see Fig. 8 for surface creep rates). Bleis Marscha is a stack of three overriding lobes composed of units I–II, unit III, and units IV–V, separated by over-steepened terrain steps. Historical maps suggest that the Holocene maximum extent of the cirque glacier, reached during the Little Ice Age (LIA) around 1850, remained within the Bleis Marscha cirque (orthophoto reproduced with the authorization of the Swiss Federal Office of Topography, swisstopo).

The lowermost front of the Bleis Marscha rock glacier rises roughly 30–50 m from the edge of the Err valley trough shoulder at an elevation of 2380 m a.s.l. (Fig. 2a). The frontal part, denoted as unit I (Figs. 3, 4), exhibits several features suggesting that it is apparently inactive (see Sect. 4.3). This includes signs of settling and thus incipient degradation of the rock glacier body, patches of vegetation, and marked soil development, as well as extensive lichen cover, iron staining, and weathering rinds. Yet, a fresh frontal boulder apron indicates that the movement of this apparently old body has not ceased completely. The boundary between unit I and II is a steep, ca. 2–3 m high terrain step that extends upstream as a stable, grassy sidewall along the two lobes (margin of unit I; Fig. 2a). Where unit II rests on unit I, it is recessed by ∼5 m forming a ledge along the sides (Fig. 5c). The boulder weathering and abundance of black and green lichen give the lower lobes (units I–II) a much darker brownish-gray appearance in comparison to the higher elevation lobes. Blocks in units I–II are subangular to subrounded; weathering of the Err Granodiorite blocks plays an important role. The surface of unit II is gently inclined (∼10^∘) with a well-developed furrow-and-ridge microtopography of downstream crescent-shaped transverse ridges that are regularly spaced ∼50 m apart and separated by <5 m deep furrows (Fig. 5b). The mean rock glacier surface slope and presumably also the basal slope steepen from ∼10 to 20^∘ at an elevation of 2500 m a.s.l. causing units I–II to decelerate. The break in slope induced along-flow compressive stresses (Fig. 5b). Buckle folding of the layered rock glacier (stiff boulder mantle, deformable ice-rich core) in response to compressive flow likely was the dominant formation mechanism of the transverse furrow-and-ridge microtopography of unit II (cf. Frehner et al., 2015; Sect. 3.4).

Figure 5 Panorama views of the Bleis Marscha rock glacier (see Fig. 4 for photo locations). (a) View to the southeast into the root zone in Piz Bleis Marscha cirque. The dominant lithology of the boulder mantle, Err Granodiorite, is sourced above the thrust fault in the back of the cirque. Photo taken in August 2018. (b) View to the west onto lower rock glacier part with furrow-and-ridge microtopography (unit II). The currently advancing unit III is outlined by the prominent terrain step. Photo taken in October 2018. (c) Side view to the southeast of the middle rock glacier part, evidencing the Bleis Marscha rock glacier as a multi-unit debris stream composed of multiple stacked lobes. The fresh lateral debris apron poured over the stabilized, grassy sidewall along unit III hints at recently increased activity (possible reactivation). Unit I at the base of the stack is discernible by the stable, grassy sidewall and the ledge beneath unit II. Photo taken in October 2018.

Along the left-lateral side of units I–II, a west-southwest- to east-northeast-oriented scarp indicated by exposed fresh material dissects both units and is therefore a younger feature. The southernmost fringe of the rock glacier is slowly subsiding. Debris slides or aprons do not follow along the entire scarp (Fig. 2a). The slow, interior deformation must originate at depth rather than at shallow levels, which would push loose surface debris over the edge. The body is sagging instead of laterally advancing, for which ice loss is a possible explanation.

Unit III is clearly differentiated from units I–II by the slightly paler color of the debris (less brown) and by a steep, 5 m high, frontal terrain step (Fig. 5b). This terrain step is quite marked; the grass cover and soil development suggest long-term stability. The incipient soil development and vegetation patches, clearly differentiate unit III from the upper units IV and V. Fresh material poured over the stabilized, grassy, right-lateral margin along unit III between radiolarite rock fall deposits and its front, indicated by a light-colored boulder apron formed by debris slides exposing less weathered material, which suggests a recent increase in or renewal of activity of unit III (possible reactivation; Fig. 5c). Units I–III are bordered by a stable lateral ridge which is densely vegetated and has a thick soil cover (Fig. 5b, c). It extends upslope until the body disappears beneath the younger unit IV (Fig. 2a). We interpret this grassy ridge as the margin of the oldest, possibly relict body (unit I) that underlies the younger lobes (units II and III) and not as lateral moraines (Frauenfelder et al., 2001; cf. Barsch, 1996).

The boundary between unit III and IV is another steep 5 m step in the terrain. The steep (>20^∘) terrain here is cut by three major scarps where the two-layered stratigraphy of a coarse, clast-supported blocky mantle (thickness of ∼3 m) over a finer, matrix-supported core is exposed. These inner terrain steps are expressions of discontinuities and form the frontal boundary of units III and IV (Fig. 5b). Units IV–V are starkly different in appearance from units I–III. Again, the hue of the debris lightens (more gray than brown), the debris is much less weathered, and boulders are more angular. The maximum block size decreases from 5–6 m in diameter to 2–3 m. Vegetation and soil patches are absent. Unit IV exhibits several longitudinal ridges along the right-hand side (Fig. 4). In the bend at the lip of the cirque, the microtopography becomes more accentuated with a set of parallel longitudinal, asymmetric ridges (steep side facing outwards), whose amplitude however rarely exceeds 2 m. These are flow features that likely relate to the left turn that the rock glacier makes here. Unit V, a small rock glacier lobe (width 80 m), is well visible in the root zone emanating from the talus slope (Figs. 4, 5a).

We observed neither signs of glacier activity nor any surface ice remaining from the recent glaciation of the cirque (Dufour, 1853; Siegfried, 1887). The “small ice patch” mentioned by Frauenfelder et al. (2005) was no longer visible in 2017. The smooth, unstructured talus passes directly into the broad (180 m) rock glacier root zone (unit IV) at an elevation of ∼2700 m a.s.l. (Fig. 5a). No morphological evidence of the recent LIA glacier remains.

Figure 6 Field photographs of selected sampled boulders that are discussed in the text. In panels (d), (e), and (g), the star marks the sampled surface. The numbers refer to the boulder exposure ages (in ka; uncertainties are 1σ external errors).

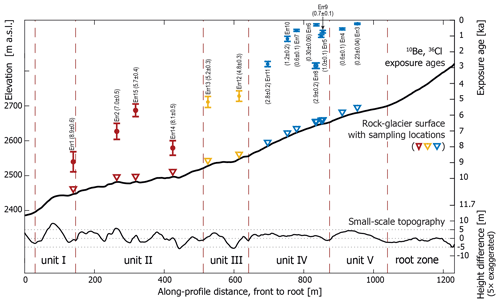
Figure 7 Longitudinal section of rock glacier surface along the profile line shown in Fig. 4 showing exposure ages (in ka; uncertainties are 1σ external errors), sample location (triangles), surface elevation, small-scale topography, and morphological units (separated by dashed red lines). Note the stratigraphically directed time axis to emphasize the general anti-correlation of the exposure ages with altitude. Exposure ages and sampling location are projected perpendicular onto the longitudinal profile, not along (unknown) surface isochrons. The small-scale topography is a high-pass-filtered topography computed by subtracting a 100 m running mean from the altitude at each point.

4.2 Boulder exposure ages

Measured ¹⁰Be concentrations are in the range of (0.7±0.1 to 23.6±1.2) × 10⁴ atoms g⁻¹. The measured ³⁶Cl concentration is $(\mathrm{3.1}\pm \mathrm{0.1})\times {\mathrm{10}}^{\mathrm{5}}$ atoms g⁻¹ (Tables 1, 2). Cosmogenic nuclide exposure ages (¹⁰Be and ³⁶Cl) range from 0.23±0.04 to 8.95±0.64 ka (Figs. 4, 7; Tables 1, 2).

For the lowermost, oldest part of the rock glacier (unit I), we obtained one ¹⁰Be exposure age: Err1 at 8.95±0.64 ka (Figs. 4, 6a, 7). The three ages for unit II are, from lowest elevation to highest, 7.03±0.51 ka (Err2; Fig. 6b), 5.70±0.40 ka (Err15; Fig. 6c), and 8.08±0.46 ka (Err14; Fig. 6d). From the next higher unit III, we obtained two ¹⁰Be ages: 5.17±0.35 ka (Err13; Fig. 6d) and 4.80±0.33 ka (Err12; Fig. 6e). In the higher elevation, the more active parts of the Bleis Marscha rock glacier, nine ages were determined, seven from unit IV and two from unit V. The ¹⁰Be ages for unit IV are from lower to higher elevation Err11 at 2.77±0.17 ka (Fig. 6f), Err10 at 1.18±0.16 ka, Err7 at 0.65±0.06 ka, Err6 at 0.30±0.06 ka, Err9 at 0.73±0.08 ka, and Err5 at 1.00±0.08 ka. The ³⁶Cl age for a dolomite boulder in unit IV is 2.89±0.18 ka (Err8; Fig. 6g). The ages from the highest youngest lobe, unit V, are 0.56±0.06 ka for Err4 and 0.23±0.04 ka for Err3 (Fig. 6h).

Ages generally decrease from the lowermost toe of the rock glacier (unit I) to the uppermost lobe (unit V). Nevertheless, ages on different morphological units of different ages show a similar degree of geologic scatter in terms of the relative dispersion. In stark contrast to nearly all exposure dating projects whereby the cosmogenic nuclide concentration records the time elapsed since the boulder reached its final position (e.g., on a moraine or a landslide deposit), we have exposure dated an active, moving landform. This requires a different way of interpreting the exposure ages. The cosmogenic nuclide concentrations comprise all the nuclides acquired during exposure of the sampled surfaces. This includes exposure in the bedrock (inheritance), at the talus foot, and on the rock glacier surface including while it is moving and at the final boulder position. Effects already discussed in other studies (Heyman et al., 2011) such as boulder rolling, toppling, or spalling can also affect the nuclide concentration. This is discussed in detail in Sect. 5.2.

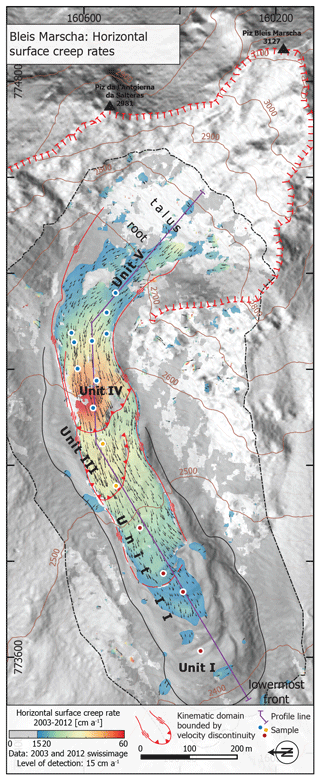
Figure 8 Modern horizontal surface creep rates derived from two orthophotos from 2003 and 2012. Level of detection is 15 cm a⁻¹. The long temporal baseline of 9 years averages interannual variabilities in rock glacier creep rates and is a robust estimate of modern, short-term surface kinematics. Important morphological (Fig. 4) and kinematic discontinuities (decorrelation gaps and stepwise changes in surface creep rate) largely coincide along morphological unit boundaries. Areas below the level of detection are considered immobile except for the lowermost front (unit I), where a fresh frontal boulder apron and comparison with the 1988 orthophoto indicate slow surface movement (5–10 cm a⁻¹) (hillshade background map reproduced with the authorization of the Swiss Federal Office of Topography, swisstopo).

4.3 Modern surface creep rates

By correlating two orthophotos from late summer 2003 and 2012, we obtain a noise-filtered horizontal surface creep rate field for the Bleis Marscha rock glacier and its immediate surroundings (Fig. 8). Surface creep rates are in the range of 25–60 cm a⁻¹. There are data gaps in which the image correlation failed due to decorrelation (non-translational movement, toppling, or vegetation) or inadequate input images (textureless snow fields). Since considerable presumably stable adjacent off-rock glacier areas show apparent surface movements of up to 15 cm a⁻¹, we adopt this conservative value as the significance level. Areas with speeds lower than this level of detection are classified as non-moving (dark gray areas in Fig. 8).

The lowermost unit I is mostly below the level of detection and considered close to immobile. Surface creep rates increase gradually upslope to 25 cm a⁻¹ on unit II, while the creep pattern changes from the slow deformation of a central, narrow stripe with outward, gradually decreasing creep rates to a laterally sharply confined, lobe-wide en bloc movement. On units II–IV, surface creep rates increase more stepwise up to 60 cm a⁻¹ until the mid-section of unit IV, along with the average surface slope (Fig. 10b). The “steps” or decorrelation gaps in surface speed coincide with terrain steps that delimit the lobes laterally and frontally. This suggests differential movement of the lobes that override each other, agreeing with field observations of boulder toppling at the over-steepened, “active” terrain steps (Fig. 4). Important discontinuities are in front of unit III (Fig. 5b) and unit IV (Figs. 7, 10b). Towards the talus, surface creep rates decrease. The orographic left side of the root zone, where unit V is, is more active.

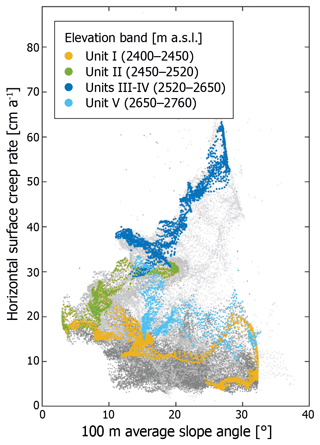
Figure 9 Slope–creep rate relation. Scatter plot showing the correlation between the 100 m averaged slope (from smoothed DEM) and the horizontal surface creep rate for different elevation bands of the Bleis Marscha rock glacier. The gray dots are data points from the entire rock glacier (lowermost part <2450 m a.s.l. in dark gray, lobes >2450 m a.s.l. in light gray). Data points restricted to a 20 m stripe along the central profile, where the effect of lateral drag is minimal, are colored. The good correlation between surface slope and surface creep rates suggests that on units II–IV, topographically controlled creep is the dominant deformation mechanism.

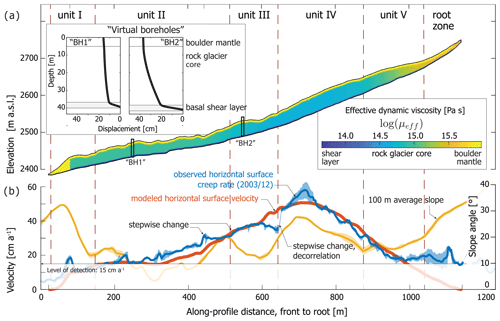
Figure 10 (a) Inferred effective viscosity distribution on the longitudinal transect (profile line shown in Figs. 4, 8). The inferred effective dynamic viscosity does not vary significantly over units II–IV. Along-profile variations in surface creep rates are primarily controlled by the surface slope. Insets: modeled yearly horizontal displacements in “virtual boreholes”. The strain localization near the base despite the linear stress–strain rate relationship arises from the rock glacier parameterization with the three-part mechanical layering (boulder mantle, core, basal shear layer). The simple Newtonian model with depth-varying viscosity generates synthetic velocity profiles that resemble borehole deformations measured on other rock glaciers. (b) Longitudinal section of observed surface creep rate (blue line), modeled or synthetic horizontal surface velocity (orange), and the 100 m filtered slope (yellow). Horizontal surface creep rate of sections dominated by viscous creep roughly follow the average surface slope (units II–IV). Correlation is lost on the lowermost front and talus. The morphologically defined units I–II, unit III, and units IV–V are separated by sharp speed gradients (stepwise changes in surface creep rate, kinematic discontinuities; Fig. 7).

Data points from the entire rock glacier surface drawn in a slope–surface creep rate scatter plot (average slope within 100 m radius; Fig. 9, gray dots) are clustered in a wedge-shaped domain; the few outliers are due to non-translational movement (e.g., sliding, tumbling) and not due to large-area cohesive creep. Higher creep rates are reached at higher surface slope angles, in accordance with the concept of shear-stress-driven creep. A clearer slope-velocity relation emerges when data from a 20 m wide stripe along the central profile are highlighted (Fig. 8) because they are unaffected by boundary effects such as lateral drag and non-translational movements. The clear correlation between creep rate and average surface slope suggests that surface creep rates on units II–IV (altitude bands 2475–2653 m a.s.l.) are controlled by topography (via average surface slope) rather than by material properties (effective viscosity). The correlation is lost on the lowermost frontal area (lowermost ∼100 m, unit I), where incipient stabilization and possibly loss of ice hampers viscous creep, and on the uppermost unit V, possibly because slope-independent deformation processes other than creep are dominant (Fig. 10b). We explore the relationship between surface creep rate, topography, and material properties numerically in Sect. 4.4.

4.4 Controls on modern surface creep rates

For a given rock glacier thickness, layering, and density, the effective viscosity distribution is fitted to the 2003 to 2012 surface creep rates. We obtain a simplified but plausible rock glacier structure (Fig. 10a) that reproduces the image-correlation data within their uncertainty (Fig. 10b). The result suggests that the viscosity in the more slowly moving, apparently inactive low-elevation lobes are only slightly higher than in the active, more rapidly moving high-elevation lobes (Fig. 10a), i.e., that surface creep rates on units II–IV can be explained by topographical parameters (thickness, surface slope) alone. In contrast, the external parts of unit I move more slowly than potentially possible given the comparable surface slope and thickness to unit II. This modeling result corroborates our hypothesis of topographically controlled creep on units II–IV and incipient degradation of unit I.

We used the FE code presented in Frehner et al. (2015). The aspects discussed therein (incompressibility, boundary effects) apply analogously in this study. Our synthetic vertical deformation profiles (“virtual boreholes”; Fig. 10a, insets) resemble measured borehole deformation profiles from other rock glaciers (Arenson et al., 2002). No boreholes have been drilled on Bleis Marscha rock glacier. Although the simple Newtonian continuum model with vertical viscosity layering does not accurately reproduce deformation mechanisms at the microscale, it does capture the essential deformation effects that lead to the observed surface creep rates.

The solution to Eq. (1) is non-unique as higher surface speed can be achieved with any combination of greater thickness, steeper surface slope, or lower viscosity. Large errors in the topographical parameters would undermine the goal of separating topographical from material controls. However, the driving stress and ultimately the deformation is largely governed by the well-constrained average surface slope (not by the basal slope; Nye, 1952) and the reasonably assessable rock glacier thickness and density. The remaining unknown viscosity can be estimated with sufficient accuracy.

5 Discussion

By examining the exposure ages and considering the image correlation and FE modeling results, we decipher the history of the Bleis Marscha rock glacier over the past 9 kyr and put it into the framework of the known regional climate history (Ivy-Ochs et al., 2009; Böhlert et al., 2011a).

5.1 Exposure dating an active rock glacier

Cosmogenic nuclide ages include all of the time that a rock surface is exposed to cosmic rays. However, in nearly all previous studies, the sought-after age encompasses only the nuclides produced since the boulder reached its final position (e.g., in a moraine or landslide deposit). Unlike single-age landforms that for the most part formed in short-lived events, active rock glaciers are continually moving and grow over centuries to millennia. Rock surfaces are exposed to cosmic rays in various stages of the landform evolution.

Rock glaciers form on an inclined slope (e.g., a talus slope) when an accumulation with favorable debris-ice proportions reaches a critical thickness (Kirkbride and Brazier, 1995; Haeberli et al., 2003, 2006). Viscous creep emerges as the dominant deformation mechanism, and the mobilized material begins to creep downslope under its own weight. Coarse blocks on the rock glacier surface that form the boulder mantle are sourced in the rock glacier root and carried towards the front. Conceptually, boulder residence time on the rock glacier surface is the time since the initial deposition in the rock glacier root and comprises the travel time (creep-induced, passive transportation during active periods) and, for an inactive to relict landform, the time since the stabilization of the landform (relict period) (Haeberli et al., 1998, 2003). This model predicts a spatially correlated age signal with downstream systematically increasing surface ages. The conveyor-belt-like advance mechanism affects the rock glacier age structure and the relations between surface velocity, length, and age (Kääb et al., 1997; Kääb and Reichmuth, 2005). Due to the decrease in horizontal speeds with depth and the frontal volume loss mainly from excess ice meltout, the rock glacier surface moves faster than the advancing landform itself (Haeberli et al., 1998; Frauenfelder et al., 2005; Kääb and Reichmuth, 2005). Surface exposure ages atop the front of rock glaciers give the lower bound of the landform age (Scapozza et al., 2014; Winkler and Lambiel, 2018).

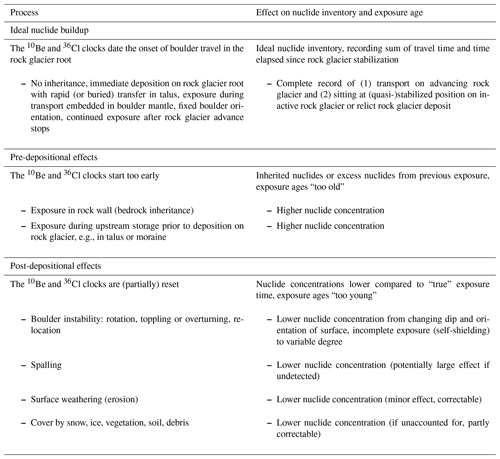
On an active rock glacier, the cosmogenic nuclide concentration adds up all of the following periods of exposure (Table 4):

1. pre-exposure in the headwall (bedrock inheritance)

2. transit time in the talus or during intermediate upstream storage

3. transport on the moving (active) rock glacier (travel time)

4. sitting at the (quasi-)stabilized position (inactive rock glacier or relict rock glacier deposit).

As in other cosmogenic nuclide studies, post-depositional surface processes like boulder surface weathering, spalling, unaccounted for shielding, rotation, and toppling lead to a lower total boulder nuclide inventory (Ivy-Ochs et al., 2007; Heyman et al., 2011).

Table 4 Processes that affect measured cosmogenic nuclide concentration in a boulder on an active rock glacier (see text for discussion). Surface processes like exposure in the bedrock (inheritance), post-depositional weathering, spalling, unaccounted for cover or shielding, rotation, and toppling affects single boulders to variable degrees and largely independently from their neighbors.

5.2 Interpretation of the Bleis Marscha boulder exposure ages

Our exposure ages in general anticorrelate with elevation and correlate with downflow distance from the rock glacier root (Figs. 4, 7), conformable to the rock glacier formation model. Nevertheless, ages from individual lobes show geologic scatter. How do the processes listed in Table 4 apply to the Bleis Marscha rock glacier?

5.2.1 Boulder nuclide inventories on a moving rock glacier

Significant pre-exposure in the cirque headwalls seems unlikely because for talus rock glaciers like Bleis Marscha, fed by scree from the retreating headwall, headwall erosion is rapid (cf. Mohadjer et al., 2020; Steinemann et al., 2020). Back-of-the-envelope estimates of long-term average debris fluxes of the rock glacier lobe IV and V are in the order of 720 (<900) m³ a⁻¹, calculated from mean speeds of 400 m $/$ 1200 a (length of lobe divided by exposure age) and a rock glacier width of 120 m (<150 m), a height of 30 m, and a debris fraction of 0.6. These debris fluxes correspond to head-wall erosion rates of ∼2.3–2.9 mm a⁻¹. At this accumulation rate meters of talus are built-up at the foot slope in decades to centuries as testified by the abundant fresh talus cones within the footprint of the LIA Bleis Marscha cirque glacier (Fig. 5a). With respect to their ice-cored moraine study, Crump et al. (2017) point out that it may be difficult to detect low levels of ¹⁰Be inheritance but that it becomes unlikely for boulders larger than ca. 1 m side length because of strong self-shielding in the bedrock wall (rapid drop-off of ¹⁰Be production with depth). Boulders can also be exposed in the talus or any other reservoir (e.g., moraine deposit) prior to entering the rock glacier system. A comparison of aerial photos over several years shows the rapid accumulation of talus since the LIA (see above), suggesting that nuclide accumulation in a boulder while in the talus or at the talus foot is likely not significant as the scree is quickly covered. Critically, the young exposure ages in unit V (see also below) verify rapid deposition onto the rock glacier. If inheritance from bedrock exposure is unlikely and storage in the talus with exposure at the surface is likely to be brief, then nuclide concentrations should record the time elapsed on the rock glacier surface. This would include travel time and all of the time that a boulder is stable, whether in final relict deposit or when the rock glacier is less active. This suggests that most of the geologic scatter of our data is due to post-depositional processes (Table 4), with instability in boulder position being the prime candidate.

Continuous boulder GPS data reported by Lambiel and Delaloye (2004) demonstrate small (cm), slow, rotational movement of boulders at the surface, pointing to the slightly variable orientation of the sampled surface and to the possibility of toppling or overturning over longer periods of time. Boulders might roll or slide down steep scarps in front of rock glacier ridges (Kääb and Reichmuth, 2005) or topple into furrows. Ulrich et al. (2021) detected creep-independent boulder movement over a 3 week period at the steep (∼30^∘) frontal part of the Äußeres Hochebenkar rock glacier with repeated terrestrial laser scans. Boulder instabilities are likely greater the faster the rock glacier moves (e.g., Wirz et al., 2016, for fast moving rock glaciers in the Mattertal, Valais) and exacerbated by displacements within the boulder mantle (e.g., Buchli et al., 2013) or by frost heave, thaw settlement, or the degradation or collapse of the active layer or the underlying ice-rich core (similar to ice-cored moraines, e.g., Crump et al., 2017). We did not observe evidence of severe disturbances on Bleis Marscha. Boulders are subangular to subrounded even in the youngest parts of the rock glacier (units IV–V; Fig. 6), evidence that knocking off of boulder corners during movement (jostling) or falling off the front of ridges is occurring. The addition of a boulder to a lobe due to recent rock fall as observed at Murtèl (Upper Engadine) in August 2020 (personal observation) would also yield an age that is “too young”. In the case of recent events, fresh boulder appearance calls this out. The effect of (∼ uniform) boulder surface weathering is accounted for in the age calculation. It is only a few percent and lies within the uncertainties of an individual exposure age. On the other hand, (non-uniform) spalling, e.g., from frost shattering or friction between the boulders, potentially leads to more severe lowering in nuclide concentration. Recently spalled surfaces, as revealed by their “fresh” appearance, were not sampled. Unaccounted for shielding also leads to exposure ages that are “too young”. The effect of snow cover was likely more pronounced for the smaller, less windswept boulders in the high-elevation lobes (units IV–V) where snow cover lasts longer but also more uniform over the less rough surface. Strict constraints on how much snow and for how long hinder such a correction whose effect is limited to a few percent. No corrections for snow cover were made in this study.

5.2.2 Three Bleis Marscha rock glacier generations

In light of the above general discussion of the various factors contributing to cosmogenic nuclide concentrations in active rock glacier boulders, we now discuss the specific Bleis Marscha exposure ages. The cumulative effect of material loss and small underexposure from boulder instabilities and rotation adding up over centuries to millennia likely is the primary contributor to the geologic scatter. We think that the effect of stochastic boulder instabilities in general exceeds inheritance, although the latter cannot be excluded in individual cases. The Bleis Marscha exposure ages are tendentially skewed towards “too young”. It is within this framework that we interpret the exposure ages.

The morphologically continuous units I and II are the lower elevation, thus oldest, units at Bleis Marscha. The exposure age of unit I is 8.9 ka (Err1; Fig. 6a). Of the three ages from boulders across unit II, two ages Err2 (7.0 ka) and Err15 (5.7 ka) are younger than the further up-slope boulder age Err14 at 8.1 ka (Fig. 6c, d). Boulders Err1 and Err14 are large and flat-lying with basal side lengths >3 m, making it more likely that they roughly maintained their orientation as the rock glacier moved. In contrast, boulders Err2 and 15 are cigar-shaped, i.e., prone to rolling, and not firmly embedded in the boulder mantle (Fig. 6b, c). We consider the ages for the latter two as being “too young”. We suggest that units I–II started forming at ∼8.9 ka. Unit III occupies an intermediate topographic position in the Bleis Marscha rock glacier and is separated by a morphological discontinuity from the lower units I–II (Figs. 4, 5b). Two consistent ages Err13 (5.2 ka; Fig. 6d) and Err12 (4.8 ka; Fig. 6e) also point to a time gap between units I–II and unit III. The partly stabilized and vegetated terrain step immediately downstream of Err13 is the stabilized front of this lobe which we interpret to have formed at ∼5.2–4.8 ka. Rock glacier units IV and V comprise the higher elevation, more rapidly moving lobe of Bleis Marscha (Fig. 5a). Ages for unit IV range from 2.9 to 0.3 ka. The ³⁶Cl age of 2.9 ka for Err8 seems incongruous with its position, and the fact that a nearby boulder (Err9) is, at 0.7 ka ¹⁰Be age, 2 kyr younger. In comparison to the several dated boulders on unit IV, it is likely that boulder Err8 experienced pre-exposure in the bedrock. Inheritance is plausible given the small dimensions of the sampled boulder ($\mathrm{0.7}\times \mathrm{1.0}\times \mathrm{1.5}$ m; Fig. 6g; see discussion above on Crump et al., 2017) and the crucial fact that ³⁶Cl is produced deeper into rock than ¹⁰Be (Alfimov and Ivy-Ochs, 2009). This does not affect our interpretation that lobe IV initiated at ∼2.8 ka (age of Err11; Fig. 6f). The time gap to unit III coincides with a morphological (frontal terrain step) and kinematic discontinuity (Figs. 4, 8, 10b). Unit V is the highest elevation, youngest unit. It emanates from the footprint of the LIA glacier 100–150 m away from the foot of the talus. Our two ages of 0.56 and 0.23 ka from unit V are in agreement with this concept.

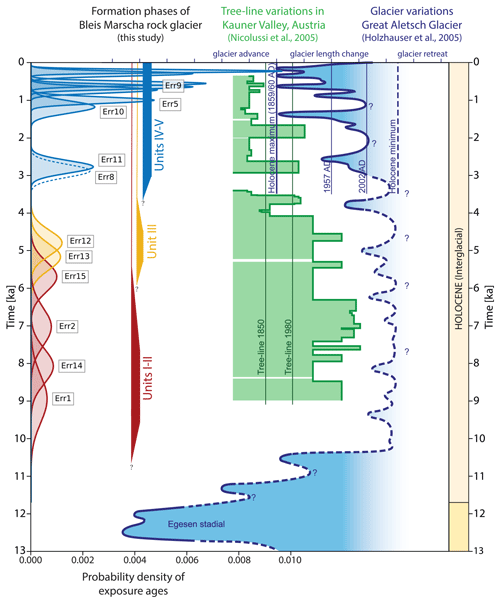
Figure 11 Bleis Marscha rock glacier formation phases in the framework of the climate evolution in the Central–Eastern Alps during the Younger Dryas and the Holocene (modified from Ivy-Ochs et al., 2009; Singeisen et al., 2020). Climate proxies are Great Aletsch glacier length variations (modified from Holzhauser et al., 2005) and Kauner valley tree-line variations (Nicolussi et al., 2005). Bleis Marscha exposure ages are plotted as probability density functions (in ka; uncertainties are 1σ external errors). We interpret three distinct generations: Early Holocene (∼8.9–8.0 ka, after retreat of the Egesen glaciers of the Younger Dryas cold phase) of low-elevation units I–II, Middle Holocene (∼5.2–4.8 ka, after the Middle Holocene warm period) of unit III, and Late Holocene until present (since ∼2.8 ka, roughly coeval with Late Holocene cooling and glacier re-advances) of high-elevation units IV–V. The formation phases of the three Bleis Marscha rock glacier generations appear to correlate with Holocene climate oscillations.

We summarize the three interpreted Bleis Marscha formation phases (Fig. 11). Our data suggest that the Early Holocene generation (units I–II) began forming at ∼8.9 ka. The formation phase lasted at least until ∼8.1 ka as indicated by the most upstream exposure age. The root zone of units I–II was afterwards overridden and buried by subsequent rock glacier generations. At the latest at ∼5.2 ka, the minimum formation age of the Middle Holocene generation (unit III), units I–II must have been cut off from their debris source in the cirque. Analogously, the formation phase of the Middle Holocene generation with ages in the range ∼5.2–4.8 ka ended at ∼2.8 ka at the latest, when it was overridden by unit IV and disconnected from the talus. The youngest Late Holocene generation (units IV–V) began forming at ∼2.8 ka. Coinciding morphological discontinuities (over-steepened terrain steps; Fig. 4), time gaps, and kinematic discontinuities (stepwise changes in surface creep rate, data gaps; Fig. 8) separate units I–II, III, and IV–V from each other. Our interpretation is that Bleis Marscha is not a continuous “stream” but a stack of three overriding lobes, each with its own discrete formation phase.

5.3 Implications

5.3.1 Episodic formation

In the Bleis Marscha cirque, Holocene rock glacier formation occurred in three distinct phases. These appear to be correlated to major Holocene climate shifts. The Early Holocene generation (units I–II) is confined within but not connected to Egesen lateral moraines (Schlosser, 1990). From this crosscutting relationship and the oldest and lowermost (minimum) formation age atop its front of 8.9 ka (Err1), it follows that these lobes must have formed after the Egesen cirque glacier starvation during the late Younger Dryas (Frauenfelder et al., 2001; Kerschner and Ivy-Ochs, 2008; Ivy-Ochs et al., 2009; Ivy-Ochs, 2015). After 10 ka, the climate shifted towards warmer conditions (Schimmelpfennig et al., 2014; Solomina et al., 2015). Already by the Middle Holocene, the lower continuous permafrost boundary rose to likely above 2600 m a.s.l. (current −2 ^∘C MAAT isotherm; Fig. 3), and the tree line was higher than today (Fig. 11; Nicolussi et al., 2005). The Early Holocene debris volume (units I–II) is twice the Late Holocene debris volume (units IV–V) that took ∼3 kyr to build up. This is a conservative estimate from the corresponding lengths (factor of 1100 m/480 m ≈2.3) and surfaces areas (factor of ∼2.7), assuming similar thickness and debris content and that units I–II must extend as far up to their source of Err Granodiorite as both younger generations. Given the Early Holocene warming and the formation timing of the Middle Holocene generation (∼5.2–4.8 ka), it seems unlikely that the formation phase of the Early Holocene generation was longer than 6 kyr. This rough comparison of debris supply rates points at a more intense Early Holocene debris release compared to the Late Holocene average. Possibly, the rapid Early Holocene buildup was conditioned by debris from warming-induced rapid head wall weathering (Kenner and Magnusson, 2017; Kenner, 2018). Considering the climate resilience of debris-mantled Bleis Marscha lobes (discussed below), the end of the formation phase seems more likely to be linked to declining or imbalanced supply of debris and ice in proportions no longer susceptible for rock glacier creep.

The ages of the Middle Holocene unit III suggest a period of enhanced Bleis Marscha rock glacier activity at around 5 ka (∼5.2–4.8 ka). Several lines of evidence, including radiocarbon data (Joerin et al., 2006), suggest a dominantly warm interval around that time perhaps punctuated by brief cold snaps (Solomina et al., 2015, 2016; Nicolussi et al., 2005; Kaufmann et al., 2020). Nevertheless, data from Tschingelgletscher (Berner Oberland; Wipf, 2001) and the Miage glacier (Mont Blanc massif; Deline and Orombelli, 2005) point to glacier advances around 5 ka, which is so well documented by the preservation of the Tyrolean Iceman after 5320–5050 cal BP (Kutschera et al., 2017) due to ice coverage which roughly persisted until 1991. Bohleber et al. (2020) point out an elevation dependency at the onset of the Middle to Late Holocene glacier advances, suggesting that at the elevation of Bleis Marscha, the transition to colder conditions may have already begun.

In the Late Holocene, after approximately 4 ka, climate cooled, timberline moved to lower elevations, and glacier advances became more frequent, longer, and more severe compared to the Middle Holocene, culminating in the LIA at ∼1350–1850 CE (Fig. 11; Joerin et al., 2006; Ivy-Ochs et al., 2009; Le Roy et al., 2015; Solomina et al., 2016; Badino et al., 2018). Air temperature oscillations and concomitant freeze–thaw cycles weakened the headwall and increased frost shattering and debris production, enhanced by the tectonically weakened fault zone in the headwall (Figs. 3–5a). Our data suggest that the Late Holocene generation began forming roughly coeval with this climatic shift.

According to the dual-threshold model presented in Kirkbride and Brazier (1995), initiation of a new rock glacier lobe occurs when an external climate threshold and an internal talus thickness (shear-stress threshold) are crossed simultaneously. In Bleis Marscha cirque, debris production is high, as shown by the overfilled talus with lots of fresh rock fall since the LIA (Fig. 5a). The internal threshold is not a limiting factor, and the Bleis Marscha rock glacier generations seem to reflect more the external climate threshold.

5.3.2 Slow degradation

The creep of the Early–Middle Holocene generations (units II–III), although with 15–35 cm a⁻¹ moving not as fast as the younger unit IV at 40–60 cm a⁻¹, is topographically controlled rather than by the creep susceptibility of the rock glacier body. This is shown by the good slope–creep rate correlation (Fig. 9) and the FE modeling results (Fig. 10). Moreover, cohesive creep and en bloc movement of these entire morphologically delineated lobes with sharp lateral velocity steps (Figs. 4, 7) indicate stress transmission and require (excess) ice as “cement” – notably beneath an Early–Middle Holocene boulder mantle, currently located below the −2 ^∘C MAAT isotherm (Fig. 3). Merely the southernmost fringe of the lowermost units I–II shows signs of incipient degradation (Fig. 2a). For lack of direct data on the interior of Bleis Marscha, the age of the inferred Bleis Marscha ice is not known and can principally be original or later recharged ice (Giardino and Vitek, 1988; Colucci et al., 2019). From the impression of a still intact looking microtopography (Fig. 5b), we think that the ice in units I–II and III is largely as old as its covering debris mantle, thus of Early and Middle Holocene age, respectively. Otherwise, if advanced meltout occurred, the surface would look more disrupted and collapsed.

Persistence of ice is characteristic for rock glaciers, owing to the insulating openwork debris mantle (∼ active layer) and the cooling effect of air circulation (Colucci et al., 2019; Jones et al., 2019; Kellerer-Pirklbauer, 2019). For example, preservation of Early Holocene ice through the Middle Holocene warm period is interpreted by Krainer et al. (2015) for the Lazaun rock glacier (South Tyrol). The close connection between surface substrate and ice preservation seems exemplified on Bleis Marscha by a stabilized right-lateral part of unit III immediately upstream of the “reactivated” area (Figs. 3, 5c) that does not move despite the mechanical load of the rapidly overriding unit IV. The local ground thermal regime beneath the fine-grained surface cover (fractured radiolarite deposited by a rock fall) is less susceptible to permafrost conditions (Harris and Pedersen, 1998; Schneider et al., 2012).

5.3.3 Late Holocene glacier–rock glacier coexistence

During the Late Holocene cold phases, the Bleis Marscha cirque was intermittently occupied at most by a perennial ice patch or a glacieret (Frauenfelder et al., 2005) likely not larger than the LIA extent as mapped in the mid-19th century (Dufour, 1853; Siegfried, 1887). The thin, stagnant cirque glaciers could neither mechanically nor thermally erode the rock glacier; permafrost and the pre-existing rock glacier persisted beneath the ice patches (Frauenfelder et al., 2001, 2005). Stable cryotic conditions during the Late Holocene are plausible in the high-elevation (>2700 m a.s.l.) cirque floor that is in the continuous permafrost belt even today (Gruber et al., 2006; Boeckli et al., 2012). “Mild” periods apparently were not long and warm enough for permafrost degradation, the more so in view of the climate resilience of the debris-mantled ice-rich bodies. The equilibrium line altitude in the steep Bleis Marscha cirque headwalls oscillated in elevation, as likely did relative accumulation rates of ice and debris, with higher relative debris input during ice-free “mild” phases (Anderson et al., 2018; Kenner, 2018). Also, the coarse debris transport alternated between glacial transport during cold phases and permafrost creep during glacial “mild” phases (Zasadni, 2007). Despite these oscillating growth conditions in the rock glacier root, the morphologically continuous surface (absent topographic steps) of unit IV with boulder exposure ages ranging from 0.5–2.8 ka suggests undisturbed growth from ∼2.8 ka to pre-LIA.

6 Conclusions

We constrained the formation phases and reconstructed the development of the active Bleis Marscha rock glacier (Val d'Err, eastern Switzerland) with morphostratigraphic relations from field observations, 15 cosmogenic nuclide exposure ages (14 ¹⁰Be and 1 ³⁶Cl sample), modern 2003 to 2012 surface creep quantification from aerial image correlation, and finite element modeling. We used the latter to separate the control of topography (mainly surface slope) and material properties (e.g., ice content) on the surface movement. In contrast to earlier research in the Alps that exposure dated relict rock glaciers, the Bleis Marscha lobes are presently active. We found that boulder nuclide inventories are stochastically overprinted primarily by the cumulative effect of small boulder instabilities (rotational movement, creep-independent displacement) while traveling on the rock glacier surface. This leads to exposure ages that are tendentially “too young”, although bedrock inheritance (ages that are “too old”) cannot be excluded in individual cases. The correlation of two orthophotos from 2003 and 2012 indicates average movement at creep rates of 25–60 cm a⁻¹. Bleis Marscha is a 1100 m long, active, polymorphic talus rock glacier at an elevation range of 2400–2700 m a.s.l. Coinciding morphological discontinuities (over-steepened terrain steps) and kinematic discontinuities (decorrelation gaps, stepwise changes in surface creep rate) separate the Bleis Marscha rock glacier into a stack of three lobes, each with its own formation phase. Our cosmogenic nuclide data suggest that the formation of each of the three lobes appears to correlate with Holocene climate shifts: Early Holocene, ∼8.9–8.0 ka; Middle Holocene, ∼5.2–4.8 ka; and Late Holocene, since ∼2.8 ka.

Crosscutting relationships in the field indicate that the low-elevation, Early Holocene generation of the Bleis Marscha rock glacier formed after the retreat of the Egesen Bleis Marscha glacier, with exposure ages pointing at ∼8.9–8.0 ka. The rapid buildup of voluminous rock glacier bodies in the rapidly warming climate of the Early Holocene was likely conditioned by warming-induced high rock fall activity. The end of the formation phase could be linked to an insufficient or imbalanced supply of debris and ice in proportions no longer susceptible for rock glacier creep. The Middle Holocene generation formed at ∼5.2–4.8 ka during a dominantly warm period interrupted by short cold spells as documented by glacier advances at some sites in the Alps. The formation phase of the high-elevation youngest Late Holocene generation likely began at ∼2.8 ka as indicated by its oldest exposure age atop its front, which is roughly coeval with the onset of the Late Holocene climate oscillations. Although these lobes are sourced during the Late Holocene intermittently glacierized Bleis Marscha cirque, their morphological continuity suggests undisturbed growth. Due to favorable topo-climatic conditions in the high-elevation cirque (>2650 m a.s.l., MAAT −2 ^∘C) and small, stagnant cirque glacierets, ground thermal conditions in the rock glacier root zone remained cryotic, and interactions with the glacieret were not disruptive for the rock glacier development. Ongoing cohesive surface deformation on old, Early and Middle Holocene Bleis Marscha lobes requires the presence of ice as a stress transmitter. Although these lobes are below the current −2 ^∘C isotherm, we believe from the intact microtopography that the ice is largely original, preserved from the Early–Middle Holocene. Degradation of this azonal, ice-rich permafrost body, in contrast to its rapid formation, is slow and attenuated by the debris mantle. We find contrasting responses to external forcing of Bleis Marscha rock glacier parts: the successive initiation of three lobes in the Holocene suggests that rock glacier formation processes in the Bleis Marscha cirque were climate-sensitive and enabled by high rock fall activity so that debris availability is not a limiting factor. Contrariwise, once formed, the boulder-mantled, ice-rich lobes reacted less sensitively to climate forcing, with permafrost degradation protracted over millennia.