the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Exceptionally high heat flux needed to sustain the Northeast Greenland Ice Stream
Basile de Fleurian
Nicole Schlegel
Helene Seroussi
Kerim Nisancioglu
The Northeast Greenland Ice Stream (NEGIS) currently drains more than 10 % of the Greenland Ice Sheet area and has recently undergone significant dynamic changes. It is therefore critical to accurately represent this feature when assessing the future contribution of Greenland to sea level rise. At present, NEGIS is reproduced in ice sheet models by inferring basal conditions using observed surface velocities. This approach helps estimate conditions at the base of the ice sheet but cannot be used to estimate the evolution of basal drag in time, so it is not a good representation of the evolution of the ice sheet in future climate warming scenarios. NEGIS is suggested to be initiated by a geothermal heat flux anomaly close to the ice divide, left behind by the movement of Greenland over the Icelandic plume. However, the heat flux underneath the ice sheet is largely unknown, except for a few direct measurements from deep ice core drill sites. Using the Ice Sheet System Model (ISSM), with ice dynamics coupled to a subglacial hydrology model, we investigate the possibility of initiating NEGIS by inserting heat flux anomalies with various locations and intensities. In our model experiment, a minimum heat flux value of 970 mW m−2 located close to the East Greenland Ice-core Project (EGRIP) is required locally to reproduce the observed NEGIS velocities, giving basal melt rates consistent with previous estimates. The value cannot be attributed to geothermal heat flux alone and we suggest hydrothermal circulation as a potential explanation for the high local heat flux. By including high heat flux and the effect of water on sliding, we successfully reproduce the main characteristics of NEGIS in an ice sheet model without using data assimilation.
- Article
(10892 KB) - Full-text XML
- Comment
- BibTeX
- EndNote
The Greenland Ice Sheet (GrIS) displays large spatial variations in surface velocity, with a few fast-flowing outlets draining most of the interior (Rignot and Mouginot, 2012). It is therefore critical to capture the complex flow pattern of GrIS in models used for future sea level projections. Recent developments in ice sheet models such as efficient parallel computation (Khroulev and PISM-Authors, 2015), better representation of flow equations (Larour et al., 2012), detailed basal topography (Morlighem et al., 2014) and the inclusion of subglacial hydrology have contributed to greatly improving the representation of this spatially varying flow (Aschwanden et al., 2016). In addition to these advances, inversion for basal friction using surface velocities has proved to be a powerful tool (Morlighem et al., 2013), and models are now able to capture most of the complex flow pattern of the ice sheet. Inversions are useful to capture present-day velocity, but they mask information that is needed to evolve these conditions in time. Therefore, we cannot fully rely on inversions for future projections, as basal conditions may evolve as a result of a changing climate and in turn influence ice dynamics.
The Northeast Greenland Ice Stream (NEGIS) drains more than 10 % of the GrIS and is exceptional by displaying high velocities all the way to the ice divide (Rignot and Mouginot, 2012). Despite its large impact on the GrIS mass balance, NEGIS is not accurately represented in ice sheet models without inverting for basal friction (Goelzer et al., 2018). Aschwanden et al. (2016) simulated NEGIS in the Parallel Ice Sheet Model, capturing high velocities using a simple hydrology model, however lacking the far inland onset of the ice stream. Beyer et al. (2018) used the basal melt rates from the model by Aschwanden et al. (2016) in a more sophisticated hydrology model to reproduce NEGIS in the Ice Sheet System Model (ISSM). They capture the high velocity flow of the outlets well, but the representation of the transition areas outside of the main trunk are more diffuse compared to the observed values. These studies illustrate how we are getting closer to reproducing present-day NEGIS in ice sheet models. However, the characteristic clearly defined shear margins, and high velocities upstream at the onset of the ice stream are still lacking.
To understand why high upstream velocities are not reproduced in models, one must look into how the ice stream is initiated. The origin of NEGIS has been explained by a geothermal heat flux (GHF) anomaly left behind by the passage of the Icelandic plume (Fahnestock et al., 2001; Rogozhina et al., 2016; Martos et al., 2018; Alley et al., 2019). Interpretation of radar data points to unusually high basal melt rates at the head of the ice stream, corresponding to an exceptionally high GHF of 970 mW m−2 (Fahnestock et al., 2001; Macgregor et al., 2016; Alley et al., 2019; Keisling et al., 2014). A local increase in GHF intensifies basal water production and potentially enhances basal sliding. Unfortunately, GHF maps for Greenland display a large spread of values (Rogozhina et al., 2012; Shapiro and Ritzwoller, 2004; Fox Maule et al., 2009; Martos et al., 2018; Rogozhina et al., 2016; Greve, 2019). These large uncertainties in the estimates of the GHF have been shown to dominate the uncertainty on the ice flux in this region (Smith-Johnsen et al., 2019). In addition, the GHF maps are coarse and may not capture local anomalies like the one suggested to exist at the head of NEGIS (Fahnestock et al., 2001; Macgregor et al., 2016; Alley et al., 2019). Accurately capturing such a feature and explicitly representing the effect of high melt rates on basal sliding are key to reproduce the distinct velocity pattern of NEGIS in ice sheet models.
Here, we study the impact of the presence and intensity of a mantle plume, at the head of NEGIS on the ice flow structure. We do not suggest the presence of a mantle plume, but rather use an existing mantle plume model to generate feasible GHF scenarios in the model sensitivity study. We use a sophisticated hydrology model (de Fleurian et al., 2014, 2016) coupled to ice dynamics in the Ice Sheet System Model (ISSM; Larour et al., 2012) to capture the influence of enhanced basal melt on ice dynamics. We first describe the models and different plume experiments. Finally, we present and discuss resulting basal conditions and surface velocities corresponding to the various plume configurations.
2.1 Ice flow model
To simulate the NEGIS ice flow, we apply the model configuration from Schlegel et al. (2013, 2015) further developed and coupled to a subglacial hydrology model by Smith-Johnsen et al. (2019). We use the Ice Sheet System Model (Larour et al., 2012), a 3D thermomechanical ice flow model, and explicitly represent the effect of high melt rates on subglacial hydrology (de Fleurian et al., 2014, 2016), which provides the effective pressure (N, the difference between ice overburden pressure and water pressure at the bed) that controls basal sliding through a linear friction law (Cuffey and Paterson, 2010):
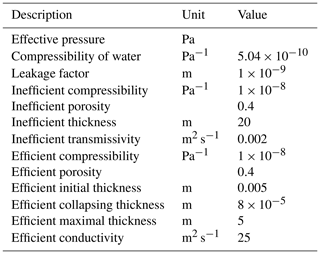
where τb is the basal drag, α the basal friction coefficient and vb the basal velocity. The hydrology model takes the basal melt rates as input and computes the effective pressure. Nodes with no basal melt are given an effective pressure equal to the ice overburden pressure. The hydrology model consists of two porous sediment layers, representing the inefficient and efficient drainage system. The efficient drainage system is activated when N reaches zero and may be deactivated as the water is evacuated and N increases again. Definitions and values of variables in the subglacial hydrology model are given in Table 1. The hydrology model and its implementation in ISSM are described in detail in de Fleurian et al. (2014, 2016).
For the thermal model we rely on the enthalpy formulation by Aschwanden et al. (2012), implemented in ISSM (Seroussi et al., 2013) with surface temperatures from Ettema et al. (2009) and GHF from Fox Maule et al. (2009). In addition we use a mantle plume module in ISSM to create elevated GHF anomalies (Seroussi et al., 2017). Ice is treated as a purely viscous incompressible material (Cuffey and Paterson, 2010), with viscosity, μ, defined as
where B is the temperature-dependent ice hardness varying with depth, n is Glen's flow law exponent and is the effective strain rate.
Basal topography is from BedMachine (Morlighem et al., 2014) (Fig. 1a) and we apply submarine melt rates under the floating ice (Rignot et al., 2001). For the stress balance equation, we use a 3D higher-order approximation (Pattyn, 2003). Our model domain consists of 9974 horizontal elements, ranging from 1 km in areas with high velocity gradients to a maximum of 15 km at the ice divide (Fig. 1b). We use linear P1 elements to solve the stress balance equations and quadratic P2 elements for the thermal analysis, in order to capture sharp temperature gradients, despite using only five layers (Cuzzone et al., 2018).
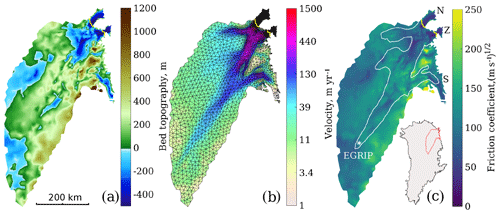
Figure 1(a) Bed topography from BedMachine (Morlighem et al., 2014) interpolated onto the model mesh; (b) InSAR-derived surface velocities (Rignot and Mouginot, 2012) and anisotropic model mesh refined in areas with high velocity gradients; (c) friction coefficient as a linear function of bed topography (Eq. 3) used in Eq. (1). The white contour shows the area of the NEGIS with observed surface velocity of 50 m yr−1 and the star shows the position of the East Greenland Ice-Core Project (EGRIP). N, Z and S indicate the outlets of the ice stream: 79N, Zachariæ and Storstrømmen, respectively. The yellow line in all panels represents the grounding line, and the inset map in the lower right corner shows Greenland with the model domain outlined in red.
We aim to represent the observed NEGIS velocity pattern in an ice sheet model without inverting for the basal friction coefficient. However, to initialise the hydrology model, we do simulate the present-day ice stream by inferring basal friction from present-day velocities (Fig. 1b). The basal melt rates from this simulation are used to initialise the subglacial hydrology model, which we run for 150 years in order to reach an equilibrium in terms of water pressure. The resulting effective pressure field computed by the hydrology model, N, is used in the friction law (Eq. 1) and kept constant in time. Finally, we run a 4 kyr simulation with the basal condition generated by the hydrology model to provide steady-state surface velocities. Note that we do not use the friction coefficient, α, from the inversion in the forward ice flow simulation, as it is only used to initialise the subglacial hydrology model.
Previous modelling studies lack sharp velocity gradients defining NEGIS (Aschwanden et al., 2016; Beyer et al., 2018). To capture this we let the basal friction coefficient, α, depend linearly on the bed elevation using the following equation:
where 100 (m s−1)1∕2 is the mean value of the inversion alpha used in Smith-Johnsen et al. (2019), and we cap the values between 1 and 250 (m s−1)1∕2. The factor 0.13 is tuned to approximately match the observed velocities at the grounding line of 79N. The resulting friction coefficient, α, is shown in Fig. 1c. We argue that low-lying topography will have more marine sediments, and thus a softer and less resistive bed, allowing high velocities of the outlet glaciers. A similar approach with basal shear stress defined as a function of bed elevation was previously used by Åkesson et al. (2018) and by Aschwanden et al. (2016). Our simple friction relationship is supported by observations, as bed topography roughness for the NEGIS region shows a pattern inversely correlated with bed elevation (Cooper et al., 2019). This relation might however not hold on smaller scales under the NEGIS trunk where the till distribution is independent of the bed geometry (Christianson et al., 2014). Some alternatives to using this parameterisation are given in the discussion section of this paper.
2.2 Experiments
In order to capture the high upstream velocity of NEGIS, we alter the GHF by simulating a mantle plume close to the head of the ice stream, at the onset of fast flow (Seroussi et al., 2017). The mantle plume module in ISSM computes the GHF, given the plume parameters in Table 2. To disentangle the effect of the mantle plume we run a control simulation without a mantle plume, using only the GHF from Fox Maule et al. (2009). This GHF map ranges from 40 mW m−2 in the northwest to 77 mW m−2 in the northeast below the Storstrømmen outlet, with an average value of 54 mW m−2.
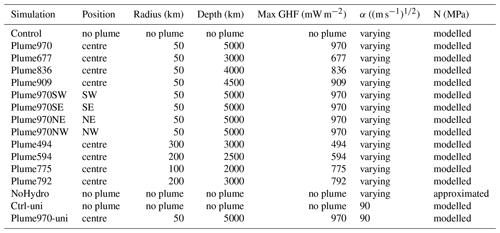
In our main experiment, plume970, the plume parameters were chosen to generate a GHF anomaly coherent with the magnitude of the GHF anomaly hypothesised by Fahnestock et al. (2001). The resulting GHF anomaly is ∼ 50 km in diameter with a maximum GHF value of 970 mW m−2 (Table 3), and we position it directly underneath the EGRIP deep ice core drilling site (Fig. 1c).
To determine the minimum GHF needed to initiate the onset of NEGIS close to the ice divide, we compute three alternative plume configurations with lower intensity. We obtain the lower GHF by decreasing the bottom plume depth parameter to 4500, 4000 and 3000 km for simulations plume909, plume836 and plume677, respectively (Table 3). Additionally, we compute four plume configurations where we change the position of the plume. We move plume970 75 km to the southwest, southeast, northeast and northwest in the plume970SW, plume970SE, plume970NE and plume970NW experiments, respectively (Table 3). To investigate the influence of the area of the mantle plume, we compute four plume configurations with larger area, compensated for by a smaller heat flux. To obtain this we increase the plume radius to values of 100–300 km, and we decrease the bottom plume depth to values of 2000–3000 km, resulting in the experiments plume494, plume594, plume775 and plume792 (Table 3).
Finally, to investigate the influence of our friction coefficient distribution, we run three additional simulations. First, we run a simulation without modelled effective pressure, but instead using effective pressure approximated to hydrostatic pressure, commonly used in ISSM (noHydro, Table 3). Then we run two simulations with a uniform friction of α=90 (m s−1)1∕2: one without a plume (Ctrl-uni, Table 3) and one with the 970 mW m−2 plume (plume970-uni, Table 3).
In the control simulation we use the GHF from Fox Maule et al. (2009) (Fig. 2a), and the corresponding basal melt rates are shown in Fig. 2f. Melt rates at the head of the ice stream (at EGRIP) are 1–2 mm yr−1, and the highest basal melt rates (600 mm yr−1) occur at the grounding line of Zachariæ, with surface velocities reaching 1500 m yr−1. Friction is the dominating heat source in the fast-flowing regions, and melt rates thus increase with increasing velocities towards the grounding line. Low melt rates in regions with high velocity are due to low-lying bed topography causing low basal drag and hence less frictional heat. The effective pressure for the control experiment is shown in Fig. 2k, and the values increase upstream toward the ice divide as ice thickness increases and basal melt decreases. The lowest values of effective pressure coincide with low bed elevation in the main trunk, 100 km upstream of the grounding line.
The resulting velocity field for the control simulation captures the main features of NEGIS: the three outlets with high velocities across the grounding lines and sharp shear margins (Fig. 2p). The northern branch feeding into 79N is slower and less defined than in the observed velocities, and the velocities of Storstrømmen are also slower than observed. Velocities of the floating tongues of 79N and Zachariæ are not well represented, and floating shelves are not shown here. The western branch, feeding into the main trunk of NEGIS, shows a more diffuse pattern with higher velocities than observed.
To evaluate how well the model simulations reproduce the observed velocity pattern, we plot the 50 m yr−1 velocity contour (black contour in Fig. 2), and we compare how far upstream this contour reaches (in kilometres from the ice divide) relative to the observed velocity (white contour in Fig. 2). The modelled velocity contour in the control simulation reaches 305 km from the ice divide (Fig. 2p) and thus further downstream than the observed velocity (120 km, Fig. 2a, f, k). The control simulation does not capture the characteristics of NEGIS, with high upstream velocities close to the ice divide.
To capture the upstream velocities, we enhance the GHF locally at the onset of the ice stream in the plume970 simulation to reach the maximum magnitude proposed by Fahnestock et al. (2001). The addition of the mantle plume results in high GHF, with values up to 970 mW m−2, rapidly decreasing to the values used in the control simulation (Fig. 2b) within a radius of less than 100 km. High geothermal heat leads to high basal melt rates, with ∼ 100 mm yr−1 above the plume (Fig. 2g), compared to 1–2 mm yr−1 in the control experiment. The increase in basal melt rates causes a reduction in effective pressure to 1.2 MPa directly above the plume, resulting in a local floatation fraction (ratio of water pressure over overburden pressure) of 0.95. The resulting velocity field in the plume970 experiment is similar to the control experiment, except for the higher velocities simulated at the head of the ice stream. In the plume970 simulation the 50 m yr−1 velocity contour reaches 131 km from the ice divide (black contour Fig. 2q), which is close to the observed 120 km. However, the spatial pattern upstream is more diffuse and the ice stream is wider than observed. The Storstrømmen outlet shows higher velocities relative to the control simulation, but still lower than observed. The 79N and Zachariæ outlets, on the other hand, display higher velocities than observed. Overall, with this approach, we capture most of the characteristics of NEGIS, although the ice stream is more diffuse and displays velocities slightly higher than the observations.
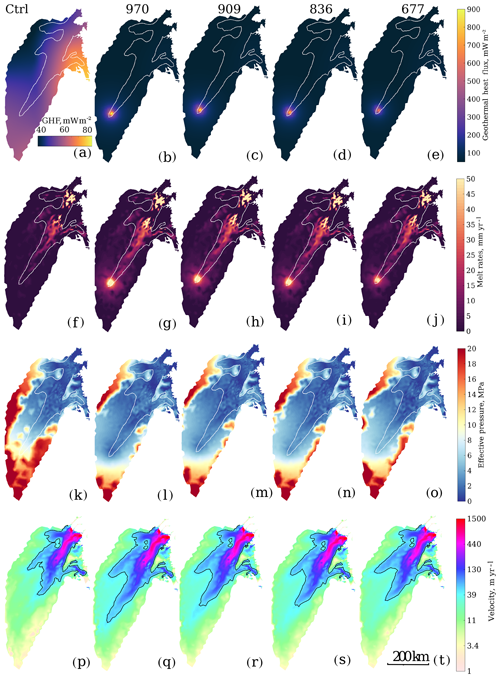
Figure 2Model results for the control simulation and the plume677, plume836, plume909 and plume970 simulations. Panels (a–e) show the modelled GHF (note the different colour scale for the control simulation) and (f–j) show the corresponding basal melt rates, forcing the hydrology model which computes the corresponding effective pressure (k–o) and finally the resulting surface velocity (p–t). White lines show the 50 m yr−1 observed velocity contour, and black lines show the 50 m yr−1 modelled velocity contour.
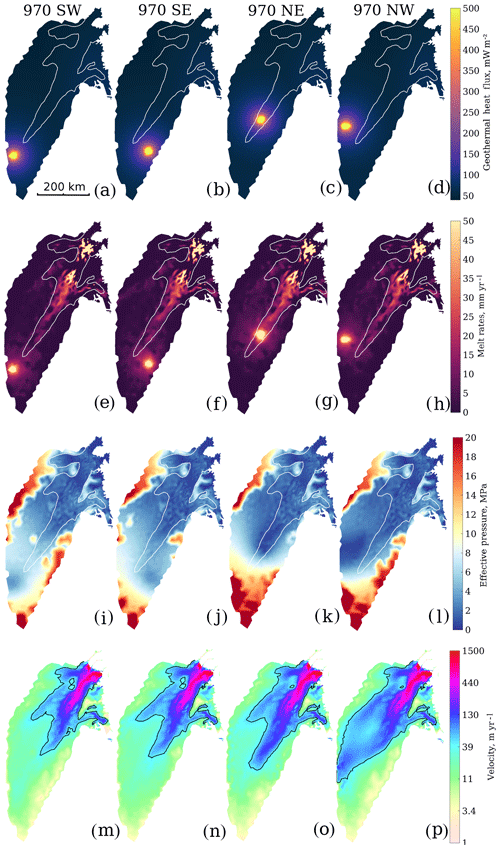
Figure 3Model results from the sensitivity simulations investigating the position of the mantle plume by moving the plume970 75 km. The first column shows results from plume970SW, with a plume 75 km to the southwest; the second column represents the 970 SE plume; the third column represents plume970NE; and the last column is plume970NW. Panels (a–d) show the GHF, (e–h) the resulting basal melt rates, (i–l) the computed effective pressure and (m–p) the modelled surface velocity. White lines show the 50 m yr−1 observed velocity contour, and black lines show the 50 m yr−1 modelled velocity contour.
To determine whether a lower GHF may induce a similar high-velocity pattern, we run three simulations with a less intense mantle plume. Figure 2c–e show the GHF values computed by increasing the plume depth to 3000, 4000 and 4500 km, respectively, obtaining maximum basal melt rates of ∼ 70 (Fig. 2j), ∼ 85 (Fig. 2i) and ∼ 95 mm yr−1 (Fig. 2h). The modelled effective pressure for the three plumes (Fig. 2m–o) results in slower velocities than plume970, with 50 m yr−1 velocity contours reaching 253, 245 and 210 km from the ice divide, respectively (Fig. 2r–t). This shows that GHF values of 677, 836 and 909 mW m−2 produce weaker ice stream signatures than observed and, given our model set-up, are not sufficient to induce the upstream fast flow of NEGIS.
To investigate the sensitivity of the position of the plume in plume970, we moved the plume 75 km to the southwest, southeast, northeast and northwest (Fig. 3). The computed GHF distribution is shown in Fig. 3a–d and the basal melt rates are of the same magnitude as in plume970. The computed effective pressures for the southwest and southeast (plume970SW and plume970SE, Fig. 3i, j) have minimum values of 3.2 and 2.9 MPa above the plume, which are not sufficient to initiate fast flow (Fig. 3m, n). When the plume is located further downstream, the effective pressure reaches lower values (Fig. 3k, l) and the ice stream flows faster than in plume970 (Fig. 3o, p), however, with the 50 m yr−1 contour only reaching 204 km from the ice divide. The plume970NE induces the fastest flow, and the plume970NW creates an interesting double-branched ice stream starting from the ice divide. The experiments in Fig. 3 indicate that the elevated heat required to initiate the NEGIS in our model must be located close to EGRIP.
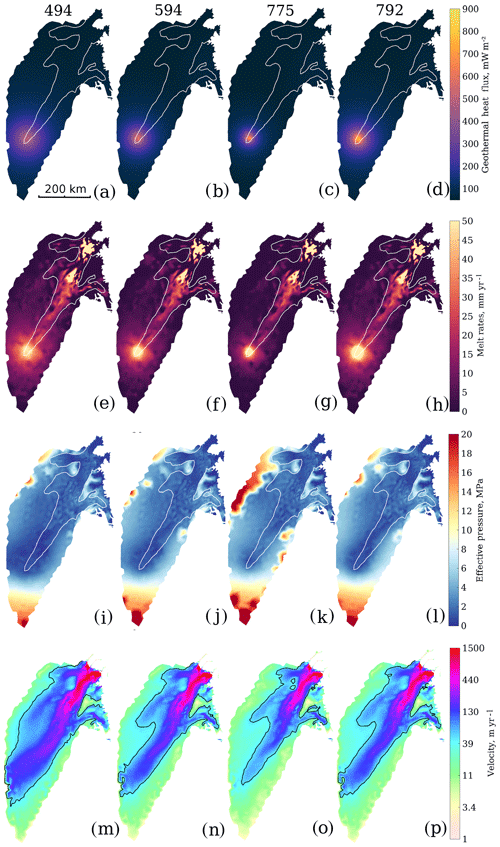
Figure 4Model results from the sensitivity simulations investigating a reduced magnitude and increased size of the mantle plume. The first column shows results from the 494 plume with a 300 km radius at 3000 km depth, the second column represents the 594 plume with a 200 km radius and 2500 km depth, the third column represents the 775 plume with a 100 km radius and 2000 km depth, and the last column represents plume 792 with a 200 km radius and 3000 km depth. Panels (a–d) show the GHF, (e–h) the resulting basal melt rates, (i–l) the computed effective pressure and (m–p) the modelled surface velocity. White lines show the 50 m yr−1 observed velocity contour, and black lines show the 50 m yr−1 modelled velocity contour.
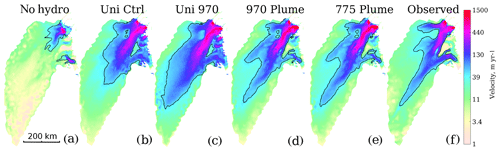
Figure 5Surface velocity results from the noHydro simulation (a) with effective pressure approximated to the hydrostatic pressure assuming direct connection to the ocean, commonly used in ISSM. Uni control (b) and plume970-uni experiments (c) use a uniform friction coefficient α set equal to 90 (ms−1)1∕2. Corresponding GHF, basal melt rates and effective pressure are the same as the control simulation and plume970, shown in Fig. 2. For reference we include (d) and (e), respectively, showing the plume970 and plume775 simulations (same as Figs. 2q, and 4o), and (f) showing the observed surface velocities interpolated onto the model mesh. Black lines show the 50 m yr−1 velocity contour.
To determine whether a lower GHF value over a larger area could induce high upstream velocities, we investigate the influence of four weaker plumes with larger plume radii (Fig. 4). The weakest but most extensive plume (plume494, Fig. 4a) produces basal melt rates of a maximum of 51 mm yr−1 (Fig. 4e), resulting in a large area of low effective pressure (minimum 0.2 MPa; Fig. 4i). The corresponding surface velocity for the plume494 displays a faster and wider ice stream (Fig. 4m) relative to the observations. Plume594 gives basal melt rates of 60 mm yr−1 (Fig. 4f) and the ice stream becomes wide, reaching all the way to the ice divide (Fig. 4n). Plume775 is twice the size of plume970 (Fig. 4c), and with melt rates of ∼ 75 mm yr−1 over a larger area (Fig. 4g) the velocity of the ice stream (Fig. 4o) is similar to plume970. However, the 50 m yr−1 velocity contour reaches too close to the ice divide and the ice stream is wider than the observed one. Plume792 produces melt rates of ∼ 75 mm yr−1 (Fig. 4d), resulting in velocities similar to those of plume594 (Fig. 4p). This shows that plumes with a restricted extent, ∼50 km × 50 km, produce model results more consistent with the observed flow behaviour in the upstream reaches of NEGIS.
Finally, we investigate the influence of varying the parameters in the friction law (Eq. 1), presented in Fig. 5. The noHydro simulation with an effective pressure approximated to the hydrostatic pressure shows very little resemblance to the observed NEGIS (Fig. 5a), with too slow velocities. The simulation with a uniform friction coefficient and no mantle plume captures the main feature of NEGIS (Ctrl-uni, Fig. 5b): with a main trunk, the northern branch and three outlets, with the fastest flow in Zachariæ. However, the velocity pattern is more diffuse than the observed pattern (Fig. 5e). The high upstream velocities are better captured in the simulation with plume970 and a uniform friction (plume970-uni, Fig. 5c). For plume970-uni, high velocities reach slightly closer to the ice divide than plume970, but the velocities of the main trunk are less confined than in experiment plume970 (Fig. 5d) and the observations (Fig. 5f).
Most of the spatial velocity pattern of NEGIS is represented in our control run, apart from the upstream one-third of the main trunk. This indicates that the downstream area of the NEGIS catchment is largely controlled by topography, while the upstream area is controlled by its basal conditions, which is in agreement with Keisling et al. (2014). The control simulation captures the main outlets and the observed snake-shaped velocity pattern of the trunk. High velocities coincide with low-lying bed elevation. However, we do not capture the high velocity of Storstrømmen, or the floating tongues of the Zachariæ and 79North outlets. This could be caused by the simple friction coefficient approach not being representative of these areas, where basal properties display a more complex pattern.
We performed experiments with various mantle plume configurations introduced at the head of NEGIS to assess if the presence of an anomalously high GHF can explain the pattern of ice flow of this region. The different plume configurations vary in intensity, position and extent. In the control simulation we use present-day surface velocity and GHF from Fox Maule et al. (2009). Without the presence of a plume, the GHF does not reach more than 54 mW m−2 and leads to underestimating velocities in the upstream part of the catchment. These low values of GHF are not sufficient to initiate the onset of NEGIS close to the ice divide. By testing with four mantle plume configurations of increasing intensity (Fig. 2), we find that the GHF (GHF) needed to induce the observed upstream velocity of NEGIS in our model is ∼ 970 mW m−2.
A GHF of 970 mW m−2 is consistent with the maximum value presented in Fahnestock et al. (2001) and Keisling et al. (2014) for regions in proximity to EGRIP, where plume970 is located. It also compares well to the anomaly modelled by Macgregor et al. (2016) in the trunk of NEGIS but does not include the high GHF that they find upstream. These GHF values are imposed based on basal melt estimates from radar internal stratigraphy. Our modelled basal melt rates (∼ 100 mm yr−1) are thus consistent with their proposed values. By directly comparing the basal melt rates of our plume970 experiment to the basal melt rate estimates from Macgregor et al. (2016) in Fig. 6, it can be seen that our plume produces a basal melt pattern that matches the position, extent and values of the northeastern branch of their anomaly. The sensitivity simulations in Fig. 3m, n show that more than 970 mW m−2 is needed to initiate high velocity, when the plume is located further upstream in a region with thicker ice relative to downstream. This suggests that the area of high basal melt estimated by Macgregor et al. (2016) in the trunk of NEGIS is probably more consequential than the larger melt anomaly that they modelled closer to the divide.
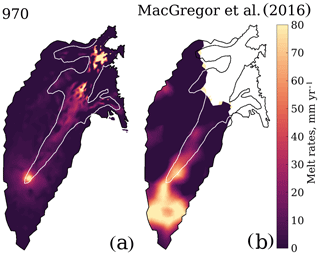
Figure 6Comparison of the basal melt rates computed for the plume970 experiment (a) and the gridded basal melt rate estimates of Macgregor et al. (2016) interpolated onto our model mesh (b). White lines show the observed 50 m yr−1 velocity contour.
The GHF at the head of NEGIS is suggested to be high due to lithospheric thinning as a result of the Iceland plume passage (Rogozhina et al., 2016; Martos et al., 2018). However, 970 mW m−2 is an extremely high GHF value, 10 to 20 times higher than the values suggested by GHF models for Greenland (Shapiro and Ritzwoller, 2004; Fox Maule et al., 2009; Martos et al., 2018; Rogozhina et al., 2016). Greve (2019) derived GHF values for five deep ice core boreholes in Greenland, using the SICOPOLIS model (SImulation COde for POLythermal Ice Sheets; http://www.sicopolis.net/, last access: 4 March 2020), such that the simulated and observed basal temperatures match. This resulted in a local elevated GHF anomaly around NGRIP of 135 mW m−2, located at the ice divide ∼ 150 km away from the head of NEGIS. Our GHF anomaly has a magnitude 7 times higher than that of Greve (2019) and 3 times as high as the highest current GHF observations in Greenland (Rysgaard et al., 2018). In summary, plume970 produces a basal melt pattern with magnitude and extent in line with previous estimates from the radar data for the region within the 50 m a−1 isoline; however there is a large discrepancy between the necessary GHF to produce this melt and the GHF estimates for Greenland.
To explain the high GHF value of 970 mW m−2, we need to investigate processes that may locally elevate the GHF. Alley et al. (2019) and Stevens et al. (2016) explained high GHF in this region by the passing of the Iceland plume, leaving behind partly molten rock that may have migrated up in response to glacial–interglacial cycles, as the crust is loaded and unloaded. A study showed that glacial rebound may have caused young intraplate volcanism in Greenland, despite the old age of the tectonic plate and no mantle plume present (Uenzelmann-Neben et al., 2012). The plume passage could have lead to shallow magma emplacements, which may feed hydrothermal systems, causing hot fluid percolation that enhances high heat transport to the base of the ice sheet (Stevens et al., 2016; Alley et al., 2019; Mordret, 2018). It is important to note that the term GHF is defined as the heat flux from the Earth's interior as a purely conductive heat transfer. Hence, the 970 mW m−2 heat flux can not be explained by GHF alone but rather also with surface heat flow from locally elevated GHF due to advective heat transfer from the processes mentioned above (Artemieva, 2019).
Comparing the velocity field in the plume970 experiment to previous studies without inversion shows that combining a basal hydrology model with an elevated GHF at the head of NEGIS captures the observed high, confined, upstream velocities of the NEGIS. The simulations in Goelzer et al. (2018) show that the ice flow models capturing the upstream onset of NEGIS all rely on inversions to initialise the basal drag in the simulations (Elmer/Ice, ISSM, BISICLES, GRISLI and f.Etish). The models without inversion underestimate the velocities in the upper part of the NEGIS catchment and lack the sharp velocity gradients. Aschwanden et al. (2016) simulated the high upstream velocity of NEGIS without inverting for basal conditions in Parallel Ice Sheet Model (PISM), but their simulation lacks the clearly defined main trunk and underestimates the high upstream velocity. Beyer et al. (2018) further improved the simulation by using a subglacial hydrology model to compute effective pressure, which allowed higher velocities in the outlets. However, high upstream velocities are still lacking, similar to our control simulation. The last two studies used GHF from Shapiro and Ritzwoller (2004), which proposed slightly lower values at the head of NEGIS compared to the values of Fox Maule et al. (2009) used in our study.
Beyer et al. (2018) used the same friction law as we use in ISSM, but with a uniform friction coefficient. We tested a uniform friction coefficient, which led to a more diffuse ice stream (Fig. 5b, c), but with more confined outlets compared to the Beyer et al. (2018) study. The difference can be explained by different basal melt rates used as input and different hydrology models. In order to capture sharp gradients in the velocity field, we find it important that the areas without any basal melt have effective pressure equal to the ice overburden pressure.
We invert for basal friction to get the basal melt rates that are used to initialise the subglacial hydrology model, and the model is then free to evolve. We do not use the inverted friction in the forward ice flow simulation; instead we use the simple friction coefficient from Eq. (3). To investigate whether the modelled velocity pattern is caused by the effective pressure distribution or the friction coefficient, we run the simulation noHydro, where the effective pressure is approximated to the hydrostatic pressure, commonly used in ISSM. The modelled velocity pattern (Fig. 5a) does not resemble the observed pattern, and we conclude that including the subglacial hydrology model is responsible for the improved velocity pattern in the control simulation and plume970. By using our friction coefficient distribution, combined with initialising with present-day basal melt from velocity observations, both the control and plume970 experiments display velocity patterns similar to the observations (Fig. 5d, e).
The middle western branch of the ice stream displays too high velocity in both the control and plume970 experiments, correlating with low-lying bed elevation (Fig. 1). Too high velocities in this region were also modelled by Aschwanden et al. (2016) using PISM and a similar bed-elevation-dependent friction law. When performing additional simulations with the GHF values from Martos et al. (2018), this branch becomes more pronounced in velocity (not shown here). This may indicate that the GHF values in this region of Greenland are even lower than those in Martos et al. (2018) and Fox Maule et al. (2009), and the glacier base is frozen to the ground. This region is recognised as “uncertain” in the synthesis of Greenland's basal thermal regime by Macgregor et al. (2016). Other explanations for too high velocities in this branch may be a higher bed roughness, errors in the bed topography or “sticky spots”.
Given the model configuration, an exceptionally high heat flux of 970 mW m−2 is needed to reproduce NEGIS. We acknowledge that this value may be overestimated due to uncertainties and assumptions in our model set-up, and we discuss these in the following sections. We use a simple friction law linearly dependent on effective pressure, and we are aware that the results are likely to change with a different choice of friction law. For example, in the friction law used in the MISMIP+ experiments (Asay-Davis et al., 2016; Tsai et al., 2015), effective pressure is included only where the coulomb criterion is met, normally a few kilometres upstream of the grounding line. This may result in a smaller dynamic response from the mantle plume in the slow upstream regions of NEGIS. However, the use of a non-linear friction law may enhance the sensitivity of the ice dynamics to effective pressure, also upstream, as we compute low effective pressure above the plume. This implies that the use of a non-linear friction law may result in a lower GHF needed to sustain NEGIS in a model.
By using a coarse model mesh we may underestimate the softening occurring due to strain heating in the shear margins and hence overestimate the lateral drag. Refining the mesh and inducing damage softening of the ice in the shear margins (Bondzio et al., 2017) would decrease the lateral drag. In this case, the observed high upstream velocity of NEGIS may have been reproduced with higher basal drag and hence lower GHF. The underestimation of modelled ice softness may also explain why our modelled upstream velocity field is wider and more diffuse than the observed field.
In the simulations where we investigate the influence of an increased plume radius (Fig. 4), we show that lower values of GHF can induce even faster flow, when the plume is more extensive (Fig. 4). However, with a larger mantle plume the ice stream becomes wider and does not match the observed velocity of NEGIS (Fig. 5e). The basal melt pattern of Macgregor et al. (2016) in Fig. 6 consists of two melt anomalies near EGRIP. It would be interesting to investigate the velocity response of two weaker elevated GHF anomalies closely located. There is also room for improvement of the model in the treatment of the shear margin or the use of a non-linear friction law (Gagliardini et al., 2007; Schoof, 2005). Both those improvements would lead to sharper transition from slow to fast velocities and might allow a plume with a larger radius.
We parameterise the friction coefficient with a simplified estimate linearly dependent on the bed elevation. In other studies this coefficient is inverted for by matching observed surface velocity, producing low values in the main trunk of NEGIS (Smith-Johnsen et al., 2019). By lowering the friction in the main trunk, we may reproduce fast flow with a lower GHF value. However, this would make the friction coefficient relate to the velocity, which we are trying to avoid. The bed topography used is from BedMachine (Morlighem et al., 2014), so datasets used to create this map impact the choice of friction. A uniform lowering of the friction coefficient, also outside the trunk, would increase velocities all over the domain; hence we would lose the sharp velocity gradients and overestimate the outlet velocity even further. Additionally, the modelled ice surface in the control experiment is lower than the observed ice surface (Scambos and Haran, 2002), and a uniform reduction of friction will enhance this mismatch. We do not observe a local depression in the surface topography above the 970 mW m−2 plume, which agrees with the observed ice surface for the region (Scambos and Haran, 2002).
Hydrology parameters are unfortunately highly uncertain, and different choices would lead to a more or less responsive hydrological system and hence possibly a lower GHF value to sustain the fast flow. However, we have a rather low transmissivity of the inefficient drainage system, resulting in low efficiency in water evacuation, causing our system to be sensitive to an increase in water input. If the transmissivity was lowered further, the efficient drainage system is likely to activate in the GHF anomaly region, lowering the water pressure and becoming less sensitive to increased water input. For this reason, we do not expect that a different hydrology configuration would reproduce NEGIS with a lower heat flux. In addition, the subglacial hydrology is only one-way coupled to ice dynamics, so we do not capture the positive feedback expected with higher velocities leading to more melt, and lower effective pressure, giving even higher velocities. With a more responsive and fully coupled system, one might be able to reproduce NEGIS with lower heat flux.
With a simple bed-elevation-dependent friction and hydrology model forced by melt rates from GHF, we capture the overall pattern of NEGIS velocity. This has implications for studies trying to predict the response of NEGIS to a future climatic warming. Basal friction may not remain constant in time, and thus we cannot fully rely on inversion as it masks unknown time-varying basal properties. By using our approach (with or without the GHF anomaly) one can capture complex velocity patterns and then invert for the remaining basal properties. These may in turn be assumed to be constant in time, while the subglacial hydrology will evolve with a changing climate, accounting for varying basal conditions. Unfortunately, observations and estimates of GHF and subglacial hydrology are challenged by large uncertainties. Therefore, it is critical for future observational and modelling studies to better constrain the basal conditions of the Greenland Ice Sheet.
Present-day basal melt rates from GHF maps and frictional heat are not sufficient to sustain the observed upstream velocities of the Northeast Greenland Ice Stream (NEGIS). The downstream velocities appear to be driven by topography, and the spatial pattern is well captured by the subglacial hydrology model. Our findings suggest that a local heat flux anomaly may explain the characteristic high upstream velocity of NEGIS and hence is consistent with previous studies (Fahnestock et al., 2001; Macgregor et al., 2016; Alley et al., 2019). To reproduce high upstream velocities at the onset of NEGIS, a sustained basal melt rate of 100 mm yr−1 is needed in a local region close to EGRIP, where observed present-day velocities reach 50 m yr−1. Hence, the minimal heat flux value needed to initiate the ice stream in our model is 970 mW m−2, as proposed by Fahnestock et al. (2001). This magnitude is too high to be explained by GHF alone, and we suggest that processes such as hydrothermal circulation may locally elevate the heat flux of the area.
ISSM software is open source and can be downloaded at https://issm.jpl.nasa.gov/ (last access: 29 January 2020, Larour et al., 2012). The surface mass balance forcing used in this study, from Jason E. Box, is available from https://zenodo.org/record/3359192 (Box, 2019).
SSJ designed the study with help from BdF and KHN. SSJ ran the simulations. NS helped greatly in set up the ice flow model, BdF helped set up the hydrology model, and HS helped setting up the mantle Plume model. SSJ wrote the manuscript with substantial contributions from all co-authors. The research related to the paper was discussed by all co-authors.
The authors declare that they have no conflict of interest.
Silje Smith-Johnsen, Basile de Fleurian and Kerim Nisancioglu were funded by the Ice2Ice project that has received funding from the European Research Council under the European Community's Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no. 610055. Basile de Fleurian is also funded by the SWItchDyn NRC grant (287206). Funding for Helene Seroussi and Nicole Schlegel was provided by grants from the NASA Cryospheric Science and Modeling, Analysis and Prediction (MAP) programmes. We would like to thank the reviewers Nicholas Holschuh and Signe Hillerup Larsen for greatly improving the manuscript. We would also like to thank Irina Rogozhina and Ralf Greve for good discussions and recommendations.
This research has been supported by the European Research Council (ICE2ICE, grant no. 610055) and the Norwegian Research Council (SWItchDyn, grant no. 287207).
This paper was edited by Nanna Bjørnholt Karlsson and reviewed by Nicholas Holschuh and Signe Hillerup Larsen.
Åkesson, H., Morlighem, M., Nisancioglu, K., Svendsen, J., and Mangerud, J.: Atmosphere-driven ice sheet mass loss paced by topography: Insights from modelling the south-western Scandinavian Ice Sheet, Quaternary Sci. Rev., 195, 32–47, https://doi.org/10.1016/j.quascirev.2018.07.004, 2018. a
Alley, R. B., Pollard, D., Parizek, B. R., Anandakrishnan, S., Pourpoint, M., Stevens, N. T., MacGregor, J., Christianson, K., Muto, A., and Holschuh, N.: Possible Role for Tectonics in the Evolving Stability of the Greenland Ice Sheet, J. Geophys. Res.-Earth, 124, 97–115, https://doi.org/10.1029/2018JF004714, 2019. a, b, c, d, e, f
Artemieva, I. M.: Lithosphere thermal thickness and geothermal heat flux in Greenland from a new thermal isostasy method, Earth-Sci. Rev., 188, 469–481, https://doi.org/10.1016/j.earscirev.2018.10.015, 2019. a
Asay-Davis, X. S., Cornford, S. L., Durand, G., Galton-Fenzi, B. K., Gladstone, R. M., Gudmundsson, G. H., Hattermann, T., Holland, D. M., Holland, D., Holland, P. R., Martin, D. F., Mathiot, P., Pattyn, F., and Seroussi, H.: Experimental design for three interrelated marine ice sheet and ocean model intercomparison projects: MISMIP v. 3 (MISMIP +), ISOMIP v. 2 (ISOMIP +) and MISOMIP v. 1 (MISOMIP1), Geosci. Model Dev., 9, 2471–2497, https://doi.org/10.5194/gmd-9-2471-2016, 2016. a
Aschwanden, A., Bueler, E., Khroulev, C., and Blatter, H.: An enthalpy formulation for glaciers and ice sheets, J. Glaciol., 58, 441–457, https://doi.org/10.3189/2012JoG11J088, 2012. a
Aschwanden, A., Fahnestock, M., and Truffer, M.: Complex Greenland outlet glacier flow captured, Nat. Commun., 7, 10524, https://doi.org/10.1038/ncomms10524, 2016. a, b, c, d, e, f, g
Beyer, S., Kleiner, T., Aizinger, V., Rückamp, M., and Humbert, A.: A confined–unconfined aquifer model for subglacial hydrology and its application to the Northeast Greenland Ice Stream, The Cryosphere, 12, 3931–3947, https://doi.org/10.5194/tc-12-3931-2018, 2018. a, b, c, d, e
Bondzio, J. H., Morlighem, M., Seroussi, H., Kleiner, T., Rückamp, M., Mouginot, J., Moon, T., Larour, E. Y., and Humbert, A.: The mechanisms behind Jakobshavn Isbræ's acceleration and mass loss: A 3-D thermomechanical model study, Geophys. Res. Lett., 44, 6252–6260, https://doi.org/10.1002/2017GL073309, 2017. a
Box, J.: Greenland monthly surface mass balance 1840–2012, Zenodo, https://doi.org/10.5281/zenodo.3359192, 2019. a
Christianson, Knut, Peters, Leo E., Alley, Richard B., Anandakrishnan, Sridhar, Jacobel, Robert W., Riverman, Kiya L., Muto, Atsuhiro, Keisling, Benjamin A.:Dilatant till facilitates ice-stream flow in northeast Greenland, Earth Planet. Sc. Lett., 401, 57–69, https://doi.org/10.1016/j.epsl.2014.05.060, 2014. a
Cooper, M. A., Jordan, T. M., Schroeder, D. M., Siegert, M. J., Williams, C. N., and Bamber, J. L.: Subglacial roughness of the Greenland Ice Sheet: relationship with contemporary ice velocity and geology, The Cryosphere, 13, 3093–3115, https://doi.org/10.5194/tc-13-3093-2019, 2019. a
Cuffey, K. M. and Paterson, W. S. B.: The physics of glaciers, Academic Press, 2010. a, b
Cuzzone, J. K., Morlighem, M., Larour, E., Schlegel, N., and Seroussi, H.: Implementation of higher-order vertical finite elements in ISSM v4.13 for improved ice sheet flow modeling over paleoclimate timescales, Geosci. Model Dev., 11, 1683–1694, https://doi.org/10.5194/gmd-11-1683-2018, 2018. a
de Fleurian, B., Gagliardini, O., Zwinger, T., Durand, G., Le Meur, E., Mair, D., and Råback, P.: A double continuum hydrological model for glacier applications, The Cryosphere, 8, 137–153, https://doi.org/10.5194/tc-8-137-2014, 2014. a, b, c
de Fleurian, B., Morlighem, M., Seroussi, H., Rignot, E., van den Broeke, M. R., Kuipers Munneke, P., Mouginot, J., Smeets, P. C. P., and Tedstone, A. J.: A modeling study of the effect of runoff variability on the effective pressure beneath Russell Glacier, West Greenland, J. Geophys. Res.-Earth, 121, 1834–1848, https://doi.org/10.1002/2016JF003842, 2016. a, b, c
Ettema, J., Bales, R. C., Box, J. E., van Meijgaard, E., van den Broeke, M. R., van de Berg, W. J., and Bamber, J. L.: Higher surface mass balance of the Greenland ice sheet revealed by high-resolution climate modeling, Geophys. Res. Lett., 36, 1–5, https://doi.org/10.1029/2009gl038110, 2009. a
Fahnestock, M., Abdalati, W., Joughin, I., Brozena, J., and Gogineni, P.: High Geothermal Heat Flow, Basal Melt, and the Origin of Rapid Ice Flow in Central Greenland, Science, 294, 2338–2342, 2001. a, b, c, d, e, f, g, h
Fox Maule, C., Purucker, M. E., and Olsen, N.: Inferring magnetic crustal thickness and geothermal heat flux from crustal magnetic field models, Danish Meteorological Institute, Danish Climate Centre Report 09-09, November, 2009. a, b, c, d, e, f, g, h
Gagliardini, O., Cohen, D., Råback, P., and Zwinger, T.: Finite-element modeling of subglacial cavities and related friction law, J. Geophys. Res., 112, F02027, https://doi.org/10.1029/2006JF000576, 2007. a
Goelzer, H., Nowicki, S., Edwards, T., Beckley, M., Abe-Ouchi, A., Aschwanden, A., Calov, R., Gagliardini, O., Gillet-Chaulet, F., Golledge, N. R., Gregory, J., Greve, R., Humbert, A., Huybrechts, P., Kennedy, J. H., Larour, E., Lipscomb, W. H., Le clec'h, S., Lee, V., Morlighem, M., Pattyn, F., Payne, A. J., Rodehacke, C., Rückamp, M., Saito, F., Schlegel, N., Seroussi, H., Shepherd, A., Sun, S., van de Wal, R., and Ziemen, F. A.: Design and results of the ice sheet model initialisation experiments initMIP-Greenland: an ISMIP6 intercomparison, The Cryosphere, 12, 1433–1460, https://doi.org/10.5194/tc-12-1433-2018, 2018. a, b
Greve, R.: Geothermal heat flux distribution for the Greenland ice sheet, derived by combining a global representation and information from deep ice cores, Polar Data, 3, 22–36, https://doi.org/10.20575/00000006, 2019. a, b, c
Keisling, B., Christianson, K., Alley, R. B., Peters, L. E., Christian, J. E. M., Anandakrishnan, S., Riverman, K. L., Muto, A., and Jacobel, R. W.: Basal conditions and ice dynamics inferred from radar-derived internal stratigraphy of the northeast Greenland ice stream, Ann. Glaciol., 55, 127–137, https://doi.org/10.3189/2014AoG67A090, 2014. a, b, c
Khroulev, C. and PISM-Authors: PISM, a Parallel Ice Sheet Model: User's Manual, 408, 2015. a
Larour, E., Seroussi, H., Morlighem, M., and Rignot, E.: Continental scale, high order, high spatial resolution, ice sheet modeling using the Ice Sheet System Model (ISSM), J. Geophys. Res.-Earth, 117, F01022, https://doi.org/10.1029/2011JF002140, 2012. a, b, c, d
Macgregor, J., Fahnestock, M., Catania, G., Aschwanden, A., Clow, G., Colgan, W., Gogineni, S., Morlighem, M., Nowicki, S., Paden, J., Price, S., and Seroussi, H.: A synthesis of the basal thermal state of the Greenland Ice Sheet, J. Geophys. Res.-Earth, 121, 1328–1350, https://doi.org/10.1002/2015JF003803, 2016. a, b, c, d, e, f, g, h, i
Martos, Y. M., Jordan, T. A., Catalan, M., Jordan, T. M., Bamber, J. L., and Vaughan, D. G.: Geothermal heat flux reveals the Iceland hotspot track underneath Greenland, Geophys. Res. Lett., 45, 8214–8222, https://doi.org/10.1029/2018GL078289, 2018. a, b, c, d, e, f
Mordret, A.: Uncovering the Iceland Hot Spot Track Beneath Greenland, J. Geophys. Res.-Sol. Ea., 123, 4922–4941, https://doi.org/10.1029/2017JB015104, 2018. a
Morlighem, M., Seroussi, H., Larour, E., and Rignot, E.: Inversion of basal friction in Antartica using exact and incomplete adjoints of a higher-order model, J. Geophys. Res.-Earth, 118, 1746–1753, https://doi.org/10.1002/jgrf.20125, 2013. a
Morlighem, M., Rignot, E., Mouginot, J., Seroussi, H., and Larour, E.: Deeply incised submarine glacial valleys beneath the Greenland ice sheet, Nat. Geosci., 7, 18–22, https://doi.org/10.1038/ngeo2167, 2014. a, b, c, d
Pattyn, F.: A new three-dimensional higher-order thermomechanical ice sheet model: Basic sensitivity, ice stream development, and ice flow across subglacial lakes, J. Geophys. Res., 108, 2382, https://doi.org/10.1029/2002JB002329, 2003. a
Rignot, E. and Mouginot, J.: Ice flow in Greenland for the International Polar Year 2008–2009, Geophys. Res. Lett., 39, 1–7, https://doi.org/10.1029/2012GL051634, 2012. a, b, c
Rignot, E., Gogineni, S., Joughin, I., and Krabill, W.: Contribution to the glaciology of nothern Greenland from satellite radar interferometry, J. Geophys. Res., 106, 34007–34019, 2001. a
Rogozhina, I., Hagedoorn, J. M., Martinec, Z., Fleming, K., Soucek, O., Greve, R., and Thomas, M.: Effects of uncertainties in the geothermal heat flux distribution on the Greenland Ice Sheet: An assessment of existing heat flow models, J. Geophys. Res., 117, 1–16, https://doi.org/10.1029/2011JF002098, 2012. a
Rogozhina, I., Petrunin, A. G., Vaughan, A. P. M., Steinberger, B., Johnson, J. V., Kaban, M. K., Calov, R., Rickers, F., Thomas, M., and Koulakov, I.: Melting at the base of the Greenland ice sheet explained by Iceland hotspot history, Nat. Geosci., 9, 366–369, https://doi.org/10.1038/ngeo2689, 2016. a, b, c, d
Rysgaard, S., Bendtsen, J., Mortensen, J., and Sejr, M. K.: High geothermal heat flux in close proximity to the Northeast Greenland Ice Stream, Sci. Rep., 8, 1–8, https://doi.org/10.1038/s41598-018-19244-x, 2018. a
Scambos, T. A. and Haran, T.: An image-enhanced DEM of the Greenland ice sheet, Ann. Glaciol., 34, 291–298, https://doi.org/10.3189/172756402781817969, 2002. a, b
Schlegel, N. J., Larour, E., Seroussi, H., Morlighem, M., and Box, J. E.: Decadal-scale sensitivity of Northeast Greenland ice flow to errors in surface mass balance using ISSM, J. Geophys. Res.-Earth, 118, 667–680, https://doi.org/10.1002/jgrf.20062, 2013. a
Schlegel, N.-J., Larour, E., Seroussi, H., Morlighem, M., and Box, J. E.: Ice discharge uncertainties in Northeast Greenland from climate forcing and boundary conditions of an ice flow model, J. Geophys. Res. Earth, 120, 29–54, https://doi.org/10.1002/2014JF003359, 2015. a
Schoof, C.: The effect of cavitation on glacier sliding, Proc. R. Soc., Ser. A, 461, 609–627, https://doi.org/10.1098/rspa.2004.1350, 2005. a
Seroussi, H., Morlighem, M., Rignot, E., Khazendar, A., Larour, E., and Mouginot, J.: Dependence of century-scale projections of the Greenland ice sheet on its thermal regime, J. Glaciol., 59, 1024–1034, https://doi.org/10.3189/2013JoG13J054, 2013. a
Seroussi, H., Ivins, E. R., Wiens, D. A., and Bondzio, J.: Influence of a West Antarctic mantle plume on ice sheet basal conditions, J. Geophys. Res.-Sol. Ea., 122, 7127–7155, https://doi.org/10.1002/2017JB014423, 2017. a, b
Shapiro, N. M. and Ritzwoller, M. H.: Inferring surface heat flux distributions guided by a global seismic model: Particular application to Antarctica, Earth Planet. Sc. Lett., 223, 213–224, https://doi.org/10.1016/j.epsl.2004.04.011, 2004. a, b, c
Smith-Johnsen, S., Schlegel, N.-J., de Fleurian, B., and Nisancioglu, K.: Sensitivity of the Northeast Greenland Ice Stream to Geothermal Heat, J. Geophys. Res.-Earth, 125, e2019JF005252, https://doi.org/10.1029/2019JF005252, 2019. a, b, c, d
Stevens, N. T., Parizek, B. R., and Alley, R. B.: Enhancement of volcanism and geothermal heat flux by ice-age cycling: A stress modeling study of Greenland, J. Geophys. Res. Earth Surf., 121, 1456–1471, https://doi.org/10.1002/2016JF003855, 2016. a, b
Tsai, V. C., Stewart, A. L., and Thompson, A. F.: Marine ice-sheet profiles and stability under Coulomb basal conditions, Journal of Glaciology, 61, 205–215, https://doi.org/10.3189/2015JoG14J221, 2015. a
Uenzelmann-Neben, G., Schmidt, D. N., Niessen, F., and Stein, R.: Intraplate volcanism off South Greenland: Caused by glacial rebound?, Geophys. J. Int., 190, 1–7, https://doi.org/10.1111/j.1365-246X.2012.05468.x, 2012. a