Micromechanical modeling of snow failure

Dry-snow slab avalanches start with the formation of a local failure in a highly porous weak layer underlying a cohesive snow slab. If followed by rapid crack propagation within the weak layer and finally a tensile fracture through the slab, a slab avalanche releases. While the basic concepts of avalanche release are relatively well understood, performing fracture experiments in the laboratory or in the field can be difficult due to the fragile nature of weak snow layers. Numerical simulations are a valuable tool for the study of micromechanical processes that lead to failure in snow. We used a three-dimensional discrete element method (3-D DEM) to simulate and analyze failure processes in snow. Cohesive and cohesionless ballistic deposition allowed us to reproduce porous weak layers and dense cohesive snow slabs, respectively. To analyze the micromechanical behavior at the scale of the snowpack (∼1 m), the particle size was chosen as a compromise between low computational costs and detailed representation of important micromechanical processes. The 3-D-DEM snow model allowed reproduction of the macroscopic behavior observed during compression and mixed-mode loading of dry-snow slab and the weak snow layer. To be able to reproduce the range of snow behavior (elastic modulus, strength), relations between DEM particle and contact parameters and macroscopic behavior were established. Numerical load-controlled failure experiments were performed on small samples and compared to results from load-controlled laboratory tests. Overall, our results show that the discrete element method allows us to realistically simulate snow failure processes. Furthermore, the presented snow model seems appropriate for comprehensively studying how the mechanical properties of the slab and weak layer influence crack propagation preceding avalanche release.

1 Introduction

Dry-snow slab avalanches require initiation and propagation of a crack in a weak snow layer buried below cohesive slab layers. Crack propagation occurs if the initial zone of damage in the weak layer is larger than the so-called critical crack size. Weak layer fracture during crack propagation is generally accompanied by the structural collapse of the weak layer due to the high porosity of snow (van Herwijnen et al., 2010). If the crack propagates across a steep slope, a slab avalanche may release (McClung, 1979; Schweizer et al., 2003). Our understanding of crack propagation was greatly improved by the introduction of the propagation saw test (PST; Gauthier and Jamieson, 2006; Sigrist and Schweizer, 2007; van Herwijnen and Jamieson, 2005). The PST involves isolating a snow column and initiating a crack by sawing in a pre-defined weak layer until the critical crack length is reached and self-propagation starts. The PST allows analysis of the onset and dynamics of crack propagation and derivation of important mechanical properties using particle tracking velocimetry (van Herwijnen et al., 2016). The essential mechanical properties related to the onset of crack propagation are slab elasticity, slab load and tensile strength, as well as the weak layer strength and specific fracture energy (e.g., Reuter and Schweizer, 2018). However, no theoretical framework exists that describes how these mechanical properties and possibly other ones such as the weak layer failure envelope, weak layer elasticity or microstructure relate to the dynamics of crack propagation at the slope scale. Whereas field experiments are difficult to perform at this scale, numerical simulations may provide insight into the drivers of propagation dynamics.

Johnson and Hopkins (2005) were the first to apply the discrete element method (DEM) to model snow deformation. They simulated creep settlement of snow samples, which consisted of 1000 randomly oriented cylinders of random length with hemispherical ends. More recently, the DEM was used to model the mechanical behavior based on the complete 3-D microstructure of snow (Hagenmuller et al., 2015). Gaume et al. (2015) developed a discrete element model to simulate crack propagation and subsequently derived a new analytical expression for the critical crack length (Gaume et al., 2017b). Their approach allows the generation of highly porous samples and was used to perform 2-D simulations of the PST in agreement with field experiments. However, the oversimplified shape (triangular structure) and the 2-D character of the weak layer employed by Gaume et al. (2015) prevented a detailed analysis of the internal stresses during crack propagation. On the other hand, microstructure-based DEM models adequately reproduce the mechanical behavior (Mede et al., 2018). However, the computational costs of these complex 3-D models are too high to generate samples large enough to investigate the dynamics of crack propagation at the slope scale on a standard personal computer (Intel Core i7, eight processors, 3.4 GHz, RAM 16Gb).

Our aim is to develop a 3-D-DEM snow model that adequately takes into account snow microstructure, but is not too costly in terms of computational power so that simulations at the slope scale become feasible on a high-performance computer (HPC). To relate DEM parameters to macroscopic snow behavior, we will validate the model by simulating basic load cases. Finally, we numerically simulate mixed-mode loading experiments and compare results to those obtained during laboratory experiments.

2 Data and methods

2.1 Formulation of the model

2.1.1 Discrete element method

To simulate the failure behavior of layered snow samples, we used the discrete element method (DEM). DEM, first introduced by Cundall and Strack (1979), is a numerical tool, commonly employed to study granular-like assemblies composed of a large number of discrete interacting particles. We used the PFC3D (v5) software developed by Itasca Consulting Group (http://www.itascacg.com, last access: 20 December 2019).

2.1.2 Contact model

We used the parallel-bond contact model (PBM) introduced by Potyondy and Cundall (2004). The PBM provides the mechanical behavior of a finite-sized piece of cement-like material that connects two particles. The PBM component acts in parallel with a classical linear contact model and establishes an elastic interaction between the particles. The mechanical parameters include the contact elastic modulus E_u, Poisson's ratio ν_u=0.3, restitution coefficient e_u=0.1 and friction coefficient ${\mathit{\mu }}_{\mathrm{u}}=\mathrm{0.2}.$ If particles are bonded, the bond part will act in parallel to the contact part. The bonded part is described by the bond elastic modulus E_b, the bond Poisson's ratio ν_b=0.3 and the bond strength, shear and tensile strength σ_s and σ_t. To reduce the number of variables we assume E_u=E_b≜E_particle and ${\mathit{\sigma }}_{\mathrm{s}}={\mathit{\sigma }}_{\mathrm{t}}\mathit{\triangleq }{\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$. Figure 1 illustrates the PFC parallel-bond model (PBM) with the mechanical parameters for the bonded and unbonded states. Four different bond behaviors (tension–compression, shear, bending and torsion) are shown in Fig. 2. The maximum bond shear and tensile stresses are calculated via beam theory depending on the normal and shear forces in the bond, M_b,1 the bending moment, M_b,2 the twisting moment, r_b the bond radius, A the area of the bond, I the moment of inertia of the bond cross section and J the polar moment of inertia. More details on the PBM can be found in previous studies (Gaume et al., 2015, 2017a, b). Once a bond breaks, only particle frictional contact occurs, and no new bonds are created (i.e., no sintering occurs). This assumption is motivated by the fact that the strain rate is large and the timescale is seconds during the post-failure phase.

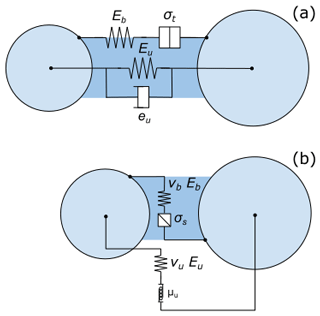
Figure 1 Representation of the PFC parallel-bond model (PBM) used in the simulations. (a) Normal mechanical parameter bonded and unbonded, where E_b represents the bond elastic modulus, σ_t the tensile strength, E_u the contact elastic modulus and e_u the restitution coefficient. (b) Shear mechanical parameter bonded and unbonded, where E_b represents the bond elastic modulus, σ_s the shear strength, E_u the contact elastic modulus, ν_b the bond Poisson's ratio, ν_u the contact Poisson's ratio and μ_u the friction coefficient.

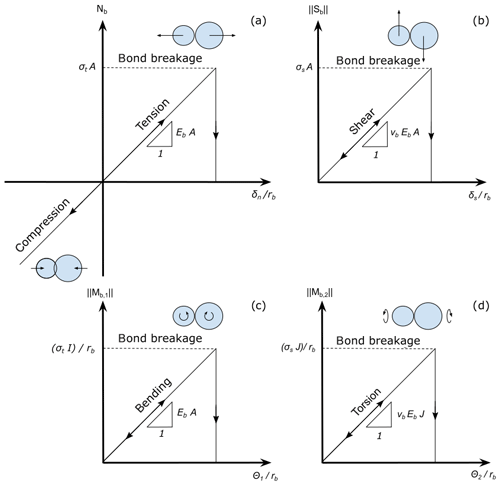
Figure 2 Representation of the bonded behavior of PBM used in the simulations. (a) Bond normal force N_b as a function of the normal interpenetration δ_n scaled by the bond radius r_b. (b) Bond shear force ∥S_b∥ as a function of tangential interpenetration δ_s scaled by the bond radius r_b. (c) Bond-bending moment ∥M_b,1∥ as a function of bending rotation θ₁ scaled by the bond radius r_b. (d) Torsion moment ∥M_b,2∥ as a function of twist rotation θ₂ scaled by the bond radius r_b.

2.1.3 System generation

The simulated three-dimensional system consisted of a rigid basal layer (Fig. 3, blue particles), the layer studied (weak layer or slab layer, green particles), and an “actuator” layer used to apply the load (red particles). The basal layer is composed of a single layer of particles with a radius of r=5 mm. The weak layer was created by cohesive ballistic deposition (Löwe et al., 2007) to reproduce the porous and anisotropic structure of natural weak layers. Doing so, we obtained a porosity of 80 % for a particle radius of r=2.5 mm. The layer thickness (3 cm) can be modified by homothetic transformation while keeping the same mechanical behavior. A short weak layer scaling study is provided in the Supplement.

Figure 3 (a) Coordinate system and diagram of the setup consisting of the basal layer (blue), the tested layer, in this case a weak layer (green), and the actuator layer (red). The violet arrow points to the interface between basal and tested layer where the stress is measured. (b) slice of a generated system consisting of a slab layer (large red particles) and a porous weak layer (small green particles). A zoom of the weak layer is shown in the circle. The lines represent bonds between particles. Applied gravity is defined on the right where ψ is the loading angle.

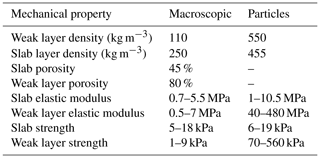
We used cohesionless ballistic deposition to generate dense layers (Kadau and Herrmann, 2011) as typically found in snow slab layers. For these layers we used a particle radius of $r=\mathrm{11}\pm \mathrm{1}$ mm (uniform distribution). The radius variation was introduced to prevent close packing, resulting in a porosity of 45 %. Layer density (ρ) was adjusted by changing the particle density. The size of the particles is not intended to represent the real snow grains. The particle size was chosen as a trade-off between an acceptable computation time (minutes to days) and avoiding particle size effects in the numerical experiments. At the defined particle scale (larger than the snow grains) the ice properties (e.g., strength, elastic modulus, Poisson's ratio) cannot be used directly. Therefore, the particle scale can be considered a mesoscale between the macroscopic scale (sample scale) and the microscale (individual snow grains). Hence, we adjusted the particle density to represent the macroscopic snow densities in accordance with the macroscopic sample porosity.

To characterize the mechanical behavior of these two types of snow-like layers (weak layer or slab layer), unconfined load-controlled tests were performed and compared to experimental results. We also performed confined compression tests, but we found no difference in behavior compared to the unconfined tests due to the porosity of 80 % (shown in the Supplement). To simulate the tests, we added an “actuator” layer generated by cohesionless ballistic deposition, composed of particles with a radius r=10 mm on top of the studied layer (Fig. 3, red particles). This layer is defined as a rigid clump with initially low density. A clump is a rigid collection of n rigid particles that form one DEM element. The volume is defined by the particle positions and radius. The mass properties are defined by the clump density and clump volume. Clumps can translate and rotate but cannot deform. Clump motion obeys the equations of motion induced by the definition of mass properties, loading conditions and velocity conditions.

The samples were generated in a box; the box walls were then removed to create unconfined test conditions. To avoid a packing effect at the sidewalls, samples were generated 10 particle radii larger and cutout before the simulation. In order to model macroscopic mechanical behavior of the studied layers, we tuned the particle elastic moduli and the bond strength. A large range of particle elastic modulus and bond strengths were tested to characterize the relation between particle parameters and macroscopic behavior. In some materials, strength and elastic modulus are related, while in other materials these properties are independent. For snow, it remains unclear whether the two properties are related. Our goal was to independently control both parameters in order to have a precise control on the macroscopic elastic modulus and macroscopic strength of the snow.

2.1.4 Load-controlled test

Load-controlled simulations were performed by linearly increasing the actuator layer density. To avoid a sample size effect (see below), 30 cm×30 cm samples were generated. Our DEM model does not take into account viscous effects or sintering of snow; therefore the results do not depend on the loading rate. We chose a high loading rate of 20 kPa s⁻¹ simply to reduce the simulation time but we verified that the loading rate did not affect the results (not shown). By changing the angle of gravity (ψ in Fig. 3), mixed-mode loading was simulated. Failure was defined as the point of maximum shear or normal stress during the two first phases (linear elastic and softening phases). Table 1 summarizes the particle mechanical properties used for simulations and their corresponding macroscopic values.

Table 1 Mechanical properties used for simulation.

2.1.5 Time step

The length of the time step was determined as a function of the particle properties according to

$$\begin{array}{}\text{(1)}& \mathrm{\Delta }t\approx r\sqrt{{\displaystyle \frac{\mathit{\rho }}{E}}},\end{array}$$

where ρ and r are the smallest particle density and radius, respectively, and E is the largest bond or particle elastic modulus. Choosing the time step in this manner ensures the stability of the DEM model (Gaume et al., 2015).

2.1.6 Stress and strain

The average stress and strain were calculated at the interface between the rigid base layer and the studied layer (Fig. 3, violet arrow). Normal stress ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_z$ was computed as ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_z=F_z/A$ and shear stress as ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_x=F_x/A$. Here F_x and F_z are the sum of the contact forces acting on the basal layer in the tangential and normal directions, respectively, and A is the total area of the basal layer over which the stresses were determined. We define the engineering strains as normal strain, ${\mathit{\epsilon }}_z=\frac{u_z}{D}$, and shear strain, ${\mathit{\gamma }}_x=\frac{u_x}{D}$, with the displacement of the actuator u in the z and x directions and the thickness D of the studied layer. The macroscopic strength (σ^th) was defined as the maximum stress before catastrophic failure. The macroscopic elastic modulus (E) was defined on the normal stress–strain curve as the derivative of the stress between 0 % and 70 % of the stress peak.

2.1.7 Fabric tensor

If the particle arrangement during layer creation is not isotropic, the mechanical quantities of the layer show directional dependency. For any heterogeneous, anisotropic material (e.g., bones, concrete, snow), the fabric tensor characterizes the geometric arrangement of the porous material microstructure. The fabric tensor, referred to here as the contact tensor C, is the volume average of the tensor product of the contact unit normal vectors $\stackrel{\mathrm{‾}}{n}$. The 2nd-order contact tensor coefficients are defined in Ken-Ichi (1984) as

$$\begin{array}{}\text{(2)}& C_{ij}={\displaystyle \frac{\mathrm{1}}{N}}{\sum }_{\mathit{\alpha }=\mathrm{1}}^N{n}_i^{\mathit{\alpha }}{n}_j^{\mathit{\alpha }},\end{array}$$

where N is the total number of particle contacts, and $n_i^{\mathit{\alpha }}$ represents the normalized projections of the contact with respect to the x_i Cartesian coordinate (Shertzer et al., 2011). The contact tensor C was used to estimate the physical properties of the simulated sample.

2.1.8 Laboratory experiments

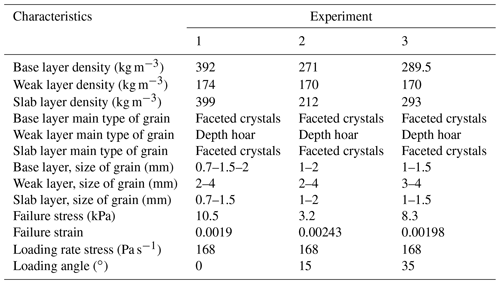
For model validation, we used data of cold laboratory experiments obtained with a loading apparatus described in Capelli et al. (2018). They performed load-controlled failure experiments on artificially created, layered snow samples, consisting of a weak layer of depth hoar crystals between harder layers of fine-grained snow. The load applied to the samples was increased linearly until the sample failed. For more information on the experiments, see Capelli et al. (2018). We selected three experiments (Table 2) for validating the numerical simulations. For the validation we focused on the normal strain, since for the experimental shear strain data (measure of the horizontal displacement) the signal-to-noise ratio was too low. Furthermore, due to the method used to load the snow samples, data from the force sensor after failure contained experimental artifacts. To select the model parameters E_particle and ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$, we used the elastic modulus computed as the derivative of the normal stress–strain curve and the strength values from the experiments (Table 2), as well as the relations for strength and modulus derived below. Digital image analysis of the experiments had revealed that the deformation was concentrated in the weak layer (Capelli et al., 2018). We therefore simulated the weak layer with a rigid actuator layer on the top.

Table 2 Characteristics of the three cold laboratory experiments used for model validation.

3 Results

This section first presents the structural properties of the two generated layers. The two generated layers were analyzed based on an unconfined compression test. Then, the link between macroscopic behavior and particle properties is described. Finally, the model setup for the weak layer is validated by comparing numerical mixed-mode loading simulations to experimental data.

3.1 Structural properties of generated samples

For the sample used to generate the slab, the coefficients of the contact tensor C were (Eq. 2)

$$\begin{array}{}\text{(3)}& C_{\mathrm{slab}}=\left[\begin{array}{ccc}\mathrm{0.32}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0.32}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0.35}\end{array}\right].\end{array}$$

This shows that the slab samples are nearly isotropic, which is in line with results reported for snow types typically found in snow slab layers (Gerling et al., 2017; Srivastava et al., 2016).

For the weak layer samples, five in total, the contact tensor was

$$\begin{array}{}\text{(4)}& C_{\mathrm{weak}\mathrm{layer}}=\left[\begin{array}{ccc}\mathrm{0.27}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0.27}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0.46}\end{array}\right].\end{array}$$

It shows transverse isotropic symmetry that is again in line with data from snow samples representative for weak layers (i.e., layers of depth hoar, surface hoar or facets), which also show transverse isotropy (Gerling et al., 2017; Shertzer, 2011; Shertzer et al., 2011; Srivastava et al., 2016).

3.2 Characterization of macroscopic properties

3.2.1 Slab layer

To establish a relationship between the macroscopic elastic modulus and the particle elastic modulus, we performed 100 simulations (with 10 different values of E_particle and 10 different values of ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}})$ in pure compression to relate macroscopic and particle parameters. The macroscopic elastic modulus increased linearly with E_particle:

$$\begin{array}{}\text{(5)}& E_{\mathrm{slab}\mathrm{macro}}={\mathit{\beta }}_{\mathrm{0}}+{\mathit{\beta }}_{\mathrm{1}}{E}_{\mathrm{particle}},\end{array}$$

with the coefficients ${\mathit{\beta }}_{\mathrm{0}}=\mathrm{1.5}\times {\mathrm{10}}^{\mathrm{5}}$ Pa and β₁=0.526 (dashed line in Fig. 4a).

The macroscopic strength also increased linearly with bond strength:

$$\begin{array}{}\text{(6)}& {\mathit{\sigma }}_{\mathrm{slab}\mathrm{macro}}^{\mathrm{th}}={\mathit{\gamma }}_{\mathrm{0}}+{\mathit{\gamma }}_{\mathrm{1}}{\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}},\end{array}$$

with the coefficients ${\mathit{\gamma }}_{\mathrm{0}}=-\mathrm{318}$ Pa and γ₁=0.982 (dashed line in Fig. 4b; R²=0.999).

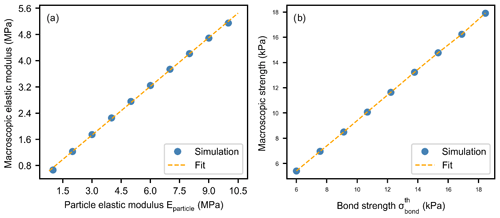
Figure 4 (a) Slab macroscopic elastic modulus as a function of particle elastic modulus. The blue dots correspond to the mean of 10 simulations with different values of ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$. (b) Slab macroscopic strength as a function of slab particle strength obtained with unconfined load-controlled compression simulations. The blue dots correspond to the mean of 10 simulations with different values of E_particle.

3.2.2 Weak layer

For the weak layer we performed 81 simulations (with nine different values of E_particle and nine different values of ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}})$ in pure compression to relate macroscopic and particle parameters. The macroscopic elastic modulus increased linearly with E_particle:

$$\begin{array}{}\text{(7)}& E_{\mathrm{wl}\mathrm{macro}}={\mathit{\beta }}_{\mathrm{0}}+{\mathit{\beta }}_{\mathrm{1}}{E}_{\mathrm{particle}},\end{array}$$

with coefficients ${\mathit{\beta }}_{\mathrm{0}}=\mathrm{7.3}\times {\mathrm{10}}^{\mathrm{4}}$ Pa and β₁=0.014 (Fig. 5a; R²=0.985).

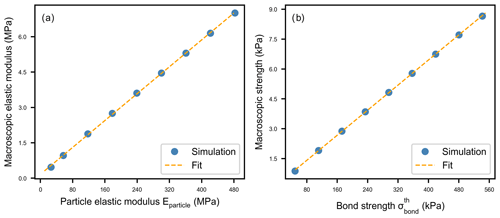
Figure 5 (a) Weak layer macroscopic elastic modulus as a function of particle elastic modulus. The blue dots correspond to the mean of nine simulations with different values of ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$. (b) Weak layer macroscopic strength as a function of weak layer particle strength obtained with unconfined load-controlled compression simulations. The blue dots correspond to the mean of nine simulations with different values of E_particle.

The macroscopic strength also increased linearly with bond strength:

$$\begin{array}{}\text{(8)}& {\mathit{\sigma }}_{\mathrm{wl}\mathrm{macro}}^{\mathrm{th}}={\mathit{\gamma }}_{\mathrm{0}}+{\mathit{\gamma }}_{\mathrm{1}}{\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}},\end{array}$$

with coefficients γ₀=76.7 Pa and γ₁=0.016 (Fig. 5b; R²=0.998).

Hence, based on Eqs. (7) and (8), any values of the macroscopic quantities ${\mathit{\sigma }}_{\mathrm{wl}\mathrm{macro}}^{\mathrm{th}}$ and E_wl macro can be obtained by tuning E_particle and ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$.

3.3 Mechanical behavior of layers

3.3.1 Slab layer

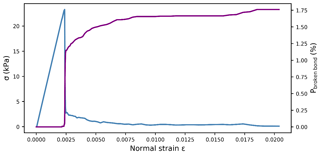
To investigate the mechanical behavior of the slab layer, we performed load-controlled tension tests. Two phases can be distinguished: linear elastic deformation followed by sample fracture. During the linear elastic deformation, no bond damage appears, and the stress linearly increases up to ε=0.0025 (Fig. 6). At failure, the stress dropped rapidly and bond damage drastically increased with increasing strain.

Figure 6 Slab layer behavior under load-controlled tension test. The blue line showing the normal stress and the violet line corresponding to the bond breaking ratio are plotted as functions of the normal strain.

3.3.2 Weak layer

The large-deformation, unconfined load-controlled compression tests of weak layer samples revealed four different phases (grey dashed–dotted lines in Fig. 7). First, there was a linear elastic phase without bond breaking (a.1); nonlinearity appears right before the stress peak induced by some damage prior to failure, in good agreement with the quasi-brittle behavior of weak snow layers (Fig. 8). When the macroscopic strength was reached, the normal stress dropped sharply during the softening phase as bond damage increased drastically (a.2). During the brittle crushing phase, the sample density as well as the proportion of broken bonds (P_{broken bond}) steadily increased (a.3). Finally, the densification phase (a.4) was reached when the stress prominently increased again as the particles were closely packed.

By varying the particle modulus E_particle and the bond strength ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$, the micromechanical behavior in terms of bond breaking and acceleration (a) of the actuator layer was also investigated more closely up to the start of the brittle crushing phase (Fig. 9). Before reaching the macroscopic strength, the normal stress increased linearly with increasing strain while the number of broken bonds and the acceleration were low. The strain at failure depended on both E_particle and ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$. During the softening the stress sharply dropped while both the number of broken bonds and the acceleration increased. Both E_particle and ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$ controlled the amount of stress drop as well as the rate of increase in P_{broken bond} and a. During the brittle crushing phase, both strength and acceleration did not change while P_{broken bond} increased, independent of the values of E_particle and ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$.

The stress at the end of the softening phase was characterized by the softening ratio $R=\frac{{\widehat{\mathit{\sigma }}}_{\mathrm{residual}}}{{\mathit{\sigma }}_{\mathrm{wl}\mathrm{macro}}^{\mathrm{th}}}$, with ${\mathit{\sigma }}_{\mathrm{wl}\mathrm{macro}}^{\mathrm{th}}$ the macroscopic strength and ${\widehat{\mathit{\sigma }}}_{\mathrm{residual}}$ the mean residual stress during the brittle crushing phase. The test with the highest softening ratio (Fig. 9 solid light blue line: R=0.45) showed the lowest damage and the lowest acceleration. In contrast, the lowest softening ratio (Fig. 9 dark blue dashed line: R=0.21) corresponded to the largest proportion of broken bonds and the largest acceleration. Concerning the two other tests, they exhibited the same residual stress but different softening ratios. We observed that the softening ratio followed a nonlinear relation with E_particle and ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$.

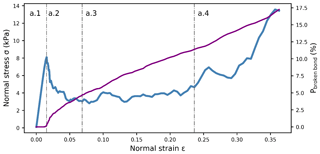
Figure 7 Weak layer behavior under load-controlled compression test (E_particle=30 MPa and ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}=\mathrm{500}\mathrm{kPa})$. The blue line shows the normal stress during the four phases of weak layer failure. It includes the linear elastic phase (a.1), softening (a.2), brittle crushing (a.3) and densification (a.4). The violet line corresponds to the proportion of broken bonds.

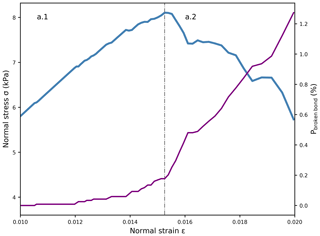
Figure 8 Weak layer behavior close to failure under load-controlled compression (E_particle=30 MPa and ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}=\mathrm{500}\mathrm{kPa}$). The blue line shows the normal stress during the two first phases of weak layer failure. It includes the elastic (a.1) and the softening phases (a.2). The violet line corresponds to the proportion of broken bonds.

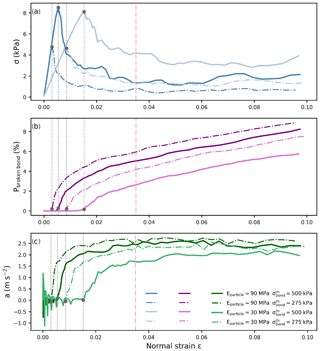
Figure 9 Weak layer behavior under load-controlled compression for four combinations of E_particle (solid lines) and ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$ (same color, dashed–dotted lines). (a) Normal stress vs. normal strain. (b) Percentage of broken bonds (damage). (c) Acceleration of the actuator layer. The orange dashed–dotted line represents the approximate beginning of the brittle crushing phase. The grey dotted lines represents the beginning of the softening phase defined by the strength (grey dot).

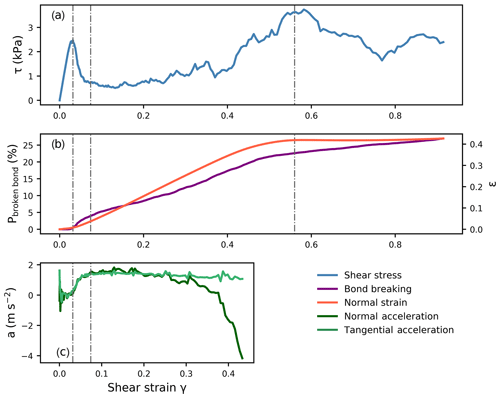
Figure 10 Weak layer behavior in load-controlled mixed-mode testing at 35^∘ from the horizontal (E_particle=30 MPa and ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}=\mathrm{500}\mathrm{kPa}$). (a) Shear stress, (b) bond damage (violet) and normal strain (orange, right scale), and (c) normal and tangential accelerations are shown as a function of the shear strain.

Similar to the behavior under compression, the mechanical response in shear exhibited different phases: an elastic phase, softening and simultaneously normal brittle crushing and shear displacement, and finally shear displacement only (grey dashed–dotted lines in Fig. 10). Also, the damage dynamics were similar to in pure compression (Fig. 10b). No critical bond breaking was observed during the linear elastic phase followed by catastrophic damage after failure. Subsequently, the damage further increased during the brittle crushing. The normal strain increased during the brittle crushing phase and did not change thereafter. The normal deformation was closely related to the proportion of broken bonds, similar to behavior in the pure compression. Shear and normal accelerations reached their maximum at the end of the softening phase (Fig. 10c) as observed in pure compression (Fig. 7). During the brittle crushing phase, the normal acceleration decreased due to the creation of new contacts that decelerate the actuator layer. The tangential acceleration did not change much during the shear displacement phase.

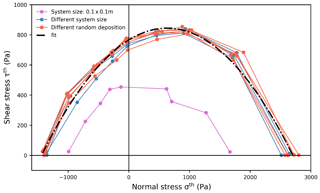
Figure 11 Failure envelopes for different sample sizes and types of random particle deposition. The blue lines correspond to different sample sizes from 0.3 m×0.3 m to 0.6 m×1 m. The pink line corresponds to a sample size of 0.1 m×0.1 m. The orange lines correspond to a sample size of 0.3 m×0.3 m generated with different random depositions. The black dashed–dotted line corresponds to a 2nd-order polynomial fit of all data apart from those obtained with the sample size of 0.1 m×0.1 m.

3.3.3 Weak layer failure envelope

Unconfined load-controlled tests with nine loading angles were performed to create the failure envelope. Figure 11 compiles the values of macroscopic strength for different loading angles resulting in a failure envelope including tension (negative normal stress), pure shear, pure compression and mixed-mode loading states. To investigate the influence of sample size, we performed a sensitivity analysis by varying the sample size from 0.1 m×0.1 m to 1 m×0.6 m and the random deposition (generation of different ball positions for the ballistic deposition). Apart from the smallest sample, all samples had very similar failure envelopes, which were fitted with a 2nd-order polynomial with coefficients ${\mathit{\beta }}_{\mathrm{0}}^{\mathrm{FE}}=-\mathrm{7.66}\times {\mathrm{10}}^{\mathrm{2}}\mathrm{Pa}$, ${\mathit{\beta }}_{\mathrm{1}}^{\mathrm{FE}}=-\mathrm{0.25}$ and ${\mathit{\beta }}_{\mathrm{2}}^{\mathrm{FE}}=\mathrm{1.97}\times {\mathrm{10}}^{-\mathrm{4}}$ (dashed–dotted black line in Fig. 11, R²=0.97):

$$\begin{array}{}\text{(9)}& {\mathit{\tau }}^{\mathrm{th}}={\mathit{\beta }}_{\mathrm{2}}^{\mathrm{FE}}{\mathit{\sigma }}^{{\mathrm{th}}^{\mathrm{2}}}+{\mathit{\beta }}_{\mathrm{1}}^{\mathrm{FE}}{\mathit{\sigma }}^{\mathrm{th}}+{\mathit{\beta }}_{\mathrm{0}}^{\mathrm{FE}}.\end{array}$$

For a sample length of 0.3 m or larger, no effect of sample size on the failure envelope was observed. The sample heterogeneity induced by different types of random deposition did not influence the failure envelope either. Given the expression for the macroscopic strength (Eq. 9), where σ^th represents the normal strength and τ^th the shear strength, the failure envelope is directly related to ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$.

As the macroscopic strength ${\mathit{\sigma }}_{\mathrm{wl}}^{\mathrm{th}}$ is related to ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$ (Eq. 8), the failure envelope can be scaled by using the scaling factor ($\frac{{\mathit{\sigma }}_{\mathrm{wl}}^{\mathrm{th}}}{{\mathit{\sigma }}_{\mathrm{wl}\mathrm{ref}}^{\mathrm{th}}})$:

$$\begin{array}{}\text{(10)}& {\mathit{\tau }}^{\mathrm{th}}=\left({\mathit{\beta }}_{\mathrm{2}}^{\mathrm{FE}}{\mathit{\sigma }}^{{\mathrm{th}}^{\mathrm{2}}}+{\mathit{\beta }}_{\mathrm{1}}^{\mathrm{FE}}{\mathit{\sigma }}^{\mathrm{th}}+{\mathit{\beta }}_{\mathrm{0}}^{\mathrm{FE}}\right){\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{wl}}^{\mathrm{th}}}{{\mathit{\sigma }}_{\mathrm{wlref}}^{\mathrm{th}}}},\end{array}$$

with ${\mathit{\sigma }}_{\mathrm{wl}\mathrm{ref}}^{\mathrm{th}}=\mathrm{2650}\mathrm{Pa}$, which corresponds to the maximum strength in pure compression (Fig. 11). Equation (10) allows the derivation of the failure envelope for any value of the bond strength ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$ (green dashed–dotted lines in Fig. 12).

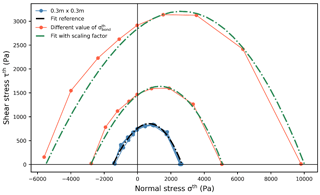
Figure 12 Failure envelopes for different values of bond strength ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$ and fit only based on Eq. (10). The blue lines correspond to the data shown in Fig. 11, and the black dashed–dotted line corresponds to the corresponding fit (Eq. 8). The orange lines correspond to failure envelopes with different values of bond strength ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$. The green dashed–dotted lines indicate the corresponding fits defined in Eq. (10), which do not depend on orange line data.

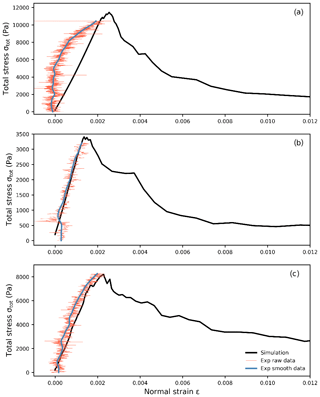
Figure 13 Total stress as function of normal strain for three simulations and the corresponding experimental results. (a) For a loading angle of 0^∘, (b) 15^∘ and (c) 35^∘. The orange lines show the raw stress data, the blue lines are the smoothed stress using a Kalman filter (Capelli et al., 2018) and the black lines are the simulation results.

3.4 Comparison with experimental data

To validate the behavior of our simulated weak layer samples, we used data from laboratory experiments performed by Capelli et al. (2018) (Table 2). For each of the three experiments with different loading angles, the simulated total stress (${\mathit{\sigma }}_{\mathrm{tot}}=\sqrt{{\mathit{\sigma }}^{\mathrm{2}}+{\mathit{\tau }}^{\mathrm{2}}})$ as a function of normal strain (ε) was in good agreement with the experimental results (Fig. 13).

4 Discussion

We used 3-D discrete element modeling to study the mechanical behavior of simplified snow samples generated by different ballistic deposition techniques. Cohesive ballistic deposition produced transversally isotropic weak layers with high porosity (80 %). Cohesionless ballistic deposition produced isotropic slab layers of lower porosity (45 %), in general agreement with key properties of natural snow samples (Shertzer, 2011). The DEM particles do not represent real snow grains to keep the computational costs reasonable (i.e., ∼10 min on a standard personal computer for a sample of 50 cm×50 cm in size, corresponding approximately to 26 500 particles). By varying the DEM particle parameters E_particle and ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$, the macroscopic properties can be modified to fit different types of snow.

First, tension tests were simulated to study the behavior of dense slab layers. The results evidenced an almost perfectly brittle behavior (Fig. 6) in good agreement with the tensile behavior reported by Hagenmuller et al. (2014) and by Sigrist (2006).

The mechanical behavior we observed for our weak layer samples, in particular the four phases (Fig. 7) during a load-controlled compression test, was very similar to that reported by Mede et al. (2018), who simulated snow behavior with microstructure-based snow samples. More generally, Gibson and Ashby (1997) also described these four distinct phases for elastic–brittle foam samples.

The unconfined load-controlled tests under mixed-mode loading conditions showed shear behavior in good agreement with previously reported results (Mede et al., 2018; Mulak and Gaume, 2019; Reiweger et al., 2015).

The obtained failure envelopes were qualitatively in good agreement with the Mohr–Coulomb–cap (MCC) model proposed by Reiweger et al. (2015) and with the ellipsoid (cam clay) model proposed by Gaume et al. (2018) and Mede et al. (2018). The model qualitatively reproduced the snow failure envelopes found in other numerical studies (Mede et al., 2018; Mulak and Gaume, 2019). In our case, the failure envelope is directly linked to ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$, since any failure envelope can be expressed as a function of ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$. Weak layer failure behavior was not affected by the heterogeneity induced by different types of random ball deposition and by the sample size if the sample size was larger than 0.3 m×0.3 m. This size is typically found in field tests (PST, extended column test; Bair et al., 2014; Reuter et al., 2015; van Herwijnen et al., 2016) and laboratory experiments (Capelli et al., 2018).

Based on these purely numerical investigations, the particle and contact parameters were selected to reproduce the results of cold laboratory experiments with real snow samples (Fig. 13). The numerical results were qualitatively in good agreement for the three loading angles. However, the comparison to the experimental results is hindered by the lack of adequate experimental data. Due to vibrations in the actuator plate, the experimental shear strain data could not be used. Hence, there are no experimental data to validate the post-failure behavior. Still, as shown above, the post-failure behavior was in agreement with results of other numerical studies (e.g., Mede et al., 2018).

We showed that the onset of failure corresponded to a strong increase in the number of broken bonds and in actuator layer acceleration (Fig. 9). The maximum acceleration was reached towards the end of the softening phase. In fracture mechanics, the zone where softening occurs is generally referred to as the fracture process zone (FPZ) (Bazant and Planas, 1998). Hence, our findings suggest that slab acceleration may be used to accurately track the crack tip location in the weak layer during crack propagation experiments.

Introducing the softening ratio (R) showed that the stress decrease in softening only depends on particle modulus E_particle and bond strength ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}}$, which allows estimation of the maximum acceleration of the actuator layer and the damage dynamics. In the present formulation of our model, the softening ratio is fixed for a given pair of parameters (E_particle and ${\mathit{\sigma }}_{\mathrm{bond}}^{\mathrm{th}})$.

To limit the number of model parameters we made two assumptions: the contact and the bond elastic moduli are equal and the bond cohesive and tensile strengths are equal. The choice of weak layer creation technique (cohesive ballistic deposition) caused unique structural anisotropy that was reflected in the mechanical behavior and added a limitation to the post-failure behavior and the shape of the failure envelope. Investigating the influence of microstructure by modifying the porosity or the coordination number as the sticky hard sphere (Gaume et al., 2017a) and/or modifying the assumption on contact/bond elastic moduli would allow us to generate a larger range of stress decrease during the softening phase.

Furthermore, in the future, the influence of the ratio between the bond tensile strength and the bond cohesive strength, and/or the weak layer microstructure on the yield surface might be explored.

The developed simulation tool does not take into account snow sintering processes, as we limited the study to fast loading rates. In the context of a dry-snow slab avalanche formation, this means that we can only study artificially induced cracks due to skiers or explosives. In the future, we plan to extend the work to larger systems with the objective of studying the micromechanics of the dynamics of crack propagation. Using the presented tool to model a PST already showed some promising preliminary results (Bobillier et al., 2018).

5 Conclusions

Understanding the failure behavior of slab and weak layer independently and characterizing the influence of the main parameters are prerequisites for studying the dynamics of crack propagation leading to the release of a dry-snow slab avalanche.

We developed a mesoscale (between snow grain and slope scale) simulation tool based on 3-D discrete element simulations to generate snow layers of varying properties and investigate micromechanical processes at play during snow failure. Two types of snow layers were generated using a ballistic deposition technique: (1) a uniform snow slab and (2) a porous transversally isotropic weak snow layer. These two types of snow layers are the two main components of dry-snow slab avalanches. The layers were characterized by a linear relation between particle and contact parameters and macroscopic properties. By deliberately making the choice of not representing the real snow microstructure, the computational time decreases and allows the creation of relatively large systems.

We found an elastic–brittle mechanical behavior for slab layers in tension. The weak layer behavior under mixed-mode loading included four distinct phases of deformation (elastic, softening, simultaneous brittle crushing and shear displacement, and finally shear displacement) as recently reported in the literature. The weak layer failure envelope, derived from a series of mixed-mode loading simulations under different loading angles, was in good agreement with previous experimental and numerical results. The closed-form failure envelope can be tuned by adjusting the bond strength parameter.

Analyzing weak layer features such as the proportion of broken bonds, normal acceleration and softening ratio showed some of the limitations induced by our assumptions on particle parameters and the uniqueness of the microstructure generation. Still, the validation results suggest that the presented simulation tool can reproduce the main behavior of weak layers under mixed-mode loading conditions – even though we strongly simplified the microstructure to limit the computational costs.

In the future, we intend to increase the system size and simulate a propagation saw test and explore the dynamics of crack propagation that eventually lead to dry-snow slab avalanche release.