the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The role of history and strength of the oceanic forcing in sea level projections from Antarctica with the Parallel Ice Sheet Model
Anders Levermann
Torsten Albrecht
Hélène Seroussi
Ricarda Winkelmann
Mass loss from the Antarctic Ice Sheet constitutes the largest uncertainty in projections of future sea level rise. Ocean-driven melting underneath the floating ice shelves and subsequent acceleration of the inland ice streams are the major reasons for currently observed mass loss from Antarctica and are expected to become more important in the future. Here we show that for projections of future mass loss from the Antarctic Ice Sheet, it is essential (1) to better constrain the sensitivity of sub-shelf melt rates to ocean warming and (2) to include the historic trajectory of the ice sheet. In particular, we find that while the ice sheet response in simulations using the Parallel Ice Sheet Model is comparable to the median response of models in three Antarctic Ice Sheet Intercomparison projects – initMIP, LARMIP-2 and ISMIP6 – conducted with a range of ice sheet models, the projected 21st century sea level contribution differs significantly depending on these two factors. For the highest emission scenario RCP8.5, this leads to projected ice loss ranging from 1.4 to 4.0 cm of sea level equivalent in simulations in which ISMIP6 ocean forcing drives the PICO ocean box model where parameter tuning leads to a comparably low sub-shelf melt sensitivity and in which no surface forcing is applied. This is opposed to a likely range of 9.1 to 35.8 cm using the exact same initial setup, but emulated from the LARMIP-2 experiments with a higher melt sensitivity, even though both projects use forcing from climate models and melt rates are calibrated with previous oceanographic studies. Furthermore, using two initial states, one with a previous historic simulation from 1850 to 2014 and one starting from a steady state, we show that while differences between the ice sheet configurations in 2015 seem marginal at first sight, the historic simulation increases the susceptibility of the ice sheet to ocean warming, thereby increasing mass loss from 2015 to 2100 by 5 % to 50 %. Hindcasting past ice sheet changes with numerical models would thus provide valuable tools to better constrain projections. Our results emphasize that the uncertainty that arises from the forcing is of the same order of magnitude as the ice dynamic response for future sea level projections.
- Article
(3187 KB) - Full-text XML
-
Supplement
(3428 KB) - BibTeX
- EndNote
Observations show that the Antarctic Ice Sheet is currently not in equilibrium and that its contribution to global sea level rise is increasing (Shepherd et al., 2018). Its future contribution is the largest uncertainty in sea level projections (Oppenheimer, 2020) with its evolution driven by snowfall increases (e.g., Ligtenberg et al., 2013; Frieler et al., 2015) that are counteracted by increased ocean forcing (e.g., Hellmer et al., 2012; Naughten et al., 2018) and potentially instabilities such as the marine ice sheet instability (Weertman, 1974; Schoof, 2007) and the marine ice cliff instability (DeConto and Pollard, 2016). In recent years, sea level projections of the Antarctic Ice Sheet were conducted with individual ice sheet models (e.g., DeConto and Pollard, 2016; Golledge et al., 2019) and extended by comprehensive community efforts such as the Ice Sheet Model Intercomparison Project for CMIP6 (ISMIP6; Nowicki et al., 2016, 2020; Seroussi et al., 2020) and the Linear Antarctic Response Model Intercomparison Project (LARMIP-2; Levermann et al., 2014, 2020) projects. In ISMIP6, a protocol for Antarctic projections was developed and ice sheet model responses to oceanic and atmospheric forcing from selected CMIP5 models (Barthel et al., 2020) were gathered and compared for the first time. As a first step of ISMIP6, initMIP-Antarctica did test the effect of different model initializations on idealized experiments (Seroussi et al., 2019). While the response of the ice sheet to surface mass balance forcing was similar among the models, they showed very different responses to basal melt rate changes. Similarly, in ISMIP6 a large spread in model projections is found, with ice volume changes from −7.8 to 30.0 cm of sea level equivalent (SLE) under the highest greenhouse gas emission scenario (Representative Concentration Pathway RCP8.5) with the largest uncertainties coming from ocean-induced melt rates, the calibration of melt rates and the ice dynamic response to oceanic changes. The ISMIP6 projections are given with respect to the control simulation, hence not considering current trends of mass loss.
Sea level estimates in ISMIP6 are in many cases substantially lower than the ocean-driven mass loss projected by LARMIP-2. In LARMIP-2, the sea level contribution of the Antarctic Ice Sheet is emulated from step-forcing experiments using linear response function theory (Winkelmann and Levermann, 2013). A median mass loss of 17 cm with a likely range from 9 to 36 cm and a very likely range of 6 to 58 cm is found. In contrast to ISMIP6, atmospheric changes, which add mass gains between −2.5 and 84.5 mm SLE to the ice sheet depending on the CMIP5 forcing, are not considered in LARMIP-2, and we here also focus on the dynamic, ocean-driven response of the ice sheet.
In projections of the future Antarctic sea level contribution following the ISMIP6 and LARMIP-2 protocols, oceanic forcing is obtained from subsurface ocean conditions in general circulation models, e.g., from results of the Coupled Model Intercomparison Project Phase 5 (CMIP5; Taylor et al., 2012). This approach takes into account that sub-shelf melt rates are mainly driven by inflow of ocean water masses at depth (Jacobs et al., 1992). However, CMIP5 models do not include ice-shelf cavities and related feedbacks that might increase the future oceanic forcing on the ice shelves (Timmermann and Goeller, 2017; Donat-Magnin et al., 2017; Bronselaer et al., 2018; Golledge et al., 2019). Ocean temperatures from CMIP5 models therefore have to be extrapolated into ice-shelf cavities (Jourdain et al., 2019). Alternatively, output from high-resolution models that resolve ocean dynamics on the continental shelf and within the ice-shelf cavities could be used (e.g., Hellmer et al., 2012; Naughten et al., 2018).
The subsurface ocean forcing informs parameterizations that provide melt rates underneath the ice shelves for ice sheet models. For the ISMIP6 experiments, a depth-dependent, nonlocal parameterization and a depth-dependent, local parameterization have been proposed (Jourdain et al., 2019) that both mimic a quadratic dependency of melt rates on thermal forcing (Holland et al., 2008). As an alternative, more complex modules that capture the basic physical processes within ice-shelf cavities have been developed recently (Lazeroms et al., 2018; Reese et al., 2018a). We here analyze results as submitted to ISMIP6 that apply the Potsdam Ice-shelf Cavity mOdel (PICO; Reese et al., 2018a), which extends the ocean box model (Olbers and Hellmer, 2010) for application in three-dimensional ice sheet models. The model has been tested and compared to other parameterizations for an idealized geometry (Favier et al., 2019). In this case, the induced ice sheet response matches the response driven by a three-dimensional ocean model. In contrast to ISMIP6, the LARMIP-2 experiments are forced by basal melt rate changes directly. Scaling factors between global mean temperature changes and Antarctic subsurface temperature changes are determined from CMIP5 models. These are used to generate ocean temperature forcing under different RCP scenarios emulated from MAGICC6.0 RCP realizations (Meinshausen et al., 2011). Sub-shelf melt rates are assumed to increase by 7 to 16 m a−1 per degree Celsius of subsurface ocean warming, based on Jenkins (1991) and Payne et al. (2007).
Here we compare simulations with the Parallel Ice Sheet Model as submitted to ISMIP6 with results obtained following the LARMIP-2 protocol and analyze (1) the effect of the oceanic forcing and (2) the effect of a historic simulation preceding the projections. In Sect. 2 we describe the methods used and the initial configurations of PISM. This is followed by an analysis of the experiments for ISMIP6 with only ocean forcing applied and the results obtained when following the LARMIP-2 protocol in Sect. 3. These are compared and discussed in Sects. 4 and 5.
We use the comprehensive, thermo-mechanically coupled Parallel Ice Sheet Model (PISM; Bueler and Brown, 2009; Winkelmann et al., 2011; The PISM authors, 2019) which employs a superposition of the shallow-ice and shallow-shelf approximations (Hutter, 1983; Morland, 1987; MacAyeal, 1989). We apply a power-law relationship between shallow-shelf approximation (SSA) basal sliding velocities and basal shear stress with a Mohr–Coulomb criterion relating the yield stress to parameterized till material properties and the effective pressure of the overlaying ice on the saturated till (Bueler and Pelt, 2015). Basal friction and sub-shelf melting are linearly interpolated on a sub-grid scale around the grounding line (Feldmann et al., 2014). In order to improve the approximation of driving stress across the grounding line, the surface gradient is calculated using centered differences of the ice thickness across the grounding line. We apply eigen-calving (Levermann et al., 2012) in combination with the removal of ice that is thinner than 50 m or extends beyond present-day ice fronts (Fretwell et al., 2013).
2.1 Initial configurations
We use two model configurations of the Antarctic Ice Sheet that were submitted to ISMIP6, one with a preceding historic simulation from 1850 to 2014 and one starting from a steady state. Both configurations share the same initialization procedure: starting from Bedmap2 ice thickness and topography (Fretwell et al., 2013), a spin-up is run for 400 000 years with constant geometry to obtain a thermodynamic equilibrium with present-day climate on 16 km resolution. Based on this, an ensemble of simulations with varying model parameters is run for several thousand years towards dynamic equilibrium on 8 km horizontal resolution. The simulations employ 121 vertical layers with a quadratic spacing from 13 m at the ice shelf base to 100 m towards the surface. We vary parameters of PICO (heat exchange coefficient γT and overturning coefficient C) as well as the minimum till friction angle in the parameterized till material properties (Φmin). The initial configuration is selected in two steps: after 5000 years of model simulation, five candidates that compare best to present-day observations of ice geometry and speed (Fretwell et al., 2013; Rignot et al., 2011) are selected and continued. After 12 000 years the best fit equilibrium result was selected among them and used as initial configuration for the projections; see Fig. S1 in the Supplement. We assess the ensemble members at each step using a scoring method (Pollard et al., 2016; Albrecht et al., 2020) that tests for root-mean-square deviation to present-day ice thickness, ice-stream velocities, and deviations in grounded and floating area, and the average distance to the observed grounding line position. We lay a specific focus on the Amundsen region, Filchner–Ronne and Ross ice shelves, by additionally evaluating each indicator for these drainage basins individually. The historic simulation is based on the same initial steady state configuration and additionally applies atmospheric and oceanic forcing over the period from 1850 to 2014 as described below. The initial state for the experiments without historic simulation, hereafter referred to as INIT*, and the initial configuration after the historic simulation, hereafter referred to as INIT, are shown in Fig S2. The INIT* configuration is very close to a steady-state with ice volume change rates being 5 mm over 85 years while the INIT state is out of balance with ice volume change rates being −1.5 cm over 85 years; see Table 1. The INIT state in 2014 after the historic simulation scores very similar to the best-scoring initial configuration INIT*. For example, the root-mean-square deviation in stream velocity in the Amundsen Sea region is 113 m a−1 for INIT (improved from 116 m a−1 for INIT*), in the Ross Sea 35 m a−1 (compared to 33 m a−1), in the Weddell Sea 47 m a−1 (38 m a−1) and in the entire domain 290 m a−1 (262 m a−1). The root-mean-square deviation in grounded ice thickness is 166 m (165 m) in the Amundsen Sea, 188 m (189 m) in the Ross Sea, 167 m (167 m) in the Weddell Sea and 250 m (250 m) for the entire continent. The mean grounding line deviation is 12 km (13 km) in the Amundsen Sea, 24 km (24 km) in the Ross Sea, 14 km (15 km) in the Weddell Sea and 17 km (17 km) in the entire domain.
2.2 Experiments
We here present experiments based on the ISMIP6, LARMIP-2 and initMIP protocols that were done for both initial configurations. A list of all experiments is given in Table S1 in the Supplement. The initMIP experiments employ idealized forcing designed to test the model response to simplified forcing of the surface mass balance (experiment “asmb”) and the basal mass balance (experiment “abmb”), which increase linearly for 50 years and are kept constant afterwards (Seroussi et al., 2019).
For LARMIP-2, constant step-forcing perturbations of the basal mass balance (4,8 and 16 m a−1) are applied in five Antarctic regions (Antarctic Peninsula, East Antarctica, Ross Sea, Amundsen Sea, Weddell Sea). From the modeled sea level response, linear response functions are derived that can be used to emulate the model's response to arbitrary melt forcing.
The ISMIP6 protocol prescribes atmospheric and oceanic forcing from CMIP5 models. We use the forcing data provided by ISMIP6 for (1) NorESM1-M for RCP8.5 (Bentsen et al., 2013; Iversen et al., 2013), (2) MIROC-ESM-CHEM for RCP8.5 (Watanabe et al., 2011), (3) NorESM1-M for RCP2.6 and (4) CCSM4 for RCP8.5 (Gent et al., 2011) as further described in experiments 1–4 in Nowicki et al. (2020) and Seroussi et al. (2020). To be consistent with LARMIP-2, we here only apply the ocean forcing in projections and keep the surface mass balance constant.
We run experiments for both initial configurations with * indicating simulations starting from the pseudo-steady state in 2015, INIT*. The control experiments for both initial configurations employ constant climate conditions as described in the following two subsections.
2.3 Atmosphere forcing
Surface mass balance and ice surface temperatures for the initial configuration without historic forcing are from RACMOv2.3p2 (1986 to 2005 averages, Van Wessem et al., 2018), remapped from 27 km resolution. The historic simulation is started from the same conditions with historic surface mass balance and surface temperature changes following the NorESM1-M simulation as suggested by ISMIP6 (Bentsen et al., 2013). The historic forcing from NorESM1-M is normalized to its initial period (1950–1980) and the anomalies are then added to the constant climatology from RACMO. Since the provided data start in 1950, surface mass balance and temperatures are constant between 1850 and 1949. Over that period, the aggregated yearly surface mass balance is very similar to the RACMO climatology, as shown in Fig. S3.
In contrast to ISMIP6, where surface mass balance and surface temperature changes are driven by CMIP5 data, we here keep surface conditions – in line with LARMIP-2 – constant throughout the projections. Note that due to changes in the ice sheet extent, surface mass balance integrated over the entire ice sheet might change slightly; see Table 1. Surface mass balance and temperatures in the projections that start from the pseudo-steady-state INIT* are given by the RACMO climatology. For the projections based on the historic simulation we created a new climatology to account for increases in surface mass balance and temperatures in the historic simulation. We avoid using exceptionally high or low values that arise from interannual variability at a specific snapshot in time by using the 1995 to 2014 average of the respective fields.
2.4 Ocean forcing
Sub-shelf melt rates are calculated by PICO which extends the ocean box model by Olbers and Hellmer (2010) for application in three-dimensional ice sheet models (Reese et al., 2018a). It mimics the vertical overturning circulation in ice-shelf cavities and has two model parameters that apply for all Antarctic ice shelves simultaneously: C related to the strength of the overturning circulation and γT related to the vertical heat exchange across the ice–ocean boundary layer. We here use parameters and m s−1 that were found to yield realistic melt rates in comparison to present-day estimates (Reese et al., 2018a; Rignot et al., 2013). The value of γT is slightly higher than the reference value as an outcome of the ensemble study; see Fig. S1 in the Supplement.
We initialize PICO with an ocean data compilation from the World Ocean Atlas 2018 pre-release (Locarnini et al., 2018; Zweng et al., 2018) and Schmidtko et al. (2014). PICO is driven by ocean temperature and salinity averaged over the depth of the continental shelf within each drainage basin. The data from the WOA2018 pre-release are processed by determining the relevant depth from bathymetric access to ice-shelf cavities. In Dronning Maud Land (PICO basins 2 to 5), where ocean temperatures have a warm bias due to the lack of data along narrow continental shelves, values from Schmidtko et al. (2014) were used. Using the currently observed “warm” conditions in the Amundsen Sea, we found that region to collapse in the initial ensemble irrespective of basal sliding parameters. As this region is out of balance today due to oceanic forcing (e.g., Konrad et al., 2018; Shepherd et al., 2018), it would be inconsistent to initialize our model by running it towards equilibrium over several thousand years applying constant present-day climate forcing. We hence reduced temperatures in the Amundsen Sea to “cold” conditions (−1.25 ∘C; Jenkins et al., 2018).
Ocean temperature and salinity forcing is calculated from CMIP5 models using an anomaly approach as suggested for ISMIP6 (Barthel et al., 2020; Jourdain et al., 2019). We average these values over 400 to 800 m depth to obtain suitable input for PICO. The historic forcing is based on NorESM1-M (as suggested for ISMIP6) and anomalies are normalized to the initial period (here 1850–1900), similar to the atmosphere forcing. A new ocean climatology for the experiments starting from the historic simulation is obtained from the 1995 to 2014 average conditions.
For LARMIP-2, we add melt rate anomalies to the underlying PICO melt rates in different Antarctic regions as described in Levermann et al. (2020). Using linear response theory, the probability distribution of the sea level contribution for RCP8.5 is then calculated following the LARMIP-2 protocol.
We present here (1) the results for the two initial configurations submitted to ISMIP6 and (2) the sea level estimates for RCP8.5 obtained following the LARMIP-2 and ISMIP6 experiments based on the historic configuration.
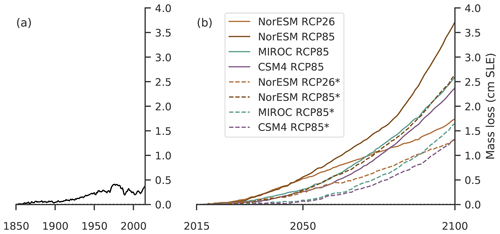
Figure 1Historic simulation and projections of the Antarctic Ice Sheet driven by ISMIP6 ocean forcing. Shown is the evolution of the sea level contribution (a) for the historic simulation relative to its control simulation and (b) for the projections with respect to the control simulations, in centimeters of sea level equivalent (SLE). Experiments are initialized either from a historic run (solid lines) or from the initial state (dashed lines) and forced with changes in ocean temperature and salinity from ISMIP6 experiment nos. 1 to 4 with the respective CMIP5 model indicated in the legend.
3.1 Initial configurations and historic simulation
The two initial configurations for 2015, one based on a pseudo-equilibrium and one on a historic simulation from 1850 to 2014, do not differ much in terms of state variables such as ice thickness, volume or speed (see Sect. 2.1). However, the configurations have opposed change rates: INIT* has a small tendency to gain mass and INIT is clearly out of balance and loses mass (compare the control simulations in Table 1). Over the historic period, the ice sheet thins along its margins through increased sub-shelf melting and at the same time thickens in the interior due to more snowfall. These signals are smaller than 50 m over grounded regions; see Fig. S2. The thinning of ice shelves around the margins and subsequent reduction of buttressing cause the ice streams and ice shelves to slightly speed up over the historic simulation. The sensitivity of the modeled ice thickness and velocities to the historic forcing is smaller than the sensitivity to different parameters in the initial ensemble; see Fig. S1. Overall, continent-wide aggregated basal mass balance decreases more strongly than the aggregated surface mass balance increases, leading to mass loss of 3.6 mm SLE between 1850 and 2014 in comparison to the historic control simulation; see Figs. 1 and S3. This is smaller than the observed mass loss of 7.6±3.9 mm SLE between 1992 and 2017 (Shepherd et al., 2018).
Table 1Mass loss and evolution of surface and basal mass balance in ISMIP6 simulations. All values, except for the ctrl simulations, are relative to the respective control simulation.
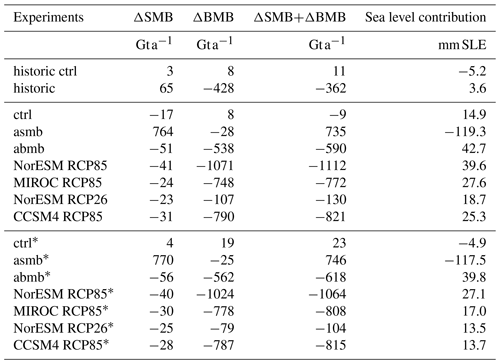
Experiments without the historic run are indicated by *. Changes in basal and surface mass balance from the first to the last time steps in the experiments (i.e., from 1850 to 2014 in the historic run and from 2015 to 2100 in the other experiments).
The patterns of present-day thickness changes (here 2014) are more realistic in the historic configuration INIT than for the pseudo-equilibrium state INIT*. Furthermore, the highest mass losses are simulated in the Amundsen Sea and Totten regions, which agrees with observations (Shepherd et al., 2018). Both initial configurations are further compared to other model configurations and to present-day ice thickness and velocities in Seroussi et al. (2020).
3.2 Comparison to initMIP Antarctica
Results from the idealized surface mass balance experiment “asmb” as described in initMIP Antarctica (Seroussi et al., 2019) are very similar for initial states with both 119 mm SLE of mass gains for the “historic” configuration INIT and 118 mm SLE for the “cold-start” configuration INIT* after 85 years of simulation with respect to the control simulations; see Table 1. This is close to the response of the different models that participated in initMIP Antarctica which showed mass gains between 125 and 186 mm SLE after 100 years.
For the idealized basal melt rate experiment “abmb” from initMIP Antarctica, both states are also quite similar with mass loss of 43 and 40 mm SLE after 85 years; see Table 1. In comparison, in Seroussi et al. (2019) a model spread of 13 to 427 mm SLE after 100 years is reported. Results for both configurations presented here are close to the median of model results for both experiments tested in initMIP Antarctica.
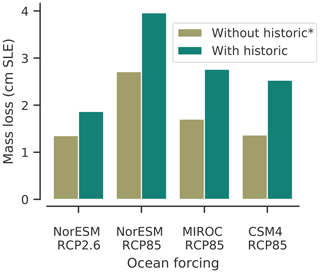
Figure 2A preceding historic simulation increases the susceptibility of the ice sheet to ocean forcing in projections. Shown is the mass loss in simulations started directly from the initial state compared to simulations based on a historic run. The mass loss in 2100 is given with respect to the control simulation, after 85 years of applying the ocean forcing from ISMIP6 experiment nos. 1 to 4 with the respective emission scenario/CMIP5 model indicated on the x axis.
3.3 ISMIP6 ocean-forcing experiments
We here compare simulations for both initial configurations that are driven by ocean forcing from the ISMIP6 experiment nos. 1 to 4 (see Sect. 3.3; Seroussi et al., 2020). In general, the ice sheet's mass loss increases with stronger ocean forcing as projected for RCP8.5 in comparison to RCP2.6; see Fig. 1. The highest losses for RCP8.5 are found for NorESM1-M. The magnitude of mass loss ranges from 1.4 to 4.0 cm SLE in comparison to the control simulation, which is substantially smaller than previous estimates of Antarctica's sea level contribution (e.g., DeConto and Pollard, 2016; Golledge et al., 2019; Edwards et al., 2019) or expert judgment (Bamber et al., 2019). Furthermore, we find that the historic simulation makes the configuration more susceptible to ocean forcing; see Fig. 2. Ocean-driven mass loss in comparison to the control run is increased by about 50 % (factor of 1.5) when starting from the historic simulation in contrast to the cold-start simulation.
3.4 LARMIP-2 basal melt rate forcing experiments
In LARMIP-2, sea level probability distributions from the Antarctic Ice Sheet are derived using linear response functions as described in Levermann et al. (2020). The response functions are derived from experiments in which constant basal melt rate forcing is applied for five different regions of Antarctica. We here perform the same experiments for both configurations described in Sect. 2.
We find that for all regions the ice sheet response compares with the responses found in LARMIP-2 as, for example, in the PISM-PIK contribution that is based on a different initial state with 4 km horizontal resolution and that does not apply subgrid melting; compare Fig. 3 with Fig. 4 from Levermann et al. (2020). A detailed comparison of both PISM-PIK contributions is given in Table S2. Similar to the ISMIP6 simulations, the experiments show different responses for the two initial configurations, especially in the Weddell Sea, East Antarctica and Amundsen Sea regions. The overall difference is smaller than in the ISMIP6 experiments for the stronger forcing applied here.
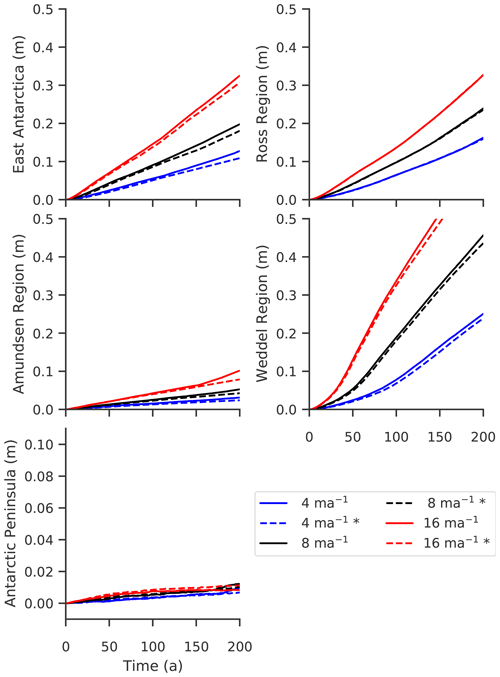
Figure 3Mass loss of the different regions in Antarctica (indicated on the y axis) driven by constant LARMIP-2 basal melt rate forcing. For the experiments from the LARMIP-2 protocol we show the changes in volume above flotation initialized from a historic simulation (solid line) and from the initial state directly (dashed line, indicated by *). Mass loss is shown relative to the respective control simulation. From the response of the ice sheet to a constant melt rate forcing over 200 years, a response function is derived which then serves to emulate the sea level contribution under various climate scenarios. This figure is similar to Fig. 4 in Levermann et al. (2020).
Table 2Percentiles of the probability distribution of the sea level contribution from Antarctica under the RCP8.5 climate scenario from 2015 to 2100, estimated following the LARMIP-2 protocol.
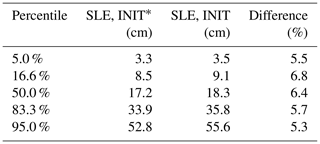
Following the procedure in LARMIP-2, we derive response functions from the idealized experiments for the five Antarctic regions. We then convolve the response function with basal melt rate forcing, given in Fig. 4, to obtain a probability distribution of the future sea level contribution for RCP8.5 which is given in Fig. 5. The ocean-driven mass loss from 2015 to 2100 has a very likely range of 3.5 to 55.6 cm SLE, a likely range of 9.1 to 35.8 cm SLE and a median of 18.3 cm SLE (percentiles 5 to 95, 16.6 to 83.3, and 50, respectively; see Table 2). Similar to the ISMIP6 simulations, these results obtained for the historic initial configuration are larger than the results for the steady-state configuration, with increases between 5 % and 7 %. In comparison, the PISM-PIK contribution of LARMIP-2 has a very likely range of 7 to 48 cm SLE, a likely range of 11 to 31 cm SLE and a median of 19 cm SLE for the 21st century. The resulting sea level probability distribution is hence in line with the estimates presented in LARMIP-2.
In the following, we compare the results found in the ISMIP6 and LARMIP-2 experiments and discuss the role of the ocean forcing and of the historic simulation.
4.1 Comparison of LARMIP-2 and ISMIP6 sea level projections
The projected mass loss in LARMIP-2 is an order of magnitude larger than the ocean-driven mass loss in our ISMIP6 experiments for RCP8.5; see Sect. 3. In order to understand this difference better, we here investigate the ocean forcing in more detail.
Both intercomparison projects, ISMIP6 and LARMIP-2, are based on CMIP5 model subsurface ocean temperature changes (Levermann et al., 2014; Barthel et al., 2020; Jourdain et al., 2019). While they are directly applied in ISMIP6, they are used to derive a scaling between global mean temperatures and Antarctic subsurface temperatures in LARMIP-2. While minor differences in ocean forcing might occur due to different processing steps, a more significant difference is that the LARMIP-2 experiments are driven by basal melt rate changes emulated from the forcing, while in the ISMIP6 simulations ocean forcing is translated into basal melt rates via sub-shelf melt parameterizations, in our case PICO.
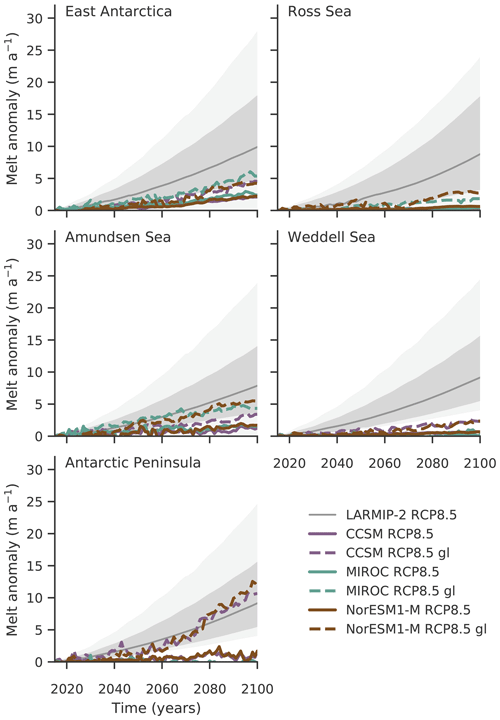
Figure 4Projected basal melt rate changes in the different Antarctic regions from LARMIP-2 and in the ISMIP6 contribution forced with NorESM1-M, CCSM and MIROC ocean changes under RCP8.5. In LARMIP-2 spatially constant basal melt rate forcing is applied with corresponding very likely ranges (5th to 95th percentiles, light gray shading), likely ranges (66th percentile around the median, dark gray shading) and median (gray line) for the RCP8.5 scenario. In the ISMIP6 contribution, basal melt rates are calculated by PICO, which shows higher increases close to the grounding line (PICO box 1, indicated by “gl”) than averaged over the ice shelves. Figure is similar to Fig. 3 in Levermann et al. (2020).
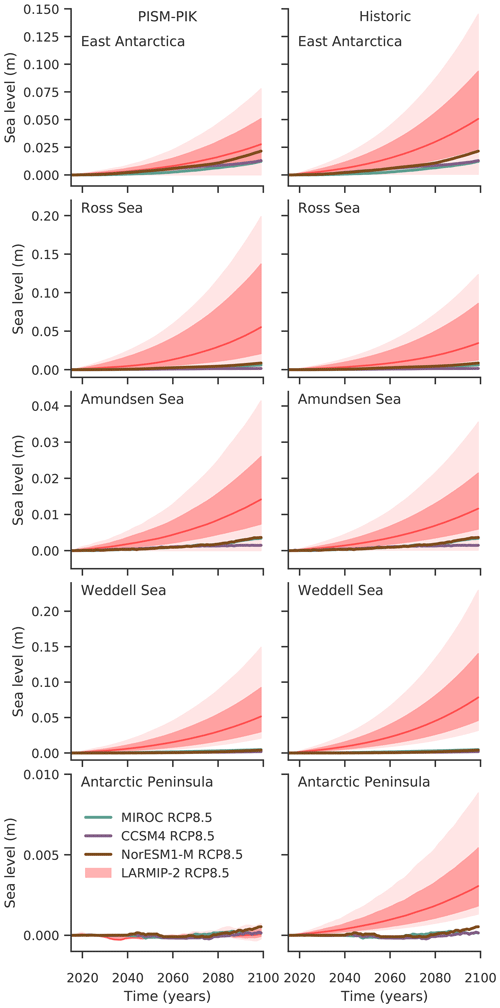
Figure 5Projections of Antarctica’s sea level contribution under the RCP8.5 climate scenario for the different Antarctic regions for LARMIP-2 and for the ISMIP6 experiments driven by NorESM1-M, MIROC and CCSM4 ocean forcing. The very likely ranges (5th to 95th percentiles, light red shading), likely ranges (percentiles 16.6 to 83.3, dark red shading) and the respective median (50th percentile, red lines) of mass loss are shown for (left panels) the PISM-PIK simulations submitted to LARMIP-2 (Levermann et al., 2020) and for comparison (right panels) estimated following LARMIP-2 for the setup as submitted to ISMIP6.
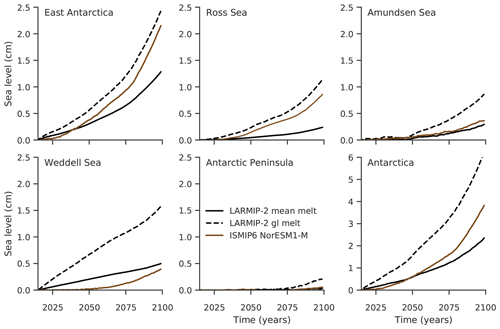
Figure 6Projections using PICO forced with NorESM1-M ocean conditions compared to projection obtained by the response function. The response function is derived for the INIT configuration. It is applied to the basal melt rate forcing from PICO using average conditions underneath the shelves in the corresponding sector (generally an underestimation) and using the melting at the grounding line (generally an overestimation) from Fig. 4.
Figure 4 shows projected basal melt rates and their uncertainty ranges for RCP8.5 used in LARMIP-2 together with the basal melt rate changes in the ISMIP6 simulations. Note that LARMIP-2 assumes constant changes in basal melt rates over the entire ice shelf. In contrast, since PICO mimics the vertical overturning circulation in ice-shelf cavities, basal melt rates in the ISMIP6 simulations increase more strongly along the grounding line (in PICO's first box) and less towards the ice shelf front. The melt rate changes in PICO along the grounding line are hence an upper limit for the comparison to the LARMIP-2 forcing while the shelf-wide averaged changes provide a lower limit. Overall, we find that in the ISMIP6 simulations, basal melt rates increase more in regions with smaller ice shelves than in the Ross and Weddell seas. Furthermore, we find that the basal melt rate changes in our ISMIP6 contribution in all Antarctic regions are located in the lower range (percentiles) of the LARMIP-2 forcing. Only for the Antarctic Peninsula do PICO melt rates along the grounding line increase more strongly than the median in LARMIP-2 for NorESM1-M and MIROC. For all other regions, melt rate changes along the grounding line are smaller than the median in LARMIP-2 (50th percentile). For the Amundsen Sea region, they lie within the likely range (percentiles 16.6 to 83.3). For East Antarctica and the Ross Sea, they are around the lower margin of the likely range, and for the Weddell Sea, they are lower than the very likely range (5th to 95th percentiles). Shelf-wide changes are generally smaller than the likely range; for the Weddell Sea and the Antarctic Peninsula they are also smaller than the very likely range.
This is consistent with the mass loss in the ISMIP6 simulations being lower than the likely range of LARMIP-2 for almost all regions; see Fig. 5. These findings are underlined by the direct comparison with the PISM-PIK contribution to LARMIP-2 which is based on a different initial setup; see Sect. 3.4. Note that basal melt rate changes in East Antarctica seem similar in Fig. 4 for NorESM1-M and MIROC but mass loss is higher for NorESM1-M, because the ocean forcing in the ISMIP6 simulations varies across the different ice shelves in East Antarctica. While there is stronger ocean warming in Dronning Maud Land and Amery in the MIROC forcing, the ocean warms substantially more in the Totten region for NorESM1-M. The higher vulnerability of the Totten region then causes higher overall mass loss.
In Fig. 6 we assess for each region the mass loss by applying the response functions to the corresponding PICO melt rate changes driven by NorESM1-M ocean forcing, once averaged over the entire ice shelves and once close to the grounding lines. When comparing the respective mass loss with the ISMIP6 simulation, we find that indeed the changes at the grounding line provide an upper limit while the changes over the entire ice shelf provide a lower limit for the actual mass loss.
Overall, we find that mass losses in the ISMIP6 projections are generally lower than the likely range in LARMIP-2, and in the Weddell Sea losses are smaller than the very likely range, as the basal melt rate changes in the LARMIP experiments are an order of magnitude higher than those estimated with PICO and ISMIP6 forcing.
4.2 Role of ocean forcing and basal melt rate sensitivity
In order to gain a better understanding of the conversion of ocean forcing to basal melt rates in LARMIP-2 and in our ISMIP6 contribution, we further analyze the sensitivity to ocean warming.
We perform step-forcing experiments for both initial configurations and diagnose the effect on basal melt rates; see Fig. 7. Ocean temperatures are increased by and 4 ∘C, and the corresponding basal melt rates for constant ice-shelf geometries are diagnosed using PICO. We find that the sensitivity in the Amundsen Sea region is comparatively high with about 10 , while the sensitivity in the Weddell Sea is lower with about 1.5 , which yields for the entire Antarctic ice shelves an overall sensitivity of about 2.2 . The sensitivities for melting close to the grounding line are as expected a bit higher: 10.5 for the Amundsen Sea region, 3.9 for the Weddell Sea and 5.3 on average for all Antarctic ice shelves. In both cases, the Antarctic-wide sensitivity is substantially lower than the sensitivity used in LARMIP-2. In the latter study, a sensitivity between 7 and 16 , based on Jenkins (1991) and Payne et al. (2007), is assumed to translate ocean forcing into sub-shelf melt rates. This is consistent with our findings in the previous section that in the ISMIP6 simulations mass loss from the Antarctic Ice Sheet, and especially from the regions that drain the large Filchner–Ronne and Ross ice shelves, is smaller than the likely range estimated following the LARMIP-2 protocol. Jourdain et al. (2019) report that a different tuning of the ISMIP6 basal melt parameterization to fit observations in the Amundsen Sea (from Dutrieux et al., 2014; Jenkins et al., 2018) substantially increases the sensitivity to ocean changes and Seroussi et al. (2020) find that this enhances the sea level contribution by a factor of 6.
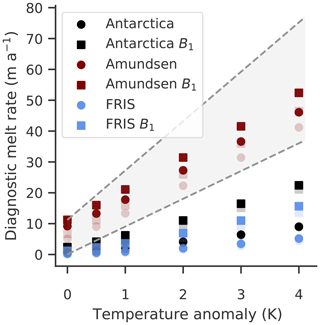
Figure 7Sensitivity of basal melt rates to ocean temperatures in PICO. Diagnosed from the historic configuration (opaque) and the cold-start configuration (transparent) in 2015 using step-wise ocean temperature increases. Dots show shelf-wide averages while boxes indicate the basal melt rates close to the grounding lines (in PICO box B1). The dashed gray lines indicate the sensitivity estimates used in Levermann et al. (2020).
Since the sensitivity in PICO depends on the parameters used, with the overturning coefficient C affecting the sensitivity in large ice shelves and the heat exchange coefficient γT affecting the sensitivity in small ice shelves, a different tuning could improve basal melt rate sensitivities and thereby lead to higher mass losses in the ISMIP6 experiments. A consistency of sub-shelf melt rates with present-day observations could be achieved by introducing additional degrees of freedom through temperature corrections that reflect uncertainties in ocean properties, as for example used in Lazeroms et al. (2018) and Jourdain et al. (2019). In addition, tuning to realistic melt rates close to the grounding lines (in PICO's first box) is potentially more important than fitting shelf-wide melt rates (e.g., Goldberg et al., 2019; Reese et al., 2018b).
Few observations exist for targeted tuning of the sensitivity of basal melt rate parameterizations to ocean temperatures; hence the use of dynamic modeling of the ocean circulation in ice-shelf cavities could be explored. We estimate that the sensitivity in Seroussi et al. (2017) varies between 6 and 16 with an average of 9.4 over the first 20 years of model simulation, which would be in line with the sensitivities used in LARMIP-2; see Fig. S5.
Note that we provide linear estimates of the sensitivity of PICO in the discussion above, while Holland et al. (2008) report a quadratic dependency of melt rates on thermal forcing. They also discuss that the sensitivity depends on ice shelf cavity properties such as the slope of the ice-shelf draft and shape of the ice shelf and that sensitivities are generally higher close to the grounding line. Further factors that influence ocean circulation, such as bathymetry, also affect the ocean sensitivity. While PICO takes into account that not all heat content of the ocean water masses that enter the cavity might be used for melting, it does not capture three-dimensional circulations in ice-shelf cavities that play a role in particular for larger ice shelves such as Filchner–Ronne.
4.3 Role of historic trajectory of the Antarctic Ice Sheet
We find that while the historic simulation has no large effect on the initial sea level volume (the overall difference being 1.6 mm SLE), it affects the mass loss in the projections. A number of reasons might cause the simulations starting from the historic configuration (INIT) to be more vulnerable to ocean forcing: both simulations have different initial trends of the sea level relevant volume and rates of ice thickness change. These trends, or the different geometry after the historic simulation, might make the configuration more susceptible to ocean forcing, for example through nonlinear changes in ice-shelf buttressing. In addition, the historic simulation might have pushed the ice sheet (closer) to a local instability that evolves in the projections. Figure S6 shows the mass loss rates for all simulations presented in Sect. 3.3. In general, the rates are higher in the simulations based on the historic configuration, and these differences increase over time. In the RCP8.5 simulation forced with NorESM1-M ocean conditions, at around year 2075 a clear shift to substantially higher differences is visible. We hypothesize that this could be linked to a local instability that is kicked off for the simulations starting from the historic configuration but not for those starting from the pseudo-steady state. This is less pronounced for CCSM4 and MIROC, maybe due to differences in the ocean forcing and regions contributing to sea level rise. In the idealized experiments for LARMIP-2 (Fig. 3), differences in simulations starting from the two initial states arise in particular in East Antarctica, the Weddell Sea and the Amundsen Sea, less in the Ross Sea. The effect of the historic simulation is reduced for the stronger basal melt rate forcing applied in the LARMIP-2 experiments, with mass loss increases in the projections between 5 % and 7 %.
Furthermore, the ice sheet's response might have changed after the historic simulation due to changes in boundary conditions. Moreover, changes in the ice sheet state could result since, for instance, the underlying equation system depends nonlinearly on the three-dimensional temperature field. The grounding line retreats slightly into deeper regions during the historic simulation, where the local freezing point at the ice shelf base near the grounding line is decreased due to its pressure dependence. Hence more heat is available for melting the ice-shelf base, which also shows an increased sensitivity to ocean changes; see Fig. 7. In particular for lower temperatures, PICO shows a nonlinear sensitivity of melt rates to ocean temperatures, as discussed in Reese et al. (2018a). Further investigations would be required to disentangle the reasons for the increased susceptibility to ocean warming after the historic simulation, also considering the strength of the forcing applied.
The sea level contribution over the historic period from 1850 to 2014 is 3.6 mm in comparison to the control simulation. This is smaller than the reported mass loss of the Antarctic Ice Sheet that amounts to 7.6±3.0 mm SLE between 1992 and 2017 (Shepherd et al., 2018). An improved understanding of the basal melt rate sensitivity, potential biases in the atmospheric or oceanic forcing, and an extension of the scoring with observed patterns of thickness changes would allow for performing “hindcasting” experiments that, in a next step, could inform future projections.
In this study we compare sea level projections for RCP8.5 from the Antarctic Ice Sheet as submitted to ISMIP6, using the PICO basal melt rate parameterization and constant surface mass balance forcing, and projections derived following the LARMIP-2 protocol that scales global temperatures to subsurface temperatures and melt rates, both using the Parallel Ice Sheet Model. Overall, we find that the sea level contribution driven by ocean forcing in ISMIP6 is smaller than the likely range of the sea level probability distribution in LARMIP-2. This difference can be explained by the comparably low sensitivity of melt rates to ocean temperature changes for the parameter tuning in PICO in comparison to LARMIP-2 where a sensitivity of 7 to 16 is used that we found to be consistent with a coupled simulation of Thwaites glacier (Seroussi et al., 2017). Future sea level projections should hence carefully consider the sensitivity of basal melt rates to ocean changes. Additional observations of ocean conditions and ocean-induced melt rates in combination with ocean modeling are needed to better constrain this sensitivity for the diverse ice-shelf cavities in Antarctica. Furthermore, we find that while the initial state resulting from a historic simulation from 1850 to 2014 is virtually indistinguishable from a steady-state simulation, the historic simulation increases the projected mass loss in 2100 by up to 50 %. This means that not only the currently committed sea level contribution in projections but also the effect of the historic forcing on the ice sheet's susceptibility to ocean changes should be considered. Hindcasting experiments, which reproduce observed thinning rates and ice loss over the past decades, would be valuable to better constrain model parameters and improve confidence in projections. Hence, further investigations are needed to assess the sensitivity of basal melting to ocean temperatures for basal melt parameterizations and the role of historical forcing and initial conditions in future sea level projections.
Model outputs from the simulations for ISMIP6 described in this paper as well as forcing datasets will be made available via the ISMIP6 project with a digital object identifier (Nowicki et al., 2020). LARMIP-2 code and data are available via the project (Levermann et al., 2020). The PISM code, the PISM simulations and the scripts to analyze the simulations and create the figures are available at https://doi.org/10.5281/zenodo.3903343 (Reese et al., 2020). The processing of the World Ocean Atlas pre-release data is described in the Bachelor thesis by Lena Nicola (2019) and will be shared upon request.
The supplement related to this article is available online at: https://doi.org/10.5194/tc-14-3097-2020-supplement.
RR and AL designed the study. All authors contributed to the interpretation of the results. RR performed the model simulations and carried out the analysis. AL calculated the response function and provided data for the LARMIP-2 comparison. TA and RR developed the scoring scheme for the PISM simulations. HS analyzed the melt sensitivity in the coupled simulations. RR prepared the manuscript with contributions from all authors.
Helene Seroussi is an editor of the special issue “The Ice Sheet Model Intercomparison Project for CMIP6 (ISMIP6)”. The authors declare that no other competing interests are present.
This article is part of the special issue “The Ice Sheet Model Intercomparison Project for CMIP6 (ISMIP6)”. It is not associated with a conference.
We thank the Climate and Cryosphere (CliC) effort, which provided support for ISMIP6 through sponsoring of workshops, hosting the ISMIP6 website and wiki, and promoting ISMIP6. We acknowledge the World Climate Research Programme, which, through its Working Group on Coupled Modelling, coordinated and promoted CMIP5. We thank the climate modeling groups for producing and making available their model output, the Earth System Grid Federation (ESGF) for archiving the CMIP data and providing access, the University at Buffalo for ISMIP6 data distribution and upload, and the multiple funding agencies who support CMIP5 and ESGF. We thank the ISMIP6 steering committee, the ISMIP6 model selection group and the ISMIP6 dataset preparation group for their continuous engagement in defining ISMIP6. This is ISMIP6 contribution no. 15. Development of PISM is supported by NASA grant NNX17AG65G and NSF grants PLR-1603799 and PLR-1644277. The authors gratefully acknowledge the European Regional Development Fund (ERDF), the German Federal Ministry of Education and Research and the Land Brandenburg for supporting this project by providing resources for the high-performance computer system at the Potsdam Institute for Climate Impact Research. Computer resources for this project have also been provided by the Gauss Centre for Supercomputing, Leibniz Supercomputing Centre (http://www.lrz.de, last access: 16 July 2020) under project IDs pr94ga and pn69ru. Ronja Reese is supported by the Deutsche Forschungsgemeinschaft (DFG) by grant WI4556/3-1 and through the TiPACCs project that receives funding from the European Union’s Horizon 2020 Research and Innovation program under grant agreement no. 820575. Torsten Albrecht is supported by the Deutsche Forschungsgemeinschaft (DFG) in the framework of the priority program “Antarctic Research with comparative investigations in Arctic ice areas” by grants WI4556/2-1 and WI4556/4-1 and in the framework of the PalMod project (FKZ: 01LP1925D), supported by the German Federal Ministry of Education and Research (BMBF) as a Research for Sustainability initiative (FONA). Hélène Seroussi was supported by grants from NASA's Cryospheric Science and Modeling, Analysis, Predictions programs.
We would like to thank the anonymous reviewers for their helpful comments on the manuscript and the editor Douglas Brinkerhoff for handling the review process. We are grateful to Matthias Mengel for supporting the development of the scoring scheme and PISM analysis tools as well as Lena Nicola for providing the processed ocean input data.
This research has been supported by the Deutsche Forschungsgemeinschaft (DFG) (grant nos. WI4556/3-1, WI4556/2-1, and WI4556/4-1), the NASA (grant no. NNX17AG65G), the NSF (grant nos. PLR-1603799 and PLR-1644277), and the Gauss Centre for Supercomputing/Leibniz Supercomputing Centre (grant nos. pr94ga and pn69ru).
The publication of this article was funded by the
Open Access Fund of the Leibniz Association.
This paper was edited by Douglas Brinkerhoff and reviewed by two anonymous referees.
Albrecht, T., Winkelmann, R., and Levermann, A.: Glacial-cycle simulations of the Antarctic Ice Sheet with the Parallel Ice Sheet Model (PISM) – Part 2: Parameter ensemble analysis, The Cryosphere, 14, 633–656, https://doi.org/10.5194/tc-14-633-2020, 2020. a
Bamber, J. L., Oppenheimer, M., Kopp, R. E., Aspinall, W. P., and Cooke, R. M.: Ice sheet contributions to future sea-level rise from structured expert judgment, P. Natl. Acad. Sci. USA, 116, 11195–11200, 2019. a
Barthel, A., Agosta, C., Little, C. M., Hattermann, T., Jourdain, N. C., Goelzer, H., Nowicki, S., Seroussi, H., Straneo, F., and Bracegirdle, T. J.: CMIP5 model selection for ISMIP6 ice sheet model forcing: Greenland and Antarctica, The Cryosphere, 14, 855–879, https://doi.org/10.5194/tc-14-855-2020, 2020. a, b, c
Bentsen, M., Bethke, I., Debernard, J. B., Iversen, T., Kirkevåg, A., Seland, Ø., Drange, H., Roelandt, C., Seierstad, I. A., Hoose, C., and Kristjánsson, J. E.: The Norwegian Earth System Model, NorESM1-M – Part 1: Description and basic evaluation of the physical climate, Geosci. Model Dev., 6, 687–720, https://doi.org/10.5194/gmd-6-687-2013, 2013. a, b
Bronselaer, B., Winton, M., Griffies, S. M., Hurlin, W. J., Rodgers, K. B., Sergienko, O. V., Stouffer, R. J., and Russell, J. L.: Change in future climate due to Antarctic meltwater, Nature, 564, 53–58, https://doi.org/10.1038/s41586-018-0712-z, 2018. a
Bueler, E. and Brown, J.: Shallow shelf approximation as a “sliding law” in a thermomechanically coupled ice sheet model, J. Geophys. Res., 114, F03008, https://doi.org/10.1029/2008JF001179, 2009. a
Bueler, E. and van Pelt, W.: Mass-conserving subglacial hydrology in the Parallel Ice Sheet Model version 0.6, Geosci. Model Dev., 8, 1613–1635, https://doi.org/10.5194/gmd-8-1613-2015, 2015. a
DeConto, R. M. and Pollard, D.: Contribution of Antarctica to past and future sea-level rise, Nature, 531, 591–597, https://doi.org/10.1038/nature17145, 2016. a, b, c
Donat-Magnin, M., Jourdain, N. C., Spence, P., Le Sommer, J., Gallée, H., and Durand, G.: Ice-Shelf Melt Response to Changing Winds and Glacier Dynamics in the Amundsen Sea Sector, Antarctica, J. Geophys. Res.-Oceans, 122, 10206–10224, 2017. a
Dutrieux, P., De Rydt, J., Jenkins, A., Holland, P. R., Ha, H. K., Lee, S. H., Steig, E. J., Ding, Q., Abrahamsen, E. P., and Schröder, M.: Strong sensitivity of Pine Island ice-shelf melting to climatic variability, Science, 343, 174–178, 2014. a
Edwards, T. L., Brandon, M. A., Durand, G., Edwards, N. R., Golledge, N. R., Holden, P. B., Nias, I. J., Payne, A. J., Ritz, C., and Wernecke, A.: Revisiting Antarctic ice loss due to marine ice-cliff instability, Nature, 566, 58–64, 2019. a
Favier, L., Jourdain, N. C., Jenkins, A., Merino, N., Durand, G., Gagliardini, O., Gillet-Chaulet, F., and Mathiot, P.: Assessment of sub-shelf melting parameterisations using the ocean–ice-sheet coupled model NEMO(v3.6)–Elmer/Ice(v8.3) , Geosci. Model Dev., 12, 2255–2283, https://doi.org/10.5194/gmd-12-2255-2019, 2019. a
Feldmann, J., Albrecht, T., Khroulev, C., Pattyn, F., and Levermann, A.: Resolution-dependent performance of grounding line motion in a shallow model compared with a full-Stokes model according to the MISMIP3d intercomparison, J. Glaciol., 60, 353–360, https://doi.org/10.3189/2014JoG13J093, 2014. a
Fretwell, P., Pritchard, H. D., Vaughan, D. G., Bamber, J. L., Barrand, N. E., Bell, R., Bianchi, C., Bingham, R. G., Blankenship, D. D., Casassa, G., Catania, G., Callens, D., Conway, H., Cook, A. J., Corr, H. F. J., Damaske, D., Damm, V., Ferraccioli, F., Forsberg, R., Fujita, S., Gim, Y., Gogineni, P., Griggs, J. A., Hindmarsh, R. C. A., Holmlund, P., Holt, J. W., Jacobel, R. W., Jenkins, A., Jokat, W., Jordan, T., King, E. C., Kohler, J., Krabill, W., Riger-Kusk, M., Langley, K. A., Leitchenkov, G., Leuschen, C., Luyendyk, B. P., Matsuoka, K., Mouginot, J., Nitsche, F. O., Nogi, Y., Nost, O. A., Popov, S. V., Rignot, E., Rippin, D. M., Rivera, A., Roberts, J., Ross, N., Siegert, M. J., Smith, A. M., Steinhage, D., Studinger, M., Sun, B., Tinto, B. K., Welch, B. C., Wilson, D., Young, D. A., Xiangbin, C., and Zirizzotti, A.: Bedmap2: improved ice bed, surface and thickness datasets for Antarctica, The Cryosphere, 7, 375–393, https://doi.org/10.5194/tc-7-375-2013, 2013. a, b, c
Frieler, K., Clark, P. U., He, F., Buizert, C., Reese, R., Ligtenberg, S. R., Van Den Broeke, M. R., Winkelmann, R., and Levermann, A.: Consistent evidence of increasing Antarctic accumulation with warming, Nat. Clim. Change, 5, 348–352, https://doi.org/10.1038/nclimate2574, 2015. a
Gent, P. R., Danabasoglu, G., Donner, L. J., Holland, M. M., Hunke, E. C., Jayne, S. R., Lawrence, D. M., Neale, R. B., Rasch, P. J., Vertenstein, M., Worley, Z.-L., and Yang, M. Z.: The community climate system model version 4, J. Climate, 24, 4973–4991, 2011. a
Goldberg, D., Gourmelen, N., Kimura, S., Millan, R., and Snow, K.: How accurately should we model ice shelf melt rates?, Geophys. Res. Lett., 46, 189–199, 2019. a
Golledge, N. R., Keller, E. D., Gomez, N., Naughten, K. A., Bernales, J., Trusel, L. D., and Edwards, T. L.: Global environmental consequences of twenty-first-century ice-sheet melt, Nature, 566, 65–72, https://doi.org/10.1038/s41586-019-0889-9, 2019. a, b, c
Hellmer, H. H., Kauker, F., Timmermann, R., Determann, J., and Rae, J.: Twenty-first-century warming of a large Antarctic ice-shelf cavity by a redirected coastal current, Nature, 485, 225–228, https://doi.org/10.1038/nature11064, 2012. a, b
Holland, P. R., Jenkins, A., and Holland, D. M.: The Response of Ice Shelf Basal Melting to Variations in Ocean Temperature, J. Climate, 21, 2558–2572, https://doi.org/10.1175/2007JCLI1909.1, 2008. a, b
Hutter, K. E.: Theoretical glaciology: material science of ice and the mechanics of glaciers and ice sheets, Springer, vol. 1, 1983. a
Iversen, T., Bentsen, M., Bethke, I., Debernard, J. B., Kirkevåg, A., Seland, Ø., Drange, H., Kristjansson, J. E., Medhaug, I., Sand, M., and Seierstad, I. A.: The Norwegian Earth System Model, NorESM1-M – Part 2: Climate response and scenario projections, Geosci. Model Dev., 6, 389–415, https://doi.org/10.5194/gmd-6-389-2013, 2013. a
Jacobs, S., Hellmer, H., Doake, C. S. M., Jenkins, A., and Frolich, R. M.: Melting of ice shelves and the mass balance of Antarctica, J. Glaciol., 38, 375–387, https://doi.org/10.3189/S0022143000002252, 1992. a
Jenkins, A.: Ice shelf basal melting: Implications of a simple mathematical model, Filchner-Ronne Ice Shelf Programme Report, 5, 32–36, 1991. a, b
Jenkins, A., Shoosmith, D., Dutrieux, P., Jacobs, S., Kim, T. W., Lee, S. H., Ha, H. K., and Stammerjohn, S.: West Antarctic Ice Sheet retreat in the Amundsen Sea driven by decadal oceanic variability, Nat. Geosci., 11, 733–738, https://doi.org/10.1038/s41561-018-0207-4, 2018. a, b
Jourdain, N. C., Asay-Davis, X., Hattermann, T., Straneo, F., Seroussi, H., Little, C. M., and Nowicki, S.: A protocol for calculating basal melt rates in the ISMIP6 Antarctic ice sheet projection, The Cryosphere, 14, 3111–3134, https://doi.org/10.5194/tc-14-3111-2020, 2020. a, b, c, d, e, f
Konrad, H., Shepherd, A., Gilbert, L., Hogg, A. E., McMillan, M., Muir, A., and Slater, T.: Net retreat of Antarctic glacier grounding lines, Nat. Geosci., 11, 258–262, 2018. a
Lazeroms, W. M. J., Jenkins, A., Gudmundsson, G. H., and van de Wal, R. S. W.: Modelling present-day basal melt rates for Antarctic ice shelves using a parametrization of buoyant meltwater plumes, The Cryosphere, 12, 49–70, https://doi.org/10.5194/tc-12-49-2018, 2018. a, b
Levermann, A., Albrecht, T., Winkelmann, R., Martin, M. A., Haseloff, M., and Joughin, I.: Kinematic first-order calving law implies potential for abrupt ice-shelf retreat, The Cryosphere, 6, 273–286, https://doi.org/10.5194/tc-6-273-2012, 2012. a
Levermann, A., Winkelmann, R., Nowicki, S., Fastook, J. L., Frieler, K., Greve, R., Hellmer, H. H., Martin, M. A., Meinshausen, M., Mengel, M., Payne, A. J., Pollard, D., Sato, T., Timmermann, R., Wang, W. L., and Bindschadler, R. A.: Projecting Antarctic ice discharge using response functions from SeaRISE ice-sheet models, Earth Syst. Dynam., 5, 271–293, https://doi.org/10.5194/esd-5-271-2014, 2014. a, b
Levermann, A., Winkelmann, R., Albrecht, T., Goelzer, H., Golledge, N. R., Greve, R., Huybrechts, P., Jordan, J., Leguy, G., Martin, D., Morlighem, M., Pattyn, F., Pollard, D., Quiquet, A., Rodehacke, C., Seroussi, H., Sutter, J., Zhang, T., Van Breedam, J., Calov, R., DeConto, R., Dumas, C., Garbe, J., Gudmundsson, G. H., Hoffman, M. J., Humbert, A., Kleiner, T., Lipscomb, W. H., Meinshausen, M., Ng, E., Nowicki, S. M. J., Perego, M., Price, S. F., Saito, F., Schlegel, N.-J., Sun, S., and van de Wal, R. S. W.: Projecting Antarctica's contribution to future sea level rise from basal ice shelf melt using linear response functions of 16 ice sheet models (LARMIP-2), Earth Syst. Dynam., 11, 35–76, https://doi.org/10.5194/esd-11-35-2020, 2020. a, b, c, d, e, f, g, h, i
Ligtenberg, S., Van de Berg, W., Van den Broeke, M., Rae, J., and Van Meijgaard, E.: Future surface mass balance of the Antarctic ice sheet and its influence on sea level change, simulated by a regional atmospheric climate model, Clim. Dynam., 41, 867–884, 2013. a
Locarnini, R. A., Mishonov, A. V., Baranova, O. K., Boyer, T. P., Zweng, M. M., Garcia, H. E., Reagan, J. R., Seidov, D., Weathers, K., Paver, C. R., and Smolyar, I.: World Ocean Atlas 2018, Volume 1: Temperature, NOAA Atlas NESDIS (Vol. 81), 2018. a
MacAyeal, D. R.: Large-scale ice flow over a viscous basal sediment: Theory and application to ice stream B, Antarctica, J. Geophys. Res.-Sol. Ea., 94, 4071–4087, 1989. a
Meinshausen, M., Raper, S. C. B., and Wigley, T. M. L.: Emulating coupled atmosphere-ocean and carbon cycle models with a simpler model, MAGICC6 – Part 1: Model description and calibration, Atmos. Chem. Phys., 11, 1417–1456, https://doi.org/10.5194/acp-11-1417-2011, 2011. a
Morland, L. W.: Unconfined Ice-Shelf Flow, Springer Netherlands, Dordrecht, 99–116, https://doi.org/10.1007/978-94-009-3745-1_6, 1987. a
Naughten, K. A., Meissner, K. J., Galton-Fenzi, B. K., England, M. H., Timmermann, R., and Hellmer, H. H.: Future projections of Antarctic ice shelf melting based on CMIP5 scenarios, J. Climate, 31, 5243–5261, 2018. a, b
Nowicki, S., Goelzer, H., Seroussi, H., Payne, A. J., Lipscomb, W. H., Abe-Ouchi, A., Agosta, C., Alexander, P., Asay-Davis, X. S., Barthel, A., Bracegirdle, T. J., Cullather, R., Felikson, D., Fettweis, X., Gregory, J. M., Hattermann, T., Jourdain, N. C., Kuipers Munneke, P., Larour, E., Little, C. M., Morlighem, M., Nias, I., Shepherd, A., Simon, E., Slater, D., Smith, R. S., Straneo, F., Trusel, L. D., van den Broeke, M. R., and van de Wal, R.: Experimental protocol for sea level projections from ISMIP6 stand-alone ice sheet models, The Cryosphere, 14, 2331–2368, https://doi.org/10.5194/tc-14-2331-2020, 2020. a, b, c
Nowicki, S. M. J., Payne, A., Larour, E., Seroussi, H., Goelzer, H., Lipscomb, W., Gregory, J., Abe-Ouchi, A., and Shepherd, A.: Ice Sheet Model Intercomparison Project (ISMIP6) contribution to CMIP6, Geosci. Model Dev., 9, 4521–4545, https://doi.org/10.5194/gmd-9-4521-2016, 2016. a
Olbers, D. and Hellmer, H.: A box model of circulation and melting in ice shelf caverns, Ocean Dynam., 60, 141–153, https://doi.org/10.1007/s10236-009-0252-z, 2010. a, b
Oppenheimer, M., Glavovic, B. C., Hinkel, J., van de Wal, R., Magnan, A. K., Abd-Elgawad, A., Cai, R., CifuentesJara, M., DeConto, R. M., Ghosh, T., Hay, J., Isla, F., Marzeion, B., Meyssignac, B., and Sebesvari, Z.: Sea Level Rise and Implications for Low-Lying Islands, Coasts and Communities, in: IPCC Special Report on the Ocean and Cryosphere in a Changing Climate, edited by: Pörtner, H.-O., Roberts, D. C., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegría, A., Nicolai, M., Okem, A., Petzold, J., Rama, B., and Weyer N. M., in press, 2020. a
Payne, A. J., Holland, P. R., Shepherd, A. P., Rutt, I. C., Jenkins, A., and Joughin, I.: Numerical modeling of ocean-ice interactions under Pine Island Bay's ice shelf, J. Geophys. Res.-Oceans, 112, c10019, https://doi.org/10.1029/2006JC003733, 2007. a, b
Pollard, D., Chang, W., Haran, M., Applegate, P., and DeConto, R.: Large ensemble modeling of the last deglacial retreat of the West Antarctic Ice Sheet: comparison of simple and advanced statistical techniques, Geosci. Model Dev., 9, 1697–1723, https://doi.org/10.5194/gmd-9-1697-2016, 2016. a
Reese, R., Albrecht, T., Mengel, M., Asay-Davis, X., and Winkelmann, R.: Antarctic sub-shelf melt rates via PICO, The Cryosphere, 12, 1969–1985, https://doi.org/10.5194/tc-12-1969-2018, 2018a. a, b, c, d, e
Reese, R., Gudmundsson, G. H., Levermann, A., and Winkelmann, R.: The far reach of ice-shelf thinning in Antarctica, Nat. Clim. Change, 8, 53–57, 2018b. a
Reese, R., Levermann, A., Albrecht, T., Seroussi, H., Winkelmann, R., Mengel, M., and other PISM authors: Data and code for publication “The role of history and strength of the oceanic forcing in sea level projections from Antarctica with the Parallel Ice Sheet Model” (Version v1) [Data set], Zenodo, https://doi.org/10.5281/zenodo.3903343, 2020. a
Rignot, E., Mouginot, J., and Scheuchl, B.: Ice flow of the Antarctic ice sheet, Science, 333, 1427–1430, 2011. a
Rignot, E., Jacobs, S., Mouginot, J., and Scheuchl, B.: Ice-shelf melting around Antarctica., Science, 341, 266–270, https://doi.org/10.1126/science.1235798, 2013. a
Schmidtko, S., Heywood, K. J., Thompson, A. F., and Aoki, S.: Multidecadal warming of Antarctic waters, Science, 346, 1227–1231, https://doi.org/10.1126/science.1256117, 2014. a, b
Schoof, C.: Ice sheet grounding line dynamics: Steady states, stability, and hysteresis, J. Geophys. Res., 112, F03S28, doi:10.1029/2006JF000664, 2007. a
Seroussi, H., Nakayama, Y., Larour, E., Menemenlis, D., Morlighem, M., Rignot, E., and Khazendar, A.: Continued retreat of Thwaites Glacier, West Antarctica, controlled by bed topography and ocean circulation, Geophys. Res. Lett., 44, 6191–6199, https://doi.org/10.1002/2017GL072910, 2017. a, b
Seroussi, H., Nowicki, S., Simon, E., Abe-Ouchi, A., Albrecht, T., Brondex, J., Cornford, S., Dumas, C., Gillet-Chaulet, F., Goelzer, H., Golledge, N. R., Gregory, J. M., Greve, R., Hoffman, M. J., Humbert, A., Huybrechts, P., Kleiner, T., Larour, E., Leguy, G., Lipscomb, W. H., Lowry, D., Mengel, M., Morlighem, M., Pattyn, F., Payne, A. J., Pollard, D., Price, S. F., Quiquet, A., Reerink, T. J., Reese, R., Rodehacke, C. B., Schlegel, N.-J., Shepherd, A., Sun, S., Sutter, J., Van Breedam, J., van de Wal, R. S. W., Winkelmann, R., and Zhang, T.: initMIP-Antarctica: an ice sheet model initialization experiment of ISMIP6, The Cryosphere, 13, 1441–1471, https://doi.org/10.5194/tc-13-1441-2019, 2019. a, b, c, d
Seroussi, H., Nowicki, S., Payne, A. J., Goelzer, H., Lipscomb, W. H., Abe-Ouchi, A., Agosta, C., Albrecht, T., Asay-Davis, X., Barthel, A., Calov, R., Cullather, R., Dumas, C., Galton-Fenzi, B. K., Gladstone, R., Golledge, N. R., Gregory, J. M., Greve, R., Hatterman, T., Hoffman, M. J., Humbert, A., Huybrechts, P., Jourdain, N. C., Kleiner, T., Larour, E., Leguy, G. R., Lowry, D. P., Little, C. M., Morlighem, M., Pattyn, F., Pelle, T., Price, S. F., Quiquet, A., Reese, R., Schlegel, N.-J., Shepherd, A., Simon, E., Smith, R. S., Straneo, F., Sun, S., Trusel, L. D., Van Breedam, J., van de Wal, R. S. W., Winkelmann, R., Zhao, C., Zhang, T., and Zwinger, T.: ISMIP6 Antarctica: a multi-model ensemble of the Antarctic ice sheet evolution over the 21st century, The Cryosphere, 14, 3033–3070, https://doi.org/10.5194/tc-14-3033-2020, 2020. a, b, c, d, e
Shepherd, A., Ivins, E. R., Rignot, E., Smith, B., Van den Broeke, M. R., Velicogna, I., Whitehouse, P. L., Briggs, K. H., Joughin, I., Krinner, G., Nowicki, S., Payne, A. J., Scambos, T. A., Schlegel, N., A, G., Agosta, C., Ahlstrøm, A. P., Babonis, G., Barletta, V. R., Blazquez, A., Bonin, J., Csatho, B., Cullather, R. I., Felikson, D., Fettweis, X., Forsberg, R., Gallée, H., Gardner, A. S., Gilbert, L., Groh, A., Gunter, B., Hanna, E., Harig, C., Helm, V., Horvath, A., Horwath, M., Khan, S., Kjeldsen, K. K., Konrad, H., Langen, P., Lecavalier, B., Loomis, B., Luthcke, S. B., McMillan, M., Melini, D., Mernild, S., Mohajerani, Y., Moore, P., Mouginot, J., Moyano, G., Muir, A., Nagler, T., Nield, G., Nilsson, J., Noël, B. P. Y., Otosaka, I., Pattle, M. E., Peltier, W. R., Pie, N., Rietbroek, R., Rott, H., Sandberg Sørensen, L., Sasgen, I., Save, H., Scheuchl, B., Schrama, E. J. O., Schröder, L., Seo, K.-W., Simonsen, S., Slater, T., Spada, G., Sutterly, T. C., Talpe, M., Tarasov, L., Van de Berg, W. J., Van der Wal, W., Van Wessem, J. M., Vishwakarma, B. D., Wiese, D., and Wouters, B.: Mass balance of the Antarctic Ice Sheet from 1992 to 2017, Nature, 558, 219–222, https://doi.org/10.1038/s41586-018-0179-y, 2018. a, b, c, d, e
Taylor, K. E., Stouffer, R. J., and Meehl, G. A.: An Overview of CMIP5 and the Experiment Design, B. Am. Meteorol. Soc., 93, 485–498, https://doi.org/10.1175/BAMS-D-11-00094.1, 2012. a
The PISM authors: PISM, a Parallel Ice Sheet Model, available at: http://www.pism-docs.org (last access: 16 July 2020), 2019. a
Timmermann, R. and Goeller, S.: Response to Filchner–Ronne Ice Shelf cavity warming in a coupled ocean–ice sheet model – Part 1: The ocean perspective, Ocean Sci., 13, 765–776, https://doi.org/10.5194/os-13-765-2017, 2017. a
van Wessem, J. M., van de Berg, W. J., Noël, B. P. Y., van Meijgaard, E., Amory, C., Birnbaum, G., Jakobs, C. L., Krüger, K., Lenaerts, J. T. M., Lhermitte, S., Ligtenberg, S. R. M., Medley, B., Reijmer, C. H., van Tricht, K., Trusel, L. D., van Ulft, L. H., Wouters, B., Wuite, J., and van den Broeke, M. R.: Modelling the climate and surface mass balance of polar ice sheets using RACMO2 – Part 2: Antarctica (1979–2016), The Cryosphere, 12, 1479–1498, https://doi.org/10.5194/tc-12-1479-2018, 2018. a
Watanabe, M., Chikira, M., Imada, Y., and Kimoto, M.: Convective control of ENSO simulated in MIROC, J. Climate, 24, 543–562, 2011. a
Weertman, J.: Stability of the junction of an ice sheet and an ice shelf, J. Glaciol., 13, 3–11, 1974. a
Winkelmann, R. and Levermann, A.: Linear response functions to project contributions to future sea level, Clim. Dynam., 40, 2579–2588, 2013. a
Winkelmann, R., Martin, M. A., Haseloff, M., Albrecht, T., Bueler, E., Khroulev, C., and Levermann, A.: The Potsdam Parallel Ice Sheet Model (PISM-PIK) – Part 1: Model description, The Cryosphere, 5, 715–726, https://doi.org/10.5194/tc-5-715-2011, 2011. a
Zweng, M. M., Reagan, J. R., Seidov, D., Boyer, T. P., Locarnini, R. A., Garcia, H. E., Mishonov, A. V., Baranova, O. K., Weathers, K., Paver, C. R., and Smolyar, I.: World Ocean Atlas 2018, Volume 2: Salinity, NOAA Atlas NESDIS (Vol. 81), 2018. a





