the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Quantification of seasonal and diurnal dynamics of subglacial channels using seismic observations on an Alpine glacier
Ugo Nanni
Florent Gimbert
Christian Vincent
Dominik Gräff
Fabian Walter
Luc Piard
Luc Moreau
Water flowing below glaciers exerts a major control on glacier basal sliding. However, our knowledge of the physics of subglacial hydrology and its link with sliding is limited because of lacking observations. Here we use a 2-year-long dataset made of on-ice-measured seismic and in situ-measured glacier basal sliding speed on Glacier d'Argentière (French Alps) to investigate the physics of subglacial channels and its potential link with glacier basal sliding. Using dedicated theory and concomitant measurements of water discharge, we quantify temporal changes in channels' hydraulic radius and hydraulic pressure gradient. At seasonal timescales we find that hydraulic radius and hydraulic pressure gradient respectively exhibit a 2- and 6-fold increase from spring to summer, followed by comparable decrease towards autumn. At low discharge during the early and late melt season channels respond to changes in discharge mainly through changes in hydraulic radius, a regime that is consistent with predictions of channels' behaviour at equilibrium. In contrast, at high discharge and high short-term water-supply variability (summertime), channels undergo strong changes in hydraulic pressure gradient, a behaviour that is consistent with channels behaving out of equilibrium. This out-of-equilibrium regime is further supported by observations at the diurnal scale, which prove that channels pressurize in the morning and depressurize in the afternoon. During summer we also observe high and sustained basal sliding speed, which supports that the widespread inefficient drainage system (cavities) is likely pressurized concomitantly with the channel system. We propose that pressurized channels help sustain high pressure in cavities (and therefore high glacier sliding speed) through an efficient hydraulic connection between the two systems. The present findings provide an essential basis for testing the physics represented in subglacial hydrology and glacier sliding models.
- Article
(8318 KB) - Full-text XML
-
Supplement
(1898 KB) - BibTeX
- EndNote
Subglacial water flow exerts a major control on glacier and ice sheet dynamics and their response to variations in water supply (e.g. Iken and Truffe, 1997; Zwally et al., 2002; Sundal et al., 2011; Bartholomaus et al., 2011; Chandler et al., 2013; Hewitt, 2013; Brondex et al., 2017; Joughin et al., 2018). Water flowing at the base of glaciers modulates glacier basal sliding by lubricating the ice–bed interface. The higher the water pressure, the weaker the basal friction, resulting in faster glacier sliding (Iken and Bindschadler, 1986; Schoof, 2005; Gagliardini et al., 2007). Water pressure depends not only on the total water input but also on the way the water is conveyed through the subglacial drainage system (Lliboutry, 1968), a system that has, yet, yielded limited observations (Flowers, 2015).
The subglacial drainage system of hard-bedded glaciers is considered to be twofold. First, cavities form on the downstream lee of bedrock bumps and are thought to enhance basal sliding through reducing the apparent bed roughness (Lliboutry, 1968). These cavities constitute a widespread inefficient drainage system associated with high basal water pressure, slow water flow (of the order of 10−2 m s−1; see, e.g. Richards et al., 1996) and limited hydraulic conductivity. Second, subglacial channels form into the ice from conduit melt by flowing water heat dissipation and close through ice creep (Röthlisberger, 1972; Nye, 1976). These channels constitute a localized efficient drainage system associated with lower basal water pressure, faster water flow and higher hydraulic conductivity compared to within cavities. A drainage system for which a steady water input is routed through channels tends to slow basal sliding compared to if water is predominantly routed through cavities (e.g. Fountain and Walder, 1998; Schoof, 2010). Most of the current subglacial drainage models (Schoof, 2010; Hewitt, 2013; Werder et al., 2013; Gagliardini and Werder, 2018) are based on this twofold representation. These models succeed in capturing the two-way channel–cavity coupling but still strongly rely on the choice of model parameters (e.g. cavities and channels' hydraulic conductivity, channels' opening and closing rates; see de Fleurian et al., 2018). Observational constraints on these parameters (e.g. water pressure, channel properties) and on the channel–cavity-sliding link are, however, very limited because of the limited observations of the drainage system and concomitant measurements of basal sliding speed (Flowers, 2015; de Fleurian et al., 2018).
Direct observations of the drainage system on temperate glaciers have relied on the analysis of water discharge measured near glacier outlets (Collins, 1979; Hooke et al., 1985; Tranter et al., 1996, 1997; Anderson et al., 2003; Theakstone and Knudsen, 1989; Chandler et al., 2013), of dye-tracing experiments (Seaberg et al., 1988; Willis et al., 1990; Nienow et al., 1996, 1998), of recently exposed subglacial environments (Vivian and Bocquet, 1973; Walder and Hallet, 1979), of local water pressure borehole measurements (Hantz and Lliboutry, 1983; Copland et al., 1997; Sugiyama et al., 2011; Andrews et al., 2014; Hoffman et al., 2016; Rada and Schoof, 2018; Gräff et al., 2019) or of radar measurements (Church et al., 2019). These methods are mostly point scale and often focus on the cavity system due to the very narrow extent of the channel system (Rada and Schoof, 2018). As a consequence, quantitative information on channels' long-term temporal dynamics is limited such that channels' properties (e.g. size, water flow velocity) and dynamics (e.g. opening and closure rate) remain poorly constrained.
Interactions between channels and cavities are often inferred from evaluating glacier-flow-velocity variations in response to meltwater-supply variability. High and sustained water supply over monthly timescales (e.g. during the peak melt season) has been linked to glacier deceleration (Bartholomew et al., 2010; Sole et al., 2013; Tedstone et al., 2013, 2015). This behaviour is related to the fact that channels' development increases the drainage system capacity and is, therefore, expected to reduce the average basal water pressure (Fountain and Walder, 1998). On the contrary, during a short-term water-supply increase (e.g. at the early melt season or at diurnal scales), glacier velocity changes have been observed to occur concomitantly with water-supply changes (Parizek and Alley, 2004; Palmer et al., 2011; Sole et al., 2013; Doyle et al., 2014; Vincent and Moreau, 2016). This behaviour is mostly related to the pressurization of the cavity system, causing an average basal water pressure rise and subsequent basal sliding speed increase (e.g. Nienow et al., 2005; Schoof, 2010; Rada and Schoof, 2018). During periods with a well-developed channelized system (e.g. in summer), this behaviour has also been observed because of channelized system drainage capacity being overwhelmed by the water input changes (Bartholomaus et al., 2008; Andrews et al., 2014), causing pressurized channel flow. These studies have been capable to underline the overall differences between cavity and channel control on subglacial water pressure over different timescales. However, the lack of dedicated channels' observations independent of those on cavities and concomitant with glacier sliding speed measurements renders a more quantitative characterization of the physics of subglacial hydrology and its link with sliding difficult.
Here we use on-ice seismology to explore the evolution of subglacial channels over two complete melt seasons. Over the last decade an increasing number of studies have shown the high potential of analysing high-frequency (>1 Hz) ambient seismic noise to investigate turbulent water flow and sediment transport in terrestrial rivers and streams (e.g. Burtin et al., 2008, 2011; Tsai et al., 2012; Schmandt et al., 2013; Gimbert et al., 2014). The recent work of Gimbert et al. (2016) based on observations of Bartholomaus et al. (2015) suggests that passive seismology may help fill the observational gap on the physics of subglacial channels. Gimbert et al. (2016) adapted, to subglacial channels, a physical framework that describes how turbulent water flow generates seismic waves and that was initially developed for rivers by Gimbert et al. (2014). Contrary to rivers, subglacial channels have the capability to be full and thus to undergo pressurized situations. By applying this modified framework to the Mendenhall Glacier (Alaska) over a 2-month-long summer period, the authors demonstrate that one can use concomitant seismic noise and water discharge measurements to continuously and separately quantify relative changes in channel hydraulic pressure gradient and channel hydraulic radius. They inferred that channels mainly evolve through changes in hydraulic radius over long timescales (multi-weekly), whereas changes in hydraulic pressure gradient are often short-lived (sub-daily to weekly). The use of such an approach to investigate channel physics on relevant glaciological timescales (e.g. diurnal and seasonal) still remains to be conducted, and the resulting channels' properties remain to be compared to other independent observations, such as basal sliding speed. This is the objective of our study.
We conduct a unique and almost uninterrupted 2-year passive seismic survey on Glacier d'Argentière (French Alps), together with continuous measurements of subglacial water discharge, glacier basal sliding speed and local subglacial water pressure. First, we characterize the subglacial channel-flow-induced seismic power signature and use the model of Gimbert et al. (2016) to derive time series of hydraulic pressure gradient and hydraulic radius. We then compare these channel properties to the other independent measurements of glacier sliding speed and basal water pressure. We also compare our seismically derived observations with the theory for subglacial channels' physics proposed by Röthlisberger (1972) to assess the implications of these analysis for channels' physics. Finally, we investigate the equilibrium state of subglacial channels to discuss the channel–cavity interactions and their potential link with basal sliding throughout the melt season. Doing so will also allow us to discuss the applicability of such an approach to improve our general knowledge on subglacial hydrology mechanisms of mountain glaciers and ice sheets.
Here we provide a brief background on the theoretical framework of Gimbert et al. (2016), which relates seismic noise and water discharge to subglacial channel-flow properties, and that of Röthlisberger (1972), which predicts subglacial channel hydraulic pressure gradient and hydraulic radius scaling as a function of water discharge under certain assumptions. Refer to Table C1 in Appendix C for a summary of all variables, physical quantities and mathematical functions defined in the following sections.
2.1 Theory of subglacial channel-flow-induced seismic noise
Turbulent water flow in a river or a subglacial channel generates frictional forces F acting on the near boundaries (e.g. riverbed or conduit wall), which in turn cause seismic waves with given amplitude and spectral signature (Gimbert et al., 2014). By propagating through a medium (e.g. rock, gravel or ice), seismic waves cause ground motion at any location x away from the source location x0 (Fig. 1). The relationship between the force time series F(t,x0) applied at x0 in a channel and the ground velocity time series U(t,x) measured at x can be described from Aki and Richards (2002) as
where G(t) is the displacement Green's function that converts the force applied at x0 into ground displacement at x, and the notation ⊗ stands for the convolution operator. The seismic power P of such a signal is defined over a time period T as
where U(f)=ℱ(U(t)) is the Fourier transform of the ground velocity time series and f is the frequency. We denote Pw as the seismic power induced by turbulent water flow. Based on a description of the force F(f) as a function of flow parameters, Gimbert et al. (2014) demonstrated that Pw scales as
where u* is river wall shear velocity, W is river width, and ζ is a function that accounts for turbulence intensity changes with changes in the apparent roughness that depend on H, the flow depth, and ks, the wall roughness size (Fig. 1).
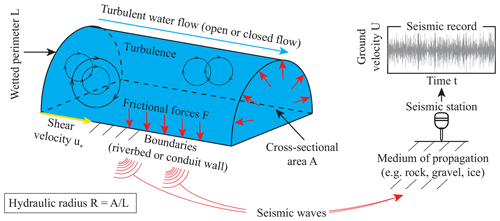
Figure 1Schematic representation of subglacial channel-flow-induced seismic noise. Representation of an idealized conduit of hydraulic radius R with a wall shear velocity u* (see Eq. 3). Turbulent flow generates frictional forces F, causing seismic waves and resulting in a ground velocity U that is recorded at a distant seismic station (see Eq. 1).
To relate Pw to subglacial channels' properties, Gimbert et al. (2016) expressed the shear velocity as , where g is gravitational acceleration, R the hydraulic radius and S the hydraulic pressure gradient. The hydraulic radius R is defined as the ratio of the cross-sectional area of the channel flow to its wet perimeter (Fig. 1). This parameter scales with flow depth for open channel flow. The hydraulic pressure gradient S is a function of both the water pressure rate of change in the flow direction and the bed slope. For free surface flow, S equals channel slope. In a case of constant channel slope and channel geometry, increasing S means closed and pressurizing channel flow.
Gimbert et al. (2016) then expressed water discharge Q as a function of water flow velocity Vw using the Manning–Strickler relation , where n′ is Manning's coefficient (Manning et al., 1891; Strickler, 1981). To study Pw for a subglacial channel flow configuration, Gimbert et al. (2016) considered that the source-to-station distance is constant such that changes in Pw are not caused by changes in source (channel) position. Gimbert et al. (2016) then assumed a constant number N of channels and thus neglected the dependency of Pw on N. Here we include the dependency of Pw on N by considering that all channels have equal hydraulic radius and hydraulic pressure gradient (i.e. are of similar size and position compared to the seismic station) such that
where β is a function of conduit shape and fullness that may be neglected (see supporting materials of Gimbert et al., 2016, for details). Combining Eqs. (4) and (5) and neglecting changes in β leads to the two following formulations for Pw:
From Eqs. (6) and (7) two end-member cases can be evaluated. If changes in discharge occur at constant channel geometry (i.e. constant R and N) from Eq. (6) we have
In contrast, if changes in discharge occur at constant hydraulic pressure gradient and channel number (regardless of whether the conduit is full or not) from Eq. (7) we have
Beyond these end-member scenarios, one can use measurements of Pw and Q to invert for relative changes in R and S using Eqs. (6) and (7) as
where the subset ref stands for a reference state, which has to be defined over the same time period for both Q and Pw but not necessarily for R and S. Details on the derivation from Eqs. (6) and (7) to Eqs. (10) and (11) can be found in Gimbert et al. (2016). In the following we consider N to be constant to invert for R and S, and later we prove that our inversions are not significantly biased by potential changes in N (Sect. 6.1).
2.2 R-channel theory
To date, state-of-the art subglacial drainage models use the theories of Röthlisberger (1972) to describe subglacial channel dynamics (see de Fleurian et al., 2018, for model inter-comparisons). Channels described in these theories are assumed to be of semi-circular shape and to form into the ice through melt by heat dissipation from the flowing water and close through ice creep. A channel evolves at steady state with water discharge Q if melt and creep rates change instantaneously with changes in Q. A steady-state channel is at equilibrium with Q if the melt (opening) rate equals the creep (closure) rate, in which case Röthlisberger (1972) predicts
For a steady-state channel not at equilibrium with Q and that responds solely through changes in pressure gradient S (i.e. R is constant), equations of Röthlisberger (1972) show that
Further details on the derivation of these equations from Röthlisberger (1972) can be found in Supplement Sect. S2. Later we compare our inversions of changes in R and S (using seismic observations) with changes in R and S as predicted by the theory of Röthlisberger (1972) for steady-state channels at equilibrium or not at equilibrium with water discharge.
3.1 Site and glaciological context
Glacier d'Argentière is a temperate glacier located in the Mont Blanc mountain range (French Alps; see Fig. 2). The glacier is ca. 10 km long and covers an area of ca. 12.8 km2. It extends from an altitude of ca. 1700 (metres above sea level) up to ca. 3600 in the accumulation zone. Its cumulative mass balance has been continuously decreasing, from −6 m water equivalent (w.e.) in 1975 to −34 m w.e. presently, compared to the beginning of the 20th century (Vincent et al., 2009). This site is ideal for studying subglacial channels' properties, since it presents a typical U-shaped narrow valley (Hantz and Lliboutry, 1983) and hard-bed conditions (Vivian and Bocquet, 1973), two conditions that favour a well-developed R-channel subglacial network (Röthlisberger, 1972).

Figure 2Monitoring set-up of Glacier d'Argentière. (a) Aerial view of Glacier d'Argentière field site (France) and location of the instruments used in this study. The aerial photography was taken in 2015. The seismic network is composed of the GDA (red circles) and ARG (red stars) borehole stations and is located according to positions in summer 2018. Station ARG.B02 is installed ca. 70 m deep in the ice, whereas the four other stations are installed ca. 5 m deep. The GLACIOCLIM (https://glacioclim.osug.fr/, last access: 28 April 2020) automatic weather station (AWS; green star) provides air temperature and precipitation. Basal sliding speed (orange circle) and water discharge (blue circle) are measured thanks to direct access to the glacier base from excavated tunnels. Basal water pressure is measured at a similar location to that of basal sliding speed measurements. (b) Picture of the seismic instrumental set-up used in this study. (c) Picture of the subglacial observatory with the bicycle wheel used to measure basal sliding speed. Photo credits: (a) IGN France, https://www.geoportail.gouv.fr/ (last access: 28 April 2020), (b) Nathan Maier and (c) Luc Moreau.
In the present study we analyse the data recorded from spring 2017 to autumn 2018 with seismometers located between 2350 and 2400 (Fig. 2). This location corresponds to cross section no. 4 monitored by the French glacier-monitoring program GLACIOCLIM (https://glacioclim.osug.fr/). There the glacier is up to ca. 280 m thick (Hantz and Lliboutry, 1983, updated from a radar campaign conducted in 2018). Subglacial water discharge is monitored 600 m downstream of the seismometers at 2173 near the glacier ice fall in subglacial excavated tunnels maintained by the hydroelectric power company Emosson S.A. Subglacial water is almost entirely evacuated through one major snout, as supported by direct observations of very limited water flowing elsewhere. Thus discharge measured at this location is well representative of discharge subglacially routed under the seismometers' location. Discharge measurements are conducted from mid-spring to early autumn with an accuracy of 0.01 m3 s−1 every 15 min by means of a Endress Hauser sensor measuring the water level in a conduit of known geometry. The minimum measurable value for water discharge is limited by the measurement accuracy, and the maximum value is 10 m3 s−1 due to the capacity of the collector. Because sediments accumulate in the collector, flushes are recorded when the collector is emptied, causing glitches in the discharge record. We remove these glitches by removing Q values that present higher than 0.2 m3 per 15 min. Within the same tunnel network, a subglacial observatory is used to measure basal sliding speed out of a bicycle wheel placed in contact with the basal ice (Vivian and Bocquet, 1973). Since August 2017 basal sliding speed has been measured at a time resolution of 5 s over a 0.07 mm space segmentation. In the close vicinity a pressure sensor, of the gauge type, is used to measure subglacial water pressure with 10 min time resolution and an accuracy of 400 Pa. The sensor is installed in a borehole drilled from the excavated tunnels up to the glacier bottom (see Vivian and Zumstein, 1973 for details). Air temperature and precipitation measurements are obtained at a 0.5 h time step through an automatic weather station maintained by the French glacier-monitoring program GLACIOCLIM and located on the moraine next to the glacier at 2400 . Precipitation is measured with an OTT Pluvio weighing rain gauge with a 400 cm2 collecting area. When air temperature is below zero, only precipitation occurrences are accurate; absolute values are not accurate because of snow clogging.
3.2 Seismic instrumentation
We use five seismic stations installed in the lower part of the glacier (Fig. 2). The instruments belong to two seismic networks, denoted as GDA (three stations) and ARG (two stations). Stations GDA.01, GDA.02 and GDA.03 were deployed in spring 2017 with ca. 200 m inter-station distances. These stations have digitizers of the type Nanometrics Taurus, set to 16 Vpp (peak-to-peak voltage) sensitivity and a 500 Hz sampling rate, and borehole type sensors (model Lennartz 3D/BH), with an eigenfrequency of 1 Hz. Station ARG.B01 was installed in October 2017 at the centre of the GDA network, at about 100 m from each GDA stations. The digitizer used for that station is a Geobit SRi32L, set to a 10 Vpp sensitivity and a 1000 Hz sampling rate. The sensor is of the borehole type (model Geobit C100), with an eigenfrequency of 0.1 Hz. Station ARG.B02 was installed in April 2018 about 50 m upglacier from station ARG.B01. The digitizer used for that station is a Geobit SRi32, set to a 0.625 Vpp sensitivity and a 1000 Hz sampling rate. The sensor is of the borehole type (model Geobit S400), with an eigenfrequency of 1 Hz. All stations were installed ca. 5 m deep below the ice surface, except ARG.B02, which was placed ca. 70 m deep. A few data gaps occurred during our study due to difficulties in ensuring continuous power supply and data storage on glaciers.
Refer to Table C1 in Appendix C for a summary of all variables, physical quantities and mathematical functions defined in the following sections.
4.1 Calculation of seismic power at a virtual station
The raw seismic record at each station is first corrected from the sensor and digitizer responses. Then, the frequency-dependent seismic noise power P is computed using the vertical component of ground motion (see Eq. 2). P is calculated with Welch's method over time windows of duration dt with 50 % overlap (Welch, 1967). The longer dt, the more likely highly energetic impulsive events are to occur and overwhelm the background noise within that time window (Bartholomaus et al., 2015). To maximize sensitivity to the continuous, low-amplitude, subglacial channel-flow-induced seismic noise and minimize that of short-lived but high-energy impulsive events, we use a short time window of dt=2 s to calculate P and average it over time windows of 15 min in the decimal logarithmic space. We express P in decibel (dB; decimal logarithmic), which allows properly evaluating its variations over several orders of magnitude.
We reconstruct a 2-year-long time series by merging records from the five available stations into one unique record at a “virtual” station. To minimize site and instrumental effects on seismic power we shift the average power at each station to a reference one taken at ARG.B01. The seismic signal at our virtual station is composed of the GDA seismic signals between May end December 2017 and of the ARG seismic signals between December 2017 and December 2018 (see Fig. S1 in the Supplement).
4.2 Evaluating bias due to anthropogenic noise
Later in Sect. 5 we show that when water discharge Q is low (in the early and late melt season) seismic power from anthropogenic noise (PA) is comparable to the subglacial channel-flow-induced seismic power (Pw). Here we evaluate how much PA adding to Pw can bias the evaluation of scaling predictions of Gimbert et al. (2016). We calculate a synthetic seismic power P as and a synthetic Pw from a synthetic Q as Pw=Qn, with n being equal to or , as expected from theory (see Eqs. 8 and 9). We quantify the relative contributions of Pw and PA to P through the parameter Sr, which we define as . When Sr tends toward 1, subglacial channel-flow-induced seismic power dominates the synthetic seismic power, and when Sr tends towards 0, anthropogenic noise power dominates.
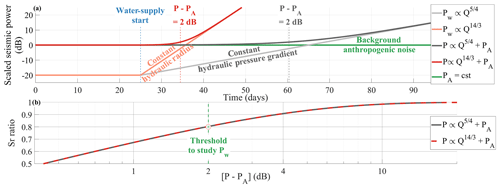
Figure 3Synthetic predictions of scaling bias due to anthropogenic noise superimposing on subglacial channel-flow-induced seismic noise. (a) Synthetic anthropogenic seismic power (green line; PA), synthetic subglacial channel-flow-induced seismic power Pw=Qn, with Q being the synthetic water discharge for (grey line) and (orange line) and synthetic seismic power for (black line) and (red line). (b) Evolution of Sr (see Sect. 4.2) ratio with respect to P-PA for (grey line) and (red line). Note that the two curves overlap.
In Fig. 3a we show the temporal evolution of synthetic P with a constant value for PA and with a Pw that responds to a synthetic evolving water supply Q. The value of P is normalized by PA, resulting in P=0 dB in winter. For (Fig. 3a; red and orange lines), Pw dominates the contribution to P within ca. 10 d of the onset of water supply. For (Fig. 3a; black and green lines) P contains both Pw and PA contributions during a period that is 3 times longer than for . The evolution of Sr with respect to P-PA (Fig. 3b) is the same for both the constant hydraulic pressure gradient (red line) and constant hydraulic radius (grey line) scenarios. For P-PA>2 dB, Sr is higher than 0.8, meaning that subglacial channel-flow-induced seismic power contributes by more than 80 % to the synthetic seismic power. Later in Sect. 5.2 we measure PA during winter and use the condition P-PA>2 dB to define the periods that evaluate Pw directly from the measurement of P and investigate the subglacial hydraulic properties.
4.3 Definition of metrics to evaluate sub-diurnal dynamics
Since the Pw-versus-Q relationship is not unique and may vary with time (see Sect. 2), we expect that the diurnal time series of Pw versus Q may exhibit different patterns throughout the melt season and that these patterns reveal changes in the subglacial hydraulic properties. To systematically quantify the diurnal variability in Pw, Q, R and S throughout the melt season we define three metrics that we calculate on an hydrological daily basis (defined as the period between two minimum Q values within a 24 h time window). To focus on the diurnal variability only, we bandpass-filter our time series within a 6–36 h range (see Appendix Fig. A1 for details). Our first metric quantifies the diurnal variability in a given variable X during a given day and corresponds to the coefficient of variation Cv, defined as
where (Xday)max and (Xday)min are the maximum and minimum value of Xday, respectively, and its average. Our second metric ϕ quantifies daily hysteresis between Pw and Q by evaluating the difference between Pw when Q is rising, e.g. in the morning, and Pw when Q is falling, e.g. in the afternoon. Following the approach of Roth et al. (2016), we define ϕ as
The larger ϕ, the more seismic energy is recorded during the rising discharge period with respect to the falling one. Hysteresis can occur either because of an asymmetry between (Pw,day)rising and (Pw,day)falling or because of a time lag between Pw and Q. To avoid ambiguity between these two hysteresis sources our third metric corresponds to the daily time lag δt between the time t((Pw,day)max), when Pw is maximum, and the time t((Qday)max), when Q is maximum, and is defined as
We set the condition that for δt to be calculated, t((Pw,day)max) has to correspond to both the time when Pw is maximum and has a null derivative within a −8–8 h time window around t((Qday)max). We note that a time delay of about 0.04 h is expected due to water flowing at ca. 1 m s−1 over the ca. 600 m separating our seismic stations to where Q is measured (see Fig. S2 for details). This means that any values of δt greater than ±0.04 h are not attributable only to water transfer time lags.
5.1 Overview of observations
Seismic power P as calculated at our virtual station based on records from our five stations (see Sect. 4) is shown in Fig. 4a as a function of time (May 2017 to December 2018) and frequency (2 to 100 Hz). Large seasonal changes in P are observed within the 2–10 Hz frequency range, in which P is higher by more than 2 orders of magnitude during the melt season (mid-May to September) compared to winter. Changes in P are also observed within the 10–20 Hz frequency range, with P during the melt season being about an order of magnitude larger than in winter. Significant changes of smaller amplitude are also observed at higher frequency (20–100 Hz). Spectral distributions of P presented in Fig. 4b and c show widely spread P values during the melt season (Fig. 4b; variations over more than 10 dB), as opposed to being comparatively much narrower in winter (Fig. 4c; variations within 1–3 dB). Seismic power within the 3–7 Hz frequency range shows the highest range of variations from winter to summer (Figs. 4a and b). Over the 2 years, the overall spectral pattern remains similar, although intra-seasonal variations in P during the 2017 melt season are more pronounced compared to the 2018 melt season.
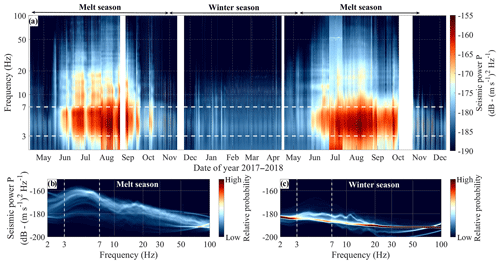
Figure 4(a) Spectrogram of the observed seismic power P as a function of time (x axis; May 2017 to December 2018) and frequency (y axis; 1–100 Hz log scale). Colours represent seismic power in decimal logarithmic space (dB; relative to (m s−1) 2 Hz−1). White bands correspond to data gaps. (b, c) Spectral distribution of seismic power during the melt seasons (b) and the winter seasons (c). Colours represent occurrence probability, and colour bars are identical for (b) and (c).
The observed meteorological and hydrological conditions at Glacier d'Argentière together with the measured basal sliding speed and the seismic power P3–7 Hz as averaged within the 3–7 Hz frequency range are shown as a function of time (May 2017 to December 2018) in Fig. 5. Water discharge Q shows a strong seasonal signal, with discharge lower than 0.1 m3 s−1 in winter and up to values higher than 10 m3 s−1 in summer. These changes are consistent with air temperature values and occur concomitantly with the evolution of P3–7 Hz (Fig. 5b). Further details on the comparison between P3–7 Hz and Q are presented in Sect. 5.2. Over the first months of the melt season (early May to mid-June 2017 and late April to mid-June 2018), Q increases by about 2 orders of magnitude, from 0.1 to 10 m3 s−1. At the same time, the amplitude of the diurnal variations in Q increase up to 3 m3 s−1 over the summer. The evolution of basal sliding speed presented in Fig. 5c depicts a rapid acceleration, from 5 mm h−1 in May 2017 and April 2018 to 7 mm h−1 over the following month. Sliding speed then stays almost constant through the summer and slowly decreases down to a minimum of 4.5 mm h−1 in February (see also comparable observations made by Vincent and Moreau, 2016, over the past decade). Basal water pressure measurements (Fig. 5c) show that at the seasonal timescale the basal water pressure tends to be higher in winter than in summer by ca. 2.51e+4 Pa. In summer 2017 the short-term (diurnal) variability in the basal water pressure is more pronounced than in winter, as also observed for the water discharge (Figs. 5b and A1). During heavy rainfall (Fig. 5a) and consequent discharge (Fig. 5b), basal water pressure variations are in phase with sliding speed (Fig. 5c; e.g. on 1 August, 7 August, 18 August, 30 August, 13 September or 2 October 2017). This evolution of the measured basal water pressure rather depicts a local behaviour, whereas changes in the basal sliding speed (Fig. 5c) represent average changes in the average basal water pressure conditions over our study area and therefore better represent the global cavity-system pressure conditions.
Measurement artefacts are observed for Q, with values having a threshold at 10 m3 s−1 and for P in July 2018, when unusually high seismic power values are observed over the whole frequency range, which we associate with the initially weak ice-sensor coupling of ARG.B02. Site specificity of the GDA network used in 2017 causes higher seismic power in the 8–20 Hz frequency band in 2017 than in year 2018. These artefacts appear to significantly affect neither P (at least not within the 2–10 Hz frequency range) nor the concomitant temporal evolution of P and Q over the 2 years.
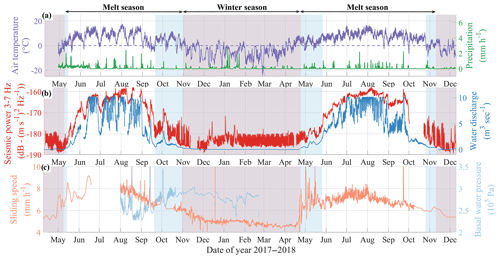
Figure 5Time series of physical quantities measured from spring 2017 to winter 2018 at Glacier d'Argentière. All data are smoothed over a 6 h time window. (a) Surface air temperature (purple line) and precipitation (green line) at the GLACIOCLIM AWS (Fig. 2). The dashed purple line shows T=0 ∘C. (b) Averaged seismic power within the 3–7 Hz frequency range at the virtual seismic station (red line; P3–7 Hz; see Sect. 5.2 for details) and subglacial water discharge Q (blue line). (c) Basal sliding speed (orange line) and subglacial water pressure (light blue line) measured at Glacier d'Argentière subglacial observatory (Fig. 2). Note that temporal resolution in the sliding speed is lower in May–July 2017 and from October 2018 on because of instrumental issues. Red shaded areas represent the winter season; blue shaded areas represent the periods when diurnal changes in anthropogenic noise are too pronounced to study Pw on a diurnal basis.
5.2 Seismic power induced by subglacial channel flow
We consider seismic power P3–7 Hz averaged within the 3–7 Hz frequency range (Fig. 5b; red line) as best representative of subglacial channel-flow-induced seismic power Pw because it shows the highest variations with changes in Q (Figs. 4 and 5). A similar frequency signature of the subglacial channel-flow-induced seismic noise has been observed by Bartholomaus et al. (2015), Preiswerk and Walter (2018), and Lindner et al. (2020). This frequency range is also comparable to those observed for water flow in rivers (Schmandt et al., 2013; Gimbert et al., 2014). As Q increases from less than 0.1 m3 s−1 in early May to about 10 m3 s−1 at the end of July, Pw increases by up to 30 dB (i.e. 3 orders of magnitude). Differences in relative variations in Pw across stations are lower than 0.5 dB, including during periods of high discharge (Fig. S2). This supports the accuracy and validity of our virtual station reconstruction to study the subglacial channel-flow-induced seismic power (Sect. 4). Variations in Pw follow those of Q during the melt season and over seasonal to weekly timescales (Fig. 5b). Both the high sub-monthly variability in Q and air temperature observed in 2017 and the rapid changes in Q occurring in fall 2017 and 2018 are also observed in the temporal evolution of Pw. In winter we observe high seismic power bursts from December to mid-January, occurring when Q is null but concomitantly with the beginning of heavy snowfall events. These bursts are not associated with subglacial channel-flow-induced seismic noise but likely correspond to repeating stick–slip events triggered by snow loading similar to those observed previously by Allstadt and Malone (2014). When Q is lower than 2 m3 s−1 during winter, early spring and fall, we observe regular weekly and daily variations in P3–7 Hz that superimpose on the background variations (Fig. 5b). This regular pattern corresponds to anthropogenic noise, as previously observed by Preiswerk and Walter (2018) in a similar set-up.
Based on the condition proposed in Sect. 4.2 (P-PA>2 dB) we use the periods 14 May–1 November 2017 and 21 April–10 November 2018 to investigate the subglacial hydraulic properties (white and blue areas in Figs. 5 and 8). During these periods we subtract the mean winter diurnal pattern of PA (defined between 29 January and 4 April 2018) from P3–7 Hz to obtain Pw (Fig. S3). At the diurnal scale, because PA can slightly vary from day to day depending on the anthropic activity (e.g. higher anthropic activity during working days than holidays), the periods with a very early and very late melt season are still strongly influenced by day-to-day changes in PA. To study diurnal changes in Pw without being biased by anthropogenic noise we limit our analysis to the periods 15 May–22 September 2017 and 27 May–28 October 2018 (white areas in Figs. 5 and 8; based on direct observation shown in Fig. S3). Later in Sect. 5.4 we filter Pw with a 5 d low-pass filter (i.e. removing variability lower than 5 d) when inverting for the hydraulic properties. Doing so allows studying the early and late melt season with confidence by reducing the influence of the diurnal variability in PA on Pw while keeping sub-weekly variations in Pw and Q (see Fig. S4 for details).
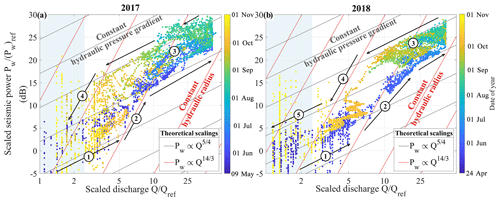
Figure 6Observed (dots) and predicted (lines) changes in subglacial channel-flow-induced seismic power versus changes in water discharge during the melt season of 2017 (a) and 2018 (b). Temporal signals are filtered with a 1 h low-pass filter. The colour scale differs for the 2 years and varies with time from early April to mid-November. Lines show predictions calculated from Eqs. (8) and (9) for constant hydraulic radii and varying hydraulic pressure gradient (red lines) and for constant hydraulic pressure gradient and varying hydraulic radii (black lines). Blue shaded areas represent the period when Q is lower than 1 m3 s−1. Arrows show the direction of time, and circled numbers refer to periods described in the main text. Reference values (Pw)ref and Qref are taken the first day of the 2017 melt season (10 May 2018).
5.3 Comparison of observations with predictions from Gimbert et al. (2016)
5.3.1 Analysis of seasonal changes
Seasonal-scale observations and predictions of the subglacial channel-flow-induced seismic power Pw versus water discharge Q are shown in Fig. 6. We find that theoretical predictions from Gimbert et al. (2016) (red and black lines) are consistent with our observations (coloured dots), which exhibit a general trend between that predicted at a constant hydraulic pressure gradient (Fig. 6; see black lines calculated using Eq. 7) and that predicted at a constant hydraulic radius (Fig. 6; red lines calculated using Eq. 6). As Q increases at the very onset of the melt season (in end of April), observed Pw values follow the trend predicted under constant hydraulic pressure gradient (Fig. 6 ①). As Q increases more rapidly from mid-May to the end of June (Fig. 5b), Pw follows a different trend of evolving hydraulic pressure gradient (Fig. 6 ②). The general trend from July to September is then dominated by changes in hydraulic radius (Fig. 6 ③). As Q decreases during the melt season termination, observed Pw values follow the trend of evolving hydraulic pressure gradient in a similar manner to during the early melt season (Fig. 6 ④). At the end of the melt season of 2018 (late October to November) our observations also show a trend of changing hydraulic radius, although this observation is not as clear in 2017 (Fig. 6 ⑤). A clear counterclockwise seasonal hysteresis of up to 10 dB power difference is observed in Fig. 6 between Pw and Q. This shows that for a similar water discharge, higher subglacial channel-flow-induced seismic power is generated in the late melt season compared to the earlier melt season. The 10 m3 s−1 measurement threshold in Q is well observable for the 2 years but does not bias the observed scaling of the changing hydraulic radius observed during summer.
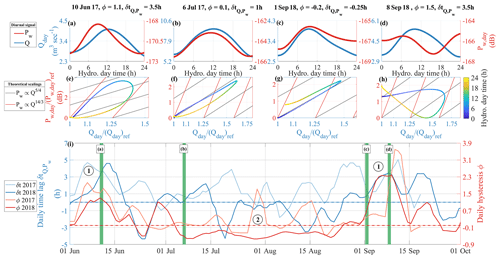
Figure 7Diurnal observations of the subglacial channel-flow-induced seismic power Pw and water discharge Q and comparison with predictions from Gimbert et al. (2016). (a–d) Daily evolution of the 6–36 h bandpass-filtered seismic power Pw,day (red line) and water discharge Qday (blue line) for 4 selected hydrological days. Values of Pw,day and Qday are centred on the average respective absolute value of the corresponding day. Corresponding values of daily and ϕ are shown at the top of the panels. (e–h) Observed (coloured dots) and predicted (red and black lines calculated with Eqs. 6 and 7) Pw-versus-Q daily relationships. Note that y axis bounds differ from panel to panel. Both variables are normalized by their daily minima. (i) Daily time lag between Pw,day and Qday peaks (blue lines) and daily hysteresis ϕ between Pw,day and Qday (red lines). Shaded lines are data from 2017, and plain ones are data from 2018. Dashed lines show (blue) and ϕ=0 (red). Time series are smoothed over 5 d. Green vertical bars show times of the 4 selected hydrological days with the corresponding panel number. Circled numbers refer to the two phases described in the main text.
5.3.2 Analysis of diurnal changes
Observations and predictions of the diurnal relationship between the subglacial channel-flow-induced seismic power Pw and water discharge Q throughout the melt season are shown in Fig. 7. We quantify the diurnal behaviours over the two melt seasons by calculating the hysteresis amplitude ϕ and time lag δt (see Sect. 4.3) and through comparing our observations with the theoretical predictions calculated for 4 selected days (Fig. 7a–h). We selected these days based on three criteria: they represent typical variations in Pw and Q over their respective periods ( d around their date), they show that our observations capture diurnal variations from unique days without multi-day averaging, and they give pedagogical support for the reader to interpret values of the hysteresis amplitude ϕ and time lag δt shown in Fig. 7i. We focus on these two indicators, as they allow evaluating respective changes of Pw versus Q.
The seasonal evolution of the daily hysteresis amplitude ϕ presents two peaks in late May–early June and in late August–early September, which are consistently observed in both 2017 and 2018 (phases ① in Fig. 7i). The seasonal evolution of the diurnal time lag between δt of Pw and Q is similar to that of ϕ, with peak values at δt>2.5 h in late May–early June and in late August–early September (Fig. 7i). This supports that hysteresis is mainly caused by phase difference between Pw and Q rather than by asymmetrical changes Pw when Q rises compared to when Q falls (Sect. 4.3). The variability in δt over the season is much larger than the predicted 0.04 h instrumental time lag (see Sect. 4.3) such that its evolution represents real changes in the relationship between Pw and Q.
In the early and late melt season (phases ① in Fig. 7i), Pw,day peaks, on average, more than 3 h before Qday (e.g. Fig. 7e). These long time delay δt values are concomitant with a pronounced asymmetrical shape in Pw,day, with a steeper rising than falling limb (e.g. Fig. 7e). This results in large clockwise hysteresis in Pw,day versus Qday as well, shown by the high hysteresis values during these periods (ϕ>1; phases ① in Fig. 7i). For example, on 10 June our observations follow the trend of evolving hydraulic pressure gradient in the morning and the one of changing hydraulic radius in the afternoon and at night. On 8 September our observations follow the trend of changing hydraulic radius in the early morning and the one of evolving hydraulic pressure gradient in the afternoon. On the contrary to these periods, in summer (phase ② in Fig. 7i), both ϕ and δt are low, with ϕ≃0 and 2 h h. At this time, δt has a more pronounced seasonal and year-to-year variability than ϕ (Fig. 7i), with values oscillating between −2 and 2 h and minimum values reaching h. In July and August (e.g. Fig. 7b and c), Pw peaks nearly at the same time as Q with δt<0.5 h and with an almost symmetrical diurnal evolution (Fig. 7i). For both summer days (6 July and 1 September), our observations mainly follow the trend of changing hydraulic radius throughout the whole day, with a non-null hysteresis that shows that hydraulic pressure gradient may also change. This two-phase seasonal evolution shows that diurnal changes in Q in the early and late melt season cause a pronounced diurnal variability in the hydraulic pressure gradient and limited diurnal changes in the hydraulic radius, whereas over the summer channels show a more marked response to diurnal changes in Q through changes in hydraulic radius.
5.4 Inversions of changes in hydraulic radius and hydraulic pressure gradient
We invert for the relative changes of hydraulic radius and hydraulic pressure gradient using Eqs. (10) and (11) and our observations of time series of Q and Pw once filtered with a 5 d low-pass filter (see Fig. S4 and Sect. 5.2 for details). In the following for the sake of readability we use the notation R, S and V to refer to , and the relative basal sliding speed . Reference values for these three variables are taken as their minimum value over the 2 years, which occur on 10 May 2017 for R, 14 May 2018 for S and 28 March 2018 for V.
5.4.1 Analysis of seasonal changes
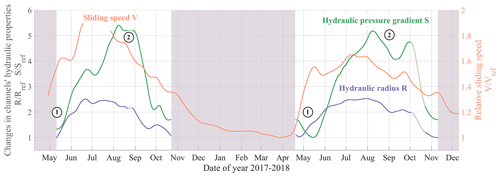
Figure 8Seasonal evolution of the hydraulic radius and hydraulic pressure gradient as inferred from seismic observations as well as of glacier basal sliding speed as measured in situ. (a) Relative hydraulic pressure gradient (green line), relative hydraulic radius (purple line) and relative sliding speed (orange line). Red shaded areas represent the winter season. Temporal signals of R and S are calculated using 5 d low-pass-filtered time series of Q and Pw and are further smoothed applying a 30 d low-pass filter. Shaded lines correspond with period with no data and show interpolated values of R and S using a cubic spline interpolation. Reference values for the three variables are taken as their minimum value of the 2 years (i.e. 10 May 2017 for R, 14 May 2018 for S and 28 March 2018 for V). Circled numbers refer to the three phases described in the main text.
The temporal evolution of R, S and V is presented in Fig. 8. We recall here that the changes in V can be considered to be a good proxy for changes in water pressure in the subglacial cavity network (see Sect. 5.1 for details). We find that all three variables show a well-marked seasonal evolution, with low values during the early and late melt season and high values in summer. However, differences between R, S and V exist over the melt season. For both years, R starts increasing from the onset of the early melt season until reaching a maximum within 2 months in late June to early July. R is then 2 times larger on average than in the early melt season. In contrast, during the first weeks of the melt season 2018, S rapidly decreases (Fig. 8 ①), concomitant with an abrupt increase in V by a factor of 1.5 compared to winter. This shows that as the average water pressure rises in cavities and enhances sliding, channels, on the contrary, undergo depressurization. During the melt season in 2017 we do not observe such behaviour, possibly because of a time series of Pw that starts about 3 weeks later than in 2018. The increase in S then occurs with a delay of about 1 month in 2018 and of about 1 week in 2017 compared to that in R, and S reaches a maximum in August (Fig. 8 ②). S is at that time on average 5 to 6 times larger than in the beginning of the melt season. As S increases, V and R have already passed their summer maximum. Contrary to the conclusions obtained on the Mendenhall Glacier (Alaska), where S presents no significant trend over the 2-month-long investigated period (Gimbert et al., 2016), seasonal changes in water discharge at Glacier d'Argentière are inferred to cause changes in both R and S. From early to mid-September, R and S decrease concomitantly and reach their minimum in late October. The summer-to-winter transition is most pronounced for S, which decreases by about a factor of 4 within less than a month (September to October), while R decreases more gently.
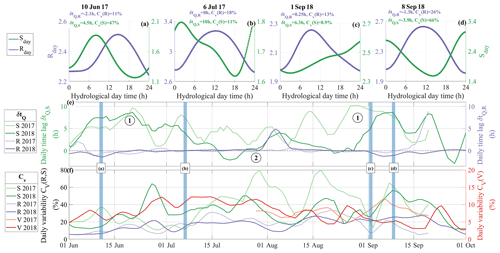
Figure 9Diurnal evolution of the hydraulic radius R and hydraulic pressure gradient S and comparison to glacier dynamics. (a–d) Daily time series of R (purple line) and S (green line) for 4 selected hydrological days across the melt season. Time series are bandpass-filtered within 6–36 h. Values of Rday and Sday are centred on the average respective absolute value of the corresponding day. Corresponding daily values of δtQ,R, δtQ,S, Cv(R) and Cv(S) are shown at the top of the panels. Note that y axis bounds differ from panel to panel. (e) Daily time lags δtQ,R between Rday and Qday peaks (purple lines) and δtQ,S between Sday and Qday peaks (green lines). (f) Sub-diurnal variability Cv in R (purple lines), S (green lines) and the basal sliding speed V (red line). Time series are smoothed over 5 d. Blue vertical bars show location of the 4 selected days with the corresponding panel. Shaded lines are data from 2017, and plain lines are data from 2018. Circled numbers refer to the two phases described in the main text.
5.4.2 Analysis of diurnal changes
Figure 9 describes how channel and cavity properties behave at the diurnal scale throughout the melt season. We quantify the diurnal behaviour throughout the two melt seasons with the time lag δt between R and Q daily maxima, denoted by δtQ,R, and between S and Q daily maxima, denoted by δtQ,S. We also calculate the amplitude of the diurnal variations Cv for R, S and V (see Sect. 4.3 for definitions). In the same scopes as in Sect. 5.3.2 we illustrate, in Fig. 9a–d, the diurnal evolution of R and S for the same 4 selected days as in Fig. 7.
Cv(R) and Cv(S) both present seasonal variation, with maximum values being reached mid-summer. The amplitude of Cv(S) is, however, up to 3 times larger than that of Cv(R), since Cv(S) reaches up to 80 % in August, while Cv(R) only increases up to 30 % (Fig. 9f). In contrast, the seasonal evolution of δtQ,R and δtQ,S drastically differs (Fig. 9e). On the one hand, the temporal evolution of δtQ,R presents no marked changes throughout the season and generally remains within a range of ±1 h (Fig. 9e), as highlighted by the 4 selected days (Fig. 9a to c). This shows that R and Q are consistently in phase on a diurnal basis throughout the melt season. On the other hand, the temporal evolution of δtQ,S presents average values of about 5 h, with two peaks of h in June and August (Fig. 9e ①) and a period of low values in the range of 0–5 h in mid-summer (Fig. 9e ②). These changes in S are clearly observed in the diurnal snapshots (e.g. Figs. 9a to d) that show a marked increase in hydraulic pressure gradient in the morning before the rise in hydraulic radius. Such a difference in diurnal dynamics between R and S shows that channels exhibit high hydraulic pressure gradients in the early morning time, while their hydraulic radius grows slowly to reach its maximum at the same time as the water discharge.
We also compare in Fig. 9f the diurnal dynamics of channel properties to the diurnal dynamics of the average water pressure conditions in cavities by comparing Cv(R) and Cv(S) with Cv(V). Over the melt season, Cv(V) exhibits a pattern that is similar to Cv(R) and Cv(S), with higher values observed for the three variables in summer (>10 %) than during the early and late melt season (<10 %). This shows that short-term variability in channels' properties (i.e. R and S) correlates well with the short-term variability in average water pressure condition in cavities. From late August to mid-September 2017, we observe that Cv(S) reaches up to 60 % over less than a week, followed ca. 1 week later by a rapid rise in Cv(V) (Fig. 9f).
5.5 Comparison of inversions with predictions from Röthlisberger (1972)
Our seismically derived S and R values are shown in Fig. 10 as a function of relative changes in water discharge Q, along with scaling predictions calculated using the theory of Röthlisberger (1972), assuming channels at equilibrium (melt rate equals creep rate) with S∝ and (Eqs. 14 and 12; green lines in Fig. 10) and channels out of equilibrium that respond to changes in Q only through changes in S with S∝Q2 and R being constant (Eq. 13; purple lines in Fig. 10). We find that R and S generally exhibit variations with Q that lie between those expected for channels at equilibrium and those expected for channels evolving at constant hydraulic radius. At low discharge (, Q<1 m3 s−1) during the early and late melt season (Fig. 10 ①) our derived changes in S and R with Q approach the theoretical prediction for channels behaving at equilibrium. At high discharge (, Q>1 m3 s−1; mid-May to early October; Fig. 10 ②) changes in S and R with changes in Q significantly depart from predictions of channels at equilibrium and approach one of the channels evolving out of equilibrium through changes in S solely. The transition between the two regimes herein observed is quite abrupt for S, which switches from being a decreasing to being an increasing function of Q. For R, the transition is marked by a weaker dependency on Q, as the latter is high. During the period when , the best data fit of R with Q gives R ∝ Q0.27 ∝ Q6∕22, and for the periods when , it gives . The latter scaling is similar to the predicted scaling of calculated using the theory of Röthlisberger (1972) assuming channels at equilibrium.
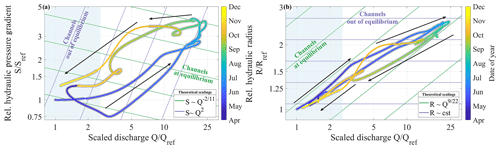
Figure 10(a) Relative hydraulic pressure gradient and (b) hydraulic radius as inverted from seismic observations and as shown as a function of measured relative water discharge . Time series of R and S are calculated from 5 d low-pass-filtered time series of Q and Pw and are then 30 d low-pass-filtered (same as in Fig. 8). Time series of Q is 30 d low-pass-filtered. Reference values for all three variables are taken as the first day of the 2017 melt season (10 May 2017). We compare our data to the predictions of Röthlisberger (1972) for subglacial channels evolving at equilibrium with Q (green lines; and ) and for subglacial channels evolving through hydraulic pressure gradient changes only (blue lines; S∝Q2 and ). Arrows show the direction of time. Blue shaded areas represent the period when Q is lower than 1 m3 s−1. Line sections without the black edges show interpolated values of R and S using a cubic spline interpolation, as in Fig. 8.
6.1 Evaluating potential bias from changes in the number and position(s) of channel(s)
As stated in Sect. 2, the subglacial channel-flow-induced seismic power Pw depends on the number of subglacial channels N (Eqs. 10 and 11) and on the source-to-station distance, which we both considered to be constant in our analysis. Here we discuss how much potential changes in N and in channels' positions may bias our inversions of S and R. On the one hand, given the glacier configuration in our study area (250 m thick, 500 m wide; Fig. 2a), channel-to-seismic station distance is similar regardless of whether channels are located at the glacier centre or on its sides. Therefore, we do not expect changes in channel spatial positions to bias our inverted values of R and S. On the other hand, we estimate how much the observed changes in Pw would require changes in N if they were to be explained only by an evolving number of channels rather than evolving S or R. From Eq. (10) we know that S weakly depends on N rather than Pw and on water discharge Q. As a result, explaining the measured variations in Pw while imposing the S constant would require N to change by more than 4 orders of magnitude (541∕6), which is unrealistic. From Eq. (11) we know that R weakly depends on N rather than Q. As a result, explaining Pw variations while imposing R as a constant would require N to change by more than factor of 30 (), which is also likely unrealistic, since at the onset of the melt season, channels are expected to form an arterial network, with few channels being kept over summer (Schoof, 2010; Werder et al., 2013). Therefore, we expect potential changes neither in channel positions nor in N to cause significant bias in our inverted values of R and S.
6.2 Implications for inferring water discharge using seismic noise
As opposed to Gimbert et al. (2016), who inferred few variations in hydraulic pressure gradient over its 2-month-long period of survey on the Mendenhall Glacier, on Glacier d'Argentière we infer high and sustained channel pressurization over the whole summer and early fall (June–October). This has implications for the physics of subglacial channels, which we further discuss in Sect. 6.3, and also for our capacity to invert for discharge Q based on observed seismic power P. If one considers the equilibrium assumption over the melt season, this yields, under Röthlisberger (1972) steady-state equilibrium assumptions, the scaling Q ∝ (see Eqs. 6 and 12). When applied over the melt season using our observations of Pw at Glacier d'Argentière, this underestimates the measured discharge by more than 65 %. As shown in Fig. 10, such an assumption is only valid for the early and late melt season, when both discharge and its variability are low. Using the approximation may be more appropriate for periods of low meltwater input and in settings with limited water input variability such as in Antarctica. If one now considers the empirical relationship obtained from the period of channels to be out of equilibrium (using Eq. 6 and ; see Sect. 5.5), this leads to an uncertainty of less than 10 % on the estimated water discharge over the melt season at Glacier d'Argentière. We therefore suggest that the relationship may be preferred for inverting discharge based on seismic observations during periods of high meltwater input and in settings with strong seasonal variability in water input (e.g. Alpine and Greenland glaciers).
6.3 Implications for subglacial hydrology and ice dynamics
6.3.1 Understanding channels approaching equilibrium at low subglacial water discharge
During the early melt season (, Q<1 m3 s−1; Figs. 5 and 10) channels are inferred to approach an equilibrium situation for which hydraulic pressure gradient scales weakly with changes in subglacial water discharge (Fig. 10). This behaviour supports that the channel's hydraulic capacity is sufficient to accommodate water input at this time of the year. We propose that, at those times, changes in water supply occur at a rate that is lower than that at which channels adjust their hydraulic radius. During the early melt season, low rates in water input changes are likely caused by water supply from melt being highly damped by the snow cover (Marshall et al., 1994; Fleming and Clarke, 2005). During the late melt season (; Fig. 10), the cause of low rates in water input is less clear. We suggest that such rates could be induced by englacial stored water being slowly released (Flowers and Clarke, 2002; Jansson et al., 2003). Because of the well-developed drainage system at those times, channels could also adjust their hydraulic radius faster than during the early melt season and therefore could behave at equilibrium for higher rates in water input than during the early melt season.
6.3.2 Using periods when channels approach equilibrium to estimate channels' size and number
Using Eqs. (6) and (8) of Hooke (1984) that predict the conditions of equilibrium for steady-state channels and assuming that total discharge is equally distributed over channels of identical geometry (R channels), we find that in our case equilibrium is predicted if the number of channels lies between four and six (using an ice thickness of 250 m, a down-glacier surface slope of 5∘ and a total water discharge of 1 m3 s−1; see Appendix B). For a lower (higher) number of channels, discharge per channel and thus channel-wall melt is higher (lower) than the expected channel-wall creep, which violates the equilibrium condition. Our estimate of four to six channels is consistent with the numerical modelling results of Werder et al. (2013) of four to five dominant channels lying below the Gornergletscher tongue (CH), a glacier which has a geometry similar to that of the tongue of Glacier d'Argentière (ca. 500 m wide, ca. 300 m maximum thickness). Further insights on the spatial evolution of the subglacial drainage system could be gained using seismic arrays to locate the source(s) of subglacial flow-induced-seismic noise (Lindner et al., 2020).
We propose estimating the absolute size of channels at the season initiation based on the channel number previously proposed. With 5±1 channels and 1 m3 s−1 equally distributed discharge, the average discharge per channel is about 0.20±0.05 m3 s−1 (uncertainty is obtained from that on channels' number). Considering that subglacial flow-induced-seismic noise is likely sensitive to water flow speed of the order of 1 m s−1 (Gimbert et al., 2016) we can estimate a minimal channel cross-section area of about 0.20±0.05 m2 and a resulting channel radius of 0.35±0.05 m (for semi-circular R-shaped channels). We note that absolute inversions of R and S could be done by explicitly formulating Green's function G in Eq. (1) and be compared to the present estimation using channels at equilibrium. However, this is beyond the scope of this study.
6.3.3 Understanding highly pressurized channels during the summer season
At water discharges higher than 1 m3 s−1 (Fig. 5b) and relative changes in water discharge Q higher than 4 (; Figs. 8 and 10) the hydraulic pressure gradient S in channels remains high (Fig. 10). Considering that bed slope is constant, these high S values require channels to be full and pressurized. During these periods of high discharge, as S increases with relative changes in Q (Fig. 10a), channels respond to changes in discharge in the same way as theoretically expected for cavities but not for channels by Schoof (2010). Such a behaviour is therefore opposed to the theoretical steady-state predictions of Schoof (2010) and Werder et al. (2013) that instead prove that channels have decreasing water pressure as they develop over the summer.
Using Hooke (1984) and our estimate of five channels made in Sect. 6.3.2, we find that in our case channel-wall melt (i.e. opening rate) is expected to dominate ice creep (i.e. closing rate) for Q>1 m3 s−1 (see Sect. B for details on the calculation). At steady state this should either lead to channel growth and/or to an abrupt decrease in S down to a free-flow situation (i.e. atmospheric pressure). These two scenarios are not observed during summer, since R stays mainly constant (i.e. limited channel growth) and S presents high values supporting closed flow over hourly timescales. We propose that the summer channel pressurization (high S) is due to channels responding to marked diurnal and short-term changes in water supply (as theoretically described in Schoof, 2010) and that channels behave out of equilibrium because changes in water input occur at a rate that is higher than that at which channels can adjust their hydraulic radius.
This interpretation is supported by our diurnal analysis on R and S evolution. In the morning, S is inferred to rise earlier than R (Fig. 9), suggesting that channel-wall melt does not accommodate the increase in Q fast enough and causes pressurized flow. As water supply increases, channels start to respond to the water input and grow by channel-wall melt, leading to a delayed hydraulic radius R increase compared to S (Fig. 9). At the same time the channel capacity increases with R (Röthlisberger, 1972), leading to a decrease in S before Q reaches a maximum, as shown in Fig. 9. During the afternoon, as the water supply decreases, R slowly decreases by much less than a percent per hour (Fig. 9). At this rate, ice creep is capable of adjusting changes in R fast enough in order to limit open channel flow (Fig. S6). This could explain why S does not show an abrupt decrease down to the early melt season values as one would expect if open channel low were to occur (Fig. 9). The hydraulic pressure gradient therefore builds up from day to day over the summer. During night-time, as Q is at its minimum, the closure rate still adjusts channel size and therefore allows R to remain nearly constant through summer. This proposed scenario is consistent with both the investigated diurnal dynamics in the hydraulic properties and may explain the unexpected pressurized channels during summer. Estimation of melt and creep rates calculated from Hooke (1984) in a similar manner to Sect. 6.3.2 supports the plausibility of such diurnal dynamics (see Appendix Sect. B for details). Further measurements remain to be conducted on glaciers with different geometries (e.g. flatter), different bed conditions (e.g. soft-bed glaciers) and different spatialization of water input (e.g. discrete water input through moulins) to evaluate the effect of such parameters on the subglacial hydrology dynamics. For instance, it is possible that our proposed channel's dynamic is limited to hard-bedded glaciers, as soft-bedded glaciers have the capacity to store water and possibly damp the pronounced short-term variability in water supply. In such a set-up, sediment erosion would complement ice wall melt and allow channels to be kept at a much lower hydraulic pressure gradient than described in our study.
6.3.4 Channel dynamics, cavity water pressure and basal sliding
Our observations and subsequent analysis (Figs. 8 and 10) indicate that over the summer channels are pressurized and behave out of equilibrium. On the other hand, during summer the glacier sliding speed remains high, especially in 2018 (Fig. 5), which shows that the average basal water pressure (which is mainly set by pressure in cavities) is also high. These concomitantly high pressures in channels and in cavities suggest that the two systems may be well connected.
During summer, because of channel-flow pressurization, the channel system does not operate under a significantly lower hydraulic potential than that of the cavity system. This would therefore prevent significant water flow from cavities to channels and leads to cavities that are kept pressurized. This sustained high water pressure at the glacier basis favours high glacier sliding speed over summer. Such a channel–cavity-sliding link has been previously suggested (Hubbard and Nienow, 1997; Andrews et al., 2014; Rada and Schoof, 2018) but was not based on an independent analysis of the cavities and channels' hydraulic conditions that we propose here through combining seismic and basal sliding speed measurements. We suggest that during these periods of pronounced short-term variability in water supply, the whole drainage system becomes well-connected, although with limited drainage capacity. Thus the channel system may participate in maintaining high pressure in cavities and thus high sliding speed during periods of high water-supply variability. Short-term variability in water supply may lead to pronounced glacier acceleration even during situations of a well-developed channel network. Such a subglacial hydrology and ice dynamics link deserves further investigation through combination of seismic observations and subglacial hydrology and ice dynamics models (e.g. Gagliardini and Werder, 2018). Indeed a better understanding of the impact of short-lived water input on glacier dynamics is necessary, as under climate warming short-term climatic variability and extreme event occurrences are expected to increase (Hynčica and Huth, 2019), potentially causing greater glacier acceleration than previously thought (e.g. Tedstone et al., 2015).
We investigate the physics of subglacial channels and its link with basal sliding beneath an Alpine glacier (Glacier d'Argentière, French Alps) through the analysis of a unique 2-year-long dataset made of on-ice-measured subglacial water-flow-induced seismic power and in situ-measured glacier basal sliding speed. Our study shows that the theory of Gimbert et al. (2016) is consistent with our observations and that the analysis of the seismic power measured within the 3–7 Hz frequency range allows studying the subglacial drainage properties over a complete melt season and down to diurnal timescales.
We quantify temporal changes in channels' hydraulic radius and hydraulic pressure gradient using the theory of Gimbert et al. (2016) and measurements of water discharge concomitant with our seismic record. Our approach allows isolating subglacial water-flow-induced seismic power from that of other seismic sources and makes observing changes at various timescales (from seasonal to hourly) and water discharge ranges (from 0.25 to 10 m3 s−1) possible. At seasonal timescales, we prove, for the first time, that hydraulic radius and hydraulic pressure gradient both present at least a 2-fold increase from spring to summer, followed by a comparable decrease towards autumn. Comparing our analysis to the theoretical predictions of Röthlisberger (1972) we identify that channel dynamics over the season is characterized by two distinct regimes still unprecedentedly reported. At low discharge during the early and late melt season our analysis proves that channels respond to changes in discharge mainly through changes in hydraulic radius and that the strong changes in hydraulic radius and weak changes in pressure gradient are similar to those predicted by theory for channels behaving at equilibrium. We propose that, at those times, changes in water input occur at a rate that is lower than that at which channels adjust their hydraulic radius. During the early melt season, these low rates in water input changes are likely caused by water supply from melt being highly damped by the snow cover. From this equilibrium channel-dynamics condition we are able to estimate the number of channels, which we find to be between four and six, with each channel having a radius of about 0.5 m in the early melt season that may go up to 2 m in summer. At high discharge and high short-term water-supply variability (often during summertime) we show that channels undergo strong changes in hydraulic pressure gradient, a behaviour that is not expected for channels at equilibrium. Instead, those changes in hydraulic pressure gradient are well reproduced by theory under the end-member consideration of no changes in channel geometry in response to changes in water input. We propose that, at those times, channels behave out of equilibrium because changes in water input occur at a rate that is much higher than that at which channels adjust their hydraulic radius. This interpretation is supported by R and S behaviours at the diurnal scale, which show that channels pressurize in the early morning and depressurize in the afternoon as their hydraulic radius slowly grows concomitantly with the water-supply rise. At night when water discharge decreases, ice creep then allows channels to recover their initial early morning hydraulic radius. We do not capture a significant decrease in the hydraulic pressure gradient during those days, which indicates that the hydraulic pressure gradient builds up from day-to-day concomitantly with a hydraulic radius that is kept nearly constant. Channels may thus remain pressurized over the whole summer because of the short-term (diurnal, rain) variability in water supply, which forces channels to respond through a transient-dynamic state. We expect our analysis of subglacial hydrology to be applicable to glaciers of similar geometry (relatively steep U-shaped valley glaciers) and similar highly variable and distributed water supply to Glacier d'Argentière.
Channels behaving out of equilibrium during most of the melt season also have implications for the use of subglacial water-flow-induced seismic power Pw to invert for water discharge Q. The empirical relationship between Q and Pw that we derive during the period when channels are out of equilibrium allows estimating a water discharge from seismic noise with an error of less than 10 %, while an error of 65 % is obtained when assuming channels at equilibrium. Our presently proposed out-of-equilibrium relationship for inverting discharge could be applied in settings with strong seasonal variability in water supply (e.g. Alpine and Greenland glaciers). During summer we also observe high and sustained basal sliding, proving that the widespread inefficient drainage system (cavities) is likely pressurized. We propose that channels also being pressurized may help sustain high pressure in cavities and thus high glacier sliding speed.
These results demonstrate that on-ice passive seismology is an efficient tool to overcome the classical observational limitations faced when investigating subglacial hydrology processes. In this respect, our results bring new constraints on channels' physics; on links between channels, cavities and sliding; and on the use of passive seismology to invert for subglacial water discharge. In future, an essential step towards strengthening our knowledge on the physics of subglacial processes would be to assess the applicability of our findings over a wider range of glacier geometries (e.g. soft bed glaciers and ice sheets) both through extended on-site seismic survey and the use of our seismically derived observations as constraints for subglacial hydrology and ice dynamics models.
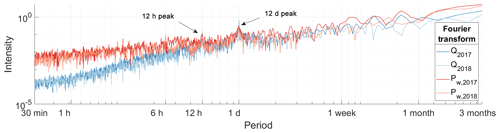
We show in Fig. A1 the power spectrum of the water discharge Q (blue lines) and subglacial channel-flow-induced seismic power Pw as a function of the period. We observe, for both variables, a well-defined peak at the 1 d and 12 h period. This shows that these signals present clear diurnal and sub-diurnal variability and supports our choice to bandpass-filter these signals within 6–36 h to study these short-term variabilities.
We used in this study the Eqs. (6) and (8) of Hooke (1984) to evaluate the theoretical melt rate and creep rate , as follows:
with H being the ice thickness, β the down-glacier surface slope, and C2 and C3 the constant. We use the values of Hooke (1984) for the two constants: and m s. For the glacier geometry we use an ice thickness of 250 m and a down-glacier surface slope of 5∘.
Table C1Summary of all variables, physical quantities and mathematical functions used in the main text.
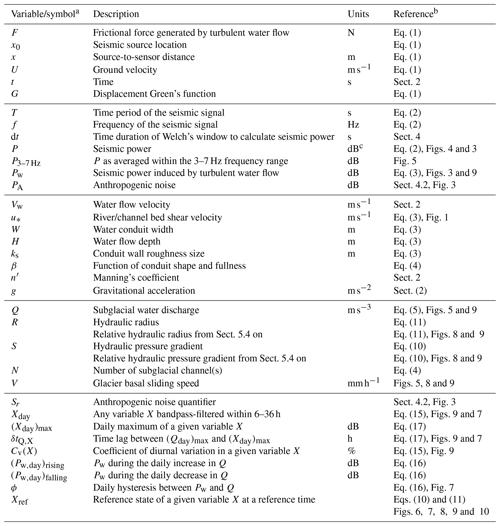
a First section lists variables characterizing the propagation of seismic wave, second section lists variables characterizing the seismic power properties, third section lists variables and constants related the physical properties of river flow, fourth section lists variables characterizing the hydraulic and glaciological properties of the subglacial drainage system, and fifth section lists the indicators defined to investigate subglacial water flow properties. b Relevant occurrences in the main text of the variables, physical quantities and mathematical functions. c Decimal logarithmic space (relative to (m s−1) 2 Hz−1).
Time series of physical quantities shown in Figs. 5 and 8 can be found at https://doi.org/10.5281/zenodo.3701520 (Nanni et al., 2020). The complete dataset will be made publicly available in future. Ongoing work is taking place to meet the format and documentation required for the release for the complete seismic survey, which is expected to happen fully or partially by mid-2021. In the meantime, it is available on request from the corresponding author. The Python and SAC codes for seismic power calculation are given in the Supplement, and additional codes can be found at https://doi.org/10.5281/zenodo.3731508 (Nanni, 2020).
The supplement related to this article is available online at: https://doi.org/10.5194/tc-14-1475-2020-supplement.
UN, FG and CV designed the study. UN performed the seismic analysis, with input from FG and FW. UN interpreted the results, with input from FG. UN led the writing of the paper, and FG, CV, FW and DG contributed to it. LP and LM were in charge of the basal sliding speed measurements. All authors participated to field installations.
The authors declare that they have no conflict of interest.
We thank Jordi Bolibar, Coline Bouchayer, Jacques Brives, Julien Brondex, Jay Chowdhry, Simon Escalle, Adrien Gilbert, Bruno Jourdain, Olivier Laarman, Bradley Lipovsky, Nathan Maier, Antoine Palenstijn, Olivier Passalacqua, Lukas Preiswerk, Antoine Rabatel, Victor Ramseyer, Victor Tsai, Benoit Urruty and Jonathan Wille for assistance in the field. We are indebted to Electricité Emosson SA (hydroelectric company) for the water discharge measurements and access to the subglacial galleries and the French GLACIOCLIM project for temperature and precipitation data (https://glacioclim.osug.fr/, last access: 28 April 2020). We thank Nikos Germenis for technical support on the ARG seismic network (https://geobit-instruments.com/, last access: 28 April 2020). Ugo Nanni would like to thank Jordi Bolibar, Basile de Fleurian and Lukas Preiswerk for fruitful discussions.
This research has been supported by the Agence Nationale de la Recherche (grant nos. ANR-17-CE01-0008 and ANR-18-CE01-0015).
This paper was edited by Nanna Bjørnholt Karlsson and reviewed by two anonymous referees.
Aki, K. and Richards, P. G.: Quantitative seismology, University Science Books, US, 2002. a
Allstadt, K. and Malone, S. D.: Swarms of repeating stick-slip icequakes triggered by snow loading at Mount Rainier volcano, J. Geophys. Res.-Earth, 119, 1180–1203, 2014. a
Anderson, S. P., Longacre, S. A., and Kraal, E. R.: Patterns of water chemistry and discharge in the glacier-fed Kennicott River, Alaska: evidence for subglacial water storage cycles, Chem. Geol., 202, 297–312, 2003. a
Andrews, L. C., Catania, G. A., Hoffman, M. J., Gulley, J. D., Lüthi, M. P., Ryser, C., Hawley, R. L., and Neumann, T. A.: Direct observations of evolving subglacial drainage beneath the Greenland Ice Sheet, Nature, 514, 80–83, 2014. a, b, c
Bartholomaus, T. C., Anderson, R. S., and Anderson, S. P.: Response of glacier basal motion to transient water storage, Nat. Geosci., 1, p. 33, 2008. a
Bartholomaus, T. C., Anderson, R. S., and Anderson, S. P.: Growth and collapse of the distributed subglacial hydrologic system of Kennicott Glacier, Alaska, USA, and its effects on basal motion, J. Glaciol., 57, 985–1002, 2011. a
Bartholomaus, T. C., Amundson, J. M., Walter, J. I., O'Neel, S., West, M. E., and Larsen, C. F.: Subglacial discharge at tidewater glaciers revealed by seismic tremor, Geophys. Res. Lett., 42, 6391–6398, 2015. a, b, c
Bartholomew, I., Nienow, P., Mair, D., Hubbard, A., King, M. A., and Sole, A.: Seasonal evolution of subglacial drainage and acceleration in a Greenland outlet glacier, Nat. Geosci., 3, 408–411, 2010. a
Brondex, J., Gagliardini, O., Gillet-Chaulet, F., and Durand, G.: Sensitivity of grounding line dynamics to the choice of the friction law, J. Glaciol., 63, 854–866, 2017. a
Burtin, A., Bollinger, L., Vergne, J., Cattin, R., and Nábělek, J.: Spectral analysis of seismic noise induced by rivers: A new tool to monitor spatiotemporal changes in stream hydrodynamics, J. Geophys. Res.-Sol. Ea., 113, 2294–2301, 2008. a
Burtin, A., Cattin, R., Bollinger, L., Vergne, J., Steer, P., Robert, A., Findling, N., and Tiberi, C.: Towards the hydrologic and bed load monitoring from high-frequency seismic noise in a braided river: The “torrent de St Pierre”, French Alps, J. Hydrol., 408, 43–53, 2011. a
Chandler, D., Wadham, J., Lis, G., Cowton, T., Sole, A., Bartholomew, I., Telling, J., Nienow, P., Bagshaw, E., Mair, D., et al.: Evolution of the subglacial drainage system beneath the Greenland Ice Sheet revealed by tracers, Nat. Geosci., 6, 195–198, 2013. a, b
Church, G., Bauder, A., Grab, M., Rabenstein, L., Singh, S., and Maurer, H.: Detecting and characterising an englacial conduit network within a temperate Swiss glacier using active seismic, ground penetrating radar and borehole analysis, Ann. Glaciol., 60, 193–205, 2019. a
Collins, D. N.: Quantitative determination of the subglacial hydrology of two Alpine glaciers, J. Glaciol., 23, 347–362, 1979. a
Copland, L., Harbor, J., and Sharp, M.: Borehole video observation of englacial and basal ice conditions in a temperate valley glacier, Ann. Glaciol., 24, 277–282, 1997. a
de Fleurian, B., Werder, M. A., Beyer, S., Brinkerhoff, D. J., Delaney, I., Dow, C. F., Downs, J., Gagliardini, O., Hoffman, M. J., Hooke, R. L., et al.: SHMIP The subglacial hydrology model intercomparison Project, J. Glaciol., 64, 897–916, 2018. a, b, c
Doyle, S. H., Hubbard, A., Fitzpatrick, A. A., As, D., Mikkelsen, A. B., Pettersson, R., and Hubbard, B.: Persistent flow acceleration within the interior of the Greenland ice sheet, Geophys. Res. Lett., 41, 899–905, 2014. a
Fleming, S. W. and Clarke, G. K.: Attenuation of high-frequency interannual streamflow variability by watershed glacial cover, J. Hydraul. Eng., 131, 615–618, 2005. a
Flowers, G. E.: Modelling water flow under glaciers and ice sheets, P. Roy. Soc. A-Math. Phy., 471, 20140907, https://doi.org/10.1098/rspa.2014.0907, 2015. a, b
Flowers, G. E. and Clarke, G. K.: A multicomponent coupled model of glacier hydrology 1. Theory and synthetic examples, J. Geophys. Res.-Sol. Ea., 107, 2287, https://doi.org/10.1029/2001JB001122, 2002. a
Fountain, A. G. and Walder, J. S.: Water flow through temperate glaciers, Rev. Geophys., 36, 299–328, 1998. a, b
Gagliardini, O. and Werder, M. A.: Influence of increasing surface melt over decadal timescales on land-terminating Greenland-type outlet glaciers, J. Glaciol., 64, 700–710, 2018. a, b
Gagliardini, O., Cohen, D., Råback, P., and Zwinger, T.: Finite-element modeling of subglacial cavities and related friction law, J. Geophys. Res.-Earth, 112, F02027, https://doi.org/10.1029/2006JF000576, 2007. a
Gimbert, F., Tsai, V. C., and Lamb, M. P.: A physical model for seismic noise generation by turbulent flow in rivers, J. Geophys. Res.-Earth, 119, 2209–2238, 2014. a, b, c, d, e
Gimbert, F., Tsai, V. C., Amundson, J. M., Bartholomaus, T. C., and Walter, J. I.: Subseasonal changes observed in subglacial channel pressure, size, and sediment transport, Geophys. Res. Lett., 43, 3786–3794, 2016. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s
Gräff, D., Walter, F., and Lipovsky, B. P.: Crack wave resonances within the basal water layer, Ann. Glaciol., 60, 158–166, 2019. a
Hantz, D. and Lliboutry, L.: Waterways, ice permeability at depth, and water pressures at Glacier d’Argentiere, French Alps, J. Glaciol., 29, 227–239, 1983. a, b, c
Hewitt, I.: Seasonal changes in ice sheet motion due to melt water lubrication, Earth Planet. Sc. Lett, 371, 16–25, 2013. a, b
Hoffman, M. J., Andrews, L. C., Price, S. F., Catania, G. A., Neumann, T. A., Lüthi, M. P., Gulley, J., Ryser, C., Hawley, R. L., and Morriss, B.: Greenland subglacial drainage evolution regulated by weakly connected regions of the bed, Nat. Commun., 7, 13903, https://doi.org/10.1038/ncomms13903, 2016. a
Hooke, R. L.: On the role of mechanical energy in maintaining subglacial water conduits at atmospheric pressure, J. Glaciol., 30, 180–187, 1984. a, b, c, d, e
Hooke, R. L., Wold, B., and Hagen, J. O.: Subglacial hydrology and sediment transport at Bondhusbreen, southwest Norway, Geol. Soc. Am. Bull., 96, 388–397, 1985. a
Hubbard, B. and Nienow, P.: Alpine subglacial hydrology, Quaternary Sci. Rev., 16, 939–955, 1997. a
Hynčica, M. and Huth, R.: Long-term changes in precipitation phase in Europe in cold half year, Atmos. Res., 227, 79–88, 2019. a
Iken, A. and Bindschadler, R. A.: Combined measurements of subglacial water pressure and surface velocity of Findelengletscher, Switzerland: conclusions about drainage system and sliding mechanism, J. Glaciol., 32, 101–119, 1986. a
Iken, A. and Truffe, M.: The relationship between subglacial water pressure and velocity of Findelengletscher, Switzerland, during its advance and retreat, J. Glaciol., 43, 328–338, 1997. a
Jansson, P., Hock, R., and Schneider, T.: The concept of glacier storage: a review, J. Hydrol., 282, 116–129, 2003. a
Joughin, I., Smith, B. E., and Howat, I.: Greenland Ice Mapping Project: ice flow velocity variation at sub-monthly to decadal timescales, The Cryosphere, 12, 2211–2227, https://doi.org/10.5194/tc-12-2211-2018, 2018. a
Lindner, F., Walter, F., Laske, G., and Gimbert, F.: Glaciohydraulic seismic tremors on an Alpine glacier, The Cryosphere, 14, 287–308, https://doi.org/10.5194/tc-14-287-2020, 2020. a, b
Lliboutry, L.: General theory of subglacial cavitation and sliding of temperate glaciers, J. Glaciol., 7, 21–58, 1968. a, b
Manning, R., Griffith, J. P., Pigot, T., and Vernon-Harcourt, L. F.: On the flow of water in open channels and pipes, Ireland, Transactions of the Institution of Civil Engineers of Ireland, 1891. a
Marshall, S., Roads, J. O., and Glatzmaier, G.: Snow hydrology in a general circulation model, J. Climate, 7, 1251–1269, 1994. a
Nanni, U.: Codes to Process Seismic Data on Glacier from Quantification of seasonal and diurnal dynamics of subglacial channels using seismic observations on an Alpine Glacier, Zenodo, https://doi.org/10.5281/zenodo.3731508, 2020. a
Nanni, U., Gimbert, F., Vincent, C., Gräff, D., Walter, F., Piard, L., and Moreau, L.: DATA of Quantification of seasonal and diurnal dynamics of subglacial channels using seismic observations on an Alpine Glacier, Zenodo, https://doi.org/10.5281/zenodo.3701520, 2020. a
Nienow, P., Sharp, M., and Willis, I.: Seasonal changes in the morphology of the subglacial drainage system, Haut Glacier d'Arolla, Switzerland, Earth Surf. Proc. Land., 23, 825–843, 1998. a
Nienow, P., Hubbard, A., Hubbard, B., Chandler, D., Mair, D. W. F., Sharp, M., and Willis, I.: Hydrological controls on diurnal ice flow variability in valley glaciers, J. Geophys. Res.-Earth, 110, F04002, https://doi.org/10.1029/2003JF000112, 2005. a
Nienow, P. W., Sharp, M., and Willis, I. C.: Velocity–discharge relationships derived from dye tracer experiments in glacial meltwaters: implications for subglacial flow conditions, Hydrol. Process., 10, 1411–1426, 1996. a
Nye, J.: Water flow in glaciers: jökulhlaups, tunnels and veins, J. Glaciol., 17, 181–207, 1976. a
Palmer, S., Shepherd, A., Nienow, P., and Joughin, I.: Seasonal speedup of the Greenland Ice Sheet linked to routing of surface water, Earth Planet. Sc. Lett., 302, 423–428, 2011. a
Parizek, B. R. and Alley, R. B.: Implications of increased Greenland surface melt under global-warming scenarios: ice-sheet simulations, Quaternary Sci. Rev., 23, 1013–1027, 2004. a
Preiswerk, L. E. and Walter, F.: High-Frequency (>2 Hz) Ambient Seismic Noise on High-Melt Glaciers: Green's Function Estimation and Source Characterization, J. Geophys. Res.-Earth, 123, 1667–1681, 2018. a, b
Rada, C. and Schoof, C.: Channelized, distributed, and disconnected: subglacial drainage under a valley glacier in the Yukon, The Cryosphere, 12, 2609–2636, https://doi.org/10.5194/tc-12-2609-2018, 2018. a, b, c, d
Richards, K., Sharp, M., Arnold, N., Gurnell, A., Clark, M., Tranter, M., Nienow, P., Brown, G., Willis, I., and Lawson, W.: An integrated approach to modelling hydrology and water quality in glacierized catchments, Hydrol. Process., 10, 479–508, 1996. a
Roth, D. L., Brodsky, E. E., Finnegan, N. J., Rickenmann, D., Turowski, J. M., and Badoux, A.: Bed load sediment transport inferred from seismic signals near a river, J. Geophys. Res.-Earth, 121, 725–747, 2016. a
Röthlisberger, H.: Water pressure in intra-and subglacial channels, J. Glaciol., 11, 177–203, 1972. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o
Schmandt, B., Aster, R. C., Scherler, D., Tsai, V. C., and Karlstrom, K.: Multiple fluvial processes detected by riverside seismic and infrasound monitoring of a controlled flood in the Grand Canyon, Geophys. Res. Lett., 40, 4858–4863, 2013. a, b
Schoof, C.: The effect of cavitation on glacier sliding, in: Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, The Royal Society, 461, 609–627, 2005. a
Schoof, C.: Ice-sheet acceleration driven by melt supply variability, Nature, 468, 803–806, 2010. a, b, c, d, e, f, g
Seaberg, S. Z., Seaberg, J. Z., Hooke, R. L., and Wiberg, D. W.: Character of the englacial and subglacial drainage system in the lower part of the ablation area of Storglaciären, Sweden, as revealed by dye-trace studies, J. Glaciol., 34, 217–227, 1988. a
Sole, A., Nienow, P., Bartholomew, I., Mair, D., Cowton, T., Tedstone, A., and King, M. A.: Winter motion mediates dynamic response of the Greenland Ice Sheet to warmer summers, Geophys. Res. Lett., 40, 3940–3944, 2013. a, b
Strickler, A.: Contributions to the question of a velocity formula and roughness data for streams, channels and closed pipelines, Lab. of Hydraul. and Water Resources, California Institute of Technology, 1981. a
Sugiyama, S., Skvarca, P., Naito, N., Enomoto, H., Tsutaki, S., Tone, K., Marinsek, S., and Aniya, M.: Ice speed of a calving glacier modulated by small fluctuations in basal water pressure, Nat. Geosci., 4, 597–600, https://doi.org/10.1038/ngeo1218, 2011. a
Sundal, A. V., Shepherd, A., Nienow, P., Hanna, E., Palmer, S., and Huybrechts, P.: Melt-induced speed-up of Greenland ice sheet offset by efficient subglacial drainage, Nature, 469, 521–524, https://doi.org/10.1038/nature09740, 2011. a
Tedstone, A. J., Nienow, P. W., Sole, A. J., Mair, D. W., Cowton, T. R., Bartholomew, I. D., and King, M. A.: Greenland ice sheet motion insensitive to exceptional meltwater forcing, P. Natl. Acad. Sci. USA, 110, 19719–19724, 2013. a
Tedstone, A. J., Nienow, P. W., Gourmelen, N., Dehecq, A., Goldberg, D., and Hanna, E.: Decadal slowdown of a land-terminating sector of the Greenland Ice Sheet despite warming, Nature, 526, 692–695, 2015. a, b
Theakstone, W. H. and Knudsen, N. T.: Temporal changes of glacier hydrological systems indicated by isotopic and related observations at Austre Okstindbreen, Okstindan, Norway, 1976–87, Ann. Glaciol., 13, 252–256, 1989. a
Tranter, M., Brown, G. H., Hodson, A. J., and Gurnell, A. M.: Hydrochemistry as an indicator of subglacial drainage system structure: a comparison of alpine and sub-polar environments, Hydrol. Process., 10, 541–556, 1996. a
Tranter, M., Sharp, M., Brown, G., Willis, I., Hubbard, B., Nielsen, M., Smart, C., Gordon, S., Tulley, M., and Lamb, H.: Variability in the chemical composition of in situ subglacial meltwaters, Hydrol. Process., 11, 59–77, 1997. a
Tsai, V. C., Minchew, B., Lamb, M. P., and Ampuero, J.-P.: A physical model for seismic noise generation from sediment transport in rivers, Geophys. Res. Lett., 39, L02404, https://doi.org/10.1029/2011GL050255, 2012. a
Vincent, C. and Moreau, L.: Sliding velocity fluctuations and subglacial hydrology over the last two decades on Argentière glacier, Mont Blanc area, J. Glaciol., 62, 805–815, https://doi.org/10.1017/jog.2016.35, 2016. a, b
Vincent, C., Soruco, A., Six, D., and Le Meur, E.: Glacier thickening and decay analysis from 50 years of glaciological observations performed on Glacier d’Argentière, Mont Blanc area, France, Ann. Glaciol., 50, 73–79, 2009. a
Vivian, R. and Bocquet, G.: Subglacial cavitation phenomena under the glacier d’Argentière, Mont Blanc, France, J. Glaciol., 12, 439–451, 1973. a, b, c
Vivian, R. A. and Zumstein, J.: Hydrologie sous-glaciaire au glacier d'Argentière (Mont-Blanc, France), IAHS-AISH P., 95, 53–64, 1973. a
Walder, J. and Hallet, B.: Geometry of former subglacial water channels and cavities, J. Glaciol., 23, 335–346, 1979. a
Welch, P.: The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms, IEEE T. Acoust. Speech, 15, 70–73, 1967. a
Werder, M. A., Hewitt, I. J., Schoof, C. G., and Flowers, G. E.: Modeling channelized and distributed subglacial drainage in two dimensions, J. Geophys. Res.-Earth, 118, 2140–2158, 2013. a, b, c, d
Willis, I. C., Sharp, M. J., and Richards, K. S.: Configuration of the drainage system of Midtdalsbreen, Norway, as indicated by dye-tracing experiments, J. Glaciol., 36, 89–101, 1990. a
Zwally, H. J., Abdalati, W., Herring, T., Larson, K., Saba, J., and Steffen, K.: Surface melt-induced acceleration of Greenland ice-sheet flow, Science, 297, 218–222, 2002. a
- Abstract
- Introduction
- Rational
- Field set-up
- Methodology
- Results
- Discussion
- Conclusions
- Appendix A: Frequency content of the water discharge and the subglacial channel-flow-induced seismic power
- Appendix B: Evaluating theoretical melt and creep rates with equations of Hooke (1984)
- Appendix C: Notations
- Code and data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Rational
- Field set-up
- Methodology
- Results
- Discussion
- Conclusions
- Appendix A: Frequency content of the water discharge and the subglacial channel-flow-induced seismic power
- Appendix B: Evaluating theoretical melt and creep rates with equations of Hooke (1984)
- Appendix C: Notations
- Code and data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement