the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Brief communication: Pancake ice floe size distribution during the winter expansion of the Antarctic marginal ice zone
Alberto Alberello
Miguel Onorato
Luke Bennetts
Marcello Vichi
Clare Eayrs
Keith MacHutchon
Alessandro Toffoli
The size distribution of pancake ice floes is calculated from images acquired during a voyage to the Antarctic marginal ice zone in the winter expansion season. Results show that 50 % of the sea ice area is made up of floes with diameters of 2.3–4 m. The floe size distribution shows two distinct slopes on either side of the 2.3–4 m range, neither of which conforms to a power law. Following a relevant recent study, it is conjectured that the growth of pancakes from frazil forms the distribution of small floes (D<2.3 m), and welding of pancakes forms the distribution of large floes (D>4 m).
- Article
(1986 KB) - Full-text XML
- BibTeX
- EndNote
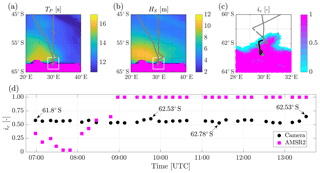
Figure 1Environmental conditions on 4 July 2017 (local time UTC+2). Peak wave period (a) and significant wave height (b) are sourced from ECMWF ERA-Interim reanalysis. The magenta area denotes ice and grey dots show the ship track. In (c), which is the subdomain indicated by a white frame in (a) and (b), ice concentration is sourced from the AMSR2 satellite with a 3.125 km resolution (Beitsch et al., 2014). The black dots denote the position during which cameras were operational and measurements were undertaken. The green cross shows the location of deployment of a wave buoy. In (d), pancake floe concentration reconstructed from the camera images is shown as black dots, and total ice concentration obtained from AMSR2 satellite at the location closest to the measurements is shown as magenta squares.
Prognostic floe size distributions are being integrated into the next generation of large-scale sea ice models (Bennetts et al., 2017; Horvat and Tziperman, 2015; Roach et al., 2018a; Zhang et al., 2015, 2016). Early results show that the floe size distribution affects ice concentration and volume close to the ice edge in the marginal ice zone, where ocean waves regulate floe sizes and floes are generally the smallest, meaning they are prone to melting in warmer seasons (Steele, 1992). However, at present the only field data available to validate and improve the models are empirical distributions derived for pack ice spanning several orders of magnitude (Toyota et al., 2016) and none resolve floes below the metre scale.
The break up of pack ice often resembles fractal behaviour similar to many brittle materials (Gherardi and Lagomarsino, 2015). It has been argued that the exceedance probability of the characteristic floe size, D, expressed as the number of floes, follows a power law , where the scaling exponent is α=2 if a fractal behaviour is assumed (Rothrock and Thorndike, 1984).
Most of the previous observations of the floe size distribution in the marginal ice zone (noting that no observations are in pancake ice conditions) conform to a truncated power law (Stern et al., 2018), with the α value varying among studies depending on season, distance from the ice edge and a range of measured diameters. Some observations of floe size distributions have been interpreted using a split power law (Toyota et al., 2016), with a mild slope for smaller floes and a steeper one for larger floes. In most cases, the sharp change in slope is an artefact due to finite size effects (Stern et al., 2018), although in few instances the split power law behaviour might be consistent with the data (Stern et al., 2018). The truncated power law cannot explain two different slopes in the probability density function n(D), suggesting that different mechanisms might in fact govern the distributions for small and large floes (Steer et al., 2008).
The power law behaviour has been verified for most cases but its universality has not been demonstrated yet (Horvat and Tziperman, 2017). Scaling parameters are typically estimated on the log–log plane with a least square fit, which leads to biased estimates of α, and, as noted by Stern et al. (2018), without rigorous goodness-of-fit tests. In comparison, Herman et al. (2018) examined the size distribution of floes under the action of waves in controlled laboratory experiments, by analysing the probability density function n(D), which revealed a fractal response due to an arbitrary strain (a power law) superimposed on a Gaussian break-up process induced by the waves. The interplay of these mechanisms is hidden in the floe number exceedance probability.
Existing observations do not provide quantitative descriptions of the floe size distribution for pancake ice floes, which form from frazil ice under the continuous action of waves and thermodynamic freezing processes (Roach et al., 2018b; Shen et al., 2004). This is important, for example, during the Antarctic winter sea ice expansion, when hundreds of kilometres of ice cover around the Antarctic continent is composed of pancake floes of roughly circular shape and characteristic diameters of 0.3–3 m (Worby et al., 2008). Pancake floes represent most of the Antarctic sea ice annual mass budget (Wadhams et al., 2018). Moreover, in the Arctic, pancakes are becoming more frequent than in the past due to the increased wave intensity associated with the ice retreat (Roach et al., 2018b; Wadhams et al., 2018).
Shen and Ackley (1991) reported pancake floe sizes from aerial observations collected during the Winter Weddell Sea Project (July 1986), showing that pancake sizes increase with distance from the ice edge, from 0.1 m in the first 50 km up to ≈1 m within 150 km from the edge (but without investigating the floe size distribution). They attributed this to the dissipation of wave energy with distance to the ice-covered ocean and proposed a relationship between wave characteristics, mechanical ice properties and pancake size (Shen et al., 2004). More recently, Roach et al. (2018b) used camera images acquired from SWIFT buoys deployed in the Beaufort Sea (Sea State cruise, October–November 2015) to quantify the lateral growth of pancakes and their welding. A correlation between wave properties and the size of relatively small pancakes (up to 0.35 m) was confirmed.
To our knowledge, the pancake floe size distribution has yet to be characterized, noting that, although Parmiggiani et al. (2017) developed an algorithm for pancake floe detection, they did not provide a quantitative indication of the shape and size of the floes. Here, a new set of images from the Antarctic marginal ice zone is used to measure the shape of individual pancakes to infer their size distribution.
At approximately 07:00 UTC on 4 July 2017, the icebreaker S.A. Agulhas II entered the marginal ice zone between 61 and 63∘ S and approximately 30∘ E during an intense storm (see Fig. 1a, b for the ship track and a snapshot of peak wave period and significant wave height as sourced from ECMWF ERA-Interim reanalysis, Dee et al., 2011). A buoy was deployed in the marginal ice zone ≈100 km from the ice edge (green mark in Fig. 1c). At the time of deployment, the significant wave height was 5.5 m, with maximum individual wave height of 12.3 m. The dominant wave period was 15 s.
A system of two GigE monochrome industrial CMOS cameras with a 2∕3 inch sensor was installed on the monkey bridge of the icebreaker to monitor the ocean surface. The cameras were equipped with 5 mm C-mount lenses (maximum aperture f∕1.8) to provide a field of view of approximately 90∘. The cameras were installed at an elevation of ≈34 m from the waterline and with their axes inclined at 20∘ with respect to the horizon. The system was operated by a laptop computer. Images were recorded with a resolution of 2448×2048 pixels and a sampling rate of 2 Hz during daylight hours on 4 July (from 07:00 to 13:30 UTC).
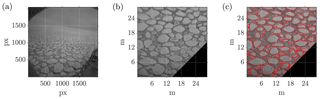
An automatic algorithm was developed using the MatLab Image Processing Toolbox (Kong and Rosenfeld, 1996) to extract sea ice metrics from the recorded images (see Fig. 2a for an example). To ensure statistical independence of the data set (i.e. to avoid sampling the same floe twice), only one camera and one image was selected every 10 s for processing (this interval guarantees no overlap between consecutive images). Images were rectified to correct for camera distortion and to project them on a common horizontal plane. A pixel to metre conversion was applied by imposing camera-dependent calibration coefficients. The resulting field of view is 28 m×28 m and the resolution of 29 px m−1 (see Fig. 2b). The image was processed to eliminate the vessel from the field of view, adjust the image contrast and convert the grey scales into a binary map based on a user-selected threshold. The mapping isolates the solid ice shapes from background water or frazil ice. The binary images, however, are noisy and require refining based on morphological image processing to improve the fidelity of the shape of identified pancake floes (i.e. erosion, filling and expansion). Threshold selection and morphological operations are optimized to detect pancake floes only and exclude interstitial frazil ice. (The optimization is performed for the specific light and ice conditions using this particular camera set-up.) The resulting separated floes are shown in Fig. 2c. Post-processed images were visually inspected for quality control, and ≈5 % of the images were discarded due to unsatisfactory reconstruction of the pancakes. Macroscopic differences between the acquired image and the reconstructed floes were noted; e.g. multiple floes were detected as one (artificial welding) or individual floes were divided by the automatic algorithm into multiple floes.
Identification of individual pancakes allows an estimation of the individual floe areas S. An overall ice concentration (ic, Fig. 1d) can be computed as the ratio of the area covered by pancake floes to the total surface in the field of view. A representative concentration was estimated every 60 consecutive images (i.e. 10 min time window), which is equivalent to a sampled area of 0.047 km2. Pancake concentration was consistently ≈60 %, with no significant variations throughout the day (Fig. 1d). The observed pancake concentration diverged from satellite observations (AMSR2) of sea ice concentration (see Fig. 1d), as the AMSR2 concentration includes the interstitial frazil ice, which is intentionally excluded from the image processing (i.e. detection of pancake ice only). Moreover, satellite data are an average over two daily swaths. Due to the intense storm activity and the associated drift of the ice edge (≈100 km eastward in a day) at that time, this average may not be fully representative of the instantaneous conditions, resulting in an under- or overestimation of the in situ ice concentration. In this regard, bridge observations following the Antarctic Sea Ice Processes and Climate protocol (Worby et al., 2008) indicated a 90 %–100 % concentration of total ice, where pancake ice was the primary ice type, with a concentration of 50 %–60 % for most of the cruise (de Jong et al., 2018), in agreement with the image processing.
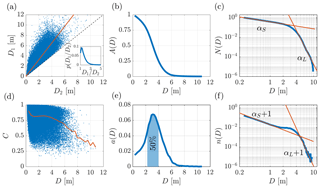
Figure 3In (a) is the scatter plot of the major and minor axis of the pancake floe with the linear fit (solid orange line), the inset shows the probability density function of D1∕D2. In (b) is the ice area distribution as a function of the floe diameter expressed as the exceedance probability. In (c) is the floe number exceedance probability N(D) as a function of the floe diameter with two power laws (solid orange lines) fitted for small (D<2.3 m) and large floes (D>4 m). In (d) is the scatter plot of the circularity of the floes against the equivalent diameter and the average value (solid orange line). In (e) is the ice area distribution as a function of the floe diameter expressed as probability density function. In (f) is the floe number probability density function n(D) as a function of the floe diameter with two power laws (solid orange lines) fitted for small (D<2.3 m) and large floes (D>4 m).
By approximating the floe shape as an ellipse, major (D1) and minor (D2) axes are extracted. It is common practice, however, to define one representative dimension as a characteristic diameter , by assuming that the pancake is a disk (Toyota et al., 2016), noting that other metrics are also widely used, e.g. the mean caliper diameter (Rothrock and Thorndike, 1984). Only floes entirely within the field of view are considered for these operations. Detecting small floes with D<0.25 m is prone to error due to the limited number of pixels of which these floes are comprised and, thus, excluded from the analysis (Toyota et al., 2011). Moreover, a small fraction of large floes (<10 % of floes larger than 5 m) were artificially welded by the image processing. These floes were also excluded. In total, 4×105 individual floes were considered over an equivalent sampled area of ≈1.55 km2 and spanned almost 100 km of the non-contiguous marginal ice zone.
Figure 3a presents a scatter plot of the aspect ratio D1:D2. On average D1 is ≈60 % greater than D2 (slope of a linear fit). This aspect ratio is similar to the one observed for broken ice floes (Toyota et al., 2011). The inset shows the full probability distribution of the ratio D1∕D2 and indicates that floes elongated such that are infrequent. Figure 3d shows the circularity , where P is the floe perimeter (for a circle C=1), which characterizes the shape of the floes, noting that other metrics can be used to define the roundness of the floes (Hwang et al., 2017). For floes up to D≈6 m, the average circularity, denoted by the continuous line, is C≥0.75. Similar values have been reported for much larger broken floes (Lu et al., 2008).
Figure 3b and 3e display the floe size area distribution as the exceedance probability and probability density function. Figure 3e shows that, in terms of the equivalent diameter (D), 50 % of the pancake area is comprised of floes with diameters in the range 2.3–4 m. The mode of the area distribution is 3.1 m (median and mean are ≈3.1 m and ≈3.2 m) compared to D1=4 m and D2=2.6 m, using the major and the minor axes.
Figure 3c shows the exceedance probability N(D), which exhibits two distinct slopes in the log–log plot, with a smooth transition from mild to steep slopes around the dominant diameter of 3.1 m. The probability density function of the equivalent diameter n(D), shown in Fig. 3f, displays a pronounced hump in the transition between these regimes, revealing a third regime (2.3 m m) around the modal pancake diameter, which is hidden in the exceedance probability, where the small- and large-floe regimes are defined as D<2.3 m and D>4 m (somewhat arbitrarily).
Small floes (D<2.3 m) constitute the vast majority of the total detected floes (>80 %). In this regime, the mild slope of N(D) may result from a continuous process of floe accretion (from frazil to larger pancakes) regulated predominantly by thermodynamic freezing processes (Roach et al., 2018b). Floes larger than 4 m are detected far less frequently (<5 % of the total floes), and the steeper slope indicates that their size is most likely governed by different underlying physical mechanisms. Visual examination of the acquired images shows that the majority of the large floes are composed of two or more welded pancakes, suggesting that the welding process, promoted by the high concentration of pancakes and the presence of interstitial frazil ice (Roach et al., 2018b), could be the dominant underlying mechanism for the shape of the probability distribution of large floes. Finite size effects are ruled out because the change in slope occurs for D≈4 m, which is considerably smaller than the image footprint.
Assuming, as standard, a power law as a benchmark and using the maximum likelihood method following Stern et al. (2018), we determine for small floes (D<2.3 m) and for large floes (D>4 m). (Note that the maximum recorded diameter was D=10.8 m, and, therefore, the estimation of the scaling exponent is not particularly meaningful or robust in either of the two regimes, as less than a decade of length scales are available.)
The power-law fits are approximations only, and an objective Kolmogorov–Smirnov goodness-of-fit test (Clauset et al., 2009) reveals that the empirical pancake size distribution does not scale accordingly to a power law in either the small- or large-floe regime, noting the power law hypothesis is more likely to be rejected when tested over limited diameter ranges (i.e. less than a decade). A close inspection of the empirical distribution shows that N(D) possesses a slightly concave-down curvature across all the diameter ranges (in a log–log plane), which is commonly associated with a truncated power law (Stern et al., 2018). The corresponding n(D) displays an S shape in the small-floe regime (it shifts from a concave-down to a concave-up curvature at D≈1 m) in contrast to the hypothesis of a power law behaviour. Deviations from the power law scaling are prominent towards the extremes of the intervals (D→0.25 m and D→2.3 m for the small-floe regime; D→4 m and D→10 m for the large-floe regime) but become conspicuous only by examining the empirical distribution over limited diameter ranges and probability intervals (i.e. zooming in on Fig. 3c–f). We also note that the increasing a(D) in the small-floe regime (Fig. 3e) is inconsistent with a power law for αS≥1, as the area and number distributions are proportional to each other, i.e. a(D)∝D2n(D). Values of αS≥1 may be because the exponent has been estimated over a range of less of decade of diameters, making its estimation non-robust. The discrepancy between area and number distribution confirms that the underlying number distribution is not a power law, although we note that provides a qualitatively good fit for the number distribution and is consistent with the growing area distribution.
Goodness-of-fit tests also rule out floe size distributions such as the truncated power law (Stern et al., 2018), generalized Pareto (Herman, 2010) and linear combination of Gaussian distribution and power law (Herman et al., 2018). It appears that an accurate approximation of the floe size distribution (in the goodness-of-fit sense) can only be achieved by dropping any a priori assumptions on the functional shape, e.g. by using a non-parametric kernel density estimation (Botev et al., 2010). However, this does not provide any insight into the underlying physical processes responsible for the shape of the empirical distribution.
Observations of pancake ice floe sizes during the winter expansion of the Antarctic marginal ice zone were analysed. An automatic floe detection algorithm was used to extract metrics (diameter and area) of the pancake floes, for which the equivalent diameter () ranged between 0.25 and 10 m. This allowed a quantitative representation of the pancake size distribution to be discussed.
The floe size distribution displays three distinct regimes, which are visible in the probability density function that, compared to the commonly reported exceedance probability, is more informative. One regime is D=2.3–4 m, centred around the dominant pancake diameter of 3.1 m, which covers half of the total pancake area, and appears as a hump in the probability density function. Two different behaviours are observed for smaller and larger pancakes on a log–log plane. The small-floe regime (D<2.3 m), in which it is conjectured that pancakes are experiencing thermodynamic growth, is characterized by a mild negative slope (in terms of the floe number exceedance and probability density function), while the large-floe regime, in which floes are typically formed by welding (detected from visual analysis), is characterized by a much steeper slope, noting that neither of the two regimes conform to a power law scaling.
These results reflect observations collected under storm conditions and, thus, lack generality. Simultaneous measurements of waves, floe size and heat fluxes under a number of different conditions are needed to verify the conjecture that different physical mechanisms (e.g. thermodynamic growth and welding) are responsible for the peculiar shape of the pancake ice floe size distribution.
The detection algorithm and the acquired images are available upon request to the corresponding author.
The algorithm for the pancake detection is developed using the MatLab Image Processing Toolbox and built-in functions.
-
Rectification: this projects the distorted camera image on an horizontal plane based on the camera internal parameters and the angle of view.
-
Contrast adjustment: contrast in the greyscale image is enhanced based on a CLAHE algorithm (the limit for clipping and shape of the distribution are user selected) to better isolate the pancakes from the frazil ice.
-
Masking: the removes the ship from the field of view.
-
Binary conversion: the greyscale image is converted into a binary image where 1 corresponds to white (i.e. ice) and 0 to water or frazil (the threshold for conversion is user selected).
-
Cleaning: this morphological operation removes isolated white pixels (i.e. 1s completely surrounded by 0s).
-
Erosion: this morphological operation helps to separate the blobs corresponding to the pancakes (the erosion value is user selected).
-
Filling: this morphological operation substitute 0 s with 1 s in area completely enclosed by white pixels.
-
Dilatation: this morphological operation counterbalance the ice pixels lost by the erosion without merging two separate blobs.
-
Clear border: this removes blobs intersecting the border of the field of view.
-
Labelling and properties extraction: geometrical properties of each individual floe are extracted.
All thresholds are user selected and the parameters have been subjected to testing to find the combination of operations that provided the best reconstruction as evaluated by the user's visual inspection.
AA, MO and AT acquired the images. AA, MO, LB and AT conceived the manuscript. AA analysed the images. MV, CE and KM provided satellite images, buoys measurements and ASPeCt observations. All authors contributed to the data interpretation and to the writing of the manuscript.
The authors declare that they have no conflict of interest.
The cruise was funded by the South African National Antarctic Programme
through the National Research Foundation. This work was motivated by the
Antarctic Circumnavigation Expedition (ACE) and partially funded by the ACE
Foundation and Ferring Pharmaceuticals. Support from the Australian Antarctic
Science Program (project 4434) is acknowledged. Miguel Onorato was supported
by the “Departments of Excellence 2018–2022” grant awarded by the Italian
Ministry of Education, University and Research (MIUR) (L.232/2016).
Clare Eayrs was supported under NYUAD Center for the Global Sea Level Change
project G1204. The authors thank Lotfi Aouf at Meteo France for providing
reanalysis data and the editor, Ted Maksym, for useful comments.
Alberto Alberello and Alessandro Toffoli acknowledge support from the
Air-Sea-Ice Lab Project. Miguel Onorato acknowledges Barbara GiuliNico for
interesting discussions. Alberto Alberello, Alessandro Toffoli and
Miguel Onorato thank Le Fascette for technical support during the cruise.
Edited by: Ted Maksym
Reviewed
by: Christopher Horvat and one anonymous referee
Beitsch, A., Kaleschke, L., and Kern, S.: Investigating high-resolution AMSR2 sea ice concentrations during the February 2013 fracture event in the Beaufort Sea, Remote Sens., 6, 3841–3856, https://doi.org/10.3390/rs6053841, 2014. a
Bennetts, L. G., O'Farrell, S., and Uotila, P.: Brief communication: Impacts of ocean-wave-induced breakup of Antarctic sea ice via thermodynamics in a stand-alone version of the CICE sea-ice model, The Cryosphere, 11, 1035–1040, https://doi.org/10.5194/tc-11-1035-2017, 2017. a
Botev, Z. I., Grotowski, J. F., and Kroese, D. P.: Kernel density estimation via diffusion, Ann. Stat., 38, 2916–2957, 2010. a
Clauset, A., Shalizi, C., and Newman, M.: Power-Law Distributions in Empirical Data, SIAM Rev., 51, 661–703, https://doi.org/10.1137/070710111, 2009. a
Dee, D., Uppala, S., Simmons, A., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A., Haimberger, L., Healy, S., Hersbach, H., Hólm, E., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A., Monge-Sanz, B., Morcrette, J., Park, B., Peubey, C., de Rosnay, P. C. T., Thépaut, J., and Vitart, F.: The ERA–Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a
de Jong, E., Vichi, M., Mehlmann, C. B., Eayrs, C., De Kock, W., Moldenhauer, M., and Audh, R. R.: Sea Ice conditions within the Antarctic Marginal Ice Zone in WInter 2017, onboard the SA Agulhas II, https://doi.org/10.1594/PANGAEA.885211, 2018. a
Gherardi, M. and Lagomarsino, M. C.: Characterizing the size and shape of sea ice floes, Sci. Rep., 5, 10226, https://doi.org/10.1038/srep10226, 2015. a
Herman, A.: Sea-ice floe-size distribution in the context of spontaneous scaling emergence in stochastic systems, Phys. Rev. E, 81, 066123, https://doi.org/10.1103/PhysRevE.81.066123, 2010. a
Herman, A., Evers, K.-U., and Reimer, N.: Floe-size distributions in laboratory ice broken by waves, The Cryosphere, 12, 685–699, https://doi.org/10.5194/tc-12-685-2018, 2018. a, b
Horvat, C. and Tziperman, E.: A prognostic model of the sea-ice floe size and thickness distribution, The Cryosphere, 9, 2119–2134, https://doi.org/10.5194/tc-9-2119-2015, 2015. a
Horvat, C. and Tziperman, E.: The evolution of scaling laws in the sea ice floe size distribution, J. Geophys. Res.-Oceans, 122, 7630–7650, https://doi.org/10.1002/2016JC012573, 2017. a
Hwang, B., Wilkinson, J., Maksym, E., Graber, H. C., Schweiger, A., Horvat, C., Perovich, D. K., Arntsen, A. E., Stanton, T. P., Ren, J., and Wadhams, P.: Winter-to-summer transition of Arctic sea ice breakup and floe size distribution in the Beaufort Sea, Elem. Sci. Anth., 5, p. 40, https://doi.org/10.1525/elementa.232, 2017. a
Kong, T. Y. and Rosenfeld, A.: Topological algorithms for digital image processing, vol. 19, Elsevier, 1996. a
Lu, P., Li, Z. J., Zhang, Z. H., and Dong, X. L.: Aerial observations of floe size distribution in the marginal ice zone of summer Prydz Bay, J. Geophys. Res.-Oceans, 113, C02011, https://doi.org/10.1029/2006JC003965, 2008. a
Parmiggiani, F., Moctezuma-Flores, M., and Guerrieri, L.: Identifying pancake ice and computing pancake size distribution in aerial photographs, in: Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions 2017, vol. 10422, International Society for Optics and Photonics, 2017. a
Roach, L., Horvat, C., Dean, S., and Bitz, C.: An emergent Sea Ice Floe Size Distribution in a Global Coupled Ocean–Sea Ice Model, J. Geophys. Res.-Oceans, 123, 4322–4337, https://doi.org/10.1029/2017JC013692, 2018a. a
Roach, L., Smith, M., and Dean, S.: Quantifying Growth of Pancake Sea Ice Floes Using Images From Drifting Buoys, J. Geophys. Res.-Oceans, 123, 2851–2866, https://doi.org/10.1002/2017JC013693, 2018b. a, b, c, d, e
Rothrock, D. A. and Thorndike, A. S.: Measuring the sea ice floe size distribution, J. Geophys. Res.-Oceans, 89, 6477–6486, https://doi.org/10.1029/JC089iC04p06477, 1984. a, b
Shen, H. H. and Ackley, S. F.: A one-dimensional model for wave-induced ice-floe collisions, Ann. Glaciol., 15, 87–95, https://doi.org/10.3189/1991AoG15-1-87-95, 1991. a
Shen, H. H., Ackley, S. F., and Yuan, Y.: Limiting diameter of pancake ice, J. Geophys. Res.-Oceans, 109, C12035, https://doi.org/10.1029/2003JC002123, 2004. a, b
Steele, M.: Sea ice melting and floe geometry in a simple ice-ocean model, J. Geophys. Res.-Oceans, 97, 17729–17738, https://doi.org/10.1029/92JC01755, 1992. a
Steer, A., Worby, A., and Heil, P.: Observed changes in sea-ice floe size distribution during early summer in the western Weddell Sea, Deep-Sea Res. Pt. II, 55, 933–942, https://doi.org/10.1016/j.dsr2.2007.12.016, 2008. a
Stern, H., Schweiger, A., Zhang, J., and Steele, M.: On reconciling disparate studies of the sea-ice floe size distribution, Elem. Sci. Anth., 6, p. 49, https://doi.org/10.1525/elementa.304, 2018. a, b, c, d, e, f, g
Toyota, T., Haas, C., and Tamura, T.: Size distribution and shape properties of relatively small sea-ice floes in the Antarctic marginal ice zone in late winter, Deep-Sea Res. Pt. II, 58, 1182–1193, https://doi.org/10.1016/j.dsr2.2010.10.034, 2011. a, b
Toyota, T., Kohout, A., and Fraser, A. D.: Formation processes of sea ice floe size distribution in the interior pack and its relationship to the marginal ice zone off East Antarctica, Deep-Sea Res. Pt. II, 131, 28–40, https://doi.org/10.1016/j.dsr2.2015.10.003, 2016. a, b, c
Wadhams, P., Aulicino, G., Parmiggiani, F., Persson, P. O. G., and Holt, B.: Pancake Ice Thickness Mapping in the Beaufort Sea From Wave Dispersion Observed in SAR Imagery, J. Geophys. Res.-Oceans, 123, 2213–2237, https://doi.org/10.1002/2017JC013003, 2018. a, b
Worby, A. P., Geiger, C. A., Paget, M. J., Van Woert, M. L., Ackley, S. F., and DeLiberty, T. L.: Thickness distribution of Antarctic sea ice, J. Geophys. Res.-Oceans, 113, C05S92, https://doi.org/10.1029/2007JC004254, 2008. a, b
Zhang, J., Schweiger, A., Steele, M., and Stern, H.: Sea ice floe size distribution in the marginal ice zone: Theory and numerical experiments, J. Geophys. Res.-Oceans, 120, 3484–3498, https://doi.org/10.1002/2015JC010770, 2015. a
Zhang, J., Stern, H., Hwang, B., Schweiger, A., Steele, M., Stark, M., and Graber, H. C.: Modeling the seasonal evolution of the Arctic sea ice floe size distribution, Elem. Sci. Anth., 4, p. 000126, https://doi.org/10.12952/journal.elementa.000126, 2016. a