Buoyant forces promote tidewater glacier iceberg calving through large basal stress concentrations

Iceberg calving parameterisations currently implemented in ice sheet models do not reproduce the full observed range of calving behaviours. For example, though buoyant forces at the ice front are known to trigger full-depth calving events on major Greenland outlet glaciers, a multi-stage iceberg calving event at Jakobshavn Isbræ is unexplained by existing models. To explain this and similar events, we propose a notch-triggered rotation mechanism, whereby a relatively small subaerial calving event triggers a larger full-depth calving event due to the abrupt increase in buoyant load and the associated stresses generated at the ice–bed interface. We investigate the notch-triggered rotation mechanism by applying a geometric perturbation to the subaerial section of the calving front in a diagnostic flow-line model of an idealised glacier snout, using the full-Stokes, finite element method code Elmer/Ice. Different sliding laws and water pressure boundary conditions are applied at the ice–bed interface. Water pressure has a big influence on the likelihood of calving, and stress concentrations large enough to open crevasses were generated in basal ice. Significantly, the location of stress concentrations produced calving events of approximately the size observed, providing support for future application of the notch-triggered rotation mechanism in ice-sheet models.

1 Introduction

Iceberg calving from marine-terminating glaciers is an important component of the Greenland Ice Sheet mass balance. Calving accounted for a third of total mass loss between 2009 and 2012 (Enderlin et al., 2014). Moreover, calving is an important control on the flow dynamics of tidewater glaciers, reducing the backstress in the glacier snout region and leading to flow acceleration and dynamic thinning (Thomas, 2004). The acceleration of Jakobshavn Isbræ (JI, Sermeq Kujalleq in Greenlandic) by a factor of 4 since 1995, for example, is linked with its continued calving retreat following the disintegration of its ice shelf (Joughin et al., 2012).

Current models of iceberg calving fail to capture the full range of observed processes, and as such the parameterisations applied within ice sheet models are limited. Van der Veen (1996) proposed the empirical height-above-flotation criterion, whereby the glacier calves to a point where its terminus is some fixed height above the flotation thickness. Although this method successfully reproduced advance and retreat behaviour for Columbia Glacier (Vieli et al., 2001) and Helheim Glacier (Nick et al., 2009), a major shortcoming was the inability for ice to thin below the flotation thickness and form an ice tongue. A more physically based approach (Benn et al., 2007a, b) assumed that crevasses penetrating to the waterline penetrate through the full glacier thickness. This simple theory has been used in many recent modelling studies (e.g. Otero et al., 2010; Nick et al., 2013; Cook et al., 2014). However, since crevasse depths are calculated based on the equilibrium between longitudinal stretching and ice overburden pressure (Nye, 1957), calving in these models arises only as a result of ice flow dynamics. The effect of localised processes such as meltwater undercutting (Luckman et al., 2015), ice-cliff collapse (Bassis and Walker, 2012) or of super-buoyancy upon near-terminus stresses is not captured in these models.

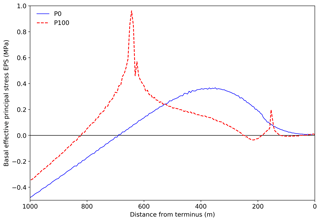
Figure 1 Proposed calving mechanism. (a) Lightly grounded terminus of a tidewater glacier with approximate dimensions of, for example, Jakobshavn Isbræ. (b) A weakness develops in the subaerial section of the front due to, for example, undercutting by a wave-cut notch at the waterline. (c) A small subaerial calving event rapidly increases the buoyant load, causing the terminus to tend to lift and rotate. Basal crevasses open and propagate rapidly upwards. (d) Full-depth crevassing results in a large, bottom-out calving event. The long-term calving rate is driven by the notch melt rate but is amplified by an unconstrained factor.

Buoyant forces have been proposed as a driver of large calving events observed at major Greenland Ice Sheet marine-terminating glaciers. Full-depth, bottom-out calving events observed at Helheim Glacier resulted from buoyant flexure of the glacier snout and the propagation of basal crevasses (e.g. Murray et al., 2015). Wagner et al. (2016) also showed that applying a buoyant force to an elastic beam model of a glacier resulted in large basal tensile stresses, which were further amplified by the emergence of a submarine protrusion of the calving face due to sea surface melting. Buoyant forces may be at play in driving as yet unexplained calving styles.

A multiple-iceberg calving event was observed at JI in August 2009 (Walter et al., 2012) that is not fully explained by existing calving models, but which we propose is tied to buoyant force changes over the course of the multi-stage calving event. In this observation, the collapse of a subaerial portion of the ice cliff was followed minutes later by a much larger, full-depth, bottom-out calving event across the same section of the front. We consider a mechanism to explain this event, whereby a substantial portion of the snout becomes buoyant immediately following a small subaerial calving event, which we term “notch-triggered rotation”. In this mechanism, visualised in Fig. 1, the sudden increase in buoyant load causes the snout to lift and rotate. The resultant basal tensile stresses initiate basal crevassing, which rapidly propagates through the full glacier thickness. This mechanism is similar to the “footloose” mechanism investigated by Wagner et al. (2014) and earlier proposed by Scambos et al. (2005) for the breakup of tabular icebergs. However, in this study we consider the very short timescales arising from abrupt changes in the geometry and analyse the viscous stresses originating at the ice–bed interface rather than the elastic stresses resulting purely from bending.

Using a diagnostic numerical glacier model, we investigate whether notch-triggered rotation is a plausible calving mechanism. With sophisticated prognostic models, calving criteria can be tested by application to real glacier geometries (e.g. Nick et al., 2010; Krug et al., 2014) and the calving rate response to various environmental forcings can be quantified (e.g. Cook et al., 2014; Todd and Christoffersen, 2014). Simpler diagnostic models provide insight into iceberg calving mechanisms by resolving the internal stresses under instantaneously imposed geometries (e.g. Hanson and Hooke, 2000, 2003; O'Leary and Christofferson, 2013). Here we use a diagnostic model that is able to quantify changes in the stress field induced by geometrical perturbations of the ice front.

2 Model setup

In this study we use a two-dimensional diagnostic flow-line model of an idealised glacier snout to determine whether the magnitude of stresses generated by the notch-triggered rotation mechanism is sufficient to result in calving. The mechanisms of crevasse propagation through the ice thickness are not examined. We apply the buoyant forcing in the model by cutting a notch into the subaerial ice cliff to a length l_n from the waterline to the surface (Fig. 2). We use a triangular mesh with a mesh resolution at the ice–bed interface of Δx=4 m at the calving front increasing linearly to Δx=8 m at the rear of the domain. The ice flow solution is calculated using the open source, full-Stokes, finite element Elmer/Ice modelling software (Gagliardini et al., 2013).

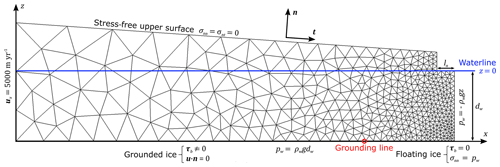
Figure 2 Example mesh and boundary conditions (not to scale). Mesh resolution increases close to the calving front and basal boundaries. Symbols: normal stress σ_nn, shear stress σ_nt.

2.1 Ice flow model

Elmer/Ice calculates velocity and stress profiles within the glacier by solving the Stokes equations for an incompressible fluid (e.g. Gagliardini et al., 2013):

$$\begin{array}{}\text{(1)}& {\displaystyle }\mathrm{\nabla }\cdot \mathit{u}=\mathrm{0},\text{(2)}& {\displaystyle }\mathrm{\nabla }\cdot \mathit{\sigma }+{\mathit{\rho }}_i\mathit{g}=\mathrm{\nabla }\cdot \mathit{\tau }-\mathrm{\nabla }p+{\mathit{\rho }}_{\mathrm{i}}\mathit{g}=\mathrm{0},\end{array}$$

where u is the velocity vector, σ the Cauchy stress tensor, ρ_i=918 kg m⁻³ the ice density, g=(0,0,−9.81) m s⁻² the acceleration due to gravity, τ the deviatoric stress tensor $\mathit{\tau }=\mathit{\sigma }+p\mathbf{I}$, p the isotropic pressure $p=-\mathrm{tr}\left(\mathit{\sigma }\right)/\mathrm{3}$ and I the identity matrix. The ice rheology is described using Glen's flow law, which relates deviatoric stress to the strain rate ${\dot{\mathit{\epsilon }}}_{ij}$ (Glen, 1958):

$$\begin{array}{}\text{(3)}& {\mathit{\tau }}_{ij}=\mathrm{2}\mathit{\mu }{\dot{\mathit{\epsilon }}}_{ij}.\end{array}$$

The effective viscosity μ is defined as follows:

$$\begin{array}{}\text{(4)}& \mathit{\mu }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{A}^{-\mathrm{1}/n}{\dot{\mathit{\epsilon }}}_{\mathrm{e}}^{\left(\mathrm{1}-n\right)/n},\end{array}$$

where ${\dot{\mathit{\epsilon }}}_{\mathrm{e}}^{\mathrm{2}}$ is the square of the second invariant of the strain rate tensor and n=3 is the commonly used exponent in Glen's flow law. The Arrhenius factor A is expressed as follows:

$$\begin{array}{}\text{(5)}& A=A_{\mathrm{0}}\exp \left(-Q/R{T}^{\prime }\right),\end{array}$$

where A₀ is a constant, Q the creep activation energy, R the universal gas constant and T^′ the temperature of ice relative to the pressure melting point (Cuffey and Patterson, 2010, p. 64). For symbols and values used in this study, see Table 1. The temperature of glacier ice is set at a constant −9 ^∘C.

Table 1 Symbols and values of physical and numerical constants and parameters used in this study.

2.2 Boundary conditions

We use typical boundary conditions for a tidewater glacier. Along the upper surface, as well as the rear and lower surfaces delineating the notch when one is present or the subaerial portion of the ice front when not present, we ignore atmospheric pressure and apply a stress-free boundary condition:

$$\begin{array}{}\text{(6)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{nn}}=\mathrm{0},\text{(7)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{nt}}=\mathrm{0},\end{array}$$

where subscripts n and t refer to normal and tangential directions. Hydrostatic pressure is applied at the ice front below the waterline:

$$\begin{array}{}\text{(8)}& p_{\mathrm{w}}=-{\mathit{\rho }}_{\mathrm{w}}\mathit{g}z,\end{array}$$

where p_w is the water pressure, ρ_w=1028 kg m⁻³ the ice density and the vertical z axis is centred at the waterline. At the rear boundary 10 km upstream, lithostatic pressure is applied along with an inflow velocity of 5000 m a⁻¹, chosen to roughly match the flow speed of JI at a similar distance from the calving front (Vieli and Nick, 2011).

At the basal boundary, a choice of sliding laws was available for grounded ice. The Weertman law (Weertman, 1957) commonly used in glacier modelling applications (e.g. Krug et al., 2014; Cornford et al., 2015) takes the following form:

$$\begin{array}{}\text{(9)}& {\mathit{\tau }}_{\mathrm{b}}=-C{\left|{\mathit{u}}_{\mathrm{b}}\right|}^{m-\mathrm{1}}\cdot {\mathit{u}}_{\mathrm{b}},\end{array}$$

with τ_b the basal shear stress, C the Weertman friction coefficient, u_b the basal sliding velocity and sliding exponent $m=\mathrm{1}/\mathrm{3}$. Values of C range from 10⁵ to 10⁸ Pa m${}^{-\mathrm{1}/\mathrm{3}}$ s^1∕3, which includes the more realistic range of modelled values of ∼10⁶ to ∼10⁷ Pa m${}^{-\mathrm{1}/\mathrm{3}}$ s^1∕3 determined from surface velocity observations around Greenland outlet glaciers (Lee et al., 2015).

Alternatively, a Coulomb-limited sliding law (Schoof, 2005; Gagliardini et al., 2007) can be applied (referred to as the “Schoof law” from here onwards). This law accounts for the effect of water pressure through an effective pressure term $N=-{\mathit{\sigma }}_{\mathrm{nn}}-P_{\mathrm{w}}$. Basal shear stress is expressed as follows:

$$\begin{array}{}\text{(10)}& {\mathit{\tau }}_{\mathrm{b}}=-C_{\mathrm{c}}\cdot N{\left({\displaystyle \frac{\mathit{\chi }{\left|{\mathit{u}}_{\mathrm{b}}\right|}^{-n}}{\mathrm{1}+\mathit{\alpha }{\mathit{\chi }}^q}}\right)}^{\frac{\mathrm{1}}{n}}\cdot {\mathit{u}}_{\mathrm{b}},\end{array}$$

where

$$\begin{array}{}\text{(11)}& \mathit{\chi }={\displaystyle \frac{\left|{\mathit{u}}_{\mathrm{b}}\right|}{C_{\mathrm{c}}^n{N}^n{A}_{\mathrm{s}}}},\end{array}$$

and

$$\begin{array}{}\text{(12)}& \mathit{\alpha }={\displaystyle \frac{(q-\mathrm{1}{)}^{q-\mathrm{1}}}{q^q}}.\end{array}$$

C_c=1 is the maximum value of $\left|{\mathit{\tau }}_{\mathrm{b}}\right|/N$, q=1 is the post-peak exponent, A_s is the value of the sliding coefficient in the absence of cavitation and n is the flow law exponent. As in previous studies (e.g. Nick et al., 2010; Krug et al., 2014), a free hydrological connection is assumed between the subglacial drainage system and the sea, so hydrostatic water pressure is applied at the ice–bed interface.

The contact problem (Durand et al., 2009) is solved at the ice–bed interface to determine where ice is grounded or floating. In this implementation, nodes touching the bedrock where the normal stress exerted by the ice is greater than the seawater pressure (σ_nn>p_w(z_b)) are considered grounded and have zero velocity normal to the bed, while nodes that have separated from the bedrock or where σ_nn≤p_w(z_b) are considered floating and have no velocity conditions imposed. The viscous flow relation (Eq. 4), friction law (Eqs. 8 or 9) and the solution-dependent grounding line position are solved during the non-linear iterations of the Stokes equations. Five steady-state loops of the non-linear iterations are performed, during which the glacier geometry is held fixed but the grounding line position is updated according to the pressure at the ice–bed interface. Beyond five iterations, further changes to the stress field are insignificant. The model is initialised with the glacier fully grounded along its entire length.

2.3 Stress analysis

As in other studies (e.g. Nick et al., 2010; Todd et al., 2014), we assess the likelihood of crevasse opening from the magnitude of the resulting stress distribution. The largest principal Cauchy stress σ₁ is coordinate system invariant, accounting for crevasse opening in any direction:

$$\begin{array}{}\text{(13)}& {\mathit{\sigma }}_{\mathrm{1}}={\displaystyle \frac{{\mathit{\sigma }}_{xx}+{\mathit{\sigma }}_{zz}}{\mathrm{2}}}+\sqrt{{\left({\displaystyle \frac{{\mathit{\sigma }}_{xx}-{\mathit{\sigma }}_{zz}}{\mathrm{2}}}\right)}^{\mathrm{2}}+{\mathit{\sigma }}_{xz}^{\mathrm{2}}}.\end{array}$$

Because the overburden pressure beneath a kilometre-thick column of ice is on the order of 10 MPa, σ₁ is negative almost everywhere at depth. Following Benn et al. (2017), we superpose the hydrostatic water pressure to define the effective principal stress (EPS):

$$\begin{array}{}\text{(14)}& \mathrm{EPS}={\mathit{\sigma }}_{\mathrm{1}}+p_{\mathrm{w}}.\end{array}$$

The hydrostatic pressure is similar in magnitude to the ice overburden pressure at the glacier bed.

In previous modelling studies (e.g. Otero et al., 2010; Cook et al., 2012), crevasses were assumed to exist in regions of the glacier where the stress is tensile (σ>0), following the method proposed by Nye (1957). Schulson (2001) suggests a fracture strength of 0.8 MPa for polycrystalline ice at −10 ^∘C with a grain size of 10 mm, with decreasing strength for increasing grain size. In this study we do not calculate crevasse penetration heights; therefore, we do not apply a crevassing or calving criterion. Instead, we infer the existence of crevasses where the EPS is of a similar magnitude to these estimates (∼0.5 MPa).

3 Model results

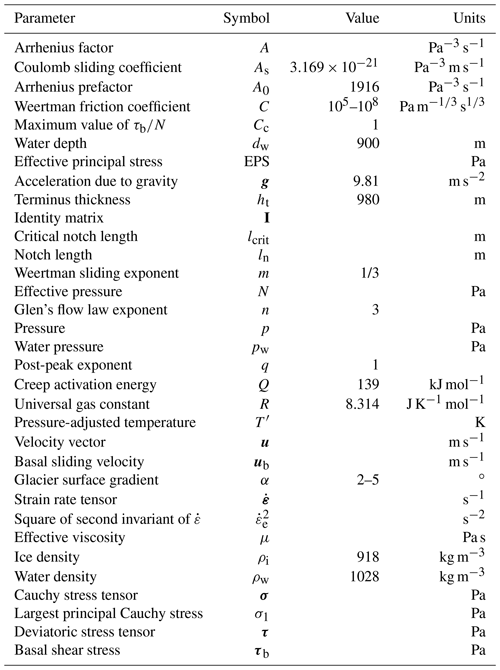
Experiments were run for a glacier with water depth d_w=900 m, terminus thickness h_t=980 m, surface slope α=3^∘ and $C=\mathrm{2.371}\times {\mathrm{10}}^{\mathrm{6}}$ Pa m${}^{-\mathrm{1}/\mathrm{3}}$ s^1∕3, with notches cut to varying lengths. For these experiments, full hydrostatic pressure (Eq. 7) was applied along the basal boundary. Figure 4 shows EPS mapped for the l_n=100 m case, with the l_n=0 m case mapped in Fig. 3 for comparison. Basal stresses are plotted for l_n=0 m, l_n=80 m and l_n=100 m (Fig. 5).

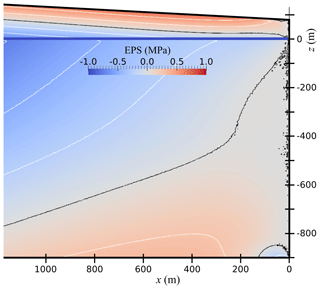
Figure 3 Effective principal stress map of the terminus of the glacier before the cutting of a notch, with d_w=900 m, h_t=980 m, α=3^∘ and $C=\mathrm{5.623}\times {\mathrm{10}}^{\mathrm{6}}$ Pa m${}^{-\mathrm{1}/\mathrm{3}}$ s^1∕3. The black contour denotes EPS = 0 MPa; white contours are spaced at 0.25 MPa intervals.

Notch cutting caused basal ice to become ungrounded between approximately 190 and 640 m upstream of the ice front for l_n=100 m (Fig. 4). Prominent stress concentrations associated with ungrounding and regrounding also appeared at the basal boundary, which were not present in the unperturbed case. The tensile stress peak centred approximately 640 m upstream of the ice front resulted from separation of basal ice from the bedrock, as the buoyant snout tended to lift. The abrupt change in basal shear stress across the grounding zone, where ice that has separated from the bedrock accelerates, gave rise to this stress peak. Further notch-cutting caused this stress peak to shift upstream and increase in magnitude. The substantial growth in concentrated stress at this location to approximately 1.4 MPa would likely result in crevasse opening.

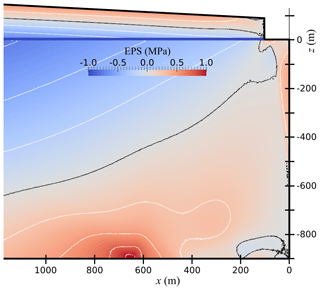
Figure 4 Effective principal stress map of the terminus of the glacier with a notch cut to a length l_n=100 m, with contours at 0.1 MPa spacing. d_w=900 m, h_t=980 m, α=3^∘ and $C=\mathrm{5.623}\times {\mathrm{10}}^{\mathrm{6}}$ Pa m${}^{-\mathrm{1}/\mathrm{3}}$ s^1∕3. Ungrounding occurred between approximately 190 and 640 m. The black contour denotes EPS = 0 MPa; white contours are spaced at 0.25 MPa intervals.

The region of compressive stress centred approximately 190 m upstream of the ice front arose from ice regrounding on the bedrock downstream of the grounding line, due to the backstress applied on the ice front by hydrostatic pressure. An imbalance between the hydrostatic and cryostatic pressure normal to the terminus tends to warp the snout downwards (see Fig. S1 in the Supplement; Reeh, 1968), with the same effect seen at the start of prognostic model runs by Benn et al. (2017). Experiments in which the hydrostatic pressure from the pro-glacial water body was removed or the bedrock lowered downstream of the grounding line, did not include this compressive stress peak while still featuring the tensile stress peak, supporting our assertion that the compressive stress concentration resulted from basal ice regrounding.

Corresponding longitudinal velocity maps for the frontal region are shown in Fig. S2 (unperturbed) and Fig. S3 (l_n=100 m). There is an acceleration of ∼2000 m a⁻¹ following the notch cutting, resulting from the reduced basal friction in the ungrounded region.

A critical notch length l_crit was required before the glacier snout became buoyant and the tensile stress peak appeared. A sensitivity study was carried out to explore the relationship of this critical notch length to the bed stickiness and the glacier surface slope (Fig. 6) and to determine how this relationship affects the maximum basal stress (Fig. 7). Setting the notch length l_n=l_crit resulted in a noisy maximum basal stress signal so we instead set $l_{\mathrm{n}}=l_{\mathrm{crit}}+\mathrm{25}$ m, which allows a coherent pattern to emerge.

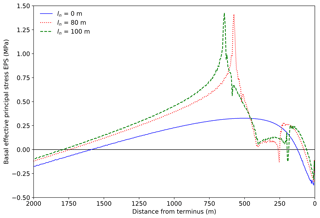
Figure 5 Plots of basal effective principal stress for l_n=0 m, 80 and 100 m. d_w=900 m, h_t=980 m, α=3^∘ and $C=\mathrm{5.623}\times {\mathrm{10}}^{\mathrm{6}}$ Pa m${}^{-\mathrm{1}/\mathrm{3}}$ s^1∕3. The large basal stress concentrations from Fig. 4 correspond to the peak and trough in the l_n=100 m plot. Ungrounding occurred between approximately 250 and 575 m for l_n=80 m and between approximately 190 and 640 m for l_n=100 m. Note that for this setup, the critical notch length l_crit=79 m.

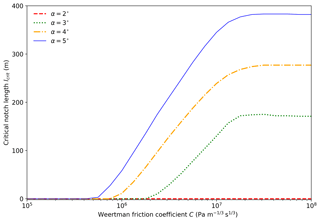
Figure 6 Critical notch length l_crit plotted for a range of Weertman coefficients C and surface gradients α.

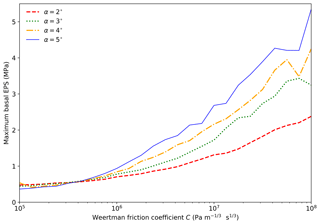
Figure 7 Basal EPS maximum plotted with the notch length equal to l_crit+25 m across a range of Weertman coefficients and surface gradients.

Ungrounding occurred even without a notch on glaciers with very slippery beds for all surface slopes and at all values of the friction coefficient for a 2^∘ surface slope. For steeper surface slopes, the critical notch length increased with bed stickiness before levelling off. For a given value of the friction coefficient, the critical notch length also increased with surface slope. Similarly, the maximum basal stress increased with both friction coefficient and surface slope. For very slippery beds the maximum stress was below the upper boundary of the tensile strength envelope, but significantly it was above the critical stress for crevasse initiation through the realistic range of friction coefficients C=10⁶ to 10⁷ Pa m${}^{-\mathrm{1}/\mathrm{3}}$ s^1∕3.

These experiments reveal a complex picture of the conditions that favour calving. An explanation for the relationship between the critical notch length and bed stickiness does not readily present itself, and this effect may warrant further investigation. The relationships of surface slope with both the critical notch length and the maximum basal stress are more easily explained. The terminus of a steeper sloped glacier is more strongly grounded, requiring the removal of more ice to render it buoyant than would be required for a more gently sloping glacier. The longer submarine foot and larger buoyant forces that result then favour larger basal stresses (e.g. Wagner et al., 2016).

Water pressure dependency

Tidewater glaciers such as JI are subject to the influence of water pressure where they meet the ocean; therefore, it is appropriate to examine the region around the grounding line and calving front using a water pressure-dependent sliding law. Since the large basal stresses were generated by the abrupt change in basal shear stress across the grounding line, a sliding law in which the basal shear stress reduces gradually as a function of effective pressure would not be expected to produce such large stress concentrations. To investigate the effects of water pressure upon the notch-triggered rotation mechanism, experiments were conducted using the Schoof law (Eq. 9). In all following experiments a similar setup as before was used, with α=3^∘, a varying notch length and the sliding coefficient $A_{\mathrm{s}}=\mathrm{3.169}\times {\mathrm{10}}^{-\mathrm{21}}$ Pa⁻³ m s⁻¹, which was chosen to produce roughly similar velocity and basal shear stress as in the Weertman law experiments. Experiments F0 and F100 were carried out with full hydraulic connectivity at the ice–bed interface, and experiments Z0 and Z100 were carried out with zero hydraulic connectivity (i.e. p_w=0 everywhere). See Table 2 for details of parameters used in Schoof law experiments.

Table 2 Hydraulic connectivity along the ice–bed interface for experiments using the Schoof law. Water pressure is 100 % of the full hydrostatic pressure (Eq. 7) downstream of position x₁. Between x₁ and x₀ water pressure reduces linearly to 0 %.

The resulting stress profiles for these experiments are highly dependent on the basal water pressure. Experiments Z0 and Z100 (Fig. 8) exhibited stress patterns very similar to those produced by the Weertman law experiments, although the stress is compressive everywhere due to the exclusion of water pressure, inhibiting any possibility of crevasses opening. However, with full water pressure applied (F0 and F100, Fig. 9), there is a region of large tensile stress that exists independent of any perturbation. Notch cutting has minimal impact on the magnitude or location of this region. This region of large stress exists because the basal shear stress in the frontal region is small, since the effective pressure is zero; therefore, the basal shear stress is increased upstream, and this upstream transferal of stress occurs via a region of increased englacial tensile stress. The magnitude of these stresses suggests an inherent instability for glaciers in such a configuration when subject to full basal water pressure.

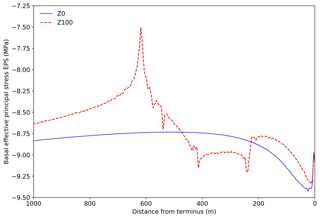
Figure 8 Comparison of basal stresses using the Coulomb sliding law with water pressure inhibited at the ice–bed interface, before (Z0) and after (Z100) cutting of a 100 m notch. Ungrounding occurred between approximately 200 and 380 m for F0, 16 and 510 m for F100 and between approximately 240 and 610 m for Z100. No ungrounding occurred for Z0.

The assumption of perfect hydraulic connectivity, however, may not hold for large distances upstream of the grounding line (Cuffey and Paterson, 2010, p. 283). We therefore carried out additional experiments P0 and P100 (Fig. 10) to simulate limited hydraulic connectivity by linearly reducing the water pressure at the ice–bed interface from full hydrostatic pressure at the front to zero at the rear of the domain (Table 2), similar to Leguy et al. (2014). Experiment P0 shows a region of large tensile stress, similar to but smaller than those seen in experiments F0 and F100. The notch perturbation in experiment P100 results in a stress peak similar to those produced by the Weertman law which is significantly larger in magnitude than the unperturbed stress peak.

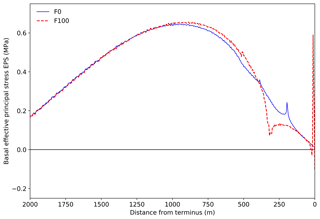
Figure 9 Comparison of basal stresses using the Coulomb sliding law with full water pressure at the ice–bed interface, before (F0) and after (F100) cutting of a 100 m notch. Ungrounding occurred between approximately 200 and 380 m for F0 and between approximately 20 and 510 m for F100.

Figure 10 Comparison of basal stresses using the Coulomb sliding law with partial hydraulic connectivity at the ice–bed interface, before (P0) and after (P100) cutting of a 100 m notch. Ungrounding occurred between approximately 160 and 640 m for P100 and not at all for P0.

4 Discussion

Our experiments show that perturbations to the ice front geometry can induce large stress concentrations in basal ice. The magnitude and location of these stress concentrations shows a strong dependency on the basal shear stress. For a glacier snout already close to flotation, only a relatively small perturbation was required to induce large stresses. This is in line with the observed relationship between calving rate and water depth (Brown et al., 1982).

The large internal stress concentrations reported here are attributed to the requirement to balance the abrupt decrease in basal shear stress across the grounding line and are not associated with bending stresses. This distinction is based on the following observations. Firstly, the region of additional high stress is sharply focused at the glacier bed and is not balanced by a region of compressive stress at the surface as would be expected for a viscous bending moment (Mosbeux et al., 2019). Secondly, the stress concentration is compressive where the ice regrounds further downstream, whereas a bending stress at this location would also be tensile. Finally, we have shown that the form and magnitude of stress is highly dependent upon the choice of sliding law and application of basal water pressure, which would be largely irrelevant for bending stresses.

The choice of diagnostic model for a calving study was criticised by Cook et al. (2014) after their prognostic model showed much greater sensitivity to atmospheric as opposed to oceanic forcing than diagnostic models (O'Leary and Christoffersen, 2013), suggesting that this was due to the inability of a diagnostic model to respond to stress perturbations through ice deformation. However, over the short timescales of interest in this study, deformation of ice is negligible. In our experiments, measured vertical velocities for the ungrounded regions of basal ice were of the order ∼10 m a⁻¹, equating to ∼0.1 mm of lifting over 5 min, which would have negligible effect on the stress field. Therefore, our choice of a diagnostic model is an appropriate one for this study.

As in other diagnostic studies, we did not apply a calving criterion, instead using the location of basal stress peaks as an indication of where crevasses may form. For this to result in calving on the timescale proposed requires the assumption of full-thickness crevassing on timescales much faster than those observed by, e.g. Murray et al. (2015). Given a sufficiently large buoyancy force, this assumption can be held as true, as once a crack has initiated, the tensile stress which opened that crack refocuses at the crack tip causing it to continue to propagate. As the crevasse increases in height, hydrostatic pressure acting to open the crevasse decreases at a faster rate than the ice overburden pressure acting to close it; therefore, larger basal stresses are required for full-depth crevassing than for crevasse initiation. However, once a crevasse has started to propagate and the downstream portion of the snout has begun to lift and rotate, elastic stresses further contribute to the crevasse growth in a feedback process. Benn et al. (2017) reported that glacier geometries that did not result in calving in Elmer/Ice via crevasse depth calving laws still produced large full-depth calving event when exported into HiDEM, a model representing glacier ice as a lattice of particles connected by breakable elastic beams. Further investigation of the rate and modes of crevasse propagation could integrate linear elastic fracture mechanics into a glacier model featuring basal crevasses (van der Veen, 1998) or use a model such as HiDEM in conjunction with Elmer/Ice (Benn et al., 2017).

Our study builds on that of O'Leary and Christoffersen (2013), which also explored the effect of geometrical perturbations at the ice front on the likelihood of calving. Their study found that undercutting led to larger calving events and a higher overall calving rate, which appears to be at odds with the results presented here: undercutting would reduce the buoyant load and potentially stabilise the terminus. Our results differ because the sharp transition in basal shear stress is not possible at the stress-free surface boundary applied here. Furthermore, the geometry of their model was set up to explore surface crevassing while ours was designed to explore basal crevassing. In reality a mixture of these effects may be working together to promote or prohibit calving.

Figure 1 suggests the subaerial calving event may result from undercutting by a waterline notch. Although this process is observed at some glaciers (e.g. Kirkbride and Warren, 1997; Röhl, 2006), it is questionable whether it could be a major factor in the Ilulissat Icefjord (where the original observation was made), in which the loosely bonded melange in summer may act to damp any wave-cutting action (Amundson et al., 2010). An alternative potential mechanism for triggering the subaerial calving event is provided by spontaneous collapse of the ice cliff. The maximum stable cliff height for damaged glacier ice was calculated by Bassis and Walker (2012) as 110 m, while Hanson and Hooke (2003) suggested a maximum stable height of ∼70 m based on diagnostic model experiments. The ice cliffs of JI approach 100 m but rarely exceed this height, suggesting that the inherent instability of ice cliffs may be the limiting factor and could induce calving through notch-triggered rotation.

Buoyancy in a glacier snout can also be induced by thinning due to high surface melt rates. However, the almost immediate increase in buoyant load resulting from the subaerial calving event proposed here occurs on timescales much faster than can be accommodated by ice creep, leading to a higher probability of calving (e.g. Boyce et al., 2007). The specific location of the basal stress peak varied with many parameters, including the notch length but tended to be within one ice thickness of the terminus, consistent with observations (e.g. Walter et al., 2012; Murray et al., 2015). The location of the peak stress always occurred much further back from the terminus than the cliff at the rear of the notch, leading to an amplification of the original subaerial calving event. The value of this amplifying factor cannot be accurately quantified within the limitations of a diagnostic model; however, it may present a method of linking environmental forcings to the calving rate.

There are a number of possible refinements to our model. We ignored lateral drag, which combines with basal shear stress to support the driving stress. Although lateral drag may be negligible along the flow line of wide ice streams, JI was able to form a floating tongue so it must be assumed that lateral drag is significant (e.g. Thomas, 2004). Its omission may have caused the model to overstate the dependence of basal stresses on the basal sliding law. Our model also omits the effect of temperature. The viscosity of ice and transmission of stresses are dependent on thermal gradients. JI has large vertical temperature gradients (Lüthi et al., 2002) and temperate basal ice, which are thought to play a role in its fast sliding. Warmer basal temperatures may act to damp the intensity of basal stress concentrations.

The reader should note that our model geometry is idealised. In reality, glacier beds are highly non-uniform, with variations in geometry, water and overburden pressure across a range of spatial and temporal scales. Bedrock bumps therefore play an important role in controlling the stress transmission upstream. It is plausible that these variations could result in basal stress concentrations of a similar magnitude to the mechanism discussed here.

The notch-triggered rotation mechanism was shown to be irrelevant when using the Schoof law with full water pressure, since a glacier in these conditions would tend to be vulnerable to buoyant calving anyway. This raises the question of whether the Schoof law with full water pressure provides an accurate representation of basal sliding for JI. We expect low effective pressure in the frontal region; however, given that the glacier snout is mostly grounded in the summer (e.g. Amundson et al., 2010), perfect hydraulic connectivity cannot be assumed along the ice–bed interface. Complete suppression of water pressure at the ice–bed interface resulted in a basal stress pattern very similar to the Weertman case, although it was strongly compressive everywhere due to the exclusion of water pressure in the calculation of EPS and is therefore very unlikely to result in crevassing. With $C_{\mathrm{c}}=q=\mathrm{1}$ and $m=\mathrm{1}/n$, as in this study, it can be easily shown that large N (∼10 MPa in the absence of water pressure) leads to small χ and Eq. (9) reduces to a Weertman power law:

$$\begin{array}{}\text{(15)}& {\mathit{\tau }}_{\mathrm{b}}=-A_{\mathrm{s}}^{-m}{\left|{\mathit{u}}_{\mathrm{b}}\right|}^{m-\mathrm{1}}\cdot {\mathit{u}}_{\mathrm{b}}.\end{array}$$

On the other hand, limiting the basal water pressure without suppressing it completely (experiments P0 and P100) resulted in a transition case displaying similar behaviour to both the Weertman and Schoof laws; the unperturbed stress profile was similar to that produced by the Schoof law, but the perturbation resulted in a significantly larger stress peak like those produced by the Weertman law. This raises the possibility that a lightly grounded glacier snout, already in a state of basal tension, could be subjected to high enough stress by a minor subaerial calving event, like that observed at JI (Walter et al., 2012), to cause full depth crevassing and buoyant calving.

5 Conclusions

Our results show that the notch-triggered rotation mechanism does produce calving for an idealised marine-terminating glacier. Although notch-triggered rotation did not significantly affect stresses when applying the Schoof law under full hydrostatic pressure, removing the assumption of perfect hydraulic connectivity at the ice–bed interface greatly enhanced the likelihood of calving through this mechanism. Significantly, a realistic length scale for calving events, on the order of hundreds of metres and generally less than one ice thickness, naturally results from the model physics. Fast-flowing glaciers near flotation and with shallow surface slopes may be especially vulnerable to buoyant calving due to basal crevassing. The notch-triggered rotation mechanism proposed here to explain the observed calving event (Walter et al., 2012) does not replace other models of calving. Instead, it bolsters our understanding of calving by providing insight into multi-stage calving events occurring particularly on large, fast-flowing tidewater glaciers.