the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Multi-year evaluation of airborne geodetic surveys to estimate seasonal mass balance, Columbia and Rocky Mountains, Canada
Brian Menounos
Shawn J. Marshall
Seasonal measurements of glacier mass balance provide insight into the relation between climate forcing and glacier change. To evaluate the feasibility of using remotely sensed methods to assess seasonal balance, we completed tandem airborne laser scanning (ALS) surveys and field-based glaciological measurements over a 4-year period for six alpine glaciers that lie in the Columbia and Rocky Mountains, near the headwaters of the Columbia River, British Columbia, Canada. We calculated annual geodetic balance using coregistered late summer digital elevation models (DEMs) and distributed estimates of density based on surface classification of ice, snow, and firn surfaces. Winter balance was derived using coregistered late summer and spring DEMs, as well as density measurements from regional snow survey observations and our glaciological measurements. Geodetic summer balance was calculated as the difference between winter and annual balance. Winter mass balance from our glaciological observations averaged 1.95±0.09 m w.e. (meter water equivalent), 4 % larger than those derived from geodetic surveys. Average glaciological summer and annual balance were 3 % smaller and 3 % larger, respectively, than our geodetic estimates. We find that distributing snow, firn, and ice density based on surface classification has a greater influence on geodetic annual mass change than the density values themselves. Our results demonstrate that accurate assessments of seasonal mass change can be produced using ALS over a series of glaciers spanning several mountain ranges. Such agreement over multiple seasons, years, and glaciers demonstrates the ability of high-resolution geodetic methods to increase the number of glaciers where seasonal mass balance can be reliably estimated.
- Article
(3957 KB) - Full-text XML
-
Supplement
(1162 KB) - BibTeX
- EndNote
Glaciers are in rapid retreat across western Canada (Menounos et al., 2019). Deglaciation is projected to have pronounced impacts on streamflow in western Canada (Clarke et al., 2015), with the greatest reductions in August and September streamflow as glaciers shrink (Huss and Hock, 2018; Jost et al., 2012). In the Canadian Columbia River basin, peak glacier runoff from ice wastage is either currently underway (Huss and Hock, 2018) or will occur within the next decade (Clarke et al., 2015). Improved projections of changes in glacier runoff will require refined treatment of seasonally varying processes that nourish and deplete glaciers, namely the redistribution of snow by wind and gravitational processes and changes in surface albedo. Seasonal mass balance records are also required to calibrate and validate these physically based mass balance models. These records do not currently exist for the Columbia River basin, however.
In addition to their use in refining estimates of future changes in glacier runoff, mass balance observations provide a valuable synopsis of a glacier's mass budget and its implications for glacier runoff (Jost et al., 2012; Ragettli et al., 2016; Stahl and Moore, 2006), water storage, regional climate (Huss et al., 2008; Radić and Hock, 2014), and contribution to sea level rise (Huss and Hock, 2018). Glacier mass balance is a function of accumulation and ablation processes, responding directly to meteorological forcing at timescales of a season or more (Oerlemans et al., 1998). Measurement of seasonal mass change via in situ and geodetic methods provides a means to assess the importance of meteorological drivers of glacier nourishment and melt. These observations can reveal trends and patterns in glacier mass evolution and are valuable calibration and validation datasets for global (Huss and Hock, 2018; Maussion et al., 2019) and regional glacier models (Clarke et al., 2015), as well as for ingestion into regional hydrologic models (Schnorbus et al., 2014).
Seasonal balance is logistically and financially difficult and globally few seasonal mass balance records exist (Ohmura, 2011). Currently, seasonal balance measurements for western Canadian glaciers are not publicly available (WGMS, 2018). Seasonal snowpack forms a critical component of glacier mass balance (Østrem and Brugman, 1991); it controls the volume and timing of runoff in the snowmelt-dominated tributaries to the Columbia River (Brahney et al., 2017). Like many regions (Barnett et al., 2005), high-elevation snow and precipitation records are limited in the Columbia River basin of Canada. Snow data are routinely only monitored at or below treeline, and much of the basin, including its glaciated terrain, exists above this elevation. Some models suggest snowpack may be increasing at high elevations (Schnorbus et al., 2014), though existing snow observations below treeline indicate decreased water equivalent through the 1980–2011 period (Brahney et al., 2017). This data gap hinders accurate estimates of alpine snowpack in the region, which is critical for glacier nourishment, ecosystems, hydropower, and flood forecasts (Hamlet et al., 2005).
Geodetic methods are now regularly used to measure seasonal snow depth on glaciers via surface (Helfricht et al., 2014; McGrath et al., 2015) or helicopter-borne ground-penetrating radar (Dadic et al., 2010; Machguth et al., 2006; Sold et al., 2015), airborne laser scanning (ALS) surveys (Helfricht et al., 2012, 2014; Sold et al., 2013), airborne photogrammetry (Nolan et al., 2015), and stereoscopic satellite imagery (Belart et al., 2017). Geodetic surveys offer the ability to greatly expand the number of glaciers over which snow depth and mass change estimates can be made (Berthier et al., 2014; Nolan et al., 2015). For hydrological applications, snow depth must be converted into snow water equivalent (SWE), and thus snow density must be known or estimated. Physical modeling of snow density is difficult (Sold et al., 2015), and in situ density measurements are sparse and are expensive in terms of cost and effort. Density measurements for snow over glacier surfaces often show little relation to either elevation or snow depth (Fausto et al., 2018; Machguth et al., 2006; McGrath et al., 2015). Density thus introduces uncertainty to geodetic winter SWE estimates which are vital to calibrate and validate hydrological modeling and to measure seasonal mass balance (Belart et al., 2017; Sold et al., 2013). The primary objective of our study is to evaluate the reliability of geodetic surveys and density assumptions for estimation of seasonal mass change of temperate glaciers over multiple years.
1.1 Study area
1.1.1 Columbia Mountains
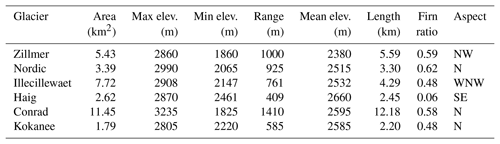
The transboundary Columbia River basin (668 000 km2) spans seven US states and the province of British Columbia (BC), Canada. The Canadian portion of the basin represents 15 % of the watershed's total area yet provides between 30 %–40 % of its total runoff, largely due to the presence of mountainous terrain with high amounts of orographic precipitation and extensive glacial cover (Cohen et al., 2000; Hamlet and Lettenmaier, 1999). There are 2200 glaciers covering 1760 km2 in the Columbia Mountains (Bolch et al., 2010); these glaciers primarily exist within the Cariboo, Monashee, Selkirk, and Purcell ranges, with the highest elevations rising to over 3000 m above sea level (a.s.l.).
The Columbia Mountains are transitional between maritime and continental (Demarchi, 2011). Monthly average temperatures in the Canadian Columbia River basin (elevation range from 420 to 3700 m a.s.l.) range from −9.2 ∘C in January to +13.3 ∘C in July (Najafi et al., 2017; Schnorbus et al., 2014). General circulation is dominated by westerly flow, which brings consistent Pacific moisture, particularly in the winter months. Approximately 65 % of annual precipitation falls as snow, with snowfall possible throughout the year (Schnorbus et al., 2014). The snow accumulation season in both the Columbia and Canadian Rocky Mountains extends from October to May. The summer melt season runs from May through September. From 1981 to 2010, Rogers Pass, located in the center of the Columbia Mountains (Fig. 1), at an elevation of 1330 m a.s.l., had an average annual temperature of +1.9 ∘C, an average winter (December–February) temperature of −8.0 ∘C, and experienced 1056±49 mm w.e. (millimeter water equivalent) of precipitation through the accumulation season (October–April) (Environment Canada, 2019).
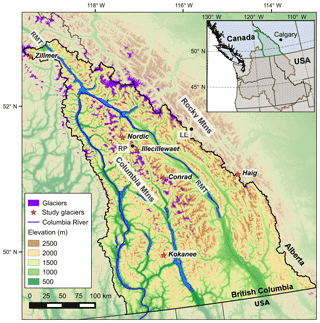
Figure 1Map of the Canadian Columbia River basin (black outline, brighter topography) and locations of study sites. Inset shows regional context of the Canadian portion of the Columbia River basin which contributes to the river where it crosses the international border (green). The remainder of the basin is also depicted (brown). The Columbia and Rocky Mountains are separated by the Rocky Mountain Trench (RMT). Weather stations (black dots) at Rogers Pass (RP) and Lake Louise (LL) are referred to in the introduction. Map coordinates are in NAD83/BCAlbers.
1.1.2 Rocky Mountains
The southern Canadian Rocky Mountains are located east of the Columbia Mountains (Fig. 1) across the Rocky Mountain Trench and are home to 1090 glaciers covering 1350 km2 (Bolch et al., 2010).
The eastern slopes of the Canadian Rocky Mountains experience a continental climate with mild summers and cold winters. However, winter precipitation along the continental divide is greatly influenced by moist Pacific air masses, with persistent westerly flow driving orographic uplift on the western flanks of the Rocky Mountains (Sinclair and Marshall, 2009). This combination of continental and maritime influences fosters extensive glaciation along the continental divide in the Canadian Rockies, with glaciers at elevations from 2200 to 3500 m a.s.l. on the eastern slopes. From 1981 to 2010, Lake Louise, located in the center of the southern Canadian Rockies (Fig. 1), at an elevation of 1524 m a.s.l., had an average annual temperature of +0.2 ∘C, an average winter temperature of −11.6 ∘C, and experienced 298±9 mm w.e. of precipitation through the accumulation season (Environment Canada, 2019). As evidenced by comparing Lake Louise and Rogers Pass, the Canadian Rocky Mountains are drier and colder in winter than the Columbia Mountains.
2.1 Study sites
Over the period 2014–2018 we measured seasonal mass balance of six alpine glaciers (Table 1): (1) Zillmer Glacier (5.4 km2) in the Cariboo Mountains; (2) Nordic Glacier (3.4 km2) and (3) Illecillewaet Glacier (7.7 km2) in the Selkirk Mountains; (4) Conrad Glacier (11.5 km2) and (4) Kokanee Glacier (1.8 km2) in the Purcell Mountains; and (5) Haig Glacier (2.6 km2), which straddles the continental divide. Haig Glacier is in the Rocky Mountains, whereas the other five glaciers lie in the Columbia Mountains.
2.2 Geodetic mass balance
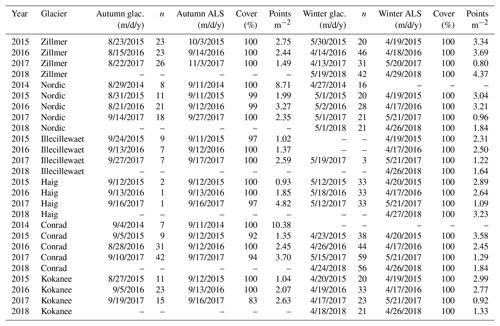
We performed repeat fixed-wing ALS surveys from late summer 2014 to late summer 2016 (Table 2) using a Riegl VQ-580 infrared (1024 micron) laser scanner with dedicated Applanix POS AV Global Navigation Satellite System (GNSS) inertial measurement unit (IMU). Later surveys used the same GNSS IMU and a Riegl Q-780 infrared (1024 micron) laser scanner. The VQ-580 and Q-780 were respectively flown at flying heights of around 500 and 2500 m above the terrain that yielded swath widths of 500–1000 and 2000–3000 m. Effective sampling diameter was 10–20 cm per laser shot. We planned the airborne surveys with 53 % overlap between flight lines to yield return point densities that averaged 1–3 laser shots m−2 (Table 2) and to minimize systematic bias from off-nadir laser shots.
Table 2Date and number of observation locations (n) for glaciological visits and geodetic acquisition dates and point density. Field dates are the median date of glacier visit.
2.2.1 ALS post-processing
Post-processing of the ALS survey flight trajectory data used the PosPac Mobile Mapping Suite (Applanix), with Trimble CenterPoint RTX with vertical and horizontal positional uncertainties that were typically better than ±15 cm (1σ). We post-processed point clouds and exported data into LAS (lidar data exchange file) files, a binary file format that can be efficiently processed with LAStools (https://rapidlasso.com/lastools/, last access: 30 May 2017, Isenburg, 2014). We used the LAStools las2dem algorithm to create 1 m resolution digital elevation models (DEMs). Las2dem triangulates ground classified ALS points from LAS files into a temporary triangulated irregular network (TIN). A DEM is then created from this using nearest-neighbor interpolation. Given an average point density of greater than 2 points m−2 (Table 2), little interpolation was required. We coregistered all DEMs following the method detailed in Nuth and Kääb (2011). For late summer surveys, one master DEM was chosen and all other late summer DEMs were coregistered to that DEM for stable terrain (e.g., off-glacier) only. Stable terrain was identified in satellite imagery and excluded forests, lakes, and ice- and snow-covered areas. For winter DEMs, the previous late summer DEM was used as the master DEM to mitigate against any surface height changes in areas defined as stable terrain, due to processes such as rockfall or vegetation height change. During the spring surveys, there was little to no snow-free terrain, except rocky features with extreme slopes which are not used in the coregistration (slope excluded). We thus did not apply any vertical shift during coregistration of winter DEMs.
We utilized satellite imagery from Landsat 7 and 8, Sentinel-2, and PlanetScope at 30, 10, and 3–5 m resolution respectively (Bevington et al., 2018), to guide surface classification used to coregister DEMs and calculate geodetic mass change. We selected the latest snow-free imagery from September or late August and used a band ratio and threshold method (Kääb, 2005) to classify areas of snow, firn, and ice. In some cases, we manually corrected surface maps where our automated methods failed to differentiate between firn and snow surfaces.
To calculate annual mass change (Ba), we (1) difference two DEMs to create a height change DEM (ΔDEM); (2) bias correct the height change by the mean height difference over stable terrain between two DEMs after coregistration (BiasΔh, Table 3); (3) derive a mask based on surface classification of ice, firn, and snow from satellite imagery (Fig. S1 in the Supplement); and then (4) apply the density of each respective surface type (Table 4), to the ΔDEM to calculate mass balance. We chose not to use digital terrain models (DTMs), which represent gridded elevation based on last returns from the laser scanner, since our gridding algorithms employed in LAStools filled crevasses and did not preserve sharp ridges that aided in coregistration of the DEMs.
Table 3Seasonal balance and uncertainty estimates for geodetic (geod) and glaciological mass balance (glac) in meter water equivalent (m w.e.). Kinematic-GPS-survey-derived corrections applied to glaciological data (surv.corr). Statistical analysis of the DEMs over stable terrain include NMAD, median height difference, and bias correction applied over the glacier (BiasΔh). Mean density of Ba_geod is . Average values include only cases where both geodetic and glaciologic data were collected. Bw_geod.gl is calculated using glaciological densities (Table S1), and Bw_geod.ss is calculated using snow survey data (Fig. 2). Listed Bs_geod is derived using Bw_geod.ss. Regional late summer snow density (Table 5) was used to calculate Ba_geod.
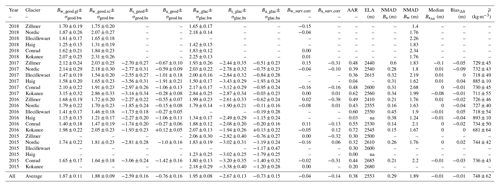
Table 4Density values used for geodetic and glaciological balance. Glaciological values are average values.
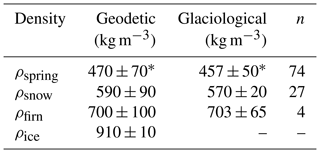
* Geodetic spring snow density (ρspring) is 440±50 kg m−3 for Haig Glacier and glaciological is 420±45 kg m−3 (n=46).
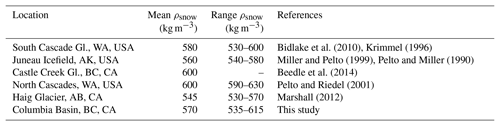
Table 5Late summer snow density observations from regional studies. We use 570 kg m−3 as our density of late summer snow for geodetic mass balance but also separately calculate mass balance using the average for regional studies excluding those from glaciers in this study (590 kg m−3).
Annual glacier mass balance is defined as the sum of accumulation and ablation throughout the balance year (Cuffey and Paterson, 2010), which can be expressed as the sum of winter and summer balance:
For geodetic and glaciological mass balance, we measure winter and annual balance and calculate summer balance as the difference between them:
To calculate geodetic winter balance (Bw_geod), we created a ΔDEM from a given spring DEM and the previous late summer DEM and then applied spring snow density (Table 4). We did not independently estimate Bs_geod because of the added uncertainty of partitioning elevation change due to melt or compaction of snow and firn.
2.2.2 Density estimates
While ALS provides an accurate estimate of snow depth with vertical uncertainties of ±0.1–0.3 m (Abermann et al., 2010; Bollmann et al., 2011; Joerg et al., 2012), it provides no information regarding snow density. We use manual snow survey measurements available from the British Columbia River Forecast Center (BCRFC) (Weber and Litke, 2018) as independent data to estimate spring snow density, and we compare this with our measured glaciological snow densities. These snow surveys are conducted as part of the BC snow survey program eight times per year, with most sites located between 1000 and 2000 m a.s.l. We use these BCRFC data to evaluate whether reliable estimates of snow density can be obtained for regions where no snow observations over glaciers exist. The mean date of our spring field visits was 1 May (Table 2), so we chose 1 May snow survey data (n=10 169) to derive a relation between SWE (kg m−2) and snow depth (m) (Fig. 2). The linear relation (regression fit) yields a slope of 470±70 kg m−3 (r2=0.97), which we use as the average 1 May snow density which we applied for our geodetic Bw calculations. For Haig Glacier, we chose only snow survey measurements from the Rocky Mountains for a linear relation yielding 440±50 kg m−3 (n=629). The estimated uncertainty in bulk snow density (±70 and ±50 kg m−3) represents the standard deviation (σ) of the snow survey data. For our glaciological density-informed Bw_geod, we use the observed glacier-wide snow density (Table S1 in the Supplement) and a linear regression of density versus day and used the slope (3.0 kg m−3 d−1, r2=0.43) and days between the survey and the observations to adjust for change in snow density (Fig. 3). The lack of an altitudinal trend in snow density observed on many glaciers (Fausto et al., 2018; McGrath et al., 2015, 2018; Sold et al., 2016) and those of this study, coupled with the absence of high-elevation snow density measurements and the annual variability of snow density evolution, required the use of a single value for spring snow density.
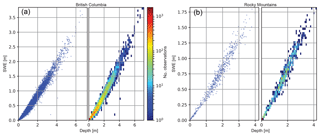
Figure 2Snow depth versus snow water equivalent from 1 May provincial snow survey data. The mean date of our spring field seasons was 1 May, and so we chose 1 May BC snow survey data (a) to derive a SWE–snow-depth regression from which we determined the average 1 May snow density (470±70 kg m−3 (r2=0.97, n=10 169)). For Haig Glacier, we derived a regression from only snow stations within the Rocky Mountains south of Pine Pass to derive winter density (440±50 kg m−3 (r2=0.97, n=629)).
Regional observations of late summer snow density are consistent (Table 5), ranging from 530 to 630 kg m−3 for glaciers across the Pacific Northwest (Table 5). This is expected for temperate, midlatitude glaciers, where snow densities range from the critical density of about 550 kg m−3 (Benson, 1962; Herron and Langway, 1980) to around 600 kg m−3 depending upon regional climatology. Since we independently evaluate glaciological versus geodetic estimates of mass change, we compare application of our late summer glaciological snow density measurements to calculate net balance with estimates based on the average of typical observations from four regional sources (590±60 kg m−3; Table 5), to test the impact of uncertainties of up to 10 % in this parameter. Firn density has not been reported for the study area, so we estimate 700±100 kg m−3 for multi-year firn based on observations in the Alps (Ambach et al., 1966). This value is also consistent with our firn core measurements for firn 2 or more years old (Table S2; average density of 703±65 kg m−3, n=4). Measurements of 1-year-old firn averaged 619±47 kg m−3 (n=8). Given the sustained mass loss of Pacific Northwest glaciers (Bolch et al., 2010; Menounos et al., 2019; Pelto, 2006), exposed firn is generally more than 1 year old, and we apply an uncertainty of 2 times the σ of our multi-year firn core observations (±15 %), which captures the range of observed firn densities (664–776 kg m−3). We use an ice density of 910±10 kg m−3 (Clarke et al., 2013). After performing a pixel-based surface classification for each late summer, we used these classification masks to assign a density (Table 4) to each pixel (snow/firn/ice).
2.2.3 Firn processes
Firn meltwater retention and densification are neglected in our study. Firn densification (Belart et al., 2017; Sold et al., 2013) can be modeled, but this approach assumes that net annual surface elevation change corresponds to the average annual accumulation layer transformed from end-of-year snow density to ice (Sold et al., 2013). Glaciers in this study have a low average accumulation ablation area ratio (AAR, 38 %, Table 3), and ice area ratios range from 38 % to 94 % (mean: 47 %). In most years, a significant amount of multi-year firn is exposed on these glaciers, similar to other glaciers experiencing strong mass loss (Fischer, 2011; Klug et al., 2018). Firn area and thickness losses interrupt the normal cycle of firn densification. Using the firn model of Sold et al. (2013) yields an estimated annual surface lowering over a given accumulation area due to densification of ∼0.20 m; yet uncertainty in estimating surface lowering resulting from densification is high since we lack knowledge of the required input parameters. Because of this, and because firn densification is unlikely to produce firn densities outside the range of our estimate (700±100 kg m−3), we chose not to estimate firn densification in our study. Firn compaction therefore comprises one systematic uncertainty term in our analysis.
2.3 Glaciological mass balance
We collected glacier mass balance measurements using the glaciological method (Cogley et al., 2011) with a two-season stratigraphic approach (Østrem and Brugman, 1991). Spring glaciological field campaigns typically occurred between mid-April and mid-May, and the summer/annual balance visits took place between mid-August and mid-September (Table 2). Measurements of Ba and Bw allow the calculation of summer balance Bs (Eq. 1). Glacier mass balance measurements included snow depth, snow density, ablation, and kinematic GPS surveys of the glacier surface (Fig. 4).
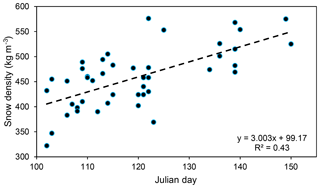
Figure 3Snow density versus Julian day for all discrete snow pit and snow core locations (n=46). For our glaciological density-informed estimates, we use the observed glacier-wide snow density and a linear regression of density versus day and used the slope (3.0 kg m−3 d−1 (r2=0.43)) and days between the survey and the observations to adjust for change in snow density (Table S1).
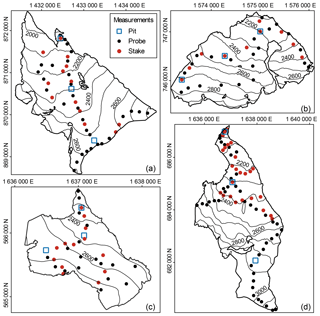
Figure 4Measurement networks for the (a) Zillmer, (b) Nordic, (c) Kokanee, and (d) Conrad glaciers. Snow depth measurement locations, ablation stakes, and snow pit/core locations are pictured. Refer to Marshall (2014) for the Haig Glacier and to Hirose and Marshall (2013) for the Illecillewaet Glacier. Map coordinates are in WGS84/UTM11N.
Our methods apply to the four glaciers studied by the University of Northern British Columbia (UNBC): the Zillmer, Nordic, Conrad, and Kokanee glaciers. For Haig Glacier, winter mass balance measurements followed the same field protocols, but summer mass balance is derived from a combination of point observations and a distributed model of glacier melt (Marshall, 2014; Samimi and Marshall, 2017). The glacier melt model has 30 m resolution and uses a surface energy balance, driven by automatic-weather-station data collected on the upper glacier and in the glacier forefield. Illecillewaet Glacier has been monitored by Parks Canada since 2009 (Hirose and Marshall, 2013). We calculated Ba_glac for Illecillewaet Glacier using the contour method since there were insufficient point measurements to estimate mass balance using the profile method.
Others have shown that snow depth is more variable than density (Elder et al., 1991; Pelto, 1996; Pulwicki et al., 2018), so we designed a sampling strategy that measures snow depth much more than density (an approximate sampling ratio of 25:1). We used G3 industrial aluminum probes to collect over 1750 estimates of snow depth over the period of study. The probe can penetrate thick ice lenses and allowed us to measure snow depths of up to 8 m. The boundary between snow and firn is typically made up of clearly defined ice lenses of variable thickness, which can be detected with a probe on midlatitude glaciers (Østrem and Brugman, 1991; Pelto, 1996; Sold et al., 2013). This end-of-summer surface at the glaciers in this study has such strength that an industrial probe can penetrate no more than a couple centimeters, in contrast with internal ice lenses in seasonal snowpack, which can be penetrated due to weak underlying support. Initially, we collected four probe measurements per location, but after two spring seasons we determined that two measurements were sufficient per location. The average σ for probe measurements for four (two) measurements was 0.14 m (0.07 m) for spring and 0.10 m (0.08 m) for late summer. Two measurements per location allowed additional locations to be measured, since our observed low variability between proximal measurements is consistent with other studies (Beedle et al., 2014; Pelto et al., 2013).
We measured snow density with a 100 cm3 box cutter (Hydro-Tech) in snow pits and from snow cores using a 7.25 cm diameter Kovacs corer. Our rationale to use a snow corer was that average spring snow depth exceeded 4 m and we chose to have as many sites as possible to estimate snow density. The corer also allowed us to sample internal ice lenses, which are difficult to measure with a snow sampler (Proksch et al., 2016). We measured spring snow density at low, middle, and high elevations for each glacier. If we observed an elevation trend in our density measurements, we applied a linear regression of density and elevation to our depth measurements prior to converting these data to water equivalent (mass). When there was no linear gradient, we averaged the snow density measurements to produce a glacier-wide snow density.
We conducted nine side-by-side pit–core comparisons that revealed density measured in our snow pits was comparable, with density from snow pits about 0.2±5.7 % heavier than measured by subsampling snow cores (Fig. S4). The mean absolute difference between pit and core density was 4.8 %, similar to observations made at Alto dell'Ortles Glacier (Gabrielli et al., 2010). Methodological differences (Sect. S1 in the Supplement) are within the range expected between duplicate field-based measurements of snow density (1 %–6 %) and with different cutters (3 %–12 %) (Conger and McClung, 2009; Proksch et al., 2016).
Aluminum and PVC ablation stakes were used on each glacier to measure ice and firn ablation. The stake heights were measured (±1 cm) and redrilled during each late summer visit. As a check on stake elevation, we measured depth to the previous snow surface for all stakes in firn, as stakes may self-drill in firn (Østrem and Brugman, 1991). Stakes were generally aligned along the centerline of a given glacier; however, we added a second transect of stakes to cover each branch to improve spatial coverage on each study site (Fig. 4). Conrad Glacier also featured three latitudinal sets of ablation stakes.
To calculate mass balance, we used the profile method (Escher-Vetter et al., 2009), applied over 100 m hypsometric elevation bins. The area–altitude distribution of a given glacier was obtained using our annual late summer ALS DEMs. The boundary of each glacier was manually delineated using the ALS DEM hillshade of the previous late summer and a ΔDEM (Abermann et al., 2010). We also calculated mass balance using linear regression. For Zillmer, Nordic, and Conrad glaciers, we separately considered the measurements from two distinct branches or sides of each glacier and then separately applied the profile and linear methods to each branch.
To account for mass change between a given field visit and the associated ALS survey, we completed kinematic GPS surveys using a Topcon GB-1000 receiver as a rover and a second receiver as a base station. We corrected base station data using Natural Resources Canada Precise Point Positioning (https://webapp.geod.nrcan.gc.ca/geod/tools-outils/ppp.php, last access: 1 June 2018) before post-processing surveys using Topcon Tools. Height changes observed between the ALS DEM surface and survey points were binned by elevation (Fig. S5) and assigned a density based upon surface classification as determined from satellite imagery. Since ALS surveys were essentially synchronous (typically flown over 2 to 3 d), we chose to apply the correction to the glaciological estimates of mass balance. We surveyed 2–6 control points at each site to determine the survey reliability and found that horizontal and vertical uncertainties respectively averaged ±0.04 and ±0.06 m.
2.4 Uncertainty assessment
We analyzed stable terrain to derive statistical indicators of bias and data dispersion from ΔDEM using a late summer DEM as a reference. We report the mean, median, and normalized median absolute deviation (NMAD) over stable terrain (Table 3), which generally covered 10–20 km2. To calculate uncertainty in ALS-derived height change, we also account for spatial correlation as assessed over stable terrain based on semivariogram analysis (Fig. S3) as described in Rolstad et al. (2009). We bias correct the height change over the glacier surfaces using the systematic elevation difference over stable terrain (BiasΔh) in the ΔDEMs (Table S3). This bias correction ranged from −0.09 to 0.05 m and averaged −0.01 m. NMAD reveals random errors that are typically below ±0.3 m, with a maximum of 0.6 m (Table 3). This maximum error occurred for Zillmer Glacier in late summer 2017 when the separation between site visit and ALS survey was large and new snow covered the glacier during the ALS survey (Table 2).
Random uncertainty stems from three sources that we assume to be independent: (i) elevation change uncertainty (σhΔDEM), (ii) glacier zone delineation uncertainty (σA), and (iii) volume-to-mass density conversion uncertainty (σρ). We define σhΔDEM following the methods detailed in Menounos et al. (2019) and found an average decorrelation length of 0.75 km (Fig. S3). Below, we have abbreviated our geodetic and glaciological uncertainty assessment (detailed version: Sect. S2 in the Supplement).
For delineation of ice/firn/snow zones from satellite imagery (Fig. S1), we applied a buffering method (Granshaw and Fountain, 2006) to the perimeter of each zone that was not at the glacier boundary. Our satellite imagery resolution varied from 3 to 15 m, so we chose a buffer of 4 times the largest pixel size to derive an uncertainty in area per zone. This 60 m buffer accounts for uncertainty in zone delineation and changes in the positions of the zone boundaries occurring between ALS and satellite imagery acquisition dates. Total random uncertainty in volume change is
where A is the area of a given glacier and p is the percentage of surveyed area, which averaged 99.1 % (Table 2). Random uncertainty on geodetic mass balance is
where ρi is individual density conversion values with associated uncertainties (±σρi) for spring snow, late summer snow, firn, and ice (Table 4). Prior to being summed to produce a final uncertainty, each zone (ice/firn/snow) is considered separately for Ba, with ΔVi and Ai the volume and area change of each zone respectively.
Firn compaction or fresh snow on the surveyed surface introduce systematic uncertainty on geodetic balance. On Drangajökull ice cap, where Bw is more than 1 m w.e. greater than our average Bw, firn compaction and fresh snow densification increased geodetic Bw by 8 %. Fresh snow off-glacier was negligible in all but a few cases. We thus assume a systematic uncertainty (σΔMsys) of 10 % on Ba,w. Collectively, random and systematic uncertainty thus yield total uncertainty in mass balance:
To determine uncertainty in glaciological mass balance, we derive a mean density () of mass change (Table 3) and uncertainty in height change for both observations and GPS survey corrections. Uncertainty in glaciological mass balance is calculated as
where σρ is the uncertainty on density taken to be 10 % of to account for uncertainty in density measurements and extrapolation of those measurements. The uncertainty in extrapolation of glaciological observations to glacier-wide mass balance is taken as the σ of the different calculations of mass balance for each season.
For both geodetic and glaciological mass balance, Bs was derived as the difference of annual and summer balance (Eq. 1), and thus uncertainty on Bs yields
3.1 Glaciological versus geodetic balance
Comparison of seasonal balance from glaciological and geodetic methods showed strong agreement (Fig. 5), with glaciological winter balance (Bw_glac) averaging 1.95±0.08 m w.e., which is 4 % greater than our geodetic estimate. Average summer and annual glaciological balance estimates were 3 % smaller and 3 % larger, respectively, than our geodetic estimates (Fig. 6). Bw_glac was 5 % greater relative to Bw_geod, and Bs_glac was 4 % more positive relative to Bs_geod when considering individual glaciers. For Bw and Bs, geodetic and glaciological balance were within 20 % for over 85 % of cases. Average mean annual balance from 2015 to 2017 was and m w.e. for glaciological and geodetic methods respectively (Table 3). Mean Bs_glac was m w.e. All individual estimates of seasonal and annual balance are within 2σ uncertainties, and only in three instances are they outside 1σ uncertainties (Fig. 6).
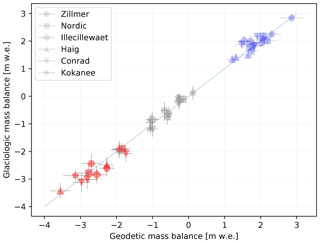
Figure 5Geodetic versus glaciological mass balance estimates for 2015 through 2018 for all six study glaciers with a one-to-one line. Blue shows the winter balance covering the accumulation season from mid-September to late April; red shows the summer balance spanning the remaining months; gray shows the annual balance. Errors depicted are 1σ uncertainties. Average Bw_glac was 4 % greater than Bw_geod, and Bs_glac and Ba_glac were 3 % smaller and 3 % larger, respectively, than our geodetic estimates.
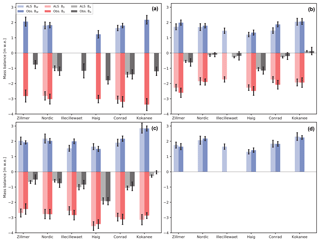
Figure 6Seasonal and annual mass balance for all study glaciers from both geodetic and glaciological measurements for each balance year from 2014 to 2018 with 1σ uncertainties. (a) 2014 to 2015 balance year, (b) 2015 to 2016 balance year, (c) 2016 to 2017 balance year, and (d) 2017 to 2018 winter balance.
We created a ΔDEM from the first and last late summer DEM for each site (Fig. 7) and compared calculated mass change from this ΔDEM to the sum of the individual balance years that comprised that given period (Fig. 8). We found that all cumulative seasonal Ba estimates from glaciological and geodetic balance were within uncertainty (2σ) of the last–first mass change approach (Fig. 8). Glaciological balance was in net more positive (average +0.09 m w.e.) and had an average absolute difference of 0.20 m w.e. from the last–first ΔDEM. Summed Ba_geod agree with our last–first estimates, with an average deviation of only 0.03 m w.e.
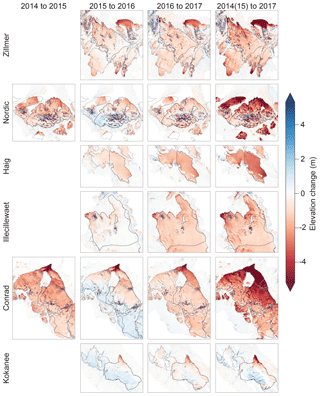
Figure 7Surface height change for the Zillmer, Nordic, Haig, Illecillewaet, Conrad, and Kokanee glaciers from the first late summer DEM (2014 or 2015) until late summer 2017. Study glaciers are outlined with thick black line and other glaciers with a thin black line. Off-ice areas deemed stable terrain were used for error analysis and coregistration.
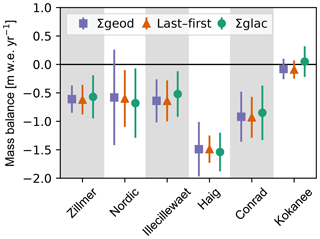
Figure 8Summed annual mass balance from glaciological data (∑glac), geodetic data (∑geod), and last–first ΔDEM. Last–first ΔDEMs were created by differencing the first available DEM (2014 or 2015 late summer) from the last available DEM (2017) for each site (Table 2). Errors denote 2σ uncertainties.
3.2 Glaciological density observations
Glacier averaged snow density from snow pits and cores for spring is 457±48 kg m−3, with a coefficient of variation (CV) of 0.14 (n=74). This estimate is 13 kg m−3 less than our snow-survey-based geodetic ρspring but is within uncertainty (Table 4). For Haig Glacier, average spring density is 420±45 kg m−3, which is 20 kg m−3 lighter than our estimate obtained from nearby snow survey measurements but again within uncertainty. Our average late summer glaciological density of 570±20 kg m−3 (n=27) ranged from 536 to 617 kg m−3 (CV =0.04). Assigned geodetic ρsnow is 18 kg m−3 greater than observations. Average probe depth for spring is 4.20±0.06 m, with a CV of 0.33 (n=1754). Average probe depth in late summer is 1.85±0.10 m, with a CV of 0.78 (n=777). Observed glacier-wide average snow depths are between 3.4 and 6.9 m and average 4.56±0.21 m. While spring snow density showed greater variability than late summer snow density, snow depth is far more variable than snow density in both seasons.
Over the period 2015–2017 average AAR was 38 % (Table 3), with multi-year firn exposed over 13 % of the glacier surface, thus leaving the remaining 49 % of glacier area as bare ice. Located in the Rocky Mountains, Haig Glacier is the easternmost site in our study and is in a lower accumulation environment. It has lost nearly all its firn cover over the last 20 years, with firn area at 6 % in 2015. The study glaciers that lie in the Columbia Mountains had an AAR of 45 % with 15 % exposed multi-year firn cover and 40 % bare glacier ice.
3.2.1 Geodetic density sensitivity
The effect of using a regional late summer snow density (Table 5) versus our glaciological density values (Table S1) depends on the amount of retained snow and glaciological density but produces a <0.01 m w.e. Ba_geod decrease on average, which is a negligible contribution. Varying firn density by ±15 % also has an average effect on Ba_geod of ±0.01 m w.e., with the largest impact (0.04 m w.e.) experienced at Conrad Glacier in 2015, when 17 % of the glacier was exposed firn. However, misclassifying a given area of glacier surface has a significant impact, as ρfirn is 17 % greater than snow and 26 % less than ρice. If we produce a single glacier-wide density () instead of distributing density based on surface classification, we change absolute magnitudes of Ba_geod by an average of ±0.10 m w.e. Though we did not use it for mass conversion, our of Ba_geod ranged from 681 (Kokanee 2016) to 895 kg m−3 (Haig 2017) and averaged 748±61 kg m−3.
Applying snow survey density values for spring snow (Table 4) versus our glaciological snow density observations (Table S1) reduces average Bw_geod by 0.03 m w.e. (1.7 %) and causes Bw_geod to be 7 % greater rather than 5 % relative to Bw_glac. For individual glaciers, Bw_geod values between the two methods differ by 1 to 13 % but only 2 % on average.
3.3 Glaciological and geodetic balance discrepancies
Estimates of seasonal and annual balance for individual glaciers were outside 1σ uncertainties in a few cases. Conrad Bw_glac was 24 % greater than Bw_geod in 2016. Snow accumulation may have occurred in the 8 d between the Conrad Glacier ALS survey and field visit, as we observed over 1 m of fresh snow over 4 d during that interval while on Kokanee Glacier. Automatic snow weather stations near both glaciers at around 2050 m a.s.l. showed no accumulation, highlighting the steep balance gradient of the Columbia Mountains. Additionally, ALS acquisition failed over the terminus of the Conrad and Illecillewaet glaciers in late summer 2015 (Table 2), and our extrapolation based upon the typical gradient over the terminus may have underestimated melt (Fig. 7). Kokanee Glacier Ba_glac in 2017 was 0.25 m w.e. more positive than Ba_geod, likely due to the burial of a few ablation stakes and subfreezing temperatures which limited our ability to take adequate snow measurements. Illecillewaet Glacier Bw_glac in 2017 was 46 % higher than Bw_geod, but this difference may stem from limited Bw_glac observations that year (n=3).
3.4 Interannual and spatial variability
Varied climatological conditions provided a range of balance outcomes for the period of study. The lowest Bw_glac of the four studied winters (1.81±0.12 m w.e.) occurred in 2016 yet also the least mass loss with an average Ba_glac of m w.e. (Fig. 5). The 2016–2017 winter brought the greatest snowpack of our study period, 2.08±0.18 m w.e., yet substantial mass loss was observed (average Ba_glac: m w.e.). The balance year of 2014–2015 saw high sustained mass loss (average Ba_glac of m w.e.), despite having an Bw_glac within 0.01 m w.e. of 2016.
The standard deviation between the seasonal and annual balances for each glacier reveals that Bw (σ=0.14 m w.e., 7 %) experiences lower interannual variability than Bs (σ=0.38 m w.e., 14 %) and Ba (σ=0.35 m w.e., 56 %). Kokanee Glacier experienced the highest Bw in all four years 2015–2018 averaging 2.34±0.30 m w.e. (Fig. 6). Haig Glacier had the lowest Bw, averaging 1.37±0.11 m w.e., and the highest mass loss (average Ba_glac: m w.e.).
We did not investigate the influence of crevasses for each glacier and each season, but for a test case for each glacier (n=6) we created DEMs with filled crevasses in the late summer and then produced a ΔDEM. We found that crevasse-free ΔDEM Bw was on average <1 % smaller than our standard Bw, with discrepancies up to −0.05 m w.e or −3 %. The amount of crevassing is important, however, as some of the studied glaciers such as the Zillmer, Nordic, and Conrad feature large crevasse fields.
The consistency between our geodetic and glaciological seasonal balance estimates among six glaciers over multiple years implies that high-resolution geodetic surveys can be used to reliably measure both winter and summer mass balance. Our study builds upon previous work that established the feasibility of geodetic methods to accurately produce Bw (Belart et al., 2017; Sold et al., 2013) and Ba (Klug et al., 2018). While others show that geodetic surveys can be applied for a single winter (Belart et al., 2017; Sold et al., 2013) or for one glacier over a number of years (Klug et al., 2018), our study demonstrates remotely measured seasonal balance is possible for widely varying rates of accumulation and ablation for multiple glaciers across entire mountain ranges.
4.1 Geodetic seasonal balance
Our small estimate of σhΔDEM (Table S3) and bias correction (Table 3) highlight that height change uncertainty is generally minor but it remains important to quantify (Joerg et al., 2012; Klug et al., 2018). As described below, density distribution and conversion factors comprise a large portion of total mass change uncertainty, with firn compaction, fresh snow at the time of ALS acquisition, and crevasses also contributing.
The spatial coverage of ALS is superior to glaciological observations; however, isolating the mass change component of surface height change at a given location is difficult and requires detailed input data (Belart et al., 2017; Sold et al., 2013). While we can develop balance gradients from glaciological data, we have not attempted to do so using our ALS data. To date, studies have differenced their glaciological and geodetic data regarding surface height change and assigned the difference as a combination of vertical ice velocity and firn compaction (Beedle et al., 2014; Belart et al., 2017; Sold et al., 2013) or used the full-Stokes ice flow model with a bedrock DEM, a surface DEM, and in situ GPS velocities as inputs (Belart et al., 2017). Then, after applying a simple firn model, vertical ice velocity is estimated. While this method appears robust, and differencing of our glaciological observations of height change from our ΔDEMs produces realistic emergence/submergence velocities, it is beyond the scope of this study.
4.1.1 Density distribution and conversion factors
Converting volume to mass change is a major challenge for geodetic studies (Huss, 2013; Moholdt et al., 2010). Over multiple years to decades, a constant value of density can produce tolerable uncertainty of mass change (Huss, 2013). For shorter timescales, and particularly for seasonal balance, a careful consideration of density is necessary (Klug et al., 2018). Klug et al. (2018) used ALS intensity data and satellite imagery for a pixel-based classification of the glacier surface as firn and ice. Our study built on this work and mapped areas of ice but also distinguished between snow and firn. Varying the density assigned to each surface class to the maximum and minimum values within our conservative uncertainties has a minor effect on seasonal balance, but failing to distribute them appropriately has a large impact. If a single density value is used, the range of values of of Ba_geod indicates that 750±60 kg m−3 would be most appropriate for seasonal mass change over this period (Table 3). Given the spread of between glaciers, however, a glacier-specific would be best.
Like Klug et al. (2018), our applied firn density was selected based on a core from a temperate glacier in the Alps (Ambach et al., 1966), and our in situ density measurements for firn ≥2 years old matched this value (Table 4). Our glaciological density values for 1-year-old firn and late summer snow density are respectively 13.1 % and 22.4 % (Table 4) less than the assumed value of 700 kg m−3 for both snow and firn taken by Klug et al. (2018). Had we also combined snow and firn density, we would have biased Ba_geod by varying magnitudes depending upon the surface cover. As glacier mass loss rates continue to accelerate (Menounos et al., 2019), it is reasonable to expect more and older exposed firn during the ablation season, which for geodetic studies may imply a higher density conversion factor for firn.
Applying glaciological late summer snow density versus our independent regional average density (Table 5) had little effect on Ba_geod. Future geodetic studies should use the best available local data, however, as different regions and mountain ranges have different late summer densities (Table 5).
Using our glaciological winter density values to produce Bw_geod estimates resulted in a slightly greater discrepancy relative to Bw_glac than applying our snow-survey-based densities (Table 3). The two Bw_geod estimates produced similar results in net and only a 2 % average difference between Bw_geod estimates for individual glaciers. In the Columbia and Rocky Mountains, the first significant warming event of the spring typically occurs between early April and early May (Marshall, 2012). Springtime warming tends to homogenize and increase snow density (Adams, 1976; Elder et al., 1991). Our linear regression approach (Fig. 3) to adjust glaciological observations of spring snow density (Table S1), appears suitable over the period from mid-April through late-May, but we caution against its use for other periods of the year when densification is far slower and less predictable. For Haig Glacier, a linear relation also exists between mid-April through late May (Marshall, 2012, p. 18, Fig. 2.3). The tendency for a more homogenous snow density and lack of a consistent altitudinal trend both lend credence to using a single snow density (Fausto et al., 2018; McGrath et al., 2018).
4.1.2 Firn and internal processes
While firn compaction is only incorporated in our uncertainty analysis; others estimate its effect to derive Bw_geod (Belart et al., 2017; Sold et al., 2013) but not Ba_geod (Klug et al., 2018). For Bw_geod, firn compaction was estimated based upon the annual balance in the accumulation zone over a decade (Sold et al., 2013) or over a single balance year (Belart et al., 2017). Currently accumulation areas on alpine glaciers are in constant flux and are typically discontinuous. Exposed firn is common (Fig. S1), implying that the firn zone on our study sites is shrinking in area and thickness, interrupting the cycle of firnification, and invalidating firnification models which assume that one annual layer is transformed from snow to ice annually. Nevertheless, a carefully considered treatment of firn could improve seasonal geodetic balance estimates, but as demonstrated by Belart et al. (2017), firn and fresh snow densification have little effect on Bw_geod if the magnitude of winter accumulation is large. For regions with low winter balance, or a colder climate, compaction would have a larger relative influence on Bw.
Meltwater retention is not incorporated into our annual balance estimates. At Haig Glacier, firn meltwater retention has not been measured, but meltwater retention in the supraglacial snowpack is a negligible contributor to mass balance, though it does create an effective energy sink, which should be accounted for in mass balance modeling (Samimi and Marshall, 2017). For glaciers in Svalbard, coupled energy balance and snow/hydrology models have been used to quantify the effects of meltwater freezing and retention on glacier mass balance (Van Pelt et al., 2012; Van Pelt and Kohler, 2015). Rates of meltwater retention are decreasing for Svalbard glaciers (Van Pelt and Kohler, 2015) and on the Devon Ice Cap (Bezeau et al., 2013), due to decreasing firn area and, in particular, warmer temperature. Like at our glaciers, melt–freeze cycles form thick summer surface layers on these Svalbard glaciers and Devon Ice Cap, which could act as a barrier for vertical water transport and is likely to promote near-surface lateral water flow, limiting deep firn water storage (Gascon et al., 2013; Van Pelt and Kohler, 2015).
Geodetic balance implicitly includes internal and basal mass change, which are not captured by the glaciological method. Studies of these processes are rare and are based upon estimates rather than verified measurements. Estimates of annual mass loss from geothermal heat, potential energy released by runoff or ice motion, and basal friction are typically around 0.01 to 0.10 m w.e. (Huss et al., 2009; Oerlemans, 2013; Sold et al., 2016). Crevasses and internal processes likely combine to be 0 % to 4 % of the magnitude of average annual ablation (e.g., Klug et al., 2018; Sold et al., 2016) and thus are likely minor contributors to seasonal balance in the Columbia Mountains. Modeled meltwater accumulation in firn would tend to increase mass balance, possibly offsetting typical basal/internal mass loss, but would not be captured by geodetic or glaciological measurements. Most mass balance models only assume vertical percolation of meltwater, yet given thick impermeable ice layers observed in our cores and snow pits, and in other studies (Gascon et al., 2013; Van Pelt and Kohler, 2015), this assumption would lead to an overestimation of refreezing. Without regional data to constrain firn processes it is difficult to incorporate them into mass balance calculations. Regionally, a better understanding of firn processes could improve annual balance and runoff estimates and likely has a greater influence on the large ice fields in western North America, which have received little attention. Although firn processes are not resolved, our approach markedly improves the quality of annual results compared to calculations based on a fixed glacier-wide conversion density.
4.1.3 Fresh snow
Presence of fresh snow at the time of acquisition is a challenge for any geodetic survey estimating mass change (Belart et al., 2017; Joerg et al., 2012; Klug et al., 2018). Fresh snow can change the height of the target surface by tens of centimeters. Our bias correction of ΔDEM height change (Fig. S2, Table 3) corrected for small quantities of fresh snow, assuming that snow was present over stable terrain. In late summer, we could detect fresh snow visually, as a hillshade of the glacier surface at 1 m resolution captures intricate details which are easily disguised by snow depths of 0.2 m or more. Off-glacier, the depth and distribution of fresh snow is variable due to redistribution and the thermal properties of bedrock and other surfaces. In spring, we are unable to detect fresh snow as the only snow-free pixels in our scenes are typically rock faces with extreme slopes and tree tops. Our σΔMsys attempts to approximate the systematic uncertainty introduced by fresh snow and firn compaction.
4.1.4 Crevasses
Crevasses can affect both Bw_geod and Bw_glac since crevasses bridged by winter snowpack will overestimate Bw_geod snow volume, and crevasses filled by snow would not be captured by Bw_glac. We produced crevasse-free glacier surfaces by resampling late summer DEMs to 10 m using the maximum elevations within the smoothing window to avoid in-crevasse height measurements. Using the 10 m crevasse-free DEMs versus the original 1 m DEMs had little influence on Bw_geod, with only the Zillmer and Nordic glaciers showing a difference >1 %. We did not extend these test cases to cover Ba_geod estimates because the area of exposed crevasses varied little year to year. On Hintereisferner, crevasse effects biased Ba_geod by only 0.03 % (−0.047 m w.e.) over a decade (Klug et al., 2018). Despite the small influence of crevassing on Ba_geod observed in this study, additional studies should quantify the magnitude of this bias in greater detail than presented here.
4.2 Glaciological seasonal balance
Observational biases include the representativeness of sampling sites and number of measurements (Cogley, 1999; Fountain and Vecchia, 1999), as well as the extrapolation of those measurements to produce a glacier-wide balance estimate (Sold et al., 2016; Thibert and Vincent, 2009). The difficulty of comparability between methods and sites (Cogley, 1999; Fountain and Vecchia, 1999) is an ongoing challenge due to logistical and financial obstacles to in situ mass balance studies. Areas of a glacier may be inaccessible, and preferred paths chosen for measurement may be biased to areas which better retain snowpack for safety purposes (Østrem and Brugman, 1991).
4.2.1 Snow depth
We observed best agreement between geodetic and glaciological measurements of winter balance during years of dense field surveys. Safety or logistical constraints prevented us from completing all transects of snow depth measurements in some years, with greater discrepancies between estimates in cases with incomplete coverage. In both spring and late summer, we encountered internal ice layers at some or all sites. Ice lenses were most common in the accumulation zone, but they were also found in the ablation zone in spring. These internal layers form via rain-on-snow events (McCabe et al., 2007) or, as the melt season progresses, via internal storage of meltwater (Pfeffer and Humphrey, 1996). Ice layers 2–6 cm thick were present nearly every year in the accumulation zone of the Conrad Glacier and often at other sites. We were able to penetrate these layers and successfully measure spring snow depth using our industrial avalanche probe. A conventional avalanche probe is unsuitable for glaciological observations in the Columbia Mountains.
The greater Bw_geod of 2016 on Conrad Glacier is likely due to both snow accumulation between the glaciological visit and ALS survey, as well as due to the late summer 2015 ALS survey missing the lowest reaches of the glacier, preventing calculation of surface height change for that portion of the glacier. We estimated the snow depth for the lower reaches of the glacier based upon the ratio of snow depth observed there for other years relative to the rest of glacier. The Bw discrepancy for Zillmer Glacier in 2016 is likely due to glaciological sampling bias, as the east transect (Fig. 4), which has a lesser snowpack, was not sampled, and the 30 d difference between field and ALS survey date (Table 2) may not be adequately resolved by the GPS survey correction.
4.2.2 Mass change between measurements
Previous studies account for mass change that occurs between measurements by using a distributed temperature index model (Sold et al., 2013) or degree-day model (Belart et al., 2017), but these models do not account for mass gain. We utilized in situ GPS surveys of the glacier height which were then compared with ALS DEMs. We averaged our height change estimates into 100 m elevation bins (Fig. S5) and then applied a density to each bin based on satellite observations of a given surface class. Limitations in our approach include (1) fresh snowfall between the GPS and ALS surveys and (2) significant densification of the snowpack in spring. Terrain presents a further challenge to kinematic GPS survey observations. The GPS antenna is securely mounted in the backpack of a field member, but the measured height of the antenna above the glacier surface may vary due to the uneven glacier terrain, particularly during travel on steep slopes (Beedle et al., 2014).
Our median dates of late summer glaciological visits and geodetic surveys are 6 and 18 September respectively (Table 2). Snowfall can occur at any time of the year in the Columbia and Rocky Mountains (Schnorbus et al., 2014), and in late August, throughout September, and even into early October, either melt or accumulation can prevail (Marshall, 2014). Lowering of the surface via ablation post ALS survey dates (Table 2) is not accounted for and would cause an underestimated winter snowpack. While our methods are comparable year to year, and between sites, our Bw and Bs values are not the total amount of snow and runoff during a year. We do not include snow which falls between May and August and melts off and cannot measure ablation after our ALS survey or glaciological visit, whichever occurs later. Our Bw and Bs values thus represent a conservative estimate of runoff contributions from snow and ice melt.
Estimates of seasonal mass balance presented here show strong agreement between glaciological and geodetic methods for individual glaciers and are within 1σ uncertainties for average winter, summer, and annual balance. These independent estimates of seasonal mass change accord over 3 years from glaciers separated by hundreds of kilometers. Our findings suggest that high-resolution geodetic methods, such as from ALS (Klug et al., 2018; Sold et al., 2013), aerial photogrammetry (Nolan et al., 2015), and stereo satellite imagery (Belart et al., 2017; Berthier et al., 2014), can be used to produce accurate seasonal and annual balance estimates over large areas. The quality of geodetic annual balance estimates depends more on distributing density via surface classification (Klug et al., 2018) than on the density values themselves. The spatial coverage, density of observations, and measurement precision of high-resolution geodetic terrain analysis compensate for uncertainty associated with fresh snow and firn compaction, internal and basal mass change, and crevasses (Belart et al., 2017; Klug et al., 2018). The minimal impact of these factors on mass balance stems from the large mass changes observed at our sites, as reported elsewhere (Belart et al., 2017; Klug et al., 2018). For glaciers with low mass turnover, errors introduced by firn compaction, crevasses, and fresh snow may be considerably larger than observed in our study.
Our estimate of spring snow density for geodetic measurements from provincial snow survey observations (Fig. 2) is within the uncertainty of our measured glaciological spring snow density (Table 4). Our approach holds promise for being able to use regional density estimates when in situ measurements are unavailable, yet discrepancies of up to 13 % between geodetic and glaciological winter balance estimates indicate the uncertainty introduced when using density values which are not site-specific. Estimates of end-of-season snow density introduce a possible bias, but given the regional consistency of late summer snow density and the overall lack of a density–altitude gradient in spring, using a single snow density is a robust method for converting snow depth to water equivalence (Fausto et al., 2018; McGrath et al., 2018). We observed greater variability in Bs relative to Bw, highlighting the need for models of glacier mass balance that can be able to reliably reproduce widely varying rates of mass change corresponding to the multitude of energy fluxes that influence alpine glaciers (Fitzpatrick et al., 2017).
The hydrologic cycle of western North America is dominated by snowfall in the mountains, but observations of alpine snowpack above 2000 m a.s.l. are sparse. As the climate continues to change, there is a growing need for a more detailed understanding of the seasonal balance of glaciers and snowpack. Geodetic methods are needed to supplement in situ observations across many mountain regions in order to address the contribution of glaciers to changes in freshwater runoff availability and to sea level rise. To date, the majority of high-resolution geodetic balance studies of seasonal or annual balance have been conducted in the European Alps, where extensive, multi-decadal glaciological data are available (Klug et al., 2018; Sold et al., 2013, 2016). Our study suggests that geodetic methods can be used to assess seasonal balance of glaciers, even in mountain ranges lacking long-term records of mass balance, if density is carefully considered (Belart et al., 2017; Klug et al., 2018). Recent advances in high-resolution, optical satellite imagery (Berthier et al., 2014; Marti et al., 2016) suggest that such efforts can be made with increasing spatial and temporal coverage, greatly adding to our understanding of the seasonal contribution of snow and glaciers to mountain hydrology.
Glaciological mass balance data will be available through the WGMS (https://doi.org/10.5904/wgms-fog-2018-06, WGMS, 2018).
The supplement related to this article is available online at: https://doi.org/10.5194/tc-13-1709-2019-supplement.
All authors contributed to the writing of the manuscript. BMP conducted the field work with the help of many invaluable volunteers and conducted the ALS processing and analysis.
The authors declare that they have no conflict of interest.
The authors wish to thank Amaury Dehecq for assistance with DEM coregistration. We thank two anonymous referees and the handling editor, Chris Derksen, for providing detailed reviews that substantially improved our manuscript.
This research has been supported by the Columbia Basin Trust, BC Hydro, the Pacific Institute for Climate Solutions, the Natural Resources and Engineering Research Council of Canada, the Canada Chairs Program, the Tula Foundation, and the Canada Foundation for Innovation. Funding for Ben M. Pelto was provided via the Pacific Institute for Climate Solutions, the University of Northern British Columbia, and the Columbia Basin Trust.
This paper was edited by Chris Derksen and reviewed by two anonymous referees.
Abermann, J., Fischer, A., Lambrecht, A., and Geist, T.: On the potential of very high-resolution repeat DEMs in glacial and periglacial environments, The Cryosphere, 4, 53–65, https://doi.org/10.5194/tc-4-53-2010, 2010.
Adams, W.: Areal differentiation of snow cover in east central Ontario, Water Resour. Res., 12, 1226–1234, 1976.
Ambach, W., Bortenschlager, S., and Eisner, H.: Pollen-analysis investigation of a 20 m Firn Pit on the Kesselwandferner (Ötztal Alps), J. Glaciol., 6, 233–236, 1966.
Barnett, T. P., Adam, J. C., and Lettenmaier, D. P.: Potential impacts of a warming climate on water availability in snow-dominated regions, Nature, 438, 303–309, https://doi.org/10.1038/nature04141, 2005.
Beedle, M. J., Menounos, B., and Wheate, R.: An evaluation of mass-balance methods applied to Castle Creek Glacier, British Columbia, Canada, J. Glaciol., 60, 262–276, https://doi.org/10.3189/2014JoG13J091, 2014.
Belart, J. M. C., Berthier, E., Magnússon, E., Anderson, L. S., Pálsson, F., Thorsteinsson, T., Howat, I. M., Aðalgeirsdóttir, G., Jóhannesson, T., and Jarosch, A. H.: Winter mass balance of Drangajökull ice cap (NW Iceland) derived from satellite sub-meter stereo images, The Cryosphere, 11, 1501–1517, https://doi.org/10.5194/tc-11-1501-2017, 2017.
Benson, C. S.: Stratigraphic studies in the snow and firn of the Greenland Ice Sheet, US Army SIPRE (now CRREL) Research Report, 70, 93, 1962.
Berthier, E., Vincent, C., Magnússon, E., Gunnlaugsson, Á. Þ., Pitte, P., Le Meur, E., Masiokas, M., Ruiz, L., Pálsson, F., Belart, J. M. C., and Wagnon, P.: Glacier topography and elevation changes derived from Pléiades sub-meter stereo images, The Cryosphere, 8, 2275–2291, https://doi.org/10.5194/tc-8-2275-2014, 2014.
Bevington, A., Gleason, H., Giroux-Bougard, X., and de Jong, J. T.: A Review of Free Optical Satellite Imagery for Watershed-Scale Landscape Analysis, Conflu, J. Watershed Sci. Manag., 2, https://doi.org/10.22230/jwsm.2018v2n2a18, 2018.
Bezeau, P., Sharp, M., Burgess, D., and Gascon, G.: Firn profile changes in response to extreme 21st-century melting at Devon Ice Cap, Nunavut, Canada, J. Glaciol., 59, 981–991, 2013.
Bidlake, W. R., Josberger, E. G., and Savoca, M. E.: Modeled and measured glacier change and related glaciological, hydrological, and meteorological conditions at South Cascade Glacier, Washington, balance and water years 2006 and 2007, Report, available at: http://pubs.er.usgs.gov/publication/sir20105143 (last access: 12 February 2018), 2010.
Bolch, T., Menounos, B., and Wheate, R.: Landsat-based inventory of glaciers in western Canada, 1985–2005, Remote Sens. Environ., 114, 127–137, https://doi.org/10.1016/j.rse.2009.08.015, 2010.
Bollmann, E., Sailer, R., Briese, C., Stötter, J. and Fritzmann, P.: Potential of airborne laser scanning for geomorphologic feature and process detection and quantifications in high alpine mountains, Z. Geomorphol. Supp., 55, 83–104, 2011.
Brahney, J., Weber, F., Foord, V., Janmaat, J., and Curtis, P. J.: Evidence for a climate-driven hydrologic regime shift in the Canadian Columbia Basin, Can. Water Resour. J., 42, 179–192, 2017.
Clarke, G. K. C., Anslow, F. S., Jarosch, A. H., Radić, V., Menounos, B., Bolch, T., and Berthier, E.: Ice Volume and Subglacial Topography for Western Canadian Glaciers from Mass Balance Fields, Thinning Rates, and a Bed Stress Model, J. Climate, 26, 4282–4303, https://doi.org/10.1175/JCLI-D-12-00513.1, 2013.
Clarke, G. K. C., Jarosch, A. H., Anslow, F. S., Radić, V., and Menounos, B.: Projected deglaciation of western Canada in the twenty-first century, Nat. Geosci., 8, 372–377, https://doi.org/10.1038/ngeo2407, 2015.
Cogley, J., Hock, R., Rasmussen, L., Arendt, A., Bauder, A., Braithwaite, R., Jansson, P., Kaser, G., Möller, M., and Nicholson, L.: Glossary of glacier mass balance and related terms, IHP-VII technical documents in hydrology No. 86, IACS Contribution No. 2, Int. Hydrol. Program UNESCO Paris, 2011.
Cogley, J. G.: Effective sample size for glacier mass balance, Geogr. Ann. A, 81, 497–507, 1999.
Cohen, S. J., Miller, K. A., Hamlet, A. F., and Avis, W.: Climate change and resource management in the Columbia River Basin, Water Int., 25, 253–272, 2000.
Conger, S. M. and McClung, D. M.: Comparison of density cutters for snow profile observations, J. Glaciol., 55, 163–169, 2009.
Cuffey, K. M. and Paterson, W. S. B.: The physics of glaciers, Academic Press, Elsevier, Burlington, MA, Edn. 4, 2010.
Dadic, R., Mott, R., Lehning, M., and Burlando, P.: Wind influence on snow depth distribution and accumulation over glaciers, J. Geophys. Res., 115, F01012, https://doi.org/10.1029/2009JF001261, 2010.
Demarchi, D. A.: An introduction to the ecoregions of British Columbia, Wildlife Branch, Ministry of Environment, Lands and Parks, Victoria, British Columbia, Canada, 2011.
Elder, K., Dozier, J., and Michaelsen, J.: Snow accumulation and distribution in an alpine watershed, Water Resour. Res., 27, 1541–1552, 1991.
Environment Canada: Canadian Climate Normals, Gov. Can., available at: http://climate.weather.gc.ca/climate_normals/index_e.html, last access: 21 April 2019.
Escher-Vetter, H., Kuhn, M., and Weber, M.: Four decades of winter mass balance of Vernagtferner and Hintereisferner, Austria: methodology and results, Ann. Glaciol., 50, 87–95, https://doi.org/10.3189/172756409787769672, 2009.
Fausto, R. S., Box, J. E., Vandecrux, B., van As, D., Steffen, K., MacFerrin, M. J., Machguth, H., Colgan, W., Koenig, L. S., McGrath, D., Charalampidis, C., and Braithwaite, R. J.: A Snow Density Dataset for Improving Surface Boundary Conditions in Greenland Ice Sheet Firn Modeling, Front. Earth Sci., 6, 51, https://doi.org/10.3389/feart.2018.00051, 2018.
Fischer, A.: Comparison of direct and geodetic mass balances on a multi-annual time scale, The Cryosphere, 5, 107–124, https://doi.org/10.5194/tc-5-107-2011, 2011.
Fitzpatrick, N., Radić, V., and Menounos, B.: Surface Energy Balance Closure and Turbulent Flux Parameterization on a Mid-Latitude Mountain Glacier, Purcell Mountains, Canada, Front. Earth Sci., 5, 67, https://doi.org/10.3389/feart.2017.00067, 2017.
Fountain, A. G. and Vecchia, A.: How many stakes are required to measure the mass balance of a glacier?, Geogr. Ann. A, 81, 563–573, 1999.
Gabrielli, P., Carturan, L., Gabrieli, J., Dinale, R., Krainer, K., Hausmann, H., Davis, M., Zagorodnov, V., Seppi, R., Barbante, C., Dalla Fontana, G., and Thompson, L. G.: Atmospheric warming threatens the untapped glacial archive of Ortles mountain, South Tyrol, J. Glaciol., 56, 843–853, https://doi.org/10.3189/002214310794457263, 2010.
Gascon, G., Sharp, M., Burgess, D., Bezeau, P., and Bush, A. B.: Changes in accumulation-area firn stratigraphy and meltwater flow during a period of climate warming: Devon Ice Cap, Nunavut, Canada, J. Geophys. Res.-Earth, 118, 2380–2391, 2013.
Granshaw, F. D. and Fountain, A. G.: Glacier change (1958–1998) in the north Cascades national park complex, Washington, USA, J. Glaciol., 52, 251–256, 2006.
Hamlet, A. F. and Lettenmaier, D. P.: Columbia River streamflow forecasting based on ENSO and PDO climate signals, J. Water Res. Pl., 125, 333–341, 1999.
Hamlet, A. F., Mote, P. W., Clark, M. P., and Lettenmaier, D. P.: Effects of temperature and precipitation variability on snowpack trends in the Western United States, J. Climate, 18, 4545–4561, 2005.
Helfricht, K., Schöber, J., Seiser, B., Fischer, A., Stötter, J., and Kuhn, M.: Snow accumulation of a high alpine catchment derived from LiDAR measurements, Adv. Geosci., 32, 31–39, https://doi.org/10.5194/adgeo-32-31-2012, 2012.
Helfricht, K., Kuhn, M., Keuschnig, M., and Heilig, A.: Lidar snow cover studies on glaciers in the Ötztal Alps (Austria): comparison with snow depths calculated from GPR measurements, The Cryosphere, 8, 41–57, https://doi.org/10.5194/tc-8-41-2014, 2014.
Herron, M. M. and Langway, C. C.: Firn densification: an empirical model, J. Glaciol., 25, 373–385, 1980.
Hirose, J. M. R. and Marshall, S. J.: Glacier Meltwater Contributions and Glaciometeorological Regime of the Illecillewaet River Basin, British Columbia, Canada, Atmos. Ocean, 51, 416–435, https://doi.org/10.1080/07055900.2013.791614, 2013.
Huss, M.: Density assumptions for converting geodetic glacier volume change to mass change, The Cryosphere, 7, 877–887, https://doi.org/10.5194/tc-7-877-2013, 2013.
Huss, M. and Hock, R.: Global-scale hydrological response to future glacier mass loss, Nat. Clim. Change, 8, 135–140, https://doi.org/10.1038/s41558-017-0049-x, 2018.
Huss, M., Bauder, A., Funk, M., and Hock, R.: Determination of the seasonal mass balance of four Alpine glaciers since 1865, J. Geophys. Res., 113, F01015, https://doi.org/10.1029/2007JF000803, 2008.
Isenburg, M.: LAStools – efficient LiDAR processing software, version 141017, unlicensed, available at: http://rapidlasso.com/LAStools, last access: 30 May 2017.
Joerg, P. C., Morsdorf, F., and Zemp, M.: Uncertainty assessment of multi-temporal airborne laser scanning data: A case study on an Alpine glacier, Remote Sens. Environ., 127, 118–129, https://doi.org/10.1016/j.rse.2012.08.012, 2012.
Jost, G., Moore, R. D., Menounos, B., and Wheate, R.: Quantifying the contribution of glacier runoff to streamflow in the upper Columbia River Basin, Canada, Hydrol. Earth Syst. Sci., 16, 849–860, https://doi.org/10.5194/hess-16-849-2012, 2012.
Kääb, A.: Remote sensing of mountain glaciers and permafrost creep, Geographisches Institut der Universität Zürich, Zürich, 2005.
Klug, C., Bollmann, E., Galos, S. P., Nicholson, L., Prinz, R., Rieg, L., Sailer, R., Stötter, J., and Kaser, G.: Geodetic reanalysis of annual glaciological mass balances (2001–2011) of Hintereisferner, Austria, The Cryosphere, 12, 833–849, https://doi.org/10.5194/tc-12-833-2018, 2018.
Krimmel, R. M.: Water, ice, and meteorological measurements at South Cascade Glacier, Washington, 1995 balance year, Report, available at: http://pubs.er.usgs.gov/publication/wri964174 (last access: 2 February 2018), 1996.
Machguth, H., Eisen, O., Paul, F., and Hoelzle, M.: Strong spatial variability of snow accumulation observed with helicopter-borne GPR on two adjacent Alpine glaciers, Geophys. Res. Lett., 33, L13503, https://doi.org/10.1029/2006GL026576, 2006.
Marshall, S.: The Cryosphere, Princeton University Press, Princeton, Princeton, New Jersey, 288 pp., 2012.
Marshall, S. J.: Meltwater run-off from Haig Glacier, Canadian Rocky Mountains, 2002–2013, Hydrol. Earth Syst. Sci., 18, 5181–5200, https://doi.org/10.5194/hess-18-5181-2014, 2014.
Marti, R., Gascoin, S., Berthier, E., de Pinel, M., Houet, T., and Laffly, D.: Mapping snow depth in open alpine terrain from stereo satellite imagery, The Cryosphere, 10, 1361–1380, https://doi.org/10.5194/tc-10-1361-2016, 2016.
Maussion, F., Butenko, A., Champollion, N., Dusch, M., Eis, J., Fourteau, K., Gregor, P., Jarosch, A. H., Landmann, J., Oesterle, F., Recinos, B., Rothenpieler, T., Vlug, A., Wild, C. T., and Marzeion, B.: The Open Global Glacier Model (OGGM) v1.1, Geosci. Model Dev., 12, 909–931, https://doi.org/10.5194/gmd-12-909-2019, 2019.
McCabe, G. J., Hay, L. E., and Clark, M. P.: Rain-on-Snow Events in the Western United States, B. Am. Meteorol. Soc., 88, 319–328, https://doi.org/10.1175/BAMS-88-3-319, 2007.
McGrath, D., Sass, L., O'Neel, S., Arendt, A., Wolken, G., Gusmeroli, A., Kienholz, C., and McNeil, C.: End-of-winter snow depth variability on glaciers in Alaska, J. Geophys. Res.-Earth, 120, 1530–1550, https://doi.org/10.1002/2015JF003539, 2015.
McGrath, D., Sass, L., O'Neel, S., McNeil, C., Candela, S. G., Baker, E. H., and Marshall, H.-P.: Interannual snow accumulation variability on glaciers derived from repeat, spatially extensive ground-penetrating radar surveys, The Cryosphere, 12, 3617–3633, https://doi.org/10.5194/tc-12-3617-2018, 2018.
Menounos, B., Hugonnet, R., Shean, D., Gardner, A., Howat, I., Berthier, E., Pelto, B., Tennant, C., Shea, J. and Noh, M.: Heterogeneous Changes in Western North American Glaciers Linked to Decadal Variability in Zonal Wind Strength, Geophys. Res. Lett., 46, 200––209, https://doi.org/10.1029/2018GL080942, 2019.
Miller, M. M. and Pelto, M. S.: Mass balance measurements on the Lemon Creek Glacier, Juneau Icefield, Alaska 1953–1998, Geogr. Ann. a, 81, 671–681, 1999.
Moholdt, G., Nuth, C., Hagen, J. O., and Kohler, J.: Recent elevation changes of Svalbard glaciers derived from ICESat laser altimetry, Remote Sens. Environ., 114, 2756–2767, https://doi.org/10.1016/j.rse.2010.06.008, 2010.
Najafi, M. R., Zwiers, F., and Gillett, N.: Attribution of the Observed Spring Snowpack Decline in British Columbia to Anthropogenic Climate Change, J. Climate, 30, 4113–4130, https://doi.org/10.1175/JCLI-D-16-0189.1, 2017.
Nolan, M., Larsen, C., and Sturm, M.: Mapping snow depth from manned aircraft on landscape scales at centimeter resolution using structure-from-motion photogrammetry, The Cryosphere, 9, 1445–1463, https://doi.org/10.5194/tc-9-1445-2015, 2015.
Nuth, C. and Kääb, A.: Co-registration and bias corrections of satellite elevation data sets for quantifying glacier thickness change, The Cryosphere, 5, 271–290, https://doi.org/10.5194/tc-5-271-2011, 2011.
Oerlemans, J., Anderson, B., Hubbard, A., Huybrechts, P., Johannesson, T., Knap, W. H., Schmeits, M., Stroeven, A. P., Van de Wal, R. S. W., Wallinga, J., nd Zuo, Z.: Modelling the response of glaciers to climate warming, Clim. Dynam., 14, 267–274, 1998.
Ohmura, A.: Observed mass balance of mountain glaciers and Greenland ice sheet in the 20th century and the present trends, Surv. Geophys., 32, 537–554, 2011.
Østrem, G. and Brugman, M.: Glacier massbalance measurements: a manual for field and office work, Saskatoon: National Hydrology Research Institute, and Oslo: the Norwegian Water Resources and Electricity Board, 1991.
Pelto, M. S.: Annual net balance of North Cascade glaciers, 1984–94, J. Glaciol., 42, 3–9, 1996.
Pelto, M. S.: The current disequilibrium of North Cascade glaciers, Hydrol. Process., 20, 769–779, https://doi.org/10.1002/hyp.6132, 2006.
Pelto, M. S. and Miller, M. M.: Mass balance of the Taku Glacier, Alaska from 1946 to 1986, Northwest Sci., 64, 121–130, 1990.
Pelto, M. S. and Riedel, J.: Spatial and temporal variations in annual balance of North Cascade glaciers, Washington 1984–2000, Hydrol. Process., 15, 3461–3472, https://doi.org/10.1002/hyp.1042, 2001.
Pelto, M., Kavanaugh, J., and McNeil, C.: Juneau Icefield Mass Balance Program 1946–2011, Earth Syst. Sci. Data, 5, 319–330, https://doi.org/10.5194/essd-5-319-2013, 2013.
Pfeffer, W. and Humphrey, N.: Determination of timing and location of water movement and ice-layer formation by temperature measurements in sub-freezing snow, J. Glaciol., 42, 292–304, 1996.
Proksch, M., Rutter, N., Fierz, C., and Schneebeli, M.: Intercomparison of snow density measurements: bias, precision, and vertical resolution, The Cryosphere, 10, 371–384, https://doi.org/10.5194/tc-10-371-2016, 2016.
Pulwicki, A., Flowers, G. E., Radić, V., and Bingham, D.: Estimating winter balance and its uncertainty from direct measurements of snow depth and density on alpine glaciers, J. Glaciol., 64, 781–795, https://doi.org/10.1017/jog.2018.68, 2018.
Radić, V. and Hock, R.: Glaciers in the Earth's Hydrological Cycle: Assessments of Glacier Mass and Runoff Changes on Global and Regional Scales, Surv. Geophys., 35, 813–837, https://doi.org/10.1007/s10712-013-9262-y, 2014.
Ragettli, S., Immerzeel, W. W., and Pellicciotti, F.: Contrasting climate change impact on river flows from high-altitude catchments in the Himalayan and Andes Mountains, P. Natl. Acad. Sci. USA, 113, 9222–9227, 2016.
Samimi, S. and Marshall, S. J.: Diurnal Cycles of Meltwater Percolation, Refreezing, and Drainage in the Supraglacial Snowpack of Haig Glacier, Canadian Rocky Mountains, Front. Earth Sci., 5, 6, https://doi.org/10.3389/feart.2017.00006, 2017.
Schnorbus, M., Werner, A., and Bennett, K.: Impacts of climate change in three hydrologic regimes in British Columbia, Canada, Hydrol. Process., 28, 1170–1189, https://doi.org/10.1002/hyp.9661, 2014.
Sinclair, K. and Marshall, S.: Temperature and vapour-trajectory controls on the stable-isotope signal in Canadian Rocky Mountain snowpacks, J. Glaciol., 55, 485–498, 2009.
Sold, L., Huss, M., Hoelzle, M., Andereggen, H., Joerg, P. C., and Zemp, M.: Methodological approaches to infer end-of-winter snow distribution on alpine glaciers, J. Glaciol., 59, 1047–1059, https://doi.org/10.3189/2013JoG13J015, 2013.
Sold, L., Huss, M., Eichler, A., Schwikowski, M., and Hoelzle, M.: Unlocking annual firn layer water equivalents from ground-penetrating radar data on an Alpine glacier, The Cryosphere, 9, 1075–1087, https://doi.org/10.5194/tc-9-1075-2015, 2015.
Sold, L., Huss, M., Machguth, H., Joerg, P. C., Leysinger Vieli, G., Linsbauer, A., Salzmann, N., Zemp, M., and Hoelzle, M.: Mass balance re-analysis of Findelengletscher, Switzerland; benefits of extensive snow accumulation measurements, Front. Earth Sci., 4, 18, https://doi.org/10.3389/feart.2016.00018, 2016.
Stahl, K. and Moore, R. D.: Influence of watershed glacier coverage on summer streamflow in British Columbia, Canada, Water Resour. Res., 42, W06201, https://doi.org/10.1029/2006WR005022, 2006.
Thibert, E. and Vincent, C.: Best possible estimation of mass balance combining glaciological and geodetic methods, Ann. Glaciol., 50, 112–118, 2009.
Van Pelt, W. and Kohler, J.: Modelling the long-term mass balance and firn evolution of glaciers around Kongsfjorden, Svalbard, J. Glaciol., 61, 731–744, https://doi.org/10.3189/2015JoG14J223, 2015.
van Pelt, W. J. J., Oerlemans, J., Reijmer, C. H., Pohjola, V. A., Pettersson, R., and van Angelen, J. H.: Simulating melt, runoff and refreezing on Nordenskiöldbreen, Svalbard, using a coupled snow and energy balance model, The Cryosphere, 6, 641–659, https://doi.org/10.5194/tc-6-641-2012, 2012.
Weber, F. and Litke, T.: Standard Operating Procedure Maintainence and Sampling Procedure Manual Snow Surveying, BC Hydro., 2018.
WGMS: Fluctuations of Glaciers Database, World Glacier Monit. Serv., https://doi.org/10.5904/wgms-fog-2018-11, 2018.