the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Cold-to-warm flow regime transition in snow avalanches
Anselm Köhler
Jan-Thomas Fischer
Riccardo Scandroglio
Mathias Bavay
Jim McElwaine
Betty Sovilla
Large avalanches usually encounter different snow conditions along their track. When they release as slab avalanches comprising cold snow, they can subsequently develop into powder snow avalanches entraining snow as they move down the mountain. Typically, this entrained snow will be cold ( ∘C) at high elevations near the surface, but warm ( ∘C) at lower elevations or deeper in the snowpack. The intake of warm snow is believed to be of major importance to increase the temperature of the snow composition in the avalanche and eventually cause a flow regime transition. Measurements of flow regime transitions are performed at the Vallée de la Sionne avalanche test site in Switzerland using two different radar systems. The data are then combined with snow temperatures calculated with the snow cover model SNOWPACK. We define transitions as complete when the deposit at runout is characterized only by warm snow or as partial if there is a warm flow regime, but the farthest deposit is characterized by cold snow. We introduce a transition index Ft, based on the runout of cold and warm flow regimes, as a measure to quantify the transition type. Finally, we parameterize the snow cover temperature along the avalanche track by the altitude Hs, which represents the point where the average temperature of the uppermost 0.5 m changes from cold to warm. We find that Ft is related to the snow cover properties, i.e. approximately proportional to Hs. Thus, the flow regime in the runout area and the type of transition can be predicted by knowing the snow cover temperature distribution. We find that, if Hs is more than 500 m above the valley floor for the path geometry of Vallée de la Sionne, entrainment of warm surface snow leads to a complete flow regime transition and the runout area is reached by only warm flow regimes. Such knowledge is of great importance since the impact pressure and the effectiveness of protection measures are greatly dependent on the flow regime.
- Article
(10824 KB) - Full-text XML
- BibTeX
- EndNote
For avalanche practitioners dealing with situations where they need to judge the avalanche hazard for infrastructure, flow regime transitions can cause large uncertainties. Which flow regime reaches the valley bottom is of great interest from two perspectives. Firstly, the usefulness of permanent protection measures like avalanche dams depends strongly on the flow regime (Jóhannesson et al., 2009). Indeed, deflecting and catching dams are relatively ineffective against the highly fluidized intermittent frontal regime of powder snow avalanches, whereas dense flow regimes, especially warm regimes, can more easily be diverted or even stopped. Secondly, the force generated by an avalanche on a structure in the path depends strongly on flow regime (Gauer et al., 2008b). A velocity-dependent grain-inertia induced pressure is dominant in cold–dry flow regimes, whereas a flow-depth dependent, quasi-static gravitational contribution is dominant in warm–wet flow regimes (Sovilla et al., 2016).
Recent studies identified snow temperature as a key parameter causing the agglomeration of snow (Steinkogler et al., 2014) and a change of the flow dynamics by altering the velocity and the effective friction (Gauer and Kristensen, 2016; Naaim et al., 2013) as well as the stopping dynamics (Köhler et al., 2018). A temperature value of −1 ∘C is proposed by a study on snow granulation (Steinkogler et al., 2015a), where they observed a significant change from millimetre-sized grains to the formation of decimetre-sized granules above this temperature. We emphasize the temperature of the snow by calling avalanches warm and cold rather than wet and dry since the flow behaviour changes already at a threshold of −1 ∘C. That this transition occurs below 0 ∘C is presumably due to the existence of a quasi-liquid layer even at sub-zero temperatures (Dash et al., 2006; Turnbull, 2011). Liquid water may cause the cohesion of snow to increase by the formation of granules, but may also lubricate the contacts between snow aggregates and result in slush flows.
The avalanche flow regime – a region inside the avalanche where the same physical processes are dominant – can be deduced from radar signatures of flow processes by use of the radar GEODAR (Köhler et al., 2018). Cold flow regimes are identified by the starving mechanism, in which the avalanche loses mass from the tail until finally the front comes to halt. We call cold regimes those flow regimes which contain cold snow ( ∘C) and are categorized as either the cold dense regime or as the intermittent regime of the dilute frontal region of powder snow avalanches. In contrast, warm flow regimes are identified by either abrupt stopping or a backward propagating shock; either a large flowing part stops instantaneously or the front comes to a halt and incoming material piles up. We call warm regimes those flow regimes which occur for warm snow temperatures ( ∘C) and are categorized as either the warm shear regime or the warm plug regime. Köhler et al. (2018) differentiated flow regimes comprising cold and warm snow further in detail. However, relevant for the discussion here is that the majority of large avalanches show transitions between cold and warm flow regimes. These transitions and the relation with snow cover properties are the focus of this paper.
This study deals exclusively with avalanches that start in a cold–dry regime, and parts of which undergo a transition to a warm–wet regime; that is, those avalanches exhibit a cold-to-warm flow regime transition. We define these transitions as partial transition or complete transition, depending on whether only parts, or the entire avalanche, transform. A partial transition often becomes visible at the tail of the flowing avalanche, as cold and warm flow regimes separate due to different velocities and the final runout is still cold-dominated. With a complete transition, all the snow becomes warm and the final runout is determined by the dynamical properties of the warm flow regime.
Large avalanches composed mostly of cold snow are powder snow avalanches and have been described by many authors (Issler, 2003; Sovilla et al., 2015). They usually release as a slab containing cold snow, and the runout area is reached by fast flowing cold snow. In addition to the typical structure of a suspension cloud, a frontal intermittent region and a cold dense core and tail, GEODAR images often reveal warm flow regimes in the tail, indicating that a partial transition happened (Köhler et al., 2018). Issler (2003) introduced the nomenclature “mixed powder snow avalanche” to describe the occurrence of dilute and dense flow regimes together in one avalanche event. The definition applies mostly for cold, dense and dilute regimes, but Issler (2003) reported damp deposits which are not covered by dust of the dilute regimes and thus had been flowing later and more slowly.
Warm-dominated avalanches release similarly to cold-dominated ones but transform completely somewhere along the path. In this case, the runout is dominated by warm regimes. Literature on this type of avalanche is hard to find since to our knowledge such a transition is rarely recognized, and the events are rather described as wet avalanches. There are some measurements with radar and picture in Gauer et al. (2008a) indicating a complete transition, but have been interpreted as a secondary wet slab released by the primary dry–cold avalanche. An example of an avalanche with a complete transition released spontaneously near the village of Moos in Passeiertal, Italy, on 6 February 2014. A video of this avalanche drew a lot of attention because most of the avalanche travelled along a road in front of houses with people on their balconies (https://www.youtube.com/watch?v=f5waSw2mMfY, last access: 20 November 2018). The avalanche released on the south-east facing slopes below the summit of Scheibkopf (2816 m a.s.l.) after a major snowstorm and developed a large powder cloud and thus contained cold snow. At around 15 s after the start of the video, the powder cloud began to decay so that the cold parts stopped at approximately 1700 m a.s.l. A dense flow continued and flowed over a cliff into a shallow valley, where finally a slow-moving plug flow developed. The avalanche transformed completely from a cold powder snow avalanche into a warm flow, which finally flowed slowly along the road.
The present study tries to answer the question of how the degree of transition relates to the snow cover properties along the avalanche track. To quantitatively describe the degree of transition as a continuum between partial and complete, we define the transition index Ft, which is a function of the path length of warm and cold flow regimes.
We then explore the relationship with snow cover characteristics, focusing on the snow temperature averaged over the uppermost 0.5 m of the snow cover. This depth is expected to be frequently entrained into the avalanche, though of course there may be more or less entrainment. This assumption is backed up by field observations on typical entrainment depths and underpinned in Sect. 2.2. We find that is a representative indicator for the thermal energy intake due to entrainment, and we will show that it can be used to give a good prediction of the transition index.
The study starts by introducing the test site and sensor equipment (Sect. 2.1), the method to derive the snow cover temperatures by simulations with the numerical model SNOWPACK (Sect. 2.2), and a short description of the avalanche data (Sect. 2.3). The following results section is divided in two parts. Firstly, we detail the kinematic and dynamic characteristics of partial and complete transitions by means of two different radar systems (Sects. 3.1 and 3.2). Secondly, we present the analysis of the degree of transition with the snow cover temperatures (Sect. 3.3). Finally, the discussion (Sect. 4) is divided into two sections which bring results into a wider context and points out limitations of our methodology.
2.1 Test site and radar sensors
The full-scale avalanche test site Vallée de la Sionne (VdlS) is situated in the west of Switzerland. The east-facing avalanche path extends from high altitudes at 2700 m a.s.l. to intermediate altitudes with a total drop height of 1300 m. The VdlS avalanche track can be roughly characterized with a 40∘ steep release area above 2300 m a.s.l., followed by a flatter section which leads into two 35∘ steep couloirs between 1800 and 2100 m a.s.l., with the runout area starting below and continuing into the valley floor at 1400 m a.s.l. Especially in the early and late season, there can be minimal snow in the lower part of the slope but still sufficient snow for avalanches in the release areas at higher elevations.
The test site is equipped with multiple sensor systems at different locations. On a 20 m high pylon near the start of the runout area, sensors give high-resolution vertical profiles of flow velocity, flow height, density and impact pressure (Sovilla et al., 2013). Upward-looking flow profiling radars and seismic sensors are situated in two locations along the flow path. Data are also collected over the entire slope by two complementary radar systems: the GEODAR (Ash et al., 2010), which allows tracking of avalanche features with high spatial and temporal resolution and the pulse-Doppler system (Schreiber et al., 2001), which complements this with complete velocity distributions of the avalanche flow. An automatic seismic trigger enables measurement of even spontaneous avalanches.
GEODAR is a high-resolution frequency modulated continuous wave radar and was first installed in winter season 2009–2010 (Ash et al., 2014). The system has been continually improved and currently has a range resolution of 0.75 m at 110 Hz over the entire slope (Köhler et al., 2018). GEODAR is able to resolve internal flow structures below the powder cloud. By means of feature tracking, comparison with other data and qualitative interpretations, new and very detailed insights into processes during an avalanche descent have been gained (Köhler et al., 2016, 2018; Vriend et al., 2013). The data processing, feature extraction and terrain registration are done here with the same methods as described in these three publications. An approach velocity va(t) of the avalanche front towards the radar is calculated by the derivative of the range–time trajectory r(t), which is corrected for the angle between terrain and the radar beam θ (Köhler et al., 2016):
The processed GEODAR data are usually shown as range–time plots with the colour representing the intensity of the moving-target identification (MTI) filter (e.g. left panels of Fig. 2). This filter suppresses static targets and background clutter and highlights moving structures. Often the front and tail give the clearest signature from light to dark colours and vice versa. In between, the avalanche signature is usually dark coloured with line and streak patterns (Köhler et al., 2018). The distance between front and the tail along the range axis is the avalanche's flowing length, which in general increases between release area and the fastest parts that reach the valley floor.
The other radar, a pulse-Doppler radar, was permanently installed at Vallée de la Sionne for the winter season 2009–2010 and upgraded in 2016–2017. The older system provided a spatial resolution of Rg=50 m (Schreiber et al., 2001), and the newer system gives Rg=25 m (Fischer et al., 2016). This resolution is referred to as a range gate extent (Rg), and the Doppler measurements provide an intensity distribution of velocities over time Ik(t,v) of the flowing material within each range gate Rk with a running number k (e.g. Figs. 3 and 4). The peak of this distribution describes the velocity of maximum intensity and gives the velocity at which most of the material is travelling (Fischer et al., 2014; Gauer et al., 2007). The data can also be transformed into a range–time representation (Fischer et al., 2016), which is very similar to GEODAR intensity–range plots but represents the mean velocity in each range gate k at each time as
(middle panels in Fig. 2). This can then be converted from a discrete function of range to a continuous function, using finite volume interpolation methods.
2.2 Snow cover reconstruction
The test site Vallée de la Sionne is equipped with three weather stations. The bottom station, VDS3 (indicated with subscript 3) at elevation H3=1680 m a.s.l., is representative for the runout area. The top weather station, VDS2 (subscript 2) at elevation H2=2390 m a.s.l., gives a good approximation for the release area even though it is situated 3 km to the north of the avalanche path. Both weather stations are installed in flat fields sheltered from winds to most accurately represent the undisturbed snow height. Both weather stations measure air temperature, humidity, wind speed, snow height, radiation and snow surface temperature, which are the complete set of parameters necessary to simulate the desired snow cover profiles. A third station VDS1 is situated directly on the ridge above the release area and especially measures wind speed and therefore wind loading.
The meteorological data have been prepared with the library meteoIO (Bavay and Egger, 2014), i.e. missing values have been interpolated, and temperature and snow height data have been filtered. Corrections according to Huwald et al. (2009) were necessary for the air temperature, as unventilated temperature sensors are used, and these usually overestimate the temperature for situations with low wind speed but strong radiation. Special attention has also been given to the snow height data at the VDS3 station, since for low snow heights the measurements were biased by vegetation so that the values had to be manually reset to 0 m.
To obtain snow temperature profiles, the snow cover has to be modelled, as these are not measured automatically. The snow cover at the location of the weather stations has been reconstructed with the numerical energy balance model SNOWPACK (Lehning et al., 2002) to obtain vertical snow profiles as a function of time. We have applied the simulation set-up for the operational simulations of the Intercantonal Measurement and Information System (IMIS), the high-alpine weather station network in Switzerland (Schmucki et al., 2014).
In this publication, we explore how the temperature of the snow cover entering an avalanche determines the degree of a cold-to-warm transition. There is no common approach to reduce the temperature profile of the snow cover to a single representative value. Naaim et al. (2013) used the average snow temperature in the full path without differentiating between release and runout area. This approach is very broad, but suitable for situations where it is necessary to compare a large number of avalanche events. In a detailed study, Steinkogler et al. (2014) averaged over an estimated entrainment depth. This is most accurate but requires very detailed entrainment data and therefore is only suited for studies with a few avalanches. Köhler et al. (2018) approximated this depth by assuming that the uppermost 0.5 m of snow was entrained. Sovilla et al. (2006) showed that significant entrainment occurs along the full avalanche path. If we divide the typical volume of large avalanches in VdlS of m3 by the typical affected area of m3 (Dufour et al., 2000; Steinkogler et al., 2014), the average entrainment depth of m appears to be a reasonable assumption. The approach with a constant averaging depth can be regarded as a trade-off between accuracy and practicability for analysing many avalanche events, even though large avalanches can usually dig much deeper into the snow cover (Gauer and Issler, 2004; Sovilla et al., 2006).
Thus, we average the simulated snow temperature:
from the layers i with thickness hi and layer temperature Ti in the uppermost of the simulated snow cover. With SNOWPACK simulations we compute only at the location of VDS2 and VDS3 (squares in right panel of Fig. 1), though we are interested in the snow cover temperatures along the entire avalanche path.
We parameterize along the avalanche path with the altitude Hs of the −1 ∘C line. Hs represents the altitude where crosses the threshold from above to below −1 ∘C, similar to the zero-degree level in meteorology. Motivated by the work of Steinkogler et al. (2014), we estimate Hs with a linear relation between the altitude of the weather stations H2 and H3 and the average temperatures and of the uppermost 0.5 m of the snow cover by
The elevation uncertainty ΔHs is estimated with the temperature variation of the uppermost 0.5 m snow temperature at both weather stations. In fact, is the standard deviation of the simulated layer temperatures in the uppermost 0.5 m of the snowpack. The right panels of Fig. 1 graphically show the linear interpolation of , and Hs and ΔHs is found at the intercept of the grey area with the dashed line at temperature −1 ∘C. ΔHs is not the uncertainty of Hs, but rather a spread of possible values.
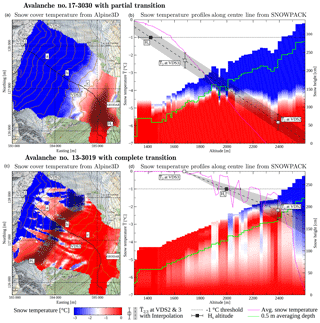
Figure 1Snow cover simulations for avalanche no. 17-3030 with partial transition (a, b) and no. 13-3019 with complete transition (c, d). The left panels (a, c) show the averaged temperatures of the uppermost 0.5 m snow cover from Alpine3D gridded over the VdlS catchment. The area overlay in grey denotes Hs±ΔHs. For reference, the location of the pylon (c) and profiling radars (a, b) are shown. The right panels (b, d) show the snow temperature profiles along the path of steepest descent (black line in left panels a, b). The purple curve indicates the average temperature of the top 0.5 m of each vertical profile. The values at the top and bottom weather stations are shown with white squares together with the temperature variations. Hs is calculated using linear interpolation between the weather stations as the intercept of grey area with −1 ∘C and shown with black squares.
Our parameterization of the snow cover temperatures in the avalanche path and the temperature gradient is in fact only dependent on altitude. To check the validity of these strong assumptions (flat field simulations, linear elevation gradient; see Eq. 4), we have additionally performed Alpine3D simulations to compare the results (Lehning et al., 2006). Alpine3D performs physically based spatial interpolations of all the meteorological input data over a domain, i.e. the area of the VdlS test site. This domain is sliced into grid cells with a resolution of 25 m × 25 m, and for each cell a SNOWPACK simulation is performed (Schlögl et al., 2016). While our single SNOWPACK simulations are calculated for flat fields, Alpine3D simulates the snow cover at each cell with their local slope and aspect. The Alpine3D outputs are grids of a parameter like the 0.5 m snow temperature for every simulation step, and a full SNOWPACK output can be generated at any point of interest.
Results of Alpine3D and SNOWPACK simulations for two example avalanches are shown in Fig. 1. The left panels show the spatial distribution of the temperature over the catchment of VdlS from Alpine3D. The right panels display the vertical profiles of layer temperatures Ti along the line of steepest descent from the release area. These profiles are generated by the Alpine3D simulations as full outputs at points of interest. Additionally, in the right panels are the data of SNOWPACK simulations for both weather stations (denoted with white squares) together with a graphical representation of the interpolation in Eq. (4), which gives Hs at the intercept with the temperature threshold of −1 ∘C (denoted with black squares).
Table 1Summary of the avalanche events with the extracted path lengths P, the transition index and altitude of transition Ht, as well as the snowpack conditions Hs and mean temperatures at both weather stations . Data of avalanche events indicated with a * in front of the row can be received from the GEODAR repository (McElwaine et al., 2017).
The two examples in Fig. 1 have the largest deviation between Eq. (4) and the Alpine3D simulations in our data sets. The no. 17-3030 event (top) occurred in springtime, when the flat fields receive more sun than the eastern aspect and thus show higher temperature for at the station VDS2. The no. 13-3019 event corresponds to a rain event, and the right panel shows isothermal 0 ∘C snow in the runout area but very cold snow in the release area. However, if compared with the gridded of the Alpine3D output in the left panels, both Hs estimates (grey areas) reflect the pattern of warm and cold temperatures reasonably well. Thus, we expect a deviation from Eq. (4) for situations like springtime with strong radiation influence, and Hs will be less accurate if large regions are isothermal. In particular, rain-on-snow events may be overlooked, as the water ingress is difficult to measure and to capture with SNOWPACK (Würzer et al., 2017).
2.3 Data set
In this study, we selected avalanche events from Vallée de la Sionne that fulfill three criteria. (1) They were large enough to pass the measurement pylon at range 655 m near the start of the runout area. This criterion implies a minimum drop height of 1000 m. (2) The avalanche stopped where it was visible to GEODAR, that is before the counter slope. (3) A cold-to-warm transition as described by Köhler et al. (2018) occurred somewhere in the avalanche.
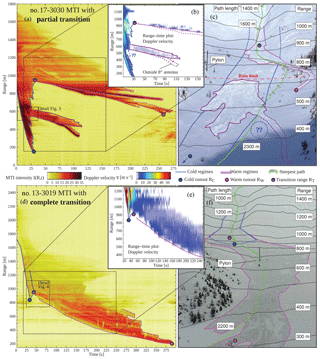
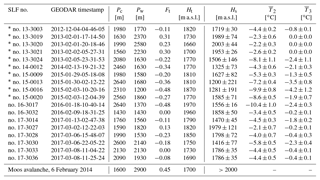
Figure 2Avalanche examples for a partial (top, a–c) and a complete (bottom, d–f) cold-to-warm transition. The avalanches are visualized by means of GEODAR data (a, d), mean Doppler velocities (b, e) and geo-referenced pictures of the deposits (c, f). Flow features extracted from GEODAR are highlighted in the other panels. The warm regimes are identified by typical coarse-grained and rough deposits (purple and magenta), while the fine-grained and smooth cold deposits can only be sketched (blue). The path along the steepest descent is drawn in green. The cold and warm runout distances and the transition point are indicated with coloured dots.
Since the lower weather station (VDS3) first became operational in the winter season 2012–2013, we selected large avalanche events from then until the season 2016–2017. From totally measured 130 avalanche events, 18 avalanches fulfill these criteria and were selected. Two of them are compared in detail in Fig. 2. The selected avalanches cover the full variability between partial (Sect. 3.1) and complete flow regime transitions (Sect. 3.2). Noteworthy is that avalanches with a complete transition are relatively rare in our data set. There was a 3-day period at the beginning of February 2013 when three out of the four of these avalanches occurred. Avalanches with a partial transition could occur all winter from December to March. The avalanche and snow cover data used in this publication are summarized in Table 1.
A release location was assigned to each avalanche event by the use of additional data from the VdlS test site such as photographs and data from flow profiling radars (Köhler et al., 2018). We map the radar range R onto the line of steepest descent from the release location (i.e. green line in Fig. 2). Such a procedure can be thought of as a transfer function between radar range R, real world coordinates and the path length P (Köhler et al., 2016). The path length P is the projected ground parallel distance from the release point P0=0 m. Whereas the radar range R is the line-of-sight distance, and is generally smaller than P. Since we often do not know precisely the release coordinates, the highest point of the most likely release area was used, giving an uncertainty of 50–100 m in path length P.
From the MTI plots of the GEODAR data (left in Fig. 2), we manually extracted the following ranges and calculated the corresponding path lengths.
-
Pc is the path length of front containing cold snow, primarily identified by a stopping with the starving mechanism.
-
Pw is the path length of front containing warm snow, primarily identified by a backward propagating shock or abrupt stopping.
-
Pt is the path length until the point of transition between a cold front and a warm front. For avalanches with a complete transition, Pt was relatively precise. For partial transitions, Pt could be identified only as soon as the warm front separated from the rest of the flow (Fig. 2), and this gave rise to an uncertainty of ± 50 m in path length.
The coloured dots in Fig. 2 show the features in the MTI images to which the three points RC, RW and RT belong for two example avalanches. The transfer function between radar range R and path length P is roughly given by the labels in the photographs in Fig. 2.
This section starts with a qualitative characterization of the two cold-to-warm flow regime transition types by means of GEODAR and pulse-Doppler data. Then we relate the degree of transition of all 18 avalanches with the snow cover data. Here, we do not differentiate the flow regimes classified by Köhler et al. (2018) in detail, but simply consider cold and warm flow regimes only. We call cold regimes those flow regimes which contain cold snow ( ∘C), i.e. the cold dense regime and intermittent regime. And we call warm regimes those flow regimes which occur for warm snow temperatures ( ∘C), i.e. the warm shear regime and warm plug regime. Warm and cold regimes differ clearly in their MTI stopping signatures. We refer to Köhler et al. (2018) for a detailed description of stopping signatures in the GEODAR signal and the differentiation between cold and warm flow regimes.
Note, we can not validate the temperature threshold for snow granulation of −1 ∘C with our data. We focus on snow temperature as the driving factor; other influences like liquid water content or salt content in maritime snow are neglected. Furthermore, as we use snow cover simulations to examine the temperature of the flowing avalanche, we explicitly assume that the temperatures of the flow and the snow cover are the same. This is clearly an assumption, which depends for example on the entrainment rate, but it is the best we can do.
Figure 2 gives an overview of how cold-to-warm transitions manifest themselves in an MTI image, in the mean velocity from the Doppler radar and in a picture of the deposit structures. In the pictures, it is feasible to clearly define the deposits of the warm flow regimes (purple and magenta), while the lateral extent of the cold regimes (blue) can only be sketched. The outlines around regions of the flow regimes can also be extracted from the GEODAR and Doppler data (annotated with the same colours). Due to a smaller opening angle of the Doppler radar antenna, features on the far right side of the track are not captured (dashed).
When the most distal deposits are cold, a partial transition happens higher up in the avalanche path and deposits of warm snow can be identified (no. 17-3030, top panels). In contrast, a complete transition happens when an initially cold avalanche starves and transforms into a warm avalanche (no. 13-3019, bottom panels). While cold regimes are rather quick, warm flow regimes separate in range and time, as they are much slower (Fig. 2). The timing when the avalanche reaches the farthest runout distance is therefore different. Avalanche no. 13-3019 with a complete transition reaches the farthest runout around 350 s later than avalanche no. 17-3030 with partial transition.
3.1 Example of a partial transition
The upper panel of Fig. 2 shows avalanche no. 17-3030 as an example of a partial transition. This avalanche originated from the right-hand side of the release area and followed the right couloir. The snow mainly consisted of freshly fallen cold snow and was, for most of the avalanche track, colder than −1 ∘C (upper panels of Fig. 1). The −1 ∘C line was estimated at m a.s.l. (≈200 m range) and thus close to the valley floor. Avalanche no. 17-3030 was a typical powder snow avalanche for the Vallée de la Sionne path, with an intermittent regime at the front and followed by a slow moving dense tail (Sovilla et al., 2015). The geo-referenced picture on the top right of Fig. 2 was taken after 1.5 days of intense snowfall. Still, the rough deposition patterns of the warm flow regimes can be easily identified, whereas the fine-grained deposits from the cold flow regimes were hidden under the new snow cover.
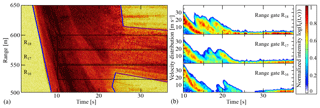
Figure 3Detail of a partial transition from avalanche no. 17-3030 from the top panels of Fig. 2. (a) Zoomed MTI plot with the location of Doppler range gates. (b) Doppler velocity distribution in the range gates R16 (525–550 m), R17 (550–575 m) and R18 (575–600 m).
The GEODAR data are complemented by velocity data captured by the Doppler radar (top middle in Fig. 2), which shows the mean velocity in a range–time plot, i.e. the expected value of the velocity distribution for every time t and range R (Eq. 2). Unfortunately, the start of the Doppler radar was delayed by 10 s, thus most of the front is missing, but the regions inside the avalanche, where fast and slower flow regimes prevail, can be clearly identified. Several fast surges are visible and were characterized by a velocity of up to 30 m s−1. These surges belonged to the cold regimes which can be identified on the basis of their starving stopping signatures. The farthest point reached by the avalanche was the runout of the cold front at RC=150 m range (blue dot, Fig. 2, top), which corresponds to Pc=2600 m path length. This avalanche had a cold-dominated runout.
Two slowly flowing tails followed after the front had passed and were characterized by a homogeneous velocity of 2 to 5 m s−1. Both tails show the characteristic abrupt stopping signatures of warm snow. The transition into the magenta tail becomes visible in the MTI plot at the end of the steep couloir at a range RT=950 m (blue and magenta dot). Interestingly, the avalanche's flowing length started to increase already at a range of 1300 m, which suggests that a transition towards the warm and slower regime may have started higher up. However, the warm tail continued to flow for another 250 s until it finally stopped at RW=550 m range, corresponding to Pw=2140 m path length. A warm tail like this one is characteristic for most of the powder snow avalanches observed in VdlS. Sometimes, an avalanche can have two of them flowing in both couloirs at the same time. In this case, the warm runout is defined by the tail which went farthest.
The tail at a 400 to 600 m range (outlined in dark purple, Fig. 2) is an unusual feature which we only observe in this data set. However, it enables an excellent opportunity to detail the formation of such a warm tail. It originated from entrainment of warm snow in the 20∘ slope of the runout area. Interestingly, the upper boundary of the entrainment corresponds to a rain limit at 1600 m a.s.l. a few days before the avalanche. The liquid water ingress may have caused a weakening of the snow cover.
Figure 3 gives a detailed look of the transition leading towards this warm tail. In the right panels, the velocity distributions of the corresponding range gates R16, R17 and R18 from the Doppler radar are shown. Three surges are visible in these range gates, with high velocities at their fronts that decline towards their tails. For the first two fronts, the velocity distribution ranges from 10 to 30 m s−1. The lower signal intensity at smaller velocities indicates that most of the snow moves fast. By comparison, the approach velocity of the front va extracted from the GEODAR data is around 25 m s−1. The Doppler data show that the velocity during the transition changed rather rapidly from fast to slow inside one range gate. Along the three range gates, the first front continues with similar velocity distribution, but the second and third surge diminish. The third front in R18 already contains low velocities at its beginning, possibly corresponding to the formation of the warm tail. The terminal velocity (later than 30 s) of the warm tail is characterized by a narrow velocity distribution, as expected for a plug flow regime in all three range gates.
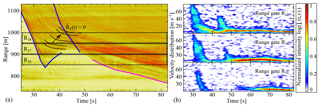
Figure 4A detailed look of the complete transition from bottom panels of Fig. 2. (a) MTI with location of Doppler range gates. The location of transition RT is not fixed but moves upward with time . (b) Doppler velocity distribution in range gates R16 (850–900 m), R17 (900–950 m) and R18 (950–1000 m).
3.2 Example of a complete transition
The lower panels of Fig. 2 show the GEODAR data, Doppler data and a picture of avalanche no. 13-3019 as an example of a complete cold-to-warm transition. The avalanche descended from the left hand side and followed the left couloir. The snow cover was wetted by rain up to around 2000 m a.s.l. The temperature pattern was highly dependent on the aspect (bottom left of Fig. 1), but the altitude m a.s.l. (≈ 1400 m range) summarizes the simulated snow cover reasonably well. Avalanche no. 13-3019 would normally be classified as a warm–wet event since the deposit showed the typical rough and coarse-grained surface and levees could be identified. But the GEODAR data reveal that a complete flow regime transition occurred at RT=950 m (magenta and blue dot, bottom left in Fig. 2).
Above the transition at RT, two major surges can be identified with high velocities. The approach velocity va measured with GEODAR was 30 to 35 m s−1, while the Doppler data showed material velocities of 50 to 60 m s−1 (Gauer et al., 2007). Such a velocity difference is usually found in the intermittent regime of the frontal region in powder snow avalanches (Sovilla et al., 2018) and corroborates on the turbulent character of both surges (Köhler et al., 2016). The first surge continued for another 100 m after the transition point RT and finally starved at the RC=840 m range (blue dot, Fig. 2, bottom), corresponding to Pc=1630 m path length. Note, all avalanches with a complete transition in the data set show the starving stopping signature for the cold front. The starving front is a primary indicator for cold regimes, so we can clearly exclude any other flow regime transition, such as a transition from the warm shear regime to the warm plug regime (Köhler et al., 2018). Therefore, the path length of the cold regimes is always farther than the transition point.
Below the transition, the avalanche quickly decelerated and revealed the MTI signature of a warm plug regime – the parallel streaks are interpreted as the signature of large granules riding on a fairly stable surface of the flow due to a homogeneous velocity field (Köhler et al., 2018). The mean velocity decreased after the transition to around 3 to 5 m s−1 and was very homogeneous in the full body of the avalanche (bottom middle in Fig. 2). The warm flow regime continued to flow for another 300 s before reaching the farthest runout at the RW=200 m range (magenta dot) and Pw=2370 m path length. Thus, this avalanche had a warm-dominated runout.
Figure 4 shows a zoom of the transition region as an MTI image (left) and distributions of the Doppler velocity in three range gates (right). In R18, the front of the first surge showed low intensity for small velocities but a broad spectrum of velocities between 20 to 70 m s−1. In general, the second surge was slower and showed large intensities in a narrow and slow velocity band. The MTI image indicates that streak signatures (black lines) crossed the second surge and suggests that the low velocities belonged originally to the first front. The duration of the high velocity region in each surge was rather short with 5 s, compared to fully developed powder snow avalanches where this region can last up to 40 s (Steinkogler et al., 2014). However, the velocity distribution after the transition was narrow, with the centre at low and constant velocity indicating a plug flow. Interestingly, the velocity distribution in the plug regime showed very little intensity for velocities between zero and 2–3 m s−1, which indicated a very coherent movement of the avalanche (Fig. 4, Doppler data R17 and R18 at t>50 s).
The flow regime transition happened rather quickly in this avalanche as well as in the other avalanches with complete transition in our data set. The transition occurs within around 100 m of the travelled distance and over a period of less than 15 s. Furthermore, the location of the transition seemed to have travelled uphill () as the black lines in the left of Fig. 4 indicate. Note, no material is travelling upwards at the transition point, but the shock front of the deceleration is moving. This may be caused by a piling up of incoming fast material on top of the already decelerated material. Or an alternative explanation could be that material flowing into the range gate later is already slower and therefore stops more easily at higher locations. However, a complicated model-based dynamic interpretation of the MTI plot and the Doppler data would be needed to decide between both possible interpretations.
As in avalanche no. 17-3030, the flowing length started to increase at a range of 1500 m (bottom left Fig. 2), indicating a separation of fast and slow material in direction of the flow. Faster and possibly cold material may have been concentrated towards the front, while slower and maybe warm material segregated towards the tail.
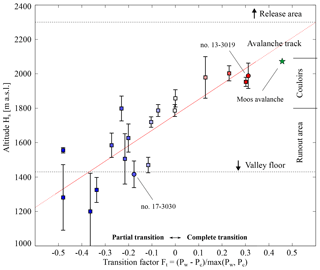
Figure 5Transition index Ft as a function of Hs with a linear regression in red. The transition index Ft has an uncertainty of ±0.05 to 0.1.The green star belongs to the Moos avalanche mentioned in the introduction. Horizontal dashed lines and annotations on the right side roughly characterize the VdlS terrain.
3.3 Snow cover influence on transition type
To differentiate between avalanches with partial and complete transitions, we quantify the degree of transition by defining the transition index
as the difference between the path length from cold (PC) and warm (PW) flow regimes divided by the total path length reached by the avalanche. For avalanches with a partial transition (e.g. Sect. 3.1), the transition index is negative, and the runout is dominated by cold regimes. For events with Ft≈0, the cold regime and the warm regimes reach the same runout. For a positive transition index, the runout is dominated by warm regimes, corresponding to avalanches with a complete transition (e.g. Sect. 3.2). A value of ± 0.5 means that the dominant regime reaches twice as far as the other regime. The limits of Ft to both sides, i.e. and Ft=1, correspond to avalanche types made of purely cold regimes and purely warm regimes, respectively. The avalanches from the examples in Fig. 2 have transition indices of (no. 17-3030) and Ft=0.31 (no. 13-3019). Note, we do not give an uncertainty of the transition index Ft explicitly in Table 1. However, an uncertainty of 50 to 100 m in the path lengths PC and PW propagates into the transition index Ft as an uncertainty of ±0.05 to 0.1.
The transition index Ft together with the altitude Hs for all avalanches are shown in Fig. 5. The 18 analysed avalanches cover Ft in the range between −0.5 and 0.4, and the set of values is well distributed over this range. A linear regression gives with a correlation coefficient of r=0.85. For pure warm avalanches (Ft=1), the regression gives Hs at 2660 m a.s.l., which corresponds to the altitude of the release area. For pure cold avalanches (), the regression would give Hs at 860 m a.s.l., which is far below the runout area of Vallée de la Sionne at 1400 m a.s.l. However, we do not think that the extrapolation towards purely cold avalanches () has any validity in this setting.
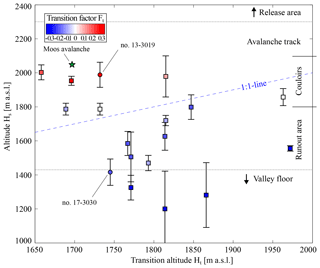
Figure 6Altitude of transition, Ht, against the altitude of the −1 ∘C line, Hs. The 1 : 1 line (dashed blue) divides the avalanches into cases where the transition occurs above or below the Hs line. Horizontal dashed lines and annotations on the right side roughly characterize the VdlS terrain. The colours indicate the transition index from Fig. 5.
Figure 6 compares the altitude Hs against the altitude Ht, which is where the snow cover changes from −1 ∘C against where the transition occurs. We find the altitudes of the transitions Ht scatter on both sides of the 1 : 1 line (blue dashed); in other words, the transition can happen above or below the Hs line. Furthermore, Ht can be up to 500 m in elevation away from Hs. The majority of the avalanches perform the transition above the Hs line, i.e. avalanches with a partial transition (blue symbols). For these events we find that Hs lies below 1880 m a.s.l. and thus in the runout area. And for a few of them, the Hs line is even below the valley floor (below 1450 m a.s.l.), which in turn means that it can not practically be reached, and entrainment of surface snow can not be the cause for a partial transition.
The remaining avalanches perform the transition below the Hs; i.e. these events express either a complete transition and the warm regimes are dominant in the runout (red symbols), or cold and warm regimes reach similar runouts (white symbols). For these events we find that Hs is consequently higher than 1800 m a.s.l., which corresponds approximately to the altitude of the middle of the avalanche path so that the entrainment of surface snow increases the avalanche temperature.
4.1 Discussion of results
We find a continuous degree of transition between partial and complete flow regime transitions (Fig. 5). This continuous degree can be related to the altitude Hs, the altitude where the average modelled temperature of the surficial snow layer changes from below to above −1 ∘C. This means that the flow regime type in the runout area – but not the runout distance itself – can be estimated when Hs is known.
This (semi-) quantitative attempt to capture an aspect of the flow regime transitions with a minimum number of observable quantities needs further investigations to find out if the proposed linear fit or other relations are valid. Even if the linear fit appears to work at least for a certain range of Ft values, one still needs to find answers to the asymptotic behaviours when Ft tends towards −1 or +1. Similar, we can not test the path dependency of our results since all our data are from the VdlS avalanche path. However, we think that at least the following three limitations are important to bear in mind for the discussion of the results.
-
The transition index will probably be most useful for avalanches with drop heights of more than 500 m. For smaller avalanches, Hs tends to be either above the release area or below the runout area.
-
While Hs can be determined wherever and whenever there is enough meteorological data for running snow-cover simulations, finding Ht for a given event requires either detailed investigation of the avalanche deposits or measurements with a GEODAR or Doppler radar.
-
For use as a predictive tool, e.g. for road closures or evacuations, a plot like Fig. 5, containing many events, would be necessary. Probably, such copious and detailed data are available only for a handful of avalanche paths worldwide as of now.
Avalanches with a cold-dominated runout occur in Vallée de la Sionne when Hs is up to 300 m in elevation above the valley floor. The nomenclature of UNESCO (1981) would classify such an avalanche as “C1G7”, with the code 7 meaning the deposit consists of a mix of cold–dry and warm–wet snow. We find that the point Ht where the transition becomes visible lies exclusively above Hs for cold-dominated avalanches. Thus, the transition can not be caused by snow erosion from the surface, and the entrainment of deeper and therefore warmer layer of the snow cover must be accounted for. Since the surface (i.e. new snow) is cold, a powder snow avalanche maintains its dynamics from surface entrainment, but later flowing parts like the denser core may eventually dig deeper into the snow cover, erode the warmer snow layers and develop a warm tail even above Hs.
We observe that nearly every large powder snow avalanche in Vallée de la Sionne undergoes a partial transition. This suggests that large purely cold–dry powder snow avalanches are very rare. In all GEODAR data acquired over the last 7 years (140 in total with 20 powder snow avalanches), only 1 large powder snow avalanche (no. 15-0017, Köhler et al., 2016) without a clear partial transition can be found. This avalanche was released shortly after avalanche no. 15-0016 (), which had entrained and removed most of the snow in the track. Purely cold–dry avalanches do exist, but perhaps, only as long as they stay small and thus only entrain layers of cold snow close to the surface.
Warm-dominated avalanches are usually classified as wet avalanches since such a description is mostly based on the deposit texture. Our data show that initially cold–dry avalanches can produce completely warm–wet deposits (Ft>0). A special nomenclature for those avalanches does not exist or is not used consistently, even though the UNESCO avalanche classification scheme allows for different wetness classes in the release and runout areas. An avalanche with a complete transition could be denoted as “C1G2” (UNESCO, 1981). The results in Fig. 5 indicate that such avalanches occurred in VdlS when Hs is more than 500 m in altitude above the valley floor. We find that Ht, the point where the transition is initiated, is consequently 200 to 300 m below Hs (Fig. 6). This indicates that entrainment of warm snow from the surface is most likely the cause for the transition but also that a previously developed cold flow regime may be able to flow over a surface of warm snow for about this distance. As soon as the transition towards warm regimes begins, it happens instantaneously and not gradually, i.e. in only 100 m and 15 s (Fig. 4).
Interestingly, the actual altitude of the transition Ht differs for events with partial and complete transitions (Fig. 6). All partial transitions in cold-dominated avalanches occurred in the elevation band between 1750 and 1850 m a.s.l., which corresponds to the altitude at the end of the steep couloir. Complete transitions could occur even at lower elevations down to around 1650 m a.s.l., which correspond to the gently inclined runout area and even the altitude of the pylon. We think that the above mentioned change in the terrain does not necessarily cause the transition, but gentle terrain may favour the warm and presumably slower flowing snow to separate from fast cold regimes in flow direction. Such a separation can be observed at higher elevations, where the flowing length starts to increase and the avalanche extends in range in the MTI plots (Fig. 2). This lengthening occurs most often above Ht and may indicate an earlier start of the transition and a separation of slower and faster flowing regions.
Both transition types are relevant for the dynamics at the avalanche front, especially during deposition in the runout area. For partial transitions, the relevance is indirect as the runout is still cold-dominated, but the slow warm tail keeps mass away from the front and reduces the size of the cold flow regimes. For complete transitions the relevance is obvious, as the runout is warm-dominated even though a cold avalanche released. The timescale when a warm-dominated avalanche reaches the runout is delayed by several hundreds of seconds due to slower velocities of the warm flow regimes (Fig. 2). More importantly, the pressure exerted on structures in the runout depends strongly on the flow regime, and in general is a function of velocity, density and flow height together with a geometric factor (Sovilla et al., 2016). Cold-dominated flow regimes have a dominant velocity-squared contribution, and the hydrostatic term vanishes due to small densities. In contrast for warm flow regimes, the dynamic term can be neglected due to smaller velocities, but the large density increases the importance of the hydrostatic pressure contribution. Sovilla et al. (2016) presented an example which deviates from the cold or warm pressure scheme, and both dynamic and hydrostatic contributions are found to be important. We can imagine that avalanches with a complete transition may generate similar high pressures during the transition process as result of remnant high velocities together with an increase in density. Such an argument seems to be different for avalanches with a partial transition. As mentioned above, the warm tail most likely results from deep entrainment by the dense core where the velocities are slower than at the front, and thus the dynamic pressure contribution probably stays small.
Another important topic is the extent to which frictional heating due to dissipation processes during the avalanche descent may play a role in flow regime transitions (Vera Valero et al., 2015). Frictional heating compared to a temperature increase due to entrainment was recently investigated experimentally on two medium-sized purely cold avalanches by Steinkogler et al. (2015b). They concluded that frictional heating depends mainly on the effective height drop, but the contribution due to entrainment was found to be more variable and dependent on the erosion depth and snow temperature. Here, we can not differentiate between both heating mechanisms on the basis of our data set. In fact, we include the frictional heating of the flowing snow as it affects Pw and Pc indirectly. However, the relation in Fig. 5 indeed indicates that snow erosion and the temperature of the eroded snow have an important effect on the flow dynamics.
4.2 Limitations of methodology
Two limitations in regard to temperature exist in our methods. Throughout the whole study, we have assumed that the flowing snow temperature is similar to the snow cover temperature. This is a vague and untested assumption, and the effect depends possibly on the entrainment rate and the temperature difference between the flowing snow and the snow cover. This assumption does not affect the correlation between Hs and Ft observed in the data. However, it would be an important factor for a generalization of the presented empirical approach. Furthermore, the history of avalanche activity in the avalanche path can significantly alter the snow cover by entrainment and deposition (Steinkogler et al., 2014). The SNOWPACK model can account for this with reinitialization of the snow cover. But this can only be done for artificial avalanches where precise mass-balance measurements are available. Our approach disregards this fact. However, we are interested in the surface layers consisting of the recent new snow precipitation. The simulation of these new top layers is more dependent on the meteorological data than on the older snow layer underneath.
The estimation of Hs by linear interpolation between two weather stations also appears questionable. We imply that the snow temperature changes only due to an altitude gradient, and this altitude gradient is found to be in the range of 100 to 400 m ∘C−1. The estimate of Hs could be improved with detailed analysis performed with distributed snow cover models like Alpine3D. Such analysis has been done by Steinkogler et al. (2014), but their results show only a small deviation from a linear trend along the Vallée de la Sionne avalanche path. However, we wanted to use a simple parameterization for Hs. “Simple” means that Hs can be estimated from different data sources, e.g. field observations or regional snow reports, since for many avalanche paths and past events, much less information about the snow cover characteristics is generally available.
The presented method is based on the temperature threshold of −1 ∘C with respect to the uppermost 0.5 m of the snow cover. To validate this −1 ∘C temperature threshold is not the scope of this study, but we have also tested our method for −2 and 0.5 ∘C. The effect is a shift in the Hs altitude, e.g. in Figs. 5 and 6. Our results indicate that −1 ∘C is a reasonable value. For −2 ∘C, the partial (blue) and complete transitions (red) are not split anymore by the 1 : 1 line in Fig. 6. And for −0.5 ∘C, the regression in Fig. 5 predicts only a Hs altitude of 2150 m a.s.l. for pure warm avalanches (Ft=1), which is clearly below the release areas so that regions with cold flow regimes are expected.
Another difficulty is how to generalize our results to other avalanche tracks since we have only investigated a single slope. We expect a path dependence of the correlation between snow cover and the transition index Ft. Vallée de la Sionne is known to be a relatively gentle avalanche path, so avalanches normally stop naturally in the runout area. But for steeper paths, i.e. 40∘ from top to bottom, we expect that both flow regimes may reach the valley floor more often. Our analysis should be extended to take into account other variables, such as volume or mass estimates and path geometry. To directly extend our method to other avalanche paths, regional snow and avalanche reports as well as path length estimation from worldwide available digital terrain models may already be sufficiently accurate. As an example, the Moos avalanche from the introduction fits into the relation found for VdlS (star in Figs. 5 and 6), but it is noteworthy to say that the geometry of this avalanche path, in terms of altitude, slope and path length, is very similar to the VdlS.
GEODAR measurements have shown that flow regime transitions are common in large snow avalanches. One of these transitions occurs between cold and warm snow when agglomeration of snow grains causes larger granules to form. In first order, this happens as soon as the flowing snow temperature changes from below to above −1 ∘C. Such a flow regime transition is very important for the dynamics of the avalanching snow, as the flow regime influences the flow mobility and the pressure exerted on structures in the path. However, we want to stress that the runout distance itself does not depend on the flow regime, as cold and warm avalanches can reach unexpectedly long runouts.
We find two types of cold-to-warm flow regime transitions depending on whether part or the complete avalanche changes the flow regime. A partial flow regime transition can occur at the tail and depends on the entrainment of deeply buried warm snow layers by the avalanche's dense core. In contrast, a complete flow regime transition can occur at the front due to the entrainment of warm snow at the surface. We find a continuous degree of transition between both types and a relation between this and the snow cover temperature along the avalanche track. More specifically, the transition index Ft is linearly related to the altitude Hs, where the average snow cover temperature in the uppermost 0.5 m changes between warm and cold at a threshold of −1 ∘C.
At Vallée de la Sionne, almost all large powder snow avalanches exhibit a transition. Given the chosen assumption of a threshold temperature of −1 ∘C measured in the uppermost 0.5 m, we find that when Hs is found no higher than 300 m above the valley floor, a partial transition (Ft<0) is observed and results in a warm tail. For complete transitions (Ft>0), the altitude Hs is located more than 500 m above the valley floor and results in only warm flow regimes in the runout area.
This work can be regarded as a first step in developing a method for predicting the dominant flow regime in the runout area – but not the runout length – based on knowledge of the snow cover temperature along the path. It is worth mentioning that meteorological and snow cover data from the release area are not representative for the avalanche dynamics in the runout area. Therefore, any hazard and risk evaluation should be made with additional information. Knowing the flow regime in the runout area may improve risk assessment; for example, the effectiveness of a dam may be evaluated in real time. Nevertheless, the presented approach is strongly dependent on the track geometry, and this requires care in adapting our results to other avalanche paths.
Compared to the complexity of temperature influence on avalanche dynamics, our presented method is rather simple. Effects such as frictional heating, temperature difference between entrained and flowing snow, entrainment depth, and mixing and separation of snow at differently temperatures are important factors, and to identify their significance on the flow dynamics is a challenging task. We are convinced that future measurement procedures with laser scans for mass balance, infrared radiation thermography in combination with temperature measurement during the passage of an avalanche, and manual or simulated snow profiles will be very useful to further understand the interplay between these factors. Finally, investigating flow regime transitions in greater detail may become important in respect to climate change. Less snow cover at lower altitudes, strong temperature gradients and quickly varying weather systems may lead to a snow cover situation favouring transitions in avalanches. Warm flow regimes may reach runout areas more frequently and thus require that hazard mitigation procedures be adapted accordingly.
The data used in this publication are available upon request to the corresponding author. Most of the GEODAR data can be sourced from the GEODAR data repository (McElwaine et al., 2017).
Data analysis and writing were done by AK with assistence from JTF. RS and MB did the snow cover modelling. JME and BS contributed greatly with the interpretation and discussion of the results.
The authors declare that they have no conflict of interest.
The research was funded by the Swiss National Science Foundation (SNSF)
project “High Resolution Radar Imaging of Snow Avalanches”, grant
200021_143435. Special thanks are due to our colleagues at the electronics
and workshop of SLF for their invaluable support. We are grateful to Dieter
Issler, Alexander Densmore and one anonymous reviewer for their valuable
comments, which increased the clarity and quality of this paper.
Edited by: Guillaume Chambon
Reviewed by: Dieter Issler and one anonymous referee
Ash, M., Brennan, P. V., Chetty, K., McElwaine, J. N., and Keylock, C. J.: FMCW Radar Imaging of Avalanche-like Snow Movements, in: Proceedings of the 2010 IEEE Radar Conference, Arlington, Va., 10–14 May 2010, IEEE, 102–107, https://doi.org/10.1109/RADAR.2010.5494643, 2010. a
Ash, M., Brennan, P. V., Keylock, C. J., Vriend, N. M., McElwaine, J. N., and Sovilla, B.: Two-Dimensional Radar Imaging of Flowing Avalanches, Cold Reg. Sci. Technol., 102, 41–51, https://doi.org/10.1016/j.coldregions.2014.02.004, 2014. a
Bavay, M. and Egger, T.: MeteoIO 2.4.2: a preprocessing library for meteorological data, Geosci. Model Dev., 7, 3135–3151, https://doi.org/10.5194/gmd-7-3135-2014, 2014. a
Dash, J. G., Rempel, A. W., and Wettlaufer, J. S.: The physics of premelted ice and its geophysical consequences, Rev. Mod. Phys., 78, 695–741, https://doi.org/10.1103/RevModPhys.78.695, 2006. a
Dufour, F., Gruber, U., Bartelt, P., and Ammann, W.: Overview of the 1999 measurements at the SLF test site Vallée de la Sionne, in: International Snow Science Workshop, Big Sky, Montana, USA, 2–6 October 2000, 527–534, 2000. a
Fischer, J.-T., Fromm, R., Gauer, P., and Sovilla, B.: Evaluation of probabilistic snow avalanche simulation ensembles with Doppler radar observations, Cold Reg. Sci. Technol., 97, 151–158, https://doi.org/10.1016/j.coldregions.2013.09.011, 2014. a
Fischer, J.-T., Köhler, A., Kofler, A., Sovilla, B., and McElwaine, J.: Front and internal velocity distribution in powder snow avalanches, International Snow Science Workshop, Breckenridge, Colorado, USA, 3–7 October 2016, 218–221, 2016. a, b
Gauer, P. and Issler, D.: Possible erosion mechanisms in snow avalanches, Ann. Glaciol., 38, 384–392, https://doi.org/10.3189/172756404781815068, 2004. a
Gauer, P. and Kristensen, K.: Four decades of observations from NGI's full-scale avalanche test site Ryggfonn – Summary of experimental results, Cold Reg. Sci. Technol., 125, 162–176, https://doi.org/10.1016/j.coldregions.2016.02.009, 2016. a
Gauer, P., Kern, M., Kristensen, K., Lied, K., Lambert, R., and Schreiber, H.: On pulsed Doppler radar measurements of avalanches and their implication to avalanche dynamics, Cold Reg. Sci. Technol., 50, 55–71, https://doi.org/10.1016/j.coldregions.2007.03.009, 2007. a, b
Gauer, P., Issler, D., Lied, K., Kristensen, K., and Sandersen, F.: On snow avalanche flow regimes: Inferences from observations and measurements, International Snow Science Workshop, Whistler, Canada, 21–27 September 2008, 717–723, 2008a. a
Gauer, P., Lied, K., and Kristensen, K.: On avalanche measurements at the Norwegian full-scale test-site Ryggfonn, Cold Reg. Sci. Technol., 51, 138–155, https://doi.org/10.1016/j.coldregions.2006.09.010, 2008b. a
Huwald, H., Higgins, C. W., Boldi, M.-O., Bou-Zeid, E., Lehning, M., and Parlange, M. B.: Albedo effect on radiative errors in air temperature measurements, Water Resour. Res., 45, W08431, https://doi.org/10.1029/2008WR007600, 2009. a
Issler, D.: Experimental Information on the Dynamics of Dry-Snow Avalanches, in: Dynamic Response of Granular and Porous Materials under Large and Catastrophic Deformations, edited by: Hutter, K. and Kirchner, N., Springer, https://doi.org/10.1007/978-3-540-36565-5_4, 109–160, 2003. a, b, c
Jóhannesson, T., Gauer, P., Issler, P., Lied, K.: The design of avalanche protection dams: recent practical and theoretical developments, in: Climate Change and Natural Hazard Research, Series 2, EUR 23339, European Commission, Brussels, 2009. a
Köhler, A., McElwaine, J. N., Sovilla, B., Ash, M., and Brennan, P. V.: The dynamics of surges in the 3 February 2015 avalanches in Vallée de la Sionne, J. Geophys. Res., 121, 2192–2210, https://doi.org/10.1002/2016JF003887, 2016. a, b, c, d, e
Köhler, A., McElwaine, J. N., and Sovilla, B.: GEODAR Data and the Flow Regimes of Snow Avalanches, J. Geophys. Res., 123, 1272–1294, https://doi.org/10.1002/2017JF004375, 2018. a, b, c, d, e, f, g, h, i, j, k, l, m, n
Lehning, M., Bartelt, P., Brown, B., and Fierz, C.: A physical SNOWPACK model for the Swiss avalanche warning Part III: meteorological forcing, thin layer formation and evaluation, Cold Reg. Sci. Technol., 35, 169–184, https://doi.org/10.1016/S0165-232X(02)00072-1, 2002. a
Lehning, M., Völksch, I., Gustafsson, D., Nguyen, T. A., Stähli, M., and Zappa, M.: ALPINE3D: a detailed model of mountain surface processes and its application to snow hydrology, Hydrol. Process., 20, 2111–2128, https://doi.org/10.1002/hyp.6204, 2006. a
McElwaine*, J. N., Köhler*, A., Sovilla, B., Ash, M., and Brennan, P. V.: GEODAR data of snow avalanches at Vallée de la Sionne: Seasons 2010/11, 2011/12, 2012/13 & 2014/15, Data set, Zenodo, https://doi.org/10.5281/zenodo.1042108, *equally contributing authors, 2017. a, b
Naaim, M., Durand, Y., Eckert, N., and Chambon, G.: Dense avalanche friction coefficients: influence of physical properties of snow, J. Glaciol., 59, 771–782, https://doi.org/10.3189/2013JoG12J205, 2013. a, b
Schlögl, S., Marty, C., Bavay, M., and Lehning, M.: Sensitivity of Alpine3D modeled snow cover to modifications in DEM resolution, station coverage and meteorological input quantities, Environ. Modell. Softw., 83, 387–396, https://doi.org/10.1016/j.envsoft.2016.02.017, 2016. a
Schmucki, E., Marty, C., Fierz, C., and Lehning, M.: Evaluation of modelled snow depth and snow water equivalent at three contrasting sites in Switzerland using SNOWPACK simulations driven by different meteorological data input, Cold Reg. Sci. Technol., 99, 27–37, https://doi.org/10.1016/j.coldregions.2013.12.004, 2014. a
Schreiber, H., Randeu, W. L., Schaffhauser, H., and Rammer, L.: Avalanche dynamics measurement by pulsed Doppler radar, Ann. Glaciol., 32, 275–280, https://doi.org/10.3189/172756401781819021, 2001. a, b
Sovilla, B., Burlando, P., and Bartelt, P.: Field experiments and numerical modeling of mass entrainment in snow avalanches, J. Geophys. Res., 111, F03007, https://doi.org/10.1029/2005JF000391, 2006. a, b
Sovilla, B., McElwaine, J., Steinkogler, W., Hiller, M., Dufour, F., Suriñach, E., Guillen, C. P., Fischer, J.-T., Thibert, E., and Baroudi, D.: The full-scale avalanche dynamics test site Vallée de la Sionne, International Snow Science Workshop, Grenoble, France, 7–11 October 2013, 1350–1357, 2013. a
Sovilla, B., McElwaine, J. N., and Louge, M. Y.: The structure of powder snow avalanches, C. R. Phys., 16, 97–104, https://doi.org/10.1016/j.crhy.2014.11.005, 2015. a, b
Sovilla, B., Faug, T., Köhler, A., Baroudi, D., Fischer, J.-T., and Thibert, E.: Gravitational wet avalanche pressure on pylon-like structures, Cold Reg. Sci. Technol., 126, 66–75, https://doi.org/10.1016/j.coldregions.2016.03.002, 2016. a, b, c
Sovilla, B., McElwaine, J. N., and Köhler, A.: The intermittency region of powder snow avalanches, J. Geophys. Res., 123, 2525–2545, https://doi.org/10.1029/2018JF004678, 2018. a
Steinkogler, W., Sovilla, B., and Lehning, M.: Influence of snow cover properties on avalanche dynamics, Cold Reg. Sci. Technol., 97, 121–131, https://doi.org/10.1016/j.coldregions.2013.10.002, 2014. a, b, c, d, e, f, g
Steinkogler, W., Gaume, J., Löwe, H., Sovilla, B., and Lehning, M.: Granulation of snow: From tumbler experiments to discrete element simulations, J. Geophys. Res., 120, 1107–1126, https://doi.org/10.1002/2014JF003294, 2015a. a
Steinkogler, W., Sovilla, B., and Lehning, M.: Thermal energy in dry snow avalanches, The Cryosphere, 9, 1819–1830, https://doi.org/10.5194/tc-9-1819-2015, 2015b. a
Turnbull, B.: Scaling Laws for Melting Ice Avalanches, Phys. Rev. Lett., 107, 258001, https://doi.org/10.1103/PhysRevLett.107.258001, 2011. a
UNESCO: Avalanche atlas: Illustrated international avalanche classification, International Commission on Snow and Ice, UNESCO, Paris, Tech. rep., 1981. a, b
Vera Valero, C., Wikstroem Jones, K., Bühler, Y., and Bartelt, P.: Release temperature, snow-cover entrainment and the thermal flow regime of snow avalanches, J. Glaciol., 61, 173–184, https://doi.org/10.3189/2015JoG14J117, 2015. a
Vriend, N. M., McElwaine, J. N., Sovilla, B., Keylock, C. J., Ash, M., and Brennan, P. V.: High-resolution Radar Measurements of Snow Avalanches, Geophys. Res. Lett., 40, 727–731, https://doi.org/10.1002/grl.50134, 2013. a
Würzer, S., Wever, N., Juras, R., Lehning, M., and Jonas, T.: Modelling liquid water transport in snow under rain-on-snow conditions – considering preferential flow, Hydrol. Earth Syst. Sci., 21, 1741–1756, https://doi.org/10.5194/hess-21-1741-2017, 2017. a





