Seasonal mass variations show timing and magnitude of meltwater storage in the Greenland Ice Sheet

The Greenland Ice Sheet (GrIS) is currently losing ice mass. In order to accurately predict future sea level rise, the mechanisms driving the observed mass loss must be better understood. Here, we combine data from the satellite gravimetry mission Gravity Recovery and Climate Experiment (GRACE), surface mass balance (SMB) output of the Regional Atmospheric Climate Model v. 2 (RACMO2), and ice discharge estimates to analyze the mass budget of Greenland at various temporal and spatial scales. We find that the mean rate of mass variations in Greenland observed by GRACE was between −277 and −269 Gt yr⁻¹ in 2003–2012. This estimate is consistent with the sum (i.e., $-\mathrm{304}\pm \mathrm{126}$ Gt yr⁻¹) of individual contributions – surface mass balance (SMB, 216±122 Gt yr⁻¹) and ice discharge (520±31 Gt yr⁻¹) – and with previous studies. We further identify a seasonal mass anomaly throughout the GRACE record that peaks in July at 80–120 Gt and which we interpret to be due to a combination of englacial and subglacial water storage generated by summer surface melting. The robustness of this estimate is demonstrated by using both different GRACE-based solutions and different meltwater runoff estimates (namely, RACMO2.3, SNOWPACK, and MAR3.9). Meltwater storage in the ice sheet occurs primarily due to storage in the high-accumulation regions of the southeast and northwest parts of Greenland. Analysis of seasonal variations in outlet glacier discharge shows that the contribution of ice discharge to the observed signal is minor (at the level of only a few gigatonnes) and does not explain the seasonal differences between the total mass and SMB signals. With the improved quantification of meltwater storage at the seasonal scale, we highlight its importance for understanding glacio-hydrological processes and their contributions to the ice sheet mass variability.

1 Introduction

During the last decade (2006–2015), the Greenland Ice Sheet (GrIS) has been rapidly losing mass, contributing on average 0.9 mm yr⁻¹ to global mean sea level rise (Enderlin et al., 2014; Stocker et al., 2013; van den Broeke et al., 2016). The NASA/German Space Agency (DLR) Gravity Recovery and Climate Experiment (GRACE) mission is a powerful tool with which to monitor ice mass variations in Greenland, including the ice sheet and its peripheral glaciers and ice caps, from monthly to multi-year timescales. The total mass balance (TMB) of the ice sheet represents the summation of processes summarized in Eq. (1): (i) surface mass balance (SMB); (ii) ice discharge (D); and (iii) mass variations (Δm∕Δt), which include all processes not related to SMB and ice discharge, for instance, en- and subglacial meltwater storage. GRACE ice mass balance is calculated after removing the impacts of glacial isostatic adjustment (GIA), atmospheric and oceanic variability, and other time-variable geophysical processes.

$$\begin{array}{}\text{(1)}& \mathrm{TMB}=\mathrm{SMB}-D+\mathrm{\Delta }m/\mathrm{\Delta }t\end{array}$$

The quantities in Eq. (1) refer to fluxes (in mass per unit time). Recent GrIS mass loss has been quantified in numerous studies (Schrama et al., 2014; Shepherd et al., 2012; Velicogna et al., 2014). Furthermore, several authors have estimated the contribution to this mass loss from SMB and ice discharge individually (Enderlin et al., 2014; Velicogna et al., 2014; van den Broeke et al., 2009, 2016). To quantify the contribution of SMB, regional climate models (RCMs) are typically used, such as the Regional Atmospheric Climate Model v. 2 (RACMO2) (Ettema et al., 2009), Modèle Atmosphérique Régional (MAR) (Fettweis et al., 2005, 2017), and HIRHAM (Christensen et al., 1996). The annual ice discharge rates are estimated by combining ice flow velocity data and ice thickness data at the flux gates (Thomas et al., 2000). Importantly, ice flow velocities have increased during the last decade and shown different spatial and temporal patterns (Moon et al., 2012).

The analysis of GrIS mass variations at the seasonal timescale is still limited. This is largely because (i) the accuracy and spatial resolution of GRACE monthly solutions is relatively poor, as compared to long-term trend estimates, and (ii) ice velocity data at this timescale are scarce (typically, only a few estimates per year are available, often spanning only a few years). A first attempt to combine GRACE data and SMB modeling in order to evaluate an ice dynamics model of the GrIS at the monthly timescale was made by Schlegel et al. (2016). Alexander et al. (2016) examined spatial patterns of GrIS seasonal mass variations using a regional climate model, a model of ice dynamics, and GRACE. The seasonal variabilities of the ice velocities of a few marine-terminating glaciers were investigated by, e.g., Howat et al. (2010), Ahlstrøm et al. (2013), and Moon et al. (2015). The only study of multi-regional seasonal variations of GrIS outlet glacier velocities was conducted by Moon et al. (2014), who analyzed 55 marine-terminating glaciers in northwest and southeast Greenland over the period 2009–2013.

GrIS mass balance also depends on supra-, en-, and subglacial meltwater storage. An example is the abundance of supraglacial lakes primarily in west Greenland, which store water during the melt season (Selmes et al., 2011). Subglacial hydrology is an area of active research (Chandler et al., 2013; Slater et al., 2015). However, time-varying total englacial and subglacial meltwater storage (included in Δm∕Δt of Eq. 1) has been poorly quantified and mostly investigated at a local scale. For instance, Rennermalm et al. (2013) quantified meltwater storage in a small watershed (36–65 km²) near Kangerlussuaq. They suggested that ∼ 54 % of liquid water is retained for 1–6 months in this watershed. To date, only one study has utilized GRACE data to quantify meltwater storage at ice-sheet-wide scales (Van Angelen et al., 2014). By fitting de-trended GRACE observations and SMB model output, it was found that the mean period of meltwater storage at the whole-ice-sheet scale is ∼18 days. So far, no attempt to quantify the meltwater storage with GRACE has been made at the drainage system scale.

In this study, we analyze the individual mass variation contributors (see Eq. 1) to total interannual and seasonal mass variations over Greenland at both regional and whole-ice-sheet scales. In particular, this study makes a first ice-sheet-wide attempt to quantify the amplitude and timing of short-term meltwater storage. For this purpose, we combine observations of total mass variations from GRACE with observations of ice discharge to the ocean (Enderlin et al., 2014; Moon et al., 2014), as well as modeled SMB output from RACMO2.3 (Noël et al., 2015), SNOWPACK (Steger et al., 2017), and MAR3.9 (Fettweis et al., 2017). Since the spatial resolution of GRACE data is limited, the obtained estimates cover both the GrIS and the parts of Greenland outside the GrIS, including the tundra and the peripheral glaciers disconnected from the GrIS. Furthermore, there are also meltwater storage estimates of the Greenland Ice Sheet using in situ core data (Forster et al., 2014; Harper et al., 2012; Machguth et al., 2016). Usually, the authors collected the data during a short period, to characterize the state of the firn in a transect, in order to understand the capacity of the firn to store meltwater. These findings are then applied to the whole ice sheet based on a firn model. The meltwater storage estimated by those studies is significant, e.g., at the level of a few hundred or even thousand gigatonnes. Those studies, however, are quite different from this study. Those studies estimated the total meltwater storage in the firn, whereas our study addresses the water storage (i) in all components (supra-, en-, and subglacial) and (ii) at the short timescale.

In Sect. 2, we discuss the methods and data utilized. The results are presented and analyzed in Sect. 3. Finally, the conclusions are presented in Sect. 4.

2 Data and methods

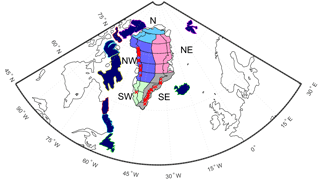
Figure 1 The 28-mascon parameterization of Greenland used in this study for GRACE data processing. For the purpose of further analysis, these patches are merged into five drainage systems (N, NE, SE, SW, and NW). Nine mascons (filled in blue) outside Greenland are added to absorb signals from the surrounding areas. Fifty-five glaciers utilized to compute seasonal ice discharge variations are marked in red.

2.1 GRACE

We use the fifth release of GRACE monthly gravity field solutions from the Center for Space Research (CSR) at the University of Texas as input to compute total mass variations. Each solution is provided as a set of spherical harmonic coefficients up to degree/order 96 and supplied with a full error covariance matrix. For the sake of consistency with previous GRACE-based estimates, we limit the considered time interval to January 2003–December 2013. Since data for 9 months are missing, 123 months in total are used. Furthermore, a reduced time interval (January 2003–December 2012) is also considered in order to make the obtained estimates consistent with ice discharge data from Enderlin et al. (2014); see Sect. 2.3 for a further discussion. Due to strong noise in the C_2,0 coefficients, we replaced them with available estimates based on satellite laser ranging (Cheng et al., 2013). The degree-one coefficients, which are not included in the GRACE products, are taken from Swenson et al. (2008). The GRACE solutions are corrected for GIA, which is triggered by a relief of ice load since the Last Glacial Maximum, with the model from A et al. (2013).

To estimate mass variations over Greenland at a regional scale, we make use of a novel data processing methodology (Ran et al., 2018b), which is based on the mascon approach. Greenland is split into 28 patches, or “mascons” (Fig. 1), which are complemented by nine patches outside Greenland to absorb signals from the surrounding areas. Temporal variations (anomalies) of surface density (i.e., mass variations per unit area) within each patch are assumed to be spatially homogeneous. Thus, the total mass anomaly within each patch is just a product of surface density anomaly and patch area. Those mass anomalies are computed for each month independently, without any regularization. Ultimately, mass anomalies are summed up over individual drainage systems or the entirety of Greenland.

A further description of the adopted GRACE data processing methodology is provided in the Appendix A. In order to investigate the robustness of GRACE-based mass anomalies, we estimate them using different processing parameters. This leads to multiple sets of GRACE solutions: two primary ones (estimated with and without applying data weighting) and alternative ones. We also consider the estimates produced by other research teams: the Jet Propulsion Laboratory (JPL) mascon solutions by Watkins et al. (2015), the CSR mascon solutions by Save et al. (2016), the Goddard Space Flight Center (GSFC) mascon solutions by Luthcke et al. (2013), and the solutions by Wouters et al. (2008).

Similar to van den Broeke et al. (2009), we aggregate the 28 mascons inside Greenland into five drainage systems. We refer to these drainage systems as (a) north (N), (b) northwest (NW), (c) southeast (SE), (d) southwest (SW), and (e) northeast (NE) (Fig. 1). We slightly shifted southwards the border between NW and SW drainage systems as compared to van den Broeke et al. (2009), in order to ensure that the SW drainage system is mostly limited to land-terminating glaciers.

2.2 SMB modeling

SMB values over 2003–2013 from three models (i.e., RACMO2.3, SNOWPACK, and MAR3.9) are analyzed. The SMB estimates are obtained as the sum of individual SMB components:

$$\begin{array}{}\text{(2)}& \mathrm{SMB}=P_{\mathrm{tot}}-{\mathrm{SU}}_{\mathrm{tot}}-{\mathrm{ER}}_{\mathrm{ds}}-\mathrm{RU},\end{array}$$

where P_tot and SU_tot are the total precipitation and sublimation, respectively; ER_ds is erosion/deposition due to drifting snow; and RU is runoff. The units are mass per unit time. The SMB mass anomalies used in this study are from RACMO2.3 unless stated otherwise. The output from SNOWPACK is included to evaluate the robustness of our findings with respect to the choice of SMB outputs simulated by different snow/firn models. Output of another regional climate model, MAR3.9, is also investigated in this study to demonstrate the robustness of the results, considering the large discrepancies among SMB outputs from different regional climate models in the past (Vernon et al., 2013).

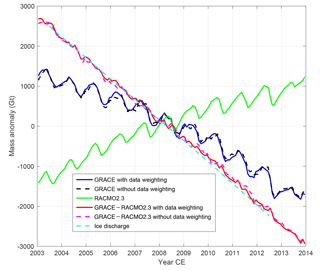
Figure 2 Time series of mass anomalies over the period 2003–2013 for the entire GrIS: total mass anomalies from GRACE produced with and without data weighting (solid blue and dashed black, respectively), cumulative SMB anomalies from RACMO2.3 (green), the difference between them, the “total–SMB” residuals (solid red and dashed pink: with and without data weighting, respectively), and cumulative ice discharge (cyan).

2.2.1 RACMO2.3

RACMO2.3 was developed by the Royal Netherlands Meteorological Institute (KNMI) and Institute for Marine and Atmospheric Research (IMAU), which is a part of Utrecht University in the Netherlands (Noël et al., 2015). RACMO2.3 provides daily SMB values with a spatial resolution of 11 km.

2.2.2 SNOWPACK

In addition to the daily SMB provided by RACMO2.3, we use SMB output from SNOWPACK (Steger et al., 2017). SNOWPACK is a state-of-the-art snow model that offers a more physically based snow densification scheme, the simulation of microstructural snow properties, and a higher near-surface vertical resolution compared with the snow/firn module of RACMO2.3. A comparison of SNOWPACK with IMAU-FDM, a snow/firn model nearly identical to the one implemented in RACMO2.3, revealed a better performance of SNOWPACK for the GrIS, particularly for locations with comparably high amounts of liquid water input due to snowmelt and rainfall (Steger et al., 2017). SNOWPACK was coupled offline to RACMO2.3 and run for the full period 1960–2014 with the same surface mask (ocean, tundra, ice sheet) and horizontal resolution as RACMO2.3. As a consequence of forcing SNOWPACK with mass fluxes from RACMO2.3 at the snow–atmosphere interface, differences in the simulated SMB from SNOWPACK and RACMO2.3 are thus only caused by unequal partitioning of meltwater and rainfall into refreezing and runoff.

2.2.3 MAR3.9

The MAR3.9 model was developed by the Laboratory of Climatology at the Department of Geography, University of Liège (Fettweis et al., 2017). It provides daily SMB values for both the ice sheet and tundra areas with a spatial resolution of 5 km and uses ERA-Interim as forcing like RACMO2.3. The only differences between the version 3.8 of MAR used in Delhasse et al. (2018) and the version 3.9 used here are improvements in the MAR stability when it is applied at high resolution as well as in its computational efficiency.

2.2.4 Processing the SMB outputs from RACMO2.3, SNOWPACK, and MAR3.9

In this study, we integrate SMB outputs from RACMO2.3, SNOWPACK, or MAR3.9 in time, which results in cumulative values that can be interpreted as daily SMB mass anomalies. These values are averaged over monthly intervals for the sake of temporal consistency with the GRACE solutions. In order to make the SMB outputs (11 km resolution for RACMO2.3 and SNOWPACK, or 5 km in the case of MAR3.9) spatially match the GRACE resolution (around 300 km), we process them consistently with the GRACE data. This scheme is similar to the GRACE-like processing of SMB data by Alexander et al. (2016) and Velicogna et al. (2014). More specifically, we convert the SMB outputs to gravity disturbances at the satellite altitude and limit their spectra to spherical harmonic degree/order 96. Then the SMB per mascon is estimated by a least-squares adjustment (see the Appendix A).

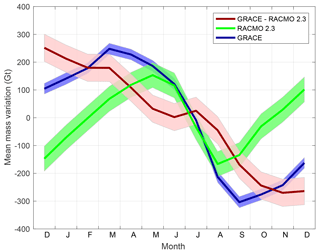
Figure 3 Greenland mean annual cycle of total mass anomalies from GRACE produced with data weighting (dark-blue), cumulative SMB anomalies (green), and the difference between them (brown) for the period 2003–2013. The latter curve reflects the cumulative sum of seasonal ice discharge variations and meltwater storage, as well as GRACE errors and SMB model bias. The shaded strips show the 1σ error bars. Labels at the horizontal axis indicate month of the year (e.g., month “J” denotes January, while month “D” is December).

Previous studies on the sources of current GrIS mass loss used relative SMB outputs, i.e., anomalies with respect to an equilibrium state (1961–1990) (Velicogna et al., 2014; van den Broeke et al., 2009). Effectively, this means that the time series of mass anomalies were de-trended to ensure that they are close to zero during the reference equilibrium period. In other words, it assumes that the ice discharge and SMB were balanced during the reference period. In contrast, we use time series of absolute SMB mass anomalies, i.e., without referring to a hypothesized equilibrium state. In this way, we are able to extract more information from the data sets: absolute mass anomalies related to ice discharge (i.e., the difference between GRACE- and SMB-based mass anomalies) cannot increase over time, which is a valuable constraint that facilitates the correct interpretation of the obtained results.

2.3 Ice discharge

We examine ice discharge from two different data sets. The first set was presented in Enderlin et al. (2014). Here, it is used to reconstruct the 2003–2012 multi-year mass trends and accelerations, as well as to separate the contributions from SMB and ice discharge. It covers 178 outlet glaciers with annual resolution. Ice discharge observations of these glaciers are estimated by multiplying ice flow velocities with ice thickness values. Annual velocities are retrieved by means of feature tracking from (winter) Landsat 7 Enhanced Thematic Mapper Plus and the Advanced Spaceborne Thermal and Reflectance Radiometer (ASTER) data. Ice discharge is calculated within 5 km of the grounding lines. The ice thicknesses at the flux gates are computed by subtracting bed elevations from surface elevations. Bed elevations are derived from NASA's Operation IceBridge airborne ice-penetrating radar data, whereas surface elevations are obtained from digital elevation models (Enderlin et al., 2014; Xu et al., 2015).

In addition, we produce the second data set, which is used to examine monthly variations of ice discharge. It covers 55 marine-terminating glaciers with sub-annual resolution for 2009–2013. The exploited ice flow velocities were obtained from TerraSAR-X images delivered by DLR (Moon et al., 2014). Ice thicknesses at the flux gates are interpolated from the IceBridge BedMachine Greenland version 2 data (Morlighem et al., 2015). Ice discharge (D) for a given glacier is defined as the ice mass flux across the flux gate (f) close to the glacier terminus (within ∼5 km):

$$\begin{array}{}\text{(3)}& D=\mathit{\rho }\int h(\mathit{\upsilon }\cdot \mathit{n})\mathrm{d}f,\end{array}$$

where h is the ice thickness, n is the unit vector directed outwards normally to the flux gate, υ is the ice flow velocity, and ρ is the ice density. When selecting flux gates, we pay attention to variations of the terminus position by checking the images of glaciers during the whole time interval, to make sure that the flux gate is upstream of the terminus all the time. Furthermore, a flux gate should span the whole outlet glacier to the ice flow edges. To compute D, we discretize the flux gates into nearly 200 m long intervals. The length of the last interval is adjusted to make sure that the ice flow edge is sampled. We then use the values (h, υ, and n) defined for the center of each interval, assuming that they are constant over the interval. Then Eq. (3) becomes

$$\begin{array}{}\text{(4)}& D=\mathit{\rho }\sum _{i=\mathrm{1}}^N{d}^i{h}^i({\mathit{\upsilon }}^{\mathit{i}}\cdot \mathit{n}),\end{array}$$

where N is the total number of intervals of the flux gate and dⁱ is the length of the ith interval.

3 Results and discussion

3.1 Multi-year mass trend and acceleration budgets

First, we examine multi-year mass trends and accelerations in terms of the total mass balance and the contributions thereto from SMB and ice discharge. For more details about the estimation of multi-year trend and accelerations, please refer to Appendix B.

Our estimate of the total-mass linear trend, which is based on the primary GRACE data time series produced with optimal data weighting, is $-\mathrm{286}\pm \mathrm{21}$ Gt yr⁻¹ for 2003–2013. The estimate obtained without data weighting is $-\mathrm{279}\pm \mathrm{21}$ Gt yr⁻¹. The individual contributors to the errors in the trend estimates are shown in Table A1. Our estimates are in agreement with those published earlier for the time interval 2003–2013: $-\mathrm{280}\pm \mathrm{58}$ Gt yr⁻¹ (Velicogna et al., 2014) and $-\mathrm{278}\pm \mathrm{19}$ Gt yr⁻¹ (Schrama et al., 2014).

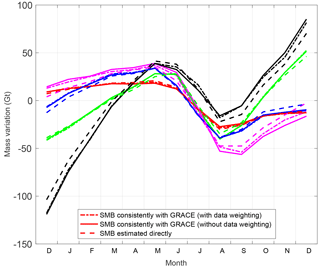
Figure 4 Similar to Fig. 3, but only for mean annual cycle of cumulative SMB anomalies of different drainage systems (SE: black; NW: green; NE: blue; N: red; SW: pink). The SMB outputs are computed in three different ways: (i) consistently with GRACE data (with or without data weighting) and (ii) by a direct estimation of mass anomalies per drainage system.

We also examine the SMB and ice discharge contributions to the total mass trend. In this case, we consider the reduced time interval, 2003–2012, in order to be consistent with the ice discharge record, which ends in 2012 (Table 1). The multi-year average mass gains from SMB (RACMO2.3) over that period processed consistently with GRACE via data weighting and without data weighting are 216±122 and 214±122 Gt yr⁻¹, respectively. The uncertainty is computed by assuming a 9 % error in accumulation and a 15 % error in meltwater runoff signals modeled by RACMO2.3, which is the typical uncertainty of RACMO2.3 (van den Broeke et al., 2016). The time series of cumulative mass anomalies due to ice discharge and other processes not related to SMB is obtained as the difference between the total mass variations and the cumulative SMB-related ones; this difference will be referred to as the “total–SMB” residuals (“total minus SMB”; cf. red and pink curves in Fig. 2). The associated rates of linear changes over 2003–2012 estimated with and without data weighting are 493±124 and 483±124 Gt yr⁻¹, respectively. Those estimates agree with the ice discharge estimate from Enderlin et al. (2014), 520±31 Gt yr⁻¹, shown as the cyan curve in Fig. 2, which is shifted to best fit the GRACE-SMB time series. Notice that the GRACE time series obtained with the optimal weighting shows a smoother behavior than that produced without data weighting. This is consistent with the analysis presented in Ran et al. (2018a, b), who found that data weighting substantially reduces the level of random noise in the GRACE GrIS mass change time series.

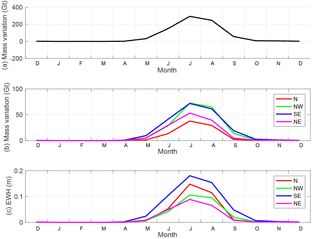
Figure 5 Mean monthly meltwater production per calendar month (gigatonnes) for the entirety of Greenland (a), for individual drainage systems in gigatonnes (b), and for individual drainage systems in meters of equivalent water height (c) modeled by RACMO2.3.

Next, we present the results of a similar analysis for the individual drainage systems. The greatest total mass losses are observed by GRACE in drainage systems NW and SE (cf. Fig. A2 and Table 1). These two drainage systems account for ∼73–76 % of the total mass loss over Greenland, depending on whether data weighting is applied or not. The interannual behavior of these drainage systems is, however, different. SE loses mass with an approximately constant rate over the whole considered period. In contrast, NW is relatively stable over the period 2003–2005, but starts losing mass thereafter. The remaining three drainage systems lose mass at much smaller rates. Remarkably, two of these drainage systems (N and SW) show a similar behavior: they are relatively stable over the period 2003–2009 but start losing mass in 2010. These findings are consistent with Velicogna et al. (2014). The SMB is negative in two drainage systems (N and SW) (cf. Table 1). However, with a large fraction of land-terminating glaciers, ice losses from ice discharge are an order of magnitude lower there than in the NW and SE drainage systems (cf. Fig. A2), resulting in only modest total mass loss in spite of the negative SMB.

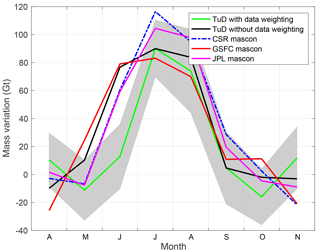
Figure 6 Estimates of seasonal meltwater storage, obtained as the monthly deviations from the April–May and September–November linear fit of “total–SMB” residuals (brown line in Fig. 3): for the whole GrIS (in gigatonnes). Labels along the horizontal axis represent months between April (“A”) and November (“N”). The shaded strip shows the 1σ error bar for the estimates by Delft University of Technology (TuD) with data weighting (the mean standard deviation is 23 Gt).

The long-term trends of total–SMB residuals in the drainage systems of NW, NE, and SW are consistent with the ice discharge estimates from Enderlin et al. (2014) within the error bar (Table 1). This suggests robustness of RACMO2.3 long-term SMB trends there, under the assumption that the meltwater storage signal is mainly seasonal. In the SE and N, however, we find relatively large discrepancies between the total–SMB residuals and ice discharge observations from Enderlin et al. (2014). Under the conditions of realistic GRACE error estimates and minimal multi-year meltwater storage, all these inconsistencies suggest a precipitation overestimation in the SE and underestimation in the N in RACMO2.3.

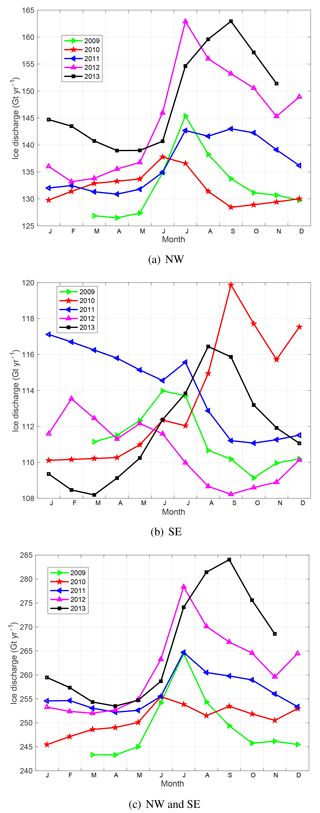
Figure 7 Monthly ice discharge estimates from 55 major marine-terminating glaciers for the glaciers in the NW drainage system (a) and the SE drainage system (b) individually, and for the NW and SE drainage systems together (c).

Average accelerations of mass change anomalies over the period 2003–2012 are also estimated using Eq. (B1) (parameter a₃). Over the entirety of Greenland, the SMB ($-\mathrm{23.3}\pm \mathrm{2.7}$ Gt yr⁻²) contributes 75 % of the total acceleration observed by GRACE (Table A2). This is close to the estimates of Velicogna et al. (2014), who assessed the contribution of SMB to the total GrIS mass loss acceleration as 79 %. The contribution of the total–SMB residuals to the mass loss acceleration for the entirety of Greenland is statistically insignificant. Analysis of individual drainage systems leads to similar conclusions (cf. Table A2). However, we note that the acceleration estimates cannot be simply extrapolated onto a longer time interval and may not properly represent the ice sheet behavior at the decadal timescale, because of the large climate variability in a limited time span of data (Wouters et al., 2013).

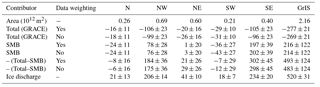
Table 1 Linear mass change rates over the period 2003–2012 for individual drainage systems and the entirety of Greenland: total, SMB-related, and total–SMB residuals (GRACE–SMB), as well as ice discharge (Gt yr⁻¹). The sign of total–SMB residuals is changed to make them directly comparable with ice discharge estimates.

3.2 Seasonal mass variations

We analyze the mean annual cycles of total (GRACE) and cumulative SMB (RACMO2.3) mass anomalies over the period 2003–2013 (Fig. 3). To derive them, we divide the entire period into 11 overlapping 13-month time intervals, each of which starts in December of the previous year and ends in December of the current year. Then, the mean mass anomaly for each calendar month is estimated by linear regression, together with one bias parameter per time interval, which accounts for a long-term variability. This scheme is less sensitive to gaps in data time series than the plain averaging of mass anomalies per calendar month. For more details about this scheme, we refer the reader to Ran et al. (2018a). The uncertainties of mean mass anomalies from GRACE are propagated from errors in each monthly GRACE estimate. The uncertainties of cumulative SMB mean mass anomalies are computed by assuming 9 % and 15 % errors in modeled mean mass anomalies due to precipitation and runoff, respectively, as suggested by van den Broeke et al. (2016). The uncertainties of the total–SMB residuals are the mean root sum square of the standard deviations of noise in GRACE and cumulative SMB estimates.

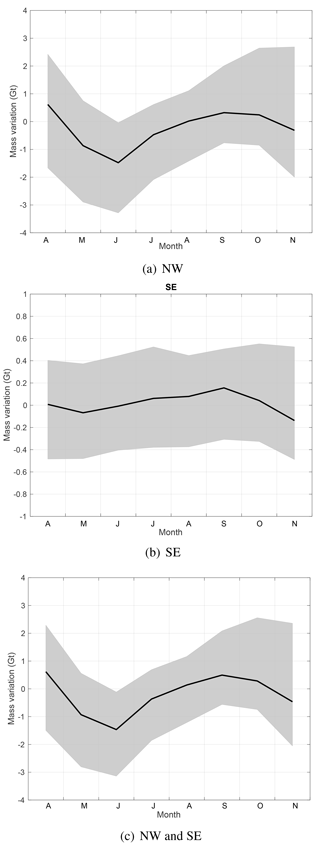
Figure 8 Similar to Fig. 6 but for mean ice-discharge-related variations over 2009–2013. The cumulative mass anomalies are computed from glaciers in NW (a) and SE (b) drainage systems individually, and for glaciers in NW and SE together (c).

The whole-Greenland mean annual cycles of total and cumulative SMB mass anomalies present smooth month-to-month variations (Fig. 3). Importantly, the estimates of both types refer to the mean values for the months considered. The total mass anomaly from GRACE reaches its maximum in March and then steadily decreases until September. The most rapid monthly mass loss is observed in July–August (∼200 Gt). In contrast, the cumulative SMB decreases over a much shorter period – only from May to August.

Alexander et al. (2016) suggested that the inconsistency between the spatial resolution of GRACE-based estimates and that of the SMB model (11 km) may have a large impact on the difference between the two time series. In response to this concern, we investigate the effect of using an alternative scheme to process SMB mass anomalies. Instead of processing them consistently with GRACE data, as was explained in Sect. 2.2.4, we directly compute SMB-related mass anomalies per drainage system from the RACMO2.3 grid with a spatial resolution of 11 km. We find that the difference for the entirety of Greenland is negligible: smaller than 2 Gt. For individual drainage systems, we find that the impact is also relatively small (<12 Gt, which is around 10 % of the signal) (see Fig. 4). Still, this effect shows a systematic behavior and may introduce some bias into GRACE-SMB estimates. For this reason, we prefer to process SMB estimates consistently with GRACE data (Alexander et al., 2016; Velicogna et al., 2014).

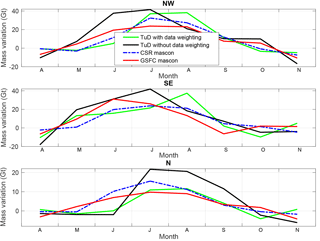
Figure 9 Similar to Fig. 6, but the estimates of seasonal meltwater storage are extracted from different mascon solutions for individual drainage systems: NW, SE, and N. The errors are not shown in the plot for the sake of its readability. The mean standard deviations of the errors for NW, SE, and N are 25, 26, and 9 Gt, respectively.

3.2.1 A simple method of quantifying short-term meltwater storage

The total–SMB residuals show some periods of almost null variations (nearly flat segments in Fig. 3): February–March, May–July, and November–December. The total–SMB residuals represent the cumulative sum of ice discharge, meltwater storage, GRACE errors, and SMB model biases. If we assumed that the main contributor to the total–SMB residuals is ice discharge, these nearly flat features would indicate that ice discharge is negligible or even negative, which is unphysical, since this implies that discharge is contributing to Greenland mass gain. Therefore, these features should be explained either by meltwater storage or by errors in SMB- and GRACE-based estimates. Based on the robustness analysis of the total–SMB estimates in Appendix C, we infer that the quasi-null total–SMB variations during February–March and November–December are likely caused by noise in the estimates. In the following, therefore, they will not be discussed. The summer flat feature of May–July, however, always persists, no matter what data processing scenario is followed. Thereby, we suggest that it is attributed to a physical signal, i.e., short-term meltwater storage.

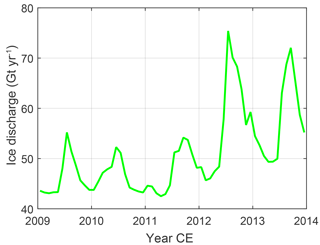
Figure 10 Monthly variations of ice discharge of Jakobshavn Glacier over the period 2009–2013 (Gt yr⁻¹).

Hereafter, we propose a simple method with which to elucidate and quantify short-term meltwater storage. According to RACMO2.3, meltwater is mostly produced between May and September, and peaks in July (cf. Fig. 5). Averaged over the GRACE period, approximately 800 Gt of meltwater is produced on average in Greenland during the melt season from May to September, of which ∼250 Gt is estimated to refreeze within the snowpack, and the rest runs off of the ice sheet. RACMO2.3 does not calculate lateral meltwater transport, i.e., the time lag between meltwater production and the moment when the runoff reaches the ocean. During late spring and early summer, this lag is particularly significant due to an inefficient subglacial channelized network (Rennermalm et al., 2013) and replenishing of firn aquifers (mainly in the SE and NW) (Forster et al., 2014; Miège et al., 2016).

In order to estimate the instantaneous amount of meltwater subject to runoff, we first fit the total–SMB residuals in two periods, before and after the flat feature (i.e., in April–May and September–November), with a linear function. This function can be interpreted as an empirical estimation of the mean combined effect of ice discharge and the difference between the modeled meltwater refreezing and the actual one. Then, we force the mass budget at the beginning and the end of the melt season to be closed by subtracting the obtained linear function from the total–SMB residuals (Fig. 6). In this way, we find that meltwater is retained in Greenland between May and October, with a 100±20 Gt maximum in July. Note that the estimates of meltwater storage are sufficiently robust with respect to the choice of the GRACE-based mascon solution, but they may vary in a small range in timing and amplitude (Fig. 6). The uncertainties of meltwater storage are computed as the root sum square of the standard deviations of noise in GRACE- and SMB-based estimates. It is worth mentioning that the error in the SMB estimates is then computed assuming 9 % and 15 % errors in modeled mean mass anomalies due to precipitation and runoff signals, respectively, after applying the same linear regression function (see above) to each component.

Estimates of non-SMB mass anomalies could reflect the delayed release of meltwater into the ocean and the variability of ice discharge. We test the effects of ice discharge variability using a monthly resolved data set of ice discharge for 55 glaciers in Greenland (See Fig. 1). These glaciers are largely located in the NW and SE Greenland drainage systems, which are the largest contributors of ice mass wastage into the ocean. The sum of the obtained estimates over all 55 glaciers is shown in Fig. 7a. One can see that at the whole-ice-sheet scale the increase in ice discharge during the melt season is minor in all years (∼10 % or less). In the absence of complete coverage of the GrIS with observations of glacier velocities at the seasonal timescale, we compute a scale factor as the ratio between the ice discharge estimates from 55 glaciers considered in this study and the discharge over the entire GrIS in terms of the long-term linear trend by Enderlin et al. (2014), and apply this scale factor (i.e., ∼2) to the ice discharge estimate of each glacier. Then, similar to Fig. 6, we represent the ice discharge related mean mass anomaly per calendar month in terms of the deviation from the linear function fitting the values in April–May and September–November (cf. Fig. 8c). One can see that the effect of ice discharge amounts to only a few gigatonnes; i.e., its contribution to the total signal is negligible. This supports our hypothesis that that delayed runoff is likely the major contributor to the signal isolated in Fig. 6.

Finally, we examine individual drainage systems (cf. Figs. 9 and A6). We refrain from an analysis of the SW and NE regions due to a relatively high level of noise in the obtained meltwater storage estimates. Regionally, the SE shows the largest meltwater accumulation per unit area. This is consistent with the fact that the rate of meltwater production is large in the sector (Fig. 5), as is the storage potential owing to high accumulation rates (Miège et al., 2016). In the N and NW regions, the signal related to meltwater storage is less pronounced, which can be explained by the dry climate of this region, meaning that less pore space is available in the firn layer to store liquid water.

In terms of the total mass, the largest meltwater accumulation takes place in the NW and SE regions: the contribution of each region may reach around 40 Gt in July–August (cf. Figs. 9 and A6).

As for the increase in ice discharge during the melt season, we find that it is relatively minor for both NW and SE drainage systems (less than 20 % and 10 %, respectively; see Fig. 7). As such, the contribution of ice discharge to the signal reported in Figs. 9 and A6 is minor for both drainage systems: not more than 2.0±1.9 and 0.3±0.5 Gt, respectively (cf. Fig. 8). Interestingly, a much larger increase in ice discharge during the melt season is found for the single major contributor to ice discharge, Jakobshavn Glacier: up to 60 % in 2012 (Fig. 10). This finding is consistent with that of Joughin et al. (2008, 2012).

Note that the meltwater storage signal at the drainage system scale is present in all GRACE mascon solutions but shows some discrepancies in the timing and amplitude. This means that further effort is still needed to improve the accuracy of GRACE-based estimates.

4 Conclusions

GRACE monthly solutions have been applied to systematically analyze the mass budget in the territory of Greenland at various temporal and spatial scales. The obtained estimate of the mean rate of mass loss produced from CSR RL05 solutions with the new variant of the mascon approach with and without data weighting is $-\mathrm{277}\pm \mathrm{21}$ and $-\mathrm{269}\pm \mathrm{21}$ Gt yr⁻¹ over the period 2003–2012, respectively. The rate of SMB accumulation, as modeled by RACMO2.3 and processed consistently with GRACE data, is 216 or 214±122 Gt yr⁻¹, depending on whether data weighting is applied or not. The differences between GRACE- and RACMO-based trends with or without data weighting are 493±124 or 483±124 Gt yr⁻¹, which are consistent with 2003–2012 ice discharge observations by Enderlin et al. (2014): 520±31 Gt yr⁻¹. On the other hand, we observe relatively large discrepancies between the estimates for the SE and N drainage systems. Those discrepancies imply that the adopted climate model likely overestimates precipitation in the SE drainage system and underestimates it in the N drainage system.

Our estimates of accelerations in SMB-related ($-\mathrm{23.3}\pm \mathrm{2.7}$ Gt yr⁻²), ice discharge-related (2.6±1.5 Gt yr⁻²), and total ($-\mathrm{31.1}\pm \mathrm{8.1}$ Gt yr⁻²) mass anomalies are consistent within error bars. Most of the observed acceleration in mass loss can be attributed to changes in SMB. This is consistent with Velicogna et al. (2014), who found that 79 % of the mass loss acceleration can be explained by the contribution of SMB. Furthermore, our results indicate that most of the total mass acceleration observed by GRACE is attributed to the SW and NW drainage systems, which is in agreement with Velicogna et al. (2014).

We found a remarkable seasonal cycle in the difference between monthly total and SMB cumulative mass anomalies (“total–SMB” residuals), which likely reflects significant meltwater storage in the early summer months due to an inefficiency of the subglacial channelized network. The maximum storage is observed in July: 80–120 Gt. To estimate the potential contribution of ice discharge to the observed signals, we exploited the estimates of ice discharge over 55 outlet glaciers obtained with the flux gate method. We showed that seasonality in ice discharge is on the order of a few gigatonnes; i.e., it is negligible compared with meltwater storage. We also analyzed the short-term meltwater storage per drainage system. Our results suggest that the meltwater storage is large in NW and SE drainage systems, whereas it is weak in the northern drainage system.

A comparison of estimates derived from GRACE data with different processing parameters and from different mascon products (e.g., JPL, CSR, and GSFC) revealed the presence of the short-term meltwater storage signal in all the considered solutions. At the same time, noticeable discrepancies are observed in timing and amplitude in meltwater storage estimates. These indicates that further work is needed to improve GRACE-based estimates at both Greenland-wide and drainage system scales.

Finally, this work illustrates the potential of combining multiple observational data sets and model output complemented by simple physical constraints, to better understand the contributors to GrIS mass variations at various timescales. Improving the estimates of (natural and forced) mass variations associated with individual processes is important for robust projections of future GrIS evolution and its contribution to sea level rise.

Appendix A: Adopted method for estimating mass variation from GRACE

Our GRACE-based estimates of total mass variations are derived using a new variant of the mascon approach (Ran, 2017). The method is adapted from the computational procedures proposed by Forsberg and Reeh (2007) and Baur and Sneeuw (2011). The procedure consists of two steps: (1) synthesizing temporal variations of gravity disturbances at a set of data points located at a specific satellite altitude (500 km). The data points are homogeneously distributed over Greenland (extended with a 800 km buffer zone) with a 37.5 km separation. The full error covariance matrix C_d of the gravity disturbances is computed on the basis of the full error covariance matrix of the spherical harmonic coefficients. (2) The synthesized gravity disturbances are converted into mass anomalies per patch. The procedure is based on a linear functional model:

$$\begin{array}{}\text{(A1)}& \mathit{d}=\mathbf{\text{A}}\mathit{x}+\mathit{n},\end{array}$$

where d is a vector composed of synthesized gravity disturbances, x is the vector consisting of mass anomalies, A is the design matrix relating the two vectors to each other in line with Newton's attraction law, and n is the data noise vector. A straightforward implementation of this functional model may lead to some additional errors due to a spectral inconsistency between the matrix A and the data vector d. The ith column of A can be interpreted as a set of gravity disturbances caused by a unit mass anomaly in the ith patch; its spatial spectrum is unlimited. The spatial spectrum of gravity disturbances d is limited to the maximum degree of the input spherical harmonic coefficients (here, 96). We eliminate this inconsistency by a low-pass filtering of all the columns of the matrix A, so that the contribution of the spherical harmonics above degree 96 is suppressed. The mass anomalies are computed from gravity disturbances by means of a least-squares adjustment:

Figure A1 Parameterization of the ocean area around Greenland with one (a) and four (b) patches.

$$\begin{array}{}\text{(A2)}& \mathit{x}=({\mathbf{\text{A}}}^T\mathbf{\text{PA}}{)}^{-\mathrm{1}}{\mathbf{\text{A}}}^T\mathbf{\text{P}}\mathit{d},\end{array}$$

where P is the weight matrix computed by an approximate inversion of the error covariance matrix of gravity disturbances C_d. The exact inverse of C_d cannot be computed because the matrix C_d is ill posed. Therefore, an approximate inversion of C_d is introduced, which is based on the eigenvalue decomposition of C_d; only a limited number of the largest eigenvalues are retained. The usage of the matrix P ensures a (nearly) statistically optimal data weighting. From a preliminary numerical study we found that the optimal choice is to retain 600 eigenvalues. No spatial regularization is applied in the course of inversion.

This procedure is used to produce one of the primary solutions, referred to as the “solution obtained with data weighting”; the other primary solution, referred as the “solution obtained without data weighting”, is produced with the ordinary least-squares adjustment

$$\begin{array}{}\text{(A3)}& \mathit{x}=({\mathbf{\text{A}}}^T\mathbf{\text{A}}{)}^{-\mathrm{1}}{\mathbf{\text{A}}}^T\mathit{d}.\end{array}$$

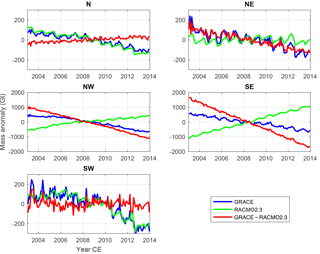
Figure A2 Same as Fig. 2 but for the GRACE-based estimates produced with data weighting at the drainage system scale. The estimates produced without data weighting are not shown as they are very similar to those with data weighting.

Table A1 Contribution of different error sources to the error in the total GrIS mass trend estimated from GRACE data both with and without data weighting (in Gt yr⁻¹).

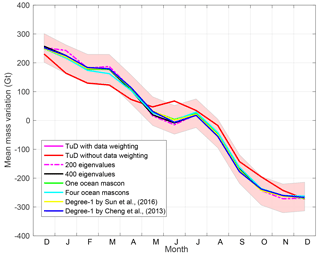
Figure A3 The mean mass anomalies per calendar month of the total–SMB residuals over the entirety of Greenland estimated by applying different GRACE data processing schemes.

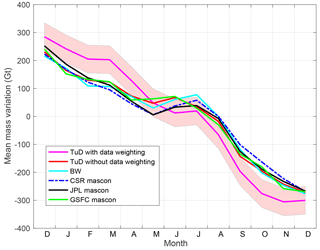
Figure A4 The mean mass anomalies per calendar month of the total–SMB residuals over the entirety of Greenland estimated from different GRACE solutions. “BW” refers to the solution of Wouters et al. (2008).

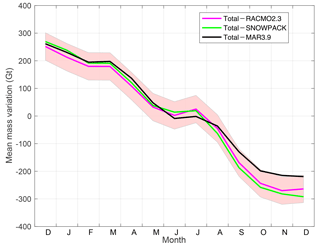
Figure A5 The mean mass anomalies per calendar month of the total–SMB residuals over the entirety of Greenland estimated from different SMB outputs.

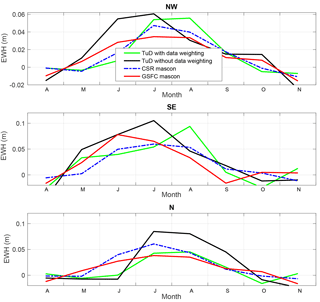
Figure A6 Similar to Fig. 9 but in meters of equivalent water height. The mean standard deviations of the errors for NW, SE, and N are 0.04, 0.07, and 0.03 m, respectively.

Table A2 Acceleration of mass change over the period 2003–2012 for individual drainage systems and the entirety of Greenland: total, SMB-related, and total–SMB residuals (GRACE minus SMB), as well as ice discharge (Gt yr⁻²). The sign of total–SMB residuals is changed to make them directly comparable with ice discharge estimates.

Appendix B: The estimation of multi-year trend and acceleration

We approximate each mass anomaly time series (cf. Fig. 2) with the following analytic function:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }f\left(t\right)=a_{\mathrm{1}}+a_{\mathrm{2}}(t-t_{\mathrm{0}})+a_{\mathrm{3}}{\displaystyle \frac{(t-t_{\mathrm{0}}{)}^{\mathrm{2}}}{\mathrm{2}}}+a_{\mathrm{4}}\sin \mathit{\omega }t+a_{\mathrm{5}}\cos \mathit{\omega }t\\ \text{(B1)}& {\displaystyle }& {\displaystyle }+a_{\mathrm{6}}\sin \mathrm{2}\mathit{\omega }t+a_{\mathrm{7}}\cos \mathrm{2}\mathit{\omega }t,\end{array}$$

where a₁, …, a₇ are parameters to be estimated; t₀ is a reference epoch defined as the middle of the considered time interval (i.e., 1 July 2008 for the time interval 2003–2013; 1 January 2008 for the time interval 2003–2012); and $\mathit{\omega }=\mathrm{2}\mathit{\pi }/T$, with T=1 year.

In addition, we calculate the uncertainty of the trend estimate, a₂. This uncertainty of the GRACE-based estimate (see Table A1) is composed of the error of the GIA model (we set it as 50 % of the signal; Jacob et al., 2012), the measurement errors of GRACE propagated from the full variance–covariance matrix of monthly solutions, the uncertainty associated with a particular choice of the oceanic mascon layout (cf. Fig. A1), and signal leakage. The latter (including both signals which leaked from outside Greenland and signals from inside Greenland which leaked between the mascons) was simulated numerically by defining the trend from ICESat as the reference. Note that the individual errors are summed up quadratically, by assuming that they are not correlated with each other. We do not consider errors from atmospheric and ocean circulation corrections, as the impact of those errors is negligible (Ran et al., 2018a, b). A similar approach is applied to estimate the uncertainty of acceleration (parameter a₃).

Appendix C: Robustness of the total–SMB residuals at the seasonal timescale

In this section, we investigate the robustness of total–SMB residuals with respect to those errors. To assess a possible impact of errors in GRACE-based mass anomalies, we try different processing schemes in our variant of the mascon method. The following modifications of the GRACE data processing scheme were considered: (i) retaining a different number of eigenvalues of the noise covariance matrix C_d when inverting this matrix within the frame of the weighted least-squares estimation: 200, 400, or 600 eigenvalues (600 eigenvalues is the primary option); (ii) different handling of the surrounding ocean: parameterization with one patch, parameterization with four patches (cf. Fig. A1), or without estimating mass anomalies over ocean (the latter is the primary option); and (iii) a different choice of spherical harmonic degree-one coefficients: from Swenson et al. (2008), Cheng et al. (2013), or Sun et al. (2016) (the former is the primary option). Note that only one parameter varies at a time, while the primary option is chosen to define the other parameters (see also the Appendix A). The optimal data weighting is exploited in all these experiments. In addition, we consider an effect of switching to the ordinary least-squares adjustment (when the data weighting is not used). We also consider alternative GRACE-based estimates: JPL mascon solutions by Watkins et al. (2015), CSR mascon solutions by Save et al. (2016), GSFC mascon solutions by Luthcke et al. (2013), and mascons solutions of Wouters et al. (2008).

The results are depicted in Figs. A3–A4. The presence and appearance of the nearly zero total–SMB month-to-month variations during February–March and November–December vary between GRACE estimates. When the surrounding ocean is parameterized with four patches, the February–March feature becomes less flat; the November–December flat feature is not significant either in the estimates based on the ordinary least-squares estimator and on Wouters et al. (2008). In addition, the flat features of February–March and November–December do not appear in the total–SMB residuals obtained from the CSR and JPL mascon solutions. Therefore, we infer that the nearly zero total–SMB variations during February–March and November–December, which are clearly visible in Fig. 3, are likely caused by noise in the GRACE-based estimates. In the following, therefore, they will not be discussed. On the other hand, the flat feature of May–July persists, no matter what processing parameters are chosen and which GRACE product is utilized. Therefore, it cannot be explained by uncertainties associated with GRACE data processing. Remarkably, switching data weighting on/off has the maximum impact on the obtained estimates of mass anomalies per calendar month. Since it is not clear at this moment which of the two options leads to better estimates, the results produced both without and with optimal data weighting will be considered in the further discussion of the main text.

To assess a possible impact of uncertainties in the SMB output, we analyze the SMB mass anomalies from RACMO2.3, SNOWPACK, and MAR3.9. As shown in Fig. A5, the May–July flat feature persists in the total–SMB residuals estimated from RACMO2.3, SNOWPACK, and MAR3.9. Therefore, we conclude that the May–July flat feature is likely not triggered by noise in the SMB estimates. As such, it must be attributed to a physical signal. We suggest that this signal is caused by short-term meltwater storage.