the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The influence of atmospheric grid resolution in a climate model-forced ice sheet simulation
Johan Liakka
Coupled climate–ice sheet simulations have been growing in popularity in recent years. Experiments of this type are however challenging as ice sheets evolve over multi-millennial timescales, which is beyond the practical integration limit of most Earth system models. A common method to increase model throughput is to trade resolution for computational efficiency (compromise accuracy for speed). Here we analyze how the resolution of an atmospheric general circulation model (AGCM) influences the simulation quality in a stand-alone ice sheet model. Four identical AGCM simulations of the Last Glacial Maximum (LGM) were run at different horizontal resolutions: T85 (1.4∘), T42 (2.8∘), T31 (3.8∘), and T21 (5.6∘). These simulations were subsequently used as forcing of an ice sheet model. While the T85 climate forcing reproduces the LGM ice sheets to a high accuracy, the intermediate resolution cases (T42 and T31) fail to build the Eurasian ice sheet. The T21 case fails in both Eurasia and North America. Sensitivity experiments using different surface mass balance parameterizations improve the simulations of the Eurasian ice sheet in the T42 case, but the compromise is a substantial ice buildup in Siberia. The T31 and T21 cases do not improve in the same way in Eurasia, though the latter simulates the continent-wide Laurentide ice sheet in North America. The difficulty to reproduce the LGM ice sheets in the T21 case is in broad agreement with previous studies using low-resolution atmospheric models, and is caused by a substantial deterioration of the model climate between the T31 and T21 resolutions. It is speculated that this deficiency may demonstrate a fundamental problem with using low-resolution atmospheric models in these types of experiments.
- Article
(9193 KB) - Full-text XML
-
Supplement
(5899 KB) - BibTeX
- EndNote
Experiments with coupled climate–ice sheet models have become increasingly popular in recent years, much thanks to coordinated international modeling initiatives such as the ”Ice Sheet Model Intercomparison Project” (ISMIP6) (Nowicki et al., 2016) and the ”Pliocene Ice Sheet Modelling Intercomparison Project” (PLISMIP) (Dolan et al., 2012). These types of experiments are however challenging, as ice sheets have a high thermal inertia that makes their response time greater than almost all other components of the climate system – the timescale depends on the application but typically ranges from 103 to 105 years. Simulations of this length are beyond the practical integration limit of most Earth system models, and a number of techniques to increase the model throughput have therefore been devised. Some of the more popular approaches for simulating ice sheets over glacial timescales include the following simplifications:
- i.
Force a stand-alone ice sheet model with a transient climate record obtained by interpolating between the climate extremes over the period of interest (often simulations of the pre-industrial and the Last Glacial Maximum; PI and LGM, respectively). The interpolation weights are typically derived from oxygen isotope ratios in Greenland and Antarctic ice cores (Charbit et al., 2007; Fyke et al., 2014).
- ii.
Use an asynchronous coupling between an ice sheet model and a general circulation model (GCM). The ice sheet model, which is computationally cheaper than the GCM, is then run multiple years between each update of the model climate (Herrington and Poulsen, 2012; Liakka, 2012; Liakka et al., 2011; Löfverström et al., 2015).
- iii.
Utilize a computationally efficient intermediate complexity model (EMIC) that can be run transiently over glacial timescales (Beghin et al., 2014; Bonelli et al., 2009; Calov et al., 2005; Ganopolski et al., 2010; Roe and Lindzen, 2001).
Although no attempt is made here to assess how these different modeling approaches compare to one another, we conclude that they all rely on a number of assumptions and simplifications that can potentially influence the results. For example, (i) assumes that the glacial climate evolved as a linear combination of the PI and LGM states, which is at odds with both modeling and proxy-data evidence of highly nonlinear circulation changes over the last glacial period (Jackson, 2000; Lora et al., 2016; Löfverström and Lora, 2017; Löfverström et al., 2014, 2016; Pausata and Löfverström, 2015; Zhang et al., 2014); (ii) accelerating the ice sheet component introduces abrupt changes in the GCM boundary conditions, which may force the model climate into an unphysical state at the beginning of each (GCM) run segment; and (iii) simplified models often rely on statistical dynamics/physics, where almost all interactions are prescribed or represented by first-order linear assumptions.
In addition, one issue that has received little attention in the literature is what role the atmospheric grid resolution – the horizontal mesh on which the model equations are discretized – plays in coupled climate–ice sheet experiments. Simplified circulation models often utilize coarse horizontal grids for computational efficiency. For example, the atmospheric component of CLIMBER-2 has a horizontal resolution of approximately 10∘ × 51∘ (Petoukhov et al., 2000), LOVECLIM runs on a 5.6∘ × 5.6∘ resolution grid (Goosse et al., 2010), and FAMOUS on a 5∘ × 7.5∘ grid (Smith et al., 2008). These are to be compared with the nominal 1∘ × 1∘ resolution of many modern GCMs (Flato et al., 2013).
Although a higher resolution is not automatically synonymous with a better model, it generally means that smaller scale phenomena can be resolved, which in turn reduces the need for explicit (parameterized) diffusion. Note that diffusion is not only influencing (damping) horizontal motions, but it can also impact vertical transport (Polvani et al., 2004). Several studies have shown that the numerical convergence breaks down somewhere between the T31 (3.8∘) and T21 (5.6∘) resolutions in an atmospheric GCM, which (Magnusdottir and Haynes, 1999) degrades the representation of even the largest scale atmospheric phenomena, such as jet streams and planetary waves (Dong and Valdes, 2000; Löfverström et al., 2016; Magnusdottir and Haynes, 1999; Polvani et al., 2004). This resolution limit appears to be an inherent property of the model dynamics, and thus largely independent of model physics; for example, Polvani et al. (2004) and Löfverström et al. (2016) found a similar limit using a dry primitive equation model (no model physics), and a comprehensive atmospheric circulation model (fairly sophisticated physics), respectively.
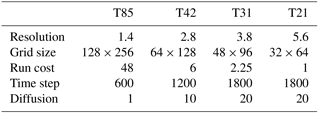
Table 1Resolution specific details. The top two rows show the horizontal resolution in degrees (∘) and in number of grid cells (lat×long), respectively. The run cost (third row) is normalized with respect to the T21 case and estimates the number of numerical operations required to simulate one model year, based on the grid size and the nominal time step (s) for each resolution (fourth row). The horizontal biharmonic (fourth order) diffusion coefficient is given in units of 1015 m4 s−1 (bottom row).
Motivated by the discussion above, the objective of this study is to illustrate that the atmospheric model resolution can have a strong influence on the ice development in climate-model-forced ice sheet experiments. In order to isolate the influence of the atmospheric model resolution we resort to a simplified experiment design (see Sect. 2) and run an ice sheet model to equilibrium (starting from an ice-free state), using atmospheric forcing data from four identical LGM simulations run at progressively coarser horizontal grids: T85, T42, T31, and T21 (Table 1). This modeling approach takes several steps away from reality, and the study is therefore perhaps best viewed in an abstract light. For example, by prescribing perpetual LGM conditions we ignore the low-frequency, multi-millennial variations in insolation, greenhouse gas concentrations, and atmosphere and ocean circulation that are typically associated with glacial cycles. Moreover, the presence of LGM ice sheets in the atmospheric simulations primes both northwestern Eurasia and northern North America to be susceptible to ice formation. However, in this context this may be considered an asset, as all ice sheet model experiments should theoretically have a similar bias towards ice formation in the ”correct” areas. Also, running the ice sheet model to equilibrium may seem excessive (it is doubtful that the LGM was an equilibrium state), but it ensures a more objective comparison of the different experiments than is offered by an arbitrarily chosen integration limit.
These shortcomings aside, the ice sheet model run with the T85 climate forcing manages to reproduce the LGM reconstruction to a high accuracy. The intermediate resolution cases (T42 and T31), on the other hand, fail to reproduce the Eurasian ice sheet, and the T21 case fails in both continents. These results suggest that a ”sufficiently” high atmospheric resolution may be required to ensure the quality of (coupled) climate–ice sheet model experiments.
The models and experimental design are presented in Sect. 2, the results from the atmospheric model and the ice sheet model are described in Sects. 3 and 4, followed by a more general discussion in Sect. 5.
2.1 Ice sheet model
We use the three-dimensional ice sheet model SICOPOLIS (SImulation COde for POLythermal Ice Sheets, version 3.1), run at a 80 km resolution grid that covers most of the Northern Hemisphere. The model treats ice as an incompressible, viscous, and heat-conducting fluid (Greve, 1997), using the shallow-ice approximation (Hutter, 1983) subjected to Glen's flow law (with stress exponent n=3) (Van der Veen, 2013). A Weertman-type sliding scheme is also applied (Weertman, 1964).
We run the model in the so-called ”cold-ice mode”, which means that temperatures exceeding the pressure melting point are artificially reset to the pressure melting temperature. The global sea level is lowered by 120 m to reflect LGM conditions, and marine ice is allowed to form where the bathymetry is less than 500 m, otherwise instantaneous calving is applied. The geothermal heat flux is set to a constant global value of 55 mW m−2, and the bedrock relaxes toward isostatic equilibrium with a timescale of 3 kyr, assuming a local lithosphere and relaxing asthenosphere (Greve and Blatter, 2009). All simulations started from ice-free conditions (interpolation of atmospheric fields is described in Sect. 2.3) and were run for 150 000 years to ensure an objective comparison of the ice sheets' steady-state extent.
2.2 Ablation parameterizations
SICOPOLIS uses the positive degree day (PDD) method to parameterize ablation. The annual melt-potential is estimated from the integrated sum of positive temperatures each year (Braithwaite and Olesen, 1989; Reeh, 1991), assuming that the daily temperatures are normally distributed about the monthly mean value (Calov and Greve, 2005).
Following Charbit et al. (2013), we test the sensitivity of the surface-mass balance scheme using three different PDD-based ablation models: the default parameterizations in SICOPOLIS (Reeh, 1991), plus the ones presented in Fausto et al. (2009b), and Tarasov and Peltier (2002) (henceforth referred to as SICOdef, FST09, and TP02, respectively).
These parameterizations use different methods for calculating the degree-day factors for snow and ice (βsnow and βice, respectively), refreezing fraction of melt water (Pmax), and standard deviation (day-to-day variability) of temperature (σ). All these parameters are set to numerical constants in SICOdef (βsnow=3 mm day−1 K−1, βice=12 mm day−1 K−1, Pmax=0.6 and σ=5 ∘C), while they take on slightly more elaborate expressions in the other parameterizations (see below).
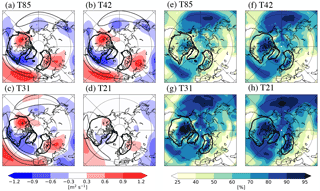
Figure 1(a–d) Summer (JJA) 500 hPa eddy stream function (m2 s−1) (shading; zonal mean removed) and zonal wind (m s−1) (contours; 10 m s−1 intervals starting at 20 m s−1); (e–h) vertically integrated (total) cloudiness (%). The 500 m ice sheet topography from the LGM reconstruction is indicated by the heavy contours (interpolated to the different horizontal resolutions).
2.2.1 The FST09 model
The standard deviation of daily temperature (σ) is assumed here to change with elevation at a rate of 1.2224 ∘C km−1, starting from σ=1.574 ∘C at sea level (σ≈4 ∘C at 2000 m elevation). A similar elevation dependence is also applied to Pmax to account for the increasing probability of melt water refreezing at higher elevation. No refreezing of melt water (Pmax=0) is assumed below 800 m, and total refreezing (Pmax=1) above 2000 m.
In addition, the FST09 model uses a temperature dependent degree-day factor for ice that varies from βice=7 mm day−1 K−1 for warm boreal summer (June–August; JJA) conditions (≥10 ∘C), to βice=15 mm day−1 K−1 for cold summer temperatures ( ∘C). A cubic change is applied for intermediate temperatures. The degree-day factor for snow is a constant with the same numerical value as in SICOdef (βsnow=3 mm day−1 K−1).
2.2.2 The TP02 model
The TP02 model uses a similar temperature-dependent parameterization of βice as in FST09, but with the following bounds: βice=8.3 mm day−1 K−1, and βice=17.22 mm day−1 K−1 for warm (≥10 ∘C) and cold ( ∘C) summer (JJA) temperatures, respectively. A similar temperature-based parameterization is also applied to βsnow that varies between βsnow=4.3 mm day−1 K−1 and βsnow=2.65 mm day−1 K−1, respectively. The standard deviation of temperature is set to a constant value of σ=5.2 ∘C. The refreezing scheme is also more comprehensive (Janssens and Huybrechts, 2000; Pfeffer et al., 1991), including both thermodynamics (latent heat release due to refreezing) and pore trapping components.
2.3 Climate evolution in SICOPOLIS
The surface temperature and precipitation (over the evolving ice sheets) are calculated using the method described in Liakka et al. (2016), which in turn is based on the general methodology outlined in Charbit et al. (2002, 2007). While the temperature decreases linearly with height at a fixed lapse rate γ ( K m−1; the ”standard” atmospheric lapse rate is assumed as the actual value over the LGM ice sheets is unknown; see Sect. 5 for a motivation of this choice), the precipitation amount changes exponentially as a function of temperature (see Eqs. (1) and (2) in Liakka et al. (2016)). The distribution of liquid and solid precipitation is also assumed to vary with temperature: 100 % solid precipitation falls if the monthly mean surface air temperature is below −10 ∘C, and 100 % liquid if it is higher than 7 ∘C. The distribution changes linearly for intermediate temperatures (Marsiat, 1994). The surface mass balance (SMB) is calculated from the climatological monthly-mean temperature and precipitation fields, which are (bilinearly) interpolated from the atmospheric (LGM) simulations, using the above lapse rate to correct for elevation biases due to different grids and horizontal resolutions.
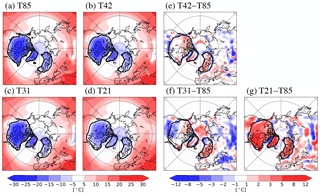
Figure 2Summer (JJA) surface temperature (∘C) from the different resolution atmospheric climatologies. The full fields are shown in the left panels (a–d), and the difference with respect to the T85 case is shown on the right (e–g). The 500 m ice sheet topography from the LGM reconstruction is indicated by the heavy contours (interpolated to the different horizontal resolutions).
2.4 Atmosphere model
The atmospheric climate forcing is produced with the Community Atmosphere Model version 3 (CAM3) (Collins et al., 2004, 2006b), using four different spectral (horizontal) resolutions: T85, T42, T31, and T21, corresponding to an approximate grid spacing of 1.4, 2.8, 3.8, and 5.6 ∘, respectively (Table 1). The model uses identical parameterizations (same equations) at all horizontal resolutions (Collins et al., 2004, 2006b), but the climate is tuned by varying 12 parameters governing the representation of clouds and precipitation (convective and stratiform), biharmonic diffusion, and integration time step in order to satisfy the Courant–Friedrichs–Lewy (CFL) condition; some of the resolution-dependent parameter settings are presented in Table 1 (Collins et al., 2004). Note that the model physics is represented in grid space, while the dynamics is discretized in spectral space. The effective diffusion rate is thus scale dependent and modulated by (horizontal) wave number in the vorticity and divergence equations (Collins et al., 2004).
The planetary boundary conditions are set to reflect LGM conditions, including the orbital parameters and greenhouse gas concentrations outlined by the Paleoclimate Modeling Intercomparison Project (PMIP) (Kageyama et al., 2017), the ice sheet reconstruction presented by Kleman et al. (2013) (raised to the height of the ICE-5G reconstruction, Peltier, 2004, to encourage ice formation in the ”correct” areas in SICOPOLIS), and prescribed monthly varying sea-surface conditions (LGM sea-surface temperature and sea-ice extent) from Otto-Bliesner et al. (2006). Motivated by the official PMIP boundary conditions (Kageyama et al., 2017), the vegetation cover in non-glaciated areas is prescribed as the modern distribution.
The grid-resolved boundary conditions were spectrally interpolated (using the same spectral transforms as in the atmospheric model) from the T85 grid to the coarser resolutions in order to ensure an identical setup. However, the spectral smoothing in the interpolation process lowers the resolved topography (including the ice sheets) on the coarser resolution grids. The interior of the Laurentide ice sheet is at most a few hundred meters lower in the T21 case, but somewhat larger differences (500 to 1000 m; Fig. S1 in the Supplement) are found over the Eurasian ice sheet as this is of smaller horizontal extent, and thus less well defined at lower resolutions. All simulations were run for 12 years, from which monthly climatologies were created over the last 10 years. The short integration length is motivated by the idealized experimental design (see Sect. 1) and the prescribed (perpetual LGM) sea-surface conditions that help dampen atmospheric interannual variability. A longer sampling rate may alter details in the climatologies, but is not expected to change the first order conclusions from the study.
In order to understand how the model climate responds to the horizontal resolution, we begin by comparing fields that are strongly related to model dynamics/physics, using the T85 case as a benchmark for the comparison. Figure 1a–d shows the 500 hPa eddy stream function (proportional to high- and low-pressure regions) and zonal wind in boreal summer (JJA). In agreement with previous studies (Dong and Valdes, 2000; Löfverström et al., 2016; Magnusdottir and Haynes, 1999; Polvani et al., 2004), the large scale atmospheric dynamics is well captured at the T42 and T31 resolutions – the circulation patterns have similar amplitude and spatial distribution as the T85 case – but it deteriorates substantially at the T21 resolution. A somewhat more gradual change is seen in the (vertically integrated) cloud cover (Fig. 1e–h), which is strongly controlled by the physics parameterization. The cloud cover changes from about 50 % over the ice sheets in the T85 case, to almost 100 % in the T21 case.
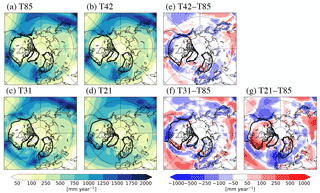
Figure 3Cumulative sum of precipitation (liquid + solid) over the year (total annual amount) (mm year−1) from the different resolution atmospheric climatologies. The full fields are shown in the left panels (a–d), and the difference with respect to the T85 case is shown on the right (e–g). The 500 m ice sheet topography from the LGM reconstruction is indicated by the heavy contours (interpolated to the different horizontal resolutions).
Related to this discussion, Figs. 2 and 3 show the surface temperature and precipitation climatologies that are used as forcing of the ice sheet model; the full fields are presented in the left columns (panels a–d), and the difference with respect to the T85 case are shown on the right (panels e–g). We focus on the surface temperature in boreal summer as this is the primary ablation season, but the cumulative sum of precipitation over the year (total annual amount), as ice can form in all seasons in regions with a positive surface mass balance.
The JJA surface temperature is to first order similar in the two intermediate resolution cases (T42 and T31; Figs. 2e, f), featuring a localized warming with respect to the T85 simulation over the northern parts of the Laurentide ice sheet, the interior of the Greenland ice sheet, and most of the Eurasian ice sheet. This is partially a response to the lowering (smoothing) of the resolved topography on the coarser grids, but the majority of the warming is related to changes in the surface energy balance induced by the increased cloudiness (see discussion in Sect. 5). The largest differences in precipitation are found in the midlatitude storm tracks that shift equatorward relative to the T85 case, especially in the North Atlantic (Fig. 3e–g). A similar resolution-induced storm-track shift has been found in several atmospheric models (Demory et al., 2014; Guemas and Codron, 2011; Hourdin et al., 2012), and thus appears to be fairly robust and largely independent of grid type and physics parameterizations.
The T21 case shows a fairly different response with a considerable warming over most of the world's topography (including the ice sheets; Fig. 2g). This is partly a response to the lower mean-height of the resolved topography (smoothing from the interpolation process), but also from a general degradation of the model climate and an enhanced downwelling of longwave radiation due to the increased cloudiness (Fig. 1; see further discussion in Sect. 5). The midlatitude precipitation field is also considerably altered with respect to the T85 case, with substantially lower precipitation in the eastern parts of the midlatitude storm tracks and thus over the southwestern parts of the ice sheets (Fig. 3). Note that this is presumably a response to the model's inability to resolve planetary waves (and hence individual cyclones) at coarse horizontal resolutions (Guemas and Codron, 2011; Hourdin et al., 2012; Löfverström et al., 2016; Magnusdottir and Haynes, 1999; Polvani et al., 2004).
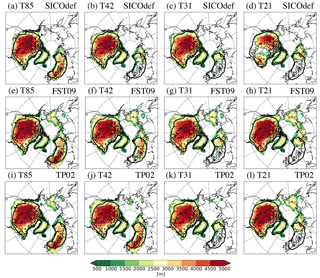
Figure 4Equilibrium ice thickness (m) when using different ablation parameterizations in the surface mass balance scheme: (a–d) default method in SICOPOLIS; (e–h) method by Fausto et al. (2009b); and (i–l) method by Tarasov and Peltier (2002), using the atmospheric climatologies from the (a, e, i) T85; (b, f, j) T42; (c, g, k) T31; and (d, h, l) T21 resolution simulations, respectively. The 500 m ice sheet topography from the LGM reconstruction is indicated by the heavy contours (interpolated to the different horizontal resolutions).
The left column in Fig. 4 shows the equilibrium ice sheet extent when using the default SMB parameterization in SICOPOLIS (SICOdef). The ice sheets forming under the high resolution atmospheric climatology (T85; Fig. 4a) are in close resemblance with the target extent (Kleman et al., 2013), with only slightly too much ice extending in western Canada and along the Siberian Arctic coast.
The ice sheets forced by the intermediate resolution climatologies (T42 and T31; Fig.4b, c) adequately reproduce the North American ice sheet, but they fail to build the Eurasian counterpart in agreement with the reconstruction. This one-sided mismatch can be understood from the atmospheric climatologies described in Sect. 3. The warm summer temperature over the southwestern parts of the Eurasian ice sheet (Fig. 2e, f) is the main reason why ice is not forming in this region. Note that although there is a relatively small reduction of precipitation with respect to the T85 case (the interior of Scandinavia is actually showing larger values than the T85 case), the warm surface temperatures are by far the most pronounced feature over the Eurasian Ice Sheet (cf. Figs. 2 and 3; see discussion in Sect. 5). These results are in broad agreement with Abe-Ouchi et al. (2013), who showed that the Eurasian ice sheet is more sensitive to temperature changes than its North American counterpart. The relatively small temperature change over the Eurasian ice sheet is thus strong enough to influence the ice sheet expansion there. The warm signal in northwestern North America (Fig. 2e, f) is located in a relatively cold region with a short ablation season, and therefore has a comparatively smaller influence on the local ice sheet evolution.
The T21 case, on the other hand, struggles to reproduce the LGM ice sheets in both continents. Although ice forms in North America, it fails to build the continent-wide Laurentide ice sheet and instead forms two distinct ice sheets – a smaller eastern and a larger western dome – separated by a wide gap in the region around Hudson Bay. This response bears some structural similarity to the low-resolution model results shown in Beghin et al. (2014) and Charbit et al. (2013), and also the pre-LGM ice sheets in Calov et al. (2005), and Bonelli et al. (2009). In a similar fashion to the T42 and T31 cases, the T21 climate forcing is too warm (and presumably too dry) over the southwestern parts of the Eurasian ice sheet area to reproduce the LGM ice sheet reconstruction.
The sensitivity experiments with different SMB parameterizations in SICOPOLIS are presented in Fig. 4e–l. The middle row (panels e, f, g, h) uses the FST09 ablation model, and the bottom row (panels i, j, k, l) the ablation model described in TP02. Both these alternative SMB parameterizations help improve the Eurasian ice extent in the T42 case (Fig. 4f, j), though at the price of a fairly substantial ice buildup in northern Siberia and Beringia (particularly pronounced in Fig. 4f), which are areas that were largely ice free at the LGM (Kleman et al., 2013; Löfverström and Liakka, 2016; Svendsen et al., 2004). A broadly similar buildup in these regions is also seen in the T85 case when using these SMB parameterizations.
These alternative SMB parameterizations do not improve the ice sheet simulations in Eurasia when using the lower resolution climatologies (T31 and T21; Fig. 4g, h, k, l), but they help the formation of a continent-wide Laurentide ice sheet in the T21 case (Fig. 4k, l).
The results presented in this paper attempt to illustrate, albeit in a highly qualitative way, the influence of atmospheric resolution on climate-forced ice sheet model simulations. By adopting a simplified modeling approach we can effectively isolate the resolution dependence of the atmospheric model, and by prescribing LGM boundary conditions (sea-surface conditions and continental ice sheets), the ice formation is primed to occur in the ”correct” areas in the subsequent ice sheet model experiments. This methodology appears to work well when using the high resolution atmospheric climatology (Liakka et al., 2016), but is less successful when using the climatologies from the lower resolution simulations (T42, T31, and T21; Fig. 4). The analysis shows that both the simulated surface temperature (Fig. 2) and precipitation (Fig. 3) fields are changing in ways that hinder ice from forming in the ”desired” areas at the lower resolutions. The precipitation changes are, however, found to be secondary, hence we devote the first part of this discussion to exploring the origin of the warmer surface temperatures.
There are two primarily explanations for why surface temperatures increase at lower horizontal resolutions: (i) lapse-rate effects due to differences in resolved topography; and (ii) changes in the simulated climate that are conducive for warm surface temperatures over the LGM ice sheets. We discuss these processes in the next two paragraphs:
- i.
Moving to a coarser horizontal resolution typically results in a lapse-rate induced surface warming, as the resolved topography is both lower and smoother as a result of the increased grid spacing. In this study we employed the modern global-average lapse rate of 6.5 ∘C km−1 for vertical interpolation/extrapolation. This is about 1 to 2 ∘C km−1 higher than observations over the Greenland ice sheet in boreal summer (Fausto et al., 2009a), but is motivated by the generally drier conditions in glacial climates that shift the lapse rate towards higher values (Braconnot et al., 2007) – Loomis et al. (2017) showed that the tropical atmospheric lapse rate may have increased from about 5.8 ∘C km−1 in the modern climate, to 6.7 ∘C km−1 at the LGM. The elevation difference in the interior of the Laurentide ice sheet is around 200 m between the T85 and T21 cases (Fig. S1), hence the lapse-rate effect only accounts for 5–10 % of the local warming signal in Fig. 2. The lapse-rate effect is however more important on the ice sheet edges and in Eurasia (accounting for 30 to 50 % of the warming signal), where the difference in topography is larger.
- ii.
The majority of the temperature difference in Fig. 2 is induced by changes in the atmospheric circulation. The stationary planetary waves are considerably weaker in the T21 case (Fig. 1), resulting in reduced cold-air advection over the Laurentide ice sheet (Fig. S3). The total cloudiness is simultaneously significantly higher (Fig. 1). While clouds help regulate the amount of downwelling shortwave radiation at the surface, upper level ice-clouds increase the re-emission of longwave radiation back to the surface. Changes in cloudiness are found to increase the surface radiative heating effect (SWnet + LWdown) by 10 to 30 W m−2 over the LGM ice sheets (Fig. S4).
As a result, while the T42 and T31 cases struggle to build ice in Eurasia, the T21 experiment also fails to build the continent-wide Laurentide ice sheet in North America (when using the default SMB parameterization; SICOdef). Instead it builds two spatially disconnected ice sheets, with a larger dome on the western side of the continent (Fig. 4d). Several coupled climate–ice sheet experiments with a low-resolution atmospheric model have shown qualitatively similar results, for example Calov et al. (2005), Charbit et al. (2013) and Beghin et al. (2014). The common denominator for these studies is that they all used CLIMBER-2 to produce the atmospheric forcing fields. We stress that it is not our intention to single out this particular model, but it appears to suffer from similar deficiencies as our T21 case and may therefore help us understand some of these results. In the aforementioned papers the ice sheet tends to be limited to the western/northwestern side of the North American continent (Beghin et al., 2014; Charbit et al., 2013), little or no ice is established in western Eurasia (Beghin et al., 2014; Calov et al., 2005; Charbit et al., 2013), and attempts to remedy these shortcomings typically result in substantial ice formation in Siberia and Alaska (Charbit et al., 2013). These results appear to be largely independent of both the choice of ice sheet model (the above studies used SICOPOLIS and GRISLI), and the complexity of the SMB parameterization (Bauer and Ganopolski, 2017; Charbit et al., 2013). Although it is not completely fair to compare CLIMBER-2 to a low resolution version of CAM3 (the complexity and general purpose of these models are extremely different), it is possible that these similarities demonstrate a fundamental problem with low-resolution climate models that transcends model complexity.
One piece of information that is rarely mentioned in the literature is that most Earth system models are tuned to reproduce the climate of the instrument era (∼ 1850 to present). These models are of course valuable tools for exploring other time periods as well, but it generally means that inter-model discrepancies tend to increase under more extreme forcing scenarios, for example, glacial conditions (Braconnot et al., 2007). The results presented here suggest that the model spread may be further exacerbated by differences in horizontal resolution.
The atmosphere model used here has been tuned and extensively tested at the T85, T42, and T31 grids (Collins et al., 2006a; Yeager et al., 2006). However, the T21 resolution only has ”functional support”, which means that boundary conditions are provided but the model climate has not been tuned to the same standard as the other resolutions. This is probably at least a partial explanation for the apparent degradation of the model climate, though it is possible that this manifests a more general breakdown of the numerical convergence that has been identified in previous modeling studies (Dong and Valdes, 2000; Magnusdottir and Haynes, 1999; Polvani et al., 2004). Some evidence of this is seen in Fig. 1: while the model physics shows a fairly gradual change between the T85 and T21 resolutions (Fig. 1e–h) – including a generally increased cloudiness and an equatorward migration of the mid-latitude precipitation field (Demory et al., 2014; Guemas and Codron, 2011; Hack et al., 2006; Hourdin et al., 2012) – fields more strongly associated with the model dynamics retain much of their amplitude and general structure at the T31 resolution, but deteriorate significantly when going to T21. What manifests an acceptable simulation quality is subjective and highly dependent on application. However, since ice sheets are sensitive to feedback loops triggered by deviations from “expected” climate conditions (both in terms of mean state and variability), coupled climate–ice sheet simulations generally require a higher simulation quality than more traditional modeling experiments.
Conversely, resorting to a lower horizontal resolution can both increase the model throughput (number of simulated years per day), and reduce the simulation cost (Yeager et al., 2006). As shown in Table 1, simulating one model year on the T85 resolution requires around 21× as many numerical operations as one model year on the T31 grid, and 48× as many operations for the same integration length on the T21 grid. This encapsulates the challenges of coupled climate–ice sheet experiments, as it is common to trade resolution (”accuracy”) for computational efficiency (”speed”) in order to run transient simulations over glacial timescales.
Lastly, it is possible that some of the shortcomings discussed here – e.g., the lack of ice forming in western Eurasia in the T42 and T31 cases, and in east-central North America in the T21 case – may be due to the simplified experiment design and selected parameter values (some evidence of this is seen in Fig. S2). However, it is important to stress that ice evolution is ultimately controlled by the quality of the atmospheric forcing data, which we can show is strongly compromised at sufficiently coarse horizontal grids. Based on these results we conclude that a lower practical resolution bound for traditional climate model experiments is likely to be somewhere around T31, and possibly somewhat higher (nominal T42 or even T85 resolution) for coupled climate–ice sheet simulations.
Data is available upon request from the authors.
The supplement related to this article is available online at: https://doi.org/10.5194/tc-12-1499-2018-supplement.
The authors declare that they have no conflict of interest.
We thank the editor Thomas Mölg, two anonymous reviewers, and Irina Rogozhina and Raymond Sellevold for critically evaluating this manuscript. We acknowledge Bette Otto-Bliesner and Johan Kleman and their collaborators for producing and making publicly available the CCSM3 LGM simulation and LGM ice sheet reconstruction that were used as the basis for our experiments. The AGCM simulations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputing Center (NSC) which is financially supported by Swedish Research Council (Vetenskapsrådet; VR). The ice sheet model simulations were carried out on resources provided by LOEWE Frankfurt Centre for Scientific Computing (LOEWE-CSC).
This work was financially supported by the National Science Foundation (NSF)
and the US Department of Energy (DOE).
Edited by: Thomas Mölg
Reviewed by: two anonymous referees
Abe-Ouchi, A., Saito, F., Kawamura, K., Raymo, M. E., Okuno, J., Takahashi, K., and Blatter, H.: Insolation-driven 100,000-year glacial cycles and hysteresis of ice-sheet volume, Nature, 500, 190–193, https://doi.org/10.1038/nature12374, 2013. a
Bauer, E. and Ganopolski, A.: Comparison of surface mass balance of ice sheets simulated by positive-degree-day method and energy balance approach, Clim. Past, 13, 819–832, https://doi.org/10.5194/cp-13-819-2017, 2017. a
Beghin, P., Charbit, S., Dumas, C., Kageyama, M., Roche, D. M., and Ritz, C.: Interdependence of the growth of the Northern Hemisphere ice sheets during the last glaciation: the role of atmospheric circulation, Clim. Past, 10, 345–358, https://doi.org/10.5194/cp-10-345-2014, 2014. a, b, c, d, e
Bonelli, S., Charbit, S., Kageyama, M., Woillez, M.-N., Ramstein, G., Dumas, C., and Quiquet, A.: Investigating the evolution of major Northern Hemisphere ice sheets during the last glacial-interglacial cycle, Clim. Past, 5, 329–345, https://doi.org/10.5194/cp-5-329-2009, 2009. a, b
Braconnot, P., Otto-Bliesner, B., Harrison, S., Joussaume, S., Peterchmitt, J.-Y., Abe-Ouchi, A., Crucifix, M., Driesschaert, E., Fichefet, Th., Hewitt, C. D., Kageyama, M., Kitoh, A., Laîné, A., Loutre, M.-F., Marti, O., Merkel, U., Ramstein, G., Valdes, P., Weber, S. L., Yu, Y., and Zhao, Y.: Results of PMIP2 coupled simulations of the Mid-Holocene and Last Glacial Maximum – Part 1: experiments and large-scale features, Clim. Past, 3, 261–277, https://doi.org/10.5194/cp-3-261-2007, 2007. a, b
Braithwaite, R. J. and Olesen, O. B.: Calculation of glacier ablation from air temperature, West Greenland, in: Glacier fluctuation and climate change, edited by: Oerlemans, J., 219–233, Kluwer, Dordrecht, 1989. a
Calov, R. and Greve, R.: A semi-analytical solution for the positive degree-day model with stochastic temperature variations, J. Glaciol., 51, 173–175, 2005. a
Calov, R., Ganopolski, A., Claussen, M., Petoukhov, V., and Greve, R.: Transient simulation of the last glacial inception. Part I: glacial inception as a bifurcation in the climate system, Clim. Dynam., 24, 545–561, 2005. a, b, c, d
Charbit, S., Ritz, C., and Ramstein, G.: Simulations of Northern Hemisphere ice-sheet retreat:: sensitivity to physical mechanisms involved during the Last Deglaciation, Quaternary Sci. Rev., 21, 243–265, 2002. a
Charbit, S., Ritz, C., Philippon, G., Peyaud, V., and Kageyama, M.: Numerical reconstructions of the Northern Hemisphere ice sheets through the last glacial-interglacial cycle, Clim. Past, 3, 15–37, https://doi.org/10.5194/cp-3-15-2007, 2007. a, b
Charbit, S., Dumas, C., Kageyama, M., Roche, D. M., and Ritz, C.: Influence of ablation-related processes in the build-up of simulated Northern Hemisphere ice sheets during the last glacial cycle, The Cryosphere, 7, 681–698, https://doi.org/10.5194/tc-7-681-2013, 2013. a, b, c, d, e, f, g
Collins, W. D., Rasch, P. J., Boville, B. A., Hack, J. J., McCaa, J. R., Williamson, D. L., Kiehl, J. T., Briegleb, B., Bitz, C., Lin, S.-J., Zhang, M., and Dai, Y.: Description of the NCAR Community Atmosphere Model (CAM3), Tech. Rep. NCAR/TN464-STR, National Center for Atmospheric Research, Boulder, CO, p. 226, 2004. a, b, c, d
Collins, W. D., Bitz, C. M., Blackmon, M. L., Bonan, G. B., Bretherton, C. S., Carton, J. A., Chang, P., Doney, S. C., Hack, J. J., Henderson, T. B., Flato, G., Marotzke, J., Abiodun, B., Braconnot, P., Chou, S. C., Collins, W. J., Cox, P., Driouech, F., Emori, S., Eyring, V., Forest, C., Gleckler, P., Guilyardi, E., Jakob, C., Kattsov, V., Reason, C., and Rummukaines, M.: The community climate system model version 3 (CCSM3), J. Climate, 19, 2122–2143, 2006a. a
Collins, W. D., Rasch, P. J., Boville, B. A., Hack, J. J., McCaa, J. R., Williamson, D. L., Briegleb, B., Bitz, C., Lin, S.-J., and Zhang, M.: The Formulation and Atmospheric Simulation of the Community Atmosphere Model Version 3 (CAM3), J. Climate, 19, 2144–2161, 2006b. a, b
Demory, M.-E., Vidale, P. L., Roberts, M. J., Berrisford, P., Strachan, J., Schiemann, R., and Mizielinski, M. S.: The role of horizontal resolution in simulating drivers of the global hydrological cycle, Clim. Dynam., 42, 2201–2225, https://doi.org/10.1007/s00382-013-1924-4, 2014. a, b
Dolan, A. M., Koenig, S. J., Hill, D. J., Haywood, A. M., and DeConto, R. M.: Pliocene Ice Sheet Modelling Intercomparison Project (PLISMIP) – experimental design, Geosci. Model Dev., 5, 963–974, https://doi.org/10.5194/gmd-5-963-2012, 2012. a
Dong, B. and Valdes, P. J.: Climates at the last glacial maximum: Influence of model horizontal resolution, J. Climate, 13, 1554–1573, 2000. a, b, c
Fausto, R. S., Ahlstrom, A. P., Van As, D., Boggild, C. E., and Johnsen, S. J.: A new present-day temperature parameterization for Greenland, J. Glaciol., 55, 95–105, 2009a. a
Fausto, R. S., Ahlstrøm, A. P., Van As, D., Johnsen, S. J., Langen, P. L., and Steffen, K.: Improving surface boundary conditions with focus on coupling snow densification and meltwater retention in large-scale ice-sheet models of Greenland, J. Glaciol., 55, 869–878, 2009b. a, b
Flato, G., Marotzke, J., Abiodun, B., Braconnot, P., Chou, S. C., Collins, W. J., Cox, P., Driouech, F., Emori, S., Eyring, V., Forest, C., Gleckler, P., Guilyardi, E., Jakob, C., Kattsov, V., Reason, C., and Rummukaines, M.: Evaluation of Climate Models, in: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Climate Change, 5, 741–866, 2013. a
Fyke, J. G., Sacks, W. J., and Lipscomb, W. H.: A technique for generating consistent ice sheet initial conditions for coupled ice sheet/climate models, Geosci. Model Dev., 7, 1183–1195, https://doi.org/10.5194/gmd-7-1183-2014, 2014. a
Ganopolski, A., Calov, R., and Claussen, M.: Simulation of the last glacial cycle with a coupled climate ice-sheet model of intermediate complexity, Clim. Past, 6, 229–244, https://doi.org/10.5194/cp-6-229-2010, 2010. a
Goosse, H., Brovkin, V., Fichefet, T., Haarsma, R., Huybrechts, P., Jongma, J., Mouchet, A., Selten, F., Barriat, P.-Y., Campin, J.-M., Deleersnijder, E., Driesschaert, E., Goelzer, H., Janssens, I., Loutre, M.-F., Morales Maqueda, M. A., Opsteegh, T., Mathieu, P.-P., Munhoven, G., Pettersson, E. J., Renssen, H., Roche, D. M., Schaeffer, M., Tartinville, B., Timmermann, A., and Weber, S. L.: Description of the Earth system model of intermediate complexity LOVECLIM version 1.2, Geosci. Model Dev., 3, 603–633, https://doi.org/10.5194/gmd-3-603-2010, 2010. a
Greve, R.: Application of a Polythermal Three-Dimensional Ice Sheet Model to the Greenland Ice Sheet: Response to Steady-State and Transient Climate Scenarios, J. Climate, 10, 901–918, 1997. a
Greve, R. and Blatter, H.: Dynamics of ice sheets and glaciers, Springer Science & Business Media, 2009. a
Guemas, V. and Codron, F.: Differing impacts of resolution changes in latitude and longitude on the midlatitudes in the LMDZ atmospheric GCM, J. Climate, 24, 5831–5849, 2011. a, b, c
Hack, J. J., Caron, J. M., Danabasoglu, G., Oleson, K. W., Bitz, C., and Truesdale, J. E.: CCSM–CAM3 climate simulation sensitivity to changes in horizontal resolution, J. climate, 19, 2267–2289, 2006. a
Herrington, A. and Poulsen, C.: Terminating the Last Interglacial: The role of ice sheet – climate feedbacks in a GCM asynchronously coupled to an ice sheet model, J. Climate, 25, 1871–1882, 2012. a
Hourdin, F., Foujols, M.-A., Codron, F., Guemas, V., Dufresne, J.-L., Bony, S., Denvil, S., Guez, L., Lott, F., Ghattas, J., Braconnot, P., Marti, O., Meurdesoif, Y., and Bopp, L.: Climate and sensitivity of the IPSL-CM5A coupled model: impact of the LMDZ atmospheric grid configuration, Clim. Dynam., online first: https://doi.org/10.1007/s00382-012-1411-3, 2012. a, b, c
Hutter, K.: Theoretical glaciology: material science of ice and the mechanics of glaciers and ice sheets, Reidel, Dordrecht, 1983. a
Jackson, C.: Sensitivity of stationary wave amplitude to regional changes in Laurentide ice sheet topography in single-layer models of the atmosphere, J. Geophys. Res., 105, 24443—24454, https://doi.org/10.1029/2000JD900377, 2000. a
Janssens, I. and Huybrechts, P.: The treatment of meltwater retention in mass-balance parameterizations of the Greenland ice sheet, Ann. Glaciol., 31, 133–140, 2000. a
Kageyama, M., Albani, S., Braconnot, P., Harrison, S. P., Hopcroft, P. O., Ivanovic, R. F., Lambert, F., Marti, O., Peltier, W. R., Peterschmitt, J.-Y., Roche, D. M., Tarasov, L., Zhang, X., Brady, E. C., Haywood, A. M., LeGrande, A. N., Lunt, D. J., Mahowald, N. M., Mikolajewicz, U., Nisancioglu, K. H., Otto-Bliesner, B. L., Renssen, H., Tomas, R. A., Zhang, Q., Abe-Ouchi, A., Bartlein, P. J., Cao, J., Li, Q., Lohmann, G., Ohgaito, R., Shi, X., Volodin, E., Yoshida, K., Zhang, X., and Zheng, W.: The PMIP4 contribution to CMIP6 – Part 4: Scientific objectives and experimental design of the PMIP4-CMIP6 Last Glacial Maximum experiments and PMIP4 sensitivity experiments, Geosci. Model Dev., 10, 4035–4055, https://doi.org/10.5194/gmd-10-4035-2017, 2017. a, b
Kleman, J., Fastook, J., Ebert, K., Nilsson, J., and Caballero, R.: Pre-LGM Northern Hemisphere ice sheet topography, Clim. Past, 9, 2365–2378, https://doi.org/10.5194/cp-9-2365-2013, 2013. a, b, c
Liakka, J.: Interactions between topographically and thermally forced stationary waves: implications for ice-sheet evolution, Tellus A, 64, 11088, https://doi.org/10.3402/tellusa.v64i0.11088, 2012. a
Liakka, J., Nilsson, J., and Löfverström, M.: Interactions between stationary waves and ice sheets: linear versus nonlinear atmospheric response, Clim. Dynam., 38, 1249–1262, 2011. a
Liakka, J., Löfverström, M., and Colleoni, F.: The impact of the North American glacial topography on the evolution of the Eurasian ice sheet over the last glacial cycle, Clim. Past, 12, 1225–1241, https://doi.org/10.5194/cp-12-1225-2016, 2016. a, b, c
Löfverström, M. and Liakka, J.: On the limited ice intrusion in Alaska at the LGM, Geophys. Res. Lett., 43, 11030–11038, https://doi.org/10.1002/2016GL071012, 2016. a
Löfverström, M. and Lora, J. M.: Abrupt regime shifts in the North Atlantic atmospheric circulation over the last deglaciation, Geophys. Res. Lett., 44, 8047–8055, https://doi.org/10.1002/2017GL074274, 2017. a
Löfverström, M., Caballero, R., Nilsson, J., and Kleman, J.: Evolution of the large-scale atmospheric circulation in response to changing ice sheets over the last glacial cycle, Clim. Past, 10, 1453–1471, https://doi.org/10.5194/cp-10-1453-2014, 2014. a
Löfverström, M., Liakka, J., and Kleman, J.: The North American Cordillera – An impediment to growing the continent-wide Laurentide Ice Sheet, J. Climate, 28, 9433–9450, 2015. a
Löfverström, M., Caballero, R., Nilsson, J., and Messori, G.: Stationary wave reflection as a mechanism for zonalising the Atlantic winter jet at the LGM, J. Atmos. Sci., 73, 3329–3342, https://doi.org/10.1175/JAS-D-15-0295.1, 2016. a, b, c, d, e
Loomis, S. E., Russell, J. M., Verschuren, D., Morrill, C., De Cort, G., Damsté, J. S. S., Olago, D., Eggermont, H., Street-Perrott, F. A., and Kelly, M. A.: The tropical lapse rate steepened during the Last Glacial Maximum, Science Adv., 3, e1600815, https://doi.org/10.1126/sciadv.1600815, 2017. a
Lora, J. M., Mitchell, J. L., and Tripati, A. E.: Abrupt reorganization of North Pacific and western North American climate during the last deglaciation, Geophys. Res. Lett., 43, 11796–11804, https://doi.org/10.1002/2016GL071244, 2016. a
Magnusdottir, G. and Haynes, P. H.: Reflection of planetary waves in three-dimensional tropospheric flows, J. Atmos. Sci., 56, 652–670, 1999. a, b, c, d, e
Marsiat, I.: Simulation of the Northern Hemisphere continental ice sheets over the last glacial-interglacial cycle: experiments with a latitude-longitude vertically integrated ice sheet model coupled to a zonally averaged climate model, Paleoclimates, 1, 59–98, 1994. a
Nowicki, S. M. J., Payne, A., Larour, E., Seroussi, H., Goelzer, H., Lipscomb, W., Gregory, J., Abe-Ouchi, A., and Shepherd, A.: Ice Sheet Model Intercomparison Project (ISMIP6) contribution to CMIP6, Geosci. Model Dev., 9, 4521–4545, https://doi.org/10.5194/gmd-9-4521-2016, 2016. a
Otto-Bliesner, B. L., Brady, E. C., Clauzet, G., Tomas, R., Levis, S., and Kothavala, Z.: Last glacial maximum and Holocene climate in CCSM3, J. Climate, 19, 2526–2544, 2006. a
Pausata, F. S. R. and Löfverström, M.: On the enigmatic similarity in Greenland δ18O between the Oldest and Younger Dryas, Geophys. Res. Lett., 42, 10470–10477, https://doi.org/10.1002/2015GL066042, 2015. a
Peltier, W.: Global glacial isostasy and the surface of the ice-age Earth: The ICE-5G (VM2) model and GRACE, Annu. Rev. Earth Planet. Sci., 32, 111–149, 2004.
Petoukhov, V., Ganopolski, A., Brovkin, V., Claussen, M., Eliseev, A., Kubatzki, C., and Rahmstorf, S.: CLIMBER-2: a climate system model of intermediate complexity. Part I: model description and performance for present climate, Clim. Dynam., 16, 1–17, 2000. a
Pfeffer, W. T., Meier, M. F., and Illangasekare, T. H.: Retention of Greenland runoff by refreezing: implications for projected future sea level change, J. Geophys. Res.-Oceans, 96, 22117–22124, 1991. a
Polvani, L. M., Scott, R., and Thomas, S.: Numerically converged solutions of the global primitive equations for testing the dynamical core of atmospheric GCMs, Mon. Weather Rev., 132, 2539–2552, 2004. a, b, c, d, e, f
Reeh, N.: Parameterization of melt rate and surface temperature on the Greenland ice sheet, Polarforschung, 59, 113–128, 1991. a, b
Roe, G. H. and Lindzen, R. S.: The Mutual Interaction between Continental-Scale Ice Sheets and Atmospheric Stationary Waves, J. Climate, 14, 1450–1465, 2001. a
Smith, R. S., Gregory, J. M., and Osprey, A.: A description of the FAMOUS (version XDBUA) climate model and control run, Geosci. Model Dev., 1, 53–68, https://doi.org/10.5194/gmd-1-53-2008, 2008. a
Svendsen, J. I., Alexanderson, H., Astakhov, V. I., Demidov, I., Dowdeswell, J. A., Funder, S., Gataullin, V., Henriksen, M., Hjort, C., Houmark-Nielsen, M., Hubberten, H., Ingolfsson, O., Jakobsson, M., Kjaer, K., Larsen, E., Lokrantz, H., Lunkka, J. P., Lyså, A., Mangerud, J., Matiouchkov, A., Murray, A., Möller, P., Niessen, F., Nikolskaya, O., Polyak, L., Saarnisto, A., Siegert, C., Siegert, M. J., Spielhagen, R. F., and Stein, R.: Late Quaternary ice sheet history of northern Eurasia, Quaternary Sci. Rev., 23, 1229–1271, 2004. a
Tarasov, L. and Peltier, R.: Greenland glacial history and local geodynamic consequences, Geophys. J. Int., 150, 198–229, 2002. a, b
Van der Veen, C. J.: Fundamentals of glacier dynamics, CRC Press, 2013. a
Weertman, J.: The theory of glacier sliding, J. Glaciol., 5, 287–303, 1964. a
Yeager, S. G., Shields, C. A., Large, W. G., and Hack, J. J.: The low-resolution CCSM3, J. Climate, 19, 2545–2566, 2006. a, b
Zhang, X., Lohmann, G., Knorr, G., and Purcell, C.: Abrupt glacial climate shifts controlled by ice sheet changes, Nature, 512, 290–294, 2014. a





